A novel time integration method for structural dynamics utilizing uniform quintic B-spline functions

Abstract

The authors have proposed a new integration method for structural dynamics by utilizing uniform quintic B-spline polynomial interpolation. In this way, with two adjustable parameters, the proposed method is successfully formulated for solving of the differential equation of motion governing a SDOF system and later generalized for a MDOF system. In the proposed method, the straightforward recurrence formulas were derived based on quintic B-spline interpolation approximation and collocation method, and the calculation process for MDOF systems was also provided. Stability analysis shows that the proposed method can attain both conditional and unconditional stability. The validity of the proposed method is verified with three numerical simulations. Compared with the latest Bathe and Noh–Bathe methods, the proposed method not only has higher computation efficiency, but also possesses better numerical dissipation characteristics.

1 Introduction

During the last few years, a large amount of researches have been devoted to the investigation of effective time integration methods for the linear and nonlinear analysis of structures [1–9]. In general, there are two major categories of step-by-step time integration methods. One is explicit method [10], and the other is implicit method [11]. A method is explicit if the equation of motion of the current time step is not employed to ascertain the current displacement, while it is implicit if that is involved. Both explicit and implicit methods have their own advantages and disadvantages. More details of time integration methods can be found in the work of Wen et.al [12] and the references therein.

Recently, Bathe et.al [13] developed a simple implicit time integration method which can remain unconditional stable without the use of adjustable parameters. This implicit method shows very desirable calculation accuracy and high-frequency dissipation characteristics. However, this method consists of two sub-steps within each time step and thus consumes much more computation time than other conventional methods. Subsequently, Noh et.al [14] presented an explicit time integration method which possesses second-order accuracy for systems with and without damping. By use of two sub-steps within each time step, this scheme can achieve a desired numerical damping to suppress undesirable spurious oscillations of high frequencies, but results in more time consumption than other conventional methods. Then, the authors [12] proposed an explicit method by utilizing a family of uniform septuple (seventh-degree) B-splines. The presented method possesses far higher calculation accuracy and more desirable numerical dissipation than other conventional methods. However, this method consumes more computation time than other conventional methods due to its complex formulations, especially for the dynamic system with very large DOFs.

As is well known, in finite element problems, the use of explicit time integration method may introduce spurious oscillations of high-frequency modes which have to be effectively suppressed or smoothed. It is well known that the high-frequency modes of discretized equations generally do not represent the genuine behavior of the real problem. Hence, it is advantageous for time integration methods to possess controllable numerical dissipation so as to filter high-order frequencies induced by the finite element spatial discretization. One critical difficulty in designing such methods is that the addition of high-frequency dissipation should neither incur a substantial loss of accuracy nor introduce excessive algorithmic damping in the important low-frequency modes. One effective approach is to introduce some damping into a time integration method by use of adjustable parameters. Actually, most of present-day time integration methods, such as the higher-order mixed method with parameters $\beta$ and $\theta$ [15], the two-step lambda method [16], and the Newmark-type integration schemes [xx-xx], have parameters that can control the degree of numerical dissipation as well as the stability and accuracy, while more details of numerical dissipation about time integration schemes can be found in references [17–19]. Apart from numerical dissipation, it is desirable for the algorithms to possess unconditional stability so that time increment of any size can be adopted without introducing numerical instability.

With due consideration of the drawbacks of aforementioned methods, the objective of this study was to propose a novel high-efficiency explicit method. This paper is organized as follows. In Sect. 2, the definition and expression of quintic B-spline interpolation are given. Then, quintic B-spline interpolation is employed to solve the equation of motion governing the SDOF and MDOF systems in Sects. 3 and 4, respectively. In Sect. 5, stability and accuracy analyses are conducted by comparing different methods. In Sect. 6, three numerical simulations are introduced to demonstrate the superiority of the proposed method in calculation accuracy, time consumption and high-frequency dissipation over other latest methods. Finally, Sect. 7 is allocated for concluding remarks.

2 The overview of B-splines

2.1 The definition of B-spline basis functions

There are many definitions for B-spline basis functions. Here we adopt a simple recurrence formula to define B-spline basis functions [20, 21]. Then, the $i$th B-spline basis of the $d$th degree $B_{i,d} \left( t \right)$, briefly denoted by $B_{i,d}$, is defined as follows:

$$\begin{aligned} B_{i,0} \left( t \right)= & {} \left\{ {{\begin{array}{l@{\quad }l} 1, &{} t_i \le t\le t_{i+1} \\ 0, &{} \mathrm{{otherwise}} \\ \end{array} }} \right. \end{aligned}$$

(1)

$$\begin{aligned} B_{i,d} \left( t \right)= & {} \left( {\frac{t-t_i }{t_{d+i} -t_i }} \right) B_{i,d-1} \left( t \right) +\left( {\frac{t_{d+i+1} -t}{t_{d+i+1} -t_{i+1}}} \right) B_{i+1,d-1} \left( t \right) \end{aligned}$$

(2)

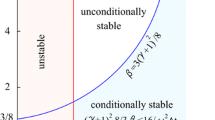
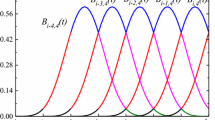
where knot span $\left\{ {t_0 ,t_1 ,\ldots ,t_i ,t_{i+1} ,\ldots } \right\}$ must be a non-decreasing sequence of real numbers, i.e., $t_i \le t_{i+1}$. Equation (2) can yield the quotient $0/0$, we define this quotient to be zero. Without going into details, $B_{i,d} \left( t \right)$ is nonzeros over an interval $t_i \le t\le t_{i+d+1}$. As shown in Fig. 1, for quintic B-spline basis functions used in this study, the usable parameter range of $B_{i,5} \left( t \right)$ is $t_i \le t\le t_{i+6}$.

Fig. 1

Quintic B-spline basis functions (usable interpolation range is from $t_{i}$ to $t_{i+1}$)

2.2 Quintic B-spline interpolation scheme

In this study, we only consider the uniform quintic B-spline basis functions with a equidistantly distributed set of time nodes $a=t_0 <t_1 <\cdots <t_n =b$ over the time domain $\left[ {a,b} \right]$, and the time step length (or, time increment) is denoted by $h$, where $h=\mathrm{{\Delta }} t=t_{i+1} -t_i ( i=0,1,\ldots ,n-1)$. To construct the quintic B-splines, we need to extend the set of nodal points as

$$\begin{aligned} t_{-5} <\cdots <t_{-1} <a=t_0 <t_1 <\cdots <t_n =b<\cdots <t_{n+5} \end{aligned}$$

For any node $t_{j} \left( {j=-5,-4,\cdots ,t_{n+5} } \right)$, we have $t_j =t_i +\left( {j-i} \right) h$, and thus, $B_{j,5} \left( t \right)$ is the shifted(or translated) instance of $B_{i,5} \left( t \right)$, i.e., $B_{j,5} \left( t \right) =B_{i,5} \left( {t-\left( {j-i} \right) h} \right)$.

Using Eq. (2), $B_{i,5} \left( t \right) \left( {i=0,1,\ldots ,n-1} \right)$ can be defined by

$$\begin{aligned} B_{i,5} \left( t \right) =\frac{1}{5!h^{5}}\left\{ {{\begin{array}{l@{\quad }l} \left( {t-t_i } \right) ^{5}&{}\;\, t_i \le t\le t_{i+1} \\ \left( {t-t_i } \right) ^{5}-6\left( {t-t_{i+1}} \right) ^{5} &{}\;\, t_{i+1} \le t \le t_{i+2} \\ \left( {t-t_i } \right) ^{5}-6\left( {t-t_{i+1}} \right) ^{5}+15\left( {t-t_{i+2}} \right) ^{5}&{}\;\, t_{i+2} \le t\le t_{i+3} \\ \left( {t_{i+6} -t} \right) ^{5}-6\left( {t_{i+5} -t} \right) ^{5}+15\left( {t_{i+4} -t} \right) ^{5}&{}\;\, t_{i+3} \le t\le t_{i+4} \\ \left( {t_{i+6} -t} \right) ^{5}-6\left( {t_{i+5} -t} \right) ^{5}&{}\;\, t_{i+4} \le t\le t_{i+5} \\ \left( {t_{i+6} -t} \right) ^{5}&{}\;\, t_{i+5} \le t\le t_{i+6} \\ \end{array}}} \right. \end{aligned}$$

(3)

Actually, for any time subinterval $I_i \equiv \left[ {t_i ,t_{i+1} }\right]$, the usable piecewise quintic B-splines, as illustrated in Fig. 2, are $B_{i-5,5} ,B_{i-4,5} ,\ldots ,B_{i,5}$. Let $\tau _i =(t-t_i )/\mathrm{{\Delta }} t$ (i.e., $t=t_i + \tau _i \mathrm{{\Delta }} t$), these B-splines coupled with their $l$th derivatives with respect to variable $t$ can be given as

$$\begin{aligned} B_{-5,5}^{(l)} \left( {\tau _i} \right)= & {} \frac{\left( {-\Delta t} \right) ^{-l}}{\left( {5-l)!} \right. }\left( {1-\tau _i } \right) ^{5-l}\end{aligned}$$

(4)

$$\begin{aligned} B_{\hbox {-}4,5}^{\left( l \right) } \left( {\tau _i } \right)= & {} \frac{\left( {-\Delta t} \right) ^{-l}}{\left( {5-l)!} \right. }\left( \left( {2-\tau _i } \right) ^{5-l}-6\left( {1-\tau _i } \right) ^{5-l}\right) \end{aligned}$$

(5)

$$\begin{aligned} B_{-3,5}^{(l)} \left( {\tau _i} \right)= & {} \frac{\left( {-\Delta t} \right) ^{-l}}{\left( {5-l)!}\right. }\left( \left( {3-\tau _i } \right) ^{5-l}-6\left( {2-\tau _i } \right) ^{5-l}+15\left( {1-\tau _i } \right) ^{5-l}\right) \end{aligned}$$

(6)

$$\begin{aligned} B_{-2,5}^{\left( l \right) } \left( {\tau _i } \right)= & {} \frac{\left( {\Delta t} \right) ^{-l}}{\left( {5-l)!} \right. }\left( \left( {\tau _i +2} \right) ^{5-l}-6\left( {\tau _i +1} \right) ^{5-l}+15\left( {\tau _i } \right) ^{5-l}\right) \end{aligned}$$

(7)

$$\begin{aligned} B_{-1,5}^{\left( l \right) } \left( {\tau _i } \right)= & {} \frac{\left( {\Delta t} \right) ^{-l}}{\left( {5-l)!} \right. }\left( \left( {\tau _i +1} \right) ^{5-l}-6\left( {\tau _i } \right) ^{5-l}\right) \end{aligned}$$

(8)

$$\begin{aligned} B_{0,5}^{\left( l \right) } \left( {\tau _i } \right)= & {} \frac{\left( {\Delta t} \right) ^{-l}}{\left( {5-l)!} \right. }\left( {\tau _i } \right) ^{5-l} \end{aligned}$$

(9)

For any usable interpolate range $I_{i}$ as shown in Figs. 1 and 2, a quintic B-spline interpolation function can be given by

$$\begin{aligned} S_{i} \left( t \right) =\sum \limits _{k=-5}^{0}C_{i+k} B_{i+k,5} \left( t \right) \end{aligned}$$

(10)

where $C_{i+k}$ (control points) are unknown real coefficients. $S_i\left( t \right)$ is four times differentiable and compatible.

Fig. 2

Usable piecewise B-splines within any time subinterval $I_i$

With Eqs. (4)–(10) can be extended to a matrix form as

$$\begin{aligned} S_{i}^{\left( l \right) } \left( t \right) ={\varvec{B}}^{\left( l \right) }\left( {\tau _i } \right) {\varvec{C}}_i , \quad \left. {t\in \left[ {t_i ,t_{i+1} } \right] \tau _i \in [0,1} \right] \end{aligned}$$

(11)

where

$$\begin{aligned} {\varvec{B}}^{\left( l \right) }\left( {\tau _i } \right)= & {} \left[ {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l} B_{-5,5}^{\left( l \right) } \left( {\tau _i } \right) &{} B_{-4,5}^{\left( l \right) } \left( {\tau _i } \right) &{} \cdots &{} B_{0,5}^{\left( l \right) } \left( {\tau _i } \right) \\ \end{array} }} \right] \end{aligned}$$

(12)

$$\begin{aligned} {\varvec{C}}_{i}= & {} \left[ {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l} C_{i-5} &{} C_{i-1} &{} \cdots &{} C_i \\ \end{array} }} \right] ^{T} \end{aligned}$$

(13)

In order to solve the second-order initial value problem in Sects. 3 and 4, $B_{i,5}^{\left( l \right) } (i=-5,-4,\ldots ,0;l=0,1,2)$, evaluated at the discrete time instant $t=t_i$ (i.e., $\tau _i =0$) and $t_{i+1}$ (i.e., $\tau _i =1$), are used for subsequent deduction. These values are listed in Table 1.

Table 1 Values of$\hbox { }B_{i,5}$, $B_{i,5}^{\left( 1 \right) }$, $B_{i,5}^{\left( 2 \right) }$

3 The implementation of quintic B-spline on SDOF systems

The equation of motion for a linear system with single degree of freedom can be written as

$$\begin{aligned} x^{\left( 2 \right) }\left( t \right) +2\xi \omega x^{\left( 1 \right) }\left( t \right) +\omega ^{2}x\left( t \right) =f\left( t \right) \end{aligned}$$

(14)

where $\xi$ is the damping ratio, $\omega$ is the undamped circular natural frequency of the system and $f\left( t \right)$ is the modal forcing excitation. $x\left( t \right)$, $x^{\left( 1 \right) }\left( t \right)$, and $x^{\left( 2 \right) }\left( t \right)$ are the displacement, velocity, and acceleration, respectively. The initial value problem is to solve Eq. (14) to meet the given initial conditions of $x\left( { t_0 } \right) = u_0$ and $x^{\left( 1 \right) }\left( { t_0 } \right) = v_0$.

Employing Eq. (11), the approximate solution of Eq. (14) ,within any time subinterval $I_{i}$, can be expressed as

$$\begin{aligned} x^{\left( l \right) }\left( t \right) ={\varvec{B}}^{\left( l \right) }\left( {\tau _i } \right) {\varvec{C}}_i , \quad t\in \left[ {t_i ,t_{i+1} } \right] \tau _i \in \left[ {0,1} \right] \end{aligned}$$

(15)

Actually, since the proposed B-spline time element is fourth-order compatible as illustrated in Sect. 2.2, all discrete unknown physical variables $x^{\left( l \right) }\left( {t_i } \right)$ can be degraded into the solving of ${\varvec{C}}_i$.

Generally, to determine Eq. (15), unknown coefficients vector ${\varvec{C}}_{i}$ needs to be solved. Nevertheless, to circumvent the direct solving of ${\varvec{C}}_{i}$, we use the numerical displacement, velocity, and acceleration at the start and end points of the time interval $\left[ {t_i ,t_{i+1}} \right]$ to represent ${\varvec{C}}_{i}$. Specifically, for $l=0,1,2$, when substituting $t=t_{i}$ (i.e., $\tau _i =0$) and $t=t_{i+1}$ (i.e., $\tau _i =1$) into Eq. (15), we have,

$$\begin{aligned} {\overline{\varvec{x}}}_{i} ={\overline{\varvec{P}}} {\varvec{C}}_{i}\; \hbox { or }\; {\varvec{C}}_{i} ={\overline{\varvec{P}}}^{-1} {\overline{\varvec{x}}}_{i} \end{aligned}$$

(16)

where

$$\begin{aligned} {\overline{\varvec{P}}} =\frac{1}{120}\left[ {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 1&{}\, 26&{}\,66&{}\,26&{}\,1&{}\,0 \\ -5&{}\,-50&{}\,0&{}\,50&{}\,5&{}\,0 \\ 20&{}\,40&{}\,-120&{}\,40&{}\,20&{}\,0 \\ 0&{}1&{}\,26&{}\,66&{}\,26&{}\,1 \\ 0&{}-5&{}\,-50&{}\,0&{}\,50&{}\,5 \\ 0&{}20&{}\,40&{}\,-120&{}\,40&{}\,20 \\ \end{array}}} \right] \end{aligned}$$

(17)

$$\begin{aligned} {\overline{\varvec{x}}}_{i}= & {} \left[ {\widetilde{\varvec{x}}}_{i} ^{T}\quad {\widetilde{\varvec{x}}}_{i+1}^{T}\right] ^{T}\end{aligned}$$

(18a)

$$\begin{aligned} {\widetilde{\varvec{x}}}_{i}= & {} \left[ x\left( {t_i } \right) \quad \Delta t\cdot x^{\left( 1 \right) }\left( {t_i } \right) \quad \left( {\Delta t} \right) ^{2}\cdot x^{\left( 2 \right) }(t_i) \right] ^{T}\end{aligned}$$

(18b)

$$\begin{aligned} {\widetilde{\varvec{x}}}_{i+1}= & {} \left[ x\left( {t_{i+1} } \right) \Delta t\cdot x^{\left( 1 \right) }\left( {t_{i+1} } \right) \left( {\Delta t} \right) ^{2}\cdot x^{\left( 2 \right) }(t_{i+1}) \right] ^{T} \end{aligned}$$

(18c)

Substituting Eq. (16) into Eq. (15) yields:

$$\begin{aligned} x^{\left( l \right) }\left( t \right) ={\varvec{B}}^{\left( l \right) }\left( {\tau _{i}} \right) {\overline{\varvec{P}}}^{-1}{\overline{\varvec{x}}}_{i}, \quad l=0,1,2. \end{aligned}$$

(19)

Inserting Eq. (20) into Eq. (14), the equation of motion evaluated at time $t_{i}$ can be expressed as

$$\begin{aligned}&\left( \left( {\Delta t} \right) ^{2}{\varvec{B}}^{\left( 2 \right) }\left( {\tau _i } \right) +2\xi \omega \cdot \left( {\Delta t} \right) ^{2}{\varvec{B}}^{\left( 1 \right) }\left( {\tau _i} \right) +\omega ^{2}\cdot \left( {\Delta t} \right) ^{2}{\varvec{B}}^{\left( 0 \right) }(\tau _i)\right) {\overline{\varvec{P}}}^{-1} {\overline{\varvec{x}}}_{i} =\left( {\Delta t} \right) ^{2}\cdot f\left( {t_i +\tau _{i} \Delta t} \right) ;\nonumber \\&\quad \left. t\in \left[ {t_i ,t_{i+1}} \right] \tau _i \in [0,1 \right] \end{aligned}$$

(20)

Further, we let

$$\begin{aligned} E\left( {\tau _i } \right)= & {} \left( (\Delta t)^{2}{\varvec{B}}^{(2)}\left( {\tau _i } \right) +2\xi \omega \cdot \left( {\Delta t} \right) ^{2}{\varvec{B}}^{\left( 1 \right) }\left( {\tau _i } \right) +\omega ^{2}\cdot \left( {\Delta t} \right) ^{2}{\varvec{B}}^{\left( 0 \right) }(\tau _i) \right) {\overline{\varvec{P}}}^{-1}\nonumber \\= & {} \left[ {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l} \left. {E_1 (\tau _i} \right) &{} \left. {E_2 (\tau _i } \right) &{} \cdots &{} \left. {E_6 (\tau _i } \right) \\ \end{array} }} \right] \end{aligned}$$

(21)

Substituting Eq. (21) into Eq. (20) and using Eq. (18), render the following residual equation:

$$\begin{aligned} R\left( {\tau _i} \right)= & {} \left[ E_1 (\tau _i)\quad E_2 (\tau _i) \quad E_3 (\tau _i) \right] {\widetilde{\varvec{x}}}_i \nonumber \\&+ \left[ E_4 (\tau _i)\quad E_5 (\tau _i)\quad E_6 (\tau _i) \right] {\widetilde{\varvec{x}}}_{i+1} - (\Delta t)^{2}f (t_i +\tau _i \Delta t); t\in \left[ {t_i ,t_{i+1}} \right] \tau _i \in [0,1] \end{aligned}$$

(22)

In this study, the proposed method is built upon the collocation method. Prescribing that Eq. (22) satisfies $R\left( {\tau _i } \right) =0$ at $\tau _i =1$(i.e., $t=t_{i+1}$), $\tau _i =r_1$ (i.e., $t=t_i +r_1 \mathrm{{\Delta }} t$), and $\tau _i =r_2$ (i.e., $t=t_i +r_2 \mathrm{{\Delta }} t$), then we have

$$\begin{aligned} \left[ E_1 (1)\quad E_2 (1)\quad E_3(1)\right] {\widetilde{\varvec{x}}}_{i}+ \left[ E_4 (1) \quad E_5 (1) \quad E_6 (1) \right] {\widetilde{\varvec{x}}}_{i+1}= & {} (\Delta t)^{2}f(t_i+\Delta t)\end{aligned}$$

(23)

$$\begin{aligned} \left[ E_1(r_1)\quad E_2 (r_1)\quad E_3 (r_1)\right] {\widetilde{\varvec{x}}}_i +\left[ E_4 (r_1)\quad E_5 (r_1)\quad E_6 (r_1)\right] {\widetilde{\varvec{x}}}_{i+1}= & {} (\Delta t)^{2}f(t_{i} +r_{1} \Delta t)\end{aligned}$$

(24)

$$\begin{aligned} \left[ E_1 (r_2)\quad E_2 (r_2)\quad E_3 (r_2)\right] {\widetilde{\varvec{x}}}_i +\left[ E_4 (r_2)\quad E_5 (r_2)\quad E_6 (r_2)\right] {\widetilde{\varvec{x}}}_{i+1}= & {} (\Delta t)^{2}f(t_i +r_2 \Delta t) \end{aligned}$$

(25)

Equations (23)–(25) can be written in a matrix form as

$$\begin{aligned} \left[ {{\begin{array}{l@{\quad }l@{\quad }l} E_1 (1)&{}\, E_2 (1)&{}\, E_3 (1) \\ E_1 (r_1)&{}\, E_2 (r_1)&{}\,E_3 (r_1) \\ E_1 (r_2)&{}\, E_2 (r_2)&{}\, E_3 (r_2) \\ \end{array}}} \right] {\widetilde{\varvec{x}}}_i+ \left[ {{\begin{array}{l@{\quad }l@{\quad }l} E_4 (1)&{}\, E_5 (1)&{}\, E_6 (1) \\ E_4 (r_1)&{}\, E_5 (r_1)&{}\, E_6 (r_1) \\ E_4 (r_2)&{}\, E_5 (r_2)&{}\, E_6 (r_2) \\ \end{array}}} \right] {\widetilde{\varvec{x}}}_{i+1} = \left[ {{\begin{array}{l} (\Delta t)^{2}f(t_i +\Delta t) \\ (\Delta t)^{2}f(t_i +r_1 \Delta t) \\ (\Delta t)^{2}f(t_i +r_2 \Delta t) \\ \end{array}}} \right] \end{aligned}$$

(26)

where $r_1$ and $r_2$ are parameters that govern the stability and accuracy of the proposed method. To meet the requirements of matrix inversion, $r_1$ and $r_2$ should satisfy conditions, $0<r_1 ,r_2 <1$ and $r_{1}\ne r_2$.

With matrix calculation, Eq. (26) can be further transformed into a simplified expression as

$$\begin{aligned} {\widetilde{\varvec{x}}}_{i+1} =\varvec{A}{\widetilde{\varvec{x}}}_i +{\varvec{f}}_i \end{aligned}$$

(27)

where

$$\begin{aligned} {\varvec{A}}= & {} -\left[ {{\begin{array}{l@{\quad }l@{\quad }l} E_4 (1)&{}\, E_5 (1)&{}\, E_6 (1) \\ E_4 (r_1)&{}\, E_5 (r_1)&{}\, E_6 (r_1) \\ E_4 (r_2)&{}\, E_5 (r_2)&{}\, E_6 (r_2) \\ \end{array}}} \right] ^{-1}\left[ {{\begin{array}{l@{\quad }l@{\quad }l} E_1 (1) &{}\, E_2 (1)&{}\, E_3 (1) \\ E_1 (r_1)&{}\, E_2 (r_1)&{}\, E_3 (r_1) \\ E_1 (r_2)&{}\, E_2 (r_2)&{}\, E_3 (r_2) \\ \end{array} }} \right] \end{aligned}$$

(28)

$$\begin{aligned} {\varvec{f}}_{i}= & {} \left[ {{\begin{array}{l@{\quad }l@{\quad }l} E_4 (1)&{}\, E_5 (1) &{}\, E_6 (1) \\ E_4 (r_1)&{}\, E_5 (r_1)&{}\, E_6 (r_1) \\ E_4 (r_2)&{}\, E_5 (r_2)&{}\, E_6 (r_2) \\ \end{array}}} \right] ^{-1}\left[ {{\begin{array}{l} (\Delta t)^{2}\cdot f\left( {t_i +\Delta t} \right) \\ (\Delta t)^{2}\cdot f\left( {t_i +r_1 \Delta t} \right) \\ (\Delta t)^{2}\cdot f\left( {t_i +r_2 \Delta t} \right) \\ \end{array}}} \right] \end{aligned}$$

(29)

4 The implementation of quintic B-spline on MDOF systems

The equation of motion for a linear system with multiple degree of freedom can be written as

$$\begin{aligned} {\varvec{MX}}^{(2)}(t)+{\varvec{DX}}^{(1)}(t)+{\varvec{KX}}(t)={\varvec{F}}(t) \end{aligned}$$

(30)

where ${\varvec{M}}, {\varvec{D}}$, and ${\varvec{K}}$ are the mass, damping, and stiffness matrices, respectively. ${\varvec{F}}$ is the vector of externally applied loads. The initial conditions at $t=0$ are ${\varvec{X}}\left( {t_0}\right) ={\varvec{X}}_{0}, {\varvec{X}}^{(1)}\left( {t_0}\right) ={\dot{{\varvec{X}}}_{0}}$. ${\varvec{X}}(t),\,{\varvec{X}}^{(1)}\left( t \right)$, and ${\varvec{X}}^{\left( 2\right) }\left( t \right)$ are the unknown displacement, velocity, and acceleration function vector. Then we have

$$\begin{aligned} {\varvec{X}}^{(l)}(t)=\left[ x_1^{\left( l\right) } \left( t \right) \quad x_{2}^{\left( l\right) } \left( t \right) \quad \cdots \quad x_{k'}^{(l)}(t) \quad \cdots \quad x_{N}^{(l)}(t) \right] ^{T},\quad l=0,1,2 \end{aligned}$$

(31)

As discussed in Sect. 3 for the SDOF system, Eq. (15) continues to be employed to represent the approximate solution of Eq. (30). Hence, we have

$$\begin{aligned} x_{k'}^{(l)}(t)= & {} {\varvec{B}}^{(l)}\left( \tau _i\right) {\varvec{C}}_{k', i}\end{aligned}$$

(32)

$$\begin{aligned} {\varvec{X}}^{(l)}\left( t \right)= & {} {\widetilde{\varvec{B}}}^{(l)}\left( {\tau _i }\right) {\varvec{C}}_i \end{aligned}$$

(33)

where

$$\begin{aligned} {\varvec{C}}_{i}= & {} \left[ {\varvec{C}}_{1,i}^{T}\quad {\varvec{C}}_{2,i}^{T}\quad {\varvec{C}}_{k', i}^{T} \quad ... \quad {\varvec{C}}_{N,i}^{T}\quad \right] ^{T}\end{aligned}$$

(34)

$$\begin{aligned} {\widetilde{\varvec{B}}}^{\left( l \right) }\left( {\tau _i } \right)= & {} \left( {{\begin{array}{l@{\quad }l@{\quad }l} {\varvec{B}}^{\left( l \right) }(\tau _i) &{}\, &{}\, \\ &{}\, \ddots &{}\, \\ &{}\, &{}\, {\varvec{B}}^{\left( l \right) }(\tau _i) \\ \end{array}}}\right) _{N\times N} \end{aligned}$$

(35)

In which ${\varvec{C}}_{k', i}(k'=1,2,\ldots , N)$ is the unknown coefficients vector of size $6\times 1$, and ${\widetilde{\varvec{B}}} ^{\left( l \right) }\left( {\tau _i } \right)$ are block diagonal matrices with element ${\varvec{B}}^{\left( l\right) }\left( {\tau _i}\right)$

Like for the SDOF system in Sect. 3, by setting $t=t_i$ (i.e., $\tau _i =0$) and $t=t_{i+1}$ (i.e., $\tau _i =1$) in Eq. (33), we obtain

$$\begin{aligned} {\overline{\varvec{X}}}_i ={\widetilde{\varvec{P}}} \varvec{C}_i \hbox { or } \varvec{C}_i ={\widetilde{\varvec{P}}} ^{-1}{\overline{\varvec{X}}} _i \end{aligned}$$

(36)

where

$$\begin{aligned} {\overline{\varvec{X}}}_i= & {} \left[ {\widetilde{\varvec{X}}}_i ^{T} \quad {\widetilde{\varvec{X}}} _{i+1} ^{T} \right] ^{T}\end{aligned}$$

(37a)

$$\begin{aligned} {\widetilde{\varvec{X}}}_i= & {} \left[ {\varvec{X}}(t_i)\quad \Delta t {\varvec{X}}^{\left( 1 \right) }(t_i) \quad (\Delta t)^{2}{\varvec{X}}^{\left( 2 \right) }(t_i)\right] ^{T}\end{aligned}$$

(37b)

$$\begin{aligned} {\widetilde{\varvec{X}}}_{i+1}= & {} \left[ {\varvec{X}}(t_{i+1}) \quad \Delta t {\varvec{X}}^{\left( 1 \right) }(t_{i+1})\quad \left( \Delta t\right) ^{2}{\varvec{X}}^{\left( 2 \right) }(t_{i+1})\right] ^{T} \end{aligned}$$

(37c)

$$\begin{aligned} {\widetilde{\varvec{P}}} =\left( {{\begin{array}{l} {\varvec{G}}_{1} \\ {\varvec{G}}_{2} \\ \end{array}}} \right) ; \quad {\varvec{G}}_1 =\left[ {{\begin{array}{l} {\widetilde{\varvec{B}}} \left( 0 \right) \\ \left( {\Delta t} \right) {\widetilde{\varvec{B}}} ^{\left( 1 \right) }\left( 0 \right) \\ \left( {\Delta t} \right) ^{2}{\widetilde{\varvec{B}}} ^{\left( 2 \right) }\left( 0 \right) \\ \end{array}}} \right] _{3N\times 6N};\quad {\varvec{G}}_2 =\left[ {{\begin{array}{l} {\widetilde{\varvec{B}}} \left( 1 \right) \\ \left( {\Delta t} \right) {\widetilde{\varvec{B}}} ^{\left( 1 \right) }\left( 1 \right) \\ \left( {\Delta t} \right) ^{2}{\widetilde{\varvec{B}}} ^{\left( 2 \right) }\left( 1 \right) \\ \end{array}}} \right] _{3N\times 6N} \end{aligned}$$

(38)

Actually, ${\widetilde{\varvec{P}}}$ is a sparse and block matrix. By use of $\overline{\varvec{P}}$ in Eq. (17), the calculation of ${\widetilde{\varvec{P}}} ^{-1}$ can be simplified as

$$\begin{aligned} {\overline{\varvec{P}}} ^{-1}=\left[ {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} q_{11} &{}\, q_{12} &{}\, \cdots &{}\, q_{16} \\ q_{21} &{}\, q_{22} &{}\, \cdots &{}\, q_{26} \\ \vdots &{}\, \vdots &{}\, \ddots &{}\, \vdots \\ q_{61} &{}\, q_{62} &{}\, \cdots &{}\, q_{66} \\ \end{array}}} \right] \!, \quad {\widetilde{\varvec{P}}} ^{-1}=\left[ {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} q_{11} [{\varvec{I}}] &{}\, q_{12} [{\varvec{I}}]&{}\, \cdots &{}\, q_{16} [{\varvec{I}}] \\ q_{21} [{\varvec{I}}] &{}\, q_{22} [{\varvec{I}}]&{}\, \cdots &{}\, q_{26} [{\varvec{I}}] \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ q_{61} [{\varvec{I}}] &{}\, q_{62} [{\varvec{I}}]&{}\, \cdots &{}\, q_{66} [{\varvec{I}}] \\ \end{array}}} \right] \end{aligned}$$

(39)

where $\left[ {\varvec{I}}\right]$ is the unit matrix of size $N\times N$.

Inserting Eq. (36) into Eq. (33) renders:

$$\begin{aligned} {\varvec{X}}^{\left( l \right) }\left( t \right) ={\widetilde{\varvec{B}}}^{ \left( l \right) }\left( {\tau _i } \right) {\widetilde{\varvec{P}}}^{-1}{\overline{\varvec{X}}} _i \end{aligned}$$

(40)

Substituting Eq. (40) into Eq. (30) gives the following residual equation:

$$\begin{aligned} {\varvec{R}}\left( {\tau _i} \right) =\left( {\varvec{M}}{\widetilde{\varvec{B}}} ^{ \left( 2 \right) }\left( {\tau _i }\right) +{\varvec{D}}{\widetilde{\varvec{B}}} ^{\left( 1 \right) }\left( {\tau _i }\right) +{\varvec{K}}{\widetilde{\varvec{B}}} ^(\tau _i) \right) {\widetilde{\varvec{P}}} ^{-1}{\overline{\varvec{X}}} _i -\left( {\Delta t} \right) ^{2}\cdot {\varvec{F}}\left( t \right) \end{aligned}$$

(41)

By setting

$$\begin{aligned} \left( {\varvec{M}}{\widetilde{\varvec{B}}}^{\left( 2\right) }\left( {\tau _i } \right) +{\varvec{D}}{\widetilde{\varvec{B}}}^{ \left( 1\right) }\left( {\tau _i } \right) +{\varvec{K}}{\widetilde{\varvec{B}}} (\tau _i)\right) {\widetilde{\varvec{P}}} ^{-1}= \left[ {\widetilde{\varvec{E}}}_1\left( {\tau _i}\right) {\widetilde{\varvec{E}}}_2 \left( {\tau _i } \right) \cdots {\widetilde{\varvec{E}}}_6 (\tau _i) \right] \end{aligned}$$

(42)

Equation (41) can be written as

$$\begin{aligned} {\varvec{R}}\left( {\tau _i}\right) =\left[ {\widetilde{\varvec{E}}}_{1} (\tau _i)\quad {\widetilde{\varvec{E}}}_{2}(\tau _i)\quad {\widetilde{\varvec{E}}}_{3}(\tau _i)\right] {\widetilde{\varvec{X}}}_i +\left[ {\widetilde{\varvec{E}}}_{4}(\tau _i)\quad {\widetilde{\varvec{E}}}_{5}(\tau _i)\quad {\widetilde{\varvec{E}}}_{6}(\tau _i)\right] {\widetilde{\varvec{X}}}_{i+1} -\left( {\Delta t} \right) ^{2}\cdot {\varvec{F}} \left( t \right) \end{aligned}$$

(43)

As illustrated in Sect. 3, after conducting the collocation method with Eq. (41), we derive the recurrence formula for calculation as

$$\begin{aligned} {\widetilde{\varvec{X}}}_{i+1} =\varvec{A}_{1}^{-1}\varvec{A}_{2}{\widetilde{\varvec{X}}}_{i} +\varvec{A}_{1}^{-1}{\widetilde{\varvec{f}}}_{i} =\varvec{A}{\widetilde{\varvec{X}}} _i +{\widetilde{\varvec{F}}}_{i} \end{aligned}$$

(44)

where

$$\begin{aligned} {\varvec{A}}_{1}= & {} \left[ {{\begin{array}{l@{\quad }l@{\quad }l} {\widetilde{\varvec{E}}}_{4} (1)&{}\, {\widetilde{\varvec{E}}}_{5}(1) &{}\, {\widetilde{\varvec{E}}}_{6} (1) \\ {\widetilde{\varvec{E}}}_{4} (r_1) &{}\, {\widetilde{\varvec{E}}} _{5} (r_1) &{}\, {\widetilde{\varvec{E}}}_{6} (r_1) \\ {\widetilde{\varvec{E}}}_{4} (r_2) &{}\, {\widetilde{\varvec{E}}} _{5} (r_2) &{}\, {\widetilde{\varvec{E}}}_{6} (r_2) \\ \end{array}}} \right] ,\quad {\varvec{A}}_{2} =\left[ {{\begin{array}{l@{\quad }l@{\quad }l} {\widetilde{\varvec{E}}}_{1} (1) &{}\, {\widetilde{\varvec{E}}}_{2} (1)&{}\, {\widetilde{\varvec{E}}}_{3} (1) \\ {\widetilde{\varvec{E}}}_{1} (r_1)&{}\, {\widetilde{\varvec{E}}}_{2} (r_1)&{}\, {\widetilde{\varvec{E}}}_{3} (r_1) \\ {\widetilde{\varvec{E}}}_{1} (r_2)&{}\,{\widetilde{\varvec{E}}}_{2} (r_2)&{}\, {\widetilde{\varvec{E}}}_{3} (r_2) \\ \end{array}}}\right] \end{aligned}$$

(45)

$$\begin{aligned} {\widetilde{\varvec{f}}}_{i}= & {} \left[ {{\begin{array}{l} \left( {\Delta t} \right) ^{2}\cdot \varvec{F}\left( {t_i +\Delta t} \right) \\ \left( {\Delta t} \right) ^{2}\cdot \varvec{F}\left( {t_i +r_1 \Delta t} \right) \\ \left( {\Delta t} \right) ^{2}\cdot \varvec{F}\left( {t_i +r_2 \Delta t} \right) \\ \end{array} }} \right] \end{aligned}$$

(46)

For small element number $N$, ${\varvec{A}}_{1} ^{-1}$ can be efficiently solved with direct matrix inversion by use of some general mathematical softwares. However, the direct inversion of ${\varvec{A}}_{\mathbf{1}}$ is not desirable for large element number $N$. Thus, a new technique is proposed here to avoid the direct inversion of matrix ${\varvec{A}}_{\mathbf{1}}$. First, we introduce the following well-known theorem and corollary [8, 22].

Theorem 1

Let a non-singular square matrix ${\widetilde{\varvec{R}}}$ can be partitioned into $2\times 2$ blocks as

$$\begin{aligned} {\widetilde{\varvec{R}}} =\left[ {{\begin{array}{l@{\quad }l} {\varvec{G}}_1 &{} {\varvec{G}}_2 \\ {\varvec{G}}_3 &{} {\varvec{G}}_4 \\ \end{array} }} \right] \end{aligned}$$

(47)

Assume ${\varvec{G}}_{4}$ is non-singular; then, the matrix ${\widetilde{\varvec{R}}}$ is invertible if and only if the Schur complement ${\varvec{G}}_{1}-{\varvec{G}}_{2}{\varvec{G}}_{4}^{-1}{\varvec{G}}_{3}$ is invertible; meanwhile, we have

$$\begin{aligned} {\widetilde{\varvec{R}}} ^{-1}= & {} \left[ {{\begin{array}{l@{\quad }l} {\varvec{G}}_{5}^{-1}&{} -{\varvec{G}}_{5}^{-1}{\varvec{G}}_{2} {\varvec{G}}_{4}^{-1} \\ -{\varvec{G}}_{4}^{-1}{\varvec{G}}_{3} {\varvec{G}}_{5}^{-1}&{}\, {\varvec{G}}_{4}^{-1}\quad +\quad {\varvec{G}}_{4}^{-1}{\varvec{G}}_{3} {\varvec{G}}_{5} ^{-1}{\varvec{G}}_{2} {\varvec{G}}_{4}^{-1} \\ \end{array} }} \right] \end{aligned}$$

(48)

$$\begin{aligned} {\varvec{G}}_{5}= & {} {\varvec{G}}_{1} -{\varvec{G}}_{2} {\varvec{G}}_{4}^{-1}{\varvec{G}}_{3} \end{aligned}$$

(49)

Corollary 1

Assume ${\varvec{G}}_{4}$ is non-singular; then ${\varvec{G}}_{5}$ is invertible if the matrix ${\widetilde{\varvec{R}}}$ is invertible.

With above theorem and corollary, the invertible matrix ${\varvec{A}}_{\mathbf{1}}$ can be expressed as

$$\begin{aligned} {\varvec{A}}_{1} =\left[ {{\begin{array}{l@{\quad }l} {\varvec{S}}_{1} &{}\, {\varvec{S}}_{2} \\ {\varvec{S}}_{3} &{}\, {\varvec{S}}_{4} \\ \end{array}}} \right] ; \quad {\varvec{S}}_{4} =\left[ {{\begin{array}{l@{\quad }l} ({\widetilde{\varvec{E}}}_{5}(r_1)&{}\, ({\widetilde{\varvec{E}}} _{6}(r_1) \\ {\widetilde{\varvec{E}}}_{5}(r_2)&{}\, {\widetilde{\varvec{E}}}_{6}(r_2) \\ \end{array}}} \right] \end{aligned}$$

(50)

Equation (50) implies

$$\begin{aligned} {\varvec{S}}_{1}= & {} {\widetilde{\varvec{E}}}_{1}\left( 1 \right) ; \quad {\varvec{S}}_{2} =\left[ {\widetilde{\varvec{E}}}_2 \left( 1 \right) \quad {\widetilde{\varvec{E}}}_{6}\left( 1 \right) \right] ; \quad S_3 =\left[ {{\begin{array}{l} {\widetilde{\varvec{E}}}_{4} (r_1) \\ {\widetilde{\varvec{E}}}_{4} (r_2) \\ \end{array}}} \right] \end{aligned}$$

(51)

Then, we have

$$\begin{aligned} {\varvec{A}}_{1}^{-1}= & {} \left[ {{\begin{array}{l@{\quad }l} {\varvec{S}}_{5}^{-1}&{}\, -{\varvec{S}}_{5} ^{-1}{\varvec{S}}_{2} {\varvec{S}}_{4}^{-1} \\ -{\varvec{S}}_{4}^{-1}{\varvec{S}}_{3} {\varvec{S}}_{5}^{-1}&{}\,{\varvec{S}}_{4}^{-1}+{\varvec{S}}_{4}^{-1}{\varvec{S}}_{3}{\varvec{S}}_{5}^{-1}S_2 {\varvec{S}}_{4}^{-1} \\ \end{array}}} \right] \end{aligned}$$

(52)

$$\begin{aligned} {\varvec{S}}_{5}= & {} {\varvec{S}}_{1} -{\varvec{S}}_{2} {\varvec{S}}_{4}^{-1}{\varvec{S}}_{3} \end{aligned}$$

(53)

where ${\varvec{S}}_{4}^{-1}$ can be directly solved by use of Eq. (48).

From Eq. (42), we can see that ${\widetilde{\varvec{E}}}_{k} \left( {\tau _i } \right) (k=1,2,\ldots ,6)$ are all symmetric matrices of size $N\times N$. Thus, the solving of ${\varvec{A}}_{1}^{-1}$ can be degraded into the inversion of several $N\times N$ matrices, which, to some extent, illustrates the proposed matrix inverse scheme is more efficient than conventional Gauss algorithm where more time is needed for asymmetric matrices. Meanwhile, after the time increment $\mathrm{{\Delta }}t$ is selected, parallel computation can be adopted for symmetric matrices inversion.

To write a computer code, the complete calculation procedure for the MDOF system is outlined in Table 2.

Table 2 The calculation procedure for the response of MDOF systems using the proposed method

5 Stability and accuracy analyses

5.1 Stability analysis

In general, any global equation of motion can be degraded into a set of uncoupled SDOF systems by use of the modal decomposition. Meanwhile, the integration of the uncoupled equations is equivalent to the integration of the original system. Therefore, to study the stability properties of the proposed method, it suffices to only consider the SDOF system [8].

As elucidated in Sect. 3, the recurrence formula of the proposed method for any SDOF system can be written in an explicit form as

$$\begin{aligned} \left\{ {{\begin{array}{c} x(t_{i+1}) \\ \Delta t\cdot x^{(1)}(t_{i+1}) \\ (\Delta t)^{2}\cdot x^{(2)}(t_{i+1}) \\ \end{array}}} \right\}= & {} {\varvec{A}}\left\{ {{\begin{array}{c} x(t_i) \\ \Delta t\cdot x^{(1)} (t_i) \\ ( \Delta t )^{2}\cdot x^{(2)}(t_i) \\ \end{array}}} \right\} +\,{\varvec{f}}_{i} \end{aligned}$$

(54)

where ${\varvec{A}}$ is the amplification matrix which transfers the state at the time instant $t_{i}$ to the state at the time instant $t_{i+1}$. Because ${\varvec{A}}$ contains too many terms, the complete expression of ${\varvec{A}}$ is not presented here. Actually, we can easily derive the expression of ${\varvec{A}}$ by virtue of some general mathematical softwares.

We conduct the stability analysis by solving the eigenproblem of the amplification matrix ${\varvec{A}}$, and the eigenvalues of ${\varvec{A}}$ are calculated by using $\left| {{\varvec{A}}-\lambda {\varvec{I}}} \right| =0$. Here we denote $\lambda _{j} (j=1,2,3)$ are the eigenvalues of ${\varvec{A}}$. To acquire a stable numerical solution, namely a convergent algorithm, we should have $\rho \left( {\varvec{A}}\right) =\hbox {max}(||\lambda _{1}||, ||\lambda _{2}||,||\lambda _{3}||)\le 1$, where $\rho ({\varvec{A}})$ is the spectral radius.

For a step-by-step explicit time integration, it suffices to investigate $\rho ({\varvec{A}})$ only at $\xi =0$. At this moment, $\rho \left( {\varvec{A}}\right)$ is a function in terms of parameters, $r_{1}$ and $r_{2}$, and $\omega \mathrm{{\Delta }}t$. The natural frequency $\omega$ satisfies $\omega =2\pi /T$, where $T$ is the period of system. To ascertain the stability of the proposed method, the effects of parameters $r_{1}$ and $r_{2}$ on the spectral radius $\rho \left( {\varvec{A}}\right)$ need to be investigated.

Here the stability analysis is conducted through numerical experimentation, and some representative parameters combinations are deliberately discussed.

The variation in spectral radius $\rho \left( {\varvec{A}}\right)$ versus $\mathrm{{\Delta }} t/T$ is illustrated in Fig. 3; especially, various combinations of parameters $r_{1}$ and $r_{2}$ for conditional and unconditional stability are illustrated in Figs. 3a, b, respectively.

Fig. 3

The spectral radius $\rho \left( {\varvec{A}}\right)$ versus $\mathrm{{\Delta }} t/T$ for different parameters combinations. a Conditionally stable. b Unconditionally stable

In Fig. 3a, for $0<\mathrm{{\Delta }} t\le 0.1T$, the spectral radius curves remain 1 for different parameter combinations. Figure 3 demonstrates that the increase in $r_{1}$ and $r_{2}$ can greatly change stability of the proposed method by augmenting the stable regions for conditionally stable cases in Fig. 3a and decreasing the value of spectral radius $\rho \left( {\varvec{A}}\right)$ in the limit $\mathrm{{\Delta }} t/T\rightarrow \infty$ for unconditionally stable cases in Fig. 3b. Thus, the unconditionally stable cases with larger parameters are certainly more dissipative in the high-frequency modes. Notably, the minimum points of these curves move downward and rightward as two algorithmic parameters increase, and the abrupt turning points in the figure indicate that the eigenvalues of amplification matrix ${\varvec{A}}$ alter between real values and complex conjugate values. However, these small turnings have no substantial influence on algorithmic stability and high-frequency dissipation characteristics.

As shown in Fig. 3, a valid parameter condition for unconditional stability can be suggested as $0.8\le r_1 <1$, $0.9\le r_2 <1$, and $r_{1} \ne r_{2}$. For simplicity, only four parameters combinations are considered. They are given as

• Quintic B-spline $I$:   $r_1\,$=$\, 0.6,\;r_2\,$=$0.8$; $\mathrm{{\Delta }} t\le 2.22T$

• Quintic B-spline II:   $r_1\,$=$\, 0.7,\; r_2\,$=$0.8$; $\mathrm{{\Delta }} t\le 2.91T$

• Quintic B-spline III:   $r_1\,$=$\, 0.8,\;r_2\,$=$0.9$ (unconditionally stable)

• Quintic B-spline IV:   $r_1\,$=$\, 0.94,\;r_2\,$=$0.96$ (unconditionally stable)

For comparison, the spectral radii of various methods versus $\mathrm{{\Delta }} t/T$ are plotted in Fig. 4. Figure 4a shows that the quintic B-splines $I$ and II have far wider stable regions than the Noh–Bathe method [14]. Figure 4b illustrates that the spectral radii from the quintic B-splines III and IV remain 1 for a larger frequency bandwidth than other methods; thus, theoretically, the proposed method has less dissipation in the low-frequency modes. For middle-frequency band, the spectral radii from the proposed method decrease more rapidly than other presented methods such as the Bathe method and the generalized-$\alpha$ method [23]. As for high-frequency band, the spectral radii curve rebound from their lowest points and then gradually approaches a constant as $\mathrm{{\Delta }} t/T\rightarrow \infty$. As revealed in Fig. 3, this constant decreases as the increase in algorithmic parameters. This property makes the proposed method very flexible in filtering high-frequency modes.

Fig. 4

The spectral radius comparison between the proposed method and other given methods. a Conditionally stable b Unconditionally stable

5.2 Accuracy analysis

To ascertain the calculation accuracy of the proposed method, numerical damping ratio(i.e., amplitude decay) and period elongation are employed for error estimation [8].

Numerical experiment demonstrates that the proposed method has no period elongation. Figure 5 shows how the numerical damping ratio varies with the ratio $\mathrm{{\Delta }} t/T$ for different parameter combinations. Conditionally stable cases in Fig. 5a give smaller numerical damping ratios than the unconditionally stable cases in Fig. 5b. The damping ratio curves in Fig. 5 are extremely small for $0<\mathrm{{\Delta }} t/T<0.1$. Figure 5 also shows that the proposed method allows the degree of dissipation to be continuously controlled by the algorithmic parameters. Figure 5 shows that the smaller the parameters $r_{1}$ and $r_{2}$, the smaller the numerical damping ratio. All damping ratios in Fig. 5 are almost two order of magnitude less than the Bathe and Noh–Bathe methods [13, 14]; thus, for clarity, damping ratios of these two methods are not delineated here.

Fig. 5

Numerical damping ratio vs $\mathrm{{\Delta }}t/T$ for the proposed method a Unconditionally stable. b Conditionally stable

6 Numerical simulations

To demonstrate the validity of the proposed method for dynamic analysis, three numerical simulations are given in this section, and four parameter cases previously given in Sect. 5.1 are used for computation. For comparison, the generalized-$\alpha$ ($\alpha _{f} =\frac{1}{3},\alpha _m =0, \beta =\frac{1}{2}, \gamma =\frac{5}{6})$ method [23], the Bathe method [13], and the Noh–Bathe method [14] are employed for numerical simulations. For the Noh–Bathe method, we adopt the suggested parameter value $p=0.54$ for computation.

6.1 A SDOF system

A SDOF system used for numerical simulation is described by the following equation:

$$\begin{aligned} u^{\left( 2 \right) }\left( t \right) +4u^{\left( 1 \right) }\left( t \right) +5u\left( t \right) =sin2t, \quad u\left( 0 \right) =57/65, \quad u^{\left( 1 \right) }\left( 0 \right) =2/65 \end{aligned}$$

(55)

For which the exact solution is $u\left( t \right) =e^{-2t}\left( {\hbox {cos}t+2\hbox {sin}t} \right) -(8\hbox {cos}2t-\hbox {sin}2t)/65$.

To illustrate the calculation accuracy of the proposed method, the relative errors of different methods are compared in Fig. 6 where we select time increment $\mathrm{{\Delta }} t=0.1$s for simulation and the relative errors are defined by

$$\begin{aligned} \eta _{i} =\frac{\left| u_{num}^{\left( i \right) } -u_{exact}^{\left( i \right) } \right| }{\left| {u_{exact}^{\left( i \right) } } \right| }100\,\%\quad \left( i=0,1,2.\right) \end{aligned}$$

(56)

in which $u_{num}^{\left( i \right) }$ and $u_{exact}^{\left( i \right) }$ are the numerical result and the exact solution at some given time, respectively.

As elucidated in Sect. 5.2, the accuracy of the proposed method improves with the decrease in parameters $r_{1}$ and $r_{2}$; thus, it suffices to only employ the quintic B-splines $I$ and IV for error analysis. Figure 6 shows that the proposed method yields far less relative errors than the Bathe and Noh–Bathe methods.

Fig. 6

The relative error comparison between the proposed method and other given methods a Displacement b Velocity c Acceleration

In Table 3, $\mathrm{{\Delta }} t=0.05s$ and various time step $n_{g}$ are selected for time consumption analysis of example 6.1. Notably, the proposed method spend less computation time than the Noh–Bathe method and more time than the Bathe method. However, the proposed method is more efficient than the Noh–Bathe and Bathe methods in terms of its high calculation accuracy as shown in Fig. 6.

Table 3 Time consumption(s) analysis for example 6.1

6.2 A 2D Howe truss under impact loads

To demonstrate the feasibility of the proposed method for dynamic response of the MDOF system, A Howe truss under four concentrated impact loads is shown in Fig. 7 [24]. Material properties for all elements are denoted in the figure. For comparison, the generalized-$\alpha$ method and the Bathe method are used for computation. The least period of this system ($T_{min}$) is equal to 0.0082s. Thus, we select $\mathrm{{\Delta }} t=1\times 10^{-2}s(\mathrm{{\Delta }} t\le 2.22T_{min})$ for the conditionally stable quintic B-spline $I$ and $\mathrm{{\Delta }} t=2\times 10^{-2}s$ for the unconditionally stable quintic B-spline IV and the Bathe method. In Figs. 8 and 9, we select ${rm{\Delta }} t=4\times 10^{-4}s$ for the generalized-$\alpha$ method to obtain the referred exact curves.

Fig. 7

A Howe truss under impact loads

Fig. 8

Vertical displacement of node 5

The time history of vertical displacement in a time interval between 0 and 2  s for node 5 is illustrated in Fig. 8, and the horizontal displacement of node 13 is plotted in Fig. 9. Obviously, the displacement curves from the quintic B-splines $I$ and IV match very well with the curves from the generalized-$\alpha$ method, while the curves from the Bathe method are clearly less accurate than the proposed method. As a sample, the results of time consumption analysis for example 6.2 have been tabulated in Table 4 where all methods use $\mathrm{{\Delta }} t=4\times 10^{-4}s$ for computation. Figures 8, 9, and Table 4 indicate that the proposed method has very desirable computation efficiency.

Fig. 9

Horizontal displacement of node 13

Table 4 Time consumption(s) analysis for example 6.2

6.3 Free vibration of a simply supported uniform continuous beam

To verify the validity of the proposed method for finite element method (FEM) calculation, a simply supported uniform continuous beam under a distributed load is shown in Fig. 10. The dimensions and parameters for simulation are the length $L=8\,\,\hbox {m}$, the radius of circular section $R=2\times 10^{-2}$  m, the cross-sectional area $A=\pi R^{2}$, the sectional inertia moment $I=\pi R^{4}/2$, Young’s modulus $E$=100  GPa, Poisson’s ratio $\mu =0.3$, the material density of the beam $\rho =4\times 10^{4}/\left( {\hbox {kg}/\hbox {m}^{3}}\right)$, the damping ratio $\xi =0$, and the distributed load $q\left( t\right) =F_{0}\mathrm{{\delta }} (t-0^{-})$. Here we select $F_0 =1\,\hbox {KN}$ and $\omega _{0} =4\, \hbox {rad}/\hbox {s}$. The analytical solution of the beam’s bending deflection can be represented by

$$\begin{aligned} w\left( {x,t} \right) =\frac{4F_0 L^{4}}{EI\pi ^{5}}\sum \limits _{r=1,3,5,\ldots }^{\infty } \quad \frac{1}{r^{5}}\hbox {sin}\frac{r\pi x}{L}\cdot \hbox {cos}\omega _r t \end{aligned}$$

(57)

where the natural frequency $\omega _{r}$ is calculated by $\omega _r =\frac{r^{2}\pi ^{2}}{L^{2}}\sqrt{\frac{EI}{\rho A}}\left( {r=1,2,\ldots } \right)$.

The equilibrium equation of this problem is formulated by use of the cubic Hermite finite element with its element number $N_s =10$. The boundary conditions are satisfied by directly setting $w=0$ at $x=0$ and $x=L$. The time history of displacement and velocity between 0 and 12  s for the middle point is illustrated in Fig. 11 where we select $\mathrm{{\Delta }} t=2\times 10^{-1}$  s for different methods. Figure 11 shows that the proposed method gives far more accurate displacements and velocities than the generalized-$\alpha$ method and the Bathe method.

Fig. 10

The scheme of bending vibration beam with two simple supports

Fig. 11

Numerical displacements and velocities of different methods at the beam’s middle point a Displacement b Velocity

To investigate the numerical dissipation characteristics of the proposed method, we select a relatively large element number $N_{s}=20$ to make first several natural frequencies more accurate and only consider the acceleration response for analysis. However, in FEM, a larger element number definitely engenders more unneeded or spurious high-frequency responses, and these frequencies need to be smoothed out effectively.

As is well known, for most numerical methods, an effective high-frequency dissipation entails a relatively large $\mathrm{{\Delta }} t$ which in return decreases the computational accuracy greatly. Thus, to manifest the superior capability of the proposed method in numerical dissipation and computational accuracy, the quintic B-spline IV is especially compared with the latest high-accuracy Bathe method which has far better high-frequency dissipation characteristics than the Newmark’s method [9]. In Fig. 4b, we assume $L_{U}$ be the critical length of $\mathrm{{\Delta }} t/T$ for $\rho \left( {\varvec{A}}\right) =1$; then, we can easily obtain $L_{U}=0.08$ and $L_{U} =0.0305$ for the quintic B-spline IV and the Bathe method, respectively. Meanwhile, the corresponding critical time increment $\mathrm{{\Delta }} t_{i}$ for first four natural frequencies $\omega _{i}$ has been listed in Table 5 where $\mathrm{{\Delta }} t_i$ is calculated by $\mathrm{{\Delta }} t_i =2\pi L_U / \omega _i$.

First, we assume that only the first term of Eq. (86) is the substantial part of exact response(briefly denoted by Exact $I$). Then, to retain the first natural frequency and filter out other natural frequencies, the adopted $\mathrm{{\Delta }} t$ should satisfy $\mathrm{{\Delta }} t_2 <\mathrm{{\Delta }} t\le \mathrm{{\Delta }} t_1$. Therefore, in Fig. 12, we select $\mathrm{{\Delta }} t=0.12$  s and $\mathrm{{\Delta }} t=0.05$  s for the quintic B-spline IV and the Bathe method, respectively. In Fig. 12, there is an ‘overshoot’ for the quintic B-spline IV at the first time step; however, the proposed method shows higher calculation and more efficient high-frequency dissipation than the Bathe method.

Fig. 12

Numerical acceleration comparison for Exact $I$

Table 5 The critical time increments of $\rho \left( {\varvec{A}}\right) =1$ for first four natural frequencies

Further, we assume the first two terms of Eq.(86) are the substantial part of exact response(briefly denoted by Exact II). Then, to retain the third natural frequency and filter out other larger natural frequencies, the adopted $\mathrm{{\Delta }}t$ should satisfy $\mathrm{{\Delta }}t_4 <\Delta t\le \mathrm{{\Delta }}t_3$. Therefore, in Fig. 13, we select $\mathrm{{\Delta }} t=0.015$  s and $\mathrm{{\Delta }} t=0.005$  s for the quintic B-spline IV and the Bathe method, respectively. As shown in Fig. 13a, at the first stage of dynamic response, both the proposed method and the Bathe method give undesirable accelerations. But Fig. 13b illustrates that the proposed method can filter out unneeded high-frequency modes more effectively and rapidly than the Bathe method. Conclusively, the proposed methods possess higher calculation accuracy and more desirable high-frequency dissipation than the Bathe method.

Fig. 13

Numerical acceleration comparison for Exact II a Acceleration between 0 and 4s b Acceleration between 14s and 18s

7 Conclusions

In this study, a new explicit time integration was proposed for structural dynamics using quintic B-spline functions. In this way, the recurrence formulas for the linear dynamic analysis of the SDOF and MDOF systems were formulated through employing quintic B-spline interpolation to solve differential equations of motion.

With adjustable algorithmic parameters, the proposed method can obtain both conditional and unconditional stability; meanwhile, algorithmic parameters conditions for stability were also given.

The clear advantages of the proposed method over other methods are that the proposed method give minimal numerical damping ratio and have no period elongation.

Numerical examples illustrate that the proposed method has far higher computation efficiency and more desirable high-frequency dissipation than the Bathe and Noh–Bathe methods.