Full Dynamic Compound Inverse Method: Extension to General and Rayleigh damping

Abstract

The present paper takes from the original output-only identification approach named Full Dynamic Compound Inverse Method (FDCIM), recently published on this journal by the authors, and proposes an innovative, much enhanced version, in the description of more general forms of structural damping, including for classically adopted Rayleigh damping. This has led to an extended FDCIM formulation, which offers superior performance, on all the targeted identification parameters, namely: modal properties, Rayleigh damping coefficients, structural features at the element-level and input seismic excitation time history. Synthetic earthquake-induced structural response signals are adopted as input channels for the FDCIM approach, towards comparison and validation. The identification algorithm is run first on a benchmark 3-storey shear-type frame, and then on a realistic 10-storey frame, also by considering noise added to the response signals. Consistency of the identification results is demonstrated, with definite superiority of this latter FDCIM proposal.

1 Introduction

This paper constitutes a refined extension of work [15], leading to superior performance in terms of output-only identification of structural dynamic properties in the seismic engineering range, namely: modal parameters, structural features at the element-level and input seismic excitation time history.

The renewed formulation starts from a more general description of structural damping, including both a general tridiagonal structure, with a higher number of damping coefficients to be identified, “General damping”, and the special case of “Rayleigh damping”, and arrives at an identification procedure leading to superior performance, also for the basic damping case previously analysed in [15], thus achieving a more effective and general validity.

For the present investigation on the Full Dynamic Compound Inverse Method (FDCIM) approach and the description of its framing in the pertinent literature, and for the main technical steps of the algorithm, this paper highly relies on what extensively presented in [15], and references quoted and discussed therein. Due credit to the specific original contributions on the FDCIM approach is instead reported below, for the sake of consistency and self-containedness.

In the branch of Operational Modal Analysis (OMA) methods, the use of earthquake input with specifically developed algorithms has been attempted by only a few works, either in the Time Domain (e.g. [4, 16, 18]) or in the Frequency Domain (e.g. [10,11,12,13,14]). In such Earthquake Engineering research context, the FDCIM approach goes ahead, towards the Time Domain OMA identification of modal parameters, element-level structural features and seismic base excitation. Focusing on the element-level identification and input estimation techniques, the fundamental works that have inspired the present FDCIM technique are briefly recalled below.

The first work that shall be delineated as an ancestor of Dynamic Compound methods came in 1994 from Wang and Haldar [20], which proposed an iterative Time Domain method founded on Finite Elements, for the stiffness and damping matrices element-level estimation and input force identification. In 1997, Haldar et al. [5] improved that previous algorithm, to work with limited observations, i.e. with structures where only a few DoFs are monitored.

In 2000, Li and Chen [7] proposed a method for identifying the structural parameters and inverse input time history, by introducing some computational improvements on their earlier work, Li and Chen [6]. Further refinements were implemented also in 2002, Chen et al. [1], where they used a combination of iterative Least-Squares and of a Statistical Average technique. They named the method as Dynamic Compound Inverse Method (DCIM), a main landmark in the present context. In 2003, Li and Chen [8] published in Computational Mechanics an improved Statistical Average technique, while in 2004 Chen and Li [2], again in Computational Mechanics, proposed another DCIM implementation, which adopted Rayleigh damping ${\mathbf {C}}=\alpha {\mathbf {M}}+\beta {\mathbf {K}}$, instead of generic viscous damping used until then. They developed a two-stage iterative method to bypass the difficulties added by the Rayleigh damping assumption in solving the resulting non-linear identification problem, due to the coupling between the unknown $\alpha$ and $\beta$ damping coefficients and the ${\mathbf {K}}$ stiffness matrix parameters (mass matrix ${\mathbf {M}}$ was assumed to be known).

In 2004, Ling and Haldar [9] developed a further approach which was also able to deal with Rayleigh damping, based on a modified Iterative Least-Squares method, which adopted Taylor series approximations to transform the non-linear set of Rayleigh-damped identification equations into a set of linear equations. Differently from the previous works, in Li and Chen [8] and Ling and Haldar [9] no earthquake excitations were considered.

Among the seminal DCIM methods above, a common critical point was that of assuming the knowledge of the mass matrix, in its structure and its single parameters. In this respect, the innovative Full Dynamic Compound Inverse Method (FDCIM) [15] was proposed by the authors, in continuity on Computational Mechanics, in order to alleviate the severe hypotheses of the earlier techniques, as that of the mandatory knowledge of the full mass matrix, and also by systematically operating with earthquake-induced structural response signals linked to unknown seismic excitation. That with the purpose of providing an effective identification tool of modal parameters, element-level structural properties and seismic input. So, the present FDCIM approach works with the required knowledge of seismic structural response signals only, i.e. accelerations, velocities and displacements.

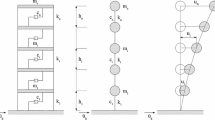
The original FDCIM [15] is based on a two-stage iterative algorithm, working jointly with a Statistical Average technique, a modification process and a parameter projection strategy, which are adopted at each identification iteration to achieve a faster and more reliable convergence. Initial hypotheses affect only the supposed behaviour of the structural matrices, i.e. diagonal mass matrix and tridiagonal symmetric damping and stiffness matrices, where the structural coefficients are coupled to each other. Damping behaviour is treated as viscous, where the damping parameters are considered as lumped between two consecutive floors, in terms of n damping coefficients $c_{i}$, where n is the number of floors, as it is for stiffness coefficients $k_i$.

By relying on the previous FDCIM approach [15], the present work proposes a new implementation that widens and generalizes the earlier FDCIM algorithm, by adopting a more general damping behaviour (in the presentation, associated results will be labelled as FDCIM-2). In this way, each single damping parameter $c_{ij}$ is uncoupled from the remaining ones, by allowing for the analysis and identification of structures characterized by unknown “General damping”. Further, as a particular case, it becomes possible to effectively identify “Rayleigh damping” (${\mathbf {C}} = \alpha {\mathbf {M}} + \beta {\mathbf {K}}$), as it was considered by the earlier DCIM attempts quoted above. This actually constitutes a much challenging case, since it leads to non-linear identification equations in terms of the unknown structural parameters (see [2, 9] and Sect. 3 in the paper). Then, starting from the formulation on General damping, the main focus of the present work moves then to the treatment of Rayleigh damping.

The use of General and Rayleigh damping becomes possible by introducing several dedicated modifications and improvements into the original FDCIM formulation, in terms of different iteration matrices and dimensions, modified vectors of unknown variables, innovative parameter projection technique, novel procedure for Rayleigh damping coefficients estimation, and so on (Sect. 2). Despite the added complexity, the current FDCIM approach still displays all the good properties of the previous one, e.g. the completely deterministic State-Space formulation, the non-required transformation from continuous to discrete time, the non-dependence on the initial conditions adopted for the iteration vectors of the unknowns and the possibility of integration or support to different output-only State-Space parametric Time Domain methods.

Presentation of the paper is organised as follows. Sect. 2 outlines the mathematical model, the governing equations and the theoretical framework of the present FDCIM approach, by focusing on the salient differences from previous FDCIM formulation [15]. The particular case of Rayleigh damping is investigated thoroughly. Section 3 presents a detailed comparison between the present and the earlier FDCIM implementation, with synthetic response data from a benchmark 3-storey frame. Results for estimated modal parameters, element-level features and input earthquake excitation are derived, as a function of the adopted number of signal points. Section 4, by adopting the same benchmark structure, derives comprehensive results on the application of the new FDCIM implementation with noise addition to the response signals; various levels of added noise have been considered, ranging from $0.5\%$ to the very high level of $20\%$. In Sect. 5, further analyses with a realistic 10-storey frame from the literature are produced, again as a function of the adopted number of signal points and of the level of added signal noise. Finally, main conclusions of the whole work are gathered in Sect. 6.

2 Full Dynamic Compound Inverse Method with General and Rayleigh damping

The present implementation follows from [15], where the Full Dynamic Compound Inverse Method (FDCIM) was introduced. There, the model and the algorithm were developed in order to deal with a specific form of viscous damping, as modelled by a peculiar tridiagonal symmetric structure, where damping coefficients $c_{ij}$ were coupled to each other, in terms of n independent inter-floor damping coefficients $c_i$ (see Eq. (2) in [15]). When the damping modelling comes out from this specific definition, the algorithm may encounter increasing problems in achieving reliable estimates, especially as concerning to the identification of the damping matrix and of the modal damping ratios, as it is going to be revealed by the analysis in Sect. 3.

Then, the present original implementation deals with different damping modellings. Specifically, it focuses on a General damping behaviour based on coefficients $c_{ij}$ and, as a particular case, on well-known Rayleigh damping ${\mathbf {C}}=\alpha {\mathbf {M}}+\beta {\mathbf {K}}$ (damping matrix made by a linear combination of mass and stiffness matrices). General damping means that the structure of the damping matrix still continues to be tridiagonal and symmetric, but its each single coefficient $c_{ij}$ is uncoupled from the remaining ones. Then, the particular case of Rayleigh damping relies on unknown coefficients $\alpha$ and $\beta$, which are coupled to the unknown mass and stiffness parameters of matrices ${\mathbf {M}}$ and ${\mathbf {K}}$, respectively. This brings to a set of non-linear identification equations, in terms of the unknown structural parameters. So, the present algorithm is reformulated and reimplemented in order to achieve effective element-level identification and input estimation with structures characterized by such General and Rayleigh damping modellings. The following subsections explain the theoretical framework and the functioning of the present extended FDCIM procedure, by referring just to the differences from the previous implementation [15].

2.1 Basic mathematical model with General and Rayleigh damping

For a linear MDoF shear-type frame under seismic excitation, the motion of the n building’s floors is controlled by a classical system of n second-order time differential equations (Eq. (1) in [15]), i.e. ${\mathbf {M}}\ddot{{\mathbf {u}}}(t)+{\mathbf {C}}\dot{{\mathbf {u}}}(t)+{\mathbf {K}}{\mathbf {u}}(t) = -{\mathbf {M}} \ddot{{\mathbf {u}}}_g(t)$. Terms ${\mathbf {M}}$, ${\mathbf {C}}$ and ${\mathbf {K}} \in {\mathcal {R}}^{n \times n}$ are the mass, damping and stiffness matrices, respectively, ${\mathbf {u}} \in {\mathcal {R}}^{n \times 1}$ is the displacement response vector (in terms of absolute, i.e. relative to the ground, displacements of each floor), while $\dot{{\mathbf {u}}}$ and $\ddot{{\mathbf {u}}}$ are the corresponding velocities and accelerations; the input excitation vector is described by the product between the mass matrix ${\mathbf {M}}$ and the ground acceleration vector $\ddot{{\mathbf {u}}}_g(t)$.

Mass and stiffness matrices ${\mathbf {M}}$ and ${\mathbf {K}}$ take here the classical definitions for shear-type frames (see Eq. (2) in [15]), with a diagonal mass matrix ${\mathbf {M}}$ (with masses $m_i$, associated to each floor $i=1,\ldots ,n$) and a tridiagonal symmetric stiffness matrix ${\mathbf {K}}$ (with lateral column stiffness $k_i$, between floor i and $(i-1)$).

With viscous damping, as treated in [15], damping matrix ${\mathbf {C}}$ shares the same tridiagonal symmetric structure as for matrix ${\mathbf {K}}$, with n damping coefficients $c_i$, leading to a matrix where damping coefficients $c_{ij}$ are coupled to each other. This damping matrix definition is not able to describe more General damping, where the damping characteristics are spread all over the structure, and do not depend only on the lateral column dissipative coefficients between floor i and $(i-1)$. In the present FDCIM algorithm the first expedient to bypass the coupling of the damping coefficients $c_{ij}$ comes from a different writing of damping matrix ${\mathbf {C}}$ for General damping, with an augmented number of damping coefficients:

$$\begin{aligned}&{\mathbf {C}} = \underbrace{\left[ \begin{array}{lllll} c_1+c_2 &{}\quad -c_2 &{}\quad 0 &{}\quad \ldots &{}\quad 0 \\ -c_2 &{}\quad c_2+c_3 &{}\quad -c_3 &{}\quad \ldots &{}\quad 0 \\ 0 &{}\quad -c_3 &{}\quad c_3+c_4 &{}\quad \ldots &{}\quad 0 \\ \vdots &{}\quad \vdots &{}\quad \vdots &{} \quad \ddots &{} \quad \vdots \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad \ldots &{}\quad c_n \end{array}\right] }_{n \; \hbox {parameters} \; c_i} \,[\hbox {Ns/m}] \nonumber \\&\Rightarrow {\mathbf {C}} = \underbrace{\left[ \begin{array}{lllll} c_{11} &{}\quad c_{12} &{}\quad 0 &{}\quad \ldots &{}\quad 0 \\ c_{21} &{}\quad c_{22} &{}\quad c_{23} &{}\quad \ldots &{}\quad 0 \\ 0 &{}\quad c_{32} &{}\quad c_{33} &{}\quad \ldots &{}\quad 0 \\ \vdots &{} \quad \vdots &{} \quad \vdots &{} \quad \ddots &{} \quad \vdots \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad \ldots &{}\quad c_{nn} \end{array}\right] }_{2n-1 \; \hbox {parameters} \; c_{ij}=c_{ji}} \,[\hbox {Ns/m}] \end{aligned}$$

(1)

In this way, the tridiagonal symmetric structure of matrix ${\mathbf {C}}$ with n coefficients $c_{i}$ ($i=1,\ldots ,n$), which is in common with stiffness matrix ${\mathbf {K}}$, may be neglected, on behalf of a more general (still symmetric) tridiagonal structure, where $2n+1$ coefficients $c_{ij}$ ($i,j=1,\ldots ,n$) are generic damping parameters, decoupled from each other and thanks to the symmetry of matrix ${\mathbf {C}}$, decrease to $2n-1$ different coefficients. Thus, this is the first step when dealing with General or Rayleigh damping (or when hypotheses on damping behaviour cannot be made).

The adoption of Rayleigh damping, as a particular case of General damping, is very interesting from the inverse analysis point of view, since it brings to a set of non-linear identification equations in terms of the unknown stiffness and mass parameters. Below, it is brought to light how the ${\mathbf {C}}$ matrix formulation of Eq. (1) can be the adopted to address such an identification issue for Rayleigh damping.

By adopting Rayleigh damping, ${\mathbf {C}} = \alpha {\mathbf {M}} + \beta {\mathbf {K}}$, the n classical equations of motion (Eq. (1) in [15]) may be rewritten as ${{\mathbf {M}} \left[ \ddot{{\mathbf {u}}}(t) + \alpha \dot{{\mathbf {u}}}(t) \right] + {\mathbf {K}} \left[ \beta \dot{{\mathbf {u}}}(t) \!+\! {\mathbf {u}}(t) \right] \!=\! -{\mathbf {M}} \ddot{{\mathbf {u}}}_g(t)}$. Towards FDCIM system identification, structural dynamic responses ${\mathbf {u}}(t)$, $\dot{{\mathbf {u}}}(t)$ and $\ddot{{\mathbf {u}}}(t)$ are the only known quantities. Mass ${\mathbf {M}}$, damping ${\mathbf {C}}$ (with Rayleigh damping coefficients $\alpha$ and $\beta$) and stiffness ${\mathbf {K}}$ matrices and seismic ground acceleration ${\ddot{u}}_g(t)$ are the unknown variables to be identified. By following the theoretical background of FDCIM [15], the two basic identification equations for Rayleigh damping may be written as:

$$\begin{aligned}&{\left( \alpha {\mathbf {M}}+\beta {\mathbf {K}} \right) \dot{{\mathbf {u}}}(t)+{\mathbf {K}}{\mathbf {u}}(t) = -{\mathbf {M}}\Big (\ddot{{\mathbf {u}}}(t)+\ddot{{\mathbf {u}}}_g(t)\Big )} \end{aligned}$$

(2)

$$\begin{aligned}&{{\mathbf {M}}^{-1}\Big [\left( \alpha {\mathbf {M}}+\beta {\mathbf {K}} \right) \dot{{\mathbf {u}}}(t)+{\mathbf {K}}{\mathbf {u}}(t)\Big ] = -\ddot{{\mathbf {u}}}(t)-\ddot{{\mathbf {u}}}_g(t)} \end{aligned}$$

(3)

where the unknown mass matrix ${\mathbf {M}}$ can always be inverted, since it is taken as a diagonal, non-singular matrix. Equations (2) and (3) constitute a set of non-linear identification equations in terms of the unknown structural parameters, since unknown coefficients $\alpha$ and $\beta$ are strictly coupled to the unknown stiffness and mass terms in matrices ${\mathbf {K}}$ and ${\mathbf {M}}$, respectively.

The identification problem based on Eqs. (2) and (3) is quite difficult to be handled by the FDCIM (and, in general, by DCIM techniques). Therefore, the general formulation below is adopted. In this way, Rayleigh damping is treated as a special case of General damping, with Rayleigh damping coefficients that may be then estimated as outlined in following Sect. 2.3.

The expedient to bypass the set of non-linear identification Eqs. (2)–(3) comes from the different writing of damping matrix ${\mathbf {C}}$, earlier exposed in Eq. (1). Accordingly, Eqs. (2) and (3) may be brought back to the definitions made in the original FDCIM algorithm (Eqs. (5) and (6) in [15]), which constitute the basic concatenated relations on which the recursive FDCIM method is built.

By following the treatment developed in [15], subsequent steps may be originally adapted and modified in order to define the equations of the two identification stages in case of General damping or Rayleigh damping. Then, Eq. (2), by recalling Eq. (5) in [15]—the origin of the first stage of the FDCIM identification method—may be rewritten from Eq. (10) in [15] as:

$$\begin{aligned} {{\mathbf {H}}_{ck}(t)\,\varvec{\theta }_{ck}}= & {} {\mathbf {P}}_{ck}(t) \nonumber \\\Rightarrow & {} { \underbrace{\begin{bmatrix} {\mathbf {H}}^1_{ck}(t)&\;\; {\mathbf {0}}_{n \times (3n-1)} \\ {\mathbf {0}}_{n \times n}&\;\; {\mathbf {H}}^2_{ck}(t) \end{bmatrix}}_{2n \times (4n-1)} \underbrace{\begin{Bmatrix} \varvec{\theta }^1_{ck} \\ \varvec{\theta }^2_{ck} \end{Bmatrix}}_{(4n-1) \times 1}} = \underbrace{\begin{Bmatrix} {\mathbf {P}}^1_{ck}(t) \\ {\mathbf {P}}^2_{ck}(t) \end{Bmatrix}}_{2n \times 1} \nonumber \\ \end{aligned}$$

(4)

where zero matrices take dimensions as suggested by the related subscripts. In earlier Eq. (4), matrix ${\mathbf {H}}_{ck}(t)$ contains the velocity and displacement responses (knowns, input for the FDCIM), vector $\varvec{\theta }_{ck}$ contains all $c_{ij}$ damping and $k_{i}$ stiffness parameters (unknowns, to be identified) and vector ${\mathbf {P}}_{ck}(t)$ contains both velocity and acceleration responses (knowns), $m_{i}$ mass terms and input ground motion excitation ${\ddot{u}}_g(t)$ (unknowns, to be identified). At a generic time instant $t=t_i$, $i=1,\ldots ,L$, being L the length of the recorded input signal, ${\mathbf {H}}^1_{ck}(t_i)$, $\varvec{\theta }^1_{ck}$, ${\mathbf {P}}^1_{ck}(t_i)$ and ${\mathbf {P}}^2_{ck}(t_i)$ elements can be expressed as reported by Eqs. (13) and (14c) in [15], while ${\mathbf {H}}^2_{ck}(t_i)$ and $\varvec{\theta }^2_{ck}$ take a different expression, which may be outlined as:

$$\begin{aligned} {\mathbf {H}^2_{ck}(t_i)}&=\underbrace{\left[ \begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} \dot{u}_1 &{} \dot{u}_2 &{} 0 &{} 0 &{} 0 &{} \cdots &{} 0 &{} \;\;\; {u}_1 &{} {u}_1-{u}_2 &{} 0 &{} \cdots \; &{} 0 \\ 0 &{} \dot{u}_1 &{} \dot{u}_2 &{} \dot{u}_3 &{} 0 &{} \cdots &{} 0 &{} \;\;\; 0 &{} {u}_2-{u}_1 &{} {u}_2-{u}_3\; &{} \cdots \; &{} 0 \\ 0 &{} 0 &{} 0 &{} \dot{u}_2 &{} \dot{u}_3 &{} \cdots &{} 0 &{} \;\;\; 0 &{} 0 &{} {u}_3-{u}_2\; &{} \cdots \; &{} 0 \\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots &{} \;\;\; \vdots &{} \vdots &{} \vdots &{} \ddots \; &{} \vdots \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \cdots &{} \dot{u}_n &{} \;\;\; 0 &{} 0 &{} 0 &{} \cdots \; &{} {u}_n\!-{u}_{n-1} \end{array}\right] }_{n \times (3n - 1)} \end{aligned}$$

(5a)

$$\begin{aligned} {\varvec{\theta }^2_{ck}}&={\lbrace \,\underbrace{c_{11}\;c_{12}\;c_{22}\;\ldots \;c_{ij}\;\ldots \;c_{nn},\,k_{1}\;k_{2}\;k_{3}\;\ldots \;k_{i}\;\ldots \;k_{n}}_{1 \times (3n-1)}\,\rbrace ^\mathrm {T}} \end{aligned}$$

(5b)

The definitions of terms contained in Eq. (4) may be expressed by collecting all the sampling time instants, i.e. as ${\mathbf {H}}_{ck}\,\varvec{\theta }_{ck} = {\mathbf {P}}_{ck}$ (Eq. (11) in [15]), where full matrix components now have dimensions ${\mathbf {H}}_{ck} \in {\mathcal {R}}^{(L \times 2n) \times (4n-1)}$, $\varvec{\theta }_{ck} \in {\mathcal {R}}^{(4n-1) \times 1}$ and ${\mathbf {P}}_{ck} \in {\mathcal {R}}^{(L \times 2n) \times 1}$. Then, the ${\mathbf {H}}_{ck}$ and ${\mathbf {P}}_{ck}$ matrices take the definitions in Eqs. (12a) and (12c) in [15], while unknown vector $\varvec{\theta }_{ck} \in {\mathcal {R}}^{(4n-1) \times 1}$ is now defined by n ones, $2n-1$ coefficients $c_{ij}$ and n coefficients $k_i$.

In the end, the unknown parameters of vector $\varvec{\theta }_{ck}$ may be estimated via Least-Squares, on the latter full matrix definitions, as first outlined in [15] (see Eq. (15) there).

In a similar way, the second identification stage (Sect. 2.2) can be deduced from Eq. (3), as outlined in [15], and allows to estimate the second unknown parameter vector $\varvec{\theta }_{m} \in {\mathcal {R}}^{2n \times 1}$, which contains the inverse of the $m_i$ mass parameters. See Eqs. (16)–(21) in [15] for more details.

The so-formulated identification problem is not one of a simple solution, since the unknown parameters are contained not only in the $\varvec{\theta }_{ck}$ and $\varvec{\theta }_{m}$ vectors, but also in the ${\mathbf {P}}_{ck}$, ${\mathbf {H}}_{m}$ and ${\mathbf {P}}_{m}$ matrices. Obviously, the price to be paid for the possibility of identifying also Generally-damped and Rayleigh-damped systems is the increase of the number of unknowns from 3n to $4n-1$ and $4n+1$, respectively. Besides, convergence is guaranteed and results turn out to be very effective, as it is going to be presented in Sects. 3–5. Then, the $4n-1$ unknown structural parameters (which becomes $4n+1$ in case of Rayleigh damping, with the additional $\alpha$ and $\beta$ unknown Rayleigh damping coefficients) and the unknown input ground motion signal may be identified by the present original modification of the two-stage iterative algorithm of the FDCIM in [15]. This is treated next.

2.2 Two-stage identification algorithm with general and Rayleigh damping

Through a consistent modification of the seminal two-stage iterative Least-Squares (LS) algorithm [15], the identification estimates may be extracted from the knowledge of the acquired building structural responses only, i.e. accelerations, velocities and displacements (if only acceleration responses would be known, velocities and displacements may be integrated numerically, as done in Concha et al. [3]).

As it concerns the first stage of identification, which allows for the realization of stiffness and damping parameters, the present FDCIM novelty is constituted by the innovative parameter projection technique adopted after the estimation of the damping and stiffness parameters at iteration 1. This step is different from that in [15] (Step 1.9), and it becomes necessary to achieve strictly-positive estimates of some selected $\big ({^{1}{\varvec{\theta }_{ck}}}\big )_{ij}$ parameters, without the need of solving constrained LS problems. This because the diagonal $c_{ij}$ terms and all the $k_{ij}$ terms need to be positive, while non-diagonal terms $c_{ij}$ are free to assume their own signs and values:

$$\begin{aligned}&\big ({^{1}{\varvec{\theta }_{ck}}}\big )_{ij}=\nonumber \\&\quad = {\left\{ \begin{array}{ll} \mathrm {sgn}\Big [\big ({^{1}{\varvec{\theta }_{ck}}}\big )_{ij}\Big ]\cdot \big ({^{1}{\varvec{\theta }_{ck}}}\big )_{ij} \;\;\; &{}\text {for} \;\, \big ({^{1}{\varvec{\theta }_{ck}}}\big )_{ij}=c_{ij},\; \text {if} \;\, i=j \\ \big ({^{1}{\varvec{\theta }_{ck}}}\big )_{ij} \;\;\; &{}\text {for} \;\, \big ({^{1}{\varvec{\theta }_{ck}}}\big )_{ij}=c_{ij},\; \text {if} \;\, i \ne j \\ \mathrm {sgn}\Big [\big ({^{1}{\varvec{\theta }_{ck}}}\big )_{ij}\Big ]\cdot \big ({^{1}{\varvec{\theta }_{ck}}}\big )_{ij} \;\;\; &{}\text {for} \;\, \big ({^{1}{\varvec{\theta }_{ck}}}\big )_{ij}=k_{ij},\; \forall i,j = 1,\ldots ,n \end{array}\right. }\nonumber \\ \end{aligned}$$

(6)

where $\mathrm {sgn}[\ldots ]$ is the sign function, i.e. the odd function which extracts the sign of its argument.

Then, as it concerns the second stage of identification, which allows for the realization of the mass parameters, computational steps do not require variations from the original FDCIM version, including for the $\varepsilon _{\theta }$ and $\varepsilon _{g}$ convergence tolerances. Refer to [15] for more details.

Once convergence is reached, the final $\varvec{\theta }_{ck}$ and $\varvec{\theta }_{m}$ estimates return a realization of state matrix ${\mathbf {A}}$ and output matrix ${\mathbf {C}}_0$ (Eq. (4) in [15]), together with a realization of final mass, damping and stiffness matrices. The averaged input vector $\bar{{\ddot{u}}}_{g,m}(t)$ obtained from Step 2.5 in [15] represents the estimated time history of the ground motion excitation. See Steps in [15] for further deepening. Finally, Rayleigh damping coefficients $\alpha$ and $\beta$ may be estimated as outlined in following Sect. 2.3.

2.3 Estimation of Rayleigh damping coefficients

After the computation of the final $\varvec{\theta }_{ck}$ and $\varvec{\theta }_{m}$ vectors, i.e. of the final mass, damping and stiffness matrices, it is possible to estimate the Rayleigh damping coefficients via the following original procedure. The following important comments apply:

• Notice that the present procedure may be applied not only to specific Rayleigh-damped systems, as a particular case of General damping, but also to systems characterized by General damping itself, as discussed in Sect. 2.1.

• Thus, for the broader case of General damping, the present procedure will return the best possible estimate of the $\alpha$ and $\beta$ Rayleigh damping coefficients related to the estimated modal and structural properties of the system under investigation.

First, starting from the realizations of mass ${\mathbf {M}}$, damping ${\mathbf {C}}$ and stiffness ${\mathbf {K}}$ matrices, it is possible to calculate the modal properties, i.e. natural frequencies $f_i$, mode shapes $\varvec{\phi }_i$ and modal damping ratios $\zeta _i$, as usually done in classical modal analysis.

By knowing eigenvector matrix $\varvec{\Phi }$, gathering all $i=1,\ldots ,n$ eigenvectors $\varvec{\phi }_i$ as columns, modal mass ${\mathcal {M}}=\varvec{\Phi }^\mathrm {T}{\mathbf {M}}\varvec{\Phi }=\mathrm {diag}[\textit{m}_i]$, modal damping ${\mathcal {C}}=\varvec{\Phi }^\mathrm {T}{\mathbf {C}}\varvec{\Phi }=\mathrm {diag}[\textit{c}_i]$ and modal stiffness ${\mathcal {K}}=\varvec{\Phi }^\mathrm {T}{\mathbf {K}}\varvec{\Phi }=\mathrm {diag}[\textit{k}_i]$ matrices can be classically calculated for the estimated system.

So, by starting from the definition of Rayleigh damping coefficients $\alpha$ and $\beta$ in modal coordinates, i.e. ${\mathcal {C}} = \alpha {\mathcal {M}} + \beta {\mathcal {K}}$, the following relations may be obtained:

$$\begin{aligned}&{\varvec{z}}_{i,j} = \begin{bmatrix} \alpha _{\,i,j} \\ \beta _{\,i,j} \end{bmatrix} = \begin{bmatrix} \textit{m}_i&\textit{k}_i \\ \textit{m}_j&\textit{k}_j \end{bmatrix}^{-1} \cdot \begin{bmatrix} \textit{c}_i \\ \textit{c}_j \end{bmatrix}, \;\;\; \forall \, i,j = 1, \ldots , n \nonumber \\&\quad \Rightarrow {\mathcal {Z}} = \begin{bmatrix} {\varvec{z}}_{1,2}&\;\;{\varvec{z}}_{1,3}&\;\;{\varvec{z}}_{2,2}&\;\;\ldots&\;\;{\varvec{z}}_{i,j}&\;\;\ldots&\;\;{\varvec{z}}_{n,n} \end{bmatrix} \end{aligned}$$

(7)

where the solutions of the previous linear system, made by the calculated modal mass, damping and stiffness as known terms, are the unknown Rayleigh coefficients, for every possible combination of i and j indexes. Then, matrix ${\mathcal {Z}} \in {\mathcal {R}}^{2 \times r}$ collects each of the r ${\varvec{z}}_{i,j}$, being r the number of possible combinations without repetitions of indexes i and j, which can be calculated as:

$$\begin{aligned} r = {\mathscr {C}}_{n,2} = \frac{n!}{2! (n-2)!} \end{aligned}$$

(8)

Finally, the estimation of the $\alpha$ and $\beta$ coefficients may be evaluated as the mean value of such r collected parameters:

$$\begin{aligned} \alpha = \frac{1}{r} \sum ^{r}_{i,j=1} {\alpha }_{i,j}, \;\;\; \beta = \frac{1}{r} \sum ^{r}_{i,j=1} {\beta }_{i,j} \end{aligned}$$

(9)

With reference to the analysed case, this type of estimation of the Rayleigh damping coefficients demonstrated to be very powerful, as it is going to be shown in the results produced in forthcoming Sects. 3–5.

2.4 Element-level identification procedure

By adopting the FDCIM approach, estimates of modal parameters, of structural (mass, damping and stiffness) matrices at the element-level, of Rayleigh damping coefficients and of input ground motion excitation can be achieved. The mass, damping and stiffness matrices, as well as the identified State-Space matrices, represent a realization of the system under investigation.

Then, the modal properties of the system (natural frequencies, mode shapes and modal damping ratios) can be obtained in a straight-forward manner from the estimated realizations of the State-Space matrices or, equivalently, of mass, damping and stiffness matrices.

Finally, as first discussed in [15], it is possible to accurately identify the element-level values of the structural parameters. This can be done since from the FDCIM procedure matrices ${\mathbf {M}}$, ${\mathbf {C}}$ and ${\mathbf {K}}$ are always identified correctly, unless for a Fixing Factor, i.e. a real positive multiplying parameter $\delta = P_{real}/P_{est}$, where $P_{real}$ is a known (or estimated) quantity from the real building and $P_{est}$ is a quantity from the estimated model. For instance, examples of $P_i$ comparison values may be the total mass of the building under investigation, or any other single parameter of one of three matrices ${\mathbf {M}}$, ${\mathbf {C}}$ and ${\mathbf {K}}$ (namely any single parameter among $m_i$, $c_{ij}$ and $k_i$).

Then, Fixing Factor $\delta$ allows to rescale the estimated elements, since from the FDCIM application the proper orders of magnitude between each element are preserved, so different realizations of structural matrices differ only for an unknown proportionality factor. In Sects. 3–5, as in [15], $P= m_{tot}$ has been adopted as a rescaling parameter, since it appears as a convenient parameter that may be roughly judged in practical cases.

3 First identification outcomes and comparison with reference FDCIM

The developed Full Dynamic Compound Inverse Method (FDCIM), that is now able to work also with General damping and Rayleigh damping, is presented through first numerical examples. This in order to validate the algorithm and to demonstrate the improvements of the present wider FDCIM version, with respect to earlier attempt [15].

The adopted example is a three-storey shear-type frame, taken from the work of Chen et al. [1] and revisited here to take into account Rayleigh damping, by setting the first two modal damping ratios equal to $\zeta _1=1\%$ and $\zeta _2=1.25\%$. Then, the third modal damping ratio is taken equal to $\zeta _3=2.70\%$, resulting into $\alpha = 0.23050$ and $\beta = 0.0004321$ Rayleigh damping coefficients. Accordingly, the $c_{ij}$ damping coefficients are 2260.24, $-136.22$, 264.79, $-68.108$ and $108.48 \times 10^3\,\mathrm {kN}\,\mathrm {s}/\mathrm {m}$ for $c_{11}$, $c_{12}$, $c_{22}$, $c_{23}$ and $c_{33}$, respectively.

Remaining structural and modal characteristics remain unchanged, by referring to Tables 1 and 2 in [15]. The synthetic earthquake-induced response signals, input channels for the FDCIM identification algorithm, are generated from direct time integration of the equations of motion, via classical Newmark’s method. The adopted earthquake input excitation, namely the El Centro 1940 earthquake, has been adopted also in the earlier FDCIM work [15] (see Table 3 in [15]). The El Centro 1940 earthquake shows a duration of $40\,\mathrm {s}$, with $100\,\mathrm {Hz}$ frequency sampling, for a total number of 4000 signal points.

Table 1 Comparison between estimates from previous (FDCIM) and present (FDCIM-2) identified natural frequencies $f_i$ and modal damping ratios $\zeta _i$ (calculated Modal Assurance Criterion indexes are all unitary), three-storey frame, 50 and 1000 adopted points; $m_{tot}$ Fixing Factor parameter; Rayleigh damping; El Centro earthquake

Table 2 Comparison between estimates from previous (FDCIM) and present (FDCIM-2) identified mass $m_i$, damping $c_i$ and stiffness $k_i$ parameters, Rayleigh damping coefficients $\alpha$ and $\beta$, PGA and RMS, three-storey frame, 50 and 1000 adopted points; $m_{tot}$ Fixing Factor parameter; Rayleigh damping; El Centro earthquake

Fig. 1

Comparison between absolute percentage deviations of estimates from previous (FDCIM) and present (FDCIM-2), identified natural frequencies $f_i$ and modal damping ratios $\zeta _i$ as a function of adopted number of points, three-storey frame; $m_{tot}$ Fixing Factor parameter; Rayleigh damping; El Centro earthquake

As previously detected in [15], also the present FDCIM implementation is independent from the adopted initial values of iteration vectors ${^{0}{\varvec{\theta }_{ck}}}$ and ${^{0}{\varvec{\theta }_{m}}}$ and from chosen Fixing Factor $\delta$. This since no significant differences can be found among the obtained values, in terms of estimated values, number of iterations and computational time. Then, they have been selected as ${^{0}{\varvec{\theta }_{ck}}}= \lbrace 1\;1\;1\;\ldots \;1 \rbrace ^\mathrm {T}$, ${^{0}{\varvec{\theta }_{m}}} = \lbrace 1\;1\;1\;\ldots \;1 \rbrace ^\mathrm {T}$ and $\delta = P_{real}/P_{est} = m_{tot,real}/m_{tot,est}$.

For the analyses and comparisons with the previous FDCIM implementation, different numbers of signal points are used. By starting from the initial time instant, attempts from a minimum of 50 points (time duration of $0.5\,\mathrm {s}$), to a maximum of 4000 points ($40\,\mathrm {s}$ full signal) have been performed. Iteration tolerance levels are set to $\varepsilon _{\theta }=10^{-6}$ and $\varepsilon _{g}=10^{-4}$.

Sample comparisons between previous and present FDCIM are reported in Tables 1 and 2, for the 50 and 1000 signal points cases. Target values, identified values and absolute percentage deviations (calculated as $\Delta \mathrm {Par} = |\mathrm {Par}_{i,id}-\mathrm {Par}_{i,targ}|/\mathrm {Par}_{i,targ}\cdot 100$ for each $\mathrm {Par}$ parameter) are shown for natural frequencies $f_i$ and modal damping ratios $\zeta _i$ (MAC indexes are always unitary), mass $m_i$, damping $c_{ij}$ and stiffness $k_i$ element-level features, $\alpha$ and $\beta$ Rayleigh coefficients, and Peak Ground Acceleration (PGA) and Root Mean Square (RMS) of the estimated seismic excitation. Identified parameters significantly improve from FDCIM to FDCIM-2, especially as concerning to the modal damping ratios, damping parameters and Rayleigh coefficients. In all the cases and instances, ameliorations are at least of one order of magnitude.

Then, a global comparison among all FDCIM and FDCIM-2 analysed cases is reported in Figs. 1, 2, 3 and 4. Absolute percentage deviations are shown in logarithmic scale, for each considered parameter and length of the signal (50, 100, 200, 500, 1000, 2000 and 4000 points).

By going in order, estimated frequencies and modal damping ratios show maximum percentage deviations of 0.058 and $35.79\%$ for FDCIM (both 200 p.), while these become only 0.0021 and $0.0193\%$ (50 and 100 p.) for FDCIM-2. Mode shapes are always very well identified, since they always lead to unitary Modal Assurance Criterion (MAC) indexes; consequently, they are not reported here.

For the estimated element-level features, maximum deviations are: $0.1800\%$ (FDCIM, 200 p.) and $0.0043\%$ (FDCIM-2, 50 p.) for $m_i$; $53.77\%$ (FDCIM, 100 p.) and $0.0156\%$ (FDCIM-2, 50 p.) for $c_{ij}$; $0.1098\%$ (FDCIM, 50 p.) and $0.0041\%$ (FDCIM-2, 50 p.) for $k_{i}$. Maximum deviations for the Rayleigh damping coefficients are: $22.38\%$ (FDCIM, 200 p.) and $0.0235\%$ (FDCIM-2, 100 p.) for $\alpha$; $12.22\%$ (FDCIM, 50 p.) and $0.0012\%$ (FDCIM-2, 50 p.) for $\beta$. Finally, maximum deviations for the estimated earthquake input excitation are: $0.2363\%$ (FDCIM, 100 p.) and $0.0061\%$ (FDCIM-2, 100 p.) for PGA; $0.3527\%$ (FDCIM, 1000 p.) and $0.0065\%$ (FDCIM-2, 100 p.) for RMS; seismic time histories are practically indistinguishable from the source input.

Then, some final remarks on the achieved estimates follow. For both methods, modal damping ratios deviations are greater than for natural frequency ones (see Fig. 1). The same can be seen in Fig. 2, where the stiffness parameters offer the best performance with respect to the mass and damping coefficients, in the order. In Fig. 3, Rayleigh damping (${\mathbf {C}}=\alpha {\mathbf {M}} + \beta {\mathbf {K}}$) coefficient $\beta$ offers a much better performance, as compared to coefficient $\alpha$. Finally, PGA and RMS perform more or less equally, for both methods, as confirmed by the results in Fig. 4. In Figs. 3 and 4, results for FDCIM-2 actually appear really striking.

Fig. 2

Comparison between absolute percentage deviations of estimates from previous (FDCIM) and present (FDCIM-2), identified mass $m_i$, damping $c_i$ and stiffness $k_i$ parameters as a function of adopted number of points, three-storey frame; $m_{tot}$ Fixing Factor parameter; Rayleigh damping; El Centro earthquake

Fig. 3

Comparison between absolute percentage deviations of estimates from previous (FDCIM) and present (FDCIM-2), identified $\alpha$ and $\beta$ Rayleigh damping coefficients as a function of adopted number of points, three-storey frame; $m_{tot}$ Fixing Factor parameter; Rayleigh damping; El Centro earthquake

All the achieved estimates and results demonstrate the wideness and goodness of the present FDCIM method and its superiority with respect to the previous one by operating with systems characterized by Rayleigh damping behaviour. Estimates are always very effective, for each parameter under target, by showing very limited percentage deviations. This validates and corroborates the present more general FDCIM proposal. In the following sections, further examples with more complex structures and with signal noise addition are proposed too, in order to further demonstrate the higher performance achieved by the present FDCIM-2 implementation.

Fig. 4

Comparison between absolute percentage deviations of estimates from previous (FDCIM) and present (FDCIM-2), identified input ground motion excitation in terms of PGA and RMS as a function of adopted number of points, three-storey frame; $m_{tot}$ Fixing Factor parameter; Rayleigh damping; El Centro earthquake

Fig. 5

FDCIM-2; Percentage deviations of identified natural frequencies $f_i$ and modal damping ratios $\zeta _i$; three-storey frame, no-noise and noise-corrupted cases; 4000 points; $m_{tot}$ Fixing Factor parameter; Rayleigh damping; El Centro earthquake

Fig. 6

FDCIM-2; Percentage deviations of identified mass $m_i$, damping $c_i$ and stiffness $k_i$ parameters; three-storey frame, no-noise and noise-corrupted cases; 4000 points; $m_{tot}$ Fixing Factor parameter; Rayleigh damping; El Centro earthquake

4 Addition of noise to the earthquake-induced structural response signals

In order to further validate the present FDCIM algorithm and to approach increasingly realistic conditions, several analyses with the addition of noise to the original earthquake-induced synthetic response signals are now considered. Every acquisition channel, in terms of displacements, velocities and accelerations, takes the addition of a zero-mean Gaussian white noise as a percentage of the Root Mean Square ratio between the noise process and the original response recording. Starting from a level of $0.5\%$, the noise has considered increasing levels of 1, 3, $5\%$ and then the very challenging ones of 10 and $20\%$.

As done in previous Sect. 3, the absolute percentage deviations (in logarithmic scale) for all the analysed noise cases, for each considered parameter, are summarized in Figs. 5, 6 and 7. By recalling the achieved results, estimated frequencies and modal damping ratios show maximum percentage deviations of $1.96\%$ ($20\%$ noise) and $76.26\%$ ($20\%$ noise), respectively. This last rather high deviation shall be considered as an outlier, since the remaining estimates show much smaller deviations. As before, mode shapes show always unitary MAC indexes, for all the adopted noise cases, and are not reported.

Fig. 7

FDCIM-2; Percentage deviations of identified $\alpha$ and $\beta$ Rayleigh damping coefficients and estimated input ground motion excitation in terms of PGA and RMS; three-storey frame, no-noise and noise-corrupted cases; 4000 points; $m_{tot}$ Fixing Factor parameter; Rayleigh damping; El Centro earthquake

Table 3 Structural features of the adopted ten-storey shear-type frame (adapted from Villaverde and Koyama [19])

Table 4 Modal characteristics of the adopted ten-storey shear-type frame (adapted from Villaverde and Koyama [19])

As it concerns to the estimated element-level parameters, maximum deviations shows to be: $2.51\%$ ($20\%$ noise) for $m_i$; $88.82\%$ ($10\%$ noise) for $c_{ij}$; $6.45\%$ ($20\%$ noise) for $k_{i}$. For the Rayleigh damping coefficients, maximum deviations are $57.61\%$ ($20\%$ noise) and $7.34\%$ ($10\%$ noise) for the $\alpha$ and $\beta$ parameters, respectively. Finally, for the estimated earthquake input base excitation, the maximum deviations show to be $44.22\%$ ($20\%$ noise) for PGA and $11.97\%$ ($20\%$ noise) for RMS. By looking at the figures, it is possible to appreciate that the higher deviations can certainly be considered as outliers, thanks to the noticeably smaller deviations related to the remaining estimates. Thus, despite for the heavy added noise level in some cases (up to $20\%$), FDCIM identification keeps very much effective.

As before, by looking at Fig. 5 it is possible to see that deviations are greater for the modal damping ratios than for the natural frequencies. The same happens in Fig. 6, where the stiffness and mass parameters show to be comparable in terms of deviations, while the damping coefficients are the less accurate identified features. Then, in Fig. 7, Rayleigh damping (${\mathbf {C}} = \alpha {\mathbf {M}} + \beta {\mathbf {K}}$) parameter $\beta$ offers again a better performance than for coefficient $\alpha$, which is affected by higher deviations, especially for noise cases from 5 up to $20\%$. In the same figure, also PGA and RMS deviations are reported; they perform more or less equally, except for the 10 and $20\%$ cases, where $\Delta$RMS shows to be higher than for $\Delta$PGA.

Again, as demonstrated also in Sect. 3, all the achieved estimates prove the reliability and effectiveness of the present FDCIM algorithm, also with noise-corrupted cases.

5 FDCIM identification of a realistic ten-storey frame building

In this section, the present FDCIM algorithm is adopted towards modal dynamic identification, element-level characterization and input ground motion estimation of a realistic ten-storey shear-type frame taken and adapted (for damping modelling) from Villaverde and Koyama [19], whose characteristics are summarized in Table 3.

The present ten-storey frame displays all its natural frequencies within a $5\,\mathrm {Hz}$ interval, i.e. very close modes, that are concomitant here with assumed high modal damping ratios, in terms of identification challenge. In Table 4, these modal parameters are summarized, while mode shapes are omitted here for brevity.

The El Centro 1940 earthquake is taken again as base excitation for the performed analyses (see Table 3 in [15]). The initial values of ${^{0}{\varvec{\theta }_{ck}}}$ and ${^{0}{\varvec{\theta }_{m}}}$ vectors are adopted as in the previous analyses in Sects. 3 and 4, jointly with a Fixing Factor $\delta$ set on $m_{tot}$.

Fig. 8

FDCIM-2; Percentage deviations of identified natural frequencies $f_i$ and modal damping ratios $\zeta _i$ as a function of adopted number of points; ten-storey frame; $m_{tot}$ Fixing Factor parameter; Rayleigh damping; El Centro earthquake

Fig. 9

FDCIM-2; Percentage deviations of identified mass $m_i$, damping $c_i$ and stiffness $k_i$ parameters as a function of adopted number of points; ten-storey frame; $m_{tot}$ Fixing Factor parameter; Rayleigh damping; El Centro earthquake

Fig. 10

FDCIM-2; Percentage deviations of identified $\alpha$ and $\beta$ Rayleigh damping coefficients and estimated input ground motion excitation in terms of PGA and RMS as a function of adopted number of points; ten-storey frame; $m_{tot}$ Fixing Factor parameter; Rayleigh damping; El Centro earthquake

As it concerns the performed analysis, these are structured as in the previous sections. Figures 8, 9 and 10 display the absolute deviations of the achievable estimates, in terms of natural frequencies, modal damping ratios, element-level parameters, Rayleigh damping coefficients and PGA and RMS of the estimated input earthquake excitation, as a function of the adopted number of signal points. These are taken from the beginning of the signal, and go from a minimum of 100 points (duration of $1\,\mathrm {s}$) until a maximum of 4000 points (entire signal of $40\,\mathrm {s}$).

Fig. 11

FDCIM-2; Percentage deviations of identified natural frequencies $f_i$ and modal damping ratios $\zeta _i$, no-noise and noise-corrupted cases; ten-storey frame, 4000 points; $m_{tot}$ Fixing Factor parameter; Rayleigh damping; El Centro earthquake

Fig. 12

FDCIM-2; Percentage deviations of identified stiffness $k_i$, damping $c_i$ and mass $m_i$ parameters, no-noise and noise-corrupted cases; ten-storey frame, 4000 points; $m_{tot}$ Fixing Factor parameter; Rayleigh damping; El Centro earthquake

Fig. 13

FDCIM-2; Percentage deviations of identified $\alpha$ and $\beta$ Rayleigh damping coefficients and estimated input ground motion excitation in terms of PGA and RMS, no-noise and noise-corrupted cases; ten-storey frame, 4000 points; $m_{tot}$ Fixing Factor parameter; Rayleigh damping; El Centro earthquake

For the natural frequencies and the modal damping ratios, maximum deviations are $0.0014\%$ (200 p.) and $0.0903\%$ (200 p.), respectively. Mode shapes are always very well estimated, leading to unitary MAC indexes, for every adopted case. For the estimated element-level parameters, the maximum deviations are: $0.0123\%$ (100 p.) for $m_i$, $0.0540\%$ (100 p.) for $c_{ij}$ and $0.0031\%$ (4000 p.) for $k_i$. The required number of iterations is 2492, 1444, 141, 256, 315 and 300 for the 100, 200, 500, 1000, 2000 and 4000 points cases, respectively.

Then, for the Rayleigh damping coefficients, maximum deviations show to be $0.3827\%$ (100 p.) and $0.0141\%$ (100 p.) for $\alpha$ and $\beta$, respectively. Finally, for the estimated earthquake input base excitation, maximum deviations are $0.0012\%$ (200 p.) and $0.0004\%$ (200 p.) for PGA and RMS, respectively. Again, present FDCIM-2 results in Fig. 10 are specifically striking, especially for a number of signal points over 500.

The achieved results confirm that, although the larger number of parameters to be estimated and the increase of complexity of the structure under target, the estimates are still very effective.

5.1 Noise addition

Even here, towards validation purposes and to get closer to realistic scenarios, further attempts with added noise have been performed, devised as already described in Sect. 4.

All the examined noise-corrupted outcomes are reported in Figs. 11, 12 and 13, in terms of achieved absolute deviations of the FDCIM estimates. Maximum natural frequency and modal damping ratio deviations are $0.1714\%$ ($20\%$ noise) and $17.32\%$ ($10\%$ noise), respectively. As before, MAC indexes are always unitary, showing the goodness of the estimated mode shapes.

For the element-level parameters, maximum deviations are $1.4726\%$ for $m_i$ ($20\%$ noise), $4.0662\%$ for $c_{ij}$ ($10\%$ noise) and $1.1415\%$ for $k_i$ ($20\%$ noise). Rayleigh damping coefficients display maximum deviations of $55.94\%$ ($20\%$ noise) and $2.3289\%$ ($10\%$ noise) for the $\alpha$ and $\beta$ parameters, respectively. Finally, PGA and RMS maximum deviations are $13.59\%$ ($20\%$ noise) and $5.9047\%$ ($20\%$ noise), respectively. Results in Fig. 13 are specifically remarkable for noise levels up to $5\%$. Levels of 10 and $20\%$ disrupt more the identification results. So, although the increasing complexity of the structure and the use of heavy noise-corrupted cases, the present FDCIM-2 identification keeps very effective.

6 Conclusions

This work has demonstrated the remarkable effectiveness of the present innovative Full Dynamic Compound Inverse Method (FDCIM), with considerable generalisation and improvement from the original FDCIM implementation in [15], which was conceived to deal only with a specific form of viscous damping. The present implementation, instead, allows for consistent modal parameter identification, element-level structural parameter characterization, damping coefficient determination and input ground motion time history estimation, by adopting General or Rayleigh damping behaviours. The following main outcomes and issues may be summarized:

• The parameter projection strategy has been totally rescheduled, to deal with the new formulations required by the current FDCIM approach and to achieve stronger and faster convergence.

• The estimation of Rayleigh damping coefficients $\alpha$ and $\beta$ becomes now possible, through an innovative, specifically-developed procedure, working with the solution of a pre-determined set of linear systems and of an average technique, bypassing then the problem of a challenging non-linear identification as attempted in previous DCIM works.

• A detailed comparison between the latter and the present FDCIM approaches has been addressed for a benchmark three-storey shear-type frame, as a function of the different adopted number of signal points. Present FDCIM looks definitely superior in working with General or Rayleigh damping behaviours, with respect to the previous implementation, with results that are from one to three orders of magnitude better than those coming from the former version.

• Still on the same three-storey shear-type frame, effectiveness of the FDCIM approach has been definitely proven also with the presence of noise, with levels up to $20\%$ . Maximum deviations are always very limited, by extensively validating the present FDCIM method in getting closer to real earthquake excitation scenarios.

• Then, a realistic ten-storey RC frame from the literature has been considered for further validation. This constitutes a more complex case, characterized by very close modes and heavy damping conditions. Analyses have been performed, as before, as a function of the adopted number of signal points and of the level of added noise. These analyses and the very performing identification results have demonstrated the remarkable effectiveness of the present wider FDCIM implementation.

Attempts with additional complex structures and earthquakes may be the target of further research, jointly with the use of real earthquake-induced structural response signals. Then, studies on the integration or support and comparison of the FDCIM with other parametric Time and Frequency Domain output-only methods may be addressed, too.