A simple triangular finite element for nonlinear thin shells: statics, dynamics and anisotropy

Abstract

This work presents a simple finite element implementation of a geometrically exact and fully nonlinear Kirchhoff–Love shell model. Thus, the kinematics are based on a deformation gradient written in terms of the first- and second-order derivatives of the displacements. The resulting finite element formulation provides $C^1$-continuity using a penalty approach, which penalizes the kinking at the edges of neighboring elements. This approach enables the application of well-known $C^0$-continuous interpolations for the displacements, which leads to a simple finite element formulation, where the only unknowns are the nodal displacements. On the basis of polyconvex strain energy functions, the numerical framework for the simulation of isotropic and anisotropic thin shells is presented. A consistent plane stress condition is incorporated at the constitutive level of the model. A triangular finite element, with a quadratic interpolation for the displacements and a one-point integration for the enforcement of the $C^1$-continuity at the element interfaces leads to a robust shell element. Due to the simple nature of the element, even complex geometries can be meshed easily, which include folded and branched shells. The reliability and flexibility of the element formulation is shown in a couple of numerical examples, including also time dependent boundary value problems. A plane reference configuration is assumed for the shell mid-surface, but initially curved shells can be accomplished if one regards the initial configuration as a stress-free deformed state from the plane position, as done in previous works.

1 Introduction

Shear deformable finite element shell models have been developed and discussed in the last decades extensively, see, e.g., [40, 53, 55, 56] among many others. Their main benefit, compared to shear-rigid deformable approaches, is that these models merely require $C^0$-continuity for the unknown fields. However, shear deformable formulations have certain theoretical and implementational drawbacks. In order to circumvent these inconveniences, several advanced techniques have been developed, like reduced and selective integration [33], assumed natural strain [9, 24] and the enhanced assumed strain [10, 54]. An elegant approach seems to be the use of non-conforming triangular elements, as done in [15]. Despite these special techniques, shear deformable shell models, still may generate poor results for the case of very thin structures, as they appear for example in case of membranes. An alternating approach, with rising popularity, is to follow the rotation-free deformable Kirchhoff–Love model for thin shells. Here, the basic kinematic quantities are expressed in terms of the first- and second-order derivatives of the displacements, which leads to the requirement of a $C^1$-continuous functional space for the numerical implementation. In the last years several Kirchhoff–Love models have been developed and successfully implemented using for example moving least-squares [43], a maximum entropy scheme [35, 36], subdivision surfaces [19, 20], isogeometric analysis [25, 28, 29], generalized moving least-squares within a meshless method [26] and $C^1$ TUBA finite elements [27]. The main drawback of those approaches are the high complexity of the shape functions and the associated difficulty of numerical implementation.

In statics, shear deformable shell model results (also known as Reissner–Mindlin models) should be, in the limit of vanishing thickness, equivalent to those obtained with a shear rigid shell model (Kirchhoff–Love). This can be controversial in presence of singularities, like corners or concentrated loads. Approximate results obtained with the aid of finite elements for the former can present some undesirable stiffening effects known as locking phenomena. This is especially true for simple quadrilateral elements. The Kirchhoff–Love model, in other hand, can be a solution for this problems, but requires $\hbox {C}^1$-continuity, what can be very difficult to achieve by finite elements. In dynamics, both models can differ substantially, particularly for high frequencies, and a deeper investigation is still a demanding task. Our approach combines the simplicity of a quadratic Lagrangian element with a discontinuous enforcing of the $\hbox {C}^1$-continuity, leading to an astonishingly simple, but robust, shell finite element.

The scope of the proposed work is to present a novel approach for the application of the Kirchhoff–Love kinematics, based on the work of [42]. This novel approach enables the use of well known and convenient $C^0$-continuous approximations of the displacements, enforcing the required $C^1$-continuity by a penalty formulation. In this sense, our approach can be regarded as a discontinuous Galerkin method. Following the ideas of [5, 6, 23, 51] we apply polyconvex anisotropic elastic strain energies $\psi$ for the modeling of anisotropic shells. The concept of polyconvexity, introduced by [2, 3] guarantees that the variational functional $\int \psi dV$ to be minimized is sequentially weakly lower semicontinuous (s.w.l.s). In large strain elasticity the existence of minimizers is guaranteed if $\int \psi dV$ is s.w.l.s. and coercive, in this context see, e.g., [17, 21, 34]. An extension of isotropic polyconvex functions to anisotropic polyconvex free energies was firstly proposed by [47, 48], in this context we also refer to [4, 46, 50].

The resulting finite element exhibits great flexibility, which is shown in a couple of numerical examples. A wide range of highly nonlinear applications are covered, using isotropic as well as anisotropic polyconvex strain energies for the calculation of static and dynamic boundary value problems. Due to the triangular structure of the element, powerful mesh generation tools can be easily used, in order to construct unstructured meshes, even for complicate geometries.

Remark on the notation Greek indices range from 1 to 2, while Latin indices range from 1 to 3.

2 Shear-rigid shell kinematics

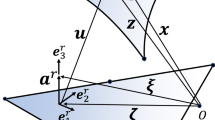
The middle plane of the shell body in the reference configuration is constrained to be plane and is denoted with $\Omega ^r\subset \mathbb {R}^2$ parametrized in $\varvec{\zeta },$ with its boundary $\Gamma ^r=\partial \Omega ^r.$ In the current configuration the middle surface of the shell body is denoted with $\Omega ^r\subset \mathbb {R}^3$ parametrized in ${{\varvec{z}}}.$ Furthermore, the reference volume $V^r$ and thickness $H^r=[-h^r_b,\,h^r_t]$ are introduced, such that the total shell thickness is $h^r=h^r_b+h^r_t.$ The superscripts b and t denote the bottom and the top external surfaces. The orthonormal right-handed coordinate system ${{\varvec{e}}}_i^r$ placed on $\Omega ^r$ is defined. Thus, an arbitrary material point in the reference configuration can be described by

$$\begin{aligned} \varvec{\xi }=\varvec{\zeta }+{{\varvec{a}}}^r, \end{aligned}$$

(1)

where $\varvec{\zeta }=\xi _\alpha {{\varvec{e}}}_\alpha ^r,\, \xi _\alpha \in \Omega ^r$ describes the middle plane and ${{\varvec{a}}}^r=\xi _3 {{\varvec{e}}}^r_3,\, \xi _3 \in H^r,$ is the director, normal to $\Omega ^r.$ In contrast to that, an arbitrary material point in the current configuration is given by

$$\begin{aligned} {{\varvec{x}}}={{\varvec{z}}}+{{\varvec{a}}}, \end{aligned}$$

(2)

where ${{\varvec{a}}}={{\varvec{Q}}}{{\varvec{a}}}^r$ is the current director and ${{\varvec{z}}}=\varvec{\zeta }+{{\varvec{u}}}$ corresponds to the middle surface in the current configuration. The first and second spatial derivatives of ${{\varvec{z}}}$ follow by

$$\begin{aligned} {{\varvec{z}}}_{\alpha }={{\varvec{e}}}_\alpha ^r+{{\varvec{u}}}_{\alpha } \quad \mathrm{and} \quad {{\varvec{z}}}_{\alpha \beta }={{\varvec{u}}}_{\alpha \beta },\quad \mathrm{with} \quad (\bullet )_\alpha =\frac{\partial (\bullet )}{\partial \xi _\alpha }.\nonumber \\ \end{aligned}$$

(3)

The rotation tensor ${{\varvec{Q}}}$ can be defined, due to the Kirchhoff–Love assumption, which states that the director ${{\varvec{a}}}$ remains orthogonal to the middle surface of the shell, by

$$\begin{aligned} {{\varvec{Q}}}={{\varvec{e}}}_i\otimes {{\varvec{e}}}_i^r. \end{aligned}$$

(4)

The local orthogonal system in the current configuration is introduced as

$$\begin{aligned} e_1= & {} \left| |{{\varvec{z}}}_{1}\right| |^{-1} {{\varvec{z}}}_{1}, \nonumber \\ {{\varvec{e}}}_2= & {} {{\varvec{e}}}_3 \times {{\varvec{e}}}_1,\nonumber \\ {{\varvec{e}}}_3= & {} \left| |{{\varvec{z}}}_{1} \times {{\varvec{z}}}_{2}\right| |^{-1}\left( {{\varvec{z}}}_{1} \times {{\varvec{z}}}_{2}\right) . \end{aligned}$$

(5)

It can be noted, that ${{\varvec{e}}}_\alpha$ are tangent to the shell middle surface in the current configuration, while ${{\varvec{e}}}_3$ is orthogonal to the shell middle surface. Note also that only ${{\varvec{e}}}_1$ and ${{\varvec{e}}}_3$ are material, i.e., permanently tangent to same material fibers, while ${{\varvec{e}}}_2$ is not. The nonlinear deformation map $\varvec{\varphi }_t{\text {:}}\,\varvec{\xi }\rightarrow {{\varvec{x}}}$ maps material points at time $t\in \mathbb {R}_+$ from the reference to the current placement. The basic kinematical quantity, the deformation gradient ${{{\varvec{F}}}=\text {Grad}\varvec{\varphi }_t(\varvec{\xi })}$ is given by

$$\begin{aligned} {{\varvec{F}}}= & {} \frac{\partial {{{\varvec{x}}}}}{\partial \varvec{\xi }} = \frac{\partial ({{\varvec{z}}}+{{\varvec{Q}}}{{\varvec{a}}}^r )}{\partial \xi _\alpha } \otimes {{\varvec{e}}}_\alpha ^r \nonumber \\&+\; \frac{\partial ({{\varvec{z}}}+ {{\varvec{Q}}}{{\varvec{a}}}^r )}{\partial \xi _3} \otimes {{\varvec{e}}}_3^r ={{\varvec{f}}}_\alpha \otimes {{\varvec{e}}}_\alpha ^r+{{\varvec{f}}}_3\otimes {{\varvec{e}}}_3^r, \end{aligned}$$

(6)

where the vectors ${{\varvec{f}}}_i$ are introduced for the spatial derivatives as (Fig. 1)

$$\begin{aligned} {{\varvec{f}}}_\alpha = {{\varvec{z}}}_{\alpha }+{{\varvec{Q}}}_{\alpha }{{\varvec{a}}}^r \quad \text {and}\quad {{{\varvec{f}}}_3}= {{\varvec{Q}}}{{\varvec{e}}}_3^r= {{\varvec{e}}}_3. \end{aligned}$$

(7)

Fig. 1

Description of the basic kinematical quantities for a typical finite element in the reference and the actual configuration

The curvature tensors and its corresponding axial curvature vectors are defined as

$$\begin{aligned} {{\varvec{K}}}_\alpha ={{\varvec{Q}}}_{\alpha } {{\varvec{Q}}}^T \quad \text {and} \quad \varvec{\kappa }_\alpha =\text {axial}\left( {{\varvec{K}}}_\alpha \right) , \end{aligned}$$

(8)

which hold ${{\varvec{K}}}_\alpha \varvec{\nu } =\varvec{\kappa }_\alpha \times \varvec{\nu }, \, \forall \, \varvec{\nu }.$ The axial curvature vector can be rewritten as

$$\begin{aligned} \varvec{\kappa }_\alpha =\varvec{\Gamma }_\beta {{\varvec{u}}}_{\beta \alpha }, \end{aligned}$$

(9)

where ${\varvec{\Gamma }}_\alpha$ are introduced by

$$\begin{aligned} \varvec{\Gamma }_1= & {} \left( {{\varvec{e}}}_1\cdot {{\varvec{z}}}_{1}\right) ^{-1}\left[ \text {Skew}\left( {{\varvec{e}}}_1\right) \right. \nonumber \\&\left. -\;\left( {{\varvec{e}}}_1\cdot {{\varvec{z}}}_{2}\right) \left( {{\varvec{e}}}_2\cdot {{\varvec{z}}}_{2}\right) ^{-1}\left( {{\varvec{e}}}_1\otimes {{\varvec{e}}}_3\right) \right] ,\nonumber \\ \varvec{\Gamma }_2= & {} \left( {{\varvec{e}}}_2\cdot {{\varvec{z}}}_{2}\right) ^{-1}\left( {{\varvec{e}}}_1\otimes {{\varvec{e}}}_3\right) , \end{aligned}$$

(10)

with the Skew operator defined for an arbitrary vector $\varvec{\theta }$ as

$$\begin{aligned} \mathrm{Skew}(\varvec{\theta }) = \begin{pmatrix} 0 &{} -{\theta }_3 &{} {\theta }_2 \\ {\theta }_3 &{} 0 &{} -{\theta }_1 \\ -{\theta }_2 &{} {\theta }_1 &{} 0 \end{pmatrix}. \end{aligned}$$

(11)

Thus, we are able to reformulate Eq. (7)$_1$ as

$$\begin{aligned} \begin{array}{rcl} {{\varvec{f}}}_\alpha &{} = &{} {{\varvec{z}}}_{\alpha }+ \varvec{\kappa }_\alpha \times {{\varvec{a}}}. \\ \end{array} \end{aligned}$$

(12)

The Jacobian, which maps a infinitesimal volume element from the reference to the current configuration, can be denoted as

$$\begin{aligned} J={\text {det}}{{{\varvec{F}}}}={{\varvec{f}}}_1\cdot \left( {{\varvec{f}}}_2\times {{\varvec{f}}}_3\right) . \end{aligned}$$

(13)

Another basic kinematic quantity is the cofactor of ${{\varvec{F}}}.$ If the inverse of the deformation gradient exists it can be given as

$$\begin{aligned} {\text {Cof}}{{{\varvec{F}}}}=J{{\varvec{F}}}^{-T}={{\varvec{g}}}_i\otimes {{\varvec{e}}}_i, \end{aligned}$$

(14)

where we use

$$\begin{aligned} {{\varvec{g}}}_1={{\varvec{f}}}_2\times {{\varvec{f}}}_3,\quad {{\varvec{g}}}_2={{\varvec{f}}}_3\times {{\varvec{f}}}_1\quad \text {and}\quad {{\varvec{g}}}_3={{\varvec{f}}}_1\times {{\varvec{f}}}_2,\nonumber \\ \end{aligned}$$

(15)

note that

$$\begin{aligned} {{\varvec{g}}}_i=\frac{1}{2}\varepsilon _{ijk}{{\varvec{f}}}_j\times {{\varvec{f}}}_k \quad \text {with} \quad \varepsilon _{ijk}={{\varvec{e}}}_i\cdot {{\varvec{e}}}_j\times {{\varvec{e}}}_k. \end{aligned}$$

(16)

It is worthwhile to introduce here also the back-rotated deformation gradient as

$$\begin{aligned} \begin{array}{rcl} {{\varvec{F}}}^r &{}=&{} {{\varvec{Q}}}^T{{\varvec{F}}}\\ &{}=&{} {{\varvec{I}}}+\varvec{\gamma }_\alpha ^r\otimes {{\varvec{e}}}_\alpha ^r, \end{array} \end{aligned}$$

(17)

with the back rotated strains

$$\begin{aligned} \varvec{\gamma }_\alpha ^r=\varvec{\eta }_\alpha ^r +\varvec{\kappa }_\alpha ^r\times {{\varvec{a}}}^r. \end{aligned}$$

(18)

Here the cross-sectional generalized back rotated strains are introduced as

$$\begin{aligned} \varvec{\eta }_\alpha ^r={{\varvec{Q}}}^T{{\varvec{z}}}_{\alpha }-{{\varvec{e}}}_\alpha ^r \quad \text {and}\quad \varvec{\kappa }_\alpha ^r=\text {axial}\left( {{\varvec{Q}}}^T{{\varvec{Q}}}_{\alpha }\right) , \end{aligned}$$

(19)

where $\varvec{\eta }_\alpha$ constitute the membrane strains.

3 Anisotropic hyperelasticity in a polyconvex framework

In the following we restrict ourselves to hyperelasticity and postulate the existence of a so-called Helmholtz free energy function $\psi = \psi ({{\varvec{F}}}),$ here defined per unit reference volume. We consider perfect elastic materials, which means that the internal dissipation is zero for every admissible process, i.e., ${{\varvec{P}}}{\text {:}}\, \dot{{\varvec{F}}}- \dot{\psi }= ( {{\varvec{P}}}- \partial _F \psi ){\text {:}}\, \dot{{\varvec{F}}}\ge 0,$ where ${{\varvec{P}}}$ denotes the first Piola–Kirchhoff stress tensor and $\dot{{\varvec{F}}}$ denotes the material time derivative of the deformation gradient. Thus, we conclude

$$\begin{aligned} {{\varvec{P}}}= \dfrac{\partial \psi }{\partial {{\varvec{F}}}} =: {\partial _{F} \psi }. \end{aligned}$$

(20)

In the following it is helpful to express the first Piola–Kirchhoff stress tensor by a decomposition on Cartesian axes with the nominal stress vectors $\varvec{\tau }_i$ acting on the planes, whose normal unitary vector are ${{\varvec{e}}}_i^r,$ as

$$\begin{aligned} {{\varvec{P}}}=\varvec{\tau }_i\otimes {{\varvec{e}}}_i^r \quad \text {with} \quad \varvec{\tau }_i=\frac{\partial \psi }{\partial {{\varvec{f}}}_i}. \end{aligned}$$

(21)

For the constitutive modeling we concentrate on the notion of polyconvexity introduced by [2, 3].

3.1 Definition of polyconvexity

${{\varvec{F}}}\mapsto \psi ({{\varvec{F}}})$ is polyconvex if and only if there exists a function $P{\text {:}}\,\mathbb {R}^{3\times 3}\times \mathbb {R}^{3\times 3}\times \mathbb {R}\mapsto \mathbb {R}$ (in general non-unique) such that

$$\begin{aligned} \psi ({{\varvec{F}}})= P({{\varvec{F}}},\, {\text {Cof}}{{{\varvec{F}}}},\, {\text {det}}{{{\varvec{F}}}}), \end{aligned}$$

(22)

and the function $({{\varvec{F}}},\, {\text {Cof}}{{{\varvec{F}}}},\, {\text {det}}{{{\varvec{F}}}}) \in \mathbb {R}^{19} \mapsto P( {{\varvec{F}}},\, {\text {Cof}}{{{\varvec{F}}}},\, {\text {det}}{{{\varvec{F}}}} ) \in \mathbb {R}$ is convex for all points ${{\varvec{X}}}\in \mathbb {R}^3.$ (For simplicity we dropped the ${{\varvec{X}}}$-dependency of the individual functions.)

Particularly for practical use polyconvexity is an important concept, because it is relative easy to proof. It should be noted, that the arguments $( {{\varvec{F}}},\, {\text {Cof}}{{{\varvec{F}}}}, \, {\text {det}}{{{\varvec{F}}}} )$ govern the transformations of the infinitesimal line, vectorial area and volume elements from the reference onto the actual placement. Calculation rules concerning the cofactor are, e.g., given [48], more advanced rules are given in [22],¹ and a reformulation of this framework is given in [14]. Furthermore, polyconvex functions are always sequential-weak-lower-semicontinuous (s.w.l.s.); this in combination with the coercivity of the stored energy function $\int _{\mathcal {B}} \psi ({{\varvec{F}}})$dV is a sufficient condition for the existence of minimizers. In this context of the direct methods of variations we refer to [1, 18, 21, 34, 52]. In the context of anisotropic polyconvex energies we refer to [48, 49]. An important invariance condition is the principle of material frame indifference, which requires the invariance of the constitutive equation under superimposed rigid body motions onto the current configuration, i.e., $\widehat{{{\varvec{Q}}}} {\text {:}}\, {{\varvec{x}}}\in \mathcal{B}_t \mapsto \widehat{{{\varvec{Q}}}} {{\varvec{x}}}=: {{\varvec{x}}}^+.$ In order to fulfill this condition a priori we use the well-known reduced constitutive equations, see, e.g., [57]. Therefore we formulate the free energy in terms of the right Cauchy–Green tensor, which guarantees $\psi ({{\varvec{C}}}) = \psi ( {{\varvec{C}}}^+)\, \text {with}\, {{\varvec{C}}}^+:= ({\nabla }_{X}{{{\varvec{x}}}^+})^T ({\nabla }_{X}{{{\varvec{x}}}^+})$ for all $\widehat{{{\varvec{Q}}}} \in \text{ SO }(3).$ In the following we formulate the strain energy $\psi ({{\varvec{C}}}) = \psi ^\mathrm{i\_p} ({{\varvec{C}}}) + \psi ^\mathrm{a\_p} ({{\varvec{C}}})$ as an isotropic tensor function, whereas we introduce here the abbreviations $^\mathrm{i\_p}$ and $^\mathrm{a\_p}$ for the isotropic- and the anisotropic part. Thus, the isotropic part of the free energy $\psi ^\mathrm{i\_p} ({{\varvec{C}}})$ can be expressed in terms of the principal invariants

$$\begin{aligned} I_1= & {} {\text {tr}}{{{\varvec{C}}}} = {{\varvec{f}}}_i\cdot {{\varvec{f}}}_i , \nonumber \\ I_2= & {} {\text {tr}}[{{\text {Cof}}{{{\varvec{C}}}}}] = {{\varvec{g}}}_i \cdot {{\varvec{g}}}_i, \nonumber \\ I_3= & {} {\text {det}}{{{\varvec{C}}}} = \left( {{\varvec{f}}}_1\cdot \left( {{\varvec{f}}}_2 \times {{\varvec{f}}}_3\right) \right) ^2. \end{aligned}$$

(23)

The derivatives of the isotropic invariants with respect to ${{\varvec{f}}}_i$ follow as

$$\begin{aligned} \frac{\partial I_1}{\partial {{\varvec{f}}}_{i}}= & {} 2{{\varvec{f}}}_i, \nonumber \\ \frac{\partial I_2}{\partial {{\varvec{f}}}_{i}}= & {} 2\frac{\partial {{\varvec{g}}}_j}{\partial {{\varvec{f}}}_i} {{\varvec{g}}}_j={-}2\varepsilon _{ijk}{{\varvec{f}}}_j\times {{\varvec{g}}}_k \quad \text {and}\nonumber \\ \frac{\partial I_3}{\partial {{\varvec{f}}}_{i}}= & {} 2J{{\varvec{g}}}_i. \end{aligned}$$

(24)

For transverse isotropy, we introduce a preferred direction vector ${{\varvec{m}}}$ of unit length. Let $\widehat{{{\varvec{Q}}}} (\alpha ,\, {{\varvec{m}}})$ characterize all rotations about the ${{\varvec{m}}}$-axis, then the associated material symmetry group is defined by

$$\begin{aligned} \mathcal{G}^\mathrm{ti} := \{ { \pm } \mathbf{1}; \; \widehat{{{\varvec{Q}}}} (\alpha ,\, {{\varvec{m}}}) | 0 \le \alpha < 2 \pi \}. \end{aligned}$$

(25)

For the formulation of anisotropic free energies in terms of isotropic tensor functions we apply the concept of structural tensors. This was first introduced in an attractive way with important applications by [11, 12], see also [13], although some similar ideas might have been touched on earlier. Structural tensors have to reflect the material symmetries, here we introduce the rank one tensor

$$\begin{aligned} {{\varvec{M}}}= {{\varvec{m}}}\otimes {{\varvec{m}}}\quad \text {with}\quad \Vert {{\varvec{m}}}\Vert = 1. \end{aligned}$$

(26)

The invariance group of ${{\varvec{M}}}$ preserves the material symmetry group $\mathcal{G}^\mathrm{ti},$ i.e.,

$$\begin{aligned} {{\varvec{M}}}= \widehat{{{\varvec{Q}}}} {{\varvec{M}}}\widehat{{{\varvec{Q}}}}^T \quad \forall \; \widehat{{{\varvec{Q}}}} \in \mathcal{G}^\mathrm{ti}. \end{aligned}$$

(27)

The strain energy $\psi ^{ti}$ can be formulated as an isotropic tensor function with respect to the arguments $\{{{\varvec{C}}},\, {{\varvec{M}}}\}.$ Exploiting the fact, that the powers of the structural tensor are the structural tensor itself, two mixed invariants of the two symmetric tensors ${{\varvec{C}}}$ and ${{\varvec{M}}}$ can be introduced

$$\begin{aligned} I_4= & {} {\text {tr}}[{{{\varvec{C}}}{{\varvec{M}}}}] =A_{ij}{{\varvec{f}}}_i\cdot {{\varvec{f}}}_j \quad \text {and}\nonumber \\ I_5= & {} {\text {tr}}[{{\text {Cof}}[{{{\varvec{C}}}}] {{\varvec{M}}}}]=A_{ij} {{\varvec{g}}}_i\cdot {{\varvec{g}}}_j, \end{aligned}$$

(28)

where

$$\begin{aligned} A_{ij}=\left( {{\varvec{e}}}_i\cdot {{\varvec{m}}}\right) \left( {{\varvec{e}}}_j\cdot {{\varvec{m}}}\right) ={{\varvec{e}}}_i\cdot {{\varvec{M}}}{{\varvec{e}}}_j. \end{aligned}$$

(29)

The derivatives of the additional transversal isotropic invariants follow as

$$\begin{aligned} \begin{array}{rcl} &{}&{}\displaystyle \frac{\partial I_4}{\partial {{\varvec{f}}}_i} = 2 A_{ij}{{\varvec{f}}}_j \quad \text {and} \\ &{}&{}\displaystyle \frac{\partial I_5}{\partial {{\varvec{f}}}_i} = 2 A_{mn}\displaystyle \frac{\partial {{\varvec{g}}}_n}{\partial {{\varvec{f}}}_i} {{\varvec{g}}}_m={-}2\varepsilon _{ijk} A_{nk}{{\varvec{f}}}_j \times {{\varvec{g}}}_n. \end{array} \end{aligned}$$

(30)

With the aid of the results above, the nominal stress vectors may be expressed by

(31)

4 Hyperelasticity for shear-rigid shell models

Due to the Kirchhoff–Love assumption we observe that

$$\begin{aligned} \varvec{\gamma }_\alpha ^r\cdot {{\varvec{e}}}_3^r=\varvec{\eta }_\alpha ^r\cdot {{\varvec{e}}}_3^r=0. \end{aligned}$$

(32)

A consequence of Eq. (32) is

$$\begin{aligned} \varvec{\eta _\alpha }\cdot {{\varvec{e}}}_3={{\varvec{z}}}_{\alpha }\cdot {{\varvec{e}}}_3=0 \quad \text {and} \quad {{\varvec{f}}}_\alpha \cdot {{\varvec{e}}}_3=0. \end{aligned}$$

(33)

The isotropic invariant simplify in the framework of shear rigid shells to

$$\begin{aligned} \begin{array}{rcl} &{}&{} I_1 = {{\varvec{f}}}_\alpha \cdot {{\varvec{f}}}_\alpha +1, \\ &{}&{} I_2 = {{\varvec{g}}}_\alpha \cdot {{\varvec{g}}}_\alpha +J^2=\left( {{\varvec{f}}}_\alpha \times {{\varvec{e}}}_3\right) \cdot \left( {{\varvec{f}}}_\alpha \times {{\varvec{e}}}_3\right) +(J)^2, \\ &{}&{} I_3 = J^2 =\left( {{\varvec{e}}}_3\cdot \left( {{\varvec{f}}}_1\times {{\varvec{f}}}_2\right) \right) ^2. \end{array}\nonumber \\ \end{aligned}$$

(34)

For the anisotropic invariants we state the basic assumption that in the reference configuration the preferred directions are parallel to the middle plane of the shell such that

$$\begin{aligned} {{\varvec{m}}}^r \cdot {{\varvec{e}}}^r_3=0. \end{aligned}$$

(35)

This leads, due to the Kirchhoff–Love assumption, to

$$\begin{aligned} {{\varvec{m}}}\cdot {{\varvec{e}}}_3=0. \end{aligned}$$

(36)

Therefore the anisotropic invariants can be simplified to

$$\begin{aligned}&I_4=A_{\alpha \beta }{{\varvec{f}}}_{\alpha }\cdot {{\varvec{f}}}_{\beta },\nonumber \\&I_5=A_{\alpha \beta }{{\varvec{g}}}_\alpha \cdot {{\varvec{g}}}_\beta \quad \text {with}\quad A_{\alpha \beta }=\left( {{\varvec{e}}}_\alpha \cdot {{\varvec{m}}}\right) \left( {{\varvec{e}}}_\beta \cdot {{\varvec{m}}}\right) . \end{aligned}$$

(37)

Due to the kinematic assumptions the derivatives of the invariants are given by

$$\begin{aligned} \begin{array}{rcl} \displaystyle \frac{\partial I_1}{{{\varvec{f}}}_\alpha }&{}=&{} 2{{\varvec{f}}}_\alpha , \\ \displaystyle \frac{\partial I_2}{{{\varvec{f}}}_\alpha }&{}=&{} 2{{\varvec{e}}}_3 \times \left( {{\varvec{f}}}_\alpha \times {{\varvec{e}}}_3\right) +2J\varepsilon _{\alpha \beta }{{\varvec{f}}}_\beta \times {{\varvec{e}}}_3,\\ \displaystyle \frac{\partial I_3}{{{\varvec{f}}}_\alpha }&{}=&{} 2J\varvec{\varepsilon }_{\alpha \beta }{{\varvec{f}}}_\beta \times {{\varvec{e}}}_3, \\ \displaystyle \frac{\partial I_4}{{{\varvec{f}}}_\alpha }&{}=&{} 2 A_{\alpha \beta }{{\varvec{f}}}_\beta , \\ \displaystyle \frac{\partial I_5}{{{\varvec{f}}}_\alpha }&{}=&{} 2 A_{\gamma \beta }\varvec{\varepsilon }_{\alpha \beta }\varvec{\varepsilon }_{\gamma \delta }{{\varvec{e}}}_3\times \left( {{\varvec{f}}}_\delta \times {{\varvec{e}}}_3\right) .\\ \end{array} \end{aligned}$$

(38)

Thus, the nominal stress vectors are then given by

(39)

Note that $\varvec{\tau }_\alpha \cdot {{\varvec{e}}}_3=0,$ hence the stress vectors $\varvec{\tau }_\alpha$ are normal to ${{\varvec{e}}}_3$ what is consistent with the shell kinematics.

4.1 Plane stress condition

The plane stress condition states, that the stresses in the normal direction of the shell mid-plane vanishes, i.e., $(\varvec{\tau }{{\varvec{e}}}_3)\cdot {{\varvec{e}}}_3=0.$ For the derivation of the plane stress condition we introduce the local transversal strain $\gamma _{33}$ as an additional degree of freedom which can be eliminated on a constitutive level as

$$\begin{aligned} {{\varvec{f}}}_3=\left( 1+\gamma _{33}\right) {{\varvec{e}}}_3. \end{aligned}$$

(40)

Now, one may write

$$\begin{aligned} \begin{array}{lll} &{}&{} J={{\varvec{f}}}_3\cdot \left( {{\varvec{f}}}_1\times {{\varvec{f}}}_2\right) =\left( 1+\gamma _{33}\right) \overline{J},\\ &{}&{}{{\varvec{g}}}_{\alpha } = \left( 1+\gamma _{33}\right) \overline{{{\varvec{g}}}}_\alpha , \\ &{}&{}{{\varvec{g}}}_3 = {{\varvec{f}}}_1\times {{\varvec{f}}}_2=\overline{J}{{\varvec{e}}}_3, \end{array} \end{aligned}$$

(41)

where

$$\begin{aligned} \overline{J}={{\varvec{e}}}_3\cdot \left( {{\varvec{f}}}_1\times {{\varvec{f}}}_2\right) \quad \text {and} \quad \overline{{{\varvec{g}}}}_\alpha =\varvec{\varepsilon }_{\alpha \beta }{{\varvec{f}}}_\beta \times {{\varvec{e}}}_3. \end{aligned}$$

(42)

Therefore the modified invariants follow as

$$\begin{aligned} \begin{array}{rcl} I_1 &{}=&{} {{\varvec{f}}}_\alpha \cdot {{\varvec{f}}}_\alpha +\left( 1+\gamma _{33}\right) ^2, \\ I_2 &{}=&{} \left( 1+\gamma _{33}\right) ^2 \left( {{\varvec{f}}}_\alpha \times {{\varvec{e}}}_3\right) \cdot \left( {{\varvec{f}}}_\alpha \times {{\varvec{e}}}_3\right) +\overline{J}^2, \\ I_3 &{}=&{} \left( 1+\gamma _{33}\right) ^2 \overline{J}^2, \\ I_4 &{}=&{} A_{\alpha \beta }{{\varvec{f}}}_\alpha \cdot {{\varvec{f}}}_\beta , \\ I_5 &{}=&{} \left( 1+\gamma _{33}\right) ^2 A_{\alpha \beta } \varvec{\varepsilon }_{\alpha \gamma }\varvec{\varepsilon }_{\beta \delta }\left( {{\varvec{f}}}_\gamma \times {{\varvec{e}}}_3\right) \cdot \left( {{\varvec{f}}}_\delta \times {{\varvec{e}}}_3\right) , \end{array} \end{aligned}$$

(43)

and their derivatives by

$$\begin{aligned} \begin{array}{rcl} \displaystyle \frac{\partial I_1}{\partial {{\varvec{f}}}_{\alpha }} &{}=&{} 2{{\varvec{f}}}_\alpha ,\\ \displaystyle \frac{\partial I_1}{\partial \gamma _{33}} &{}=&{} 2\left( 1+\gamma _{33}\right) ,\\ \displaystyle \frac{\partial I_2}{\partial {{\varvec{f}}}_{\alpha }} &{}=&{} 2\left( 1+\gamma _{33}\right) ^2 \left( {{\varvec{f}}}_\alpha \times {{\varvec{e}}}_3\right) +2\overline{J}\left( 1+\gamma _{33}\right) \varvec{\varepsilon }_{\alpha \beta }{{\varvec{f}}}_\beta \times {{\varvec{e}}}_3,\\ \displaystyle \frac{\partial I_2}{\partial \gamma _{33}} &{}=&{} 2\left( 1+\gamma _{33}\right) \left( {{\varvec{f}}}_\alpha \times {{\varvec{e}}}_3\right) \cdot \left( {{\varvec{f}}}_\alpha \times {{\varvec{e}}}_3\right) ,\\ \displaystyle \frac{\partial I_3}{\partial {{\varvec{f}}}_{\alpha }} &{}=&{} 2\left( 1+\gamma _{33}\right) ^2 \overline{J}\varvec{\varepsilon }_{\alpha \beta }{{\varvec{f}}}_\beta \times {{\varvec{e}}}_3,\\ \displaystyle \frac{\partial I_3}{\partial \gamma _{33}} &{}=&{} 2\left( 1+\gamma _{33}\right) \overline{J}^2, \\ \displaystyle \frac{\partial I_4}{\partial {{\varvec{f}}}_{\alpha }} &{}=&{} 2 A_{\alpha \beta }{{\varvec{f}}}_\beta ,\\ \displaystyle \frac{\partial I_4}{\partial \gamma _{33}} &{}=&{} 0, \\ \displaystyle \frac{\partial I_5}{\partial {{\varvec{f}}}_{\alpha }} &{}=&{} 2\left( 1+\gamma _{33}\right) ^2 A_{\delta \beta }\varvec{\varepsilon }_{\delta \gamma }\varvec{\varepsilon }_{\beta \alpha }\left( {{\varvec{f}}}_\gamma \times {{\varvec{e}}}_3\right) \times {{\varvec{e}}}_3 ,\\ \displaystyle \frac{\partial I_5}{\partial \gamma _{33}} &{}=&{} 2\left( 1+\gamma _{33}\right) A_{\alpha \beta }\varvec{\varepsilon }_{\alpha \gamma }\varvec{\varepsilon }_{\beta \delta }\left( {{\varvec{f}}}_\gamma \times {{\varvec{e}}}_3\right) \cdot \left( {{\varvec{f}}}_\delta \times {{\varvec{e}}}_3\right) . \end{array} \end{aligned}$$

(44)

Thus, the nominal stress vectors are given by

(45)

and

(46)

Due to the physical condition $\gamma _{33}>{-}1$ we obtain with the plane stress condition $\tau _{33}=0$ the solution as

(47)

which has to be solved in order to obtain $\gamma _{33}$ that satisfies $\tau _{33}=0.$ Equation (47) is in general a non-linear equation in $\gamma _{33}$ which can be solved iteratively by the Newton method as follows

$$\begin{aligned} \gamma _{33}^{k+1}=\gamma _{33}^k-\left( \frac{\partial \tau _{33}}{\partial \gamma _{33}}\right) ^{-1}\tau _{33}\left( \gamma _{33}^k\right) ,\quad k=0,\,1,\,2,\ldots \nonumber \\ \end{aligned}$$

(48)

4.1.1 Example for analytical enforcement of the plane stress condition

For special cases it is possible to find an analytical solution for the enforcement of the plane stress condition, which is exemplary depicted in this section for an anisotropic polyconvex strain energy function. Let us regard a strain energy function of the form

(49)

where

(50)

Therefore the plane-stress condition from Eq. (47) leads to

$$\begin{aligned} \frac{1}{2}\mu +\frac{1}{4}\overline{J}^2 \left( \lambda -\frac{\lambda +2\mu }{(1+\gamma _{33})^2\overline{J}^2}\right) =0. \end{aligned}$$

(51)

Solving with respect to $\gamma _{33}$ yields the non-trivial solution

$$\begin{aligned} \gamma _{33}=\sqrt{\frac{\lambda +2\mu }{\lambda \overline{J}^2+2\mu }}-1. \end{aligned}$$

(52)

5 Variational formulation

The main differential equation in solid mechanics is the local statement of the balance of linear momentum

$$\begin{aligned} {\text {Div}}{{\varvec{P}}}+\rho _0 (\overline{{{\varvec{b}}}}-\ddot{{{\varvec{u}}}})=0, \end{aligned}$$

(53)

with the initial density $\rho _0,$ the body forces $\overline{{{\varvec{b}}}}$ and the acceleration $\ddot{{{\varvec{u}}}}.$ This leads with the help of the theorem of virtual work to a local equilibrium of the form

$$\begin{aligned} \delta W=\delta W_{\text {int}}-\delta W_{\text {ext}}=0, \quad \forall \,\delta {{\varvec{u}}}, \end{aligned}$$

(54)

whereas $\delta {{\varvec{u}}}$ are virtual displacements and with the internal and external parts of the virtual work as

$$\begin{aligned} \begin{array}{rcl} \delta W_{int} &{}=&{} \displaystyle \int _\mathcal{{B}} {{\varvec{P}}}{\text {:}}\,\delta {{\varvec{F}}}dV +\int _\mathcal{{B}}\rho _0 \delta {{\varvec{u}}}\cdot \ddot{{{\varvec{u}}}} dV, \\ \delta W_{ext} &{}=&{} \displaystyle \int _{\partial \mathcal {B}} \overline{{{\varvec{t}}}}\cdot \delta {{\varvec{x}}}dA +\int _\mathcal{{B}}\overline{{{\varvec{f}}}}\cdot \delta {{\varvec{x}}}dV. \end{array} \end{aligned}$$

(55)

Here $\overline{{{\varvec{t}}}}$ denotes the normal surface stresses and the external volume forces $\overline{{{\varvec{f}}}}=\rho _0\overline{{{\varvec{b}}}}.$ Introducing the Eqs. (17) and (21) into the internal part of the weak form (55)$_1$ yields

$$\begin{aligned} \delta W_{int}= & {} \displaystyle \int _{\mathcal{{B}}}\left( \varvec{\tau }^r_\alpha \cdot \delta \varvec{\eta }_\alpha ^r+\left( {{\varvec{a}}}^r\times \varvec{\tau }^r_\alpha \right) \cdot \delta \varvec{\kappa }_\alpha ^r \right) dV \nonumber \\&+\; \int _\mathcal{{B}}\rho _0 \delta {{\varvec{u}}}\cdot \ddot{{{\varvec{u}}}} dV. \end{aligned}$$

(56)

For simplicity we use the assumption that the shell mid-surface is the medium surface, i.e., $H=[-h/2,\,h/2].$ Thus, the cross-sectional generalized strains and the acceleration are constant over the shell thickness H we split the integral and by introducing the back rotated counterparts of the true forces ${{\varvec{n}}}_\alpha$ and the true moments ${{\varvec{m}}}_\alpha ,$ both defined per unit length at reference configuration and the inertia property of the cross section $\overline{M}$ as

$$\begin{aligned}&{{\varvec{n}}}_\alpha ^r =\int _H \varvec{\tau }_\alpha ^r dH,\nonumber \\&{{\varvec{m}}}_\alpha ^r =\int _H \left( {{\varvec{a}}}^r \times \varvec{\tau }_\alpha ^r\right) dH \quad \text {and}\nonumber \\&\overline{M}=\int _H \rho _0 dH, \end{aligned}$$

(57)

we obtain

$$\begin{aligned} \delta W_{int}= & {} \int _{\varvec{\Omega }^r} \left( \varvec{\sigma }_\alpha ^r\cdot \delta \varvec{\varepsilon }_\alpha ^r + \overline{M}\ddot{{{\varvec{u}}}}\cdot \delta {{\varvec{u}}}\right) d\varvec{\Omega }^r. \end{aligned}$$

(58)

Here we introduced for convenience the vectors $\varvec{\varepsilon }^r_\alpha =[\varvec{\eta }_\alpha ^r \quad \varvec{\kappa }_\alpha ^r]^T$ and $\varvec{\sigma }_\alpha ^r=[{{\varvec{n}}}_\alpha ^r \, {{\varvec{m}}}_\alpha ^r]^T.$ Following the procedure given in [42], we introduce a vector $\varvec{\Delta }$ for the differential operations

$$\begin{aligned} \varvec{\Delta }=\left[ {{\varvec{I}}}\quad {{\varvec{I}}}\frac{\partial }{\partial \xi _1} \quad {{\varvec{I}}}\frac{\partial }{\partial \xi _2} \quad {{\varvec{I}}}\frac{\partial ^2}{\partial \xi _1^2} \quad {{\varvec{I}}}\frac{\partial ^2}{\partial \xi _1\partial \xi _2} \quad {{\varvec{I}}}\frac{\partial ^2}{\partial \xi _2^2}\right] ^T. \end{aligned}$$

(59)

Therefore, we may rewrite

$$\begin{aligned} \delta \varvec{\varepsilon }^r_\alpha = \varvec{\Lambda }^T \varvec{\Psi }_\alpha \varvec{\Delta }\delta {{\varvec{u}}}, \end{aligned}$$

(60)

where the two operators $\varvec{\Lambda }$ and $\varvec{\Psi }_\alpha$ are defined as follows

$$\begin{aligned} \begin{array}{lll} \varvec{\Lambda } &{}=&{} \begin{bmatrix} {{\varvec{Q}}}&{} \varvec{0} \\ \varvec{0} &{} {{\varvec{Q}}}\end{bmatrix}, \\ \varvec{\Psi }_\alpha &{}=&{} \left[ \begin{array}{llllll} \varvec{0} &{} \delta _{1\alpha }{{\varvec{I}}}+{{\varvec{Z}}}_{\alpha }\varvec{\Gamma }_1 &{} \delta _{2\alpha }{{\varvec{I}}}+{{\varvec{Z}}}_{\alpha }\varvec{\Gamma }_2 &{} \varvec{0} &{} \varvec{0} &{} \varvec{0} \\ \varvec{0} &{} \varvec{\Gamma }_{1,\alpha } &{} \varvec{\Gamma }_{2,\alpha } &{} \delta _{1\alpha } \varvec{\Gamma }_{1} &{} \delta _{1\alpha }\varvec{\Gamma }_2+\delta _{2\alpha }\varvec{\Gamma }_1 &{} \delta _{2\alpha }\varvec{\Gamma }_2 \end{array}\right] , \end{array}\nonumber \\ \end{aligned}$$

(61)

with $\delta _{\alpha \beta }$ as the Kronecker delta. Thus, Eq. (58) can be rearranged as

$$\begin{aligned} \delta W_{int}=\int _{{\Omega }^r} \varvec{\Delta } \delta {{\varvec{u}}}\cdot \varvec{\Psi }_{\alpha }^T\varvec{\Lambda }\varvec{\sigma }_\alpha ^r + \delta {{\varvec{u}}}\cdot \overline{M}\ddot{{{\varvec{u}}}} d{\Omega }^r. \end{aligned}$$

(62)

For the external part of the weak form we split the surface traction vector into the top and bottom surface tractions $\overline{{{\varvec{t}}}}^t,\,\overline{{{\varvec{t}}}}^b$ and the tractions along the lateral surface $\overline{{{\varvec{t}}}}^l.$ Such that we may write

$$\begin{aligned} \int _{\partial {\mathcal B}} \overline{{{\varvec{t}}}} dA= & {} \int _{\Omega ^r} \left( \overline{{{\varvec{t}}}}^t+\overline{{{\varvec{t}}}}^b\right) d\Omega ^r\nonumber \\&+\; \int _{\partial \Omega ^r}\int _{H^r} \overline{{{\varvec{t}}}}^l dH^r d\partial \Omega ^r. \end{aligned}$$

(63)

Therefore we may rewrite Eq. (55)$_2$ as

$$\begin{aligned} \delta W_{ext}= & {} \int _{{\Omega ^r}} \left( \overline{{{\varvec{t}}}}^t+\overline{{{\varvec{t}}}}^b+\int _{H^r} \overline{{{\varvec{f}}}}dH^r\right) \cdot \delta {{\varvec{x}}}d{\Omega }^r\nonumber \\&+\;\int _{\partial \Omega ^r}\int _H \overline{{{\varvec{t}}}}^l \cdot \delta {{\varvec{x}}}dH^r d\partial \Omega ^r. \end{aligned}$$

(64)

Introduction of $\delta {{\varvec{x}}}=\delta {{\varvec{u}}}+(\varvec{\Gamma }_\alpha \delta {{\varvec{u}}}_{\alpha })\times {{\varvec{a}}}$ and Eq. (63) yield

$$\begin{aligned} \delta W_{ext}= & {} \int _{\Omega ^r}\overline{{{\varvec{q}}}}^{\Omega ^r}\cdot \widetilde{{\varvec{\Delta }}}\delta {{{\varvec{u}}}} d\Omega ^r \nonumber \\&+\; \int _{\partial \Omega ^r}\overline{{{\varvec{q}}}}^{\partial \Omega ^r}\cdot \widetilde{{\varvec{\Delta }}}\delta {{{\varvec{u}}}} d\partial \Omega ^r, \end{aligned}$$

(65)

where the displacements, its spatial derivatives and the generalized cross-sectional forces

$$\begin{aligned} \overline{{{\varvec{n}}}}^{\Omega ^r}=\overline{{{\varvec{t}}}}^t+\overline{{{\varvec{t}}}}^b+\int _{H^r} \overline{{{\varvec{f}}}} dH^r, \quad \overline{{{\varvec{n}}}}^{\partial \Omega ^r}=\int _{H^r} \overline{{{\varvec{t}}}}^l dH^r, \end{aligned}$$

(66)

and moments

$$\begin{aligned}&\overline{{{\varvec{m}}}}^{\Omega ^r}={{\varvec{a}}}\times \overline{{{\varvec{t}}}}^t+{{\varvec{a}}}\times \overline{{{\varvec{t}}}}^b+\int _{H^r} {{\varvec{a}}}\times \overline{{{\varvec{f}}}} dH^r, \nonumber \\&\overline{{{\varvec{m}}}}^{\partial \Omega ^r}=\int _{H^r} {{\varvec{a}}}\times \overline{{{\varvec{t}}}}^l dH^r, \end{aligned}$$

(67)

have been gathered in the following vectors

$$\begin{aligned}&\widetilde{{\varvec{\Delta }}}= \begin{bmatrix} {{\varvec{I}}}\\ {{\varvec{I}}}\frac{\partial }{\partial \xi _1} \\ {{\varvec{I}}}\frac{\partial }{\partial \xi _2} \end{bmatrix}, \quad \overline{{{\varvec{q}}}}^{\Omega ^r}= \begin{bmatrix} \overline{{{\varvec{n}}}}^{\Omega ^r} \\ \varvec{\Gamma }_1^T \overline{{{\varvec{m}}}}^{\Omega ^r}\\ \varvec{\Gamma }_2^T \overline{{{\varvec{m}}}}^{\Omega ^r} \end{bmatrix} \quad \text {and}\nonumber \\&\overline{{{\varvec{q}}}}^{\partial \Omega ^r}= \begin{bmatrix} \overline{{{\varvec{n}}}}^{\partial \Omega ^r} \\ \varvec{\Gamma }_1^T \overline{{{\varvec{m}}}}^{\partial \Omega ^r}\\ \varvec{\Gamma }_2^T \overline{{{\varvec{m}}}}^{\partial \Omega ^r} \end{bmatrix}. \end{aligned}$$

(68)

5.1 Linearization of the weak form

In order to solve a nonlinear boundary value problem with the Newton–Raphson scheme a consistent linearization of the weak form (55) is needed. Under the assumption of conservative loading the linearization follows as

$$\begin{aligned} \Delta \delta W= & {} \int _{\Omega ^r} \left( {\varvec{\Delta }}\delta {{\varvec{u}}}\cdot \left( {{\varvec{G}}}+{\varvec{\Psi }}_\alpha ^T{{\varvec{D}}}_{\alpha \beta }{\varvec{\Psi }}_\beta \right) \cdot {\varvec{\Delta }}\Delta {{\varvec{u}}}\right. \nonumber \\&\left. + \;\delta {{\varvec{u}}}\cdot \overline{M}\cdot \Delta \ddot{{{\varvec{u}}}} \right) d\Omega ^r, \end{aligned}$$

(69)

where the material and geometrical stiffnesses are given by

$$\begin{aligned} {{\varvec{D}}}_{\alpha \beta }=\frac{\partial {\varvec{\sigma }}_\alpha ^r}{\partial {\varvec{\epsilon }}_\alpha ^r} = \begin{bmatrix} \displaystyle \frac{\partial {{\varvec{n}}}^r_\alpha }{\partial \varvec{\eta }_\beta ^r}&\displaystyle \frac{\partial {{\varvec{n}}}^r_\alpha }{\partial \varvec{\kappa }_\beta ^r} \\ \displaystyle \frac{\partial {{\varvec{m}}}^r_\alpha }{\partial \varvec{\eta }_\beta ^r}&\displaystyle \frac{\partial {{\varvec{m}}}^r_\alpha }{\partial \varvec{\kappa }_\beta ^r} \end{bmatrix} \quad \text {and}\quad {{\varvec{G}}}=\frac{\partial ({\varvec{\Psi }}^T_\alpha {\varvec{\sigma }}_\alpha ^r)}{\partial {\varvec{\Delta }}\delta {{\varvec{u}}}}.\nonumber \\ \end{aligned}$$

(70)

The parts of the material tangent matrices can be evaluated similar to the procedure given in [15]. A description of the geometric stiffness ${{\varvec{G}}}$ is given in [26]. Due to a lack of space, a detailed derivation of these parts is omitted herein and the interested reader is referred to the specific literature.

5.2 Discretization in space and time

In this subsection the finite element equations for triangular shell elements are specified. In general, the Kirchhoff–Love shell theory requires $C^1$-continuous approximations. The novel approach adopted herein is to enforce $C^1$-continuity at the element boundaries by imposing preservation of the angles between elements, as shown in Sect. 6. Therefore it is sufficient to employ a $C^0$ interpolation. For the approximation of the triangular shaped finite elements we apply shape functions based on baricentric parent coordinates. The position vector of the middle surface in the current configuration, the displacement vector and its spatial derivatives are interpolated as

$$\begin{aligned}&\varvec{\zeta }^h=\sum _I^{nen} {{\varvec{N}}}_I \varvec{\zeta }_I,\nonumber \\&{{\varvec{u}}}^h=\sum _I^{nen} {{\varvec{N}}}_I {{\varvec{d}}}_I, \nonumber \\&{{\varvec{u}}}^h_{\alpha }=\sum _I^{nen} {{\varvec{N}}}_{I,\alpha } {{\varvec{d}}}_I, \nonumber \\&{{\varvec{u}}}^h_{\alpha \beta }=\sum _I^{nen} {{\varvec{N}}}_{I,\alpha \beta }{{\varvec{d}}}_I, \end{aligned}$$

(71)

where the superscript h indicates the finite element discretization, nen the number of element nodes and ${{\varvec{N}}}_I$ a suitable matrix including the shape functions. Furthermore $\varvec{\zeta }_I$ denote the nodal coordinates and ${{\varvec{d}}}_I=[d_I^1,\,d_I^2,\,d_I^3]^T,\, \dot{{{\varvec{d}}}}_I=[\dot{d}_I^1,\,\dot{d}_I^2,\,\dot{d}_I^3]^T$ and $\ddot{{{\varvec{d}}}}_I=[\ddot{d}_I^1,\,\ddot{d}_I^2,\,\ddot{d}_I^3]^T$ are the nodal degrees of freedom for the displacements, velocities and accelerations, respectively. The discretized forms of the variation and linearization of the displacements and its first and second spatial derivatives follow by

$$\begin{aligned}&\displaystyle \delta {{\varvec{u}}}^h = \displaystyle \sum _I^{nen} {{\varvec{N}}}_I \delta {{\varvec{d}}}_I,\nonumber \\&\delta {{\varvec{u}}}^h_{\alpha }=\displaystyle \sum _I^{nen} {{\varvec{N}}}_{I,\alpha }\delta {{\varvec{d}}}_I,\nonumber \\&\delta {{\varvec{u}}}^h_{\alpha \beta }=\displaystyle \sum _I^{nen} {{\varvec{N}}}_{I,\alpha \beta } \delta {{\varvec{d}}}_I, \nonumber \\&\displaystyle \Delta {{\varvec{u}}}^h = \displaystyle \sum _I^{nen} {{\varvec{N}}}_I \Delta {{\varvec{d}}}_I, \nonumber \\&\Delta {{\varvec{u}}}^h_{\alpha }=\displaystyle \sum _I^{nen} {{\varvec{N}}}_{I,\alpha } \Delta {{\varvec{d}}}_I,\nonumber \\&\Delta {{\varvec{u}}}^h_{\alpha \beta }=\displaystyle \sum _I^{nen} {{\varvec{N}}}_{I,\alpha \beta } \Delta {{\varvec{d}}}_I. \end{aligned}$$

(72)

The acceleration, its variation and linearization is discretized in space by

$$\begin{aligned}&\ddot{{{\varvec{u}}}}^h = \displaystyle \sum _I^{nen} {{\varvec{N}}}_I \ddot{{{\varvec{d}}}}_I,\quad \delta \ddot{{{\varvec{u}}}}^h = \displaystyle \sum _I^{nen} {{\varvec{N}}}_I \delta \ddot{{{\varvec{d}}}}_I \quad \text {and} \nonumber \\&\Delta \ddot{{{\varvec{u}}}}^h = \displaystyle \sum _I^{nen} {{\varvec{N}}}_I \Delta \ddot{{{\varvec{d}}}}_I. \end{aligned}$$

(73)

In order to solve a time dependent boundary value problem, an updated description of the motion is deployed. Thus, a time-increment notation is adopted here. An arbitrary time step is denoted by $\Delta t=t_{i+1}-t_i.$ We introduce the notation $(\cdot )(t_i)=(\cdot )_{i},\, (\cdot )(t_i+1)=(\cdot )_{i+1}$ and $(\cdot )(t_i+1)-(\cdot )(t_i)=\Delta (\cdot ).$ Assume that all quantities of the previous time step, at time $t_i,$ are known. The well known Newmark method was applied for the time integration, with $0\le \beta \le 0.5$ and $0\le \gamma \le 1$ as the Newmark parameters. Thus, the acceleration and the velocity of the actual configuration at time $t=t_{i+1}$ are computed by

$$\begin{aligned} \ddot{{{\varvec{d}}}}_{i+1}= & {} \frac{1}{\beta \Delta t^2}\left( {{\varvec{d}}}_{i+1}-\widehat{\ddot{{{\varvec{d}}}}}_i\right) \quad \text {and}\nonumber \\ \dot{{{\varvec{d}}}}_{i+1}= & {} \frac{\gamma }{\beta \Delta t}{{\varvec{d}}}_{i+1}+\widehat{\dot{{{\varvec{d}}}}}_i-\frac{\gamma }{\beta \Delta t}\widehat{\ddot{{{\varvec{d}}}}}_{i+1}, \end{aligned}$$

(74)

whereas $\widehat{\ddot{{{\varvec{d}}}}}_i$ and $\widehat{\dot{{{\varvec{d}}}}}_i$ are predictors, only depending on the previous time step given by

$$\begin{aligned} \widehat{\ddot{{{\varvec{d}}}}}_i= & {} {{\varvec{u}}}_{i}+\dot{{{\varvec{d}}}}_i \Delta t+\left( \frac{1}{2}-\beta \right) \ddot{{{\varvec{d}}}}_{i} \quad \text {and}\nonumber \\ \widehat{\dot{{{\varvec{d}}}}}_i= & {} \dot{{{\varvec{d}}}}_i+(1-\gamma )\ddot{{{\varvec{d}}}}_i\Delta t. \end{aligned}$$

(75)

Variation and linearization of (74)$_1$ leads to

$$\begin{aligned} \delta \ddot{{{\varvec{d}}}}_{i+1}=\frac{1}{\beta \Delta t^2}\delta {{\varvec{d}}}_{i+1} \quad \text {and} \quad \Delta \ddot{{{\varvec{d}}}}_{i+1}=\frac{1}{\beta \Delta t^2}\Delta {{\varvec{d}}}_{i+1}. \end{aligned}$$

(76)

We obtain the system of equations for a typical finite element e

$$\begin{aligned} {{\varvec{k}}}^e \Delta {{\varvec{d}}}={-}{{\varvec{r}}}^e, \end{aligned}$$

(77)

with the typical right-hand side vector from (62) and (65) as

$$\begin{aligned} {{\varvec{r}}}^e= & {} \int _{{\Omega }^r} \left( (\varvec{\Delta }{{\varvec{N}}})^T \varvec{\Psi }_{\alpha }^T\varvec{\Lambda }\varvec{\sigma }_\alpha ^r + {{\varvec{N}}}^T \overline{M}{{\varvec{N}}}\ddot{{{\varvec{d}}}}\right. \nonumber \\&\left. +\; (\widetilde{{\varvec{\Delta }}} {{\varvec{N}}})^T \overline{{{\varvec{q}}}}^{\Omega ^r} \right) d\Omega ^r + \int _{\partial \Omega ^r} (\widetilde{{\varvec{\Delta }}} {{\varvec{N}}})^T \overline{{{\varvec{q}}}}^{\partial \Omega ^r} d\partial \Omega ^r, \end{aligned}$$

(78)

and the typical stiffness matrix from (69) as

$$\begin{aligned} {{\varvec{k}}}^e= & {} \int _{\Omega ^r} \left( ({\varvec{\Delta }}{{\varvec{N}}})^T \left( {{\varvec{G}}}+{\varvec{\Psi }}_\alpha ^T{{\varvec{D}}}_{\alpha \beta }{\varvec{\Psi }}_\beta \right) {\varvec{\Delta }}{{\varvec{N}}}\right. \nonumber \\&\left. +\; {{\varvec{N}}}^T \frac{1}{\beta \Delta t^2} \overline{M} {{\varvec{N}}}\right) d\Omega ^r. \end{aligned}$$

(79)

6 Enforcement of the $\hbox {C}^1$-continuity

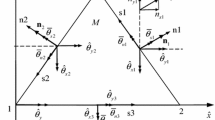
The shell kinematics is based on the Kirchhoff–Love assumption, thus the deformation gradient is written in terms of first- and second-order derivatives of the displacements. Therefore the finite element construction has to guarantee $C^1$-continuity. In this work, this condition is imposed by a penalty approach, which penalizes the kinking of the edge of two neighboring elements. Considering two arbitrary neighboring elements A and B,  we define for each element a local orthogonal system at the boundary $\Gamma ^r$ in the reference configuration, expressed by ${{\varvec{e}}}_\Gamma ^r=\{\varvec{\tau }^r,\,\varvec{\nu }^r,\,{{\varvec{e}}}_3^r\}.$ Here $\varvec{\nu ^r}$ is the inward unitary normal to the boundary $\Gamma ^r$ and

$$\begin{aligned} \varvec{\tau }^r=\varvec{\nu }^r\times {{\varvec{e}}}^r_3, \end{aligned}$$

(80)

is tangent to $\Gamma ^r.$ Associated with ${{\varvec{e}}}_\Gamma ^r,$ we introduce a local orthogonal system at the boundary of the current configuration denoted by ${{\varvec{e}}}_\Gamma =\{\varvec{\tau },\,\varvec{\nu },\,{{\varvec{e}}}_3\}.$ The angle between ${{\varvec{e}}}_3^r$ of element A and element B is denoted by $\beta ^r$ and its counterpart in the current configuration by $\beta ,$ compare Fig. 2. The $C^1$-continuity is asymptotically satisfied (as $h\rightarrow \infty$) if this angle does not change during the deformation, such that the condition $\beta -\beta ^r=0$ holds. In order to enforce this condition, the difference of these angles is penalized which can be expressed by a minimization problem as

$$\begin{aligned} \Pi ^\mathrm{pen}= & {} \int _{\Gamma ^r} \frac{1}{2}k \left( \left( {{\varvec{e}}}_{3,B}^r \times {{\varvec{e}}}_{3,A}^r\right) \cdot \varvec{\tau }_B^r\right. \nonumber \\&\left. -\; \left( {{\varvec{e}}}_{3,B} \times {{\varvec{e}}}_{3,A}\right) \cdot \varvec{\tau }_B\right) ^2 d\Gamma ^r, \end{aligned}$$

(81)

where k denotes the penalty parameter. The integral in Eq. (81) is solved by a one point integration or a collocation at the mid-point. The idea of the enforcement of the continuity condition only at the midpoint is that it leads to a sufficient $\hbox {C}^1$-continuity with mesh refinement, as it was shown by [15], and this formulation is equivalent to an equilibrium bending or a constant curvature element. The same procedure can be applied for clamped boundary conditions, as depicted in Fig. 3a. Therefore the clamping condition is induced by the minimization of

$$\begin{aligned} \Pi ^\mathrm{pen,clamp}= & {} \int _{\Gamma ^r} \frac{1}{2}k \left( \left( {{\varvec{e}}}_{3,A}^r \times {{\varvec{e}}}_{3,A}^r\right) \cdot \varvec{\tau }_A^r\right. \nonumber \\&\left. -\; \left( {{\varvec{e}}}_{3,A}^r \times {{\varvec{e}}}_{3,A}\right) \cdot \varvec{\tau }_A^r \right) ^2 d\Gamma ^r. \end{aligned}$$

(82)

Fig. 2

Enforcement of $C^1$-continuity; local coordinate system in reference (a) and current (b) configuration

In case of multiple branched elements, as exemplary depicted for the case of three branching elements in Fig. 3b, the penalty functional can be adopted as

$$\begin{aligned} \Pi ^\mathrm{pen,mult}= & {} \displaystyle \int _{\Gamma ^r} \frac{1}{2}k \left( \left( {{\varvec{e}}}_{3,B}^r \times {{\varvec{e}}}_{3,A}^r\right) \cdot \varvec{\tau }_B^r- \left( {{\varvec{e}}}_{3,B} \times {{\varvec{e}}}_{3,A}\right) \cdot \varvec{\tau }_B \right) ^2 d\Gamma ^r \nonumber \\&+\; \displaystyle \int _{\Gamma ^r} \frac{1}{2}k \left( \left( {{\varvec{e}}}_{3,C}^r \times {{\varvec{e}}}_{3,A}^r\right) \cdot \varvec{\tau }_C^r- \left( {{\varvec{e}}}_{3,C} \times {{\varvec{e}}}_{3,A}\right) \cdot \varvec{\tau }_C \right) ^2 d\Gamma ^r.\nonumber \\ \end{aligned}$$

(83)

Fig. 3

Enforcement of $C^1$-continuity at mid-edge nodes for a a clamped edge, and b branching of multiple elements

This procedure is analogously expandable for systems with multiple branching elements. In place of the penalty method, one can also use the Lagrangian or augmented Lagrangian method. For instance in place of Eq. (81) one can write in case of the Lagrange method

$$\begin{aligned} \Pi ^\mathrm{lag}=\int _{\Gamma ^r}\lambda \left( \left( {{\varvec{e}}}_{3,B}^r \times {{\varvec{e}}}_{3,A}^r\right) \cdot \varvec{\tau }_B^r- \left( {{\varvec{e}}}_{3,B} \times {{\varvec{e}}}_{3,A}\right) \cdot \varvec{\tau }_B \right) d\Gamma ^r,\nonumber \\ \end{aligned}$$

(84)

with $\lambda$ as a Lagrange multiplier, or in case of the augmented Lagrange method

$$\begin{aligned} \Pi ^{\text {aug-lag}}=\Pi ^\mathrm{lag}+\Pi ^\mathrm{pen}. \end{aligned}$$

(85)

The construction of the corresponding right-hand side vectors and the stiffness matrices is performed using the automatic differentiation capabilities of AceGen, see [30–32].

7 Numerical examples

In the this section a couple of numerical examples are discussed in order to demonstrate the reliability and flexibility of the proposed finite element formulation. The chosen boundary value problems cover isotropic as well as anisotropic material behavior using polyconvex strain energy functions. In addition to that a time dependent problem is analyzed and an application of branched shells is depicted. The solution of the boundary value problems are calculated by a classical incremental solution scheme with Newton iterations.

7.1 Pinched cylinder with rigid ends

In the first example a common shell benchmark problem of a thin cylinder with rigid ends is considered in a non time-dependent setup, as depicted in Fig. 4. The isotropic cylindrical shell has a length of $L=200,$ a radius $R=100$ and a height $h=1.$ The neo-Hookean material is described by a polyconvex strain energy as

$$\begin{aligned} \psi =\frac{1}{4}\lambda \left( \left( I_3-1\right) -{\text {ln}}{I_3}\right) +\frac{1}{2}\mu \left( I_1-3-{\text {ln}}{I_3}\right) , \end{aligned}$$

(86)

compare Sect. 4.1.1, whereas the material parameter are for the Young’s modulus $E=6.825\times 10^7$ and for the Poisson ratio $\nu =0.3$. The penalty parameter is chosen as $k=d_0 10^5$ with the bending stiffness $d_0=(Eh^3)/(12(1-\nu ^2))$. The point loads of $F=5.4\times 10^4$ pinches the cylinder on two opposing sides. Due to the symmetry conditions this boundary value problem can be modeled by only one octant of the cylinder, which is done in this contribution by a $2\times 30\times 30$ uniform mesh. The plot of the load over the vertical displacements at point A and the horizontal displacements at point B,  depicted in Fig. 5, are in perfectly shape with the results which can be found in the literature, e.g., for the shear deformable theory [45] or [15] but also in the framework of Kirchhoff–Love formulations in [27]. In addition to that it can be recognized, considering the final deformed configuration, that the proposed finite element formulation behaves very robust even for large deformations including huge curvatures.

Fig. 4

Pinched cylinder; sketch of the boundary value problem

Fig. 5

Pinched cylinder; plot of the load F over the displacements and the final (unscaled) deformed configuration

7.2 Dynamic reversion of a clamped dome

In this example a clamped half sphere is pushed down by a displacement driven boundary condition using a dynamic analysis, as presented in [39]. The boundary value problem is sketched in Fig. 6. The edge of the half sphere is clamped and the top point has a prescribed displacement of $\overline{u}_3={-}u_3(t)$, plotted on the right in Fig. 6, with a maximal value of $u_3^{\text {max}}={-}2r$. The radius of the half sphere is given by $r=0.05$ and the thickness of the shell is $h=10^{-3}$. The material model is equivalent to the same above, whereas the material parameter are chosen such that it corresponds to polyvinyl siloxane. Therefore the Young’s modulus is given by $E=10^5$, the Poisson’s ratio by $\nu =0.499$ and the initial density by $\rho =1000$. For the time integration the implicit Newmark-beta method has been applied whereas the Newmark parameter are set to $\beta =0.3025$ and $\gamma =0.6$, which induces a slight amount of numerical damping. This boundary value problem is very complex since during the simulation various snap-throughs and snap-backs appear and in addition to that very high deformations and bending occur. Due to the high complexity we used 28,806 triangular elements in order to model the dome. The results correspond to the reference results, which have been calculated with a shear deformable formulation, published in [39]. We expect to return to the issue of energy conservation and dissipation in a future work where also the necessary damping of high frequency vibrations will be investigated. For the proposed formulation this damping was done by the choice of the Newmark Parameter (Fig. 7).

Fig. 6

Clamped dome; sketch of the geometry and plot of $u_3(t)$

Fig. 7

Clamped dome: deformed configurations at different times

7.3 Hyperbolic shell subjected to locally distributed loads

In the following example a hyperbolic shell loaded by four pairs of locally distributed axial loads is investigated, compare for example [5, 7, 8]. The geometry of the hyperbolic shell is sketched, with its boundary conditions in Fig. 8a and the reference mesh is depicted in Fig. 8b. The radius of the system is given by the function

$$\begin{aligned} R=\hat{R}(z)=R_T \sqrt{1+\left( \frac{z-H/2}{4.5}^2\right) }. \end{aligned}$$

(87)

Fig. 8

Hyperbolic shell; a system with boundary conditions, taken from [5], and b discretized system with 16,448 elements

The minimal radius is $R_T=3$, which leads to a maximal radius of $R_0=5$. The total height is defined by $H=12$ and the thickness of the shell $h=0.05$, respectively. As in [5], two sets of materials are investigated here. In the first example an isotropic material model is chosen given by

$$\begin{aligned} \psi ^\mathrm{i\_p}=c_1\left( \frac{I_1}{I_3^{1/3}}-3\right) +\epsilon _1\left( I_3^{\epsilon _2}+\frac{1}{I_3^{\epsilon _2}}-2\right) . \end{aligned}$$

(88)

This strain energy satisfies the polyconvexity conditions for $c_1>0,\, \epsilon _1>0$ and $\epsilon _2>1$. The material parameter are set for the numerical example to

$$\begin{aligned} c_1=100.0 ,\quad \epsilon _1=2000.0,\quad \epsilon _2=10.0. \end{aligned}$$

(89)

In addition to that, a transversely isotropic shell is investigated where the preferred direction ${{{\varvec{m}}}}$ is aligned as a helix around the hyperbolic shell with $\beta =45^\circ$. The strain energy for the anisotropic material is given by

$$\begin{aligned} \psi =\psi ^\mathrm{i\_p}+\alpha _1 \left\langle I_1 J_4-J_5-2 \right\rangle ^{\alpha _2}, \end{aligned}$$

(90)

whereas the additional anisotropic part is polyconvex for $\alpha _1>0$ and $\alpha _2>2$ and $\langle (\bullet ) \rangle :=((\bullet )+\Vert (\bullet )\Vert )/2$ denoting the Macaulay bracket. The additional material parameter are chosen as

$$\begin{aligned} \alpha _1=1000.0, \quad \alpha _2=2.3. \end{aligned}$$

(91)

The plane stress condition is solved iteratively using a Newton scheme, as presented in Sect. 4.1. The penalty parameter for the enforcement of the $\hbox {C}_{1}$ condition is set to $k=10^4$. In order to compare the deformations of the isotropic and the anisotropic model, we follow the approach of [5], and apply a load q such that a maximal vertical displacement of approximately $u_3=2.0$ is reached. The final deformed configurations, which are in good agreements with the reference results, are depicted in Fig. 9. The attached transversely isotropic terms lead to a significant different material response. The symmetric material behavior of the isotropic shell is in complete difference to the twisting response of the transversely isotropic shell.

Fig. 9

Hyperbolic shell; deformed configurations: a isotropic and b transversely isotropic shell

7.4 Wrinkling of a membrane

Wrinkling effects of a thin membrane are analyzed in this numerical example. We consider a square membrane with truncated corners as depicted in Fig. 10, c.f. [38]. The length and thickness are given by $l_1=0.9$, $l_2=0.05$ and $h=0.001$. At two opposing truncated corners the displacements are fixed. A distributed load of $q=0.1$ is applied at the remainder truncated corners. The membrane is modeled by a superimposed transversal isotropic material model, whereas two cases are taken into account. In case (a), tension in warp direction, the preferred directions are given by ${{\varvec{m}}}_1=[1,\,0,\,0]^T$ and ${{\varvec{m}}}_2=[0,\,1,\,0]^T$, whereas in case (b), tensions in weft direction, we choose ${{\varvec{m}}}_1=[0,\,1,\,0]^T$ and ${{\varvec{m}}}_2=[1,\,0,\,0]^T$, respectively. The corresponding strain energy is additively split into an isotropic and a transversal isotropic part $\psi =\psi ^\mathrm{i\_p}+\psi ^\mathrm{a\_p}$. The isotropic part corresponds to the strain energy given in (50)$_1$ whereas the transversal isotropic part reads as

$$\begin{aligned} \psi ^\mathrm{a\_p}=\sum _i^{2} \alpha ^{\{i\}}_{1} \left\langle I^{\{i\}}_4-1 \right\rangle ^{\alpha ^{\{i\}}_2}, \end{aligned}$$

(92)

with the material parameters $\alpha ^{\{i\}}_{1},$ $\alpha ^{\{i\}}_{2}$ and the invariants $I_4^{\{i\}}={\text {tr}}[{A^{\{i\}}_{ij} {{\varvec{f}}}_i \cdot {{\varvec{f}}}_j}]$ where $A^{\{i\}}_{ij}$ is given by Eq. (37). The isotropic material parameters are for the $E=200$, $\nu =0.3$. The transversal isotropic material parameters for the warp direction are $\alpha _1^\mathrm{warp}=4$ and $\alpha _2^\mathrm{warp}=2.3$ whereas for the weft direction $\alpha _1^\mathrm{weft}=1$ and $\alpha _2^{\mathrm{weft}}=2.3$. The penalty parameter is chosen as $k=(E h^3)/(12(1-\nu ^2))10^5$. In order to obtain a wrinkling effect a imperfection is applied to the reference coordinates. Therefore six distributed nodes are initially displaced by $\overline{{{\varvec{u}}}}_3=0.001$. The deformed configuration is depicted in Fig. 11, whereas the altering wrinkles due to the different preferred directions be recognized.

Fig. 10

Wrinkling of a membrane; boundary value problem for case (a)

Fig. 11

Wrinkling of a membrane; deformed configurations of the membrane. a Tension in warp direction and b tension in weft direction

Fig. 12

Plate with varying stiffeners; boundary value problem and cross sections for (a) unstiffened-, (b) eccentric stiffened-, and (c) concentric stiffened plate

7.5 Plate with varying stiffeners

The proposed finite element formulation can be used without further modifications for the simulation of boundary value problems with branched geometries. In order to demonstrate this ability, a simple supported square plate with diagonal stiffeners is analyzed, c.f. [19, 37, 44]. The deflection of the square plates, which are loaded by a uniform distributed pressure p,  are compared for three different stiffening conditions, compare Fig. 12. The length and the thickness are given by $l=25.4$ and $h=0.254,$ respectively. The length of the flange is $h_s=1.27$ in case of the eccentric stiffening and $h_s=0.508$ in case of the concentric stiffening. The material model is described by the polyconvex strain energy

$$\begin{aligned} \psi =\frac{1}{4}\lambda \left( \left( I_3-1\right) -{\text {ln}}{I_3}\right) +\frac{1}{2}\mu \left( I_1-3-{\text {ln}}{I_3}\right) , \end{aligned}$$

(93)

compare Sect. 4.1.1. The material parameters are $E=117.25$ for the Young’s modulus, $\nu =0.3$ for the Poisson’s ratio and the penalty parameter is chosen as $k=d_0 10^5$ with the bending stiffness $d_0=(Eh^3)/(12(1-\nu ^2)).$ The plate is meshed by $8\times 8 \times 2$ elements, whereas the flange is discretized by 2, respectively one element over the thickness for the eccentric and concentric stiffening. In order to demonstrate the stiffening effects, the out of plane displacements in the center of the plate are compared in Fig. 13. The applied material model differs to the material model which is recently used for this numerical example. In the literature the common material model is the Saint-Venant–Kirchhoff model, which does not satisfy the polyconvexity condition. However, the obtained results are in very close agreement compared to the results from [19, 37, 44], which can be explained by the relatively small strains, which are obtained in this example.

Fig. 13

Plate with varying stiffeners; Scaled (by factor 10) deformed configuration of the eccentric stiffened plate and load–displacement plot for (a) unstiffened-, (b) eccentric stiffened-, and (c) concentric stiffened plate

8 Conclusion

In this work, an astonishingly simple finite element formulation is presented, following the geometrically exact Kirchhoff–Love theory as discussed in [42]. Therein we have used a penalty formulation in order to fulfill the required $C^1$-continuity, which is the crucial implementational aspect of the shear-rigid shell model. This enables the use of well known and elementary $C^0$ quadratic continuous shape functions which also simplifies the handling of the boundary conditions drastically. In this approach the plane stress condition is satisfied on a constitutive level which leads to great flexibility regarding the material model. This work deals with finite elasticity using isotropic and anisotropic polyconvex energy densities. In this framework the existence of minimizers is guaranteed. Due to the generality of the shell model the formulation can also be extended to inelastic materials. The deployed time integration scheme is not energy conserving but an extension to an exact conserving scheme, as for example proposed in [16], is considered in detail in a next work. Combined with powerful mesh generators the proposed triangular finite element can be used to discretize and solve boundary value problems with complex geometries. A plane reference configuration is used in the proposed work. An extension to initially curved shells, as done in [41], can be regarded using an initial stress-free deformation.