A continuity re-relaxed thin shell formulation for static and dynamic analyses of linear problems

Abstract

This paper presents a curvature-constructed triangular element for static, free vibration and explicit dynamic analyses of shell structures by using a continuity re-relaxed technique. In the present method, the formulation is based on the classical thin shell theory, and only the translational displacements are treated as the filed variables that are assumed piecewisely linear. A set of three-node triangular background cells is adopted to discretize the problem domain. The curvature field in an element is constructed using the continuity re-relaxed technique, which can relax the continuity requirement of the trial function. The membrane strain filed is formulated same as the practice of standard FEM. Based on the principle of virtual work, the discertized system equations are finally formed. As the rotational displacements are not considered as the basic degrees of freedom, the essential boundary conditions of this part are imposed in the process of forming the curvature field. In order to validate the efficiency and accuracy of the present method, several numerical examples are studied. The results demonstrate that the present formulation can achieve very stable and accurate solutions with the less consuming of CPU time.

1 Introduction

With the widely application of thin shells in civil, mechanical and aerospace engineering, analyses of such structures have always been the focal point of research. As the analytical solutions are limited to problems with very simple geometries, various numerical approaches including the finite difference method (FDM), finite element method (FEM), finite volume method (FVM), boundary element method (BEM), spline strip element method and meshless method are always adopted to analyze and simulate the behaviors of shells. Among these numerical approaches, the FEM is still so far the most reliable tool.

Based on the finite element method (FEM), many efficient shell elements have been proposed by researchers in the last century, such as the 4-node Belytschko–Tsay quadrilateral element  [1], Hughes–Liu quadrilateral element  [2], mixed interpolation of tensorial components quadrilateral element (MITC4)  [3], physical stabilization of the 4-node shell element  [4]. All these methods possess higher computational accuracy in the numerical simulations. However, meshing complex geometry such as aircraft structures with quadrilaterals often brings great burdens in preprocess of analysis. Besides, quadrilateral element is inefficient in solving problems with warped elements, which ineluctably occurs in complex geometry. Furthermore, for large deformation analysis, folding may occur along the diagonals of the quadrilateral element, which leads to deterioration in accuracy, even invalidation of the computation.

Compared with quadrilateral elements, 3-node triangular elements are more attractive to engineers for their simplicity, easy in automatic meshing and re-meshing in adapting analysis. However, the direct application of Reissner–Mindlin theory to 3-node C0 shell problems with linear interpolation, such as the LSDYNA triangular element  [5, 6], often leads to an element with a “stiffer” stiffness, which surely affect the computational accuracy. In order to overcome this deficiency, Specht  [7] proposed a three-node plate bending element based on a polynomial displacement basis, which provided us a general convergence criterion for nonconforming shell elements. Civalek  [8, 9] presented a discrete singular convolution (DSC) method and analyzed the free vibration problems of shell structures. Zenkour  [10] studied the static and dynamic responses of anisotropic spherical shells using a mixed shear deformation modal. Another numerical difficulty for Reissner–Mindlin plate is the shear-locking phenomenon caused by parasitic internal energy. Thus, various numerical approaches, including reduced integration or selective integration  [11], discrete Kirchhoff theory (DKT)  [12, 13], mixed shear projected  [14], assumed natural strains (ANS)  [15], discrete shear gap (DSG) method  [16], improved absolute nodal coordinate-based shear deformable element  [17], have already been proposed by researches to reduce the locking effect. Among the various schemes proposed to derive reliable C0 triangular shell elements, the imposition of discrete Kirchhoff constraints constitutes a mean to deal with problems inherent in formulations, which accommodate the effect of transverse shear. Soon after, Wu et al.  [18] successfully applied the DKT element to dynamic large deformation analysis. However, the discrete Kirchhoff approach involves approximations for the normal rotations within the element; thus, high computational cost is needed to derive the stiffness matrix. The formulations directly derived from the Kirchhoff hypotheses are free of locking phenomena, and only transverse displacements are treated as the independent field variables. However, for Kirchhoff theory element, the C1 continuity requirement is needed when constructing the deflection field, and this is not an easy task. The other works of shell structure analysis in recent years include those given by Naghdabadi et al.  [19], Liu et al.  [20, 21], Wang et al.  [22].

In the effects to construct reliable Kirchhoff shell elements, many efficient works have been done by researchers in the past decades. In 1971, Morley  [23] first proposed a nonconforming displacement triangular finite element for plate bending problems. The accuracy of this element is very low, but convergence rate is assured with the refinement of mesh size. In 2001, Kolahi and Crisfield  [24] carried out a large-strain elasto-plastic shell formulation by using the “Morley triangle” element. Before long, Sabourin and Brunet  [25] presented a rotation-free triangular element for shell analysis. Onate et al.  [26, 27] formulated a simply triangular thin plate element with only one degree of freedom (DOF) per node by using the finite volume-like approach and gave detailed scheme for rotation-free triangular plate and shell elements. All these methods are very interesting and laid the foundation for our research in this work.

Based on the fundamental works presented above, we further give a thin shell model based on the Kirchhoff hypothesis by using linear shape functions in this paper. Three-node triangular elements that can be generated automatically for any complicated geometries are adopted to discrete the problem domain. The translational displacement fields are interpolated through linear shape functions same as the practice of standard FEM. Based on the generalized gradient smoothing technique (GST)  [28, 29], the smoothed slopes at each edge for an element are obtained by using the gradients of the cell and its neighboring cells sharing common edges. As the curvature and membrane strain in each triangular cells are constants, the system stiffness matrices can be computed via a simple summation operation. The principle of virtual work is then used to create the discretized system equations. In order to examine the efficiency and accuracy of the proposed formulation, a set of benchmark examples is studied and comparisons are made with results available in literatures. The excellent results demonstrate that the present method exhibits superior performance for both static and dynamic problems.

2 Shell formulations

2.1 Basic equations for thin shell

Based on the Kirchhoff hypothesis for thin shell analysis, the relationship between the local deflection ($\hat{{w}})$ in the normal direction and the rotations ($\hat{{\theta }}_x$,$\hat{{\theta }}_y )$ is given as follows

$$\begin{aligned} \hat{{\theta }}_x =\frac{\partial \hat{{w}}}{\partial \hat{{x}}}, \hat{{\theta }}_y =\frac{\partial \hat{{w}}}{\partial \hat{{y}}} \end{aligned}$$

(1)

Dividing the problem domain into several triangular cells, the local translational displacement fields $\hat{{u}}$, $\hat{{v}}$ and $\hat{{w}}$ in each element can be interpolated using the nodal displacements at the nodes of the element by the linear shape functions, which gives

$$\begin{aligned} \left\{ {{\begin{array}{l} {\hat{{u}}} \\ {\hat{{v}}} \\ {\hat{{w}}} \\ \end{array} }} \right\} =\sum _{i=1}^3 {\varphi _i \left( {\hat{{\mathbf{x}}}} \right) \left\{ {{\begin{array}{l} {\hat{{u}}_i } \\ {\hat{{v}}_i } \\ {\hat{{w}}_i } \\ \end{array} }} \right\} } \end{aligned}$$

(2)

where $\varphi _i \left( \hat{{{\mathbf{x}}}} \right)$ is the linear shape function value at node i and $\left\{ {{\begin{array}{ccc} {\hat{{u}}_i }&{} {\hat{{v}}_i }&{} {\hat{{w}}_i } \\ \end{array} }} \right\} ^{\mathrm{T}}$ is the local nodal displacement vector of node i.

The membrane strain in an element can be defined by

$$\begin{aligned} \hat{{{\varvec{\upvarepsilon } }}}_m =\left\{ {{\begin{array}{l} {\left( {\hat{{\varepsilon }}_m } \right) _{\hat{{x}}\hat{{x}}} } \\ {\left( {\hat{{\varepsilon }}_m } \right) _{\hat{{y}}\hat{{y}}} } \\ {\left( {\hat{{\varepsilon }}_m } \right) _{\hat{{x}}\hat{{y}}} } \\ \end{array} }} \right\} =\left\{ {{\begin{array}{l} {\frac{\partial \hat{{u}}}{\partial \hat{{x}}}} \\ {\frac{\partial \hat{{v}}}{\partial \hat{{y}}}} \\ {\frac{\partial \hat{{u}}}{\partial \hat{{y}}}+\frac{\partial \hat{{v}}}{\partial \hat{{x}}}} \\ \end{array} }} \right\} \end{aligned}$$

(3)

The curvature in a triangular cell can be expressed as

$$\begin{aligned} \hat{{{\varvec{\upkappa } }}}=\left\{ {{\begin{array}{l} {\hat{{\kappa }}_{\hat{{x}}\hat{{x}}} } \\ {\hat{{\kappa }}_{\hat{{y}}\hat{{y}}} } \\ {\hat{{\kappa }}_{\hat{{x}}\hat{{y}}} } \\ \end{array} }} \right\} =-\left\{ {{\begin{array}{l} {\frac{\partial ^{2}\hat{{w}}}{\partial \hat{{x}}^{2}}} \\ {\frac{\partial ^{2}\hat{{w}}}{\partial \hat{{y}}^{2}}} \\ {2\frac{\partial ^{2}\hat{{w}}}{\partial \hat{{x}}\partial \hat{{y}}}} \\ \end{array} }} \right\} =\mathbf{L}\hat{{w}} \end{aligned}$$

(4)

where $\mathbf{L}$ is the differential operator defined as

$$\begin{aligned} \mathbf{L}=\left\{ {{\begin{array}{lll} {-\frac{\partial ^{2}}{\partial \hat{{x}}^{2}}}&{} {-\frac{\partial ^{2}}{\partial \hat{{y}}^{2}}}&{} {-2\frac{\partial ^{2}}{\partial \hat{{x}}\partial \hat{{y}}}} \\ \end{array} }} \right\} \end{aligned}$$

(5)

2.2 Continuity re-relaxed and curvature-constructed

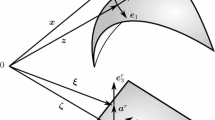
From Eq. (4), we can clearly find that the strict C1 continuity requirement for deflection field must be satisfied to obtain the curvature field in each cell. In order to relax the continuity requirement for deflection field, the area integral of the curvature in each cell can be converted into the boundary integral along the cell boundary through the generalized gradient smoothing operation. As shown in Fig. 1, the curvature in the triangular cell M can be constructed as follows

$$\begin{aligned} \overline{{ \hat{{{\varvec{\upkappa } }}}}}=\frac{1}{A_m }\int _{\Omega _m } {\mathbf{L}\hat{{w}}\left( \hat{{{\mathbf{x}}}} \right) } \hbox {d}\Omega =\frac{1}{A_m }\int _{\Gamma _m } {\mathbf{n}\nabla \hat{{w}}\left( \hat{{{\mathbf{x}}}} \right) } \hbox {d}\Gamma =\frac{1}{A_m }\int _{\Gamma _m } \mathbf{n}\hat{{\varvec{\uptheta } }}\left( \hat{{{\mathbf{x}}}} \right) \hbox {d}\Gamma =\frac{1}{A_m }\sum _{k=1}^3 {l_k \mathbf{n}_k^m \hat{{{\varvec{\uptheta } }}}_k \left( \hat{{{\mathbf{x}}}} \right) } \end{aligned}$$

(6)

where $\Gamma _m$ is the boundary of cell M, $A_m$ is the area of cell M, $l_k$ is the length of the $k\hbox {th}$ edge, $\mathbf{n}_k^m$ is the outward normal matrix containing the components of the outward normal vector on the edge k in the local coordinate system given by

$$\begin{aligned} \mathbf{n}_k^m =\left[ {{\begin{array}{ccc} {-n_{xk}^m }&{} 0 \\ 0&{} {-n_{yk}^m } \\ {-n_{yk}^m }&{} {-n_{xk}^m } \\ \end{array} }} \right] \end{aligned}$$

(7)

and $\hat{{{\varvec{\uptheta } }}}_k \left( \hat{{{\mathbf{x}}}} \right)$ is the local rotations on the $k\hbox {th}$ edge of cell M defined as

$$\begin{aligned} \hat{{{\varvec{\uptheta } }}}_{\mathrm{k}} =\left\{ {\left. {{\begin{array}{c} {\hat{{\theta }}_{xk} } \\ {\hat{{\theta }}_{yk} } \\ \end{array} }} \right\} } \right. =\mathbf{T}_{mk} \overline{{{\varvec{\uptheta } }}}_k \end{aligned}$$

(8)

in which

$$\begin{aligned} \mathbf{T}_{mk} =\left[ {{\begin{array}{cc} {-n_{yk}^m }&{} {-n_{xk}^m } \\ {n_{xk}^m }&{} {-n_{yk}^m } \\ \end{array} }} \right] \end{aligned}$$

(9)

and

$$\begin{aligned} \overline{{{\varvec{\uptheta } }}}_k =\left\{ {\left. {{\begin{array}{c} {\overline{{\theta }}_{sk} } \\ {\overline{{\theta }}_{nk} } \\ \end{array} }} \right\} } \right. \end{aligned}$$

(10)

is the smoothed slope corresponding to edge k obtained using the gradients of the cell and its neighboring cell sharing common edge k.

Fig. 1

Local slopes and outer normal components for each edge of the triangular cell

Fig. 2

Local coordinate systems for master and slave cells and the smoothed slopes at the edges of the master cell

Figure 2 shows a representative triangular cell M with three neighboring cells (named S1, S2 and S3). The local coordinate systems for each cell are also given in the figure. The smoothed slope $\overline{{{\varvec{\uptheta } }}}_k$ at the edge k can then be expressed as

$$\begin{aligned} \left\{ {\left. {{\begin{array}{l} {\overline{{\theta }}_{sk} } \\ {\overline{{\theta }}_{nk} } \\ \end{array} }} \right\} } \right. =\frac{1}{A_m +A_{sk} }\left( {A_m \left\{ {\left. {{\begin{array}{l} {\theta _{sk}^m } \\ {\theta _{nk}^m } \\ \end{array} }} \right\} +A_{sk} \left\{ {\left. {{\begin{array}{l} {\theta _s^{sk} } \\ {\theta _n^{sk} } \\ \end{array} }} \right\} } \right. } \right. } \right) \end{aligned}$$

(11)

where $A_m$ is the area of cell M, $A_{sk}$ is the area of $k\hbox {th}$ neighboring cell Sk. $\theta _{nk}^m$, $\theta _{sk}^m$, $\theta _n^{sk}$and $\theta _s^{sk}$ presented in Eq. (11) will be computed using the local deflections presented next.

In the global coordinate system, the nodal displacement vector at each node can be expressed as

$$\begin{aligned} \mathbf{d}_i =\left\{ {{\begin{array}{l} {u_i } \\ {v_i } \\ {w_i } \\ \end{array} }} \right\} \end{aligned}$$

(12)

As shown in Fig. 2, the local nodal deflections for cell M can be obtained through the global nodal displacement vector $\mathbf{d}_1$, $\mathbf{d}_2$ and $\mathbf{d}_3$, which gives

$$\begin{aligned} \left\{ {{\begin{array}{c} {w_1^m } \\ {w_2^m } \\ {w_3^m } \\ \end{array} }} \right\}= & {} \left[ {{\begin{array}{ccc} {\mathbf{c}_{\hat{{z}}} }&{} \mathbf{0}&{} \mathbf{0} \\ \mathbf{0}&{} {\mathbf{c}_{\hat{{z}}} }&{} \mathbf{0} \\ \mathbf{0}&{} \mathbf{0}&{} {\mathbf{c}_{\hat{{z}}} } \\ \end{array} }} \right] \left\{ {{\begin{array}{c} {\mathbf{d}_1 } \\ {\mathbf{d}_2 } \\ {\mathbf{d}_3 } \\ \end{array} }} \right\} =\mathbf{T}_w^m \left\{ {{\begin{array}{c} {\mathbf{d}_1 } \\ {\mathbf{d}_2 } \\ {\mathbf{d}_3 } \\ \end{array} }} \right\} \nonumber \\ \mathbf{c}_{\hat{{z}}}= & {} \left\{ {{\begin{array}{ccc} {c_{\hat{{z}}x} }&{} {c_{\hat{{z}}y} }&{} {c_{\hat{{z}}z} } \\ \end{array} }} \right\} ,\quad {\mathbf{0}=\left\{ {{\begin{array}{ccc} 0&{} 0&{} 0 \\ \end{array} }} \right\} } \end{aligned}$$

(13)

where $c_{\hat{{z}}x}$ is the cosine of the angle between the $\hat{{z}}$ and x axes, etc.

Similarly, the local nodal deflections for the neighboring cell S1, S2 and S3 can be obtained by

$$\begin{aligned} \left\{ \begin{array}{c} {w_1^{s1} } \\ {w_2^{s1} } \\ {w_3^{s1} } \\ \end{array} \right\}= & {} \left[ {{\begin{array}{ccc} {\mathbf{c}_{z^{1}} }&{} \mathbf{0}&{} \mathbf{0} \\ \mathbf{0}&{} {\mathbf{c}_{z^{1}} }&{} \mathbf{0} \\ \mathbf{0}&{} \mathbf{0}&{} {\mathbf{c}_{z^{1}} } \\ \end{array} }} \right] \left\{ {{\begin{array}{c} {\mathbf{d}_2 } \\ {\mathbf{d}_4 } \\ {\mathbf{d}_3 } \\ \end{array} }} \right\} =\mathbf{T}_w^{s1} \left\{ {{\begin{array}{c} {\mathbf{d}_2 } \\ {\mathbf{d}_4 } \\ {\mathbf{d}_3 } \\ \end{array} }} \right\} ,\quad {\mathbf{c}_{z^{1}} =\left\{ {{\begin{array}{ccc} {c_{z^{1}x} }&{} {c_{z^{1}y} }&{} {c_{z^{1}z} } \\ \end{array} }} \right\} } \end{aligned}$$

(14)

$$\begin{aligned} \left\{ \begin{array}{c} {w_1^{s2} } \\ {w_2^{s2} } \\ {w_3^{s2} } \\ \end{array} \right\}= & {} \left[ {{\begin{array}{ccc} {\mathbf{c}_{z^{2}} }&{} \mathbf{0}&{} \mathbf{0} \\ \mathbf{0}&{} {\mathbf{c}_{z^{2}} }&{} \mathbf{0} \\ \mathbf{0}&{} \mathbf{0}&{} {\mathbf{c}_{z^{2}} } \\ \end{array} }} \right] \left\{ {{\begin{array}{c} {\mathbf{d}_3 } \\ {\mathbf{d}_5 } \\ {\mathbf{d}_1 } \\ \end{array} }} \right\} =\mathbf{T}_w^{s2} \left\{ {{\begin{array}{c} {\mathbf{d}_3 } \\ {\mathbf{d}_5 } \\ {\mathbf{d}_1 } \\ \end{array} }} \right\} ,\quad {\mathbf{c}_{z^{2}} =\left\{ {{\begin{array}{ccc} {c_{z^{2}x} }&{} {c_{z^{2}y} }&{} {c_{z^{2}z} } \\ \end{array} }} \right\} } \end{aligned}$$

(15)

$$\begin{aligned} \left\{ {{\begin{array}{c} {w_1^{s3} } \\ {w_2^{s3} } \\ {w_3^{s3} } \\ \end{array} }} \right\}= & {} \left[ {{\begin{array}{ccc} {\mathbf{c}_{z^{3}} }&{} \mathbf{0}&{} \mathbf{0} \\ \mathbf{0}&{} {\mathbf{c}_{z^{3}} }&{} \mathbf{0} \\ \mathbf{0}&{} \mathbf{0}&{} {\mathbf{c}_{z^{3}} } \\ \end{array} }} \right] \left\{ {{\begin{array}{c} {\mathbf{d}_1 } \\ {\mathbf{d}_6 } \\ {\mathbf{d}_2 } \\ \end{array} }} \right\} =\mathbf{T}_w^{s3} \left\{ {{\begin{array}{c} {\mathbf{d}_1 } \\ {\mathbf{d}_6 } \\ {\mathbf{d}_2 } \\ \end{array} }} \right\} , \quad {\mathbf{c}_{z^{3}} =\left\{ {{\begin{array}{ccc} {c_{z^{3}x} }&{} {c_{z^{3}y} }&{} {c_{z^{3}z} } \\ \end{array} }} \right\} } \end{aligned}$$

(16)

From Eq. (2), the local deflection in the cell M can be computed by

$$\begin{aligned} w^{m}=\sum _{i=1}^3 {\varphi _i } \left( \hat{{{\mathbf{x}}}} \right) w_i^m \end{aligned}$$

(17)

Substituting Eq. (17) into Eq. (1) yields

$$\begin{aligned} \left\{ \begin{array}{c} {\theta _x^m } \\ {\theta _y^m } \\ \end{array} \right\}= & {} \sum _{i=1}^3 {\left\{ {{\begin{array}{c} {\frac{\partial \varphi _i \left( \hat{{{\mathbf{x}}}} \right) }{\partial \hat{{x}}}} \\ {\frac{\partial \varphi _i \left( \hat{{{\mathbf{x}}}} \right) }{\partial \hat{{y}}}} \\ \end{array} }} \right\} } w_i^m \end{aligned}$$

(18)

$$\begin{aligned} \left\{ {{\begin{array}{c} {\theta _s^m } \\ {\theta _n^m } \\ \end{array} }} \right\}= & {} \left[ {{\begin{array}{cc} {-n_{yk}^m }&{} {n_{xk}^m } \\ {-n_{xk}^m }&{} {-n_{yk}^m } \\ \end{array} }} \right] \left\{ {{\begin{array}{c} {\theta _x^m } \\ {\theta _y^m } \\ \end{array} }} \right\} =\left[ {\mathbf{T}_{mk} } \right] ^{{\mathrm{T}}}\left\{ {{\begin{array}{l} {\theta _x^m } \\ {\theta _y^m } \\ \end{array} }} \right\} \end{aligned}$$

(19)

Similarly, $\theta _n^{sk}$ and $\theta _s^{sk}$ can be given by

$$\begin{aligned} \left\{ {{\begin{array}{c} {\theta _x^{sk} } \\ {\theta _y^{sk} } \\ \end{array} }} \right\}= & {} \sum _{i=1}^3 {\left\{ {{\begin{array}{c} {\frac{\partial \varphi _i \left( {\mathbf{x}^{k}} \right) }{\partial x^{k}}} \\ {\frac{\partial \varphi _i \left( {\mathbf{x}^{k}} \right) }{\partial y^{k}}} \\ \end{array} }} \right\} } w_i^{sk} \end{aligned}$$

(20)

$$\begin{aligned} \left\{ {{\begin{array}{c} {\theta _s^{sk} } \\ {\theta _n^{sk} } \\ \end{array} }} \right\}= & {} \left[ {{\begin{array}{cc} {-n_y^{sk} }&{} {n_x^{sk} } \\ {-n_x^{sk} }&{} {-n_y^{sk} } \\ \end{array} }} \right] \left\{ {{\begin{array}{c} {\theta _x^{sk} } \\ {\theta _y^{sk} } \\ \end{array} }} \right\} =\left[ {\mathbf{T}_{sk} } \right] ^{{\mathrm{T}}}\left\{ {{\begin{array}{c} {\theta _x^{sk} } \\ {\theta _y^{sk} } \\ \end{array} }} \right\} \end{aligned}$$

(21)

in which $n_x^{sk}$ and $n_y^{sk}$ are the components of the outward normal vector on the edge k in the local coordinate system $(x^{k},y^{k},z^{k})$.

Based on the above equations, the curvature in the triangular cell M can be obtained using the global displacements, which gives

$$\begin{aligned} {\overline{\hat{\varvec{\upkappa }}}}=\mathbf{B}_b \mathbf{d}_m , \quad \mathbf{d}_m =\left\{ {{\begin{array}{c} {\mathbf{d}_1 } \\ {\mathbf{d}_2 } \\ {\mathbf{d}_3 } \\ {\mathbf{d}_4 } \\ {\mathbf{d}_5 } \\ {\mathbf{d}_6 } \\ \end{array}}} \right\} \end{aligned}$$

(22)

where $\mathbf{B}_b$ is the curvature displacement matrix presented in detail in Appendix A.

2.3 Membrane strain displacement matrix

The local in-plane displacement field in the cell M is interpolated by the local nodal displacements using the linear shape function same as in standard FEM

$$\begin{aligned} \left\{ {{\begin{array}{c} {u^{m}} \\ {v^{m}} \\ \end{array} }} \right\} =\left[ {{\begin{array}{cccccc} {\varphi _1 \left( \hat{{{\mathbf{x}}}} \right) }&{} 0&{} {\varphi _2 \left( \hat{{{\mathbf{x}}}} \right) }&{} 0&{} {\varphi _3 \left( \hat{{{\mathbf{x}}}} \right) }&{} 0 \\ 0&{} {\varphi _1 \left( \hat{{{\mathbf{x}}}} \right) }&{} 0&{} {\varphi _2 \left( \hat{{{\mathbf{x}}}} \right) }&{} 0&{} {\varphi _3 \left( \hat{{{\mathbf{x}}}} \right) } \\ \end{array} }} \right] \left\{ {{\begin{array}{c} {u_1^m } \\ {v_1^m } \\ {u_2^m } \\ {v_2^m } \\ {u_3^m } \\ {v_3^m } \\ \end{array} }} \right\} \end{aligned}$$

(23)

From Eq. (3), the membrane strain in the cell M is given by

$$\begin{aligned} \hat{{{\varvec{\upvarepsilon } }}}_m =\left[ {{\begin{array}{cccccc} {\frac{\partial \varphi _1 \left( \hat{{{\mathbf{x}}}} \right) }{\partial \hat{{x}}}}&{} 0&{} {\frac{\partial \varphi _2 \left( \hat{{{\mathbf{x}}}} \right) }{\partial \hat{{x}}}}&{} 0&{} {\frac{\partial \varphi _3 \left( \hat{{{\mathbf{x}}}} \right) }{\partial \hat{{x}}}}&{} 0 \\ 0&{} {\frac{\partial \varphi _1 \left( \hat{{{\mathbf{x}}}} \right) }{\partial \hat{{y}}}}&{} 0&{} {\frac{\partial \varphi _2 \left( \hat{{{\mathbf{x}}}} \right) }{\partial \hat{{y}}}}&{} 0&{} {\frac{\partial \varphi _3 \left( \hat{{{\mathbf{x}}}} \right) }{\partial \hat{{y}}}} \\ {\frac{\partial \varphi _1 \left( \hat{{{\mathbf{x}}}} \right) }{\partial \hat{{y}}}}&{} {\frac{\partial \varphi _1 \left( \hat{{{\mathbf{x}}}} \right) }{\partial \hat{{x}}}}&{} {\frac{\partial \varphi _2 \left( \hat{{{\mathbf{x}}}} \right) }{\partial \hat{{y}}}}&{} {\frac{\partial \varphi _2 \left( \hat{{{\mathbf{x}}}} \right) }{\partial \hat{{x}}}}&{} {\frac{\partial \varphi _3 \left( \hat{{{\mathbf{x}}}} \right) }{\partial \hat{{y}}}}&{} {\frac{\partial \varphi _3 \left( \hat{{{\mathbf{x}}}} \right) }{\partial \hat{{x}}}} \\ \end{array} }} \right] \left\{ {{\begin{array}{c} {u_1^m } \\ {v_1^m } \\ {u_2^m } \\ {v_2^m } \\ {u_3^m } \\ {v_3^m } \\ \end{array} }} \right\} \end{aligned}$$

(24)

Using the global nodal displacement vector, the local nodal displacements $u_i^m$ and $v_i^m$ can be computed by

$$\begin{aligned} \left\{ \begin{array}{c} {u_1^m } \\ {v_1^m } \\ {u_2^m } \\ {v_2^m } \\ {u_3^m } \\ {v_3^m } \\ \end{array} \right\}= & {} \left[ {{\begin{array}{cccccc} {\mathbf{c}_{\hat{{x}}} }&{} \mathbf{0}&{} \mathbf{0}&{} \mathbf{0}&{} \mathbf{0}&{} \mathbf{0} \\ {\mathbf{c}_{\hat{{y}}} }&{} \mathbf{0}&{} \mathbf{0}&{} \mathbf{0}&{} \mathbf{0}&{} \mathbf{0} \\ \mathbf{0}&{} {\mathbf{c}_{\hat{{x}}} }&{} \mathbf{0}&{} \mathbf{0}&{} \mathbf{0}&{} \mathbf{0} \\ \mathbf{0}&{} {\mathbf{c}_{\hat{{y}}} }&{} \mathbf{0}&{} \mathbf{0}&{} \mathbf{0}&{} \mathbf{0} \\ \mathbf{0}&{} \mathbf{0}&{} {\mathbf{c}_{\hat{{x}}} }&{} \mathbf{0}&{} \mathbf{0}&{} \mathbf{0} \\ \mathbf{0}&{} \mathbf{0}&{} {\mathbf{c}_{\hat{{y}}} }&{} \mathbf{0}&{} \mathbf{0}&{} \mathbf{0} \\ \end{array} }} \right] \left\{ {{\begin{array}{c} {\mathbf{d}_1 } \\ {\mathbf{d}_2 } \\ {\mathbf{d}_3 } \\ {\mathbf{d}_4 } \\ {\mathbf{d}_5 } \\ {\mathbf{d}_6 } \\ \end{array} }} \right\} =\mathbf{T}_u^m \mathbf{d}_m \nonumber \\ \mathbf{c}_{\hat{{x}}}= & {} \left\{ {{\begin{array}{ccc} {c_{\hat{{x}}x} }&{} {c_{\hat{{x}}y} }&{} {c_{\hat{{x}}z} } \\ \end{array} }} \right\} ,\quad {\mathbf{c}_{\hat{{y}}} =\left\{ {{\begin{array}{ccc} {c_{\hat{{y}}x} }&{} {c_{\hat{{y}}y} }&{} {c_{\hat{{y}}z} } \\ \end{array} }} \right\} } \end{aligned}$$

(25)

Substituting Eq. (25) into (24), the membrane strain in the triangular cell M can be obtained using those in global system

$$\begin{aligned} \hat{{{\varvec{\upvarepsilon } }}}_m =\mathbf{B}_m \mathbf{d}_m \end{aligned}$$

(26)

in which $\mathbf{B}_m$ is the membrane strain displacement matrix given by

$$\begin{aligned} \mathbf{B}_m =\left[ {{\begin{array}{cccccc} {\frac{\partial \varphi _1 \left( \hat{{{\mathbf{x}}}} \right) }{\partial \hat{{x}}}}&{} 0&{} {\frac{\partial \varphi _2 \left( \hat{{{\mathbf{x}}}} \right) }{\partial \hat{{x}}}}&{} 0&{} {\frac{\partial \varphi _3 \left( \hat{{{\mathbf{x}}}} \right) }{\partial \hat{{x}}}}&{} 0 \\ 0&{} {\frac{\partial \varphi _1 \left( \hat{{{\mathbf{x}}}} \right) }{\partial \hat{{y}}}}&{} 0&{} {\frac{\partial \varphi _2 \left( \hat{{{\mathbf{x}}}} \right) }{\partial \hat{{y}}}}&{} 0&{} {\frac{\partial \varphi _3 \left( \hat{{{\mathbf{x}}}} \right) }{\partial \hat{{y}}}} \\ {\frac{\partial \varphi _1 \left( \hat{{{\mathbf{x}}}} \right) }{\partial \hat{{y}}}}&{} {\frac{\partial \varphi _1 \left( \hat{{{\mathbf{x}}}} \right) }{\partial \hat{{x}}}}&{} {\frac{\partial \varphi _2 \left( \hat{{{\mathbf{x}}}} \right) }{\partial \hat{{y}}}}&{} {\frac{\partial \varphi _2 \left( \hat{{{\mathbf{x}}}} \right) }{\partial \hat{{x}}}}&{} {\frac{\partial \varphi _3 \left( \hat{{{\mathbf{x}}}} \right) }{\partial \hat{{y}}}}&{} {\frac{\partial \varphi _3 \left( \hat{{{\mathbf{x}}}} \right) }{\partial \hat{{x}}}} \\ \end{array} }} \right] \mathbf{T}_u^m \end{aligned}$$

(27)

3 Discretized system equations

Applying the principle of virtual work, the weak form of kinematic equation can now be written as

$$\begin{aligned} \delta W=\delta W^{{\mathrm{int}}}+\delta W^{{\mathrm{kin}}}-\delta W^{{\mathrm{ext}}}=0 \end{aligned}$$

(28)

In Eq. (28), $\delta W^{\mathrm{ext}}$ is the virtual external work since it results from the external loads. Due to the virtual displacement $\delta \mathbf{u}$, the virtual external work is given by

$$\begin{aligned} \delta W^{\mathrm{ext}}=\int _\Omega {\delta \mathbf{u}^{\mathrm{T}}\tilde{\mathbf{f}}} \hbox {d}\Omega +\int _\Gamma {\delta \mathbf{u}^{\mathrm{T}}\tilde{\mathbf{t}}} \hbox {d}\Gamma \end{aligned}$$

(29)

where $\tilde{\mathbf{f}}$ is the external load applied over the problem domain $\Omega$, and $\tilde{\mathbf{t}}$ is the traction applied on the natural boundary $\Gamma$.

$\delta W^{\mathrm{int}}$ is the virtual internal work given by

$$\begin{aligned} \delta W^{\mathrm{int}}=\int _\Omega \delta \hat{{{\varvec{\upvarepsilon } }}}_m { }^{\mathrm{T}}\mathbf{D}_m \hat{{{\varvec{\upvarepsilon } }}}_m \hbox {d}\Omega +\int _\Omega \delta {\overline{\hat{\varvec{\upkappa }}}}^{\mathrm{T}}\mathbf{D}_b {\overline{\hat{\varvec{\upkappa }}}}\hbox {d}\Omega \end{aligned}$$

(30)

where the membrane stiffness constitutive coefficients ($\mathbf{D}_m )$ and the bending stiffness constitutive coefficients ($\mathbf{D}_b )$ are defined as

$$\begin{aligned} \mathbf{D}_m= & {} \int _{-\frac{t}{2}}^{\frac{t}{2}} {\mathbf{D}_0 } \hbox {d}z=t\mathbf{D}_0 \end{aligned}$$

(31)

$$\begin{aligned} \mathbf{D}_b= & {} \int _{-\frac{t}{2}}^{\frac{t}{2}} {z^{2}\mathbf{D}_0 } \hbox {d}z=\frac{t^{3}}{12}\mathbf{D}_0 \end{aligned}$$

(32)

and the matrix $\mathbf{D}_0$ is the constitutive coefficients given by

$$\begin{aligned} \mathbf{D}_0 =\frac{E}{1-\nu ^{2}}\left[ {{\begin{array}{ccc} 1&{} \nu &{} 0 \\ \nu &{} 1&{} 0 \\ 0&{} 0&{} {\left( {1-\nu } \right) /2} \\ \end{array} }} \right] \end{aligned}$$

(33)

in which E is Young’s modulus and $\nu$ is Poisson ratio.

$\delta W^{{\mathrm{kin}}}$ is the virtual kinetic work given by

$$\begin{aligned} \delta W^{{\mathrm{kin}}}=\int _\Omega {\rho t\delta \mathbf{u}^{\mathrm{T}}\ddot{\mathbf{u}}} \hbox {d}\Omega \end{aligned}$$

(34)

where $\rho$ is the density of the material, and $\ddot{\mathbf{u}}$ the acceleration that can be expressed in terms of the nodal acceleration $\ddot{\mathbf{d}}_i$ and the shape functions $\varphi _i \left( \mathbf{x} \right)$.

$$\begin{aligned} \ddot{\mathbf{u}}\left( \mathbf{x} \right) =\sum _{i=1}^3 {\varphi _i } \left( \mathbf{x} \right) \ddot{\mathbf{d}}_i \end{aligned}$$

(35)

3.1 Static analysis

For static analysis, the kinetic work item vanishes and Eq. (28) can be rewritten as

$$\begin{aligned} \delta W=\delta W^{\mathrm{int}}-\delta W^{\mathrm{ext}}=0 \end{aligned}$$

(36)

Substituting Eqs. (2), (22) and (26) into Eq. (36), a set of discretized algebraic system equations can be obtained in the following matrix form

$$\begin{aligned} \mathbf{Kd}-\mathbf{F}^{\mathrm{ext}}=\mathbf{0} \end{aligned}$$

(37)

where $\mathbf{d}$ is the vector of global nodal displacement at all of the nodes, $\mathbf{F}^{\mathrm{ext}}$ is the force vector defined as

$$\begin{aligned} \mathbf{F}^{\mathrm{ext}}=\int _\Omega {{\varvec{\upvarphi }}^{\mathrm{T}}} \left( \mathbf{x} \right) \tilde{\mathbf{f}}\hbox {d}\Omega +\int _\Gamma {{\varvec{\upvarphi }}^{\mathrm{T}}} \left( \mathbf{x} \right) \tilde{\mathbf{t}}\hbox {d}\Gamma \end{aligned}$$

(38)

in which ${\varvec{\upvarphi }}^{\mathrm{T}}\left( \mathbf{x} \right)$ is the shape function vector.

In Eq. (37), $\mathbf{K}$ is the global stiffness matrix assembled in the form of

$$\begin{aligned} \mathbf{K}=\sum _{M=1}^{N_{{\mathrm{ele}}} } {\mathbf{K}_{\left( M \right) } } \end{aligned}$$

(39)

where $N_{{\mathrm{ele}}}$ is the total number of triangular cells for the whole problem domain $\Omega$, and $\mathbf{K}_{(M)}$ is the stiffness matrix associated with cell M calculated using

$$\begin{aligned} \mathbf{K}_{\left( M \right) }= & {} \mathbf{K}_{m\left( M \right) } +\mathbf{K}_{b\left( M \right) } \end{aligned}$$

(40)

$$\begin{aligned} \mathbf{K}_{m\left( M \right) }= & {} \mathbf{B}_m^{\mathrm{T}} \mathbf{D}_m \mathbf{B}_m A_m \end{aligned}$$

(41)

$$\begin{aligned} \mathbf{K}_{b\left( M \right) }= & {} \mathbf{B}_b^{\mathrm{T}} \mathbf{D}_b \mathbf{B}_b A_m \end{aligned}$$

(42)

in which $A_k$ is the area of cell M.

3.2 Free vibration analysis

For the free vibration analysis of Kirchhoff shell, the generalized weak form can be deduced by simply eliminating the external work item presented in Eq. (28), which gives

$$\begin{aligned} \delta W=\delta W^{\mathrm{int}}+\delta W^{\mathrm{kin}}=0 \end{aligned}$$

(43)

Substituting Eqs. (2), (30) and (34) into Eq. (40) yields

$$\begin{aligned} \mathbf{Kd}+\mathbf{M}{\ddot{\mathbf{d}}}=\mathbf{0} \end{aligned}$$

(44)

in which the global stiffness matrix $\mathbf{K}$ has the same expression as presented in Eq. (39), $\mathbf{M}$ is the global mass matrix defined by

$$\begin{aligned} \mathbf{M}=\sum _{M=1}^{N_{\mathrm{ele}} } {\mathbf{M}_{\left( M \right) } } \end{aligned}$$

(45)

and $\mathbf{M}_{(M)}$ is sub-matrices of the mass matrix related to cell M given by

$$\begin{aligned} \mathbf{M}_{\left( M \right) } =\int _{\Omega _{(M)} } {{\varvec{\upvarphi }}^{T}\left( \mathbf{x} \right) \mathbf{m}} {\varvec{\upvarphi }}\left( \mathbf{x} \right) d\Omega \end{aligned}$$

(46)

where $\mathbf{m}$ is the matrix containing the mass density of the material $\rho$ and thickness t as

$$\begin{aligned} \mathbf{m}=\hbox {diag}\left\{ {{\begin{array}{ccc} {\rho t}&{} {\rho t}&{} {\rho t} \\ \end{array} }} \right\} \end{aligned}$$

(47)

A general solution of such a homogeneous equation can be written as

$$\begin{aligned} \mathbf{d}=\lambda \exp (i\omega t) \end{aligned}$$

(48)

where $\lambda$ indicates the eigenvector, t is time and $\omega$ is natural frequency. On it substitution into Eq. (44), the natural frequency $\omega$ can then be obtained by solving the following eigenvalue equation

$$\begin{aligned} \left( {-\omega ^{2}\mathbf{M}+\mathbf{K}} \right) \mathbf{\uplambda }=\mathbf{0} \end{aligned}$$

(49)

3.3 Explicit dynamic analysis

The previous thin shell formulation is extended for explicit dynamic analysis in this subsection. An updated Lagrangian formulation is established, and elastic constitutive is used. The discrete equations of motion can be given by

$$\begin{aligned} \mathbf{F}^{\mathrm{ext}}-\mathbf{F}^{\mathrm{int}}=\mathbf{M}{\ddot{\mathbf{d}}} \end{aligned}$$

(50)

in which the mass matrix $\mathbf{M}$ has been given in Sect. 3.2. It should be noted that the lumped mass matrix will be used in this subsection, and the mass matrix corresponding to cell M can then be rewritten as

$$\begin{aligned} \mathbf{M}_{\left( M \right) } =\hbox {diag}\left\{ {m_1 ,m_2 ,m_3 } \right\} \end{aligned}$$

(51)

and $m_i$ is the lumped mass at the node i given by

$$\begin{aligned} m_i ={\rho tA_m }\big /3 \end{aligned}$$

(52)

In Eq. (50), $\mathbf{F}^{\mathrm{int}}$ is the internal force vector computed by

$$\begin{aligned} \mathbf{F}^{\mathrm{int}}= & {} \sum _{M=1}^{N_{\mathrm{ele}} } {\mathbf{f}_{\left( M \right) }^{\mathrm{int}} } \end{aligned}$$

(53)

$$\begin{aligned} \mathbf{f}_{\left( M \right) }^{\mathrm{int}}= & {} \left( {\mathbf{B}_m^{\mathrm{T}} {\varvec{\upsigma } }_m +\mathbf{B}_b^{\mathrm{T}} \mathbf{m}} \right) A_m \end{aligned}$$

(54)

where ${\varvec{\upsigma } }_m$ is the membrane stress and $\mathbf{m}$ is the bending moment given by

$$\begin{aligned} {\varvec{\upsigma } }_m^{n+1}= & {} {\varvec{\upsigma } }_m^n +\mathbf{D}_m \Delta \hat{{{\varvec{\upvarepsilon } }}}_m \end{aligned}$$

(55)

$$\begin{aligned} \mathbf{m}^{n+1}= & {} \mathbf{m}^{n}+\mathbf{D}_b \Delta {\overline{\hat{\varvec{\upkappa }}}} \end{aligned}$$

(56)

$$\begin{aligned} \Delta \hat{{{\varvec{\upvarepsilon } }}}_m= & {} \mathbf{B}_m \Delta \mathbf{d}_m \end{aligned}$$

(57)

$$\begin{aligned} \Delta {\overline{\hat{\varvec{\upkappa }}}}= & {} \mathbf{B}_b \Delta \mathbf{d}_m \end{aligned}$$

(58)

4 Impose essential boundary conditions

In the present work, the independent variables only contain the translational displacements, and the rotational displacements are not considered as the basic degrees of freedom. The translational displacement boundary conditions can be prescribed when solving the global system equations same as the practice of standard FEM. However, the rotational displacement boundary conditions must be imposed when building the curvature displacement matrix.

For cell M, if one of the edge (suppose edge k) located at the boundary line, the $k\hbox {th}$ neighboring cell vanishes as shown in Fig. 3, then we will not consider the contribution of the cell Sk for $\overline{{{\varvec{\uptheta } }}}_k$ in Eq. (10) when building the curvature displacement matrix. The side rotations on the boundary lines only contributed from cell M. The prescription of the rotational boundary conditions is a simple process as the side rotations are formulated in terms of the normal and tangential rotation values. The potential rotational conditions may be classified as:

(a) $\theta _{nk} =0$, $\theta _{sk} =0$: The rotational boundary condition $\theta _{nk} =0$ is imposed by neglecting the terms contributed by the second column of matrix $\mathbf{T}_{mk}$ in Eq.  (8) when building the curvature displacement matrix. Similarly, $\theta _{sk} =0$ is imposed by neglecting the terms contributed by the first column of matrix $\mathbf{T}_{mk}$. It must be point out that the condition $\theta _{sk} =0$ is automatically satisfied when prescribing the side displacements $\mathbf{d}_i =\mathbf{d}_j =\mathbf{0}$ ($\mathbf{d}_i$ and $\mathbf{d}_j$ are the nodal displacements).

(b) $\theta _{xk} =0$, $\theta _{yk} =0$: The rotational boundary condition $\theta _{xk} =0$ is imposed by neglecting the terms contributed by the first row of matrix $\mathbf{T}_{mk}$ in Eq. (8) when building the displacement matrix. Similarly, $\theta _{yk} =0$ is imposed by neglecting the terms contributed by the second row of matrix $\mathbf{T}_{mk}$.

5 Numerical examples

The present formulation has been coded using Matlab program. For comparison, several other elements such as C0  [5], DKT  [13] and S3R have also been implemented in our package. The CPU time is measured using the hardware platform CPU: Intel(R) Core(TM) i5-3450 (3.1 GHz); RAM 8.00 GB.

For explicit dynamic analysis, the time step $\Delta t$ is determined by  [30, 31]

$$\begin{aligned} \Delta t=\alpha \Delta t_\mathrm{crit} \end{aligned}$$

(59)

with

$$\begin{aligned} \Delta t_\mathrm{crit} =\mathop {\min }\limits _e \frac{l_e }{c_e } \end{aligned}$$

(60)

in which $\Delta t_\mathrm{crit}$ denotes the critical time step; $l_e$ is a characteristic length of element e and $c_e$ the wavespeed of element e. $\alpha \in \left[ {0.8,0.98} \right]$ is the Courant number which is set to 0.90 in this study.

Fig. 3

Triangular cell next to the boundary line

Fig. 4

Scordelis–Lo roof with diaphragm ends

Fig. 5

Deflection at middle node of the free edge for different DOFs

Fig. 6

Vertical displacement of support line

Fig. 7

Longitudinal displacement of support line

Fig. 8

Model of the hood of an automobile

Fig. 9

Displacements at the loading point for different DOFs: a x-direction; b y-direction

Fig. 10

Displacements along the line AB: a x-direction; b y-direction

5.1 Scordelis–Lo roof problem

The Scordelis–Lo roof shown in Fig. 4 is a famous benchmark problem for shell analysis to test a numerical method. The length of the shell is $L=50\,\hbox {ft}$, the radius is $R=25\,\hbox {ft}$, the thickness is $t=0.25\,\hbox {ft}$, and the span angle is $\theta _0 =40^{\circ }$. The material properties are as follows: Poisson’s ratio $\nu =0.0$ and Young’s modulus $E=4.32\,\times \,10^{8}\hbox {N}/{\hbox {ft}^{{2}}}$. The boundary conditions at each end are supported by a rigid diaphragm. The loading is a uniform vertical gravity load of $q_0 =90\, \hbox {N}/{\hbox {ft}^{{2}}}$. Owing to the symmetry, only a quarter of the roof is modeled.

The reference solution for the vertical deflection at the midpoint of the free edge is 0.3024 ft  [32, 33]. The results obtained from present element and those of other methods are given in Fig. 5. It can be observed that the results were two flexible in the coarse meshes for all element types. However, among these numerical solutions, the proposed element exhibited good convergence. The vertical displacement along the central line of the roof is plotted in Fig. 6, and the longitudinal displacement along the supported end is shown in Fig. 7. From these figures, we can clearly find that the present results agree very well with the reference solutions.

Table 1 First 12 natural frequencies of the automobile hood

5.2 Stiffness analysis of an automobile hood

In this subsection, an actual structure component of a car hood shown in Fig. 8 is studied using the present element. The dent resistance of a car hood is one of the most important considerations in the process of car design. The thickness of the shin shell is 1.0 mm; Young’s modulus of the material is taken to be $2.1\,\times \,10^{5}\,\hbox {N}/{\hbox {mm}^{{2}}}$ and Poisson’s ratio is 0.3. In order to test the dent resistance, clamped boundary condition is considered during the analysis, and a concentrated load $\hbox {F}=-\hbox {150\,N}$ is imposed along the y-direction as illustrated in Fig. 8.

Several existing shell elements are used here to compare with the present method. Because the analytical solution is unavailable, the numerical solution using quadrilateral shell element S4R in ABAQUS with large number of (42306) nodes is provided as the reference. Figure 9 shows the convergence of the central displacements obtained using unstructured meshes and different shell elements. It is noticed that the present element can provide very accurate results compared with the other two methods. Figure 10 illustrates the displacement distribution along the defined path AB. Here, the problem domain is discretized using 1457 irregular nodes with 2690 elements. Again, the present CCT element can provide a much closer result compared with the reference one.

5.3 Modal analysis of an automobile hood

The automobile hood presented in Fig. 8 is now investigated for free vibration analysis. The geometric and material parameters are same as those given in Sect. 5.2. The mass density is taken to be $7.8\,\times \,10^{-6}\, {\hbox {kg}}/{\hbox {mm}^{{3}}}$. Numerical results are obtained using 1457 irregular distributed nodes, and the reference solutions are obtained using commercial software ABAQUS with 42306 nodes.

Fig. 11

First twelve vibration modes of the automobile hood

Fig. 12

CPU time in solving the eigenvalue problem

Fig. 13

Geometry of the clamped spherical cap

Fig. 14

Four mesh types for a quarter of the cap

Fig. 15

Convergence of the dynamic solution with the CCT element

Modal analysis of the car hood is performed based on the same mesh discretization. The first 12 natural frequencies deduced from the present method are given in Table 1. For comparison, the numerical solutions obtained from C0, DKT and S3R elements are also included in our package. It can be observed that the present approach can provide very accurate eigenfrequencies than the other three methods. The first 12 eigenmodes are plotted in Fig. 11. One can clearly find that there is no spurious nonzero energy modes. Thus, the present CCT element could provide a stable solution for dynamic problems.

Now, we mention the computational efficiency of present method compared with C0 and DKT models. Figure 12 illustrates the CPU time consumed by present CCT element together with the other two methods in solving above eigenvalue problem. From the figure, we can observed that the present approach spends less than half times compared with C0 and DKT elements but achieves higher computational accuracy.

5.4 Clamped spherical cap

Finally, a clamped spherical cap subjected to a uniform pressure load of 600psi as shown in Fig. 13 is investigated for explicit dynamic analysis. This example has been studied by a number of researchers using the finite element methods. The geometric parameters are radius $R=22.27\,\hbox {in.}$ and thickness $t=0.41\,\hbox {in.}$ The material properties are as follows: Young’s modulus $E=1.05\,\times \,10^{7}\hbox {psi}$, Poisson’s ratio $\nu =0.33$ and mass density $\rho =2.45\,\times \,10^{-4}{\hbox {psi}\,\times \,\hbox {s}^{{2}}}/{\hbox {in}^{{2}}}$. Due to double symmetry of geometry and deformations, only one-quarter of the cap is modeled in the following analysis. Four different meshes are used to solve this problem, as shown in Fig. 14.

Fig. 16

Comparison of results obtained with the CCT element, the 3-node C0 triangular element, DKT element and S3R element

Fig. 17

Comparison of computational efficiency between the CCT element and the 3-node C0 triangular element

Figure 15 plots the convergence of the central deflection obtained using different structured meshes. It can be seen that the present approach converges quickly. In Fig. 16, the dynamic response obtained with the CCT element for mesh 3 is compared to those from several other types of element. It is observed that the results from these elements agree reasonably well.

In order to validate the efficiency of the present method for dynamic problems, Fig. 17 illustrates the CPU time against the number of time steps obtained using CCT element and C0 triangular element. Similar to Sect. 5.3, the present method spends only half times compared with the C0 element but achieves a reasonable result. Thus, the present CCT element is a good competitor to other methods.

6 Conclusion

In this paper, a curvature-constructed triangular element is proposed for thin shell analysis. Three-node triangular elements that can be generated automatically for any complicated geometries are adopted to discretize the problem domain. The translational displacement field in each background cell is interpolated using the nodal displacements by the linear shape functions. A continuity re-relaxed technique is utilized to formulate the curvature filed. The membrane strain filed is constructed same as the practice of standard FEM. The principle of virtual work is then adopted to discretize the governing partial difference equations. As only the translational displacements are considered as the basic degrees of freedom (DOF), the rotational displacement boundary conditions are imposed in the process of curvature displacement matrix formed. The numerical examples have confirmed the significant features of the present method:

• (1) The present method uses only three translational displacements as the basic DOFs, which significantly reduces the computing scale for practical engineering problems.

• (2) There is no need to perform the numerical integration as the curvature and membrane strain fields are constants in each background element; thus, the proposed CCT element possesses a superior computational efficiency.

• (3) Numerical comparisons illustrate that the present method could provide very accurate and effective solutions for both static and dynamic problems.

Appendix A

The linear shape function is given as follows

$$\begin{aligned} \varphi _i \left( x \right)= & {} \frac{1}{2A_e }\left( {a_i +b_i x+c_i y} \right) \nonumber \\ a_i= & {} x_j y_k -x_k y_j ,\quad b_i =y_j -y_k ,\quad c_i =x_k -x_j \end{aligned}$$

(61)

where $A_e$ is the area of the triangular cell, the subscript i varies from 1 to 3, j and k are determined by the cyclic permutation in the order of i, j, k. Then, Eq. (18) can be rewritten as

$$\begin{aligned} \left\{ {{\begin{array}{c} {\theta _x^m } \\ {\theta _y^m } \\ \end{array} }} \right\}= & {} \frac{1}{2A_m }\left[ {{\begin{array}{ccc} {b_1^m }&{} {b_2^m }&{} {b_3^m } \\ {c_1^m }&{} {c_2^m }&{} {c_3^m } \\ \end{array} }} \right] \left\{ {{\begin{array}{c} {w_1^m } \\ {w_2^m } \\ {w_3^m } \\ \end{array} }} \right\} =\frac{1}{2A_m }\nabla {\varvec{\upvarphi }}^{m}\mathbf{T}_w^m \left\{ {{\begin{array}{c} {\mathbf{d}_1 } \\ {\mathbf{d}_2 } \\ {\mathbf{d}_3 } \\ \end{array} }} \right\} \end{aligned}$$

(62)

$$\begin{aligned} \left\{ {{\begin{array}{c} {\theta _{nk}^m } \\ {\theta _{sk}^m } \\ \end{array} }} \right\}= & {} \frac{1}{2A_m }\left[ {\mathbf{T}_{mk} } \right] ^{\mathrm{T}}\nabla {\varvec{\upvarphi }}^{m}\mathbf{T}_w^m \left\{ {{\begin{array}{c} {\mathbf{d}_1 } \\ {\mathbf{d}_2 } \\ {\mathbf{d}_3 } \\ \end{array} }} \right\} \end{aligned}$$

(63)

in which

$$\begin{aligned} b_i =\hat{{y}}_j -\hat{{y}}_k ,\quad c_i =\hat{{x}}_k -\hat{{x}}_j \end{aligned}$$

(64)

Similarly,

$$\begin{aligned} \left\{ {{\begin{array}{c} {\theta _x^{s1} } \\ {\theta _y^{s1} } \\ \end{array} }} \right\}= & {} \frac{1}{2A_{s1} }\left[ {{\begin{array}{ccc} {b_1^{s1} }&{} {b_2^{s1} }&{} {b_3^{s1} } \\ {c_1^{s1} }&{} {c_2^{s1} }&{} {c_3^{s1} } \\ \end{array} }} \right] \left\{ {{\begin{array}{c} {w_1^{s1} } \\ {w_2^{s1} } \\ {w_3^{s1} } \\ \end{array} }} \right\} =\frac{1}{2A_{s1} }\nabla {\varvec{\upvarphi }}^{s1}\mathbf{T}_w^{s1} \left\{ {{\begin{array}{c} {\mathbf{d}_2 } \\ {\mathbf{d}_4 } \\ {\mathbf{d}_3 } \\ \end{array} }} \right\} \end{aligned}$$

(65)

$$\begin{aligned} \left\{ {{\begin{array}{c} {\theta _x^{s2} } \\ {\theta _y^{s2} } \\ \end{array} }} \right\}= & {} \frac{1}{2A_{s2} }\left[ {{\begin{array}{ccc} {b_1^{s2} }&{} {b_2^{s2} }&{} {b_3^{s2} } \\ {c_1^{s2} }&{} {c_2^{s2} }&{} {c_3^{s2} } \\ \end{array} }} \right] \left\{ {{\begin{array}{c} {w_1^{s2} } \\ {w_2^{s2} } \\ {w_3^{s2} } \\ \end{array} }} \right\} =\frac{1}{2A_{s2} }\nabla {\varvec{\upvarphi }}^{s2}\mathbf{T}_w^{s2} \left\{ {{\begin{array}{c} {\mathbf{d}_3 } \\ {\mathbf{d}_5 } \\ {\mathbf{d}_1 } \\ \end{array} }} \right\} \end{aligned}$$

(66)

$$\begin{aligned} \left\{ {{\begin{array}{c} {\theta _x^{s3} } \\ {\theta _y^{s3} } \\ \end{array} }} \right\}= & {} \frac{1}{2A_{s3} }\left[ {{\begin{array}{ccc} {b_1^{s3} }&{} {b_2^{s3} }&{} {b_3^{s3} } \\ {c_1^{s3} }&{} {c_2^{s3} }&{} {c_3^{s3} } \\ \end{array} }} \right] \left\{ {{\begin{array}{c} {w_1^{s3} } \\ {w_2^{s3} } \\ {w_3^{s3} } \\ \end{array} }} \right\} =\frac{1}{2A_{s3} }\nabla {\varvec{\upvarphi }}^{s3}\mathbf{T}_w^{s3} \left\{ {{\begin{array}{c} {\mathbf{d}_1 } \\ {\mathbf{d}_6 } \\ {\mathbf{d}_2 } \\ \end{array} }} \right\} \end{aligned}$$

(67)

$$\begin{aligned} \left\{ {{\begin{array}{c} {\theta _n^{s1} } \\ {\theta _s^{s1} } \\ \end{array} }} \right\}= & {} \frac{1}{2A_{s1} }\left[ {\mathbf{T}_{s1} } \right] ^{\mathrm{T}}\nabla {\varvec{\upvarphi }}^{s1}\mathbf{T}_w^{s1} \left\{ {{\begin{array}{c} {\mathbf{d}_2 } \\ {\mathbf{d}_4 } \\ {\mathbf{d}_3 } \\ \end{array} }} \right\} \end{aligned}$$

(68)

$$\begin{aligned} \left\{ {{\begin{array}{c} {\theta _n^{s2} } \\ {\theta _s^{s2} } \\ \end{array} }} \right\}= & {} \frac{1}{2A_{s2} }\left[ {\mathbf{T}_{s2} } \right] ^{\mathrm{T}}\nabla {\varvec{\upvarphi }}^{s2}\mathbf{T}_w^{s2} \left\{ {{\begin{array}{c} {\mathbf{d}_3 } \\ {\mathbf{d}_5 } \\ {\mathbf{d}_1 } \\ \end{array} }} \right\} \end{aligned}$$

(69)

$$\begin{aligned} \left\{ {{\begin{array}{l} {\theta _n^{s3} } \\ {\theta _s^{s3} } \\ \end{array} }} \right\}= & {} \frac{1}{2A_{s3} }\left[ {\mathbf{T}_{s3} } \right] ^{\mathrm{T}}\nabla {\varvec{\upvarphi }}^{s3}\mathbf{T}_w^{s3} \left\{ {{\begin{array}{c} {\mathbf{d}_1 } \\ {\mathbf{d}_6 } \\ {\mathbf{d}_2 } \\ \end{array} }} \right\} \end{aligned}$$

(70)

From Eq. (11)

$$\begin{aligned} \left\{ {{\begin{array}{c} {\overline{{\theta }}_{n1} } \\ {\overline{{\theta }}_{s1} } \\ \end{array} }} \right\}= & {} \frac{1}{2\left( {A_m +A_{s1} } \right) }\left( {\left[ {\mathbf{T}_{m1} } \right] ^{\mathrm{T}}\nabla {\varvec{\upvarphi }}^{m}\mathbf{T}_w^m \left\{ {{\begin{array}{c} {\mathbf{d}_1 } \\ {\mathbf{d}_2 } \\ {\mathbf{d}_3 } \\ \end{array} }} \right\} +\left[ {\mathbf{T}_{s1} } \right] ^{\mathrm{T}}\nabla {\varvec{\upvarphi }}^{s1}\mathbf{T}_w^{s1} \left\{ {{\begin{array}{c} {\mathbf{d}_2 } \\ {\mathbf{d}_4 } \\ {\mathbf{d}_3 } \\ \end{array} }} \right\} } \right) = \overline{{\mathbf{B}}}_1 \mathbf{d}_m \end{aligned}$$

(71)

$$\begin{aligned} \left\{ {{\begin{array}{c} {\overline{{\theta }}_{n2} } \\ {\overline{{\theta }}_{s2} } \\ \end{array} }} \right\}= & {} \frac{1}{2\left( {A_m +A_{s2} } \right) }\left( {\left[ {\mathbf{T}_{m2} } \right] ^{\mathrm{T}}\nabla {\varvec{\upvarphi }}^{m}\mathbf{T}_w^m \left\{ {{\begin{array}{c} {\mathbf{d}_1 } \\ {\mathbf{d}_2 } \\ {\mathbf{d}_3 } \\ \end{array} }} \right\} +\left[ {\mathbf{T}_{s2} } \right] ^{\mathrm{T}}\nabla {\varvec{\upvarphi }}^{s2}\mathbf{T}_w^{s2} \left\{ {{\begin{array}{c} {\mathbf{d}_3 } \\ {\mathbf{d}_4 } \\ {\mathbf{d}_1 } \\ \end{array} }} \right\} } \right) = \overline{{\mathbf{B}}}_2 \mathbf{d}_m \end{aligned}$$

(72)

$$\begin{aligned} \left\{ {{\begin{array}{c} {\overline{{\theta }}_{n3} } \\ {\overline{{\theta }}_{s3} } \\ \end{array} }} \right\}= & {} \frac{1}{2\left( {A_m +A_{s3} } \right) }\left( {\left[ {\mathbf{T}_{m3} } \right] ^{\mathrm{T}}\nabla {\varvec{\upvarphi }}^{m}\mathbf{T}_w^m \left\{ {{\begin{array}{c} {\mathbf{d}_1 } \\ {\mathbf{d}_2 } \\ {\mathbf{d}_3 } \\ \end{array} }} \right\} +\left[ {\mathbf{T}_{s3} } \right] ^{\mathrm{T}}\nabla {\varvec{\upvarphi }}^{s3}\mathbf{T}_w^{s3} \left\{ {{\begin{array}{c} {\mathbf{d}_1 } \\ {\mathbf{d}_6 } \\ {\mathbf{d}_2 } \\ \end{array} }} \right\} } \right) = \overline{{\mathbf{B}}}_3 \mathbf{d}_m \end{aligned}$$

(73)

where

$$\begin{aligned} \overline{{\mathbf{B}}}_1= & {} \frac{1}{2\left( {A_m +A_{s1} } \right) }\left( {\begin{array}{l} \left[ {{\begin{array}{cc} {-n_{y1}^m }&{} {n_{x1}^m } \\ {-n_{x1}^m }&{} {-n_{y1}^m } \\ \end{array} }} \right] \left[ {{\begin{array}{ccc} {b_1^m }&{} {b_2^m }&{} {b_3^m } \\ {c_1^m }&{} {c_2^m }&{} {c_3^m } \\ \end{array} }} \right] \left[ {{\begin{array}{cccccc} {\mathbf{c}_{\hat{{z}}} }&{} \mathbf{0}&{} \mathbf{0}&{} \mathbf{0}&{} \mathbf{0}&{} \mathbf{0} \\ \mathbf{0}&{} {\mathbf{c}_{\hat{{z}}} }&{} \mathbf{0}&{} \mathbf{0}&{} \mathbf{0}&{} \mathbf{0} \\ \mathbf{0}&{} \mathbf{0}&{} {\mathbf{c}_{\hat{{z}}} }&{} \mathbf{0}&{} \mathbf{0}&{} \mathbf{0} \\ \end{array} }} \right] + \\ \left[ {{\begin{array}{cc} {-n_y^{s1} }&{} {n_x^{s1} } \\ {-n_x^{s1} }&{} {-n_y^{s1} } \\ \end{array} }} \right] \left[ {{\begin{array}{ccc} {b_1^{s1} }&{} {b_2^{s1} }&{} {b_3^{s1} } \\ {c_1^{s1} }&{} {c_2^{s1} }&{} {c_3^{s1} } \\ \end{array} }} \right] \left[ {{\begin{array}{cccccc} \mathbf{0}&{} {\mathbf{c}_{z^{1}} }&{} \mathbf{0}&{} \mathbf{0}&{} \mathbf{0}&{} \mathbf{0} \\ \mathbf{0}&{} \mathbf{0}&{} \mathbf{0}&{} {\mathbf{c}_{z^{1}} }&{} \mathbf{0}&{} \mathbf{0} \\ \mathbf{0}&{} \mathbf{0}&{} {\mathbf{c}_{z^{1}} }&{} \mathbf{0}&{} \mathbf{0}&{} \mathbf{0} \\ \end{array} }} \right] \\ \end{array}} \right) \end{aligned}$$

(74)

$$\begin{aligned} \overline{{\mathbf{B}}}_2= & {} \frac{A_m }{2\left( {A_m +A_{s2} } \right) }\left( {\begin{array}{l} \left[ {{\begin{array}{cc} {-n_{y2}^m }&{} {n_{x2}^m } \\ {-n_{x2}^m }&{} {-n_{y2}^m } \\ \end{array} }} \right] \left[ {{\begin{array}{ccc} {b_1^m }&{} {b_2^m }&{} {b_3^m } \\ {c_1^m }&{} {c_2^m }&{} {c_3^m } \\ \end{array} }} \right] \left[ {{\begin{array}{cccccc} {\mathbf{c}_{\hat{{z}}} }&{} \mathbf{0}&{} \mathbf{0}&{} \mathbf{0}&{} \mathbf{0}&{} \mathbf{0} \\ \mathbf{0}&{} {\mathbf{c}_{\hat{{z}}} }&{} \mathbf{0}&{} \mathbf{0}&{} \mathbf{0}&{} \mathbf{0} \\ \mathbf{0}&{} \mathbf{0}&{} {\mathbf{c}_{\hat{{z}}} }&{} \mathbf{0}&{} \mathbf{0}&{} \mathbf{0} \\ \end{array} }} \right] + \\ \left[ {{\begin{array}{cc} {-n_y^{s2} }&{} {n_x^{s2} } \\ {-n_x^{s2} }&{} {-n_y^{s2} } \\ \end{array} }} \right] \left[ {{\begin{array}{ccc} {b_1^{s2} }&{} {b_2^{s2} }&{} {b_3^{s2} } \\ {c_1^{s2} }&{} {c_2^{s2} }&{} {c_3^{s2} } \\ \end{array} }} \right] \left[ {{\begin{array}{cccccc} \mathbf{0}&{} \mathbf{0}&{} {\mathbf{c}_{z^{2}} }&{} \mathbf{0}&{} \mathbf{0}&{} \mathbf{0} \\ \mathbf{0}&{} \mathbf{0}&{} \mathbf{0}&{} \mathbf{0}&{} {\mathbf{c}_{z^{2}} }&{} \mathbf{0} \\ {\mathbf{c}_{z^{2}} }&{} \mathbf{0}&{} \mathbf{0}&{} \mathbf{0}&{} \mathbf{0}&{} \mathbf{0} \\ \end{array} }} \right] \\ \end{array}} \right) \end{aligned}$$

(75)

$$\begin{aligned} \overline{{\mathbf{B}}}_3= & {} \frac{A_m }{2\left( {A_m +A_{s3} } \right) }\left( {\begin{array}{l} \left[ {{\begin{array}{cc} {-n_{y3}^m }&{} {n_{x3}^m } \\ {-n_{x3}^m }&{} {-n_{y3}^m } \\ \end{array} }} \right] \left[ {{\begin{array}{ccc} {b_1^m }&{} {b_2^m }&{} {b_3^m } \\ {c_1^m }&{} {c_2^m }&{} {c_3^m } \\ \end{array} }} \right] \left[ {{\begin{array}{cccccc} {\mathbf{c}_{\hat{{z}}} }&{} \mathbf{0}&{} \mathbf{0}&{} \mathbf{0}&{} \mathbf{0}&{} \mathbf{0} \\ \mathbf{0}&{} {\mathbf{c}_{\hat{{z}}} }&{} \mathbf{0}&{} \mathbf{0}&{} \mathbf{0}&{} \mathbf{0} \\ \mathbf{0}&{} \mathbf{0}&{} {\mathbf{c}_{\hat{{z}}} }&{} \mathbf{0}&{} \mathbf{0}&{} \mathbf{0} \\ \end{array} }} \right] + \\ \left[ {{\begin{array}{cc} {-n_y^{s3} }&{} {n_x^{s3} } \\ {-n_x^{s3} }&{} {-n_y^{s3} } \\ \end{array} }} \right] \left[ {{\begin{array}{ccc} {b_1^{s3} }&{} {b_2^{s3} }&{} {b_3^{s3} } \\ {c_1^{s3} }&{} {c_2^{s3} }&{} {c_3^{s3} } \\ \end{array} }} \right] \left[ {{\begin{array}{cccccc} {\mathbf{c}_{z^{3}} }&{} \mathbf{0}&{} \mathbf{0}&{} \mathbf{0}&{} \mathbf{0}&{} \mathbf{0} \\ \mathbf{0}&{} \mathbf{0}&{} \mathbf{0}&{} \mathbf{0}&{} \mathbf{0}&{} {\mathbf{c}_{z^{3}} } \\ \mathbf{0}&{} {\mathbf{c}_{z^{3}} }&{} \mathbf{0}&{} \mathbf{0}&{} \mathbf{0}&{} \mathbf{0} \\ \end{array} }} \right] \\ \end{array}} \right) \end{aligned}$$

(76)

The relation between the local rotations $\hat{{{\varvec{\uptheta } }}}_k$ and global displacement vector can be expressed as

$$\begin{aligned} \hat{{{\varvec{\uptheta } }}}_k =\mathbf{T}_{mk} \overline{{\mathbf{B}}}_k \mathbf{d}_m \end{aligned}$$

(77)

The curvature in the triangular cell M is given by

$$\begin{aligned} {\overline{\hat{\varvec{\upkappa }}}}= & {} \left( {\frac{1}{A_m }\sum _{k=1}^3 {l_k \mathbf{n}_k^m \mathbf{T}_{mk} \overline{{\mathbf{B}}}_k } } \right) \mathbf{d}_m =\mathbf{B}_b \mathbf{d}_m \end{aligned}$$

(78)

$$\begin{aligned} \mathbf{B}_b= & {} \frac{1}{A_m }\sum _{k=1}^3 {l_k \mathbf{n}_k^m \mathbf{T}_{mk} \overline{{\mathbf{B}}}_k } \end{aligned}$$

(79)