1 Introduction

Interfacial debonding often results in failure of laminated or generally jointed structures. Laminated structures are widely used e.g. for aerospace, civil and mechanical applications due to their good thermo-electro-mechanical performances combined with low weight and high toughness. The development of damage at the interfaces between laminae results in the formation and growth of interlaminar cracks through a non-linear and irreversible process which is known as debonding.

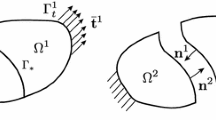
A widely used modeling approach to simulate the onset and the propagation of debonding is represented by cohesive zone (CZ) models. These interpret the progressive decay of the cohesive forces and the formation of traction-free surfaces at a bi-material interface or within a material or at the interlaminar interface in a laminated structure, provided that the path of the potential crack is known a priori [2, 43]. CZ models were originally introduced by [7, 22] as an alternative approach to singularity driven fracture mechanics and have been widely used to describe the fracture process in a number of materials, such as ductile [32, 33, 54, 55, 59] or composite materials [3, 4, 9, 11, 37, 43].

The numerical application of CZ models for debonding problems within finite element frameworks, however, has shown some difficulties because of the localization of the fracture process zone (FPZ) ahead of the crack tip. Unless a sufficiently fine mesh discretizes the process zone of a cohesive crack, local softening in the interface elements results in a sudden release of the elastic strain energy stored in the surrounding bulk material. This causes a sequence of artificial (non physical) snap-through or snap-back branches in the global load-deflection response, which leads to failure of a standard Newton–Raphson iterative scheme [1]. The simplest strategy to circumvent this problem consists in reducing the oscillations through mesh refinement, so that the FPZ is adequately resolved. For realistic interface parameters leading to a small process zone size, the element size has to be extremely small.

In contrast to refinement of the entire domain, local refinement close to the potentially debonded interface is a computationally more efficient alternative. To this end, different surface enrichment strategies have been developed in the literature using different types of enrichment functions for CZ interface elements [13, 24, 38, 39, 41, 42]. These techniques, however, do not increase the degree of continuity of the parameterization at the inter-element boundaries which is also partly responsible for the unphysical stress oscillations at the interface.

The advent of isogeometric analysis (IGA), introduced recently by [27], has provided a framework in which an exact description of the geometry is combined with the possible achievement of the desired degree of continuity at the element boundaries, as well as with additional advantageous features including variation diminishing and convex hull properties, and non-negativeness of the basis function. The core idea of IGA is the tight connection between computer aided design (CAD) and finite element analysis (FEA), since the same basis fuctions are used with this approach to represent geometry in CAD and approximate the solutions fields in FEA. In addition, it has been shown that the use of a smooth, higher-order geometric basis can deliver significant advantages as an analysis technique, independently of the integration with CAD. This has been verified for many application areas, see [27] and references therein. In particular, the application of IGA to the solution of contact problems has been recently shown to deliver significantly superior results in comparison with conventional Lagrange discretizations [16, 17, 30, 31, 52, 53].

The development of local refinement strategies within IGA is a subject of active research. Local refinement techniques include T-splines [8, 45, 46, 58, 61], hierarchical B-splines [44, 57], polynomial splines over hierarchical T-meshes [18, 34], and locally-refinable splines [20]. The application of T-spline discretizations for the solution of contact problems was first demonstrated in Dimitri et al. [19].

The attempts to apply IGA to the modeling of cohesive interface debonding have been very limited. In [56], problems involving cohesive cracks were solved by introducing discontinuities in the IGA parameterization by means of knot insertion at the location of existing knots. Non uniform rational B-splines (NURBS) were used for the discretization of pre-defined interfaces, whereas T-splines were applied to the case of propagating cracks, due to their ability to generate localized discontinuities. Nguyen and Nguyen-Xuan [35] employed Bézier elements based on Bernstein basis functions to solve delamination problems using zero-thickness cohesive interface elements. The utilization of high order Bézier elements was shown to deliver improved results compared to standard linear elements.

This paper presents a simple isogeometric framework for the 2D and 3D analysis of interfaces undergoing contact and cohesive debonding. These two phenomena are here treated within a unified framework, by developing an IGA-based generalized contact element which embeds the enforcement of the non-penetration contact conditions in compression as well as a bilinear mode-I CZ model in tension. In contrast to the vast majority of the existing investigations based on interface elements, the presented generalized contact element allows for non-matching discretizations of the interacting surfaces, thereby allowing for a much greater flexibility in the meshing of complicated geometries.

Using a terminology sometimes used in the literature [56], the focus in this paper is on “adhesive” interfaces, where a non-infinite initial stiffness of the CZ law in tension is introduced to simulate the finite stiffness of an adhesive layer. However, the same approach can be applied to “cohesive” interfaces within a single material, where the initial stiffness of the CZ law in tension plays the role of a penalty parameter and should be taken as large as possible compatibly with ill-conditioning issues. As follows, the term “cohesive” will be used throughout without distinction between the previous two cases.

Unlike in [56], we make no use of knot insertion procedures to generate the discontinuity within a single patch, but rather assemble different patches along the desired potential interfaces. The stress conditions then automatically lead to the enforcement of the proper boundary conditions at these interfaces, i.e. non-penetration under compression and the desired CZ behavior in tension.

Unlike in Nguyen and Nguyen-Xuan [35], we adopt here NURBS and T-splines discretizations as well as conventional Lagrange discretizations for a comparative assessment of their performance. In contrast to Bézier elements based on Bernstein basis functions, which feature \(C^{0}\) inter-element continuity also for higher-order discretizations, IGA basis functions are able to naturally achieve a \(C^{p-1}\) inter-element continuity, with \(p\) as the order of the discretization (provided that no knots are repeated).

The IGA-based discretizations are developed in this work from a finite element point of view, utilizing the so called Bézier extraction. The idea is to extract the linear operator which maps the Bernstein polynomial basis on Bézier elements to the global NURBS or T-spline basis. In this way the isogeometric discretizations are automatically generated for any analysis-suitable CAD geometry and easily incorporated into existing finite element frameworks [10, 45]. A recently released commercial T-spline plugin for Rhino3d is capable of defining and exporting analysis-suitable T-spline or NURBS models based on Bézier extraction. This plugin was used to build the analysis models adopted in this study.

The paper is organized as follows. Sect. 2 briefly describes basic NURBS and T-spline concepts. Sect. 3 presents the formulation of the large deformation frictionless contact and mode-I debonding problem in the discretized setting. Finally, in Sect. 4, numerical examples are presented and discussed.

2 A brief introduction to NURBS and T-splines

In this section NURBS and T-splines discretizations are briefly reviewed. Further details and extensive references can be found in the fundamental works of Hughes and co-workers [12, 27], as well as in further references which will be cited at the appropriate locations. In what follows we denote the spatial and parametric dimensions by \(d_{s}\) and \(d_{p}\), respectively.

2.1 NURBS discretizations

Univariate B-splines in all spatial dimensions are generated from \(d_{s}\) knot vectors

$$\begin{aligned} \Xi ^{i}=\left\{ \xi _{1}^{i},\ldots .,\xi _{n_{i}+p_{i}+1}^{i}\right\} \end{aligned}$$
(1)

In the above equation \(i=1,..,d_{s}, p_{i}\) is the polynomial order of the B-spline basis functions along parametric direction \(i, \xi _{j}^{i}\) is the \(j\)th knot, \(n_{i}\) is the number of associated control points, and \(n_{i}-p_{i}\) is the resulting number of elements. Let \(N_{d_{i},p_{i}}^{i}\left( \xi ^{i}\right) \) be univariate B-spline basis functions associated with knot vectors \(\Xi ^{i}\). The continuity and order of \(N_{d_{i},p_{i}}^{i}\) depend on \(\Xi ^{i}\) only. If \(\Xi ^{i}\) has no repeated interior knot \(\xi _{j}^{i}, j\in [p_{i}+1,n_{i}]\), then the order-\(p_{i}\) basis function \(N_{d_{i},p_{i}}^{i}\) has continuity \(C^{p_{i}-1}\). The order of continuity at a certain knot is decreased by one for each repetition of this knot in the knot vector.

The knot vectors together with the associated control points and their weights constitute a patch. To mantain a single-index notation, which is also used for T-splines, we introduce a mapping between the tensor product space and the global indexing of the basis functions and control points. Let \(d_{1}=1,\ldots ,n_{1}, d_{2}=1,\ldots ,n_{2}, d_{3}=1,\ldots ,n_{3}\), then in two dimensions we define

$$\begin{aligned} \tilde{A}(d_{1},d_{2})=n_{2}(d_{1}-1)+d_{2} \end{aligned}$$
(2)

and in three dimensions

$$\begin{aligned} \tilde{A}(d_{1},d_{2},d_{3})=n_{3}n_{2}(d_{1}-1)+ n_{3}(d_{2}-1)+d_{3} \end{aligned}$$
(3)

With this definition, the control point coordinates and their weights will be denoted as \(\mathbf {P}_{A}\) and \(w_{A}\), respectively, where \(A=\tilde{A}(d_{1},d_{2}), A=1,\ldots ,n_{1}n_{2}\) for surfaces, and \(A=\tilde{A}(d_{1},d_{2},d_{3}), A=1,\ldots ,n_{1}n_{2}n_{3}\) for volumes.

NURBS basis functions for surfaces (\(d_{s}=2\)) and volumes (\(d_{s}=3\)) are defined via a tensor product of univariate B-spline basis functions. In two dimensions, the surface NURBS basis functions are defined as

$$\begin{aligned} R_{A}^{p_{1},p_{2}}\left( \xi ^{1},\xi ^{2}\right) =\frac{N_{d_{1},p_{1}}^{1}\left( \xi ^{1}\right) N_{d_{2},p_{2}}^{2}\left( \xi ^{2}\right) w_{A}}{\sum _{d_{1}=1}^{n_{1}}\sum _{d_{2}=1}^{n_{2}}N_{d_{1},p_{1}}^{1}\left( \xi ^{1}\right) N_{d_{2},p_{2}}^{2}\left( \xi ^{2}\right) w_{A}}\nonumber \\ \end{aligned}$$
(4)

Similarly, in three dimensions, the volume NURBS basis functions are defined as

$$\begin{aligned}&R_{A}^{p_{1},p_{2},p_{3}}\left( \xi ^{1},\xi ^{2},\xi ^{3}\right) \nonumber \\&\quad =\frac{N_{d_{1},p_{1}}^{1}\left( \xi ^{1}\right) N_{d_{2},p_{2}}^{2}\left( \xi ^{2}\right) N_{d_{3},p_{3}}^{3}\left( \xi ^{3}\right) w_{A}}{\sum _{d_{1}=1}^{n_{1}}\sum _{d_{2}=1}^{n_{2}}\sum _{d_{3}=1}^{n_{3}}N_{d_{1},p_{1}}^{1}\left( \xi ^{1}\right) N_{d_{2},p_{2}}^{2}\left( \xi ^{2}\right) N_{d_{3},p_{3}}^{3}\left( \xi ^{3}\right) w_{A}}\nonumber \\ \end{aligned}$$
(5)

Finally, we can define a NURBS surface as

$$\begin{aligned} \mathbf {S}(\xi ^{1},\xi ^{2})=\sum _{A=1}^{n_{1}n_{2}}R_{A}^{p_{1},p_{2}}\left( \xi ^{1},\xi ^{2}\right) \mathbf {P}_{A} \end{aligned}$$
(6)

and a NURBS volume as

$$\begin{aligned} \mathbf {V}(\xi ^{1},\xi ^{2},\xi ^{3})=\sum _{A=1}^{n_{1}n_{2}n_{3}}R_{A}^{p_{1},p_{2},p_{3}}\left( \xi ^{1},\xi ^{2},\xi ^{3}\right) \mathbf {P}_{A} \end{aligned}$$
(7)

2.2 Limitations of NURBS discretizations

As a design tool NURBS surfaces and volumes have two main shortcomings: their tensor product structure, and the inability to produce watertight multi-patch geometries with no gaps or overlaps. These NURBS-based design deficiencies lead to corresponding drawbacks for the analysis [8]:

  1. 1.

    Many NURBS control points in a mesh are often only needed to satisfy topological constraints and do not contain significant geometric information. This implies that a large percentage of the degrees of freedom (DOFs) are needed just for topological reasons.

  2. 2.

    NURBS refinement is inherently global, due to the tensor product structure of multi-dimensional meshes. Resolution of local features propagates globally and knot lines extend through the entire domain, resulting in a prohibitive computational cost. In the context of contact or delamination problems, this global propagation of refinement is especially deleterious as the interfacial response may be highly localized and an accurate resolution of the cohesive zone may only be needed along the bondline ahead of the crack tip.

  3. 3.

    Complex geometry of arbitrary genus can only be represented by multiple NURBS patches which are generally discontinuous across patch boundaries. For multi-patch domains inconsistencies at patch boundaries lead to \(C^{0}\) continuity at the interface or gaps and overlaps between patches. This lack of watertightness destroys the analysis-suitable nature of the discretization. By “analysis-suitable” we mean the exact representation of the geometry due to the smooth geometric basis functions with efficient mathematical properties (i.e. partition of unity, non-negativity, convex hull property, linear independence), whereas “smooth” refers to the \(C^{l}\) interelement continuity, where \(0\le l<p\), and \(p\) is the polynomial order.

T-splines [47, 49] have been proposed as a step forward with respect to NURBS in the aforementioned respects. They can be locally refined and can represent complicated engineering designs as a single, watertight geometry [21, 45, 46]. Multiple NURBS patches can be merged into a single, watertight T-spline surface and any trimmed NURBS model can be represented as a watertight T-spline model [50].

2.3 T-spline fundamentals

Hereafter, we briefly overview the main concepts of the T-spline technology. Additional details can be retrieved in [8, 45–49], and references therein. We focus on cubic T-spline surfaces due to their predominance in industry. An element index is denoted by \(e\) and the number of non-zero basis functions over an element \(e\) is denoted by \(n\).

T-splines allow to build spaces that are complete up to a desired polynomial degree, as smooth as those of an equivalent NURBS basis, and capable of being locally refined while keeping the original geometry and parameterization unchanged. A T-spline is constructed from a global structure, named T-mesh, that defines the topology and parameterization for the entire T-spline object. For surfaces (\(d_{p}=2\)) the T-mesh is a mesh of quadrilateral elements whose edges are allowed to contain T-junctions, i.e. vertices that are analogous to hanging nodes in finite elements. An element with T-junctions is composed of four corner vertices and any number of additional vertices on any side. Another possibility allowed for by T-splines is the presence of extraordinary points in the T-mesh. An extraordinary point is a vertex which is not a T-junction and whose valence, i.e. the number of edges touching the vertex, is different from four. The edges that touch an extraordinary point are referred to as spoke edges, and the elements contained in its two-ring neighborhood are denoted as irregular elements.

A control point of coordinates \(\mathbf {P}_{A}\in \mathbb {R}^{d_{s}}\) (in the reference configuration), a control weight \(w_{A}\in \mathbb {R}^{+}\) and a T-spline basis function are all associated to each vertex \(A\) of the T-mesh. While global knot vectors are sufficient to define all NURBS basis functions, for T-splines the T-mesh does not contain enough information to construct the basis. A valid knot interval configuration must be additionally assigned, in order to endow the T-mesh with local parametric information [48]. A knot interval is a non-negative real number assigned to each edge of the T-mesh, and a valid knot interval configuration is such that knot intervals on the opposite sides of each element sum to the same value.

Once the T-mesh is equipped with a valid knot interval configuration, the construction of the T-spline basis function associated to each vertex starts by inferring sequences of knot intervals from the T-mesh in the neighborhood of the vertex. A local knot interval vector is thus defined as a sequence of knot intervals \(\triangle \Xi =\left\{ \triangle \xi _{1},\triangle \xi _{2},\ldots ..,\triangle \xi _{p+1}\right\} \), such that \(\triangle \xi _{i}=\xi _{i+1}-\xi _{i}\), from which a local knot vector can be derived as a sequence of non-decreasing knots, \(\Xi =\left\{ \xi _{1},\xi _{2},\ldots \ldots ,\xi _{p+2}\right\} \). A local knot interval vector possesses all the information in a local knot vector except an origin. In general, for T-splines, knot intervals are the method of choice for assigning and retrieving parameter information to and from the T-mesh since no origin is required. All classical B-spline algorithms can be rewritten in terms of knot intervals [45].

For \(d_{p}>1\), a set of local knot interval vectors, \(\varvec{\triangle }\varvec{\Xi }_{A}=\left\{ \triangle \Xi _{A}^{i}\right\} _{i=1}^{d_{p}}\) is assigned to each vertex \(A\), from which a corresponding set of local knot vectors, \(\varvec{\Xi }_{A}=\left\{ \Xi _{A}^{i}\right\} _{i=1}^{d_{p}}\) can be derived. Each set \(\varvec{\Xi }_{A}\) defines a local basis function domain \(\hat{\Omega }_{A}\subset \mathbb {R}^{d_{p}}\), which carries a coordinate system \(\varvec{\xi }_{A}=\left( \xi _{A}^{i}\right) _{i=1}^{d_{p}}\).

Over each \(\hat{\Omega }_{A}\) the T-spline basis function \(N_{A}\) is defined as the tensor product of the univariate basis functions, i.e.

$$\begin{aligned} N_{A}\left( \varvec{\xi }_{A}|\varvec{\Xi }_{A}\right) =\prod _{i=1}^{d_{p}}N_{A}^{i}\left( \xi _{A}^{i}|\Xi _{A}^{i}\right) \end{aligned}$$
(8)

and the univariate T-spline basis functions, \(N_{A}^{i}\left( \xi _{A}^{i}|\Xi _{A}^{i}\right) \), are computed by the Cox-de Boor recursion formula applied over the local knot vectors [45]. If \(A\) is not adjacent to an extraordinary point, \(N_{A}\) is comprised of a \(4\times 4\) grid of polynomials. Otherwise, the polynomials comprising \(N_{A}\) form an unstructured grid. In either case, the polynomials can be represented in Bézier form. Hence, Bézier extraction can be applied to an entire T-spline to generate a finite set of Bézier elements such that

$$\begin{aligned} \mathbf {N}^{e}(\varvec{\xi })=\mathbf {C}^{e}\mathbf {B}(\varvec{\xi }) \end{aligned}$$
(9)

where \(\varvec{\xi }\in \tilde{\Omega }\) is a coordinate in a standard Bézier parent element domain, \(\mathbf {N}^{e}(\varvec{\xi })=\{N_{a}^{e}(\varvec{\xi })\}_{a=1}^{n}\) is a vector of T-spline basis functions which are non-zero over Bézier element \(e, \mathbf {B}(\varvec{\xi })=\{B_{i}(\varvec{\xi })\}_{i=1}^{m}\) is a vector of tensor product Bernstein polynomial basis functions defining Bézier element \(e\), and \(\mathbf {C}^{e}\in \mathbb {R}^{n\times m}\) is the element extraction operator featuring the following structure

$$\begin{aligned} \mathbf {C}^{e}=\left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} c_{1,1}^{e} &{} c_{1,2}^{e}&{}\ldots &{} c_{1,m}^{e}\\ c_{2,1}^{e} &{} c_{2,2}^{e} &{}&{} c_{2,m}^{e}\\ \vdots &{} \vdots &{}&{} \vdots \\ c_{n,1}^{e} &{} c_{n,2}^{e} &{}&{} c_{n,m}^{e} \end{array}\right] \end{aligned}$$
(10)

The coefficients in the above matrix can be computed using standard knot insertion algorithms for B-splines, see [10] and [45] for more details. The matrix dimensions follow from \(n\) T-spline basis functions and \(m\) Berstein polynomials being defined over element \(e\).

2.4 T-spline discretizations

The element geometric map, \(\mathbf {X}^{e}:\tilde{\Omega }\rightarrow \Omega ^{e}\), from the parent element domain onto the physical domain in the reference configuration can be defined as

$$\begin{aligned} \mathbf {X}^{e}(\varvec{\xi })&= \frac{1}{\left( \mathbf {w}^{e}\right) ^{T}\mathbf {N}^{e}(\varvec{\xi })}\left( \mathbf {P}^{e}\right) ^{T}\mathbf {W}^{e}\mathbf {N}^{e}(\varvec{\xi })\end{aligned}$$
(11)
$$\begin{aligned}&= \left( \mathbf {P}^{e}\right) ^{T}\mathbf {R}^{e}(\varvec{\xi }) \end{aligned}$$
(12)

where we introduced \(\mathbf {R}^{e}(\varvec{\xi })=\{R_{a}^{e}(\varvec{\xi })\}_{a=1}^{n}\), i.e. a vector of rational T-spline basis functions, the element weight vector \(\mathbf {w}^{e}=\{w_{a}^{e}\}_{a=1}^{n}\), and the diagonal weight matrix \(\mathbf {W}^{e}=\mathrm{diag}(\mathbf {w}^{e})\). Moreover, \(\mathbf {P}^{e}\) is a matrix of dimension \(n\times d_{s}\) that contains the reference coordinates of the element control points. For \(d_{s}=3\) it is

$$\begin{aligned} \mathbf {P}^{e}=\left[ \begin{array}{c@{\quad }c@{\quad }c} X_{1}^{e} &{} Y_{1}^{e} &{} Z_{1}^{e}\\ X_{2}^{e} &{} Y_{2}^{e} &{} Z_{2}^{e}\\ \vdots &{} \vdots &{} \vdots \\ X_{n}^{e} &{} Y_{n}^{e} &{} Z_{n}^{e} \end{array}\right] \end{aligned}$$
(13)

Using Eqs. (11) and (12) it is

$$\begin{aligned} \mathbf {R}^{e}(\varvec{\xi })=\frac{1}{\left( \mathbf {w}^{e}\right) ^{T}\mathbf {N}^{e}(\varvec{\xi })}\mathbf {W}^{e}\mathbf {N}^{e}(\varvec{\xi }) \end{aligned}$$
(14)

and using eq. (9)

$$\begin{aligned} \mathbf {R}^{e}(\varvec{\xi })=\frac{1}{\left( \mathbf {w}^{e}\right) ^{T}\mathbf {C}^{e}\mathbf {B}(\varvec{\xi })}\mathbf {W}^{e}\mathbf {C}^{e}\mathbf {B}(\varvec{\xi }) \end{aligned}$$
(15)

Note that all quantities in Eq. (15) are written in terms of the Bernstein basis defined over the parent element domain, \(\tilde{\Omega }\).

In the isoparametric framework, element mappings analogous to Eq. (12) are introduced for the unknown displacement field, its variation, and the coordinates in the current configuration

$$\begin{aligned} \displaystyle \mathbf {u}(\varvec{\xi })&= {\displaystyle \begin{matrix}{\displaystyle \sum _{a=1}^{n}}R_{a}({\varvec{\xi }}){\mathbf {u}}_{a}\end{matrix}\qquad \mathbf {\delta u}({\varvec{\xi }})={\displaystyle \begin{matrix}{\displaystyle \sum _{a=1}^{n}}R_{a}(\varvec{\xi }){\delta \mathbf {u}}_{a}\end{matrix}\qquad }}\nonumber \\ \mathbf {x}(\varvec{\xi })&= \begin{matrix}{\displaystyle \sum _{a=1}^{n}}R_{a}(\varvec{\xi }){\mathbf {p}}_{a}\end{matrix} \end{aligned}$$
(16)

where the superscript \(e\) has been dropped for convenience and \({\mathbf {u}}_{a}, {\delta \mathbf {u}}_{a}\) and \({\mathbf {p}}_{a}\) are the unknown displacement, displacement variation, and current coordinate of the control point \(\mathbf {P}_{A}\), respectively, with \({\mathbf {p}}_{a}=\mathbf {P}_{a}+{\mathbf {u}}_{a}\). \(A=IEN(a,e)\) is a mapping from the local element numbering to the global control point numbering [26]. Equation (16) can also be applied to a NURBS interpolation as a special case where the number of control points \(n\) pertaining to each element is fixed, as well as to a Lagrangian interpolation, in which case \(n\) is simply the number of nodes per element.

Parameterization of the surfaces follows immediately from that of the bulk by fixing the value of the appropriate parametric coordinate. In this paper, we assume that the third parametric coordinate takes a constant value on the contact/cohesive surface. Additionally, the parameterization of the slave and master surfaces, introduced in the interfacial treatment, will be denoted by the superscripts \(s\) and \(m\), respectively.

3 Large deformation frictionless contact and mode-I debonding problem

The formulation reported hereafter is largely based on the GPTS contact formulation illustrated in [19]. This is an extension to the T-spline case of the NURBS-based formulation termed “knot-to-surface” in [52] and “non-mortar” in [16]. In turn, this formulation is the isogeometric counterpart of the contact algorithm proposed by [23] in the context of Lagrange linear elements. A clarification regarding the terminology has been reported in [19].

Hereafter, the formulation in [19] is extended to encompass cohesive mode-I debonding in the tensile regime. Many details which are shared with the unilateral contact formulation are omitted, except for those that are needed to ensure a self-consistent presentation. Further details can be retrieved in the original reference.

3.1 Problem description

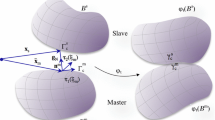
Two hyperelastic bodies are assumed to undergo finite deformations including contact and cohesive debonding along a pre-defined interface. One of them is denoted as the slave body, \(\mathcal {B}^{s}\), and the other one is the master body, \(\mathcal {B}^{m}\). This classical choice introduces a bias between the two interacting surfaces, however, alternative unbiased formulations are also possible [36, 40]. The deformation of both bodies is expressed by the coordinates of their generic point in the current configuration \(\mathbf {x}^{i}=\mathbf {X}^{i}+\mathbf {u}^{i}\), where \(\mathbf {X}\) is the coordinate of the same point in the reference configuration, \(\mathbf {u}\) is its displacement, and the superscript \(i=(s,m)\) refers to the slave and master bodies, respectively.

On the master surface, the convective coordinates \({\varvec{\xi }}_{m}=\{\xi _{m}^{\alpha }\}_{\alpha =1}^{d_{s}-1}\) coincide with the parametric coordinates and define the covariant vectors \({\varvec{\tau }}_{\alpha }=\mathbf {x}_{,\alpha }^{m}\). We introduce the distance function \(d:=\Vert \mathbf {x}^{ s }-\mathbf {x}^{m}({\varvec{\xi }}_{m})\Vert \), describing the distance between a fixed point \(\mathbf {x}^{ s }\) on the contact/cohesive boundary \(\gamma _{c}^{s}\) of the slave surface and an arbitrary point \(\mathbf {x}^{m}(\mathbf {\varvec{\xi }}_{m})\) on the contact/cohesive boundary of the master surface \(\gamma _{c}^{m}\). Each point \(\mathbf {x}^{s}\) is assumed to have a unique interacting partner on the master surface, \({\bar{\mathbf{x}}}^{m}=\mathbf {x}^{m}({\bar{\varvec{\xi }}}_{m})\), whose position is computed via the closest-point projection of \(\mathbf {x}^{s}\) onto \(\gamma _{c}^{m}\). This is equivalent to minimizing the distance \(d\) previously defined. The closest projection point and the related variables are often identified in the literature with the \(\left( \bar{\bullet }\right) \) notation.

The contact/cohesive interface is pulled back to \(\Gamma _{c}:=\Gamma _{c}^{s}\ne \Gamma _{c}^{m}\), where \(\Gamma _{c}^{i}\) is the contact/cohesive boundary of body \(\mathcal {B}^{i}\) in the reference configuration. The interface integrals are all evaluated on \(\Gamma _{c}^{s}\) for ease of linearization.

The normal gap, \(g_{N}\), between the two bodies is defined as

$$\begin{aligned} g_{N}=\left( \mathbf {x}^{s}-{\bar{\mathbf{x}}}^{m}\right) \cdot \mathbf {n} \end{aligned}$$
(17)

where \(\mathbf {n}=\bar{\mathbf {n}}^{m}\) is the outward normal unit vector to the master surface at the projection point. With this definition, for negative \(g_{N}\) penetration between the bodies takes place and the contact algorithm is activated, while for positive \(g_{N}\) cohesive tractions arise. The normal traction \(p_{N}\) is defined as the normal component of the Piola traction vector \(\mathbf {t}=\mathbf {t}^{m}=-\mathbf {t}^{s}\)

$$\begin{aligned} \mathbf {t}={\displaystyle p_{N}\mathbf {n}\qquad p_{N}=\mathbf {t}\cdot \mathbf {n}} \end{aligned}$$
(18)

The non-penetration condition is here enforced in the normal direction using the penalty method. Depending on the gap status, an automatic switching procedure is used to choose between contact and cohesive models. In the latter case a bilinear CZ law is considered (Fig. 1). This simple shape is able to capture the main characteristic parameters of the interface, i.e. the cohesive strength, \(p_{Nmax}\), the ultimate value of the normal relative displacement, \(g_{Nu}\), as well as the linear-elastic stiffness (slope of the curve in the ascending branch, \(\frac{p_{Nmax}}{g_{Nmax}}\), where \(g_{Nmax}\) is the normal relative displacement at peak cohesive stress). Thus the interface law reads

$$\begin{aligned} p_{N}=\left\{ \begin{array}{l@{\quad }l@{\quad }l} \varepsilon _{N}g_{N} &{} \quad {\mathrm {for}} &{} g_{N}<0\\ \frac{p_{Nmax}}{g_{Nmax}}g_{N} &{} \quad {\mathrm {for}} &{} 0\le g_{N}<g_{Nmax}\\ p_{Nmax}\frac{g_{Nu}-g_{N}}{g_{Nu}-g_{Nmax}} &{} \quad {\mathrm {for}} &{} g_{Nmax}\le g_{N}<g_{Nu}\\ 0 &{} \quad {\mathrm {for}} &{} g_{N}\ge g_{Nu} \end{array}\right. \end{aligned}$$
(19)

where \(\varepsilon _{N}>0\) is the normal penalty parameter. The non-penetration condition in compression is enforced exactly in the limit as \(\varepsilon _{N}\) tends to infinity.

Fig. 1
figure 1

Relationship between interfacial tractions and relative displacements in the normal direction

Full size image

Note that, in this formulation, the interacting locations at the two sides of the crack are continuously updated through the closest-point projection procedure typical of large deformation contact algorithms [60]. Through this choice, the tangential components of contact and cohesive interfacial forces vanish automatically, which is reasonable for frictionless contact and mode-I cohesive debonding. In cases involving mode II or mixed-mode debonding where the interacting bodies undergo significant relative displacements in the normal as well as in the tangential directions as well as for frictional contact, a different formulation is needed. E.g. a possible approach is to assume that the cohesive force acting across the interface at each slave Gauss point continuously connects it to the same master projection point identified in the initial bonded configuration, at least during the initial stage of loading.

3.2 Interface contribution to the virtual work

The contribution of the interfacial tractions to the virtual work can be expressed as

$$\begin{aligned} \delta W_{c}=\int _{\Gamma _{c}}p_{N}\delta g_{N}\, d\Gamma \end{aligned}$$
(20)

where \(\delta \) is the symbol for virtual variation, the integral is evaluated on the pull back of the currently active interfacial region (see also Sect. 3.4) and the normal component of the interfacial traction, \(p_{N}\), takes one of the expressions in Eq. (19) depending on the sign and magnitude of \(g_{N}\). Linearization of Eq. (20) for use in the Newton–Raphson iterative procedure yields

$$\begin{aligned} \triangle \delta W_{c} =\int _{\Gamma _{c}}\frac{\partial p_{N}}{\partial g_{N}}\Delta g_{N}\delta g_{N}d\Gamma +\int _{\Gamma _{c}}p_{N}\Delta \left( \delta g_{N}\right) d\Gamma \end{aligned}$$
(21)

where \(\Delta \) is the symbol for linearized increment. Based on Eq. (19), it is

$$\begin{aligned} \frac{\partial p_{N}}{\partial g_{N}}=\left\{ \begin{array}{l@{\quad }l@{\quad }l} \varepsilon _{N} &{} \quad {\mathrm {for}} &{} g_{N}<0\\ \frac{p_{Nmax}}{g_{Nmax}} &{} \quad {\mathrm {for}} &{} 0\le g_{N}<g_{Nmax}\\ -\frac{p_{Nmax}}{g_{Nu}-g_{Nmax}} &{} \quad {\mathrm {for}} &{} g_{Nmax}\le g_{N}<g_{Nu}\\ 0 &{} \quad {\mathrm {for}} &{} g_{N}\ge g_{Nu} \end{array}\right. \end{aligned}$$
(22)

For the detailed expressions of \(\delta g_{N}, \Delta g_{N}\), and \(\Delta \left( \delta g_{N}\right) \) needed in Eqs. (20) and (21), see [29, 60]. These are also reported in [19].

3.3 Variation and linearization of the contact and debonding variables in discretized form

The quantities \(\delta g_{N}, \Delta g_{N}\) and \(\Delta \left( \delta g_{N}\right) \) can be rewritten in matrix form as follows (Dimitri et al. [19])

$$\begin{aligned} \delta g_{N}=\mathbf {\delta u}^{T}\mathbf {N}\qquad \triangle g_{N}=\mathbf {N}^{T}\triangle \mathbf {u} \end{aligned}$$
(23)

where the following vectors have been defined

$$\begin{aligned} \delta \mathbf {u}\!=\!\left[ \begin{array}{c} \delta \mathbf {u}_{1}^{s}\\ \vdots \\ \delta \mathbf {u}_{n^{s}}^{s}\\ \delta \mathbf {u}_{1}^{m}\\ \vdots \\ \delta \mathbf {u}_{n^{m}}^{m} \end{array}\right] \quad \triangle \mathbf {u}\!=\!\left[ \begin{array}{c} \triangle \mathbf {u}_{1}^{s}\\ \vdots \\ \triangle \mathbf {u}_{n^{s}}^{s}\\ \triangle \mathbf {u}_{1}^{m}\\ \vdots \\ \triangle \mathbf {u}_{n^{m}}^{m} \end{array}\right] \quad \mathbf {N}\!=\!\left[ \begin{array}{c} R{}_{1}^{s}(\mathbf {\varvec{\xi }}_{s})\mathbf {n}\\ \vdots \\ R{}_{n^{s}}^{s}(\varvec{\mathbf {\xi }}_{s})\mathbf {n}\\ -R{}_{1}^{m}({\bar{\varvec{\xi }}}_{m})\mathbf {n}\\ \vdots \\ -R{}_{n^{m}}^{m}({\bar{\varvec{\xi }}}_{m})\mathbf {n} \end{array}\right] \nonumber \\ \end{aligned}$$
(24)

In Eq. (24) \(n^{s}\) and \(n^{m}\) are the number of basis functions having support on the element of the slave and master body, respectively, where the quantities are currently being evaluated; \(\mathbf {\varvec{\xi }}_{s}=\{\xi _{s}^{\alpha }\}_{\alpha =1}^{d_{s}-1}\) are the parametric coordinates of the point on the slave surface where the quantities are being evaluated, and \(\mathbf {\varvec{\bar{\xi }}}_{m}=\{\bar{\xi }_{m}^{\alpha }\}_{\alpha =1}^{d_{s}-1}\) are the parametric coordinates of the respective projection point on the master surface. The linearization of the variation can be expressed as

$$\begin{aligned} \triangle \left( \delta g_{N}\right) =\delta \mathbf {u}^{T}\mathbf {k}_{geo}\Delta \mathbf {u} \end{aligned}$$
(25)

with

$$\begin{aligned} \mathbf {k}_{geo}=g_{N}\bar{\mathbf {N}}\mathbf {m}^\mathbf{-1} \bar{\mathbf {N}}^{T}+\mathbf {D}{\hat{\mathbf{N}}^{ T }}+{\hat{\mathbf{N}} \mathbf {D}^{ T }}-\mathbf {D}\mathbf {k}\mathbf {D}^{T} \end{aligned}$$
(26)

Here \(\mathbf {m}^{-1}\) is the inverse metric tensor, whose components \(m^{\alpha \beta }\) are the inverse of those of the metric tensor evaluated at the projection point, \(m_{\alpha \beta }:=\bar{{\varvec{\tau }}}_{\alpha }\cdot \bar{{\varvec{\tau }}}_{\beta }\), and \(\mathbf {k}\) is the curvature tensor also evaluated at the projection point, \(k_{\alpha \beta }={\bar{\mathbf{x}}}_{\alpha ,\beta }^{m}\cdot \mathbf {n}\). Moreover, the following definitions have been introduced

$$\begin{aligned}&\mathbf {T_{\alpha }}\!=\!\left[ \begin{array}{c} R{}_{1}^{s}(\mathbf {\varvec{\xi }}_{s}) {\varvec{\tau }}_{\alpha }\\ \vdots \\ R{}_{n^{s}}^{s}(\mathbf {\varvec{\xi }}_{s}){\varvec{\tau }}_{\alpha }\\ -R{}_{1}^{m}({\bar{\varvec{\xi }}}_{m}){\varvec{\tau }}_{\alpha }\\ \vdots \\ -R{}_{n^{m}}^{m}(\mathbf {\varvec{\bar{\xi }}}_{m}){\varvec{\tau }}_{\alpha } \end{array}\right] \quad \mathbf {N}_{\alpha }\!=\! \left[ \begin{array}{c} 0\\ \vdots \\ 0\\ -R{}_{1,\alpha }^{m}(\mathbf {\varvec{\bar{\xi }}}_{m})\mathbf {n}\\ \vdots \\ -R{}_{n^{m},\alpha }^{m}(\mathbf {\varvec{\bar{\xi }}}_{m})\mathbf {n} \end{array}\right] \end{aligned}$$
(27)
$$\begin{aligned}&{\hat{\mathbf{N}}}=\left[ \begin{array}{cc} \mathbf {N}_{1}&\mathbf {N}_{2}\end{array}\right] \qquad {\hat{\mathbf{T}}}=\left[ \begin{array}{cc} \mathbf {T}_{1}&\mathbf {T}_{2}\end{array}\right] \qquad \left( d_{s}=3\right) \end{aligned}$$
(28)
$$\begin{aligned}&\mathbf {D}=\left[ {\hat{\mathbf{T}}}-g_{N}{\hat{\mathbf{N}}}\right] \mathbf {A}^{-1}\qquad \overline{\mathbf {N}}={\hat{\mathbf{N}}}-\mathbf {D}\mathbf {k} \end{aligned}$$
(29)

where \(\mathbf {A}^{-1}\) is the inverse of tensor \(A_{\alpha \beta }=m_{\alpha \beta }-g_{N}k_{\alpha \beta }\). All the equations reported in this section are valid for both 2D and 3D cases, except for Eq. (28) that in the 2D case is substituted by \({\hat{\mathbf{N}}}=\mathbf {N}_{1}\) and \({\hat{\mathbf{T}}}=\mathbf {T}_{1}\).

For Lagrange and NURBS discretizations, the size of all vectors is fixed and dictated by the order of the discretization, while for T-spline discretizations the above vectors have variable size depending on the number of basis functions having support on each given slave or master element. This is dictated not only by the polynomial order but also by the presence and number of T-junctions and extraordinary points.

3.4 The Gauss-point-to-surface (GPTS) contact and cohesive debonding algorithm

As mentioned earlier, the interface is discretized with generalized contact elements which account for both contact and cohesive debonding. The computation of the interface contribution is based on the GPTS algorithm. This formulation was originally proposed by [23] for the solution of contact problems, extended to NURBS discretizations in [16, 52] and then to T-splines discretizations in [19]. The formulation is characterized by the independent enforcement of the interfacial constraints at each quadrature point associated with the contribution \(\delta W_{c}\) in Eq. (20). In other words, the interfacial contribution to the virtual work \(\delta W_{c}\) in Eq. (20) is integrated in a straightforward fashion by locating a predetermined number of Gauss-Legendre quadrature points (GPs) on each element of the slave contact surface.

The GPTS algorithm is characterized by a remarkable simplicity of formulation and implementation. It is also computationally inexpensive and passes (up to within the integration error) the so-called contact patch test, which is a necessary condition for convergence to the correct solution [23]. Its main drawback is its overconstrained nature, as the interface constraints are enforced (in simple but not rigorous terms) at an “excessive” number of locations. This leads to LBB instability when using the penalty method with very large values of the penalty parameter. In our examples the values of the penalty parameter for which the drawbacks of instability become appreciable for the GPTS algorithm seem to lay beyond those needed for a solution of satisfactory quality from the engineering perspective. Nevertheless, an interfacial formulation in the framework of mortar methods would certainly be more performant and may be pursued by the authors in future research.

By substitution of Eq. (23) into Eq. (20), the contact contribution to the residual vector for the Newton–Raphson iterative solution of the non-linear problem is obtained as follows

$$\begin{aligned} \mathbf {R}=\int _{\Gamma _{c}}p_{N}\mathbf {N}\, d\Gamma \end{aligned}$$
(30)

which is numerically computed on \(\Gamma _{c}\) as

$$\begin{aligned} \mathbf {R}={\displaystyle \sum _{GP,active}p_{Ng}\mathbf {N}_{g}w_{g}j_{g}} \end{aligned}$$
(31)

where the subscript \(g\) indicates that the quantity is computed at the \(g^{th}\) GP on \(\Gamma _{c}, w_{g}\) and \(j_{g}\) are respectively the weight and the jacobian associated to the same GP, and the summation is extended to all active GPs. From Eq. (21) combined with Eqs. (23) and (25) the expression of the consistent tangent stiffness matrix results as

$$\begin{aligned} \mathbf {K}_{T} =\mathbf {K}_{T,main}+\mathbf {K}_{T,geo} \end{aligned}$$
(32)

where the “main” and “geometric” components are given by

$$\begin{aligned}&\mathbf {K}_{T,main} =\int _{\Gamma _{c}}\frac{\partial p_{N}}{\partial g_{N}}\mathbf {N}\mathbf {N}^{T}d\Gamma \end{aligned}$$
(33)
$$\begin{aligned}&\mathbf {K}_{T,geo} =\int _{\Gamma _{c}}p_{N}\mathbf {k}_{geo}d\Gamma \end{aligned}$$
(34)

with \(\mathbf {k}_{geo}\) given by Eq. (26). Finally, the numerical integration of Eqs. (33) and (34) yields

$$\begin{aligned}&\mathbf {K}_{T,main} ={\displaystyle \sum _{GP,active}}\left. \frac{\partial p_{N}}{\partial g_{N}}\right| _{g}\mathbf {N}_{g}\mathbf {N}_{g}^{T}w_{g}j_{g} \end{aligned}$$
(35)
$$\begin{aligned}&\mathbf {K}_{T,geo} ={\displaystyle \sum _{GP,active}}p_{Ng}\mathbf {k}_{geo,g}w_{g}j_{g} \end{aligned}$$
(36)

A final remark is needed regarding the concept of “active” GPs and, correspondingly, of “active” interface region. Unlike in a unilateral contact formulation, in the presented setting all GPs belonging to the predefined contact/cohesive surface are potentially active, as the contact or cohesive constrains are activated for negative and positive normal gap, respectively. However, in general loading cases attention must be paid to distinguish between loading and unloading conditions as well as to the previous history of each GP. E.g., a GP which has fully debonded by reaching \(g_{N}\ge g_{Nu}\) can no longer be considered active if its gap is found to decrease below \(g_{Nu}\) at subsequent loading stages, unless the gap changes sign and leads to contact conditions. Such general situations can be accounted for e.g. within a damage formulation but are not encountered in the examples reported hereafter.

4 Numerical examples

The algorithm illustrated above has been implemented in the finite element code FEAP (courtesy of Prof. Taylor [51]). Some numerical examples are presented hereafter to demonstrate its performance in combination with NURBS and T-spline-based parameterizations. A user module has been added to FEAP to input the control points, elements and Bézier extraction operators of T-spline models exported from the Autodesk T-spline plugin for Rhino3d [6].

T-splines, NURBS and Lagrange discretizations with the same number of DOFs \(\left( D_{0}\right) \), or equivalently with the same number of control variables (control points or nodes) are employed. The current T-spline technology only encompasses third-degree interpolations, whereas for NURBS and Lagrange different degrees are adopted. Cubic T-spline discretizations are denoted by \(T\), while NURBS and Lagrange discretizations with order \(p\) in all parametric directions are denoted as \(Np\) and \(Lp\), respectively. Lagrange and NURBS meshes are uniform, whereas in the T-spline parameterizations T-junctions are locally added to the meshes near the interfaces.

The sets of comparisons presented hereafter should be intended as follows. First, Lagrange and NURBS models with the same number of DOFs are compared. Despite Lagrange interpolations are capable of local refinement, this possibility is not exploited here, in order for the Lagrange/NURBS comparison to focus on the effect of the different basis functions on performance. Second, NURBS and T-spline models with the same number of DOFs are compared, to quantify the increase in accuracy obtained through the local refinement capability for a given computational cost. The accuracy of NURBS for given DOFs may be improved by using non-uniform knot vectors such as done e.g. in [19]. However, this possibility is not general enough and is not exploited herein to avoid introducing additional problem-dependent variables such as the grading ratios, which are not believed to be significant for the purpose of the present investigation.

The three presented examples consider the 2D double cantilever beam (DCB) specimen, the 2D peel test for bimaterial joints and 3D edge peeling of thin laminates. Unless specified otherwise, a fixed number of 2 GPs is adopted for the evaluation of the interface integrals on each surface element in each surface parametric direction.

4.1 DCB test

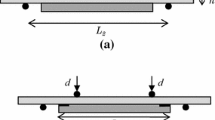
As a first example, we consider the classical mode-I DCB test, used in the ASTM3433 [5] standard to determine the mode-I fracture toughness, and we assume plane stress conditions. A specimen with length \(L=14\,{\mathrm {mm}}\), width \(w=1\,{\mathrm {mm}}\), thickness \(h=0.2\,{\mathrm {mm}}\), and precrack length \(a_{0}=4\,{\mathrm {mm}}\), is gradually pulled apart (Fig. 2) by applying a vertical displacement \(u=2.5\) mm in 2500 time steps. An elastic isotropic behavior is assumed for both master (upper) and slave (lower) bodies, with material properties \(E=120\,{\mathrm {GPa}}\) and \(\nu =0.2\). A penalty parameter \(\varepsilon _{N}=10^{5}\,{\mathrm {MPa/mm}}\) is chosen as the default value.

Fig. 2
figure 2

DCB problem: scheme

Full size image

A prerequisite for accurate debonding computations is that the element size ahead of the crack tip is sufficiently smaller than the length of the FPZ where the cohesive traction-separation law is activated and the energy is dissipated. While the element size is obviously dictated by the discretization, the length of the FPZ is essentially a function of the CZ parameters. In particular, for a given interfacial fracture energy, \(G_{IC}\), and for a given ratio between the ultimate and maximum opening displacements, \(g_{Nu}/g_{Nmax}\), the length of the FPZ is known to decrease as the cohesive strength increases (see [14, 15] for detailed analytical solutions).

To investigate on the effect of the FPZ resolution on results, both mesh refinement and size of the FPZ are varied in the numerical analyses. The problem is solved with uniform Lagrange and NURBS meshes, as well as with locally refined T-spline meshes. Lagrange and NURBS discretizations of different orders are first considered. Then, all third-order discretizations including T-splines are compared. All comparisons are made for the same number of total DOFs. Two different levels of mesh refinement are studied, corresponding to \(D_{0}=1698\) (mesh 1) and \(D_{0}=3108\) (mesh 2). Figure 3 shows a close-up of the two meshes for Lagrange, NURBS and T-spline discretizations in the vicinity of the crack tip. Whereas Lagrange and NURBS meshes are uniform, T-discretizations have a larger number of elements concentrated in the vicinity of the interface due to analysis-suitable T-spline local refinement [46]. Also, two different cohesive strengths are considered (\(p_{Nmax}\!=\!3\,{\mathrm {MPa}}\) and \(p_{Nmax}\!=\!6\,{\mathrm {MPa}}\)), whereas \(G_{IC}=0.1\,{\mathrm {N/mm}}\) and \(g_{Nu}/g_{Nmax}=12.5\) are kept fixed (Fig. 4).

Fig. 3
figure 3

DCB problem: cubic Lagrange, NURBS and T-spline meshes (close-up). a–c \(D_{0}\) = 1698, d–f \(D_{0}\) = 3108

Full size image
Fig. 4
figure 4

DCB problem: the CZ laws

Full size image

The response is evaluated in terms of load-deflection behavior. The numerical results are compared with analytical predictions obtained by combining the concepts of elastic bending theory and linear elastic fracture mechanics (LEFM) [25]. Note that LEFM can be considered as the limit case of CZ modeling where the cohesive strength tends to infinity and the size of the FPZ accordingly tends to zero, so that the crack tip singularity is recovered. As a result, the load-deflection response as predicted by LEFM is not expected to agree with the numerically computed response. Nevertheless, the analytical curve is a useful benchmark which is expected to be approached more closely as the cohesive strength is increased.

Linear and higher-order interpolations are first considered with Lagrange and NURBS basis functions, see Figs. 5 and 6a, b for the lowest cohesive strength (CZM 1) and Figs. 7 and 8a, b for the highest cohesive strength (CZM 2). \(L1\) and \(N1\) interpolations are coincident in this case due to the uniform weights.

Fig. 5
figure 5

DCB problem: load-displacement response for a Lagrange discretizations of different orders, b NURBS discretizations of different orders, c cubic Lagrange, NURBS and T-spline discretizations. \(D_{0}\) = 1698, CZM 1

Full size image
Fig. 6
figure 6

DCB problem: load-displacement response for a Lagrange discretizations of different orders, b NURBS discretizations of different orders, c cubic Lagrange, NURBS and T-spline discretizations. \(D_{0}\) = 3108. CZM 1

Full size image
Fig. 7
figure 7

DCB problem: load-displacement response for a Lagrange discretizations of different orders, b NURBS discretizations of different orders, c cubic Lagrange, NURBS and T-spline discretizations. \(D_{0}\) = 1698. CZM 2

Full size image
Fig. 8
figure 8

DCB problem: load-displacement response for a Lagrange discretizations of different orders, b NURBS discretizations of different orders, c cubic Lagrange, NURBS and T-spline discretizations. \(D_{0}\) = 3108. CZM 2

Full size image

Linear interpolations deliver too stiff results in the ascending branch of the curves, due to shear locking effects. This phenomenon is less pronounced for the finest mesh as this features a more favorable element aspect ratio. Note that the seemingly good agreement of the stiffer results with the analytical curve in Figs. 5 and 7 does not imply a better accuracy, as analytical results refer to the LEFM case.

NURBS discretizations evidently deliver results of higher quality in comparison with conventional Lagrange finite elements. This is likely due to the higher (\(C^{p-1}\)) order of inter-element continuity achieved with NURBS, as opposed to \(C^{0}\) in the Lagrange case. The load-deflection curves obtained from NURBS discretizations are smoother than the Lagrange ones and are nearly unaffected by the interpolation order. Conversely, results from higher-order Lagrange parameterizations are quite irregular. For a given resolution, increasing the order of the Lagrange discretization does not alleviate the magnitude of oscillations but is rather unfavorable, as even larger oscillations are produced. These results qualitatively resemble those presented in [16, 17, 52] for unilateral contact problems.

As the mesh is refined, the cohesive/contact regions are better resolved and the quality of the solution improves, as visible by comparing Figs. 5 with 6 and 7 with 8. More elements are enclosed within a FPZ of given size and the debonding process is more accurately described. On the other hand, the effect of the increase of the interfacial strength for a constant fracture energy (i.e. for a decreasing ultimate separation, \(g_{Nu}\)) is also to reduce the length of the FPZ and therefore to decrease the number of elements spanning this zone. It is expected that if the fracture strength \(p_{Nmax}\) is increased to a point where less than one element spans the FPZ, convergence is no longer achieved or inaccurate results are found. By comparing Figs. 5 with 7 and 6 with 8, it is clear that increasing the cohesive strength leads to more severe irregularities and oscillations in the global response both for Lagrange and NURBS discretizations. The FPZ is localized in a smaller region, and a higher mesh resolution near the crack tip is necessary to improve the results.

The same problem is then solved with locally refined cubic T-spline meshes, whose results are compared with those from cubic Lagrange and NURBS interpolations in Figs. 5, 6, 7 and 8c. The curves obtained with T-splines feature significantly smaller oscillations during the progressive debonding phase (i.e. in the softening branch of the curves) in comparison with those from NURBS interpolations with the same \(D_{0}\), as a direct consequence of the locally refined FPZ.

For completeness, the number of GPs where the interface constraints are enforced is varied in Fig. 9 for the most unfavourable case here analysed, corresponding to the highest fracture strength \(p_{Nmax}\) (i.e. CZM 2), and the coarsest mesh (i.e. mesh 1). An increasing number of GPs is beneficial as it improves the resolution in the computation of the cohesive or contact forces, especially for this coarse mesh. This is much more evident for \(L_{3}\) and \(N_{3}\) discretizations, for which the magnitude of the oscillations is reduced for increasing number of GPs, until macroscopically smooth curves are obtained. T-spline discretizations are less sensitive to the number of GPs as a smooth curve is already obtained with 2 GPs. From a qualitative observation valid for this case, the T-spline curve with 2 GPs is similar to the NURBS curve with 8 GPs and to the Lagrange curve with 16 GPs. These results indicate that increasing the number of interface GPs in the GPTS formulation allows for the use of coarse meshes even when the interface parameters lead to a very small FPZ, thus decreasing the overall computational cost. With IGA-based (and in particular T-spline-based) discretizations, coarse meshes with a small number of interface GPs can be used.

Fig. 9
figure 9

DCB problem: effect of the number of Gauss points per parametric direction on each contact element. a L3, b N3, c T. \(D_{0}\) = 1698. CZM 2

Full size image

4.2 Bimaterial peel test

The second example considers a peel test between a fiber-reinforced polymer strip with length \(L_{2}=150\,{\mathrm {mm}}\) and thickness \(h_{2}=2\,{\mathrm {mm}}\) and a concrete substrate with length \(L_{1}=120\,{\mathrm {mm}}\) and thickness \(h_{1}=10\,{\mathrm {mm}}\). The strip, initially bonded to the substrate throughout its length, is peeled away by applying at the right boundary a vertical displacement of 10 mm in 200 time steps, as shown in Fig. 10. An elastic isotropic behavior is assumed for both bodies, with material properties \(E_{1}=5\,{\mathrm {MPa}}\) and \(\nu _{1}=0.2\) for the substrate and \(E_{2}=250\,{\mathrm {MPa}}\) and \(\nu _{2}=\nu _{1}\) for the strip. The lower surface of the strip is treated as slave, and the upper surface of the substrate as master. A bilinear CZ law is adopted with cohesive parameters \(p_{Nmax}=6\,{\mathrm {MPa}}, G_{IC}=0.1\,{\mathrm {N/mm}}, g_{Nu}/g_{Nmax}=10\). Figure 11 shows the meshes for the cubic Lagrange, NURBS and T-spline discretizations. The penalty parameter \(\varepsilon _{N}\) is set to \(10^{5}\,{\mathrm {MPa/mm}}\), and 2 GPs are considered for each element of the interface.

Fig. 10
figure 10

Peel test problem: scheme

Full size image
Fig. 11
figure 11

Peel test problem: cubic Lagrange, NURBS and T-spline meshes (close-up)

Full size image

Figure 12 describes the peeling process in terms of load-displacement curves for Lagrange and NURBS interpolations of different orders. As in the previous example, the Lagrange interpolations are shown to produce significant and irregular load oscillations during the softening stage. These oscillations tend to increase with the order of the discretization and strongly affect the iterative convergence behavior. Using NURBS parameterizations greatly improves the quality of results, as visible from the reduced magnitude of the oscillations and the regularity of the pattern. Increasing the order of the discretization from \(p=2\) to \(p=3\) does not produce appreciable changes in results, although probably smoother results would be obtained with further order elevation.

Fig. 12
figure 12

Peel test problem: load-displacement response for a Lagrange discretizations of different orders, b NURBS discretizations of different orders, c cubic Lagrange, NURBS and T-spline discretizations

Full size image

Figure 12b compares all third-order discretizations, including the locally refined T-spline mesh. This performs even better than the cubic NURBS mesh and leads to a macroscopically smooth curve due to the local refinement close to the contacting/cohesive surfaces. This confirms T-spline-based IGA as the most accurate and efficient choice when studying debonding problems.

As finally shown in Fig. 13, increasing the number of GPs reduces significantly the magnitude of oscillations for Lagrange and NURBS discretizations, while having virtually no effect for T-spline discretizations as smooth results are obtained already with 2 GPs. In this case, the T-spline curve with 2 GPs is similar to the NURBS curve with 4 GPs, whereas results of Lagrange interpolations remain oscillatory even for the largest number of GPs investigated.

Fig. 13
figure 13

Peel test problem: effect of the number of Gauss points per parametric direction on each contact element. a L3, b N3, c T

Full size image

4.3 3D thin-walled laminates

In this section, the T-spline-based integrated contact and CZ formulation is applied to a 3D laminated structure. The primary goal of this example is to demonstrate the effectiveness of the proposed formulation in conjunction with 3D T-spline discretizations using shell elements for the continuum. Figure 14 depicts two square laminae (dimensions \(25 \times 25 \times 0.2~\mathrm{mm}^{3}\)) bonded to each other and fixed on two orthogonal sides. A concentrated displacement \(U_{z}=12\,{\mathrm {mm}}\) is applied in 120 time steps to the control point located at the free corner of the upper lamina. The two laminae are discretized with 3D isogeometric Kirchoff-Love shell elements [28]. Some irregular elements are generated in the T-mesh by including T-junctions around the loaded control point. Also in this case, the analysis is carried out by importing into FEAP the extraction operator generated by the T-spline plugin in the Rhino environment, where the mesh is generated using standard CAD operations. An elastic isotropic material behaviour is assumed for both bodies, with constants \(E=10^{6}\,{\mathrm {MPa}}\) and \(\nu =0.3\). The lower shell is here treated as master and the upper shell as slave. A bilinear cohesive model with \(p_{Nmax}=10\,{\mathrm {MPa}}\) and \(G_{IC}=0.3\,{\mathrm {N/mm}}\) is assigned to the interface, and \(4\times 4\) GPs are used for integration of the interface contribution to the virtual work.

Fig. 14
figure 14

3D thin-walled laminates: T-spline mesh and deformed shape for time step 80

Full size image

Figure 14 shows the deformed mesh at time step 80, along with the contours of the vertical displacement, whereas the load-deflection history is reported in Fig. 15. In the initial loading phase, the two shells are bonded throughout the interface and the slope of the load-deflection curve corresponds to the stiffness of a single shell having double the thickness of each lamina (dashed line). Soon thereafter debonding starts taking place, leading to a markedly non-linear behavior. The peak is reached approximately when the debonding front reaches the diagonal of the laminate, at which point a sudden drop in load is observed. The subsequent behavior returns to linearity but the stiffness corresponds to that of the upper lamina, now fully detached from the lower one (dash-dotted line). The load-deflection response appears remarkably smooth throughout all phases, including the abrupt transition from the partially debonded to the fully debonded stage. This suggests that the \(C^{2}\) continuity of the interface determines a well-resolved deformed FPZ. Due to the large deformation range, the slave GPs are projected onto different master segments as the deformation progresses. However, these transitions occur quite smoothly and do not lead to appreciable oscillations in the global response despite the coarseness of the mesh. A similarly smooth behaviour is also expected for more complex meshes including extraordinary points with \(C^{1}\)-continuous local parameterizations. This has been succesfully verified in Dimitri et al. [19] for examples including extraordinary points in unilateral frictionless contact.

Fig. 15
figure 15

3D thin-walled laminates: reaction-displacement global response

Full size image

5 Conclusions

This paper proposes a NURBS- and T-spline-based isogeometric formulation for 2D and 3D interface problems with non-matching meshes encompassing contact and mode-I CZ debonding. A GPTS discretization of the interface constraints is adopted whereby a desired number of quadrature points is located on the slave contact/cohesive surface and the contact/CZ constraints are enforced independently at each of these points. The performance of Lagrange, NURBS and T-spline discretizations is evaluated comparatively based on the load-displacement responses from a DCB specimen, a bimaterial peel test, and an edge debonding test between thin laminates.

The results of the Lagrange discretizations are shown to feature oscillations of increasing magnitude and irregularity as the order of the parameterization is increased. These oscillations in turn lead to important iterative convergence issues and potentially loss of convergence. Conversely, the NURBS discretizations lead to very small oscillations whose magnitude is approximately constant with the interpolation order within the range of order analyzed herein. In the comparison between NURBS and T-spline models with the same number of DOFs, T-splines deliver macroscopically smooth results due to their ability of local refinement, which leads to a better resolution of the FPZ in the vicinity of the interface and ahead of the cohesive crack. Finally, increasing the number of interface GPs in the GPTS formulation allows for the use of coarse meshes even when the interface parameters lead to a very small FPZ, thus decreasing the overall computational cost. With IGA-based (and in particular T-spline-based) discretizations, coarse meshes with a small number of interface GPs can be used.

In summary, the proposed formulation, combined with T-spline isogeometric discretizations featuring high inter-element continuity and local refinement ability, appears to be a computationally accurate and efficient technology for the solution of interface problems.