1 Introduction

The motion of droplet within a bulk fluid medium takes place in numerous natural and engineering processes such as blood-flow, air entrainment at ocean surfaces, cloud cavitation, boiling heat transfer, petroleum refining, spraying of liquid fuel and paint, and bubble reactors in the chemical industry [1–3]. This motion in a viscous liquid is a dynamically complicated, nonlinear, and non-stationary hydrodynamical process, and is usually associated with a significant deformation in the droplet geometry due to the complex interactions among fluid convection, viscosity, gravitational and interfacial forces. Deforming droplet can acquire complex shapes, thereby resulting in a large variety of flow patterns around droplets [1, 4–6].

In multiphase systems of different electrical permittivities and conductivities, the utilization of electric fields provides a promising way to control the motion and deformation of droplets which can be crucial for a variety of engineering applications such as electrospray ionization, electro-coalescence and mixing, electrostatic printing and electro-spinning [2, 3, 7]. To state more explicitly, if a droplet suspended in a quiescent viscous liquid is exposed to an externally applied electric field, in addition to the gravitational force induced deformation and motion if exist, it will also be deformed depending on the strength of the applied electric field and the fluid properties such as viscosity, surface tension, electrical conductivity, and permittivity [7–9].

Although a number of experimental, theoretical, and numerical studies have addressed the buoyancy-driven motion of a droplet through a quiescent fluid [6, 10–12], there are only a few works that consider the effect of the applied electric field on the dynamics of bubble deformation [5, 7, 8], and a complete understanding of the underlying mechanisms has not yet been achieved, which necessitates further studies in this field. Additionally, not only the problem in question but also the large majority of other multiphase flow problems have generally been modeled using mesh dependent techniques [5, 6, 8, 13] and the validity and accuracy of mesh free methods for modeling droplet deformation under the influence of electric field need to be further investigated.

In multiphase systems, modeling the evolution of interface is a crucial part of the flow simulations, and needs to be performed correctly in order to obtain reliable numerical results. Mesh-dependent methods are generally associated with the difficulties in handling large topological deformation, and hence, depending on the problem in hand (i.e., if the topology of the flows deforms significantly), mesh-refinement might be required. In literature, within the context of mesh dependent methods, different approaches have been proposed and studied to simulate the interface evolution on a regular grid. The majority of these techniques utilizes Eulerian interface-capturing method wherein the interface is represented as either by a discontinuity line of some characteristic function or a zero-level set of some implicit function reconstructed from the properties of some relevant field variables such as fluid fractions or density. The former method is referred to as the “discontinuous approach” (for example, volume of fluid (VOF) method) while the later one is called as the “continuous approach” (for instance, Level Set method). In both approaches, the interface is modeled through a solution of an additional transport equation and treated as a material line propagating with the fluid. The term “interface-capturing” comes from the fact that the interface is recovered using the current distribution of the relevant field variable. Two main steps of the interface-capturing algorithm are (i) the propagation and (ii) the reconstruction. Both of these steps should be implemented with a great care since the propagation step may introduce some difficulties for the numerical method while the reconstruction step may significantly affect the viscous stress and surface tension forces’ approximation at the interface (calculated from the location, orientation and curvature of the interface). The main advantages of the interface-capturing methods are: (i) easy treatment of reconnection or merging of interfaces, (ii) mass conservation in a natural way, and (iii) its extendibility to three-dimensional problems. The major disadvantages of the method can be named as: (i) the advection of either discontinuous or continuous interface function, (ii) the complexities in determining the exact interface location, normal and curvature, (iii) numerical smearing of the interfacial boundary conditions as well as the interface details.

An alternative to the above-mentioned interface capturing approaches can be the Lagrangian meshless methods which are inherently combined with the interface-tracking approaches and are holding the benefits of: (i) precise tracking and the delineation of material interface, (ii) easy implementation of the interface boundary conditions and (iii) the absence of nonlinear convective term in the momentum equation. The main reason for choosing the Smoothed Particle Hydrodynamics (SPH) technique, as a well-advanced member of Lagrangian meshless methods, for the problems considered in the present work is due to the fact that in comparison to the conventional mesh-dependent computational fluid dynamics methods, the SPH method possesses the above mentioned unique features for modeling multiphase fluid flows and associated transport phenomena. Being more specific, in the SPH technique, the complexities in determining the interface position are easily avoided, and breaking and reconnection of interface can be treated naturally since phases can be easily distinguished due to the fact that each individual particle holds material properties, and the particle positions mark the locations of the interface because of the movable nature of the SPH particles. Additionally, discontinuities in transport coefficients, and interfacial forces can be easily included in governing equations or numerical scheme. The flow modeling with large topological deformations is possible since the SPH method does not require connected grid points and spatial partial derivatives in governing equations are computed directly from the differentiation of the weighting function analytically instead of taking the derivatives of the field variables on grid points. Numerical instabilities which might be observed in mesh dependent methods due to the discretization of nonlinear convective terms in the momentum balance equations is automatically eliminated owing to the non-existence of convective term in the numerical approximation scheme. The SPH method can be conveniently extended to three-dimensional problems without facing significant challenges in the course of modifying the numerical algorithm. Due to above substantiated attributes, the SPH method has recently received a great deal of attention for modeling multiphase flow problems. For more details about numerical modeling of multiphase flows with the SPH method, interested readers are referred to [14].

In this study, we numerically investigate the effect of an electric field on the neutrally buoyant droplet in a quiescent Newtonian fluid. The dynamics of the droplet is simulated computationally by solving conservation of mass and momentum equations together with associated interface and boundary conditions. These governing equations and relevant interface and boundary conditions are discretized by employing the SPH method. The leaky dielectric model is used in order to account for the effects of the electric field, and electrical properties of liquids. In the leaky dielectric model, the droplet with finite electrical conductivity and with no free electrical charge is considered. Under these model assumptions, electric stresses are supported only at the droplet interface, and are absent in the bulk. The interface of the droplet is modeled as a transition zone with a finite-thickness across which the material properties vary smoothly. The surface tension and electric field effects are integrated into momentum balance equations as volumetric forces by using the continuum surface force (CSF) and the divergence of the Maxwell stress tensor, respectively. The extensive amount of computations performed have enabled us to study the complex nature of droplet dynamics under the combined effect of Maxwell stresses, surface tension, and viscous forces.

2 Mathematical formulation

2.1 Mechanical balance laws of continua

All constituents of the multiphase system are considered to be viscous, Newtonian and incompressible liquids with constant material properties \(D\varGamma /Dt=0\) where \(D/Dt\) is the material time derivative operator, and the arbitrary field \(\varGamma \) may represent the density, and viscosity, among others. The set of equations governing the electrohydrodynamics (EHD) of viscous fluids is composed of Maxwell’s equations, and the conservation of mass and linear momentum which are written in their local form for the volume and the discontinuity surface, respectively as

$$\begin{aligned}&\!\!\!\!\frac{D\rho }{Dt}=-\rho \nabla \cdot \mathbf{v},\end{aligned}$$
(1)
$$\begin{aligned}&\!\!\!\! \rho \frac{D\mathbf{v}}{Dt}= \nabla \cdot T+\rho \mathbf{f}^{b}+\mathbf{f}^{E},\end{aligned}$$
(2)
$$\begin{aligned}&\!\!\!\! \Vert \rho \,(\mathbf{v}-\mathbf{u})\Vert \cdot \mathbf{n}=0,\end{aligned}$$
(3)
$$\begin{aligned}&\!\!\!\! \Vert \rho \,\mathbf{v}\,(\mathbf{v}-\mathbf{u})-T-T^E\Vert \cdot \mathbf{n}=\mathbf{f}^s, \end{aligned}$$
(4)

where Eq. (1) and (2) are valid in \(V-\xi \) which denotes the volume excluding points lying on the discontinuity surface \(\xi \) while Eqs. (3) and (4) are valid only on the discontinuity surface and represent the jump condition across \(\xi \). Here, \(\rho \) is the density, \(\mathbf{v}\) is the divergence-free velocity vector, \(T\) is the symmetric total stress tensor, \(\mathbf{f}^{b}\) is the body force, and \(\mathbf{f}^{E}\) is the Lorentz force per unit volume, which can be shown to be equal to the divergence of the so-called Maxwell stress tensor \(T^E\) as \(\mathbf{f}^{E}=\nabla \cdot T^E\) [15]. As can be noted, the electrostatics and hydrodynamics are coupled together through the Maxwell stress tensor. Furthermore, the symbol \(\Vert \Vert \) indicates the jump of the enclosed quantities across the discontinuity surface \(\xi \); for instance, \(\Vert \varGamma \Vert =\varGamma ^+-\varGamma ^-\) where \(\varGamma ^+\) and \(\varGamma ^-\) are the values of \(\varGamma \) on the positive and negative sides of the discontinuity surface, \(\mathbf{u}\) is the velocity of the discontinuity surface, and \(\mathbf{n}\) is the unit normal to the discontinuity surface, and finally, \(\mathbf{f}^{s}\) is the surface force per unit area on the interface due to the surface tension. For a Newtonian fluid, the total stress tensor can be defined as \(T=-pI+\tau \) where \(p\) is the absolute pressure, \(I\) is the identity tensor, and \(\tau =\mu (\nabla \mathbf{v}+(\nabla \mathbf{v})^{ +})\) is the viscous part of the total stress tensor, where \(\mu \) is the dynamic viscosity, and the sign \({ +}\) denotes transpose operation.

The surface tension force acting on the interface \(\xi \) in the unit normal direction can be formulated as

$$\begin{aligned} \mathbf{f}^s= \nabla _s\gamma +\gamma \, \kappa \, \mathbf{n}, \end{aligned}$$
(5)

where \(\nabla _s\) is the surface gradient operator, and defined as \(\nabla _s=P\cdot \nabla =\nabla -\mathbf{n}(\mathbf{n} \cdot \nabla )\) where \(P=I-\mathbf{n} \otimes \mathbf{n}\) is the projection tensor which extracts the tangential component of a vector field, \(\otimes \) is a dyadic product, \(\gamma \) is the surface tension coefficient, and \(\kappa =-P:\nabla \mathbf{n}=-\nabla \cdot \mathbf{n}\) is the curvature where the notation \(:\) indicates the inner product. Here, one can note that the surface gradient of surface tension gives rise to a tangential force while surface tension on a curved surface leads to a normal force.

Assuming that the discontinuity surface is a material interface (which requires that \(\mathbf{v}=\mathbf{u}\)), the momentum fluxes are continuous across the fluid-fluid interface, namely, \(\Vert \tau \Vert \cdot \mathbf{n}=0\), and \(\Vert T^E\Vert \cdot \mathbf{n}=0\), and the surface tension is independent of position, i.e., \(P\cdot \nabla \gamma =0\), the interface mass balance is satisfied identically, and the momentum balance on the interface reduces to

$$\begin{aligned} \mathbf{f}^s=\Vert p\Vert \cdot \mathbf{n}=\gamma \, \kappa \, \mathbf{n}. \end{aligned}$$
(6)

It should be noted that the surface tension force \(\mathbf{f}^s\) is a local surface force and the calculation of which requires the solution of the jump condition for the momentum balance. For the sake of computational convenience and efficiency, it is a common practice to express the local surface force \(\mathbf{f}^s\) as an equivalent volumetric force \(\mathbf{f}^v\)(the force per unit volume) as is done in the CSF method originally proposed by Brackbill et al. in [16]. The basic concept behind this approach is to replace the sharp interface between two fluids with a transition region of a finite thickness. This can be fulfilled through multiplying the local surface tension force with a dirac delta function \(\delta \), and the effect of surface tension can be consequently included in the momentum balance equation in the form of an external force term as [17, 18]

$$\begin{aligned} \mathbf{f}^v=\gamma \, \kappa \, \mathbf{n} \, \delta . \end{aligned}$$
(7)

2.2 Electrohydrodynamics balance Laws

Electrohydrodynamics is a science concerned with the interactions of electric fields and electric charges in fluids. The electrical conductivity of fluids may range from exceedingly low value to high value hence allowing for a fluid to be classified as extremely good insulator (dielectrics) or highly conducting. In EHD transport phenomena, due to the transient nature of the problems, the electric current distribution is not steady. Therefore, in accordance with the Ampere-Maxwell’s law,

$$\begin{aligned} \nabla \times \mathbf{B}&= \mu _M \mathbf{J}+ \mu _M \varepsilon \frac{\partial \mathbf{E}}{\partial t}, \end{aligned}$$
(8)

dynamic currents in the system give rise to a time-varying induced magnetic field. Here, \(\mathbf{B}\) and \(\mathbf{E}\) respectively are magnetic and electric field vectors, \(\mu _M\) is the magnetic permeability, and \(\mathbf{J}\) is total volume current. In EHD, the dynamic currents are so small that the influence of magnetic induction is negligible whereby the electromagnetic part of the system can be described by a quasi-static electric field model. Additionally, in the system considered, there is no externally applied time-varying magnetic field. In light of these assumptions, the coupling between the electric and magnetic field quantities in the Faraday’s law \(\nabla \times \mathbf{E}=- \partial \mathbf{B}/\partial t\) disappears which requires that the electric field vector be irrotational as [19]

$$\begin{aligned} \nabla \times \mathbf{E}=0, \end{aligned}$$
(9)

which necessitates that the gradient of the electric field vector be a symmetric tensor, namely, \(\nabla \mathbf{E}=(\nabla \mathbf{E})^{ +}\). The total volume current is defined as

$$\begin{aligned} \mathbf{J}= q^v \mathbf{v} + \mathbf{j}, \end{aligned}$$
(10)

where the first term on the right hand side is the convection current due to the free charges, \(q^v\) is the volume-charge density of free charges, and \(\mathbf{j}\) is the volume conduction current density, ohmic current, which is related to electric field vector through

$$\begin{aligned} \mathbf{j}= \sigma \mathbf{E}, \end{aligned}$$
(11)

where \(\sigma \) is the electrical conductivity.

The Gauss’ law for electricity in a dielectric material with the absolute permitivity (hereafter referred to as the permitivity) \(\varepsilon \) can be written in terms of the electric displacement vector, \(\mathbf{D}=\varepsilon \mathbf{E}\) as

$$\begin{aligned} \nabla {\cdot } \mathbf{D}=q^v. \end{aligned}$$
(12)

On taking the divergence of the differential form of Ampere’s law, and using the entity \(\nabla \cdot \nabla \times \mathbf{B}=0\) (the divergence of the curl is equal to zero) together with the Gauss’ law (Eq. (12)) for electricity, one can write the charge conservation as

$$\begin{aligned} \frac{D q^v}{D t}+\nabla \cdot \mathbf{j}=0. \end{aligned}$$
(13)

Considering a homogeneous fluid with the constant permittivity and the electrical conductivity, and then substituting the Gauss’ law for electricity in a dielectric material (Eq. (12)) together with the volume conduction current density (Eq. (11)) into the charge conservation equation (Eq. (13)), one can write

$$\begin{aligned} \dot{q}^v=-q^v \frac{\sigma }{\varepsilon }. \end{aligned}$$
(14)

The integration of this differential equation produces

$$\begin{aligned} q^v=q_o^v \exp \bigg (\frac{-t}{t^E}\bigg ), \end{aligned}$$
(15)

which describes the time relaxation of the net free charges along fluid particles line. Hence, homogeneous fluids support no net free charges. However, in inhomogeneous materials, free charges can be generated by an electric field component along the gradients of conductivity and/or permittivity. Here, \(t^E=\varepsilon /\sigma \) is referred to as the bulk relaxation time. For EHD problems, the time \(t\) can be considered as the viscous time scale of the fluid motion, which is defined as \(t^\mu =\rho L^2/\mu \), where \(L\) is the characteristic length scale. A two-fluid system can be classified as dielectric-dielectric, dielectric-conducting, or conducting-conducting by comparing the magnitude of \(t^E\) with \(t^\mu \) where the last case is the focus of this work.

As in the case of mechanical balance laws, in the surface-coupled model for a sharp interface, the electrical material properties are also piecewise constant on either side of the interface. However, jump conditions are also needed for Maxwell’s equations to relate interfacial and bulk properties. The jump conditions corresponding to Eqs. (9), (12) and (13) are written respectively as [15, 19]

$$\begin{aligned}&\mathbf{n} \times \Vert \mathbf{E}\Vert =0,\end{aligned}$$
(16)
$$\begin{aligned}&\mathbf{n} \cdot \Vert \mathbf{D}\Vert =q^s,\end{aligned}$$
(17)
$$\begin{aligned}&\displaystyle \frac{\overline{\delta } q^s}{\delta t}+\mathbf{n} \cdot \Vert \mathbf{J}-q^v\mathbf{v}\Vert +\nabla _s\cdot \mathbf{K}=0, \end{aligned}$$
(18)

where \(q^s\) is a surface density of free charge (charge per unit surface area), \(\overline{\delta }/\delta t\) is the total time derivative in following the motion of the discontinuity surface \(\xi \) along its normal, and defined as \(\overline{\delta }/\delta t= \partial /\partial t+(\mathbf{v} \cdot \mathbf{n})(\mathbf{n} \cdot \nabla )\) wherein the velocity of the discontinuity surface \(\mathbf{u}\) is replaced by \(\mathbf{v}\) based on the assumption that the discontinuity surface is a material interface. Here, \(\mathbf{K}\) is the total surface current defined as \(\mathbf{K}=\mathbf{k}+q^s\mathbf{u}\) where \(\mathbf{k}\) and \(q^s\mathbf{u}\) are the surface conduction and convection currents, respectively. Eq. (16) states that the tangential component of the electric field vector is continuous across the discontinuity surface while Eq. (17) reveals that the normal component of the electric displacement vector is discontinuous at the interface. Equation (18) is the conservation of charge on the discontinuity surface.

As stated previously, the electrostatics and hydrodynamics of a fluid system can be coupled together in the momentum balance equation through the Maxwell stress tensor which accounts for the stress induced in an incompressible liquid medium due to the presence of an electric field. The Maxwell stress tensor can be written as [19, 20]

$$\begin{aligned} T^E=\mathbf{D}\mathbf{E}-0.5(\mathbf{D} {\cdot } \mathbf{E}) I, \end{aligned}$$
(19)

where in Eq. (19), the contribution from the induced magnetic field was neglected. Upon taking the divergence of the Maxwell stress tensor and then using Eq. (12) and the symmetry of the gradient of the electric field vector as well as the product rule of differentiation, one can obtain the electric force \(\mathbf{f}^E\) per unit volume as [19, 20]

$$\begin{aligned} \mathbf{f}^E= q^v \mathbf{E}-0.5\mathbf{E}{\cdot }\mathbf{E}\nabla \varepsilon , \end{aligned}$$
(20)

Here, the first term on the right hand side of Eq. (20) is the electric force acting along the direction of the electric field due to the interaction of the free charges with the electric field while the second term accounts for the polarization force due to the pairs of charges, which acts along the normal direction to the interface as a result of term \(\nabla \varepsilon \).

2.3 Leaky dielectric model

For a two-fluid system with finite electrical conductivities in a quasistatic electric field and \(t^\mu >> t^E\) and in the absence of buoyancy forces, both volume and surface charge conservation equations in Eqs. (13) and (18) can attain steady state condition (i.e., \(Dq^v/Dt=0\) and \(\overline{\delta } q^s/\delta t\)=0) in a time scale much smaller than the viscous time scale of the fluid motion. Such a system can be referred to as conducting-conducting. Therefore, relying on the quasistatic assumption, the conservation of charge in Eq. (13) can be simplified to

$$\begin{aligned} \nabla \cdot (\sigma \mathbf{E})=0. \end{aligned}$$
(21)

Additionally, since the electric field is irrotatioal (\(\nabla \times \mathbf{E}=0\)), due to the mathematical entity of \(\nabla \times \nabla \phi =0\) (the curl of the gradient of a scalar function is equal to zero), which holds for any arbitrary scalar field, the electric field vector can be expressed in terms of electric potential as

$$\begin{aligned} \mathbf{E}=-\nabla \phi , \end{aligned}$$
(22)

where \(\phi \) is the electric potential. This would mean that the charge conservation equation (Eq. (21)) in the domain can be re-written as

$$\begin{aligned} \nabla \cdot (\sigma \nabla \phi )=0. \end{aligned}$$
(23)

Following the work of Saville [19], if the conservation of charge equation for the interface given in Eq. (18) is written in dimensionless form, one can show that the effect of surface current to the physics of problems with \(t^\mu >>t^E\) is negligible. The interface condition for Eq. (23) can then be written as

$$\begin{aligned} \Vert \sigma \mathbf{E}\Vert \cdot \mathbf{n}=0, \end{aligned}$$
(24)

by justifiably ignoring the surface current. This interface condition is referred to as the continuity of the current across the interface. Further interface condition can be written as the continuity of the electric potential across the interface as \(\Vert \phi \Vert =0\). For a two-fluid system, having a constant electrical conductivity in each fluid, Eq. (23) for electrical potential reduces to Laplace equation (\(\nabla ^2 \phi =0\)) in each medium.

With the solution of Eq. (23), the electric potential can be obtained, and then the electric field strength is calculated by \(\mathbf{E}=-\nabla \phi \). Based on Eq. (12), we can obtain the distribution of volume charge density as \(q^v=\nabla \cdot (\varepsilon \mathbf{E})\). Having calculated the distributions of electric charge density and electric field strength, the electric force within the liquid bulk in the vicinity of interface can then be determined through Eq. (20) for incompressible fluid.

Upon combining Eq. (2) with Eqs. (7) and (20), one can obtain the equation of motion including volumetric surface tension and electric field forces as

$$\begin{aligned} \rho \frac{D\mathbf{v}}{Dt}&= -\nabla p+ \mu \nabla ^2\mathbf{v}+\gamma \kappa \mathbf{n}\delta \nonumber \\&+q^v\mathbf{E}-0.5\mathbf{E}{\cdot }\mathbf{E}\nabla \varepsilon +\rho \mathbf{f}^{b}. \end{aligned}$$
(25)

3 Smoothed particle hydrodynamics

Smoothed particle hydrodynamics method is a meshless particle based approach which was originally introduced separately by Monaghan and Gingold [21], and Lucy [22] to simulate astrophysical problems. Later on, it was adapted to be able to carry out simulations in other fields of engineering and natural sciences, especially fluid dynamics and solid mechanics. Recent developments empowered this method to model more complicated physical phenomena such as multiphase flows, and fluid-solid interactions. Benefiting from its particle based nature, distributed particles in the continuum are influenced by their neighboring particles by means of a weighting or kernel function \(W(r_{{ ij}},h)\), or in a concise notation, \(W_{ ij}\). Any arbitrary kernel function \(W_{ ij}\), which satisfies certain conditions, can relate the particle of interest \({ i}\) to its neighboring particles \({ j}\) through the magnitude of the distance vectors for pairs of particles \(r_{ ij}=|\mathbf{r}_{ ij}|\) and the smoothing length \(h\), where \(\mathbf{r}_{ ij}=\mathbf{r}_{ i}-\mathbf{r}_{ j}\). A particle \({ j}\) is called a neighbor particle to \({ i}\) as long as \(r_{ ij}<\kappa h\) where \(\kappa \) is a constant associated with the particular weighting function and \(\kappa h\) is referred to as a smoothing radius (cut-off distance, support or localized domain) beyond which the weighting function goes to zero. For the clarity of the presentation, it is worthy of introducing notational conventions to be used in the rest of this article. Latin italic indices (i; j) are used only as particle identifers to denote particles and will always be placed as subscripts that are not summed unless used under the summation symbol. When a vector is written in a componet form, suffix notation is employed with Latin italic indices placed as superscripts. As well, throughout this article the Einstein summation convention is employed whereby any repeated component index is summed over the range of the index.

The integral approximation of any arbitrary function for particle \({ i}, \,f_{{ i}}\), can be written as

$$\begin{aligned} f_{{ i}}\cong \left\langle f_{{ i}}\right\rangle \equiv \int _{\varOmega } f_{{ j}}W_{{ ij}} \mathrm d \mathbf{r}_{{ j}}, \end{aligned}$$
(26)

where \(\mathrm d \mathbf{r}_{{ j}}\) is a differential volume element and \(\varOmega \) represents the total bounded volume of the domain. Upon replacing the integral operation over the volume of the bounded domain by the mathematical summation operation over all neighboring particles \({ j}\) of the particle of interest \({ i}\), and the differential volume element by the inverse of the number density \(\psi _{{ j}}\) for a particle \({ j}\), one thus obtains the discrete representation of Eq. (26) as

$$\begin{aligned} f_{{ i}}=\sum _{{ j}} \frac{1}{\psi _{{ j}}} f_{{ j}}W_{{ ij}}. \end{aligned}$$
(27)

The number density for the particle i can be calculated as

$$\begin{aligned} \psi _{{ i}}=\sum _{{ j}}W_{{ ij}}. \end{aligned}$$
(28)

It may also be expressed in terms of the particle density \(\rho \) and the mass \(m\) by

$$\begin{aligned} \psi _{{ i}}={\rho _{{ i}}}/{m_{{ i}}}. \end{aligned}$$
(29)

Upon substituting \(f_{{ j}}\) by \(\partial f_{{ j}}/{\partial x^k_{{ j}}}\) in Eq. (26) and then performing the integration by parts, then converting the following volume integral \(\int _{\varOmega } \partial (f_{{ j}} W_{{ ij}})/{\partial x^k_{{ j}}} \mathrm d \mathbf{r}_{{ j}}\) to the surface integral through using the divergence theorem and noting that this surface integral should be zero due to the fact that the kernel function goes to zero beyond its support domain, and finally knowing that \(\partial W_{{ ij}}/{\partial x^k_{{ j}}}=-\partial W_{{ ij}}/{\partial x^k_{{ i}}}\), one may obtain the simplest form of the SPH discretization for the gradient of the arbitrary function \(f_{{ i}}\) as

$$\begin{aligned} \frac{\partial f_{{ i}}}{\partial x^k_{{ i}}} =\sum _{{ j}}\frac{1}{\psi _{{ j}}}f_{{ j}} \frac{\partial W_{{ ij}}}{\partial x^k_{{ i}}}. \end{aligned}$$
(30)

The above SPH approximation for the spatial discretization of a gradient operation has been known to be incapable of providing sufficient accuracy, wherefore more accurate discretization schemes have been proposed in literature. One of them is known as a corrective SPH gradient discretization [17] which can be obtained upon using a Taylor series expansion and the properties of a second-rank isotropic tensor, and written for an arbitrary vector valued function as

$$\begin{aligned} \frac{\partial f^p_{{ i}}}{\partial x^k_{{ i}}}a^{ks}_{{ i}}=\sum _{{ j}}\frac{1}{\psi _{{ j}}} \big (f^p_{{ j}}-f^p_{{ i}}\big ) \frac{\partial W_{{ ij}}}{\partial x^s_{{ i}}}, \end{aligned}$$
(31)

where \(a^{ks}_{{ i}}=\sum _{{ j}} \frac{1}{\psi _{{ j}}} r^k_{{ ji}} \frac{\partial W_{{ ij}}}{\partial x^s_{{ i}}}\) is a second rank tensor. The SPH Laplacian formulation can be written in two different ways as,

$$\begin{aligned}&\!\!\!\! \frac{\partial }{\partial x^k_{{ i}}}\left( \zeta _{{ i}}\frac{\partial f^p_{{ i}}}{\partial x^k_{{ i}}}\right) {=\,}8(a^{pm}_{{ i}})^{-1} \sum _{{ j}}\frac{2}{\psi _{{ j}}} \frac{\zeta _{{ i}}\zeta _{{ j}}}{\zeta _{{ i}}+\zeta _{{ j}}} f^p_{{ ij}} \frac{r^p_{{ ij}}}{r^2_{{ ij}}} \frac{\partial W_{{ ij}}}{\partial x^m_{{ i}}},\end{aligned}$$
(32)
$$\begin{aligned}&\!\!\!\! \frac{\partial }{\partial x^k_{{ i}}}\left( \zeta _{{ i}}\frac{\partial f^p_{{ i}}}{\partial x^k_{{ i}}}\right) {=}\frac{8}{(2+a^{ll}_{{ i}})} \sum _{{ j}}\frac{2}{\psi _{{ j}}} \frac{\zeta _{{ i}}\zeta _{{ j}}}{\zeta _{{ i}}+\zeta _{{ j}}} f^p_{{ ij}} \frac{r^s_{{ ij}}}{r^2_{{ ij}}} \frac{\partial W_{{ ij}}}{\partial x^s_{{ i}}}.\end{aligned}$$
(33)

In above equations, \(\zeta \) might denote \(\mu , \,\rho ^{-1}\), and \(\sigma \) and \(f^p_{{ ij}}=f^p_{{ i}}-f^p_{{ j}}\). In this work, Eq. (32) is used for the Laplacian of velocity while Eq. (33) is used for the Laplacian of pressure in the Poisson pressure equation. In a multiphase system, the accurate treatment of the jump in transport parameters across the interface is important for the accuracy and robustness of the SPH scheme wherefore a weighted harmonic mean interpolation is applied in above equations as

$$\begin{aligned} \zeta _{{ i}}=2\zeta _{{ i}}\zeta _{{ j}}/({\zeta _{{ i}} +\zeta _{{ j}}}). \end{aligned}$$
(34)

It has been previously noted that the smoothing kernel has to satisfy several conditions. The first one is the normalization condition that requires

$$\begin{aligned} \int _{\varOmega } W(r_{{ ij}},h) \mathrm d \mathbf{r}_{{ j}}=1. \end{aligned}$$
(35)

The second one is the Dirac-delta function property. That is, as the smoothing length approaches to zero, the Dirac-delta function is recovered. Hence,

$$\begin{aligned} \lim _{h\rightarrow 0} W(r_{{ ij}},h) =\delta (r_{{ ij}}). \end{aligned}$$
(36)

The third one is the compactness or compact support property, which necessitates that the kernel function be zero beyond its compact support domain.

$$\begin{aligned} W(r_{{ ij}},h)=0\quad \text{ when} r_{{ ij}}>\kappa h, \end{aligned}$$
(37)

and be positive within the support domain.

The fourth one is that the kernel function has to be spherically symmetric even function

$$\begin{aligned} W(r_{{ ij}},h) =W(-r_{{ ij}},h). \end{aligned}$$
(38)

Finally, the value of the smoothing function should decay with increasing distance away from the center particle.

In literature, it is possible to find a variety of kernel function which satisfies above-listed conditions. Most commonly used ones are spline kernel (for instance, cubic or quintic) and Gaussian functions. The smoothing kernels might be considered as discretization schemes in mesh dependent techniques such as finite difference and volume. The stability, accuracy and the speed of the SPH simulation heavily depend on the choice of the smoothing kernel function as well as the smoothing length. Considering the stability and the accuracy of the simulations, throughout the present work, the compactly supported two-dimensional quintic spline kernel is used at the expense of higher computational cost. For example, the utilization of the higher order quintic spline in simulations is at least two times computationally more expensive than that of the cubic spline. The two-dimensional quintic spline kernel function has the form of

$$\begin{aligned} W_{{ ij}} = \chi \left\{ \begin{array}{ll} (3-q)^{5} - 6 (2-q)^{5} + 15 (1-q)^{5} &{} 0 \le q \le 1 \\ (3-q)^{5} - 6 (2-q)^{5} &{} 1 \le q \le 2 \\ (3-q)^{5} &{} 2 \le q \le 3 \\ 0 &{} 3 \le q \end{array}\right. , \end{aligned}$$
(39)

where \(q=r_{{ ij}}/h\) and \(\chi \) is \(\frac{7}{478} \pi h^2\) for 2-D simulations.

4 Numerical scheme

Here, we briefly introduce the initial and boundary conditions as well as describe the sequence of the numerical algorithm implemented in this work. The computational domain is represented by a set of discrete points (so-called SPH particles) initially located on a Cartesian grid which have an equidistant particle spacing. Depending on their initial position, particles are associated with different integer labels whereby fluid and boundary particles as well as boundary particles with different boundary conditions can be distinguishable from each other. The constituents of the multiphase system are also distinguished from each other through integer labels known as color function

$$\begin{aligned} c=\left\{ \begin{array}{ll} 0 &{} \text{ fluid} 1\\ 1 &{} \text{ fluid} 2 \end{array}.\right. \end{aligned}$$
(40)

The color function value of each phase remains the same during the entire simulation. Each particle is endowed with transport variables and initial conditions.

Boundary conditions are applied onto solid boundaries by means of the multiple boundary tangent (MBT) method [24]. According to the MBT method, the field variables of each fluid particle \(\varGamma \) (i.e. velocity or pressure) is extrapolated to its neighbor ghost particles across the tangent line (or tangent plane in 3-D) of the solid boundary thereby imposing different boundary conditions, namely, \(\varGamma _g=2\varGamma _s-\varGamma _f\) and \(\varGamma _g=\varGamma _f\) for the Dirichlet and Neumann boundary conditions respectively. Here subscripts \(g, \,s\), and \(f\) indicate that the field variable \(\varGamma \) is associated with the ghost, boundary, and fluid particles, respectively. Other properties of a ghost particle (i.e. mass, density, number density, viscosity, and electric permittivity and conductivity) is identical to those of its “mother” fluid particle. Boundary conditions are enforced upon the inclusion of ghost and solid boundary particles into the solution of governing equations.

The initial mass of each particle is calculated using the relation \(m_{{ i}}=\rho _{{ i}}/{\psi _o}\) where \(\psi _o=max(\psi _{ i})\) is the initial or reference particle number density which is retained constant during the computation. To enhance the robustness of the model, and circumvent the particle disorderness and fracture induced numerical problems, an artificial particle displacement (APD) term is added to the advection equation [24]. The APD vector \(\delta \mathbf{r}_{{ i}} =\beta V_{max}r_{{ i},o}^2 \sum _{{ j}}\mathbf{r}_{{ ij}}/{r_{{ ij}}^3}\) is calculated for all fluid particles where the \(\beta \) is a problem-dependent parameter which is set to be equal to \(0.03\) for all test cases, and \(r_{{ i},o}=\sum _{{ j}}{r_{{ ij}}}/{N}\) is the average the cut off distance for a given particle with \({N}\) being the number of neighbor particles. As one may note that the APD vector is an odd function and therefore has a non zero value only for asymmetric particle distribution.

For all test cases, time step is initially set to \(\varDelta t = 2 \times 10^{-4} s\) and is updated afterward using the Courant- Friedrichs-Lewy (CFL) condition wherein the recommended time-step is \( \varDelta t = C_{CFL} h/v_{max}\) where \(v_{max}\) is the maximum velocity magnitude of particles and \(C_{CFL} = 0.125\). For the time marching, we have used a first-order Euler time step scheme along with a projection method based ISPH approach [25]. Thus, we first move particles from their current positions \(\mathbf{r}_{{ i}}^{(n)}\) with their current divergence free velocities \(\mathbf{v}_{{ i}}^{(n)}\) at time \(t\) to the temporary or intermediate positions \(\mathbf{r}_{{ i}}^{*}\) using

$$\begin{aligned} \mathbf{r}_{{ i}}^{*}=\mathbf{r}_{{ i}}^{(n)}+\mathbf{v}_{{ i}}^{(n)} \varDelta t + \delta \mathbf{r}_{{ i}}. \end{aligned}$$
(41)

Having advected particle positions to their intermediate positions, their neighbors (both real and ghost particles) are recalculated. For simulations involving small topological changes in flow, which is the case for test problems considered in this work, fluid particles experience rather small changes in positions at each time step in comparison to particle spacing whereby one may assume that the neighbor of a given particle will not change significantly. To reduce the computational cost incurred due the neighbor finding process, the neighbor lists and ghost particles are updated every tenth time step. However, for numerical modeling that may have large topological changes in flow, the neighbor list needs to be updated more frequently or at each time step.

Afterward, in the interface subroutine, the surface tension force in Eq. (7) is computed as

$$\begin{aligned} \mathbf{f}^{v} = -\gamma (\nabla \cdot (\nabla C/|\nabla C|)) \nabla C, \end{aligned}$$
(42)

where \(C\) is a smoothed color function which can be written for particle i as

$$\begin{aligned} C_{{ i}}=\frac{\sum _{{ j}} W_{{ ij}} c_{{ j}}}{\sum _{{ j}} W_{{ ij}}}. \end{aligned}$$
(43)

In converting Eq. (7) into Eq. (42), the unit normal and delta dirac function are calculated respectively as \(\mathbf{n}=\nabla C/|\nabla C|\), and \(\delta =|\nabla C|\) where \(|\nabla C|\) is the magnitude of the gradient of the smoothed color function.

It is noted that unlike the initial color function \(c\), the smoothed color function \(C\) is updated for all particles at each time step and its value differs from unsmoothed color function only for particles at the vicinity of interface.

Since each fluid particle has constant \(\rho , \,\mu , \,\varepsilon \) and \(\sigma \) which are discontinuous across the interface, the numerical scheme might have instabilities especially in the case of a large mismatch in the transport parameters of constituents [17, 18]. Thus, these transport parameters are smoothed using a weighted arithmetic mean interpolation

$$\begin{aligned} \rho _{{ i}}&= (1-C_{{ i}}) \rho _1 + C_{{ i}} \rho _2,\end{aligned}$$
(44)
$$\begin{aligned} \mu _{{ i}}&= (1-C_{{ i}}) \mu _1 + C_{{ i}} \mu _2,\end{aligned}$$
(45)
$$\begin{aligned} \varepsilon _{{ i}}&= (1-C_{{ i}}) \varepsilon _1 + C_{{ i}} \varepsilon _2, \end{aligned}$$
(46)

and

$$\begin{aligned} \sigma _{{ i}}= (1-C_{{ i}}) \sigma _1 + C_{{ i}} \sigma _2, \end{aligned}$$
(47)

where \(\sum _{\alpha } C_{{ i}}^{\alpha }=1\) where \(C_{{ i}}^{\alpha }\) is the smoothed color function of \(\alpha \) th phase. In essence, the smoothed color function provides a finite transition region along the interface at which the field variables can smoothly change from one phase into another thereby avoiding sharp jump at the interface.

Afterward, the intermediate velocity \(\mathbf{v}_{{ i}}^{*}\) is computed on temporary particle locations through the solution of the momentum balance equations with the forward time integration as

$$\begin{aligned} \mathbf{v}_{{ i}}^{*}=\mathbf{v}_{{ i}}^{(n)}+ \mathbf{f}_{{ i}}^{(n)} \varDelta t. \end{aligned}$$
(48)

Here, \(\mathbf{f}_{{ i}}^{(n)}\) represents the right hand side of the momentum balance equation given in Eq. (25), which embodies viscous, volumetric surface tension and electric forces excluding the pressure gradient term, calculated using old velocities, updated transport properties and intermediate positions. Given the intermediate particle positions and velocities, the intermediate number densities

$$\begin{aligned} \psi _{{ i}}^{*}=\psi _{{ i}}^{(n)}-\varDelta t \psi _{{ i}}^{(n)} (\nabla \cdot \mathbf{v}_{{ i}}^{*}), \end{aligned}$$
(49)

and mixture densities

$$\begin{aligned} \rho _{{ i}}^{*}=\psi _{{ i}}^{*} \sum _{\alpha } m_{{ i}}^{\alpha } C_{{ i}}^{\alpha }, \end{aligned}$$
(50)

as well as divergences of intermediate velocities are calculated, which will be used at the correction step in the pressure Poisson equation. Then, at the correction step, we add the effect of pressure gradient term into intermediate velocity \(\mathbf{v}_{{ i}}^{*}\) to obtain the divergence free velocity vector \(\mathbf{v}_{{ i}}^{(n+1)}\) at the new time

$$\begin{aligned} \mathbf{v}_{{ i}}^{(n+1)}=\mathbf{v}_{{ i}}^{*}-\frac{\varDelta t}{\rho ^*} \nabla p^{(n+1)}_{{ i}}, \end{aligned}$$
(51)

where the pressure \(p^{(n+1)}\) has been obtained through the solution of the pressure–Poisson equation, which can be formulated in general form as

$$\begin{aligned} \frac{\nabla \cdot \mathbf{v}^{*}}{\varDelta t}=\nabla \cdot \left( \frac{\nabla p}{\rho ^*}\right) , \end{aligned}$$
(52)

by taking the divergence of Eq. (51) and noting that the incompressibility condition requires that \( \nabla \cdot \mathbf{v}_{{ i}}^{(n+1)}=0\). Eq. (52) is solved using a direct solver based on the Gauss elimination. The boundary condition for pressure is obtained by projecting Eq. (52) on the outward unit normal vector \(\mathbf{n}\) to the boundary. Thus, one can obtain the Neumann boundary condition as

$$\begin{aligned} \left( \frac{\rho ^*}{\varDelta t}\right) (\mathbf{v}^{*}-\mathbf{v}^{(n+1)}) \cdot \mathbf{n} = \nabla p \cdot \mathbf{n}. \end{aligned}$$
(53)

Upon approximating the boundary condition for \(\mathbf{v}^{*}\) by \(\mathbf{v}^{(n+1)}\), namely, \((\mathbf{v}^{*}-\mathbf{v}^{(n+1)})\cdot \mathbf{n}=0\), the pressure boundary condition reduces to \(\nabla p\cdot \mathbf{n}= 0\).

Finally, with the correct velocity field for \(t^{(n+1)}\), all fluid particles are advected to their new positions \(\mathbf{r}_{{ i}}^{(n+1)}\) using an average of the previous and current particle velocities as

$$\begin{aligned} \mathbf{r}_{{ i}}^{(n+1)}=\mathbf{r}_{{ i}}^{(n)}+ 0.5 (\mathbf{v}_{{ i}}^{(n)}+\mathbf{v}_{{ i}}^{(n+1)})\varDelta t + \delta \mathbf{r}_{{ i}}. \end{aligned}$$
(54)

Neighbor and ghost particle lists are updated, and then the initial (reference) number density of the fluid is restored.

5 Results

In this section, we consider two main test cases. The first test case is the deformation of static circular droplet under the influence of the surface tension force only, which is modeled to validate the implementation of surface force and the numerical scheme. The second one is also the deformation of a droplet which is this time subjected to both surface tension and a constant externally applied electric field. The second test case has been numerically simulated under various combinations of fluid properties to reveal the capability and the accuracy of the SPH method in modeling the multiphase EHD problems.

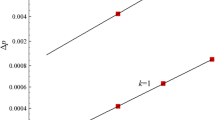
The deformation of a static circular droplet under the surface tension force is a commonly utilized test case for validating the accuracy of numerically computed pressure jump across the interface in multiphase systems, which can also be calculated analytically from the relation, \(p_{in}-p_{out}={\gamma }/{r}\). This relation is known as the Laplace’s law that relates pressure difference between inside and outside of the droplet to the surface tension coefficient and the curvature. For this test problem, the computations are performed in a square domain with the edge length of \(H=0.04\) \([m]\). The origin of the static circular droplet with a radius of \(r=0.005\) \([m]\) is placed at the center of the square domain, which is represented by an array of \(100\times 100\) particles in \(x-\) and \(y-\) directions, and the smoothing length for all particles is set equal to 1.6 times the initial particle spacing. The simulations are performed for constant density and viscosity values of \(\rho _1=\rho _2=1000\) \([kg/m^3], \,\mu _1=\mu _2=1\) \([Pa.s]\), respectively, and for several values of the surface tension coefficient \(\gamma \) \([N/m]\). Here, subscripts \(1\), and \(2\) are used to denote parameters associated with the inner and outer fluids, respectively. As for the boundary conditions of the current test case, the pressure on the boundaries is set equal to zero, and the no-slip boundary condition is imposed for velocity on all solid walls. The initial velocity field is zero. Pressure jumps computed across the interface for various surface tension coefficients are presented in Fig. 1 together with the results of the analytical solution, where the linear continuous line represents the results obtained from the analytical relation while the outcomes of the numerical simulations are shown with filled-in circles. From this figure, one can notice the good agreement between numerical and analytical results. Here, we would like to note that the current multiphase ISPH algorithm has been extensively validated in our previous works by solving a wide variety of multiphase flow test cases such as single vortex flow, square bubble deformation, bubble deformation in a shear flow, Newtonian bubble rising in viscous and viscoelastic fluids, and Rayleigh-Taylor instability, which can be found in [17, 18, 26].

Fig. 1
figure 1

The comparison of numerically computed pressure jumps as a function of surface tension coefficient with that calculated by the analytical equation, namely, Laplace’s law

Full size image

In Fig. 2 is shown the two dimensional problem geometry for the second test problem which is composed of a square domain occupied by the immiscible background fluid and the initially circular droplet having the radius of \(r_o\) whose origin is located at the center of the square domain. The size of the computational domain as well as the boundary conditions of flow equations for this test case are identical to that for first one unless stated otherwise. Likewise, the modeling domain is represented by particles generated on a rectangular grid with identical and equidistant particle spacing. Additionally, for all simulations, the domain size is eight times greater than initial droplet radius. The smoothing length for all particles is set equal to 1.6 times the initial particle spacing as in the case of the first test case. In the present test case, both the droplet and background fluids have identical densities and viscosities, which are \(\rho _1=\rho _2=1000\) \([kg/m^3]\) and \(\mu _1=\mu _2=1\) \([Pa.s]\), respectively, and a constant surface tension coefficient \(\gamma \) is used. However, the inner fluid’s electric permittivity \(\varepsilon _1\) and conductivity \(\sigma _1\) may differ from that of the background fluid depending on the test case studied. The boundary conditions for Eq.(23) are Dirichlet and Neumann boundary (\(\nabla \phi \cdot \mathbf{n}= 0\)) conditions for horizontal and vertical walls, respectively.

Fig. 2
figure 2

The schematic of the problem domain. Upon setting an electric potential at the upper and lower horizontal boundaries, a constant electric field in the downward direction is obtained in the model domain

Full size image

The relative differences in the electric permittivity and conductivity of both constituent phases are represented by their ratios as

$$\begin{aligned} S=\frac{\varepsilon _{in}}{\varepsilon _{out}}=\frac{\varepsilon _{1}}{\varepsilon _{2}},\,\,\, R=\frac{\sigma _{in}}{\sigma _{out}}=\frac{\sigma _1}{\sigma _2}, \end{aligned}$$
(55)

which are two significant parameters that play an important role in simulations which will be discussed later in details.

One of the main features that can be compared in bubble dynamics research is the droplet deformation parameter \(D\), which is defined as

$$\begin{aligned} D=\frac{A-B}{A+B}, \end{aligned}$$
(56)

where \(A\) and \(B\) are the diameters of the elliptic droplet which are parallel and perpendicular to the direction of the applied electric, respectively, at the steady state condition. The droplet deformation parameter quantifies the deviation in the geometry of a droplet from its original circular shape to an elliptic one. The higher the value of \(D\), the larger the ellipticity whereas as the \(D\) goes to zero, the droplet approaches to the circular shape. Besides, the positive value of \(D\) indicates that the droplet is stretched in the electric field direction thus acquiring a prolate shape while the negative value denotes that it is lengthened perpendicularly to the electric field direction (transverse direction) hence forming an oblate shape.

The numerical findings of this test case are compared with two different theories in terms of the droplet deformation parameter. The first one is the analytical equation developed by Taylor [27] which formulates the droplet deformation parameter as

$$\begin{aligned} D_T=\frac{9f_{d,T}E_o^2\varepsilon _2 r_o}{8(2+R)^2\gamma }, \end{aligned}$$
(57)

where \(E_o\) is the magnitude of the electric field vector (set to be \(E_o=1\) unless stated otherwise) which is calculated as \((\phi _+-\phi _-)/H\) with \(\phi _-=0\), and \(f_{d,T}\) is the discriminating function, which is evaluated as

$$\begin{aligned} f_{d,T}=R^2+1-2S+\frac{3}{2}(R-S), \end{aligned}$$
(58)

which determines the sign of \(D_T\) in the above equation so that according to \(f_{d,T}\), the droplet may oblate or prolate.

Taylor also showed that the fluid rotation in the droplet and surrounding fluid is only dependent on the ratios between electric permittivity and conductivities. Figure 3 shows fluid vorticities inside and outside of a droplet subjected to a constant electric field for the conditions of the \(R<S\) (left) and \(R>S\) (right). Taylor’s theory suggests that for the condition of \(R<S\), there are four vortices inside the droplet which have identical flow patterns. Namely, the flow direction is from the center of the drop toward the pole along vertical axis, from the pole to the equator along the perimeter of the drop, and from the equator to the center of the drop along the horizontal axis. However, for the condition of \(R>S\), the fluid circulates in the opposite direction in comparison to the first case.

Fig. 3
figure 3

Schematics for two types of induced flow a \(R<S\) and b \(R>S\)

Full size image

The second theoretical analysis which is used to evaluate our results is the one introduced by Feng [13] wherein the droplet deformation parameter \(D\) is formulated as

$$\begin{aligned} D_F=\frac{f_{d,F} E_o^2\varepsilon _1 r_o}{3(1+R)^2S\gamma }. \end{aligned}$$
(59)

In the above equation, the sign of \(D_F\) also depends on the sign of \(f_{d,F}\) because all the other terms have positive sign. The discriminating function \(f_{d,F}\) in Eq. (59) is defined as

$$\begin{aligned} f_{d,F}=R^2+R+1-3S. \end{aligned}$$
(60)

If \(f_{d,F}\) is positive, the droplet deformation parameter \(D_F\) will be positive, wherefore the droplet will prolate, while the negative values of \(f_{d,F}\) result in oblate deformation of the droplet.

In order to compare numerical results with those obtained by using Taylor and Feng theories quantitatively, Table 1 is presented. In this table, the droplet deformation parameter \(D\) is presented for six different sets of input parameters. As one may infer from the sign of evaluated droplet deformation \(D\) in Table 1, the input parameters given in the first three rows of the table lead to prolate deformation while the input parameters in the fourth and fifth rows causes the droplet to deform in the oblate form. However, the simulation with input parameters given in the last row is an exception, which will be discussed in details later by referring to Fig. 4.

Fig. 4
figure 4

S–R map, and particle positions for three different simulations a The relation between the permittivity and the conductivity ratios: b \(R > S, \,f_{d,F}>0\); c \(R < S, \,f_{d,F}<0\); and d \(R < S, \,f_{d,F}> 0\). Only a half of the central regions is displayed; different particle shape and size are also shown to indicate the fluid-fluid interfaces and drop deformations

Full size image
Table 1 The comparison of SPH and theoretical results (Eqs. (57) and (59)) in terms of the discriminating function \(f_d\) and the deformation parameter \(D\) for different combinations of conductivity and permittivities
Full size table

One may notice from Table 1 that for small deformation parameter values in both oblate and prolate conditions, the results of numerical simulations agree very well with those of analytical analysis except that there are rather small deviations between the analytical and simulation results. However, for relatively higher values of the droplet deformation parameter, the results of numerical simulations deviate observably from those of both theories. It is important to state that the theoretical analysis of both Taylor and Feng assume that the droplet remains circular hence being accurate for small droplet deformations only. Therefore, our findings are in mesh with what have been reported in literature [4, 7, 28] wherein it was shown both experimentally and numerically that for large droplet deformations, these two analytical expressions underestimate the droplet deformation parameter. Another important point worthy of mentioning here is that for the prolate deformation, our results are closer in magnitude to those of the Taylor’s theory. On the other hand, when the droplet oblates, our findings have better agreement with the results of the Feng’s theory rather than the Taylor’s theory. In other words, in the prolate deformation, the Taylor’s theory calculates higher values for the droplet deformation parameter and the relative difference between Taylor data and ours are less than the Feng’s theory. Yet, in oblate deformation, the opposite situation is observed. The reason for such a controversy is hidden in Eqs. (57) and (59) where in Feng’s theory, the inner fluid permittivity is used while in Taylor’s theory, the droplet deformation parameter is evaluated using the outer fluid’s permittivity.

The relation between the permittivity ratio \(S\) and the conductivity ratio \(R\) is shown in Fig. 4a, which is hereafter referred to as \(S-R\) map. In this figure, the dashed straight line represents the situation of \(S=R\). For the case of \(R<S\) which is the region above the dashed straight line on the map, the fluid particles inside and outside of droplet circulate with the pattern explained earlier and depicted in Fig. 3a. As for the case of \(R>S\), the opposite flow circulation pattern should be expected. Moreover, in the same figure, the variation of \(S\) as a function of \(R\) is plotted by utilizing the discrimination functions \(f_{d,T}\) and \(f_{d,F}\) in Eqs. (58) and (60) for the values of \(f_{d,T}=0\) and \(f_{d,F}=0\), and the curves are denoted by solid and dash-dot lines, respectively. Since these two curves are almost equivalent to each other, we have provided our discussion below referring to the Feng’s theory. The regions above and below this curve represent the conditions of \(f_{d,F}<0\) and \(f_{d,F}>0\) in the given order, which correspond to the oblate and prolate droplet deformations, respectively. Three different combinations or configurations might be formed out of the above given situations, which are plotted in Figs.4b, c, and d, where the right half of each sub-figure shows particle velocity vectors and the left half represents droplet (dark) and surrounding (light) particle distribution for corresponding simulations. The first configuration, which is shown in Fig. 4b, belongs to the situation where \(R>S\) and in turn \(f_{d,F}>0\), which can be obtained using the input parameters given in the first three rows of Table1. The results in Fig. 4b are obtained by using the simulation parameters provided in the second row of the Table1. As a result, the flow circulation inside the droplet is according to Fig. 3b, and the droplet prolates. The second combination shown in Fig. 4c represents the \(R<S\) and as a result \(f_{d,F}<0\),which leads to the formation of the flow pattern as illustrated in Fig. 3a and oblate droplet deformation. Under this configuration, the droplet deformation is a representative figure for the fourth and fifth rows of Table1. The input parameters for the Fig. 4c is given in the forth row of the Table1. The third configuration (i.e., \(R<S\) and \(f_{d,F}>0\)) forms when the problem conditions belong to the small region flanked by the straight and curved lines. In this configuration, as can observed from Fig. 4d for which the input parameters are given in the last row of the Table1, the droplet tends to prolate due to the fact that \(f_{d,F}>0\) while the flow pattern is opposite to Fig. 4b. One can note that the droplet does not prolate severely, which is a quite expected result since the input parameters result in \(S, R\), and \(f_{d,F}\) values that fall into the region between the straight and curved lines in the \(S-R\) map.

Figure 5 shows the variation of droplet deformation as a function of different parameters. In subfigures, electric field strength, droplet initial radius, inner fluid permittivity, and surface tension coefficient are separately varied to show the dependency of droplet deformation to each parameter. In these figure, the solid lines and unfilled circles represent the results of Feng and Taylor theories, respectively, while the numerical values are shown with filled circles. It is observed that for all cases, our numerical simulations for larger droplet deformations have overestimated values of \(D\) calculated by both theoretical analyses. However, as discussed before, for small deformations, the overestimation is relatively small.

Fig. 5
figure 5

The variation of droplet deformation parameter \(D\) as a function of a the electric field strength \(E_o\), b the permittivity \(\varepsilon _i\), c the initial droplet radius \(r_o\), and d the reciprocal of the surface tension \(1/\gamma \)

Full size image

Other parameters that can be compared with the theory are the velocity profiles of fluid media inside and outside of droplet. Thanks to Feng [13], the fluid velocity inside and outside the droplet may be evaluated theoretically as,

$$\begin{aligned}&v_{r,in}=U^*[(r/r_o)^3-(r/r_o)] \cos 2\theta ,\end{aligned}$$
(61)
$$\begin{aligned}&v_{\theta ,in}=U^*[(r/r_o)-2(r/r_o)^3] \sin 2\theta ,\end{aligned}$$
(62)
$$\begin{aligned}&v_{r ,out}=U^*[(r_o/r)-(r_o/r)^3] \cos 2\theta ,\end{aligned}$$
(63)
$$\begin{aligned}&v_{\theta ,out}=-U^*[(r_o/r)^3] \sin 2\theta , \end{aligned}$$
(64)

where \(r\) is the radial position, \(v_r\) and \(v_\theta \) are the radial and tangential velocities in the given order. Also, the \(U^*\) is the characteristic velocity, which corresponds to the maximum velocity

$$\begin{aligned} U^*=\frac{R-S}{2S(1+R)^2} \frac{\varepsilon _1 E_o^2 r_o}{\mu _1+\mu _2}. \end{aligned}$$
(65)

These equations carry some valuable conceptual facts which are perfectly captured by current simulations. First, for the radial velocity, in both expressions for inner and outer fluid velocities, the fluid velocity approaches zero near the droplet boundary. Moreover, the maximum radial velocity may be observed where the cosine function in Eqs. (61) and (63) is maximized. This happens at angles like \(\theta =0\), and \(\pi /2\). On the other hand, for the angles like \(\pi /4\) at which the sinusoidal function has its maximum value, the tangential velocity is maximized.

Figure 6 shows the profiles of the radial and tangential velocity components for two different angles at which one of the velocity components is maximized. In this figure, the theoretical velocity profile for radial and tangential components are shown with solid and dashed lines, respectively. Also, the numerical data for radial and tangential velocity components are represented with unfilled and filled circles, respectively. In accordance with Eqs. (62) and (64), the tangential velocity component has to be zero at \(\theta =0\), which is observed in Fig. 6a where the radial velocity may have its maximize values. Eqs. (61) and (63) require that for the circular droplet, the radial velocity should be zero at the droplet interface where \(r=r_o\). Nevertheless, after the droplet gets deformed, its interface is no longer at \(r=r_o\). Thus, the numerical results show a slight deviation in evaluation of zero radial velocity prediction, which is again due to the assumption made in theory that the droplet remains circle.

Fig. 6
figure 6

The profiles for the components of the velocity profile and their comparison with analytical results a for the case of \(\theta =0\), b for the case of \(\theta =\pi /4\). This figures are generated from the simulation with input parameters provided in the forth row of Table 1 after the steady state has been reached

Full size image

Finally, to show the convergence of our results with respect to particle resolution, one of the test cases is reexamined here. In this case, the numerical parameters are set to \(S=0.5, \,R=2.0, \,\sigma _1=40, \,\varepsilon _1=0.3\), and the surface tension coefficient has the value of \(0.012\). Under this condition, the droplet prolates as the calculated deformation parameter is equal to \(D=0.077\). Fig. 7a represents the fluid particles’ positions for four different particle resolutions of \(60 \times 60, \,80 \times 80, \,100 \times 100\), and \(120 \times 120\) for the quarter of the entire domain. Figure 7b shows the corresponding velocity vectors inside and outside the droplet.

Fig. 7
figure 7

Numerical convergence a Particle position distribution, and b velocity vectors, for different particle resolutions of \(60 \times 60, \,80 \times 80, \,100 \times 100\), and \(120 \times 120\)

Full size image

A close observation on Fig. 7a reveals that for low particle resolution cases, i.e. \(60 \times 60\) and \(80 \times 80\), the droplet deformation is dependent on the particle resolution. However, as the particle resolution increases, this dependency vanishes so that the droplet deformation is identical for \(100 \times 100\), and \(120 \times 120\) particle resolutions. Moreover, Fig. 7b clearly reveals that as the particle resolution increases, the center of vorticities inside and outside of droplet converges to a certain location, so that the position of vorticity centers are independent of particle resolution at high values. This brings the conclusion that considering the computational costs and the satisfactory accuracy of \(100 \times 100\) particle resolution, as well as minor quantitative and qualitative difference between the results of \(100 \times 100\), and \(120 \times 120\) results, the particle resolution of \(100 \times 100\) has been employed for all the simulations for which results are presented.

6 Conclusion

In this work, the SPH method has been used to model EHD of a droplet suspended inside a neutral viscous fluid with different electrical and hydrodynamical properties. To be able to couple electric field forces, surface tension forces, droplet deformation, and flow fields, momentum balance equations including electric field and surface tension forces are solved together with a set of Maxwell equations simplified by the using leaky dielectric model. The electric field and surface tension forces are included in the momentum balance equations as volumetric forces through taking the divergence of the Maxwell stress tensor and using the CSF approach, respectively. The interface between phases is tracked by means of color functions which are also used for the calculation of surface normals, curvature and properties of the mixture across the interface. Quite many simulations have been performed to investigate the effects of the electric field strength, permittivity ratios, and electrical conductivity ratios, surface tension and the initial droplet radius on the droplet deformation parameter. It is found that in the leaky dielectric model, droplets deform in either prolate or oblate manners depending on the ratios of electrical conductivity and permittivity. The simulation results have been validated by two theories and shown to agree well with those predicted by both theories for small droplet deformation parameters. However, it is observed that the numerical results overestimate the analytically calculated droplet deformation parameters for high deformations, which was also underscored in some other relevant works in literature. The reason behind this discrepancy lies in the assumption made by theories such that the droplet deformation is rather small, and hence the droplet remains nearly circular after the deformation. Depending on the relative magnitudes of the electric permittivity and conductivity ratios (i.e., the case of \(R>S\), or \(S>R\)), flow circulations have different patterns. The electric field strength only affects the magnitude of the droplet deformation. The intensity of the circulatory flow motion gets stronger when the droplet is subject to a larger deformation due to the high value of the steady electric field. The results of the current work suggest that the SPH method is able to capture the physics behind the droplet deformation under the influence of a steady electric field in a robust and accurate manner. The SPH model will be further extended to study other complex and interesting EHD problems such as the deformation of a non-Newtonian droplet in a Newtonian fluid.