Modification of the phase-field model to reach a high-density ratio and tunable surface tension of two-phase flow using the lattice Boltzmann method

Abstract

This paper presents a modified phase-field model to reach a two-phase flow with a high-density ratio and tunable surface tension. For this purpose, the gradient of the potential function in the pressure distribution function is discretized by combining the direct and indirect methods, which increases the method’s stability and enables it to simulate two-phase flows with a high-density ratio (in the order of 1000). The modified model is validated with the Laplace law, relaxation of a square droplet and the layered Poiseuille flow. Also, an impact of a droplet on the thin liquid film for We = 8000 and Re = 20, 100 and 500, as well as the Rayleigh–Taylor instability in two Reynolds numbers of 256 and 2048, is simulated, and the results are compared and validated with those of previous works. Finally, a droplet falling under gravity is investigated and its results are compared with the classic phase-field model. Comparisons show that for a cases with low deformation (Eötvös numbers smaller than 87 and Ohnesorge number greater than 0.2), the results are similar to previous works, but for the cases with high deformation the present model accurately estimates the droplet breakup, which confirms the ability of the present model to simulate a two-phase flow with complex patterns.

1 Introduction

Investigation of two-phase flows, especially droplet dynamics due to their wide application in engineering and natural phenomena, including boiling, evaporation, fuel spray and fluid flow in microchannel’s, is of specific importance [1,2,3]. On the other hand, the application of the lattice Boltzmann method (LBM) for simulating two-phase flows has been widely developed as a powerful numerical method for simulating two-phase flows. In this regard, some methods such as the pseudo-potential model [4,5,6], the free energy [7,8,9] and the phase-field [10,11,12] formulations are extensively developed.

The technique of force application and discretizing its terms is one of the important issues in simulating two-phase flows, and especially increasing its stability. In the framework of the pseudo-potential model, some techniques such the Shan and Chen [13] and the exact difference methods [14,15,16] are known for applying the force terms. However, both of these methods suffer from discrete lattice effects and do not cover the correct macroscopic equations. Despite the simplicity of the pseudo-potential model, the dependence of the surface tension on the equation of state and the density ratio is a limitation for this model, and efforts have been made to correct this issue [17]. In the free energy model, a non-ideal thermodynamic pressure is reached by modifying the equilibrium density distribution function. This approach causes some non-Navier–Stokes terms that break Galilean invariance. To solve this problem, some correction terms should be added to equilibrium distribution function [18].

Another approach to model the two-phase flows is known as the phase-field model. This model benefits from the two distribution functions for capturing the species and momentum conservation equations [10]. Tunable surface tension and reduced spurious velocities at the interface along with the simple coding are the advantages of this method. Lee and Liu [19] proposed a model for incompressible binary fluids based on the phase-field formulation. They also developed a model to consider the contact line dynamics with ability of eliminating the parasitic currents to machine accuracy in the presence of a wall boundary. Liang et al. [20] developed a model based on the phase-field lattice Boltzmann method to simulate the incompressible multiphase flows. In this model, a proper source term is incorporated in the Chan–Hilliard equation and a pressure distribution function is defined to recover the correct hydrodynamic equations. Along with improving the stability, their multiple-relaxation-time model effectively reduces the spurious velocities compared with the single-relaxation-time. Also, they used the phase-field formulation to model three-phase incompressible flows [21]. The interfaces of three different fluids are captured using two equations, and the flow field is solved by defining another distribution function. Kumar et al. [22] present a lattice Boltzmann model for simulating water–air flow with a high Reynolds number. This model uses two separate distribution functions to obtain the velocity field and solve the conservative Allen–Cahn equation. The presented model has successfully passed the numerical tests such as the rise of an air bubble, splash of a water droplet on a wet bed and Rayleigh–Taylor instability. Zhang et al. [23] proposed a modified phase-field model using the lattice Boltzmann method for simulating two-phase flows with a high-density ratio. The conserved Allen–Cahn equation is correctly recovered considering an improved multiple-relaxation-time model for the collision term and modifying both the equilibrium distribution function and discrete source term.

Fakhari and Rahimian [24] simulated the deformation and breakup of a falling droplet using the phase-field model [10]. The verification process was performed with the Laplace test and relaxation of a square droplet. They proved that for small Eötvös numbers the droplet deforms slowly and for large Eötvös numbers it breaks up. Fakhari et al. [25] presented a conservative three-dimensional phase-field model. In the conservative model, the vector perpendicular to the surface must be found. Their verification was studying the dynamics of a slotted droplet in a rotational flow. Also, Liang et al. [26] presented a new model based on the index function considering two distribution functions: The first one solves the Allen–Cahn equation and the next one is for covering the Navier–Stokes equations. They added a new force term to the Boltzmann equation without adding complexity to the problem. Verifications were performed by a static droplet, the layered Poiseuille flow and the spinodal decomposition.

In this paper, the original phase-field model with a low-density ratio and tunable surface tension is modified by correcting the numerical calculation of the gradient terms. In that way, the stability of numerical results improves and the density ratio increases remarkably up to 1000. The present model investigates the impact of a droplet with the thin liquid film and Rayleigh–Taylor instability. Also, the droplet falling under gravity is examined and droplet breakup is well examined.

2 Mathematical formulation

According to the model of He et al. [10], the equation for the density distribution function f is given by:

$$\frac{\partial f}{{\partial t}} + {\mathbf{e}}.\nabla f = - \frac{{f - f^{{{\text{eq}}}} }}{\tau } + \frac{{\left( {{\mathbf{e}} - {\mathbf{u}}} \right).\left( {{\mathbf{F}} + {\mathbf{G}}} \right)}}{\rho RT}f^{{{\text{eq}}}}$$

(1)

Here e and u are the lattice and macroscopic velocities, respectively. ρ is the density, R is the gas constant, T is the temperature, $f^{{{\text{eq}}}}$ expresses the equilibrium distribution function, τ is the relaxation time, F represents the effective intermolecular interactions and G refers to the gravitational force. Considering the intermolecular attraction and exclusion volume effect, F is written as [10, 24]

$${\mathbf{F}} = \rho \nabla \left( {2a\rho + k\nabla^{2} \rho } \right) - b\rho^{2} RT\chi \nabla \left( {\ln \rho^{2} \chi } \right),$$

(2)

where parameters a and b determine the strength of the molecular interaction and exclusion volume effects, respectively. The condition of a > 10.601RT must be applied to separate the two phases. Here, we choose a = b = 4. $\chi$ indicates an increase in the probability of particles colliding with each other due to the increase in fluid density and is given by:

$$\chi \left( \rho \right) = 1 + \frac{5}{8}b\rho + 0.2869\left( {b\rho } \right)^{2} + 0.1103\left( {b\rho } \right)^{3} + \cdots$$

(3)

The effective intermolecular interactions, F, can be related to the gradient of potential function ψ as

$${\mathbf{F}} = - \nabla \psi + {\mathbf{F}}_{s},$$

(4)

where ψ is given by

$$\psi \left( \rho \right) = b\rho^{2} RT\chi - a\rho^{2}$$

(5)

The potential function can also be related to the equation of state by [24]

$$\psi \left( \rho \right) = p - \rho RT.$$

(6)

Consequently, one obtains the pressure, p, as follows:

$$p = \rho RT\left( {1 + b\rho \chi } \right) - a\rho^{2}.$$

(7)

F_s in Eq. (4) corresponds to the surface tension and can be written in the form of a density function:

$${\mathbf{F}}_{{\mathbf{s}}} = k\rho \nabla \nabla^{2} \rho,$$

(8)

where k is a coefficient that controls the strength of the surface tension.

To avoid the presence of large amounts of forces at the interface that causes numerical instability, the pressure distribution function, g, is defined as [10]

$$g = fRT + \psi \left( \rho \right)\Gamma \left( 0 \right).$$

(9)

In this equation, $\Gamma \left( {\mathbf{u}} \right)$ is obtained by the following equation:

$$\Gamma \left( {\mathbf{u}} \right) = \frac{{f^{{{\text{eq}}}} }}{\rho }.$$

(10)

The material derivative of Eq. (9) gives [10]:

$$\frac{Dg}{{Dt}} = RT\frac{Df}{{Dt}} + \Gamma \left( 0 \right)\frac{D\psi \left( \rho \right)}{{Dt}}.$$

(11)

For incompressible flow after substituting Eq. (1) into Eq. (11), the last form of the pressure distribution function is obtained.

$$\frac{Dg}{{Dt}} = - \frac{{g - g^{{{\text{eq}}}} }}{\tau } + \left( {{\mathbf{e}} - {\mathbf{u}}} \right) \cdot \left[ {\Gamma \left( {\mathbf{u}} \right)\left( {{\mathbf{F}}_{s} + {\mathbf{G}}} \right) - \left( {\Gamma \left( {\mathbf{u}} \right) - \Gamma \left( 0 \right)} \right)\nabla \psi \left( \rho \right)} \right].$$

(12)

Here $\nabla \psi \left( \rho \right)$ is multiplied by a small amount, and that is why, the new distribution function makes numerical simulation more stable. Another distribution function defining the index function φ captures the interface of two phases.

$$\frac{Df}{{Dt}} = - \frac{{f - f^{{{\text{eq}}}} }}{\tau } - \frac{{\left( {{\mathbf{e}} - {\mathbf{u}}} \right).\nabla \psi \left( \varphi \right)}}{RT}\Gamma \left( {\mathbf{u}} \right),$$

(13)

where $\psi \left( \varphi \right)$ follows the equation of state [24].

$$\psi \left( \varphi \right) = \varphi^{2} RT\frac{4 - 2\varphi }{{\left( {1 - \varphi } \right)^{3} }} - a\varphi^{2}.$$

(14)

In Eq. (12), $\nabla \psi \left( \rho \right)$ and its factor play an important role in the numerical stability of the solution. By defining the pressure distribution function, the value of the coefficient of $\nabla \psi \left( \rho \right)$ was reduced. Now, by combining the direct and indirect methods in calculating the gradient of $\psi \left( \rho \right)$, the stability of the method is further increased. It is suggested to explain the potential function as [27]:

$$\nabla \psi = - 2\phi \nabla \phi,$$

(15)

where $\phi = \sqrt { - \psi \left( \rho \right)}$. The substantial point is to calculate the force term using the both direct derivative of the potential function, $\nabla \psi$, and the equivalent derivative of the potential function, $- 2\phi \nabla \phi$, together. Consequently, the last form of the gradient of the potential function reduces to

$$\nabla \psi = \frac{1}{\alpha \Delta x}\left[ {A\sum\limits_{k = 1}^{N} {\frac{{G_{k} }}{{G_{1} }}} \phi^{2} ({\mathbf{x}} + {\mathbf{e}}_{k} \Delta t){\mathbf{e}}_{k} + (1 - 2A)\phi ({\mathbf{x}})\sum\limits_{k = 1}^{N} {\frac{{G_{k} }}{{G_{1} }}\phi ({\mathbf{x}} + {\mathbf{e}}_{k} \Delta t){\mathbf{e}}_{k} } } \right],$$

(16)

where Δx is the lattice length, α is a coefficient equal to 3/2, A is the weight factor, and G_1:4 = 1 and G_5:8 = 1/4 [27]. This discretization is the isotropic finite difference approximation, which ensures the total mass of the system is conserved [28]. The authors experimentally found that applying Eqs. (16)–(13) had no effect on stability. Also, the values of coefficient A were manually changed in the range of − 0.125–0.25, and finally, the value of − 0.152 was selected as suggested in [27].

3 Discretization of equations

To solve Eqs. (12) and (13) and obtaining distribution functions, the following discrete equations are proposed [10]:

$$\begin{aligned} & \overline{{f_{i} }} \left( {{\mathbf{x}} + {\mathbf{e}}_{i} \Delta t,t + \Delta t} \right) - \overline{{f_{i} }} \left( {{\mathbf{x}},t} \right) \\ & \quad = - \frac{{\overline{{f_{i} }} \left( {{\mathbf{x}},t} \right) - \overline{{f_{i}^{{{\text{eq}}}} }} \left( {{\mathbf{x}},t} \right)}}{\tau } - \frac{{\left( {2\tau - 1} \right)}}{2\tau }\frac{{\left( {{\mathbf{e}}_{i} - {\mathbf{u}}} \right)\nabla \psi \left( \phi \right)}}{RT}\Gamma_{i} \left( {\mathbf{u}} \right)\Delta t ,\\ \end{aligned}$$

(17)

$$\begin{aligned} & \overline{{g_{i} }} \left( {{\mathbf{x}} + {\mathbf{e}}_{i} \Delta t,t + \Delta t} \right) - \overline{{g_{i} }} \left( {{\mathbf{x}},t} \right) = - \frac{{\overline{{g_{i} }} \left( {{\mathbf{x}},t} \right) - g_{i}^{{{\text{eq}}}} \left( {{\mathbf{x}},t} \right)}}{\tau } \\ & \quad + \frac{{\left( {2\tau - 1} \right)}}{2\tau }\left( {{\mathbf{e}}_{i} - {\mathbf{u}}} \right).\left[ {\Gamma_{i} \left( {\mathbf{u}} \right)\left( {{\mathbf{F}}_{s} + {\mathbf{G}}} \right) - \left( {\Gamma_{i} \left( {\mathbf{u}} \right) - \Gamma_{i} \left( 0 \right)} \right)\nabla \psi \left( \rho \right)} \right]\Delta t, \\ \end{aligned}$$

(18)

where $g_{i}^{{{\text{eq}}}}$, $f_{i}^{{{\text{eq}}}}$ and $\Gamma_{\alpha }$ are given by:

$$f_{i}^{{{\text{eq}}}} = w_{i} \varphi \left[ {1 + \frac{{3{\mathbf{e}}_{i} .{\mathbf{u}}}}{{c^{2} }} + \frac{{9\left( {{\mathbf{e}}_{i} .{\mathbf{u}}} \right)^{2} }}{{2c^{2} }} - \frac{{3{\mathbf{u}}^{2} }}{{2c^{2} }}} \right],$$

(19)

$$g_{i}^{{{\text{eq}}}} = w_{i} \left[ {p + \rho \left( {1 + \frac{{3{\mathbf{e}}_{i} .{\mathbf{u}}}}{{c^{2} }} + \frac{{9\left( {{\mathbf{e}}_{i} .{\mathbf{u}}} \right)^{2} }}{{2c^{2} }} - \frac{{3{\mathbf{u}}^{2} }}{{2c^{2} }}} \right)} \right],$$

(20)

$$\Gamma_{i} = w_{i} \left[ {1 + \frac{{3{\mathbf{e}}_{i} .{\mathbf{u}}}}{{c^{2} }} + \frac{{9\left( {{\mathbf{e}}_{i} .{\mathbf{u}}} \right)^{2} }}{{2c^{2} }} - \frac{{3{\mathbf{u}}^{2} }}{{2c^{2} }}} \right].$$

(21)

Also, the lattice velocity is c = Δx/Δt and Δx = Δt = 1. The mesoscopic velocities e_i and coefficients w_i are equal to the following values:

$$e_{i} = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {} \hfill & {i = 0} \hfill \\ {c\left( {\cos \theta_{i} ,\sin \theta_{i} } \right),} \hfill & {\theta_{i} = \left( {i - 1} \right){\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-\nulldelimiterspace} 2},} \hfill & {i = 1,2,3,4} \hfill \\ {\sqrt 2 c\left( {\cos \theta_{i} ,\sin \theta_{i} } \right),} \hfill & {\theta_{i} = \left( {i - 5} \right){\pi \mathord{\left/ {\vphantom {\pi {2 + {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-\nulldelimiterspace} 4}}}} \right. \kern-\nulldelimiterspace} {2 + {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-\nulldelimiterspace} 4}}},} \hfill & {i = 5,6,7,8} \hfill \\ \end{array} } \right.$$

(22)

$$w_{i} = \left\{ \begin{gathered} 4/9, \, i = 0 \hfill \\ 1/9, \, i = 1,2,3,4 \hfill \\ 1/36, \, i = 5,6,7,8 \, \hfill \\ \end{gathered} \right.$$

(23)

The mesoscopic quantities must be integrated to calculate the macroscopic quantities. Thus, the values of the index function, pressure and velocity are calculated from the following equations, respectively:

$$\phi = \sum\limits_{i = 0}^{8} {\overline{{f_{i} }} },$$

(24)

$$p = \sum\limits_{i = 0}^{8} {\overline{{g_{i} }} } - \frac{1}{2}{\mathbf{u}}.\nabla \psi \left( \rho \right)\Delta t,$$

(25)

$$\rho RT{\mathbf{u}} = \sum\limits_{i = 0}^{8} {{\mathbf{e}}_{i} \overline{{g_{i} }} + \frac{RT}{2}\left( {{\mathbf{F}}_{s} + {\mathbf{G}}} \right)} \Delta t.$$

(26)

In the above equations, RT = 1/3. Fluid thermophysical properties such as density, ρ, and kinematic viscosity, ν, will be obtained by interpolating between liquid- and gas-state values with the index function.

$$\rho = \rho_{{\text{g}}} + \frac{{\phi - \phi_{{\text{g}}} }}{{\phi_{{\text{l}}} - \phi_{{\text{g}}} }}\left( {\rho_{{\text{l}}} - \rho_{{\text{g}}} } \right),$$

(27)

$$\upsilon \left( \varphi \right) = \upsilon_{{\text{g}}} + \frac{{\varphi - \varphi_{{\text{g}}} }}{{\varphi_{{\text{l}}} - \varphi_{{\text{g}}} }}\left( {\upsilon_{{\text{l}}} - \upsilon_{{\text{g}}} } \right),$$

(28)

where ρ_l and ρ_g are the densities of the liquid and gas phase, respectively, and φ_l and φ_g are the maximum and minimum values of the index function, respectively. Finally, the kinematic viscosity is related to the relaxation time, τ, by:

$$\upsilon = \left( {\tau - 0.5} \right)/3.$$

(29)

The equations of mass and momentum conservations can be obtained by the Chapman–Enskog analysis on the pressure distribution equation. Details of this derivation are mentioned in “Appendix 1”. Accordingly, the equation of mass conservation has been derived as:

$$\left( {\frac{\partial }{\partial t} + {\mathbf{u}}.\nabla } \right)p + c_{s}^{2} \rho \nabla \cdot {\mathbf{u}} = 0.$$

(30)

In incompressible flows, ${{\partial p} \mathord{\left/ {\vphantom {{\partial p} {\partial t}}} \right. \kern-\nulldelimiterspace} {\partial t}}$ is very small, and ${\mathbf{u}}.\nabla p$ is the order of O (Ma³). Hence, the equation of continuity simplifies to $\nabla \cdot {\mathbf{u}} = 0$.

Also, the momentum conservation equations are obtained as:

$$\frac{{\partial \left( {\rho {\mathbf{u}}} \right)}}{\partial t} + \nabla \cdot \left( {\rho {\mathbf{uu}}} \right) = - \nabla p + \upsilon \nabla \cdot \Pi + k\rho \nabla \nabla^{2} \rho + {\mathbf{G}},$$

(31)

where $\Pi = \rho \left( {\nabla {\mathbf{u}} + {\mathbf{u}}\nabla } \right)$ is the viscous stress tensor. It is important to note that the choice of $\psi \left( \rho \right) = p - \rho RT$ ensures Galilean invariance of the model, which is shown in Appendix 1.

The interface dynamics that is described by an order parameter follows the Cahn–Hilliard equation (Cahn–Hilliard-like equation [29]), which can be derived from Eq. (17):

$$\frac{\partial \phi }{{\partial t}} + \nabla \cdot \left( {\phi {\mathbf{u}}} \right) = \frac{1}{2}\left( {1 - \frac{1}{2\tau }} \right)\nabla^{2} \left( {p - c_{s}^{2} \phi } \right).$$

(32)

4 Initial and boundary conditions

The distribution of the index function, φ, inside the domain is initialized using a hyperbolic tangent function.

$$\varphi \left( {x,y} \right) = \varphi_{m} - \frac{{\varphi_{l} - \varphi_{{\text{g}}} }}{2}\tanh \left( {z - r} \right),$$

(33)

$$\varphi_{m} = \frac{{\varphi_{l} + \varphi_{g} }}{2},$$

(34)

$$z = \sqrt {\left( {x - z_{x} } \right)^{2} + \left( {y - z_{y} } \right)^{2} },$$

(35)

where z_x and z_y are the x and y coordinates of the center of the droplet, respectively.

Any distribution function N_i at each point can be considered as a sum of equilibrium $N_{i}^{{{\text{eq}}}}$ and non-equilibrium $N_{i}^{{{\text{neq}}}}$ parts such as [30]:

$$N_{i} = N_{i}^{{{\text{eq}}}} + N_{i}^{{{\text{neq}}}}.$$

(36)

Since the distribution functions coming from the outside of the domain are not known after streaming, the non-equilibrium part cannot be obtained at the collision step at the boundary points. To yield the distribution function at the boundary point, N_i,b the equilibrium part $N_{i,b}^{{{\text{eq}}}}$ is computed owning to the macroscopic parameter at the boundary and corresponding equilibrium equation. But the non-equilibrium part $N_{i,b}^{{{\text{neq}}}}$ could be estimated by the first-order extrapolation with neighbor points, $N_{i,n}^{{{\text{neq}}}}$. Knowing that $N_{i,n}^{{{\text{neq}}}} = N_{i,n} - N_{i,n}^{{{\text{eq}}}}$, Eq. (36) at the boundary points is written as

$$N_{i,b} = N_{i,b}^{eq} + \left( {N_{i,n} - N_{i,n}^{eq} } \right).$$

(37)

Hence, the collision term for the boundary points can be obtained as follows:

$$N_{i,b}^{*} = N_{i,b}^{{{\text{eq}}}} + \left( {1 - {1 \mathord{\left/ {\vphantom {1 {\tau_{N} }}} \right. \kern-\nulldelimiterspace} {\tau_{N} }}} \right)\left( {N_{i,n} - N_{i,n}^{{{\text{eq}}}} } \right).$$

(38)

In Eq. (38), $N_{i,b}^{*}$ is the post-collision distribution function and τ_N is the relaxation time related to N.

5 Results and discussion

5.1 Determination of numerical parameters

Before simulating droplet dynamics, it is important to find the maximum and minimum values of index function, φ_l and φ_g. For the flat interface of two phases, one writes the following equation for surface tension:

$$\sigma = kI,$$

(39)

where

$$I = \int\limits_{ - \infty }^{ + \infty } {\left( {\frac{\partial \varphi }{{\partial n}}} \right)}^{2} {\text{d}}n.$$

Initial guess for the index function is φ_g = 0.002 and φ_l = 0.27. After about 100,000 iterations, the solution of two-layered two phases is converged and numerical results including φ_g, φ_l and I are given in Table 1. As it is seen, for different density ratios of γ = 1000, γ = 100 and γ = 10 the variable I keeps constant (constant surface tension) and φ_g and φ_l remain almost unchanged. Note that δ = μ_l/μ_g is the dynamic viscosity ratio, Nx and Ny are the lattice numbers in x and y directions, respectively, and T is the number of iterations. For this case, periodic boundary conditions are set in all walls.

5.2 Laplace law

Here, the Laplace test is performed for a static droplet. First, for a droplet with the radius of R = 20 and density ratio of γ = 1000 the values of φ_g = 0.02442 and φ_l = 0.2521 are obtained. Then for three different radiuses and also three different surface tensions, the numerical parameters are obtained and listed in Table. 2. In this table, τ_g is a constant input, R, φ_g, φ_g I and the pressure difference between the inside and outside of the droplet Δp are measured after the convergence. Also, surface tension is calculated using σ = kI, and the ratio of mass changes to the initial mass is computed by E = Δm₀/m₀.

Table 1 Numerical values of φ_g, φ_l and I for the test case of two-layered two phases

Table 2 Numerical parameters of τ_g, R, φ_g, φ_l, I, ∆p, σ and E for the Laplace test

Figure 1 shows the variation of Δp with respect to the inverse of the droplet radius. To better display the changes in all three cases, the scale of vertical axis has been changed from ∆p = 0.0009. Here, two points should be clear. First, in all cases ratio of mass changes to the initial mass is less than 3.44%. This means that the principle of mass conservation is satisfied in a good way. Second, in all cases the linear variation of pressure difference between the inside and outside of the droplet Δp with respect to inverse of the droplet radius is observed, which passes through the origin of the coordinates. This correctly confirms the Laplace law for the two-dimensional droplet.

Fig. 1

Laplace test for different surface tension coefficients

5.3 Relaxation of a square droplet

Here, the relaxation of a square droplet with the length of 50 lattice units is investigated, and the results are provided in Fig. 2. Table 3 reports numerical parameters, where λ = ν_l/ν_g is the kinematic viscosity ratio. Simulations are performed in a 100 × 100 domain, and φ_g and φ_l are set to 0.00042 and 0.27889, respectively. Figure 2 shows that as time progresses, sharp corners of the square tend to be smooth and eventually turns into a circle. In this case, the initial square droplet turns into a circle without oscillation. This is while the oscillation of the droplet from the square to the circle and vice versa until it reaches the convergence is observed in some conditions [24].

Fig. 2

Relaxation of a square droplet for γ = 100, λ = 0.1, τ_l = 0.65 and k = 10 at different time step numbers T

Table 3 Numerical parameters for the relaxation of a square droplet

5.4 Spurious velocities

Unrealistic velocities at the interface of two phases are known as parasitic or spurious velocities which appear because of the imbalance between the pressure and surface tension forces due to the numerical discretization. The magnitude of spurious velocities, U_s are computed by

$$U_{{\text{s}}} = \max \left( {\sqrt {u\left( {x,y} \right)^{2} + v\left( {x,y} \right)^{2} } } \right),$$

(40)

where x and y belong to the whole computing domain. Table 4 shows the magnitude of spurious velocities for two density ratios of γ = 2 and γ = 1000 at three different surface tension coefficients, k = 0.1, 1 and 10. Also, Fig. 3 shows the spurious velocities with a magnification of 10,000 for two density ratios of γ = 2 and γ = 1000 when k = 10. The computational domain is 100 × 100, the droplet radius is 20, the kinematic viscosity ratio is 0.1, and relaxation times for liquid and gas phases are 0.55 and 1, respectively. Also, the boundary conditions are periodic in all directions.

Table 4 The magnitude of spurious velocities for γ = 2 and γ = 1000 at k = 0.1, 1 and 10

Fig. 3

Representation of the spurious velocities for k = 10 with the magnification of 10.⁴, a γ = 2, b γ = 1000

It is shown that by increasing the surface tension, the values of spurious velocities are increased. This fact shows that with increasing the surface tension, the balance of forces in the interface is weakened and this has led to an increase in the values of parasitic flows. In contrast, it is observed that increasing the density ratio has reduced the spurious velocities. In other words, with increasing density difference on both sides of the interface, the balance between pressure and surface tension forces has increased so that it has weakened the parasitic flows.

5.5 Layered Poiseuille flow

Two-phase Poiseuille flow analysis is often performed at densities less than 10 due to numerical instability [26]. Here, two-phase Poiseuille flow in three centerline velocities is investigated. To do this, a computational dimension of 400 × 100 is created. The pressure gradient is ignored in the whole field so that the inlet and outlet use the periodic boundary condition. On the other hand, in order to generate the flow, a uniform gravity field g = (g,0) is applied to the computational domain. The analytical solution for the fluid velocity when the lower half of the channel filled by the liquid and the upper half of the channel occupied by the vapor phase leads to the following relation:

$$u_{x} (y) = \left\{ {\begin{array}{*{20}c} {\frac{{g_{x} h^{2} }}{{2\mu_{g} }}\left[ { - \left( \frac{y}{h} \right)^{2} - \frac{y}{h}\left( {\frac{{\mu_{g} - \mu_{l} }}{{\mu_{g} + \mu_{l} }}} \right) + \frac{{2\mu_{g} }}{{\mu_{g} + \mu_{l} }}} \right],\quad 0 < y \le h}, \\ {\frac{{g_{x} h^{2} }}{{2\mu_{l} }}\left[ { - \left( \frac{y}{h} \right)^{2} - \frac{y}{h}\left( {\frac{{\mu_{g} - \mu_{l} }}{{\mu_{g} + \mu_{l} }}} \right) + \frac{{2\mu_{l} }}{{\mu_{g} + \mu_{l} }}} \right],\quad - h \le y < 0}. \\ \end{array} } \right.$$

(41)

In Eq. (41), h is the half-height of the channel and μ_g and μ_l are the dynamic viscosity of the vapor and the liquid phase, respectively. Also, the centerline velocity is equal to $u_{{\text{c}}} = {{g_{x} h^{2} } \mathord{\left/ {\vphantom {{g_{x} h^{2} } {\left( {\mu_{{\text{l}}} + \mu_{{\text{g}}} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\mu_{{\text{l}}} + \mu_{{\text{g}}} } \right)}}$. Numerical results for the horizontal velocity, u_x, along with analytical ones for u_c = 0.01 are presented in Fig. 4. As can be seen in this figure, there is a good agreement between the numerical and analytical results in predicting the velocity values. A slight difference between the analytical and numerical results is observed in the interface of two phases and also in the maximum velocity of the vapor phase. This difference will be reduced by reducing the centerline velocity and satisfying the condition of incompressibility. To see this issue, the following relative error is defined:

$$E_{u} = \frac{{\sum\nolimits_{y} {\left| {u_{x}^{n} \left( y \right) - u_{x}^{a} \left( y \right)} \right|} }}{{\sum\nolimits_{y} {\left| {u_{x}^{a} \left( y \right)} \right|} }},$$

(42)

Fig. 4

Presentation of analytical and numerical velocity profiles in the layered Poiseuille flow

where the subscripts n and a denote the numerical and analytical solutions, respectively.

Calculations show that the relative error for the centerline velocity of 0.05, 0.01 and 0.001 is 6.88%, 3.59% and 1.49%, respectively. In other words, as the velocity decreases, numerical results tend to analytical ones.

5.6 Droplet impact on a thin liquid film

Droplet impact on a thin liquid film of the same fluid is one of the important problems for two-phase flows [31], where achieving a high-density ratio and high-dynamic-viscosity ratio has been a challenging [11, 32,33,34] issue. After hitting the thin liquid film with an initial height of h by a droplet, the liquid film takes a crown shape for high-density ratios.

Reynolds number, Re = u₀D/υ_l, and Weber number, We = ρ_lu_y0²D/σ, along with dimensionless time, t^* = − tu₀/D, explain this problem. Boundary conditions for sidewalls are periodic, top and bottom walls are bounce-back, and the second-order extrapolation is used for all parameters at top and bottom walls. First, we compare the results of current model with the model of He et al. [10] for the case of γ = 10, Re = 100, We = 500 and δ = 10. Numerical parameters are given in Table 5, and liquid shape at t^* = 1.6 is shown in Fig. 5. Observation of density contours in two models shows that the present model gives almost the same results compared with He et al. [10]. Also in the present model, fine drops can be seen which are falling from the top of the crown.

Table 5 Numerical parameters for droplet impact with a thin liquid film for γ = 10 (comparison between the current model and method of He et al. [10])

Fig. 5

Droplet impact with a thin liquid film for γ = 10, δ = 10, Re = 100 and We = 500 at t^* = 1.6, a Model of He et al. [10], b current model

Now, consider the droplet splashing for three Re = 20, 100 and 500 when We = 8000 and γ = 1000. Also, the dynamic viscosity ratios of 1000, 200 and 40 are considered in such a way that the viscosity ratio decreases with increasing the Reynolds number [35]. Table 6 reports the details of numerical parameters, and Figs. 6, 7, 8 show the interface position of two phases. Here, for Re = 20 the deposition process with a wavy surface and for Re = 100 and 500 splashing phenomenon are observed. In the deposition process, the droplet moves slowly on the liquid film, and it does not take the shape of a crown. But in the splashing phenomenon, the droplet removes the thin liquid film, and when the liquid film rises, the droplet takes the shape of a crown. This behavior is well observed in [11, 36]. In this simulations, the minimum applicable liquid kinematic viscosity is υ_l = 0.0116 for Re = 500, λ = 0.038 and φ_min = 0.01542.

Table 6 Numerical parameters for droplet impact with a thin liquid film of high-density ratio at three Reynolds numbers

Fig. 6

Droplet impact with a liquid film for Re = 20, We = 8000, γ = 1000 and δ = 1000, a t^* = 0, b t^* = 0.2, c t^* = 0.8, d t^* = 1.6

Fig. 7

Droplet impact with a liquid film for Re = 100, We = 8000, γ = 1000 and δ = 200, a t^* = 0, b t^* = 0.2, c t^* = 0.8, d t^* = 1.6

Fig. 8

Droplet impact with a liquid film for Re = 500, We = 8000, γ = 1000 and δ = 40, a t^* = 0, b t^* = 0.2, c t^* = 0.8, d t^* = 1.6

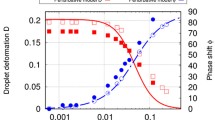
To quantify the splashing phenomenon, consider the dimensionless parameter of spread ratio. The spread ratio is defined as the ratio of the crown radius to the droplet diameter. This parameter follows a power law as r/D = C(u₀t/D)^0.5 [31, 37]. In this equation, C is a coefficient relating to the flow geometry. For three-dimensional flows, it is found to be 1.1, and for two-dimensional flows, it should be greater than 1.1 [38]. Figure 9 shows the spread ratio for Re = 100 and 500 and compares them with analytical ones. According to this figure, it is shown that the current results are completely consistent and the behavior of their changes is consistent with the analytical prediction. It should be noted that in the theoretical equation, we set C = 1.35 [26] and its numerical value is obtained as 1.8. Since the splashing phenomenon has not appeared for Re = 20, the spread ratio has not been drawn for this case.

Fig. 9

Theoretical and numerical variation of spread ratio for Re = 100 and 500

As a final point in this section, we examine the mass change of the liquid phase during the deposition and splashing phenomena. For this purpose, the percentage changes of the total mass (liquid and vapor phase) to the initial total mass ∆m/m₀ with respect to time for three splashing problems and a Laplace test are reported in Fig. 10. According to this figure, it can be seen that the total mass changes are always less than 0.2%.

Fig. 10

Percentage of changes in the total mass to the initial total mass ∆m/m₀ with respect to time for three splashing problems and a Laplace test

5.7 Rayleigh–Taylor instability

One of the complex and important problems in two-phase flows is the Rayleigh–Taylor instability, where two phases meet each other, while the denser fluid is at the top. As it is clear, a perturbation is needed to dense fluid coming down from the center and light fluid coming up from sides of the domain. Perturbation, S, follows a cosine relation which makes the interface curvature

$$S = B_{y} + 0.1\left( {Nx - 1} \right)\cos \left( {\frac{{2\pi \left( {x - 1} \right)}}{Nx - 1}} \right),$$

(43)

where B_y = Ny/2. If z = y−S, then the index function will initialize as

$$\varphi = \varphi_{m} + \frac{{\varphi_{{\text{l}}} - \varphi_{{\text{g}}} }}{2}\tanh \left( \frac{z}{w} \right),$$

(44)

where w = 4 is the thickness of the interface.

Characteristic velocity is defined as $U_{c} = \sqrt {\left( {Nx - 1} \right)g}$, so the Reynolds number for this problem will be given by ${\text{Re}} = U_{c} \left( {Nx - 1} \right)/\upsilon_{l}$. Also, the Atwood number is given by ${\text{At}} = (\rho_{{\text{l}}} - \rho_{{\text{g}}} )/(\rho_{{\text{l}}} + \rho_{{\text{g}}} )$. The characteristic time is $T_{c} = \sqrt {\left( {N_{x} - 1} \right)/g}$ and t^* = t/T_c. Table 7 represents the numerical parameters for two Reynolds numbers, and the results are shown in Figs. 11 and 12. The present results are comparable with those of previous works [10, 39]. It can be seen that with increasing the Reynolds number, the growth of perturbation occurs more rapidly, so that the two-phase interface in the second case (Re = 2048) is more turbulent and entangled than in the first case (Re = 256). These results are consistent with the results of previous works [10, 39].

Table 7 Numerical parameters for simulation of Rayleigh–Taylor instability for two Reynolds numbers

Fig. 11

Rayleigh–Taylor instability for Re = 256, At = 0.5 and U_c = 0.04

Fig. 12

Rayleigh–Taylor instability for Re = 2048, At = 0.5 and U_c = 0.04

Figure 13 displays the spike and bubble positions with time. The spike is defined as the distance of the liquid phase tip from the center of the domain to the length of the domain, and the bubble is the distance of the gas phase peak from the center of the domain to the length of the domain.

Fig. 13

Spike and bubble position of Rayleigh–Taylor instability for Re = 256 and 2048

A substantial point to check for this phenomenon is that the spike and bubble positions are independent of Reynolds number [10, 39]. It is shown that the bubble position is almost independent of the Reynolds number, but there is little difference between the spike positions between the two Reynolds numbers. This difference can occur due to the mass changes of the two phases.

5.8 Droplet deformation and breakup under gravity

Here, we investigate the moving, deformation and breakup of a single droplet under gravity. For this reason, the Eötvös (Bond) number is defined as ${\text{Eo}} = g\Delta \rho D^{2} /\sigma$, the Ohnesorge number is given by ${\text{Oh}} = \mu_{{\text{l}}} /(\rho_{{\text{l}}} D\sigma )^{0.5}$ and the dimensionless time is $t^{*} = t/\sqrt {D/g}$. Boundary conditions are bounce-back at the sidewalls and free-slip at up and down walls [24].

5.8.1 Effect of Eötvös number

Increasing the Eötvös number decreases the effects of surface tension and intensifies the deformation of the droplet. Figure 14 shows the interface of a falling droplet for γ = 5, δ = 5 and Oh = 0.3 at four Eötvös numbers of 22, 43, 65 and 87.

Fig. 14

Effect of Eötvös number on the droplet falling for γ = 5, δ = 5 and Oh = 0.3. Current work: a, b, c and d, Fakhari and Rahimian [24]: e, f, g and h

For this case, the computational domain is 150 × 300, the droplet radius is 15 and the relaxation time for the gas phase is τ_g = 0.8. It is shown that for Eo > 43 shear breakup is starting. Comparing results of the present work with those of Fakhari and Rahimian [24], which is based on the model of He et al. [10], shows that up to Eo = 65 there is a good match between them, but by increasing the Eötvös number to 87, we see a difference in the results. In other words, in Eo = 87 we expect a further decrease in the effects of surface tension and thus an increase in droplet deformation, which is shown in Fig. 14d. But in [24], in Eo = 87 we see a decrease in drop deformation and shear breakup is stopped (Fig. 14h). This comparison shows that the proposed model is successful in simulating two-phase flow with high deformations.

5.8.2 Effect of Ohnesorge number

Unlike the Eötvös number, increasing the Ohnesorge number reduces the deformation of the droplet. Therefore, in this section, small Ohnesorge numbers of Oh = 0.2, 0.3, 0.5 and 1 are selected, and the results are represented in Fig. 15. Also, Table 8 gives the necessary numerical parameters. Comparing the current results with those of Fakhari and Rahimian [24] shows a good agreement. Nonetheless, similar to the previous case, when the amount of droplet deformation is high (Oh = 0.2), there is a difference between the results of the present model and [24], which is due to the modified discretization of the source term in the pressure distribution function.

Fig. 15

Effect of Ohnesorge number on the droplet falling for, γ = 5, δ = 5 and Eo = 43

Table 8 Ohnesorge number effect

5.8.3 Limited case in the absence of surface tension

In this part, to see the pure effect of gravity on a droplet falling, the surface tension is assumed to be zero. In this situation, droplet deformation is stronger, and also, the bag breakup for the smallest gravity accelerations is shown in Fig. 16. Numerical parameters are given in Table 9. Similar to previous sections, droplet falling and deformation are in good agreement with [24].

Fig. 16

Interface of falling droplet for the limited case in the absence of surface tension (γ = 5, υ_l = υ_g = 1 and σ = 0)

Table 9 Limited state in the absence of surface tension

6 Conclusion

In this paper, a modified version of phase-field model for simulating the two-phase flows with a high-density ratio and tunable surface tension is presented. In this regard, the combined method for discretizing the potential function which has been well performed in the pseudo-potential model is used. As a result, a modified model with capability to reach the high-density ratio has been yielded. This model is validated with common test such as the Laplace law and circling a square droplet. Also, an impact of the droplet with a thin liquid film, Rayleigh–Taylor instability and falling a droplet under gravity is investigated. These problems are well simulated and confirm the ability of the current model.

Appendix 1: Macroscopic equations of mass and momentum conservations

As it is stated in Sect. 2 (Mathematical formulation), two distribution functions of g_i and f_i are introduced to recover the incompressible Navier–Stokes and a macro interface-tracking equation (a Cahn–Hilliard-like equation), respectively [40]:

$$\overline{{g_{i} }} \left( {{\mathbf{x}} + {\mathbf{e}}_{i} \Delta t,t + \Delta t} \right) - \overline{{g_{i} }} \left( {{\mathbf{x}},t} \right) = - \frac{{\overline{{g_{i} }} \left( {{\mathbf{x}},t} \right) - g_{i}^{{{\text{eq}}}} \left( {{\mathbf{x}},t} \right)}}{\tau } + S_{i},$$

(45)

$$\overline{{f_{i} }} \left( {{\mathbf{x}} + {\mathbf{e}}_{i} \Delta t,t + \Delta t} \right) = \overline{{f_{i} }} \left( {{\mathbf{x}},t} \right) - \frac{{\overline{{f_{i} }} \left( {{\mathbf{x}},t} \right) - \overline{{f_{i}^{{{\text{eq}}}} }} \left( {{\mathbf{x}},t} \right)}}{\tau } + S^{\prime}_{i},$$

(46)

where

$$S_{i} = \frac{{\left( {2\tau - 1} \right)}}{2\tau }\left( {{\mathbf{e}}_{i} - {\mathbf{u}}} \right).\left[ {\Gamma_{i} \left( {\mathbf{u}} \right)\left( {k\rho \nabla \nabla^{2} \rho } \right) - \left( {\Gamma_{i} \left( {\mathbf{u}} \right) - \Gamma_{i} \left( 0 \right)} \right)\nabla \psi \left( \rho \right)} \right]\Delta t,$$

(47)

$$S^{\prime}_{i} = - \frac{{\left( {2\tau - 1} \right)}}{2\tau }\frac{{\left( {{\mathbf{e}}_{i} - {\mathbf{u}}} \right)\nabla \psi \left( \phi \right)}}{RT}\Gamma_{i} \left( {\mathbf{u}} \right)\Delta t.$$

(48)

Define the Chapman–Enskog expansions:

$$\frac{\partial }{\partial t} = \frac{\partial }{{\partial t_{1} }} + \varepsilon \frac{\partial }{{\partial t_{2} }} + \cdots$$

(49)

$$\overline{g}_{i} = \overline{g}_{i}^{\left( 0 \right)} + \varepsilon \overline{g}_{i}^{\left( 1 \right)} + \varepsilon^{2} \overline{g}_{i}^{\left( 2 \right)} + \cdots$$

(50)

One applies the Taylor expansion to Eq. (45):

$$\begin{aligned} & \varepsilon \left( {\frac{\partial }{{\partial t_{1} }} + \varepsilon \frac{\partial }{{\partial t_{2} }} + e_{i\alpha } \frac{\partial }{\partial \alpha }} \right)\left( {\overline{g}_{i}^{\left( 0 \right)} + \varepsilon \overline{g}_{i}^{\left( 1 \right)} + \varepsilon^{2} \overline{g}_{i}^{\left( 2 \right)} } \right) \\ & \quad + \frac{{\varepsilon^{2} }}{2}\left( {\frac{\partial }{{\partial t_{1} }} + \varepsilon \frac{\partial }{{\partial t_{2} }} + e_{i\alpha } \frac{\partial }{\partial \alpha }} \right)^{2} \left( {\overline{g}_{i}^{\left( 0 \right)} + \varepsilon \overline{g}_{i}^{\left( 1 \right)} } \right) = - \frac{1}{\tau }\left( {\overline{g}_{i}^{\left( 0 \right)} + \varepsilon \overline{g}_{i}^{\left( 1 \right)} + \varepsilon^{2} \overline{g}_{i}^{\left( 2 \right)} - g_{i}^{{{\text{eq}}}} } \right) + S{}_{i}\Delta t. \\ \end{aligned}$$

(51)

The equations associated with scales ε, ε² and ε³ result in:

$$\frac{1}{\tau }\left( {\overline{g}_{i}^{\left( 0 \right)} - g_{i}^{{{\text{eq}}}} } \right) = 0,$$

(52)

$$\left( {\frac{\partial }{{\partial t_{1} }} + e_{i\alpha } \frac{\partial }{\partial \alpha }} \right)\overline{g}_{i}^{\left( 0 \right)} + \frac{1}{\tau }\overline{g}_{i}^{\left( 1 \right)} - S_{i} = 0,$$

(53)

$$\frac{{\partial \overline{g}_{i}^{\left( 0 \right)} }}{{\partial t_{2} }} + \left( {1 - \frac{1}{2\tau }} \right)\left( {\frac{\partial }{{\partial t_{1} }} + e_{i\alpha } \frac{\partial }{\partial \alpha }} \right)\overline{g}_{i}^{\left( 1 \right)} + \frac{1}{2}\left( {\frac{\partial }{{\partial t_{1} }} + e_{i\alpha } \frac{\partial }{\partial \alpha }} \right)S{}_{i} + \frac{1}{\tau }\overline{g}_{i}^{\left( 2 \right)} = 0.$$

(54)

From the definition of the pressure, we have:

$$\sum\limits_{i = 0}^{8} {\overline{g}_{i} = } \sum\limits_{i = 0}^{8} {\overline{g}_{i}^{\left( 0 \right)} } + \Delta t\sum\limits_{i = 0}^{8} {\overline{g}_{i}^{\left( 1 \right)} } + \Delta t^{2} \sum\limits_{i = 0}^{8} {\overline{g}_{i}^{\left( 2 \right)} } + \cdots = p + \frac{1}{2}u_{\beta } \frac{\partial \psi \left( \rho \right)}{{\partial \beta }}\Delta t.$$

(55)

By substituting the equilibrium distribution function $g_{i}^{{{\text{eq}}}}$ in Eq. (52), one obtains:

$$\sum\limits_{i = 0}^{8} {\overline{g}_{i}^{\left( 0 \right)} } = \sum\limits_{i = 0}^{8} {\overline{g}_{i}^{{{\text{eq}}}} = } p.$$

(56)

Considering Eqs. (56) and (55), we have:

$$\sum\limits_{i = 0}^{8} {\overline{g}_{i}^{\left( 1 \right)} } = \frac{1}{2}u_{\beta } .\frac{\partial \psi \left( \rho \right)}{{\partial \beta }}\Delta t, \,\quad \sum\limits_{i = 0}^{8} {\overline{g}_{i}^{\left( 2 \right)} } = 0.$$

(57)

Also, combining Eqs. (28) and (50) results in:

$$\sum\limits_{i = 0}^{8} {e_{i\alpha } \overline{g}_{i}^{\left( 0 \right)} = } c_{s}^{2} \rho u_{\alpha } , \,\quad \sum\limits_{i = 0}^{8} {e_{i\alpha } \overline{g}_{i}^{\left( 1 \right)} } = - \frac{1}{2}c_{s}^{2} k\rho \frac{\partial }{\partial \alpha }\left( {\frac{{\partial^{2} \rho }}{{\partial \delta^{2} }}} \right).$$

(58)

The zeroth and first moments of the source term S_i take the form:

$$\sum\limits_{i = 0}^{8} {S_{i} } = - \left( {1 - \frac{1}{2\tau }} \right)u_{\alpha } \frac{\partial \psi \left( \rho \right)}{{\partial \alpha }}, \, \quad\sum\limits_{i = 0}^{8} {e_{i\beta } S_{i} } = c_{s}^{2} \left( {1 - \frac{1}{2\tau }} \right)k\rho \frac{\partial }{\partial \alpha }\left( {\frac{{\partial^{2} \rho }}{{\partial \delta^{2} }}} \right).$$

(59)

From Eq. (22), one can write:

$$\sum\limits_{i = 0}^{8} {\overline{g}_{i}^{\left( 0 \right)} } e_{i\alpha } e_{i\beta } = c_{s}^{2} \left( {p\delta_{\alpha \beta } + \rho u_{\alpha } u_{\beta } } \right).$$

(60)

Using Eq. (47), and omitting higher-order terms of O(u³), we have:

$$\begin{aligned} & \sum\limits_{i = 0}^{8} {e_{i\alpha } e_{i\beta } S_{i} } = c_{s}^{2} \left( {1 - \frac{1}{2\tau }} \right) \\ & \quad \times \left[ { - \frac{\partial \psi \left( \rho \right)}{{\partial \gamma }}\left( {u_{\alpha } \delta_{\beta \gamma } + u_{\beta } \delta_{\alpha \gamma } + u_{\gamma } \delta_{\beta \alpha } } \right) + k\rho \frac{\partial }{\partial \beta }\left( {\frac{{\partial^{2} \rho }}{{\partial \delta^{2} }}} \right)u_{\alpha } + k\rho \frac{\partial }{\partial \alpha }\left( {\frac{{\partial^{2} \rho }}{{\partial \delta^{2} }}} \right)u_{\beta } } \right]. \\ \end{aligned}$$

(61)

Summing both sides of Eq. (53) over i and using Eqs. (56), (57), (58) and (59) gives:

$$\frac{\partial p}{{\partial t_{1} }} + c_{s}^{2} \frac{\partial }{\partial \alpha }\left( {\rho u_{\alpha } } \right) + u_{\alpha } \frac{\partial \psi \left( \rho \right)}{{\partial \alpha }} = 0.$$

It is easy to get the equivalent of Eq. (62):

$$\begin{aligned} \frac{\partial p}{{\partial t_{1} }} + c_{s}^{2} \frac{\partial }{\partial \alpha }\left( {\rho u_{\alpha } } \right) + u_{\alpha } \frac{\partial \psi \left( \rho \right)}{{\partial \alpha }} & = \frac{\partial p}{{\partial t_{1} }} + c_{s}^{2} \rho \frac{{\partial u_{\alpha } }}{\partial \alpha } + c_{s}^{2} u_{\alpha } \frac{\partial \rho }{{\partial \alpha }} + u_{\alpha } \frac{\partial \psi \left( \rho \right)}{{\partial \alpha }} \\ & = \frac{\partial p}{{\partial t_{1} }} + u_{\alpha } \frac{\partial }{\partial \alpha }\left( {c_{s}^{2} \rho + \psi } \right) + c_{s}^{2} \rho \frac{{\partial u_{\alpha } }}{\partial \alpha } \\ \end{aligned}$$

On the other hand, we know that $p = c_{s}^{2} \rho + \psi$, so:

$$\frac{\partial p}{{\partial t_{1} }} + c_{s}^{2} \frac{\partial }{\partial \alpha }\left( {\rho u_{\alpha } } \right) + u_{\alpha } \frac{\partial \psi \left( \rho \right)}{{\partial \alpha }} = \left( {\frac{\partial }{{\partial t_{1} }} + u_{\alpha } \frac{\partial }{\partial \alpha }} \right)p + c_{s}^{2} \rho \frac{{\partial u_{\alpha } }}{\partial \alpha } = 0.$$

(62)

Using Eqs. (56), (57), (58) and (59) and summing both sides of Eq. (54) over i give:

$$\begin{aligned} & \frac{\partial p}{{\partial t_{2} }} + \left( {1 - \frac{1}{2\tau }} \right)\left( {\frac{\partial }{{\partial t_{1} }}\left( {\frac{1}{2}u_{\beta } .\frac{\partial \psi \left( \rho \right)}{{\partial \beta }}\Delta t} \right) + \frac{\partial }{\partial \alpha }\left( { - \frac{1}{2}c_{s}^{2} k\rho \frac{\partial }{\partial \alpha }\left( {\frac{{\partial^{2} \rho }}{{\partial \delta^{2} }}} \right)} \right)} \right) \\ & \quad + \frac{1}{2}\left( {\frac{\partial }{{\partial t_{1} }}\left( { - \left( {1 - \frac{1}{2\tau }} \right)u_{\alpha } \frac{\partial \psi \left( \rho \right)}{{\partial \alpha }}} \right) + \frac{\partial }{\partial \alpha }\left( { - \left( {1 - \frac{1}{2\tau }} \right)u_{\alpha } \frac{\partial \psi \left( \rho \right)}{{\partial \alpha }}} \right)} \right) = 0 .\\ \end{aligned}$$

It follows from the above equation that:

$$\frac{\partial p}{{\partial t_{2} }} = 0.$$

(63)

According to Eq. (49) and Eqs. (62) and (63), the subscript 1 in Eq. (62) can be omitted.

$$\left( {\frac{\partial }{\partial t} + u_{\alpha } \frac{\partial }{\partial \alpha }} \right)p + c_{s}^{2} \rho \frac{{\partial u_{\alpha } }}{\partial \alpha } = 0.$$

(64)

In incompressible flows, ${{\partial p} \mathord{\left/ {\vphantom {{\partial p} {\partial t}}} \right. \kern-\nulldelimiterspace} {\partial t}}$ is very small, and ${\mathbf{u}}.\nabla p$ is the order of O (Ma³). Hence, the equation of continuity leads to $\nabla \cdot {\mathbf{u}} = 0$:

Multiplying Eq. (53) by e_iβ, summing over i and using Eqs. (59) and (60) gives:

$$\frac{\partial }{{\partial t_{1} }}\left( {\rho u_{\beta } } \right) + \frac{\partial }{\partial \alpha }\left( {p\delta_{\alpha \beta } + \rho u_{\alpha } u_{\beta } } \right) - k\rho \frac{\partial }{\partial \beta }\left( {\frac{{\partial^{2} \rho }}{{\partial \delta^{2} }}} \right) = 0.$$

(65)

In order to extract the momentum equations, the similar approach should be done, so that by some manipulations, it can be shown that [40]:

$$\begin{aligned} & \frac{\partial }{{\partial t_{2} }}\left( {\rho u_{\beta } } \right) - \left( {\tau - 0.5} \right)\left\{ \begin{gathered} \frac{\partial }{\partial \alpha }\frac{\partial }{{\partial t_{1} }}\left( {p\delta_{\alpha \beta } } \right) + \frac{\partial }{\partial \alpha }\frac{\partial }{{\partial t_{1} }}\left( {\rho u_{\alpha } u_{\beta } } \right) \hfill \\ + c_{s}^{2} \frac{\partial }{\partial \alpha }\frac{\partial }{\partial \gamma }\left[ {\rho \left( {u_{\alpha } \delta_{\beta \gamma } + u_{\beta } \delta_{\alpha \gamma } + u_{\gamma } \delta_{\beta \alpha } } \right)} \right] \hfill \\ \end{gathered} \right\} \\ & \quad + \left( {\tau - 0.5} \right)\left\{ \begin{gathered} \frac{\partial }{\partial \alpha }\left( {k\rho \frac{\partial }{\partial \beta }\left( {\frac{{\partial^{2} \rho }}{{\partial \delta^{2} }}} \right)u_{\alpha } + k\rho \frac{\partial }{\partial \alpha }\left( {\frac{{\partial^{2} \rho }}{{\partial \delta^{2} }}} \right)u_{\beta } } \right) \hfill \\ + \frac{\partial }{\partial \alpha }\left[ { - \frac{\partial \psi \left( \rho \right)}{{\partial \gamma }}\left( {u_{\alpha } \delta_{\beta \gamma } + u_{\beta } \delta_{\alpha \gamma } + u_{\gamma } \delta_{\beta \alpha } } \right)} \right] \hfill \\ \end{gathered} \right\} = 0. \\ \end{aligned}$$

(66)

On the other hand, from Eq. (62) we know

$$\frac{{\partial \left( {p\delta_{\alpha \beta } } \right)}}{{\partial t_{1} }} = \left( { - u_{\gamma } \frac{\partial p}{{\partial y}} - c_{s}^{2} \rho \frac{{\partial u_{\gamma } }}{\partial \gamma }} \right)\delta_{\alpha \beta }.$$

(67)

Substituting this equation and $\frac{\partial \psi \left( \rho \right)}{{\partial \gamma }} = \frac{\partial }{\partial \gamma }\left( {p - c_{s}^{2} \rho } \right)$ into Eq. (66), we have:

$$\begin{aligned} & \frac{\partial }{{\partial t_{2} }}\left( {\rho u_{\beta } } \right) - \left( {\tau - 0.5} \right)\left[ {\underbrace {{\frac{\partial }{\partial \alpha }\left( {u_{\alpha } \frac{\partial p}{{\partial \beta }} + u_{\beta } \frac{\partial p}{{\partial \alpha }}} \right)}}_{{}} + \underline{{\frac{\partial }{\partial \alpha }\frac{\partial }{{\partial t_{1} }}\left( {\rho u_{\alpha } u_{\beta } } \right)}} + c_{s}^{2} \frac{\partial }{\partial \alpha }\left( {\rho \frac{{\partial u_{\alpha } }}{\partial \beta } + \rho \frac{{\partial u_{\beta } }}{\partial \alpha }} \right)} \right] \\ & \quad + \left( {\tau - 0.5} \right)\left[ {\underbrace {{\frac{\partial }{\partial \alpha }\left( {k\rho \frac{\partial }{\partial \beta }\left( {\frac{{\partial^{2} \rho }}{{\partial \delta^{2} }}} \right)u_{\alpha } + k\rho \frac{\partial }{\partial \alpha }\left( {\frac{{\partial^{2} \rho }}{{\partial \delta^{2} }}} \right)u_{\beta } } \right)}}_{{}}} \right] = 0. \\ \end{aligned}$$

(68)

In Eq. (68), term $\frac{\partial }{\partial \alpha }\left( {u_{\alpha } \frac{\partial p}{{\partial \beta }} + u_{\beta } \frac{\partial p}{{\partial \alpha }}} \right)$ breaks Galilean invariance when the pressure gradient is large [41]. Fortunately, it is shown that the underbraced terms can be canceled with the underlined term $\underline{{\frac{\partial }{\partial \alpha }\frac{\partial }{{\partial t_{1} }}\left( {\rho u_{\alpha } u_{\beta } } \right)}}$ [40]. Finally, all these terms that may break Galilean invariance will disappear. So, Eq. (68) changes to:

$$\frac{\partial }{{\partial t_{2} }}\left( {\rho u_{\beta } } \right) - c_{s}^{2} \left( {\tau - 0.5} \right)\left\{ {\frac{\partial }{\partial \alpha }\left( {\rho \frac{{\partial u_{\alpha } }}{\partial \beta } + \rho \frac{{\partial u_{\beta } }}{\partial \alpha }} \right)} \right\} = 0.$$

(69)

From Eqs. (65) and (69) and using $\frac{\partial }{\partial t}\left( {\rho u_{\beta } } \right) = \frac{\partial }{{\partial t_{1} }}\left( {\rho u_{\beta } } \right) + \Delta t\frac{\partial }{{\partial t_{2} }}\left( {\rho u_{\beta } } \right)$, we have the N–S equations:

$$\frac{\partial }{\partial t}\left( {\rho u_{\beta } } \right) + \frac{\partial }{\partial \alpha }\left( {\rho u_{\alpha } u_{\beta } } \right) = - \frac{\partial p}{{\partial \beta }} + \upsilon \frac{\partial }{\partial \alpha }\left\{ {\rho \left( {\frac{{\partial u_{\alpha } }}{\partial \beta } + \frac{{\partial u_{\beta } }}{\partial \alpha }} \right)} \right\} + k\rho \frac{\partial }{\partial \beta }\left( {\frac{{\partial^{2} \rho }}{{\partial \delta^{2} }}} \right),$$

(70)

where $\upsilon = c_{s}^{2} \left( {\tau - 0.5} \right)\Delta t$. Hence, the choice of $\psi \left( \rho \right) = p - \rho RT$ ensures Galilean invariance of the model.