1 Introduction

Applications of layered structures are numerous and continuously increasing an example being the massive use of composite materials in aeronautical industry at present. Usually the interfaces between these rather bulk laminas consist of very thin adhesive layers. For efficient computations, these adhesive layers may be approximated by zero thickness interface layers. There are many situations where an adhesive layer is found to be partially or fully damaged. This process is frequently referred to as delamination or debonding of adjacent material laminas. In this work the description of the damage is based on a scalar damage quantity (variable, cf. [14]), which is defined at interfaces and takes values from the interval \([0,1]\), with zero value meaning no adhesion due to the total damage of the adhesive while the unit value meaning complete operation of the adhesive without any damage. During a damage evolution the damage variable decays in time, and it is assumed that a specific amount of energy has to be released (dissipated). This simplified approach, motivated essentially by Griffith [15], is often inadequate as it is observed experimentally that considerably more energy is usually needed to perform delamination in shear Mode II than in opening Mode I [1, 19, 24, 42]. Motivated by the microscopical idea of interface plasticity [24, 42], an extra inelastic parameter is introduced [36, 37], which describes some plastic slip that may occur in the tangent direction of an interface before its debonding.

An alternative approach to model fracture-mode-sensitive delamination uses only the delamination variable but makes the dissipated energy directly dependent on the so-called fracture mode mixity angle, cf. (10)–(11) below. This approach has frequently been used in engineering models [40, 41] but, it does not seem amenable to a rigorous mathematical analysis. In the present work we consider the delamination as a unidirectional process, i.e. no healing (or reconstruction) of adhesive is allowed, which covers most of engineering applications.

The goal of this article is to present and analyse from an engineering as well as numerical implementation viewpoint some basic features of the delamination model devised in [36, 37] with different dissipated energies in Modes I and II. In particular, in Sect. 2 we briefly present the energetic approach employed. In Sect. 3, we concisely introduce the present model, while some engineering insight on this model is provided. Then, in Sect. 4, the numerical implementation of the model is presented. Finally, in Sect. 5, two-dimensional simulations are developed, showing that the model is suitable for solving realistic problems of delamination between elastic layers.

2 Theoretical background

2.1 Problem definition

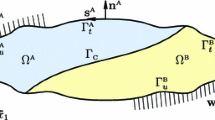
Let us consider an assemblage of \(N\) elastic bodies, each of them defined by a reference domain \(\Omega _i\) \((i=1,\ldots ,N)\), with the Lipschitz boundary \(\Gamma _i=\partial \Omega _i\), see Fig. 1.We denote by \(\Gamma _{ij}=\partial \Omega _i \cap \partial \Omega _j\) the (possibly empty) interface boundary between \(\Omega _i\) and \(\Omega _j\) \((i,j=1,\ldots ,N)\),which may undergo delamination. We also consider possible delamination on some parts of the outer boundary \(\Gamma _{0i}\), which is assumed to be in adhesive (unilateral) contact with a fixed rigid surface, Fig. 1. The union of these parts is denoted as \(\Gamma _{0}=\bigcup _{1\le i \le N} \Gamma _{0i}\). We will denote \({\Gamma }_{\mathrm{C}}:=\bigcup _{1\le i<j\le N}\Gamma _{ij}\cup \Gamma _{0}\). We assume that the rest of the outer boundary \(\partial \Omega \) is the union of two disjoint subsets \({\Gamma _{\mathrm{D}}}\) and \({\Gamma }_{\mathrm{N}}\), where Dirichlet (prescribed displacements \(u_{\mathrm{D}}=u_{\mathrm{D}}(t)\)) and Neumann boundary conditions (prescribed tractions \(p_{\mathrm{N}}=p_{\mathrm{N}}(t)\)) are imposed, respectively. For the sake of simplicity of the following considerations, vanishing tractions \(p_{\mathrm{N}}=0\) will be considered hereinafter, except for Sects. 4.2, 4.3 and 5.1.2. The intersection of the closures of \({\Gamma }_{\mathrm{C}}\) and \({\Gamma _{\mathrm{D}}}\) is assumed to be the empty set, i.e. \(\overline{\Gamma }_{\mathrm{C}}\cap \overline{\Gamma }_{\mathrm{D}}{=}\emptyset \). Any \(\Gamma _{ij}\) is considered as an infinitely thin adhesive layer, represented by springs distributed continuously, similarly to the Winkler spring model, with distinct normal and tangential elastic stiffnesses of values ranging from zero to infinity. Both the elastic subdomains and the adhesive layers are assumed to store energy, which is given by a stored energy functional \({\fancyscript{E}}(t,u,z)\) a function of time \(t\), the displacements \(u\) and the inelastic (internal) parameters collected in \(z\). It is considered that two elastic subdomains \(\Omega _i\) and \(\Omega _j\), may debond along the interface \(\Gamma _{ij}\). During this process the material of the adhesive can be damaged and plastified. The onset and growth of the damage and plastification, represented by the \(z\) variables, does not depend on some internal time scale and therefore the process is considered as rate-independent. The damage and plastification of the adhesive layer are accompanied by a release of stored energy. The dissipation potential \({\fancyscript{R}}(\dot{z})\), with \(\dot{z}:=\frac{\mathrm{d}z}{\mathrm{d}t}\), for a rate-independent process can be represented by a degree-1 homogeneous functional [31]. The processes described in this work are assumed to be quasistatic, i.e. no inertia effects are taken into account. The rate-independent evolution we have in mind is governed by the following system of doubly nonlinear degenerate abstract static/evolution inclusions, referred sometimes as Biot’s equations generalizing the original work [5, 6]:

$$\begin{aligned} \partial _u{\fancyscript{E}}(t,u,z)\ni 0\quad \text{ and}\quad \partial {\fancyscript{R}}\big (\dot{z}\big )+\partial _z{\fancyscript{E}}(t,u,z) \ni 0, \end{aligned}$$
(1)

where the symbol “\(\partial \)” refers to a (partial) subdifferential, relying on that \({\fancyscript{R}}(\cdot ),\,{\fancyscript{E}}(t,\cdot ,z)\), and \({\fancyscript{E}}(t,u,\cdot )\) are convex functionals. The first optimality condition of Eq. (1) represents the minimum energy principle, while the latter one, the minimum dissipation potential principle [36].

Fig. 1
figure 1

Schematic illustration of the geometry and notation for a two-dimensional case of two bonded subdomains, i.e. \(N{=}2\)

Full size image

For the sake of simplicity, throughout this work, we will restrict ourselves to the two-dimensional case, i.e. \(\Omega _i\subset \mathbb{R }^2\) will be planar domains, \(i=1,\dots ,N\), and \(\Gamma _{ij}\) will be one-dimensional surfaces.

2.2 Energetic solutions

A fruitful concept of a certain weak solution to the doubly nonlinear inclusion with degree-1 homogeneous dissipation potential \({\fancyscript{R}}\), called energetic solution, was developed by Mielke et al. [32, 33]. In the convex case, this concept is essentially equivalent to conventional weak-solution concept, while in our case where \({\fancyscript{E}}(t,\cdot ,\cdot )\) is non-convex this concept represents a certain generalization; cf. [27] for a survey on the concept of energetic solutions and [28] for comparison with other concepts.

The process \((u({t}),z({t})),\ {t}\in [0,T]\) is called an energetic solution to the initial-value problem (1), if it satisfies the following three conditions:

  1. (i)

    The energy equality:

    $$\begin{aligned}&\begin{array}[t]{c}\begin{array}[t]{c}\underbrace{{\fancyscript{E}}(T,u(T),z(T))_{_{_{_{_{_{}}}}}}\!\!\!}\quad \end{array}\quad \quad \\ _{\text{ stored} \text{ energy}}\quad \quad \\ _{\text{ at} \text{ time} t=T}\end{array} + \!\!\begin{array}[t]{c}\begin{array}[t]{c}\underbrace{\mathrm{Diss}_\mathcal{R } (z;[0,T])_{_{_{_{_{_{}}}}}}\!\!\!}\quad \end{array}\quad \quad \\ _{\text{ energy} \text{ dissipated}}\quad \quad \\ _{\text{ during} [0,T]}\end{array} \\ \nonumber&\qquad =\!\!\begin{array}[t]{c}\begin{array}[t]{c}\underbrace{\int _0^T\!\!\!{\fancyscript{E}}_t^{\prime }(t,u,z)\,\mathrm{d}t}\quad \end{array}\quad \quad \\ _{\text{ work} \text{ done} \text{ by}}\quad \quad \\ _{\text{ mechanical} \text{ load}}\end{array}\!\! +\!\!\begin{array}[t]{c}\begin{array}[t]{c}\underbrace{{\fancyscript{E}}(0,u_0,z_0)_{_{_{_{_{_{_{}}}}}}}\!\!\!}\quad \end{array}\quad \quad \\ _{\text{ stored} \text{ energy}}\quad \quad \\ _{\text{ at} \text{ time} t=0}\end{array}\!, \end{aligned}$$
    (2)

    where

    $$\begin{aligned} \mathrm{Diss}_\mathcal{R } (z;[0,T]):=\sup \sum _{j=1}^N {\mathcal{R }}(z(t_{j})-z(t_{j-1})), \end{aligned}$$
    (3)

    with the supremum taken over all partitions \(0\le t_0<t_1 <\cdots <t_{N-1}\le t_N\le T\).

  2. (ii)

    Stability inequality for any \(t\in [0,T]\):

    $$\begin{aligned} \ \ {\fancyscript{E}}(t,u,z)\le {\fancyscript{E}}(t,\tilde{u},\tilde{z})+{\fancyscript{R}}(\tilde{z}{-}z) \ \ \ \text{ for} \text{ any} (\tilde{u},\tilde{z}), \end{aligned}$$
    (4)
  3. (iii)

    The initial conditions: \(u(0)=u_0\) and \(z(0)=z_0\).

In Eq. (2), \({\fancyscript{E}}_t^{\prime }\) is the partial derivative of \({\fancyscript{E}}\) with respect to time \(t\).

3 Model of interface damage and plasticity

In this section we present the specific model adopted, in order to simulate the nonlinear inelastic behaviour of an adhesive layer, by defining a suitable stored energy functional as well as a dissipation potential. The present plastic-type model with kinematic-type hardening [16, 39] for the delamination problem, was devised essentially in [36] without any mathematical or computational justification, and further scrutinized in [37]. Beside the displacement \(u\), two internal parameters are used in order to describe the nonlinear behaviour of the adhesive: the damage variable \(\zeta \) and the plastic tangential slip variable \(\pi \), which together constitute the pair of inelastic variables \(z=(\zeta ,\pi )\).

3.1 Stored energy

Stored energy \({\fancyscript{E}}\) includes the elastic bulk contribution and the additional adhesive-surface contribution:

$$\begin{aligned} {{\fancyscript{E}}}(t,u,z)={{\fancyscript{E}}}_{\mathrm{el}}(t,u)+{{\fancyscript{E}}}_{\mathrm{adh}}(u,z) \end{aligned}$$
(5)

with

$$\begin{aligned} {{\fancyscript{E}}}_{\mathrm{el}}(t,u)=\!\left\{ \begin{array}{ll} \sum _{i=1}^N\int _{\Omega _i}\mathbb C _i e(u){:}e(u)\,\mathrm{d}x, \text{ if}\,u|_{{\Gamma _{\mathrm{D}}}}=u_{\mathrm{D}}(t),\\ \infty \quad \quad \text{ elsewhere.} \end{array}\right. \end{aligned}$$
(6)

where \(\mathbb C _i\) is the elastic moduli tensor in \(\Omega _i\), and

$$\begin{aligned} {{\fancyscript{E}}}_{\mathrm{adh}}(u,z):=\!\left\{ \begin{array}{ll} \displaystyle {\ \!\int _{{\Gamma }_{\mathrm{C}}}\!\! \Big (\zeta \Big ( \frac{\kappa _{\mathrm{n}}}{2} {[}\![u]\!]_{\mathrm{n}}^{2}\!+ \frac{\kappa _{\mathrm{t}}}{2}\big ({[}\![u]\!]_t\!{-}\pi \big )^2\Big )}&{}\\ \quad \displaystyle {\ \ \ +\,\frac{\kappa _{_{\mathrm{H}}}}{2} \pi ^2 +\frac{\kappa _0}{r}\big |\partial _{s}\zeta \big |^r \Big )} \displaystyle {\,\mathrm{d}S}\\ \quad \quad \quad \quad \quad \quad \quad \text{ if} 0\le \zeta \le 1 \text{ and} \\ \quad \quad \quad \quad \quad \quad \quad \quad {[}\![u]\!]_n 0 \text{ on} {\Gamma }_{\mathrm{C}},\\ \infty \quad \quad \quad \quad \quad \quad \text{ elsewhere,} \end{array}\right. \end{aligned}$$
(7)

where \(\kappa _{\mathrm{n}}>0\) and \(\kappa _{\mathrm{t}}>0\) are the phenomenological elastic constants describing the stiffnesses of the linearly elastically responding adhesive in the normal and tangential directions, respectively, \(\kappa _0>0\) is the so-called factor of influence of damage [29], \({[}\![u]\!]={[}\![u]\!]_n\nu +{[}\![u]\!]_t\tau \) with \({[}\![u]\!]_n={[}\![u]\!] \cdot \nu \) and \({[}\![u]\!]_t={[}\![u]\!] \cdot \tau ,\,\nu \) and \(\tau \) being unit normal and tangential vectors to \({\Gamma }_{\mathrm{C}}\), and \(\partial _{s}\) is the tangential derivative defined on \({\Gamma }_{\mathrm{C}}\). For \(\Gamma _{0}\) the outward normal \(\nu \) is typically taken. Constant parameter \(\kappa _{_{\mathrm{H}}}\) stands for the plastic modulus of kinematic hardening. Here we used the notation \({[}\![u]\!]\) for the differences of displacements from both sides of \({\Gamma }_{\mathrm{C}}\). We also assume \(r>1\). The last term in Eq. (7), although bearing a physical interpretation [2], is here introduced mainly for mathematical reasons in order to facilitate a proof of convergence; for further details see [37], but in specific simulations one may expect reasonable numerical results even if this term is neglected by setting \(\kappa _0=0\). The constraint \({[}\![u]\!]_n\ge 0\) in Eq. (7) is actually the Signorini non-penetration condition of unilateral contact [22].

3.2 Dissipation potential

A suitable functional for the dissipation potential, describing both inelastic processes of damage and plastic slip in the adhesive layer, and actually being a degree-1 homogeneous functional, is defined as:

$$\begin{aligned}&{\fancyscript{R}}(\dot{z})={\fancyscript{R}}(\dot{\zeta },\dot{\pi }):= {\left\{ \begin{array}{ll}\displaystyle {\int _{{\Gamma }_{\mathrm{C}}}\!\!G_{_{{\mathrm{I}} \mathrm{c}}}\,\big |\dot{\zeta }\big | +\sigma _{\mathrm{t,yield}}\big |\dot{\pi }\big |\mathrm{d}S}\\ \quad \quad \quad \quad \quad \quad \text{ if} \dot{\zeta }\le 0 \text{ a.e.} \text{ on} {\Gamma }_{\mathrm{C}},\\ \infty \quad \quad \quad \quad \quad \text{ otherwise}. \end{array}\right. } \end{aligned}$$
(8)

Parameter \(G_{_{{\mathrm{I}} \mathrm{c}}}>0\) is the minimal energy required for complete damage (debonding) of a unit area of the interface. In particular, we assume it represents the interface fracture energy in Mode I. Parameter \(\sigma _{\mathrm{t,yield}}>0\) is the interface yield shear stress for initiation of tangential plastic slip along the interface. The constraint \(\dot{\zeta }\le 0\) in (8) makes the evolution of \(\zeta \) irreversible, i.e. the model does not permit healing, which means that a debond appeared at some point can not be restored.

Note that, except trivial case when \(u_{\mathrm{D}}\) is constant in time, \({\fancyscript{E}}_t^{\prime }\) in 2 would not be well defined. One way how to avoid this drawback, well consistent with BEM, is to restrict the displacement only on \({\Gamma }_{\mathrm{C}}\), assuming that \({\Gamma }_{\mathrm{C}}\) and \({\Gamma _{\mathrm{D}}}\) are not touching each other. The restricted displacement \(u|_{{\Gamma }_{\mathrm{C}}}\) will be denoted by \(u_{\mathrm{C}}\); in fact, in the case of \(\Gamma _{ij}\), it is a couple of traces of \(u\) from both sides of \(\Gamma _{ij}\). As \(u\) does not occur in Eq. (8) and thus it is fully nondissipative, Eq. (4) implies that \(u\) minimizes \({\fancyscript{E}}(t,\cdot ,z)\) and thus, in fact, \(u_{\mathrm{C}}\) and \(z\) determines \(u\) at a given time \(t\). Thus, \({\fancyscript{E}}\) can be considered as a function of \(u_{\mathrm{C}}\) instead of \(u\), which makes \({\fancyscript{E}}_t^{\prime }(t,u_{\mathrm{C}},z)\) well defined if \(u_{\mathrm{D}}\) is smooth in time. On the other hand, we will not distinguish between \({[}\![u]\!]\) and \({[}\![u_\mathrm{C}]\!]\). We will use this convention through the rest of this article.

3.3 Engineering analysis of the traction-relative displacement law

In the case of a linear elastic-perfectly brittle interface model [40, 41], the interface failure criterion is connected to the energy release rate (ERR) concept. It can be shown [9, 23] that the energy stored in the adhesive at the crack tip equals the ERR of a mixed mode crack propagating along a linear elastic interface, and can be evaluated as:

$$\begin{aligned} G=G_{\mathrm{I}}+G_{\mathrm{II}}=\frac{\kappa _{\mathrm{n}}{[}\![u]\!]_{\mathrm{n}}^{2}}{2}+\frac{\kappa _{\mathrm{t}}{[}\![u]\!]_{\mathrm{t}}^{2}}{2}. \end{aligned}$$
(9)

The so-called fracture mode mixity angles, denoted as \(\psi _G,\,\psi _u\), or \(\psi _\sigma \), can be defined in terms of ERR as,

$$\begin{aligned} \tan ^2{\psi _G}=\frac{G_{\mathrm{II}}}{G_{\mathrm{I}}}, \end{aligned}$$
(10)

as well as in terms of relative displacements and tractions, respectively,

$$\begin{aligned} \tan {\psi _u}=\frac{{[}\![u]\!]_t}{{[}\![u]\!]_n} \ \text{ and} \ \tan {\psi _{\sigma }}=\frac{\sigma _t}{\sigma _n}=\frac{\kappa _{\mathrm{t}}{[}\![u]\!]_t}{\kappa _{\mathrm{n}}{[}\![u]\!]_n}. \end{aligned}$$
(11)

Thus, the following relations hold:

$$\begin{aligned} |\tan {\psi _{\sigma }}|=\sqrt{\frac{\kappa _{\mathrm{t}}}{\kappa _{\mathrm{n}}}}\tan {\psi _G} \ \text{ and} \ |\tan {\psi _u}|=\sqrt{\frac{\kappa _{\mathrm{n}}}{\kappa _{\mathrm{t}}}}\tan {\psi _G}. \end{aligned}$$
(12)

It is assumed that a crack propagates along a linear elastic-perfectly brittle interface if the ERR \(G\) reaches the fracture energy \(G_c\) (cf. [40, 41]), that means:

$$\begin{aligned} \frac{\kappa _{\mathrm{n}}{[}\![u]\!]_{\mathrm{n}}^{2}}{2}+\frac{\kappa _{\mathrm{t}}{[}\![u]\!]_{\mathrm{t}}^{2}}{2}=G_c. \end{aligned}$$
(13)

A strong dependence of \(G_c\) on the fracture mode mixity has been observed in extensive experiments [1, 12, 19, 24]. In accordance with other experimental observations [21, 42], the associated plastic zones in the adjacent bulk, near the crack tip, are larger in Mode II than in Mode I and these plastic phenomena are localized in a relatively narrow plastic zone in the bulk in the interface vicinity. In order to provide a better representation of these experimental results, a plastic tangential slip variable \(\pi \) has been introduced at the interface, which allows us, firstly, to distinguish between fracture Mode I and II in the sense that some additional dissipated energy is associated to interface fracture in Mode II, and secondly to simulate these narrow plastic zones. In such a case we can model an inelastic behaviour in the tangential response of the interface, while the response in the normal direction remains linear elastic, as shown in Fig. 2. An engineering insight into the present interface constitutive law can be summarized by the two conditions which activate the two inelastic processes included in the formulation [37]. The first one is the activation criterion for damage initiation which, for the case of \(\kappa _0=0\), reads as

$$\begin{aligned} \frac{1}{2}\left( \kappa _{\mathrm{n}}{[}\![u]\!]_{\mathrm{n}}^{2}+ \kappa _{\mathrm{t}}\left( {[}\![u]\!]_t\!{-}\pi \right) ^2\right) = G_{_{{\mathrm{I}} \mathrm{c}}}, \end{aligned}$$
(14)

where the left hand side represents the elastic energy stored in the adhesive. The second one concerns the evolution of \(\pi \) which is triggered when \(|\sigma _{\mathrm{t}}-\kappa _{_{\mathrm{H}}}\pi |\) reaches the activation threshold \(\sigma _{\mathrm{t,yield}}\), and then,

$$\begin{aligned} |\zeta \kappa _{\mathrm{t}}({[}\![u]\!]_t{-}\pi )-\kappa _{_{\mathrm{H}}}\pi | =\sigma _{\mathrm{t,yield}}. \end{aligned}$$
(15)

A more detailed analysis of the model may be found in [37]. The model produces the desired results if

$$\begin{aligned} \frac{1}{2}\sqrt{2\kappa _{\mathrm{t}}G_{_{{\mathrm{I}} \mathrm{c}}}}<\sigma _{\mathrm{t,yield}} \le \sqrt{2\kappa _{\mathrm{t}}G_{_{{\mathrm{I}} \mathrm{c}}}}. \end{aligned}$$
(16)

The upper bound of yield stress is necessary for making possible to initiate plastic slip before the total interface damage, while the lower one is required to avoid plastic slip evolution at some point which has already been debonded.

Fig. 2
figure 2

Schematic illustration of the traction-relative displacement law in the model. a pure normal (opening) mode and b pure tangential (shear) mode, considering \(\zeta _0=1\) and \(\pi _0=0\). Contribution of the delamination-gradient term is neglected, i.e. \(\kappa _0{=}0\)

Full size image

Thus, the ERR of a mixed mode crack for the present model is defined by the:

$$\begin{aligned} G=\frac{\kappa _{\mathrm{n}} {[}\![u]\!]_{\mathrm{n}}^{2}}{2} +\frac{\kappa _{\mathrm{t}}\left( {[}\![u]\!]_t{-}\pi \right) ^2}{2}+\sigma _{\mathrm{t,yield}}|\pi |+\frac{\kappa _{\scriptscriptstyle \mathrm H } \pi ^2}{2},\end{aligned}$$
(17)

where it may be seen that, referring to Eq. (9), ERR is here augmented by terms concerning inelastic slip \(\pi \).

In the following we will try to determine the dependence of \(G_c\) on the fracture mode mixity angle \(\psi _{u}\) similarly as in [43]. To accomplish this task, first we eliminate the plastic slip \(\pi \), which in our kinematic-hardening model may be written, for \(\pi >0\), as:

$$\begin{aligned} \pi =\frac{\kappa _{\mathrm{t}}}{\kappa _{\mathrm{t}}+\kappa _{\scriptscriptstyle \mathrm H }}\left( {[}\![u]\!]_t-\frac{\sigma _{t,\mathrm yield}}{\kappa _{\mathrm{t}}}\right) . \end{aligned}$$
(18)

Substituting Eq. (18) into the damage initiation criterion of Eq. (14), leads to the relation,

$$\begin{aligned} \frac{1}{2}\left( \kappa _{\mathrm{n}}{[}\![u]\!]_{\mathrm{n}}^{2}{+} \kappa _{\mathrm{t}}\left( \frac{\kappa _{\mathrm{H }}}{\kappa _{\mathrm{H }}{+}\kappa _{\mathrm{t}}}\right) ^2\left( {[}\![u]\!]_t{+}\frac{\sigma _{t, \mathrm{yield}}}{\kappa _{\mathrm{H }}}\right) ^2\right) {=}G_{_{{\mathrm{I}} \mathrm{c}}}\end{aligned}$$
(19)

when some interface plasticity occurs, i.e. \({[}\![u]\!]_t\ge \frac{\sigma _{t,\mathrm{yield}}}{\kappa _{\mathrm{t}}}\).

In a similar way as in Eq. (13), which is valid if no plasticity has occurred, Eq. (19) defines the relation between the two components of the relative displacement at the crack tip leading to the crack growth, if some plasticity has already appeared. This relation can be written in a parameterized form through the use of a parametric angle \(\phi \), as:

$$\begin{aligned} {[}\![u]\!]_n&= \sqrt{\frac{2 G_{_{{\mathrm{I}} \mathrm{c}}}}{\kappa _{\mathrm{n}}}}\cos {\phi },\nonumber \\ {[}\![u]\!]_t&= \sqrt{\frac{2 G_{_{{\mathrm{I}} \mathrm{c}}}}{\kappa _{\mathrm{t}}}}\frac{\kappa _{\mathrm{t}}+\kappa _{\mathrm{H }}}{\kappa _{\mathrm{H }}}\sin {\phi }-\frac{\sigma _{t, \mathrm{yield}}}{\kappa _{\mathrm{H }}}, \end{aligned}$$
(20)

for \(\arcsin {\frac{\sigma _{t,\mathrm{yield}}}{\sqrt{2 \kappa _{\mathrm{t}} G_{_{{\mathrm{I}} \mathrm{c}}}}}}\le \phi \le \frac{\pi }{2}\). Before plasticity occurs, i.e. for \(0\le \phi \le \arcsin {\frac{\sigma _{t,\mathrm{yield}}}{\sqrt{2 \kappa _{\mathrm{t}} G_{_{{\mathrm{I}} \mathrm{c}}}}}}\), the analogous parameterization writes as

$$\begin{aligned}&{[}\![u]\!]_n=\sqrt{\frac{2G_{_{{\mathrm{I}} \mathrm{c}}}}{\kappa _{\mathrm{n}}}}\cos {\phi },\nonumber \\&{[}\![u]\!]_t=\sqrt{\frac{2G_{_{{\mathrm{I}} \mathrm{c}}}}{\kappa _{\mathrm{t}}}}\sin {\phi }, \end{aligned}$$
(21)

and angle \(\phi \) coincides with the fracture mode mixity angle \(\psi _G\) defined in Eq. (10). Parameterization of Eq. (20), defines an ellipse whose center is at the point \(\left( 0,-\frac{\sigma _{t,\mathrm{yield}}}{\kappa _{\scriptscriptstyle \mathrm H }}\right) \), which continuously switches from the ellipse with the center at the origin of coordinates Eq. (21), which corresponds to a state of zero plasticity.

The relation \(G_c=G_c(\psi _u)\), for the case of non-zero interface plasticity, can be obtained by substitution of Eqs. (20), (19) and (18) into Eq. (17), leading after some algebra to:

$$\begin{aligned} G_{_{{\mathrm{I}} \mathrm{c}}}\left( 1+\frac{\kappa _{\mathrm{t}}}{\kappa _{\scriptscriptstyle \mathrm H }}\sin ^2{\phi } \right) -\frac{\sigma ^2_{t,\mathrm{yield}}}{2\kappa _{\scriptscriptstyle \mathrm H }}=G_c(\phi ). \end{aligned}$$
(22)

Finally, finding the relation between the angles \(\phi \) and \(\psi _u\)

$$\begin{aligned} \tan {\psi _u}=\sqrt{\frac{\kappa _{\mathrm{n}}}{\kappa _{\mathrm{t}}}} \frac{\kappa _{\mathrm{t}}{+}\kappa _{\scriptscriptstyle \mathrm H }}{\kappa _ {\scriptscriptstyle \mathrm H }}\tan {\phi } -\sqrt{\frac{\kappa _{\mathrm{n}}}{2G_{_{{\mathrm{I}} \mathrm{c}}}}}\frac{\sigma _t,\mathrm{yield}}{\kappa _{\scriptscriptstyle \mathrm H }} \frac{1}{\cos {\phi }}, \end{aligned}$$
(23)

we obtain the desired relation \(\phi =\phi (\psi _u)\) to be substituted into Eq. (22). However, an explicit relation of \(G_c(\psi _u)\) is rather cumbersome. Nevertheless, according to plots presented in [43] the functional dependence of \(G_c(\psi _u)\) qualitatively represents the expected behaviour in view of the previous experimental results [1, 12, 19, 24].

4 Numerical implementation

The theoretical framework, briefly presented up to this point, provides an implementable and efficient numerical scheme. An emerging global minimization problem, inherent in Eq. (4) may be defined by an implicit time discretization. By discretizing the time incremental formulation in space by some appropriate method, the problem may be casted in a standard algebraic form. Since the problem may be (and here is) formulated on the boundary, as all nonlinear processes considered occur exclusively on the boundary \({\Gamma }_{\mathrm{C}}\) only, a boundary element method seems to be a natural approach especially if the bulk equations can efficiently be solved, which is in particular the case of isotropic linear elastic materials considered in this article. Such a formulation was developed in [37], using the collocation BEM but without providing a thorough description of the numerical implementation. A related symmetric Galerkin SGBEM formulation can be found in [43] and a FEM implementation in [36]. A preliminary comparison with the SGBEM formulation has shown an excellent agreement in a few specific case studies. An advantage of the present approach with respect to a related FEM approach is that no bulk discretization is required here, and in the analysis and optimization procedures we directly work with a relatively small number of variables associated to boundaries in particular to \({\Gamma }_{\mathrm{C}}\).

4.1 Minimization problem

Making an implicit time discretization by adopting, for simplicity, an equidistant partition of \([0,T]\) with a fixed time-step \(\tau >0\), assuming \(T/\tau \in \mathbb{N }\), Eq. (4) leads to a recursive minimization problem:

$$\begin{aligned} \left. \begin{array}{ll} \text{ minimize}&{}{\fancyscript{F}}^k(u_{\mathrm{C}},z)={\fancyscript{E}}(k\tau ,u_{\mathrm{C}},z)+{\fancyscript{R}}(z{-}z^{k-1})\\ \text{ subject} \text{ to}\ &{}B_I u_{\mathrm{C}}{ } 0,\quad 0{\le }\zeta {\le }\zeta ^{k-1}, \end{array}\right\} \end{aligned}$$
(24)

to be solved successively for \(k=1,\ldots ,T/\tau \), starting from \(u_0\) and \(z_0\). Operator \(B_I\) represents the non-penetration Signorini conditions, while the further constraint in (24) refers to the non-negativity and irreversibility of damage parameter evolution. According to the convention of Sect. 3.2, only \(u_{\mathrm{C}}\), the displacement at interfaces (or adhesive contact zones), appears in Eq. (24) making clear that only this part of the displacement field is a minimizer of the problem.

We denote by \((u_{\mathrm{C}}^k,z^k)\) some (generally not unique) solution to the problem (24).

In order to numerically solve the emerging minimization problems (24), we have utilized and test in this work several algorithms, such as the L-BFGS-B [8] for general large scale simply bounded problems, the GLPK routines for linear programming problems [25] as well as a conjugate gradient based algorithm with constraints, see [11], for solving quadratic programming problems. Notably, the minimization problem appears to have an \(L_1\)-type non-smooth term with respect to the plastic tangent slip variable \(\pi \), see Eq. (8). In order to overcome this difficulty we take advantage of gradient projection algorithm presented in [13] for such kind of non-smoothness.

4.1.1 Alternate minimization algorithm

The functional \({\fancyscript{F}}^k\) in Eq. (24) is not convex and as such leads to a difficult minimization problem. In order to overcome this difficulty we utilize a special technique, originally proposed in [7], called as alternate minimization algorithm (AMA). The AMA procedure, in our case, consists in splitting the original nonconvex minimization problem to two distinct convex problems with respect to the kinematical variables (\(u, \pi \)) and to damage variable \(\zeta \), respectively. Convergence is succeeded through an iterative procedure by alternation of this two convex problems. A flowchart of AMA may be seen in Table 1. It is worth mentioning that the individual subproblems emerging by using such alternation consist of a nonsmooth quadratic programming problem, step (2-b), and a linear programming problem, step (2-c) of Table 1, respectively, for which we may use appropriate specialized algorithms such as those mentioned above.

Table 1 Pseudocode of the alternate minimization algorithm
Full size table

4.1.2 Back-tracking technique

The above AMA procedure does not necessarily lead to a globally minimizing solution which is, however, one of the main condition behind the energetic-solution concept, as shown in Sect. 2. In order to execute the global minimization more successfully at particular time levels we use heuristic back-tracking algorithm (BTA), devised and tested on this kind of problems in [3, 4, 31, 36, 37]. The BTA technique is based on checking a two-sided energy estimate, the integral expression in Table 2, where also some pseudo-code of BTA is given. This two-sided inequality has been constructed by use of the energy stability condition Eq. (4) and a full deduction of it can be found in [27, 30, 36]. The upper and lower energy estimates are given as time integrals of the power while \((\overline{u}_{\mathrm{C}},\overline{z})\) and \((\underline{u}_{\mathrm{C}},\underline{z})\) are piecewise constant interpolants in time defined by

$$\begin{aligned}&\overline{u}_{\mathrm{C}}(t)=u_{\mathrm{C}}^k \quad \quad \quad \quad \quad \quad \mathrm{for}\, t\in \big ((k{-}1)\tau ,k\tau \big ], \end{aligned}$$
(25a)
$$\begin{aligned}&\underline{u}_{\mathrm{C}}(t)=u_{\mathrm{C}}^{k-1} \quad \quad \quad \quad \quad \mathrm{for}\, t\in \big [(k{-}1)\tau ,k\tau \big ). \end{aligned}$$
(25b)

Similar notation concerns also \(\overline{z}\) and \(\underline{z}\). A thorough deduction of the boundary forms for these integrals of power, amenable into the boundary element context, is given in Sects. 4.2 and 4.3. Although there is no proof that BTA converges to the global minimum, definitely it leads to solutions of lower energy than those obtained if we used AMA only.

Table 2 Pseudocode of the energy-based backtracking algorithm
Full size table

4.2 Boundary element method

The boundary element method is closely related to the map between the prescribed boundary conditions in displacements or tractions and the unknown boundary displacements or tractions. In pure Dirichlet and Neumann boundary-value problems (BVPs), these maps are called Steklov–Poincaré and Poincaré–Steklov maps [20, 38], respectively, and BEM can be considered as an approach to discretize these maps. In the present computational procedure, the role of the BEM analysis, applied to each subdomain \(\Omega _i\) separately (which, in fact, makes this problem very suitable for parallel computers), is to solve the corresponding BVPs on each \(\Omega _i\). For this goal, we numerically solve the Somigliana displacement identity [35, 38]

$$\begin{aligned} c^i_{ml}(\xi )u^i_m(\xi )+{\int \!\!\!\!\!\!\!\,-}_{\Gamma _i} \ u^i_m(x)T^i_{ml}(x,\xi )\,\mathrm{d}S_x\nonumber \\ {=}\int _{\Gamma _i} p^i_m(x)U^i_{ml}(x,\xi )\,\mathrm{d}S_x, \end{aligned}$$
(26)

where \(\xi \in \Gamma _i=\partial \Omega _i\) and \(u^i_m(x)\) and \(p^i_m(x)\) denote the \(m\)-component of the displacement and traction vector, respectively. The superscript \(i\) used in this section refers to a subdomain \(\Omega _i\) in difference to previous and next sections where it denotes time step. The weakly singular integral kernel \(U^i_{ml}(x,\xi )\), two-point tensor field, given by the Kelvin fundamental solution (free-space Green’s function) represents the displacement at \(x\) in the \(m\)-direction originated by a unit point force at \(\xi \) in the \(l\)-direction in the unbounded elastic medium whose material properties coincide with those of \(\Omega _i\). The strongly singular integral kernel \(T^i_{ml}(x,\xi )\), two-point tensor field, represents the corresponding tractions at \(x\) in the \(m\)-direction. The coefficient-tensor \(c^i_{ml}(\xi )\) of the free-term is a function of the local geometry of the boundary \(\Gamma _i\) at \(\xi \), and may be evaluated by a closed analytical formula for isotropic elastic solids [26]. The symbol \(\int \!\!\!\!\!\!\,-\) in Eq. (26) stands for the Cauchy principal value of an integral.

Consider a discretization of the boundary \(\Gamma _i\) by a boundary element mesh, which is also used to define a suitable discretization of boundary displacements \(u^i(x)\) and tractions \(p^i(x)\) by interpolations of their nodal values. By imposing (collocating) the Somigliana identity (26) at all boundary nodes (called collocation points) we set the BEM system of linear equations for \(\Gamma _i\). The solution of this system defines the unknown nodal values of displacements and tractions along \(\Gamma _i\) representing a part of arrays of all nodal values denoted as \(\mathbf u ^i\) and \(\mathbf p ^i\), respectively. The arrays \(\mathbf u ^i\) and \(\mathbf p ^i\) also include the known nodal values of displacements and tractions along \(\Gamma _i\) given by the prescribed boundary conditions. The BEM system obtained from Eq. (26) is usually written as \(\mathbf H ^i\mathbf u ^i=\mathbf G ^i\mathbf p ^i\) [35]. In our computer implementation of BEM, we employ straight elements with continuous and piecewise linear interpolation for displacements and possibly discontinuous piecewise linear interpolation for tractions.

Then, to compute an approximation of the elastic energy, \({\fancyscript{E}}_{\mathrm{el}}\) in Eq. (6), stored in each bulk \(\Omega _i\), by using the obtained approximations of boundary displacements \(u_m^i\) and of the corresponding boundary tractions \(p_m^i\) along \(\Gamma _i\), we utilize the following general relation [17], assuming zero body forces:

$$\begin{aligned}&{{\fancyscript{E}}}_{\Omega _i} (t,u^i):=\!\left\{ \begin{array}{ll} \displaystyle {\ \!\frac{1}{2}\int _{\Gamma _i}\!\! u^i p^i(u^i) } \displaystyle {\,\mathrm{d}S} &{} \text{ if} \;u^i{=}{u^i_{\text{ D}}}(t) \text{ on}\,{\Gamma ^i_{\mathrm{D}}},\\ \infty &{} \text{ elsewhere,} \end{array}\right. \!\!\!\! \end{aligned}$$
(27)

while the corresponding total potential energy is

$$\begin{aligned} \Pi _{\Omega _i} (t,u^i) ={{\fancyscript{E}}}_{\Omega _i} (t,u^i)-\int _{{\Gamma ^i_{\mathrm{N}}}} u^i {p^i_{\text{ N}}}(t)\,\mathrm{d}S. \end{aligned}$$
(28)

Notice that both Eq. (27) and (28) provide pure boundary expressions of energy. If \({\fancyscript{E}}_{\mathrm{el}}\) in Eq. (5) is replaced by the sum of potential energies \(\Pi _{\Omega _i}\) for all subdomains, the functional \({\fancyscript{E}}\) defined by Eq. (5) will represent the total potential energy of the whole problem.

We will also need to compute integrals of time derivatives of energy, appearing in Table 2, were it is presupposed that displacements on the adhesive contact boundary part \(u_{\mathrm{C}}\) are defined in time steps \(k\) and \(k-1\). In order to do such calculations we need to separate the problem into three different subproblems, in each of them either the adhesive contact or prescribed Dirichlet or Neumann data are defined on the boundary. This separation to subproblems may also serve to express and solve the minimization problem, considering the integral on \({\Gamma }_{\mathrm{C}}\) only.

4.3 Boundary forms of the total potential energy for a single domain

Consider the BVP for a subdomain \(\Omega _i\). In this section we will omit index \(i\), for the sake of simplicity. Let \(u_\eta \) and \(p_\eta \), respectively, denote the displacement and traction solutions of this BVP restricted to \(\Gamma _\eta ,\,\eta =\text{ C},\,\text{ D}\) and \(\text{ N}\), e.g. \(u_{\mathrm{C}}=u|_{{\Gamma }_{\mathrm{C}}}\) and \(p_{\text{ D}}=p|_{{\Gamma _{\mathrm{D}}}}\).We assume here a mixed-type operator \({\fancyscript{M}}\) which formally assigns \((p_{\text{ C}},p_{\text{ D}},u_{\text{ N}})\) to the known boundary data \((u_{\mathrm{C}},u_{\mathrm{D}}(t),p_{\mathrm{N}}(t))\) of the original BVP \(P\) shown in Fig. 3, and may be expressed using the following block structure as:

$$\begin{aligned} \left( \!\begin{array}{l}p_{\text{ C}}\\ p_{\text{ D}}\\ u_{\text{ N}}\end{array}\!\right) = \left( \!\begin{array}{ccc} {\fancyscript{M}}_{\mathrm{CC}}&{}{\fancyscript{M}}_{\text{ CD}}&{}{\fancyscript{M}}_{\mathrm{CN}} \\ {\fancyscript{M}}_{\mathrm{DC}}&{}{\fancyscript{M}}_{\text{ DD}}&{}{\fancyscript{M}}_{\mathrm{DN}}\\ {\fancyscript{M}}_{\mathrm{NC}}&{}{\fancyscript{M}}_{\text{ ND}}&{}{\fancyscript{M}}_{\mathrm{NN}} \end{array}\!\right) \left( \!\begin{array}{l}u_{\mathrm{C}}\\ u_{\mathrm{D}}\\ p_{\mathrm{N}}\end{array} \!\right) . \end{aligned}$$
(29)

The columns of the above defined block operator \({\fancyscript{M}}\) are associated to the subproblems \(P^\eta \) defined in Fig. 3. The displacement solution of a subproblem \(P^\eta \) is denoted as \(u^\eta \). From the principle of superposition the displacement solution of \(P\) may be reconstructed by the sum:

$$\begin{aligned} u=u^{\text{ C}}+u^{\text{ D}}+u^{\text{ N}}\,. \end{aligned}$$
(30)

The total potential energy for the mixed type BVP \(P\) can be written in an expanded form as,

$$\begin{aligned} \Pi =\frac{1}{2}\int _{{\Gamma }_{\mathrm{C}}}\!\! u_{\mathrm{C}}p_{\text{ C}}\mathrm{d}S{+}\frac{1}{2}\int _{{\Gamma _{\mathrm{D}}}}\!\! u_{\mathrm{D}}p_{\text{ D}}\mathrm{d}S {-}\frac{1}{2}\int _{{\Gamma }_{\mathrm{N}}}\!\! u_{\text{ N}}p_{\mathrm{N}}\mathrm{d}S. \end{aligned}$$
(31)

By substituting the unknown data for the problem \(P\) from Eq. (29) the total potential energy writes as

$$\begin{aligned}&\Pi (t,u_{\mathrm{C}})=\frac{1}{2}\left( \int _{{\Gamma }_{\mathrm{C}}}\!\! u_{\mathrm{C}}{\fancyscript{M}}_{\mathrm{CC}}u_{\mathrm{C}}\,\mathrm{d}S {+}\int _{{\Gamma }_{\mathrm{C}}}\!\! u_{\mathrm{C}}{\fancyscript{M}}_{\mathrm{CD}}u_{\mathrm{D}}\,\mathrm{d}S \right. \nonumber \\&\quad +\int _{{\Gamma }_{\mathrm{C}}}\!\! u_{\mathrm{C}}{\fancyscript{M}}_{\mathrm{CN}}p_{\mathrm{N}}\,\mathrm{d}S {+}\int _{{\Gamma _{\mathrm{D}}}}\!\! u_{\mathrm{D}}{\fancyscript{M}}_{\mathrm{DC}}u_{\mathrm{C}}\,\mathrm{d}S \nonumber \\&\quad +\int _{{\Gamma _{\mathrm{D}}}}\!\! u_{\mathrm{D}}{\fancyscript{M}}_{\mathrm{DD}}u_{\mathrm{D}}\,\mathrm{d}S{+}\int _{{\Gamma _{\mathrm{D}}}}\!\! u_{\mathrm{D}}{\fancyscript{M}}_{\mathrm{DN}}p_{\mathrm{N}}\,\mathrm{d}S \nonumber \\&\quad -\int _{{\Gamma }_{\mathrm{N}}}\!\! p_{\mathrm{N}}{\fancyscript{M}}_{\mathrm{NC}}u_{\mathrm{C}}\,\mathrm{d}S{-}\int _{{\Gamma }_{\mathrm{N}}}\!\! p_{\mathrm{N}}{\fancyscript{M}}_{\mathrm{ND}}u_{\mathrm{D}}\,\mathrm{d}S \left. {-}\int _{{\Gamma }_{\mathrm{N}}}\!\! p_{\mathrm{N}}{\fancyscript{M}}_{\mathrm{NN}}p_{\mathrm{N}}\,\mathrm{d}S\right) . \nonumber \\ \end{aligned}$$
(32)

From Eq. (32) it is clear, that since \(u_{\mathrm{D}}(t)\) and \(p_{\mathrm{N}}(t)\) are known, the total potential energy is in fact a function of the contact displacement \(u_{\mathrm{C}}\) only, in addition to be a function of time \(t\). We further modify Eq. (32), in order to hold the unknown variables in the integral on \({\Gamma }_{\mathrm{C}}\) only, by utilizing the second Betti reciprocity relation between the elastic solutions of \(P^{\text{ C}}\) and \(P^{\text{ N}}\),

$$\begin{aligned} \int _{{\Gamma }_{\mathrm{N}}}\!\! p_{\mathrm{N}}{\fancyscript{M}}_{\mathrm{NC}}u_{\mathrm{C}}\,\mathrm{d}S =- \int _{{\Gamma }_{\mathrm{C}}}\!\! u_{\mathrm{C}}{\fancyscript{M}}_{\mathrm{CN}}p_{\mathrm{N}}\,\mathrm{d}S , \end{aligned}$$
(33)

as well as between the solutions of \(P^{\text{ C}}\) and \(P^{\text{ D}}\),

$$\begin{aligned} \int _{{\Gamma _{\mathrm{D}}}}\!\! u_{\mathrm{D}}{\fancyscript{M}}_{\mathrm{DC}}u_{\mathrm{C}}\,\mathrm{d}S = \int _{{\Gamma }_{\mathrm{C}}}\!\! u_{\mathrm{C}}{\fancyscript{M}}_{\mathrm{CD}}u_{\mathrm{D}}\,\mathrm{d}S. \end{aligned}$$
(34)

Then, by substituting Eqs. (33) and (34) into Eq. (32),

$$\begin{aligned}&\Pi (t,u_{\mathrm{C}})= \int _{{\Gamma }_{\mathrm{C}}}\!\! u_{\mathrm{C}}\left( \frac{1}{2}{\fancyscript{M}}_{\text{ CC}}u_{\mathrm{C}}{+}{\fancyscript{M}}_{\mathrm{CD}}u_{\mathrm{D}}{+}{\fancyscript{M}}_{\text{ CN}}p_{\mathrm{N}}\right) \,\mathrm{d}S \nonumber \\&\quad +\frac{1}{2}\int _{{\Gamma _{\mathrm{D}}}}\!\! u_{\mathrm{D}}{\fancyscript{M}}_{\mathrm{DD}} u_{\mathrm{D}}\,\mathrm{d}S{+}\frac{1}{2}\int _{{\Gamma _{\mathrm{D}}}}\!\! u_{\mathrm{D}}{\fancyscript{M}}_{\mathrm{DN}}p_{\mathrm{N}}\,\mathrm{d}S \nonumber \\&\quad -\frac{1}{2}\int _{{\Gamma }_{\mathrm{N}}}\!\! p_{\mathrm{N}}{\fancyscript{M}}_{\mathrm{ND}}u_{\mathrm{D}}\,\mathrm{d}S{-}\frac{1}{2}\int _{{\Gamma }_{\mathrm{N}}}\!\! p_{\mathrm{N}}{\fancyscript{M}}_{\mathrm{NN}}p_{\mathrm{N}}\,\mathrm{d}S. \end{aligned}$$
(35)

The partial time derivative of the total potential energy expression in Eq. (35) writes as

$$\begin{aligned}&\!\!\!\!\!\frac{\partial \Pi }{\partial t} (t,u_{\mathrm{C}})= \int _{{\Gamma }_{\mathrm{C}}}\!\! u_{\mathrm{C}}\big ({\fancyscript{M}}_{\text{ CD}}\dot{u}_{\text{ D}}{+}{\fancyscript{M}}_{\mathrm{CN}}\dot{p}_{\text{ N}}\big ) \,\mathrm{d}S \nonumber \\&\qquad \qquad \qquad \quad +\frac{1}{2}\int _{{\Gamma _{\mathrm{D}}}}\!\! \dot{\overline{u_{\mathrm{D}}{\fancyscript{M}}_{\mathrm{DD}}u_{\mathrm{D}}}} \,\mathrm{d}S {+}\frac{1}{2}\int _{{\Gamma _{\mathrm{D}}}}\!\! \dot{\overline{u_{\mathrm{D}}{\fancyscript{M}}_{\mathrm{DN}}p_{\mathrm{N}}}} \,\mathrm{d}S \nonumber \\&\qquad \qquad \qquad \quad -\frac{1}{2}\int _{{\Gamma }_{\mathrm{N}}}\!\! \dot{\overline{p_{\mathrm{N}}{\fancyscript{M}}_{\mathrm{ND}}u_{\mathrm{D}}}} \,\mathrm{d}S{-}\frac{1}{2}\int _{{\Gamma }_{\mathrm{N}}}\!\! \dot{\overline{p_{\mathrm{N}}{\fancyscript{M}}_{\mathrm{NN}}p_{\mathrm{N}}}} \,\mathrm{d}S,\nonumber \\ \end{aligned}$$
(36)

where the bar with dot denotes the time derivative of the expression below the bar. The integral corresponding to that on the left-hand side in the two-sided inequality in Table 2, can be evaluated using Eq. (36) as,

$$\begin{aligned}&\int _{(k-1)\tau }^{k\tau }\frac{\partial \Pi }{\partial t} (t,u_{\mathrm{C}}^k)\nonumber \\&\quad = \int _{{\Gamma }_{\mathrm{C}}}\!\!\! u_{\mathrm{C}}^{k} \left( {\fancyscript{M}}_{\text{ CD}}u_{\mathrm{D}}^{k}{+}{\fancyscript{M}}_{\mathrm{CN}}p_{\mathrm{N}}^{k} \right) \,\mathrm{d}S \nonumber \\&\qquad {-}\int _{{\Gamma }_{\mathrm{C}}}\!\!\! u_{\mathrm{C}}^{k} \left( {\fancyscript{M}}_{\text{ CD}}u_{\mathrm{D}}^{k-1}{+}{\fancyscript{M}}_{\mathrm{CN}}p_{\mathrm{N}}^{k-1} \right) \,\mathrm{d}S \nonumber \\&\qquad {+}\frac{1}{2}\int _{{\Gamma _{\mathrm{D}}}}\!\!\! u_{\mathrm{D}}^{k} {\fancyscript{M}}_{\mathrm{DD}}u_{\mathrm{D}}^{k} \,\mathrm{d}S{-}\frac{1}{2}\int _{{\Gamma _{\mathrm{D}}}}\!\!\! u_{\mathrm{D}}^{k-1} {\fancyscript{M}}_{\text{ DD}}u_{\mathrm{D}}^{k-1} \,\mathrm{d}S \nonumber \\&\qquad {+}\frac{1}{2}\int _{{\Gamma _{\mathrm{D}}}}\!\!\! u_{\mathrm{D}}^{k} {\fancyscript{M}}_{\mathrm{DN}}p_{\mathrm{N}}^{k} \,\mathrm{d}S{-}\frac{1}{2}\int _{{\Gamma _{\mathrm{D}}}}\!\!\! u_{\mathrm{D}}^{k-1} {\fancyscript{M}}_{\text{ DN}}p_{\mathrm{N}}^{k-1} \,\mathrm{d}S \nonumber \\&\qquad {-}\frac{1}{2}\int _{{\Gamma }_{\mathrm{N}}}\!\!\! p_{\mathrm{N}}^{k} {\fancyscript{M}}_{\mathrm{ND}}u_{\mathrm{D}}^{k} \,\mathrm{d}S{+}\frac{1}{2}\int _{{\Gamma }_{\mathrm{N}}}\!\!\! p_{\mathrm{N}}^{k-1} {\fancyscript{M}}_{\text{ ND}}u_{\mathrm{D}}^{k-1} \,\mathrm{d}S \nonumber \\&\qquad {-}\frac{1}{2}\int _{{\Gamma }_{\mathrm{N}}}\!\!\! p_{\mathrm{N}}^{k} {\fancyscript{M}}_{\mathrm{NN}}p_{\mathrm{N}}^{k} \,\mathrm{d}S{+}\frac{1}{2}\int _{{\Gamma }_{\mathrm{N}}}\!\!\! p_{\mathrm{N}}^{k-1} {\fancyscript{M}}_{\text{ NN}}p_{\mathrm{N}}^{k-1} \,\mathrm{d}S, \end{aligned}$$
(37)

and similarly for the integral on the right-hand side of the two-sided inequality in Table 2,

$$\begin{aligned}&\int _{(k-1)\tau }^{k\tau }\frac{\partial \Pi }{\partial t} (t,u_{\mathrm{C}}^{k-1})\nonumber \\&\quad = \int _{{\Gamma }_{\mathrm{C}}}\!\! u_{\mathrm{C}}^{k-1} \left( {\fancyscript{M}}_{\text{ CD}}u_{\mathrm{D}}^{k}{+}{\fancyscript{M}}_{\mathrm{CN}}p_{\mathrm{N}}^{k} \right) \,\mathrm{d}S \nonumber \\&\qquad {-}\int _{{\Gamma }_{\mathrm{C}}}\!\! u_{\mathrm{C}}^{k-1} \left( {\fancyscript{M}}_{\mathrm{CD}}u_{\mathrm{D}}^{k-1}{+}{\fancyscript{M}}_{\text{ CN}}p_{\mathrm{N}}^{k-1} \right) \,\mathrm{d}S \nonumber \\&\qquad {+}\frac{1}{2}\int _{{\Gamma _{\mathrm{D}}}}\!\! u_{\mathrm{D}}^{k} {\fancyscript{M}}_{\mathrm{DD}}u_{\mathrm{D}}^{k} \,\mathrm{d}S{-}\frac{1}{2}\int _{{\Gamma _{\mathrm{D}}}}\!\! u_{\mathrm{D}}^{k-1} {\fancyscript{M}}_{\text{ DD}}u_{\mathrm{D}}^{k-1} \,\mathrm{d}S \nonumber \\&\qquad {+}\frac{1}{2}\int _{{\Gamma _{\mathrm{D}}}}\!\! u_{\mathrm{D}}^{k} {\fancyscript{M}}_{\mathrm{DN}}p_{\mathrm{N}}^{k} \,\mathrm{d}S{-}\frac{1}{2}\int _{{\Gamma _{\mathrm{D}}}}\!\! u_{\mathrm{D}}^{k-1} {\fancyscript{M}}_{\text{ DN}}p_{\mathrm{N}}^{k-1} \,\mathrm{d}S \nonumber \\&\qquad {-}\frac{1}{2}\int _{{\Gamma }_{\mathrm{N}}}\!\! p_{\mathrm{N}}^{k} {\fancyscript{M}}_{\mathrm{ND}}u_{\mathrm{D}}^{k} \,\mathrm{d}S{+}\frac{1}{2}\int _{{\Gamma }_{\mathrm{N}}}\!\! p_{\mathrm{N}}^{k-1} {\fancyscript{M}}_{\text{ ND}}u_{\mathrm{D}}^{k-1} \,\mathrm{d}S \nonumber \\&\qquad {-}\frac{1}{2}\int _{{\Gamma }_{\mathrm{N}}}\!\! p_{\mathrm{N}}^{k} {\fancyscript{M}}_{\mathrm{NN}}p_{\mathrm{N}}^{k} \,\mathrm{d}S{+}\frac{1}{2}\int _{{\Gamma }_{\mathrm{N}}}\!\! p_{\mathrm{N}}^{k-1} {\fancyscript{M}}_{\text{ NN}}p_{\mathrm{N}}^{k-1} \,\mathrm{d}S. \end{aligned}$$
(38)

For the case where homogeneous boundary conditions are prescribed on \({\Gamma }_{\mathrm{N}}\), i.e. \(p_{\mathrm{N}}=0\), the above equations are simplified further. In such a case the total potential energy will coincide with the elastic strain energy and Eq. (35) takes the form,

$$\begin{aligned} \Pi (t,u_{\mathrm{C}})&= \int _{{\Gamma }_{\mathrm{C}}} u_{\mathrm{C}}\left( \frac{1}{2}{\fancyscript{M}}_{\text{ CC}}u_{\mathrm{C}}{+}{\fancyscript{M}}_{\mathrm{CD}}u_{\mathrm{D}}\right) \,\mathrm{d}S \nonumber \\&+\frac{1}{2}\int _{{\Gamma _{\mathrm{D}}}} u_{\mathrm{D}}{\fancyscript{M}}_{\mathrm{DD}} u_{\mathrm{D}}\,\mathrm{d}S. \end{aligned}$$
(39)

In this case, the time derivative, given by Eq. (36), is written as,

$$\begin{aligned} \frac{\partial \Pi }{\partial t} (t,u_{\mathrm{C}})= \int _{{\Gamma }_{\mathrm{C}}}\!\!u_{\mathrm{C}}\big ({\fancyscript{M}}_{\mathrm{CD}}\dot{u}_{\text{ D}}\big ) \,\mathrm{d}S{+}\frac{1}{2}\int _{{\Gamma _{\mathrm{D}}}}\!\!\dot{\overline{u_{\mathrm{D}}{\fancyscript{M}}_{\mathrm{DD}}u_{\mathrm{D}}}} \,\mathrm{d}S. \end{aligned}$$
(40)

Furthermore, in this case \((p_{\mathrm{N}}=0)\), the lower and upper energy estimates in the two-sided inequality are further simplified as

$$\begin{aligned} \int _{(k-1)\tau }^{k\tau }\!\!\frac{\partial \Pi }{\partial t} (t,u_\mathrm{C}^{k})&= \int _{{\Gamma }_{\mathrm{C}}}\! u_{\mathrm{C}}^{k} \left( {\fancyscript{M}}_{\text{ CD}}u_{\mathrm{D}}^{k}{-}{\fancyscript{M}}_{\mathrm{CD}}u_{\mathrm{D}}^{k-1} \right) \,\mathrm{d}S \nonumber \\&+\frac{1}{2}\int _{{\Gamma _{\mathrm{D}}}}\! (u_{\mathrm{D}}^{k}{-}u_{\mathrm{D}}^{k-1}) \left( {\fancyscript{M}}_{\mathrm{DD}}u_{\mathrm{D}}^{k}{+}{\fancyscript{M}}_{\text{ DD}}u_{\mathrm{D}}^{k-1} \right) \,\mathrm{d}S,\nonumber \\ \end{aligned}$$
(41)

and

$$\begin{aligned}&\int _{(k-1)\tau }^{k\tau }\!\!\frac{\partial \Pi }{\partial t} (t,u_\mathrm{C}^{k-1})\nonumber \\&\quad = \int _{{\Gamma }_{\mathrm{C}}}\! u_\mathrm{C}^{k-1} \left( {\fancyscript{M}}_{\text{ CD}}u_{\mathrm{D}}^{k}{-}{\fancyscript{M}}_{\mathrm{CD}}u_{\mathrm{D}}^{k-1} \right) \,\mathrm{d}S \nonumber \\&\qquad +\frac{1}{2}\int _{{\Gamma _{\mathrm{D}}}}\! (u_{\mathrm{D}}^{k}{-}u_{\mathrm{D}}^{k-1}) \left( {\fancyscript{M}}_{\mathrm{DD}}u_{\mathrm{D}}^{k}{+}{\fancyscript{M}}_{\text{ DD}}u_{\mathrm{D}}^{k-1} \right) \,\mathrm{d}S, \end{aligned}$$
(42)

respectively.

Fig. 3
figure 3

Solution of a mixed BVP \(P\) for a single elastic domain given as a superposition of the solutions of the three subproblems \(P^{\text{ C}},P^{\text{ D}}\) and \(P^{\text{ N}}\)

Full size image

The above formulation assumes the solution of each of the three subproblems in all time steps, while the total response results by their superposition. It is worth mentioning that for proportional external loading, which is separable with respect to spatial coordinates and time, that means

$$\begin{aligned} u_{\mathrm{D}}(t,x)&= \phi (t)\,u_{\mathrm{D}}(x)\ \quad \text{ for} \, x\, \in {\Gamma _{\mathrm{D}}},\end{aligned}$$
(43a)
$$\begin{aligned} p_{\mathrm{N}}(t,x)&= \psi (t)\,p_{\mathrm{N}}(x)\ \quad \text{ for} \, x\, \in {\Gamma }_{\mathrm{N}}, \end{aligned}$$
(43b)

the \(P^{\text{ D}}\) and \(P^{\text{ N}}\) problems need to be solved just once for the first time step, while for the subsequent steps the solutions will be generated by using functions \(\phi \) and \(\psi \) from Eq. (43) as appropriate multipliers.

Summarizing, expressions where the minimizer of the total potential energy is the displacement field defined at the adhesive contact boundary part \({\Gamma }_{\mathrm{C}}\) have been established in this section. Moreover, appropriate formulas for computing the lower and upper energy estimates shown in Table 2 have been given.

4.4 Interface elements

The interconnection of the subdomains as well as the consideration of Signorini kinematical conditions is attained by intermediate elements referred to as interface elements. A local reference system is associated to each interface element defining a normal and a tangential component of relative displacements. In the case of adhesive contact problems of two deformable bodies where only small changes in the geometry are assumed and conforming meshes of elastic domains are considered along the interface, it is possible to incorporate the contact constraints on a purely nodal basis. For a general case of nodes arbitrarily distributed along the possible contact interface between two bodies, which can occur e.g. when automatic meshing is used for two different bodies, further considerations must be taken into account about the definition of Signorini contact conditions, this case not being considered here. The mechanical properties of springs distributed continuously at the interface, are given by their normal and tangential stiffnesses \(\kappa _{\mathrm{n}}\) and \(\kappa _{\mathrm{t}}\), respectively, and additionally in the tangent direction also by the so-called plastic modulus \(\kappa _{\scriptscriptstyle \mathrm H }\) and the factor of influence of damage \(\kappa _{\mathrm{0}}\). The shape functions used to approximate the distribution of variables at interface elements are linear and continuous for the displacements, while for the inelastic variables, \(\zeta \) and \(\pi \), might be constant or (continuous or discontinuous) linear. In addition to the continuous distribution of springs, the interfaces and interface elements may be equipped by a “dissipative mechanism” whose properties are the mode-I fracture energy \(G_{_{{\mathrm{I}} \mathrm{c}}}\) and the critical stress \(\sigma _{\mathrm{t,yield}}\) used in (8).

5 Numerical examples

The above introduced formulation has been implemented in a two-dimensional BEM code [34] using continuous piecewise linear boundary elements [35], and also supplied with all the necessary modules for the EC-BEM, where the acronym EC-BEM refers to the Energetic approach for the solution of adhesive Contact problems by BEM. The geometry of the problem solved is shown in Fig. 4. With reference to Fig. 1, only one subdomain (i.e. \(N=1\)) is used to model in a simple way an experimental test motivated by the pull-push shear test used in engineering practice [10]. Thus, the debonding occurs between the domain and the rigid foundation interface \({\Gamma }_{\mathrm{C}}\).

Fig. 4
figure 4

Problem geometry and boundary conditions

Full size image

The length and height of the rectangular domain \(\Omega \), respectively, are \(L=250\,\)mm and \(h=12.5\) mm. The length of the initially glued part \({\Gamma }_{\mathrm{C}}\) placed at the bottom side of \(\Omega \) is \(L_\mathrm{C}=0.9 L=225\) mm. The isotropic elastic material of the bulk is aluminium with the Young modulus \(E=70\) GPa and the Poisson ratio \(\nu =0.35\). Elastic plain strain state is considered. The material of the adhesive layer is epoxy resin, with elastic properties \(E_a=2.4\,\)GPa and \(\nu _a=0.33\). Assuming the thickness of the adhesive layer \(h_a=0.2\,\)mm, and following [41], the corresponding stiffness parameters are represented by the normal stiffness \(\kappa _\mathrm{n}=\frac{E_a(1-\nu _a)}{h_a(1+\nu _a)(1-2\nu _a)}=\)18 GPa/mm and the tangential stiffness \(\kappa _{\mathrm{t}}=\frac{\kappa _\mathrm{n}(1-2\nu _a)}{2(1-\nu _e)}=\kappa _{\mathrm{n}}/4\). The parameters for the dissipation mechanisms are the mode-I fracture energy \(G_{_{{\mathrm{I}} \mathrm{c}}}=0.01\) J/mm\(^2\) as well as the yield shear stress \(\sigma _{t,\mathrm{yield}}=\)168 MPa. Then, \(\sigma _{n,\mathrm{crit}}=\sqrt{2\kappa _\mathrm{n}G_{_{{\mathrm{I}} \mathrm{c}}}}=\)600 MPa and \(\sigma _{t,\mathrm{crit}}=\sqrt{2\kappa _\mathrm{t}G_{_{{\mathrm{I}} \mathrm{c}}}}=\)300 MPa. Finally, the hardening slope for plastic slip is \(\kappa _{\scriptscriptstyle \mathrm H } =\kappa _{\mathrm{t}}/9\).

5.1 Numerical experimentation

A few sample problem cases are solved in order to illustrate the capabilities of the numerical procedure developed. In Sect. 5.1.1 we experiment with a non-monotonic Dirichlet loading, for a variety of combination of dissipation properties. In the next Sect. 5.1.2 we present results for a monotonic Neumann loading on a modified geometry of the problem in order to avoid the absence of a Dirichlet boundary part especially after the total delamination of the interface. Both examples allow us to illustrate the behaviour of the numerical solution of the present energetic formulation for delamination problems, and do not aim to analyze the problem solutions in a thorough manner. In all the numerical computations, linear continuous elements have been used for the interface displacement and plastic slip variables, also referred to as kinematical variables (\(u,\pi \)), while constant discontinuous elements have been assumed for the damage variable \(\zeta \).

5.1.1 Non-monotonic loading

A hard-device loading is assumed by prescribing cyclic horizontal and vertical displacements, \(u_1(t,x)=\sin (7\,t) w_1(x)\), where \(t \in [0,1]\) while \(w_1\)=1 mm, and \(u_2=0.6 u_1\), respectively, at the right-hand side of the rectangle \(\Gamma \), defining the Dirichlet boundary \({\Gamma _{\mathrm{D}}}\). In accordance with Eq. (43a), \(\phi (t){=}\sin (7\,t)\). All the other boundary parts are considered to be traction free, defining the Neumann boundary \({\Gamma }_{\mathrm{N}}\), except for the adhesive contact surface \({\Gamma }_{\mathrm{C}}\). The boundary \(\Gamma \) is discretized by 64 elements using a uniform boundary element mesh along each side, 27 elements being used for \({\Gamma }_{\mathrm{C}}\). Four combinations of properties of the dissipative mechanism of the adhesive are considered:

  1. (a)

    Absence of any dissipation, leading to a pure adhesive contact problem,

  2. (b)

    Interface plasticity is considered, the damage variable \(\zeta \) being excluded from the minimization procedure,

  3. (c)

    Interface damage is considered, the plastic slip variable \(\pi \) being excluded from the minimization procedure,

  4. (d)

    Both interface damage and plasticity are considered.

Cases (a) and (b) are mainly included for the comparison purposes and also in order to analyse an inelastic response due to interface plasticity. The horizontal resultant force with respect to the displacement on \({\Gamma _{\mathrm{D}}}\) is plotted in Fig. 5. For the case of an inelastic response due to a cyclic loading, a hysteresis cycle appears as expected. Furthermore, for these two cases also the shear stresses with respect to the relative tangential displacements at an interface point \(x_1=208.33\) mm are plotted in Fig. 6, where a typical hysteretic behaviour for the kinematic type hardening plasticity is successfully computed in case (b).

Fig. 5
figure 5

The horizontal resultant force versus the horizontal displacement on \({\Gamma _{\mathrm{D}}}\): (a) pure adhesive contact and (b) interface plasticity included

Full size image
Fig. 6
figure 6

Stress-relative displacement behaviour computed at the interface point \(x_1=208.33\,\)mm of \({\Gamma }_{\mathrm{C}}\): (a) pure adhesive contact and (b) interface plasticity included

Full size image

More complicated behaviour is obtained for cases (c) and (d) where interface damage is included. This may be observed in Figs. 7 and 8 where the horizontal and vertical resultant forces with the respective displacements at \({\Gamma _{\mathrm{D}}}\) are depicted. For these cases upon the first uploading a damage initially appears, for case (c) by breaking one element that corresponds to a crack opening of \(L_{\mathrm{crack}}\,=\,0.037 L_\mathrm{C}=8.33\) mm, while for case (d) in a following time step, by breaking six elements simultaneously which corresponds to a crack opening of \(L_{\mathrm{crack}}=0.22 L_\mathrm{C}=50.0\) mm. For the same time step, that crack initiates in case (d) with a crack opening of \(L_{\mathrm{crack}}=50.0\) mm, for case (c) after some progressive damage propagation, a crack of the same length exists. This behaviour is the expected one, since because of plasticity appearance in case (d), damage delayed to appear in comparison with case (c) where it is assumed that an energy may be released only due to damage. Then, after change of the direction of loading no further damage appears, while plasticity still evolves on the remaining glued part of \({\Gamma }_{\mathrm{C}}\) upon the respective uploading periods. This behavior can be better understood from Fig. 9, where the evolution of the accumulated dissipation with respect to the time \(t\) is shown. In fact, \(t\) is a kind of pseudo-time or process time which can arbitrarily be re-scaled since the considered system is rate-independent. Finally, the evolution of stored energies in the adhesive layer due to opening and shear are shown in Fig. 10.

Fig. 7
figure 7

The horizontal resultant force versus the horizontal displacement on \({\Gamma _{\mathrm{D}}}\): (c) interface damage and (d) both interface damage and plasticity

Full size image
Fig. 8
figure 8

The vertical resultant force versus the vertical displacement on \({\Gamma _{\mathrm{D}}}\): (c) interface damage and (d) both interface damage and plasticity

Full size image
Fig. 9
figure 9

Evolution of the dissipated energies: (c) interface damage and (d) both interface damage and plasticity

Full size image
Fig. 10
figure 10

Evolution of the stored energies in the adhesive for case (d) considering both interface damage and plasticity

Full size image

5.1.2 Traction instead of displacement loading

From an engineering point of view, we are highly interested in the case of external loading given by nonvanishing Neumann boundary conditions. This is because in numerous experiments or real applications, loading is described through external forces, moments or tractions. For these reasons a modified problem configuration shown in Fig. 11 is studied in this section. The length of \({\Gamma }_{\mathrm{C}}\) is \(L_\mathrm{C}=200\) mm, while the homogeneous Neumann boundary parts \({\Gamma }_{\mathrm{N}h}\) on the left and right hand side of \({\Gamma }_{\mathrm{C}}\) have lengths equal to \(0.125 L_\mathrm{C}\). The length and height of \(\Omega \) as well as the material properties are the same as in the previous example. The left vertical side of \(\Omega \) is fixed, defining \({\Gamma _{\mathrm{D}}}\), while uniform normal tractions applied on the right vertical side of \(\Omega \), defining \({{{\Gamma }_{\mathrm{N}}}}_n\), are increasing in time, i.e. \(p_1(t,x)=\psi (t) p_0\) and \(p_2=0\) therein, with \(p_0>0\) being a constant and \(\psi (t)>0\) an increasing function, see Eq. (43b). Both interface damage and plasticity are considered.

Fig. 11
figure 11

Modified geometry and boundary conditions used for the problem with prescribed non-zero tractions

Full size image

The evolution of the horizontal resultant force on \({\Gamma }_{\mathrm{N}n}\) is plotted in Fig. 12. The computational analysis, including BTA together with the two-sided energy inequality checking, stops at a point, marked in Fig. 12 as point (L), where after some plasticity development the first and at the same time the total damage of the adhesive layer occurs. A dashed line in the same plot represents the tangent line to the initial purely elastic part of the resultant force-displacement curve. Both lines separate due to the appearance of some plastic slip at \({\Gamma }_{\mathrm{C}}\). To capture a progressive damage propagation along \({\Gamma }_{\mathrm{C}}\) would require decreasing the applied load after the peak load is achieved.

Fig. 12
figure 12

The horizontal resultant force on \({{\Gamma }_{\mathrm{N}n}}\) versus the horizontal displacement of the lower right corner of \(\Omega \)

Full size image

Finally, in order to analyse the pointwise behaviour of the numerical solution at \({\Gamma }_{\mathrm{C}}\), in particular regarding the evolution of plastic slip, the same problem is solved again but including interface plasticity only, i.e. no damage at \({\Gamma }_{\mathrm{C}}\) is possible. Numerically computed shear stress versus the relative tangential displacement at the rightmost node of \({\Gamma }_{\mathrm{C}}\) is shown in Fig. 13, together with the expected tangential stress-relative displacement law of Fig. 2. An “overshooting” phenomenon takes place when plasticity occurs, a similar behaviour may also be observed in Fig. 6. This phenomenon is essentially associated to the time and spatial discretization of the problem, in particular possibly due to some oscillations of the traction solution near the crack tip, and therefore can gradually be eliminated by a spatial discretization refinement as observed in Fig. 13.

5.2 Practical application

The problem configuration shown in Fig. 4 is considered again. A monotonic hard-device loading is assumed by prescribing horizontal and vertical displacements, respectively, as \(u_1(t,x)=t\,w_1(x)\) with \(w_1(x)=0.6\)mm and \(u_2(t,x)=0.6u_1(t,x)\) at the right-hand side of the rectangle \(\Gamma \), defining the Dirichlet boundary \({\Gamma _{\mathrm{D}}}\). All the other boundary parts are considered to be traction free, defining the Neumann boundary \({\Gamma }_{\mathrm{N}}\), except for the adhesive contact surface \({\Gamma }_{\mathrm{C}}\). The problem evolution is represented as a function of the pseudo- time \(t\).

Fig. 13
figure 13

Shear stress-relative tangential displacement relation as computed at the rightmost point of the interface \({\Gamma }_{\mathrm{C}}\). For this case, only plasticity is considered, damage being excluded

Full size image

An advantage of the present method considering a continuous distribution of springs along the interface in comparison with the classical fracture mechanics, which assumes a perfect interface except for some cracked zones, is that no special mesh refinement is needed near the crack tip and a uniform mesh can be employed along \({\Gamma }_{\mathrm{C}}\), similarly as in the Cohesive Zone Models, see [18] and further references therein. The tractions along the adhesive layer of the present type are bounded although traction concentrations can be expected at the end-points of the adhesive layer, which may correspond to crack tips, cf. [23, 40]. Actually, in the present model, these tractions are limited by the critical values of normal and tangential tractions \(\sigma _{n,\mathrm{crit}}\) and \(\sigma _{t,\mathrm{crit}}\), respectively. If the adhesive layer at \({\Gamma }_{\mathrm{C}}\) in the present problem in Fig. 4 would be replaced by perfect bonding conditions, stress singularities would appear at both extremes of the bonded part \({\Gamma }_{\mathrm{C}}\). The stress singularity at the right extreme of \({\Gamma }_{\mathrm{C}}\), corresponding to the classical oscillatory singularity of the open model of an interface crack between an elastic and an infinitely rigid solid, cf. [44], would be more severe than that at the left extreme. In such a case, a strongly refined mesh or special singular elements would be needed for a proper problem discretization of the crack tip neighbourhood. It should be mentioned here that intuitive refinement without having rigorous local error indicators is sometimes dangerous and may destroy convergence which is standardly guaranteed on uniformly refined meshes only.

Nevertheless, in the present model, the fact that a local mesh refinement at the crack tip is not needed makes easy the modeling of damage progression with the crack tip moving along the interface. In order to check this statement, we have solved the problem in Fig. 4 by using a series of uniform boundary element meshes, the three finest meshes having 126 (60 and 3 elements along each horizontal and vertical side, respectively), 252 and 504 elements on \(\Gamma \) (that corresponds to 54, 108 and 216 elements on \({\Gamma }_{\mathrm{C}}\)). The traction solutions along \({\Gamma }_{\mathrm{C}}\) for these three finest meshes shown in Fig. 14 correspond to horizontal prescribed displacement \(u_1=0.28\)mm, when no damage appears although some interface plasticity has evolved. A strong traction concentration at the right extreme of \({\Gamma }_{\mathrm{C}}\) can be observed in these plots which, however, indicate that even for the coarsest mesh (54 elements on \({\Gamma }_{\mathrm{C}}\)) the solution obtained is sufficiently accurate for the purpose of the present study. An additional checking is shown in Fig. 15, where the percentage differences of the computed strain energy in the bulk, the computed total energy (that is the sum of the stored energy and the dissipated energy at time \(t,\,{\fancyscript{E}}(t,u(t),z(t))+\mathrm{Diss}_{\mathcal{R }}(z;[0,t]\)), see (2), and the maximum absolute value of normal tractions at \({\Gamma }_{\mathrm{C}}\) computed by a coarse mesh and the finest mesh (216 elements on \({\Gamma }_{\mathrm{C}}\)) are plotted. These plots confirm that the percentage difference of the strain energy and of the maximum normal traction for the mesh with 54 elements on \({\Gamma }_{\mathrm{C}}\) is sufficiently small, in particular it is about 1 %. Therefore, this mesh is used in the following complete numerical study of the present problem.

Fig. 14
figure 14

a Normal and b tangent tractions along the adhesive zone \({\Gamma }_{\mathrm{C}}\), for the three finest uniform boundary element meshes, \(n\) the number of boundary elements at \({\Gamma }_{\mathrm{C}}\)

Full size image
Fig. 15
figure 15

Percentage difference of a the total energy, b the elastic strain energy and c the maximum normal tractions at the adhesive zone \({\Gamma }_{\mathrm{C}}\), for uniform, along the horizontal and vertical edges, boundary element meshes

Full size image

Figure 16 shows the evolution of different energies computed, in particular, the energy stored in the elastic bulk, in the adhesive layer and the dissipated energy. Also the total energy, which is actually minimized in the time stepping procedure, together with the lower and upper estimates of energy are shown. As it can be seen in Fig. 16, the global minimization procedure defines the end of the delamination process, where the remaining undamaged part of the adhesive layer is debonded, as the point where the sum of the stored energy in the bulk and the adhesive layer is basically equal to the energy needed to delaminate the undamaged part of the adhesive layer, which is given by the dissipated energy in the last time step. In Fig. 17, the deformed shape of the bulk, is plotted for two time steps, just before and after the first damage, respectively.

Fig. 16
figure 16

Evolution of the energies

Full size image
Fig. 17
figure 17

Deformed shape of the elastic domain for two time steps, just before and after damage initiation. A scale factor of 150 has been used

Full size image

Figures 18 and 19 present the normal and tangential tractions vector along the adhesive zone \({\Gamma }_{\mathrm{C}}\). A very good agreement exists between the computed tractions for each subdomain by BEM and those computed in the adhesive layer, although the equilibrium has not been imposed directly but it results as a consequence of the energy minimization. Progressive extension of the traction free portion of the original \({\Gamma }_{\mathrm{C}}\) because of the damage propagation (\(\zeta =0\)) can be observed in Figs. 18(b) and 19(b). It should be mentioned that the portion of \({\Gamma }_{\mathrm{C}}\) which is totally damaged is still kept as a part of the minimization procedure, where nodal displacement values participate as unknowns in the minimization procedure and their values are used in the BEM solution of the pertinent BVP. For this reason, in fact an approximation of the developed traction-free zone is computed by BEM for each subdomain. Obviously other algorithms might be used where after the total damage of a portion of the adhesive layer a switch in the type of the boundary condition (e.g. from Dirichlet to vanishing Neumann boundary condition) is taken into account along this boundary portion in the BEM computation for each subdomain. Nevertheless, we have been interested in the results obtained by the present simple procedure. Normal compressive tractions computed by BEM can be observed in Fig. 18 in zones where vanishing normal tractions are obtained in the interface elements. This is due to the fact that the rigid obstacle undertakes these compressive tractions.

Fig. 18
figure 18

Normal tractions along the adhesive zone \({\Gamma }_{\mathrm{C}}\), just a before and b after the first crack opening, computed by BEM as well as in the interface elements

Full size image
Fig. 19
figure 19

Tangential tractions along the adhesive zone \({\Gamma }_{\mathrm{C}}\), just a before and b after the first crack opening, computed by BEM as well as in the interface elements

Full size image

Finally, in Fig. 20 the resultant forces acting at \({\Gamma _{\mathrm{D}}}\) versus the pseudo-time \(t\) are shown. These two plots have some similarities in the behaviour that may come up through the characteristic points (A)–(E). Up to point (A) the linear elastic behaviour manifests in both the solid and adhesive, at this point a plastic slip appears. Then, at point (B) the first damage appears in the first 11 boundary elements that are situated on the right-hand side of the adhesive layer. This new crack length results in a “jump down” of the resultant forces up to point (C). Then, up to point (D) the damaged zone is progressively extended and finally after point (D) the remaining adhesive zone is damaged instantaneously. The problem evolution ends up at point (E), where a rigid body motion of the elastic body takes place. The increment of the crack length from point (B) to (C) equals 45.83 mm. In the same figures also the linear elastic responses, obtained for the same configuration taking into account only adhesive contact without any interface damage and plasticity, are plotted in order to facilitate the observation of the initiation of plasticity and/or damage.

Fig. 20
figure 20

Evolution of a the horizontal and b vertical resultant force on \({\Gamma _{\mathrm{D}}}\)

Full size image

6 Conclusions

A boundary element implementation of a computational procedure based on an energetic-solution framework for the delamination problems has been presented. A specific model for the adhesive interfaces, which distinguishes the amount of energy dissipated in opening Mode I and shear Mode II has been adopted. This model involves two inelastic internal variables on delaminating surfaces, namely the damage variable \(\zeta \) and the plastic slip \(\pi \). Some details regarding the formulation of the collocation BEM as well as the optimization procedures necessary for solving the global minimization problem, inherent in the formulation, have been discussed. A few numerical tests have been presented in order to analyse the behaviour of the present delamination model and performance of the algorithms implemented in a collocational BEM code.