Crack propagation using the continuum strong discontinuity approach by the BEM: some numerical remarks

Abstract

Some numerical remarks regarding the crack evolution in failure analysis by the BEM using cells with embedded strong discontinuities are addressed in this work. A comparative study between the generation of these cells at any iteration or only after a step convergence is firstly performed. Moreover, an analysis is carried out related to the cells size growth throughout the iterative-incremental process. As reference, some classical problems whose experimental results are available in the literature are used for the numerical analysis which is performed considering the implicit formulation of the boundary element method together with the continuum strong discontinuity approach. It was verified that the results are coincident for different numbers of steps considered in the simulations when cells are generated during any iteration, showing step size independence in this case, while the same is not true for the case of cells generated only after step convergence, in which a large number of steps are required for a good accuracy. Finally, it is shown that a small increase in cell size throughout the analysis contributes to the reduction in numerical processing time without significantly affecting the results accuracy.

1 Introduction

The progress in the development of computational resources in recent years has led to an increase in the use of numerical methods in engineering. In this sense, the numerical study of material failure has been one of the most prominent areas, since analytical solutions are limited to simple cases and experimental tests are usually expensive and laborious. Moreover, this kind of study is of great importance in the design and avaliation of several types of structures, since it allows a determination of the post-critical behaviour, contributing to the establishment of techniques to predict structural collapse. In this context, the boundary element method (BEM), which presents some advantages when compared to classical domains methods, has assumed a prominent role, mainly after the development of the so-called Dual BEM [24, 25]. In this method, cracks are treated as part of the boundary, which increases during propagation. Another way to address loss of strength is to consider a total or partial domain discretization by internal cells, where the inelastic fields are interpolated, as for example in [2, 4,5,6,7, 20, 27]. More recently, the continuum strong discontinuity approach (CSDA) originally introduced by [26] was used in BEM analyses by the adoption of cells with embedded discontinuities as in [9,10,11, 23].

In the CSDA, a kinematics characterized by the presence of finite discontinuities in the displacement field is considered and, consequently, infinite discontinuities in the strain field are obtained. In this way, it is shown that continuous constitutive models, equipped with a strain softening law, are compatible with the kinematics of strong discontinuities and thus induce a discrete constitutive model on the discontinuous surface [14, 18]. Later on, in [12] and [13], a more rigorous detailing of the process of identifying the characteristics that make conventional continuous constitutive models consistent with the strong discontinuity regime was carried out. In addition, a more general numerical treatment with the finite element method, using isotropic damage and elastoplastic models, to show that the analysis methodology is easily extended to any constitutive model was considered.

In many cases, the strong discontinuity kinematics can be induced directly after the elastic regime. However, in other cases, it becomes necessary to consider an intermediate phase when the so-called strong discontinuity conditions are not met at the moment of bifurcation which is characterized by the inception of a strain localization zone. These conditions consist of a set of equations necessary for the adequation of the continuous constitutive model to the strong discontinuity regime. In this case, a transitional phase between the bifurcation and the strong discontinuity, based on weak discontinuity kinematics, is considered in the works of [8, 15, 16, 21]. This kinematics is characterized by continuous displacements fields and the presence of finite discontinuities in the strain field. In addition, these works also take into account a regularized kinematics capable of representing both (weak and strong) kinematics through a single set of equations, where a variable bandwidth model is introduced. It is shown that this methodology is more suitable to represent the regions of the fracture process zone.

Despite the CSDA have been extensively explored in finite element analyses, its application with boundary elements remains limited to few works, deserving further study on some points. In this sense, [10] and [11] considered constant triangular cells with embedded discontinuity and used associative elastoplastic constitutive models with a specific yield criterion, together with an exponential softening law, to represent the behaviour of cracks in quasi-brittle materials. In [9], the same idea of these works was adopted, however, using an isotropic damage model and a cells generation algorithm to follow the crack path. Also, the strong discontinuity was imposed directly after the end of the elastic regime with the discontinuity line direction defined as perpendicular to the maximum principal stress. Moreover, in [23], quadrilateral cells were used together with another automatic cells generation algorithm. Besides that, in [9] the cell generation occurs only after step convergence while that in [23], the generation is allowed at any iteration inside the steps.

In this article, a material failure analysis is performed through the implicit formulation of the boundary element method using the continuum strong discontinuity approach that was implemented in the INSANE software (INteractive Structural ANalysis Environment) through the work of [23]. In this work, the cell generation was performed at any iteration, which is not the most adequate procedure from the numerical point of view since it is associated to an unbalanced state. Such strategy was adopted due to the previous lack of knowledge of the progression rate of the crack during the analysis and for believing that for monotonic loads this would not be a problem. Therefore, in this article we seek to evaluate the accuracy and efficiency of this methodology comparing the cell generation at any iteration with the generation only after step convergence of the nonlinear analysis. Thus, considering these two cases, two classical problems in the literature with monotonic load are analysed using an automatic cell generation algorithm. Furthermore, a study on the cells size growth throughout the iterative-incremental process is also carried out which, in turn, has not been addressed in previous works. Being thus, step size independence with satisfactory results is observed for cell generation at any iteration while a large number of steps are required for better accuracy when cells are generated only after step convergence. Finally, it is shown that a small increase in cell size throughout the analysis contributes to the reduction in numerical processing time without relevant impact on the results accuracy.

2 Integral equations for problems with strong discontinuities

2.1 Strong discontinuity kinematics

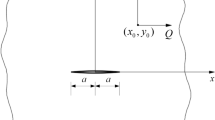
A strong discontinuity kinematics capable to distribute the effects of the discontinuous surface on a finite region of the domain is presented. Thus, with reference to Fig. 1, a subdomain $\varOmega _{\varphi }$ is defined around the discontinuity line ${\mathcal {S}}$ and contained in the domain $\varOmega$. In this case, the discontinuity is inserted during the analysis according to a predefined criterion as described further in Sect. 4.4.

Fig. 1

Discontinuous surface contained in an arbitrary subdomain $\varOmega _{\varphi }$

Also, it is defined a continuous and arbitrary function, $\varphi ({\mathbf {X}})$, in $\varOmega _{\varphi }({\mathbf {X}})$, such that $\varphi ({\mathbf {X}})=0$ in $\varOmega ^{-} \backslash \varOmega _{\varphi }^{-}$ and $\varphi ({\mathbf {X}})=1$ in $\varOmega ^{+} \backslash \varOmega _{\varphi }^{+}$. In this case, the expression $a \backslash b$ means the domain a excluding the domain b, that is, $a \backslash b = a-(a \cap b)$ and, besides this, the material points are designated by ${\mathbf {X}}$. Thus, the following equation can be defined:

$$\begin{aligned} \begin{aligned} {\dot{u}}_i({\mathbf {X}}, t)&=\underbrace{\dot{\bar{u}}_i({\mathbf {X}}, t) + \varphi ({\mathbf {X}})[\![ {\dot{u}}_i]\!] ({\mathbf {X}},t)}_{{\dot{\hat{u}}}_{i}({\mathbf {X}},t)} + \underbrace{[{\mathcal {H}}_{{\mathcal {S}}}({\mathbf {X}})-\varphi ({\mathbf {X}})]}_{{\mathcal {M}}_{{\mathcal {S}}}^{\varphi }({\mathbf {X}})}[\![ {\dot{u}}_i]\!] ({\mathbf {X}}, t) \\&= {\dot{\hat{u}}}_{i}({\mathbf {X}},t) + {\mathcal {M}}_{{\mathcal {S}}}^{\varphi }({\mathbf {X}})[\![ {\dot{u}}_i]\!] ({\mathbf {X}},t) \end{aligned} \end{aligned}$$

(1)

where the terms $\dot{\bar{u}}_i({\mathbf {X}}, t)$, $[\![ {\dot{u}}_{i}]\!] ({\mathbf {X}},t)$ and ${\mathcal {H}}_{{\mathcal {S}}}({\mathbf {X}})$ represent, respectively, the displacement field regular part components, the displacement jumps components on the discontinuity surface ${\mathcal {S}}$ and the Heaviside function (${\mathcal {H}}_{{\mathcal {S}}}=1$ for ${\mathbf {X}} \in \varOmega ^{+}$ and ${\mathcal {H}}_{{\mathcal {S}}}=0$ for ${\mathbf {X}} \in \varOmega ^{-}$). In addition, ${\dot{\hat{u}}}_{i}({\mathbf {X}},t)$ are continuous functions and ${\mathcal {M}}_{{\mathcal {S}}}^{\varphi }({\mathbf {X}})$ has null value for all ${\mathbf {X}}$ in $\varOmega$, except for ${\mathbf {X}} \in \varOmega _{\varphi }$.

Therefore, with the kinematic defined by Eq. (1) the essential boundary conditions (prescribed displacements) can be applied exclusively to the terms ${\dot{\hat{u}}}_{i}$, since $\varGamma _{u}~\cap ~\varOmega _{\varphi }~=~0$, provided that $\varGamma _{u}$ represents the region of the boundary where the essential boundary conditions are applied.

The strains are given by the symmetric part of the gradient of Eq. (1), that is:

$$\begin{aligned} \begin{aligned} {\dot{\epsilon }}_{ij}({\mathbf {X}}, t)&= \underbrace{\frac{1}{2}\left( {\dot{\hat{u}}}_{i,j}+{\dot{\hat{u}}}_{j,i}\right) }_{\dot{{\hat{\epsilon }}}_{ij}}+ \underbrace{\frac{{\mathcal {M}}_{{\mathcal {S}}}^{\varphi }}{2}\left( [\![ {\dot{u}}_{i,j}]\!] +[\![ {\dot{u}}_{j,i}]\!] \right) -\frac{1}{2}\left( \varphi _{,i}[\![ {\dot{u}}_{j}]\!] +\varphi _{,j}[\![ {\dot{u}}_{i}]\!] \right) }_{-{\dot{\epsilon }}_{ij}^{\varphi }} \\&\quad +\,\frac{\delta _{{\mathcal {S}}}}{2}\left( [\![ {\dot{u}}_{i}]\!] n_{j}+[\![ {\dot{u}}_{j}]\!] n_{i}\right) \\&= \dot{{\hat{\epsilon }}}_{ij} - {\dot{\epsilon }}_{ij}^{\varphi } + \frac{\delta _{{\mathcal {S}}}}{2}\left( [\![ {\dot{u}}_{i}]\!] n_{j}+[\![ {\dot{u}}_{j}]\!] n_{i}\right) \end{aligned} \end{aligned}$$

(2)

where the term ${\dot{{\hat{\epsilon }}}}_{ij}$ represents the strain field regular portion and the term ${{\dot{\epsilon }}}_{ij}^{\varphi }$ has nonzero values only in $\varOmega _{\varphi }$.

2.2 Integral equations with discontinuities

The boundary value problem for a solid medium with the presence of a discontinuity surface ${\mathcal {S}}$ is represented by the following equations:

$$\begin{aligned}&{\dot{\sigma }}_{ij,j} + \dot{b}_{i} = 0 \quad \text {for}\,\,\,{\mathbf {X}} \in \varOmega \backslash {\mathcal {S}} \end{aligned}$$

(3)

$$\begin{aligned}&{\dot{\sigma }}_{ij}^{+}n_{j} - {\dot{\sigma }}_{ij}^{-}n_{j} = 0 \quad \text {for}\,\,\,{\mathbf {X}} \in {\mathcal {S}} \end{aligned}$$

(4)

$$\begin{aligned}&{\dot{\sigma }}_{ij}^{+}n_{j} - {\dot{\sigma }}_{ij}^{{\mathcal {S}}}n_{j} = {\dot{\sigma }}_{ij}^{-}n_{j} - {\dot{\sigma }}_{ij}^{{\mathcal {S}}}n_{j} = 0 \quad \text {for} \quad {\mathbf {X}} \in {\mathcal {S}} \end{aligned}$$

(5)

$$\begin{aligned}&{\dot{\epsilon }}_{ij} - \frac{1}{2}({\dot{u}}_{i,j} + {\dot{u}}_{j,i}) = 0 \quad \text {for}\,\,\,{\mathbf {X}} \in \varOmega \end{aligned}$$

(6)

$$\begin{aligned}&{\dot{\sigma }}_{ij} = {\dot{\sigma }}_{ij}^{{\mathcal {S}}}({\dot{\epsilon }}_{ij}) \quad \text {for}\,\,\,{\mathbf {X}} \in {\mathcal {S}} \end{aligned}$$

(7)

$$\begin{aligned}&{\dot{\sigma }}_{ij} = {\dot{\sigma }}_{ij}^{\varOmega \backslash {\mathcal {S}}}({\dot{\epsilon }}_{ij}) = E_{ijkl}^{o}{\dot{\epsilon }}_{kl} \quad \text {for} \,\,\, {\mathbf {X}} \in \varOmega \backslash {\mathcal {S}} \end{aligned}$$

(8)

$$\begin{aligned}&{\dot{\hat{u}}}_{i} = {\dot{\mathbb {u}}}_{i} \quad \text {for} \,\,\, {\mathbf {X}} \in \varGamma _{u} \end{aligned}$$

(9)

$$\begin{aligned}&{\dot{\sigma }}_{ij}n_{j} = {\dot{\mathbb {t}}}_{i} \quad \text {for} \,\,\, {\mathbf {X}} \in \varGamma _{\sigma } \end{aligned}$$

(10)

Equations (3) to (10) represent internal equilibrium, surface forces external continuity, surface forces internal continuity, kinematic compatibility, the constitutive compatibility in ${\mathcal {S}}$, the constitutive compatibility in $\varOmega \backslash {\mathcal {S}}$, the essential boundary conditions and the natural boundary conditions, respectively. In these expressions, the terms $\dot{b}_{i}$, ${\dot{\sigma }}_{ij}^{+}$, ${\dot{\sigma }}_{ij}^{-}$, ${\dot{\sigma }}_{ij}^{{\mathcal {S}}}$, ${\dot{\sigma }}_{ij}^{{\varOmega \backslash\mathcal {S}}}({\dot{\epsilon }}_{ij})$, ${\dot{\mathbb {u}}}_{i}$ and ${\dot{\mathbb {t}}}_{i}$ represent the rates of: body forces, stresses in $\varOmega ^{+}$, stresses in $\varOmega ^{-}$, stresses in ${\mathcal {S}}$, an appropriate continuous constitutive relation, prescribed displacements and prescribed surface forces, respectively. In addition, in Eq. (9), as mentioned previously, $\varGamma _{u}$ is the boundary region where the displacements are prescribed and $\varGamma _{\sigma }$, in Eq. (10), is the boundary region where surface forces are prescribed. It should also be noted, through Eq. (8), that a linear constitutive relation is considered for $\varOmega \backslash {\mathcal {S}}$ despite the effects of the strong discontinuity kinematics have been numerically distributed in the subdomain $\varOmega _{\varphi }$.

The constitutive relation presented in Eqs. (7) and (8) can be rewritten, after applying Eq. (2), as follows:

$$\begin{aligned} {\dot{\sigma }}_{ij}^{{\mathcal {S}}}({\dot{\epsilon }}_{ij}) &= {\dot{\sigma }}_{ij}^{{\mathcal {S}}}\left( \dot{{\hat{\epsilon }}}_{ij},[\![ {\dot{u}}_{i}]\!] ,[\![ {\dot{u}}_{i,j}]\!] \right) \end{aligned}$$

(11)

$$\begin{aligned} {\dot{\sigma }}_{ij}^{\varOmega \backslash {\mathcal {S}}}({\dot{\epsilon }}_{ij}) &=E_{ijkl}^{o}{\dot{\epsilon }}_{kl} = E_{ijkl}^{o} \left[ \dot{{\hat{\epsilon }}}_{kl} - {\dot{\epsilon }}_{kl}^{\varphi }\left( [\![ {\dot{u}}_{i}]\!] ,[\![ {\dot{u}}_{i,j}]\!] \right) \right] \end{aligned}$$

(12)

where the arbitrariness of the function $\varphi ({\mathbf {X}})$ and the material character of ${\mathcal {S}}$ were considered, that is, once the orientation of an discontinuity surface increment is established, it becomes fixed throughout the analysis.

In addition, from Eqs. (2) and (12) one can write:

$$\begin{aligned} {\dot{\sigma }}_{ij}^{\varOmega \backslash {\mathcal {S}}} = E_{ijkl}^{o}{\dot{\hat{u}}}_{k,l} - E_{ijkl}^{o}{\dot{\epsilon }}_{kl}^{\varphi } \end{aligned}$$

(13)

where the symmetries associated to the regime of small strains in isotropic media were taken into account.

Therefore, a first integral formulation of this problem can be obtained on the basis of the following weighted residues equation, that is:

$$\begin{aligned} \begin{aligned}&\int _{\varOmega \backslash {\mathcal {S}}}^{} \left( {\dot{\sigma }}_{ij,j}^{\varOmega \backslash {\mathcal {S}}} + \dot{b}_{i}\right) u_{i}^{*} \text {d}\varOmega + \int _{{\mathcal {S}}}^{} n_{j}\left( {\dot{\sigma }}_{ij}^{+} - {\dot{\sigma }}_{ij}^{-}\right) u_{i}^{*} \text {d}\varGamma \\&\quad + \int _{\varGamma _{\sigma }}^{} \left( {\dot{\mathbb {t}}}_{i} - \dot{t}_{i}\right) u_{i}^{*} \text {d}\varGamma + \int _{\varGamma _{u}}^{} \left( {\dot{u}}_{i} - {\dot{\mathbb {u}}}_{i}\right) t_{i}^{*} \text {d}\varGamma = 0 \end{aligned} \end{aligned}$$

(14)

where $u_{i}^{*}$ and $t_{i}^{*}$ represent weighted fields which, for the time being, are arbitrary.

In this way, based on Eq. (14), and considering also Eq. (13), we arrive at the integral governing equations of the boundary value problem (for more details, see [23]), that is:

$$\begin{aligned}{\dot{\hat{u}}}_{i}({\varvec{\xi }}) &= \int _{\varGamma }^{} u_{ij}^{*}({\varvec{\xi }},{\mathbf {X}})\dot{t}_{j}({\mathbf {X}}) \text {d}\varGamma ({\mathbf {X}}) - \int _{\varGamma }^{} t_{ij}^{*}({\varvec{\xi }},{\mathbf {X}}){\dot{\hat{u}}}_{j}({\mathbf {X}}) \text {d}\varGamma ({\mathbf {X}}) \nonumber \\&\quad + \int _{\varOmega }^{} u_{ij}^{*}({\varvec{\xi }},{\mathbf {X}})\dot{b}_{j}({\mathbf {X}}) \text {d}\varOmega ({\mathbf {X}}) + \int _{\varOmega }^{} \sigma _{ijk}^{*}({\varvec{\xi }},{\mathbf {X}}){\dot{\epsilon }}_{jk}^{\varphi }({\mathbf {X}}) \text {d}\varOmega ({\mathbf {X}}) \end{aligned}$$

(15)

$$\begin{aligned}c_{ij}({\varvec{\xi }}){\dot{\hat{u}}}_{i}({\varvec{\xi }})& = \int _{\varGamma }^{} u_{ij}^{*}({\varvec{\xi }},{\mathbf {X}})\dot{t}_{j}({\mathbf {X}}) \text {d}\varGamma ({\mathbf {X}}) - \int _{\varGamma }^{} t_{ij}^{*}({\varvec{\xi }},{\mathbf {X}}){\dot{\hat{u}}}_{j}({\mathbf {X}}) \text {d}\varGamma ({\mathbf {X}}) \nonumber \\&\quad + \int _{\varOmega }^{} u_{ij}^{*}({\varvec{\xi }},{\mathbf {X}})\dot{b}_{j}({\mathbf {X}}) \text {d}\varOmega ({\mathbf {X}}) + \int _{\varOmega }^{} \sigma _{ijk}^{*}({\varvec{\xi }},{\mathbf {X}}){\dot{\epsilon }}_{jk}^{\varphi }({\mathbf {X}}) \text {d}\varOmega ({\mathbf {X}}) \end{aligned}$$

(16)

$$\begin{aligned}\dot{{\hat{\epsilon }}}_{ij}({\varvec{\xi }}) &= \int _{\varGamma }^{} u_{ijk}^{*}({\varvec{\xi }},{\mathbf {X}})\dot{t}_{k}({\mathbf {X}}) \text {d}\varGamma ({\mathbf {X}}) - \int _{\varGamma }^{} t_{ijk}^{*}({\varvec{\xi }},{\mathbf {X}}){\dot{\hat{u}}}_{k}({\mathbf {X}}) \text {d}\varGamma ({\mathbf {X}}) \nonumber \\&\quad + \int _{\varOmega }^{} u_{ijk}^{*}({\varvec{\xi }},{\mathbf {X}})\dot{b}_{k}({\mathbf {X}}) \text {d}\varOmega ({\mathbf {X}}) + \int _{\varOmega }^{} \sigma _{ijkl}^{*}({\varvec{\xi }},{\mathbf {X}}){\dot{\epsilon }}_{kl}^{\varphi }({\mathbf {X}}) \text {d}\varOmega ({\mathbf {X}})\nonumber \\&\quad + F_{ijkl}^{\epsilon \epsilon }{\dot{\epsilon }}_{kl}^{\varphi }({\varvec{\xi }}) \end{aligned}$$

(17)

In Eqs. (15–17), the tensors $u_{ij}^{*}({\varvec{\xi }}, {\mathbf {X}})$, $t_{ij}^{*}({\varvec{\xi }}, {\mathbf {X}})$ and $\sigma _{ijk}^{*}({\varvec{\xi }}, {\mathbf {X}})$ are the Kelvin’s fundamental solutions and represent, respectively, displacements and surface forces in the j direction and jk stress components, at a field point ${\mathbf {X}}$, due to a concentrated unit load at the source point ${\varvec{\xi }}$ applied in the i direction. Already the tensors $u_{ijk}^{*}({\varvec{\xi }}, {\mathbf {X}})$, $t_{ijk}^{*}({\varvec{\xi }}, {\mathbf {X}})$ and $\sigma _{ijkl}^{*}({\varvec{\xi }}, {\mathbf {X}})$ represent the Kelvin’s fundamental solutions derivatives with respect to the source point ${\varvec{\xi }}$ and the terms $F_{ijkl}^{\epsilon \epsilon }$ and $c_{ij}({\varvec{\xi }})$ are free terms associated with particular analytical integrations.

2.3 Equilibrium equation of the discontinuous interface

The integral equations presented in Sec. 2.2 do not completely define the boundary value problem, since the internal continuity condition of the surface forces [Eq. (5)] is not met. Therefore, this condition is imposed separately, as in [19], adopting the strong form of the equation.

Initially we note that Eq. (5) is equivalent to the following equation:

$$\begin{aligned} t_{i}({\mathbf {X}},t) = \sigma _{ij}^{\varOmega \backslash {\mathcal {S}}}({\mathbf {X}},t)n_{j}({\mathbf {X}})= \sigma _{ij}^{{\mathcal {S}}}({\mathbf {X}},t)n_{j}({\mathbf {X}}) \end{aligned}$$

(18)

Therefore, considering Eq. (18), together with Eqs. (11) and (12), we obtain the interface equilibrium equation that is given by:

$$\begin{aligned} f_{i} = \left\{ E_{ijkl}^{o} \left[ {\hat{\epsilon }}_{kl} - \epsilon _{kl}^{\varphi }\left( [\![ u_{i}]\!] ,[\![ u_{i,j}]\!] \right) \right] - \sigma _{ij}^{{\mathcal {S}}}(\epsilon _{ij})\right\} n_{j} = 0 \end{aligned}$$

(19)

where $\epsilon _{ij}$ is given by the time integration of Eq. (2) which, for points on ${\mathcal {S}}$, corresponds to the following expression:

$$\begin{aligned} \epsilon _{ij} = {\hat{\epsilon }}_{ij} - \epsilon _{ij}^{\varphi } + \frac{1}{2h}\left( [\![ u_{i}]\!] n_{j} + [\![ u_{j}]\!] n_{i}\right) \end{aligned}$$

(20)

In the context of the boundary element method, Eq. (19) can be solved numerically by the adoption of cells with embedded discontinuities that, in this case, provide the displacements jump components $([\![ u_{i}]\!] )$ required to calculate $\epsilon _{ij}^{\varphi }$. Furthermore, these components are considered to be constant within the cells causing null values for the gradient tensors, that is, $[\![ u_{i,j}]\!] =0$. In this way, considering a given regular strain ${\hat{\epsilon }}_{ij}$ and taking into account  Eq. (20), we can be written Eq. (19) as $f_{i} \equiv f_{i}([\![ u_{i}]\!] )=0$. Therefore, after the linearization of this equation its solution can be obtained through Newton’s method.

From these considerations, a regularized constitutive equation that relates stresses and regular strains $({\hat{\epsilon }}_{ij})$ is defined. Therefore, using Eq. (12), we find:

$$\begin{aligned} \tilde{\sigma }_{ij}({\hat{\epsilon }}_{ij}) = \sigma _{ij}^{\varOmega \backslash {\mathcal {S}}}\left( {\hat{\epsilon }}_{ij} - \epsilon _{ij}^{\varphi } \left( [\![ u_{i}]\!] ({\hat{\epsilon }}_{ij})\right) \right) = E_{ijkl}^{o}\left( {\hat{\epsilon }}_{kl} - \epsilon _{kl}^{\varphi }\right) \end{aligned}$$

(21)

where $[\![ u_{i}]\!] ({\hat{\epsilon }}_{ij})$ represents the solution of Eq. (19).

3 Implicit formulation of the BEM for problems with discontinuities

Equations (15–17) can be rewritten in matrix form, after BEM standard discretization, as:

$$\begin{aligned} \{{\dot{\hat{u}}}^{\varOmega }\}& = [G^{u}]\{\dot{t}\} - [H^{u}]\{{\dot{\hat{u}}}\} + [Q_{\epsilon ^{\varphi }}^{u}]\{{\dot{\epsilon }}^{\varphi }\} \end{aligned}$$

(22)

$$\begin{aligned}{}[H]\{{\dot{\hat{u}}}\} &= [G]\{\dot{t}\} + [Q_{\epsilon ^{\varphi }}]\{{\dot{\epsilon }}^{\varphi }\} \end{aligned}$$

(23)

$$\begin{aligned} \{\dot{{\hat{\epsilon }}}\} &= [G^{\epsilon }]\{\dot{t}\} - [H^{\epsilon }]\{{\dot{\hat{u}}}\} + [Q_{\epsilon ^{\varphi }}^{\epsilon }]\{{\dot{\epsilon }}^{\varphi }\} \end{aligned}$$

(24)

From an algebraic manipulation of these equations, we arrive at a single nonlinear equation, as in the implicit formulation developed by [28]. Therefore, through consideration of the essential and natural boundary conditions, Eqs. (22) to (24) are rewritten as:

$$\begin{aligned} \{{\dot{\hat{u}}}^{\varOmega }\} &= [A^{u}]\{\dot{x}\} + [B^{u}]\{\dot{y}\} + [Q_{\epsilon ^{\varphi }}^{u}]\{{\dot{\epsilon }}^{\varphi }\} \end{aligned}$$

(25)

$$\begin{aligned}{}[A]\{\dot{x}\} &= [B]\{\dot{y}\} + [Q_{\epsilon ^{\varphi }}]\{{\dot{\epsilon }}^{\varphi }\} \end{aligned}$$

(26)

$$\begin{aligned} \{\dot{{\hat{\epsilon }}}\} &= [A^{\epsilon }]\{\dot{x}\} + [B^{\epsilon }]\{\dot{y}\} + [Q_{\epsilon ^{\varphi }}^{\epsilon }]\{{\dot{\epsilon }}^{\varphi }\} \end{aligned}$$

(27)

where in $\{\dot{y}\}$ and $\{\dot{x}\}$ are grouped, respectively, the prescribed and the unknown values of the boundary stemming from the vectors $\{{\dot{\hat{u}}}\}$ or $\{\dot{t}\}$. In addition, the matrices [A] and [B] are composed, respectively, by the coefficients from the matrices [H] and [G].

Isolating the vector $\{\dot{x}\}$ in Eq. (26), we find:

$$\begin{aligned} \{\dot{x}\} = [N]\{\dot{y}\} + [M_{\epsilon ^{\varphi }}]\{{\dot{\epsilon }}^{\varphi }\} \end{aligned}$$

(28)

where we have that:

$$\begin{aligned}{}[N] = [A]^{-1}[B], \quad [M_{\epsilon ^{\varphi }}] = [A]^{-1}[Q_{\epsilon ^{\varphi }}] \end{aligned}$$

(29)

Now replacing Eq. (28) in Eqs. (25) and (27), it is found:

$$\begin{aligned} \{{\dot{\hat{u}}}^{\varOmega }\} = [N^{u}]\{\dot{y}\} + [M_{\epsilon ^{\varphi }}^{u}]\{{\dot{\epsilon }}^{\varphi }\} \end{aligned}$$

(30)

$$\begin{aligned} \{\dot{{\hat{\epsilon }}}\} = [N^{\epsilon }]\{\dot{y}\} + [M_{\epsilon ^{\varphi }}^{\epsilon }]\{{\dot{\epsilon }}^{\varphi }\} \end{aligned}$$

(31)

where:

$$\begin{aligned}{}[N^{u}] &= [A^{u}][A]^{-1}[B] + [B^{u}], \quad [M_{\epsilon ^{\varphi }}^{u}] = [A^{u}][A]^{-1}[Q_{\epsilon ^{\varphi }}] + [Q_{\epsilon ^{\varphi }}^{u}] \end{aligned}$$

(32)

$$\begin{aligned}{}[N^{\epsilon }] &= [A^{\epsilon }][A]^{-1}[B] + [B^{\epsilon }], \quad [M_{\epsilon ^{\varphi }}^{\epsilon }] = [A^{\epsilon }][A]^{-1}[Q_{\epsilon ^{\varphi }}] + [Q_{\epsilon ^{\varphi }}^{\epsilon }] \end{aligned}$$

(33)

The constitutive model considered in this work is time independent, so the rates can be replaced by finite increments, that is, $\dot{(\cdot )} = \varDelta (\cdot ) \equiv (\cdot )_{i} - (\cdot )_{i-1}$, where the i term is an incremental index. Thus, considering the i-th increment of prescribed loads, $\{y\}$, Eqs. (28), (30) and (31) are rewritten as follows:

$$\begin{aligned} \{x\}^{i} &= \lambda ^{i}[N]\{y\} + [M_{\epsilon ^{\varphi }}]\{\epsilon ^{\varphi }\}^{i} \end{aligned}$$

(34)

$$\begin{aligned} \{\hat{u}^{\varOmega }\}^{i} &= \lambda ^{i}[N^{u}]\{y\} + [M_{\epsilon ^{\varphi }}^{u}]\{\epsilon ^{\varphi }\}^{i} \end{aligned}$$

(35)

$$\begin{aligned} \{{\hat{\epsilon }}\}^{i} &= \lambda ^{i}[N^{\epsilon }]\{y\} + [M_{\epsilon ^{\varphi }}^{\epsilon }]\{\epsilon ^{\varphi }\}^{i} \end{aligned}$$

(36)

where the term $\lambda ^{i}$ is a cumulative scalar value called load factor whose evolution depends on a specific control method, see for example [7, 20].

From Eq. (36), and taking into account the matrix form of the regularized constitutive equation [Eq. (21)] applied to the complete set of internal cells, we define an equilibrium vector, $\{Q\}^{i} \equiv \{Q({\hat{\epsilon }}^{i},\lambda ^{i})\}$, as a function of the regular strains and the load factor, that is:

$$\begin{aligned} \{{Q}\}^{i} = \lambda ^{i}[N^{\epsilon }]\{y\} + [M_{\epsilon ^{\varphi }}^{\epsilon }]\left( \{{\hat{\epsilon }}\}^{i} - [E^{o}]^{-1}\{\tilde{\sigma }({\hat{\epsilon }})\}^{i}\right) - \{{\hat{\epsilon }}\}^{i} = \{0\} \end{aligned}$$

(37)

where $[E^{o}]$ now represents the linear elastic quasi-diagonal matrix and the vector $\{\tilde{\sigma }({\hat{\epsilon }})\}$ represents the appropriate stress vector.

In this work, this equation is solved using the solution strategy implemented in INSANE software through the work of [23] where, in this case, the load factor is considered an additional variable of $\{Q\}^{i}$.

4 Numerical aspects

4.1 Cells with embedded discontinuity

From the definition of the function $\varphi ({\mathbf {X}})$ (Sect. 2.1), we can see that the dissipative effects are restricted to the subdomain $\varOmega _{\varphi }$. Therefore, only this region needs to be discretized by cells, as illustrated by Fig. 2a.

Fig. 2

BEM discretization of a solid with discontinuity surface: a boundary and domain discretization, b cell with embedded discontinuity [23]

Thus, for each internal cell with embedded discontinuity, typically represented in Fig. 2b, only one collocation point is adopted and, besides this, the field $\epsilon _{ij}^{\varphi }$ is considered constant inside the entire cell domain, that is, for ${\mathbf {X}} \in \varOmega _{c}$:

$$\begin{aligned} \begin{aligned} \begin{Bmatrix} \epsilon ^{\varphi }_{11}({\mathbf {X}}) \\ \epsilon ^{\varphi }_{22}({\mathbf {X}}) \\ \epsilon ^{\varphi }_{12}({\mathbf {X}}) \end{Bmatrix}&\approx \begin{Bmatrix} \epsilon ^{\varphi ,c}_{11} \\ \epsilon ^{\varphi ,c}_{22} \\ \epsilon ^{\varphi ,c}_{12} \end{Bmatrix} = \{\epsilon ^{\varphi ,c}\} \end{aligned} \end{aligned}$$

(38)

However, the cells geometry is parametrized by conventional linear functions defined by the natural coordinates $\eta _{i}$, that is:

$$\begin{aligned} X_{j}(\eta _{1}, \eta _{2}) \approx M^{\alpha }(\eta _{1}, \eta _{2}) X^{\alpha }_{j} \end{aligned}$$

(39)

where the $\alpha$ index refers to the corner points (numbered from 1 to 4 in Fig. 2b).

Therefore, in a cell with embedded discontinuity, an internal collocation point and a set of geometric interpolation points can be distinguished. In addition, the discontinuity line orientation is defined by the unit normal vector and a very small value parameter, k, is used to regularize the Dirac delta function.

The geometry interpolation functions can also be used to define the function $\varphi ({\mathbf {X}})$ inside the cell since the conditions ($\varphi ({\mathbf {X}})=0$ in $\varOmega ^{-} \backslash \varOmega _{\varphi }^{-}$ and $\varphi ({\mathbf {X}})=1$ in $\varOmega ^{+} \backslash \varOmega _{\varphi }^{+}$) are satisfied by the choice:

$$\begin{aligned} \varphi ({\mathbf {X}}(\eta _{1}, \eta _{2})) = \sum _{\alpha ^{+}} M^{\alpha ^{+}}(\eta _{1}, \eta _{2}) \end{aligned}$$

(40)

In this case, the summation is performed considering the interpolation functions associated with the corners located in $\varOmega _{c}^{+}$ (e.g. points 2 to 4 in Fig. 2b).

4.2 Evaluation of displacement jumps

The displacement jump inside a cell is obtained through the numerical solution of the interface equilibrium equation [Eq. (19)]. Thus, it is considered that the displacement jump, $[\![ u_{i}]\!] ({\mathbf {X}})$, is constant inside the cell, that is:

$$\begin{aligned} \left\{ \begin{array}{ll} {[\![ u_{i} ]\!] ({\mathbf {X}}) \approx \begin{Bmatrix} [\![ u^{c}_{1} ]\!] &{} [\![ u^{c}_{2} ]\!] \end{Bmatrix}^T = \{ [\![ u^{c} ]\!] \}} &{}\quad \text {for }\;\;{\mathbf {X}} \in \varOmega _{c} \\ {[\![ u_{i,j} ]\!] ({\mathbf {X}}) = 0} &{}\quad \text {for }\;\;{\mathbf {X}} \in \varOmega _{c} \end{array}\right. \end{aligned}$$

(41)

Also, we assume a Dirac delta function regularization through a very small value parameter k, that is:

$$\begin{aligned} {\left\{ \begin{array}{ll} \delta _{{\mathcal {S}}} \approx \dfrac{1}{k} &{}\quad \text {for }\;\;{\mathbf {X}} \in {\mathcal {S}} \\ \delta _{{\mathcal {S}}} = 0 &{}\quad \text {for }\;\;{\mathbf {X}} \in \varOmega \backslash {\mathcal {S}} \end{array}\right. } \end{aligned}$$

(42)

Using Eqs. (2) and (41), one can write the vector of Eq. (38) in terms of the displacement jump:

$$\begin{aligned} \{\epsilon ^{\varphi ,c}\} = \begin{Bmatrix} \epsilon ^{\varphi ,c}_{11} \\ \epsilon ^{\varphi ,c}_{22} \\ \epsilon ^{\varphi ,c}_{12} \end{Bmatrix} = \begin{bmatrix} \varphi ,_{1}(\varvec{\xi }^c)&\quad 0 \\ 0&\quad \varphi ,_{2}(\varvec{\xi }^c) \\ \frac{1}{2} \varphi ,_{2}(\varvec{\xi }^c)&\quad \frac{1}{2} \varphi ,_{1}(\varvec{\xi }^c) \end{bmatrix} \begin{Bmatrix} [\![ u^{c}_{1} ]\!] \\ [\![ u^{c}_{2} ]\!] \end{Bmatrix} =[\nabla ^{s} \varphi ^{c}] \{ [\![ u^{c} ]\!] \} \end{aligned}$$

(43)

where ${\varvec{\xi }}^{c}$ are the collocation points coordinates of the cell c and, from Eqs. (39) and (40),

$$\begin{aligned} \varphi ,_{i} = \dfrac{\partial \varphi }{\partial \eta _{k}} \dfrac{\partial \eta _{k}}{\partial X_{i}} = \left( \dfrac{\partial M^{\alpha } }{\partial \eta _{k}} X^{\alpha }_{i} \right) ^{-1} \left( \dfrac{\partial }{\partial \eta _{k}} \left[ \sum _{\alpha ^{+}} M^{\alpha ^{+}} \right] \right) \end{aligned}$$

(44)

Therefore, using Eqs. (42) and (43), we obtain the following matrix form for Eq. (19):

$$\begin{aligned} \begin{aligned} \{ f \}&= [{\bar{N}}^{c}]^{T} \left( [E^{o}] \{ {\hat{\epsilon }}^{c} \} - [E^{o}] [\nabla ^s \varphi ^c] \{ [\![ u^c ]\!] \} \right. \\&\quad \left. - \{ \sigma ^{{\mathcal {S}}} (\{{\hat{\epsilon }}^{c}\} - [\nabla ^s \varphi ^c] \{ [\![ u^c ]\!] \} + \frac{1}{k} [N^{c}] \{ [\![ u^c ]\!] \} ) \} \right) = \{ 0 \} \end{aligned} \end{aligned}$$

(45)

where:

$$\begin{aligned}{}[{\bar{N}}^{c}] = \begin{bmatrix} n_{1}&\quad 0&\quad n_{2} \\ 0&\quad n_{2}&\quad n_{1} \end{bmatrix}^T \text {;}\quad [N^{c}] = \begin{bmatrix} n_{1}&\quad 0&\quad \frac{1}{2} n_{2} \\ 0&\quad n_{2}&\quad \frac{1}{2} n_{1} \end{bmatrix}^T \end{aligned}$$

(46)

Finally, Eq. (45) is solved by the Newton iterative method, noting that its linearized form, for a known value of $\{{\hat{\epsilon }}^{c}\}$, is given by:

$$\begin{aligned} \{ f \}_{j-1} + \left[ \dfrac{\partial \{ f \}}{\partial \{ [\![ u^c ]\!] \}} \right] _{j-1} \{ \delta [\![ u^c ]\!] \}_{j} \approx \{ 0 \} \end{aligned}$$

(47)

where j is an iterative index and

$$\begin{aligned} \left[ \dfrac{\partial \{ f \}}{\partial \{ [\![ u^c ]\!] \}} \right] _{j-1} = [{\bar{N}}^{c}]^{T} \left[ - [E^{o}] [\nabla ^s \varphi ^c] - \left[ \dfrac{\partial \sigma ^{{\mathcal {S}}}}{\partial \epsilon } \right] _{j-1} \left[ \frac{1}{k} [N^{c}] - [\nabla ^s \varphi ^c] \right] \right] \end{aligned}$$

(48)

In Eq. (48), the term $\left[ \frac{\partial \sigma ^{{\mathcal {S}}}}{\partial \epsilon } \right]$ is the tangent operator of the continuous constitutive model used to represent the dissipative effects on the discontinuity line ${\mathcal {S}}$.

4.3 Regularized constitutive model

The matrix form of Eq. (21) for an internal cell is given by:

$$\begin{aligned} \{ \tilde{\sigma }({\hat{\epsilon }}^{c}) \} = [E^{o}] (\{{\hat{\epsilon }}^{c}\} - [\nabla ^s \varphi ^c] \{ [\![ u ]\!] \}) = [E^{o}] (\{{\hat{\epsilon }}^{c}\} - \{\epsilon ^{\varphi ,c}\}) \end{aligned}$$

(49)

Thus, the tangent operator associated to this regularized constitutive model and necessary for the solution of the implicit BEM formulation’s equilibrium condition vector of Eq. (37) can be obtained from Eq. (49), that is:

$$\begin{aligned} \left[ \dfrac{\partial \tilde{\sigma }}{\partial {\hat{\epsilon }}^{c}} \right] = [E^{o}] \left( [I] - [\nabla ^s \varphi ^c] \left[ \dfrac{\partial \{ f \}}{\partial \{ [\![ u^c ]\!] \}} \right] ^{-1} [{\bar{N}}^{c}]^{T} \left( [E^{o}] - \left[ \dfrac{\partial \sigma ^{{\mathcal {S}}}}{\partial \epsilon } \right] \right) \right) \end{aligned}$$

(50)

4.4 Discontinuity line tracking algorithm

In the INSANE software, an automatic cell generation algorithm was implemented to allow the discontinuity line propagation along the solid domain. A schematic drawing of the algorithm operation is shown in Fig. 3.

Fig. 3

Automatic cell generation algorithm [23]

In front of the last generated cell with embedded discontinuity (Cell $i-1$), there is always a cell in elastic regime (Cell i). When the elastic limit is reached or the bifurcation condition is met in this cell, a straight discontinuity segment is introduced ensuring discontinuous line continuity (line ${\mathcal {S}}_{i-1}$ and ${\mathcal {S}}_{i}$). In this case, the segment orientation will be defined according to a predefined criterion: perpendicular to maximum principal stress, as in [23], or following a bifurcation analysis, as in [21]. Then, a new cell $(i+1)$ is generated from the following steps:

• 1. The edge of the cell (i) that contains the end of the discontinuity line is assumed to be the starting edge of the cell ($i+1$);

• 2. A straight segment is drawn from the end point of the discontinuity segment of the previous cell following the same orientation as this, but with length weighted by a scalar factor, $\beta$;

• 3. The opposite side of the new cell is created perpendicularly to this segment, with its same size and taking its final point as the side’s midpoint;

• 4. The other two sides of the new cell are created by connecting the end points of these first two sides.

Numerically speaking, the introduction of a new cell corresponds to the amplification of the matrices presented in Sect. 3, as described in [22], which can be done in any iteration or only after step convergence in the incremental-iterative solution strategy.

The adoption of a progressive cell size growth becomes important in some cases to prevent the occurrence of numerical instabilities. In addition, the use of small values for the $\beta$ parameter can contribute to a shorter numerical processing time. However, as will be seen further in the numerical examples, the adoption of high values for this parameter can result in the generation of oversized cells. This event, in turn, generates discrepant results since much of the crack trajectory is approximated by straight segments. Furthermore, a large distance between cells collocation points also leads to a loss of accuracy, since the crack progression is delayed.

5 Isotropic damage constitutive model

5.1 Constitutive equations

In the numerical analyses performed in this work, an isotropic damage constitutive model is used. This model can be synthesized through the following equations [23]:

$$\begin{aligned} \psi (\epsilon _{ij},r) &= [1-D(r)]\psi _{o}(\epsilon _{ij}), \quad \psi _{o}(\epsilon _{ij})=\frac{1}{2}\epsilon _{ij}E_{ijkl}^{o}\epsilon _{kl} \end{aligned}$$

(51)

$$\begin{aligned} \sigma _{ij} &= \frac{\partial \psi (\epsilon _{ij},r)}{\partial \epsilon _{ij}}= (1-D)E_{ijkl}^{o}\epsilon _{kl} = E_{ijkl}\epsilon _{kl} \end{aligned}$$

(52)

$$\begin{aligned} D \equiv D(r) &= 1 - \frac{q(r)}{r}, \quad D \in [0,1] \end{aligned}$$

(53)

$$\begin{aligned} \dot{r} &= {\dot{\gamma }}, \quad {\left\{ \begin{array}{ll} r \in [r_{o}, \infty ), \\ r_{o} = r|_{t=0} = \frac{f_{t}}{\sqrt{E}} \end{array}\right. } \end{aligned}$$

(54)

$$\begin{aligned} \bar{F}(\epsilon _{ij},r) &= \tau _{\epsilon }-r \end{aligned}$$

(55)

$$\begin{aligned} \bar{F}\leqslant & {} 0, \quad {\dot{\gamma }} \geqslant 0, \quad {\dot{\gamma }}\bar{F}=0, \quad {\dot{\gamma }}\dot{\bar{F}}=0 \end{aligned}$$

(56)

$$\begin{aligned} \dot{q} &= H(r)\dot{r}, \quad (H=q'(r) \leqslant 0), \quad {\left\{ \begin{array}{ll} q \in [0,r_{o}], \\ q|_{t=0} = r_{o} \end{array}\right. } \end{aligned}$$

(57)

Equation (51) represents the expression for Helmholtz free energy. In this equation, the term r is the strain-like scalar internal variable. In addition, D is the damage variable and $E_{ijkl}^{o}$ represents the elastic constitutive tensor for isotropic materials which is given by:

$$\begin{aligned} E_{ijkl}^{o} = {\bar{\lambda }}\delta _{ij}\delta _{kl} + \mu (\delta _{ik}\delta _{jl}+\delta _{il}\delta _{jk}) \end{aligned}$$

(58)

where $\delta _{ij}$ is the Kronecker delta and the terms $\mu$ and ${\bar{\lambda }}$ represent the Lamé constants that are expressed as:

$$\begin{aligned} \mu = \frac{E}{2(1+\nu )}; \quad {\bar{\lambda }} = \frac{2\mu \bar{\nu }}{1-2\bar{\nu }} \end{aligned}$$

(59)

where E is the elasticity modulus, $\nu$ is the Poisson’s ratio and $\bar{\nu }$ is given by:

$$\begin{aligned} \bar{\nu }={\left\{ \begin{array}{ll} \nu , &{}\quad \text {for 3D and plane strain state} \\ \dfrac{\nu }{1 + \nu } ,&{}\quad \text {for plane stress state} \end{array}\right. } \end{aligned}$$

(60)

Already Eqs. (52) to (57) represent, respectively, a constitutive equation, an expression for the damage variable, the evolution law of the internal variable, a damage criterion, the Kuhn–Tucker conditions and a softening law. In these expressions, the term $\sigma _{ij}$ represents the Cauchy stress tensor, $E_{ijkl}$ represents the secant tensor of the constitutive relation, q is the stress-like internal scalar variable, $\gamma$ is the damage multiplier, $f_{t}$ refers to the tensile strength, $\bar{F}$ represents the damage function in the strain space, $\tau _{\epsilon }$ is the equivalent strain and H is the hardening–softening modulus.

Different damage criteria can be obtained from the choice of the $\tau _{\epsilon }$ parameter [Eq. (55)]. In this work, the same damage criterion used by [17] is adopted, that is:

$$\begin{aligned} \tau _{\epsilon } = \sqrt{\epsilon _{ij}^{+}E_{ijkl}^{o}\epsilon _{kl}} \end{aligned}$$

(61)

In Eq. (61), the tensor $\epsilon _{ij}^{+}$ is defined, taking into account a coordinate system aligned with the strain principal directions, such as:

$$\begin{aligned} \epsilon _{ij}^{+} = \sum _{k=1}^{n_{dim}}\langle \epsilon _{k} \rangle {\mathbf {\hat{e}}}_{k} \otimes {\mathbf {\hat{e}}}_{k} \end{aligned}$$

(62)

where the term $\epsilon _{k}$ represents the k-th principal strain, ${\mathbf {\hat{e}}}_{k}$ represents a unit vector in the corresponding principal direction and $\langle \epsilon _{k}\rangle = (|\epsilon _{k}| + \epsilon _{k})/2$. Thus, this model becomes suitable for the representation of quasi-brittle materials, since the degradation will occur in traction states preferentially.

And finally, an incremental constitutive equation can be obtained from Eq. (52) considering the inelastic loading condition $(\dot{r}=\dot{\tau }_{\epsilon })$, that is:

$$\begin{aligned} \begin{aligned} {\dot{\sigma }}_{ij}&= (1-D)E_{ijkl}^{o}{\dot{\epsilon }}_{kl} - \dot{D}E_{ijkl}^{o}\epsilon _{kl} \\&= E_{ijkl}{\dot{\epsilon }}_{kl} - \left( \frac{\partial D}{\partial r}\right) \dot{r}E_{ijkl}^{o}\epsilon _{kl} \\&= \left[ E_{ijkl} - \left( \frac{\partial D}{\partial r}\right) \left( \frac{\partial \tau _{\epsilon }}{\partial \epsilon _{kl}} \right) E_{ijrs}^{o}\epsilon _{rs}\right] {\dot{\epsilon }}_{kl} \\&= E_{ijkl}^{t}{\dot{\epsilon }}_{kl} \end{aligned} \end{aligned}$$

(63)

where $E_{ijkl}^{t}$ is the constitutive tangent tensor.

5.2 Softening law

For the strong discontinuity regime, an exponential softening law that compatibilizes the continuous constitutive model with the strong discontinuity kinematics [9, 23] is adopted for Eq. (57), that is:

$$\begin{aligned} q(r) = r_{o}e^{\frac{r_{o}^{2}k}{G_{f}}\left( 1-\frac{r}{r_{o}}\right) } \end{aligned}$$

(64)

where $G_{f}$ represents the fracture energy and k is a small value parameter later presented in Eq. (42).

From Eqs. (53) and (64), we find the following expression for the damage variable evolution:

$$\begin{aligned} D(r) = 1-\frac{r_{o}}{r}e^{\frac{r_{o}^{2}k}{G_{f}}\left( 1-\frac{r}{r_{o}}\right) } \quad \text {for} \quad r>r_{o} \end{aligned}$$

(65)

6 Numerical examples

In this section, the above formulation is used for the numerical simulations of two problems whose experimental results are available in the literature. The simulations were performed using only cells with constant jumps for the displacement components, and the isotropic damage constitutive model presented in Sec. 5.1 together with the exponential softening law outlined in Sec. 5.2 was taken into account. Beside this, we considered the plane stress state with the parameter $k=0.01 \, \text {mm}$ [Eqs. (64) and (65)] and a convergence tolerance equal to $1\times 10^{-4}$ was adopted in the incremental-iterative process. Analyses were performed with cell generation only after step convergence and at any iteration considering, for each of these cases, simulations with 40, 70 and 170 steps. Moreover, an analysis of the growth rate of the cells size was performed. In this case, the same problem was simulated by adopting 70 steps and different values for the parameter $\beta$ which is defined in Sect. 4.4.

6.1 Example 1: Arrea and Ingraffea (1982) [1]

Initially the mixed-mode fracture simulation of a pre-notched concrete beam subjected to shear with forces at four points is considered. A schematic model of this test, which has been studied experimentally by [1], is presented in Fig. 4 where the geometric properties, loads, boundary conditions and the approximate crack path obtained in the experiments are shown. In addition, the values considered in the numerical analysis for the elasticity modulus E, Poisson’s ratio $\nu$, tensile strength $f_{t}$ and fracture energy $G_{f}$ are also presented.

Fig. 4

Shear test with forces at four points [23]

The boundary discretization was performed considering 642 linear elements, and a square cell with a diagonal of $1.6 \, \text {mm}$ was pre-introduced at the notch tip. Furthermore, the origin of the discontinuity segment within the cell was established as the midpoint of the side common to the boundary of the notch.

In the automatic cells generation algorithm (Sec. 4.4), a progressive increase in cell size was considered using $\beta =1.001$ as shown in Fig. 3. However, when a new discontinuity segment exceeded $8 \, \text {mm}$ the cell growth was stopped. As previously mentioned in Sect. 4.4, the adoption of a progressive increase in the cells size is mandatory in some cases, since it can reflect in the reduction of instabilities during the analysis.

The nonlinear analysis was controlled by vertical displacement component of point A (Fig. 4), and the direct introduction of strong discontinuity at the end of the elastic regime was considered. Thus, the results for the applied load versus the relative vertical displacement between the two sides at the initial tip of the notch (the crack mouth sliding displacement—CMSD) are presented through Fig. 5a, b. In these figures, the experimental envelope obtained by [1] is also outlined. In addition, the initial an the final (after cells generation) meshes are presented through Fig. 6a, b, respectively.

Fig. 5

Example 1: Results for load P versus CMSD; a cell generation at any iteration, b cell generation after step convergence

Fig. 6

Example 1: a initial mesh, b final mesh

6.1.1 Growth rate analysis of the cells size

The same example was also considered to analyse the impact of parameter $\beta$ on the numerical results. In this case, all analyses were performed with 70 steps and cells generation was allowed at any iteration. Thus, the following $\beta$ values were adopted: 1.001, 1.005 and 1.010. No interruption was forced in cells growth rate, and therefore, the next cell generated was always larger than the previous one. The results for the applied load versus the CMSD are presented in Fig. 7.

Fig. 7

Example 1: Results for load P versus CMSD with cell generation at any iteration; $\beta$ evaluation

Moreover, the final meshes obtained for the different $\beta$ values are presented in Fig. 8.

Fig. 8

Final mesh for different $\beta$ values: a $\beta = 1.010$, b $\beta = 1.005$, c $\beta = 1.001$

6.2 Example 2: García-Álvarez et al. (2012) [3]

The second example analysed in this paper is the eccentrically notched beam under three points bending which has been experimentally studied by [3]. In Fig. 9, a schematic drawing of this problem together with the values considered for the parameters E, $\nu$, $f_{t}$ and $G_{f}$ is presented.

Fig. 9

Eccentrically notched beam under three points bending

Three different values were considered for each parameter e and d, totalling nine different kinds of specimens. They were: d = 80 mm, 160 mm, 320 mm and e = 0.0 mm, 0.3125d, 0.625d. However, in this work we only analysed the problem with $d=160$ mm and, besides this, the dark grey area shown in Fig. 9 was disregarded in order to reduce computational costs.

In the numerical simulations of this problem were used a factor $\beta =1.000$ (cells with the same size); however, unlike the previous problem (Sec. 6.1) it was necessary to adopt a bifurcation analysis for discontinuity line progression, as detailed described in [21], due to the occurrence of numerical instabilities. In this way, the boundary discretization was performed considering 542 linear elements and a square cell with edge size of $2.0 \, \text {mm}$ was pre-introduced at the notch tip. In addition, the vertical displacement of point B (Fig. 9), located 0.5 mm to the right of the application load point, was used to control the nonlinear analysis.

Thus, the results for the applied load versus the relative horizontal displacement between the two sides at the initial tip of the notch (the crack mouth opening displacement—CMOD) were obtained and are shown in Figs. 10, 11 and 12 together with the experimental envelopes obtained from [3].

Fig. 10

Example 2: Results for load P versus CMOD for $d=160$ mm and $e=0.0$ mm; a cell generation at any iteration, b cell generation after step convergence

Fig. 11

Example 2: Results for load P versus CMOD for $d=160$ mm and $e=0.3125d$; a cell generation at any iteration, b cell generation after step convergence

Fig. 12

Example 2: Results for load P versus CMOD for $d=160$ mm and $e=0.625d$; a cell generation at any iteration, b cell generation after step convergence

Besides this, as for example 1, the initial and final meshes are also shown through Figs. 13, 14 and 15 for cases in which $e=0.0$ mm, $e=0.3125d$ and $e=0.625d$, respectively.

Fig. 13

Example 2: a Initial mesh for $e=0.0$ mm, b final mesh for $e=0.0$ mm

Fig. 14

Example 2: a initial mesh for $e=0.3125d$, b final mesh for $e=0.3125d$

Fig. 15

Example 2: a Initial mesh for $e=0.625d$, b final mesh for $e=0.625d$

In [3], experimental results are also presented for the crack paths considering $e=0.3125d$ and $e=0.625d$. Therefore, in Figs. 16 and 17 the obtained numerical trajectories for the simulations with cells generation at any iteration and only after step convergence are compared to those experimental results.

Fig. 16

Example 2: Results for the crack trajectory; $e=0.3125d$

Fig. 17

Example 2: Results for the crack trajectory; $e=0.625d$

7 Discussions

7.1 Cell generation criteria

As can be seen from Figs. 5a, 10a, 11a and 12a, the curves obtained for all the three simulations (40, 70 and 170 steps) were practically coincident and also had a good approximation with the experimental results. However, the same is not observed for the curves obtained considering cell generation only after step convergence (Figs. 5b, 10b, 11b and 12b). In this case, the three curves presented very different profiles and, besides this, in Figs. 5b, 10b and 11b only the curves obtained in the simulation with 170 steps presented good agreement with the experimental results and converge to the same results obtained with generation at any iteration. Already for $e=0.625d$, as can be seen in Fig. 12b, more steps are needed for a better approximation with the experimental results.

For this last case, the number of cells with embedded discontinuity generated is proportional to the number of steps used in the analysis. Thus, the smaller the number of steps the more rigid the model will be, which explains, therefore, the different profiles sketched through Figs. 5b, 10b, 11b and 12b. On the other hand, increasing the number of steps, better is the agreement with the experimental results.

Regarding Figs. 16 and 17, a good agreement of the crack trajectories obtained numerically with cells generation at any iteration and after the step convergence is observed. Moreover, these results presented a good approximation with respect to the experimental results, especially for the case where $e=0.3125d$ (Fig. 16).

7.2 Growth rate of cells size

Using example 1 as reference, an initial $\beta$ value equal to 1.010 was stipulated in the analysis to define the growth rate of the cells size. However, as can be seen from Fig. 8a, the generated cells have reached a very high size thus compromising the good delineation of the discontinuity line. Also, the results for the applied load versus the CMSD did not presented a satisfactory agreement with the experimental ones as can be seen from Fig. 7.

On the other hand, for the $\beta$ value equal to 1.005 the results were slightly better than the previous one. However, large size cells were still observed (Fig. 8b) and non-acceptable results for the applied load versus CMSD were again verified (Fig. 7).

Finally, the last $\beta$ value tested was 1.001. In this case, the cells did not reach a very large size so as to impair the crack path prediction (Fig. 8c). Besides that, as shown by Fig. 7, the numerical results showed a very satisfactory agreement with the experimental ones.

The adoption of a progressive increase in cell size becomes important in some cases in the prevention of numerical instabilities. In addition, the use of the $\beta$ factor contributes to a decrease in the numerical processing time. However, as can be seen from Figs. 7 and 8, care must be taken in the use of high values for this variable.

8 Conclusion

In this work, two studies related to material failure analysis using the implicit formulation of the boundary element method were presented. For this purpose, numerical simulations of two classical problems whose experimental results are available in the literature were performed. In the first of these studies, two different cells generation criteria along the nonlinear analysis were considered: cells generation at any iteration and cells generation only after step convergence. For each of these cases, three different step sizes were adopted in the incremental-iterative process. In the second of these studies, an analysis on the cell size growth rate was performed considering three values for the cell growth factor (parameter $\beta$). For this case, in all the simulations 70 steps were used and only the cells generation at any iteration was considered.

In the cell generation criteria analysis, where the cells generation was considered at any iteration, step size independence was observed in the structural response. In addition, the results showed good accuracy with the experimental results even with the cells generation occurring in an unbalanced state. For cells generated after step convergence, that is the most correct form from the numerical point of view, a strong dependence on the step size was observed. In this case, we verified that the number of steps is proportional to the number of cells generated which, in turn, are directly related to the softening or hardening branch of the model.

Regarding the analysis of the growth rate of the cells size, it was found that small values must be used for the growth factor in order to prevent numerical instabilities or to reduce the computational cost. However, the use of high values may lead to discrepant results due to the emergence of large cells. Thus, the use of this factor must be done with some care and a balance between results precision and processing time must be performed in order to obtain the ideal $\beta$ value for the problem under analysis.

It is important to note that only monotonic loads were considered in the numerical analyses; therefore, for other types of loads the conclusions obtained in this work may not be valid.