1 Introduction

Dynamic changes in the effective connectivity of neuronal networks are thought to underlie moment-by-moment changes in brain function (e.g., Friston 1994, 2011). Such changes can arise rapidly in fixed anatomical networks by dynamic modulation of the synaptic gains (Tononi et al. 1994; Sporns et al. 2000). How those changes interact with ongoing neural activity remains an active research question (see Jirsa and McIntosh 2007). The present study explores the effect of dynamic changes in lateral connectivity on the spatial synchronization of neural oscillations. Specifically, we use numerical simulation and linear stability analysis to investigate the formation and dissolution of spatial waves of synchronization among laterally connected neural oscillators when the gain of lateral inhibition is dynamically modulated.

Spatial waves of synchronized neural activity are ubiquitous in the brain (see Wu et al. 2008, for a review). Traveling waves have been observed in the local field potential of olfactory bulb (Delaney et al. 1994), motor cortex (Rubino et al. 2006), visual cortex (Huang et al. 2004; Benucci et al. 2007) and hippocampus (Lubenov and Siapas 2009). Stimulus-induced changes in the amplitude and traveling distance of waves in visual cortex have been directly attributed to dynamic modulation of the lateral connections (Nauhaus et al. 2009). In olfactory bulb, stimulus-induced transitions from spontaneous traveling waves to uniform synchrony have been attributed to modulation of the inhibitory connections in particular (Ermentrout et al. 1998; Ermentrout and Kleinfeld 2001; Kazanci and Ermentrout 2007).

Following Ermentrout and Kleinfeld (2001), we model the oscillatory neural dynamics as a spatial network of weakly coupled oscillators where the phase of each oscillator represents the timing of the local neural activity. In such models, spatial synchronization patterns are governed by the strength and topology of the lateral coupling as well as the shape of the oscillator’s phase interaction function. The latter describes the extent to which the phase of the oscillator is advanced or retarded according to the timing of a perturbation. Phase interaction functions that only ever advance the oscillator are classified as Type I whereas those capable of both advancing and retarding the oscillator are classified as Type II. Oscillators with Type II phase interaction functions are generally better at synchronizing than those with Type I (Hansel et al. 1995; Ermentrout 1996, 1998; Rinzel and Ermentrout 1998).

Many cortical neurons have Type II phase interaction functions which can be modeled using the Kuramoto (1984) oscillator. It represents a minimal Type II neural oscillator in which the phase interaction is reduced to a simple sinusoidal term. The lack of even components in the sinusoidal phase interaction does preclude some exotic types of synchronization patterns, such as chimeras (Abrams and Strogatz 2004; Laing 2009). Nonetheless, spatially coupled Kuramoto oscillators adequately serve as a minimal neurobiological model of synchronization in cortex (Breakspear et al. 2010; Heitmann et al. 2012, 2013).

Following Amari (1977), we model the lateral spread of excitatory and inhibitory connection densities by the Mexican hat function which defines the combined densities as a difference of Gaussians. We fix the spatial spread of inhibition at twice that of excitation, unless noted otherwise, and manipulate the strength of the inhibitory density to mimic dynamic modulation of the inhibitory synaptic gains. The stability of wave solutions in this network is then formally analyzed using linear perturbation methods (Ermentrout 1985; Kazanci and Ermentrout 2007). Wiley et al. (2006) use a similar method to analyze waves in a ring of oscillators with short-range uniform excitatory connectivity. Their model has since been extended to include transmission delays (Sethia et al. 2011), uniform inhibitory connectivity (Girnyk et al. 2012) and heterogeneous oscillation frequencies (Omel’chenko et al. 2014). The latter study derives an analytic expression for the stability of the wave solution in terms of the local mean field continuum. Kazanci and Ermentrout (2007) analyzed the stability of the wave solution when short-range excitation was augmented with long-range inhibitory connections. Heitmann et al. (2012) extended analysis to consider inhibitory surround connectivity where the strength of inhibition could be varied dynamically. In that study, the spatial coupling was modeled on the fourth derivative of the Gaussian. Here we consider Mexican hat connectivity, which is more biologically principled, and extend the analysis from the case of the infinite ring to that of the finite ring.

Lastly, we analyze a non-wave solution—which we call ripple—that emerges from the uniformly synchronous state when it loses stability. Wiley et al. (2006) had correctly predicted the existence of such a solution but had never observed it. Girnyk et al. (2012) and Omel’chenko et al. (2014) observed non-wave solutions which they call multi-twisted states, but those solutions did not emerge from synchrony. Our findings suggest that multi-twisted states and ripple states belong to the same branch of solutions.

2 Model

Neural activity was modeled as a one-dimensional ring of non-locally coupled Kuramoto (1984) oscillators

$$\begin{aligned} \dfrac{\partial \theta _x}{\partial t} = \omega - \int _0^L G(|x-x'|) \, \sin \left( \theta _x - \theta _{x'}\right) \, \hbox {d}x' \end{aligned}$$
(1)

where \(\omega \) is the intrinsic oscillation frequency and \(\theta _x\) is the phase of oscillatory neural activity at spatial position \(x\). The ring has a finite spatial length \(L\) and periodic boundary conditions by definition. The distance metric \(|x-x'|\) was defined as the distance along the circumference of the ring. The spatial coupling kernel, \(G(|x-x'|)\), was defined by the Mexican hat function,

$$\begin{aligned} G(x) = \exp \left( -x^2/(2 \sigma _\mathrm{e}^2)\right) - h\; \exp \left( -x^2/(2 \sigma _\mathrm{i}^2)\right) , \end{aligned}$$
(2)

where \(\sigma _\mathrm{e}\) and \(\sigma _\mathrm{i}\) represented the spread of the excitatory and inhibitory connection densities, respectively. Parameter \(h\in [0,1]\) controls the contribution of the inhibitory coupling. It was systematically manipulated, while the contribution of the excitatory coupling remained fixed at unity.

3 Results

Three structurally distinct synchronization patterns were observed depending upon the strength of lateral inhibition and the initial choice of oscillator phases: Spatially uniform solutions (Fig. 1a) arose from random initial phases when lateral inhibition was absent or very weak \((h\approx 0)\). These types of solutions have a winding number of zero and are commonly referred to as synchrony because all oscillators have identical phases. Wave solutions (Fig. 1b) arose from random initial conditions with moderate–high levels of lateral inhibition \((h \gtrsim 0.5)\). Waves have a nonzero winding number that is commensurate with the length of the ring. Lastly, ripple solutions (Fig. 1c) arose from near-uniform initial conditions when lateral inhibition was weak \((h=0.2)\). Ripples have a net winding of zero and resemble spatially periodic deviations of phase from the uniform solution.

Fig. 1
figure 1

Spatially uniform, wave and ripple solutions that arise on the ring under differing levels of lateral inhibition. The longitudinal axis of the cylinder represents spatial distance \((x)\), and the polar angle represents oscillator phase \((\theta _x)\). Boxes illustrate the corresponding Mexican hat coupling function. a Uniform synchrony occurs when lateral inhibition is absent \((h=0)\). b Wave solutions occur when lateral inhibition is moderate \((h=0.5)\). c Ripple solutions occur when lateral inhibition is weak \((h=0.2)\), and initial conditions are close to synchrony. Ripples are structurally distinct from waves. The relative spread of inhibition and excitation \((\sigma _\mathrm{i} = 2 \sigma _\mathrm{e})\) is identical in all panels

Full size image

Ripples have previously been reported in two-dimensional arrays of Kuramoto oscillators with lateral inhibitory coupling based on the fourth derivative of the Gaussian (Heitmann et al. 2012). Here we confirm the existence of ripple solutions in one dimension with conventional Mexican hat coupling. We will later present a formal stability analysis of the normal form approximation of ripples near the onset of bifurcation. First we formally analyze the stability of waves and uniform synchrony in the one-dimensional ring. These have the known analytic solution,

$$\begin{aligned} \theta (x,t) = \omega t + mx, \end{aligned}$$
(3)

where \(\omega \) is the intrinsic oscillation frequency (Hz) and \(m\) is the wavenumber (rads/distance) of the spatial periodicity. Uniform synchrony corresponds to \(m=0\). Spatially periodic solutions are free to select any wavenumber \(m\) in the case of the infinite ring but are restricted to wavelengths that are commensurate with ring length \(L\) in the case of the finite ring.

3.1 Stability analysis of waves on an infinite ring

The stability of the wave solution (3) was formally analyzed by considering the growth or decay of spatial perturbations, \(\psi (x,t)\), applied to the wave. Namely,

$$\begin{aligned} \theta (x,t) = \omega t + mx + \psi (x,t), \end{aligned}$$
(4)

where \(\psi (x,t)\) is some spatially periodic function (Ermentrout 1985). See also Wiley et al. (2006), Kazanci and Ermentrout (2007), Sethia et al. (2011), Heitmann et al. (2012), Omel’chenko et al. (2014). Substituting (4) into (1) yields the growth rate of the perturbation,

$$\begin{aligned} \dfrac{\partial \psi _x}{\partial t} = - \int _{-\infty }^{+\infty } G(|x-x'|) \, H\left( m x - m x' + \psi _x - \psi _{x'}\right) \, \hbox {d}x' \end{aligned}$$
(5)

where \(H(\theta )=\sin (\theta )\) is the phase interaction function for the Kuramoto model, and the \((x,t)\) parameter notation has been omitted for brevity. For any even coupling function, \(G(x)\), and any odd phase interaction function, \(H(\theta )\), the linearization of (5) has solution,

$$\begin{aligned} \psi _x = e^{inx} e^{\lambda _nt}, \end{aligned}$$
(6)

where \(n\) is the spatial wavenumber of the perturbation and \(\lambda _n\) is its eigenvalue. Furthermore, those eigenvalues \(\lambda _n\) are readily computed as,

$$\begin{aligned} \begin{aligned} \lambda _n&= \int _{-\infty }^{+\infty } G(x) \, H'(mx) \, e^{-inx} \, \hbox {d}x\\&\quad -\,\int G(x) \, H'(mx) \, e^{-i0x} \, \hbox {d}x \\&= \text {FT}\big [J(x)\big ]_{n} - \text {FT}\big [J(x)\big ]_{0} \end{aligned} \end{aligned}$$
(7)

where \(J(x) = G(x) H'(mx)\) and \(\text {FT}\) is the Fourier transform. The real part of \(\lambda _n\) is the growth rate of the perturbation with wavenumber \(n\). Any arbitrary spatial perturbation can be represented as a linear combination of such perturbations with a range of wavenumbers. For the perturbed wave (4) to be stable, the growth rate of all such periodic perturbations must be negative. In other words, the real part of \(\lambda _n\) must be negative for all \(n\). The set of all \(\lambda _n\) for a given wavenumber \(m\) is called a dispersion curve.

3.2 Exact Fourier integral

In the case of Kuramoto oscillators, the Fourier integral

$$\begin{aligned} \text {FT}\big [J(x)\big ]_{n} = \int _{-\infty }^{+\infty } G(x) \, H'(mx) \, e^{-inx} \, \hbox {d}x \end{aligned}$$
(8)

can be solved exactly by substituting \(H'(mx)=\cos (mx)\) and expanding the \(e^{-inx}\) term with Euler’s formula. This yields,

$$\begin{aligned} \begin{aligned} \text {FT}\big [J(x)\big ]_{n}&= \int _{-\infty }^{+\infty } G(x) \cos (mx) \cos (nx) \, \hbox {d}x \\&\quad -\,i \int _{-\infty }^{+\infty } G(x) \cos (mx) \sin (nx) \, \hbox {d}x \end{aligned} \end{aligned}$$
(9)

where \(\int G(x) \cos (mx) \sin (nx) \, \hbox {d}x = 0\) because it is the integral of an odd function. Applying the trigonometric identity,

$$\begin{aligned} 2 \cos (mx) \cos (nx)=\cos (mx+nx) + \cos (mx-nx) \end{aligned}$$

to the remaining integral term and substituting the Mexican hat function (2) for \(G(x)\) allows (9) to be written as,

$$\begin{aligned} \begin{aligned} \text {FT}\big [J(x)\big ]_{n}&= \int _{-\infty }^{+\infty } \exp \left( \frac{-x^2}{2 \sigma _\mathrm{e}^2}\right) \, \cos (mx+nx) \, \hbox {d}x \\&\quad +\,\int _{-\infty }^{+\infty } \exp \left( \frac{-x^2}{2 \sigma _\mathrm{e}^2}\right) \, \cos (mx-nx) \, \hbox {d}x \\&\quad -\,h\,\int _{-\infty }^{+\infty } \exp \left( \frac{-x^2}{2 \sigma _\mathrm{i}^2}\right) \, \cos (mx+nx) \, \hbox {d}x \\&\quad -\,h\,\int _{-\infty }^{+\infty } \exp \left( \frac{-x^2}{2 \sigma _\mathrm{i}^2}\right) \, \cos (mx-nx) \, \hbox {d}x. \end{aligned} \end{aligned}$$
(10)

Substituting the known integral,

$$\begin{aligned} \int _{-\infty }^{+\infty } \exp \left( \frac{-x^2}{2 \sigma ^2}\right) \, \cos (2\pi k x) \, \hbox {d}x \!=\! \sqrt{2\pi }\,\sigma \exp \left( -2 \pi ^2 k^2 \sigma ^2\right) , \end{aligned}$$

into (10) gives the exact solution,

$$\begin{aligned} \begin{aligned} \text {FT}\big [J\left( x\right) \big ]_{n}&= \sqrt{\pi /2}\; \sigma _\mathrm{e} \exp \left( -\tfrac{1}{2} \left( m+n\right) ^2 \, \sigma _\mathrm{e}^2\right) \\&\quad +\,\sqrt{\pi /2}\; \sigma _\mathrm{e} \exp \left( -\tfrac{1}{2}\left( m-n\right) ^2 \, \sigma _\mathrm{e}^2\right) \\&\quad -\,h\,\sqrt{\pi /2}\; \sigma _\mathrm{i} \exp \left( -\tfrac{1}{2}\left( m+n\right) ^2 \, \sigma _\mathrm{i}^2\right) \\&\quad -\,h\,\sqrt{\pi /2}\; \sigma _\mathrm{i} \exp \left( -\tfrac{1}{2}\left( m-n\right) ^2 \, \sigma _\mathrm{i}^2\right) , \end{aligned} \end{aligned}$$
(11)

from whence the growth rates \(\lambda _n\) of each perturbation mode (wavenumber \(n)\) to a given wave solution (wavenumber \(m)\) are obtained exactly (Eq. 7).

3.3 Dispersion relations

Dispersion curves \((\lambda _n)\) for selected wave solutions, \(m\in [0,0.2,0.3,0.4]\), under moderate inhibition \((h=0.5)\) are presented in Fig. 2a. Those parts of the dispersion curve where \(\lambda _n>0\) correspond to unstable spatial modes of the wave solution. In this case, wave solutions \(m=0\) (the uniform solution) and \(m=0.3\) are both unstable because they have at least some spatial modes \(n\) where \(\lambda _n>0\).

Fig. 2
figure 2

Stability of wave solutions on an infinite ring. a Dispersion curves for selected waves (\(m=0,0.1,0.2,0.3)\) for the case of Mexican hat coupling parameters \(\sigma _\mathrm{e}=1,\,\sigma _\mathrm{i}=2\) and \(h=0.5\). Each dispersion curve represents the growth rates \(\lambda _n\) of spatially periodic perturbations (wavenumber \(n\)) applied to the wave (wavenumber \(m\)). b Stability map for all waves \((m)\) at all inhibitory coupling strengths \((h)\) with the lateral spread of excitation fixed at \(\sigma _\mathrm{e}=1\) and the spread of inhibition fixed at \(\sigma _\mathrm{i}=2\). The green shaded region indicates stable wave solutions. The four small crosses at \(h=0.5\) correspond to the wavenumbers \((m=0,0.1,0.2,0.3)\) from panel a. The region bounded by the horizontal dashed lines corresponds to those wave solutions \((0.13<m<0.16)\) which are stable for all \(h\in [0,1]\). c Same as the previous panel except here, the lateral spread of inhibition \(\sigma _\mathrm{i}\) is varied while the strength of inhibition \((h=0.5)\) is fixed. In this case, the horizontal dashed lines bound those wave solutions \((0.088<m<0.16)\) that are stable for all \(\sigma _\mathrm{i} \in [0,4]\). Those waves that are stable at all parameter values are robust against changes in network connectivity (color figure online)

Full size image

Wave solutions \(m=0.1\) and \(m=0.2\) appear to be stable because \(\lambda _n<0\) for \(n\in [0,0.4]\). However, we must ascertain that \(\lambda _n<0\) for all \(n\) to be strict. From (7), we require that

$$\begin{aligned} \text {FT}\big [J(x)\big ]_{n} < \text {FT}\big [J(x)\big ]_{0} \end{aligned}$$
(12)

for all \(n\). For large \(n\), we may neglect the \(m\) terms in (11) and write the left-hand side of (12) as,

$$\begin{aligned} \text {FT}\big [J(x)\big ]_{n}&\approx \sqrt{2\pi }\; \sigma _\mathrm{e} \exp \left( -\tfrac{1}{2} n^2 \, \sigma _\mathrm{e}^2\right) \nonumber \\&\quad - h\,\sqrt{2\pi }\; \sigma _\mathrm{i} \exp \left( -\tfrac{1}{2}n^2 \, \sigma _\mathrm{i}^2\right) , \end{aligned}$$
(13)

and observe that \(\text {FT}\big [J(x)\big ]_{n} \rightarrow 0\) as \(n \rightarrow \infty \). We conclude that a given wave solution is stable against all large perturbation modes provided that the right-hand side of (12), namely

$$\begin{aligned} \text {FT}\big [J\left( x\right) \big ]_{0}&= \sqrt{2\pi }\; \sigma _\mathrm{e} \exp \left( -\tfrac{1}{2} m^2 \, \sigma _\mathrm{e}^2\right) \nonumber \\&\quad - h\,\sqrt{2\pi }\; \sigma _\mathrm{i} \exp \left( -\tfrac{1}{2}m^2 \, \sigma _\mathrm{i}^2\right) , \end{aligned}$$
(14)

is greater than zero. For the case of \(h=0.5\) and \(\sigma _\mathrm{e}=2\sigma _\mathrm{i}\) (Fig. 2a), condition (14) simplifies to

$$\begin{aligned} \exp \left( -\tfrac{1}{2} m^2 \, \sigma _\mathrm{e}^2\right) < 1 \end{aligned}$$

which is true for all \(m\). Hence, we may be confident that \(\lambda _n<0\) for all \(n\) in the examples of \(m=0.1\) and \(m=0.2\).

3.4 Stability maps

Wave stability maps (Fig. 2b, c) were constructed from the dispersion curves of a range of wave solutions \(m\in [0,0.4]\) with Mexican hat coupling parameters in the range \(h\in [0,1]\) and \(\sigma _\mathrm{i}\in [1,4]\), respectively. The spread of excitation was fixed at \(\sigma _\mathrm{e}=1\). These maps reveal the region of parameter space (shaded green) where Mexican hat coupling supports stable waves on the infinite ring. The results generalize to arbitrary values of \(\sigma _\mathrm{e}\) by appropriate scaling of the spatial variables \(m,\,n\) and \(\sigma _\mathrm{i}\).

The first map (Fig. 2b) shows the effect of inhibitory strength, \(h\), when the lateral spread is fixed at \(\sigma _\mathrm{i}=2\). The lateral inhibitory coupling is found to support a band of stable waves for any given level of inhibition. That band of stability spans the uniform solution \((m=0)\) at low levels of inhibition \((h<0.12)\). As inhibition increases, the band shifts monotonically upward into higher wavenumbers. The bandwidth of stable waves can thus be controlled by modulating the strength of the lateral inhibition. Nonetheless, that bandwidth is broad enough that some wave solutions \((0.13<m<0.16)\) remain stable irrespective of the strength of inhibition. The existence of these persistent wave solutions shows that some synchronization patterns are immune to changes in network connectivity.

The second map (Fig. 2c) similarly reveals a broad band of stable wave solutions at all spreads of lateral inhibition \(\sigma _\mathrm{i}\in [1,4]\) when the strength of inhibition is held fixed at \(h=0.5\). In this case, the band of stable solutions does not shift monotonically with the spread of inhibition, \(\sigma _\mathrm{i}\). This is emphasized by the broad span of waves \((0.088<m<0.16)\) that are stable irrespective of the spread of the lateral inhibition. We conclude that manipulating the spread of inhibition (relative to excitation) exerts only weak influence over the emergent wave patterns. In any event, such a manipulation is biologically implausible. Consequently, we fix \(\sigma _\mathrm{e}=1\) and \(\sigma _\mathrm{i}=2\) for the remainder of the study and focus exclusively on modulating the strength of inhibition, \(h\).

3.5 Stability maps for the finite ring

In the case of finite rings, the spatial periodicity of the solution must be commensurate with ring length. The same restriction applies to the spatial perturbations. Hence, perturbations that are not commensurate with ring length must be excluded from the analysis. These exclusions subtly impact the stability of the wave, most notably for small rings.

We extend the stability analysis of the previous section to consider waves on a finite ring of length \(L\) by restricting the continuous wavenumbers \(m\) and \(n\) to multiples of the ring length, \(m \rightarrow 2\pi \hat{m}/L\) and \(n \rightarrow 2\pi \hat{n}/L\), where \(\hat{m}\) and \(\hat{n}\) are integers. This gives the exact solution (11) to the Fourier integral an explicit dependence on ring length,

$$\begin{aligned} \begin{aligned} \text {FT}\big [J(x)\big ]_{n}&= \sqrt{\pi /2}\; \sigma _\mathrm{e} \exp \left( -2\pi ^2 (\hat{m}+\hat{n})^2 \, \sigma _\mathrm{e}^2 \,/ L^2\right) \\&\quad +\,\sqrt{\pi /2}\; \sigma _\mathrm{e} \exp \left( -2\pi ^2 (\hat{m}-\hat{n})^2 \, \sigma _\mathrm{e}^2 \,/ L^2\right) \\&\quad -\,h\,\sqrt{\pi /2}\; \sigma _\mathrm{i} \exp \left( -2\pi ^2 (\hat{m}+\hat{n})^2 \, \sigma _\mathrm{i}^2 \,/ L^2\right) \\&\quad -\,h\,\sqrt{\pi /2}\; \sigma _\mathrm{i} \exp \left( -2\pi ^2 (\hat{m}-\hat{n})^2 \, \sigma _\mathrm{i}^2 \,/ L^2\right) . \end{aligned} \end{aligned}$$
(15)

Together, Eqs. (7) and (15) describe the growth of spatial perturbations \((\hat{n})\) to commensurate wavenumbers \((\hat{m})\) in a finite ring of Kuramoto oscillators with Mexican hat connectivity.

Figure 3a illustrates how the exclusion of non-commensurate perturbations bolsters the stability of the uniform solution \((m=0)\) for a finite ring of length \(L=5\). The filled circles show the eigenvalues \(\lambda _n\) of only those perturbation modes \((n=0,0.2,0.4\) cycles/distance) which are commensurate with the ring \((\hat{n}=0,1,2).\) The smooth curve shows the matching dispersion curve for an infinite ring. The uniform solution is stable on the finite ring because \(\lambda _n \le 0\) for all of the commensurate perturbation modes. This is despite the existence of unstable perturbation modes \((0<n<0.18)\) on the infinite ring. Those unstable modes are not commensurate with the \(L=5\) ring and so do not impact stability.

Fig. 3
figure 3

Effects of finite ring length on wave stability. a Dispersion curve for the uniform solution \((m=0)\) with moderate inhibitory coupling \((h=0.25)\). The filled circles indicate the eigenvalues of those perturbation modes \((n=0,0.2,0.4)\) which are commensurate with the ring \((L=5)\). Solid line is the matching dispersion curve for the infinite ring. The wave solution \((m=0)\) is stable on the finite ring because all of the commensurate perturbations have eigenvalues \(\lambda _n \le 0\). The same wave is unstable on the infinite ring. b Horizontal lines map the stability of waves \((m=0,0.2,0.4)\) commensurate with a ring of length \(L=5\). Green shaded region reproduces the stability map of the infinite ring. c Same as b except for a ring of length \(L=20\). The lateral spread of excitation \((\sigma _\mathrm{i}=1)\) and inhibition \((\sigma _\mathrm{i}=2)\) is the same in all panels (color figure online)

Full size image

Small rings are especially prone to finite length effects. For example, a ring of length \(L=5\) only supports stable waves \(m=0\) and \(m=0.2\) (Fig. 3b). The stability limits of those waves also extend significantly beyond the region predicted by the infinite ring (green shaded region). This extended stability is due to the exclusion of non-commensurate perturbation modes that would otherwise cause the wave to be unstable. Larger rings, on the other hand, support a greater number of commensurate modes. For example, the ring of length \(L=20\) has stable waves at \(m=0,0.05,0.10,\ldots ,0.25\) (Fig. 3c). Moreover, the stability boundaries for the finite ring quickly approach that of the infinite ring as ring length is increased.

3.6 Hysteresis

The analytic findings of broad bands of stable wave solutions suggest that individual wave solutions will exhibit hysteresis when the lateral inhibition is dynamically modulated. Specifically, the stability map for the infinite ring (Fig. 2b) predicts that slowly increasing (decreasing) the strength of inhibition, \(h\), should cause existing stable solutions to smoothly track along the lower (upper) boundary of the region of stability. Reversals in the direction of change will not affect the current state until the inhibition has changed sufficiently for that solution to become unstable.

The prediction for the finite ring (Fig. 3b, c) is similar except that the waves will abruptly jump between the commensurate wavenumbers in a discrete fashion. Nonetheless, hysteresis is still predicted to occur. To test these predictions, we simulated the evolution of wave patterns in a finite ring \((L=20)\) while lateral inhibition was slowly ramped between \(h=0\) and \(h=1\). Small Gaussian noise fluctuations were applied to the oscillator phases after each increment in \(h\) to ensure that unstable solutions were escaped. The initial conditions were chosen according to the starting level of inhibition.

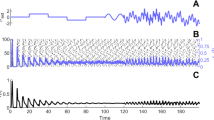
As predicted, wave solutions on the finite ring discretely stepped down through the commensurate wavenumbers \((m=0.25,0.20,0.15)\) when inhibition was slowly ramped down from \(h=1\) to \(h=0\) (Fig. 4a, b). Upon reaching \(h=0\), the \(m=0.15\) wave maintained its stability even after inhibition had returned to \(h=1\). The final synchronization pattern remained stable even after substantial changes in lateral inhibition. This despite the injection of noise at each increment in \(h\) (see Sect. 5). See Supplementary Movie S1 for an animated version of Fig. 4a,b.

Fig. 4
figure 4

Hysteresis in synchronization patterns on a finite ring \((L=20)\) when inhibition is slowly ramped up and down. a Heavy black line shows the evolution of an initial stable wave solution \((m=0.25)\) as inhibition is slowly ramped from \(h=1\) to \(h=0\) and back to \(h=1\). The initial wave steps down from \(m=0.25\) to \(m=0.20\) as inhibition decreases below \(h=0.70\). It steps down again to \(m=0.15\) as inhibition decreases below \(h=0.13\). The wave then remains stable at \(m=0.15\) for all subsequent values of \(h\in [0,1]\). Thin horizontal lines indicate the theoretical stability for the finite ring. b Exemplar wave solution \(m=0.25\) corresponding to label b in the previous panel. c Evolution of initial uniform synchrony \((m=0)\) as inhibition is ramped from \(h=0\) to \(h=1\) and back. The uniform solution gives way to spatial ripple as inhibition increases above \(h=0.13\). The ripple solution continues to increase in amplitude as inhibition is increased to \(h=1\). Stability is maintained, and the ripple returns to synchrony by the same path when inhibition ramps back down to \(h=0\). Ripple solutions do not have unique wavenumbers, so the mean wavenumber \(\bar{m}\) is plotted instead (Sect. 5). d Exemplar ripple solution corresponding to label d in the previous panel. The lateral spreads of excitation \((\sigma _\mathrm{i}=1)\) and inhibition \((\sigma _\mathrm{i}=2)\) are the same in all panels. See Supplementary Movies S1 and S2 for animated versions of this figure

Full size image

However, ramping inhibition in the reverse direction did not cause waves to discretely step upward as predicted. Instead, a low-amplitude ripple solution emerged when the uniform solution lost stability at \(h=0.13\). The ripple maintained its stability and grew in amplitude as inhibition increased to \(h=1\) (Fig. 4c, d). The ripple returned to synchrony by the same path when inhibition was subsequently ramped back to \(h=0\). See Supplementary Movie S2.

The failure of the second simulation (Fig. 4c) to follow the predicted path is due to the existence of solutions other than waves. The analysis of wave stability correctly predicts the loss of stability of the uniform solution at \(h=0.13\). However, that analysis provides no information on the stability or existence of non-wave solutions, such as ripple. In the absence of an analytical expression for ripple, we must revert to numerical continuation techniques to map the bifurcation structure of this system.

3.7 Numerical continuation

Bifurcation maps of the finite ring \((L=20)\) were constructed numerically by continuing both stable and unstable solutions while allowing the strength of inhibition, \(h\), to vary as a free parameter (Figs. 5, 6). The commensurate waves of the ring \((m=0,0.05,0.10,\ldots ,0.35)\) served as the initial solutions for each continuation. Rotational invariance was eliminated by constraining the oscillator phases to solutions with odd symmetry about \(x=0\) (see Sect. 5).

Fig. 5
figure 5

Bifurcation map for a finite ring of length \(L=20\) with spread of lateral inhibition fixed at \(\sigma _\mathrm{i}=2\). a Numerical continuation of wave solutions \(m=0,0.05,\ldots ,0.35\) (horizontal black lines) superimposed on the stability map of the infinite ring (shaded green). Solid lines indicate stable branches. Dashed lines indicate unstable branches. Branch points (BP) indicate bifurcations of the solution curves. b Branch of stable ripple solutions emerging from the uniform solution \((m=0)\) at \(h=0.13\). Labels c–f mark the exemplar solutions shown in the remaining panels. c Uniform solution at \(h=0.05\). d–f Exemplar ripple solutions at \(h=0.2,\,h=0.4\), and \(h=0.9\), respectively

Full size image
Fig. 6
figure 6

Emergence of ripple from waves on the finite ring \((L=20)\). a Bifurcation plot showing the emergence of ripple solutions from the first commensurate wave \((m=0.05)\) at \(h=0.21\). This branch is initially unstable, as shown in the inset. Stability emerges at the first LP \((h=0.19, m=0.061)\) and is lost at the second LP \((h=0.96, m=0.20)\). The branch beyond the second LP is unstable (not shown). Labels c–f correspond to the exemplar solutions shown in the lower panels. b Bifurcation of ripple solutions from other commensurate waves \((m=0.10,0.20,0.25)\). All of these ripple branches are unstable. c The first commensurate wave solution \((m=0.05)\) at \(h=0.05\). d–f Exemplar ripple solutions on the branch emerging from the first commensurate wave

Full size image

The stability of wave solutions computed by numerical continuation (Fig. 5a) agrees with the analytic results for the finite ring (Sect. 3.5, Fig. 3c). The wave loses stability via pitchfork bifurcation which gives rise to a conjugate pair of ripple solutions as inhibition is increased. The conjugate ripple solutions are equivalent after reflection about the origin \((x=0)\); hence, we only need follow one of each pair.

Stable ripple solutions were found to bifurcate from the uniform solution \((m=0)\) via a supercritical pitchfork bifurcation when inhibition exceeds the critical value \(h=0.13\) (Fig. 5b). This branch of ripple solutions corresponds to that observed in the hysteresis simulation (Sect. 3.6, Fig. 4c). Selected solutions from this branch (Fig. 5c–f) illustrate the monotonic growth in amplitude (peak phase deviation) of the ripple as inhibition increases beyond the critical value. Notice that these ripple solutions have a net winding of zero.

Ripple solutions with a net winding of 1 were found to bifurcate from the first commensurate wave \((m=0.05)\) via a subcritical pitchfork bifurcation at the critical value \(h=0.22\) (Fig. 6). Close inspection reveals that the ripple branch is unstable at it emerges from the wave (Fig. 6a, inset). Stability is onset at the first limit point (LP) where the branch folds backward \((m=0.061, h=0.19)\) and subsequently lost through another fold bifurcation indicated by the second LP \((m=0.20, h=0.96)\). In theory, this branch of stable solutions is not accessible by modulation of the lateral inhibitory coupling because of the lack of a stable path from waves. Nonetheless, the basins of attraction are sufficiently close that stable ripple-on-wave solutions can be achieved from stable waves in practice.

In contrast, ripple solutions bifurcating from the other commensurate waves \((m=0.10,0.20,0.25)\) were never stable for this ring length (Fig. 6b). These unstable branches did not warrant further consideration.

3.8 Normal form of the bifurcation to ripple

The use of sinusoidal coupling (or, in fact, any odd periodic function for the coupling) makes it easy to determine the direction of bifurcation of ripple since there will be no quadratic terms in the Taylor expansion of \(\sin (\theta )\) about the synchronous solution. We can subtract off the rotation motion and write \(\sin (\theta )\) in a truncated Taylor series (up to third order) to convert the existence of the ripple solution to Eq. (1) to a solution to the integral equation:

$$\begin{aligned}&0=\int _0^L G\left( |x-x'|,h\right) \nonumber \\&\qquad \left[ (\theta (x')-\theta (x)) - \frac{1}{6} (\theta (x')-\theta (x))^3\right] \ \hbox {d}x' \end{aligned}$$
(16)

where we have specifically included the dependence of the weight function, \(G\) on the inhibition parameter, \(h\). If we ignore the cubic terms, then this equation has a nontrivial solution (\(\theta (x)\) not a constant) if and only if \(h=h_0\) where \(h_0\) is the point at which the synchronous solution loses stability at a zero eigenvalue (cf. Figs. 3b, c, 5b). Figure 5d and the linear stability analysis show that the spatial mode that emerges at \(h=h_0\) is a single sine mode that has period \(L\). The model is on a ring so there will be arbitrary spatial translation, thus, as in the numerical diagrams, we will restrict our analysis to odd periodic functions (this is unnecessary, but allows us to easily directly compare the analysis to the numerics). We proceed as follows. We write

$$\begin{aligned}&h = h_0 + \epsilon ^2 h_2 \end{aligned}$$
(17)
$$\begin{aligned}&\theta (x) = \epsilon r \sin (2\pi x/L) + \epsilon ^3 v(x). \end{aligned}$$
(18)

We skip order \(\epsilon \) terms in \(h\) and order \(\epsilon ^2\) terms in \(\theta \) since the nonlinearity contains no even terms. The unknown function \(v(x)\) must be an odd periodic function. At \(h_0\), the linear part of Eq. (16) has a one-dimensional nullspace (in the space of odd periodic functions) and is self-adjoint, so that the nullspace of the adjoint is the same; both are spanned by \(\sin (2\pi x/L).\) We write

$$\begin{aligned} G(x,h) = G(x,h_0) + (h-h_0)G_1(x) + \mathcal {O}(h-h_0)^2 \end{aligned}$$

where, for our choice of \(G\) (Eq. 2),

$$\begin{aligned} G_1(x) = - \exp \left( -x^2/\left( 2 \sigma _\mathrm{i}^2\right) \right) . \end{aligned}$$

Plugging the expansion for \(\theta (x)\) into (16) and looking at the order \(\epsilon ^3\) terms, we see that we are left with

$$\begin{aligned}&-\int _0^L G(|x-x'|,h_0)[v(x')-v(x)]\ \hbox {d}x' \\&\quad = h_2 r \int _0^L G_1(|x-x'|)[\sin (2\pi x'/L)-\sin (2\pi x/L)] \ \hbox {d}x' \\&\qquad + -\frac{r^3}{3}\int _0^L\!\! G(|x{-}x'|,h_0)[\sin (2\pi x'/L){-}\sin (2\pi x/L)]^3\ \hbox {d}x'. \end{aligned}$$

The function \(v(x)\) is unknown, and the convolution equation has a nontrivial nullspace so that the right-hand side must be in the range of the integral operator for there to be a solution \(v(x)\), whence we apply the Fredholm alternative theorem to the right-hand side; namely, we multiply it by \(\sin 2\pi x/L\), integrate from 0 to \(L\), and set the result to zero. Using a symbolic algebra program such as Maple or Reduce makes this quite simple, and we obtain the bifurcation equations:

$$\begin{aligned} 0 = r [ h_2 \alpha + \beta r^2] \end{aligned}$$
(19)

where \(\alpha ,\beta \) are the results of the integration. For example, using our parameters, \(\sigma _\mathrm{e}=1,\sigma _\mathrm{i}=2\), we obtain

$$\begin{aligned} \alpha =2\,\sqrt{\pi }\sqrt{2} \left( -1+{\mathrm{e}^{8\,{\frac{{\pi }^{2}}{{L }^{2}}}}} \right) {\mathrm{e}^{-8\,{\frac{{\pi }^{2}}{{L}^{2}}}}} \end{aligned}$$

The expression for \(\beta \) is considerably more complicated so we do not write it down explicitly here. Noting that the amplitude of the solutions is \(A:=\epsilon r\) and using the fact that \(h-h_0 = \epsilon ^2 h_1\), we see from (19), that

$$\begin{aligned} A = q \sqrt{h-h_0} \end{aligned}$$
(20)

where \(q=\sqrt{-\alpha /\beta }.\) The parameter \(q\) depends on \(L, \sigma _\mathrm{e},\sigma _\mathrm{i}\) and describes how rapidly the magnitude grows with deviation from the critical value of \(h\). Figure 7a shows the predicted amplitude of the solution for \(L=20\) along with the true magnitude. Panels b and c show the numerical solutions (gray) compared to the sinusoidal solutions (black) predicted from the analysis. Even for solutions with quite a large amplitude (close to \(\pi \)), the theory matches well. If \(q^2<0\), then we must have \(h<h_0\) and the bifurcation is subcritical and unstable. For \(q^2>0\), the bifurcation is supercritical and implies that small stable ripple solutions will bifurcate from the synchronous state. The function \(q=q(L)\) is plotted in Fig. 7d and for all \(L>0\), is positive for \(\sigma _\mathrm{e}=1,\sigma _\mathrm{i}=2.\)

Fig. 7
figure 7

Comparison of the numerical continuation with the analytic calculation for the ripple. a Comparison of the amplitude of the numerical solution with the normal form approximation (Eq. 20) for a ring of length \(L=20\). b The shape of the ripple obtained numerically (gray) along with the normal form approximation (black) for the case of weak inhibition \((h=0.2)\). c Same as panel b but in this case for medium inhibition \((h=0.4)\). d Dependence of the magnitude parameter \(q\) on the ring length \(L\)

Full size image

In sum, this analysis predicts that for all ring sizes, the bifurcation will be supercritical, and ripple solutions are stable. Furthermore, the rate of growth as a function of the ring size is minimized for rings about length 5. Numerical results for rings of size 5, 10 and 20 confirm this.

3.9 Two spatial dimensions

To test the generality of our findings, we repeated our hysteresis simulation (Sect. 3.6) in two spatial dimensions using a square domain of side length \(L=20\), with periodic boundary conditions in both directions. The torus was spatially coupled using an isotropic Mexican hat function (Eq. 2 with \(x\in \mathbf {R}^2)\). As before, the strength of the lateral inhibition was slowly ramped up and down between \(h=0\) and \(h=1\). The torus was initialized with either a linear spatial wave solution or uniform synchrony depending upon whether initial inhibition was strong \((h=1)\) or absent \((h=0)\). The presence of a given wavenumber \((m)\) in the two-dimensional solution was characterized by spatially filtering the pattern with the appropriate planar wave grating and averaging the result across all possible wave orientations. The resulting metric is the spectral power of wavenumber \(m\) irrespective of wavefront orientation. The average wavenumber \(\bar{m}\) in the spectrum, weighted by the magnitude of the spectral response, equates to the mean spatial phase gradient of the pattern.

For the case of strong initial inhibition (Fig. 8), the initial wave pattern (Fig. 8a; \(\bar{m}=0.28)\) maintained stability until inhibition dropped below \(h=0.79\). The subsequent commensurate wave (Fig. 8b; \(\bar{m}=0.21)\) emerged and maintained stability until inhibition dropped below \(h=0.07\). The next commensurate wave (Fig. 8d; \(\bar{m}=0.14)\) remained stable thereafter, even when inhibition was abolished altogether \((h=0)\). That wave solution persisted during the return of inhibition until inhibition reached \(h=0.25\). Spatial rippling (Fig. 8g, f) smoothly emerged out of the \(\bar{m}=0.14\) wave as inhibition increased from \(h=0.25\) to \(h=0.79\). Finally, the spatial ripple lost stability when inhibition exceeded \(h=0.79\). The ripple abruptly gave way to the pattern shown in Fig. 8e \((\bar{m}=0.21)\).

Fig. 8
figure 8

Hysteresis in two-dimensional synchronization patterns on a finite (\(20 \times 20\)) torus continuum. a–h Tracks the evolution of spatial waves when inhibition is gradually ramped from \(h=1\) to \(h=0\) and back to \(h=1\) (clockwise). Each panel shows the spatial pattern of synchronization where gray scale indicates oscillator phase, \(\theta _x \in [0,2\pi ]\). The waves step through a discrete sequence of spatial frequencies as inhibition is ramped down (a–d). Spatial rippling emerges smoothly upon the return of inhibition (h–e). i Spectral decomposition of the spatial patterns during the ramping procedure. Color indicates spectral power of the wavenumber irrespective of wave orientation. Blue is low, and red is high. Labels a–h mark the positions of the corresponding figure panels. The horizontal dashed line indicates the lower Nyquist limit of the spectral analysis. The spectrum highlights those wavenumbers that are recruited by the pattern irrespective of wavefront orientation. j Weighted average wavenumber present in the spectral signature. It represents the mean spatial phase gradient of the observed pattern. Compare with Fig. 4a (color figure online)

Full size image

The sequential stepping through wavenumbers is clearly seen in the spectral signature of the spatial patterns (Fig. 8i). The spectrum shows the spatial wavenumbers present in the pattern irrespective of wavefront orientation (Sect. 5). While single wavenumbers are sequentially recruited when inhibition ramps down, multiple wavenumbers are simultaneously recruited when inhibition returns. These wavenumbers combine linearly to form spatial ripples. The smooth emergence of ripple is revealed by the mean wavenumber of the patterns (Fig. 8j). The sequential stepping down of the wavenumber in the two-dimensional ring is consistent with that of the one-dimensional ring (compare Fig. 8j with Fig. 4). There is no counterpart to spatial ripple in one dimension.

For the case of zero initial inhibition (Fig. 9), the two-dimensional wave patterns followed a similar course to that of the ripple patterns observed in one dimension. Namely, the synchronous solution (Fig. 9a) gives way to a small-amplitude ripple pattern with spatial frequency that increases smoothly as inhibition is ramped from \(h=0.07\) to \(h=0.60\) (Fig. 9b–d). These smoothly changing patterns tended to revert abruptly to waves when inhibition exceeded \(h\approx 0.65\). We therefore restricted our range of manipulation to \(0\le h \le 0.5\). In doing so, we demonstrate that these patterns return to synchrony (Fig. 9e–h) by the same route as which they arrived (Fig. 9a–d). However, the return is not perfect. The patterns in panels f and g exhibit well-defined pinwheels that are absent in their counterparts (Fig. 9b, c). Nonetheless, the gross topology of the solution is retained. The spectral signature (Fig. 9i) highlights the smooth rise and fall of the wavenumbers that are recruited. Even though only commensurate wavenumbers are selected, they combine in ways to yield smooth changes in the mean wavenumber (Fig. 9j). This behavior is consistent with the emergence of ripple from synchrony in the one-dimensional ring (compare Fig. 9j with Fig. 4c).

Fig. 9
figure 9

Two-dimensional ripple solutions emerge from the uniform solution. a–h Evolution of spatial patterns when inhibition is ramped up and then down (clockwise). Color scales are the same as Fig. 8. Uniform synchrony (a) loses stability at \(h=0.07\). A low-frequency spatial ripple pattern emerges which increases in spatial frequency as inhibition increases (b–d). The pattern retreats by a similar path when inhibition recedes (h–e). i Spectral decomposition of the spatial patterns during the ramping procedure. Solid white line is the spectrally weighted average wavenumber. j Weighted average wavenumber redrawn versus inhibition. The advancing and retreating paths are close but not identical. Compare with Fig. 4c (color figure online)

Full size image

In both cases just described, the evolution of the two-dimensional pattern is reminiscent of that observed in the one-dimensional ring but with qualitative differences due to the additional degree of spatial freedom. For example, if we bisect Fig. 9d through the two localized extrema in that pattern, then we obtain a one-dimensional cross section which resembles a ripple solution of the ring (Fig. 5f). Similarly in Fig. 8, spatial ripples (Fig. 8g) emerge from planar waves (Fig. 8g) by the growth of spatial deviations to the wavefront. If we bisect that pattern along a line parallel to the original wavefronts, then we observe a one-dimensional cross section that likewise resembles a ripple solution of the ring. Intuitively, these two-dimensional patterns may be interpreted as contiguous sets of one-dimensional ripple solutions embedded in space.

4 Discussion

Spatial neural network models typically approximate inhibitory surround coupling with the Mexican hat function because it assumes little more than Gaussian spreading of excitatory and inhibitory connection densities. In sinusoidally phase-coupled oscillator networks, our analysis shows that Mexican hat connectivity supports a broad range of spatially synchronized wave solutions provided that the spread of inhibition exceeds the spread of excitation. The range of stable wavenumbers depends upon the strength of the inhibitory surround. Hence, a specific range of wave solutions can be selected by an appropriate choice of inhibitory strength. Likewise, transitions between neighboring wave solutions can be achieved by dynamic manipulation of inhibition. However, those transitions exhibit substantial hysteresis due to the coexistence of multiple stable wavenumbers at any given level of inhibition. In some cases, a wavenumber is stable at all levels of inhibition and thus cannot be escaped by manipulation of inhibition alone.

By analyzing the linear stability of the wave solution, we obtained exact solutions to the dispersion relation (5) describing the growth of spatial perturbations to waves in both the infinite ring (11) and the finite ring (15). Stability maps for a range of wave solutions were obtained numerically by evaluating the growth of a range of perturbations to each wave solution. The broad band of multi-stability is most evident in the case of the infinite ring where coexisting wave solutions occupy a continuum of wavenumbers (Fig. 2). Multi-stability is likewise observed in the case of the finite ring where solutions are restricted to wavenumbers that are commensurate with ring length (Fig. 3). At very small ring lengths (e.g., \(L=5)\), the stability of each wave extends beyond the region predicted by the infinite ring. This is due to the exclusion of non-commensurate perturbation modes that would otherwise render the wave unstable. This stabilizing effect of small ring length quickly diminishes with increasing ring length whereby fewer perturbation modes are excluded. Formally, it is possible to find a ring length \(L\) such that a commensurate wave in a finite ring is arbitrarily close to the critical wavenumber of the infinite ring (see Fife 1978; Ermentrout 1981). Hence, for large rings, the stable wavenumbers approach those of the infinite ring.

Irrespective of ring length, the band of stable wavenumbers in the stability map shifts monotonically higher with inhibition. Numerical simulation confirmed the predicted stepping down through commensurate stable wavenumbers of the finite ring as inhibition was gradually decreased from its maximum. However, the predicted stepping up to higher commensurate wavenumbers was not observed when inhibition was gradually increased from zero. Instead, the wave solution—notably uniform synchrony—gave way to the non-wave solution that we call ripple. Such solutions have previously been reported in two-dimensional models with inhibitory surround coupling based on the fourth derivative of the Gaussian (Heitmann et al. 2012). The present findings confirm the existence of ripple solutions with Mexican hat coupling in both one and two dimensions.

Wiley et al. (2006) correctly predicted the existence of ripple-like solutions even though they never observed them. They reasoned that such solutions, which they call non-uniform twisted states, were the only conceivable way that the uniform state could lose stability. Using numerical continuation, we observed stable ripple solutions emerge from the uniform state via a supercritical pitchfork bifurcation. The normal form calculation of this bifurcation provides a fairly good approximation to the numerical continuation. In particular, it showed that the dependence of the amplitude on the strength of the lateral inhibition strongly depends on the ring size. Intuitively, larger rings support more extensive local winding of the ripple solution even though the net winding is always zero.

Similar solutions—called multi-twisted states—have been reported in rings of non-locally coupled oscillators with uniform inhibitory coupling (Girnyk et al. 2012) as well as uniform inhibitory coupling combined with heterogeneous oscillator frequencies (Omel’chenko et al. 2014). In those cases, the solutions were observed far from the uniform state. Our analysis suggests that non-uniform twisted states (Wiley et al. 2006) and multi-twisted states (Girnyk et al. 2012; Omel’chenko et al. 2014) are extremes of the same branch of solution that we call ripple.

We also observed ripple-like solutions emerging from wave solutions as they lost stability. These ripple solutions inherit the winding number of the wave from which they bifurcate. In all cases observed, the ripple emerged from the wave via a subcritical pitchfork bifurcation and was locally unstable. The branch that bifurcated from the first commensurate wave \((\hat{m} = 1)\) quickly returned to stability through a subsequent fold bifurcation; hence, stable solutions on that branch could be observed in practice. However, no stable ripple solutions were observed emerging from other wavenumbers.

In two spatial dimensions, stable ripple readily emerges from both the uniform state and the wave state. Unlike wave solutions, ripple solutions lack hysteresis and exhibit smooth changes in spatial frequency in response to dynamic changes in lateral inhibition. Ripple patterns therefore have the potential to encode continuous changes in neural state variables that wave patterns cannot. Further research is required to investigate the properties of ripple solutions in two dimensions.

Throughout this paper, we used the simplest possible interaction function for the oscillators, namely \(\sin (\theta ),\) following Kuramoto (1984). In general, the interaction function can be any periodic function. The existence of waves and synchrony still holds, but the stability calculation is more difficult. The loss of stability for the synchronous solution will still be via zero eigenvalue, but the addition of even terms into the interaction function makes the calculations much more tedious with little qualitative difference. Thus, while we have the simplest possible interaction function, results will not qualitatively change. In general, equations of the form (1) arise from more general oscillatory neural networks when the interactions between neurons are small (“weak coupling” ansatz), so we expect to see the same types of dynamics in much more general systems of spatially coupled neural oscillators.

5 Methods

For computational efficiency, Eq. (1) was reformulated as

$$\begin{aligned} \dfrac{\partial \theta _x}{\partial t}&= \omega + \cos (\theta _x) \int _0^L G(|x-x'|) \, \sin (\theta _{x'}) \, \hbox {d}x' \nonumber \\&\quad -\,\sin (\theta _x) \int _0^L G(|x-x'|) \, \cos (\theta _{x'}) \, \hbox {d}x' \end{aligned}$$
(21)

by applying the trigonometric identity \(\sin (u-v)=\sin u \cos v - \cos u \sin v\). Equation (21) was then numerically integrated in the form

$$\begin{aligned} \dfrac{\hbox {d} \mathbf {\theta }}{\hbox {d}t} = \mathbf {\omega }+ \cos (\mathbf {\theta }) \Big [ \mathbf {G} \otimes \sin (\mathbf {\theta }) \Big ] - \sin (\mathbf {\theta }) \Big [ \mathbf {G} \otimes \cos (\mathbf {\theta }) \Big ] \end{aligned}$$
(22)

using a variable time-step Runge–Kutta method where \(\otimes \) denotes spatial convolution with periodic boundary conditions. Eq. (22) applies to both one-dimensional \((x\in \mathbf {R}^1)\) and two-dimensional \((x\in \mathbf {R}^2)\) networks. For the one-dimensional network: \( \mathbf {\theta }\) and \(\mathbf {\omega }\) are both \((m \times 1)\) vectors and \(\mathbf {G}\) is a \((p \times 1)\) vector, where \(m\) is the number of sample points on the ring and \(p\) is the number of sample points on the coupling kernel. For the two-dimensional network: \( \mathbf {\theta }\) and \(\mathbf {\omega }\) are both \((m \times n)\) matrices, and \(\mathbf {G}\) is a \((p \times q)\) matrix, where \(m\) x \(n\) is the number of sample points on the torus and \(p\) x \(q\) is the number of sample points on the coupling kernel. The intrinsic oscillation frequency was set to \(\mathbf {\omega }=0\) without loss of generality by moving onto a co-rotating frame.

5.1 Numerical continuation

Numerical continuation (Sect. 3.7) was done using the CL_MATCONT software package (Dhooge et al. 2003). Degenerate solutions due to rotational invariance were eliminated by constraining the oscillator phases to solutions with odd spatial symmetry \((\theta _x=-\theta _{-x})\). This constraint pinned the oscillator phase at position \(x=0\) to \(\theta =0\). The imposed symmetry also meant that only half of the ring \((0<x<L/2)\) needed to be explicitly computed.

5.2 Hysteresis in the one-dimensional model

The hysteresis study (Sect. 3.6) approximated a continuous ring of length \(L=20\) spatial units by simulating \(n=400\) oscillators equally spaced at \(\hbox {d}x=0.05\) units. Inhibition was incremented in steps of \(\hbox {d}h=0.01\). At each step, the dynamics were integrated for \(t=100\) time units using a variable time-step Runge–Kutta method. Prior to each step, all oscillator phases \(\theta _x\) were perturbed by a small amount of Gaussian noise, \(N(0,2\pi /100)\), to permit escape from unstable solutions. Wave solutions were characterized by wavenumber, \(m\), as defined by Eq. (3).

Ripple solutions do not have a unique wavenumber, so were instead characterized by the mean wavenumber,

$$\begin{aligned} \bar{m} = \frac{1}{\hbox {d}x} \frac{1}{n} \sum _{i=1}^{n} \Big |\theta _{i+1} - \theta _{i}\Big |, \end{aligned}$$
(23)

where \(\hbox {d}x\) is the spatial distance between oscillators, \(n\) is the number of oscillators, and \(\theta _{i}\) is the phase of the \(i\)th oscillator. The mean wavenumber \(\bar{m}\) is equivalent to \(m\) when the phase solution is a true wave.

5.3 Hysteresis in the two-dimensional model

The two-dimensional hysteresis study (Sect. 3.9) followed the same basic procedure as the one-dimensional study (Sect. 3.6). Here, a continuous torus of \(20 \times 20\) spatial units was approximated by a grid of \(200 \times 200\) oscillators equally spaced at \(\hbox {d}x=0.1\) units. Spatial coupling was implemented with the isotropic form of the Mexican hat function (Eq. 2 with \(x\in \mathbf {R}^2\)). Boundary conditions were periodic in both spatial dimensions. Inhibition was incremented in steps of \(\hbox {d}h=0.01\). At each step, the dynamics were integrated for \(t=10\) time steps. In the first simulation (Fig. 8), inhibition was manipulated through the full range \(0<h<1\). In the second simulation (Fig. 9), inhibition was manipulated through the smaller range \(0<h<0.6\) where ripple was stable.

5.4 Spectrograms

The spectrograms in Figs. 8 and 9 were computed by sweeping each two-dimensional wave pattern with an isotropic bandpass filter that progressively filtered spatial wavenumbers from \(m=0\) to \(m=0.4\) in steps of 0.025. The average power within each passband served as a measure of wave power that is independent of wavefront orientation. Prior to filtering, each pattern was tiled \(10 \times 10\) to reduce the lower Nyquist frequency to \(\frac{2}{10L}=0.01\) where \(L=20\) is the length (width) of the torus. The periodic boundary conditions preserve the spatial pattern under tiling. Filtering was performed in the Fourier domain using the MATLAB two-dimensional fast Fourier transform with 2,000 frequency bins per dimension. Bandpass filtering was implemented using a 10th-order Butterworth filter with a bandwidth of 0.005. Wavenumbers below the lower Nyquist frequency were eliminated using a 10th-order Butterworth high-pass filter with frequency cutoff set to 0.01.