Mathematical modelling of the acid–base chemistry and oxygenation of blood: a mass balance, mass action approach including plasma and red blood cells

Abstract

Mathematical models of the acid–base chemistry of blood based upon mass action and mass balance equations have become popular as diagnostic tools in intensive care. The reference models using this approach are those based on the strong ion approach, but these models do not currently take into account the effects of oxygen on the buffering characteristics of haemoglobin. As such these models are limited in their ability to simulate physiological situations involving simultaneous changes of O₂ and CO₂ levels in the blood. This paper describes a model of acid–base chemistry of blood based on mass action and mass balance equations and including the effects of oxygen. The model is used to simulate the mixing of venous blood with the same blood at elevated O₂ and reduced CO₂ levels, and the results compared with the mixing of blood sampled from 21 healthy subjects. Simulated values of pH, PCO₂, PO₂ and SO₂ in the mixed blood compare well with measured values with small bias (i.e. 0.000 pH, −0.06 kPa PCO₂, −0.1% SO₂, −0.02 kPa PO₂), and values of standard deviations (i.e. 0.006 pH, 0.11 kPa PCO₂, 0.8% SO₂, 0.13 kPa PO₂) comparable to the precision seen in direct measurement of these variables in clinical practice. These results indicate that the model can reliably simulate the mixing of blood and has potential for application in describing physiological situations involving the mixing of blood at different O₂ and CO₂ levels such as occurs in the mixing of lung capillary and shunted pulmonary blood.

Introduction

The mathematical models of acid–base chemistry of the blood proposed by Siggaard-Andersen and colleagues are considered by many to be the reference models for this field (Siggaard-Andersen 1974; Siggaard-Andersen et al. 1988). Most clinical interpretation of acid–base status continues to come from either consideration of plasma pH and bicarbonate concentration (Schwartz and Relman 1963), or from use of the parameters of models of Siggaard-Andersen and colleagues. This is despite the formulation of newer models by Stewart (1983) which have found some acceptance in the scientific literature and have even been proposed as a revolution in our understanding of acid–base balance (Constable 2003; Honore et al. 2009).

The approach based on strong ion theory, made popular by Stewart, has been seen as an improvement over the models of Siggaard-Andersen and colleagues for several reasons. The link between electrolyte and acid–base status is explicitly modelled, through the strong ion difference (SID), i.e. the difference between strong cations and anions, which should equal the total buffer base. This point was in itself not new, and was recognized much earlier by Singer and Hastings (1948). Indeed, the Siggaard-Andersen models including anion gap, provide this link, and where plasma protein is measured and anion gap is represented in its corrected form (Figge et al. 1998), Siggaard-Andersen’s approach has been shown to be clinically as useful as the strong ion approach (Dubin et al. 2007). The contribution of Stewart in this respect has probably then been to focus attention on the causes of metabolic acidosis, in particular in disorders like hyperchloraemic acidosis, where changes in buffer base can be due solely to electrolyte disturbances (Constable 2003).

The other major advantage seen in the strong ion approach concerns the modelling methodology adopted by Stewart. Stewart formulated his model from mass balance and mass action equations. This enabled formulation of a set of six simultaneous equations, which could be solved numerically from knowledge of only three variables, with each of these variables describing the necessary components of plasma, i.e. protein/phosphate (Atot), carbon dioxide (PCO₂) and buffer base (SID). Stewart considered variables describing the components as the only variables influenced from outside the system, and as such called these independent variables. This mathematical simplicity represented a systematic approach to formulating the model equations, and the use of numerical methods possible through ‘modern’ computers meant that it was unnecessary to manipulate the equations into an algebraic form which often results in mathematical expressions that are difficult to understand. The approach was also seen by Stewart to be a general representation of the acid–base chemistry of all body fluids (Stewart 1983). Typically, Stewart’s equations are used to describe plasma (Wooten 1999) and other cell free fluids, e.g. cerebrospinal fluid (Duffin 2005). Indeed, applying the Stewart approach to fluid containing more than one compartment, such as whole blood, may be seen as difficult in that ion transfer between compartments influences the SID in both compartments but to differing extents, making prediction difficult. Recently, models have been developed looking at the application of Stewarts approach within muscle cells (Lindinger et al. 2005), and in fluid containing cells, e.g. blood (Wooten 2003).

Despite the apparent advantages and generality of the approach, the model of Stewart has a major shortcoming in comparison with the models of Siggaard-Andersen when used to represent whole blood. The three independent variables applied in Stewart’s model do not take into account the effects of oxygen, which can also be seen as an independent variable, influencing the buffering characteristics of red blood cells (RBC). As such even the most advanced models of blood based on the strong ion approach (Wooten 2003) do not include oxygen binding to haemoglobin or the competitive binding of oxygen, hydrogen ions and carbon dioxide on haemoglobin. This limitation means that their use as predictive models are, in some situations, limited. Physiological situations involving simultaneous changes of both oxygen and carbon dioxide levels in blood, such as the difference between the arterial blood supplying and venous blood draining tissues cannot be simulated; and neither can the mixing of blood with different oxygen and carbon dioxide levels, such as occurs when shunted pulmonary blood is mixed with lung capillary blood returning from normal regions of the lung.

Recently a new model of acid–base chemistry has been proposed including the acid–base and oxygenation aspects of the RBC including the competitive binding of O₂, CO₂ and H⁺ on haemoglobin (Rees and Andreassen 2005). This model is similar to Stewart’s in model formulation, where equations are formulated by considering mass balance, and mass action, such that a set of 28 simultaneous equations are formulated which can be solved simultaneously using six variables. This model can be seen as having the mathematical simplicity of Stewart’s formulation but with the biochemical coverage of the Siggaard-Andersen model.

This paper summarizes the model of Rees and Andreassen (2005), comparing its formulation with that of Stewart, and illustrating how an approach based on mass balance and mass action equations can be used to model complete blood, including the effects of oxygen. Furthermore, the model of Rees and Andreassen is validated, in part, by simulating the effects of mixing blood samples at different levels of O₂, CO₂ and pH, i.e. the functionality not possible using other models formulated using a strong ion approach. Model simulations are compared with experiments involving the mixing of blood samples with different partial pressures of O₂ and CO₂. In addition, simulations are performed by the models of Stewart and Rees and Andreassen in a range of interesting physiological situations.

Methods

Mathematical models’ descriptions

To illustrate the similarities and differences in model formulation between Stewart’s (1983) model and the model of Rees and Andreassen (2005), Fig. 1 illustrates both models as in Fig. 1a, b, respectively.

Fig. 1

a The mathematical model of acid–base chemistry proposed by Stewart (1983), and b the mathematical model of acid–base chemistry of the blood proposed by Rees and Andreassen (2005). See text for details

In Stewart’s model, plasma and other body fluids can be considered as having three components mixed in water: CO₂, weak acid (Atot) in this case plasma protein and phosphate, and SID or buffer base (BB). Each of these components is involved in a number of reaction equations (R1s–R4s) in which the components can present in different chemical forms. To keep track of the concentration of each component in each chemical form three mass balance equations are required 1s–3s. 1s accounts for the total CO₂ as dissolved (CO₂), bound as bicarbonate (HCO₃ ⁻), or as carbonate (CO₃ ²⁻); 2s accounts for the total protein and or phosphate in the plasma, and 3s accounts for the total buffer base, which in the Stewart representation can be described as the SID. In addition four mass action equations are required to account for the four chemical reactions represented in the Stewart model. Each equation may be written in a Henderson–Hasselbalch type format, i.e. in terms of pH, or as in the Stewart representation in terms of the H⁺ concentration. The four equations describe buffering of hydrogen ions by: bicarbonate (R1s, equation 4s); plasma protein and phosphate (R2s, equation 5s); hydroxyl ions (R3s, equation 6s) and carbonate (R4s, equation 7s). A simpler version of Stewart’s model has been proposed excluding the reactions R3s and R4s and hence equations 6s and 7s, these having been shown to be algebraically (Constable 1997) and graphically (Constable 2001) redundant. A further equation is required, equation 8s, to represent CO₂ solubility. This, and equation 1s were not included in Stewart’s original model, as he assumed that the value of the partial pressure of CO₂ is always known.

This model can be used in several ways. For known values of PCO₂, Atot and SID, i.e. Stewart’s independent variables, equations 2s, 3s, 4s, 5s, 7s and 8s represent six equations with six unknowns (HA, A⁻, HCO₃ ⁻, CO₃ ²⁻, pH, CO₂), which can be solved simultaneously. As suggested previously (Morgan 2005), there are some situations where the total CO₂ concentration (tCO₂) may be a more appropriate variable than PCO₂, for example when adding CO₂ to plasma rather than equilibrating plasma at a PCO₂. In this case, for known values of tCO₂, Atot, and SID, equations 1s, 2s, 3s, 4s, 5s, 7s and 8s represent seven equations with seven unknowns (CO₂, HCO₃ ⁻, CO₃ ²⁻, HA, A, pH, PCO₂) which can be solved simultaneously. Table 1a, gives the values of parameters reported by Stewart and necessary to solve these equations, and Table 1b the values of variables calculated by the model when solved for normal plasma values of PCO₂ = 5.33 kPa (40 mmHg), Atot = 19 mmol/l, and SID = 41.7 meq/l, using equations 2s, 3s, 4s, 5s, 7s and 8s. SID can be calculated from equation 9s as the difference between strong cations and anions, where X⁻ represents unmeasured anions. The number of ions used in the calculation of SID in this way is dependent on which ions are measured.

Table 1 Parameter values and values of variables in normal plasma

Figure 1b illustrates the model of Rees and Andreassen (2005). This model includes the three components included in the Stewart model for representation of plasma, plus O₂, haemoglobin (Hb(RH)_bNH₃ ⁺) and 2,3 Diphosphoglycerate (DPG). For plasma, only bicarbonate and non-bicarbonate buffer reactions (R1r, R2r) are included. Equations similar to R3s and R4s from Stewart’s model are not included, having been shown previously to be redundant (Constable 1997, 2001). For the erythrocyte fraction of blood, haemoglobin in its ‘basic’ form is written as Hb(RH)_bNH₃ ⁺ to reflect the side chain (RH)_b and amino end (–NH₃ ⁺) buffering sites. The carboxyl end of haemoglobin protein chains is fully dissociated under physiological conditions, with the dissociated H⁺ forming NH₃ ⁺ on the amino ends. Each of these components is involved in a number of reaction equations (R1r–R14r) in which the components can present in different chemical forms. Haemoglobin binding to H⁺, O₂ and CO₂ is drawn as three blocks of reaction equations A–C. Blocks A and B represent the binding of H⁺ to the various chemical forms of the amino end of the haemoglobin molecules protein chains, i.e. NH₂ in block A and NHCOO⁻ in block B, and the oxygenated and deoxygenated forms of these. Block C represents the binding of H⁺ to the side chains of the amino acids, with on average b binding sites per haemoglobin molecule, and the oxygenated and deoxygenated forms of this.

In principle, six mass balance equations are required, one to describe each of the components of blood. Equation 1r accounts for the total CO₂ in plasma (CO_2,p and HCO_3,p), and that in erythrocyte as dissolved (CO_2,e), bicarbonate (HCO_3,e), bound to deoxygenated haemoglobin (HbNHCOO⁻), and bound to oxygenated haemoglobin (HbO₂NHCOO⁻). Equation 2r is the same as 2s for describing phosphate and protein in plasma. Equation 3r accounts for the total haemoglobin in blood (Hb) and can be written in two ways: by counting the different chemical forms of the amino end of the haemoglobin chains (NH₃ ⁺, NH₂, or NHCOO⁻) (equation 3ar) on oxygenated or deoxygenated haemoglobin; or by counting the different chemical forms of the amino side chain buffers (RH, R⁻) (equation 3br) on oxygenated and deoxygenated haemoglobin. Equation 4cr, accounts for the total buffer base in whole blood (BB), defined as the total concentration of weak base in blood which is written as a weighted sum of that due to plasma buffers (BB_p) (equation 4ar) and that due to erythrocyte buffers (BB_e) (equation 4br) including buffers due to bicarbonate (HCO_3,e), side chain buffer sites on oxygenated and deoxygenated haemoglobin (Hb(R⁻)_b, HbO₂(R⁻)_b), and binding to the amino end of oxygenated and deoxygenated haemoglobin chains (HbNH₂, HbO₂NH₂, HbNHCOO⁻, HbO₂NHCOO⁻). To ensure electrical neutrality BB in the plasma and erythrocyte fractions is equal to the difference between strong cations and anions in the respective fluids (Singer and Hastings 1948). In the Stewart approach BB_p is therefore usually called the effective SID. Equation 5r accounts for the total oxygen as the small amount dissolved in the plasma and RBC and that bound to the various forms of haemoglobin. No mass balance equation is included in the model for 2,3 DPG, assuming that for most interesting situations its value remains constant.

In addition nine mass action equations are required to account for the nine reactions buffering H⁺ (R1r–R9r) by: plasma bicarbonate (R1r and 6r); plasma protein and phosphate (R2r and 7r); erythrocyte bicarbonate (R3r and 8r); the NH₂ form of the amino acid end of both oxygenated and deoxygenated haemoglobin (R4r and R5r, equations 9r, 10r, pKzd = 7.32, pKzo = 7.14); the NHCOO⁻ form of the amino acid end of both oxygenated and deoxygenated haemoglobin (R6r and R7r, equations 11r, 12r, pKcd = 4.80, pKco = 5.46); and the R⁻ form of the amino acid side chain of both oxygenated and deoxygenated haemoglobin (R8r and R9r, equations 13r, 14r, pKzd_R = 7.32, pKzo_R = 7.14).

Mass action equations could be formulated representing the remaining five reaction equations (R10r–R14r) representing the oxygen binding to the different forms of haemaglobin. A detailed model of this has already been formulated (Siggaard-Andersen et al. 1984; Siggaard-Andersen and Siggaard-Andersen 1995) in the form of the oxygen dissociation curve (ODC), describing the relationship between oxygen partial pressure (PO₂) and saturation (SO₂). This model is included in the model of Rees and Andreassen (equation 15r), and equations are required which define SO₂ from the other model variables, by counting either the amino ends (equation 16r) or the side chains (equation 17r).

Several other equations are required to describe the physico-chemical properties of blood. Equations 18r–21r describe the solubility of O₂ and CO₂ in plasma and RBC. Equation 22r states that the plasma and erythrocyte fractions sum to 1. Equation 23 states that the haemoglobin concentration in erythrocyte is a constant value of 21 mmol/l, such that the fraction of erythrocyte can be calculated as the haemoglobin concentration in blood divided by 21. The model does not simulate explicitly the transport of ions over the RBC membrane, e.g. the Hamburger shift or Jacobs–Stewart cycle. Instead a modified form (Siggaard-Andersen 1974) of the empirical relationship relating pH in the plasma and RBC derived by Funder and Weith (1966), is used, i.e. equation 24r (Fig. 1). Funder and Weith derived this relationship from measurement of chloride and hydrogen ion concentrations in plasma and RBC, using these measurements to solve the Nernst equation. The equation of Funder and Weith therefore provides a link between plasma and RBC acid–base status without the need to represent electrolyte transport across cell membranes. This simplification means that the model cannot calculate values of electrolytes in the plasma and RBC.

Equation 25r represents the calculation of base excess (BE) as the concentration of buffer base above normal (nBB). Equations 26ar and 26br, represent two different equations describing electrical neutrality. The first calculates the anion gap (A ⁻_p ), and is usually reported as a variable from Siggaard-Andersen’s models. The second represents the plasma buffer base or SID, and is usually reported as a variable from the strong ion approach.

A detailed formulation of the model including all the assumptions and their justification has been published previously (Rees and Andreassen 2005). These assumptions are summarized as follows. That O₂ and CO₂ diffuse well enough through blood so that the partial pressures of O₂ and CO₂ are the same in plasma and erythrocyte. That all chemical reactions are in steady state conditions. That plasma non-bicarbonate buffers can be represented using a single reaction with a single dissociation constant with a constant value. That in erythrocyte the binding of O₂, CO₂ and H⁺ to haemoglobin can be conveniently represented as three lumped binding sites: the binding of oxygen to haemoglobin represented by the ODC; the competitive binding of H⁺ and CO₂ to the uncharged amino end (NH₃) of the four haemoglobin polypeptide chains; and the binding of H⁺, and only H⁺, to the side chains of the amino acids of the haemoglobin polypeptide chains. That for both oxygenated and deoxygenated haemoglobin the amino and side chain sites bind H⁺ with the same affinity such that pKzo = pKzo_R and pKzd = pKzd_R.

In a similar way to Stewart’s representation, equations 1r–25r, i.e. 28 equations can be solved simultaneously using, in this case, six known values, one representing each of the components of blood. This solution makes it possible to obtain all 28 + 6 = 34 variables describing blood (tCO₂, pCO₂, CO_2,p, HCO ⁻_3,p , CO_2,e, HCO ⁻_3,e , A ⁻_p , HA_p, Atot_p, pH_e, pH_p, Hb, HbO₂NH₂, HbO₂NHCOO⁻, HbO₂NH₃, HbO₂(R⁻)_b, HbO₂(RH)_b, HbNH₂, HbNHCOO⁻, HbNH₃ ⁺, Hb(R⁻)_b, Hb(RH)_b, f_e, f_p, BB, BB_p, BB_e, BE, tO₂, O_2,p, O_2,e, pO₂, sO₂, DPG). For example, these equations can be solved using Stewart’s three independent variables Atot, PCO₂ and SID, describing plasma non-bicarbonate buffer, CO₂ and buffer base, respectively, plus three, e.g. PO₂, Hb and DPG, describing oxygenation, haemoglobin and DPG. Table 2 gives the values of parameters reported by Rees and Andreassen (2005) necessary to solve these equations, and the values of variables calculated by the model when solved for fully oxygenated blood at PCO₂ = 5.33 kPa, Atot = 23.5 mmol/l, BB_p = 41.7 meq/l, SO₂ = 100%, Hb = 9.3 mmol/l, DPG = 5 mmol/l.

Table 2 Parameter values and values of variables in normal fully oxygenated blood

Experimental procedure

Peripheral venous blood was sampled from 21 normal subjects. A butterfly needle (Multifly Set; Sarsted AG & Co., Nürbrecht, Germany), was inserted into a cubital vein. Blood was sampled into two standard 9 ml venous blood collection tubes (Li-Heparin S-Nonovette; Sarsted AG & Co., Nürbrecht, Germany) using the vacuum principle. For each of the 9 ml samples air was expelled immediately from the syringe and the following procedure was performed.

A 1–2 ml sample of blood was drawn anaerobically from the 9 ml syringe into a 5 ml syringe (BD Plastipak, Madrid, Spain) fitted with a needle (BD Microlance 3, Drogheda, Ireland). It was not necessary to use heparinized syringes as the blood was heparinized via the 9 ml syringes. The sample was drawn by piercing the 9 ml syringe’s rubber membrane with the needle. This 5 ml syringe was labelled ‘d’ for deoxygenated (i.e. venous blood), and analysed immediately to obtain values of peripheral venous acid–base, oxygenation, metabolite and electrolyte status (ABL 800, Radiometer AS, Brønshoj, Denmark). A further 1 ml sample was drawn from the same 9 ml syringe into a 5 ml syringe (BD Plastipak, Madrid, Spain) in the same manner, and this syringe labelled ‘m’ for mixed. The syringe was weighed prior to and following blood sampling (Mettler PC440 Delta Range, Mettler Toledo, Naverland 8, Glostrup, Denmark). The sample was capped and placed on a rotator for later analysis. The remaining approximately 6 ml was then poured into a beaker open to the air, and this was agitated gently for a period of about 15 min whilst exposed to room air. A 1–2 ml sample was then drawn from the beaker into a 5 ml syringe (BD Plastipak, Madrid, Spain) with this syringe labelled ‘o’ for oxygenated, capped and placed on a rotator for further analysis. A further 1 ml was then drawn into the syringe marked ‘m’, which was capped and rotated to ensure mixing. The blood samples marked ‘o’ and ‘m’ were then analysed to obtain values of acid–base, oxygenation, metabolite and electrolyte status (ABL 800, Radiometer AS, Brønshoj, Denmark).

In order to estimate the fractions of ‘d’ and ‘o’ in the mixed sample 30 μl of physiological saline containing creatinine at a concentration of 120 mmol/l, was added to the beaker at the start of the period where blood was exposed to room air. As very little creatinine is present in the deoxygenated sample, measurement of creatinine levels in each of the ‘d’ ‘o’ and ‘m’ samples enabled accurate calculation of the mixing fractions of blood. Creatinine was measured in all samples as part of acid–base, oxygenation, metabolite and electrolyte status (ABL 800, Radiometer AS, Brønshoj, Denmark).

For each subject all analysis was performed on the same blood gas analyser which was calibrated prior to use and not allowed to recalibrate during the procedure. In all the 5 ml syringes mixing beads were placed into the syringes prior to the experiment to ensure adequate mixing during rotation. These beads were taken from a 9 ml syringe identical to those used in the experiment. In all cases care was taken to ensure that no air entered the 5 ml syringes and that any was expelled immediately.

Ethical approval was obtained from the ethical committee of the North Jutland Region of Denmark, and informed written and oral consent was obtained from all subjects.

Model simulation and validation

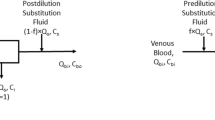
The model simulation and validation process is illustrated in Fig. 2. Measurement of pH, PCO₂, PO₂, SO₂, total haemoglobin concentration (tHb), and fractions of abnormal forms of haemoglobin, carboxyhaemoglobin (FCOHb) and methaemoglobin (FmetHb), were made in oxygenated (o) and deoxygenated (d) blood. Step A represents determination of the values of variables necessary for solution of the acid–base model of Rees and Andreassen for oxygenated and deoxygenated blood samples, i.e. pH, PCO₂, PO₂, Hb, DPG and Atot. Values of pH, PCO₂ and PO₂, are those measured in the oxygenated (o) and deoxygenated (d) samples. Hb, the effective haemoglobin concentration, are obtained by subtracting carboxyhaemoglobin and methaemoglobin from the tHb. DPG is obtained by fitting the ODC to the data obtained from the deoxygenated sample, finding values of DPG at which the ODC passes through measured values of PO₂ and SO₂, as described previously (Siggaard-Andersen and Siggaard-Andersen 1995; Rees et al. 2006b). This is only possible for SO₂ values <97% and as such values for DPG in oxygenated blood were assumed to be the same as those calculated for deoxygenated. Blood was sampled from normal subjects with normal electrolyte concentrations. Atot was therefore set to the normal value reported by Rees and Andreassen (2005) (Atot = 23.5 meq/l) for both oxygenated and deoxygenated blood.

Fig. 2

Mathematical model simulation of the mixing of blood, see text for details

The six variables pH, PCO₂, PO₂, Hb, DPG and Atot, for both oxygenated (o) and deoxygenated (d) samples were then used as input to simultaneous solution of equations 1r–25r (Fig. 1b), as illustrated in Fig. 2, Step B. This enables calculation of all variables describing these two blood samples, including BB, tCO₂, tO₂, DPG and Atot. These variables represent the concentration of each of the components, i.e. each of the mass balance equations, and as such are convenient variables to simulate mixing.

Mixing is simulated using equations a–f (Fig. 2, Step C). The concentration of each of the components of the calculated mixed blood (c) are calculated as a weighted sum of the two blood samples, depending upon the fraction of each sample mixed, the assumption being that the mass of these components is conserved in the mixing. The only exception to this being the calculation of the buffer base BBc, which is calculated as the weighted sum of the fractions minus a concentration of strong acid (Δacid). Δacid represents the strong acid added to the blood as a result of the continuing anaerobic metabolism in the RBC during the 15-min oxygenation period. Δacid was calculated as the difference between the lactate concentration measured in the mixed sample and the weighted sum of the lactate concentration in the oxygenated and deoxygenated mixed fractions, i.e.

$$ \Updelta {\text{acid}} = {\text{lactate}} - \left( {{\text{lactate}}_{\text{o}} {\text{ f}}_{\text{o}} + {\text{lactate}}_{\text{d}} {\text{ f}}_{\text{d}} } \right) $$

The respective fractions f_o and f_d in equations a–f (Fig. 2), are calculated from the measurement of creatinine in the oxygenated, deoxygenated and mixed samples.

The resulting six variables BBc, tcCO₂, tcO₂, Hbc, DPGc, Atotc then provide input to simultaneous solution of equations 1r–25r (Fig. 2, step D), enabling calculation of the variables measured in the mixed sample, e.g. pHc, PcCO₂, PcO₂ and ScO_2.

Statistical methods

Values of pH, PCO₂, PO₂ and SO₂ in the mixed sample calculated from the procedure illustrated in Fig. 2 using the model of Rees and Andreassen, are compared with those measured using Bland–Altman plots. Calculations are made of the mean bias and standard deviation of the difference between calculated and measured variables.

Model simulations of interesting physiological situations

To illustrate the differences between the models of Stewart and Rees and Andreassen, i.e. the effects of including a RBC model compartment including oxygen, several simulations were performed using each model, these simulations reflecting typical physiological situations.

For the Stewart model, respiratory acidosis and alkalosis were simulated by setting PCO₂ to 6.0 and 4.0 kPa, respectively, whilst maintaining SID (or BB_p) and Atot at normal values. For the model of Rees and Andreassen respiratory acidosis and alkalosis were similarly simulated by setting PCO₂ to 6.0 and 4.0 kPa, respectively, whilst maintaining BB, Atot, Hb, FMetHb, FCOHb and DPG to normal values. BB rather than BB_p was held constant as changes in PCO₂ cause HCO₃ ⁻–Cl⁻ exchange across the RBC membrane, meaning that BB_p may not be constant.

For the Stewart model, metabolic acidosis and alkalosis were simulated by reducing or increasing SID (or BB_p) by 5 meq/l, respectively, whilst maintaining PCO₂ and Atot at normal values. For the model of Rees and Andreassen respiratory acidosis and alkalosis were simulated by reducing or increasing BB by 2.5 meq/l, respectively, whilst maintaining PCO₂, Atot, Hb, FMetHb, FCOHb and DPG to normal values. BB was reduced by half of BB_p to simulate an equivalent addition of acid to either plasma (for the Stewart model) or whole blood for the Rees and Andreassen model.

For the model of Rees and Andreassen both respiratory and metabolic changes were simulated at normal and low levels of PO₂ to illustrate the effects of the competitive binding of H⁺, O₂ and CO₂ included in the model of haemoglobin.

Results

Table 3 includes summary statistics describing the measurement of pH, PCO₂, PO₂ and SO₂ for the deoxygenated and oxygenated blood samples (blood sample 1 in all cases).

Table 3 Measurements in deoxygenated and oxygenated blood

The differences between variables measured in deoxygenated and oxygenated blood are large in relation to the normal variation seen in blood. This is with the exception of PO₂, where oxygen content differences were large without large changes in partial pressure. Values of oxygen saturation in the oxygenated sample were on occasions quite low, indicating the relative slow diffusion of oxygen from room air into the blood sample, such that full equilibrium was not achieved within the approximately 15 min.

Table 4 illustrates five examples of the raw data used as input to the mixing algorithm and the measured and calculated values in the mixed sample. Examples were selected so as to cover the range of values given in Table 3. Subject 1 and subject 5 are typical cases with values close to the average reported in Table 3. Subject 2 has average values for pH and PCO₂, but low oxygenation. Subject 3 has high pH, low PCO₂ and high levels of oxygenation. Subject 4 has low pH, high PCO₂ and low levels of oxygenation. These cases illustrate that the model simulations function across the range of values given in Table 3, with only very small differences between measured and calculated values in the mixed blood samples.

Table 4 Examples of oxygenated, deoxygenated and mixed blood samples and calculations of mixed blood values

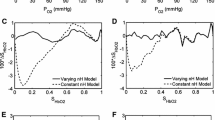
Figure 3 illustrates Bland–Altman plots comparing values of pH, PCO₂, PO₂ and SO₂ in measured (m) and calculated (c) values of mixed blood samples using the model of Rees and Andreassen. For each subject two blood samples were taken and these are plotted as crosses and circles, respectively. Data from all the 21 subjects’ first blood samples (crosses) were used in the analysis. Only 19 of the subjects’ second blood samples (circles) were used in the analysis. Two data sets were excluded due to poor handling of the blood as identified by values of PO₂ in the mixed blood sample being either higher than those in the oxygenated sample (one case), or lower than in the deoxygenated sample (one sample). Values of the mean bias and SD are given in Table 5, along with typical values for measurement errors in routine clinical measurement of blood gas and acid–base. For all variables, Fig. 3 and Table 5 show that model calculated values are close to those measured with very little bias. The precision of model predictions is also good with values of the SD of model predictions similar to those for direct measurement of blood in routine clinical practice given in Table 5.

Fig. 3

Bland–Altman plots comparing measured (m) and model calculated (c) values of mixed blood. Two blood samples were taken for each subject and are plotted as crosses and circles, respectively. Dashed lines represent the mean bias ± 2 SD for crosses, and solid lines represent the mean bias ± 2SD for circles

Table 5 Mean bias and SD when comparing measured (m) and model calculated (c) measurements in mixed blood

In two cases calculated values of pHc and PcCO₂ were substantially different from measured, as illustrated in Fig. 3. Both these cases were in the second blood sample (Fig. 3, circles) taken from the subject, used as a control. These errors were not present in the first blood sample for the same subjects and were therefore considered erroneous and omitted from calculations of bias and SD.

Table 6 gives the results of the simulations of typical physiological situations using both the models. In normal conditions values of pH are similar for each model. Respiratory alkalosis and acidosis were simulated using PCO₂ of 6.0 and 4.0 kPa, respectively. Larger changes in plasma pH were seen in the model of Stewart reflecting the smaller buffer capacity of plasma alone when compared to both plasma and RBC which include the substantial buffering of haemoglobin. A similar situation can be seen for metabolic acidosis and alkalosis where an equivalent amount of acid added or removed causes larger pH changes if a model of plasma only is used.

Table 6 Simulated examples using the models of Stewart and Rees and Andreassen

In addition, the effects of the competitive binding of H⁺, O₂ and CO₂ can be seen in the simulations performed using the model of Rees and Andreassen. For example, for respiratory acidosis at normal PO₂, the difference between pH values simulated by the models is 0.012. This increases to 0.023 on reduction of PO₂ from 15 to 5 kPa.

Discussion

This paper describes and provides a first validation of a mathematical model of the acid–base chemistry of blood. The model is novel in that it describes plasma and erythrocyte fractions of the blood using a mass balance and mass action representation of the chemical reactions, where the erythrocyte fraction is modelled in sufficient detail to include the competitive binding of H⁺, CO₂ and O₂ to haemoglobin. In this way the model incorporates the simplicity of the mathematics of the Stewart approach with the coverage of the models of Siggaard-Andersen. In doing so it is possible to simulate physiological situations involving the mixing of blood at different O₂, CO₂ and pH levels, for example the mixing of pulmonary capillary blood passing through atelectatic regions of the lung with that passing through regions with normal ventilation and perfusion.

This model has been shown to be able to simulate the mixing of blood samples with the same electrolyte and metabolite status, but with different partial pressures of O₂ and CO₂. Values of pH, PCO₂, PO₂ and SO₂ could be simulated within the routinely available measurement precision available in the clinic. Venous blood and venous blood left open to room air are analogous to arterial blood during respiratory acidosis and respiratory alkalosis, respectively. Correct mixing of these samples therefore evaluates the ability of the model to account for the effects on acid–base status of respiratory disturbances which simultaneously change O₂ and CO₂. In addition, it has been shown that when performing simulations representing typical physiological changes, a model including the erythrocyte compartment and the effects of O₂ level on buffering results in quite different simulations from a model of plasma alone. These simulations illustrate the need for models including the RBC, as the additional buffering capacity of the RBC due to haemoglobin means that changes in plasma pH are smaller when acid–base status is perturbed. In addition, this illustrates the need for models including the effects of O₂ on acid–base chemistry, as significant changes in pH can be due solely to changes in PO₂.

Previously, the model of Rees and Andreassen (2005) has been validated against existing literature data and has been shown to be capable of reproducing characteristic pH/PCO₂ buffer curves for plasma and whole blood. The model was also shown to be able to calculate accurately values of Haldane and BE coefficients in blood at a range of pH and PCO₂ values, illustrating its ability to correctly simulate the competitive binding of O₂, CO₂ and H⁺ on haemoglobin. This paper is, however, the first validation of the model using data from a study designed specifically to evaluate its functionality in an interesting physiological situation.

In order to validate the mathematical model it was necessary to sample and mix blood whilst minimizing contact with atmospheric air during the procedures. This was performed by expelling atmospheric air hidden in the ‘dead space’ of syringes immediately, and by capping syringes until analysis. The presence of air bubbles does, however, represent a potential source of error in the procedure. A further source of error is in the determination of the precise fractions of mixing of the deoxygenated and oxygenated blood. This was performed by adding a high concentration of creatinine to the oxygenated blood, and measuring creatinine in all samples. Since the CV for creatinine is only 2–3%, this was a rather exact method of determining the fractional mixing. The mixing fractions determined using creatinine were checked by weighing the mixing syringe empty and before and after addition of the respective fractions of blood. In spite of these potential errors the difference between measured and the calculated values of the mixed blood were similar to the analytic variation, illustrating that the mathematical model can reliably simulate the mixing of blood.

The mathematical model presented here is formulated in a similar approach to Stewart, i.e. using mass balance and mass action equations. The total concentrations of the six components of blood (CO₂, O₂, SID/BB, haemoglobin, DPG and Atot) are represented as mass balance equations and each of these variables represents a state variable. This representation is convenient in performing simulations such as the mixing of blood samples, such that the concentrations of the state variables can be calculated by adding the concentrations of the respective fractions of the mixing samples and calculating all other variables by solving the model equations. Whilst there are a relatively large number of equations in the model, the model can still be regarded as mathematically simple, being only mass action, mass balance and simple physicochemical properties. A one to one relationship exists between buffering reaction equations and mass action equations and the model does not include any piecewise linear constants such as buffer capacity or Bohr–Haldane coefficients, with Bohr–Haldane effects being completely described by the different pK values of the mass action equations. The ability of the model to simulate the mixing of blood samples represents an improvement in functionality when compared to other models of acid–base chemistry based on mass-balance and mass-action approaches. Even the most complex of the models using this approach (Figge et al. 1998; Wooten 1999, 2003), do not calculate the competitive binding of O₂, CO₂ and H⁺ on haemoglobin, and as such do not have predictive power in simulating changes to blood at different levels of oxygen.

The ability of the model presented here to describe the mixing of blood enables it to be applied in many situations. In describing pulmonary physiology, the model has previously been used to simulate the mixing of lung capillary blood with that from pulmonary shunt in a system aiming at optimizing the mechanical ventilation of intensive care patients (Allerød et al. 2008; Rees et al. 2006a). The model has also previously been used as part of a mathematical method for calculating the acid–base and oxygen status of arterial blood from measurements performed only on peripheral venous blood (Rees et al. 2006b), where the transport of whole blood is simulated back through tissues with addition of oxygen and removal of carbon dioxide. This method has been validated in both intensive care patients (Toftegaard et al. 2009) and in patients with chronic respiratory disease (Rees et al. 2009). Whilst the model has been used successfully in these patients care should be taken when applying it in situations of rapid changes in acid–base or electrolyte status such as occurs following maximal exercise (McKelvie et al. 1992). In these situations the assumptions included in the model of steady state of reaction equations and ion transport may not be valid.

The data presented here have been collected in normal subjects and as such the range of pH in the deoxygenated blood, electrolyte concentrations, plasma protein concentrations, anion gap and BE were all normal. In particular, all model simulations were performed with the same constant value of Atot estimated by Rees and Andreassen (2005) (Atot = 23.5 meq/l) which represents the total buffer available due to plasma non-bicarbonate buffers, mainly proteins. This may be a reasonable assumption for blood in normal conditions, but further studies are required to provide a complete validation of the model, in particular in patients with abnormal values of Atot, electrolyte concentrations and plasma protein levels and in situations of metabolic acidosis or alkalosis.

This paper describes and provides a first validation of a mathematical model of the acid–base chemistry of blood. This model is based upon a mass balance and mass action representation of the chemical reactions including the effects of oxygen. Unlike previous models of this type it includes sufficient biochemical coverage to enable simulation of physiological situations such as the mixing of blood.