Two-dimensional elasticity solution for free vibration of simple-supported beams with arbitrarily and continuously varying thickness

Abstract

This paper studies the analytical solution for the vibration of simply supported beams with arbitrarily and continuously varying thickness based on the two-dimensional elasticity theory. The general expression of stress function, which exactly satisfies the governing differential equations and the boundary conditions, is derived. Frequency equation governing the free vibration of beams with variable thickness can be obtained by using the Fourier sinusoidal series expansion on the upper and lower surfaces of the beam. The present solution method ensures a rapid convergence and meets the need of high accuracy in modern precise instruments. Several examples are provided to show the application of the proposed solution method which can be used to assess the validity of various approximate solutions and numerical methods for the beams with arbitrarily and continuously varying thickness.

1 Introduction

It is well known that in many cases, non-uniform beams may achieve a better distribution of strength and weight than uniform beams and sometimes can satisfy special architectural and functional requirements. Therefore, the vibration analysis of beams with variable cross sections has been the subject of numerous investigations because of its relevance to aeronautical, civil and mechanical engineering.

A great deal of attention had been paid to the dynamic characteristics of non-uniform beams, and most of them were based on the classical beam theory. Granch and Adler [1] presented the closed-form solutions (in terms of the Bessel functions and/or power series) for the natural frequencies and mode shapes of the unconstrained non-uniform beams with four kinds of rectangular cross sections. Heidebrecht [2] determined the approximate natural frequencies and mode shapes of a non-uniform simply supported beam from the frequency equation using a Fourier sine series. Mabie and Rogers [3] considered polynomial variation of the beam cross-sectional area and the moment of inertia and obtained natural frequencies for a double-tapered beam. Bailey [4] numerically solved the frequencies of the non-uniform cantilever beams. Gupta [5] numerically determined the natural frequencies and mode shapes of the tapered beams using a finite element method. Naguleswaran [6, 7] determined the approximate natural frequencies of the single-tapered beams and double-tapered beams with a direct solution of the mode shape equation based on the Frobenius method. Free vibration of stepped beams has also received a considerable attention, and a comprehensive review is given by Jang and Bert [8]. Klein [9] used a combination of finite element approach and Rayleigh–Ritz method to analyze the vibration of non-uniform beams. Ece et al. [10] investigated the vibration of an isotropic beam with exponentially varying width. Banerjee and Williams [11] derived the exact dynamic stiffness matrices of axial, torsional and transverse vibrations for a range of tapered beam elements. Lee et al. [12] used Green’s function method in Laplace transform domain to study the vibration of general elastically restrained non-uniform beams and obtained the approximate fundamental solution by using a number of stepped beams to represent the non-uniform beam. Furthermore, Lee and Kuo [13] used Green’s function method to study the truncated non-uniform beams on elastic foundation with polynomial varying bending rigidity and elastically constrained ends, and an exact fundamental solution is given in power series form. Sato [14] used Ritz method to study a linearly tapered beam with ends restrained elastically against rotation and subjected to an axial force. Kim and Dickinson [15] used the Rayleigh–Ritz method, with orthogonally generated polynomials as admissible functions, to analyze slender beams subject to various complicated effects.

It should be mentioned that the Bernoulli–Euler beam theory has been only successfully applied to the slender beam analysis. This classical beam theory overpredicts all the eigen frequencies for thick beams and the higher eigen frequencies for slender beams as it neglects the effects of transverse shear deformation and rotary inertia. In modern industry, particularly in some high-tech fields such as aerospace engineering and the design of micro-mechanical apparatus, refining the analysis for dynamic characteristics of the beams is often necessary. The approximate theories cannot satisfy the requirement of higher accuracy. In such case, the two-dimensional analysis on the basis of small-strain linear elasticity theory which does not rely on any hypotheses involving the kinematics of deformation should be used.

A number of researchers have studied the free vibration of beams with constant thickness based on the two-dimensional elasticity theory. For example, Chen et al. [16] presented a new approach combining the state-space method and the differential quadrature method for freely vibrating laminated beams. Moreover, Chen et al. [17] proposed a mixed method for bending and free vibration of beams resting on a Pasternak elastic foundation. Ying et al. [18] presented exact solution for bending and free vibration of functionally graded beams resting on elastic foundations. Ye and Jin [19] presented elasticity solution for vibration of generally laminated beams by a modified Fourier expansion based sampling surface method. By using the state-space differential quadrature method, Alibeigloo and Liew [20] carried out the bending and free vibrational analyses of functionally graded carbon nanotube-reinforced composite beam embedded in piezoelectric layers based on the theory of elasticity. Recently, Xu and Zhou [21] studied the two-dimensional elasticity solutions for static analysis of multi-span simply supported beams with arbitrarily and continuously variable thickness. Moreover, Xu and Zhou [22, 23] presented the two-dimensional elasticity solution for static analysis of simply supported piezoelectric beams and functionally graded beams with arbitrarily and continuously variable thickness, respectively. To the best of authors’ knowledge, no study has been reported on the two-dimensional elasticity solution for free vibration of beams with arbitrarily and continuously variable thickness. The present work attempts to address this topic.

In this paper, the vibrational characteristics of simply supported beams with arbitrarily and continuously varying thickness based on the two-dimensional elasticity theory are investigated. The general expression of stress function, which exactly satisfies the governing differential equations and the boundary conditions, is derived. Frequency equation governing the free vibration of beams with variable thickness can be obtained by using the Fourier sinusoidal series expansion on the upper and lower surfaces of the beam. Numerical results are given for the various beams with variable thickness and compared with the known results. It is seen that the eigen frequencies can be obtained with high accuracy by using only a small of terms of series. The results are new and can serve as new data for researchers interested in this type of problem.

2 Basic formulations

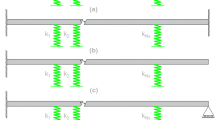
Consider an arbitrarily and continuously varying thickness beam, as shown in Fig. 1. The beam is simply supported at the two ends $x=0$ and $x=L$ (called as S–S beam). The length of beam is L, and the thickness of beam at the left end is H. The upper surface of the beam is described by the continuous functions $f_1 (x)$, and the lower surface of the beam is described by the continuous functions $f_2 (x)$.

Fig. 1

The S–S beam with arbitrarily and continuously varying thickness

The constitutive relations (plane stress) for beam read

$$\begin{aligned} \sigma _x =\frac{E}{1-\mu ^{2}}\left( \frac{\partial u}{\partial x}+\mu \frac{\partial v}{\partial y}\right) , \quad \sigma _y =\frac{E}{1-\mu ^{2}}\left( \frac{\partial v}{\partial y}+\mu \frac{\partial u}{\partial x}\right) , \quad \tau _{xy} =\frac{E}{2(1+\mu )}\left( \frac{\partial v}{\partial x}+\frac{\partial u}{\partial y}\right) \end{aligned}$$

(1)

where $\sigma _x$ and $\sigma _y$ are the normal stress components in the x and y directions, respectively, and $\tau _{xy}$ is the shear stress components, u, v are the displacement components in the $x,\,y$ directions, respectively. E is the Young’s modulus, and $\mu$ is the Poisson’s ratio.

The dynamic differential equations are

$$\begin{aligned} \frac{\partial \sigma _x }{\partial x}+\frac{\partial \tau _{xy} }{\partial y}=\rho \frac{\partial ^{2}u}{\partial t^{2}}, \quad \frac{\partial \sigma _y }{\partial y}+\frac{\partial \tau _{xy} }{\partial x}=\rho \frac{\partial ^{2}v}{\partial t^{2}} \end{aligned}$$

(2)

where $\rho$ denotes the material density.

Substituting Eq. (1) into Eq. (2), the two-dimensional differential equations expressed by displacements can be obtained as follows:

$$\begin{aligned} \frac{E}{1-\mu ^{2}}\left( \frac{\partial ^{2}u}{\partial x^{2}}+\mu \frac{\partial ^{2}v}{\partial x\partial y}\right) +\frac{E}{2(1+\mu )}\left( \frac{\partial ^{2}u}{\partial y^{2}}+\frac{\partial ^{2}v}{\partial x\partial y}\right)= & {} \rho \frac{\partial ^{2}u}{\partial t^{2}}\nonumber \\ \frac{E}{1-\mu ^{2}}\left( \frac{\partial ^{2}v}{\partial y^{2}}+\mu \frac{\partial ^{2}u}{\partial x\partial y}\right) +\frac{E}{2(1+\mu )}\left( \frac{\partial ^{2}v}{\partial x^{2}}+\frac{\partial ^{2}u}{\partial x\partial y}\right)= & {} \rho \frac{\partial ^{2}v}{\partial t^{2}} \end{aligned}$$

(3)

For a beam undergoing free vibration, its periodic displacement components can be expressed in terms of the displacement amplitude functions as follows:

$$\begin{aligned} u(x,y,t)=U(x,y)e^{i\omega t}, \quad v(x,y,t)=V(x,y)e^{i\omega t} \end{aligned}$$

(4)

where $\omega$ denotes the natural frequency of the beam and $i=\sqrt{-1}$.

Substituting Eq. (4) and into Eq. (3), one has

$$\begin{aligned} \frac{\partial ^{2}U(x,y)}{\partial x^{2}}+\frac{1+\mu }{2}\frac{\partial ^{2}V(x,y)}{\partial x\partial y}+\frac{1-\mu }{2}\frac{\partial ^{2}U(x,y)}{\partial y^{2}}+\frac{1-\mu ^{2}}{E}\rho \omega ^{2}U(x,y)= & {} 0 \nonumber \\ \frac{\partial ^{2}V(x,y)}{\partial y^{2}}+\frac{1+\mu }{2}\frac{\partial ^{2}U(x,y)}{\partial x\partial y}+\frac{1-\mu }{2}\frac{\partial ^{2}V(x,y)}{\partial x^{2}}+\frac{1-\mu ^{2}}{E}\rho \omega ^{2}V(x,y)= & {} 0 \end{aligned}$$

(5)

For a beam simply supported at two ends, the displacements and stresses boundary conditions are

$$\begin{aligned} \sigma _x =v=0\quad \hbox {at }x=0,\,L \end{aligned}$$

(6)

Assume that the displacement distributions have the following form:

$$\begin{aligned} U(x,y)= & {} \sum _{m=0}^\infty {U_m (y)} \cos \frac{m\pi x}{L} \nonumber \\ V(x,y)= & {} \sum _{m=0}^\infty {V_m (y)} \sin \frac{m\pi x}{L} , \end{aligned}$$

(7)

where $U_m (y),\,V_m (y)$ are the unknown functions about the coordinate y.

Substituting Eq. (7) and into Eq. (5), one has

$$\begin{aligned} \frac{1-\mu }{2}U_m^{(2)} (y)+\frac{1+\mu }{2}\frac{m\pi }{L}V_m^{(1)} (y)+\left( \frac{1-\mu ^{2}}{E}\rho \omega ^{2}-\frac{m^{2}\pi ^{2}}{L^{2}}\right) U_m (y)= & {} 0 \nonumber \\ V_m^{(2)} (y)-\frac{1+\mu }{2}\frac{m\pi }{L}U_m^{(1)} (y)+\left( \frac{1-\mu ^{2}}{E}\rho \omega ^{2}-\frac{1-\mu }{2}\frac{m^{2}\pi ^{2}}{L^{2}}\right) V_m (y)= & {} 0 . \end{aligned}$$

(8)

Eliminating functions $U_m (y)$, a fourth-order differential equation of $V_m (y)$ can be derived out from Eq. (8) as follows

$$\begin{aligned}&V_m^{(4)} (y)+\left[ \frac{(3-\mu )(1+\mu )}{E}\rho \omega ^{2}-\frac{2m^{2}\pi ^{2}}{L^{2}}\right] V_m^{(2)} (y)\nonumber \\&\qquad +\left( \frac{1-\mu ^{2}}{E}\rho \omega ^{2}-\frac{m^{2}\pi ^{2}}{L^{2}}\right) \left[ \frac{2(1+\mu )}{E}\rho \omega ^{2}-\frac{m^{2}\pi ^{2}}{L^{2}}\right] V_m (y)=0 \end{aligned}$$

(9)

Denoting the square of the roots of the characteristic equation related to Eq. (9) as $\lambda ^{2}$, one has

$$\begin{aligned} \left[ \lambda ^{2}-\left( \frac{m^{2}\pi ^{2}}{L^{2}}-\frac{1-\mu ^{2}}{E}\rho \omega ^{2}\right) \right] \left\{ \lambda ^{2}-\left[ \frac{m^{2}\pi ^{2}}{L^{2}}-\frac{2(1+\mu )}{E}\rho \omega ^{2}\right] \right\} =0 \end{aligned}$$

(10)

3 Solution of displacements and stresses

The solution form of Eq. (9) is dependent of the sign of the coefficient $\frac{m^{2}\pi ^{2}}{L^{2}}-\frac{1-\mu ^{2}}{E}\rho \omega ^{2}$ and $\frac{m^{2}\pi ^{2}}{L^{2}}-\frac{2(1+\mu )}{E}\rho \omega ^{2}$. Therefore, there are three possible solutions for Eq. (9):

Solution I When $\frac{2(1+\mu )}{E}\rho \omega ^{2}>\frac{m^{2}\pi ^{2}}{L^{2}}>\frac{1-\mu ^{2}}{E}\rho \omega ^{2}$

$$\begin{aligned} V_m (y)=sh(\alpha _m y)A_m +ch(\alpha _m y)B_m +\sin (\beta _m y)C_m +\cos (\beta _m y)D_m \end{aligned}$$

(11)

in which,

$$\begin{aligned} \alpha _m =\sqrt{\frac{m^{2}\pi ^{2}}{L^{2}}-\frac{1-\mu ^{2}}{E}\rho \omega ^{2}}, \quad \beta _m =\sqrt{\frac{2(1+\mu )}{E}\rho \omega ^{2}-\frac{m^{2}\pi ^{2}}{L^{2}}} \end{aligned}$$

(12)

Substituting Eq. (11) and into Eq. (8), one has

$$\begin{aligned} U_m (y)=I_m^1 [ch(\alpha _m y)A_m +sh(\alpha _m y)B_m ]+J_m^1 [\cos (\beta _m y)C_m -\sin (\beta _m y)D_m ] \end{aligned}$$

(13)

in which,

$$\begin{aligned} I_m^1= & {} \frac{\frac{1-\mu }{1+\mu }\frac{L}{m\pi }\alpha _m ^{3}+\left[ \frac{(1-\mu )^{2}}{E}\frac{L}{m\pi }\rho \omega ^{2}+\frac{2\mu }{1+\mu }\frac{m\pi }{L}\right] \alpha _m }{\frac{m^{2}\pi ^{2}}{L^{2}}-\frac{1-\mu ^{2}}{E}\rho \omega ^{2}} \nonumber \\ J_m^1= & {} \frac{-\frac{1-\mu }{1+\mu }\frac{L}{m\pi }\beta _m ^{3}+\left[ \frac{(1-\mu )^{2}}{E}\frac{L}{m\pi }\rho \omega ^{2}+\frac{2\mu }{1+\mu }\frac{m\pi }{L}\right] \beta _m }{\frac{m^{2}\pi ^{2}}{L^{2}}-\frac{1-\mu ^{2}}{E}\rho \omega ^{2}} \end{aligned}$$

(14)

Substituting Eq. (11) and Eq. (13) into Eq. (1), one has

$$\begin{aligned} \sigma _x= & {} \frac{E}{1-\mu ^{2}}e^{i\omega t}\sum _{m=1}^\infty \left\{ \left( -\frac{m\pi }{L}I_m^1 +\mu \alpha _m \right) [ch(\alpha _m y)A_m +sh(\alpha _m y)B_m ]\right. \nonumber \\&\left. + \left( -\frac{m\pi }{L}J_m^1 +\mu \beta _m\right) [\cos (\beta _m y)C_m -\sin (\beta _m y)D_m]\right\} \sin \frac{m\pi x}{L},\nonumber \\ \sigma _y= & {} \frac{E}{1-\mu ^{2}}e^{i\omega t}\sum _{m=1}^\infty \left\{ \left( -\mu \frac{m\pi }{L}I_m^1 +\alpha _m \right) [ch(\alpha _m y)A_m +sh(\alpha _m y)B_m ] \right. \nonumber \\&\left. + \left( -\mu \frac{m\pi }{L}J_m^1 +\beta _m \right) [\cos (\beta _m y)C_m -\sin (\beta _m y)D_m ]\right\} \sin \frac{m\pi x}{L},\nonumber \\ \tau _{xy}= & {} \frac{E}{2(1+\mu )}e^{i\omega t}\sum _{m=1}^\infty \left\{ \left( \frac{m\pi }{L}+\alpha _m I_m^1\right) [sh(\alpha _m y)A_m +ch(\alpha _m y)B_m ]\right. \nonumber \\&\left. + \left( \frac{m\pi }{L}-\beta _m J_m^1\right) [\sin (\beta _m y)C_m +\cos (\beta _m y)D_m ]\right\} \cos \frac{m\pi x}{L} \end{aligned}$$

(15)

Solution II When $\frac{2(1+\mu )}{E}\rho \omega ^{2}>\frac{1-\mu ^{2}}{E}\rho \omega ^{2}>\frac{m^{2}\pi ^{2}}{L^{2}}$

$$\begin{aligned} V_m (y)=\sin (\alpha _m y)A_m +\cos (\alpha _m y)B_m +\sin (\beta _m y)C_m +\cos (\beta _m y)D_m \end{aligned}$$

(16)

in which,

$$\begin{aligned} \alpha _m =\sqrt{\frac{1-\mu ^{2}}{E}\rho \omega ^{2}-\frac{m^{2}\pi ^{2}}{L^{2}}}, \quad \beta _m =\sqrt{\frac{2(1+\mu )}{E}\rho \omega ^{2}-\frac{m^{2}\pi ^{2}}{L^{2}}} \end{aligned}$$

(17)

Substituting Eq. (16) and into Eq. (8), one has

$$\begin{aligned} U_m (y)=I_m^2 [\cos (\alpha _m y)A_m -\sin (\alpha _m y)B_m ]+J_m^2 [\cos (\beta _m y)C_m -\sin (\beta _m y)D_m ] \end{aligned}$$

(18)

in which,

$$\begin{aligned} I_m^2 =\frac{-\frac{1-\mu }{1+\mu }\frac{L}{m\pi }\alpha _m ^{3}+\left[ \frac{(1-\mu )^{2}}{E}\frac{L}{m\pi }\rho \omega ^{2}+\frac{2\mu }{1+\mu }\frac{m\pi }{L}\right] \alpha _m }{\frac{m^{2}\pi ^{2}}{L^{2}}-\frac{1-\mu ^{2}}{E}\rho \omega ^{2}} \nonumber \\ J_m^2 =\frac{-\frac{1-\mu }{1+\mu }\frac{L}{m\pi }\beta _m ^{3}+\left[ \frac{(1-\mu )^{2}}{E}\frac{L}{m\pi }\rho \omega ^{2}+\frac{2\mu }{1+\mu }\frac{m\pi }{L}\right] \beta _m }{\frac{m^{2}\pi ^{2}}{L^{2}}-\frac{1-\mu ^{2}}{E}\rho \omega ^{2}} \end{aligned}$$

(19)

Substituting Eq. (16) and Eq. (18) into Eq. (1), one has

$$\begin{aligned} \sigma _x= & {} \frac{E}{1-\mu ^{2}}e^{i\omega t}\sum _{m=1}^\infty \left\{ \left( -\frac{m\pi }{L}I_m^2 +\mu \alpha _m\right) [\cos (\alpha _m y)A_m -\sin (\alpha _m y)B_m ]\right. \nonumber \\&\left. +\left( -\frac{m\pi }{L}J_m^2 +\mu \beta _m\right) [\cos (\beta _m y)C_m -\sin (\beta _m y)D_m ]\right\} \sin \frac{m\pi x}{L},\nonumber \\ \sigma _y= & {} \frac{E}{1-\mu ^{2}}e^{i\omega t}\sum _{m=1}^\infty \left\{ \left( -\mu \frac{m\pi }{L}I_m^2 +\alpha _m\right) [\cos (\alpha _m y)A_m -\sin (\alpha _m y)B_m ]\right. \nonumber \\&\left. + \left( -\mu \frac{m\pi }{L}J_m^2 +\beta _m\right) [\cos (\beta _m y)C_m -\sin (\beta _m y)D_m ]\right\} \sin \frac{m\pi x}{L},\nonumber \\ \tau _{xy}= & {} \frac{E}{2(1+\mu )}e^{i\omega t}\sum _{m=1}^\infty \left\{ \left( \frac{m\pi }{L}-\alpha _m I_m^2\right) [\sin (\alpha _m y)A_m +\cos (\alpha _m y)B_m ]\right. \nonumber \\&+\left( \frac{m\pi }{L}-\beta _m J_m^2\right) [\sin (\beta _m y)C_m +\cos (\beta _m y)D_m ]\}\cos \frac{m\pi x}{L} \end{aligned}$$

(20)

Solution III When $\frac{m^{2}\pi ^{2}}{L^{2}}>\frac{2(1+\mu )}{E}\rho \omega ^{2}>\frac{1-\mu ^{2}}{E}\rho \omega ^{2}$

$$\begin{aligned} V_m (y)=sh(\alpha _m y)A_m +ch(\alpha _m y)B_m +sh(\beta _m y)C_m +ch(\beta _m y)D_m \end{aligned}$$

(21)

in which,

$$\begin{aligned} \alpha _m =\sqrt{\frac{m^{2}\pi ^{2}}{L^{2}}-\frac{1-\mu ^{2}}{E}\rho \omega ^{2}}, \quad \beta _m =\sqrt{\frac{m^{2}\pi ^{2}}{L^{2}}-\frac{2(1+\mu )}{E}\rho \omega ^{2}} \end{aligned}$$

(22)

Substituting Eq. (21) and into Eq. (8), one has

$$\begin{aligned} U_m (y)=I_m^3 [ch(\alpha _m y)A_m +sh(\alpha _m y)B_m ]+J_m^3 [ch(\beta _m y)C_m +sh(\beta _m y)D_m ] \end{aligned}$$

(23)

in which,

$$\begin{aligned} I_m^3= & {} \frac{\frac{1-\mu }{1+\mu }\frac{L}{m\pi }\alpha _m ^{3}+\left[ \frac{(1-\mu )^{2}}{E}\frac{L}{m\pi }\rho \omega ^{2}+\frac{2\mu }{1+\mu }\frac{m\pi }{L}\right] \alpha _m }{\frac{m^{2}\pi ^{2}}{L^{2}}-\frac{1-\mu ^{2}}{E}\rho \omega ^{2}} \nonumber \\ J_m^3= & {} \frac{\frac{1-\mu }{1+\mu }\frac{L}{m\pi }\beta _m ^{3}+\left[ \frac{(1-\mu )^{2}}{E}\frac{L}{m\pi }\rho \omega ^{2}+\frac{2\mu }{1+\mu }\frac{m\pi }{L}\right] \beta _m }{\frac{m^{2}\pi ^{2}}{L^{2}}-\frac{1-\mu ^{2}}{E}\rho \omega ^{2}} \end{aligned}$$

(24)

Substituting Eq. (21) and Eq. (23) into Eq. (1), one has

$$\begin{aligned} \sigma _x= & {} \frac{E}{1-\mu ^{2}}e^{i\omega t}\sum _{m=1}^\infty \left\{ \left( -\frac{m\pi }{L}I_m^3 +\mu \alpha _m\right) [ch(\alpha _m y)A_m +sh(\alpha _m y)B_m ]\right. \nonumber \\&\left. +\left( -\frac{m\pi }{L}J_m^3 +\mu \beta _m\right) [ch(\beta _m y)C_m +sh(\beta _m y)D_m ]\right\} \sin \frac{m\pi x}{L},\nonumber \\ \sigma _y= & {} \frac{E}{1-\mu ^{2}}e^{i\omega t}\sum _{m=1}^\infty \left\{ \left( -\mu \frac{m\pi }{L}I_m^3 +\alpha _m\right) [ch(\alpha _m y)A_m +sh(\alpha _m y)B_m ]\right. \nonumber \\&\left. +\left( -\mu \frac{m\pi }{L}J_m^3 +\beta _m \right) [ch(\beta _m y)C_m +sh(\beta _m y)D_m ]\right\} \sin \frac{m\pi x}{L},\nonumber \\ \tau _{xy}= & {} \frac{E}{2(1+\mu )}e^{i\omega t}\sum _{m=1}^\infty \left\{ \left( \frac{m\pi }{L}+\alpha _m I_m^3\right) [sh(\alpha _m y)A_m +ch(\alpha _m y)B_m ]\right. \nonumber \\&\left. + \left( \frac{m\pi }{L}+\beta _m J_m^3\right) [sh(\beta _m y)C_m +ch(\beta _m y)D_m ]\right\} \cos \frac{m\pi x}{L} \end{aligned}$$

(25)

4 Upper and lower surface conditions

For free vibration problem, the surface of the beam is traction-free. Therefore, the boundary conditions on the upper surface of the beam can be written as

$$\begin{aligned} l_1 (x)\sigma _x +m_1 (x)\tau _{xy} =0, \quad m_1 (x)\sigma _y +l_1 (x)\tau _{xy} =0 \end{aligned}$$

(26)

where

$$\begin{aligned} l_1 (x)= & {} \cos (N_1 ,x)=-\frac{{\text {d}}f_1 (x)}{{\text {d}}x}\Bigg /\sqrt{1+\left[ \frac{{\text {d}}f_1 (x)}{{\text {d}}x}\right] ^{2}} \nonumber \\ m_1 (x)= & {} \cos (N_1 ,y)=-1\Bigg /\sqrt{1+\left[ \frac{{\text {d}}f_1 (x)}{{\text {d}}x}\right] ^{2}} \end{aligned}$$

(27)

The boundary conditions on the lower surface of the beam can be written as

$$\begin{aligned} l_2 (x)\sigma _x +m_2 (x)\tau _{xy} =0, \quad m_2 (x)\sigma _y +l_2 (x)\tau _{xy} =0 \end{aligned}$$

(28)

where

$$\begin{aligned} l_2 (x)= & {} \cos (N_2 ,x)=-\frac{{\text {d}}f_2 (x)}{{\text {d}}x}\Bigg /\sqrt{1+\left[ \frac{{\text {d}}f_2 (x)}{{\text {d}}x}\right] ^{2}}\nonumber \\ m_2 (x)= & {} \cos (N_2 ,y)=1\Bigg /\sqrt{1+\left[ \frac{{\text {d}}f_2 (x)}{{\text {d}}x}\right] ^{2}}, \end{aligned}$$

(29)

5 Unknown coefficients

Considering the simultaneous Eqs. (26–29), the Fourier sinusoidal series expansion to each equation can be made, namely

$$\begin{aligned} \int \limits _0^L {\sin \frac{n\pi x}{L}[} l_1 (x)\sigma _x +m_1 (x)\tau _{xy} ]{\text {d}}x= & {} \int \limits _0^L {\sin \frac{n\pi x}{L}\cdot } 0{\text {d}}x \end{aligned}$$

(30)

$$\begin{aligned} \int \limits _0^L {\sin \frac{n\pi x}{L}[} m_1 (x)\sigma _y +l_1 (x)\tau _{xy} ]{\text {d}}x= & {} \int \limits _0^L {\sin \frac{n\pi x}{L}\cdot } 0{\text {d}}x \end{aligned}$$

(31)

$$\begin{aligned} \int \limits _0^L {\sin \frac{n\pi x}{L}[} l_2 (x)\sigma _x +m_2 (x)\tau _{xy} ]{\text {d}}x= & {} \int \limits _0^L {\sin \frac{n\pi x}{L}\cdot } 0{\text {d}}x \end{aligned}$$

(32)

$$\begin{aligned} \int \limits _0^L {\sin \frac{n\pi x}{L}[} m_2 (x)\sigma _y +l_2 (x)\tau _{xy} ]dx= & {} \int \limits _0^L {\sin \frac{n\pi x}{L}\cdot } 0{\text {d}}x \end{aligned}$$

(33)

Substituting Eq. (25) into the above equations and truncating each series to $N+1$ terms yield an algebraic equations in the matrix form as follows:

(34)

From which the following frequency equation is derived for the requirement of non-trivial solutions:

$$\begin{aligned} \left| {{\begin{array}{cccccccccccc} {A_{11} ^{(1)}}&{} {\cdot \cdot \cdot }&{} {A_{1N} ^{(1)}}&{} {B_{11} ^{(1)}}&{} {\cdot \cdot \cdot }&{} {B_{1N} ^{(1)}}&{} {C_{11} ^{(1)}}&{} {\cdot \cdot \cdot }&{} {C_{1N} ^{(1)}}&{} {D_{11} ^{(1)}}&{} {\cdot \cdot \cdot }&{} {D_{1N} ^{(1)}} \\ {\cdot \cdot \cdot }&{} &{} {\cdot \cdot \cdot }&{} {\cdot \cdot \cdot }&{} &{} {\cdot \cdot \cdot }&{} {\cdot \cdot \cdot }&{} &{} {\cdot \cdot \cdot }&{} {\cdot \cdot \cdot }&{} &{} {\cdot \cdot \cdot } \\ {A_{N1} ^{(1)}}&{} {\cdot \cdot \cdot }&{} {A_{NN} ^{(1)}}&{} {B_{N1} ^{(1)}}&{} {\cdot \cdot \cdot }&{} {B_{NN} ^{(1)}}&{} {C_{N1} ^{(1)}}&{} {\cdot \cdot \cdot }&{} {C_{NN} ^{(1)}}&{} {D_{N1} ^{(1)}}&{} {\cdot \cdot \cdot }&{} {D_{NN} ^{(1)}} \\ {A_{11} ^{(2)}}&{} {\cdot \cdot \cdot }&{} {A_{1N} ^{(2)}}&{} {B_{11} ^{(2)}}&{} {\cdot \cdot \cdot }&{} {B_{1N} ^{(2)}}&{} {C_{11} ^{(2)}}&{} {\cdot \cdot \cdot }&{} {C_{1N} ^{(2)}}&{} {D_{11} ^{(2)}}&{} {\cdot \cdot \cdot }&{} {D_{1N} ^{(2)}} \\ {\cdot \cdot \cdot }&{} &{} {\cdot \cdot \cdot }&{} {\cdot \cdot \cdot }&{} &{} {\cdot \cdot \cdot }&{} {\cdot \cdot \cdot }&{} &{} {\cdot \cdot \cdot }&{} {\cdot \cdot \cdot }&{} &{} {\cdot \cdot \cdot } \\ {A_{N1} ^{(2)}}&{} {\cdot \cdot \cdot }&{} {A_{NN} ^{(2)}}&{} {B_{N1} ^{(2)}}&{} {\cdot \cdot \cdot }&{} {B_{NN} ^{(2)}}&{} {C_{N1} ^{(2)}}&{} {\cdot \cdot \cdot }&{} {C_{NN} ^{(2)}}&{} {D_{N1} ^{(2)}}&{} {\cdot \cdot \cdot }&{} {D_{NN} ^{(2)}} \\ {A_{11} ^{(3)}}&{} {\cdot \cdot \cdot }&{} {A_{1N} ^{(3)}}&{} {B_{11} ^{(3)}}&{} {\cdot \cdot \cdot }&{} {B_{1N} ^{(3)}}&{} {C_{11} ^{(3)}}&{} {\cdot \cdot \cdot }&{} {C_{1N} ^{(3)}}&{} {D_{11} ^{(3)}}&{} {\cdot \cdot \cdot }&{} {D_{1N} ^{(3)}} \\ {\cdot \cdot \cdot }&{} &{} {\cdot \cdot \cdot }&{} {\cdot \cdot \cdot }&{} &{} {\cdot \cdot \cdot }&{} {\cdot \cdot \cdot }&{} &{} {\cdot \cdot \cdot }&{} {\cdot \cdot \cdot }&{} &{} {\cdot \cdot \cdot } \\ {A_{N1} ^{(3)}}&{} {\cdot \cdot \cdot }&{} {A_{NN} ^{(3)}}&{} {B_{N1} ^{(3)}}&{} {\cdot \cdot \cdot }&{} {B_{NN} ^{(3)}}&{} {C_{N1} ^{(3)}}&{} {\cdot \cdot \cdot }&{} {C_{NN} ^{(3)}}&{} {D_{N1} ^{(3)}}&{} {\cdot \cdot \cdot }&{} {D_{NN} ^{(3)}} \\ {A_{11} ^{(4)}}&{} {\cdot \cdot \cdot }&{} {A_{1N} ^{(4)}}&{} {B_{11} ^{(4)}}&{} {\cdot \cdot \cdot }&{} {B_{1N} ^{(4)}}&{} {C_{11} ^{(4)}}&{} {\cdot \cdot \cdot }&{} {C_{1N} ^{(4)}}&{} {D_{11} ^{(4)}}&{} {\cdot \cdot \cdot }&{} {D_{1N} ^{(4)}} \\ {\cdot \cdot \cdot }&{} &{} {\cdot \cdot \cdot }&{} {\cdot \cdot \cdot }&{} &{} {\cdot \cdot \cdot }&{} {\cdot \cdot \cdot }&{} &{} {\cdot \cdot \cdot }&{} {\cdot \cdot \cdot }&{} &{} {\cdot \cdot \cdot } \\ {A_{N1} ^{(4)}}&{} {\cdot \cdot \cdot }&{} {A_{NN} ^{(4)}}&{} {B_{N1} ^{(4)}}&{} {\cdot \cdot \cdot }&{} {B_{NN} ^{(4)}}&{} {C_{N1} ^{(4)}}&{} {\cdot \cdot \cdot }&{} {C_{NN} ^{(4)}}&{} {D_{N1} ^{(4)}}&{} {\cdot \cdot \cdot }&{} {D_{NN} ^{(4)}} \\ \end{array} }} \right| =0 \end{aligned}$$

(35)

The elements in the above matrix equation are given in Appendix A. It should be noted that Eq. (35) is not a polynomial equation about $\omega$ any more as obtained by various conventional beam theories, but a transcendental equation. Consequently, the number of solutions to this equation is infinite, that is, one can obtain innumerable natural frequencies from Eq. (35) theoretically.

6 Convergence studies

In the following studies, the material properties of the beam are fixed at $E=2.06\times {10}^{11}\,\hbox {Pa}$, $\mu =0.3$, $\rho =7800\,\hbox {kg/m}^{3}$, unless otherwise stated. In order to verify the accuracy of the proposed method, the convergence of the present solutions is studied firstly. An S–S wedge-shaped beam with the linearly varying lower surface is shown in Fig. 2. The depth-to-length ratio of the beam is $H/L=0.05$.

Fig. 2

The S–S wedge-shaped beam with linearly varying lower surface

Five different series terms $N=10$, 20, 30, 40, 50 have been checked. The first eight frequency parameters with two depth ratios $H_{1}/H= 1.5$, 2 have been calculated and given in Table 1.

Table 1 Convergence of frequency parameters $\omega$ for S–S wedge-shaped beam with the linearly varying lower surface

It can be seen from Table 1 that the numerical results of $N=40$ and $N=50$ have a good agreement. The results from $N=50$ are accurate up to the fourth significant digit for both cases. The maximum relative errors of frequency between $N=40$ and $N=50$ are no more than 0.1%. This indicates the rapid convergence of the proposed method. Therefore, all the series terms are fixed at $N=40$ in the following numerical calculations. It should be mentioned that the usable number of terms in numerical calculations is limited, which is related to the effective digit of computer used. Overly increasing the number of terms in the series may lead to the ill-conditioned results.

7 Comparison studies

In order to validate the formulations, the present two-dimensional elasticity solutions are compared with the classical beam theory (CBT) and the finite element (FE) simulation. Consider an S–S beam with constant thickness, as shown in Fig. 3. The first eight frequency parameters for beams with three different depth-to-length ratio $H/L=0.01$, 0.05, 0.1 calculated using the present method are given in Table 2. Note that $H/L=0.01$ corresponds to a very thin beam, $H/L=0.1$ correspond to moderately thick beams. It can be seen from Table 2 that with the increase in the beam thickness, the error of the classical beam theory solution to the two-dimensional elasticity solution rapidly increases, especially for the higher eigenfrequency. Therefore, the solution of the two-dimensional elasticity theory is more accurate than that of the classical beam theory. However, the excellent agreement of the two-dimensional elasticity with the FE solution for both thin beams and moderately thick beams can be seen from Table 2. The maximum relative error of the two-dimensional elasticity solution to the FE solution is no more than 0.1%.

Fig. 3

The S–S beam with constant thickness

Table 2 Comparison of the first eight frequency parameters $\omega$ for S–S beam with constant thickness

A finite element (FE) simulation using the software ABAQUS has been also carried out to verify the correctness of the present two-dimensional elasticity solution for varying thickness beams. The beam with the linearly varying lower surface in two directions is considered, as shown in Fig. 4. The depth-to-length ratio of the beam is $H/L=0.05$. The depth ratio of the beam is $H_{1}/H=2$. The first eight frequency parameters for beams computed using the present method are given in Table 3 and compared with finite element simulation results. It can be seen from Table 3 that the present two-dimensional elasticity solution matches well with the FE solution. This comparison study validates the proposed method and verifies its accuracy again.

Fig. 4

The S–S beam with linearly varying lower surface in two directions

Table 3 Comparison of the first eight frequency parameters $\omega$ for S–S beam with linearly varying lower surface in two directions ($H/L=0.05$, $H_{1}/H=2$)

8 Numerical examples

A survey on the literature reveals that the available results for vibrations of beams with arbitrarily and continuously varying thickness are very limited. Therefore, it is meaningful to systematically provide some data what can serve as a benchmark of further reference for researchers and present useful information for designers. In this section, three types of beams with variable thickness are analyzed in detail. Figure 5 shows an S–S beam with parabolic concave lower surface. The maximum depth-to-length ratio of the beam is $H/L=0.1$. The first eight frequency parameters for beams with five different depth ratios $H_{1}/H =0.5$, 0.6, 0.7, 0.8, 0.9 computed using the present method are given in Table 4. From Table 4, one can see that the eigenfrequencies of beams increase with the increase in the depth ratios.

Fig. 5

The S–S beam with parabolic concave lower surface

Table 4 The first eight frequency parameters $\omega$ for S–S beam with the parabolic concave lower surface

Figure 6 shows an S–S beam with the parabolic convex lower surface. The minimum depth-to-length ratio of the beam is $H/L=0.05$. The first eight frequency parameters for beams with three different depth ratios $H_{1}/H =1.2$, 1.6, 2.0 computed using the present method are given in Table 5. From Table 5, one can find that the depth ratios $H_{1}/H$ have an important effect on the eigenfrequencies of the beams with varying thickness. It is seen that decreasing the depth ratios trends to lower the eigenfrequencies of the beam.

Fig. 6

The S–S beam with parabolic convex lower surface

Table 5 The first eight frequency parameters $\omega$ for S–S beam with the parabolic convex lower surface

Figure 7 shows an S–S varying thickness beam which can be usually found in civil engineering. The depth-to-length ratio of the beam is $H/L=0.1$. The depth ratio of the beam is $H_{1}/H=0.5$, and $L_{1}/L$ is fixed at 0.2. The effect of Poisson’s ratio on natural frequencies of the beam has been studied. The first eight frequency parameters for beams with four different Poisson’s ratios $\mu =1/6\,1/4,\,0.3,\,0.4$ are calculated and given in Table 6. It can be seen from Table 6 that increasing the Poisson’s ratios can not lower the eigenfrequencies of the beam.

Fig. 7

The S–S beam with parabolic convex lower surface

Table 6 The first eight frequency parameters $\omega$ for S–S beam with varying thickness

9 Conclusions

The general expression of stress function for S–S beams, which exactly satisfies the governing differential equations and simply supported boundary conditions at two ends, is deduced based on the two-dimensional elasticity theory. Frequency equation governing the free vibration of beams with variable thickness can be obtained by using the Fourier sinusoidal series expansion on the upper and lower surfaces of the beam. The solution can be applied to the free vibration analysis of arbitrarily and continuously varying thickness beams. A convergence study has shown that the solutions converge quickly with an increase in the series terms. A comparative study has indicated that the present solutions agree well with the results from the finite element method. To demonstrate the effectiveness of the proposed solution method, three examples have been taken. Numerical results have been presented and discussed in detail. The study has shown that the proposed solution method is effective. It preserves some advantages of the analytical solution such as maintaining a physical insight in the solution process. It is expected that the presented method offers a valid alternative in solving engineering problems in which ultra-high solution accuracy is required.

Appendix A. Elements in matrix equation (35)

$$\begin{aligned} A_{mn}^{(1)}= & {} \int \limits _0^L {l_1 (x)\sin \frac{n\pi x}{L}} \sin \frac{m\pi x}{L}\frac{E}{1-\mu ^{2}}\left( -\frac{m\pi }{L}I_m^3 +\mu \alpha _m\right) \cosh [\alpha _m f_1 (x)]{\text {d}}x\\&+ \int \limits _0^L {m_1 (x)\sin \frac{n\pi x}{L}} \cos \frac{m\pi x}{L}\frac{E}{2(1+\mu )}\left( \frac{m\pi }{L}+\alpha _m I_m^3\right) \sinh [\alpha _m f_1 (x)]{\text {d}}x,\\ B_{mn}^{(1)}= & {} \int \limits _0^L {l_1 (x)\sin \frac{n\pi x}{L}} \sin \frac{m\pi x}{L}\frac{E}{1-\mu ^{2}}\left( -\frac{m\pi }{L}I_m^3 +\mu \alpha _m \right) \sinh [\alpha _m f_1 (x)]{\text {d}}x\\&+ \int \limits _0^L {m_1 (x)\sin \frac{n\pi x}{L}} \cos \frac{m\pi x}{L}\frac{E}{2(1+\mu )}\left( \frac{m\pi }{L}+\alpha _m I_m^3\right) \cosh [\alpha _m f_1 (x)]{\text {d}}x,\\ C_{mn}^{(1)}= & {} \int \limits _0^L {l_1 (x)\sin \frac{n\pi x}{L}} \sin \frac{m\pi x}{L}\frac{E}{1-\mu ^{2}}\left( -\frac{m\pi }{L}J_m^3 +\mu \beta _m\right) \cosh [\beta _m f_1 (x)]{\text {d}}x\\&+ \int \limits _0^L {m_1 (x)\sin \frac{n\pi x}{L}} \cos \frac{m\pi x}{L}\frac{E}{2(1+\mu )}\left( \frac{m\pi }{L}+\beta _m J_m^3\right) \sinh [\beta _m f_1 (x)]{\text {d}}x,\\ D_{mn}^{(1)}= & {} \int \limits _0^L {l_1 (x)\sin \frac{n\pi x}{L}} \sin \frac{m\pi x}{L}\frac{E}{1-\mu ^{2}}(-\frac{m\pi }{L}J_m^3 +\mu \beta _m )\sinh [\beta _m f_1 (x)]{\text {d}}x\\&+ \int \limits _0^L {m_1 (x)\sin \frac{n\pi x}{L}} \cos \frac{m\pi x}{L}\frac{E}{2(1+\mu )}\left( \frac{m\pi }{L}+\beta _m J_m^3\right) \cosh [\beta _m f_1 (x)]{\text {d}}x,\\ A_{mn}^{(2)}= & {} \int \limits _0^L {m_1 (x)\sin \frac{n\pi x}{L}} \sin \frac{m\pi x}{L}\frac{E}{1-\mu ^{2}}(-\mu \frac{m\pi }{L}I_m^3 +\alpha _m )\cosh [\alpha _m f_1 (x)]{\text {d}}x\\&+ \int \limits _0^L {l_1 (x)\sin \frac{n\pi x}{L}} \cos \frac{m\pi x}{L}\frac{E}{2(1+\mu )}\left( \frac{m\pi }{L}+\alpha _m I_m^3\right) \sinh [\alpha _m f_1 (x)]{\text {d}}x,\\ B_{mn}^{(2)}= & {} \int \limits _0^L {m_1 (x)\sin \frac{n\pi x}{L}} \sin \frac{m\pi x}{L}\frac{E}{1-\mu ^{2}}(-\mu \frac{m\pi }{L}I_m^3 +\alpha _m )\sinh [\alpha _m f_1 (x)]{\text {d}}x\\&+ \int \limits _0^L {l_1 (x)\sin \frac{n\pi x}{L}} \cos \frac{m\pi x}{L}\frac{E}{2(1+\mu )}\left( \frac{m\pi }{L}+\alpha _m I_m^3\right) \cosh [\alpha _m f_1 (x)]{\text {d}}x,\\ C_{mn}^{(2)}= & {} \int \limits _0^L {m_1 (x)\sin \frac{n\pi x}{L}} \sin \frac{m\pi x}{L}\frac{E}{1-\mu ^{2}}(-\mu \frac{m\pi }{L}J_m^3 +\beta _m )\cosh [\beta _m f_1 (x)]{\text {d}}x\\&+\int \limits _0^L {l_1 (x)\sin \frac{n\pi x}{L}} \cos \frac{m\pi x}{L}\frac{E}{2(1+\mu )}\left( \frac{m\pi }{L}+\beta _m J_m^3\right) \sinh [\beta _m f_1 (x)]{\text {d}}x,\\ D_{mn}^{(2)}= & {} \int \limits _0^L {m_1 (x)\sin \frac{n\pi x}{L}} \sin \frac{m\pi x}{L}\frac{E}{1-\mu ^{2}}\left( -\mu \frac{m\pi }{L}J_m^3 +\beta _m\right) \sinh [\beta _m f_1 (x)]{\text {d}}x\\&+ \int \limits _0^L {l_1 (x)\sin \frac{n\pi x}{L}} \cos \frac{m\pi x}{L}\frac{E}{2(1+\mu )}\left( \frac{m\pi }{L}+\beta _m J_m^3\right) \cosh [\beta _m f_1 (x)]{\text {d}}x, \end{aligned}$$

$$\begin{aligned} A_{mn}^{(3)}= & {} \int \limits _0^L {l_2 (x)\sin \frac{n\pi x}{L}} \sin \frac{m\pi x}{L}\frac{E}{1-\mu ^{2}}\left( -\frac{m\pi }{L}I_m^3 +\mu \alpha _m\right) \cosh [\alpha _m f_2 (x)]{\text {d}}x\\&+ \int \limits _0^L {m_2 (x)\sin \frac{n\pi x}{L}} \cos \frac{m\pi x}{L}\frac{E}{2(1+\mu )}\left( \frac{m\pi }{L}+\alpha _m I_m^3\right) \sinh [\alpha _m f_2 (x)]{\text {d}}x,\\ B_{mn}^{(3)}= & {} \int \limits _0^L {l_2 (x)\sin \frac{n\pi x}{L}} \sin \frac{m\pi x}{L}\frac{E}{1-\mu ^{2}}\left( -\frac{m\pi }{L}I_m^3 +\mu \alpha _m\right) \sinh [\alpha _m f_2 (x)]{\text {d}}x\\&+ \int \limits _0^L {m_2 (x)\sin \frac{n\pi x}{L}} \cos \frac{m\pi x}{L}\frac{E}{2(1+\mu )}\left( \frac{m\pi }{L}+\alpha _m I_m^3\right) \cosh [\alpha _m f_2 (x)]{\text {d}}x,\\ C_{mn}^{(3)}= & {} \int \limits _0^L {l_2 (x)\sin \frac{n\pi x}{L}} \sin \frac{m\pi x}{L}\frac{E}{1-\mu ^{2}}\left( -\frac{m\pi }{L}J_m^3 +\mu \beta _m \right) \cosh [\beta _m f_2 (x)]{\text {d}}x\\&+ \int \limits _0^L {m_2 (x)\sin \frac{n\pi x}{L}} \cos \frac{m\pi x}{L}\frac{E}{2(1+\mu )}\left( \frac{m\pi }{L}+\beta _m J_m^3\right) \sinh [\beta _m f_2 (x)]{\text {d}}x,\\ D_{mn}^{(3)}= & {} \int \limits _0^L {l_2 (x)\sin \frac{n\pi x}{L}} \sin \frac{m\pi x}{L}\frac{E}{1-\mu ^{2}}\left( -\frac{m\pi }{L}J_m^3 +\mu \beta _m\right) \sinh [\beta _m f_2 (x)]{\text {d}}x\\&+ \int \limits _0^L {m_2 (x)\sin \frac{n\pi x}{L}} \cos \frac{m\pi x}{L}\frac{E}{2(1+\mu )}\left( \frac{m\pi }{L}+\beta _m J_m^3\right) \cosh [\beta _m f_2 (x)]{\text {d}}x,\\ A_{mn}^{(4)}= & {} \int \limits _0^L {m_2 (x)\sin \frac{n\pi x}{L}} \sin \frac{m\pi x}{L}\frac{E}{1-\mu ^{2}}\left( -\mu \frac{m\pi }{L}I_m^3 +\alpha _m \right) \cosh [\alpha _m f_2 (x)]{\text {d}}x\\&+ \int \limits _0^L {l_2 (x)\sin \frac{n\pi x}{L}} \cos \frac{m\pi x}{L}\frac{E}{2(1+\mu )}\left( \frac{m\pi }{L}+\alpha _m I_m^3\right) \sinh [\alpha _m f_2 (x)]{\text {d}}x,\\ B_{mn}^{(4)}= & {} \int \limits _0^L {m_2 (x)\sin \frac{n\pi x}{L}} \sin \frac{m\pi x}{L}\frac{E}{1-\mu ^{2}}\left( -\mu \frac{m\pi }{L}I_m^3 +\alpha _m\right) \sinh [\alpha _m f_2 (x)]{\text {d}}x\\&+ \int \limits _0^L {l_2 (x)\sin \frac{n\pi x}{L}} \cos \frac{m\pi x}{L}\frac{E}{2(1+\mu )}\left( \frac{m\pi }{L}+\alpha _m I_m^3\right) \cosh [\alpha _m f_2 (x)]{\text {d}}x,\\ C_{mn}^{(4)}= & {} \int \limits _0^L {m_2 (x)\sin \frac{n\pi x}{L}} \sin \frac{m\pi x}{L}\frac{E}{1-\mu ^{2}}\left( -\mu \frac{m\pi }{L}J_m^3 +\beta _m\right) \cosh [\beta _m f_2 (x)]{\text {d}}x\\&+ \int \limits _0^L {l_2 (x)\sin \frac{n\pi x}{L}} \cos \frac{m\pi x}{L}\frac{E}{2(1+\mu )}\left( \frac{m\pi }{L}+\beta _m J_m^3\right) \sinh [\beta _m f_2 (x)]{\text {d}}x,\\ D_{mn}^{(4)}= & {} \int \limits _0^L {m_2 (x)\sin \frac{n\pi x}{L}} \sin \frac{m\pi x}{L}\frac{E}{1-\mu ^{2}}\left( -\mu \frac{m\pi }{L}J_m^3 +\beta _m\right) \sinh [\beta _m f_2 (x)]{\text {d}}x\\&+ \int \limits _0^L {l_2 (x)\sin \frac{n\pi x}{L}} \cos \frac{m\pi x}{L}\frac{E}{2(1+\mu )}\left( \frac{m\pi }{L}+\beta _m J_m^3\right) \cosh [\beta _m f_2 (x)]{\text {d}}x, \end{aligned}$$