Coupled inverted pendulums: stabilization problem

Abstract

A mathematical model of an unstable system in the form of inverted coupled pendulums is developed and simulated. Dynamics of such a system is investigated, and the stability zones are identified in the explicit form. The algorithm of stabilization of the pendulums near the vertical position is constructed and verified.

1 Introduction

As is known, the problem of inverted pendulum plays a central role in the control theory [1,2,3,4,5]. In particular, the problem of inverted pendulum (as a test model) provides many challenging problems to control design. Because of their nonlinear nature, pendulums have maintained their usefulness and they are now used to illustrate many of the ideas emerging in the field of nonlinear control [6, 7]. Typical examples are the feedback stabilization, variable structure control, passivity-based control, back-stepping and forwarding, nonlinear observers, friction compensation and nonlinear model reduction. The challenges of control made the inverted pendulum systems as a classical tool in control laboratories. It should also be noted that the problem of stabilization of such a system is a classical problem of the dynamics and control theory. Moreover, the model of inverted pendulum is widely used as a standard for testing of the control algorithms (for PID controller, neural networks, fuzzy control, etc.). Such a mechanical system can be found in various fields of technical science, from robotics to cosmic technologies. For example, the stabilization of inverted pendulum is considered in the problem of missile pointing because the engine of missile is placed lower than the center of mass and such a fact leads to an aerodynamical instability. Similar problem is solved in the self-balancing transport device (the so-called segway). Moreover, the model of inverted pendulum (especially, under various kinds of control of the suspension point motion) is widely used in physics, applied mathematics, engineering science, neuroscience, economics, etc [8]. First theoretical description of the inverted pendulum was carried out by Stephenson [9], and the first experimental investigation of the stabilization process for such a system (using oscillations of the suspension point) was considered in the works of Kapitza [10]. In general, the problem of inverted pendulum is of more than one hundred years of history, but it is still relevant even in the present days. It should also be pointed out that in recent time the systems of inverted pendula, namely the double and triple pendula, have a special interest, especially in connection with the fact that in such systems can be realized the deterministic chaos. The problem of stabilization of such an otherwise unstable, autonomous, and mechanical system is a fascinating task, both from theoretical (various methods of nonlinear analysis) and applied (modeling of the real mechanical systems) point of view [11,12,13]. In this article, we investigate the dynamics of a mechanical system consisting of two inverted pendulums hinged on the moving platform and connected by a spring. The force applied to the platform (and caused its horizontal motion) is treated as a control action. The purpose of this work is to solve the problem of stabilization of the pendulums in vertical position using the horizontal motion of the platform at the presence of the information on the angles of deviation. In order to solve this problem, we developed the algorithm of stabilization of the pendulums near the vertical position, observed the stability zones and their dependence on the spring stiffness.

2 Physical model

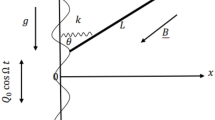
Let us consider a system of two inverted pendulums with masses $m_1$ and $m_2$ that are rigidly fixed on a movable cart and connected by a spring with stiffness k (when the pendulums are in vertical position the spring is nonstretched). The fixation point of the spring is at a distance h from the suspension points of the pendulums (see Fig. 1). We assume that the cart has no mass and moves without friction, and the control action applied to the cart determines the acceleration u. In order to describe the dynamics of such a system, we write the equations for the moments (neglecting the damping) that have the form

Fig. 1

Physical model of coupled pendulums

$$\begin{aligned} \left\{ \begin{array}{l} {I_1}\frac{{\text {d}{{\mathbf {\omega }}_1}}}{{\text {d}t}} = \mathbf {M}_1^{\left( g \right) } + \mathbf {M}_1^{\left( k \right) } - {{\mathbf {M}}^{\left( u \right) }},\\ {I_2}\frac{{\text {d}{{\mathbf {\omega }}_2}}}{{\text {d}t}} = \mathbf {M}_2^{\left( g \right) } - \mathbf {M}_2^{\left( k \right) } - {{\mathbf {M}}^{\left( u \right) }}. \end{array} \right. \end{aligned}$$

(1)

Here $I_{1,2}$ are the moments of inertia of the pendulums, $\omega _{1,2}$ are the angular velocities, $M^{(g)}_{1,2}$ and $M^{(k)}_{1,2}$ are the returning moments of gravitational and elastic forces, respectively.

Since the motion is flat, all these vectors are directed perpendicular to the figure’s area. This fact allows us to transform the vector equations to scalar. Positions of the pendulums will be characterized by the deviation angles (relative to the vertical axis) $\varphi _{1,2}$, and we will consider the small (linear) oscillations of the pendulums (we assume that ${\varphi _{1,2}} \ll 1$). Then, for the elongation of the spring $\Delta x$ we can write the following approximate expression:

$$\begin{aligned} \Delta x \approx h\left( {{\varphi _2} - {\varphi _1}} \right) . \end{aligned}$$

(2)

Then, for a moment of the elastic forces we have

$$\begin{aligned} \left\{ \begin{array}{l} M_1^{\left( k \right) } = k{h^2}\left( {{\varphi _2} - {\varphi _1}} \right) ,\\ M_2^{\left( k \right) } = - k{h^2}\left( {{\varphi _2} - {\varphi _1}} \right) . \end{array} \right. \end{aligned}$$

(3)

and for a moment of gravitational force:

$$\begin{aligned} \left\{ \begin{array}{l} M_1^{\left( g \right) } = {m_1}g{l_1}{\varphi _1},\\ M_2^{\left( g \right) } = {m_2}g{l_2}{\varphi _2}. \end{array} \right. \end{aligned}$$

(4)

where $m_{1,2}$ are the masses of the pendulums and l is the distance from the fixing point to the center of mass. The control moment we can write in the similar way:

$$\begin{aligned} \left\{ \begin{array}{l} M_1^{\left( u \right) } = - {m_1}{l_1}u,\\ M_2^{\left( u \right) } = - {m_2}{l_2}u. \end{array} \right. \end{aligned}$$

(5)

Thus, from the system (1), taking into account (3)–(5), we obtain the following equation:

$$\begin{aligned} \left\{ \begin{array}{l} {I_1}{{\ddot{\varphi }}_1} = {m_1}g{l_1}{\varphi _1} + k{h^2}\left( {{\varphi _2} - {\varphi _1}} \right) - {m_1}{l_1}u,\\ {I_1}{{\ddot{\varphi }}_2} = {m_2}g{l_2}{\varphi _2} - k{h^2}\left( {{\varphi _2} - {\varphi _1}} \right) - {m_2}{l_2}u. \end{array} \right. \end{aligned}$$

(6)

In the next step, we introduce the eigen-frequency for isolated pendulum:

$$\begin{aligned} \omega = \sqrt{\frac{{mgl}}{I}}. \end{aligned}$$

(7)

In the case $I = m{l^2}$, $\omega =\sqrt{\frac{g}{l}}$ we have the point-like pendulum. Then, the system (6) takes the form

$$\begin{aligned} \left\{ \begin{array}{l} {{\ddot{\varphi }}_1} = \omega _1^2{\varphi _1} + \frac{{k{h^2}}}{{{I_1}}}\left( {{\varphi _2} - {\varphi _1}} \right) - \frac{u}{{{l_1}}},\\ {{\ddot{\varphi }}_2} = \omega _2^2{\varphi _2} - \frac{{k{h^2}}}{{{I_2}}}\left( {{\varphi _2} - {\varphi _1}} \right) - \frac{u}{{{l_2}}}, \end{array} \right. \end{aligned}$$

(8)

where

$$\begin{aligned} \left\{ \begin{array}{l} {\omega _1} = \sqrt{\frac{g}{{{l_1}}}}, \\ {\omega _2} = \sqrt{\frac{g}{{{l_2}}}}. \end{array} \right. \end{aligned}$$

(9)

Next, we consider the control based on the feedback principles, namely

$$\begin{aligned} u = a \cdot \text {sign}\left( {bs + \dot{s}} \right) , \end{aligned}$$

(10)

where $s = {\varphi _1} + {\varphi _2}$, ${a = \text {const}}$, ${b = \text {const}}$.

Obviously that if ${\varphi _1} + {\varphi _2} = 0$ (i.e., when the pendulums are on the opposite sides relative to vertical axis) the control u does not act, and the spring stiffness k will define the position of the pendulums.

The purpose of this work is to: research the dynamics of such a mechanical system, search the coefficients a and b, provide the stabilization of the pendulums in the vicinity of the vertical position, and identify the stability zones depending on the system’s parameters (k, m, l, h).

3 Solution of the stabilization problem

Let us analyze a particular case when $l_1=l_2$ and $m_1=m_2$. The system (8) can be rewritten as follows:

$$\begin{aligned} \left\{ \begin{array}{l} {{\ddot{\varphi }}_1} = {\omega ^2}{\varphi _1} + \frac{{k{h^2}}}{I}\left( {{\varphi _2} - {\varphi _1}} \right) - \frac{u}{l},\\ {{\ddot{\varphi }}_2} = {\omega ^2}{\varphi _2} - \frac{{k{h^2}}}{I}\left( {{\varphi _2} - {\varphi _1}} \right) - \frac{u}{l}. \end{array} \right. \end{aligned}$$

(11)

Let us find the sum s and the difference d of these equations, namely we have:

$$\begin{aligned} \left\{ \begin{array}{l} {{\ddot{\varphi }}_1} + {{\ddot{\varphi }}_2} = {\omega ^2}\left( {{\varphi _1} + {\varphi _2}} \right) - \frac{{2u}}{l},\\ {{\ddot{\varphi }}_2} - {{\ddot{\varphi }}_1} = \left( {{\omega ^2} - \frac{{2k{h^2}}}{I}} \right) \left( {{\varphi _2} - {\varphi _1}} \right) , \end{array} \right. \Rightarrow \left\{ \begin{array}{l} \ddot{s} = {\omega ^2}s - \frac{{2u}}{l},\\ \ddot{d} = \left( {{\omega ^2} - \frac{{2k{h^2}}}{I}} \right) d. \end{array} \right. \end{aligned}$$

(12)

Obviously that the sum of the deviation angles s is proportional to the average position of the pendulums in the space, while the difference d determines the position of the pendulums relative to each other. As can be seen from the system (12) in the case when $l_1=l_2$ and $m_1=m_2$, the control u impacts the average position of the pendulums in the space, but does not impact their relative position. At the same time, the stiffness of the spring k affects the relative position, but does not affect the average position.

Thus, the control u is responsible for the stabilization of the pendulums in the case when ${\varphi _2} - {\varphi _1} \ne 0$, $u = a \cdot \text {sign}\left( {bs + \dot{s}} \right) \ne 0$, and the stiffness of the spring k when ${\varphi _2} - {\varphi _1} = 0$, $u = a \cdot \text {sign}\left( {bs + \dot{s}} \right) = 0$. The solution of the system (12) has the form

$$\begin{aligned} \left\{ \begin{array}{l} s = {C_1}{e^{\omega t}} + {C_2}{e^{ - \omega t}} + \frac{{2u}}{{{\omega ^2}l}},\\ d = {D_1}{e^{\sqrt{\alpha }t}} + {D_2}{e^{ - \sqrt{\alpha }t}} \begin{array}{*{20}{c}} ,&{}{\alpha = } \end{array}{\omega ^2} - \frac{{2k{h^2}}}{I}. \end{array} \right. \end{aligned}$$

(13)

Let the initial values of the deviation and velocity are $s\left( 0 \right) = {s_0}$ and $\dot{s}\left( 0 \right) = {\dot{s}_0}$, respectively. Then, the solution of Cauchy’s problem for the first equation has the following form:

$$\begin{aligned} s = \left( {\frac{{{s_0}}}{2} + \frac{{{{\dot{s}}_0}}}{{2\omega }} - \frac{u}{{{\omega ^2}l}}} \right) {e^{\omega t}} + \left( {\frac{{{s_0}}}{2} - \frac{{{{\dot{s}}_0}}}{{2\omega }} - \frac{u}{{{\omega ^2}l}}} \right) {e^{ - \omega t}} + \frac{{2u}}{{{\omega ^2}l}}. \end{aligned}$$

(14)

We investigate the phase trajectory of the system (see Fig. 2) based on the solution of (14).

Fig. 2

Phase trajectory of the system

In the case $u=0$ (as it can be seen directly from $\omega s + \dot{s} = 0$), the phase coordinates will strive to zero equilibrium position. Thus, if the control u is able to bring the pendulum to the straight line, the system will be stable [8].

$$\begin{aligned} \frac{{{s_0}}}{2} + \frac{{{{\dot{s}}_0}}}{{2\omega }} - \frac{u}{{{\omega ^2}l}} = 0. \end{aligned}$$

(15)

Here

$$\begin{aligned} u = \frac{{\omega l}}{2}\left( {\omega {s_0} + {{\dot{s}}_0}} \right) . \end{aligned}$$

(16)

So, $u = a \cdot \text {sign}\left( {bs + \dot{s}} \right)$ presents (16) as

$$\begin{aligned} u = \frac{{\omega l}}{2}\left| {\omega {s_0} + {{\dot{s}}_0}} \right| \text {sign}\left( {\omega {s_0} + {{\dot{s}}_0}} \right) . \end{aligned}$$

(17)

Thus, the control coefficients that provide the stable position of the pendulums can be obtained in the following form:

$$\begin{aligned} \left\{ \begin{array}{l} a = \frac{{\omega l}}{2}\left| {\omega {s_0} + {{\dot{s}}_0}} \right| ,\\ b = \omega . \end{array} \right. \end{aligned}$$

(18)

It should be noted that this stable position is not vertical (in the equality (18) the sum of the angles is $s = \frac{{2u}}{{{\omega ^2}l}}$). However, from the solution of (14) it also follows that in case

$$\begin{aligned} \frac{{{s_0}}}{2} + \frac{{{{\dot{s}}_0}}}{{2\omega }} - \frac{u}{{{\omega ^2}l}} < 0, \end{aligned}$$

(19)

the control affection will return the pendulum to the side of the vertical position. In the moments when the pendulums crossing the vertical point, the control’s sign will be reversed and the process will repeat. Thus, the inequality (19) is the criterion for the stabilization of the pendulums in the vicinity of the vertical position. Based on this fact, we rewrite the inequality (18):

$$\begin{aligned} \left\{ \begin{array}{l} a \ge \frac{{\omega l}}{2}\left| {\omega {s_0} + {{\dot{s}}_0}} \right| ,\\ b = \omega . \end{array} \right. \end{aligned}$$

(20)

The resulting inequality is the criterion for the stabilization of the pendulums.

Now, we investigate the phase trajectory of the system based on the criterions (20). From this inequality, it is obvious that

$$\begin{aligned} \left\{ \begin{array}{l} a \ge \frac{{\omega l}}{2}\left( {\omega {s_0} + {{\dot{s}}_0}} \right) ,\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} &{}{\text {if}} \end{array}}&{}{{s_0}> 0,}&{}{{{\dot{s}}_0} > 0}, \end{array}\\ -\, a \le \frac{{\omega l}}{2}\left( {\omega {s_0} + {{\dot{s}}_0}} \right) ,\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}}&{}{\text {if}} \end{array}}&{{s_0}< 0,}&{{{\dot{s}}_0} < 0}. \end{array} \end{array} \right. \end{aligned}$$

(21)

Inequalities (21) can be presented on the phase plane as the area of all possible initial states that correspond to possible stabilization of the system with fixed control (see Fig. 3).

Fig. 3

Stability zone of the system

So, the area A shown in Fig. 3 determines all the possible initial positions of the system when the pendulums impossible to bring to a steady vertical position, and the area B is the stability area of the system.

Let us consider the second equation of the system (13). Obviously that in the case $D_1=0$, the difference d will turn to zero. (This corresponds to stabilization of the pendulums relative to each other.) However, this situation is impossible because the value of D is determined by the initial states (different from zero) and does not depend on control u.

Thus, the coefficient $\alpha$ is only the parameter affecting the relative position of the pendulums. If $\alpha =0$ and $d=\text {const}$, it corresponds to the case when the moment of gravitational force is balanced by the restoring moment of the elastic force of the spring. If $\alpha >0$, the difference d increases with time and it leads to the loss of control. If $\alpha <0$, the complex terms appear in the solution and this fact indicates the emergence of a harmonic process. Thus, the criterion of controllability of the pendulums becomes

$$\begin{aligned} \alpha \le 0 \Rightarrow k \ge \frac{{I{\omega ^2}}}{{2{h^2}}}. \end{aligned}$$

(22)

Fig. 4

Sum of the angles s(t) (left panel) and phase trajectory (right panel). The parameters are $s\left( 0 \right) = 0.1$, $\dot{s}\left( 0 \right) = 0$, $a = 1.08$, the inequality (20) and (22) is satisfied

Fig. 5

Sum of the angles s(t) (left panel) and phase trajectory (right panel). The parameters are $s\left( 0 \right) = -0.3$, $\dot{s}\left( 0 \right) = -\,0.05$, $a = 1.08$; the inequality (20) and (22) is satisfied

Above we considered the case when the measurement of parameters s $\dot{s}$ and control impact u were instantaneous. But in real systems of automatic control, this process takes some time. In this case, we can introduce the parameter T which is the time interval of the control’s change. Let the control impact applied to the pendulums will depend on the time T. Therefore, the solution of the first equation of the system (13) can be written in the recursive form:

$$\begin{aligned} {s_k}\left( t \right) = \left( {\frac{{{s_{k - 1}}}}{2} + \frac{{{{\dot{s}}_{k - 1}}}}{{2\omega }} - \frac{{{u_{k - 1}}}}{{{\omega ^2}l}}} \right) {e^{\omega \left( {t - {t_{k - 1}}} \right) }} +\left( {\frac{{{s_{k - 1}}}}{2} - \frac{{{{\dot{s}}_{k - 1}}}}{{2\omega }} - \frac{{{u_{k - 1}}}}{{{\omega ^2}l}}} \right) {e^{ - \omega \left( {t - {t_{k - 1}}} \right) }} + \frac{{2{u_{k - 1}}}}{{{\omega ^2}l}}, \end{aligned}$$

(23)

where $t_k$ is the time of the control change, $s_{k-1}$ is the sum of the angles at the time $t_{k-1}$, and $u_{k-1}$ is the control impact at time intervals $[t_{k-1}, t_k]$.

It is obvious that Eq. (23) describes the dynamics of the system in the more realistic way. Also this form of equation can be easily realized using the numerical simulation.

4 Numerical simulation

Now we can make the numerical simulation of the dynamics of the system under consideration using Eq. (23). Let us consider the phase trajectory of the system under various initial conditions (see Figs. 4, 5, 6, 7).

Fig. 6

Sum of the angles s(t) (left panel) and phase trajectory (right panel). The parameters are $s\left( 0 \right) = 0.2$, $\dot{s}\left( 0 \right) = 0.4$, $a = 1.08$; the inequality (20) and (22) is satisfied

Fig. 7

Sum of the angles s(t) (left panel) and phase trajectory (right panel). The parameters are $s\left( 0 \right) = 0.2$, $\dot{s}\left( 0 \right) = 0$, $a = 6$; the inequality (20) and (22) is satisfied

As it can be seen from the simulation results, the considered system can be stabilized successfully near the vertical position under control in the form (10) [of course, we took into account the criterions of stabilization (20) and (22)]. It should be noted that the condition (21) imposes a restriction on the value of the coefficient a only, and, as it can be seen from Fig. 7, even fairly large values of this coefficient lead the system to the stable state (but the oscillations of the pendulums relative to the vertical axis occur with the greater amplitude).

5 Conclusions

In this paper using the numerical simulations, we have investigated the dynamics of the inverted coupled pendulums. Namely, we obtained the stability zones for such a system in the phase space depending on the system’s parameters (k, m, l, h). The analysis of the dynamics of the constructed model has shown that the stabilization of such a complex unstable system is possible using the relatively simple control action which represents the alternating force affection with a constant amplitude.