1 Introduction

As is known, the problem of inverted pendulum plays a central role in the control theory [2, 6, 7, 12, 15, 18, 24, 26, 28, 29, 36]. In particular, the problem of inverted pendulum (as a test model) provides many challenging problems to control design. Because of their nonlinear nature, pendulums have maintained their usefulness and they are now used to illustrate many of the ideas emerging in the field of nonlinear control [4]. Typical examples are feedback stabilization, variable structure control, passivity- based control, back-stepping and forwarding, nonlinear observers, friction compensation, and nonlinear model reduction. The challenges of control made the inverted pendulum systems a classic tool in control laboratories.Footnote 1 It should also be noted that the problem of stabilization of such a system is a classical problem of the dynamics and control theory. Moreover, the model of inverted pendulum is widely used as a standard for testing of the control algorithms (for PID controller, neural networks, fuzzy control, etc.).

Such a mechanical system can be found in various fields of technical science, from robotics to cosmic technologies. E.g., the stabilization of inverted pendulum is considered in the problem of missile pointing because the engine of missile is placed lower than the center of mass and such a fact leads to an aerodynamical instability. Similar problem is solved in the self-balancing transport device (the so-called segway). Moreover, such a mechanical system can be applied in various fields. Namely, the model of inverted pendulum (especially, under various kinds of control of the suspension point motion) is widely used in physics [32], applied mathematics [38], engineering science [21, 31, 33], neuroscience [39], economics [30], etc.

First theoretical description of the inverted pendulum was carried out by Stephenson [34], and the first experimental investigation of the stabilization process for such a system (using oscillations of the suspension point) was considered in the works of Kapitza [16, 17]. In general, the problem of inverted pendulum is of more than one hundred years of history, but it is still relevant even in the present days (see, e.g.,  [1, 7–9, 12, 22, 25, 28, 31, 36, 40] and related references). It should also be pointed out that in recent time the systems of inverted pendula, namely, the double and triple pendula (see [2, 3] and related references) have a special interest, especially, in connection with the fact that in such systems can be realized the deterministic chaos. The problem of stabilization of such an otherwise unstable, autonomous, and mechanical system is a fascinating task, both from a theoretical (various methods of nonlinear analysis) and practical (modeling of the real mechanical systems) point of view.

According to control purposes of the inverted pendulum, the control of inverted pendulum can be divided into three aspects. The first widely researched aspect is the swing-up control of inverted pendulum [12, 24, 28]. The interesting and important results on the time optimal control of the inverted pendulum were obtained in [12, 28]. In particular, in [28], the optimal transients (taking into account the cylindrical character of the state space of the system under control) were built for different values of the parameters and constraints on the control torque. The second aspect is the stabilization of the inverted pendulum [5, 11]. The third aspect is the tracking control of the inverted pendulum [10]. In practice, stabilization and tracking control are more useful for application.

A backlash in the suspension point is a kind of hysteretic nonlinearity. The hysteretic phenomena (especially in the form of control parameters) play an important role in such a fields as physics, chemistry, biology, economics, etc. It should also be pointed out that the hysteretic phenomena are insufficiently known in our days. The purpose of this paper is investigation of the possible stabilization (in a vicinity of vertical position) of the elastic inverted pendulum in the presence of a backlash in the suspension point together with investigation of various aspects of such a dynamical system.

The paper is organized as follows. In the first section, we consider the general view of elastic inverted pendulum together with the operator technique for hysteretic nonlinearities. Also in this section, we obtain the equation of motion of the elastic pendulum with a hysteretic nonlinearity in the form of backlash in the suspension point. The second section is dedicated to numerical solution of the obtained equations (we use the difference scheme). In the third section, we analyze the problem of optimization for the system under consideration. The numerical realization of optimization procedure is made using the so-called bionic algorithm. In the next section, the results of numerical simulations are discussed and analyzed. In the last section, the main results are summarized.

2 Elastic inverted pendulum

2.1 Problem

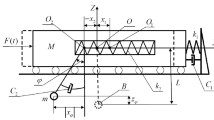
Let us consider the model of stabilization of the inverted pendulum in the vicinity of the vertical position. The pendulum is considered as an elastic rod which is hingedly fixed on the cylinder. Motion of the cylinder is excited by the horizontal motion of a piston (see the Fig. 1).

Fig. 1
figure 1

Model of elastic inverted pendulum: geometry of the problem

Full size image

Mathematical model of a similar mechanical system was considered in [37]. Investigation of the dynamics of an elastic inverted pendulum was carried out in [13, 14, 23, 35].

Here (x, y) is the coordinates of an elastic rod with mass m and density \(\rho \); the Ox axis coincides with a tangent to rod’s profile in the suspension point; \(\theta \) is an angle of slope for the coordinates of a rod, and I is a centroidal moment of inertia of the rod’s section; \((X,\bar{x})\) is the Cartesian coordinate system connected with a considered mechanical system (namely the X coordinate determines the position of the piston in a cylinder), M is a mass of a cylinder with length L, and F is a force joined to a piston with mass \(m_{p}\) (such a force is treated as control).

2.2 Hysteretic nonlinearity

In the following consideration, we use the operator technique for the hysteretic nonlinearities following the ideas of Krasnosel’skii and Pokrovskii [19]. Output of the backlash operator on the monotonic inputs can be described by the following expression:

$$\begin{aligned} X(t)\quad= & {} \varGamma [X_{0},L]Y(t)\\ \quad= & {} \left\{ \begin{array}{ll} \textstyle X_{0}, &{}\textstyle |Y(t)-X_{0}|\leqslant \frac{L}{2};\\ \textstyle Y(t)-\frac{L}{2}, &{}\textstyle Y(t)-X_{0}>\frac{L}{2}, \quad Y(t) \text{ is } \text{ an } \text{ increasing } \text{ function };\\ \textstyle Y(t)+\frac{L}{2}, &{} \textstyle Y(t)-X_{0}<-\frac{L}{2}, \quad Y(t) \text{ is } \text{ a } \text{ decreasing } \text{ function }. \end{array} \right. \end{aligned}$$

Here \(X_{0}\) is the initial position of the piston in a cylinder. Such an expression (action of such an operator) can be illustrated by the Fig. 2.Footnote 2 The detailed description of this operator as well as its properties is considered in the book of Krasnosel’skii and Pokrovskii [19].

Fig. 2
figure 2

Dynamics of input–output relation for the backlash operator

Full size image

Here X(t) is a displacement of the cylinder’s center, and Y(t) is a displacement of a piston in the horizontal plane (see Fig. 1).

2.3 Physical model

Let us assume that the deviation y and angle \(\theta \) are small, i.e., \(x\approx \bar{x}\) and the boundary conditions that determine the curvature of the pendulum areFootnote 3:

$$\begin{aligned} \left\{ \begin{array}{l} y(0,t)=y_{xx}(0,t)=0,\\ y_{xx}(l,t)=y_{xxx}(l,t)=0. \end{array} \right. \end{aligned}$$
(1)

The function \(X(\bar{x},t)\) describes the behavior of the pendulum’s profile in the time and shows the deviation of the pendulum’s points relative to the vertical axis; \((X,\bar{x})\) are the coordinates of the pendulum’s profile, and \(X(0,t)=s(t)\) is a displacement of the suspension point in the horizontal plane.

The coordinate system transformation in the matrix form is given by

$$\begin{aligned} \left( \begin{array}{c} X\\ \bar{x} \end{array}\right) = \left( \begin{array}{l@{\quad }l} \cos {\theta }&{}\sin {\theta }\\ -\sin {\theta }&{}\cos {\theta } \end{array} \right) \left( \begin{array}{c} y\\ x \end{array}\right) +\left( \begin{array}{c} X(0,t)\\ 0 \end{array}\right) . \end{aligned}$$
(2)

Let us construct the physical model of the considered mechanical system taking into account a backlash in the suspension point of an elastic rod. In order to do this, we use the Lagrange formalism.

Taking into account that y and \(\theta \) are small, the Lagrange function can be written as:

$$\begin{aligned} L(t)= & {} \frac{\mathrm{Ms}_{t}^{2}}{2}+\frac{1}{2}\int \limits _{0}^{l}\Big [\rho s_{t}^{2}+\rho y_{t}^{2}+\rho (x\theta _{t})^{2}\nonumber \\&+\,\rho (2s_{t}x\theta _{t}+2x \theta _{t}y_{t}+2s_{t}y_{t})\nonumber \\&+\,2\rho gy\theta -\mathrm{EI}y_{xx}^{2} \Big ]\,\mathrm {d}x, \end{aligned}$$
(3)

where E is the Young’s modulus, \(\rho \) is the density of a rod, g is the gravitational acceleration.

We can integrate the Eq. (3) in the interval \((t_{0},t_{f})\) and obtain the action function:

$$\begin{aligned} \displaystyle W= & {} \frac{1}{2}\int \limits _{t_{0}}^{t_{f}}\mathrm{Ms}_{t}^{2}\,\mathrm {d}t+\frac{1}{2}\int \limits _{t_{0}}^{t_{f}} \int \limits _{0}^{l}\Bigg [\rho \Big ( s_{t}^{2}+y_{t}^{2}+x^{2}\theta _{t}^{2}\nonumber \\&+\,2s_{t}x\theta _{t}+ 2x\theta _{t}y_{t}+2s_{t}y_{t}+ 2gy\theta \Big )\nonumber \\&-\frac{\mathrm{EI}}{\rho }y_{xx}^{2}\Bigg ]\,\mathrm {d}x\,\mathrm {d}t. \end{aligned}$$
(4)

Using the variational principle and using the Tailor’s expansion, we obtain the following equation:

$$\begin{aligned} y_{tt}+\frac{\mathrm{EI}}{\rho }y_{xxxx}=-s_{tt}-x\theta _{tt}+g\theta . \end{aligned}$$
(5)

Taking \(\theta \) as the generalized coordinate in the Lagrange function, we obtain:

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}t}\frac{\partial {L}}{\partial {\theta _{t}}}-\frac{\partial {L}}{\partial {\theta }}=0. \end{aligned}$$
(6)

Substitution of (3) in (6) gives:

(7)

Taking into account (5), we have

$$\begin{aligned} \int \limits _{0}^{l}x\left( g\theta -\frac{\mathrm{EI}}{\rho }y_{xxxx}\right) \,\mathrm {d}x=g\int \limits _{0}^{l}y\,\mathrm {d}x. \end{aligned}$$
(8)

or

$$\begin{aligned} \frac{gl^{2}\theta }{2}-\frac{\mathrm{EI}}{\rho }\int \limits _{0}^{l} xy_{xxxx}\,\mathrm {d}x=g\int \limits _{0}^{l}y\,\mathrm {d}x. \end{aligned}$$
(9)

Using the boundary conditions (1), we can show that the integral in the left part of (9) is equal to zero. Then, multiplying both parts of this equality on \(\frac{\rho }{g}\), we obtain

$$\begin{aligned} \frac{ml\theta }{2}=\rho \int \limits _{0}^{l}y\,\mathrm {d}x. \end{aligned}$$
(10)

Integrating (5) and multiplying on \(\rho \), we have

$$\begin{aligned} \rho \int \limits _{0}^{l}\left( y_{tt}+\frac{\mathrm{EI}}{\rho }y_{xxxx}\right) \,\mathrm {d}x=\rho \int \limits _{0}^{l} \left( -s_{tt}-x\theta _{tt}+g\theta \right) \,\mathrm {d}x, \end{aligned}$$

or, by integration:

$$\begin{aligned}&\mathrm{EI}\left[ y_{xxx}(l,t)-y_{xxx}(0,t)\right] +\rho \int \limits _{0}^{l}y_{tt}\,\mathrm {d}x\nonumber \\&\quad =-s_{tt}\rho l-\frac{\rho l^{2}\theta _{tt}}{2}+\rho gl\theta , \end{aligned}$$
(11)

Taking into account the relations \(\rho l=m\), \(y_{xxx}(l,t)=0\) (from boundary conditions), and using

$$\begin{aligned} \rho \int \limits _{0}^{l}y_{tt}\,\mathrm {d}x=\frac{ml\theta _{tt}}{2}, \end{aligned}$$

which follows from (10), we have the following equation:

$$\begin{aligned} ml\theta _{tt}+ms_{tt}=mg\theta +\mathrm{EI}y_{xxx}(0,t). \end{aligned}$$
(12)

In the next step, taking s as the generalized coordinate in the Lagrange function, we obtain:

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}t}\frac{\partial {L}}{\partial {s_{t}}}-\frac{\partial {L}}{\partial {s}}=f(t). \end{aligned}$$
(13)

Here f(t) is the force joined to the suspension point of a rod.

General peculiarity of the system under consideration is the presence of a backlash in the suspension point. Due to the fact that the backlash can be considered as a hysteretic nonlinearity, we can use the technique of hysteretic operators. According to classical patterns of Krasnosel’skii and Pokrovskii [19], the hysteretic operators are treated in an appropriate function spaces. The dynamics of such operators are described by the relation of “input-state” and “state-output.”

Thus, the force joined to the suspension point can be found from the relation:

$$\begin{aligned} f(t)= & {} \varGamma \left[ X(0,t),Y(t),L,F_{0}\right] F\nonumber \\= & {} \left\{ \begin{array}{l@{\quad }l} 0, &{} |X(0,t)-Y(t)|\leqslant L;\\ F, &{} |X(0,t)-Y(t)|>L, \end{array} \right. \end{aligned}$$
(14)

where L is the length of a cylinder and F is the force (this force affects the piston) which can be treated as a control.

The equation of motion of the piston is:

$$\begin{aligned} m_{p}Y_{tt}(t)=F. \end{aligned}$$
(15)

Here Y is a displacement of the piston in the horizontal plane.

Substitution of (3) in (13) gives the following:

$$\begin{aligned} \mathrm{Ms}_{tt}+\rho \int \limits _{0}^{l}\left( s_{tt}+x\theta _{tt} +y_{tt}\right) \,\mathrm {d}x=f(t). \end{aligned}$$
(16)

Using (5), we obtain

$$\begin{aligned} \mathrm{Ms}_{tt}+\rho \int \limits _{0}^{l}\left( g\theta -\frac{\mathrm{EI}}{\rho } y_{xxxx}\right) \,\mathrm {d}x=f(t). \end{aligned}$$
(17)

Making the same transformations as in (11), we obtain the following equality:

$$\begin{aligned} \mathrm{Ms}_{tt}=f(t)-mg\theta -\mathrm{EI}y_{xxx}(0,t). \end{aligned}$$
(18)

Thus, we have the following system of equations:

$$\begin{aligned} \left\{ \begin{array}{l} ml\theta _{tt}+ms_{tt}=mg\theta +\mathrm{EI}y_{xxx}(0,t),\\ \mathrm{Ms}_{tt}=f(t)-mg\theta -\mathrm{EI}y_{xxx}(0,t). \end{array} \right. \end{aligned}$$
(19)

Passing to coordinate system \((X,\bar{x})\) (using the Eq. 2), the system of equation which describes the physical model of the considered mechanical system will have the following form:

$$\begin{aligned} \left\{ \begin{array}{l} \textstyle X_{tt}+\frac{\mathrm{EI}}{\rho }X_{xxxx}=gX_{x}(0,t),\\ MX_{tt}(0,t)=f(t)-mgX_{x}(0,t)-\mathrm{EI}X_{xxx}(0,t),\\ ml(X_{tt})_{x}(0,t)+mX_{tt}(0,t)\\ \quad =mgX_{x}(0,t)+\mathrm{EI}X_{xxx}(0,t),\\ f(t)=\varGamma \left[ X(0,t),Y(t),L,F_{0}\right] F,\\ m_{p}Y_{tt}(t)=F, \end{array} \right. \end{aligned}$$
(20)

where \(X=X(x,t)\) due to \(\bar{x}\approx x\).

Let us express \(X_{tt}(0,t)\) from the first equation of the system and substitute it into the second equation:

$$\begin{aligned} g(M+m)X_{x}(0,t)-\frac{\mathrm{MEI}}{\rho }X_{xxxx}+\mathrm{EI}X_{xxx}=f(t). \end{aligned}$$
(21)

Let us integrate the Eq. (21) over x. The result is

$$\begin{aligned}&g(M+m)X(0,t)-\frac{\mathrm{MEI}}{\rho }X_{xxx}+\mathrm{EI}X_{xx}\nonumber \\&\quad = \int \limits _{0}^{l}f(t)\,\mathrm {d}x=lf(t). \end{aligned}$$
(22)

Taking into account (1), we have:

$$\begin{aligned} g(M+m)X(0,t)-\frac{\mathrm{MEI}}{\rho }X_{xxx}=lf(t). \end{aligned}$$
(23)

Finally, the system of equations which describes the dynamics of the system under consideration has the following form:

$$\begin{aligned} \left\{ \begin{array}{l} \textstyle X_{tt}+\frac{\mathrm{EI}}{\rho }X_{xxxx}=gX_{x}(0,t),\\ MX_{tt}(0,t)+mgX_{x}(0,t)+\mathrm{EI}X_{xxx}(0,t)=f(t),\\ (M+m)X_{tt}(0,t)+ml(X_{tt})_{x}(0,t)=f(t),\\ \textstyle g(M+m)X(0,t)-\frac{\mathrm{MEI}}{\rho }X_{xxx}=lf(t),\\ f(t)=\varGamma \left[ X(0,t),Y(t),L,F_{0}\right] F,\\ m_{p}Y_{tt}(t)=F. \end{array} \right. \end{aligned}$$
(24)

2.4 Stabilization

Let us consider the problem of control of the pendulum using the feedback principles, i.e., the force which affects the piston can be presented by the following equality:

$$\begin{aligned} F=k\,\mathrm {sign}(\alpha e_{1}+e_{2}), \end{aligned}$$
(25)

where \(\alpha >0,\,k>0\) and

$$\begin{aligned} e_{1}= & {} \int \limits _{0}^{l}X_{x}\,\mathrm {d}l, \end{aligned}$$
(26)
$$\begin{aligned} e_{2}= & {} \int \limits _{0}^{l}(X_{t})_{x}\,\mathrm {d}l. \end{aligned}$$
(27)

Here \(e_{1}\) is an average angle of the rod’s deviation, and \(e_{2}\) is an average angular velocity of the rod.

Thus, in order to solve the stabilization problem for the elastic inverted pendulum, we should use the system of Eq. (24) together with the equalities (25)–(27):

$$\begin{aligned} \left\{ \begin{array}{l} \textstyle X_{tt}+\frac{\mathrm{EI}}{\rho }X_{xxxx}=gX_{x}(0,t),\\ MX_{tt}(0,t)+mgX_{x}(0,t)+\mathrm{EI}X_{xxx}(0,t)=f(t),\\ (M+m)X_{tt}(0,t)+ml(X_{tt})_{x}(0,t)=f(t),\\ \textstyle g(M+m)X(0,t)-\frac{\mathrm{MEI}}{\rho }X_{xxx}=lf(t),\\ f(t)=\varGamma \left[ X(0,t),Y(t),L,F_{0}\right] F,\\ m_{p}Y_{tt}(t)=F,\\ F=k\,\mathrm {sign}(\alpha e_{1}+e_{2}),\\ \textstyle e_{1}=\int _{0}^{l}X_{x}\,\mathrm {d}l,\\ \textstyle e_{2}=\int _{0}^{l}(X_{t})_{x}\,\mathrm {d}l. \end{array} \right. \end{aligned}$$
(28)

The solution of the posed problem on stabilization of the elastic inverted pendulum in the vicinity of the upper position is consisted in search of the optimal values for the coefficients \(\alpha \) and k.

3 Numerical realization

3.1 Difference scheme

Let us introduce the rectangular net. In order to do this, let us cross the domain of function \(X=X(x,t)\) by the net of straight lines parallel to the coordinate axis (see the Fig. 3).

Fig. 3
figure 3

Rectangular net which corresponds to domain of the function X(x, t)

Full size image

It is evident that the value of X(x, t) in the knots of presented net is:

$$\begin{aligned} X_{i,j}=X(ih_{x},jh_{t}), \end{aligned}$$
(29)

where \(h_{x}\) is the step of a net by the x axis, \(h_{t}\) is the step of a net by the t axis, \(i=\overline{0,n}\), \(j=\overline{0,m}\), \(h_{x}=\frac{L}{n}\), \(h_{t}=\frac{T}{m}\), T is the time interval for calculation of the single iteration by the time.

For calculation of the derivatives, we can use the right finite difference:

$$\begin{aligned}&X_{x}(x,t)\approx \frac{X_{i+1,j}-X_{i,j}}{h_{x}}, \end{aligned}$$
(30)
$$\begin{aligned}&X_{t}(x,t)\approx \frac{X_{i,j+1}-X_{i,j}}{h_{t}}. \end{aligned}$$
(31)

Then, the system (28) in the finite differences will have the following form:

$$\begin{aligned} \left\{ \begin{array}{l} \begin{array}{l} \displaystyle \frac{X_{i,j+2}-2X_{i,j+1}+X_{i,j}}{h_{t}^{2}}+\\ \displaystyle \quad +\frac{EI}{\rho }\frac{6X_{i+2,j}-4X_{i+1,j}-4X_{i+3,j} +X_{i+4,j}+X_{i,j}}{h_{x}^{4}}\\ \quad =g\frac{X_{1,j}-X_{0,j}}{h_{x}}, \end{array}\\ \begin{array}{l} \displaystyle M\frac{X_{0,j+2}-2X_{0,j+1}+X_{0,j}}{h_{t}^{2}}+mg\frac{X_{1,j}-X_{0,j}}{h_{x}}\\ \displaystyle \quad +EI\frac{3X_{1,j}-3X_{2,j}+X_{3,j}-X_{0,j}}{h_{x}^{3}}\\ \quad =f_{j}, \end{array}\\ \begin{array}{l} \displaystyle (M+m)\frac{X_{0,j+2}-2X_{0,j+1}+X_{0,j}}{h_{t}^{2}}\\ \displaystyle \quad +ml\frac{2X_{0,j+1}-X_{0,j+2}-2X_{1,j+1} +X_{1,j+2}-X_{0,j}+X_{1,j}}{h_{t}^{2}h_{x}}\\ \quad =f_{j}, \end{array}\\ \displaystyle g(M+m)X_{0,j}-\frac{MEI}{\rho }\frac{3X_{1,j}-3X_{2,j} +X_{3,j}-X_{0,j}}{h_{x}^{3}}\\ \quad =f_{j}h_{x},\\ \displaystyle f_{j}=\varGamma \left[ X_{0,j},Y_{j},L,F_{0}\right] F_{j},\\ \displaystyle m_{p}\frac{Y_{j+2}-2Y_{j+1}+Y_{j}}{h_{t}^{2}} =F_{j},\\ \displaystyle F_{j}=k\,\mathrm {sign}(\alpha e_{1j}+e_{2j}),\\ \displaystyle e_{1j}=\sum \limits _{i=0}^{n} \left( X_{i+1,j}-X_{i,j}\right) ,\\ \displaystyle e_{2j}=\sum \limits _{i=0}^{n}\frac{X_{i,j}-X_{i,j+1}- X_{i+1,j}+X_{i+1,j+1}}{h_{t}}, \end{array} \right. \end{aligned}$$
(32)

together with the initial conditions, namely the angle, linear and angular velocities:

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \frac{X_{1,0}-X_{0,0}}{h_{\mathrm {x}}}=\varphi ,\\ \displaystyle \frac{X_{0,1}-X_{0,0}}{h_{\mathrm {t}}}=V,\\ \displaystyle \frac{X_{0,0}-X_{0,1}-X_{1,0}+X_{1,1}}{h_{\mathrm {t}}h_{\mathrm {x}}}=V_{\varphi },\\ \displaystyle \frac{X_{2,j}-2X_{1,j}+X_{0,j}}{h_{\mathrm {x}}^{2}}=0. \end{array}\right. \end{aligned}$$
(33)

On the basis of (32) and (33), we can obtain the explicit difference scheme. In the Fig. 4, we show all the knots of a net that take part in the solution of the system (28) on each consequent iteration together with the direction of calculation. In brackets, we show the number of equation in the system (32).

Fig. 4
figure 4

Calculation scheme

Full size image

In the next step, we would like to construct the algorithm for solution of (28) taking into account the explicit difference scheme (32) together with the initial conditions (33).

3.2 Algorithm

The algorithm contains two stages of calculations, namely the forward and inverse stages. In the forward stage, we compute the lower four layers by i, i.e., the values of \(X_{i,j}\), where \(i=\overline{0,3}\), \(j=\overline{0,m}\). In the inverse stage, we compute the residuary layers, i.e., \(X_{i,j}\), where \(i=\overline{4,n}\), \(j=\overline{0,m}\). At the same time, in order to find the position of the rod’s profile at the present time moment, it is enough to find the values of \(X_{i,j}\) in the region bordered by a triangle (see Fig. 5). In other words, we need to organize the net with \(n=2m\) for the comfortable simulations.

Fig. 5
figure 5

Domain of calculations

Full size image

The algorithm

  1. 1.

    Let us assign the parameters of the system m, M, l, I, E, \(\rho \);

  2. 2.

    Let us assign the initial conditions \(X_{0,0}\), \(Y_{0}\), \(\varphi \), V, \(V_{\varphi }\);

  3. 3.

    Let us assign the parameters of the difference schema n, m, \(h_{\mathrm {x}}\), \(h_{\mathrm {t}}\);

  4. 4.

    Let us assign the parameters of the control \(F_{0}\), \(\alpha \), k.

  5. 5.

    Forward stage From the initial conditions (33) and fourth equation of the system (32), we find:

    $$\begin{aligned}&f_{j}=\varGamma \left[ X_{0,j},Y_{j},L,F_{0}\right] F;\\&j=0,\\&X_{1,0}=\varphi h_{\mathrm {x}}+X_{0,0},\\&X_{2,j}=2X_{1,j}-X_{0,j},\\&X_{3,j}=\left[ (M+m)gX_{0,j}-f_{j}h_{\mathrm {x}}\right] \frac{\rho h_{\mathrm {x}}^{3}}{\mathrm{MEI}}\\&\qquad \,\,\,\, +\,3X_{2,j}+X_{0,j}-3X_{1,j};\\&j=1,\\&X_{0,1}=V h_{\mathrm {t}}+X_{0,0},\\&X_{1,1}=V_{\varphi }h_{\mathrm {t}}h_{\mathrm {x}}-X_{0,0}+X_{0,1}+X_{1,0},\\&X_{2,j}=2X_{1,j}-X_{0,j},\\&X_{3,j}=\left[ (M+m)gX_{0,j}-f_{j}h_{\mathrm {x}}\right] \frac{\rho h_{\mathrm {x}}^{3}}{\mathrm{MEI}}\\&\qquad \,\,\,\, +\,3X_{2,j}+X_{0,j}-3X_{1,j}; \end{aligned}$$
  6. 6.

    Let us calculate the residuary points at \(i=\overline{0,3}\), \(j=\overline{0,m}\):

    $$\begin{aligned}&j=0\ldots (m-2),\\&Y_{j+2}=\frac{Fh_{\mathrm {t}}^{2}}{m_{p}}+2Y_{j+1} -Y_{j},\\&f_{j}=\varGamma \left[ X_{0,j},Y_{j},L,F_{0}\right] F,\\&X_{0,j+2}=\frac{h_{\mathrm {t}}^{2}}{M} \Bigg (f_{j}-mg\frac{X_{1,j}-X_{0,j}}{h_{\mathrm {x}}}\\&\qquad \quad \,\,-\,\mathrm{EI}\frac{3X_{1,j}-3X_{2,j}+X_{3,j}-X_{0,j}}{h_{\mathrm {x}}^{3}}\Bigg )\\&\qquad \quad \,\, +\,2X_{0,j+1}-X_{0,j},\\&X_{1,j+2}=\frac{h_{\mathrm {t}}^{2}h_{\mathrm {x}}}{ml}\times \left[ f_{j}-(M+m)\frac{X_{0,j+2}-2X_{0,j+1}+X_{0,j}}{h_{\mathrm {t}}^{2}}\right] \\&\qquad \quad \,\,+2X_{0,j+1}+X_{0,j+2}+2X_{1,j+1}\\&\qquad \quad \,\,+\,X_{0,j}-X_{1,j},\\&X_{2,j+2}=2X_{1,j+2}-X_{0,j+2},\\&X_{3,j+2}=\left[ (M+m)gX_{0,j+2}-f_{j}h_{\mathrm {x}}\right] \frac{\rho h_{\mathrm {x}}^{3}}{\mathrm{MEI}}\\&\qquad \quad \,\,+\,3X_{2,j+2}+X_{0,j+2}-3X_{1,j+2}; \end{aligned}$$
  7. 7.

    Inverse stage Let us find \(X_{i,j}\) at \(i=\overline{4,n},\,j=\overline{0,m}\):

    $$\begin{aligned}&i=0\ldots (n-4), j=0\ldots (m-2),\\&X_{i+4,j}\\&\quad =\left( g\frac{X_{1,j}-X_{0,j}}{h_{x}}-\frac{X_{i,j+2}-2X_{i,j+1}+X_{i,j}}{h_{t}^{2}}\right) \\&\qquad \times \frac{\rho h_{\mathrm {x}}^{4}}{\mathrm{EI}}-6X_{i+2,j} +\,4X_{i+1,j}+\,4X_{i+3,j}-X_{i,j}; \end{aligned}$$
  8. 8.

    Let us redefine the initial parameters \(X_{0,0}\), \(\varphi \), V, \(V_{\varphi }\);

  9. 9.

    Let us redefine the control parameters

    $$\begin{aligned}&e_{1}=\sum \limits _{i=0}^{n} \left( X_{i+1,0}-X_{i,0}\right) ,\\&e_{2}=\sum \limits _{i=0}^{n} \frac{X_{i,0}-X_{i,1}-X_{i+1,0}+X_{i+1,1}}{h_{\mathrm {t}}},\\&F=k\,\mathrm {sign}(\alpha e_{1}+e_{2}); \end{aligned}$$
  10. 10.

    Let us turn to the step 5.

As we can see from this algorithm, the numerical value of the force F should be recalculated in the each new time interval T.

4 Optimization problem

As was mentioned above, the solution of the problem on stabilization of elastic inverted pendulum in the vicinity of the upper position is consisted in search of the optimal values for coefficients \(\alpha \) and k from the equality (25).

In many technical problems, the question on stabilization has a general interest. However, together with the stabilization of the system, there is the problem of optimization (this problem corresponds to asymptotically optimal characteristics of the system). In the system under consideration, the problem of optimization corresponds to minimizing of the functional which determines the deviation of the pendulum from the vertical position. Let us consider the functional (the so-called objective functional) as follows:

$$\begin{aligned} \mathfrak {J}=\frac{1}{T}\int \limits _{0}^{T} \left\{ \int \limits _{0}^{l}\left( X_{x}\right) ^{2}\mathrm {d}l+\int \limits _{0}^{l}\left[ (X_{t})_{x}\right] ^{2}\mathrm {d}l\right\} \mathrm {d}t. \end{aligned}$$
(34)

Here T is the time interval in which we find an optimal control.

Solution of the Eq. (28) that describes the dynamics of the system under consideration should be obtained under conditions that provide the minimization of the functional (34). Physically, this means that the problem is equivalent to minimization of the mean-square deviation of the pendulum relative to the vertical position.

In order to solve the optimization problem in the system under consideration, we use the bionic algorithms of adaptation because the hysteretic peculiarities in the considered pendulum’s model lead to some difficulties in use of the classical optimization algorithms due to nondifferentiability of the functions in the system of equations.

Such algorithms are the part of the line of investigation which can be called as an “adaptive behavior.” Main method of this line consists in the investigation of artificial organisms (in the form of computer program or a robot) that can be named as animats (these animats can be adapted to environment). The behavior of animats emulates the behavior of animals.

Actual line of investigation in the frame of the animat approach is an emulation of searching behavior of the animals [20, 27]. Let us consider the bionic model of adaptive searching behavior on the example of caddisflies larvae or Chaetopteryx villosa. The main schema of searching behavior can be characterized by the two stages:

  • Motion in a chosen direction (conservative tactics);

  • Random change of the motion direction (stochastic searching tactics).

We consider this model for the simple case of maximum search for the function of two variables. Let us describe the main stages of the considered model:

  1. 1.

    We consider an animat which is moved in the two-dimensional space x, y. Main purpose of animat is maximum search for the function f(x, y).

  2. 2.

    Animat is functioned in discrete time \(t=0,1,2,\ldots \). Animat estimates the change of current value of f(x, y) in comparison with the previous time \(\varDelta f(t)=f(t)-f(t-1)\).

  3. 3.

    Every time animat moves so its coordinates x and y change by \(\varDelta x(t)\) and \(\varDelta y(t)\), respectively.

  4. 4.

    Animat has two tactics of behavior: a) conservative tactics; b) stochastic searching tactics.

The displacement of an animat in the next time \(\varDelta x(t+1)\), \(\varDelta y(t+1)\) for these tactics determines in different ways. Switching between the cycles drives by M(t). Time dependence of M(t) can be determined using the equation:

$$\begin{aligned} M(t)=k_{1}M(t-1)+\xi (t)+I(t), \end{aligned}$$
(35)

where \(k_{1}\) is a parameter which determines the switching persistence of tactics \((0<k_{1}<1)\), \(\xi (t)\) is a normal distributed variate with an average value equal to zero and mean-square deviation equal to \(\sigma \), and I(t) is an intensity of irritant. For the value of I(t), there are two possibilities:

$$\begin{aligned} I(t)=k_{2}\Delta f(t) \end{aligned}$$
(36)

and

$$\begin{aligned} I(t)=k_{2}\frac{\Delta f(t)}{f(t-1)}, \end{aligned}$$
(37)

where \(k_{2}>0\). As follows from (36) and (37), the intensity is positive when the step leads to increasing of function; otherwise, the intensity is negative. It should be noted also that the Eq. (37) can be applied in the case \(f(t)>0\).

We assume that at \(M(t)>0\) the animat follows the tactic a) and at \(M(t)<0\) it follows tactic b). So, the value of M(t) can be considered as a motivation to selection of tactic a).

Thus, the algorithm of maximum search can be considered as follows:

Tactics a Animat moves in the chosen direction. The displacement of an animat is determined by \(R_{0}\)

$$\begin{aligned} \varDelta x(t+1)= & {} R_{0}\cos {\varphi _{0}}, \end{aligned}$$
(38)
$$\begin{aligned} \varDelta y(t+1)= & {} R_{0}\sin {\varphi _{0}}, \end{aligned}$$
(39)

where the angle \(\varphi _{0}\) defines the constant direction of motion of the animat:

$$\begin{aligned} \cos {\varphi _{0}}= & {} \frac{\Delta x(t)}{\sqrt{\varDelta x^{2}+\varDelta y^{2}}}, \end{aligned}$$
(40)
$$\begin{aligned} \sin {\varphi _{0}}= & {} \frac{\Delta y(t)}{\sqrt{\varDelta x^{2}+\varDelta y^{2}}}. \end{aligned}$$
(41)

Tactics b Animat makes an accidental turn. The displacement of the animat is determined by \(r_{0}\), but the direction of motion is accidentally varied

$$\begin{aligned} \varDelta x(t+1)= & {} r_{0}\cos {\phi }, \end{aligned}$$
(42)
$$\begin{aligned} \varDelta y(t+1)= & {} r_{0}\sin {\phi }, \end{aligned}$$
(43)

where \(\varphi =\varphi _{0}+w\), \(\varphi _{0}\) is an angle which characterizes the direction of motion at current time t, w is a normal distributed variate (average value of w equal to zero and mean-square deviation equal to \(w_{0}\)), and \(\varphi \) is an angle which characterizes the direction of motion at time \(t+1\).

In that way, we can use the proposed algorithm for searching the optimal control in the problem of stabilization of the elastic inverted pendulum. Taking into account the reasoning presented above, we can apply the presented algorithm to the functional \(\mathfrak {J}(\alpha ,k)\) where the coefficients \(\alpha \) and k determine the character of control of the mechanical system under consideration following the Eq. (25). Due to the fact that the presented bionic algorithm is used to maximum search of the function of two variables, we will consider the minimization of the functional (34) as a procedure for finding the coefficients \(\alpha \) and k that lead to realization of the condition

$$\begin{aligned} -\mathfrak {J}(\alpha ,k)\rightarrow \max . \end{aligned}$$
(44)

5 Simulation results

5.1 Elastic inverted pendulum

Now we can make a simulation of the behavior of elastic inverted pendulum using the corresponding difference scheme in the absence of a backlash (\(L=0\)). Using the bionic algorithm, we can find the optimal values of the coefficients \(\alpha \) and k.

The characteristics and initial conditions for the mechanical system under consideration are:

$$\begin{aligned}&m=1,\, M=10,\, l=1,\, \rho =0.5,\, E=10,\\&\quad I=4,\, \theta _{0}=0.06^{\circ }. \end{aligned}$$

In the searching process for optimization (using the bionic algorithm), we have obtained the following values of the coefficients: \(\alpha =22.04\) and \(k=1.15\).

In order to estimate the stability of the system under consideration, we use the Lyapunov criterion. Namely, we use the following Lyapunov function:

$$\begin{aligned} V=e_{1}^{2}+e_{2}^{2}. \end{aligned}$$

The phase trajectory of such a system together with the dynamics of Lyapunov function in time (namely in discrete time which corresponds to the difference scheme) are presented in the Fig. 6. In this figure, the integral angle \(e_{1}\) and integral angular velocity \(e_{2}\) correspond to Eqs. (26) and (27), respectively.

In the Fig. 7, we present the phase trajectory and Lyapunov function for another values of \(\alpha \) and k, namely \(\alpha =50\) and \(k=0.4\).

Fig. 6
figure 6

Phase trajectory (left panel) and dynamics of Lyapunov function (right panel) in the absence of a backlash (\(L=0\)). The parameters are \(\alpha =22.04\) and \(k=1.15\)

Full size image
Fig. 7
figure 7

The same as in Fig. 6 but for another values of parameters \(\alpha \) and k, namely \(\alpha =50\) and \(k=0.4\)

Full size image

As we can see from the presented figures, the Lyapunov function satisfies the following condition (during all the considered time interval):

$$\begin{aligned} V_{t}(t)\leqslant 0. \end{aligned}$$

This means that the considered inverted pendulum eventually tends to stable vertical position.

5.2 Elastic inverted pendulum with backlash in suspension

Now, let us add a backlash in the suspension point of a considered mechanical system and let us investigate the behavior of such a system with the same parameters as in previous subsection. Using the bionic algorithm, we have obtained the following optimal values of the coefficients: \(\alpha =9\) and \(k=2\).

The mass of a piston is \(m_{p}=1\,\text{ kg }\). The main parameters of the system are the same as in previous section. The phase trajectories of such a system (as previously we use \((e_{1},e_{2})\) coordinates) and dynamics of the Lyapunov function for different values of the control coefficients are presented in the Fig. 8.

Fig. 8
figure 8

Phase trajectories (left panels) and dynamics of Lyapunov function (right panels) in the presence of a backlash in the suspension point. Parameters of the backlash and the control coefficients are as follows: a \(L=0.01\,\text{ m }\), \(\alpha =9\), \(k=2\); b \(L=0.02\,\text{ m }\), \(\alpha =9\), \(k=2\); c \(L=0.02\,\text{ m }\), \(\alpha =10.5\), \(k=1.5\)

Full size image

As we can see from the presented figure (both from the phase trajectories and Lyapunov function), the considered system (at the same main parameters and different values of L and control coefficients \(\alpha \) and k) also eventually tends to stable state.

6 Conclusions

In this paper, we have considered the stabilization problem of the elastic inverted pendulum under hysteretic control in the form of a backlash in the suspension point. Also the problem of optimization for the system under consideration is analyzed. Main coefficients, namely \(\alpha \) and k, that provide the solution of the optimization problem for the considered system are obtained using the so-called bionic algorithm. In particular, in the case of the absence of a backlash in the suspension point (\(L=0\)), we have obtained the following values of the coefficients: \(\alpha =22.04\) and \(k=1.15\) (for the parameters of the system presented in the main text). In the case of a backlash in the suspension point (corresponding characteristics of a backlash are \(L=0.01\,\text{ m }\) and \(m_{p}=1\,\text{ kg }\)), the corresponding coefficients are \(\alpha =9\) and \(k=2\). All the results on stabilization of the system under consideration have obtained using the corresponding numerical methods based on the difference scheme. The results of numerical simulations show that the considered system eventually tends to the stable state both in the case of the absence of a backlash and in the case of its presence. These facts are presented in the form of the corresponding phase portraits for the considered system. Moreover, in order to estimate the stability of the elastic pendulum with the hysteretic nonlinearity in the suspension point, we have used the Lyapunov criterion and the dynamics of the corresponding Lyapunov function has also been presented.