Winding angle optimization of filament-wound cylindrical vessel under internal pressure

Abstract

The maximum strength ratio and more uniform strength for all layers can be achieved by variation of winding angle of filament-wound (FW) vessel. The deformation and stresses of a thick-walled cylinder with multi-angle winding filament under uniform internal pressure are proposed. The stresses of each orthotropic unit of fiber layers, as well as longitudinal stress along the fiber direction, transverse stresses perpendicular to the fiber direction and shear stress in the fiber layer are derived analytically. An optimization model of FW closed ends vessel under uniform internal pressure subjected to Tsai–Wu failure criterion to maximize the lowest strength ratio through thickness with optimal variation of winding angle is built. Two optimization methods are adopted to find the optimized winding angle sequence through different ways, and their combination led to more efficient algorithm is suggested. The research shows that the material utilization and working pressure can be increased by proper winding angle variation, and several optimization winding angle sequence schemes are found for different thickness ratios cylindrical vessels with two typical composite materials E-glass/epoxy and T300/934, which are useful for many applications of FW vessel design and manufacture.

1 Introduction

With the development of science and technology, high-performance fiber-wound pressure vessel has been widely used in many fields, such as rocket, missile, deep diving, satellite [1]. And the mechanical performances of winding filaments differ in thousands ways. Filament-wound (FW) structure can remedy the shortcomings and take the advantages. Modern computerized equipment allows for the production of multi-angle winding structures [2]. However, how to design a FW structure with proper winding angle to maximize the material utilization is still a challenged task today.

Using internal pressure and axial force, experiments under biaxial tensile stress ratios were carried out to investigate the performance of multi-angle FW structures [3]. Multi-angle wound structures exhibit better performance in resisting damage and greater advantages over pure angle-ply lay-ups [4]. Many experimental failure analyses [5–9] have been conducted for pipes with different winding angles, and an optimum winding angle of $55^{\circ }$ has been noted for thin pipes subjected to internal pressure or biaxial loads with a hoop-to-axial stress ratio of 2:1. Researches show that stacking sequence has great influence on pressure capability [10, 11], where stacking sequence can only be computed by 3-D analysis [12]. Using 3-D orthotropic elasticity and axisymmetric thick-walled cylinder theory, deformation and stresses of a thick cylinder using multi-angle winding with different kinds of filaments with any number of layers under internal, external pressure and axial force are investigated analytically [13].

Base on 3-D anisotropic elasticity, many optimization researches of composite structure have been proposed. However, part of the optimization researches focused on minimizing the weight and thickness of composite laminates with different methods [14–17]. After that, an integrated optimization methodology is proposed to optimize the manufacturing cost as well as the structural performance of composite laminated plates manufactured by the resin transfer molding (RTM) process [18]. A new initialization strategy is proposed by Irisarri et al. following mechanical considerations. The method is applied to the optimal design of a composite plate for weight minimization and maximization of the buckling margins under three hundred load cases that make also the originality of this work [19]. A technique for the optimization design of composite laminated structures is presented, and the optimization process is performed using a genetic algorithm (GA), associated with the finite element method for the structural analysis [20]. The layer optimization was carried out for maximum fundamental frequency of laminated composite plates under any combination of three classical edge conditions [21]. A new iteration fractal branch and bound method is proposed, which does not require empirical knowledge of the target structure [22]. Gre’diac dealt with the stiffness design of laminated plates made of woven plies [23]. All the above researches are concerned about composite laminates. The optimization of FW thick-walled cylindrical vessel with variation of winding angle has been investigated early in 1988 [1]. Until 2006, an optimization of multilayered composite pressure vessels is accomplished using GA and subject to the Tsai–Wu failure criterion [24], but the optimal variation of winding angle is still undetermined for commonly used composite material.

Here, the deformation and stresses of a thick-walled cylinder using multi-angle winding with different kinds of filament with any number of layers under uniform internal pressure are investigated analytically. To be convenient for strength assessment, longitudinal stress along fiber direction, transverse stresses perpendicular to the fiber direction and shear stress are present analytically. An optimization model of multiple winding angle FW cylindrical vessel under uniform pressure is built, to maximize the lowest strength ratio in all layers by adjusting the winding angle of each layer. Two traditional optimization methods are adopted to find the optimization results, and their calculation efficiency is compared. Numeric results show that their combination has better efficiency to achieve the optimization solution.

2 Stresses in fiber layer

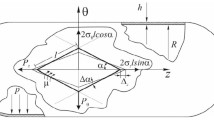
Consider a thick-walled cylinder with an inner radius of $r_{0}$, and outer radius after alternate-ply FW of $r_{n}$. Each alternate-ply layer can be regarded as an orthotropic layer. Winding filaments are divided into n orthotropic layers with outer radius of $r_{i}, (i=1, 2, {\ldots }, n)$, with different kinds of filament and winding angles in each layer.

The cylinder is subjected to uniform internal pressure $q_{a}$. Only displacement in radial r direction and axial z direction occurs, and axisymmetric stresses are developed for all orthotropic layers (Fig. 1).

Fig. 1

Axisymmetric filament-wound cylinder

2.1 On-axis stress–strain relation

The ply-oriented constitutive relationship can be expressed in matrix form as

$$\begin{aligned} \{\sigma \}=\left\{ {\begin{array}{c} \sigma _1 \\ \sigma _2 \\ \sigma _3 \\ \tau _{23} \\ \tau _{31} \\ \tau _{12} \\ \end{array}} \right\} =\left[ {{\begin{array}{cccccc} {C_{11}}&{} {C_{12}}&{} {C_{13}}&{} 0&{} 0&{} 0 \\ {C_{12}}&{} {C_{22}}&{} {C_{23}}&{} 0&{} 0&{} 0 \\ {C_{13}}&{} {C_{23}}&{} {C_{33}}&{} 0&{} 0&{} 0 \\ 0&{} 0&{} 0&{} {G_{23}}&{} 0&{} 0 \\ 0&{} 0&{} 0&{} 0&{} {G_{31} }&{} 0 \\ 0&{} 0&{} 0&{} 0&{} 0&{} {G_{12}} \\ \end{array} }} \right] \left\{ {\begin{array}{c} \varepsilon _1 \\ \varepsilon _2 \\ \varepsilon _3 \\ \gamma _{23} \\ \gamma _{31} \\ \gamma _{12} \\ \end{array}} \right\} =[C]\{\varepsilon \} \end{aligned}$$

(1)

In which

$$\begin{aligned}{}[C]=\left[ {{\begin{array}{cccccc} {1/E_1 }&{} {-\nu _{12} /E_2 }&{} {-\nu _{13} /E_3 }&{} 0&{} 0&{} 0 \\ {-\nu _{21} /E_1 }&{} {1/E_2 }&{} {-\nu _{23} /E_3 }&{} 0&{} 0&{} 0 \\ {-\nu _{31} /E_1 }&{} {-\nu _{32} /E_2 }&{} {1/E_3 }&{} 0&{} 0&{} 0 \\ 0&{} 0&{} 0&{} {1/G_{23} }&{} 0&{} 0 \\ 0&{} 0&{} 0&{} 0&{} {1/G_{31} }&{} 0 \\ 0&{} 0&{} 0&{} 0&{} 0&{} {1/G_{12} } \\ \end{array} }} \right] ^{-1} \end{aligned}$$

(2)

For unidirectional orientation fiber composites, the fiber distributions are very similar in the 2 and 3 directions. Therefore, assuming transverse isotropy, and based on equivalent properties in the 2–3 plane for unidirectional material, we have

$$\begin{aligned} E_2= & {} E_3,\quad G_{31} =G_{12},\quad \nu _{12} =\nu _{13}, \nonumber \\ \nu _{21}= & {} \nu _{31},\quad G_{23} =E_2 /2/(1+\nu _{23} ) \end{aligned}$$

(3)

Then, the stiffness matrix in Eq. (2) can be simplified as

$$\begin{aligned}{}[C]_{3\times 3}= & {} \frac{1}{1-\frac{2\nu _{21}^2 }{1-\nu _{23} }\frac{E_2 }{E_1 }}\left[ {{\begin{array}{ccc} {E_1 }&{} {\frac{\nu _{21} E_2 }{1-\nu _{23} }}&{} {\frac{\nu _{21} E_2 }{1-\nu _{23} }} \\ &{} {\frac{1-\nu _{21}^2 E_2 /E_1 }{1-\nu _{23}^2 }E_2 }&{} {\frac{\nu _{23} +\nu _{21}^2 E_2 /E_1 }{1-\nu _{23}^2 }E_2 } \\ \hbox {sym.}&{} &{} {\frac{1-\nu _{21}^2 E_2 /E_1 }{1-\nu _{23}^2 }E_2 } \\ \end{array} }} \right] \nonumber \\ C_{44}= & {} \frac{E_2 }{2(1+\nu _{23} )},\quad C_{55} =C_{66} =G_{12} \end{aligned}$$

(4)

2.2 Off-axis stress–strain relation

The strain energy can be calculated with on-axis stiffness constants or off-axis stiffness constants. With coordinate transformation of the strain vector, we can get the relationship between the stiffness coefficients of on-axis and that of off-axis, which is

$$\begin{aligned}{}[\bar{{C}}]=[T_\varepsilon ]^{T}[C][T_\varepsilon ] \end{aligned}$$

(5)

The nonzero elements of $\bar{{C}}_{ij},(i,j=1,2,3)$ can be expressed in matrix form as

$$\begin{aligned} \left\{ {\begin{array}{c} \bar{{C}}_{11} \\ \bar{{C}}_{22} \\ \bar{{C}}_{33} \\ \bar{{C}}_{23} \\ \bar{{C}}_{13} \\ \bar{{C}}_{12} \\ \end{array}} \right\} =\left[ {{\begin{array}{ccccccc} {m^{4}}&{} {n^{4}}&{} 0&{} {2m^{2}n^{2}}&{} 0&{} 0&{} {4m^{2}n^{2}} \\ {n^{4}}&{} {m^{4}}&{} 0&{} {2m^{2}n^{2}}&{} 0&{} 0&{} {4m^{2}n^{2}} \\ 0&{} 0&{} 1&{} 0&{} 0&{} 0&{} 0 \\ 0&{} 0&{} 0&{} 0&{} {n^{2}}&{} {m^{2}}&{} 0 \\ 0&{} 0&{} 0&{} 0&{} {m^{2}}&{} {n^{2}}&{} 0 \\ {m^{2}n^{2}}&{} {m^{2}n^{2}}&{} 0&{} {m^{4}+n^{4}}&{} 0&{} 0&{} {-4m^{2}n^{2}} \\ \end{array} }} \right] \left\{ {\begin{array}{c} C_{11} \\ C_{22} \\ C_{33} \\ C_{12} \\ C_{13} \\ C_{23} \\ G_{12} \\ \end{array}} \right\} \end{aligned}$$

(6)

For a group of plies within an alternate-ply layer, the effective average properties of the layers are $\bar{{C}}_{ij},(i,j=1,2,3)$. For layer (i), the orthotropic stress–strain relationship can be written as

$$\begin{aligned} \left\{ {\begin{array}{c} \sigma _z^{(i)} \\ \sigma _\theta ^{(i)} \\ \sigma _r^{(i)} \\ \end{array}} \right\} =\left[ {{\begin{array}{ccc} {\bar{{C}}_{11}^{(i)} }&{} {\bar{{C}}_{12}^{(i)} }&{} {\bar{{C}}_{13}^{(i)} } \\ {\bar{{C}}_{12}^{(i)} }&{} {\bar{{C}}_{22}^{(i)} }&{} {\bar{{C}}_{23}^{(i)} } \\ {\bar{{C}}_{13}^{(i)} }&{} {\bar{{C}}_{23}^{(i)} }&{} {\bar{{C}}_{33}^{(i)} } \\ \end{array} }} \right] \left\{ {\begin{array}{c} \varepsilon _z^{(i)} \\ \varepsilon _\theta ^{(i)} \\ \varepsilon _r^{(i)} \\ \end{array}} \right\} =\left[ {{\begin{array}{ccc} {\bar{{C}}_{zz}^{(i)} }&{} {\bar{{C}}_{z\theta }^{(i)} }&{} {\bar{{C}}_{zr}^{(i)} } \\ {\bar{{C}}_{z\theta }^{(i)} }&{} {\bar{{C}}_{\theta \theta }^{(i)} }&{} {\bar{{C}}_{\theta r}^{(i)} } \\ {\bar{{C}}_{zr}^{(i)} }&{} {\bar{{C}}_{\theta r}^{(i)} }&{} {\bar{{C}}_{rr}^{(i)} } \\ \end{array} }} \right] \left\{ {\begin{array}{c} \varepsilon _z^{(i)} \\ \varepsilon _\theta ^{(i)} \\ \varepsilon _r^{(i)} \\ \end{array}} \right\} \end{aligned}$$

(7)

2.3 Deformation and stresses

Considering the equilibrium equation in radial displacement, whose solution can be expressed as

$$\begin{aligned} u_r^{(i)} (r)=D_1^{(i)} r^{s_i }+D_2^{(i)} r^{-s_i }+t_1^{(i)} \varepsilon _0 r \end{aligned}$$

(8a)

where

$$\begin{aligned} s_i =\sqrt{\bar{{C}}_{\theta \theta }^{(i)} /\bar{{C}}_{rr}^{(i)} },\quad t_1^{(i)} =\frac{\bar{{C}}_{z\theta }^{(i)} -\bar{{C}}_{zr}^{(i)} }{\bar{{C}}_{rr}^{(i)} -\bar{{C}}_{\theta \theta }^{(i)} } \end{aligned}$$

(9a)

The integral constants $D_1^{(i)}$ and $D_2^{(i)}$ can be determined by boundary conditions, radial displacement and stress continuity conditions. Then the stresses are

$$\begin{aligned} \sigma _r^{(i)}= & {} d_1^{(i)} D_1^{(i)} r^{s_i -1}+d_2^{(i)} D_2^{(i)} r^{-s_i -1}+d_3^{(i)} \varepsilon _0 \nonumber \\ \sigma _\theta ^{(i)}= & {} d_4^{(i)} D_1^{(i)} r^{s_i -1}+d_5^{(i)} D_2^{(i)} r^{-s_i -1}+d_6^{(i)} \varepsilon _0 \nonumber \\ \sigma _z^{(i)}= & {} d_7^{(i)} D_1^{(i)} r^{s_i -1}+d_8^{(i)} D_2^{(i)} r^{-s_i -1}+d_9^{(i)} \varepsilon _0 \end{aligned}$$

(10a)

where

$$\begin{aligned} d_1^{(i)}= & {} \bar{{C}}_{\theta r}^{(i)} +\bar{{C}}_{rr}^{(i)} s_i ,\quad d_2^{(i)} =\bar{{C}}_{\theta r}^{(i)} -\bar{{C}}_{rr}^{(i)} s_i ,\\ d_3^{(i)}= & {} \bar{{C}}_{zr}^{(i)} +\left( \bar{{C}}_{\theta r}^{(i)} +\bar{{C}}_{rr}^{(i)}\right) t_1^{(i)},\quad d_4^{(i)} =\bar{{C}}_{\theta \theta }^{(i)} +\bar{{C}}_{\theta r}^{(i)} s_i, \\ d_5^{(i)}= & {} \bar{{C}}_{\theta \theta }^{(i)} -\bar{{C}}_{\theta r}^{(i)} s_i,\quad d_6^{(i)} =\bar{{C}}_{z\theta }^{(i)} +\left( \bar{{C}}_{\theta \theta }^{(i)} +\bar{{C}}_{\theta r}^{(i)} \right) t_1^{(i)}, \\ d_7^{(i)}= & {} \bar{{C}}_{z\theta }^{(i)} +\bar{{C}}_{zr}^{(i)} s_i ,\quad d_8^{(i)} =\bar{{C}}_{z\theta }^{(i)} -\bar{{C}}_{zr}^{(i)} s_i, \\ d_9^{(i)}= & {} \bar{{C}}_{zz}^{(i)} +\left( \bar{{C}}_{z\theta }^{(i)} +\bar{{C}}_{zr}^{(i)}\right) t_1^{(i)}, \\ \end{aligned}$$

When $s_{i} = 1$, it corresponds to isotropic material in r- $\theta$ plane; then, the solution of Eq. (9a) becomes

$$\begin{aligned} u_r^{(i)} (r)=D_1^{(i)} r+D_2^{(i)} /r+t_2^{(i)} \varepsilon _0 r\ln (r) \end{aligned}$$

(8b)

where

$$\begin{aligned} \;t_2^{(i)} =\frac{\bar{{C}}_{z\theta }^{(i)} -\bar{{C}}_{zr}^{(i)} }{2\bar{{C}}_{rr}^{(i)} } \end{aligned}$$

(9b)

Then, the stresses in Eq. (10a) become

$$\begin{aligned} \sigma _r^{(i)}&=d_1^{(i)} D_1^{(i)} +d_2^{(i)} D_2^{(i)} r^{-2}+\left( d_{31}^{(i)} +d_{32}^{(i)} \ln (r)\right) \varepsilon _0 \\ \sigma _\theta ^{(i)}&=d_4^{(i)} D_1^{(i)} +d_5^{(i)} D_2^{(i)} r^{-2}+\left( d_{61}^{(i)} +d_{62}^{(i)} \ln (r)\right) \varepsilon _0 \\ \sigma _z^{(i)}&=d_7^{(i)} D_1^{(i)} +d_8^{(i)} D_2^{(i)} r^{-2}+\left( d_{91}^{(i)} +d_{92}^{(i)} \ln (r)\right) \varepsilon _0 \end{aligned}$$

(10b)

where

$$\begin{aligned} d_1^{(i)}= & {} \bar{{C}}_{\theta r}^{(i)} +\bar{{C}}_{rr}^{(i)} ,\quad d_2^{(i)} =\bar{{C}}_{\theta r}^{(i)} -\bar{{C}}_{rr}^{(i)},\\ d_4^{(i)}= & {} \bar{{C}}_{\theta \theta }^{(i)} +\bar{{C}}_{\theta r}^{(i)},\quad d_5^{(i)} =\bar{{C}}_{\theta \theta }^{(i)} -\bar{{C}}_{\theta r}^{(i)}, \\ d_7^{(i)}= & {} \bar{{C}}_{z\theta }^{(i)} +\bar{{C}}_{zr}^{(i)} ,\quad d_8^{(i)} =\bar{{C}}_{z\theta }^{(i)} -\bar{{C}}_{zr}^{(i)},\\ d_{31}^{(i)}= & {} \bar{{C}}_{zr}^{(i)} +\bar{{C}}_{rr}^{(i)} t_2^{(i)} ,\quad d_{32}^{(i)} =\left( \bar{{C}}_{\theta r}^{(i)} +\bar{{C}}_{rr}^{(i)} \right) t_2^{(i)}, \\ d_{61}^{(i)}= & {} \bar{{C}}_{z\theta }^{(i)} +\bar{{C}}_{\theta r}^{(i)} t_2^{(i)},\quad d_{62}^{(i)} =\left( \bar{{C}}_{\theta \theta }^{(i)} +\bar{{C}}_{\theta r}^{(i)}\right) t_2^{(i)}, \\ d_{91}^{(i)}= & {} \bar{{C}}_{zz}^{(i)} +\bar{{C}}_{zr}^{(i)} t_2^{(i)} ,\quad d_{92}^{(i)} =\left( \bar{{C}}_{z\theta }^{(i)} +\bar{{C}}_{zr}^{(i)}\right) t_2^{(i)} \end{aligned}$$

2.4 Boundary and continuity conditions

The boundary conditions on the internal ($r=r_{0}$) and external ($r= r_{n}$) surfaces are given by

$$\begin{aligned} \sigma _r^{(1)} |_{r=r_0 } =-q_a,\quad \sigma _r^{(n)} |_{r=r_n } =0 \end{aligned}$$

(11a)

At a given layer interface ($r=r_{i}$), the radial stress and displacement satisfy continuity conditions as

$$\begin{aligned} {\begin{array}{l} \sigma _r^{(i)} |_{r=r_i } =\sigma _r^{(i+1)} |_{r=r_i }, \\ u_r^{(i)} (r_i )=u_r^{(i+1)} (r_i ), \\ \end{array}}\quad (i=1,2,\ldots ,n-1) \end{aligned}$$

(11b)

The equilibrium in z direction gives

$$\begin{aligned} 2\pi \sum _{i=1}^n {\int _{r_{i-1} }^{r_i } {\sigma _z^{(i)} r dr} } =q_a \pi r_0^2 \end{aligned}$$

(11c)

Above conditions in Eq. (11) lead to a set of equations, where the integral constants and axial strain are determined by

$$\begin{aligned} {[}K{]}\{\delta \}= & {} \{q_{i}\}\nonumber \\ {[}K{]}= & {} \left[ {{\begin{array}{ccccccccccc} {a_{1,1} }&{} {a_{1,2} }&{} {\cdots }&{} 0&{} 0&{} 0&{} 0 &{}{\cdots }&{} 0&{} 0&{} {a_{1,2n+1} } \\ 0&{} 0&{} {\cdots }&{} 0&{} 0&{} 0&{} 0 &{}{\cdots }&{} {a_{2,2n-1} }&{} {a_{2,2n} }&{} {a_{2,2n+1} } \\ {\cdots }&{} {\cdots }&{} {\cdots }&{} {\cdots }&{} {\cdots }&{} {\cdots }&{} {\cdots } &{}{\cdots }&{} {\cdots }&{} {\cdots }&{} {\cdots } \\ 0&{} 0&{} {\cdots }&{} {a_{2i+1,2i-1} }&{} {a_{2i+1,2i} }&{} {a_{2i+1,2i+1} }&{} {a_{2i+1,2i+2} } &{}{\cdots }&{} 0&{} 0&{} {a_{2i+1,2n+1} } \\ 0&{} 0&{} {\cdots }&{} {a_{2i+2,2i-1} }&{} {a_{2i+2,2i} }&{} {a_{2i+2,2i+1} }&{} {a_{2i+2,2i+2} } &{}{\cdots }&{} 0&{} 0&{} {a_{2i+2,2n+1} } \\ {\cdots }&{} {\cdots }&{} {\cdots }&{} {\cdots }&{} {\cdots }&{} {\cdots }&{} {\cdots } &{}{\cdots }&{} {\cdots }&{} {\cdots }&{} {\cdots } \\ {a_{2n+1,1} }&{} {a_{2n+1,2} }&{} {\cdots }&{} {a_{2n+1,2i-1} }&{} {a_{2n+1,2i} }&{} {a_{2n+1,2i+1} }&{} {a_{2n+1,2i+2} } &{}{\cdots }&{} {a_{2n+1,2n-1} }&{} {a_{2n+1,2n} }&{} {a_{2n+1,2n+1} } \\ \end{array} }} \right] \nonumber \\ \end{aligned}$$

(12)

In which nonzero elements in the stiffness matrix [K] are given as follows,

• (1) Elements in the first two rows:

  $$\begin{aligned} a_{1,1}= & {} \left( \bar{{C}}_{\theta r}^{(1)} +\bar{{C}}_{rr}^{(1)} s_1\right) r_0^{s_1 -1} \\ a_{1,2}= & {} \left( \bar{{C}}_{\theta r}^{(1)} -\bar{{C}}_{rr}^{(1)} s_1\right) r_0^{-s_1 -1} \\ a_{1,2n+1}= & {} \left\{ {\begin{array}{ll} \bar{{C}}_{zr}^{(1)} +\left( \bar{{C}}_{\theta r}^{(1)} +\bar{{C}}_{rr}^{(1)}\right) \frac{\bar{{C}}_{z\theta }^{(1)} -\bar{{C}}_{zr}^{(1)} }{\bar{{C}}_{rr}^{(1)} -\bar{{C}}_{\theta \theta }^{(1)} },&{} s_1 \ne 1 \\ \frac{\bar{{C}}_{z\theta }^{(1)} +\bar{{C}}_{zr}^{(1)} }{2}+\left( \bar{{C}}_{\theta r}^{(1)} +\bar{{C}}_{rr}^{(1)}\right) \frac{\bar{{C}}_{z\theta }^{(1)} -\bar{{C}}_{zr}^{(1)} }{2\bar{{C}}_{rr}^{(1)} }\ln (r_0 ),&{} s_1 =1 \\ \end{array}} \right. \\ a_{2,2n-1}= & {} \left( \bar{{C}}_{\theta r}^{(n)} +\bar{{C}}_{rr}^{(n)} s_n\right) r_n^{s_n -1} \\ a_{2,2n}= & {} \left( \bar{{C}}_{\theta r}^{(n)} -\bar{{C}}_{rr}^{(n)} s_n\right) r_n^{-s_n -1} \\ a_{2,2n+1}= & {} \left\{ {\begin{array}{ll} \bar{{C}}_{zr}^{(n)} +\left( \bar{{C}}_{\theta r}^{(n)} +\bar{{C}}_{rr}^{(n)}\right) \,\frac{\bar{{C}}_{z\theta }^{(n)} -\bar{{C}}_{zr}^{(n)} }{\bar{{C}}_{rr}^{(n)} -\bar{{C}}_{\theta \theta }^{(n)} },&{} s_n \ne 1 \\ \frac{\bar{{C}}_{z\theta }^{(n)} +\bar{{C}}_{zr}^{(n)} }{2}+\left( \bar{{C}}_{\theta r}^{(n)} +\bar{{C}}_{rr}^{(n)}\right) \frac{\bar{{C}}_{z\theta }^{(n)} -\bar{{C}}_{zr}^{(n)} }{2\bar{{C}}_{rr}^{(n)} }\ln r_{n-1},&{} s_n =1 \\ \end{array}} \right. \\ \end{aligned}$$

• (2) Elements from the third row to the second row from bottom, in which loop index $i=1,2,{\ldots },n-1$.

  $$\begin{aligned} \begin{array}{l} a_{2i+1,2i-1} =\left( \bar{{C}}_{\theta r}^{(i)} +\bar{{C}}_{rr}^{(i)} s_i\right) r_i^{s_i -1}, \\ a_{2i+1,2i} =\left( \bar{{C}}_{\theta r}^{(i)} -\bar{{C}}_{rr}^{(i)} s_i\right) r_i^{-s_i -1}, \\ a_{2i+1,2i+1} =-\left( \bar{{C}}_{\theta r}^{(i+1)} +\bar{{C}}_{rr}^{(i+1)} s_{i+1}\right) r_i^{s_{i+1} -1}, \\ a_{2i+1,2i+2} =-\left( \bar{{C}}_{\theta r}^{(i+1)} -\bar{{C}}_{rr}^{(i+1)} s_{i+1}\right) r_i^{-s_{i+1} -1} \\ \end{array}\quad (i=1,2,\ldots ,n-1) \end{aligned}$$
  $$\begin{aligned}&a_{2i+1,2n+1} =e_3^{(i)} -e_4^{(i)},\quad (i=1,2,\ldots ,n-1) \\&e_3^{(i)} =\left\{ {\begin{array}{ll} {\bar{C}}_{zr}^{(i)} +\left( \bar{{C}}_{\theta r}^{(i)} +\bar{{C}}_{rr}^{(i)}\right) \frac{\bar{{C}}_{z\theta }^{(i)} -\bar{{C}}_{zr}^{(i)} }{\bar{{C}}_{rr}^{(i)} -\bar{{C}}_{\theta \theta }^{(i)} },&{}s_i \ne 1 \\ \frac{{\bar{C}}_{z\theta }^{(i)} +{\bar{C}}_{zr}^{(i)}}{2}+\left( \bar{{C}}_{\theta r}^{(i)} +\bar{{C}}_{rr}^{(i)}\right) \frac{\bar{{C}}_{z\theta }^{(i)} -\bar{{C}}_{zr}^{(i)} }{2\bar{{C}}_{rr}^{(i)} }\ln r_i,&{} s_i =1 \\ \end{array}} \right. \\&e_4^{(i)} =\left\{ {\begin{array}{ll} {\bar{C}}_{zr}^{(i+1)} +\left( \bar{{C}}_{\theta r}^{(i+1)} +{\bar{C}}_{rr}^{(i+1)}\right) \,\frac{{\bar{C}}_{z\theta }^{(i+1)} -{\bar{C}}_{zr}^{(i+1)}}{{\bar{C}}_{rr}^{(i+1)} -{\bar{C}}_{\theta \theta }^{(i+1)} },&{}s_{i+1} \ne 1 \\ \frac{{\bar{C}}_{z\theta }^{(i+1)} +{\bar{C}}_{zr}^{(i+1)} }{2}+\left( {\bar{C}}_{\theta r}^{(i+1)} +{\bar{C}}_{rr}^{(i+1)}\right) \frac{{\bar{C}}_{z\theta }^{(i+1)} -{\bar{C}}_{zr}^{(i+1)} }{2{\bar{C}}_{rr}^{(i+1)} }\ln r_i ,&{}s_{i+1} =1 \\ \end{array}} \right. \\&a_{2i+2,2i-1} =r_i^{s_i -1}, \\&a_{2i+2,2i} =r_i^{-s_i -1} \\&a_{2i+2,2i+1} =-r_i^{s_{i+1} -1} \\&a_{2i+2,2i+2} =-r_i^{-s_{i+1} -1} \\&a_{2i+2,2n+1} =e_5^{(i)} -e_6^{(i)},\quad (i=1,2,\ldots ,n-1) \\&e_5^{(i)} =\left\{ {\begin{array}{ll} \frac{\bar{{C}}_{z\theta }^{(i)} -\bar{{C}}_{zr}^{(i)} }{\bar{{C}}_{rr}^{(i)} -\bar{{C}}_{\theta \theta }^{(i)} },&{}s_i \ne 1 \\ \frac{\bar{{C}}_{z\theta }^{(i)} -\bar{{C}}_{zr}^{(i)} }{2\bar{{C}}_{rr}^{(i)} }\ln r_i,&{}s_i =1 \\ \end{array}} \right. \\&e_6^{(i)} =\left\{ {\begin{array}{ll} \frac{\bar{{C}}_{z\theta }^{(i+1)} -\bar{{C}}_{zr}^{(i+1)} }{\bar{{C}}_{rr}^{(i+1)} -\bar{{C}}_{\theta \theta }^{(i+1)} },&{}s_{i+1} \ne 1 \\ \frac{\bar{{C}}_{z\theta }^{(i+1)} -\bar{{C}}_{zr}^{(i+1)} }{2\bar{{C}}_{rr}^{(i+1)} }\ln r_i,&{}s_{i+1} =1 \\ \end{array}} \right. \\ \end{aligned}$$

• (3) Elements in the last row:

  $$\begin{aligned} \begin{array}{l} a_{2n+1,2i-1} =\frac{2\left( \bar{{C}}_{z\theta }^{(i)} +\bar{{C}}_{zr}^{(i)} s_i\right) \left( r_i^{s_i +1} -r_{i-1}^{s_i +1}\right) }{1+s_i }, \\ a_{2n+1,2i} =\left\{ {\begin{array}{ll} \frac{2\left( \bar{{C}}_{z\theta }^{(i)} -\bar{{C}}_{zr}^{(i)} s_i\right) \left( r_i^{1-s_i } -r_{i-1}^{1-s_i }\right) }{1-s_i },&{}s_i \ne 1 \\ 2\left( \bar{{C}}_{z\theta }^{(i)} -\bar{{C}}_{zr}^{(i)}\right) \ln (r_i /r_{i-1} ),&{}s_i =1 \\ \end{array}} \right. , \\ \end{array}\quad (i=1,2,\ldots ,n) \\ \end{aligned}$$
  $$\begin{aligned}&a_{2n+1,2n+1} =\sum _{i=1}^n {e_7^{(i)} } \\&e_7^{(i)} =\left\{ {\begin{array}{l} \left[ \bar{{C}}_{zz}^{(i)} +\left( \bar{{C}}_{z\theta }^{(i)} +\bar{{C}}_{zr}^{(i)}\right) \frac{\bar{{C}}_{z\theta }^{(i)} -\bar{{C}}_{zr}^{(i)}}{\bar{{C}}_{rr}^{(i)} -\bar{{C}}_{\theta \theta }^{(i)} }\right] \left( r_i^2 -r_{i-1}^2\right) ,\quad s_i \ne 1 \\ \left[ \bar{{C}}_{zz}^{(i)} -\frac{\left( \bar{{C}}_{z\theta }^{(i)} -\bar{{C}}_{zr}^{(i)}\right) ^{2}}{4\bar{{C}}_{rr}^{(i)}}\right] \left( r_i^2 -r_{i-1}^2 \right) +\frac{\bar{{C}}_{z\theta }^{(i)}{2}-\bar{{C}}_{zr}^{(i)} {2}}{2\bar{{C}}_{rr}^{(i)} }\left( r_i^2 \ln r_i -r_{i-1}^2 \ln r_{i-1}\right) ,\quad s_i =1 \\ \end{array}}\right. \quad (i=1,2,\ldots ,n) \end{aligned}$$

• (4) Vector of unknown integral constants and loading parameters:

  $$\begin{aligned} \{\delta \}= & {} \left\{ {D_1^{(1)},D_2^{(1)},\ldots ,D_1^{(i)},D_2^{(i)} ,\ldots ,D_1^{(n)},D_2^{(n)} ,\varepsilon _0 } \right\} ^{T} \\ \{q_i \}= & {} \left\{ {-q_a ,0,0,\ldots ,0,q_a r_0^2 } \right\} ^{T} \\ \end{aligned}$$

Solving Eq. (12), the displacements, strains and the stresses of each layer can be determined.

2.5 3-D stresses in fiber directions

The stresses in Eq. (10) are average values in each orthotropic layer in global coordinate system. Stresses in fiber directions such as longitudinal stress $\sigma _1^{(i)}$, transverse stresses $\sigma _2^{(i)} ,\sigma _3^{(i)}$ and shear stress $\tau _{12}^{(i)}$ in fiber layer can be determined by on-axis stress–strain relation. First, we need on-axis strains by coordinate transformation of off-axis. From deformations in Eq. (8) and strain definition, we can get strains in cylindrical coordinate system. Then the on-axis strains can be obtained with coordinate transformation of strains. Finally, the stresses in fiber directions are derived as

$$\begin{aligned} \sigma _1^{(i)}= & {} \left( n_i^2 C_{11}^{(i)} +m_i^2 C_{12}^{(i)} +s_i C_{13}^{(i)}\right) D_1^{(i)} r^{s_i -1} \nonumber \\&+\,\left( n_i^2 C_{11}^{(i)} +m_i^2 C_{12}^{(i)} -s_i C_{13}^{(i)}\right) D_2^{(i)} r^{-s_i -1} \nonumber \\&+\,\left[ C_{11}^{(i)} \left( m_i^2 +n_i^2 t_1^{(i)} \right) +C_{12}^{(i)} \left( n_i^2 +m_i^2 t_1^{(i)}\right) +C_{13}^{(i)} t_1^{(i)} \right] \varepsilon _0 \nonumber \\ \sigma _2^{(i)}= & {} \left( n_i^2 C_{12}^{(i)} +m_i^2 C_{22}^{(i)} +s_i C_{23}^{(i)}\right) D_1^{(i)} r^{s_i -1} \nonumber \\&+\,\left( n_i^2 C_{12}^{(i)} +m_i^2 C_{22}^{(i)} -s_i C_{23}^{(i)}\right) D_2^{(i)} r^{-s_i -1} \nonumber \\&+\,\left[ C_{12}^{(i)} \left( m_i^2 +n_i^2 t_1^{(i)} \right) +C_{22}^{(i)} \left( n_i^2 +m_i^2 t_1^{(i)}\right) +C_{23}^{(i)} t_1^{(i)} \right] \varepsilon _0\nonumber \\ \sigma _3^{(i)}= & {} \left( n_i^2 C_{13}^{(i)} +m_i^2 C_{23}^{(i)} +s_i C_{33}^{(i)}\right) D_1^{(i)} r^{s_i -1} \nonumber \\&+\left( n_i^2 C_{13}^{(i)} +m_i^2 C_{23}^{(i)} -s_i C_{33}^{(i)}\right) D_2^{(i)} r^{-s_i -1} \nonumber \\&+\,\left[ C_{13}^{(i)} \left( m_i^2 +n_i^2 t_1^{(i)} \right) +C_{23}^{(i)} \left( n_i^2 +m_i^2 t_1^{(i)}\right) +C_{33}^{(i)} t_1^{(i)} \right] \varepsilon _0\nonumber \\ \tau _{12}^{(i)}= & {} 2m_i n_i G_{12} \left[ D_1^{(i)} r^{s_i -1}+D_2^{(i)} r^{-s_i -1}+ (t_1^{(i)} -1)\varepsilon _0\right] \end{aligned}$$

(13a)

when $s_{i}=1$, stresses in fiber directions become

$$\begin{aligned} \sigma _1^{(i)}= & {} \left( n_i^2 C_{11}^{(i)} +m_i^2 C_{12}^{(i)} +C_{13}^{(i)} \right) D_1^{(i)} \nonumber \\&+\,\left( n_i^2 C_{11}^{(i)} +m_i^2 C_{12}^{(i)} -C_{13}^{(i)} \right) D_2^{(i)} /r^{2} \nonumber \\&+\,\left[ C_{11}^{(i)} \left( m_i^2 +n_i^2 t_2^{(i)} \ln r\right) +C_{12}^{(i)} \left( n_i^2 +m_i^2 t_2^{(i)} \ln r\right) +C_{13}^{(i)} t_2^{(i)} (1+\ln r)\right] \varepsilon _0\nonumber \\ \sigma _2^{(i)}= & {} \left( n_i^2 C_{12}^{(i)} +m_i^2 C_{22}^{(i)} +C_{23}^{(i)}\right) D_1^{(i)} \nonumber \\&+\,\left( n_i^2 C_{12}^{(i)} +m_i^2 C_{22}^{(i)} -C_{23}^{(i)} \right) D_2^{(i)} /r^{2} \nonumber \\&+\,\left[ C_{12}^{(i)} \left( m_i^2 +n_i^2 t_2^{(i)} \ln r\right) +C_{22}^{(i)} \left( n_i^2 +m_i^2 t_2^{(i)} \ln r\right) +C_{23}^{(i)} t_2^{(i)} (1+\ln r)\right] \varepsilon _0\nonumber \\ \sigma _3^{(i)}= & {} \left( n_i^2 C_{13}^{(i)} +m_i^2 C_{23}^{(i)} +C_{33}^{(i)}\right) D_1^{(i)} \nonumber \\&+\,\left( n_i^2 C_{13}^{(i)} +m_i^2 C_{23}^{(i)} -C_{33}^{(i)} \right) D_2^{(i)} /r^{2} \nonumber \\&+\,\left[ C_{13}^{(i)} \left( m_i^2 +n_i^2 t_2^{(i)} \ln r\right) +C_{23}^{(i)} \left( n_i^2 +m_i^2 t_2^{(i)} \ln r\right) +C_{33}^{(i)} t_2^{(i)} (1+\ln r)\right] \varepsilon _0 \nonumber \\ \tau _{12}^{(i)}= & {} 2m_i n_i G_{12} \left[ D_1^{(i)} +D_2^{(i)} /r^{2}+ (t_2^{(i)} \ln r-1)\varepsilon _0\right] \end{aligned}$$

(13b)

3 Optimization model and method

3.1 Failure criteria

Composite material failure criterions are the maximum stress criterion, the maximum strain criterion, Tsai–Hill criteria, Hoffman criteria, and Tsai–Wu criterion. Here three-dimensional Tsai–Wu failure criterion is adopted in strength ratio calculation. The failure surface of Tsai–Wu criterion is [25]:

$$\begin{aligned} -F_{zz} \sigma _1^2 -F_{rr} \left( \sigma _2^2 +\sigma _3^2\right) +F_{ss} \tau _{12}^2 +2F_{rz} \left( \sigma _2 +\sigma _3\right) \sigma _1 +2F_{r\theta } \sigma _2 \sigma _3 +F_r (\sigma _2 +\sigma _3 )+F_z \sigma _1 =1 \end{aligned}$$

(14)

where

$$\begin{aligned} F_{zz}= & {} 1/(X_\mathrm{t} X_\mathrm{c} ),F_{rr} =1/(Y_\mathrm{t} Y_\mathrm{c} ),\;F_{ss} =1/S^{2},\; \\ F_{rz}= & {} -0.5/\sqrt{X_\mathrm{t} X_\mathrm{c} Y_\mathrm{t} Y_\mathrm{c} },\;F_{r\theta } =1/(2Y_\mathrm{t} Y_\mathrm{c} ), \\ F_r= & {} 1/Y_\mathrm{t} +1/Y_\mathrm{c} ,\;F_z =1/X_\mathrm{t} +1/X_\mathrm{c} \end{aligned}$$

In which $X_{\mathrm{t}}, X_{\mathrm{c}}$ represent the longitudinal tensile strength and compression strength in fiber directions, respectively. $Y_{\mathrm{t}}, Y_{\mathrm{c}}$ are the fiber transverse tensile strength and compression strength, respectively. S is the shear strength. $\sigma _{1}$ is the longitudinal stress in fiber direction. $\sigma _{2 }$ and $\sigma _{3}$ are the transversed stresses. $\tau _{12}$ is the shear stress.

3.2 Strength ratio calculation

From Eq. (14), we calculate the strength ratio by

$$\begin{aligned} R=-\xi /(2\rho )+\sqrt{\xi ^{2}/(2\rho )^{2}+1/\rho } \end{aligned}$$

(15)

In which

$$\begin{aligned} \rho&=-F_{zz} \sigma _1^2 -F_{rr} \left( \sigma _2^2 +\sigma _3^2\right) +F_{ss} \tau _{12}^2 \\&\quad +\,2F_{rz} (\sigma _2 +\sigma _3 )\sigma _1 +2F_{r\theta } \sigma _2 \sigma _3 , \\ \xi&=F_r (\sigma _2 +\sigma _3 )+F_z \sigma _1 \end{aligned}$$

(Tsai-Wu criterion)

3.3 Optimization method

We used two methods, complex method (CM) and steepest descent (SD) to find the optimization solution [26].

3.3.1 Complex method

Actually, CM is a development of simplex method in constrained problems. In 1965, Box extended the simplex method of unconstrained minimization to solve constrained minimization problems of nonlinear programming:

$$\begin{aligned} \hbox {Minimize}\,f(X) \end{aligned}$$

(16a)

subject to

$$\begin{aligned}&g_{j}(X)\le 0,\quad (j=1,2,\ldots ,m) \end{aligned}$$

(16b)

$$\begin{aligned}&x^{(l)}_{i}\le x_{i}\le x^{(u)}_{i},\quad (i=1,2,\ldots ,n) \end{aligned}$$

(16c)

In general, the satisfaction of the side constraints (lower and upper bounds on the variables $x_{i})$ may not correspond to the satisfaction of the constraints $g_{j}({{\varvec{X}}}) \le 0$. The formation of a sequence of geometric figures each having $k=n+1$ vertices in an n-dimensional space (called the simplex) is the basic idea, where a sequence of geometric figures each having $k\ge n+1$ vertices is formed to find the constrained minimum point. The method assumes that an initial feasible point ${{\varvec{X}}}_{1}$ (which satisfies all the m constraints) is available.

Iterative steps in the procedure:

• (1) Find $k\ge n+1$ points, satisfied all m constraints.

• (2) The objective function is evaluated at each of the k points (vertices). If the vertex ${{\varvec{X}}}_{h }$ corresponds to the largest function value, the reflection is used to find a new point ${{\varvec{X}}}_{r}$ as

  $$\begin{aligned} X_{r}=X_{0}+ \alpha (X_{0}-X_{h}) \end{aligned}$$

  (17)

  where $\alpha = 1.3$ and ${{\varvec{X}}}_{0 }$ is the centroid of all vertices except ${{\varvec{X}}}_{h}$:

  $$\begin{aligned} X_0 =\frac{1}{k-1}{\mathop {\mathop {\sum }\limits _{l=1}}\limits _{l\ne k} ^k}X_l \end{aligned}$$

  (18)

• (3) If the point ${{\varvec{X}}}_{r }$ is feasible and $f({{\varvec{X}}}_{r})< f({{\varvec{X}}}_{h})$, then point ${{\varvec{ X}}}_{h}$ is replaced by ${{\varvec{X}}}_{r}$, and turn to step 2. If $f({{\varvec{X}}}_{r})\ge f({{\varvec{X}}}_{h})$, a new trial point ${{\varvec{X}}}_{r }$ is found by reducing the value of $\alpha$ in Eq. (16) by a factor of 2 and is tested for the satisfaction of the relation $f({{\varvec{X}}}_{r})<f({{\varvec{X}}}_{h})$. The procedure of finding a new point ${{\varvec{X}}}_{r}$ with a reduced value of $\alpha$ is repeated again. This procedure is repeated, until the value of $\alpha$ becomes very small. If an improved point ${{\varvec{X}}}_{r}$, with $f({{\varvec{X}}}_{r}) < f({{\varvec{X}}}_{h})$, cannot be obtained even with that small value of $\alpha$, the point ${{\varvec{ X}}}_{r}$ is discarded and the entire procedure of the reflection is restarted by using the point ${{\varvec{X}}}_{p}$ (which has the second-highest function value) instead of ${{\varvec{ X}}}_{h}$.

• (4) If at any stage, the reflected point ${{\varvec{ X}}}_{r}$ (found in step 3) violates any of the constraints, it is moved halfway in toward the centroid until it becomes feasible. This method will progress toward the optimum point as long as the complex has not collapsed into its centroid.

• (5) Each time the worst point ${{\varvec{ X}}}_{h }$ of the current complex is replaced by a new point, the complex gets modified, and we have to test for the convergence of the process. We assume convergence of the process whenever the following two conditions are satisfied:

  • (a) The complex shrinks to a specified small size.

  • (b) The standard deviation of the function value becomes sufficiently small.

3.3.2 Steepest descent method

SD is one of the simplest and the most fundamental minimization methods for unconstrained optimization. Since it uses the negative gradient as its descent direction, it is also called the gradient method. It can be summarized by the following steps:

• (1) Start with an arbitrary initial point ${{\varvec{ X}}}_{1}$. Set the iteration number as $i =1$.

• (2) Find the search direction $\triangledown f({{\varvec{ X}}}_{i})$.

• (3) Determine the optimal step length $h_{i}$ in the direction $\triangledown f({{\varvec{ X}}}_{i})$, and set

  $$\begin{aligned} X_{i}+1 = X_{i}-h_{i} \triangledown f(X_{i}) \end{aligned}$$

  (19)

• (4) Test the new point, ${{\varvec{X}}}_{i+1}$, for optimality. If ${{\varvec{X}}}_{i+1 }$ is optimum, stop the process. Otherwise, go to next step.

• (5) Set the new iteration number $i =i+1$, and return to step 2.

3.3.3 The combined method

In order to improve the efficiency of above methods, a combined complex–steepest descent method is developed to achieve better results. The process of the calculation is: first, we use CM to find an optimized winding angle sequence, then curve fit the results to obtain a more smooth distribution of winding angle sequence, and finally, optimize the fitted curve with SD. The combined method diagram is given in Fig. 2.

Fig. 2

Combined method diagram

3.4 Optimized winding angle sequence

Here carbon fiber epoxy (T300/934) and E-glass/epoxy are used, whose properties are listed in Table 1.

Table 1 Material property of winding filaments [24, 25, 27]

Under 0.1111111 MPa internal pressure, letting $n=1$, it describes a uniform winding angle cylinder. Letting $n=1, 3, 5, 10, 20$, multi-angle FW cylinder with different number of winding angle sequence for ratio of the inner radius to outer radius $r_{0}$/$r_{n}=0.95, 0.90, 0.85, 0.80, 0.75, 0.70, 0.65$ is simulated.

To get the optimal variation of winding angles sequence, we used CM, SD and a combined complex–steepest descent method to solve the problem.

3.4.1 Results of CM

For a series multi-layered T300/934 cylinders and E-glass/epoxy cylinders, the optimized winding angle is obtained with CM.

For different radius ratio cylindrical vessels, it is found that the variation of the optimized winding angle is unstable and fluctuating for large number of n. This result makes the distributions of strength ratio via thickness are also unstable and fluctuating, so the maximum strength ratio and more uniform strength for all layers cannot be achieved. For example, a T300/934 cylinder ($n=10$), the results were obtained and given in Table 2.

Table 2 Optimized winding angle of T300/934 ($^{\circ }$)

3.4.2 Results of SD

With SD, the results with the same geometric parameters for T300/934 cylinders and E-glass/epoxy cylinders are given.

From the results, we find that the optimized winding angle sequences are smooth, but the strength ratios do not achieve the optimal state, so the maximum strength ratio is not achieved. For example, a E-glass/epoxy cylinder ($n=10$), the results are obtained and given in Table 3.

Table 3 Optimized winding angle of E-glass/epoxy(${}^{\circ }$)

3.4.3 Results of the combined method

The optimization study shows that the optimized winding angle sequences tend to unique distribution of winding angle when the layer number n goes to large number and the lowest strength ratio achieves the optimal level.

For T300/934 cylinders and E-glass/epoxy cylinders with different radius ratio $r_{0}/r_{n}$ and layer numbers n, the results are obtained with the combined method and listed in Table 4(a,b), respectively.

Table 4 Optimized winding angle of (a) T300/934 (${}^{\circ }$), (b) E-glass/epoxy (${}^{\circ }$)

From the results, we find that the variation of the optimized winding angle is stable and smooth for large number of n, and the strength ratios achieve the optimal state. More details will be discussed in the next section.

4 Discussion of the results

Choose the combined method and different radius ratio $r_{0}/r_{n}=0.95, 0.90, 0.85, 0.80, 0.75, 0.70, 0.65$, etc., the winding angle sequence to maximize the lowest strength ratio is optimized. We choose layer number $n=1,3,5,10$ and 20, to simulate the winding angle variation for the optimized scheme of infinite thin thickness of winding layer. For a single-angle winding thin-walled cylinder, the optimized winding angle is about $55^{\circ }$ [7–11]. So $\phi =55^{\circ }$ is chosen as the original winding angle.

The optimized winding angle sequence, the maximum strength ratio and the strength ratio distribution via thickness are calculated, respectively.

4.1 T300/934 cylinders

For T300/934 cylinders, the optimized winding angle sequence for different layer number n and the corresponding strength ratio distributions via thickness are shown in Fig. 3 for $r_{0}/r_{n}=0.95,0.90,0.85,0.80,0.75,0.70$ and 0.65.

Fig. 3

The optimized winding angle and the corresponding strength ratio distributions via thickness of T300/934

From the figures we find that, for single-layered cylinder, the winding angles distribute in range 54$^{\circ }$–57$^{\circ }$ for $r_{0}/r_{n}=0.95-0.65$. This conclusion is consistent with the paper [24].

For a multi-layered thin-walled FW cylinder, such as $r_{0}/r_{n}=0.95$, the optimized winding angle, which is stable and smooth for large number of n, increases versus thickness outward, whose minimum and maximum appear on the inner and outer surface, respectively. With the increase number of n, the maximum strength ratio and more uniform strength distribution are achieved. With thicker wall thickness, such as $r_{0}/r_{n}=0.80$, the optimized winding angle increases rapidly near the inner surface and the optimized winding angle decreases rapidly near the outer surface, like a parabola. For large number of n, the maximum strength ratio and more uniform strength distribution are achieved. For very thick cylinders, such as $r_{0}$/$r_{n} =0.65$, the optimized winding angle reaches nearly $90^{\circ }$ near the inner surface and uniform strength distribution cannot be achieved. Obviously, it is difficult to achieve uniform strength ratio via thickness only by changing winding angle. A 20-layer strength ratio variation is compared in Table 5.

Table 5 The strength ratio in 20-layer cylinder of original and optimized winding angle of (a) T300/934

From the results, for original scheme, the difference of strength ratio via thickness for $r_{0}/r_{n}=0.95-0.65$ is 14.18, 15.16, 14.70, 25.61, 39.12, 51.34, 61.90 %, respectively, while that of the optimized scheme is 1.17, 2.88, 6.06, 17.98, 30.07, 41.22, 51.29 %, respectively. The optimized scheme leads to more uniform strength ratio than the original one, and the minimum strength is much higher than that of the original scheme.

4.2 E-glass/epoxy cylinders

For E-glass/epoxy cylinders, the optimized winding angle sequence for different layer number n and the corresponding maximum strength ratio are shown in Fig. 4.

Fig. 4

The optimized winding angle and the corresponding strength ratio distributions via thickness of E-glass/epoxy

The general trends of winding angle of E-glass/epoxy cylinders are the same with that of T300/934 cylinders. It is worth to emphasize that the variation of the optimized winding angle is stable and smooth for large number n, and with the increase number of n, the maximum strength ratio and more uniform strength distribution via thickness can be achieved easily. It suggests that the material property has great influence on strength ratio distribution via thickness. The more difference elasticity coefficients in different directions, the more difficult to achieve an optimal winding angle scheme and large difference distribution in strength ratio via thickness are produced.

The strength ratio variation in 20-layer cylinder is shown in Table 6. From the results, for original scheme, the difference of strength ratio via thickness for $r_{0}/r_{n}=0.95-0.65$ is 3.06, 4.73, 4.88, 4.83, 7.80, 14.91, 23.61 %, respectively, while the optimized scheme is 0.61, 0.82, 1.27, 1.55, 2.31, 2.83, 3.76 %, respectively. More uniform strength ratio distribution is achieved, and their minimum strength ratio is improved significantly.

Table 6 The strength ratio in 20-layer cylinder of original and optimized winding angle of (b) E-glass/epoxy

4.3 Comparison of multi-angle winding vessel of T300

In order to prove the accuracy of the results in this paper, here the 20-layered filament-wound cylinder in [24] is chosen and compared for strength ratio $R = 1, r_{n}$/$r_{0 }= 1.1, 1.5$.

The optimized winding angle sequence and distribution of the burst pressures via the thickness of a 20-layered cylinder are shown in Fig 5. From the results, for the thin-walled FW cylinder ($r_{n}/r= 1.1$), it is found that the two optimized winding angle sequences are very similar, and the distribution of the burst pressures of this paper is much better than those of [24]. For very thick cylinders ($r_{n}/r= 1.5$), it is found that there is no difference between the distribution of the burst pressures.

Fig. 5

The optimized winding angle and the corresponding strength ratio distributions via thickness of T300/5208

5 Conclusion

The investigation leads to conclusions:

• (1) A suitable optimization method has great influence to the optimized winding angle sequence. Numeric results show that the combined complex–steepest descent method has better efficiency to achieve the optimization solution.

• (2) The material property has great influence on strength ratio distribution via thickness. Large difference in elasticity coefficients in different directions, more evident variation winding angle should be adopted to achieve more uniform strength ratio, so the corresponding strength ratio distributions of E-glass/epoxy are much better than T300/934.

• (3) The material utilization and working pressure can be increased by proper winding angle variation, and several optimization winding angle sequence schemes are found for different radius ratio cylindrical vessels made of E-glass/epoxy or T300/934.

• (4) In this paper, more accurate calculation results are given for multi-layered thin-walled FW cylinder. It is difficult to achieve uniform strength ratio via thickness for carbon fiber cylinder by changing winding angle, and the strength ratios of the carbon fibers are approximately double the values of the glass fibers. Therefore, the carbon fiber is not suitable for a thick-walled FW cylinder.