1 Introduction

Impacts or collisions are an important part of the mechanical design and have been studied for centuries; however, due to the complexity of impact theory, our knowledge on this matter is limited. There are two main approaches on the study of impacts. In the first approach, colliding bodies are considered rigid with the exception of small deformations at the contacting points. Rigid body collision dates back to defining the kinematic coefficient of restitution by Newton [17]. Newton defined the coefficient of restitution as the ratio between post- and pre-impact relative velocities. The other definition is provided by Poisson [19] and divides the impact into compression and restitution phases. An energetic coefficient of restitution was introduced later by Stronge [25]. The coefficient of restitution replaces the effect of the contact force on the impacting objects and is used to determine the normal impulse during the impact [12]. The coefficient of restitution does not consider the effect of the contact force history during the impact, and there are many combinations of contact force and impact duration that can yield to the same coefficient of restitution.

For oblique impact, where the coefficient of friction plays an important role, the kinematic coefficient of restitution yields to an increase in the total energy of the system for certain situations[13, 20]. The recent focus has been on solving the problems of rigid body models [1, 8, 12, 16, 21–24, 26]. Pfeiffer and Foerg [18] studied the specific structure of one impact and investigated the functional dependencies with respect to the initial normal and tangential relative velocities and normal and tangential impulses before an impact. They developed the theory and gave examples. Detailed review on the rigid body collision can be found in [13, 20].

A second approach solves the problem by direct numerical integration of the equations of motion using different models for the contact force. For fully elastic impacts, one can use linear or nonlinear expressions for the contact force, as in the Hertzian theory [7]. Even at low-speed impacts, most of materials get to the plastic regime. For the elastic–plastic problems, finding an accurate contact model to calculate the impact force is essential. There are a variety of contact models that can be used, such as Johnson’s simple contact model [11] for elastic-perfectly plastic contacts, or more complicated elastic–plastic contact models such as Brake’s models [2, 3], the Jackson–Green model [9], Ghaednia et al. model [5], which uses the hardness from [10], and the Ye–Komvopoulos model [27]. In these models [2–4, 15], the impact is divided into two phases: loading and unloading. The loading phase starts when the objects touch and continues until the relative velocity of the contacting points is zero. Then, the unloading phase starts. For the unloading phase, because the deformations are not fully elastic, there will be a permanent deformation; therefore, the unloading phase ends when the relative displacement of the objects reaches the permanent deformation. A detailed comparison of these models can be found in the recent work of Ghaednia et al. [6].

In this research, we will analytically relate the normal permanent deformation to the sliding length and the impact duration. The presented formulation is based on the impact of a rounded-end rod and a flat without initial tangential and angular velocity; however, the formulation can be modified for different cases easily. An experimental setup has been built in order to measure the motion of the rod before and after the impact. The profiles of the deformed areas from the experiments have been scanned with an optical profilometer. The experimental results can be used with the presented analytical results to calculate the impact duration and the average contact force.

The impact has also been solved numerically using three different contact models: Brake [3], Ghaednia et al. [4] and Kogut–Komvopoulos [14]. The numerical solutions have been compared with the results from the experiments and the analytical approach.

The quasi-static contact models have been used with good results for the coefficient of restitution for most of the impacts. For the permanent deformations after the impact, impact duration and average force during the impact, the results given by quasi-static contact models are not in good agreement with the experimental results. A simple analytical approach has been developed so that the impact duration and contact force can be calculated more accurately using the permanent deformation profiles after the impact.

2 Mathematical approach

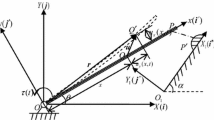
In this section, a formulation is developed to relate the impact duration to the normal permanent deformation and the sliding length. Figure 1 shows the schematic of the problem: a rigid rod with length L impacting a massive surface at an angle \(\theta \). The rod has semi-spherical ends with radius, R. The contact point between the rod and the surface is O, and the center of mass is noted by C. The origin of the system is at O, and the position of the center of mass, C, is

$$\begin{aligned} \mathbf {r}_C = \frac{L}{2}\, \cos (\theta )~{\hat{\imath }} + \left[ \frac{L}{2}\sin (\theta ) +R \right] ~{\hat{\jmath }}. \end{aligned}$$
(1)

The impact is initiated at \(t=0\). The initial impact angle is \(\theta (t=0) = \theta _i \); the initial angular velocity of the link is \(\mathbf {\mathrm {\omega }}(t=0) = \omega _i~{\hat{k}}=\mathbf{0}\); and the initial impact velocity is \(\mathbf {v}_O(t=0) = 0~{\hat{\imath }} + v_i~{\hat{\jmath }}\), where \(v_i\) is the initial vertical dropping velocity. During the impact, the velocity of the center of mass is

$$\begin{aligned} \mathbf {v}_C = \mathbf {v}_{iC} + \frac{1}{m}\int _{0}^{t}\mathbf {\mathrm {F}}\,\mathrm{d}t= \frac{1}{m}\int _{0}^{t} F_x \, \mathrm{d}t~{\hat{\imath }} + \left( v_i+ \frac{1}{m}\int _{0}^{t} F_y \, \mathrm{d}t\right) ~{\hat{\jmath }}. \end{aligned}$$
(2)

The angular velocity of the bar is calculated as

$$\begin{aligned} \mathbf {\mathrm {\omega }} = \frac{1}{I_C} \int _{0}^{t} \mathbf {\mathrm {M}}\, \mathrm{d}t = \frac{1}{I_C}\left( \frac{L}{2}\sin {\theta }+R\right) \int _{0}^{t} F_x \, \mathrm{d}t ~{\hat{\imath }} - \frac{L\cos {\theta }}{2\,I_C} \int _{0}^{t}F_y \,\mathrm{d}t~{\hat{\jmath }}, \end{aligned}$$
(3)

where \(I_C\) is the mass moment of inertia. It has been assumed that the impact angle is constant during the impact, \(\theta =\mathrm {const.}\) Using Eqs. (2) and (3), the velocity of the tip of the rod is

$$\begin{aligned} \mathbf {v}_{O} = v_{Ox}~{\hat{\imath }} + v_{Oy}~{\hat{\jmath }} =\mathbf {v}_{C} + \mathbf {\omega }\times \mathbf {\mathrm {r}}_{CO}, \end{aligned}$$
(4)

where

$$\begin{aligned} v_{Ox} = v_{x}= & {} \left[ \frac{1}{m} + \frac{1}{{I_C}}\left( \frac{L}{2}\sin {\theta }+R \right) ^2 \right] \int _{0}^{t} F_x \mathrm{d}t \nonumber \\&- \frac{L\cos {\theta } \displaystyle \left( \frac{L}{2}\sin {\theta }+R \right) }{{2\,I_C}} \int _{0}^{t} F_y \mathrm{d}t, \end{aligned}$$
(5)

and

$$\begin{aligned} v_{Oy} = v_{y} =v_{i} -\frac{L\cos {\theta } \displaystyle \left( \frac{L}{2}\sin {\theta }+R\right) }{2\,{I_C}} \int _{0}^{t} F_x \mathrm{d}t + \left( \frac{1}{m} + \frac{L\cos {\theta }}{4\, {I_C}} \right) \int _{0}^{t} F_y \mathrm{d}t. \end{aligned}$$
(6)

Assuming that

$$\begin{aligned} \int _{0}^{t} F_x \mathrm{d}t = \mu \int _{0}^{t}F_y \mathrm{d}t, \end{aligned}$$
(7)

where \(\mu \) is the coefficient of friction during impact, the previous relations yield to

$$\begin{aligned} v_{Ox} = \left[ \left( \frac{1}{m} + \frac{ (L\sin {\theta }+2\,R)^2}{4\,{I_C}} \right) \mu - \frac{L\cos {\theta } \displaystyle \left( \frac{L}{2}\sin {\theta }+R \right) }{2\,{I_C}} \right] \int _{0}^{t}F_y \mathrm{d}t, \end{aligned}$$
(8)

and

$$\begin{aligned} v_{Oy} = v_{i} + \left[ \frac{1}{m} + \frac{(L\cos {\theta })^2}{4\,{I_C}}- \frac{L\cos {\theta } \displaystyle \left( \frac{L}{2}\sin {\theta }+R \right) }{2\,{I_C}}\mu \right] \int _{0}^{t}F_y \mathrm{d}t. \end{aligned}$$
(9)

Using Eq. (9), the normal permanent deformation after the impact, \(\delta _p\), can be calculated as

$$\begin{aligned} \delta _p = \int _{0}^{T} v_{Ty} \mathrm{d}t = \int _{0}^{T} v_{i} \mathrm{d}t + \left[ \frac{1}{m} + \frac{(L\cos {\theta })^2}{4\,{I_C}} - \frac{ \displaystyle \frac{L}{2}\sin {\theta }+R }{2\,{I_C}}\mu \right] \int _{0}^{t_f}\int _{0}^{t} F_y \mathrm{d}t. \end{aligned}$$
(10)

Therefore,

$$\begin{aligned} \int _{0}^{T}\int _{0}^{t} F_y \mathrm{d}t = \frac{\delta _p-v_i T}{ \displaystyle \frac{1}{m} + \frac{(L\cos {\theta })^2}{4\,{I_C}} - \frac{\displaystyle \frac{L}{2}\sin {\theta }+R }{2\,{I_C}}\mu }, \end{aligned}$$
(11)

where T is the impact duration. Using Eqs. (8, 11), the sliding length, \(L_\mathrm{s}\), is

$$\begin{aligned} L_\mathrm{s} = \int _{0}^{t_f} v_{Tx} \mathrm{d}t = -\alpha (\delta _p - v_i T), \end{aligned}$$
(12)

where \(\alpha \) is

$$\begin{aligned} \alpha = \frac{ \displaystyle \left[ \frac{1}{m} + \frac{\displaystyle (L\sin {\theta }+R)^2}{4\,{I_C}}\right] \mu - \frac{L\cos {\theta }\left( \displaystyle \frac{L}{2}\sin {\theta }+R \right) }{2\,{I_C}}}{ \displaystyle \frac{1}{m} + \frac{(L\cos {\theta })^2}{4\,{I_C}} - \frac{ \displaystyle \frac{L}{2}\sin {\theta }+R }{2\,{I_C}}\mu }. \end{aligned}$$
(13)
Fig. 1
figure 1

Rod impacting a flat

Full size image

3 Numerical simulation

The equations of motion are solved numerically for three different contact forces during the impact. The Kogut–Komvopoulos [14], Brake [3] and Ghaednia et al. [4] models have been used for the numerical simulations. These models predict the quasi-static contact force for indentation contacts [11]. The contact force from these models has been used in the numerical integration of the equations of motion to calculate the motion of the rod during and after the impact. Equation (8) is valid for the numerical simulations because the average coefficients of friction measured from the experiments have been used for the numerical solutions.

In each of these models, the contact has been divided into different phases: elastic, elasto-plastic and restitution. For the elastic phase of the impact, all of these contact models use Hertzian theory [7]. For the elasto-plastic phase, Brake uses a transition function from the fully elastic to fully plastic phase and Kogut–Komvopoulos and Ghaednia et al. use empirical formulations created from finite element results. The numerical solutions have been compared with the experiments and with the analytical solution for permanent deformation, sliding length, impact duration, average force and coefficient of restitution. The following subsections provide formulations for each contact model.

3.1 Hertzian contact theory

Most of the models use the Hertzian theory [7] for the elastic phase and the restitution phase. The Hertzian theory uses the reduced modulus of elasticity and radius

$$\begin{aligned} E^{-1}&= \frac{1-\nu _1^2}{E_{\mathrm {r}}}+\frac{1-\nu _2^2}{E_{\mathrm {f}}}, \nonumber \\ \frac{1}{R}&=\frac{1}{R_{\mathrm {r}}}+\frac{1}{R_{\mathrm {f}}}, \end{aligned}$$

where \(\nu \) is the Poisson ratio, \(R_{\mathrm {r}},~E_{\mathrm {r}}\) and \(R_{\mathrm {f}},~E_{\mathrm {f}}\) are the radius and the modulus of elasticity of the rod and the flat, respectively. For our case, \(R=R_{\mathrm {r}}\) since \(R_{\mathrm {f}}=\infty \).

The elastic contact force, \(F_{\mathrm {e}}\), can be calculated as

$$\begin{aligned} {F}_{\mathrm {e}} = \frac{4}{3}\,E\,R^{0.5}\,\delta ^{1.5}, \end{aligned}$$
(14)

where \(\delta \) is the deformation of the flat at the contact point, as shown in Fig. 2.

Fig. 2
figure 2

Spherical contact with a flat

Full size image

3.2 Ghaednia et al. model

Our previous work modifies the Jackson–Green model [9] in order to satisfy the effects of deformation on both of the objects for specific material properties and provides a new empirical formula for the permanent deformation [4].

3.2.1 Elastic phase

The elastic phase has been considered to follow the Hertzian [7] theory. It has been considered that the effective elasto-plastic phase starts at \(\delta ^*\ge 1.9\) with

$$\begin{aligned} \delta ^*=\frac{\delta }{\delta _{\mathrm {y}}} ,~~ \delta _{\mathrm {y}} = \left( \frac{\pi \, C_{\mathrm {j}}\, S_{\mathrm {y}}}{2\,E}\right) ^2R, ~~C_{\mathrm {j}} = 1.295\,e^{0.736\nu }, \end{aligned}$$
(15)

where \(\delta _{\mathrm {y}}\) is the interference at which the yield starts and \(S_{\mathrm {y}}\) is the yield strength of the weaker material. The elasto-plastic phase starts effectively at \(\delta ^*=1.9\) according to [9]. For this phase, the contact force is given by Eq. (14).

3.2.2 Modified Jackson–Green elasto-plastic phase

For the elasto-plastic phase, the Jackson–Green (JG) expression of the contact force has been modified [4]. This expression satisfies the effects of deformation on both of the objects. The modified JG model expression for the contact force is given by

$$\begin{aligned} F_{\mathrm {ep}}=F_{\mathrm {c}}\left[ e^{\displaystyle -0.17\delta ^{*5/12}}\delta ^{*1.5} + \frac{4\,H_G}{C_{\mathrm {j}}\,S_{\mathrm {y}}}\left( 1-e^{\displaystyle -\frac{1}{78}(\delta ^*)^{5/9}}\right) \,\delta ^{*1.1}\right] , \end{aligned}$$
(16)

where

$$\begin{aligned} B&= 0.14\, e^{23\,S_{\mathrm {y}}/\,E} ,~~~ r = \sqrt{R\,\delta _{\mathrm {y}}\left( \frac{\delta }{1.9\,\delta _{\mathrm {c}}}\right) ^B}, \nonumber \\ \frac{H_G}{S_{\mathrm {y}}}&= 2.84-0.92\left[ 1-\cos \left( \pi \frac{r}{R}\right) \right] , \nonumber \\ F_{\mathrm {c}}&= \frac{4}{3}\left( \frac{R}{E}\right) ^2\left( \frac{\pi \,C_{\mathrm {j}}\, S_{\mathrm {y}}}{2}\right) ^3. \end{aligned}$$
(17)

The real radius of contact is r; the average normal pressure is \(H_G\); the critical force at the instant the yield occurs is \(F_{\mathrm {c}}\); and the contact force during the elasto-plastic phase is \(F_{\mathrm {ep}}\).

3.2.3 Restitution phase

The contact force for the restitution phase of this model has been considered to be elastic and follows the Hertzian theory. The radius of curvature \(R_{\mathrm {r}}\) is calculated as

$$\begin{aligned} R_{\mathrm {r}} = \frac{1}{(\delta _{\mathrm {m}}-\delta _{\mathrm {r}})^3}\left( \frac{3\,F_{\mathrm {m}}}{4\,E}\right) ^2. \end{aligned}$$
(18)

The permanent deformation, \(\delta _{\mathrm {r}}\), for this model is calculated from experimental results [4] using an empirical expression

$$\begin{aligned} \frac{\delta _{\mathrm {r}}}{\delta _{\mathrm {m}}}= 0.8\,\left[ 1-\left( \frac{\delta _{\mathrm {m}}/\delta _{\mathrm {y}}+5.5}{6.5}\right) ^{-2}\right] . \end{aligned}$$
(19)

3.3 Kogut–Komvopoulos indentation model

For the indentation models, \(\delta \) is defined as the deformation of the rigid sphere on the flat as shown in Fig. 2. The formulations developed by Kogut–Komvopoulos [14] are presented next.

3.3.1 Kogut–Komvopoulos elastic phase

The elastic phase starts at \(\delta =0\) and continues until

$$\begin{aligned} \frac{\delta }{r'}\le \frac{1.78\,S_{\mathrm {y}}}{E}, \end{aligned}$$

where \({r'}\) is the truncated contact radius, shown in Fig. 2; E is the reduced modulus of elasticity defined in the Hertzian theory; and \(S_{\mathrm {y}}\) is the yield strength of the flat. Using these criteria for the elastic phase, the contact force is

$$\begin{aligned}&\frac{F_{\mathrm {e}}}{a\,S_{\mathrm {y}}}=\frac{4\sqrt{2}}{3\pi }\left( \frac{E\,\delta }{S_{\mathrm {y}}\,r'}\right) , \end{aligned}$$
(20)

where \(a'\) is the truncated area of contact, \( a'=\pi \,r'^2\), and \(r'=\sqrt{R^2-(R-\delta )^2}\).

3.3.2 Kogut–Komvopoulos elasto-plastic phase

The elasto-plastic phase for this model starts when \(\delta \,/r' > 1.78\,S_{\mathrm {y}}/E\). The Kogut–Komvopoulos model suggests the following expression for the contact force

$$\begin{aligned} \frac{F_{\mathrm {ep}}}{a'\,S_{\mathrm {y}}} = \frac{0.839 + \ln \,\left[ (E\,/S_{\mathrm {y}})^{0.656}(\delta \,/r')^{0.651}\right] }{2.192 - \ln \,\left[ (E\,/S_{\mathrm {y}})^{0.394}(\delta \,/r')^{0.419}\right] }. \end{aligned}$$
(21)

3.3.3 Kogut–Komvopoulos restitution phase

The restitution phase has been considered to follow the Hertzian theory [7] with the following expression for the permanent deformation

$$\begin{aligned} \delta _{\mathrm {r}} = \delta _{\mathrm {m}}\,(1-E_{R\delta })~~~\mathrm{with}~~~~E_{R\delta }=0.591\left( \frac{E}{S_{\mathrm {y}}}\right) ^{-0.156}. \end{aligned}$$
(22)

3.4 Brake model

Brake’s model [3] divides the contact into two phases: elastic phase and elasto-plastic phase. The elastic phase follows the Hertzian theory, and for the fully plastic phase, Meyer’s hardness has been used. For the elasto-plastic phase, a transitional function that a matches the experimental results has been proposed.

3.4.1 Brake elastic phase

The elastic phase starts from \(\delta =0\) and continues until \(\delta \le \delta _y\) with

$$\begin{aligned}&\delta _y = \frac{r}{F(\nu )}\left( \frac{\pi \, S_y}{2\, E}\right) ^2, \end{aligned}$$
(23)

where

$$\begin{aligned} F(\nu ) = \mathrm{max}\left\{ -(1-\nu )\left[ 1-\frac{z}{r}\tan ^{-1} \left( \frac{r}{z} \right) \right] +\frac{3}{2}\frac{1}{1+\left( z/r \right) ^2}\right\} ^2 ~~\mathrm{for}~~ z\ge 0. \end{aligned}$$

Using these criteria for the elastic phase, the contact force is calculated from Eq. (14).

3.4.2 Brake elasto-plastic phase

The elasto-plastic phase starts when \(\delta > \delta _y\). Brake proposes the following equation for the contact force

$$\begin{aligned} F_\mathrm{ep}= & {} {\mathrm {sech}} \left[ (1+n_{\epsilon })\frac{\delta -\delta _y}{\delta _p-\delta _y}\right] \frac{4}{3} \,E\, \sqrt{r}\, \delta ^{1.5} \nonumber \\&+ \left\{ 1-\mathrm {sech}\left[ (1-n_{\epsilon })\frac{\delta -\delta _y}{\delta _p-\delta _y}\right] \right\} \,P_0\, \pi \, \frac{a^n}{a_p^{n-2}}, \end{aligned}$$
(24)

where

$$\begin{aligned} P_0 =10^6\, H\,g\,~~~\mathrm{and}~~~H = \left( \frac{2}{H_s}+\frac{2}{H_f}\right) ^{-1}. \end{aligned}$$
(25)

The Meyer’s strain hardening components are n, \(n_{\epsilon } = n -2\); H is Brinell’s hardness; and \(a_p\) can be calculated by solving the following nonlinear equation for the smallest positive root of \(\delta \)

$$\begin{aligned}&a_p = \sqrt{2 \delta R} = \left[ \frac{3P_0}{4E}2^{n/2}\pi r^{(n-1)/2} \delta ^{(n-3)/2} \right] ^{1/(n-2)}, \end{aligned}$$
(26)

with \(\delta _p = a_p^2/(2R)\).

3.4.3 Brake restitution phase

The restitution phase has been considered to follow the Hertzian theory with the following expression for the permanent deformation and radius of curvature for the unloading phase

$$\begin{aligned} \delta _r = \delta _m \, \left[ 1 - \frac{F_m}{(4\,E/3)(\delta _m-\delta )^{1.5}}\right] ~~~ \mathrm{and}~~~ R_r = \frac{F_m^2}{(4 \, E/3)^2(\delta _m-\delta )^3}. \end{aligned}$$
(27)

4 Experiments

The experimental setup is designed to perform consistent drops of a rounded-end stainless steel rod on a carbon iron flat (material properties and geometries of the rod and the flat are provided in Table 1). The setup provides the desired initial angle, zero initial tangential velocity and zero initial angular velocity. Figure 3 shows the schematic of the experimental setup from the right and front views, respectively. Two solenoids have been used to grab and release the rod with a manual trigger. The initial angle of the drop can be changed continuously from \(0^\circ \) to \(90^\circ \). The flat is clamped to a massive table.

Table 1 Material properties and geometries for the rod and the flat
Full size table
Fig. 3
figure 3

Experimental setup: a right view and b front view

Full size image

A high-speed 3D infrared camera is used to track the motion of three markers attached to the rod at 500 fps. The position of the markers is used to calculate the velocity of the center of the rod before and after the impact. Using the velocities from experiments and Eq. (7), the average coefficient of friction during the impact is measured using the equation

$$\begin{aligned} \mu = \frac{\displaystyle \int _0^T F_x \mathrm{d}t}{ \displaystyle \int _0^T F_n \mathrm{d}t}=\left| \frac{v_{Cx}(t=T)-v_{Cx}(t=0)}{v_{Cy}(t=T)-v_{Cy}(t=0} \right| . \end{aligned}$$
(28)

The deformed areas after the impact are marked, and the profiles of the deformed areas are scanned using an optical profilometer. The results from the profilometer have been used to measure the normal permanent deformation and the sliding length.

5 Results and discussion

The results are studied for three different impact angles, \(\theta = 20^\circ , 45^\circ , 70^\circ \). Using the scanned profiles, the normal permanent deformations and the sliding lengths are measured. The normal permanent deformation is defined as the maximum depth of the deformed area, and the sliding length is defined as the maximum length of the deformed area minus the width of the deformed area at the maximum deformation depth. The deformation patterns after the impact for the numerical simulations have been compared with the experiments. The positions of three markers on the rod are tracked and used to find the linear and the angular velocities of the rod before and after the impact.

5.1 Deformation patterns

In this section, the permanent deformation patterns for the numerical solutions, analytical approach and experimental results have been analyzed. For the analytical solution, the effect of \(\alpha \) on the deformation patterns will be analyzed. Three cases with initial impact angles of \(\theta _i=20^\circ , 45^\circ , 70^\circ \) have been chosen for comparison. The results are analyzed for the coefficient of restitution, e, normal permanent deformation, \(\delta _p\), and the sliding length, \(L_\mathrm{s}\). Numerical solutions have been performed to compare with the experiments and the analytical solutions.

5.1.1 Numerical solutions

The deformation patterns after the impact have been calculated by the numerical solutions. Figure 4 shows the deformation patterns for the case with an initial impact angle \(\theta =20^\circ \) and an initial velocity \(\mathbf {v}_i = -1.41{\hat{\jmath }}~\hbox {m/s}\). Using the Ghaednia et al. model, the deformation pattern is shown in Fig. 4. The numerical simulations predict a circular deformation. The predicted pattern stays the same for different impact angles and different contact models, so only one plot has been provided for the numerical solutions.

Fig. 4
figure 4

Deformation pattern for numerical simulation with an impact angle \(\theta =20^\circ \)

Full size image

5.1.2 Analytical solution

For the analytical solution, the term \(\alpha \), given by Eq. (13), is a function of the geometry and the friction coefficient and relates the sliding length to the normal permanent deformation. In Eq. (12), the following relations exist \(\delta _p \le 0\), \(v_i\le 0\) and \(T \ge 0\). For \(|v_y(t)|\le |v_i|\) then \(|\int _0^T v_n \mathrm{d}t|\le |v_iT|\); therefore, \(|\delta _p| = |\int _0^T v_n \mathrm{d}t|< |v_iT|\) and yields to \((\delta _p - v_i T) \ge 0\). This shows that the sign of \(\alpha \) determines the sliding direction. Figure 5 shows the change in \(\alpha \) with respect to the initial impact angle for different friction coefficients. For this figure, we have used data given in Table 1. From Fig. 5, the sign of \(\alpha \) changes for large impact angles, \(\theta \). The change in the sign here shows that the friction changes from sliding to sticking. This phenomenon occurs because at higher impact angles the friction force applies a larger moment than the normal force.

Fig. 5
figure 5

Variation of \(\alpha \) with respect to \(\theta \) for different coefficients of friction

Full size image

5.1.3 Experiments

Deformation patterns for the three different impact angles: \(\theta =20^\circ \), \( 45^\circ \), \(70^\circ \) have been scanned using an optical profilometer. For \(\theta =20^\circ \), the rod has an initial velocity \(\mathbf {v}_i = -1.41{\hat{\jmath }}~\hbox {m/s}\). The rebound normal velocity of the tip of the rod is, \(v_{Of}=0.71~\hbox {m/s}\). The coefficient of restitution is \(e=0.50\). The average friction coefficient is measured from the experiments using Eq. (28) and is \(\mu =0.20\).

The normal permanent deformation and the sliding length are measured using the scans of the deformed areas, as shown in Fig. 6. In Fig. 6, the sliding direction is from left to right. The profile is wider at the center and sharper at the end of the impact. The profile is approximately elliptical and symmetrical around the x-axis. From the profile of the pattern, it can be seen that the rod is continuously sliding throughout the impact. The normal permanent deformation and the sliding length are approximately \(\delta _p = 22~\upmu {\mathrm {m}}\) and \(L_\mathrm{s} = 1400~\upmu {\mathrm {m}}\), respectively.

Fig. 6
figure 6

Experimental deformation patterns for \(\theta =20^\circ \)

Full size image

For the initial impact angle \(\theta _i=45^\circ \), the initial velocity is \(\mathbf {v}_i = -2.18{\hat{\jmath }}~\hbox {m/s}\); the normal rebound velocity of the tip of the rod is \(v_{Of} =1.08~\hbox {m/s}\); and coefficient of restitution is \(e=0.49\). The average coefficient of friction measured from the experiments using Eq. (28) is \(\mu = 0.13\).

The deformation pattern for this case, shown in Fig. 7, shows a deeper deformation at the start of the impact and sharper pattern at the end compared to the previous case with \(\theta =20^\circ \). As in the previous case, based on the profile of deformed area, Fig. 7, the rod is sliding throughout the impact. The normal permanent deformation and the sliding length are measured as \(\delta _p = 26~\upmu {\mathrm {m}}\) and \(L_\mathrm{s} =1650\,\upmu \)m, respectively.

Fig. 7
figure 7

Experimental deformation patterns for \(\theta =45^\circ \)

Full size image

The same measurements have been taken for an impact with initial angle, \(\theta _i=70^\circ \), as shown in Fig. 8. The initial velocity is \(\mathbf {v}_i = -3.45~{\hat{\jmath }}~\hbox {m/s}\); the normal rebound velocity of the tip of the rod is \(v_{Of}=0.19~\hbox {m/s}\); and the coefficient of restitution is \(e=0.05\). The coefficient of friction measured from the experiment is \(\mu = 0.10\).

For this case, the scanned profile of the deformed area, Fig. 8, shows a different trend than the previous cases. In this case, the maximum normal permanent deformation is closer to the end of the impact. The profile shows sliding at the beginning of the impact and sticking or rolling at the end. A pileup is developed at the end of the deformation region. The normal permanent deformation and the sliding length are \(\delta _p = 105~\upmu \)m and \(L_\mathrm{s}=200~\upmu \)m, respectively, as shown in Fig. 8.

Fig. 8
figure 8

Experimental deformation patterns for \(\theta =70^\circ \)

Full size image

5.2 Average force and impact duration

The main outcome of the presented analytical solution is the calculation of the average force and the impact duration using the experimental measurements of the coefficient of restitution and the permanent deformations. Using the results from the experiments and Eq. (12), one can calculate the impact duration. Using the calculated impact duration from Eq. (12), the average contact force can be calculated as

$$\begin{aligned} \displaystyle \int _0^TF \mathrm{d}t = {\bar{F}}T = m\,(v_{Cf}-v_{Ci}).{\hat{\jmath }}. \end{aligned}$$
(29)

Tables 2, 3, 4 show the comparison between the numerical solutions, the experimental results and the analytical approach for the normal permanent deformation, the sliding length, the coefficient of restitution, the impact duration and the average force.

For a drop with an impact angle \(\theta =20^\circ \) and \(\mathbf {v}_i = -1.41{\hat{\jmath }}\) as shown in Fig. 6, using the measured coefficient of restitution, the permanent deformation and the sliding length along with Eqs. (12) and (29), the average contact force and the impact duration can be calculated. Table 2 shows the results for impact duration and average force from the experiments and the analytical solution. For this case, using the Ghaednia et al. model, the coefficient of restitution is \(e=0.42\); the normal permanent deformation is \(\delta _p=-67~\upmu {\mathrm {m}}\); the sliding length is \(L_\mathrm{s}=-74~\upmu {\mathrm {m}}\); the impact duration is \(T=0.256~\hbox {ms}\); and the average contact force is \({{\bar{F}}} = 2153~\hbox {N}\). Brake’s model shows \(e=0.46\), \(\delta _p=-77~\upmu {\mathrm {m}}\), \(L_\mathrm{s}=-74~\upmu {\mathrm {m}}\), \(T=0.256~\hbox {ms}\) and \({{\bar{F}}} = 2153~\hbox {N}\), and the Kogut–Komvopoulos model predicts \(e=0.43\), \(\delta _p=-64~\upmu {\mathrm {m}}\), \(L_\mathrm{s}=-64~\upmu {\mathrm {m}}\), \(T=0.25~\hbox {ms}\) and \({{\bar{F}}} = 2568~\hbox {N}\). The results predicted from all of the numerical solutions are in the same order of magnitude and are approximately the same. Compared to the experimental results, it can be seen that the predictions from the numerical solutions for the coefficient of restitution match; however, for both the impact duration and the average contact force, there is a great difference between the numerical solutions and the experiments.

Table 2 Comparison for \(\theta =20^\circ \) between experiments and Eqs. (12) and (29) and the numerical simulation results
Full size table
Table 3 Comparison for \(\theta =45^\circ \) between experiments and Eqs. (12) and (29) and the numerical simulation results
Full size table
Table 4 Comparison for \(\theta =70^\circ \) between experiments and Eqs. (12) and (29) and the numerical simulation results
Full size table

The same calculation and numerical solutions have been done for the impact angle \(\theta =45^\circ \). The results from the experiments, the analytical solutions and the numerical solutions are shown in Table 3. As in the previous case (with \(\theta =20\)), the results for the impact duration and the average force from the numerical solutions show a great difference compared to the experiments, even though for the coefficient of restitution the numerical results match the experiments.

For the impact angle \(\theta =70^\circ \), the coefficient of restitution and the impact duration are significantly smaller than the previous cases. Comparing the experiments with the numerical solutions, it can be seen that the normal permanent deformation and the sliding length are still different but closer than the previous cases. For the impact duration and the average force, the numerical solutions are closer to the experiments.

The numerical solutions that have been considered in this study have been validated for normal impacts [3, 4, 14]. Using these contact models for an oblique impact, we observe significant differences in terms of deformations, even though the coefficients of restitution are in good agreement. We have presented a solution which is a combination of experiments and analytical calculations for the average contact force and the impact duration.

5.3 Discussion

The sliding length, the impact duration and the average impact force are shown to be significantly different from the numerical predictions. One should consider that the same numerical simulations have been proven to match the experimental results for the coefficient of restitution and the permanent deformation for the normal impacts. For the impact angles, \(\theta _i = 20^\circ \) and \(\theta _i=45^\circ \), the numerical simulations and the experimental results match for the coefficient of restitution, but experiments have significantly larger values for the sliding length and the impact duration. Experiments also show smaller values for the average impact force than the numerical results. For a larger angle \(\theta _i=70^\circ \), the comparison is reversed. The deformation patterns predicted by the numerical simulations and measured by the experiments are closer. The coefficient of restitution is significantly larger for the simulations than for the experiments. It is interesting that in this case the average impact force is larger and the impact duration is smaller for the experiments, which is different from what was found for the previous impact angles. A possible reason for this phenomenon might be the existence of a relatively large pileup (see Fig. 8) at the tip of the rod. The pileup can significantly increase the tangential force and therefore can decrease the velocity of the tip of the rod.

In Eq. (12), \(\alpha \) is positive; \(\delta _p\) and \(v_i\) are negative; and T is positive. To obtain a larger sliding length in Eq. (12), the impact duration should increase. Using Eq. (29) if the impact duration increases, the average impact force should decrease. This shows that the initial condition of the collision, mainly the impact angle, significantly affects the contact force.

6 Conclusion

In this study, a new formulation for the oblique impact of a rod with a flat is presented. The formulation relates the deformation patterns after the impact to the velocity before the impact, the impact duration and the average contact force. The impact duration and the average impact force during the impact can be calculated by measuring the normal permanent deformation, sliding length, the coefficient of friction and the impact velocities. Experiments have been performed to measure the velocities before and after the impact and the permanent deformations after the impact.

The numerical simulations are in good agreement with the experiments for the normal impact, but for the oblique impact, the results are significantly different from the experimental measurements. The comparison between the analytical approach and the numerical simulations shows that for the impact angles, \(\theta _i=20^\circ , 45^\circ \), the coefficient of restitution matches and the deformation patterns are significantly different.

More analytical studies and experimental results are needed to accurately validate our results.