1 Introduction

The indentation of solids by a harder or effectively rigid object is of great importance to material property measurements via the surface. It is also an integral part of friction, wear, and contact resistance predictive models. In most cases, the load is large enough to cause significant plastic deformation and even cause the entire surface in contact to deform plastically. Indentation hardness tests are aimed at achieving this range of deformation.

In the elastic regime, and at relatively small displacements, the contact of an elastic–plastic sphere against a rigid flat (i.e., flattening) and the contact of a rigid sphere against an elastic–plastic surface (i.e., indentation) are practically equivalent. However, as the displacements increase, the two cases begin to diverge [1]. This work focuses on the case of indentation between a rigid sphere and a deformable surface.

Ishlinskii [2] performed a slip-line analysis of a spherical contact and found that the contact pressure for a perfectly plastic contact without hardening (i.e., Brinell hardness) was between 2.61 and 2.84 and did not vary significantly with the indentation depth. As will be shown later, this is in contradiction to the current work.

Hardness is the average pressure in a contact when the deformation is fully plastic. In this work, the average pressure, \(\bar{p},\) is defined by the contact force divided by the projected area of the contact in the direction of the indentation, not the total surface area. This is often defined as the Meyer’s hardness, and its equation form is: \(\bar{p} = \frac{F}{{\pi \cdot {\text{a}}^{ 2} }},\) where a is the contact radius and F is the contact force. Alternatively, Brinell suggested that the hardness be calculated by the dividing the force by the total surface area of the spherical cap in contact.

Jackson and Green [3] performed a finite element analysis of an elastic–plastic deformable sphere against a rigid flat surface (referred to as flattening). They found that as the deformation increased, the average pressure reduced from approximately 2.84 times the yield strength (i.e., the hardness found by Tabor [4] and Ishlinskii [2] for a spherical contact). This is due to the spherical geometry changing to that of a compressed cylinder (see Fig. 1). This was taken even farther by Wadwalkar et al. [5] who showed that under heavy deformation, the average pressure on a flattened sphere approaches the yield strength. Note that in these cases of severe deformation, the sphere actually begins to behave similar to a ‘barreling’ cylinder in compression. The deformation in these works is described by the ratio between the contact radius, a, and the radius of the sphere, R, as shown in Fig. 2. These previous works found an equation that captures the effect that large deformations of the sphere have on the average contact pressure, \(\bar{p},\) in relation to the yield strength, S y [6]:

$$\frac{{\bar{p}}}{{S_{y} }} = 2.84 - 0. 9 2\left( { 1 - { \cos }\left( {\pi \frac{a}{R}} \right)} \right)$$
(1)
Fig. 1
figure 1

Schematic showing how the pressure changes with the deformation of the sphere during fully plastic contact

Full size image
Fig. 2
figure 2

Schematic of the contact area between a sphere and a flat surface

Full size image

Again, note that Eq. (1) was based on the flattening case, where the flat surface is rigid and the sphere deforms. However, it could serve as a benchmark to the case of indentation.

Mesarovic and Fleck [7] studied the indentation of a rigid sphere into an elastic–plastic deformable surface both with and without hardening. They observed that at larger deformations, the average pressure-to-yield strength ratio appeared to decrease from Tabor’s value of 2.8, similar to the trend noted above. They also showed that hardening could nullify this effect in some cases. They were probably the first to observe this trend in indentation, but they did not provide an analytical description of the phenomenon.

Later, Kogut and Komvopoulos [8] investigated elastic–plastic indentation and found that the fully plastic pressure behaved similar to that of the flattening case investigated by Jackson and Green [3]. This case is important when using indentation tests for the measurement of material properties, especially the Brinell hardness test. Building from the work of Ye and Komvopoulos [9], Kogut and Komvopoulos [8] found that the pressure during elastic–plastic indentation reached a maximum value that is less than the popular value of 2.84 S y . They suggested that the pressure varied as a function of E ′/S y (the effective elastic modulus divided by the yield strength):

$$\frac{{\bar{p}}}{{S_{y} }} = 0. 2 0 1 {\text{ln}}\left( {\frac{{E^{{\prime }} }}{{S_{y} }}} \right) + 1.685$$
(2)

which is analogous to Eq. (1) for spherical indentation, rather than flattening, although in terms of the material properties rather than the deformed geometry. However, the current authors believe that the ratio is directly dependent on the geometry rather than the material properties, as will be shown for indentation in the current work. Also, the results of the current work cannot be compared to Eq. 2 because the current work assumes a perfectly plastic material that does not have a finite elastic modulus. Additional equations are provided in [8] relating contact area and pressure to the penetration depth, and the reader is advised to obtain the paper for additional information.

Later, Alcalá and Esqué-de los Ojos [10] also thoroughly analyzed the spherical indentation of strain-hardening metallic surfaces. Nonetheless, they found a similar empirical relation for the case of indentation without hardening or pileup or sink-in:

$$\frac{{\bar{p}}}{{S_{y} }} = 3. 0 4 4 - 1. 8 8 5\frac{a}{R}$$
(3)

Yu and Blanchard [11] also presented a thorough analysis and summary of many various cases of indentation, including wedge, conical, spherical and flat-ended indenters against elastic, perfectly plastic, and elastic–plastic materials. However, their perfectly plastic analysis was a curve fit to previous tabulated results in the literature. They then provided the following fit equation:

$$\frac{{\bar{p}}}{{S_{y} }} = \frac{2}{\sqrt 3 }\left( { 2. 8 4 5 - 0. 4 9 2 1\frac{a}{R}} \right)$$
(4)

The contact radius, a, could be difficult to determine. There are several models that may be employed to make an approximate prediction, or it could simply be measured.

There are many models that have been devised to account for the plastic deformation in the sphere (i.e., flattening). Most models also assume that the deformation is elastic–perfectly plastic, meaning there is no hardening in the material. However, there is no known analytical solution to this problem; therefore, many previous models did not give the correct quantitative predictions, such as the groundbreaking model by Chang, Etsion, and Bogy (CEB) [12] and the work by Zhao et al. [13], which attempted to improve on the CEB model by using a continuous template to connect the elastic and plastic regimes of deformation. Later, for the flattening case, Kogut and Etsion [14] and Jackson and Green [3] improved upon these models by using the finite element method. Jackson and Green [3] found the following equations for the prediction of initial yielding in the sphere according to the von Mises yield criterion, which in theory could also be used for indentation:

$$\omega_{c} = \left( {\frac{{\pi \cdot C \cdot S_{y} }}{{2E^{{\prime }} }}} \right)^{2} R$$
(5a)
$$C = 1.295\exp (0.736v)$$
(5b)
$$A_{c} = \pi^{3} \left( {\frac{{CS_{y} R}}{{2E^{{\prime }} }}} \right)^{2}$$
(6)
$$F_{c} = \frac{4}{3}\left( {\frac{R}{{E^{\prime}}}} \right)^{2} \left( {\frac{C}{2}\pi \cdot S_{y} } \right)^{3}$$
(7)

In Eqs. (5a–7), ω c is the indentation depth, A c is the critical contact area, and F c is the critical contact force, all at the initiation of plastic deformation. For flattening, Kogut and Etsion [14] and Jackson and Green [3] also found that fully plastic deformation begins at approximately 68–110 times the critical interference given by Eq. (5). It is plausible that this is also approximately true for indentation. There are also many other models and studies of spherical elastic–plastic indentation, in addition to those described above [15–19]. However, none of these appear to capture the decreasing average pressure-to-yield strength ratio trend.

Although much information exists in the literature for indentation and hardness tests, little information exists on how the average pressure during fully plastic contact may change during indentation due to the change in the geometry of the interface, as it does for the flattening case. The current work derives a simple equation to account for this effect based on slip-line theory. However, the current theoretical slip-line work does not include the effects of pileup or sink-in directly. A finite element model is also constructed that does include these effects and is compared to the slip-line result.

2 Methodology

The current work uses the concept of slip lines to find the relationship between the average pressure and the yield strength as a function of the magnitude of the deformation. The slip-line theory and derivation are not thoroughly described here, but additional details can be found in the book by Tabor [4]. For the theory to be applicable, the following assumptions are made: The loading is quasi-static; there are no body forces; and the material yields according to the von Mises criterion as a rigid–perfectly plastic material. No elasticity is considered. Here, the contact will be considered to be well lubricated, so no friction is considered, although this effect is often important. The effects of pileup and sink-in due to elasticity and volume conservation are also neglected.

Slip lines are defined as curved lines which are tangential along their length to directions of maximum shear stress. Slip lines in a material are made up of two curvilinear and orthogonal lines (α and β) described by the following equations:

$$h + 2k\varDelta \varphi = C_{1} {\text{along the }}\alpha \,{\text{line}}$$
(8)
$$h - 2k\varDelta \varphi = C_{2} {\text{ along the }}\beta {\text{ line}}$$
(9)

where h is the hydrostatic stress and k is the shear yield strength of the material. According to the von Mises yield criterion, h does not cause yielding or plastic deformation of the material. Note that only the α line needs to be considered. k is also related to the yield strength, S y , by

$$k = \frac{{S_{Y} }}{\sqrt 3 }$$
(10)

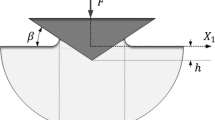
The case considered in the current work is schematically depicted in Fig. 3. On the labeled free surface, there is no normal or shear traction. Therefore, the shear stress tangential to the surface is zero there. On the indenter surface, there is an applied pressure, p, but no shear stress tangential to the surface, since the surface is frictionless. By considering these surface boundary conditions, the following equation is obtained (although some details are omitted here, this equation is identical to that found in Tabor [4]):

$$p = 2k + 2k\varDelta \varphi$$
(11)

where Δφ is the change in the angle of the slip line from the free surface to the pressurized indenter surface. Δφ is equal to the θ shown in the schematic in Fig. 3 and decreases from π/2 rad at the point of maximum indentation depth at the tip of the sphere to zero rad if the hemisphere is pressed into the half-space so that half of it is indented into the surface and the free half-space surface is perpendicular to the sphere.

Fig. 3
figure 3

Schematic of a spherical rigid indenter penetrating a rigid–perfectly plastic half-space

Full size image

Equation (11) can then be integrated over the contacting surface of the indenter to find the required normal force, F. Since the contact pressure on the indenter is always normal to it, we must consider that only the vertical portion contributes to F:

$$p_{v} = p\sin \theta$$
(12)

The resulting integration to calculate the force is then:

$$F = 2\pi \int_{0}^{a} {x \cdot p} \cdot \sin \theta {\text{d}}x$$
(13)

Noting that:

$$x = R\cos \theta ,$$
(14)

the integral can be rearranged as:

$$F = 2\pi R^{2} \int_{\pi /2}^{{\theta_{1} }} p \cdot \sin^{2} \theta \cos \theta \cdot {\text{d}}\theta$$
(15)

where θ 1 is the angle, θ, at x = a. Next Eq. 11 is substituted in for p:

$$F = 2\pi R^{2} \int_{\pi /2}^{{\theta_{1} }} {\left( {2k + 2k\theta } \right)} \cdot \sin^{2} \theta \cos \theta \cdot {\text{d}}\theta$$
(16)

This integration solves analytically to be:

$$F = 4k\pi R^{2} \left[ {\frac{{\sin^{3} \theta }}{3} + \frac{1}{36}\left( {12\theta \sin^{3} \theta + 9\cos \theta - \cos 3\theta } \right)} \right]_{\pi /2}^{{\theta_{1} }}$$
(17)

Then, normalizing the force by the contact area, substituting in Eq. 10, and simplifying further results in:

$$\frac{{\bar{p}}}{{S_{y} }} = \frac{F}{{\pi a^{2} S_{y} }} = \frac{4}{\sqrt 3 }\left( {\cos \theta_{1} } \right)^{ - 2} \left[ {\left( {\frac{1}{3} + \frac{\pi }{6}} \right) - \left( {1 + \theta_{1} } \right)\frac{{\sin^{3} \theta_{1} }}{3} - \frac{{\cos \theta_{1} }}{4} + \frac{{\cos 3\theta_{1} }}{36}} \right]$$
(18)

In addition, noting that \(\frac{a}{R} = \cos \theta\), Eq. 18 can be written as a function of a/R as:

$$\frac{{\bar{p}}}{{S_{y} }} = \frac{4}{\sqrt 3 }\left( \frac{a}{R} \right)^{ - 2} \left[ {\left( {\frac{1}{3} + \frac{\pi }{6}} \right) - \frac{1}{3}\left( {1 + \cos^{ - 1} \left( \frac{a}{R} \right)} \right)\left( {1 - \left( \frac{a}{R} \right)^{2} } \right)^{3/2} - \frac{a}{4R} + \frac{1}{36}\left( {4\left( \frac{a}{R} \right)^{3} - 3\left( \frac{a}{R} \right)} \right)} \right]$$
(19)

which can be moderately simplified to:

$$\frac{{\bar{p}}}{{S_{y} }} = \frac{4}{3\sqrt 3 }\left( \frac{a}{R} \right)^{ - 2} \left[ {\frac{1}{3}\left( \frac{a}{R} \right)^{3} - \left( {1 + \cos^{ - 1} \left( \frac{a}{R} \right)} \right)\left( {1 - \left( \frac{a}{R} \right)^{2} } \right)^{3/2} - \frac{a}{R} + \frac{\pi }{2} + 1} \right]$$
(20)

3 Finite Element Analysis

In order to verify the analytical results, an axisymmetric finite element model has been developed. The model simulates the indentation of a half-space with a sphere. Modeling the perfectly plastic behavior of the materials using the finite element method is difficult. Therefore, elastic–plastic material properties close to the perfectly plastic case have been used (i.e., a low yield strength and high elastic modulus). According to Tabor’s experiments [4], if the yield strength of the indenting sphere is 2.5 times larger than the flat, the deformation of the sphere can be neglected. Therefore, for the sphere, a yield strength of 1000 MPa is used, and for the flat, a yield strength of 100 MPa has been chosen. The modulus of elasticity and the Poisson’s ratio for both the flat and the sphere are considered to be 300 GPa and 0.3, respectively. Yield strength values smaller than this and elastic moduli larger than this tend to cause convergence problems in the finite element algorithm.

A fine mesh around the contact point has been applied on both the flat surface and the sphere. Mesh convergence for both the small and the large deformations has been verified, and a mesh with a total of 9784 elements has been chosen (see Fig. 4). To apply the boundary conditions, the following constraints have been applied: The bottom edge of the flat has been fixed for displacements in both directions, and the left edges of the sphere and the flat have been fixed for displacements in the horizontal direction. A uniform displacement downward on the top edge of the sphere has been applied to load the sphere against the flat surface.

Fig. 4
figure 4

Finite element model. A finer mesh around the contact point both on the flat and the sphere is applied

Full size image

Different displacements have been applied on the sphere, and the radius of contact and the reaction forces have been analyzed. Because of the complexity of the problem, the finite element analysis could not converge to a reliable result for larger deformations (a/R > 0.5).

4 Results

Now the predictions of Eq. 20 are shown in Fig. 5, alongside the finite element model predictions and those of Eq. (3) [10] and Eq. (4) [11]. Again, note that Eq. (2) from [8] is not compared to the other results in this work because it is dependent on the ratio of the elastic modulus to the yield strength. Since there is no elastic modulus present in Eq. 20, but the same decrease in average contact pressure is present, it suggests that Eq. 2 captured a secondary correlation that is actually sourced from the change in geometry. The current formulation appears to agree fairly well with the finite element results, even though the slip-line theory does not include sink-in or pileup and is for a perfectly plastic material, while the finite element model is for an elastic–plastic material with a relatively low yield strength to ensure that plastic deformation dominates. Note that the predictions of Eq. 4 [11] seem to over-predict the pressure, perhaps due to a factor in their paper meant to account for von Mises plasticity. The predictions of Eq. 20 appear to be very reasonable and show how the ratio of the average pressure to the yield strength can change dramatically as the geometry of the contact changes. By solving the above equation for θ 1 = π/2 (i.e., a/R = 1), a lower limit of the pressure-to-yield strength ratio is also found to be 1.465, which differs from the limit of unity for the flattening case. The upper limit is also different between the flattening and indentation cases. From Eq. 20, the maximum average pressure-to-yield strength ratio \(\left( {\frac{{\bar{p}}}{{S_{y} }}} \right)\) at a/R approaching zero is approximately 2.97, but there is a singularity at a/R = 0. This differs from the flattening value of 2.84, but is similar to the value of 2.96 provided by Ishlinskii [2], although, as Johnson [20] stated, in Ishlinskii’s work, this was for a/R = 0.376. In contrast, at a/R = 0.376, Eq. 20 predicts that \(\frac{{\bar{p}}}{{S_{y} }} = 2.589.\) Equation 20 might also be adapted to pileup [19] and sink-in, by adapting a/R and the slope at the edge of contact in the derivation.

Fig. 5
figure 5

A comparison of the current fully plastic analytical model and previous equations

Full size image

The solution given by Eq. 20 is for the indentation of a perfectly plastic surface by a rigid sphere, but it is useful for considering single asperity contact between rough surfaces within the framework of a statistical [21–28] or multiscale model [29–31]. For this equation to be applicable to any case, the case should first be in the fully plastic regime. In the fully plastic regime, the entire surface in contact, or the material supporting it, has been yielded. Although the initiation of this regime varies with the geometry and material properties, several researchers found that it initiates approximately between ω/ω c  = 68 and 80 [3, 14], although there may still be a significant influence of the elastic deformation until ω/ω c reaches approximately 110.

In addition, for Eq. 20 to be applicable, the contact should be categorized by indentation rather than flattening (i.e., the plastic deformation should mostly occur in the flat surface [1]). From a finite element analysis of elastic plastic contact, the authors believe that this transition is dictated mostly by the ratio between the yield strengths of the two contacting materials. When the yield strength of the sphere is lower, most of the plastic deformation will take place in the sphere. Equation 20 is probably not very applicable for this case (defined as flattening), and Eq. 1 is more applicable. When the yield strength of the flat surface is lower, most of the plastic deformation will occur in the flat surface, and Eq. 20 is most applicable (this case is indentation). To include both elastic and plastic deformations in such a contact, one might also replace Eq. 1 in the model by Jackson and Green [3] with Eq. 20. However, this is a crude approximation, and additional work is required to completely characterize elastic–plastic contact across the flattening and indentation regimes.

In addition and as mentioned previously, Eq. 20 could be used to approximate the yield strength from the average pressure (i.e., hardness) in spherical indentation measurements, such as in Brinell Hardness measurements. This model would probably need to be integrated with other models that account for phenomena such as hardening, pileup, and sink-in. Even then, this should be done carefully.

5 Conclusion

This work presents a new closed-form equation for the relation between the average contact pressure and yield strength as a function of a geometrical parameter for a rigid sphere indenting a fully plastic surface. This formulation is derived by using slip-line theory. The ratio of the average contact pressure-to-yield strength ratio has been shown to decrease with increasing deformation before, but no analytically derived relationship had been provided. As the deformation increases, the ratio decreases from 2.97 to 1.465, when the contact radius equals the radius of the sphere. The predictions have also been shown to compare well with finite element results, although the FEM results included some elastic deformation. This equation will be very useful in augmenting existing methodologies in rough surface contact modeling and indentation testing to account for this effect.