Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Impact is an important phenomena which plays an important role in many sports such as baseball, golf, tennis, and soccer since it affects rebound parameters of a ball; speed, angle, and spin etc. A normal and oblique impact of a ball with a flexible or rigid surface have been studied by many researches for decades. Authors mainly focus on dynamic properties of a ball and measure parameters before and after an impact. On the other hand, the behavior of a ball during the impact still attracts researchers. Measuring the motion of the ball during the impact is hard experimentally, since the impact duration is short. The friction force between a ball and a surface is also another challenge because it is difficult to measure.

A spring-damper system has been used by several authors in order to model the impact between a ball and a surface. Dignall and Haake [1] developed an analytical model of the normal impact of a tennis ball on a tennis court using a spring-damper system. The stiffness and damping coefficients were calculated analytically using the coefficient of restitution and the contact time from the experiments. Haake et al. [2] studied the impact of tennis ball with racket using the model from [1]. It was shown that the stiffness and damping coefficients of the tennis ball increase with higher initial velocity of the ball, [1, 2]. Goodwill and Haake [3] developed a new spring-damper model for the impact between a tennis ball and a head-clamped racket by adding a new linear spring in series. This extra spring is used to simulate the influence of the string-bed. Goodwill and Haake [4] developed a viscoelastic model of normal impact of a tennis ball on a rigid surface. A new damper representing the large deformation on the ball was added in parallel with the classical spring-damper model. Carre et al. [5] studied the impact of a cricket ball on a rigid surface. The spring-damper model was used to predict the force-deflection behavior. Yang et al. [6] developed a nonlinear impact model for a tennis ball and a racket. A nonlinear spring for the string-bed was connected in series with the spring-damper model. Ghaednia et al. [7] studied the oblique impact of a tennis ball with a racket. The impact is presented with a spring damper model. The stiffness and damping coefficients were found experimentally for the normal impact case, and the theory was verified with experiments for the oblique impact.

In this work, the normal and oblique impact of an elastic ball with a rigid flat has been studied theoretically. We have used a spring damper model in order to present the impact. A new expression for the damping term has been proposed in order to overcome the weakness of using a spring damper system for an impact problem.

2 Dynamics of the Ball

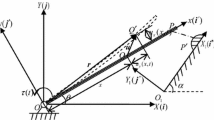
The elastic ball impacting the rigid surface is shown in Fig. 4.1. The impact angle of the rigid flat with the x0 horizontal axis is \(\upbeta\). R is the radius, and m is the mass of the ball. C is the center of the mass, and E is the contact point between the ball and the rigid flat. A global reference frame of unit vectors [I 0, J 0, k 0] and a local reference frame, with the origin at E, of unit vectors [I, J, k] are considered as shown in Fig. 4.1. The x-axis is tangential, and the y-axis is perpendicular to the rigid flat.

Fig. 4.1
figure 1

The ball in contact with a rigid surface

Full size image

The impact is divided into two phases; compression and restitution. Restitution phase is considered to be fully elastic. Compression phase starts when the ball contacts the surface and at this moment the normal contact force, P, and the indentation, \(\delta\), are zero. This phase ends at maximum compression, \({\updelta}_{\text{m}}\), and maximum normal force, P m , when the normal component of the velocity of the contact point of the ball is zero. Restitution phase starts at the moment of maximum compression, and the normal contact force decreases from maximum value to zero.

The elasto-plastic normal contact force, P, acts upward alongside the y-axis.

Contact force is defined as:

$$P = P_{static} + P_{dynamic} \quad P = k\delta - b\dot{\delta }$$
(4.1)

where \({\updelta} = q_{2} \left( t \right)\) is the normal elastic displacement during the impact, \(\dot{\updelta }\) is its rate and k, b are stiffness and damper coefficients, respectively.

The model above is modified with a new expression to overcome discontinuous problem because of the damping term. In reality, both elastic and damping forces should be initially at zero at the beginning of the impact. Equation 4.1 is modified with a new expression for the dynamic part of the contact force and it can be seen below:

$$P = k{\updelta} - b\dot{ {\updelta} }(1 - e^{{100 {\updelta} /R}} )$$
(4.2)

The total force at the point E is

$$\bf T = {\it {F}_f {\bf I} + P}{J}$$
(4.3)

where F f represents the friction force that is opposite to the tangential component of the velocity of the contact point of the ball. The friction force is given by

$${\bf F}_{f} = \mu P{\bf I}$$
(4.4)

where μ is the kinetic coefficient of friction. For the case of a rigid ball the equations of motion are

$$m{\bf{a}}_{C} = {\bf{G}} + {\bf{T}},\quad {\text{I}}_{C}{\bf \upalpha} = {\bf {r}}_{CE} \times {\bf {T}},$$
(4.5)

where G is the weight of the ball, IC is the mass moment of inertia about C. Diameter, D = 63 mm and a mass, m = 145 g, kinetic coefficient of friction, μ = 0.2, stiffness coefficient, k = 60,000 N/m, and damping coefficient, b = 10.5 Ns/m have been used for the simulation.

3 Results

The impact angle of 0° (normal impact) and 60° are used for the simulations. Initial impact velocity of the center of the ball, v C = −3J 0 m/s in the global coordinates is used for both the normal and oblique impacts. Figures 4.2 and 4.3 present the normal and tangential displacement of the center of the ball during the normal and oblique impact, respectively. For the normal impact, the maximum displacement is \({\updelta}_{\text{m}} = - 4.31 \times 10^{ - 3} \;{\text{m}}\), and compression phase ends when tm = 2.4×10−3 s. At this moment, the contact force reaches its highest point, and the restitution phase starts. Tangential displacement stays at zero since there is no force in the tangential direction. For the oblique impact, the maximum normal displacement of the center of the ball is \({\updelta}_{\text{m}} = - 2.17 \times 10^{ - 3} \;{\text{m}}\), and compression phase ends when tm = 2.44×10−3 s. The displacement in the tangential direction increases throughout the impact as seen in Fig. 4.3.

Fig. 4.2
figure 2

Normal and tangential displacement during the normal impact

Full size image
Fig. 4.3
figure 3

Normal and tangential displacement during the oblique impact at β = 60°

Full size image

Figure 4.4 shows the normal and tangential velocities of the center of the ball during the normal impact. For the normal impact, initial impact velocity is v E(t0) = −3J m/s, and the impact ends at t f  = 4.8 × 10−3 s. The final velocity at the end of the impact is v E(t f ) = 2.55J m/s. The tangential velocity is zero throughout the impact since no friction affects the ball. Figure 4.5 depicts the normal and tangential velocities of the center of the ball during the oblique impact for 60°. The initial impact velocity for the oblique is v E(t0) = 2.6I − 1.5J m/s in local coordinates. The normal component of the velocity becomes zero at tm = 2.44 × 10−3 s. At this point, maximum displacement and maximum normal contact force occur, compression phase ends, and restitution phase starts. Impact ends at tf = 4.9 × 10−3 s.

Fig. 4.4
figure 4

Normal and tangential velocity of the center of the ball during the normal impact

Full size image
Fig. 4.5
figure 5

Normal and tangential velocity of the center of the ball during the impact at β = 60o

Full size image

The final velocity at the end of the impact is v E(tf) = 0.64I + 1.3J m/s. Newtonian, coefficient of restitution is calculated as

$$e = \left| {{\bf v}_{E} \left( {t_{f} } \right) \cdot {\bf {J}}/{\bf {v}}_{E} \left( {t_{0} } \right) \cdot {\bf{J}}} \right|$$

For 60° and 0° impact angles, COR, e, is found 0.86 and 0.85, respectively. Figure 4.6 presents the angular velocity of the ball during the oblique impact for 60°. Angular velocity increases throughout the impact. Rebound angular velocity after the impacts predicted as ωf = 44 rad/s.

Fig. 4.6
figure 6

Angular velocity of the ball during the oblique impact at β = 60°

Full size image

For the normal contact force, P, as a function of displacement, the Eqs. 4.1 and 4.2 have been plotted for both the oblique and normal impact cases. The dashed and solid lines in Figs. 4.7 and 4.8 show the previous model and modified model, respectively. Figures 4.7 and 4.8 depict the normal contact force during the normal and oblique impact cases, respectively. Contact force reaches its highest point at the end of compression phase, and at this point, maximum displacement occurs. Restitution phase starts, and contact force starts to decrease from this moment. For the previous model, the contact force is not zero at the beginning of the impact as seen in both Figs. 4.7 and 4.8. This discontinuous comes from the damping term. In reality both elastic and damping forces should be zero at the beginning of the impact. On the other hand, a negative force is present at the end of the impact for the previous model as well. For the modified model with the new expression, the normal contact force starts at zero and decreases back to zero at the end of the impact as seen in both Figs. 4.7 and 4.8.

Fig. 4.7
figure 7

The normal contact force during the normal impact

Full size image
Fig. 4.8
figure 8

The normal contact force during the oblique impact at β = 60°

Full size image

4 Conclusions

The normal and oblique impact of an elastic ball with a rigid surface has been studied theoretically. The linear and angular motion of the ball during the impact have been simulated. Previous model consisting linear spring and damper is modified with a new expression for the damping term. With modified model, the normal contact force discontinuity problem is fixed and it starts at zero at the beginning of the impact. A negative contact force at the end of the impact which is seen in the previous model is not present for the modified model.