Abstract
The rheological characterization of a human blood, through modeling and analysis of transient flows and large-amplitude oscillatory shear (LAOS) flow, has made tremendous progress recently. We show how various components, and modifications of two recent scalar, structural kinetic, thixotropic models, can offer several modeling and prediction improvements, and compare our results to the Maxwell-like Bautista-Manero-Puig (BMP) model, and a recent transient model based on the Herschel-Bulkley. We explore the weakness of the legacy blood models, and then, we apply this newly improved model to recently published data from the literature in order to demonstrate its efficacy in modeling steady state, transient, and oscillatory shear flow. Following this effort, we demonstrate a novel approach using the sequence of physical phenomena (SPP) to facilitate interpretation, characterization, mapping, and “fingerprinting” of transient blood data from the literature. We compare the SPP approach to other LAOS analysis techniques in the literature and show how our approach can function as a mechanical-property diagnostic blood analysis tool. The goal of this work is a deeper understanding of the microstructural basis and validity of structural thixotropic blood models, and transient flow analysis techniques and procedures.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
Introduction
Human blood is a known shear-thinning, viscoelastic, and thixotropic complex material with a yield stress, viscosity, and structure that will undergo aging when outside of the human body (Baskurt et al. 2009; Apostolidis et al. 2015; Apostolidis and Beris 2015; Coussot 2017; Malkin et al. 2017; Bessonov et al. 2016; Flormann et al. 2016; Sousa et al. 2016; Valant et al. 2016; Ewoldt and McKinley 2017; Herrera-Valencia et al. 2017). Therefore, to mitigate aging to a limited extent, an anticoagulant protocol must be followed to get any rheological measurements (Merill 1969; Apostolidis and Beris 2015; Apostolidis et al. 2016; Baskurt et al. 2009; Bessonov et al. 2016). Working with human blood and performing rheological experiments is not trivial. For this work, we are using previously published steady state results from Sousa et al. (2013), Tomaiuolo et al. (2016), and Moreno et al. (2015), as well as transient data from Bureau et al. (1979, 1980) and large-amplitude oscillatory shear (LAOS) data from Sousa et al. (2013). This effort does not espouse a new experimental technique, or take issue with the current best practices in blood rheology, but only to shed light on a new proposed modification of an existing thixotropic model, which is a combination of best features of already proven blood and structural kinetic models (Mewis 1979; Apostolidis et al. 2015; Armstrong et al. 2016a). Our proposed modified model has a more robust predictive capability by fully taking into account the viscous nature of the blood medium, and viscous contribution from the “microstructure” of the blood, as it aggregates and breaks down during shear flow, as well as the elastic contribution to the total stress from the stretching, breaking, and reforming of the microstructure (Apostolidis et al. 2015; Moreno et al. 2015; Armstrong et al. 2016a; Larson 2015; Wei et al. 2016).
The nonthixotropic steady state modeling approaches shown here will focus on the Herschel-Bulkley model and the Casson model (Mewis and Wagner 2012; Apostolidis and Beris 2015; Apostolidis et al. 2015; Bessonov 2016). In addition, we will compare steady state modeling approaches using the Carreau and Cross models (Mewis and Wagner 2012; Bessonov et al. 2016).
With respect to the thixotropic modeling techniques showcased here, there are two generic approaches as follows:
where the total stress is the summation of an elastic contribution and a viscous contribution both functions of the current value of structure ξ and the shear rate \( \dot{\gamma} \). The nondimensional structure parameter ξ takes on values between [0 1], whereby these values represent a completely structured and unstructured material, respectively (Mujumdar et al. 2002; Dullaert and Mewis 2006; Blackwell and Ewoldt 2014; de Souza Mendes and Thompson 2013; Apostolidis et al. 2015; Armstrong et al. 2016a). The other modeling approaches highlighted in this manuscript incorporate the Maxwell paradigm. The Maxwell structure is used in the Bautista-Manero-Puig (BMP) model, albeit with a fluidity parameter φ which is the inverse of viscosity, and White-Metzner with an evolving viscosity, which is generically represented by
where σ is the deviatoric stress, η is the viscosity, and G is the elastic modulus. The BMP model uses φ a structural parameter with inverse viscosity units which becomes the fluidity only at steady state conditions, while the Stickel et al. (2013) EVP-like model uses a Herschel-Bulkley equivalent expression to represent viscosity as a function of the yield stress, power law parameter, and consistency parameter (Bautista et al. 1999; Stickel et al. 2013). We will use the shear stress component of the deviatoric stress only here.
With respect to the history of the structural kinetic models, in 1939, Goodeve first used a scalar, structural, kinetic expression for the structure parameter, denoted as ξ, which he then correlated to number of possible bonds formed with nearest neighbor aggregates or particles. The parameter ξ takes on values ranging between zero and one [0 1], where a value of 1 corresponds to a fully structured material, and a value of 0 to a fully broken down structure due to deformation (Armstrong et al. 2016a, b; Mewis and Wagner 2012). Over the years, there have been many contributions to the scalar, structure parameter models including work from Mujumdar et al. (2002), Dullaert and Mewis (2006), Saramito (2009), Mewis and Wagner (2012), Dimitriou et al. (2012), de Souza Mendes and Thompson (2013), Blackwell and Ewoldt (2014), and Armstrong et al. (2016a). Mujumdar et al. (2002) were the first to separate the elastic and viscous contributions to the evolving stress, and Dullaert and Mewis (2006) added to this with a structural viscous term. Importantly, Dimitriou et al. (2012) were able to separate the elastic and viscous components of the strain and shear rate. Most recently, there have been contributions from Larson (2015) and Wei et al. (2016) with an approach that brings in numerous thixotropic “harmonics.” With respect to human blood scalar, thixotropic, structure parameter models, Apostolidis et al. (2015) made significant contributions by allowing the elastic stress component to evolve in time by separating the elastic and viscous strain and shear rate, respectively (Apostolidis et al. 2015). All of these contributions were combined in recent work by Armstrong et al. (2016a). We are now proposing to add these recent contributions to blood modeling by way of a superposition of a structural viscosity term added to the overall stress equation from the Apostolidis et al. (2015) work, as shown in the modified Delaware thixotropic model by Armstrong et al. (2016a).
The present work focuses on the rheological characterization of human blood using contemporary steady state and scalar, structural, thixotropic models using published data from the literature. We will then explore the present state of blood modeling starting with the modeling of steady state data using well-known steady state models. We then discuss how the preponderance of these steady state models struggle in their ability to predict transient conditions. Following this, we show the ability of a recent thixotropic, structural kinetic model by Apostolidis et al. (2015) with and without modifications that have previously been shown to improve predictive capability for thixotropic systems by Armstrong et al. (2016a). The proposed modifications will be used to fit and predict the rheology of published transient data from Bureau et al. (1979, 1980). In addition, we compare our structural kinetic, thixotropic modeling to the recently published nonstructural kinetic Bautista-Manero-Puig Bautista model by Bautista et al. (1999).
The published blood data sets highlighted in this manuscript were used to further the development of a simple structural kinetic thixotropic model for blood flows that incorporates elastic and viscous contributions to the total stress that depend on a time- and shear rate-dependent structure parameter (Mujumdar et al. 2002; Dullaert and Mewis 2006; Mewis and Wagner 2012; Dimitriou et al. 2012; Apostolidis et al. 2015; Armstrong et al. 2016a, b). In addition, we highlight the novel sequence of physical phenomenon (SPP) approach as a way to analyze data. Contemporary work on thixotropy modeling using a structural kinetic approach includes a wide variety of approaches, e.g., Mewis and Wagner (2009), Mewis and Wagner (2012), de Souza Mendes and Thompson (2012, 2013), Dimitriou et al. (2013), de Souza Mendes and Thompson (2013), Larson (2015), Blackwell and Ewoldt (2014), Armstrong et al. (2016a), and Wei et al. (2016). The Dullaert and Mewis structural kinetic model for thixotropy has been the basis of “type I” models as defined by de Souza Mendes and Thompson (2012, 2013). Work to evolve Bingham-like constitutive models that incorporate a structure parameter include contributions by Mujumdar et al. (2002) and more recently, Blackwell and Ewoldt (2014), Armstrong et al. (2016a), and Wei et al. (2016) is to develop a quantitative, microstructural understanding that can ultimately be used for the rational formulation the thixotropic, shear-thinning material blood.
With this accomplished, we then highlight the use of a novel, recently published transient and LAOS data analysis technique, SPP by Rogers (2012, 2017). The SPP framework allows one to analyze a continuous, transient data flow signal and carefully compare several flow metrics such as elasticity and viscosity. This enables the construction of an elasto-viscous unique “fingerprint” or mapping allowing comparisons to other similarly constructed fingerprints for comparison. We show and compare several ways to visualize the SPP framework using our fingerprinting technique, the Cole-Cole plot, and modified Cole-Cole plot using published blood data form Bureau et al. (1980) and Sousa et al. (2013). Other metrics from SPP include the torsion and curvature (Rogers 2012, 2017), where torsion is known to be a measure of nonlinearity (Rogers 2017).
The SPP framework is a model independent to transient and LAOS analysis technique that allows one to compare elastic and viscous components of a stress signal directly by way of a Cole-Cole plot, the modified Cole-Cole (first-time derivatives of the moduli) plot, and a unique fingerprinting method demonstrated here (Rogers 2012; Rogers and Lettinga 2012). The SPP fingerprinting methodology is a novel technique to view the evolution of the elastic and viscous moduli over a period of flow with respect to strain and shear rate. Before this, the de facto Small Amplitude Oscillatory Shear (SAOS) and Large Amplitude Oscillatory Shear (LAOS) analysis technique has been the G′ and G″ analysis, as well as fast Fourier transform (FFT) harmonic analysis of the stress signal. To this, Ewoldt et al. (2008), Ewoldt (2013), and Dimitriou et al. (2013) added the Chebychev polynomial analysis technique, similar to fast Fourier time transform, but in the Chebychev space domain. These intrinsic material functions, when calculated, could then be used to construct a mapping of values in a pseudo-fingerprinting manner unique to a certain material’s rheology (Ewoldt et al. 2010). In addition, meaning was given to the Chebychev material functions (Ewoldt 2013). More recently, the asymptotically nonlinear material function framework was contributed by Blackwell and Ewoldt (2014) and Ewoldt and Bharadwaj (2013, 2014, 2015). The asymptotically nonlinear material function framework allows to explore the transition region between SAOS and LAOS (Blackwell and Ewoldt 2013; Ewoldt and Bharadwaj 2013, 2014, 2015).
We will show the efficacy of the SPP approach, and demonstrate that we can generate unique sets of viscoelastic fingerprints of evolving moduli for transient and LAOS data directly to compare elastic and viscous contributions to total stress, in addition to the Cole-Cole plot and modified Cole-Cole analysis. The above mentioned approach can be used in conjunction with transient and LAOS flows only (Rogers 2012, 2017). The SPP methodology is favored due to fact that SPP uses each data point from a given data set, whereby other LAOS analysis frameworks use only G′ and G″ to represent an entire period of oscillatory data. In addition, the traditional analysis frameworks FFT and Chebychev can only be applied to SAOS or LAOS (Gurnon and Wagner 2012). SPP allows one to use all the data, and sheds light on the significant shortcomings of the other analysis frameworks. In addition, all transient experiments can be analyzed with SPP, not only oscillatory experiments. This generalization is a significant improvement over more traditional methods, where no data is wasted, and all transient experiments can be analyzed.
There is also significant interest in using LAOS to study material properties and potentially, for determining parameters in rheological constitutive models (Hyun et al. 2011; Rogers et al. 2012; Germann et al. 2016). The models of interest here are all blood rheological models. In the following, we provide a description of the published blood data from literature, along with a summary of the models highlighted here and a brief description of the model parameter fitting algorithm used. The published blood data used here consisted of steady state data from Moreno et al. (2015), Sousa et al. (2013), and Tomaiuolo et al. (2016), while the transient data is from Bureau et al. (1980), and the LAOS data from Sousa et al. (2013).
The present work focuses on the rheological characterization of human blood using contemporary steady state and structural, thixotropic models using published data from the literature. We will then explore the present state of blood modeling starting with the modeling of steady state data using well-known steady state models. We then discuss how the preponderance of these steady state models struggle in their ability to predict transient conditions. Following this, we show the ability of a recent thixotropic, structural kinetic model by Apostolidis et al. (2015) with and without modifications shown to work for thixotropic systems by Armstrong et al. (2016a) to fit and predict the rheology of published transient data from Bureau et al. (1979, 1980). In addition, we compare our modeling efforts to one more recently published nonstructural kinetic models, the Bautista-Manero-Puig (Bautista et al. 1999).
With this accomplished, we then highlight the use of a novel, recently published transient and LAOS data analysis technique, SPP by Rogers (2012, 2017). The SPP framework allows one to analyze a continuous, transient data flow signal and carefully compare several flow metrics such as elasticity and viscosity. This enables the construction of an elasto-viscous unique fingerprint or mapping allowing comparisons to other similarly constructed fingerprints for comparison. We show and compare several ways to visualize the SPP framework using our fingerprinting technique, the Cole-Cole plot, and modified Cole-Cole plot using published blood data form Bureau et al. (1980) and Sousa et al. (2013). Other metrics from SPP include the torsion and curvature (Rogers 2012, 2017), where torsion is known to be a measure of nonlinearity (Rogers 2017).
Materials and methods
This work involved the use of already published data from three literature sources. Our intent is use published steady state human blood data from Sousa et al. (2013), Moreno et al. (2015), and Tomaiuolo et al. (2016) and transient data from Sousa et al. (2013) and Bureau et al. (1980). We will briefly discuss the respective experimental protocols here.
The Bureau et al. (1980) is the oldest data set used here. The data was taken using series of “triangular” step-up/down in shear rate functions, also known as “sawtooth” pattern, to generate hysteresis curves in stress. The rheometer used was a semi-automatic coaxial cylinder microviscometer constructed by Chaix-Meca using a cup and bob analogue geometry, and the blood was treated with the anticoagulant EDTA. The Sousa data incorporated an Anton-Paar Physica MCR301 with parallel plate geometry, with a rough surface on the upper plate, and the anticoagulant was EDTA. Tomaiuolo et al. (2016) data was taken with the Anton-Paar Physica MCR301 with a double-gap, cup and bob geometry, and EDTA as the blood anticoagulant. With the exception of the Bureau et al. (1980) data, all of the data was taken at 37 °C, while Bureau et al. was at 25 °C. All of these details can be found here (Bureau et al. 1980; Sousa et al. 2013; Moreno et al. 2015; Tomaiuolo et al. 2016). Moreno et al. (2015) used a TA Instrument AR-G2, a double concentric cylinder fixture, with EDTA as the anticoagulant. We utilize here two sets of this data with reported “high-cholesterol” measurements (H1, H2) and two sets of this data with reported “low-cholesterol” (L1, L2) (Moreno et al. 2015). The EDTA has been shown not to appreciably affect the rheological signatures Sousa et al. (2013).
With these respective data sets, we show fitting results for first a series of six simple models from literature routinely used to fit steady state data that compare well to each other in goodness of fit. We then highlight the limitations of the simple models by showing that the only models that can model transient flow appropriately are the structural kinetic models demonstrated by Apostolidis et al. (2015) and Armstrong et al. (2016a), as well as the nonstructural, but still dynamic BMP model, which has a term for an evolving fluidity term. In addition, the BMP model is demonstrated due to its pseudo-structural kinetic approach modeling an evolving fluidity (Bautista et al. 1999). We test the model fit for transient data fitting with data of Bureau et al. (1980). Finally, we demonstrate how the series of physical phenomena can be used to interrogate LAOS data for elastic and viscous signatures (Bureau et al. 1980; Sousa et al. 2013; Rogers 2017).
In each of the respective fits, the models are fit using the parallel tempering algorithm, a stochastic, global optimization technique recently developed and improved by Armstrong et al. (2016b). The values for objective functions are compared, and the Akaike information criteria were calculated, which assign a penalty for number of parameters (Akaike 1974). Brief model descriptions are offered. For the transient Bureau et al. (1980) blood data, the data was digitized, then fit to a series of empirical functions to facilitate the parameter fitting with the parallel tempering. The empirical functions were fit using the lsqcurvefit command in MATLAB. The SPP elastic and viscous signatures, Cole-Cole plots, and modified Cole-Cole plots were created in MATLAB using the SPP algorithm (Rogers 2017).
Results and discussion
In this section, we introduce the necessary details related to all of the models, discuss each of the model parameters, and show the fitting results of the models and data using the parallel tempering algorithm. The steady state and transient data fits are compared and analyzed using a cost function and the Akaike information criteria. This is followed by a demonstration of the SPP analysis technique applied to LAOS and transient flow.
This section is further broken into three subsections: the first of which will be a comparison and description of several current simple models with the ability to fit steady state human blood data; followed by the second subsection that focuses on fitting recent structural kinetic thixotropic models, the BMP model, the Stickel et al. EVP-like dynamic “Herschel-Bulkley,” and the White-Metzner with Carreau-Yasuda used to describe the evolving viscosity as a function of the shear rate to transient data; and the third subsection will first give a cursory overview of traditional ways to analyze LAOS data and then discuss and demonstrate a more contemporary, novel approach to interpreting large-amplitude oscillatory shear and transient data using the SPP framework (Rogers 2012, 2017).
First, we will explore the ability of seven different models with varying numbers of parameters from three to nine parameters to model recently published, steady state blood data. The simplest of the model is the classic Herschel-Bulkley model and it has three parameters (Mewis and Wagner 2012). For each model, we will provide a brief description of each parameter, and then compare each model by fitting the models to a series of steady state data sets from literature. We are using four steady state sets of data from Moreno et al. (2015) that have varying cholesterol levels, two sets of data from Sousa et al. (2013), and one set of steady state data from Tomaiuolo et al. (2016). The model comparison will conclude with a comparison of the cost function, and Akaike information criterion metric, which assigns a penalty for parameters. With the Akaike information criteria, we rank order the six simple models for steady state data fitting, and discuss strengths and weaknesses (Akaike 1974; Sousa et al. 2013; Moreno et al. 2015).
Our first model to be compared is the classic Herschel-Bulkley three-parameter model shown below:
where σ y0 is the yield stress, K is the consistency parameter, and n is the power law dependence. This model is extremely accurate in fitting steady state data; however, due to the fact that it is does not contain a way to bring in time dependence in its native form, it breaks down for transient flows.
For the dynamic, transient blood data of Bureau et al. (1980), we fit a “dynamic” version of the Herschel-Bulkley model recently published by Stickel and coworkers (Stickel et al. 2013). A version of this model was postulated by Saramito (2009), whereby the model was called the “elastoviscoplastic model based on the Herschel-Bulkley viscoplastic model” (Saramito 2009). In addition, Dimitriou et al. (2012) worked on a similar construct with a strain and shear rate broken into elastic and plastic components. We use the model by Stickel et al. (2013) by adding only one additional parameter to the Herschel-Bulkley, G, the elastic modulus, as follows:
where the parameters all have the same interpretation as Herschel-Bulkley shown in Eq. 3, with the addition of G, elastic modulus. In this way, we can give the Herschel-Bulkley model a characteristic time of stress evolution. The original Herschel-Bulkley cannot model the transient data without this modification as well.
We next explore the very similar Carreau-Yasuda and modified Cross models, both with five parameters each and both shown below:
where η 0 and η ∞ represent the zero and infinite shear viscosity, respectively; λ is the relaxation time; and m, n, and a are the power law-like parameters and fitting constants (Mewis and Wagner 2012; Bessonov et al. 2016). It can be argued that these models represent a slight improvement in modeling evolution due to fact that they both contain a relaxation time. It is duly noted that these models estimate the viscosity, and when multiplied into shear rate can predict the current stress as follows: \( \sigma =\eta \left(\dot{\gamma}\right)\dot{\gamma} \). A weakness with these models is the lack of a yield stress term, and blood is known to have a yield stress, which over the range of data we fit is seemingly not a factor as we take the lowest stress value at the lowest shear rate as the low shear viscosity term in Eqs. 5 and 6. In reality, it has been argued that the manifestation of a yield is in reality a very high value of a zero-shear viscosity (Barnes 1997). This is the interpretation of yield stress-like term used in the Carreau-Yasuda and modified Cross models, where a zero-shear viscosity values is used as the limiting case of low shear rate and not a yield stress term (Barnes 1997).
For the transient data fitting with the Carreau-Yasuda, we turn to the White-Metzner model, which is essentially the Maxwell model with a function for viscosity based on the shear rate. We will use Eq. 5 in conjunction with the following (Bird et al. 1987):
where G is the elastic modulus and \( \eta \left(\dot{\gamma}\right) \) is given by Eq. 5, the Carreau-Yasuda model. Again, the model by itself does not have the ability to effectively evolve its values of stress for the transient flow of blood. There is a full tensorial version of the White-Metzner, with a full deviatoric stress tensor, that we have not used here, but ostensibly could be used with an upper convected form to potentially solve for at least for the first normal stress difference if one desired.
The next model to be showcased is the classic Casson model, also has two parameters, and was originally designed to model steady state blood rheology (Merill 1969; Mewis and Wagner 2012; Apostolidis et al. 2015). It is shown below:
where again σ y0 is the yield stress and η ∞ is the infinite shear viscosity. This model is on par with the Herschel-Bulkley for accuracy, as shown in Table 1, and is well suited for fitting and modeling steady state human blood rheology data, however also lacks the capability to fit transient, oscillatory, and more complicated rheological flow conditions due to its lack of an evolutionary term to model an evolving structure, viscosity, or fluidity (Merill 1969; Mewis and Wagner 2012; Apostolidis et al. 2015).
The next three models are all either thixotropic models or have the capability to model shear thinning through an ordinary differential equation, or set of simultaneous ordinary differential equations that can model an evolving structure, fluidity/viscosity, and stress as a changing value with a certain time constant. The first models discussed here will be structural kinetic models, one which was specifically designed to fit transient human blood data, the other which includes our modifications to the first that contain additional viscous terms. The modifications we are proposing are inspired by recent work of Armstrong et al. (2016a) and were originally derived for more generic thixotropic materials undergoing transient rheological conditions. The modified Delaware thixotropic model was itself the result of a combination of several other recently published structural kinetic thixotropic models (Mujumdar et al. 2002; Dullaert and Mewis 2006; Mewis and Wagner 2012; Dimitriou et al. 2013; de Souza Mendes and Thompson 2013; Blackwell and Ewoldt 2014; Armstrong et al. 2016a). In its present incarnation, we use ξ to represent our scalar structure parameter that represents a normalized number of attachments between [0 1] to nearest neighbors, where a value of 0 would be a fully broken down structure, and a value of 1 would be the fully formed structure at rest (Goodeve 1939; Mujumdar et al. 2002; Blackwell and Ewoldt 2014; Armstrong et al. 2016a, b).
The first thixotropic blood model introduced here in the steady state comparison is the Apostolidis et al. blood thixotropic model (Apostolidis et al. 2015). Suffice to say here that this model considers the total strain and total shear rate as a linear superposition of the elastic and the plastic component as follows:
where the subscript e and p represent the elastic and plastic components, respectively (Mujumdar et al. 2002; Dullaert and Mewis 2006; Mewis and Wagner 2012; Armstrong 2015; Armstrong et al. 2016a). Note that the total strain, γ (and, correspondingly, the total shear rate, \( \dot{\gamma} \)), is decomposed within the MDT model into an elastic, γ e (correspondingly \( {\dot{\gamma}}_e \)), and a plastic, γ p (correspondingly \( {\dot{\gamma}}_p \)), contributions. Equation 9 long with the following:
where γmax is the maximum allowable strain (set to unity for blood) and γ0 is the critical strain. Together, Eqs. 9–11 communicate the full picture of how this thixotropic model is able to accomplish the breakdown of the elastic and plastic components of the strain and shear rate. In addition to this, there are a series of three ordinary differential equations in time, shown below for the evolution of the elastic strain, the structure parameter, and the elastic modulus:
where σ y0 is the yield stress, η ∞ is the blood viscosity, G is the elastic modulus, and the k i s represent the characteristic time of structure and elastic modulus evolution, respectively (Dimitriou et al. 2013; Apostolidis et al. 2015; Armstrong et al. 2016a, b). The structural evolution equation has two terms, the first to account for structure breakdown of shear rate and the second to account for Brownian buildup of structure. The elastic modulus has its own characteristic time of evolution, and it describes the evolution of the elastic modulus of the blood. Components of Eqs. 10–14 are combined to form the overall constitutive equation shown below:
To enhance the predictive capability for human blood, we propose modifying Eq. 15 by adding a term to account for structurally induced viscosity with power law dependence as follows:
where K ST is the structural consistency parameter, n is the power law dependence, and ξ is the current structure level, inspired by Armstrong et al. (2016a). The enhanced Apostolidis et al. blood thixotropic model combination allows for accurate accounting of the current level of the structural viscosity contribution. This is a legitimate addition due to the fact that it is widely known that blood forms aggregates, and structures at low shear rates, that are in turn broken down during high shear rates. This continuous evolution of blood structure contributes a viscous term to the overall shear stress that can now be accounted for with the middle term of Eq. 16.
The next model we consider is the BMP model, which is based on a Maxwell-like, tensorial framework; however, we only use the shear component in xy direction here, even though this construct does have the capability to model normal forces. The BMP bases the stress calculation on the inverse of viscosity, the fluidity, and includes an evolution term for the fluidity which as an evolution constant, k, and a relaxation time λ. The function for evolving fluidity, φ, and the constitutive equation for stress evolution as a function of the current value of the fluidity are shown below:
where G 0 is the elastic modulus and the product of G 0 and φ gives the characteristic time of stress evolution in a Maxwell-like fashion. This is the form of the BMP we use here. The other terms of the deviatoric stress tensor are not used.
For the steady state analysis, we use the steady state representation of all the model Ordinary Differential Equation (ODE) and solve for respective values at steady state. This means that at steady state, we set the values of the ODEs to zero. For the transient analysis in the next section, the full ODEs are first solved and then are fit to the transient data of Bureau et al. (1980). It is mentioned here that to calculate the infinite shear viscosity for BMP, Apostolidis et al., and the enhanced Apostolidis et al. blood thixotropic models, the empirical relationship developed by Apostolidis and Beris (2014, 2015) is used,
where np is the plasma viscosity (taken here to be 1.67E−3 Pa s or 1.67E−2 dyne/cm3 s), HCT is the hematocrit level, and T 0 and T represent the reference temperature and temperature at which the data is taken (Barbee and Cokelet 1971; Apostolidis and Beris 2014; Apostolidis et al. 2015). While the Apostolidis models also incorporate the following empirical relationship to deduce the yield stress:
where cf is the fibrinogen concentration (Apostolidis and Beris 2014, 2015; Apostolidis et al. 2015).
Table 1 below shows a comparison of each of the models fitting seven different sets of steady state blood data from literature as follows: four sets from Moreno et al. (2015), two sets from Sousa et al. (2013), and one set from Tomaiuolo et al. (2016). The comparison metrics are as follows: cost function shown in Eq. 21:
where y i is the value of the data, f i is the value of each model prediction, and N is the number of points of the data set. It was necessary to normalize our data by the data stress values due to the typical order of magnitude differences in steady state human blood data. All the steady state model fitting and transient model fitting were completed using a recently published parallel tempering algorithm, incorporating a cost function of the form shown in Eq. 21 or Eq. 26 (Armstrong et al. 2016b). There were seven published steady state, blood data sets analyzed, and the cost function values shown in Table 1 represents the average values over the seven sets of data. Furthermore, we incorporated into our comparison of the models residual sum of squares, which is defined as
In order to present a fair comparison between models, and allow a penalty for more parameters, we also incorporate the Akaike information criterion (AIC) metric, which penalizes good data fits for additional parameters (Akaike 1974),
where k is the number of model parameters and RSS is defined in Eq. 22. For success, the AIC or Akaike information criteria will be minimized, and the penalty incurred by additional parameters will be mitigated by a smaller value of RSS. The use of AIC allows a balance between model complexity and model simplicity, and discourages the addition of fitting parameters that do not directly tie to the physics of the material. This seems to be implicitly used by the authors whenever they speak of which model is “the best” when fitting a particular data set. This point could also be made more clearly. Lastly, for the purposes of comparison and to correct for small data sets, we incorporate the corrected Akaike information criteria as follows:
where n denotes the sample size and k represents the number of parameters (Akaike 1974).
Steady state fitting
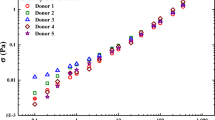
In this section, we start with the six sets of data we have received permission to show from Moreno et al. (2015) and Sousa et al. (2013) shown in Fig. 1.
Published steady state blood data from Moreno et al. (2015) and Sousa et al. (2013). The steady state blood data labeled H1 and H2 are high-cholesterol samples, while the steady state blood data labeled L1 and L2 are low-cholesterol samples. The Sousa et al. (2013) steady state blood data has two sets of data one male (A) and one female (B)
In Fig. 1, there are several trends in the data that are worthy of pointing out. The first is the obvious apparent yield stress at the lowest values of shear rate shown here. The second is that at the higher values of shear rate, several of the curves are overlapping. In the recent paper by Moreno et al. (2015), it was shown that the yield stress and viscosity of the blood have statistically significant correlations with cholesterol levels.
Below in Table 1, there are seven columns: the first is the model name, the second are the appropriate equations at steady state introduced above, the third is the number of and a listing of parameters, the fourth column is the value of the cost function from the parallel tempering parameter fitting, the fifth is the residual sum of squares value, the sixth is the Akaike information criterion, and the seventh is the corrected Akaike information criterion. For the most part, each of the seven sets of data was individually fit to each of the models, and the above mentioned metrics were calculated as shown in Table 1. The parameter values are not shown in Table 1, only the model comparisons. The parameter values from the fits are shown in Tables 2, 3, 4, 5, 6, and 7 below. In general, we can say that we want the smallest values of the individual metrics possible, where negative numbers are okay for the AIC. For example, the model that shows the best fitting capability is at the top of Table 1, and it is the Casson model. The AIC is the lowest value for this model due to the fact that it only uses two parameters, while the second place Herschel-Bulkley has three of the four lowest values of the other comparison metrics. The model in last place for this investigation was the Apostolidis et al. thixotropic blood model due to its four high values of the metrics calculated.
Table 1 shows the best fit results of the six models compared here. The parameters of each of the models were fit with the parallel tempering algorithm described by Armstrong et al. (2016b). Interestingly, we know from Moreno et al. (2015) that the high-cholesterol and low-cholesterol steady state data show that there are several parameters that are postulated to by influenced by high-density lipoproteins and low-density lipoproteins. Those results are corroborated by our fittings. With respect to the Sousa et al. (2013) data, set A is a male and set B is a female. It is extremely interesting to note that with respect to the rank ordering in Table 1, the first four models, on their own and without modifications, cannot successfully model transient and LAOS data. However, we acknowledge here that the Herschel-Bulkley can be modified as shown by Saramito (2009), Stickel et al. (2013), and Dimitriou et al. (2013) to accommodate evolving shear rate, and the Carreau-Yasuda and modified Cross can be utilized in conjunction with a Maxwell-like equation like Eq. 2, for example, as a function for the evolving viscosity term, like the White-Metzner model (Bird et al. 1987). Whereby under this construct, the elastic modulus would stay constant. A similar construct was analyzed recently by Stickel et al. (2013) and Merger et al. (2016). In this manuscript, we only utilize the base model for the Herschel-Bulkley, Carreau-Yasuda, and modified Cross models for the steady state fitting and comparison, and the other versions for the transient data.
In Tables 2, 3, 4, 5, 6, and 7, the results of each of the model fitting is shown, for each of the sets of steady state blood, in rank order from best steady state blood data fitting capability to the least. Again, here, it is interesting to note that the Casson model, originally developed for steady state modeling of blood data, is outperformed by the more generic Herschel-Bulkley model (Merill 1969; Mewis and Wagner 2012) if value of the cost function is considered alone. Additionally, we again point out that the yield stress for the high-cholesterol blood data of Moreno et al. (2015) does indeed appear to be larger in magnitude than that of the low-cholesterol blood data for several of the models. This trend is also apparent for the zero-shear and infinite shear viscosities for the Carreau-Yasuda, modified Cross, and BMP models. This suggests the existence of a possible correlation between cholesterol level and yield stress, as well as blood viscosity.
In addition, we again point out that to successfully model and fit model parameters to transient data of Bureau et al. (1980), the first four models, although at the top of the ranking for steady state model fitting, are not suitable for the transient fits due to their lack of ability to model evolving structure and viscosity. It is also obvious that through this modeling and parametric analysis, it has started to show what the expected values for “normal” or healthy blood are, whereby one can postulate that deviations from the known or accepted values could potentially indicate pathologies. The parameters referred to here are the zero-shear and infinite shear viscosities, the yield stress, and the various model relaxation times fit and shown below in Tables 2, 3, 4, 5, 6, and 7.
Furthermore, the nonthioxotropic models do not have the ability to effectively evolve viscosity (structure) values of stress for the transient flow of blood, but this effect is not easily visualized when limited to steady state analysis. As such, the steady state modeling takes out the time evolution of the structure, creating the appearance of nonthixotropic models adequately predicting steady state responses. The way to identify thixotropy is in the time dependence of the material response, which any steady state test necessarily, and by definition avoids. The transient data fitting section is the most important when it comes to the thixotropy of blood and will demonstrate the clear weakness of the nonthixotropic models.
Transient data fitting
In this subsection, we demonstrate the efficacy of the four models from the previous section that have the ability to model transient flow conditions using previously published data from Bureau et al. (1980). The fifth model depicted here is the enhanced Apostolidis thixotropic blood model (Eq. 16), which includes a structural viscosity term similar to the structural viscosity term from the modified thixotropic model (Armstrong et al. 2016a). All of the best fit parameters for each respective model used are shown in Tables 8, 9, 10, 11, and 12 for each of the four blood types from Bureau et al. (1980). First, we show in Fig. 2a, b the step-up/down in shear rate sawtooth function used by Bureau et al. (1980). We will fit the five models with the ability to predict transient data to the normal, diabetic, and anemic blood rheology data from Bureau et al. (1980). This will allow the demonstration of the five models in action, and possibly allow for parametric analysis and correlation between model parameters and blood pathology. Again, we use the stochastic, parallel tempering algorithm to perform the parameter fitting using the solution to both sets of low shear and high shear for each type of blood listed, and for each model (Armstrong et al. 2016b). The results of each fitting are shown below, with the best fit parameter values for each set of model fit shown in Tables 8, 9, 10, 11, and 12.
a Low strain amplitude step-up/down in shear rate function of Bureau et al. (1980) shown in Eq. 25 with\( {\dot{\upgamma}}_{\max, 1}=0.12\kern0.5em {\mathrm{s}}^{-1};\kern0.5em {\gamma}_{\max, 1}=0.018;\kern0.5em {t}_{\mathrm{max}}=12.5\kern0.5em \mathrm{s} \). b High strain amplitude step-up/down in shear rate function of Bureau et al. (1980) shown in Eq. 25 with \( {\dot{\upgamma}}_{\max, 2}=1.01\kern0.5em {\mathrm{s}}^{-1};\kern0.5em {\upgamma}_{\max, 2}=0.022;{t}_{\mathrm{max}}=46\kern0.5em \mathrm{s} \) (Bureau et al. 1980)
More details of the Bureau transient data are here: Bureau et al. (1980) and Apostolidis et al. (2015). The Bureau data sets include two separate sawtooth step-up/down in shear rate functions, starting from a shear rate of zero, stepping up to a maximum shear rate, then stepping back to zero. There are two sawtooths or triangle functions for each type of blood used in his paper. The first sawtooth function is a linear progression from zero up to a shear rate that is smaller in magnitude (\( {\dot{\upgamma}}_{\max, 1}=0.12\kern0.5em {\mathrm{s}}^{-1};\kern0.5em {\gamma}_{\max, 1}=0.018 \)) than the second sawtooth, before going back to zero. While the second sawtooth function is a linear progression from zero to a larger shear rate (\( {\dot{\upgamma}}_{\max, 2}=1.01\kern0.5em {\mathrm{s}}^{-1};\kern0.5em {\upgamma}_{\max, 2}=0.022 \)) than the first step-up sawtooth function, before going back to zero. In conclusion, the γMAX value of the first sawtooth is smaller in magnitude than the γMAX value of the second sawtooth. The sawtooth shear rate functions are shown in Eq. 25.
Figure 3a–d shows the results of fitting the five models to the normal blood transients from Bureau et al. (1980) with the intrinsic capability to fit transient data: BMP; Apostolidis et al.; enhanced Apostolidis et al. blood thixotropic model, respectively; Stickel et al. EVP-like; and White-Metzner with Carreau-Yasuda. While Fig. 4a, b shows the structure evolution for the normal blood using the Apostolidis et al. and enhanced Apostolidis et al. More details of the Bureau transient can be found here: Bureau et al. (1980) and Apostolidis et al. (2015).
a Normal blood undergoing a ramp-up/down in shear rate as shown in Fig. 2a for low shear rate, with best fit of Apostolidis, enhanced Apostolidis, and BMP. b Normal blood undergoing a ramp-up/down in shear rate as shown in Fig. 2b for high shear rate, with best fit of Apostolidis, enhanced Apostolidis, and BMP. c Normal blood undergoing a ramp-up/down in shear rate as shown in Fig. 2a for low shear rate, with best fit of Stickel et al. and White-Metzner with Carreau-Yasuda. d Normal blood undergoing a ramp-up/down in shear rate as shown in Fig. 2b for high shear rate, with best fit of Stickel et al. and White-Metzner with Carreau-Yasuda (Bureau et al. 1980; Apostolidis et al. 2015; Armstrong et al. 2016a)
a Normal blood structural evolution while undergoing a ramp-up/down in shear rate as shown in Fig. 2a for low shear rate, with best fit of Apostolidis, enhanced Apostolidis, and BMP. b Normal blood structural evolution undergoing a ramp-up/down in shear rate as shown in Fig. 2b for high shear rate, with best fit of Apostolidis, enhanced Apostolidis, and BMP (Bureau et al. 1980; Apostolidis et al. 2015; Armstrong et al. 2016a)
Figure 3a–d shows the best fit for the three transient models of interest. Note that in Fig. 3a, it appears that the stress (in dyne/cm3) was not enough to break down the structure substantially, and that it stays relatively formed during flow, although there is a clear and obvious hysteresis loop. The breaking of the structure was more apparent in Fig. 3b as shown by the steep slope initially, and then ramp-down staying relatively on same slope. Figures 3a–d and 4a, b show the direction of the step-up/down as well as the directions of the structural evolutions. With respect to the normal blood qualitatively, each of the models is accurately fitting the data with respect to the general trend, while the BMP struggles slightly. Tables 9, 10, and 11 bear out this conclusion. Figure 4a, b shows the evolution of the structure starting from a virgin material, ξ equal to one, or completely structured. The high shear rate case shown in Fig. 4b obviously induced a bigger structure breakdown. The modeling of the structure also bears out for the low and high shear rate cases that the structure does not return to its starting value. Although it is assumed that upon the cessation of flow, the structure will completely relax if given the time to do so. It is interesting that although the enhanced Apostolidis has a slightly lower value of cost function, the Akaike information criterion gives the best fit the original version due to the penalty of adding two addition parameters K ST and n. Due to the fact that Fig. 3d shows the inability of the White-Metzner and the Stickel et al. EVP-like model to fail to model the hysteresis loop properly, it is clear that these models struggle with thixotropic materials.
The diabetic blood transient fitting results are shown in Fig. 5a–d, while the diabetic structural evolution for the Apostolidis and enhanced Apostolidis are shown in Fig. 6a, b.
a Diabetic blood undergoing a ramp-up/down in shear rate as shown in Fig. 2a for low shear rate, with best fit of Apostolidis, enhanced Apostolidis, and BMP. b Diabetic blood undergoing a ramp-up/down in shear rate as shown in Fig. 2b for high shear rate, with best fit of Apostolidis, enhanced Apostolidis, and BMP. c Diabetic blood undergoing a ramp-up/down in shear rate as shown in Fig. 2a for low shear rate, with best fit of Stickel et al. and White-Metzner with Carreau-Yasuda. d Diabetic blood undergoing a ramp-up/down in shear rate as shown in Fig. 2b for high shear rate, with best fit of Stickel et al. and White-Metzner with Carreau-Yasuda (Bureau et al. 1980; Apostolidis et al. 2015; Armstrong et al. 2016a)
a Diabetic blood structural evolution while undergoing a ramp-up/down in shear rate as shown in Fig. 2a for low shear rate, with best fit of Apostolidis, enhanced Apostolidis, and BMP. b Diabetic blood structural evolution undergoing a ramp-up/down in shear rate as shown in Fig. 2b for high shear rate, with best fit of Apostolidis, enhanced Apostolidis, and BMP (Bureau et al. 1980; Apostolidis et al. 2015; Armstrong et al. 2016a)
As seen in Fig. 3a–d, we seem the same trends in Fig. 5a–d, where the best fits are given by the three transient models of interest that have the ability to model evolving structure or viscosity. The breaking of the structure was more apparent in Fig. 5b as shown by the steep slope initially, and then ramp-down staying relatively on same slope. Figures 5a–d and 6a, b again show the direction of the step-up/down as well as the directions of the structural evolutions. With respect to the diabetic blood qualitatively, each of the models is hitting the mark with respect to the general trend, while it appears that the original Apostolidis struggles slightly. Tables 9, 10, and 11 show for the diabetic blood fitting that each of the three models yields similar accuracy as shown by the values of the AIC. Although, in this case, the clear winner is the enhanced Apostolidis. Again, Fig. 6a, b shows the evolution of the structure starting from a virgin material, or structure value of 1, or completely structured. Even with the additional parameter penalty, the best model here was the enhanced Apostolidis. Again, due to the fact that Fig. 5d shows the inability of the White-Metzner and the Stickel et al. EVP-like model to fail to model the hysteresis loop properly, it is again clear that these models struggle with thixotropic materials (Bird et al. 1987; Stickel et al. 2013).
The anemic blood transient fitting results are shown in Fig. 7a, b, while the anemic structural evolution for the Apostolidis and enhanced Apostolidis are shown in Fig. 8a, b.
a Anemic blood undergoing a ramp-up/down in shear rate as shown in Fig. 2a for low shear rate, with best fit of Apostolidis, enhanced Apostolidis, and BMP. b Anemic blood undergoing a ramp-up/down in shear rate as shown in Fig. 2b for high shear rate, with best fit of Apostolidis, enhanced Apostolidis, and BMP. c Anemic blood undergoing a ramp-up/down in shear rate as shown in Fig. 2a for low shear rate, with best fit of Stickel et al. and White-Metzner with Carreau-Yasuda. d Anemic blood undergoing a ramp-up/down in shear rate as shown in Fig. 2b for high shear rate, with best fit of Stickel et al. and White-Metzner with Carreau-Yasuda (Bureau et al. 1980; Apostolidis et al. 2015; Armstrong et al. 2016a)
a Anemic blood structural evolution while undergoing a ramp-up/down in shear rate as shown in Fig. 1 for low shear rate, with best fit of Apostolidis, enhanced Apostolidis, and BMP. b Anemic blood structural evolution undergoing a ramp-up/down in shear rate as shown in Fig. 1 for high shear rate, with best fit of Apostolidis, enhanced Apostolidis, and BMP (Bureau et al. 1980; Apostolidis et al. 2015; Armstrong et al. 2016a)
Figure 7a–d shows the best fit for the three transient models of interest. The trends in Fig. 7a–d are similar to Figs. 3a–d and 5a–d. With respect to the anemic blood, qualitatively, each of the models is hitting the mark, while it appears that the original Apostolidis struggles slightly again. Tables 8, 10, 11, and 12 show for the anemic blood fitting that each of the three models yields similar accuracy as shown by the values of the AIC. Although, in this case, the clear winner is the BMP (according to the AIC value). Even with the additional parameter penalty, the best model here was the BMP. Again, due to the fact that Fig. 7d shows the inability of the White-Metzner and the Stickel et al. EVP-like model to fail to model the hysteresis loop properly (Bird et al. 1987; Stickel et al. 2013).
In this section, we use a slightly different version of the cost function and AIC as follows:
and
where due to the large number of points we divide the residual sum of square by number of points, the cost function is accumulated, k is the number of parameters, and do not normalize each residual by the value of the actual value of the data y i . The use of AIC here ensures a fair comparison and a penalty for number of parameters, and the smallest value shows the best fit (negative numbers are okay).
To sum up the transient fitting using the Bureau et al. (1980) transient data for four types of blood, normal, diabetic, anemic, and umbilical, according to the fitting results shown in Tables 8, 9, 10, 11, and 12, each of the five model fits appears equally capable. Each of the three top models for modeling thixotropic materials compared Apostolidis, enhanced Apostolidis, and BMP, each won in at least one category (i.e., normal, diabetic, anemic, and umbilical). With respect to lowest average cost function, the best model for fitting the four types of blood transient data from Bureau et al. (1980) was the enhanced Apostolidis et al. thixotropic blood model as shown in Table 13. With respect to the lowest value of the AIC, the best model for fitting the four types of blood transient data from Bureau et al. (1980) was the BMP as shown in Table 14. Two models must be removed from consideration due to the fact that they could not capture the crossover shown in the hysteresis loop of the Bureau et al. (1980) data as shown in Figs. 3d, 5d, and 7d.
Although this was only by a slight margin, the enhanced Apostolidis was penalized for more parameters by the Akaike information criteria as shown in Tables 13 and 14. Therefore, a conclusion cannot be drawn about which model is best for the dynamic blood fitting here. However, we hypothesize that pathological blood could require the choice of appropriate model; however, at this point, we must gather, model, and compare more normal and pathological blood data. We can say that dynamic models with the capability to model evolving structure and viscosity are required and preferred for accurate modeling results. A table of pathological model parameters may also aid in identifying appropriate correlations between respective model parameter values and the actual pathology moving forward. Again, we mention here that from Tables 8, 9, 10, 11, and 12, it is clear that one can start to accumulate a database of values for normal, healthy blood for appropriate models to begin the process of looking for correlations with pathological blood, and deviations outside normal ranges of values of respective model parameter values (Bird et al. 1987; Bautista et al.(1999); Stickel et al. 2013; Apostolidis et al. 2015; Armstrong et al. 2016a). Additionally, the only models we have shown that can more or less accurately measure steady state and the qualitative and quantitative features of the thixotropic elasto-visco-plastic blood transient data are the models that allow for a direct modeling of the evolution of either a structure parameter or viscosity and fluidity via either a relaxation time, or a kinetic rate parameter, or both (Ewoldt and McKinley 2017).
Interpreting LAOS blood data using series of physical phenomena
Traditionally, there has been in the rheology community a rote way to analyze large-amplitude oscillatory shear in one of two analogous ways, each involving a form of a fast Fourier transform or FFT. They are shown below only to give the evolution of transient flow analysis,
where γ 0 is the strain amplitude, ω is the frequency of oscillation, n is the harmonic, G′s are the elastic components, and the G″s are the viscous components of in-phase and out-of-phase contributions (Giacomin and Dealy 1993; Ewoldt et al. 2008; Blackwell and Ewoldt 2014; Ewoldt and Bharadwaj 2013; Dimitriou et al. 2013; Merger et al. 2016). There is also the expansion of each of the elastic and viscous moduli as follows in a power series:
In addition to the frameworks described in Eqs. 28 and 29, there has been much work using Chebychev coefficients to decompose stress signals into elastic and viscous components (Dimitriou et al. 2012; Dimitriou et al. 2013). With this decomposition, the elastic and viscous contributions are as follows:
where x is the nondimensionalized strain, γ/γ 0, T n (x) is the nth-order Chebychev polynomials, and e n is the elastic Chebychev polynomial. Additionally,
where y is the nondimensionalized strain, \( \dot{\gamma}/{\dot{\gamma}}_0 \), T n (y) is the nth-order Chebychev polynomials, and v n is the viscous Chebychev polynomial. Dimitriou et al. (2012) also mention that in the linear regime, e n → G ′ and v n → G ″ = ωη ′ (Ewoldt et al. 2013; Blackwell and Ewoldt 2014). From this understanding, Ewoldt and coworkers further defined a set of four local parameters, one set of elastic moduli, and one set of viscous moduli to capture local behavior, and interpret viscoelastic material LAOS data. Ewoldt and coworkers go on to say that the two elastic moduli look as follows:
and
where \( {G}_M^{\prime } \) is the minimum strain modulus and \( {G}_L^{\hbox{'}} \) is the large strain modulus. Equations 32 and 33 also show the tie between the Chebychev and Fourier coefficients. There is an analogous set of moduli for viscous measures as follows:
and
where \( {\eta}_M^{\hbox{'}} \) is the minimum-rate dynamic viscosity, \( {\eta}_L^{\hbox{'}} \) is the large-rate dynamic viscosity, and e n and v n are the elastic and viscous nth-order Chebychev polynomials. This analysis is performed by Sousa and coworkers on human LAOS data (Ewoldt et al. 2013; Sousa et al. 2013). These measures are calculated over a period of LAOS while at alternance, and presently do not aid with the interpretation of more generic flows, like those described in Bureau et al. (1980) paper shown in Fig. 2a, b. We show the mathematical evolution of LAOS analysis techniques here to explicitly acknowledge the improvement of transient flow interpretation and then to demonstrate that the techniques cannot be used to interpret or analyze generic transient flows, while SPP can be used for all transient flows. In other words, we would not be able to interpret the elastic and viscous signatures of the Bureau et al. (1980) data without the SPP technique.
More recently, Rogers (2012, 2017) has investigated and found a new way to represent transient data, which does not rely on a single metric, or series of metrics of elasticity and viscosity per oscillating period, but give an equivalent metric per data point at each time step of data recorded during the actual oscillation itself. The framework is SPP. This framework relies on first building an array consisting of strain, shear rate, and stress over a transient rheological test, which is then analyzed in the Frenet-Seret apparatus (Rogers 2012, 2017). The new framework strengths are as follows: it uses all the data, can decompose all transient data into an elastic and viscous signal, and provides interpretation of parameters including the torsion. The framework also allows for calculation and analysis of the rate at which the elasticity and viscosity are changing during flow. In addition, the Cole-Cole plots can be constructed for further interpretation (Rogers 2012, 2017) using Fig. 9 shown below from Rogers 2017.
Step 1 of Rogers SPP is to define the A matrix as \( {\mathbf{A}}_{\mathrm{LAOS}}\equiv \left[{\mathbf{A}}_{\boldsymbol{\upgamma}}\kern0.5em {\mathbf{A}}_{\dot{\boldsymbol{\upgamma}}/\boldsymbol{\upomega}}\kern0.5em {\mathbf{A}}_{\boldsymbol{\upsigma}}\right]\equiv \left[\boldsymbol{\upgamma} \left(\mathbf{t}\right)\kern0.5em \dot{\boldsymbol{\upgamma}}\left(\mathbf{t}\right)/\boldsymbol{\upomega} \kern0.5em \boldsymbol{\upsigma} \left(\mathbf{t}\right)\right] \) taken from Rogers (2017), where each of the column vectors of the A matrix consists of the data from the rheometer; the first column is the strain, the second the shear rate, and the third the stress. It is noted here that in many instances, the raw data stress signal is too noisy, and FFT reconstruction is performed to smooth the stress signal. The reconstructed stress signal is then used in the A matrix. Typically, the FFT reconstruction manipulations are performed using a form similar to Eq. 28. Series of physical phenomena has the following form:
where \( {\mathrm{G}}_{\mathrm{t}}^{\prime}\left(\mathrm{t}\right) \), the evolving elastic modulus; \( {\mathrm{G}}_{\mathrm{t}}^{{\prime\prime}}\left(\mathrm{t}\right) \), the evolving viscous modulus; and σ off(t), the offset, are evolving functions of time, while still maintaining their original character of elastic modulus and viscous modulus. The third evolving term, σ off(t), or offset, is an offset, loosely correlated with degree of nonlinearly in the flow or rheological experiment. To calculate each of these terms from Eq. 36, one must manipulate the A matrix consisting of the strain, shear rate, and stress data by constructing the Frenet-Seret apparatus of mutually orthogonal tangent, principal normal, and binormal vectors as follows (Pressley 2010; Rogers 2017):
where T is the tangent vector, pointing in the “direction of instantaneous travel,” and “dot” notation refers to the first-time derivative, while the double-line notation is the norm. With the tangent vector calculated, we calculate the normalized temporal derivative of the tangent vector as follows:
where again the dot notation is the first derivative with respect to time and N is the principal normal vector. With these calculations complete, we calculate the binormal vector as follows:
The Frenet-Seret apparatus is made up of the binormal, tangent, and principal normal vectors. It is the components of the binormal used to calculate \( {G}_t^{\hbox{'}}(t) \), \( {G}_t^{"}(t) \), and σ off(t). This is shown below in Eqs. 40–42:
and
where the B i components represent the x, y, and z components of the binormal vector, with the x corresponding to γ(t), the y to the \( \dot{\gamma}(t) \), and the z component to the σ(t). The double-dot formalism is the second derivative of the stress, and ω is the frequency. This presentation offers only a brief synopsis of the SPP and Frenet-Seret apparatus. For more background, check these references (Pressley 2010; Rogers 2012, 2017; Rogers and Lettinga 2012). The derivatives of \( {G}_t^{\hbox{'}}(t) \) and \( {G}_t^{"}(t) \) can also be calculated to construct a modified Cole-Cole plot as follows:
and
where again the dot indicates the first derivative with respect to time and τ is the torsion, a known indicator of nonlinear behavior, which is calculated as
With a series of transient experiments, one can build a series of similar rheological experiments with differing strain amplitudes, for example, a series of step-up/step-down in shear rate experiments with varying strain amplitudes or a series of LAOS experiments with varying strain amplitudes (with same frequency). Typically, in a LAOS experiment, the strain will vary as γ(t) = γ0 sin(ωt), with γ 0 equal to the strain amplitude and ω equal to the oscillation frequency. The first derivative of the strain with respect to time is the shear rate. With each of the moduli calculated for each experiment, the three-dimensional color map can then be created over each experiment, and each strain amplitude in such a way to invoke a unique fingerprint of properties. On the x axis is strain, the y axis shear rate, and the z axis, or color axis, representing some value of interest like the elastic or viscous modulus, or the instantaneous rate of change of the elastic or viscous modulus. This is approach followed here for the Bureau et al. (1980) transient, and Sousa et al. (2013) LAOS data, and the approach will demonstrate the unique set of curves, plots, and figure to assist with characterizing blood. In addition to the blood rheology fingerprint plots, one can create the standard Cole-Cole plot, which is a plot of the evolving elastic modulus on the x axis vs. the evolving viscous modulus on the y axis.
In this work, we will demonstrate the Cole-Cole plots, the LAOS modulus fingerprinting, and the SPP modulus plots to show how one can characterize transient data. First, we will analyze two sets of LAOS blood data from Sousa et al. (2013), with different values of strain amplitude, and the same value of frequency. Typically, LAOS data has two parameters, a strain amplitude γ 0 and a oscillation frequency ω. A standard strain-controlled experiment has strain as a sinusoidally oscillating function of time as shown in Eq. 46,
while the shear rate, the first-time derivative of strain, is given as
where the strain vector and the shear rate vector form the first two vectors of the A matrix described in the first paragraph of this section. The third stress vector or σ(t) vector is the measured quantity of a strain-controlled experiment from the rheometer. Both the elastic projections and the viscous projections of the two sets of LAOS data analyzed here are both shown in Figs. 10a, b and 14a, b below (Giacomin and Dealy 1993; Dimitriou et al. 2013; Rogers 2012, 2017).
Figure 10a, b shows the viscous and elastic projections, respectively, from a set of LAOS data from the work of Sousa et al. (2013) at γ0 = 10; ω = 0.631(rad/s). Starting from the number 1 in the figure, we can trace out each of the trajectories. If we had a purely viscous signature, we would see a straight line, for the viscous projection, while the elastic would show a circle. If we had a purely elastic signature, the elastic projection would be a straight line, and the viscous projection would be a circle. Clearly, we are at a combination of frequency, ω, and strain amplitude, γ 0, that leave a thixo-viscoelastic signature, which hypothetically has not caused full destruction of the structure, and furthermore, this structure is contributing to the elasticity, and to some extent evolving viscosity as the structure have a resistance to flow (Ewoldt and McKinley 2017). The Cole-Cole plot and modified Cole-Cole plot shown in Fig. 9a, b, respectively, show how the elastic \( {G}_R^{\hbox{'}} \) and viscous moduli \( {G}_R^{"} \) are evolving, and how their respective time derivatives are evolving.
Again, the arrows are shown to give the reader a general idea of the evolution of both curves. The evolution of \( {G}_R^{\hbox{'}} \) and \( {G}_R^{\hbox{'}} \) with respect to time are shown in Fig. 12a, b, and show yet another way of observing the modulus evolution. With Figs. 9 and 11a, the Cole-Cole plot legend, one can gain a better understanding of how the complex material blood behaves over a period of LAOS oscillation at this particular combination of frequency and strain amplitude. For example, in Fig. 11a, we see at point 1, we start with a purely elastic signature that soon crosses over the 45° line and is fluidized, and becomes a more viscous signature. With respect to blood, this could mean more structure at first, and as the shear rate increases, the structure is broken down leading to more viscosity and less elasticity. The signal then crosses the y axis, meaning closer to fully viscous, and there is a purely viscous signature and recoil. This is followed by reforming of the structure as the shear rate applied to the blood decreases, and the structure has time to rebuild allowing for a predominantly elastic signature.
The moduli vs. time and the first-time derivative of the moduli are shown in Fig. 12a, b. This visualization strategy is not quite as useful as the Cole-Cole and modified Cole-Cole plots. The fingerprinting technique we introduce in this manuscript is shown in Fig. 13a, b, whereby the viscous fingerprint is shown in Fig. 13a, and the elastic fingerprint is shown in Fig. 13b.
a Elastic projection fingerprint. b Viscous projection fingerprint of Sousa et al. (2013)γ0 = 10; ω = 0.631(rad/s). Black arrows show the evolution of LAOS flow
To create this imagery, two vectors are utilized and then read into Mathematica. The first array for Fig. 13a consisted of \( {\mathbf{A}}_E=\left[\boldsymbol{\upgamma}\ \dot{\boldsymbol{\upgamma}}\ {\mathbf{G}}_t^{\prime}\right] \), and the second was \( {\mathbf{A}}_{\mathbf{V}}=\left[\boldsymbol{\upgamma}\ \dot{\boldsymbol{\upgamma}}\ {\mathbf{G}}_t^{{\prime\prime}}\right] \). With the array into Mathematica, and by using the “Temperature Map” command, we can now create a three-dimensional figure, or a “heat map” with the shear rate as the x axis, strain as the y axis, and the third dimension the value of \( {G}_t^{"} \). For Fig. 13b, the value depicted is \( {G}_t^{\prime } \). In Mathematica, one can set the color scales or accept the default. One can now conceivably look up the strain and shear rate to find the corresponding values of the moduli within the confines of the flow. For a cursory consistency check, one can check the same set of (x,y) coordinates in both the viscous and elastic fingerprint and see that as one is at a maximum, the other is at a minimum and vice versa. This is one more way to visualize any transient data set of a thixo-elasto-viscous flow field with respect to the moduli (Rogers 2017; Ewoldt and McKinley 2017). One can follow the black arrows shown in Fig. 13a over the period of LAOS flow to visualize how the elastic and viscous components evolve.
Figure 10a, b shows the viscous and elastic projections, respectively, from a set of LAOS data from the work of Sousa et al. (2013) at γ0 = 100; ω = 0.631(rad/s). Starting from the number 1 in the figure, we can trace out each of the trajectories. If we had a purely viscous signature, we would see a straight line, for the viscous projection, while the elastic would show a circle. If we had a purely elastic signature, the elastic projection would be a straight line, and the viscous projection would be a circle. Clearly, we are at a combination of frequency, ω, and strain amplitude, γ 0, that leave a thixo-visco-elastic signature, which hypothetically has not caused full destruction of the structure, and furthermore, this structure is contributing to the elasticity, and to some extent evolving viscosity as the structure have a resistance to flow (Ewoldt and McKinley 2017) (Fig. 14). The Cole-Cole plot and modified Cole-Cole plot shown in Fig. 11a, b, respectively, show how the elastic \( {G}_t^{\hbox{'}} \) and viscous moduli \( {G}_t^{{\prime\prime} } \) are evolving, and how their respective time derivatives are evolving.
Again, the arrows are shown to give the reader a general idea of the evolution of both curves. The evolution of \( {G}_R^{\hbox{'}} \) and \( {G}_R^{\hbox{'}} \) with respect time are shown in Fig. 16a, b and show yet another way of observing the modulus evolution. With Figs. 9 and 15a, the Cole-Cole plot legend, one can gain a better understanding of how the complex material blood behaves over a period of LAOS oscillation at this particular combination of frequency and strain amplitude. For example, in Fig. 15a, we see that we are now starting with a more viscous signal due to the fact that the strain amplitude is 100, therefore breaking all of the structure down, giving a more pure viscous signature. With respect to blood, this could mean a lot less structure at first, and that the structure remains in this broken-down configuration during the flow almost entirely due to the larger shear rate. The signal then crosses the y axis, meaning there is a purely viscous signature and recoil here.
The moduli vs. time and the first-time derivative of the moduli are shown in Fig. 16a, b. This visualization strategy is not quite as useful as the Cole-Cole and modified Cole-Cole plots. The fingerprinting technique we introduce in this manuscript is again shown in Fig. 17a, b for this LAOS data set (Sousa et al. 2013), whereby the viscous fingerprint is shown in Fig. 17a, and the elastic fingerprint is shown in Fig. 17b.
a Elastic projection fingerprint. b Viscous projection fingerprint of Sousa et al. (2013) γ0 = 10; ω = 0.631(rad/s), γ0 = 100; ω = 0.631(rad/s). Black arrows show the evolution of LAOS flow
To create this imagery, two vectors are utilized and then read into Mathematica. The first array for Fig. 17a consisted of \( {\mathbf{A}}_E=\left[\boldsymbol{\upgamma}\ \dot{\boldsymbol{\upgamma}}\ {\mathbf{G}}_t^{\prime}\right] \) and the second \( {\mathbf{A}}_{\mathbf{V}}=\left[\boldsymbol{\upgamma}\ \dot{\boldsymbol{\upgamma}}\ {\mathbf{G}}_t^{{\prime\prime}}\right] \). With the array into Mathematica, and by using the Temperature Map command, we can now create a three-dimensional figure, or a heat map with the shear rate as the x axis, strain as the y axis, and the third dimension the value of \( {G}_t^{{\prime\prime} } \). For Fig. 17b, the value depicted is \( {G}_t^{\prime } \). As previously mentioned in Mathematica, one can set the color scales or accept the default. This is another example a way to visualize any transient data set of a thixo-elasto-viscous flow field with respect to the moduli (Rogers 2017; Ewoldt and McKinley 2017). With the full picture easily viewed in all of these visualizations, one can make comparisons between not just different flows but also different samples of blood to start to parse out effects of pathology, etc.
We essentially now show the same analysis framework for the Bureau et al. (1980) transient blood data for normal and the diabetic blood with the same functions and parameters that define the shear rate from Eq. 36. For types of transient flow that are nonoscillating, we use a different form of Eq. 36 with \( {\mathbf{A}}_{\mathrm{Trans}}\equiv \left[{\mathbf{A}}_{\boldsymbol{\upgamma}}\kern0.5em {\mathbf{A}}_{\dot{\boldsymbol{\upgamma}}}\kern0.5em {\mathbf{A}}_{\boldsymbol{\upsigma}}\right]\equiv \left[\boldsymbol{\upgamma} \left(\mathbf{t}\right)\kern0.5em \dot{\boldsymbol{\upgamma}}\left(\mathbf{t}\right)\kern0.5em \boldsymbol{\upsigma} \left(\mathbf{t}\right)\right] \), leading to a reconstruction of the stress as follows:
where \( {\upeta}_t^{\prime}\left(\mathrm{t}\right) \) is given by
and this is a good time to recall that \( {\upeta}_t^{\prime}\left(\mathrm{t}\right)=\frac{{\mathrm{G}}_t^{{\prime\prime}}\left(\mathrm{t}\right)}{\upomega} \), where ω is the frequency of oscillation. For some transient flows, ω is not always clearly defined.
Figure 18 demonstrates the Cole-Cole plot for the normal blood, with the low shear step-up and step-down sawtooth function (as seen in Fig. 2a), while Fig. 19a, b shows the evolution of the moduli with respect to time. The reader is reminded that this stress vs. shear rate (pseudo-viscous projection) of the data is shown in Fig. 3a for normal blood (Bureau et al. 1980).
From Fig. 18, it is clear that the blood starts from purely elastic signature as we expect due to the fact that the shear rate started from zero. It then evolves into a more viscous signature as the shear rate is ramped up the maximum value, and then begins to show more elastic signatures as the shear rate decreases towards the end of the shear rate sawtooth, or triangle function. With a comparison to the legend in Fig. 9 (Rogers 2017), we can see that the normal blood goes through a cycle of thinning and softening as the structure breaks down, and thickening and hardening as the structure in the blood relaxes.
To create this imagery, two vectors are utilized and then read into Mathematica. The first array for Figure 20a consists of \( {\mathbf{A}}_E=\left[\boldsymbol{\upgamma}\ \dot{\boldsymbol{\upgamma}}\ {\mathbf{G}}_t^{\prime}\right] \) and second (Fig. 20b) is \( {\mathbf{A}}_{\mathbf{V}}=\left[\boldsymbol{\upgamma}\ \dot{\boldsymbol{\upgamma}}\ {\eta}_t^{\prime}\right] \). With the array into Mathematica, and by using the Temperature Map command, we can now create a three-dimensional figure, or a heat map with the shear rate as the x axis, strain as the y axis, and the third dimension the value of \( {\eta}_t^{\hbox{'}} \). For Fig. 20b, the value depicted is \( {G}_t^{\hbox{'}} \). In Mathematica, one can set the color scales or accept the default. Similar to the LAOS data SPP analysis, the same technique can be use with a more generic transient flow, where one can now theoretically look up the strain and shear rate to find the corresponding values of the moduli within the confines of the flow and perform a consistency check in both the viscous and elastic fingerprints and see that as one is at a maximum, the other is at a minimum and vice versa (Rogers 2017; Ewoldt and McKinley 2017).
a Elastic projection. b Viscous projection using series of physical phenomenon modulus fingerprinting of normal blood (Bureau et al. 1980). Black arrows show the evolution of sawtooth function
Figure 21 demonstrates the Cole-Cole plot for the diabetic blood, with the low shear step-up and step-down sawtooth function (as seen in Fig. 2a), while Fig. 22a, b shows the evolution of the moduli with respect to time. The reader is reminded that this stress vs. shear rate (pseudo-viscous projection) of the data is shown in Fig. 5a for diabetic blood (Bureau et al. 1980). One can also reference Fig. 6a to check the various model predictions of structure evolution.
From Fig. 21, it is clear that the diabetic blood starts from purely elastic signature as we expect due to the fact that the shear rate started from zero. It then evolves into a more viscous signature as the shear rate is ramped up the maximum value, and then begins to show more elastic signatures as the shear rate decreases towards the end of the shear rate sawtooth function. With a comparison to the legend in Fig. 9 (Rogers 2017), we can see that the normal blood goes through a cycle of thinning and softening as the structure breaks down, and thickening and hardening as the structure in the blood relaxes. The bottom line here is that there is a unique Cole-Cole evolution for the diabetic blood and normal blood, which could lead to a technique in which the pathology could be identified with just the mechanical information from the sawtooth function. Figure 22 shows the evolution of the moduli for diabetic blood as a function of time.
We have demonstrated the novel new SPP framework and analysis for the normal and diabetic blood of Bureau et al. (1980) and the LAOS data from Sousa et al. (2013). This technique allows for a more robust, deep, and far-reaching understanding of what is happening to the material with respect to elastic and viscous stress during the entire evolution of a rheology experiment. It is also stated here that a reconstruction of the stress signal using Eq. 36 or Eq. 48 is spot on every time.
Each of the Cole-Cole plot interpretation via use of Fig. 9 shows how the material is behaving with respect to its original starting point, while the modified Cole-Cole plot shows the rate of change with respect to time of the Cole-Cole plot. In addition, we demonstrate several ways to view the moduli in such a way to show uniqueness of the material. For example, the novel fingerprinting technique could be used to identify pathological blood sample should there exist a database of fingerprints a priori to compare to. This could be done numerically by comparing values of the moduli over a single evolution, period, or step-up/down experiment. We anticipate pushing a more complete demonstration of this technique in future work with our own data.
Conclusions
In essence, we have here shown a snapshot of where contemporary blood modeling of steady state, transient, and LAOS analysis and mapping stands. The state of modeling has steadily improved over the years since the inception of some of the original models shown by Merill (1969) and Mewis and Wagner (2012). We have also shown that the simple steady state models can model steady state well, but lack the robust transient terms required for evolution of structure and viscosity which occur naturally as human blood undergoes transient flows. The more advanced models allow for the evolution of structure and viscosity do not perform as well for steady state but make up for this during transient flows as demonstrated. However, those models have the best chance of accurately predicting transient flows. Here, we demonstrated an enhanced thixotropic blood model based on the work of Apostolidis et al. (2015) that was at least as good as its peer models. The enhanced Apostolidis et al. model was augmented with a term to account for structural viscosity of blood, at a cost of two additional parameters a power law, n, and the structural viscosity, K ST. This follows previous work by Armstrong et al. (2016a). Tables 13 and 14 show the results tabulated with respect to overall cost function and AIC, respectively. We argue that although adding the two parameters adds an AIC penalty, in this case, the penalty does not outweigh the fact that the new terms represent the actual physics of structural viscosity contribution. The structural viscosity adds a nontrivial component to overall viscosity and is well documented in the literature (Bureau et al. 1980; Sousa et al. 2013; Apostolidis et al. 2015). We acknowledge that structural kinetic modeling is reaching a limit, and have noticed in fitting this system and other similar systems that there is still a viscoelastic timescale that is not accurately captured (Apostolidis et al. 2015; Armstrong et al. 2016a, 2017). The future now lies in constructing a model that can simultaneously model the thixotropic timescales associated with structural buildup and breakdown as well as the viscoelastic timescales of the underlying material. This may involve invoking a more thermodynamically consistent framework using tensor and/or conformation models as shown in Bird et al. (1987) and Beris et al. (2008).
The transient and LAOS visualization techniques shown here also allow for a new look at characterizing, “fingerprinting,” and mapping human blood rheological experiments. This may open up a new avenue to approach diagnosing various pathological conditions. We will demonstrate this in future work using the modeling, visualization, and interpretation methodologies outlined here. The best approach to modeling any rheological data is to simultaneously fit the steady state with transient data to more than one family of models (i.e., thixotropic, purely viscoelastic, or a combination), and use the same model and set of parameters fit to make predictions for a different set of data. A good analysis will simultaneously incorporate the LAOS and sawtooth fingerprinting using one or all of the techniques espoused here. From this type of human blood modeling, we will begin to use modeling as a tool to understand the microstructural underpinnings of blood rheology, and its connection to pathological conditions. We will move in this direction with our own data in the future.
References
Akaike H (1974) A new look at the statistical model identification. IEEE Trans Autom Control AC-19(6)
Apostolidis AJ, Armstrong MJ, Beris AN (2015) Modeling of human blood rheology in transient shear flows. J Rheol 59:275–298
Apostolidis AJ, Beris AN (2014) Modeling the blood rheology in steady-shear flows. J Rheol (1978-Present) 58(3):607–633
Apostolidis AJ, Beris AN (2015) The effect of cholesterol and triglycerides on the steady state rheology of blood. Rheol Acta 1:1–13
Apostolidis AJ, Moyer AP, Beris AN (2016) Non-Newtonian effects in simulations of coronary arterial blood flow. J Non-Newton Fluid Mech 233:155–165
Armstrong MJ (2015) Investigating and modeling the thixotropic behavior, microstructure and rheology of complex material. Ph.D. Thesis, University of Delaware
Armstrong MJ, Beris AN, Rogers SA, Wagner NJ (2016a) Dynamic shear rheology of a thixotropic suspension: comparison of an improved structure-based model with large amplitude oscillatory shear experiments. J Rheol 60:433–450
Armstrong MJ, Beris AN, Rogers SA, Wagner NJ (2017) Dynamic shear rheology and structure kinetics modeling of a thixotropic carbon black suspension. Rheol Acta 56(10):811–824
Armstrong MJ, Beris AN, Wagner NJ (2016b) An adaptive parallel tempering method for the dynamic data-driven parameter estimation of nonlinear models. AICHE J. 10.1002/aic.15577
Barbee JH, Cokelet GR (1971) Prediction of blood flow in tubes with diameters as small as 29 microns. Microvasc Res 3:17–21
Barnes HA (1997) Thixotropy—a review. J Non-Newtonian Fluid Mech 70(1–2):1–33
Baskurt KO, Boynard M, Cokelet GC, Connes P, Cooke BM, Forconi S, Liao F, Hardeman MR, Jung F, Meiselman HJ, Nash G, Nemeth N, Neu B, Sandhagen B, Shin S, Thurston G, Wautier JL (2009) New guidelines for hemorheological laboratory techniques. Clin Hemorheol Microcirc 42:75–97
Bautista F, De Santos JM, Puig JE, Manero O (1999) Understanding thixotropic and antithixotropic behavior of viscoelastic micellar solutions and liquid crystalline dispersions. J Non-Newtonian Fluid Mech 80:93–113
Beris AN, Stiakakis E, Vlassopoulos D (2008) A thermodynamically consistent model for the thixotropic behavior of concentrated star polymer suspensions. J Non-Newtonian Fluid Mech 152:76–85
Bessonov N, Sequeira A, Simakov S, Vassilevskii Y, Volpert V (2016) Methods of blood flow modeling. Math Model Nat Phenom 11(1):1–25
Bharadwaj AN, Ewoldt R (2014) The general low-frequency prediction for asymptotically nonlinear material functions in oscillatory shear. J Rheol 58(4):891–910
Bharadwaj AN, Ewoldt R (2015) Constitutive fingerprints in medium-amplitude oscillatory shear. J Rheol 59(2):557–592
Bird RB, Armstrong R, Hassager O (1987) Dynamics of polymeric liquids. John Wiley and Sons, NY
Blackwell B, Ewoldt R (2014) A simple thixotropic-viscoelastic constitutive model produces unique signatures in large-amplitude oscillatory shear (LAOS). J Non-Newtonian Fluid Mech 208-209:27–41
Bureau M, Healy JC, Bourgoin D, Joly M (1979) Etude rhéologique en régime transitoire de quelques échantillons de sangs humains artificiellement modifiés. Rheol Acta 18:756–768
Bureau M, Healy JC, Bourgoin D, Joly M (1980) Rheological hysteresis of blood at low shear rate. Biorheology 17:191–203
Coussot P (2017) Bingham’s heritage. Rheol Acta. https://doi.org/10.1007/s00397-016-0983-y
de Souza Mendes PR, Thompson RL (2012) A critical overview of elasto-viscoplastic thixotropic modeling. JNNFM 187-188: 8-15
de Souza Mendes PR, Thompson RL (2013) A unified approach to model elasto-viscoplastic thixotropic yield-stress materials and apparent yield-stress fluids. Rheol Acta 52:673–694
Dimitriou CJ, Ewoldt RH, McKinley GH (2012) Describing and prescribing the constitutive response of yield stress fluids using large amplitude oscillatory shear stress (LAOStress). J Rheol 57:27–70
Dullaert K, Mewis J (2006) A structural kinetics model for thixotropy. J Non-Newtonian Fluid Mech 139(1–2):21–30
Ewoldt RH (2013) Defining nonlinear rheological material functions for oscillatory shear. J Rheol 57:177–195
Ewoldt R, Bharadwaj AN (2013) Low-dimensional intrinsic material functions for nonlinear viscoelasticy. Rheol Acta 52:201–219
Ewoldt RH, Hosoi AE, McKinley GH (2008) New measures for characterizing nonlinear viscoelasticity in large amplitude oscillatory shear. J Rheol 52(6):1427–1458
Ewoldt RH, McKinley GH (2017) Mapping thixo-elastic-visco-plastic behavior. Rheol Acta 56:195–210
Ewoldt RH, Winter P, Maxey J, McKinley GH (2010) Large amplitude oscillatory shear of pseudoplastic and elastoviscoelastic material. Rheol Acta 49:191–212
Flormann D, Schirra K, Podgorski T, Wagner C (2016) On the rheology of red blood cell suspensions with different amounts of dextran: separating the effect of aggregation and increase in viscosity of the suspending phase. Rheol Acta 55:477–483
Germann N, Gurnon AK, Zhou L, Cook LP, Beris AN, Wagner NJ (2016) Validation of constitutive modeling of shear banding, threadlike wormlike micellar fluids. J Rheol 60:983–999
Giacomin AJ, Dealy JM (1993) Large-amplitude oscillatory shear. Techniques in Rheological Measurement. Chapman and Hall
Goodeve CF (1939) A general theory of thixotropy and viscosity. Trans Faraday Society 35:342–358
Gurnon AK, Wagner NJ (2012) Large amplitude oscillatory shear (LAOS) measurements to obtain constitutive equation model parameters: Giesekus model of banding and nonbanding wormlike micelles. J Rheol 56(2):333–351
Herrera-Valencia EE, Calderas F, Medina-Torres L, Perez-Camacho M, Moreno L, Manero O (2017) On the pulsating flow behavior of a biological fluid: human blood. Rheol Acta doi. https://doi.org/10.1007/s00397-017-0994-3
Hyun K, Wilhelm M, Klein CO, Kwang SC, Jung GN, Kyung HA, Seung JL, Ewoldt RH, McKinley GH (2011) A review of nonlinear oscillatory shear tests: analysis and application of large amplitude oscillatory shear (LAOS). Prog Polym Sci 36:1697–1753
Larson RG (2015) Constitutive equations for thixotropic fluids. J Rheol 59:595–611
Malkin A, Kulichikhin V, Ilyin S (2017) A modern look on yield stress fluids. Rheol Acta. https://doi.org/10.1007/s00397-016-0963-2
Merger D, Abbasi M, Merger J, Giacomin AJ, Saengow C, Wilhelm M (2016) Simple scalar model and analysis for large amplitude oscillatory shear. Appl Rheol. https://doi.org/10.3933/APPLRHEOL-26-53809
Merill E (1969) Rheology of blood. Physiol Rev 49:(4)
Mewis J (1979) Thixotropy—a general review. J Non-Newtonian Fluid Mech 6:1–20
Mewis J, Wagner NJ (2009) Thixotropy. Adv Coll Int Sci 147-148:214–227
Mewis J, Wagner NJ (2012) Colloidal suspension rheology. Cambridge University Press, NY
Moreno L, Calderas F, Sanchez-Olivares G, Medina-Torres L, Sanchez-Solis A, Manero O (2015) Effect of cholesterol and triglycerides levels on the rheological behavior of human blood. Korea-Australia Rheology Journal 27(1):1–10
Mujumdar A, Beris AN, Metzner AB (2002) Transient phenomena in thixotropic systems. J Non-Newtonian Fluid Mech 102:157–178
Pressley A (ed) (2010) Elementary differential geometry. Springer, London
Rogers SA (2012) A sequence of physical processes determined and quantified in LAOS: an instantaneous local 2D/3D approach. J Rheol 56(5):1129–1151
Rogers SA (2017) In search of physical meaning: defining transient parameters for nonlinear viscoelasticity. Rheol Acta. https://doi.org/10.1007/s00397-017-1008-1
Rogers SA, Lettinga MP (2012) A sequence of physical processes determined and quantified in large-amplitude oscillatory shear (LAOS): application to theoretical nonlinear models. J Rheol 56(1):1–25
Saramito P (2009) A new elastoviscoplastic model based on the Herschel-Bulkley viscoplastic model. J Non-Newtonian Fluid Mech 158:154–161
Sousa PC, Carneiro K, Vaz R, Cerejo A, Pinho FT, Alves MA, Oliveira MS (2013) Shear viscosity and nonlinear behavior of whole blood under large amplitude oscillatory shear. Biorheology 50(5–6):269–282
Sousa PC, Pinho FT, Alves MA, Oliveira M (2016) A review of hemorheology: measuring techniques and recent advances
Stickel J, Knutsen JS, Libertore MW (2013) Response of elastoviscoplastic materials to large amplitude oscillatory shear flow in the parallel-plate and cylindrical-Couette geometries. J Rheol 57(6):1569–1596
Tomaiuolo G, Carciata A, Caserta S, Guido S (2016) Blood linear viscoelasticity by small amplitude oscillatory flow. Rheol Acta 55:485–495
Valant AZ, Ziberna L, Papaharilaou Y, Anayiotos A, Gergiou GC (2016) The influence of oxygen concentration on the rheological properties and flow of whole human blood. Rheol Acta 55:921–933
Wei Y, Solomon MJ, Larson RG (2016) Quantitative nonlinear thixotropic model with stretched exponential response in transient shear flows. J Rheol 60:1301
Acknowledgements
The authors acknowledge the support funding assistance from the US Army and the Department of Chemistry and Life Science, United States Military Academy. The authors also acknowledge support in the form of helpful and insightful discussions with Jeff Horner, Dr. Antony Beris, and Dr. Norman Wagner from the University of Delaware, as well as Dr. Simon Rogers from the University of Illinois Urbana-Champaign. The views expressed herein are those of the authors and do not reflect the position of the United States Military Academy, the Department of the Army, or the Department of Defense. Sousa et al. (2013) and Moreno et al. (2015) data reprinted with permission of corresponding author, respectively.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Clarion, M., Deegan, M., Helton, T. et al. Contemporary modeling and analysis of steady state and transient human blood rheology. Rheol Acta 57, 141–168 (2018). https://doi.org/10.1007/s00397-017-1062-8
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00397-017-1062-8