A unified approach to model elasto-viscoplastic thixotropic yield-stress materials and apparent yield-stress fluids

Abstract

A constitutive model for elasto-viscoplastic thixotropic materials is proposed. It consists of two differential equations, one for the stress and the other for the structure parameter, a scalar quantity that indicates the structuring level of the microstructure. In contrast to previous models of this kind, the structure parameter varies from zero to a positive and typically large number. The lower limit corresponds to a fully unstructured material, whereas the upper limit corresponds to a fully structured material. When the upper limit is finite, the model represents a highly shear-thinning, thixotropic, and viscoelastic liquid that possesses an apparent yield stress. When it tends to infinity, the behavior of a true yield-stress material is achieved. Predictions for rheometric flows such as constant shear rate tests, creep tests, SAOS, and large-amplitude oscillatory shear (LAOS) are presented, and it is shown that, in all cases, the trends observed experimentally are faithfully reproduced by the model. Within the framework of the model, simple explanations are given for the avalanche effect and the shear banding phenomenon. The LAOS results obtained are of particular importance because they provide a piece of information that so far is absent in the literature, namely a quantitative link between the Lissajous–Bowditch curve shapes and rheological effects such as elasticity, thixotropy, and yielding.

Introduction

There is a protracted controversy in the field of rheology regarding the concept of yield stress, triggered by the article entitled “The yield stress myth?” (Barnes and Walters 1985). In this article, the authors question the existence of the yield stress: “if a material flows at high stresses, it will also flow, however slowly, at low stresses.”

The comprehensive review on the yield stress given by Barnes (1999) (which carries in its title the quotation “$\pi \alpha \nu \tau \alpha \rho \epsilon \iota$” (“everything flows”) from the ancient Greek philosopher Heraclitus) provides numerous arguments in support of the view that the yield stress does not exist. He argues that the yield-stress concept, introduced by Bingham (1922), is an idealization of the real material behavior, unveiled by a new generation of rheometric devices that are able to detect more accurately the response of materials at very low stress values. Materials previously considered to possess a yield stress were shown to deform irreversibly throughout the entire range of stress, and, accordingly, the threshold stress corresponding to a major change in the material behavior was denominated apparent yield stress. Below the apparent yield stress, in steady state, the material flows like a Newtonian fluid with a very high (but finite) viscosity. In other words, in the range of small shear rates (and below the apparent yield stress), a high-viscosity Newtonian plateau appears in the flow curve.

While the ample evidence given by Barnes (1999) proves that many materials previously believed to possess a yield stress actually do not, it is certainly not a universal disproof of the existence of the yield stress.

Hartnett and Hu (1989) advocated the existence of the yield stress. To this end, they used a Carbopol aqueous solution and immersed a nylon sphere in it. The density of the sphere was slightly higher than the one of the solution. They observed that the sphere did not move (within 1-mm accuracy) after 4 months, and then they concluded that the yield stress is an “engineering reality.” Similar experiments were reported by Schurz (1990), who concluded that the yield stress is an “empirical reality.” In a humorous “Letter to the editor” in the Journal of Rheology about the article by Hartnett and Hu (1989), Astarita (1990) argued that the yield stress should actually be seen as a “sociological reality,” given the fact that, typically, graduate students must finish up their thesis research within a limited amount of time and, hence, cannot afford to wait much longer than 4 months.

Astarita (1990) also criticized the “everything flows” point of view and defended the opinion that the yield stress should be seen as just an assumption that may be useful or not, depending on the problem at hand, in the same fashion that the incompressibility assumption is handled for fluids.

Subsequently, Evans (1992) observed that the debate actually hinges on the meaning of the term “yield stress.” The classical definition of yield stress¹ excludes the possibility of experimental proof of its existence, since it would require an infinite observation time to show that the shear rate at any given stress is exactly zero.

To circumvent this impossibility, it has been proposed that the definition of yield stress be changed to “the highest stress at which no flow is detectable within the duration of the experiment.” Such pragmatic approach is unsatisfactory both from the logical and from the fundamental points of view, because, as explained by Evans (1992), it simply “defines the yield stress into existence.” The quantity, thus obtained is not the yield stress in the classical sense (neither it is the apparent yield stress as defined above), being clearly a function of the patience of the experimentalist and of the experimental protocol (Møller et al. 2006; Nguyen and Boger 1992).

Thus, Evans (1992) concludes by stating that the yield-stress debate resolves into a rather sterile issue of semantics, and hence, it should not concern rheologists. Surprisingly, however, after almost two decades, the controversy gives no sign of dying out. It is still possible to find in the recent literature claims for the existence of the yield stress based on experiments whose waiting time for a steady state is less than 1 h!

Interestingly, the two points of view are useful in practice, notwithstanding the “faith orientation” of the rheologist. If the necessary precautions are taken, the yield-stress assumption can be used to model real fluids, and it is known to provide a realistic description for a wide variety of engineering applications. Moreover, it is often the only feasible approach, since often disproportionately long experiments would be required to capture the high-viscosity Newtonian plateau (if such exists), during the course of which evaporation and other sources of artifacts inevitably occur. However, the assumption of zero flow below the (apparent?) yield stress should not be used in the prediction of processes whose characteristic times exceed the time scale used in the “yield stress” measurements. On the other hand, as far as computer simulations are concerned, there are practical difficulties in using classical yield-stress models such as the Bingham and Herschel–Bulkley ones, due to their intrinsic singularities. Very often “regularized versions” of the original viscosity function are used instead (e.g., Papanastasiou 1987). It is clear that there is a one-to-one correspondence between the regularization parameter that arises and the high-viscosity Newtonian plateau mentioned above (de Souza Mendes and Dutra 2004; Freitas et al. 2011).

A myriad of viscoplastic materials are thixotropic. As discussed by de Souza Mendes and Thompson (2012), the great majority of the models available to describe thixotropy (e.g., Moore 1959, Houska 1981, Barnes 1997, Mujumdar et al. 2002, Mewis and Wagner 2009) take a classical yield-stress equation as a starting point and introduce a structure parameter that intends to represent the microstructure state of the material. Structural elasticity and structural viscosity are introduced via additive stress terms. A few models, however, introduce the structural elasticity and structural viscosity via additive strain terms (Quemada 1999; Bautista et al. 1999; Yziquel et al. 1999; de Souza Mendes 2009, 2011)

All the models mentioned in the previous paragraph are suitable to yield-stress materials only, except the ones recently proposed by de Souza Mendes (2009, 2011), which were developed for apparent yield-stress fluids only.

Although it is consensual that in many cases apparent yield-stress fluids can be modeled as yield-stress materials, there are engineering situations where the nonzero flow below the apparent yield stress must be taken into account. For example, the size and shape of unyielded regions as predicted in numerical simulations are known to be a function of the regularization parameter (e.g., Liu et al. 2002), or, equivalently, of the finite value assumed for the zero-shear-rate viscosity. Another example is the fact that the time required for particles to settle in apparent yield-stress fluids may be very large but is not infinite as predicted by a yield-stress model. Therefore, there is a clear demand for thixotropy models that can predict such behavior, and this fact has not received the deserved attention in the literature.

In the present work, we propose a thixotropic elasto-viscoplastic model that accommodates both viewpoints discussed above in one single backbone. Depending upon the choice of the parameters, the model will possess either an apparent yield stress (and hence a finite zero-shear-rate viscosity) or a yield stress (hence predicting an infinite zero-shear-rate viscosity). A comparison between the two approaches is given for some representative cases. Within the framework of the model, simple explanations are given for the avalanche effect (Coussot et al. 2002b) and the shear banding phenomenon.

The model is applied to different shear flows of interest. In particular, the large-amplitude oscillatory shear flow is examined, the results being presented in the form of viscous Lissajous–Bowditch curves. These results constitute an important piece of information that is not presently available in the literature, namely a quantitative link between the Lissajous–Bowditch curve shapes and rheological effects such as elasticity, thixotropy, and yielding.

The model

This section describes the proposed constitutive model for thixotropic materials. One of the key assumptions is the existence of a microstructure whose state can be described by a single nonnegative scalar parameter. Let $\lambda$ be this parameter that expresses the structuring level of the microstructure. By definition, it ranges from 0 to $\lambda _{o}$, 0 corresponding to a completely unstructured state and $\lambda _{o}$ corresponding to a fully structured state. Moreover, $\lambda$ increases monotonically as the structuring level increases.

It is worth noting that the structure parameter $\lambda$ is perhaps the simplest possible description of the microstructure state. Nevertheless, it has been proved useful as a tool for representing and accounting for the structuring level of the material’s microstructure (Barnes 1997; Mewis and Wagner 2009).

Constitutive equation

The differential equation for the shear stress $\tau$ used in the present model is the same one presented in de Souza Mendes (2011), being derived with a basis on the mechanical analog shown in Fig. 1. In this figure, $G_{s}(\lambda )$ is the structural elastic modulus (i.e., the elastic modulus of the microstructure); $\eta _{s}(\lambda )$ is the structural viscosity, a function that describes the purely viscous response of the microstructure; $\eta _{\infty }$ is the viscosity corresponding to the completely unstructured state (i.e., to $\lambda =0$), i.e., the infinite-shear-rate viscosity; $\gamma _{e}$ is the elastic strain of the microstructure; $\gamma _{v}$ is the viscous strain; and $\gamma$ is the total strain. This analog corresponds to the Jeffreys (or Oldroyd-B) constitutive model for viscoelastic liquids, except that, here, both $G_{s}$ and $\eta _{s}$ are assumed to be functions of the structure parameter $\lambda$.

Fig. 1

The mechanical analog

It is interesting to note that, in the limit when $\eta _{s}\rightarrow \infty$, the analog in Fig. 1 becomes a representation of the Kelvin–Voigt constitutive model for viscoelastic solids (with a retardation time equal to $\eta _{\infty }/G_{s}$), except that $G_{s}$ depends on $\lambda$. Conversely, in the limit when $G_{s}\rightarrow \infty$ and $\eta _{s}$ is finite, the predicted behavior is the one of a purely viscous fluid (whose viscosity is $\eta _{v}\equiv \eta _{s}+\eta _{\infty }$).

Therefore, because $G_{s}$ and $\eta _{s}$ are allowed to vary with the structuring level, this analog encompasses all types of mechanical behavior, ranging from the purely elastic to the purely viscous, and including viscoelastic, viscoplastic, and elasto-viscoplastic behaviors. This multifaceted mechanical behavior is typical of many colloids as well as other structured materials.

Following the discussion and assumptions given by de Souza Mendes (2011), the following differential equation for the stress $\tau$ corresponds to the analog shown in Fig. 1:

$$ \tau+\theta_{1}\dot\tau=\eta_{v}(\dot\gamma+\theta_{2}\ddot\gamma) $$

(1)

where

$$\begin{array}{rll} \eta_{v}=\eta_{s}+\eta_{\infty}\,\,\,;\,\,\, \theta_{1}=\left(1-\frac{\eta_{\infty}}{\eta_{v}(\lambda)}\right)\frac{\eta_{v}(\lambda)}{G_{s}(\lambda)}\\ ;\,\,\,\theta_{2}=\left(1-\frac{\eta_{\infty}}{\eta_{v}(\lambda)}\right)\frac{\eta_{\infty}}{G_{s}(\lambda)} \end{array} $$

(2)

Thus, it is always true that $\theta _{2}<\theta _{1}$.

The equation for stress as given by Eq. (1) is not appropriate for materials that do not flow when $\tau <\tau _{y}$, i.e., for materials whose structural viscosity pertaining to the fully structured state is infinite. An equivalent form which encompasses this limiting case is

$$ \dot\gamma+\theta_{2}\ddot\gamma=\frac{\theta_{2}}{\eta_{\infty}}\left(\frac{\tau}{\theta_{1}}+\dot\tau\right). $$

(3)

For yield-stress materials, when the material is fully structured, the relaxation time $\theta _{1}$ also goes to infinity, and Eq. (3) reduces to the one for the classical Kelvin–Voigt viscoelastic solid model:

$$ \dot\gamma+\frac{\eta_{\infty}}{G_{s}}\ddot\gamma=\frac{\dot\tau}{G_{s}} $$

(4)

As discussed in more detail in our previous publications (de Souza Mendes 2009, 2011), Eq. (3) can be readily generalized into a frame-indifferent, tensorial equation for usage in complex, nonhomogeneous flows.

Viscosity function $\eta$

The viscosity function is defined as

$$ \eta\equiv\frac{\tau}{\dot\gamma} $$

(5)

As shown in de Souza Mendes (2011), $\eta$ can be written as a product of two functions, one carrying the elasticity information and the other the purely viscous character:

$$ \eta=\left[1-\left(1-\frac{\theta_{2}}{\theta_{1}}\right)\frac{\dot\gamma_{e}}{\dot\gamma} \right]\eta_{v} $$

(6)

where the term between brackets is the elastic contribution to the viscosity function $\eta$.

The structural elastic modulus function $G_{s}(\lambda )$

A physically reasonable function $G_{s}(\lambda )$ should ensure that both $\theta _{1}$ and $\theta _{2}$ are monotonically increasing functions of $\lambda$ (de Souza Mendes 2011). This criterion is satisfied, for example, if (but not only if) (a) $G_{s}(\lambda )=\mbox {constant}$ and (b) $G_{s}(\lambda )$ is smallest when the material is fully structured ($\lambda =\lambda _{o}$), and increases monotonically as $\lambda$ is decreased (de Souza Mendes 2011).

One possible choice for $G_{s}(\lambda )$ that is consistent with the above discussion is

$$ G_{s}=G_{o}\exp\left[m\left(\frac{1}{\lambda}-\frac{1}{\lambda_{o}}\right)\right] $$

(7)

where $G_{o}$ is the structural elastic modulus of the completely structured material and m is a dimensionless positive constant. Note that this function remains bounded and well defined when $\lambda _{o}\rightarrow \infty$ (yield-stress material).

The structural viscosity function $\eta _{s}(\lambda )$

Equation (6) shows that, when $\dot \gamma _{e}=0$, the viscosity function reduces to $\eta =\eta _{v}=\eta _{s}+\eta _{\infty }$. In particular, when the microstructure is in equilibrium, i.e., when the buildup and breakdown rates are equal, we have

$$ \eta_{\text{eq}}=\eta_{v}(\lambda_{\text{eq}}) $$

(8)

where $\eta _{\text {eq}}$ is the equilibrium or steady-state viscosity function and $\lambda _{\text {eq}}$ is the equilibrium or steady-state structure parameter. Therefore, the equilibrium viscosity function carries useful information regarding the dependence of $\eta$ and $\eta _{v}$ on the structure parameter $\lambda$ (de Souza Mendes 2009). For example, it is clear that both $\eta _{\text {eq}}$ and $\eta _{v}$ vary from $\eta _{\infty }$ to $\eta _{o}$, where $\eta _{o}$ is the equilibrium viscosity of the completely structured material ($\lambda =\lambda _{o}$), i.e., the zero-shear-rate viscosity. Thus, the function $\eta _{v}(\lambda )$ should map the range $[0,\lambda _{o}]$ into the range $[\eta _{\infty },\eta _{o}]$.

The above considerations suggest the following form for $\eta _{v}(\lambda )$:

$$ \eta_{v}(\lambda)=\eta_{\infty}e^{\lambda} $$

(9)

Equation (9) can be seen as the definition of the structure parameter:

$$ \lambda=\ln\left(\frac{\eta_{v}}{\eta_{\infty}}\right) $$

(10)

In particular, the equilibrium structure parameter $\lambda _{\text {eq}}$ is given by

$$ \lambda_{\text{eq}}=\ln\left(\frac{\eta_{\text{eq}}}{\eta_{\infty}}\right). $$

(11)

Therefore, as in the models previously proposed by de Souza Mendes (2009, 2011), once the flow curve is determined experimentally, the equilibrium structure parameter is also determined from Eq. (11). $\lambda _{\text {eq}}$ can be seen as a dimensionless equilibrium viscosity function.

From the above discussion, it is clear that the relationship between $\lambda _{o}$ and $\eta _{o}$ is just

$$ \lambda_{o}=\ln\left(\frac{\eta_{o}}{\eta_{\infty}}\right). $$

(12)

In contrast to the models proposed in de Souza Mendes (2009, 2011), the above definitions are tailored to render the present model capable to accommodate both materials that exhibit a yield stress, for which $\eta _{o}\rightarrow \infty$ and, hence, $\lambda _{o}\rightarrow \infty$, and fluids that possess an apparent yield stress, for which $\eta _{o}$ and $\lambda _{o}$ are very large but finite.

For the sake of simplicity and to avoid the introduction of additional nomenclature, in the remainder of this text, we will use the term “structural viscosity” to refer loosely both to $\eta _{s}$ and $\eta _{v}$, unless where a clear distinction between these two quantities is needed to avoid ambiguity or confusion.

The evolution equation for the structure parameter

The structure parameter $\lambda$ is now assumed to obey the following evolution equation:

$$ \frac{d\lambda}{dt}=\frac{1}{t_{\text{eq}}}\left[\left(\frac{1}{\lambda}-\frac{1}{\lambda_{o}}\right)^{a} - f(\tau)\lambda^{b}\right] $$

(13)

where $t_{\text {eq}}$ is the equilibrium time, a characteristic time of change (of $\lambda$), and a and b are positive dimensionless constants. In this equation, the first term on the right-hand side is a structure buildup term, while the second one is a breakdown term. It is worth noting that the forms chosen for the buildup and breakdown terms guarantee that the structure parameter will always be in the range $0\leq \lambda \leq \lambda _{o}$. Moreover, the term involving $\lambda _{o}$ conveniently vanishes in the limit when $\lambda _{o}\rightarrow \infty$ (yield-stress material).

We now observe that the function $f(\tau )$ can be obtained by applying Eq. (13) to equilibrium ($d\lambda /dt=0$):

$$ f(\tau)=\frac{1}{\lambda_{\text{eq}}(\tau)^{b}}\left(\frac{1}{\lambda_{\text{eq}}(\tau)}-\frac{1}{\lambda_{o}}\right)^{a} $$

(14)

The factor $\left (\frac {\tau }{\eta _{v}(\lambda )\dot \gamma }\right )^{c}$ that was introduced in $f(\tau )$ in the previous models of this kind (de Souza Mendes 2009, 2011) is here omitted, because it is actually inconsistent with the definition of $f(\tau )$. This is particularly interesting because it eliminates the parameter c from the formulation.

Combination of Eqs. (13) and (14) gives

$$ \frac{d\lambda}{dt}=\frac{1}{t_{\text{eq}}}\left[\left(\frac{1}{\lambda}-\frac{1}{\lambda_{o}}\right)^{a} -\left(\frac{\lambda}{\lambda_{\text{eq}}(\tau)}\right)^{b}\left(\frac{1}{\lambda_{\text{eq}}(\tau)}-\frac{1}{\lambda_{o}}\right)^{a} \right] $$

(15)

The above evolution equation for $\lambda$ preserves the same features of the ones employed by de Souza Mendes (2009, 2011), viz., it uses the steady-state experimental information (i.e., the flow curve) as an input for the evolution equation, because the function $\lambda _{\text {eq}}(\tau )$ used is determined from the observed material behavior.

To obtain $\lambda _{\text {eq}}(\tau )$, we first have to determine the value of $\eta _{\text {eq}}$ corresponding to the present value of the stress $\tau$ (see Eq. (11)). Because $\eta _{\text {eq}}$ is given as a function of the shear rate $\dot \gamma$ (see “The equilibrium viscosity function”), then $\eta _{\text {eq}}(\tau )$ is obtained through the solution of

$$ \tau=\eta_{\text{eq}}(\dot\gamma_{\text{eq}})\dot\gamma_{\text{eq}} $$

(16)

where $\dot \gamma _{\text {eq}}$ (also determined from Eq. (16)) is the equilibrium shear rate that would be attained if the stress $\tau$ were imposed to the material until steady state (or equilibrium) conditions were achieved.

As discussed by de Souza Mendes (2011), Eq. (15) can also be easily adapted for usage in complex, nonhomogeneous flows, just by interpreting $d\lambda /dt$ as the material time derivative of $\lambda$.

The equilibrium viscosity function

The equilibrium viscosity function employed in the present model must be consistent with the above physical arguments and related definitions. The function proposed by (de Souza Mendes 2009, 2011) is an appropriate choice, because it accommodates both yield-stress materials and apparent yield-stress fluids. It is given by

$$\begin{array}{rll}\eta_{\text{eq}}(\dot\gamma)=\left[1-\exp\left(-\frac{\eta_{o}\dot\gamma}{\tau_{y}}\right)\right] \left\{\frac{\tau_{y}-\tau_{yd}}{\dot\gamma}e^{-{\dot\gamma}/{\dot\gamma_{yd}}}\right.\\&\left. \qquad{\kern9pc}+\frac{\tau_{yd}}{\dot\gamma}+K\dot\gamma^{n-1}\right\}+\eta_{\infty}\\ \end{array} $$

(17)

Equation (17) is plotted in Fig. 2. The parameter $\tau _{y}$ is the static yield stress, $\tau _{yd}$ the dynamic yield stress, $\dot \gamma _{yd}$ a shear rate that marks the transition in stress from $\tau _{y}$ to $\tau _{yd}, K$ the consistency index, and n the power-law index.

Fig. 2

The steady-state shear stress, viscosity, and structure parameter as a function of the shear rate. Note that the scales for $\eta _{\text {eq}}$ and $\lambda _{\text {eq}}$ were chosen such that both quantities share the same curve

Figure 2 illustrates that, in addition to $\dot \gamma _{yd}$, three other shear rates mark important transitions in the flow curve, namely $\dot \gamma _{o}, \dot \gamma _{1},$ and $\dot \gamma _{2}$. These shear rates are given by (de Souza Mendes 2009):

$$ \dot\gamma_{o}=\frac{\tau_{y}}{\eta_{o}}\ ,\ \ \dot\gamma_{1}=\left(\frac{\tau_{yd}}{K}\right)^{1/n}, \ \ \dot\gamma_{2}=\left(\frac{\eta_{\infty}}{K}\right)^{1/n-1} $$

(18)

Equation (17) is capable of predicting all the features observed in steady-state data for viscoplastic materials. For the special case of yield-stress materials ($\eta _{o}\rightarrow \infty$), it reduces to a modified version of the Herschel–Bulkley viscosity function:

$$ \eta_{\text{eq}}(\dot\gamma)=\frac{\tau_{y}-\tau_{yd}}{\dot\gamma}e^{-{\dot\gamma}/{\dot\gamma_{yd}}}+\frac{\tau_{yd}}{\dot\gamma}+K\dot\gamma^{n-1}+\eta_{\infty} $$

(19)

Instead of using the Papanastasiou exponential term (term between square brackets in Eq. (17)) to generate the Newtonian plateau, it is also possible to use the following term, inspired in the regularization procedure proposed by Bercovier and Engelman (1980) for the Bingham plastic viscosity function:

$$\begin{array}{rll} \eta_{\text{eq}}(\dot\gamma)=\left[\frac{\eta_{o}\dot\gamma}{\sqrt{(\eta_{o}\dot\gamma)^{2}+\tau_{y}^{2}}}\right]\left\{\frac{\tau_{y}-\tau_{yd}} {\dot\gamma}e^{-{\dot\gamma}/{\dot\gamma_{yd}}}\right.\\ &&\left.\qquad{\kern8.5pc}+\frac{\tau_{yd}}{\dot\gamma}+K\dot\gamma^{n-1}\right\}+\eta_{\infty}\\ \end{array} $$

(20)

In addition, the expression between the curly brackets in Eqs. (17) and (20), a modified Herschel–Bulkley viscosity function, can be replaced with any one of the viscosity functions for yield-stress materials available in the literature. One example is the viscosity function proposed by Robertson and Stiff (1976), which, modified to accommodate two yield stresses, gives

$$\begin{array}{rll}\eta_{\text{eq}}(\dot\gamma)=\left[1-\exp\left(-\frac{\eta_{o}\dot\gamma}{\tau_{y}}\right)\right] \frac{K}{\dot\gamma}\\ &{\kern3pc}\times\left\{{}\left(\frac{(\tau_{y}-\tau_{yd})e^{-{\dot\gamma}/{\dot\gamma_{yd}}}{}+\tau_{yd}}{K}\right)^{1/n}+\dot\gamma\right\}^{n}{} +{}\eta_{\infty}\\ \end{array} $$

(21)

or

$$\begin{array}{rll}\eta_{\text{eq}}(\dot\gamma)=\left[\frac{\eta_{o}\dot\gamma}{\sqrt{(\eta_{o}\dot\gamma)^{2}+\tau_{y}^{2}}}\right] \frac{K}{\dot\gamma} \\ &{\kern3pc}\times\left\{{}\left( \frac{(\tau_{y}-\tau_{yd})e^{-{\dot\gamma}/{\dot\gamma_{yd}}}{}+\tau_{yd}}{K}\right)^{1/n}{} +\dot\gamma\right\}^{n} +{}\eta_{\infty}\\ \end{array} $$

(22)

The Robertson–Stiff viscosity function is often used in the petroleum industry. It predicts a sharper transition into the power-law range of the flow curve, relative to the Herschel–Bulkley function.

Any of the above viscosity functions is compatible with the present model. The results presented in “Results and discussion” were obtained with Eq. (17), plotted in Fig. (2).

It is worth noting that all controlled-rate rheometers have a resolution for the shear rate, which may not be low enough to reach the range where the flow curve for an apparent yield-stress fluid differs from the one for a yield-stress material (see Fig. 2). In this case, it will not be possible to distinguish an apparent yield-stress fluid from a yield-stress material.

Summary of the model and evaluation of the parameters

In summary, Eqs. (2), (3), (7), (9), (11), (15), and (17) compose the thixotropy model proposed in this paper. These equations are gathered as follows:

$$ \theta_{1}=\left(1-\frac{\eta_{\infty}}{\eta_{v}(\lambda)}\right)\frac{\eta_{v}(\lambda)}{G_{s}(\lambda)}\ \ \ ;\ \ \ \theta_{2}=\left(1-\frac{\eta_{\infty}}{\eta_{v}(\lambda)}\right)\frac{\eta_{\infty}}{G_{s}(\lambda)} $$

(2)

$$ \dot\gamma+\theta_{2}\ddot\gamma=\frac{\theta_{2}}{\eta_{\infty}}\left(\frac{\tau}{\theta_{1}}+\dot\tau\right) $$

(3)

$$ G_{s}=G_{o}e^{m\left(\frac{1}{\lambda}-\frac{1}{\lambda_{o}}\right)} $$

(7)

$$ \eta_{v}(\lambda)=\eta_{\infty}e^{\lambda} $$

(9)

$$ \lambda_{\text{eq}}(\tau)=\ln\left(\frac{\eta_{\text{eq}}(\tau)}{\eta_{\infty}}\right) $$

(11)

$$ \frac{d\lambda}{dt}=\frac{1}{t_{\text{eq}}}\left[\left(\frac{1}{\lambda}-\frac{1}{\lambda_{o}}\right)^{a} -\left(\frac{\lambda}{\lambda_{\text{eq}}(\tau)}\right)^{b}\left(\frac{1}{\lambda_{\text{eq}}(\tau)}-\frac{1}{\lambda_{o}}\right)^{a} \right] $$

(15)

$$\begin{array}{rll} \eta_{\text{eq}}(\dot\gamma)=\left[1-\exp\left(-\frac{\eta_{o}\dot\gamma}{\tau_{y}}\right)\right] \left\{\frac{\tau_{y}-\tau_{yd}}{\dot\gamma}e^{-{\dot\gamma}/{\dot\gamma_{yd}}}+\frac{\tau_{yd}} {\dot\gamma}\right.\\\left.+K\dot\gamma^{n-1}{\vphantom{\left\{\frac{\tau_{y}-\tau_{yd}}{\dot\gamma}e^{-{\dot\gamma}/{\dot\gamma_{yd}}}+\frac{\tau_{yd}} {\dot\gamma}\right.}}\right\}+\eta_{\infty} \\ \end{array} $$

(17)

Thus, comparing the present model with the ones previously proposed by de Souza Mendes (2009, 2011), it is seen that the parameters that appear in the three models are the same, except that the evolution equation has one parameter fewer. For the special case of yield-stress materials, the number of parameters is further reduced, since in this case $\eta _{o}$ is infinite.

Specifically, the parameters are $\eta _{o}, \eta _{\infty }, \tau _{y}, \tau _{yd}, \dot \gamma _{yd}, K,$ $n, G_{o}, m, t_{\text {eq}}, a,$ and b.

It is interesting to compare the number of parameters of the present model with the number of parameters employed in other thixotropic elasto-viscoplastic models available in the literature. However, this comparison should be carried out at equivalent level of generality and predictive capability. To this end, we should use a simplified version of the present model in which $\tau _{y}=\tau _{yd}$ (one yield stress only); $\eta _{o}\rightarrow \infty$ (particularization to yield-stress materials only); and $a=b=1$ as usually done in the thixotropic elasto-viscoplastic models available in the literature. This simplified form involves seven parameters only ($\eta _{\infty }, \tau _{yd}, K, n, G_{o}, m$, and $t_{\text {eq}}$), while preserving the main features of the complete model that lend it a superior robustness. The model proposed by Dullaert and Mewis (2006), for example, possesses eight parameters.

The flow curve parameters can, in principle, be determined from a least-squares fit to steady-state data, except $\eta _{\infty }$, which, together with $G_{o}$, is determined directly from small-amplitude oscillatory tests (see “Analytical solutions”).

The parameters of the evolution equation, $t_{\text {eq}},a$, and b, can be determined with tests involving step changes in shear stress. An initial stress $\tau _{i}$ is imposed and kept fixed until a steady state is achieved. Then, at time $t=0$, a step change to $\tau _{f}$ is imposed, and the shear rate (or viscosity) is obtained as a function of time. According to the theoretical development detailed in de Souza Mendes (2009, 2011), when the stress is held constant ($\dot \tau =0$), after a short transient of the order of $\theta _{2}(\lambda _{i})$, the measured viscosity $\tau _{f}/\dot \gamma (t)$ becomes equal to $\eta _{v}$, i.e., there is no elastic contribution.² Therefore, this experiment provides a direct means of measuring $\lambda (t)=\ln [\tau _{f}/\dot \gamma (t)\eta _{\infty }]$ (see Eq. (9)). With the experimental data, the derivative $d\lambda /dt$ is firstly evaluated (via a second- or fourth-order finite difference scheme, for example), and then the parameters $t_{\text {eq}}, a$, and b are obtained via a curve fitting of the data to Eq. (15).

An alternate experiment to determine $t_{\text {eq}}, a$, and b—which also gives the remaining parameter, m—is described in the end of “Numerical results for an imposed sinusoidal stress.”

Results and discussion

To demonstrate the predictive capability of the model, this section presents numerical solutions of Eqs. (1) (or (3)), (2), (7), (9), (11), (15), and (17) for some selected transient flows. For all flows investigated, the initial condition is that of a relaxed ($\tau =0$ for $t<0$), at rest ($\dot \gamma =0$ for $t<0$), and fully structured material ($\lambda =\lambda _{o}$ for $t<0$). Since numerical solutions preclude the possibility of imposing an exactly infinite initial condition, for the cases pertaining to the yield-stress material, $\lambda (0)$ was set to a very large but finite number, namely $\lambda (0)=695$, which corresponds to a zero-shear-rate viscosity of the order of $10^{300}$. Everywhere else in the formulation for the cases involving the yield-stress materials, both $\lambda _{o}$ and $\eta _{o}$ were set to infinity.

The results are presented in dimensionless form, following the ideas described elsewhere (de Souza Mendes 2007). The characteristic shear rate employed in the scaling is $\dot \gamma _{1}$ (defined in Eq. (17), see also Fig. 2), whereas the characteristic shear stress is the dynamic yield stress $\tau _{yd}$.

All the results below pertain to the following set of parameter values: $n=0.5; \tau _{y}/\tau _{yd}{}={}2; \dot \gamma _{yd}/\dot \gamma _{1}{}={}10^{-4}; \eta _{\infty }\dot \gamma _{1}/\tau _{yd}{}={}10^{-2}; G_{o}/\tau _{yd}{}={}1; m{}={}1; a=1; b=1$.

Constant shear rate flows

Effect of the imposed shear rate $\dot {\gamma }_f$

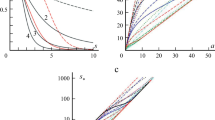
Figure 3 shows the stress evolution for a material that, when $t<0$, is relaxed, at rest, and fully structured. At time $t=0$, a constant shear rate $\dot {\gamma }_f$ is suddenly imposed. The value of the dimensionless equilibrium time is $t_{\text {eq}}\dot \gamma _1=100$. For each value of $\dot {\gamma }_f$, there are two evolution curves: a red one for a yield-stress material ($\eta _{o}\dot \gamma _{1}/\tau _{yd}\rightarrow \infty$) and a black one for an apparent yield-stress fluid ($\eta _{o}\dot \gamma _{1}/\tau _{yd}=10^{7}$). A wide range of constant shear rates is covered, from ${\dot {\gamma }_f}/{\dot {\gamma }_1}=10^{-7}$ to ${\dot {\gamma }_f}/{\dot {\gamma }_1}=10^{5}$.

Fig. 3

Time evolution of the stress for constant rate flows—effect of the imposed shear rate

At $t=0$, when the shear rate is imposed, $\tau =\eta _{\infty }\dot {\gamma }_f$ because at this moment the elastic microstructure is still relaxed and does not contribute to the total stress. At early times, the stress is below the static yield stress, and hence, the material is still fully structured. Thus, there is no creep at all in the case of the yield-stress material and essentially no creep in the case of the apparent yield-stress fluid. Therefore, the elastic deformation is given by $\dot {\gamma }_ft$, i.e., it increases linearly with time. Consequently, at early times, the total stress is given by $\tau =\eta _{\infty }\dot {\gamma }_f+G_0\dot {\gamma }_ft$, explaining the linear behavior observed at early times.

At the moment when the stress exceeds the static yield stress, the breakdown process is activated, because $\lambda _{\text {eq}}$ jumps from $\lambda _{o}$ to $\lambda _{\text {eq}}(\tau _{y})<<\lambda _{o}$. However, due to thixotropic effects, there is a finite time interval before the structuring level decreases sufficiently to cause perceptible effects. During this time lag, therefore, the material continues behaving elastically, and the stress keeps increasing linearly with time, reaching values that may be much higher than the static yield stress. The structuring level keeps decreasing at a very fast rate and finally reaches values such that the structural viscosity $\eta _{v}$ becomes low enough to allow significant flow, while the structural elastic modulus $G_{s}$ becomes large enough to reduce the elastic response of the material. Consequently, the stress decreases—initially very abruptly—and approaches asymptotically an equilibrium value equal to $\eta _{\text {eq}}(\dot {\gamma }_f)\dot {\gamma }_f$.

Stress undershoots are observed for the apparent yield-stress fluid at an imposed rate of ${\dot {\gamma }_f}/{\dot {\gamma }_1}=0.01$ and for the yield-stress material when ${\dot {\gamma }_f}/{\dot {\gamma }_1}$ is within the range 0.01–10. The undershoot occurs if, after the major microstructure breakdown, the structuring level attains values lower than the steady state structuring level, $\lambda _{\text {eq}}(\eta _{\text {eq}}(\dot \gamma _{f})\dot \gamma _{f})$. In this situation, elasticity is not important, and the viscosity $\eta \simeq \eta _{v}$ clearly attains values below $\eta _{\text {eq}}(\dot \gamma _{f})$, causing the stress undershoot.

The positive-slope portion of the flow curve, right before the power-law region and delimited by $\tau _{yd}$ and $\tau _{y}$, is attainable only if approached from above, i.e., if the microstructure reaches equilibrium after a structuring process. Therefore, it cannot be attained with creep (imposed stress) tests with the material initially fully structured. However, if we impose a constant shear rate that falls within this region, we will obtain a point of the flow curve, after a transient behavior involving a stress overshoot followed by an undershoot. A decaying sequence of overshoots followed by undershoots, i.e., a decaying oscillating approach to steady state can, in principle, also be predicted by the model for lower values of $t_{\text {eq}}$.

Stress overshoots are observed for all cases investigated, except for the lowest shear rate value imposed, namely ${\dot {\gamma }_f}/{\dot {\gamma }_1}=10^{-7}$. For such a low shear rate, the elastic stress growth is so slow that the time lag is not long enough to allow a stress overshoot.

Shear banding

Note that for ${\dot {\gamma }_f}/{\dot {\gamma }_1}=10^{-7}$, there is no corresponding curve for the yield-stress material, because while this value of the imposed shear rate falls in the Newtonian region of the flow curve of the apparent yield-stress fluid, it falls on the negative-slope portion of the flow curve of the yield-stress material (red dotted line in Fig. 2). Therefore, ${\dot {\gamma }_f}/{\dot {\gamma }_1}=10^{-7}$ corresponds to an equilibrium state for the apparent yield-stress fluid and to an unattainable state for the yield-stress material.

The unattainability of the negative-slope points of the flow curve is well documented in the literature (e.g., Coussot et al. 2002a, Olmsted 2008, Møller et al. 2008). The present model also predicts that this region of the flow curve is unattainable, as explained next with the aid of Fig. 2.

Let us imagine an experiment in which we impose a shear rate that falls on the negative-slope region of the flow curve, e.g., the central yellow point in Fig. 2. The measured stress is $\tau$, which necessarily lies between $\tau _{yd}$ and $\tau _{y}$. Note that at this point, the driving potential for changes in structuring level is not null, i.e., $\lambda _{\text {eq}}(\tau )$ has two possible values that drive the structural state away from the one corresponding to this point. One of these values corresponds to the structural state found at the yellow point on the right side. The other value is slightly below $\lambda _{o}$ (essentially fully structured), which corresponds to the yellow point on the left side for the apparent yield-stress fluid and to $\dot \gamma =0$ for the yield-stress material (fully structured).

Note that the above discussion leads to a simple and novel explanation for the shear banding phenomenon (Callaghan 2008; Dhont and Briels 2008; Li and Li 2006, 2007; Bailey et al. 2007; Manneville 2008; Møller et al. 2008; Olmsted 2008; Wakeda et al. 2008; Fall et al. 2010; Raudsepp et al. 2010; Schall and van Heckem 2010; Fielding et al. 2009; Martens et al. 2012) observed in steady flows with a homogeneous stress $\tau$: the material in one of the bands remains fully structured while, in the other band, it flows steadily with a shear rate corresponding to the yellow point on the right-hand side.

Moreover, it is not difficult to show that the thickness of the fully structured band, say $H_{fs}$, is given by

$$ \frac{H_{fs}}{H}=\frac{\dot\gamma_{\text{high}}-\dot\gamma_{\text{imposed}}}{\dot\gamma_{\text{high}}-\dot\gamma_{fs}}\simeq\frac{\dot\gamma_{\text{high}}-\dot\gamma_{\text{imposed}}}{\dot\gamma_{\text{high}}} $$

(23)

where H is the total gap, $\dot \gamma _{\text {high}}$ is the shear rate at the right-hand side yellow point, $\dot \gamma _{fs}$ is either zero (yield-stress material) or it is the shear rate at the left-hand side yellow point, which is extremely low. Thus, this equation shows that, for the example, as discussed above, ${H_{fs}}\simeq {H}$, since $\dot \gamma _{\text {high}}>>\dot \gamma _{\text {imposed}}$. That is, the thickness of the layer under high shear rate (namely ${H}-{H_{fs}}$) is negligibly small, and hence, it will seem like a situation of wall slip. For imposed shear rates still within the negative-slope region but closer to the local minimum of the flow curve (which delimits on the right the unattainable region), $\dot \gamma _{\text {high}}$ will be of the order of $\dot \gamma _{\text {imposed}}$, and hence, the two bands will be of comparable thicknesses.

It is important to observe that the ability of the model to predict the unattainability of the negative-slope region of the flow curve is a direct consequence of the assumption that the breakdown term of the evolution equation for $\lambda$ is a function of the stress.

Effect of the initial condition for the structure parameter $\lambda$

It is also observed in Fig. 3 that the time lag mentioned above is much longer for the yield-stress material, i.e., the yield-stress material stays longer in the linear elastic range. Moreover, the microstructure breakdown occurs more abruptly.

These different trends are easily understood if we recall that, for the yield-stress material, the initial value of the structure parameter was set to $\lambda (0)=695$, while for the apparent yield-stress fluid analyzed $\lambda (0)=\lambda _{o}=\ln (\eta _{o}/\eta _{\infty })=20.72$. Therefore, even though for the yield-stress material the breakdown term of Eq. (15) is always larger (and hence, so is the intensity of $d\lambda /dt$), it takes much longer for the structure parameter to decrease sufficiently and reach the level in which the departure from the elastic regime occurs.

From the above discussion, it becomes clear that the prediction of the stress overshoot is unique for apparent yield-stress fluids but unfortunately, in the case of the yield-stress material, is a strong function of the finite value guessed for the initial structure parameter. In practice, this should not represent a problem, because it is, in principle, possible to choose an appropriate guess that will reproduce the overshoot observed experimentally, but, theoretically, this should be regarded as a weakness of the model.

Effect of the equilibrium time $t_{\text {eq}}$

Figures 4 and 5 show the influence of the equilibrium time, $t_{\text {eq}}$, on the stress evolution for an apparent yield-stress fluid and a yield-stress material, respectively. The imposed shear rate is $\dot {\gamma }_f/\dot {\gamma }_1=1,000$, and there are three curves, pertaining to $t_{\text {eq}}\dot \gamma _1=\{0, 0.01, 100\}$.

Fig. 4

Time evolution of the stress for constant rate flows—effect of the equilibrium time. $\eta _{o}\dot \gamma _{1}/\tau _{yd}=10^{7}$

Fig. 5

Time evolution of the stress for constant rate flows—effect of the equilibrium time. $\eta _{o}\dot \gamma _{1}/\tau _{yd}\rightarrow \infty$

The value $t_{\text {eq}}\dot \gamma _1=0\Leftrightarrow \frac {d\lambda }{dt}\rightarrow \infty$ represents the important limit of no thixotropy, i.e., the limit in which the microstructure changes occur instantaneously. When $t_{\text {eq}}\dot \gamma _1=0$, the stress evolution is given by

$$\begin{array}{rll}\tau=\dot{\gamma}_f\left\{\eta_{\infty}+{\vphantom{\left. {\kern16pt}\times\left[1-\mathrm{exp}\left(-\frac{G_{s} (\lambda_{\text{eq}}(\tau(\dot{\gamma}_f)))} {\eta_{\text{eq}}(\dot{\gamma}_f)-\eta_{\infty}}t\right)\right]\right\}}}[\eta_{\text{eq}}(\dot{\gamma}_f)-\eta_{\infty}]\right.\\&& \left. {\kern2.5pc}\times\left[1-\mathrm{exp}\left(-\frac{G_{s} (\lambda_{\text{eq}}(\tau(\dot{\gamma}_f)))} {\eta_{\text{eq}}(\dot{\gamma}_f)-\eta_{\infty}}t\right)\right]\right\}, \end{array} $$

(24)

The steady-state limit ($t\rightarrow \infty$) is clearly given by $\eta _{\text {eq}}(\dot {\gamma }_f)\dot {\gamma }_f$. This equation—which, of course, reproduces the numerical solutions for $t_{\text {eq}}\dot \gamma _1=0$ shown in Figs. 4 and 5—illustrates that no overshoot is expected in the absolute absence of thixotropy. Since some stress overshoot is observed experimentally for many yield-stress materials, including some that are usually assumed to be nonthixotropic (e.g., Carbopol solutions), this result supports the viewpoint that some level of thixotropy is always present in structured fluids, i.e., the microstructure response to changes in stress is never exactly instantaneous.

Figures 4 and 5 illustrate that the stress overshoots increase as $t_{\text {eq}}$ is increased. This is an expected result, since, as discussed above, the stress overshoots are due to thixotropy. Hence, the slower the response of the microstructure to stress changes (i.e., the larger is $t_{\text {eq}}$), the larger the stress overshoot.

Comparing Figs. 4 and 5, we see that for $t_{\text {eq}}\dot \gamma _1=100$, the yield-stress material and the apparent yield-stress fluid reach the steady state at about the same time, while for $t_{\text {eq}}\dot \gamma _1=0.01$, the time necessary for reaching the steady state is much shorter for the apparent yield-stress fluid.

Constant shear stress flows

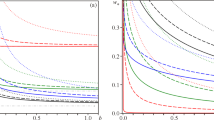
Figure 6 shows the shear rate evolution for a material that is at rest, relaxed, and fully structured when $t<0$, and, at time $t=0$, a constant shear stress $\tau _f$ is suddenly imposed. The value of the equilibrium time is $t_{\text {eq}}\dot \gamma _1=100$. For each value of $\tau _f$ imposed, this figure shows two curves, the red one corresponding to yield-stress material and the black one corresponding to the apparent yield-stress fluid. The range of imposed shear stress values goes from ${\tau _f}/{\tau _{yd}}=10^{-2}$ to $10^{2}$.

Fig. 6

Time evolution of the shear rate for constant stress flows—effect of the imposed shear stress

It is worth noting that, although the dimensionless yield stress is set at ${\tau _{y}}/{\tau _{yd}}=2$, for the apparent yield-stress fluid, the actual threshold value—which occurs between $\dot {\gamma }_{o}$ and ${\dot {\gamma }_{yd}}$ (see Fig. 2)—is 1.9855. Therefore, at ${\tau _{f}}/{\tau _{yd}}=2$, the material has already yielded.

When the material is initially fully structured and then a finite constant stress is imposed, analogously to what happens in a constant shear rate experiment, at time $t=0^{+}$, the microstructure is still relaxed, and hence, the shear rate at time $t=0^{+}$ is just equal to ${\tau _f}/{\eta _{\infty }}$, which explains the first plateau region in all curves of Fig. 6.

Analytical solution for the fully structured state

Actually, Eq. (1) can be integrated analytically, giving an exact solution for the situation in which the material is fully structured:

$$ \dot{\gamma}(t)=\frac{\tau_f}{\eta_{\infty}}\left\{\frac{\eta_{\infty}}{\eta_{o}}+\left(1-\frac{\eta_{\infty}}{\eta_{o}}\right)\exp\left[-\frac{\eta_{o}}{\eta_{o}-\eta_{\infty}}\frac{G_{o}}{\eta_{\infty}}t\right]\right\} $$

(25)

Equation (25) gives exactly the shear rate evolution for all cases where the imposed stress is smaller than the static yield stress. Moreover, for stresses beyond the static-yield stress, it is also exact while the microstructure is still intact, at early times. For the yield-stress material, Eq. (25) clearly reduces to

$$ \dot{\gamma}(t)=\frac{\tau_f}{\eta_{\infty}}\exp\left[-\frac{G_{o}}{\eta_{\infty}}t\right] $$

(26)

which describes the behavior of a Kelvin–Voigt solid. Therefore, for yield-stress materials, the shear rate goes to zero exponentially, with a dimensionless decay time scale of $\dot \gamma _{1}\eta _{\infty }/G_{o}$.

For the apparent yield-stress fluid, the solution initially coincides with the one for the yield-stress material, because $1/\eta _{o}$ is negligible when compared to $1/\eta _{\infty }$. However, once the exponential term decays to zero, the shear rate approaches $\tau _{f}/\eta _{o}$ asymptotically, instead of going to zero as it happens with the yield-stress material.

For $t_{\text {eq}}\dot \gamma _1=100$, Fig. 6 shows that, after the exponential shear rate decay, the yield-stress material remains at rest, while the apparent yield-stress fluid keeps flowing steadily at the always very low shear rate $\tau _{f}/\eta _{o}$.

The avalanche effect

For imposed yield-stress values below the static yield stress, nothing else happens. However, when the imposed shear stress is above the static yield stress, the unstructuring effects eventually become appreciable, when Eq. (25) ceases to be valid. At this moment, the shear rate suddenly undergoes a very sharp increase and shortly after steady flow conditions are reached. The final steady-state shear rate is equal to $\tau _{f}/\eta _{v}(\lambda _{\text {eq}}(\tau _{f}))=\tau _{f}/\eta _{\text {eq}}(\tau _{f})$. For the yield-stress material, the shear rate increase is sharper, and the final steady state is reached a little later.

The time period during which the yield-stress material remains at rest (and during which the apparent yield-stress fluid flows steadily at a very low shear rate) is a strongly decreasing function of the imposed stress. For a stress just above the static yield stress, this time lag can be extremely long. For this reason, the constant shear stress experiment suffers from the same limitation as any other technique for determining unequivocally the yield stress: as discussed in the “Introduction” section, the experimentalist can never be sure if, had they waited a little longer, yielding would have been observed. However, this experiment is perhaps the most suitable for determining whether or not the material will yield when subjected to a certain stress level during a period of time that is representative of a given engineering application.

The phenomenon involving the time lag between the application of the stress and the occurrence of yielding was firstly investigated by Coussot et al. (2002a), who denominated it the avalanche effect. From the above discussion, it becomes clear that the present model is capable of predicting appropriately this experimentally observed phenomenon.

We have seen that the time lag before yielding is a very strong function of the stress level, and that when the imposed stress is just above the static yield stress, the time lag may be enormous. This is a well-known experimental fact that is predicted quite well by the present model. A conclusion that is commonly drawn from this experimental observation is that the yield stress is a time-dependent quantity, which requires a major departure from the classical and intuitive concept of yield stress. The present results represent a plausible explanation for these experimental facts that preserves the classical yield-stress concept.

Effect of the equilibrium time $t_{\text {eq}}$

For all cases shown in Fig. 6 pertaining to the apparent yield-stress fluid, appreciable unstructuring occurs only after the asymptotic value $\tau _{f}/\eta _{o}$ has been reached. However, for lower values of $t_{\text {eq}}$, the effect of unstructuring effects may become important before it is reached.

Figures 7 and 8 show the influence of the equilibrium time, $t_{\text {eq}}$, on the shear rate evolution in time for an apparent yield-stress fluid and a yield-stress material, respectively. The imposed shear stress is fixed at $\tau _f/\tau _{yd}=5$, and the equilibrium time values examined are $t_{\text {eq}}\dot \gamma _1=\{0, 0.01, 100\}$.

Fig. 7

Time evolution of the shear rate for constant stress flows—effect of the equilibrium time. $\eta _{o}\dot \gamma _{1}/\tau _{yd}=10^{7}$

Fig. 8

Time evolution of the shear rate for constant stress flows—effect of the equilibrium time. $\eta _{o}\dot \gamma _{1}/\tau _{yd}\rightarrow \infty$

In the absence of thixotropy ($t_{\text {eq}}\dot \gamma _1=0$), the response to the imposed stress is instantaneous. Hence, at $t=0$, the structure parameter jumps from $\lambda _{o}$ to $\lambda _{\text {eq}}(\tau _{f})$ and remains constant thereafter. Therefore, Eq. (1) also admits an analytical solution, which has the same form of Eq. (25), with the structuring level-dependent quantities being evaluated at $\lambda _{\text {eq}}(\tau _{f})$:

$$\begin{array}{rll}\dot{\gamma}(t)=\frac{\tau_f}{\eta_{\infty}}\left\{\frac{\eta_{\infty}}{\eta_{\text{eq}}(\tau_{f})}+\left(1-\frac{\eta_{\infty}}{\eta_{\text{eq}}(\tau_{f})}\right)\right.\\&& \left.{\kern48pt} \exp\left[-\frac{\eta_{\text{eq}}(\tau_{f})}{\eta_{\text{eq}}(\tau_{f})-\eta_{\infty}}\frac{G_{s}(\lambda_{\text{eq}}(\tau_{f}))}{\eta_{\infty}}t\right]\right\} \end{array} $$

(27)

This solution is of course valid for both yield-stress materials and apparent yield-stress fluids, and reproduces exactly the numerical solution shown in Figs. 7 and 8 for $t_{\text {eq}}\dot \gamma _1\,=\,0$. Since the avalanche effect is clearly a consequence of thixotropy, it is not observed in the curve for $t_{\text {eq}}\dot \gamma _1=0$.

Figures 7 and 8 illustrate that the time lag before the flow restart increases with the equilibrium time $t_{\text {eq}}$, as expected. It is interesting to observe in Fig. 7 that, for the apparent yield-stress material and $t_{\text {eq}}\dot \gamma _1=0.01$, the unstructuring effects become appreciable, while the viscoelastic exponential decay is still far from being complete, and hence, before attaining very low values, the shear rate abruptly starts to increase sharply and then levels off at its steady-state value. For the yield-stress material (Fig. 8) at this same value of the equilibrium time ($t_{\text {eq}}\dot \gamma _1=0.01$), another trend is observed, namely the flow stops for a short period after the viscoelastic exponential decay, then restarts with an extremely sharp increase in shear rate, and finally levels off at its steady-state value somewhat later than in the case of the apparent yield-stress fluid. The period during which the material remains at rest before restarting to flow is a function of the choice of $\lambda (0)$, as discussed in the previous section.

Oscillatory flows

In this section, we illustrate the model predictive capability for oscillatory flows. Before presenting the numerical results, however, it is worth presenting some analytical solutions which will prove useful in the analysis of the results.

Analytical solutions

If a sinusoidal shear stress

$$ \tau(t)=\tau_{a}\sin(\omega t) $$

(28)

is imposed ($\tau _{a}$ is the stress amplitude and $\omega$ is the oscillation frequency), then Eq. (3) becomes

$$ \ddot\gamma+\frac{1}{\theta_{2}}\dot\gamma=\frac{1}{\theta_{1}}\frac{\tau_{a}}{\eta_{\infty}}\sin(\omega t)+\omega\frac{\tau_{a}}{\eta_{\infty}}\cos(\omega t) $$

(29)

Considering that initially the material is at rest ($\dot \gamma (0)=0$), this equation admits the following solution for the case of constant $\theta _{1}$ and $\theta _{2}$:

$$ \dot\gamma(t)=\dot\gamma_{a}[\sin(\omega t+\phi)-e^{-t/\theta_{2}}\sin\phi] $$

(30)

where $\dot \gamma _{a}$ is the shear rate amplitude and $\phi$ is the phase shift, given by

$$\begin{array}{rll} \dot\gamma_{a}&{}={}&\frac{\tau_{a}}{\eta_{\infty}} \left({}\frac{1}{1+\omega^{2}\theta_{2}^{2}}{}\right) \sqrt{ \omega^{2}\theta_{2}^{2}\left(1-\frac{\theta_{2}}{\theta_{1}}\right)^{2}+ \left(\frac{\theta_{2}}{\theta_{1}}{}+{}\omega^{2}\theta_{2}^{2}\right)^{2}}\\ &=&\frac{\tau_{a}}{\eta_{\infty}}\frac{\theta_{2}}{\theta_{1}}\sqrt{\frac{1+\omega^{2}\theta_{1}^{2}}{1+\omega^{2}\theta_{2}^{2}}} \end{array} $$

(31)

$$\begin{array}{rll} \sin\phi&=&\frac{\omega\theta_{2}\left(1-\frac{\theta_{2}}{\theta_{1}}\right)}{\sqrt{ \omega^{2}\theta_{2}^{2}\left(1-\frac{\theta_{2}}{\theta_{1}}\right)^{2}+ \left(\frac{\theta_{2}}{\theta_{1}}+\omega^{2}\theta_{2}^{2}\right)^{2} }}\\&=&\frac{\omega\left(\theta_{1}-\theta_{2}\right)}{\sqrt{\left(1+\omega^{2}\theta_{1}^{2}\right)\left(1+\omega^{2}\theta_{2}^{2}\right)}} \end{array} $$

(32)

It is interesting to examine the predictions of the model for the following limiting cases:

• 1. When $\theta _{1}\rightarrow \infty$ (or $\eta _{v}\rightarrow \infty$), the model reduces to the Kelvin–Voigt solid, which corresponds to a fully-structured yield-stress material as predicted by the present model. In this case, the expressions for $\dot \gamma _{a}$ and $\sin \phi$, respectively, become

  $$ \dot\gamma_{a}=\frac{\tau_{a}}{\eta_{\infty}} \left(\frac{\omega\theta_{2,o}}{\sqrt{1+\omega^{2}\theta_{2,o}^{2}}}\right)= \omega\frac{\tau_{a}}{\sqrt{G_{o}^{2}+\omega^{2}\eta_{\infty}^{2}}} $$

  (33)
  $$ \sin\phi=\frac{1}{\sqrt{ 1+ \omega^{2}\theta_{2,o}^{2} }}=\frac{G_{o}}{\sqrt{G_{o}^{2}+\omega^{2}\eta_{\infty}^{2}}} $$

  (34)

  Therefore, it is clear that an imposed stress frequency sweep oscillatory test with a stress amplitude below the static yield stress can be used to determine (e.g., via curve fitting) the model parameters $G_{o}$ and $\eta _{\infty }$. It is worth noting that in the limit of very large frequencies, $\tau _{a}/\dot \gamma _{a}\rightarrow \eta _{\infty }$ (Newtonian response, cf. Eq. (39) below); and in the limit of very small frequencies, $\omega \tau _{a}/\dot \gamma _{a}\rightarrow G_{o}$ (Hookean response, cf. Eq. (37) below).

• 2. When $\theta _{2}\rightarrow 0$ (or $\eta _{\infty }\rightarrow 0$), the model reduces to the Maxwell model, and the expressions for $\dot \gamma _{a}$ and $\sin \phi$ become

  $$ \dot\gamma_{a}=\frac{\tau_{a}}{\eta_{v}} \frac{\sqrt{G_{s}^{2}+\omega^{2}\eta_{v}^{2}}}{G_{s}} $$

  (35)
  $$ \sin\phi=\frac{\omega\eta_{v}}{\sqrt{G_{s}^{2}+\omega^{2}\eta_{v}^{2}}} $$

  (36)

• 3. The model reduces to a Hookean (purely elastic) solid when $\theta _{1}\rightarrow \infty$ and $\theta _{2}\rightarrow 0$ (or $\eta _{v}\rightarrow \infty$ and $\eta _{\infty }\rightarrow 0$). The corresponding expressions for $\dot \gamma _{a}$ and $\sin \phi$ are

  $$ \dot\gamma_{a}=\frac{\tau_{a}}{G_{o}}\omega $$

  (37)
  $$ \sin\phi=1 $$

  (38)

• 4. Finally, the model reduces to the Newtonian fluid model (which corresponds to a fully unstructured state) when $\theta _{1}\rightarrow 0$ and $\theta _{2}\rightarrow 0$ such that $\theta _{1}/\theta _{2}\rightarrow 1$ (or when $\eta _{v}\rightarrow \eta _{\infty }$). In this case,

  $$ \dot\gamma_{a}=\frac{\tau_{a}}{\eta_{\infty}} $$

  (39)
  $$ \sin\phi=0 $$

  (40)

Strictly speaking, the limiting cases 2 (Maxwell fluid) and 3 (Hookean solid) are never attained because they imply a null infinite-shear-rate viscosity $\eta _{\infty }$, which is physically unjustifiable. However, the Maxwell limit is often representative of the realistic situation in which $\eta _{\infty }<<\eta _{v}$, whereas the Hookean limit is often representative of the also realistic situation in which $\eta _{\infty }<<\eta _{v}\rightarrow \infty$.

Analogously, if a sinusoidal shear rate

$$ \dot\gamma(t)=\dot\gamma_{a}\sin(\omega t) $$

(41)

is imposed ($\dot \gamma _{a}$ is the shear rate amplitude and $\omega$ is the oscillation frequency), Eq. (3) becomes

$$ \dot\tau+\frac{1}{\theta_{1}}\tau=\frac{1}{\theta_{2}}(\eta_{\infty}\dot\gamma_{a})\sin(\omega t)+\omega(\eta_{\infty}\dot\gamma_{a})\cos(\omega t) $$

(42)

Equations (29) and (42) have the same form. Consequently, so do their solutions:

$$ \tau(t)=\tau_{a}[\sin(\omega t-\psi)+e^{-t/\theta_{1}}\sin\psi] $$

(43)

where $\tau _{a}$ is the shear stress amplitude and $\psi$ is the phase shift. These quantities are given by

$$\begin{array}{rll} \tau_{a}&{}={}&\eta_{\infty}\dot\gamma_{a} {}\left(\frac{1}{1{}+{}\omega^{2}\theta_{1}^{2}}{}\right) {}\sqrt{ \omega^{2}\theta_{1}^{2}\left(\frac{\theta_{1}}{\theta_{2}}{}-{}1\right)^{2}{}+{} \left(\frac{\theta_{1}}{\theta_{2}}+\omega^{2}\theta_{1}^{2}\right)^{2} }\\&=&\eta_{\infty}\dot\gamma_{a}\frac{\theta_{1}}{\theta_{2}}\sqrt{\frac{1+\omega^{2}\theta_{2}^{2}}{1+\omega^{2}\theta_{1}^{2}} } \end{array} $$

(44)

$$\begin{array}{rll} \sin\psi&=&\frac{\omega\theta_{1}\left(\frac{\theta_{1}}{\theta_{2}}-1\right)}{\sqrt{ \omega^{2}\theta_{1}^{2}\left(\frac{\theta_{1}}{\theta_{2}}-1\right)^{2}+ \left(\frac{\theta_{1}}{\theta_{2}}+\omega^{2}\theta_{1}^{2}\right)^{2} }}\\&=&\frac{\omega(\theta_{1}-\theta_{2})}{\sqrt{(1+\omega^{2}\theta_{1}^{2})(1+\omega^{2}\theta_{2}^{2})}} \end{array} $$

(45)

Thus, for any given pair $(\theta _{1},\theta _{2})$, it happens that the phase shifts $\phi$ and $\psi$ are equal. Moreover, the relationship between the shear stress and shear rate amplitudes is indifferent to whether it is the stress or the rate that is imposed, i.e., the ratio $\tau _{a}/\eta _{\infty }\dot \gamma _{a}$ as given by Eq. (31) and by Eq. (44) is the same.

Consequently, the expressions given above for the particular cases of the model can be used both for imposed stress and imposed rate. In particular, Eqs. (33) and (34) can be used to show that, in a frequency or strain amplitude sweep at imposed stress or shear rate, the model parameters $G_{o}$ and $\eta _{\infty }$ are simply given by $G_{o}=G'$ and $\eta _{\infty }=G''/\omega$ ($G',G''$ are the classic storage and loss moduli), provided (a) $\tau _{a}<\tau _{y}$ at all times during the test, and (b) the material is initially fully structured, relaxed, and at rest.

It is worth noting that, if the time scale of the microstructure changes is much larger than the period of oscillation $1/\omega$, then $\theta _{1}$ and $\theta _{2}$ do not change significantly within a cycle, which means that the response to the imposed sinusoidal oscillation will also be sinusoidal. In other words, for large enough frequencies, the above analytical solutions (Eqs. (30) to (32) and (43) to (45)) are expected to be valid even for time-dependent $\theta _{1}$ and $\theta _{2}$, which means that the amplitude and phase shift will also be time-dependent. This fact can be explored to determine experimentally the structural elastic modulus function $G_{s}(\lambda )$ and, hence, the model parameter m, as discussed by the end of “Numerical results for an imposed sinusoidal stress” section.

Numerical results for an imposed sinusoidal stress

We integrated numerically the model equations for the case of oscillatory flows with the imposed sinusoidal stress given by Eq. (28). Specifically, the shear rate differential equation (Eq. (30)) was integrated simultaneously with the evolution equation for the structure parameter $\lambda$ (Eq. (15)) and all other equations listed in “Summary of the model and evaluation of the parameters.” For all cases, the initial condition corresponded to a material at rest, relaxed, and fully structured ($\lambda (0)=\lambda _{o}$ and $\dot \gamma (0)=0$). Integration was pursued until the steady state was achieved. By steady state we mean here a state in which the structure parameter is either constant (when the cycle period is much shorter than the time scale of microstructure changes) or varies periodically around a constant value (when the cycle period is of the same order of the time scale of microstructure changes). Note that the time scale of microstructure changes is related to the equilibrium time $t_{\text {eq}}$ but is also a strong function of the stress; the larger the stress, the shorter the time scale. The equilibrium time $t_{\text {eq}}$ represents a maximum time scale of microstructure changes, namely the time scale of microstructure buildup at null stress (see Eq. (15) and note that $\lambda _{\text {eq}}(0)=\lambda _{o}$).

We present our results using viscous Lissajous–Bowditch plots for different stress amplitudes and frequencies, i.e., plots of the instantaneous shear stress versus the instantaneous shear rate, displayed in a Pipkin-like plane, following Ewoldt et al. (2008). Lissajous–Bowditch plots have been used extensively in the presentation of large-amplitude oscillatory test data of yield-stress materials (e.g., Mas and Magnin 1997, Tiu et al. 2006, Ewoldt et al. 2008, Ewoldt and McKinley 2010, Ewoldt et al. 2010, Rogers et al. 2011, Rogers and Lettinga 2012, Rogers 2012).

Figures 10, 11, 12, 13, 14, and 15 are used to unveil the wealth of information about the material mechanical behavior contained in Lissajous–Bowditch plots. These figures show plots for three different frequencies ($\omega \dot \gamma _{1}=0.2\pi ,\ 2\pi ,$ and $20\pi$) and three different stress amplitudes ($\tau _{a}/\tau _{yd}=1, 10,$ and 100). Figures 10, 12, and 14 pertain to apparent yield-stress fluids with a dimensionless zero-shear-rate viscosity $\eta _{o}\dot \gamma _{1}/\tau _{yd}=10^{7}$, and Figs. 11, 13, and 15 pertain to yield-stress materials ($\eta _{o}\dot \gamma _{1}/\tau _{yd}\rightarrow \infty$). Three different levels of thixotropy are investigated, namely $t_{\text {eq}}\dot \gamma _{1}=1$ (Figs. 10 and 11); $t_{\text {eq}}\dot \gamma _{1}=0.01$ (Figs. 12 and 13); and $t_{\text {eq}}\dot \gamma _{1}=0$ (no thixotropy, Figs. 14 and 15). To indicate the time evolution, the color of the curves changes gradually from dark blue ($t=0$) to red (steady state); as time elapses, the curves evolve in the counterclockwise direction, except in some low-frequency cases whose curves present self-crossing and, hence, secondary loops in the reverse direction.

It turned out that the response to the stress oscillations was nearly insensitive to whether the material is a yield-stress material or an apparent yield-stress fluid (for the finite $\eta _{o}$ value investigated, namely $\eta _{o}\dot \gamma _{1}/\tau _{yd}=10^{7}$), except during the short transient just after startup (corresponding to the exponential decay term in Eq. (30)). However, it seems reasonable to expect that significant differences would be observed for lower values of the zero-shear-rate viscosity $\eta _{o}$.

Shapes of the Lissajous–Bowditch figures

The shape of the curves is a strong function of the thixotropy and elasticity levels and of the imposed values of both the stress amplitude and the frequency. Ellipses³ indicate that the shear rate response is sinusoidal, which happens only in the cases of no significant variation of the structuring level within each cycle. In other words, when the Lissajous–Bowditch figure for a given cycle is an ellipse, then $\lambda$ did not change significantly along that cycle, and hence, the analytical solution given above is valid, with $\theta _{1}$ and $\theta _{2}$ evaluated at the current $\lambda$. This discussion is clearly illustrated in Fig. 9. As far as we know, this interesting and important observation has not been previously reported.

Fig. 9

Viscous Lissajous curves, shear rate, and structure parameter. $t_{\text {eq}}\dot \gamma _{1}=1$; $\eta _{o}\dot \gamma _{1}/\tau _{yd}=\rightarrow \infty$; $\tau _{a}/\tau _{yd}=100$

Indeed, we compared the numerical and analytical solutions for all cases, and confirmed that the deviation is imperceptible when the Lissajous–Bowditch figure is an ellipse, i.e., when the shear rate response is sinusoidal.

Interestingly, for the parameter values investigated, even when the shear rate response departs dramatically from a sinusoidal one, i.e., when there are large changes of structuring level within the cycles, only minor deviations between the numerical and analytical solutions (with $\theta _{1}$ and $\theta _{2}$ evaluated at the instantaneous value of $\lambda$) were observed.

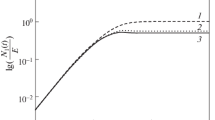
Figure 9 illustrates that the time required for the steady state to be achieved turned out to be independent of the frequency for the cases investigated. Moreover, it shows that the steady-state (mean) value of the structure parameter is a very weak decreasing function of the frequency and tends asymptotically to a constant value, say $\lambda _{s}$, for large enough frequencies. These facts were observed for all cases investigated. However, both the time required for steady state and $\lambda _{s}$ are strong decreasing functions of the stress amplitude.

It is important to point out that the steady-state value of the structure parameter, $\lambda _{s}$, is not equal to the equilibrium structure parameter evaluated at the stress amplitude, $\lambda _{\text {eq}}(\tau _{a})$. It is observed that $\lambda _{s}>\lambda _{\text {eq}}(\tau _{a})$ always. Thus, the effective stress that acts on the material, say $\tau _{eff}$, is lower than the stress amplitude $\tau _{a}$, due to the oscillations. $\tau _{eff}$ can be obtained in Fig. 2 by entering with $\lambda _{s}$ on the right-hand-side ordinate, then obtaining the corresponding equilibrium shear rate in the $\lambda _{\text {eq}}$ curve, and then entering with this equilibrium shear rate on the abscissa to obtain the effective stress on the $\tau$ curve. The fact that $\tau _{eff}<\tau _{a}$ poses a number of questions on the methods for determining the yield stress via oscillatory tests.

Linear viscoelastic regime

In Fig. 10, at a stress amplitude of $\tau _{a}/\tau _{yd}=1$, which is below the static yield stress ($\tau _{y}/\tau _{yd}=2$), and at the lower frequency ($\omega \dot \gamma _{1}=0.2\pi$), it is seen that the behavior is essentially purely elastic, i.e., the shear rate response is nearly orthogonal to the imposed stress wave ($\sin \phi \simeq 1$).

As the frequency is increased ($\omega \dot \gamma _{1}=2\pi$ and $20\pi$), the phase shift decreases, meaning that the influence of the infinite-shear-rate viscosity becomes progressively more important. These trends are independent of the thixotropy level, since below the yield stress the material microstructure remains intact, and hence, the material behaves as a viscoelastic (Kelvin–Voigt) solid, showing a single loop for all cycles (after a short transient).

Therefore, the set of curves for $\tau _{a}/\tau _{yd}=1$ is essentially the same in Figs. 10, 11, 12, 13, 14, and 15, and in this case, the analytical solution given by Eqs. (30), (33), and (34) is exact for $\eta _{o}\dot \gamma _{1}/\tau _{yd}\rightarrow \infty$ and essentially exact for $\eta _{o}\dot \gamma _{1}/\tau _{yd}=10^{7}$.

Fig. 10

Viscous Lissajous curves. $t_{\text {eq}}\dot \gamma _{1}=1$; $\eta _{o}\dot \gamma _{1}/\tau _{yd}=10^{7}$

Fig. 11

Viscous Lissajous curves. $t_{\text {eq}}\dot \gamma _{1}=1$; $\eta _{o}\dot \gamma _{1}/\tau _{yd}\rightarrow \infty$

Fig. 12

Viscous Lissajous curves. $t_{\text {eq}}\dot \gamma _{1}=0.01$; $\eta _{o}\dot \gamma _{1}/\tau _{yd}=10^{7}$

Fig. 13

Viscous Lissajous curves. $t_{\text {eq}}\dot \gamma _{1}=0.01$; $\eta _{o}\dot \gamma _{1}/\tau _{yd}=\rightarrow \infty$

Fig. 14

Viscous Lissajous curves. $t_{\text {eq}}\dot \gamma _{1}=0$; $\eta _{o}\dot \gamma _{1}/\tau _{yd}=10^{7}$

Fig. 15

Viscous Lissajous curves. $t_{\text {eq}}\dot \gamma _{1}=0$; $\eta _{o}\dot \gamma _{1}/\tau _{yd}=\rightarrow \infty$

It is clear that this case in which the stress amplitude is lower than the yield stress corresponds to the linear viscoelastic regime, while all other cases discussed in this paper belong to the realm of nonlinear viscoelasticity.

Nonlinear viscoelastic regime with thixotropy effects

Attention is now turned to Figs. 10 and 11, which pertain to $t_{\text {eq}}\dot \gamma _{1}=1$. When the imposed stress amplitude is larger than the static yield stress, the trends observed are dramatically different.

For $\tau _{a}/\tau _{yd}=10$, we see that in the first few cycles, the Lissajous–Bowditch curves are equal to the corresponding ones for $\tau _{a}/\tau _{yd}=1$, because the material is initially fully structured and, hence, responds like a Kelvin–Voigt solid. Due to thixotropy, yielding occurs only after some finite period of time after the application of the stress, evidencing the avalanche effect (Coussot et al. 2002b).

After this time lag, the microstructure breaking rate is initially very large and soon after reduces to moderate levels. Correspondingly, the curve shapes change from cycle to cycle initially fast and then more moderately, until a final constant shape corresponding to steady state is attained.

The shape of the curves and their evolution in time are strong functions of the frequency. Some of the Lissajous–Bowditch plots in these figures are not ellipses, namely the figure for $\tau _{a}/\tau _{yd}=10$, $\omega \dot \gamma _{1}=0.2\pi$ (middle left), and the figures for $\tau _{a}/\tau _{yd}=100$, $\omega \dot \gamma _{1}=0.2\pi$ and $2\pi$ (top left and top middle). As discussed above, this means that the structuring level changes within the cycles. Hence, it is possible to estimate experimentally the time scale of the microstructure response, which is the inverse of the threshold frequency above which the Lissajous–Bowditch plot becomes an ellipse.

It is interesting to observe that, for $\tau _{a}/\tau _{yd}=10$, $\omega \dot \gamma _{1}=0.2\pi$ (middle left), and $\tau _{a}/\tau _{yd}=100$, $\omega \dot \gamma _{1}=0.2\pi$ (top left), the periodic structuring and unstructuring within the cycles causes the self-crossing of the Lissajous–Bowditch curves at this frequency, forming secondary loops. This behavior has been observed experimentally for a wide variety of systems, as discussed in detail by Ewoldt and McKinley (2010).

Secondary loops occur in the present case as a consequence of thixotropy. As the stress increases within the cycle, when it is above the yield stress, it tends to break the microstructure. However, because it takes a finite time for the microstructure to respond to the stress changes, there is a time lag between the stress changes and the structuring level changes, which causes the observed self-crossing.

As the frequency is increased, the steady-state Lissajous–Bowditch figures eventually become ellipses. As discussed above, the actual frequency threshold beyond which the steady-state plots become ellipses depends on the time scale of microstructure changes, which in turn is governed both by the equilibrium time $t_{\text {eq}}$ and the stress amplitude $\tau _{a}$. For example, the elliptical shape is observed at $\omega \dot \gamma _{1}=2\pi$ and above for $\tau _{a}/\tau _{yd}=10$ (slower microstructure response) and at $\omega \dot \gamma _{1}=20\pi$ only for $\tau _{a}/\tau _{yd}=100$ (faster microstructure response).

Moreover, for larger frequencies, the elastic response becomes more important, as indicated by the larger areas within the loops. This trend is in accordance with the behavior observed in viscoelastic liquids. It is worth noting, however, that when the retardation time is nonzero, at large enough frequencies, the behavior is expected to become viscous again. This trend is not illustrated in the figures but can be easily inferred from Eq. (32), which gives that $\sin \phi \rightarrow 0$ as $\omega \rightarrow \infty$.

The qualitative trends described above for $\tau _{a}/\tau _{yd}=10$ are also observed for $\tau _{a}/\tau _{yd}=100$, except that

• unstructuring occurs much faster, and hence, for $\omega \dot \gamma _{1}=0.2\pi$, the material yields before completing the first cycle;

• the periodic variation of structuring level during the cycles observed for $\omega \dot \gamma _{1}=0.2\pi$ is significantly larger; and

• the elastic response after unstructuring is generally much milder, because the structuring level is lower.

Due to thixotropy, in the cases shown in Figs. 10 and 11 for $\tau _{a}/\tau _{yd}=10$ and 100, the material remains yielded at all times after the initial yielding, because the response of the microstructure is not fast enough. As discussed above, there is periodic structuring and unstructuring within the cycles, but the maximum level of structuring is far from full structuring.

Nonlinear viscoelastic regime without thixotropy effects

For a much lower or null level of thixotropy, namely $t_{\text {eq}}\dot \gamma _{1}=0.01$ and 0 (Figs. 12, 13, 14, and 15), the Lissajous–Bowditch plots pertaining to the nonlinear viscoelastic regime are quite different from the corresponding ones discussed above for $t_{\text {eq}}\dot \gamma _{1}=1$. The shapes of these loops are in agreement with experimental data for different nonthixotropic viscoplastic materials (e.g., Mas and Magnin 1997; Ewoldt et al. 2008, 2010).

The steady state is achieved within the first cycle in most cases shown, and the shear rate response is clearly nonsinusoidal, due to the important microstructure changes that occur within the cycles. The exception is the plot for $t_{\text {eq}}\dot \gamma _{1}=0.01$, $\tau _{a}/\tau _{yd}=10$ and $\omega \dot \gamma _{1}=20\pi$ (Figs. 12 and 13), which requires a few cycles to reach steady state and whose elliptical shapes indicate a sinusoidal shear rate response.

Moreover, because the microstructure responds very fast to stress changes (low thixotropy), the yield stress (or apparent yield stress) effect becomes visible in many of the plots pertaining to the nonlinear viscoelastic regime, as explained next. The signature of the yield stress in a viscous Lissajous–Bowditch figure are vertical portions in the vicinity of zero stress (i.e., below the yield stress), because below the yield stress, the stress is proportional to the strain, and hence, the shear rate remains constant as the stress changes.

In Figs. 14 and 15 (which pertain to $t_{\text {eq}}\dot \gamma _{1}=0$, no thixotropy whatsoever), it is observed that some characteristics are common in the shapes of the plots pertaining to $\tau _{a}/\tau _{yd}=100; \ \omega \dot \gamma _{1}=0.2\pi ; \ 2\pi ; \ 20\pi$ and to $\tau _{a}/\tau _{yd}=10; \ \omega \dot \gamma _{1}=0.2\pi ; \ 2\pi$.

To aid in extracting the information contained in these plots, let us examine, for example, the plot pertaining to $\tau _{a}/\tau _{yd}=10$ and $\omega \dot \gamma _{1}=2\pi$ in Fig. 15. At the upper right end of this plot, both the stress and the shear rate attain their maxima. At this point of the loop, the structuring level is lowest, and hence, both elasticity and the viscosity are lowest. As time elapses and the stress intensity decreases, an elastic microstructure is gradually formed, and as it is formed, it deforms, storing energy. In this situation, the motion is driven by the imposed stress while the elastic stress resists the motion. When the shear rate reaches zero, the imposed stress balances exactly with the elastic stress. From this moment on, motion restarts in the reverse direction, driven by the elastic stress, while the decreasing imposed stress resists the motion. When the imposed stress reaches the dynamic yield stress $\tau _{yd}$ (from above), the structure parameter jumps to infinity, causing the elastic module value to jump from a higher value to $G_{o}$. This jump causes a discontinuity in the curve derivative at $\tau /\tau _{yd}\simeq 1$. The stress reaches zero at a nonzero shear rate, maintained by the elastic stress which, at this moment, is exactly equal to the viscous stress related to the infinite-shear-rate viscosity. Then the imposed stress reverses direction and begins to act in the flow direction, progressively replacing the elastic force to maintain the shear rate nearly constant. When the imposed stress intensity reaches the static yield stress $\tau _{y}$ (from below), the microstructure collapses, causing a sudden drop of the elastic force. At this moment, the instantaneous imposed stress is not sufficient to maintain the shear rate, which therefore decreases momentarily. As the imposed stress intensity increases further, the viscosity progressively decreases due to unstructuring, and hence from there on, the shear rate intensity increases at an increasing rate. When the lower left extreme of the loop is reached, the sequence of events described above is repeated to complete the other half of the cycle.

With different relative importances, the same events occur in the flows pertaining to the other plots in Figs. 14 and 15 ($t_{\text {eq}}\dot \gamma _{1}=0$) and also to the corresponding plots in Figs. 12 and 13 ($t_{\text {eq}}\dot \gamma _{1}=0.01$). It is important to emphasize that some level of thixotropy is expected to be present in all real materials, especially at low stresses, because no thixotropy at all ($t_{\text {eq}}\dot \gamma _1=0$) implies that the microstructure reaches equilibrium instantaneously upon any change in stress. Therefore, the slope discontinuities observed in Figs. 14 and 15 are not expected to appear in the measurements of real systems. Accordingly, a very low level of thixotropy ($t_{\text {eq}}\dot \gamma _{1}=0.01$, Figs. 12 and 13) eliminates these discontinuities, while keeping the same general shapes observed for $t_{\text {eq}}\dot \gamma _1=0$.

Determining the parameter m

We now outline a possible procedure to determine the parameter m that appears in Eq. (7). It is assumed that $\tau _{y}$, $G_{o}$, and $\eta _{\infty }$ were already determined in separate experiments, using the procedures suggested above or any other.

Firstly, we perform time sweep oscillatory tests at different frequencies, at a stress amplitude significantly above the static yield stress. We then pick one of the test results whose Lissajous–Bowditch figures are ellipses, meaning that the analytical solution should reproduce the data exactly. More specifically, the shear rate amplitude $\dot \gamma _{a}(t)$ and the phase shift $\sin \phi (t)$, which are part of the experimental results, should obey Eqs. (31) and (32), respectively.

It is, thus, possible to solve Eqs. (31) and (32) for $\theta _{1}(t)$ and $\theta _{2}(t)$, and, using the definitions in Eq. (2), determine $G_{s}(t)$ and $\eta _{v}(t)$. The next step is to use Eq. (9) to transform $\eta _{v}(t)$ into $\lambda (t)$. This gives the function $G_{s}(\lambda )$ (in tabular form), and a simple fitting to Eq. (7) can be used to determine m. It is clear that, if it turns out that Eq. (7) is not a good representation of the data, any other more suitable function with similar properties may be adopted.

Note that the function $\lambda (t)$ obtained with this procedure can also be used to determine the parameters $t_{\text {eq}}$, a, and b, using the same data reduction described in the end of “Summary of the model and evaluation of the parameters.”

Final remarks

In this paper, we describe a constitutive model for thixotropic elasto-viscoplastic materials based on our previous work (de Souza Mendes 2009, 2011), modified to accommodate both yield-stress materials and apparent yield-stress fluids. It was shown in this paper that the proposed model is able to predict the main rheological characteristics of thixotropic elasto-viscoplastic materials.

In constant shear rate flows, it predicts stress overshoots and provides an explanation for the shear banding phenomenon that occurs in homogeneous flows. In constant shear stress flows, it predicts nicely the viscosity bifurcation (Coussot et al. 2002a) and the avalanche effect (Coussot et al. 2002b).

In large-amplitude oscillatory flows, it yields Lissajous–Bowditch figures for a wide range of flow regimes that are in excellent qualitative agreement with the experimental ones reported in the literature. These results provide, for the first time in the literature, a quantitative link between the Lissajous–Bowditch curve shapes and rheological effects such as elasticity, thixotropy, and yielding. Among other interesting findings, it is shown that a sinusoidal output shear rate wave is obtained whenever the characteristic time of change of the microstructure is much larger than the reciprocal frequency of the LAOS test.

Finally, we describe different experimental strategies for measuring all the model parameters. As discussed in the “Introduction”, strictly speaking, it is never possible to affirm that a given material possesses a yield stress, but, for practical purposes, we can use the yield-stress material version of the proposed model whenever the zero-shear-rate viscosity $\eta _{o}$ is unreachable, independently of its existence or nonexistence. In this case, the yield stress should be evaluated in rheometrical measurements whose waiting time is larger than the characteristic time of the sought-for process. In addition, $\eta _{o}$ ceases to be a parameter, and consequently, the number of parameters of the model is conveniently reduced by one.