Direct numerical simulation of surfactant-stabilized emulsions

Abstract

A 3D lattice Boltzmann model for two-phase flow with amphiphilic surfactant was used to investigate the evolution of emulsion morphology and shear stress in starting shear flow. The interfacial contributions were analyzed for low and high volume fractions and varying surfactant activity. A transient viscoelastic contribution to the emulsion rheology under constant strain rate conditions was attributed to the interfacial stress. For droplet volume fractions below 0.3 and an average capillary number of about 0.25, highly elliptical droplets formed. Consistent with affine deformation models, gradual elongation of the droplets increased the shear stress at early times and reduced it at later times. Lower interfacial tension with increased surfactant activity counterbalanced the effect of increased interfacial area, and the net shear stress did not change significantly. For higher volume fractions, co-continuous phases with a complex topology were formed. The surfactant decreased the interfacial shear stress due mainly to advection of surfactant to higher curvature areas. Our results are in qualitative agreement with experimental data for polymer blends in terms of transient interfacial stresses and limited enhancement of the emulsion viscosity at larger volume fractions where the phases are co-continuous.

Introduction

The history-dependent rheology and morphology of emulsions and the effects of surfactants on emulsions are important in a wide range of natural systems such as milk and plant latexes, foods and personal care products, and industrial applications. The work described here was motivated by oil industry applications such as the transport of mixtures of oil, water, and gas in pipelines under steady and transient flow conditions and the separation of oil and water in the presence of indigenous and synthetic polymers. The work described here is also relevant to the manufacture of polymer blends with a valuable combination of properties that cannot be obtained with individual polymers and the effects of compatibilizers such as diblock copolymers, which play a role like that of surfactants in low molecular mass multiphase fluid systems on the manufacture and properties of polymer blends. Here we present results obtained from simulations conducted using a 3D lattice Boltzmann model that includes two liquid phases and a nonionic amphiphilic surfactant, to investigate some aspects of emulsion morphology and rheology, including the shear stress under transient, start up, shear flow, and the effects of surfactant strength on shear stress and morphology. Other aspects of the rheology, including the normal stress, will be analyzed in upcoming work.

Emulsion rheology, morphology, and simulation

For dilute emulsions, in which the droplets have simple shapes and they are separated by distances that are, on average, much larger than their maximum diameter, it is sufficient to consider the response of single droplets to the applied shear. Rheological formulae can then be derived from first principles, e.g., Taylor (1932), Frankel and Achrivos (1970), Yu et al. (2002), and Derkach (2009). Choi and Schowalter (1975) obtained rheological formula for larger volume fractions and found that the relationship between the effective viscosity and droplet volume fraction becomes nonlinear.

For a simple droplet morphology, the viscoelastic response of the emulsion in a time varying shear strain rate can also be predicted. Jansseune et al. (2001) performed experiments with a cone and plate rheometer to investigate the transient behavior in Couette flow, established in blends of nearly Newtonian immiscible polymers. The rheology determined in these experiments was consistent with the prediction of a simple model based on affine deformation of the droplets. The interfacial shear stress evolution that was measured in these experiments is consistent with our simulation results, which exhibited a rapid increase of the interfacial shear stress immediately after startup and then a gradual decay as the droplets aligned with the flow. Christini et al. (2002) performed numerical modeling of the same system for both critical and subcritical capillary numbers. Similar transients were measured by Krall et al. (1993) who observed a rapid decrease of the shear viscosity and elastic shear modulus during spinodal decomposition and domain coarsening.

The role of morphology in dense emulsions and bi-continuous blends is less well understood. Doi and Ohta (1991) developed a general theoretical framework for bi-continuous blends in terms of the interface tensor and interface area for two immiscible Newtonian fluids with the same viscosity and density in low Reynolds number flows. Since only the interface tensor and the specific surface area are used to characterize the morphology, the coarse-grained Doi Ohta model predicts the evolution of the average droplet size, deformation, and orientation, but it does not provide detailed information about the droplet shapes, droplet size distribution, local fluid velocities, etc. The Doi Ohta model assumes a constant surface interfacial tension (Marangoni effects are not included), and it requires a closure approximation for the moments of the components of the unit vector perpendicular to the interface (tensor products of the unit vector normal to the interface). Subsequent work has improved the theoretical model of Doi and Ohta, by introducing more general expressions for the relaxation of the specific surface area and the interface tensor (Lee and Park 1994), by using more accurate closure approximations for the hierarchy of equations for the second rank tensor product of the unit vector normal to the interface (Wentzel and Tucker 1999; Almusallam et al. 2000; Wagner et al. 1999), and by developing different theoretical approaches such as using an advection–relaxation–diffusion equation of motion for the state variables, based on the general equation for nonequilibrium reversible–irreversible coupling (GENERIC) approach to the dynamics of complex fluids (Grmela and Öttinger 1997; Öttinger and Grmela 1997; Wagner et al. 1999; Grmela and Ati-Kadi 1994), which ensures consistency with equilibrium thermodynamics, reversible Hamiltonian dynamics, and linear irreversible thermodynamics. The Doi Ohta model and related models have also been applied to specific simplified cases such as a constant droplet volume with no coalescence or fragmentation (Almusallam et al. 2000) and extended to more general cases such as different fluid viscosities (Lee and Park 1994). All of these theories and related theories discussed in the scientific literature provide important insight into the rheology and dynamics of multiphase fluids. However, they are based on mean field approximations. Consequently, they cannot be used to address questions such as how droplets deform as they approach each other or how surfactants are distributed over complex fluid–fluid interfaces. For this purpose, experiments, which may be very difficult to perform, or detailed computer simulations are needed.

A transition to a bi-continuous morphology (a morphology with two continuous liquid phases) can occur even at volume fractions as low as 0.25 (Willemse et al. 1999). The transition occurs at a volume fraction that decreases as the capillary number is increased by reducing the interfacial tension, or by increasing the continuous phase viscosity and/or shear strain rate. Willemse et al. (1999) studied blends with viscosity ratios of 0.4 and 2.1 and devised a successful model for the critical volume fraction based on randomly oriented “rods” which represent stretched droplet filaments.

Takahashi et al. (1994) investigated the rheology of immiscible polydimethylsiloxane (PDMS)/polybutadine (PB) blends with a viscosity ratio near unity over a range of compositions up to a PDMS/PB ratio of 9. They found that both the shear stress and normal stress difference were proportional to the shear strain rate, in accordance with the predictions of the Doi Ohta model, except that the normal stress difference was not proportional to the shear strain rate for the highest PDMS/PB ratio. This deviation was attributed to the nonlinear normal stress difference/shear strain rate relationships for the component polymers. However, after correcting for the nonlinear rheology of the component polymers, the contribution of the interface to the normal stress difference scaled in a more linear fashion with the shear strain rate. Vinckier et al. (1996) investigated the effects of shear strain on blends of polyisobutylene (PIB) and PDMS with viscosity ratios of 0.15:6.57 and density ratios of ≈1.09. The blends were sheared at a constant strain rate in a cone and plate rheometer until a steady state was reached, and the shear stress and first normal stress difference were measured. After the continuous shear was stopped, low amplitude dynamic oscillatory shear measurements were used to determine the dynamic moduli, and the self-consistent effective medium theory of Palierne (1990) was used to determine the mean droplet size from the dynamic moduli measurements and the independently measured interfacial tension. The Doi Ohta model predicts that the shear stress and the first normal stress difference should both be proportional to the shear strain rate for blends of polymers with the same viscosity. The experimental results were consistent with linear scaling between the excess normal stress and shear strain rate over a range of about 1.5 decades in the shear strain rate. However, the excess shear viscosity was constant over only a small range of shear strain rates. Vinckier et al. (1996) concluded that the Doi Ohta model could be extended to mixtures of fluids with different viscosities providing that the shear strain rate is not too high and the ratio between the viscosity of the fluid in the drops and the viscosity of the continuum fluid is less than ≈4 (so that the droplet fragmentation can occur and the droplet size and shape distributions are determined by the flow conditions instead of the initial conditions). Taking into account the work of Takahashi et al. (1994), Vinckier et al. (1996) also concluded that only the contribution of the interface to the normal stress difference (not the total normal stress difference) should be expected to scale linearly with the strain rate.

Vinckier et al. (1999) measured the shear viscosity of polymer blends with a viscosity ratio of 0.44 for the full range of volume fractions. They found good agreement with the Choi and Schowalter (1975) model for high and low volume fractions corresponding to droplets embedded in a continuous phase. An important observation was that the emulsion viscosity can be significantly lower than that predicted by classical models in the intermediate range of volume fractions. A similar effect was observed by Jansseune et al. (2003) who found an interfacial shear stress plateau over a broad interval of volume fractions, and an agreement with the model of Maffettone and Minale (1998) was found only at low and high volume fractions. Yu et al. (2005) developed a model for intermediate volume fractions based on droplet morphology but found that the emulsion viscosity of Vinckier et al. (1999) was still far below their model predictions, suggesting a co-continuous morphology.

Keleşoğlu et al. (submitted for publication) studied emulsions of water droplets in a matrix of highly viscous North Sea crude oils. They found good agreement with the model of Pal and Rhodes (1989) for various temperatures and shear rates up to an aqueous phase volume fraction of about 0.65. Closer to the phase inversion point, the measured emulsion viscosity was lower than the viscosity predicted by the model. Even though oil/water emulsions have higher viscosity ratios, it is likely that the Pal and Rhodes model did not fit the data at these volume fractions because the morphology did not correspond to droplets in a continuous phase.

Important effects of surfactants include altering the phase inversion point and emulsion viscosity via morphological changes (e.g., Pal 1993, for oil and water emulsions). Clearly, the behavior near phase inversion is complex and depends on the fluid properties, surfactant concentration, and type of surfactant. Numerical simulations can be used to gain qualitative insight even for complex morphologies where analytic treatment is difficult or impossible. Simulations can now be performed on a spatial scale that is large enough to generate rheological results with reasonable statistics, using ordinary multiprocessor workstations.

Loewenberg and Hinch (1996) made a significant breakthrough by performing 3D simulations of sheared dense emulsions in 3D. Spinodal decomposition of binary mixtures under shear has been simulated by many authors, both in 2D (Rothman 1991) and more recently in 3D (Corberi et al. 2000). Kim and Hwang (2007) implemented Lees–Edwards (periodic shear) boundary conditions that eliminate wall effects in simulations of shear flow. They studied relatively dense emulsions in 2D and determined the shear stress and first normal stress difference. Roths et al. (2002) studied the interfacial area and elasticity of a sheared emulsion in 2D and found that the elasticity increased with increasing volume fraction while the interfacial area decreased. Keestra et al. (1993) studied coalescence and breakup effects in 2D.

Here we present the results of 3D rather than 2D simulations with the objective of capturing realistic morphologies and predictions of the variation of interfacial area with volume fraction that can be compared with experimental results. We include amphiphilic surfactant using the lattice Boltzmann model developed by Nekovee et al. (2000). An important advantage of the lattice Boltzmann approach is the high computational speed that can be achieved by very efficient parallelization on multiprocessor machines. The simulation domains can then be large enough for volume averaging to provide reliable estimates of the effective rheology. Using essentially the same model, Guipponi et al. (2006) and González-Segredo et al. (2006) found evidence for shear thinning and viscoelasticity in bi-continuous self-assembled ordered structures in the presence of amphiphilic surfactant. In the model, the surfactant is soluble in the fluids, and diffusion-dominated adsorption kinetics can be simulated (Skartlien et al. 2011). A version of the surfactant model based on a Cahn–Hilliard-type free energy functional (phase field model) was developed by Furtado and Skartlien (2010).

It is difficult to experimentally determine the morphology of polymer blends and emulsions during startup shear experiments and even more difficult to determine how the distribution of surfactants, including block copolymer surfactants, on the fluid–fluid interface and in the fluid phases changes during such experiments. Blends and emulsions are often opaque, and because the X-ray attenuation coefficients of polymer blend components are usually similar, attenuation contrast high-resolution X-ray tomography is not widely applicable. Recently, phase contrast X-ray tomography has been used to investigate polymer blends (Momose et al. 2005), but X-ray tomography data acquisition times are too long for transient behaviors to be investigated. If the morphology relaxation time, characterized by the interface energy (stress/strain) relaxation time $\tau^s_r = \mu a/\sigma$ and the kinetic energy (momentum) relaxation time $\tau^p_r = \rho a^2/\mu$, where μ is the viscosity, a is the characteristic morphology length such as the equilibrium droplet radius, r _∘, σ is the surface tension, and ρ is the fluid density, is large enough, the morphology of a polymer blend may be determined by stopping the deformation, rapidly cooling the material below the glass transition temperature, selectively dissolving one of the two phases, and using optical or electron microscopy to characterize the morphology of the remaining component (Scott and Macosko 1995; Lyu et al. 2000).

An important advantage of computer simulations is the great amount of detailed information that can be obtained without measurement artifacts or measurement time smearing. However, simulations do suffer from discretization errors, and they are only as good as the conceptual and mathematical models that they are based on.

The stress tensor for a surfactant-free emulsion

The average shear stress in an emulsion is determined by the fluid properties and the stress associated with the interface between the fluids. Here we focus on simulation results obtained with a viscosity ratio of unity to isolate the contribution from the interfacial stress from the contribution that arises due to the viscosity contrast between the fluids. Other viscosity ratios will be considered in the sequel to this paper.

As explained in “Appendix 1”, the shear stresses were calculated from the momentum flux density of the fluid particles (represented by population densities in lattice Boltzmann models) and the interactions between the particles using the virial theorem. This is a general approach that also incorporates the interfacial stresses, and it is valid for any volume fraction and viscosity contrast. An overview of the essential stress contributions may be obtained by considering the analytic expression for the volume averaged stress tensor for a dilute emulsion of Newtonian fluids without surfactant (e.g., Jansseune et al. 2001; Christini et al. 2002; Li and Sarkar 2005),

$$ \begin{array}{rll} \overline{\Pi}_{\alpha \beta}&=&-p\delta_{\alpha \beta}+\mu_{\rm c}(\overline{ \partial_\alpha u_\beta}+\overline{ \partial_\beta u_\alpha})\\ &&+ \frac{\mu_{\rm d}-\mu_{\rm c}}{V}\int (u_\alpha n_\beta +u_\beta n_\alpha){\rm d}S \\ &&+\frac{\sigma}{V}\int\left( \frac{1}{3}\delta_{\alpha \beta} - n_\alpha n_\beta\right){\rm d}S -\frac{1}{V} \int {u}^{\prime}_\alpha {u}^{\prime}_\beta {\rm d}V. \end{array} $$

(1)

Here, μ _c is the viscosity of the matrix (the continuous fluid), μ _d is the droplet viscosity, p is the isotropic pressure, u _α is the local velocity component, n _α is the component of the local normal vector to the interface, σ is the interfacial tension, and V is the averaging volume. The surface integrals run over the total interfacial area S in the averaging volume, and dS is the surface element. The indices α and β denote the coordinate directions, and $\overline{ \partial_\alpha u_\beta}$ is the average velocity gradient in the volume V. The fluctuating velocity components are defined as ${u}^{\prime}_\alpha = {u}_\alpha- \overline{u}_\alpha$, where the volume averaged velocity is $\overline{u}_\alpha$.

The second and third terms on the right-hand side of Eq. 1 represent the viscous stresses. The third term involves the fluid velocities at the interface, and it represents a viscous contribution if there is a viscosity contrast between the fluids. The fourth term is the interfacial stress, which is the focus of this work. This depends on the drop shape, size, and orientation. The interface tensor (e.g., Doi and Ohta 1991),

$$ q_{\alpha \beta}=\frac{1}{V}\int\left( n_\alpha n_\beta - \frac{1}{3}\delta_{\alpha \beta} \right){\rm d}S, $$

(2)

measures the degree of anisotropy of the interface (e.g., Tucker and Moldenaers 2002). The interface tensor and the interfacial anisotropy also play central roles for higher volume fractions with more complex morphologies and topologies, as we will discuss below. In this work, a viscosity ratio of unity was used, so that the contribution that arises due to the viscosity contrast (third term) vanishes. This enables us to focus on the interfacial stress. For perfectly round drops, the interface tensor and the interfacial stress are zero due to symmetry, but for tilted elliptical drops (at nonzero capillary number), the interfacial stress is significant. The degree of ellipticity is characterized by the deformation D defined as

$$ D=\frac{L-B}{L+B} $$

(3)

for spheroids, where L is the greater diameter and B is the lesser diameter (perpendicular to L).

The transient interfacial shear stress in an emulsion in starting Couette flow (with a zero-velocity initial state) at first increases and then decreases with increasing time. The average interfacial shear stress in a dilute emulsion of equal-sized spheroidal droplets can be described by affine deformation models. At early times, immediately after startup, the increasing deformation D provides an increasing interfacial stress that can be modeled with a “true affine” deformation model as discussed in Jansseune et al. (2001). At sufficiently late times and for sufficient deformation or capillary number (Jansseune et al. 2001),

$$ \overline{\Pi}_{xy}^{\rm int}=\frac{\sigma\phi}{B}F(B,L)\sin(2\theta); \;\; {\rm Uniform\;Spheroids}, $$

(4)

where θ is the tilt angle (between L and the mean flow direction), F(B,L) is an algebraic–trigonometric function of L and B, and ϕ is the droplet volume fraction. For a starting flow, the tilt angle and sin(2θ) decrease in time after startup. Initially, the droplets are slightly deformed spheres, and θ = 45°. At later times, the tilt angle is reduced further, and consequently, sin(2θ) in Eq. 4 decreases and the stress decreases. The interfacial stress is smaller for droplets that are more aligned with the mean flow (smaller tilt angle θ).

The final term in Eq. 1 (the fifth term on the right-hand side) is the “inertial stress” in the fluids, which resembles the Reynolds stress in turbulent flows. The inertial stress, which is zero for Stokes flow and increases with increasing Reynolds number, is expected to make a significant contribution to the total stress at high shear rates with larger velocity fluctuations.

Surfactant effects

An important effect of surfactants is to reduce the interfacial tension on the average. In pipe flow, this may promote emulsification so that separated water and oil phases may become a dispersion because less energy is required to increase the interfacial area. In general, the addition of surfactants generates smaller droplets in a dispersion for a given shear field or turbulence, owing to the reduction of the interfacial tension.

Apart from slip at the fluid–fluid interface, which can be characterized by the slip length, $\ell_{\rm s} = u_{\rm s}/{\dot{\epsilon}}$, where u _s is the slip velocity at the interface and ${\dot{\epsilon}}$ is the shear strain rate, the flow velocity field is continuous across the interface. Molecular dynamic simulations (Li et al. 2005; Hu et al. 2010) indicate that for fluid–fluid interfaces, with or without surfactant, the slip length is on the order of 1 nm or smaller, and the effects of slip can be safely neglected if the droplet size is greater than a few tens of nanometers. Under these conditions, the interface is advected with the fluid and gradients in the concentration of the surfactant in the interface develop. This generates gradients in the interfacial tension (tangential or Marangoni stresses), gradients in the chemical potential of the surfactant, and gradients in the rheology and rigidity of the interface. In addition, the variability in the surface tension must be taken into account when the jump in normal stress across the interface is calculated (ΔΠ _n (x _s) = κ(x _s) σ(c _s(x _s)), where κ is the surface curvature, c _s is the surfactant concentration, and x _s is the position in the interface). If the surfactant is confined to the interface, it will diffuse in the interface, down the chemical potential gradient from regions of high surfactant concentration to regions of low surfactant concentration, and an interface Péclet number, ${\rm Pe}_{\rm s} = \dot{\epsilon}r_{\circ}^2/D_{\rm s}$, where $\dot{\epsilon}$ is the strain rate, r _∘ is the radius of the undeformed drop, and D _s is the interface diffusion coefficient, can be defined. The interface Péclet number measures the relative importance of advective and diffusive transport of surfactant in the interface. When the surface Péclet number is small, the gradients in the surfactant concentration in the interface, $\nabla_{\rm s} c_{\rm s}$, and in the interfacial tension, $\nabla_{\rm s}\sigma$, are small. When Pe_s is large, $\nabla_{\rm s} c_{\rm s}$ and $\nabla_{\rm s} \sigma$ are large.

If the surfactant is soluble in one or both of the liquids, diffusive and advective transport through the bulk phase may become important, and additional Péclet numbers may be required. Pawar and Stebe (1996) have investigated how Marangoni effects influence the shapes of drops in an extensional flow for equal fluid viscosities and surfactants that are insoluble in both liquid phases with Langmuir and Frumkin equations of state. Simulations were performed for several initial surfactant coverages using a quasistatic steady state Stokes flow approximation for the two fluids (inside and outside the drops), and the capillary number was incremented by small amounts until the drop became unstable.

A second important effect is that the surfactant tends to inhibit or oppose droplet coalescence because of slower hydrodynamic draining of the liquid film between the droplets and because of molecular repulsion between the surfactant laden interfaces. Reduced draining rates occur due to Marangoni stresses if the interface is sufficiently mobile so that gradients in the interfacial surfactant concentration can be induced (Danov et al. 2001). In more dynamic or turbulent flows, the contact time (or available interaction time) between droplets is reduced, and the hydrodynamic repulsion can be more important than shorter range molecular repulsion. Van Puyvelde et al. (2001) have discussed the effects of surfactants on droplet coalescence in the context of compatibilized polymer blends for which block copolymers are used as compatibilizers (surfactants). A third surfactant effect is the modification of the topology and morphology of the interface via modified droplet deformations (e.g., Fisher and Erni 2007), formation of multiple emulsions (Pal 1993), or via altered topology in co-continuous blends.

Numerical model

Two-component lattice Boltzmann model with surfactant

A detailed description of the lattice Boltzmann model used in this work was published by Nekovee et al. (2000). The model was developed into its free energy form by Furtado and Skartlien (2010), and only a brief overview is presented here. The lattice Boltzmann approach solves the Boltzmann equation directly using a set of velocity collocation points in velocity space. This is an alternative to solving the Navier–Stokes equations using finite volume, finite difference, or finite element methods or using particle methods such as molecular dynamics or dissipative particle dynamics. An important advantage of the amphiphilic LBM is that it can simulate flows on hydrodynamic scales where the fluids can be treated as continua, while it includes mechanisms that arise from the molecular properties of the surfactant.

A simple nonionic surfactant model that uses two connected unlike “particles”, A and B, was used to represent the hydrophilic and hydrophobic parts of a surfactant molecule, S = A + B. The two ordinary fluids were assumed to be composed of particles similar to the A and B components of the surfactant, producing an A-fluid and a B-fluid. The lattice Boltzmann model used in this work is based on an underlying conceptual model that attributes separation of the fluids into A-rich and B-rich phases and the effect of the surfactant on the A–B surface tension to (relatively) long range attractive intermolecular forces. The dipole structure of the surfactant results in relatively complex forces with both radial and tangential components. The rotational degree of freedom of the surfactant adds another level of complexity compared with models that treat the surfactant as a scalar.

Furtado and Skartlien (2010) assumed short-range repulsive interactions V and longer-range attractive interactions W _pq ,

$$ {\mathcal V}_{pq} = V({\bf R}_i,{\bf R}_j) + W_{pq}({\bf R}_i,{\bf R}_j), $$

(5)

where p and q denote any of the three species and R _i is the position of particle i to derive the model of Nekovee et al. (2000). The combination of short-range repulsive interactions and somewhat longer-range attractive interactions are typical of nonionic molecules. In the model, the short-range repulsive potential is governed by the BGK collision term in the lattice Boltzmann framework (Nekovee et al. 2000). The long-range force between any two pairs of “particles” has the form

$$ \mathcal{F}_\alpha = \pm\frac{ {\mathcal G} }{C^D} C_\alpha, $$

(6)

where C = |C| = |R _j  − R _i | is the inter-particle separation and where D is the spatial dimension. The coupling constant is chosen so that like particles attract while unlike ones repel (or attract less), and this provides immiscibility between the fluids (A and B) and an affinity of the surfactant for the interface between the fluids. This basic force model gives rise to a number of coupling constants: $\mathcal{G}_{\rm AB}$ for interactions between different fluid components, $\mathcal{G}_{\rm AA}$, $\mathcal{G}_{\rm BB}$ for interactions between particles of the same kind, $\mathcal{G}_{\rm AS}$ and $\mathcal{G}_{\rm BS}$ for fluid–surfactant interactions, and $\mathcal{G}_{\rm SS}$ for surfactant–surfactant interactions. The force model is used with a standard lattice Boltzmann approach, and this is described in the cited papers, along with the kinematic viscosity relations and equations of state.

Initial and boundary conditions and flow parameters

The fluids were assumed to have the same density in order to eliminate buoyancy effects and to focus on the shear-induced interfacial dynamics without gravitational settling effects. Shear was applied at t = 0 by the upper and lower walls, which were moved in opposite directions. The boundary conditions in the flow direction (x) and transverse direction, z (parallel to the walls and perpendicular to the flow direction), were periodic, and no-slip boundary conditions were used on the moving walls at y = 0,y = L _y . A domain size of L _x  = 256, L _y  = L _z  = 128 was used.

A linear velocity profile was imposed between the moving walls at t = 0 to avoid undesirable effects of gradual diffusion of momentum into the simulation domain from the moving walls (on a timescale of $L_y^2/\nu$, where ν is the kinematic viscosity). If the initial velocity in the domain had been set to zero, the finite diffusion time would have resulted in appreciable shear only in the near wall region during the early stages of a simulation, and the coalescence rates would have been much larger near the walls than in the middle of the computational domain.

Small random fluctuations in the composition of the fluid mixture were used to initiate spontaneous phase separation (nucleation and growth for large and small volume fractions and spinodal decomposition for similar volume fractions). Phase separation gave droplets of A-rich fluid, immersed in a B-rich continuous phase, provided that there was a significant asymmetry in the volume fractions. For all volume fractions, phase separation proceeded from t = 0. The model surfactant was soluble in both fluids and exhibited diffusion-controlled adsorption kinetics (Skartlien et al. 2011).

Constant wall velocities of u _w  = ±0.1, commensurate with the lattice units Δt (time step) and Δx (grid spacing), were used, and these increments were chosen to fit a desired set of dimensional parameters of the flow. The characteristic kinematic viscosity is $\nu_{\rm c} = \Delta x ^2 /\Delta t$, and the characteristic velocity scale is u _c = Δx /Δt. With the chosen domain size, a flow Reynolds number of Re = 77 (based on the wall velocity difference) was obtained. The simulations were carried out over $N_t=10^4$ time steps, to obtain approximately steady-state conditions. This corresponds to a total strain of 2 N _t u _w /L _y  = 15.6. Highly elongated droplets were already obtained at 10³ time steps with a strain of 1.56, and the average droplet diameter perpendicular to the walls was about 0.1 times the wall separation, or about 10–15 grid points. Reliable results in terms of deformation, tilt angles, and breakup properties are obtained with lattice Boltzmann methods even for this modest grid density (e.g., Xi and Duncan 1999). At later times, the diameters are larger due to coalescence, and this corresponds to more grid points per droplet.

The average capillary number was of the order of 0.1 (below the critical capillary number for single droplets). The diffusion timescale for surfactant adsorption was on the order of 10³ Δt, or 10% of the full duration of the current simulations. The interface Péclet number was on the order of unity, so that diffusion of surfactant and advection in the interface were equally important. The surfactant diffusion coefficient was D _s = 1/3(τ _s − 1/2) (where τ _s is the relaxation time discussed below), and if the characteristic droplet diameter is ≈0.1 L _y , and the mean shear rate is $\dot{\epsilon}= u_w/L_y$, which was typical of the lattice Boltzmann simulations presented here, Pe_s ≈ 1.

Table 1 shows two physical parameter sets with two combinations of lattice units, Δx and Δt, that give droplet sizes in the micrometer and millimeter range. The interfacial tension without surfactant is ≈20 mN/m if a length scale for the system that gives droplet sizes in the millimeter range is chosen. If a length scale corresponding to droplets in the micrometer range is chosen, an interfacial tension (without surfactant) of ≈1 mN/m is obtained. The magnitudes of the surfactant-related coupling constants in the model were adjusted to two different sets of values (Table 2), corresponding to “strong” and “weak” surfactant forces. The equilibrium interfacial tension for the strong surfactant forces was ≈1/2 the equilibrium interfacial tension without surfactant (Skartlien et al. 2011). For the weak surfactant forces, the coupling constants were a factor 100 smaller, and the surfactant did not affect the interfacial tension significantly (giving an interfacial tension that was comparable to the surfactant free value). In the current model, the strength of the surfactant forces (magnitudes of the surfactant-related coupling constants) affects the interfacial tension in the system and not the Péclet number.

Table 1 Physical parameters for two different sets of lattice units, Δx and Δt

Table 2 Interaction coupling constants used with the force model

The total time span T of the simulations depends on the timescale parameter Δt chosen for the system. For the two timescales selected in Table 1, $T=\Delta t N_t = 10^{-2}$ and 1.0 s, with $N_t=10^4$. Peak shear stresses were obtained after about 1,000Δt, or 10^− 3 and 0.1 s for the two examples given in Table 1.

Model parameters

A number of simulations were performed with four different volume fractions: 0.2/0.8, 0.3/0.7, 0.4/0.6, and 0.5/0.5 (with respect to the ratio: fluid A/fluid B). Two additional simulations were also performed with the volume fractions 0.6/0.4 and 0.7/0.3. However, these runs are equivalent simulations with volume fractions of 0.4/0.6 and 0.3/0.7 for a viscosity ratio of unity and serve as additional realizations of these volume fractions. One series with weak surfactant forces and one with strong surfactant forces were simulated, giving a total of 12 runs. The strength of the surfactant forces in the model is determined by the magnitudes of the surfactant related coupling constants. These are given in the last three entries of Table 2, and strong forces correspond to coupling constants that are a factor 10² larger than the weak surfactant coupling constants.

Collisional relaxation times of τ _i  = 1.2 were chosen for both ordinary fluids and τ _S = 3.0 for the surfactant, giving a surfactant that was slightly more viscous than fluids A and B. The rotational relaxation time of the amphiphiles was set to τ _d = 2.0, and the surfactant temperature parameter was set to T _s = 0.1. Further explanation of these parameters can be found in Nekovee et al. (2000).

An average surfactant-to-ordinary fluid density ratio of 0.15 was used, and a similar density ratio was used in the studies of Nekovee et al. (2000). The relatively large surfactant density was chosen mainly for numerical stability reasons, since a small density resulted in a large acceleration of the surfactant fluid. The large surfactant density had no consequence other than altering the bulk properties of fluids via the average viscosity and density with changes on the order of the surfactant-to-ordinary fluid density ratio (0.15).

MPI processing and visualization

The code was implemented in Fortran 90 with message passing interface (MPI) for parallel processing (Sollum and Skartlien 2010). The domain was divided into equal horizontal slabs in the flow direction (x), one for each CPU. With eight or 12 CPUs, the processing time was reduced to about 36 h for $N_t=10^4$ time steps, generating 22 Gb of data per run. A D3Q19 velocity quadrature was used to eliminate the effects of lattice anisometry. The stress tensor was calculated from the force model directly using all the 19 lattice directions. Volume visualizations of iso-contours of the fluid density fields including surfactant and of the shear stress contributions were carried out using the freeware VISIT.

Benchmark testing with droplet deformation

Droplet deformation D and breakup are controlled by the capillary number,

$$ {\rm Ca}=\frac{\mu_{\rm c} a \dot{\gamma}}{\sigma}. $$

(7)

Here, μ _c is the viscosity of the fluid external to the droplet, a is the non-deformed droplet radius, $\dot{\gamma}$ is the applied strain rate, and σ is the interfacial tension (without surfactant). Droplet breakup occurs at a critical value of the capillary number, Ca_cr(λ), which is highly dependent on the viscosity ratio λ = μ _d/μ _c, where μ _d is the droplet viscosity (Grace 1982; deBruijn 1989). Breakup generally occurs when the capillary number is O(1) or greater in the range 0.1 < λ < 4. In the limit Ca ≪ 1 , the droplets are essentially spherical because the capillary forces dominate the viscous forces, and the tilt angle relative to the flow direction is near 45°. In this regime, Taylor (1932) obtained a deformation of

$$ D = {\rm Ca} \frac{19\lambda + 16}{16 \lambda + 16}. $$

(8)

Increasing Ca above 0.1 results in a droplet deformation that increases nonlinearly with increasing capillary number and that is larger than the Taylor limit (e.g., Bazhlekov et al. 2009).

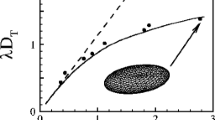
Emulsion simulations were performed with capillary numbers in the range 0.1–0.3—below the critical capillary number for a single droplet with λ = 1. A number of 3D benchmark simulations of single droplets in Couette flows were also conducted, with different viscosity ratios, surfactant strengths, and strain rates. Figure 1 shows that the benchmark results were in excellent agreement with the Taylor limit at small capillary number for λ = 0.24 and λ = 1.03 with weak surfactant forces. As expected, the droplets became more deformed than the Taylor value as the capillary number increased.

Fig. 1

Droplet deformation as a function of capillary number with weak surfactant forces. Left panel λ = 0.24, right panel λ = 1.03. There is excellent agreement with the Taylor limit (thick line) at low capillary numbers. The deformations are larger than the Taylor limit at larger capillary number, as expected

Figure 2 shows the effect of surfactant in benchmark simulations with λ = 0.69. The deformation of the droplets increased as the surfactant forces increased (triangles). With stronger surfactant forces, the deformation deviated appreciably from the Taylor result at lower capillary number, but the Taylor limit was still recovered at very low shear rates. The experimental results of Hu and Lips (2003), using polymeric liquids, also showed that surfactant increased the droplet deformation if λ < 1. In this case, the deformation was due mainly to Marangoni stress, which is captured by the current model. Bazhlekov et al. (2009) conducted similar investigations and found reasonable agreement between their insoluble surfactant model and the results of Hu and Lips (2003).

Fig. 2

Effect of surfactant on the deformation at λ = 0.69. Squares weak surfactant forces, triangles strong surfactant forces, thick line Taylor limit. As the surfactant strength was increased, the droplets became more distorted for a constant capillary number

Effects of volume fraction and surfactant activity

Morphology overview

The simulations were started with uniformly mixed liquid components and surfactant, with small concentration fluctuations. The early stages of phase separation occurred via nucleation and growth of droplets or spinodal decomposition, depending on the composition (nucleation and growth when the volume fractions are much different and spinodal decomposition when both liquid components were present in similar quantities). As time progressed, droplet growth and coalescence increased the average droplet size. The droplet sizes stabilized for long times with smaller droplets for more active surfactant. Coarsening of the morphology formed by spinodal decomposition led to co-continuous phases, with smaller length scale of the interfacial structures for more active surfactant.

Dispersed phases

Separate droplets embedded in a continuous fluid domain were formed for the volume fractions 0.2/0.8 and 0.3/0.7. Figure 3 shows the interface for the volume fraction 0.2/0.8 at early times (left panels) and at late times close to steady-state conditions (right panels). With strong surfactant (lower row), there were more but smaller droplets at late times. For weak surfactant forces (upper right panel), some of the droplets were stretched into longer filaments, and the droplet volumes were on the average larger, as expected for larger capillary numbers. At early times, the surfactant reduced the surface tension, and this caused the droplets to deform more (lower left panel versus the upper left panel), like the behavior found for single droplets.

Fig. 3

Evolution of the morphology of emulsions with volume fractions of 0.2/0.8. Upper row weak surfactant forces, lower row strong surfactant forces, left column t = 3,000 (strain = 4.5), right column, t = 9,000 (strain = 14)

Figure 4 shows how the mean effective diameter and standard deviations of the effective diameters at late times (t = 8,000–10,000) depend on volume fraction (note that the volume fractions 0.3 and 0.7 in this figure are equivalent, as are 0.4 and 0.6). The standard deviations are indicated only for systems in which distinct droplets are dispersed in a continuous fluid domain. For intermediate volume fractions, co-continuous phases were formed. The effective diameters were defined in terms of the volumes V of separate fluid domains by

$$ d_{\rm ef\/f}=2 r_{\rm ef\/f} = 2 \left( \frac{3}{4}\frac{V}{\pi}\right)^{1/3}. $$

(9)

It is evident from the figure that a more active surfactant resulted in smaller mean droplet sizes.

Fig. 4

Droplet diameters at late times: t = 8,000–10,000 (squares weak surfactant, triangles strong surfactant). The standard deviations are indicated for cases in which the droplet distribution was well defined. For the intermediate volume fractions, the phases were co-continuous. For a viscosity ratio of unity, volume fractions of 0.3 and 0.7 and volume fractions of 0.4 and 0.6 are equivalent. The particle diameters were not equal for these equivalent systems because of the different initial states (random composition fluctuations)

For strong surfactant, the mean effective diameter was reduced roughly by a factor of 0.8 compared with the mean effective diameter obtained with the weak surfactant. Another effect was the smaller standard deviations of the droplet size distributions with stronger surfactant.

Figure 5 shows an example of the evolution of the average capillary number, deformation, and orientation angle of the major axis of the droplets, for the strong surfactant case. The volume fractions 0.3 and 0.7 in this figure are equivalent, and they provide two different realizations of the same case. The capillary number (upper row) increased in time because of the increasing droplet sizes. The deformation D (middle panel) increased in time owing to a gradual response to the shear flow and larger droplet sizes. The lower row shows that the average tilt angle relative to the flow direction decreased in time as the droplets adjusted to the flow. The average capillary number was slightly larger for the volume fraction 0.3/0.7 (and 0.7/0.3) compared with the 0.2/0.8 case, due to larger droplet sizes. The average deformation was therefore also slightly larger for the higher volume fraction. For all cases, the average capillary number was in the range 0.1–0.3, and the average deformation factor was in the range 0.2–0.6 corresponding to highly elliptic droplets.

Fig. 5

Average capillary numbers, deformations and tilt angles. Results are shown for simulations conducted with a strong surfactant in which droplets were dispersed in a continuum fluid. These quantities varied in time as the droplet sizes increased, and they responded to the shear. The volume fractions 0.3 (denoted by 37) and 0.7 (denoted by 73) in this figure are equivalent realizations. Again, the results for these equivalent systems were not exactly the same because the initial conditions were not exactly the same

Co-continuous phases

For the intermediate volume fractions 0.4/0.6 and 0.5/0.5, co-continuous domains that resemble a sponge structure were formed, as shown in Fig. 6. The interfaces were connected surfaces with a complex topology, and the emulsion morphologies were elongated, on average, due to the strain. With stronger surfactant forces, the apparent length scale of the interfacial structures appears to be smaller. Figure 7 shows Fourier power spectra of the phase function ϕ = ρ _A − ρ _B (the density difference between the fluids), evaluated in the x–y plane, and averaged over the transverse direction (the z-direction). The iso-contours are plotted on a log-scale. Figure 7 indicates that there was more structure on shorter length scales with stronger surfactant (lower row), since the same iso-contours cover a larger area in the wave vectors space (k _x , k _y ). This widening can be seen in all directions. Note that the major axis of the contour levels of the power spectra is perpendicular to the average interface direction. As expected, the interfaces became more aligned with the flow direction, and the structures became more anisotropic at later times.

Fig. 6

Emulsion morphology for 0.5/0.5 volume fraction at early times. Upper panel weak surfactant forces. Lower panel strong surfactant forces. The fluid domains are bi-continuous, and the characteristic scale of the morphology is smaller with stronger surfactant

Fig. 7

Power spectra of the phase function ρ ₁ − ρ ₂, represented by iso-contours on a logarithmic scale. Right column t = 3,000, left column t = 9,000, top row weak surfactant, bottom row strong surfactant. The dashed line corresponds to the strain, and the full line corresponds to 0.4 times the strain. The latter corresponds to the major axis of the power spectrum, which is aligned perpendicular to the average interfacial direction. In general, there is more structure on shorter length scales with stronger surfactant (lower row). Furthermore, the interfaces are more aligned with the flow direction, and the structures become more anisotropic at later times, as expected. The axes show the wave numbers, k _x and k _y , normalized to the Nyquist frequency

The dashed lines in the power spectra correspond to the total strain, and the full line corresponds to 0.4 times the strain, which appear to correspond to the major axis of the spectrum. There is no clear variation of the tilt angle of the iso-contours as the wave number varies. Furthermore, the tilt angles do not change significantly as the surfactant strength changes. Analogous plots can be obtained experimentally to probe the average morphology in emulsions, using small angle light scattering (SALS). For example, Vermant et al. (1998) found small variations in the tilt angles as a function of wave number (or scattering vector) in SALS images of steady state shear flows. The varying tilt angles corresponded to the variation of the droplet tilt angles as the droplet size changed. They investigated dilute emulsions of polymer blends with a viscosity ratio of 0.27.

Shear stress transients

Figure 8 shows the evolution of the relative viscosity with weak surfactant forces. The volume fractions vary as indicated (with “28” as a short notation for 0.2/0.8, etc.). The relative viscosity is shown with a thick line, and it is defined by

$$ \mu_r = \frac{\overline{\Pi}_{xy}}{\overline{\Pi}_{xy}^{\rm c}} $$

(10)

$$ \overline{\Pi}_{xy}^{\rm c} = \mu_{\rm c} \frac{2U_w}{L_y}, $$

(11)

where $\overline{\Pi}_{xy}$ is the total volume averaged shear stress and $\overline{\Pi}_{xy}^{\rm c}$ is the shear stress for a pure single-phase fluid with viscosity μ _c. U _w is the wall velocity and L _y the distance between the walls. The calculation of the various stress contributions from the simulation data is outlined in “Appendix 1,” and the calculation of the effective viscosity is outlined in “Appendix 2.”

Fig. 8

Contributions to the effective viscosity for weak surfactant forces. The volume fractions are indicated (e.g., “28” for 0.2/0.8). Thick line relative emulsion viscosity. The different contributions are given by the following curves; thin line viscous stress, dashed line total interfacial stress, thick dashed line surfactant contribution to interfacial stress, dash-dot line Reynolds stress

The thin full lines in Fig. 8 correspond to the viscous stress integrated over the computational domain with volume V,

$$ \overline{\Pi}_{xy}^{\rm visc} = \frac{1}{V}\int_V (\mu \partial_y u_x){\rm d}V, $$

(12)

which is almost identical to the reference stress defined by $\overline{\Pi}_{xy}^{\rm c}$ (Eq. 11). The dashed line shows the total interfacial stress, $\overline{\Pi}_{xy}^{\rm int}$. The thick dashed line shows the surfactant contribution to the interfacial stress, which was negligible in these simulations with weak surfactant forces. Finally, the dash-dot line shows the volume integrated Reynolds stress contribution,

$$ \overline{\Pi}_{xy}^{R} = -\frac{1}{V}\int_V (\rho u_x^{'} u_y^{'}){\rm d}V, $$

(13)

which was also negligible. For higher shear rates, we expect that this inertial stress will be important.

Figure 8 demonstrates that the relative emulsion viscosity was significantly larger than unity due to the interfacial stress, and the peak values were comparable to the viscous stress. The total stress and effective viscosity reached maxima near t = 2,000 for all volume fractions. For the droplets, the transient stress is a consequence of the starting flow, in which the droplets are gradually distorted into tilted ellipsoids so that the net interfacial stress increases with time (dashed lines). The gradual deformation of the droplets is a consequence of work done by the shear stress. This work is partially stored in the form of increased interfacial energy (larger interfacial areas), and part of it is dissipated by viscosity due to the perturbations in the velocity field. Consequently, the rheology of the emulsion is viscoelastic. Remarkably, similar responses were also found for the co-continuous cases, and the reason for this is a similar change of the average interfacial orientation with time.

At the lowest volume fraction, a time lag due to delayed formation of interfaces was observed. Consequently, the interfacial forces and the associated shear stress profiles also show a delay. At low volume fraction, phase separation proceeds via nucleation and growth in the initial phases of the simulation. At 50/50 volume fraction, the phase separation proceeds via spinodal decomposition, and there is no such delay. At intermediate volume fractions, phase separation also occurs without a delay.

The total interfacial area decreased from the beginning of the simulations because of coalescence and/or coarsening of the morphology during surfactant modified spinodal decomposition. Figure 9 shows an example of the evolution of the interfacial area for one of the droplet cases. However, the area reduction was not sufficient to prevent the initial increase of the stress due to droplet tilting and deformation, and we therefore obtained results that are comparable to experiments with stable emulsions (e.g., Jansseune et al. 2001) where a stress maximum in time was observed. The reduction in interfacial area and tilting of the droplets at later times further reduced the interfacial stress.

Fig. 9

Total interfacial area as a function of time. For the volume fractions 0.3/0.7 and weak surfactant forces. The interfacial area decreases before the total shear stress reaches a maximum near t = 2,000

Jansseune et al. (2001) investigated starting Couette flow for a blend of nearly Newtonian, high viscosity immiscible polymers using a cone and plate rheometer. The blend consisted of 10% by volume of PDMS in PIB, with a viscosity ratio of 1.61, and PDMS droplets were dispersed in a PIB continuum. The interfacial tension was relatively low (3 mN/m), but they were able to separate the interfacial stress from the other stress components. For significant droplet deformation, the morphology evolution could be described in terms of affine deformation models. The interfacial shear stress evolution in these experiments and in the current simulations are qualitatively similar, with a rapid increase of the interfacial shear stress immediately after start-up followed by a gradual decay as the droplets align with the flow. The main difference between the simulation results and these experiments is that the simulated emulsion started out as a completely mixed system followed by droplet nucleation, growth, coalescence, and a diminishing interfacial area, while the experiments utilized stable emulsions prior to shearing.

Figure 10 shows the individual contributions to the effective viscosity during simulations with strong surfactant forces. The surfactant provided a negative contribution to the shear stress (thick dashed lines), originating from the interfaces where the surfactant accumulated. The contribution was negative because the surfactant lowered the interfacial tension and the interfacial energy (for a comparable geometry). The interfacial energy for a planar interface based on the surfactant model used in this work is discussed in “Appendix 3.” The time dependence of the surfactant contribution was similar to that of the total interfacial stress (but with opposite sign) since both quantities depend on the varying orientation and shape of the interfaces. The interfacial stress with surfactant was also influenced by altered interfacial orientations and variations in the local interfacial tension (the surfactant is not uniformly distributed over the interface in a flowing system).

Fig. 10

Contributions to the effective viscosity. Strong surfactant forces. The coding is the same as in Fig. 8

Volume fraction effects

Figure 11 compares the relative viscosities determined for strong and weak surfactant forces. The figure indicates that the shear stresses were similar for the lower volume fractions, but stronger surfactant forces reduced the shear stress significantly at higher volume fractions (thick lines). For low volume fractions, droplets were dispersed in a continuous fluid domain, while for higher volume fractions, a complex sponge structure formed (Fig. 6).

Fig. 11

Effective viscosities. Thin line weak surfactant, thick line strong surfactant. Here the time axis is replaced by the total strain or shear deformation, which increases linearly with increasing time (this is calculated using the strain rate corresponding to the wall separation and velocities, multiplied by time). This normalization can be used when simulation results are compared with experimental results obtained on various time and length scales

Stress maxima at early times

The maximum stress (near t = 2,000) increased with volume fraction up to 0.5/0.5, as shown in Fig. 12 (upper left panel). The upper right panel shows the interfacial areas averaged over the time interval t = 2,000–3,000. Both the stresses and the areas increased with increasing volume fraction, and the interfacial area was significantly larger with stronger surfactant (triangles). It is reasonable to expect that lowering of the interfacial tension with stronger surfactant would lead to emulsion morphology with smaller characteristic length scales and larger interfacial area. The increase in interfacial area with increasing volume fraction contributed to the increase in stress, but the stresses for stronger surfactant were, in fact, comparable or lower than those for the weak surfactant case, even if the interfacial area was larger. It is very interesting that the stresses were significantly lower for stronger surfactant only for the higher volume fractions.

Fig. 12

Relative viscosities. Upper left maximum relative viscosity (near t = 2,000). Upper right interfacial areas averaged over the interval t = 2,000–3,000. Triangles strong surfactant forces, squares weak surfactant forces, lower row Relative viscosity and interfacial areas at late times averaged over the interval t = 8,000–10,000. The volume fraction denoted 0.3 was averaged over the volume fractions 0.3/0.7 and 0.7/0.3 and likewise for 0.4 (0.4/0.6 and 0.6/0.4)

Late times near steady state

At later times, approximate steady-state conditions were reached. The lower right panel in Fig. 12 shows the interfacial areas averaged over the time interval t = 8,000–10,000, and the lower left panel shows the stresses averaged over the same time interval. Once again, stronger surfactant forces increased the interfacial area. The highest stresses occurred at a volume fraction of 0.5/0.5, and the shear stresses were suppressed with strong surfactant only for the higher volume fractions, as for the earlier times.

The lower left panel indicates, somewhat surprisingly, that the relative viscosity may decrease with increasing volume fraction. This behavior is consistent with the results of Loewenberg and Hinch (1996), which covered volume fractions up to 30%. A decrease in viscosity with increasing volume fraction was observed when the capillary number was larger than about 0.25, for a viscosity ratio of unity. The droplets were more aligned with the flow for large volume fractions, and this reduced the emulsion viscosity. The average capillary number in the current simulations was in the range 0.1–0.3, and our results are consistent with Loewenberg and Hinch (1996).

There was only a modest increase of the emulsion viscosity near a volume fraction of 0.5/0.5, relative to the lower volume fractions. This is consistent with the experimental results of Vinckier et al. (1999) and Jansseune et al. (2003) for PDMS/PIB polymer blends with a viscosity ratio of order unity, which had a “fibrillar” morphology under shear for a 0.5/0.5 composition.

Morphology and surfactant effects

An important effect of surfactants is reduction of the interfacial tension, which depends on the local surfactant interfacial density, and this can directly reduce the interfacial shear stress. At a lower interfacial tension, the fluid can deform the interface more easily, and this leads to smaller characteristic interfacial scales. In addition, nonuniform surfactant interfacial densities generate surface tension gradients, which is the origin of Marangoni phenomena. For example, the surfactant accumulates at the higher curvature droplet tips, and this generates Marangoni stresses which alter droplet shapes (e.g., Bazhlekov et al. 2009).

Figure 12 implies that, in the simulations, the sensitivity of the shear stress to the surfactant depended on the topology of the interface. At lower volume fractions, where well-defined droplets existed, the shear stress was insensitive to the surfactant activity. This can be explained in terms of a pure interfacial tension effect; increased interfacial area (more and smaller droplets with stronger surfactant) is compensated by reduced interfacial tension. We will show below that this picture is somewhat simplified since the changes in the droplet shape also come into play.

In the co-continuous regime, it appears from Fig. 12 that the surfactant reduced the shear stresses efficiently during early time transients and at late times as the steady state was approached. The reason for this is that the interfacial structure was altered with stronger surfactant, and surfactant accumulated near high curvature portions of the interface by advection. This gave a lowered total interfacial stress, even though the interfacial area was larger. The details are discussed below.

Stress statistics for the droplet regime

The left panel in Fig. 13 shows a histogram of the interfacial stress distributions for the lowest volume fraction (0.2/0.8). The asymmetric shape is due to droplet elongation, where a larger area of the interface is associated with positive stress (as compared to areas with negative stress), and this provides a net positive interfacial stress. The distributions appear to have similar shapes, independent of surfactant strength. However, the distributions are slightly wider with stronger surfactant, even though the interfacial tension is lowered. This reflects a difference in droplet shapes or morphology.

Fig. 13

Interfacial stress distributions for 0.2/0.8 volume fraction at late times. The thick vertical line indicates zero stress, and the two thin vertical lines indicate the stress levels 0.001 and 0.003 that are discussed in the text. Left panel total interfacial shear stress $\overline{\Pi}_{xy}^{\rm int}=\overline{\Pi}_{xy}^{\rm oo}+ \overline{\Pi}_{xy}^{\rm S}$ (thin line weak surfactant, thick line strong surfactant). Middle panel shear stress from the mutual forces between the ordinary fluids, $\overline{\Pi}_{xy}^{\rm oo}$ (thin weak surfactant, dashed strong surfactant). With weak surfactant, $\overline{\Pi}_{xy}^{\rm int} \simeq {\overline{\Pi}_{xy}^{\rm oo}}$. Right panel shear stresses for the strong surfactant case (dashed $\overline{\Pi}_{xy}^{\rm oo}$, thick total stress $\overline{\Pi}_{xy}^{\rm int}$). The line styles label the same quantity in all figures

The middle panel in Fig. 13 shows the contributions to the stresses from the forces between ordinary fluids only (see “Appendix 1”), hereafter denoted as “OO-stresses,” where “OO” stands for the ordinary fluid-to-ordinary fluid interaction. These stresses are directly related to the morphology (orientations and shapes of the droplets) through the interface anisotropy tensor (Eq. 2) via

$$ \overline{\Pi}_{\alpha \beta}^{\rm oo} = -\sigma^* q_{\alpha \beta}, $$

(14)

where σ ^* is a constant interfacial tension. The OO-stress $\overline{\Pi}_{\alpha \beta}^{\rm oo}$ is then simply a measure of the interface anisotropy tensor. Onuki (1987) provided a similar relation,

$$ {\overline{\Pi}_{xy}^{\rm oo}}=-a {\sigma^* } \; \langle n_x n_y \rangle, $$

(15)

where a is the interfacial area per unit volume and $\langle n_x n_y \rangle$ is the area averaged local interface tensor, where n _x and n _y are components of the unit vector normal to the interface. The maximum value of n _x n _y occurs at an interface orientation angle of 45° and the minimum value of zero at 0° or 90°. This stress contribution does not involve the surfactant forces directly, but the surfactant influences the orientation and morphology of the interface and hence $\langle n_x n_y \rangle$.

The middle panel of Fig. 13 shows wider tails also for the OO-distribution with stronger surfactant (dashed line). More droplets and lower interfacial tension appear to promote larger peak values of the OO-stresses. The volume rendering in Fig. 14 shows the 0.001 (yellow) and 0.003 (red) OO-stress levels for both strong (upper panel) and weak (lower panel) surfactant, and it can be seen that stronger surfactant increased the number of droplets. The more numerous red (higher stress) areas in the upper panel display, in a direct way, the more extended tails for the OO-stresses. The total size of the yellow areas for the 0.001 level are comparable for the two cases, as shown by the comparable counts in the middle panel in Fig. 13. The reason for this is that with the lower surfactant strength, the droplets were more elongated with larger yellow (lower stress) areas, and this compensated for the effect of fewer droplets.

Fig. 14

Stress contributions for 0.2/0.8 volume fraction at late times. Upper panel positive contours of the ordinary fluid–ordinary fluid stress (0.001—yellow, 0.003—red), for strong surfactant. Lower panel positive contours of the ordinary fluid–ordinary fluid stress, for weak surfactant, same contour levels

The total interfacial stress is given by

$$ \overline{\Pi}_{\alpha \beta}^{\rm int} = -\sigma^* q_{\alpha \beta} + \overline{\Pi}_{\alpha \beta}^{\rm S}, $$

(16)

where $\overline{\Pi}_{\alpha \beta}^{\rm S}$ depends on both the local interfacial orientation and the local surfactant density. The total stress was also calculated by using the force model directly (“Appendix 1”). In general, $-\sigma^* q_{\alpha \beta}$ is positive and $\overline{\Pi}_{\alpha \beta}^{\rm S}$ is negative because the surfactant reduces the interfacial tension. The wider tails for the OO-stresses for the stronger surfactant were to some degree compensated by the surfactant-related stresses $\overline{\Pi}_{xy}^{\rm S}$. This is illustrated in the right panel of Fig. 13, which displays the OO-stresses again (dashed) and the narrower total stress distribution with the surfactant stress included (full thick line). The surfactant contribution did not fully compensate for the wide OO-stress tails, and in the end, a wider total stress distribution was obtained with stronger surfactant (left panel, full thick line, Fig. 13). Even so, the total stress did not increase noticeably for stronger surfactant.

Stress statistics for the co-continuous regime

Figure 15 shows the interfacial stress distribution functions, or histograms for 0.5/0.5 volume fraction. Again, the asymmetric shape of the distributions indicates a net positive interfacial stress. The left panel demonstrates that the net stress was lower with stronger surfactant (thick line) mainly due to a reduction of the number of positive stress values (the counts are reduced in particular near 0.001 as indicated by the vertical line).

Fig. 15

Interfacial stress distributions for 0.5/0.5 volume fraction at late times. Left panel: thin line weak surfactant, thick line strong surfactant. The net stress was lower with surfactant due to a reduction of the number of positive stress values, preferentially near 0.001. The coding is the same as in Fig. 13

The same effect can be seen for the distribution of OO-stresses (middle panel), but there is also an increased number of the higher stress values (dashed line for strong surfactant). This suggests that the change of interfacial stress with stronger surfactant was partially due to a modified interfacial structure, since the shape of the OO-stress distribution is quite different with the strong surfactant.

Figure 16 shows volume renderings of the OO-stresses in red and yellow together with the interface in green. The upper panel shows the OO-stress for weak surfactant with contours at 0.003 (red) and 0.001 (yellow), corresponding to the vertical lines in the middle panel of Fig. 15. The lower values (yellow) correspond to relatively large connected areas with significant tilt angles relative to the mean flow. Note that the total interfacial shear stress is now approximately $\overline{\Pi}_{xy}^{\rm int} \simeq \overline{\Pi}_{xy}^{\rm oo}$.

Fig. 16

Stress contributions for 0.5/0.5 volume fraction at late times. Upper panel ordinary fluid–ordinary fluid stress for weak surfactant, contours at 0.001 and 0.003. Lower panel ordinary fluid–ordinary fluid stress for strong surfactant, contours at 0.001 and 0.003

The lower panel in Fig. 16 shows the OO-stress for the strong surfactant case (with the same contour levels), corresponding to the dashed line in the middle panel of Fig. 15. The increased areas of the 0.003 level is evident from the volume rendering, with more numerous red patches in the lower panel. Figure 17 shows a side view of the morphology of the total stress distribution for weak surfactant (upper panel) and strong surfactant (lower panel). The same contour levels are shown in red and yellow. Both cases display highly organized, skewed, and smooth structures for the areas that provide the dominating stress contributions (yellow). More smaller scale structure can also be seen with stronger surfactant.

Fig. 17

Total interfacial stress contributions for 0.5/0.5 volume fraction at late times. Red: stress = 0.003, yellow: stress = 0.001. The red patches correspond to the extended positive tail of the corresponding distribution function. Lower panel total stress for strong surfactant, upper panel total stress for weak surfactant. The qualitative appearance is similar to the strong surfactant case, even though the volume averaged stress was higher due to a larger area with stress levels near 0.001 (yellow)

The higher OO-stresses (red) seem to be associated with higher interface curvatures. The power spectra shown earlier indicate more smaller scale structures (higher curvatures) with stronger surfactant. The histogram in the right panel of Fig. 15 indicates that these higher stress values were counteracted by relatively strong negative surfactant contributions. Figure 18 displays a perspective more in the flow direction. Higher surfactant densities are shown in yellow and the full interface in opaque grey. It is clear that surfactant accumulated where the OO-stresses were large (red), resulting in a suppressed shear stress. Furthermore, these interfacial areas are associated with transverse liquid threads and sheets between larger domains of the same fluid.

Fig. 18

Interfacial stress contributions for 0.5/0.5 volume fraction at late times. Grey: interface, red: Ordinary fluid–ordinary fluid stress = 0.003, yellow: higher surfactant density. In this simulation, the surfactant tended to accumulate where the interfacial tensor values (OO-stresses) were relatively large (red), and this prevented large peak stress values. The left panel shows the front half of the domain, while the right panel shows the back half

The main contribution to the total interfacial stress for the strong surfactant case came from the lower curvature (smoother) portions of the interface (shown in yellow in Fig. 17). These areas were more aligned with the flow so that they provide lower shear stress contributions. For weak surfactant, these smooth portions of the interface occupied a larger area, so that the total interfacial stress became larger.

Discussion

The peak values in time for the interfacial stresses were relatively large and comparable to the viscous stresses. This is not necessarily a general result when the viscosity ratio is significantly different from unity because the interfacial contribution to the viscous stress (the third term on the right-hand side of Eq. 1) comes into play. For example, Jansseune et al. (2001) performed transient experiments with polymer blends consisting of 10% PDMS in PIB, with a viscosity ratio of 1.61 and a relatively low interfacial tension of 3 mN/m. Even though the viscosities were comparable, they found that the interfacial contribution to the viscous stress was larger than the interfacial stresses. Our simulations are representative of systems in which the interfacial tension (that increases the interfacial stress) is larger and the viscosity ratio is of order unity.

The interfacial area is a key factor in determining the rheology, together with the emulsion morphology. In most cases, we found that the interfacial area increased with volume fraction up to 0.5/0.5, as shown in Fig. 12. Using 2D simulations, Roths et al. (2002) found that the interfacial area actually decreased with increasing volume fraction due to coalescence and formation of interconnected structures that extended over the full computational domain in the flow direction. Dimensionality and finite size effects are important issues for simulation work. The probability of coalescence and droplet–droplet interaction is lower in 3D so that a larger interfacial area can be maintained even without surfactant. Furthermore, the breakup rates are larger in 3D for capillary breakup modes because there are two principal radii of curvature (rather than one in 2D), and this increases the pressure perturbations in droplet filaments.

Vinckier et al. (1999) found that the effective viscosity of an immiscible blend of approximately Newtonian polymers was significantly lower than the predictions of classical models. The morphology was not determined, but the authors suggested that it was co-continuous. A similar effect was observed by Jansseune et al. (2003) who found an interfacial shear stress plateau over a broad interval of volume fractions. For a 50/50 PDMS/PIB composition, the morphology was “fibrillar” at high shear rates and droplets dispersed in a continuous phase at lower shear rates. The fibrillar structure observed by Jansseune et al. (2003) resembles the interfacial structure in our simulations, as shown in Fig. 17.

A similar suppression of the shear stress has also been found in many crude oil- and water-based emulsions. For example, the data of Keleşoğlu et al. (submitted for publication) show a clear suppression effect close to the phase inversion point, relative to the prediction of the model of Pal and Rhodes (1989). A well-known explanation is that droplets are more aligned with the flow for higher volume fractions (e.g., Loewenberg and Hinch 1996). Our results indicate that a similar effect can occur with co-continuous phases, as already suggested by Vinckier et al. (1999) and Jansseune et al. (2003).

The transition from a droplet field to a co-continuous morphology seems to be associated with the stretching of droplets into longer filaments that can coalesce with other filaments (Willemse et al. 1999). The role of surfactant is therefore potentially important in this respect as well. More surfactant corresponds to lower interfacial tension, higher capillary number, and more droplet deformation, with a potentially lower transition point (lower volume fraction) for phase inversion. On the other hand, increased surfactant concentration is associated with smaller coalescence rates and a smaller mean droplet diameter, which implies less deformation. A transition to co-continuous morphology was observed between the volume fractions 0.3 and 0.4 for both strong and weak surfactant forces in the current system. Preliminary results show that an earlier transition point is obtained with higher continuous phase viscosity (lower viscosity ratio), in accordance with (Willemse et al. 1999).

Conclusion

Simulations of emulsions with a simple model for amphiphilic nonionic surfactants were performed on relatively large grids of dimension 128 × 128 × 256 using a three component (fluid A, fluid B, and surfactant) lattice Boltzmann model. The experimental measurement of the dynamics of surfactants on surfaces and interfaces is extremely challenging, and this is currently possible only for simple geometries (Fallest et al. 2010). Consequently, only numerical methods, such as lattice Boltzmann simulations, can reveal details such as the correlation between the concentration of the surfactant and the interface curvature under dynamic conditions, as illustrated in Fig. 18 for a bi-continuous morphology. For low volume fractions, the emulsion rheology can be predicted, to some extent, from the stress distribution on single, surfactant covered droplets. For higher volume fractions with complex morphologies (e.g., bi-continuous morphologies), the influence of the surfactant on the rheology cannot be reliably estimated without a fairly advanced numerical model. We have demonstrated how the surfactant influences the shear rheology for both high volume fraction (in a bi-continuous morphology) and for low volume fractions (for a droplet field), and the main differences are summarized below.

For high volume fractions with bi-continuous phases, the total interfacial shear stress (and shear viscosity) decreased as the magnitude of the surfactant-related forces increased. In the current model, stronger surfactant-related forces correspond to lower interfacial tension. More smaller scale structures with higher interface curvatures were formed with lower interfacial tension as shown by the volume renderings and power spectra of the fluid density fields. The surfactant density tended to be larger in higher curvature areas of the interface due to significant advective transport by the flow field (with a Péclet number of order unity), and this suppressed potentially large stress values there (Fig. 18). Stronger surfactant forces reduced the shear stresses more efficiently in these higher curvature areas, and the main contribution to the total interfacial stress then came from the lower curvature areas. These areas were more aligned with the flow for the stronger surfactant forces, so that stronger surfactant forces provided lower average shear stress values and a lower shear viscosity.

For the smaller volume fractions, for which the morphology consisted of droplets dispersed in a continuum, the surfactant modified the volume, shape, and orientation of the droplets, as expected. Weak surfactant forces resulted in larger, fewer, and more elongated/stretched droplets, while the stronger surfactant forces (lower interfacial tension) resulted in smaller and more numerous droplets. Large local interfacial stresses are associated with regions of high interfacial curvature such as the end caps of elongated droplets, and more numerous droplets can therefore potentially increase the total shear stress. Since the Péclet number was of order unity, the advection and diffusion of surfactant were equally important in the interface. Similar to the bi-continuous case, advection served to increase the surfactant concentration in the end caps (or higher curvature areas), and this prevented a significant increase of the shear stress. The total interfacial shear stress (and emulsion shear viscosity) was in this case nearly unchanged with respect to surfactant strength even though the number of droplets were larger for the stronger surfactant.

We emphasize that, for bi-continuous/high volume fractions cases, the average interfacial shear stress was significantly reduced with stronger surfactant forces (lower interfacial tension), in contrast to the low volume fraction/dispersed cases where the average shear stress was nearly unchanged. For the dependence of the emulsion viscosity and morphology on the volume fraction, we found qualitative agreement between our results and experimental data for polymer blends. The polymer blends of Vinckier et al. (1999), Yu et al. (2005), and Jansseune et al. (2003) were dispersed at low volume fraction and co-continuous at higher volume fractions, similar to our cases. These authors found only a moderate increase of the emulsion viscosity at higher volume fractions when the phases were co-continuous, similar to our results.

Appendix 1: Stress calculations

The stresses in the simulated emulsions can be determined from the forces between the fluids and the kinetic stresses that are available from the Boltzmann distribution. The virial theorem is commonly used to calculate the macroscopic (continuum) stress in molecular dynamics computations, and the same concept was used to calculate the virial stress from the populations in the Boltzmann distribution and from the mesoscale forces in the model. The virial stress is given by (e.g., Xu and Liu 2009)

$$ \Pi_{\alpha \beta}^{\rm vir}=\frac{1}{V}\left( -\sum_k m_k v_\alpha^kv_\beta^k +\frac{1}{2}\sum_{k,l\neq k} r^{kl}_\alpha \mathcal{F}^{kl}_\beta \right). $$

(17)

Here $\mathcal{F}^{kl}$ is the force on a particle k due to particle l, r ^kl = r ^l − r ^k is the separation vector pointing from particle k to particle l, V is the averaging volume, m _k is the particle mass, and $v_\alpha^k$ is the velocity components of the same particle.

The stress has the form $\Pi_{\alpha \beta}^{\rm vir}=\Pi_{\alpha \beta}^{\rm kin}+\Pi_{\alpha \beta}^{\rm int}$, where $\Pi_{\alpha \beta}^{\rm kin}$ is the kinetic (momentum flux density) and $\Pi_{\alpha \beta}^{\rm int}$ is the contribution from attractive and repulsive interactions. In general, the kinetic stress is nonzero throughout the flow volume. In terms of the population distributions in the discrete lattice Boltzmann model, the kinetic contribution for each fluid is given by

$$ \Pi_{\alpha \beta}^{\rm kin}=-\sum\limits_i f_i c_{i\alpha}c_{i\beta}=-\rho u_\alpha u_\beta - p\delta_{\alpha\beta} + \Pi_{\alpha \beta}^{\rm visc}, $$

(18)

where $\Pi_{\alpha \beta}^{\rm visc} \simeq \rho \nu(\partial_\alpha u_\beta + \partial_\beta u_\alpha)$ is the Newtonian (viscous) stress to leading order if the velocity divergence can be ignored (Dellar 2001) and p is the isotropic pressure component. Here, f _i corresponds to the particle population in a single lattice cell with volume V _c. In Eq. 18, superscripts indicating the chemical component are omitted. Since all three components (fluid A, fluid B, and surfactant) are present in each phase, the contributions from the individual components must be summed.

To calculate the interaction stress or interfacial stress, neighboring cells must be included, since the forces act between neighbor cells and not within the local cell and the corresponding volume is 2V _c. The interaction contribution to the stress is given by

$$ \Pi_{\alpha \beta}^{\rm int}=\frac{1}{2V_{\rm c}} \frac{1}{2} \sum\limits_i \left( e_\alpha^{0i} \mathcal{F}_\beta^{0i} + e_\alpha^{i0}\mathcal{F}_\beta^{i0}\right) = \frac{1}{2} \sum\limits_i e_\alpha^{0i} F_\beta^{0i}, $$

(19)

where $e_\alpha^{0i}$ is the lattice separation vector pointing from the local cell “0” to the neighbor cell “i” and $\mathcal{F}_\beta^{0i}$ is the total force on the local cell from the neighbor cell. Similarly, $e_\alpha^{i0}$ is the lattice separation vector pointing from the neighbor cell “i” to the local cell “0,” and $\mathcal{F}_\beta^{i0}$ is the total force on the neighbor cell, due to the local cell. In the case of two ordinary fluids,

$$ F_{\beta}^{0i}(\mathbf{x}) = \mathcal{G}_{\rm AB}\psi^{\rm A}(\mathbf{x}) \psi^{\rm B}(\mathbf{x}+\mathbf{c}_i) c_{i\beta}, $$

(20)

where ψ ^A and ψ ^B are monotonically increasing functions of the fluid densities and $\mathcal{G}_{\rm AB}$ is the interaction strength between A and B. With this relation, we verify the form of González-Segredo et al. (2006),

$$ \begin{array}{rll}\Pi_{\alpha \beta}^{\rm oo} &=& \frac{1}{4}\sum\limits_{\sigma,\overline{\sigma}} \mathcal{G}_{\rm AB} \\ &&\times \sum\limits_i [ \psi^\sigma(\mathbf{x}) \psi^{\overline{\sigma}}(\mathbf{x}+\mathbf{c}_i) + \psi^{\overline{\sigma}}(\mathbf{x}) \psi^\sigma (\mathbf{x}+\mathbf{c}_i)]c_{i\alpha}c_{i\beta}, \end{array} $$

where the first summation runs over the two fluid components. Volume averaging yields the interface tensor due to ordinary fluid forces, $\overline {\Pi}_{\alpha \beta}^{\rm oo}$. When surfactant forces are included, a volume averaged interfacial stress of $\overline {\Pi}_{\alpha \beta}^{\rm int} = \overline {\Pi}_{\alpha \beta}^{\rm oo} + \overline {\Pi}_{\alpha \beta}^{\rm S}$ is obtained.

Appendix 2: Calculation of the emulsion viscosity

In general, the average stress in any chosen volume V is given by

$$ \overline{\Pi}_{\alpha \beta}=\frac{1}{V}\int_V \sum\limits_\sigma (\Pi_{\alpha \beta}^{\rm kin}+\Pi_{\alpha \beta}^{\rm int}) {\rm d}V. $$

(21)

The deviation $\Delta \overline{\Pi}$ from the stress in a single-phase fluid with

$$ \Pi_{\alpha \beta}^{\rm kin,0}=-\rho u_\alpha^0 u_\beta^0 - p^0\delta_{\alpha\beta} + \Pi_{\alpha \beta}^{\rm visc,0} $$

(22)

$$\Pi_{\alpha \beta}^{\rm int,0}= 0, $$

(23)

is a central quantity. The viscous stress in the single-phase fluid is $\Pi_{\alpha \beta}^{\rm visc,0}$. In simple shear, the relations for the shear stress

$$ \Pi_{xy}^{\rm kin,0}= \Pi_{\alpha \beta}^{\rm visc,0} = \mu^{0}\partial_yu_x^0 $$

(24)

$$ \Delta \overline{\Pi}_{xy} = \frac{1}{V}\int_V \sum\limits_\sigma \left(-\rho u'_x u'_y+\mu\left(\partial_y u_x\right) + \Pi_{xy}^{\rm int}\right) {\rm d}V \\ - \mu^{0}\partial_yu_x^0. $$

(25)

are obtained assuming no pressure change. Here, u′ _x u′ _y is the macroscopic stress due to the velocity perturbations in the emulsion, and the corresponding volume average is referred to as a Reynolds stress. The excess shear viscosity for the emulsion is defined as

$$ \mu_e-\mu^{0}=\frac{\Delta \overline{\Pi}_{xy}}{\partial_yu_x^0}, $$

(26)

and the relative viscosity is defined by

$$ \mu_r = \frac{\overline{\Pi}_{xy}}{\overline{\Pi}_{xy}^{0}}=\frac{\overline{\Pi}_{xy}}{\mu^{0}\partial_yu_x^0} . $$

(27)

Appendix 3: Energy density of the planar interface

For a planar interface perpendicular to say the z-direction, the non-isotropic contribution to the total pressure in the model is given by (Furtado and Skartlien 2010),

$$ P^{ni}= \kappa \left( \frac{{\rm d}\phi}{{\rm d}z} \right)^2 + b M_z \frac{{\rm d}\phi}{{\rm d}z}, $$

(28)

where ${\bf M} = M_z \hat{{\bf z}}$ is the dipole vector of the surfactant and ϕ = (n ^A − n ^B)/n is the phase ordering function. The total fluid density n ≈ n ^A + n ^B is assumed to be constant, and b and κ depend on a number of lattice quadrature weights. These relations can be found in Furtado and Skartlien (2010). The first term in Eq. 28 corresponds to the interfacial tension or energy density of a surfactant-free interface. The second term in (Eq. 28) arises from the adsorption of surfactant molecules to the interface. If the signs of the interaction parameters $\mathcal{G}_{\rm AS}$ and $\mathcal{{G}}_{\rm BS}$ are as specified in Table 2, then the surfactant contribution results in a reduction of the interfacial tension when the dipole is aligned with its equilibrium direction perpendicular to the interface.