Entropic, electrostatic, and interfacial regimes in concentrated disordered ionic emulsions

Abstract

We develop a free energy model that describes two key thermodynamic properties, the osmotic pressure Π and the linear elastic shear modulus G′_p (i.e. plateau storage modulus), of concentrated monodisperse emulsions which have isotropic, disordered, droplet structures, and are stabilized using ionic surfactants. This model effectively incorporates the concept of random close packing or jamming of repulsive spheres into a free energy F that depends on droplet volume fraction ϕ and shear strain γ both below and above the a critical jamming point ϕ _c ≈ 0.646. This free energy has three terms: entropic, electrostatic, and interfacial (EEI). By minimizing F with respect to an average droplet deformation parameter that links all three terms, we show that the entropic term is dominant for ϕ well below ϕ _c, the electrostatic term is dominant for ϕ near but below ϕ _c, and the interfacial term dominates for larger ϕ. This EEI model describes measurements of G′_p(ϕ) for charge-stabilized uniform emulsions having a wide range of droplet sizes, ranging from nanoscale to microscale, and it also is consistent with measurements of Π(ϕ). Moreover, it describes G′_p(ϕ) for similar nanoemulsions after adding non-amphiphilic salt, when changes in the interfacial tension and the Debye screening length are properly taken into account. By unifying existing approaches, the EEI model predicts constitutive properties of concentrated ionic emulsions that have disordered, out-of-equilibrium structures through near-equilibrium free energy minimization, consistent with random driving Brownian excitations.

Introduction

Emulsions are one of the most important classes of soft materials. A first liquid is dispersed as droplets in a second immiscible liquid phase; the first liquid and second liquid are known as the dispersed phase (DP) as the continuous phase (CP), respectively. Typically, a surface-active agent, or surfactant, which is soluble in the CP but not in the DP, is added to inhibit coalescence of the droplets after they have been formed. Amphiphilic surfactants preferentially adsorb at the interfaces of the droplets, thereby providing repulsive forces that reduce or eliminate droplet recombination. Provided that the DP is highly insoluble in the CP, slow coarsening of the droplet size distribution via Ostwald ripening is negligible over practical measurement time scales ranging up to years (Taylor 1998), so such surfactant-stabilized emulsions can have droplet size distributions that are effectively time-independent. Many emulsions are stabilized using ionic surfactants, such as anionic sodium dodecyl sulfate (SDS), which are highly soluble in an aqueous or polar CP but not significantly soluble in a non-aqueous or non-polar DP. For such ionic emulsions, short-range screened-charge repulsions between droplet interfaces, imparted by adsorbed amphiphilic ions, inhibit droplet coalescence, even when the droplets are concentrated through the application of an osmotic pressure Π to high droplet volume fractions ϕ approaching and beyond the point at which droplets begin to deform as they interact with neighboring droplets.

For colloidal ionic emulsions, during the process of osmotic compression from a dilute gas-like dispersion of droplets, work is done against entropy, which is the origin of the osmotic pressure of Brownian droplets at low ϕ. As ϕ is increased further, work is done against electrostatic screened-charge repulsions and also against the interfacial tension σ of droplet interfaces populated with adsorbed ionic amphiphilic molecules. This interfacial tension sets the scale of the energetic cost of deforming droplets and creating additional interfacial area in the emulsion. Thus, there are three essential contributions to the free energy that are required to describe colloidal ionic emulsions: entropic, electrostatic, and interfacial. For emulsions having droplet radii larger than a few microns, the entropic term is typically negligible, and even the electrostatic term can often be neglected, if the Debye screening length λ_D is much smaller than the average droplet radius <a>. However, for colloidal emulsions, which have droplet radii ranging from several nanometers to several microns, accounting for all three terms is necessary when predicting their equilibrium properties, such as Π and the linear elastic shear modulus G′_p (i.e. plateau storage modulus).

For uniform emulsions that have highly peaked monomodal size distributions, the positional structure of the droplets in the emulsion also plays an important role. When rapidly concentrated by applying a substantial osmotic pressure, for instance through ultracentrifugation, droplets in these monodisperse emulsions remain disordered even as the emulsion solidifies (Mason et al. 1995). Thus, the colloidal disorder-order transition (Russel et al. 1989) is bypassed, and the droplets remain in a disordered structure as a consequence of quenching ϕ in the presence of Brownian excitations, which leads to a glassy ergodic-nonergodic transition (Pusey and van Megen 1987) and then to jamming and isotropic viscoelastic emulsions that have statistically reproducible macroscopic physical properties. The maximally probable jamming point (Torquato et al. 2000; O’Hern et al. 2003), a more precisely defined notion related to random close packing (Bernal and Mason 1960; Finnery and Woodcock 2014), for monodisperse spheres occurs at a critical volume fraction of ϕ _c ≈ 0.646. Going beyond earlier work of Princen (Princen and Kiss 1986), Mason (Mason et al. 1995, 1997) measured G′_p(ϕ) of disordered microscale monodisperse emulsions stabilized by an ionic surfactant and previously established that this ϕ _c effectively set the beginning of the rise in measurements of G′_p(ϕ) after accounting for electrostatic repulsions between droplets in an ad hoc manner. Later rheological measurements by Wilking and Mason (Wilking and Mason 2007) on uniform repulsive ionic nanoemulsions showed that jamming can be seen at ϕ well below ϕ _c, thereby revealing the increasing importance of electrostatic repulsions for nanoemulsion systems as the droplet radius gets closer to the Debye screening length.

Although analytical models (Morse and Witten 1993; Buzza et al. 1995; Mason 1995; Mason and Scheffold 2014) and numerical studies (Lacasse et al. 1996; Mason et al. 1997; O’Hern et al. 2003; Ikeda et al. 2012, 2013; Scheffold et al. 2013, 2014) have had some success in describing certain limited regimes of emulsion rheology, none have treated ionic colloidal emulsions by combining all three energetic contributions (i.e., entropic, electrostatic, and interfacial) into a total free energy that is minimized in a near-equilibrium approach to provide thermodynamic Π and G′_p. For uncharged colloidal emulsions, an energy minimization approach using a microscopic parameter describing average droplet deformation has been introduced by Mason (Mason 1995; Mason and Scheffold 2014); this model involved only entropic and interfacial terms. Exploring smaller colloidal emulsions, Wilking and Mason (Wilking and Mason 2007) measured G′_p(ϕ) of uniform disordered nanoemulsions and interpreted this data using a model based on two energetic contributions from repulsive electrostatic interactions and interfacial droplet deformation, linked by droplet jamming at ϕ _c. Through this interpretation, they deduced the electrostatic interaction potential as a function of average separation between droplet interfaces, essentially creating a macroscopic rheological form of a surface-forces measurement (Israelachvili 1992). By keeping these same two energetic contributions in an electrostatic-interfacial model that involved energy minimization, Scheffold et al. (2014) took this idea further and predicted G′_p(ϕ) for disordered, ionic emulsions while neglecting entropy, which was assumed to be a constant value of several k _B T, where T is the temperature. Following on initial simulations (Lacasse et al. 1996), recent numerical work on the jamming transition of soft spheres has been carried out in the zero-temperature limit neglecting entropic contributions (Jorjadze et al. 2013; Liu and Nagel 2010; O’Hern et al. 2003; Seth et al. 2006; van Hecke 2010). In this jamming work, where entropic excitations are absent, important scaling relations have been discovered, and these can be employed to derive measurable quantities such as the shear modulus or pressure based on the excess number of soft particle contacts and the pair interaction potential. However, none of these prior models of disordered uniform droplets, whether analytical or numerical, have combined all three relevant energetic terms in a near-equilibrium energy minimization approach.

Here, to overcome these limitations, we present a near-equilibrium free energy model for disordered colloidal ionic emulsions that includes all three terms and connects them using a model of nearest-neighboring droplet interactions that includes the disordered structure of jammed monodisperse droplets. This connection is made geometrically by introducing an average droplet deformation parameter, ϕ _d, as has been done previously in a two-term entropic-interfacial model for non-ionic emulsions (Mason 1995; Mason and Scheffold 2014). The three-term free energy is minimized with respect to ϕ _d for different droplet volume fractions ϕ relative to ϕ _c, yielding predictions of the emulsion’s osmotic equation of state Π(ϕ). By further introducing a shear strain γ into this model, performing energy minimization, and then taking appropriate thermodynamic second derivative with respect to γ, we predict G′_p as a function of ϕ. We show that these predictions closely match measurements of Π and G′_p of model disordered colloidal ionic emulsions of silicone oil in water taken at a fixed aqueous concentration of amphiphilic electrolyte (sodium dodecyl sulfate (SDS)). Moreover, we show that this model also explains measurements of G′_p(ϕ) of nanoemulsions in which a non-amphiphilic salt (sodium chloride (NaCl)) has also been added. From this, we reveal that the surface potential on the droplets increases when the concentration of added NaCl begins to exceed that of the SDS. While distributions of microscopic properties, such as coordination number, are not taken into account explicitly, this entropic-electrostatic-interfacial (EEI) model, through a near-equilibrium energy minimization approach, reasonably predicts the shear modulus and osmotic pressure of Brownian, ionic, screened-charge, uniform, disordered, colloidal emulsions.

Methods and materials

Nanoemulsion preparation, fractionation, and characterization

We first create a polydisperse microscale oil-in-water premix emulsion by emulsifying trimethyl-terminated polydimethylsiloxane (PDMS) silicone oil (viscosity 10 cSt, mass density 0.935 g/cm³, Gelest) at ϕ = 0.3 into a 20 mM aqueous SDS solution (MP Biomedicals, Ultrapure) (Meleson et al. 2004). We process this premix emulsion at a liquid pressure of 10,000 psi through a 75-μm Y-type diamond interaction chamber using a Microfluidics M-110P homogenizer, recirculating for three passes using a cooling coil immersed in an ice-water bath. The resulting submicroscale emulsion is fractionated via ultracentrifugation to reduce the polydispersity in the droplet size distribution. To size-fractionate the resulting polydisperse nanoemulsion, we dilute it to ϕ = 0.15 using a 10 mM SDS solution and ultracentrifuge at 15,000 rpm for 9 h (L8-55 Beckman, SW 28 TI Rotor). We recover cylindrical elastic plugs at the top of the ultracentrifuge tubes and divide these into three disk-like sections (i.e. top, middle, and bottom sections) having equal lengths using a stainless steel blade. Similar sections of the plugs from different centrifuge tubes are combined to create three concentrated emulsions, yielding a first size-fractionation step. We then separately dilute each of these three concentrated emulsions with 10 mM SDS solution to set ϕ = 0.15, and we perform two additional ultracentrifugal size-fractionation steps (15,000 rpm for 6 h, and 12,000 rpm for 8 h). Repeated dilution of these concentrated emulsions with 10 mM SDS during size-fractionation ensures that the final SDS concentration in the CP is fixed to 10 mM, irrespective of the SDS concentration used to make the initial polydisperse emulsion. By taking the top sections of the first step, the middle sections of the second step, and the middle sections of the third step, we obtain a fractionated emulsion that has an average droplet radius that lies between larger submicron and micron-scale droplets (Mason et al. 1997) and smaller nanoscale emulsions (Wilking and Mason 2007) at [SDS] = 10 mM as in prior published results. This concentration is only slightly higher than the critical micelle concentration of SDS near 8 mM, so energies associated with micellar-driven depletion attractions between droplets are all much less than thermal energy and can be neglected for microscale and nanoscale droplet radii (Russel et al. 1989).

We measure the average hydrodynamic radius of this new fractionated emulsion using dynamic light scattering (DLS) (90 deg, laser wavelength 633 nm, temperature 295 K, diluted using a 10 mM SDS solution to ϕ ≈10⁻⁴–10⁻⁵), yielding an average hydrodynamic radius of <a> = a = 104 ± 2 nm. The polydispersity in the size distribution of these fractionated droplets is ≈20 %, as inferred from small angle neutron scattering experiments on other emulsions that have been fractionated in a similar manner (Scheffold and Mason 2009). We also measure ϕ of the fractionated concentrated emulsion by evaporating the water from about 150 mg of emulsion at room temperature, since the oil and SDS are non-volatile (Zhu et al. 2012). To obtain smaller volumes of concentrated emulsion at desired ϕ, we dilute this stock fractionated concentrated emulsion with 10 mM aqueous SDS solutions and stir gently to avoid introducing air bubbles.

Linear shear rheometry

We load approximately 150 μL of the fractionated emulsion into a cone-and-plate shear rheometer (Rheometrics RFS II, controlled strain, 25 mm diameter, 0.1° cone angle, titanium). We perform a frequency sweep from 1.0 × 10² rad/s down to 1.0 × 10⁻² rad/s at a peak shear strain amplitude of γ = 1.0 × 10⁻² and then a strain sweep at a frequency of ω = 1.0 rad/s from γ = 2.0 × 10⁻³ to γ = 2.0. The shear strain amplitude used in the frequency sweep is below the yield shear strain of all emulsion samples. We determine the plateau elastic shear moduli using the inflection point of the G′ curve in the frequency sweep (Mason 1995; Mason et al. 1997). If no inflection point can be identified on the G′(ω) curve, then G′ at ω = 1.0 rad/s is reported. We use an enclosing vapor trap filled with water to prevent water evaporation from the emulsion during the measurements. Residual torques arising from the vapor trap are much less than the torques due to the loaded emulsions for all measurements. We have tested for the possibility of wall slip, and it is not present for these fractionated nanoemulsions in the small shear strain limit.

Interfacial tension measurements

We measure the interfacial tension between the aqueous 10 mM SDS solution, into which different concentrations of NaCl have been added, and the PDMS oil using a du Nouy ring (Hanson et al. 2008; Zuidema and Waters 1941). Before each measurement, we clean the du Nouy ring (CSC Scientific, platinum-iridium, circumference = 5.996 cm; R/r = 55.6, where R is the radius of the ring and r is the radius of the platinum wire) by rinsing it with deionized water and flaming it with a methanol flame. We pour the aqueous solution, which has a higher mass density, into a small crystallization dish (80-mm diameter) and then slowly pipette the PDMS oil on top of the aqueous layer. The du Nouy ring is attached to a custom bottom-hole surface tensiometer and submerged through the PDMS oil into the aqueous phase. This tensiometer has been previously calibrated by measuring the air-liquid surface tension of deionized water, obtaining the reported value to within ±5 %. After waiting 5 min while the ring is fully submerged, we command the tensiometer to lower the crystallizing dish using a LabVIEW-controlled motor, and we digitally record the force on the ring by the bottom hook of the balance as the ring is slowly pulled through the interface at a rate of 0.10 mm/s until the interface detaches from the ring. We use the peak force and the mass densities to calculate the interfacial tension (Zuidema and Waters 1941). All surface tension measurements have been performed at room temperature, T = 298 K, the same as has been used for the rheometry measurements.

Model

We consider a disordered colloidal emulsion system of soft, deformable, uniform droplets composed of a first viscous liquid, the dispersed phase, that effectively form a Brownian suspension in a second immiscible liquid, the continuous phase, at a temperature T. Each droplet has a fixed volume, V _drop = 4πa ³/3, where a is its undeformed radius. The number of droplets in the system is N, the system’s total volume is V, and the droplet volume fraction is ϕ = NV _drop/V. Droplet stability is assured by adding an adequate concentration of an ionic amphiphilic surfactant, presumed to be present in only the continuous phase, some of which has adsorbed onto droplet interfaces. Thus, screened-charge electrostatic repulsions exist between the interfaces of droplets, and ions only reside in the continuous phase and at the surfaces of the droplets where the charged head groups of adsorbed ionic surfactant molecules are located. Droplet interfaces can deform near regions of closest approach (ROCAs) with nearest neighboring droplets. Such volume-preserving deformation of a droplet necessarily implies that work has been done against interfacial tension σ to increase its surface area. A characteristic Laplace pressure scale of an undeformed droplet is therefore σ/a, and an applied osmotic pressure Π must approach this Laplace pressure scale to cause any significant droplet deformation.

In a dilute system of droplets at low ϕ, entropy dominates the free energy because the average separation h between neighboring droplets’ interfaces at ROCAs, on average, is significantly larger than the characteristic thickness of the Debye layers, λ_D, of the screened-charge repulsion, represented schematically by blue boundaries around droplets as shown in Fig. 1a. At higher ϕ in the near-glass regime where ϕ is still below the ergodic-nonergodic glass transition, the droplets form cages around each other but the cages are transient due to entropic fluctuations; the system remains ergodic, exhibiting a low-frequency relaxation. As the system is further concentrated (Fig. 1b), neighboring droplets no longer form transient cages, and the system becomes a non-ergodic glass; the low-frequency relaxation disappears, yet the droplets are not strictly jammed and Brownian fluctuations of droplets can still be significant. As ϕ is further increased, the separation between the droplets’ interfaces becomes small enough that adjacent Debye layers of neighboring droplets begin to overlap, and the droplets begin to repulsively jam through screened-charge repulsions as shown by the electrostatic regime in Fig. 1c. This electrostatic repulsion also leads to tiny interfacial deformations near ROCAs of neighboring droplets in order to increase the separation between the charged droplet interfaces. Droplets experience greater electrostatic repulsion upon further concentration, so this leads to greater deformation of the droplets’ surfaces to create facet-like areas of reduced curvature at ROCAs. At even larger Π, work is primarily done against interfacial tension and droplet deformation, and droplet deformation can become significant, as shown by the interfacial regime in Fig. 1d.

Fig. 1

Rapidly increasing the volume fraction ϕ of uniform colloidal droplets in ionic oil-in-water emulsions leads to a disordered structure and a shear elasticity that arises from a combination of entropic, electrostatic, and interfacial forces. Dispersed-phase oil droplets (green) and surfaces populated with ionic surfactant molecules, which cause screened-charge repulsions between droplet interfaces. The aqueous continuous phase (white) contains ions, leading to a Debye screening length λ _D (blue coronas). A central droplet (red outline) is surrounded by its nearest neighbors (black outline), and these are surrounded by second nearest neighbors (dashed outline). Osmotic compression raises ϕ from the dilute limit into the following regimes: a the entropic near-glass regime, which is ergodic, so cages of nearest neighbors are transient, as a result of entropic fluctuations; b the entropic glass regime, which is non-ergodic; c the electrostatic jammed regime, in which Debye layers of the droplet begin to overlap significantly and screened electrostatic repulsive forces dominate as the droplets are jammed together; and d the interfacial jammed regime, in which droplets become increasingly deformed, but still weakly deformed, and work is predominantly done against interfacial tension (color figure online)

As a fluid-like, dilute, Brownian dispersion of disordered droplets is concentrated by an applied Π, we assume that ϕ passes rapidly through the colloidal disorder-order transition (Snook and van Megen 1976; van Megen and Snook 1975), corresponding to 0.495 ≤ ϕ ≤ 0.545 for hard spheres, thereby suppressing crystallization, and into the near-glass regime, just below the glass transition volume fraction, corresponding to ϕ _g ≈ 0.56–0.58 for hard spheres, associated with an ergodic-nonergodic transition and the disappearance of a low-frequency relaxation. As ϕ is further raised through and beyond ϕ _g into the glass regime, and beyond that into the jamming regime, the system remains disordered (Mason and Scheffold 2014). Thus, in a colloidal ionic emulsion system, as ϕ is raised, work is done against a combination of entropy, screened-charge electrostatic interfacial repulsions, and droplet interfacial tension via deformation. Consequently, we construct a model of the system’s total free energy, which includes these three contributions, and we calculate the osmotic pressure Π and the linear shear elastic plateau storage modulus G′_p, of this system by minimizing its total free energy in the limits of small droplet deformation and infinitesimal shear strains. As ϕ is raised, we assume that the most probable out of equilibrium states of disordered droplet configurations in the highly jammed system are effectively sampled by a near-equilibrium approach to the jammed regime through the glassy regime (Mason and Scheffold 2014). Inherent in this near-equilibrium approach is the implicit assumption that the particular disordered state of the colloidal emulsion at a given ϕ, even if only one manifestation of a large ensemble of microscopic droplet positional and interfacial structures that could arise from one trial to the next in preparing the emulsion, still gives rise to highly reproducible average macroscopic properties, including G′_p and Π. Thus, the dominant contribution to the free energy progresses from an entropic regime to an electrostatic regime, and then to an interfacial regime, in which more substantial droplet deformation can occur.

As a first step in building a suitable model for the free energy of a dense ionic emulsion, we consider a simpler disordered system of N uniform spheres having volume V _sphere = 4πa ³/3 in which the only contributions are entropic and all interactions between the spheres are purely hard. When ϕ is raised rapidly enough to avoid crystallization that could otherwise be caused by the entropic colloidal disorder-order transition, these disordered spheres can pass through the glass regime, characterized by a glass transition volume fraction ϕ _g ≈ 0.56–0.58 (Bengtzelius et al. 1984; Pusey and van Megen 1987; Woodcock 1981), and jam in a disordered configuration at a critical volume fraction ϕ _c, where Π diverges. Randomly jammed or packed hard spheres are known to have ϕ _c = ϕ _MRJ = ϕ _RCP ≈ 0.646 (Bernal and Mason 1960; Torquato et al. 2000). For ϕ just below ϕ _c, the time- and ensemble-average free volume V _f corresponding to accessible translational microstates of the center of mass of a sphere has been found to be proportional to the product of the volume per sphere with the cube of the volume fraction difference away from jamming (Woodcock 1981). This implies that the number of translational microstates in the three-dimensional (3D) system is Ω ∼ (ϕ _c − ϕ)^3N. Thus, according to Boltzmann’s law, the 3D translational entropy of the hard-sphere system for ϕ near but below ϕ _c can be estimated as: S _HS = k _B ln Ω ≈ k _B ln(ϕ _c − ϕ)^3N = 3Nk _B ln(ϕ _c − ϕ). Thus, for a disordered system of hard spheres, it can be inferred that the entropic translational free energy is F _ent,HS = −TS _HS = −3Nk _B T ln(ϕ _c − ϕ).

We next consider the entropic free energy of a system of disordered uniform colloidal particles that have hard interactions, yet are not completely spherical in a special manner that we describe as follows. Starting with spherical particles in a dense jammed system, we imagine slightly deforming all particles while conserving their internal volumes, in a manner that creates tiny facet-like areas, which locally have smaller curvature, near all ROCAs of all particles. The result of such selective tiny deformations causes the particles in the jammed system to lose contact with each other, and thus, unjam. Thus, this procedure of deformation at ROCAs increases the free volume available for translational motion of the particles. For irreversible deformations, the system of deformed particles, if further compressed, would jam at a slightly higher critical volume fraction ϕ _c′ compared to ϕ _c of perfect spheres. The difference between ϕ _c′ and ϕ _c can be connected to an effective deformation volume fraction ϕ _d related to translational motion: ϕ _d = ϕ _c′ − ϕ _c, where ϕ _d > 0, but ϕ _d is still small, far from the limit of strong droplet deformation. Since the spherical particles have only been slightly deformed, the entropic contribution to the free energy of a disordered system scales in a similar manner as for spheres, but diverges at a higher ϕ _c′ instead of ϕ _c: F _ent/N ≈ −3k _B T ln(ϕ _c′ − ϕ) ≈ −3k _B T ln(ϕ _c + ϕ _d − ϕ). In the dense system, the slightly deformed particles cannot easily re-orient because of their neighbors, so we ignore rotational contributions to the entropic term in the free energy.

Next, we construct the interfacial free energy of deformable spheres based on a simplified model of droplet compression by its nearest neighbors above the jamming point for a certain applied osmotic pressure Π. We assume that the emulsion is an isotropic effective medium and therefore that there is an average near-equilibrium separation between centers of neighboring droplets as well as average local geometrical features at all ROCAs. For simplicity of representation in the schematic, we show a middle cross section of a single cubic box (see Fig. 2), implying six nearest neighboring droplets in 3D; the scaling form resulting from the following argument can also be generalized to a disordered configurational structure for the real emulsion system even if numerical prefactors differ. We define Δr to be an average deformation length along the centerline between adjacent droplets normal to a small circular facet; each facet has an area of πr _d ², where r _d is the average radius of the facet (Fig. 2). We assume weak deformation near and above the jamming point, implying Δr << a. As a consequence, there is a gain in accessible translational microstates resulting from these deformations at ROCAs, which is directly related to ϕ _d (Mason and Scheffold 2014). For ϕ near the jamming point, each droplet in a disordered system of spheres also has ≈6 nearest neighboring droplets on average; we assume that changes in coordination number around the jamming point play only a minor role in the free energy near the jamming point. In going from an uncompressed to a weakly compressed state, the osmotic pressure effectively causes a small change in volume of an imaginary box around a droplet of 6(2a)²Δr. Dividing this change in volume by the box’s original volume gives the deformation volume fraction ϕ _d = 24a ²Δr/(2a)³ = 3Δr/a, so ϕ _d is linearly proportional to Δr. Using the Pythagorean theorem, a ² = r _d ² + (a − Δr)², so the area of a deformed facet is πr _d ² ≈ πa ²[1 − (1 − Δr/a)²] ≈ πa ²(2Δr/a) ≈ 2πaΔr to leading order in Δr in the weak compression limit. The linear dependence of the facet area on Δr and therefore ϕ _d is a key geometrical result, but six times this facet area does not represent the excess surface area of a droplet as a result of the osmotic compression, since volume conservation of the droplet must be respected.

Fig. 2

Schematic two-dimensional cross-section of a single oil droplet (green) in an aqueous surfactant solution (white) that is deformed by applying a uniform osmotic compression through a small reduction in the volume of an enclosing, rigid, semi-permeable cube (dashed lines). a Prior to deformation, the droplet is spherical and has radius a; the cube’s edge length is 2a. b After deformation, the enclosed droplet is isotropically compressed by a length 2Δr from the original cube. Small circular facets having radii r _d form at regions where the droplet interface is deformed. The droplet volume is conserved (color figure online)

To obtain the connection between the interfacial free energy and ϕ _d, we use force balance to obtain Π in terms of ϕ _d and then we integrate. By Newton’s law, the force given by the weakly deformed droplet’s Laplace pressure exerted over the area of one of its facets, on average, must be equal to the force given by the applied osmotic pressure over a face of the cube where that facet is located: (2σ/a)(πr _d ²) ≈ Π(2a)². Thus, the osmotic pressure is linearly proportional to the deformation volume fraction ϕ _d: Π ≈ (πσ/a ²)Δr ≈ (π/3)(σ/a)ϕ _d. We define the interfacial free energy f _int associated with deformation of a single droplet to be a function of ϕ _d. We obtain f _int from Π using the differential equation Π(ϕ) = [ϕ ²/(4πa ³/3)]∂f _int/∂ϕ (Mason et al. 1997), which, when converted into a function of ϕ _d, is approximately Π(ϕ _d) ≈ [ϕ _c ²/(4πa ³/3)]∂f _int/∂ϕ _d, assuming that ϕ _d is significantly smaller than ϕ _c for weak droplet deformation. Using the force balance result Π(ϕ _d) ∼ ϕ _d and integrating, we obtain f _int ∼ σa ² ϕ _d ² , which is quadratic to leading order in ϕ _d, where ϕ _d ≥ 0. Thus, the change in a droplet’s surface area resulting from a uniform osmotic compressional deformation is ∼a ² ϕ _d ² to leading order. Here, as a convenient convention, we omit a constant term related to the area of an undeformed droplet in f _int; this convention does not influence calculated values of Π and G'_p, which depend on derivatives of f _int. In addition, for simplicity, we ignore small variations in the local coordination number that can occur around the jamming point, recognizing that this could be incorporated later into a more complex model.

In a real disordered material, the prefactor associated with f _int could be different than the one we have calculated from the cubic model, so we simply generalize the interfacial free energy per droplet to be: f _int = F _int/N ≅ 4πξσa ² ϕ _d ². We have introduced a dimensionless numerical parameter ξ to bridge between the cubic model and a real isotropic disordered emulsion system; ξ is related to the distribution of facet sizes and local neighbor configurations of the real emulsion system (Mason and Scheffold 2014), and it could even depend on real polydispersity in the droplet size distribution. This simple model of energy associated with droplet deformation in a disordered concentration emulsion captures the most relevant main feature. We recognize that other refinements, such as the known logarithmic correction to the harmonic dependence of the free energy (Morse and Witten 1993), changes in local coordination number near and above ϕ _c (Lacasse et al. 1996), and changes in the effective values of ϕ _c for disordered systems of spheres having differing polydispersities (Desmond and Weeks 2014), could be incorporated into more complex models in the future. Such adjustments would refine the main result of the simple deformation model for F _int/N near and just above the jamming point.

Next, we consider the contribution to the free energy per droplet associated with electrostatic interactions, F _elec/N, via screened-charge electrostatic repulsions between the surfactant-coated interfaces of the deformed droplets. In the limit of weakly deformed droplets that have pairs of opposing deformed facets near all ROCAs, we assume that the dominant contribution to the electrostatic interactions arises primary from screened repulsions between these proximate facets, which are separated by an average distance of closest approach h. The high density of droplets having charged surface regions and counterion screening layers precludes the use of simple formulae developed for pair interactions of isolated spheres that have charged surfaces. The screened electrostatic potential between two disks (i.e., proximate deformed facets of neighboring droplets) separated by a distance h in a dilute solution having an ionic strength I is F _elec/N ≈ 2πa ² ε _r ε ₀ ψ ₀ ² exp(−h/λ _D)/h, where the surface charge density is ψ ₀, the Debye screening length is λ _D = (ε _r ε ₀ k _B T/(2e ² I))^1/2, ε ₀ is the permittivity of vacuum, ε _r is the relative dielectric constant of the continuous phase, and e is the elementary charge (Larson 1999; Russel et al. 1989). Here, ψ ₀ is negative for anionic surfactants; for simplicity, we report and plot only the magnitude of ψ ₀. For common concentrations of ionic surfactants used to stabilize emulsions, λ _D is typically on the scale of few nanometers. This form for the free energy is identical to that used in a model that has successfully scaled nanodroplet elasticity (Wilking and Mason 2007), and it differs only slightly from a form used to model screened electrostatic interactions between isolated charged droplets that does not include the factor of 1/h (Scheffold et al. 2014). Inherent in the expression for F _elec/N is the use of a linearized Poisson-Boltzmann model in the Debye-Hückel limit (Russel, et al. 1989), so the surface potential on the droplets is fixed and the ionic strength is assumed to be relatively small. In the limit of small droplet deformation, changes in the total droplet surface area, which could influence the equilibrium adsorbed density and therefore the surface potential, are small and so we assume that ψ ₀ does not depend on ϕ. Thus, the assumed electrostatic free energy contribution does not attempt to treat complex effects, including surfactant adsorption equilibria, high ionic strengths, and local variations in surfactant density on droplet interfaces near and in between ROCAs. These more complex effects related to electrostatic interactions could be potentially relevant for a subset of ionic emulsions; treatment of such effects lie beyond the scope of this simplified model.

To connect the electrostatic free energy with the rest of the EEI model, we must determine the dependence of h on the deformation volume fraction ϕ _d. We define the average center-to-center distance L between neighboring droplets to be L = h + 2(a − Δr) ≈ h + 2a since the droplets are weakly deformable (Fig. 3). At the shifted jamming point ϕ _c′, we envision a slightly deformed droplet as being effectively enclosed by a larger spherical shell having volume V _eff = 4π(L/2)³/3. Our definition of the shifted volume fraction at the critical jamming volume fraction implies that Vϕ _c′ = NV _eff = N[4π(L/2)³/3]. At the shifted jamming point, the true “bare” droplet volume fraction must still satisfy Vϕ = NV _drop = N(4πa ³/3). Since N and V are fixed, dividing these two equations implies that ϕ _c′/ϕ = L/(2a)³, where ϕ _c′ = ϕ _c + ϕ _d. Solving for h in terms of ϕ, ϕ _d, and the universal jamming point ϕ _c, we find h = 2a [(ϕ _c′/ϕ)^1/3 − 1], leading to the following:

$$ h = 2a{\left({\phi}_{\mathrm{c}}+{\phi}_{\mathrm{d}}\right)}^{1/3}\left[{\phi}^{-1/3}\hbox{--}\ {\left({\phi}_{\mathrm{c}}+{\phi}_{\mathrm{d}}\right)}^{-1/3}\right]. $$

(1)

For weak deformations around and near the jamming point, ϕ _d << ϕ _c so ϕ _d will make only a minor modification to the (ϕ _c + ϕ _d)^1/3 factor in Eq. 1, but ϕ _d can still make a significant impact on the difference in brackets. Consequently, we further simplify the expression for h to

$$ h \approx 2a{\phi_{\mathrm{c}}}^{1/3}\left[{\phi}^{-1/3}\hbox{--}\ {\left({\phi}_{\mathrm{c}}+{\phi}_{\mathrm{d}}\right)}^{-1/3}\right]. $$

(2)

We modify this model of the near-equilibrium free energy of an ionic colloidal emulsion so that it can also be used to calculate the linear plateau elastic shear modulus G′_p, a rheological property based on an applied perturbative shear strain γ. The shear deformation changes the positional configurations of the droplets such that the shifted jamming point of the sheared system is lowered by a quadratic term proportional to γ ², since the free energy cannot depend on the sign of γ, from the shifted jamming point of the unsheared system, ϕ _c′. Consequently, we substitute ϕ _c′ − αγ ² = ϕ _c + ϕ _d − αγ ² into the above expressions for F _ent/N and F _elec/N (i.e., into h in Eq. 2) wherever ϕ _c′ occurs. Here, we have introduced α as a dimensionless parameter that describes the average shear effects to the configurations of the droplets and effectively incorporates non-affine local displacements that can occur in such systems during osmotic compression and shear (Lacasse et al. 1996; O’Hern et al. 2003). Thus, the complete set of equations for the free energy per droplet contributions to the sheared emulsion system are the following:

Fig. 3

Schematic showing deformation of charged interfaces of two ionically stabilized droplets (green: oil) in a concentrated oil-in-water emulsion at a region of closest approach (ROCA) for osmotic compressions approaching the Laplace pressure scale σ/a, where a is the radius of an undeformed droplet and σ is its interfacial tension. Debye layers that have a screening length λ _D (blue) overlap significantly near the ROCA. The distance between the centers of the droplets is L, the length along the centerline of droplet deformation is Δr, and the separation between the oil-water interfaces at the ROCA is h. Ions (not shown) are present in the continuous aqueous phase, and charged amphiphiles (not shown) populate droplet surfaces (color figure online)

$$ {F}_{\mathrm{int}}/N=4\pi \xi \sigma {a}^2{\phi_{\mathrm{d}}}^2 $$

(3)

$$ {F}_{\mathrm{ent}}/N=-3{k}_{\mathrm{B}}T \ln \left({\phi}_{\mathrm{c}}+{\phi}_{\mathrm{d}} - \phi - \alpha {\gamma}^2\right) $$

(4)

$$ {F}_{\mathrm{elec}}/N=2\pi {a}^2{\varepsilon}_{\mathrm{r}}{\varepsilon}_0{\psi_0}^2 \exp \left(-h/{\lambda}_{\mathrm{D}}\right)/h $$

(5)

where the separation at closest approach is

$$ h=2{\phi_{\mathrm{c}}}^{1/3}a\left[{\phi}^{-1/3}-{\left({\phi}_{\mathrm{c}}+{\phi}_{\mathrm{d}} - \alpha {\gamma}^2\right)}^{-1/3}\right]. $$

(6)

The total free energy per droplet is simply F _tot/N = (F _int + F _ent + F _elec)/N, and ϕ _d is a parameter that must be minimized in order to satisfy the near-equilibrium condition of free energy minimization, consistent with the second law of thermodynamics.

To obtain Π in the absence of shear and G′_p for an applied perturbative shear, we first minimize the total free energy:

$$ {\left.\frac{\partial {F}_{\mathrm{tot}}}{\partial {\phi}_{\mathrm{d}}}\right|}_{\phi_{\mathrm{d}}={\phi}_{\mathrm{d}}^{*}}=0 $$

(7)

from which we determine ϕ _d*, the deformation volume fraction satisfying the minimization condition, in terms of other parameters, including γ in the case when a shear has been applied. A transcendental equation arises from the minimization condition, so Mathematica’s FindRoot function (Wolfram Research Inc.) is used to solve numerically for the one positive real root of ϕ _d* that corresponds to a meaningful physical value. Once we have obtained this ϕ _d*, we substitute it back into the expression for the total free energy wherever ϕ _d occurs to obtain the minimized total free energy F _tot*. We then take appropriate thermodynamic derivatives of F _tot* to determine Π and G′_p (Mason and Scheffold 2014):

$$ \Pi =\left[{\phi}^2/\left(N{V}_{\mathrm{d}\mathrm{rop}}\right)\right]{\left[\partial {F}_{\mathrm{tot}}/\partial \phi \right]}_{\phi_{\mathrm{d}}={\phi}_{\mathrm{d}}^{*},\gamma =0} $$

(8)

$$ {G}_{\mathrm{p}}^{\prime }=\left[\phi /\left(N{V}_{\mathrm{d}\mathrm{rop}}\right)\right]{\left[{\partial}^2{F}_{\mathrm{tot}}/\partial {\gamma}^2\right]}_{\phi_{\mathrm{d}}={\phi}_{\mathrm{d}}^{*},\gamma =0.} $$

(9)

To obtain the osmotic pressure Π, solutions of ϕ _d* are found for a range of ϕ values at γ = 0, such that the local slope of F _tot* with respect to ϕ can be calculated and used in Eq. 8. The plateau elastic shear modulus G′_p is found numerically as follows. For a particular ϕ value, solutions of ϕ _d* are found over a small range of γ values from 0 to about 0.01, below the measured yield strain of concentrated disordered emulsions, corresponding to the linear rheological regime. At each ϕ, the curvature ∂² F _tot*/∂γ ² is obtained by finding the least-squares fit of parabolic F _tot*(γ) centered around γ = 0 for small γ. The parabolic coefficient from the fit is then used to determine G′_p. This process is repeated for different ϕ, yielding G′_p as a function of ϕ. We have verified this approach using a high density of ϕ and γ values (i.e., Δϕ = 0.009 and Δγ = 0.0005 intervals), and we find excellent agreement with a prior analytical solution (Mason and Scheffold 2014) when electrostatic forces have been eliminated (i.e., when ψ ₀ = 0 V). By first solving the transcendental equation for ϕ _d* to determine the minimized F _tot* and then finding slopes and curvatures of these F _tot* numerically, we obtain the thermodynamic properties Π and G′_p for a system of uniform deformable ionic droplets as a function of ϕ below, through, and above the jamming point. However, the EEI model is not expected to be appropriate in limits as ϕ → 1, away from the weak deformation limit where ϕ _d* would become large, and as ϕ → 0, where the scaling form used for the entropic term for ϕ near ϕ _c is inappropriate.

Results and discussion

We compare the predictions of the EEI free energy minimization model with five sets of G′_p(ϕ) measured for uniform, disordered, ionic, oil-in-water emulsions having microscale, sub-microscale, and nanoscale droplet radii, as shown in Fig. 4. We fix T = 298 K, since measurements have been made at room temperature, and we also fix ϕ _c = 0.646, based on the known ideal limit of maximal random jamming of perfectly monodisperse spheres, recognizing that residual polydispersity in a real emulsion could shift this value somewhat (Desmond and Weeks 2014; Zhang et al. 2015). We use a Debye screening length of λ _D ≈ 3.4 nm, predicted from λ _D = [ε _r ε ₀ k _B T/(2e ² I)]^1/2, (Russel et al. 1989) where the ionic strength I of the SDS solution is I ≈ 8.2 mM, corresponding to the known critical micelle concentration (CMC) of SDS (Scheffold et al. 2014; Umlong and Ismail 2007). This value of λ _D is only about 10 % larger than the calculated Debye length using I = 10 mM, disregarding micelle formation and the CMC. Because the diameter of SDS micelles (i.e., ≈4 nm) is larger than the Debye length and the SDS concentration is very close to its CMC, any small residual concentration of SDS micelles would not be expected to contribute significantly to the screening length. We fix the surface tension to be σ = 9.8 dyne/cm based on a prior measured value for PDMS oil and 10 mM SDS solution (Mason 1995).

Fig. 4

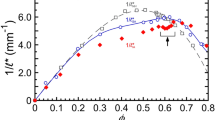
Plateau elastic shear moduli G′_p, in units of Laplace pressure scale σ/a, as a function of droplet volume fraction ϕ for uniform microscale and nanoscale 10 cSt trimethyl terminated PDMS oil-in-water emulsions stabilized by 10 mM SDS (points: measurements by mechanical shear rheometry; solid lines: calculation using Eq. 9). Droplet radii are (from left to right) a (nm): 28 (33) [red circles], 47 (47) [orange squares], 73 (67) [green diamonds], 104 (108) [blue up-triangles], and 530 (530) [black down-triangles] at T = 298 K. Values for a listed in parenthesis are used in the calculation. Data for a < 100 nm are from Wilking and Mason (2007), for a = 530 nm are from Mason (1995) and Mason et al. (1995), and for a = 104 nm are from the herein work. We fix the jamming point to be ϕ _c = 0.646 and temperature T = 298 K. We also fix σ = 9.8 dyn/cm (Mason 1995). Calculation parameters (see text) that yield the best overall fits to all data are as follows: ξ = 0.15, α = 0.85, λ _D = 3.4 nm, and |ψ ₀| = 270 mV (color figure online)

We determine the remaining parameters by optimizing the global fit of the EEI model to all sets of measurements in Fig. 4, yielding ξ = 0.15, α = 0.85, and |ψ ₀| = 270 mV. These values lie within uncertainty limits of separate entropic-interfacial and electrostatic-interfacial models (Mason and Scheffold 2014; Scheffold et al. 2014), where we have made minor modifications to measured droplet hydrodynamic radii within the range of polydispersity (i.e., approximately ±15  %) to improve the global agreement. The value of ψ ₀ obtained from the global fit is reasonably close to an estimate of |ψ ₀| = 210 mV using Grahame’s equation, ψ ₀ = [2k _B T/(ze)] sinh⁻¹[σ _e/(8c ₀ ε _r ε _o RT)^1/2], which is based on Gouy-Chapman theory (Russel et al. 1989), where c ₀ is the bulk molar concentration of the counterions in the CP, and z = 1 is appropriate for monovalent ions arising from dissociated SDS. In this calculation, we have used a measured and reported value of σ _e ≈ 2 e/nm² for the adsorbed surface density of dodecyl sulfate anions (DS−) at the interface of decane and water at c ₀ = [SDS] = 10 mM (Cockbain 1954). Differences in the dispersed phase compositions and differences in the experimental system from the assumed boundary conditions inherent in Grahame’s equation could account for at least some of the difference between the estimated and fitted values of ψ ₀. Overall, the EEI model matches the measurements over a wide range of radii from nanoscale to microscale emulsions. It captures features including the interfacial contributions to G′_p at high ϕ as well as electrostatic and entropic contributions at lower ϕ. Variations in residual droplet polydispersity, which for the measured emulsions is typically about 10 - 20 %, could account for at least some part of small deviations of the data from the model. At the lowest ϕ shown, the reported G′_p values do not necessarily correspond to a zero-frequency G′, so the frequency dependence of the storage modulus could play a role in any departures of the EEI model from the data there.

The same parameters can be used with the EEI model to describe the measured osmotic equation of state Π(ϕ) of a uniform disordered microscale oil-in-water PDMS emulsion having a = 480 nm and stabilized using 10 mM SDS, as shown in Fig. 5 (Mason 1995; Mason et al. 1997; Mason and Scheffold 2014). Given the large scatter in the data for Π at lower ϕ, and the higher difficulty in measuring precise values of Π using an ultracentrifugation technique (Mason et al. 1997), the comparison of measured and calculated Π(ϕ) using parameters that had been optimized only using G′_p(ϕ) data represents good agreement. If the five sets of G′_p(ϕ) are disregarded, even better agreement with the measured Π(ϕ) could be obtained using a slightly higher value of ξ = 0.22 in the model. Because ϕ _c = 0.646 is used in our current calculations, rather than an effective jamming volume fraction of ϕ _c,eff ≈ 0.62 in prior work (Mason and Scheffold 2014), in which electrostatic effects had only been accounted for in an ad hoc manner, the EEI model represents an improvement over prior analyses and is consistent with existing data describing the osmotic equation of state of disordered uniform emulsions. Furthermore, the largest values of ϕ _d ^* (see Fig. 5b, inset) shows the relative change in surface area per droplet in any of our calculations, ξϕ _d*², is at most few percent; thus, the droplets are only weakly deformed over the intermediate range of ϕ where we compare the EEI model with measurements.

Fig. 5

Osmotic pressure Π in units of Laplace pressure scale σ/a, for SDS-stabilized PDMS oil-in-water emulsions having average radius a = 480 nm (points: measurements by centrifugation (Mason 1995; Mason et al. 1995); solid lines: calculation using Eq. 8 and same parameter values as for G′_p in Fig. 4). The calculated deformation volume fraction, ϕ _d ^*, as a function of volume fraction ϕ for <a>= 480 nm is shown in the inset (color figure online)

Adding a solution of a non-amphiphilic salt, such as NaCl, to the aqueous continuous phase can be used to effectively melt and liquify elastic ionic nanoemulsions over a certain range of ϕ (Scheffold et al. 2014). The measured G′_p(ϕ) of monodisperse emulsions having a = 47 nm at [SDS] = 10 mM SDS concentration for several different added [NaCl] are shown in Fig. 6. At larger [NaCl], the onset of elasticity, corresponding to the rise in G′_p, occurs at larger ϕ. To explain the origin of this effect, we consider the influence of [NaCl] on several parameters in the EEI model, as follows.

Fig. 6

Plateau elastic shear moduli G′_p as a function of droplet volume fraction ϕ for a = 47 (46) nm, 10 cSt PDMS oil-in-water emulsions stabilized by 10 mM SDS with varying NaCl concentrations at T = 298 K (points: measurements by mechanical shear rheometry (Wilking and Mason 2007); solid lines: calculation using Eq. 9). The concentrations of added NaCl (mM) (from left to right) are as follows: 0 (red circles), 10 (green squares), 40 (blue diamonds), and 90 (black triangles). Surface tension and electrostatic parameters used to calculate the corresponding lines are shown in Fig. 7; all others are the same as in Fig. 4 (color figure online)

The interfacial tension between an oil and an aqueous surfactant solution is typically reduced when soluble salts are added to the aqueous solution (Kanellopoulos and Owen 1971). We have measured the interfacial tension σ between the oil and an aqueous solution containing fixed [SDS] = 10 mM while varying [NaCl] added. The results are plotted relative to σ ₀ between PDMS oil and a 10 mM SDS aqueous solution in Fig. 7a (squares). The measured reduction in σ/σ ₀ can be fit using a semi-empirical function, σ/σ ₀ = 1 + A(exp(−[NaCl]/[NaCl]*) − 1), yielding A = 0.338 ± 0.007 and [NaCl]* = 28 ± 2 mM with a correlation coefficient of R ² = 0.998. This reduction in interfacial tension by the added non-amphiphilic electrolyte indicates that DS− anions have been driven from the continuous phase onto the interfaces of the oil droplets.

Fig. 7

Parameter values used to fit G′_p(ϕ) data of emulsions to which salt NaCl has been added in Fig. 6, for uniform, concentrated, disordered PDMS emulsions in aqueous 10 mM SDS solution. a Experimental measurements of interfacial tension, measured using a du Nouy ring method, are plotted as relative surface tension σ/σ ₀, referenced to the interfacial tension of σ ₀ = 9.8 dyn/cm, between 10 mM SDS and PDMS oil are shown as blue squares. An empirical exponential model (black line) for the relative interfacial tension is shown (see text). Red points on the fitted line are used for the calculations. b Debye lengths, λ _D, used in the fits (red points) follow the prediction: λ _D = (ε _r ε ₀ k _B T/(2e ² I))^1/2 (black line). c Magnitude of the surface potential |ψ ₀| ≈ 270 mV in the absence of added NaCl and ψ ₀ increases with [NaCl] once [NaCl] approaches and exceeds the fixed [SDS] ≈ 10 mM. Reported uncertainties in ψ ₀ (error bars correspond to one standard deviation) have been determined using minimization of chi-square values of the fits to G′_p(ϕ) (color figure online)

The increased ionic strength in the aqueous phase also affects the electrostatic interactions between the droplets by reducing λ _D = [ε _r ε ₀ k _B T/(2e ² I)]^1/2, where this formula is valid only in the limit of dilute electrolyte concentrations (Russel et al. 1989; Scheffold et al. 2014). Values of λ _D for added [NaCl] = 0, 10, 40, and 90 mM used in the model are 3.4, 2.3, 1.5, and 1.1 nm, respectively (see Fig. 7b). These values of λ _D yield good agreement with the measured G′_p(ϕ) and deviate only slightly from the Debye screening equation at higher [NaCl]. Because the activities of ionic species can deviate from the ideal dilute Debye limit, slight departures of λ _D from the ideal prediction at higher [NaCl] could be anticipated.

Using the measured reduction in σ/σ ₀ and the predicted reduction in λ _D with [NaCl], we adjust ψ ₀ to obtain the best overall agreement for each G′_p(ϕ) curve in Fig. 6; the results for ψ ₀([NaCl]) are shown in Fig. 7c. For [NaCl] ≤ 10 mM, which is comparable to or smaller than [SDS], ψ ₀ does not change much within the uncertainties obtained from the fits. However, for [NaCl] ≥ 40 mM, there is a marked increase in ψ ₀, indicating a greater surface charge. At least some of this increase in ψ ₀([NaCl]) is likely to arise from additional adsorbed DS− on the surfaces of droplets, caused by the higher concentration of additional non-amphiphilic anions in the continuous phase. This increased adsorption is qualitatively consistent with the reduction in surface tension related additional DS− on the droplet surfaces, a consequence of a shift in the DS− adsorption equilibrium caused by the addition of NaCl to the continuous phase. However, considering the mass balance of free and adsorbed surfactant, we find that increased adsorption of DS− from the CP onto the surfaces of the droplets cannot be solely responsible for the increase in the value of ψ ₀. This suggests that non-ideal ionic effects, such as the development of a secondary attractive minimum in the droplet pair potential at high added non-amphiphilic salt concentrations is likely to also be happening (Bibette et al. 1993; Mason 1995). Such secondary minima are not captured by the electrostatic term in our model, so a more complex model is most likely needed to describe the regime of high concentrations of added non-amphiphilic salts. Overall, the calculated values of G′_p(ϕ) agree well with the measured data using the parameters shown in Fig. 7. Thus, we have used the EEI model in combination with the existing macroscopic measurements for G′_p(ϕ,[NaCl]) to estimate the microscopic ψ ₀([NaCl]).

Having determined appropriate parameters for the EEI model, which yield good agreement with a large number of measurements of G′_p(ϕ) over a wide range of droplet radii and added [NaCl], we vary certain parameters while fixing others in order to predict the linear rheological behavior of disordered ionic emulsion systems over a wide range of conditions. Figure 8 shows the systematic variation of predicted G′_p(ϕ) for various radii, fixing other parameters to match with PDMS oil-in-water emulsions stabilized at [SDS] = 10 mM. The smaller the droplet radii are, the more likely the crossover behavior occurs towards lower ϕ, below the maximally random jamming point ϕ _c = 0.646, as a consequence of the screened-charge electrostatic repulsion. As the characteristic droplet radius becomes closer to λ _D, the droplets effectively jam at much lower volume fractions. The EEI model appropriately captures this jamming effect as well as the entropic modulus scale for ϕ below the effective jamming point.

Fig. 8

Calculated plateau elastic shear moduli G′_p, in units of Laplace pressure scale σ/a, as a function of droplet volume fraction ϕ, based on the EEI model describing colloidal ionic emulsions for various droplet radii a in a 10 mM aqueous SDS solution (model parameters: see Fig. 4 caption) (color figure online)

In Fig. 9, we show how G′_p is influenced by different values for electrostatic parameters λ _D and ψ ₀. For nano- and micro-scale emulsions (a = 30, 270, and 2430 nm), at a given droplet size and fixed surface potential, the rapid rise in G′_p associated with disordered jamming shifts toward lower ϕ as λ _D is increased, as shown in Fig. 9a–c). The limit λ _D → 0 effectively turns off the electrostatic term in the free energy, so G′_p(ϕ) in that limit reflects only entropic and interfacial contributions. Increasing the surface potential while fixing λ _D for the same set of ionic emulsions causes this rapid rise to shift towards lower ϕ, as shown in Fig. 9d–f. Droplets having ψ ₀ = 0 mV corresponds to an absence of electrostatic effects, so interactions between neighboring surfaces of deformable droplets are effectively hard.

Fig. 9

Calculated dependence of plateau elastic shear modulus G′_p as function of droplet volume fraction ϕ on electrostatic parameters for oil-in-water emulsions in aqueous 10 mM SDS solution for droplet radii a (nm): 30 (a, d), 270 (b, e), and 2430 (c, f). For a–c, Debye length is varied, λ _D (nm): 5, 4, 3, 2, and 1 (lines from left to right) at a fixed surface potential ψ ₀ = 270 mV. For d–f, surface potential is varied ψ ₀ (mV) = 810, 270, 90, 30, and 0 mV (lines from left to right) at fixed λ _D = 3.4 nm. All other parameters are fixed and the same as those in Fig. 4 (color figure online)

We next calculate the relative contributions of entropic, electrostatic, and interfacial terms to F _tot, G′_p, and Π using the EEI model. Figures 10, 11, and 12 show the absolute and relative contributions for PDMS emulsions having a = 270 nm at [SDS] = 10 mM over a range of ϕ. The relative percent graphs, shown in Figs. 10b, 11b, and 12b, obtained from free energy minimization, are consistent with the qualitative regimes depicted in Fig. 1. Furthermore, Fig. 10a shows that the entropic free energy per droplet remains about ≈5 k _B T above the crossover to the electrostatic regime. This value resulting from free energy minimization of the EEI model is close to an assumed value in the electrostatic-interfacial energy model (Scheffold et al. 2014).

Fig. 10

Calculated free energies per droplet F as function of droplet volume fraction ϕ for uniform disordered emulsions having a = 270 nm oil droplets in 10 mM aqueous SDS solution (parameters from Fig. 4): a entropic (F _ent, dashed line), electrostatic (F _elec, dashed-dotted line), interfacial (F _int; dotted line), and total F = F _ent + F _elec + F _int (solid black line). b Percent relative contributions of F _ent, F _elec, and F _int to the total F (color figure online)

Fig. 11

Calculated plateau elastic shear moduli G′_p for a = 270 nm oil droplets in 10 mM aqueous SDS solution as a function of droplet volume fraction ϕ using parameters from Fig. 4: a entropic (G′_p,ent, dashed line); electrostatic (G′_p,elec, dashed-dotted line); and interfacial (G′_p,int, dotted line); total (G′_p = G′_p,ent + G′_p,elec + G′_p,int, solid black line). b Percent relative contributions of G′_p,ent, G′_p,elec, and G′_p,int to the total G′_p (color figure online)

Fig. 12

Calculated contributions to the osmotic pressure Π for a = 270 nm oil droplets in 10 mM aqueous SDS solution as a function of droplet volume fraction ϕ using parameters from Fig. 4. a Entropic (Π_ent, dashed line); electrostatic (Π_elec, dashed-dotted line); and interfacial (Π_int, dotted line); total (Π = Π_ent + Π_elec + Π_int, solid black line). b Percent relative contributions of Π_ent, Π_elec, and Π_int to the total Π (color figure online)

Using parameter values that correspond to PDMS droplets in 10 mM aqueous SDS solutions, we determine the two values of ϕ corresponding to crossover in G′_p between the entropic and electrostatic regimes and between the electrostatic and interfacial regime for a given droplet radius. We repeat this process for a wide range of droplet radii and show the results as lines separating the dominant contributions to G′_p in Fig. 13. The labeled areas in the plots indicate which of the three terms contribute the most to G′_p. The two lines in Fig. 13 converge to the critical jamming point ϕ _c in the limit of very large, macroscopic droplets, and the electrostatic regime effectively disappears.

Fig. 13

Calculated regimes of dominant contributions by entropic, electrostatic, or interfacial terms to the plateau elastic shear moduli G′_p for 10 cSt PDMS oil droplets stabilized by 10 mM SDS for varying radii a and droplet volume fraction ϕ at a Debye screening length of λ _D = 3.4 nm (green lines); other parameter values are the same as in Fig. 4. The dashed line represents equal relative contributions of entropic and electrostatic terms; the solid line represents equal relative contributions of the electrostatic and interfacial terms. Inset: lowering λ _D to 1.8 nm (red lines) reduces the electrostatic and interfacial zones, whereas raising λ _D to 5.0 nm (blue lines) expands the electrostatic and interfacial zones (all other parameters are fixed) (color figure online)

The dependence of G′_p on temperature has also been explored. Temperature mostly affects the magnitude of the entropic term, although temperature also affects λ _D in the electrostatic term. In the entropic regime, the calculated G′_p from the numerical minimization procedure is found to increase linearly with respect to increasing temperature, consistent with G′_p ∼ k _B T/V _f (Russel et al. 1989; Woodcock 1981). In principle, if the temperature T could be tuned to approach 0 K while preserving the CP in a liquid state, then the entropic contribution to the free energy would be effectively turned off, and the two-term electrostatic-interfacial free energy would lead to the jamming result (Wilking and Mason 2007; Scheffold et al. 2014). Given the narrow range of temperatures over which the aqueous phase exists in a liquid state (e.g., from about 273 to 373 K at atmospheric pressure), varying temperature over this range only makes a minor change in the osmotic equation of state and in the linear viscoelastic modulus. Thus, for oil-in-water emulsions, the most practical and effective means of investigating the entropic regime is not by varying temperature, but rather by reducing the droplet radius while also reducing the Debye screening length.

Conclusion

We have shown that minimizing a total free energy with respect to an average microscopic droplet deformation parameter accounts well for the shear elasticity and osmotic pressure of concentrated disordered ionic emulsions and nanoemulsions for droplet volume fractions below, near, and above ϕ _c. The EEI model connects three principal energetic terms, entropic, electrostatic, and interfacial, of this total free energy using a near-equilibrium approach that assumes disordered jamming of monodisperse deformable droplets while conserving droplet volume. Simultaneous fitting of measured G′_p(ϕ) curves for a wide range of droplet radii establishes the values of two universal parameters, ξ and α, that essentially set the relative strengths of the terms and are based fundamentally on complicated geometrical aspects of the disordered system. It is remarkable that such a simple free energy, when minimized, can properly capture such a wide range of measurements without resorting to a highly detailed microscopic description. Rapidly quenching uniform deformable objects to jam them in the presence of Brownian fluctuations creates a reproducibly statistically similar disordered structural state, so the emulsion system is technically out-of-equilibrium. Nevertheless, we have shown that near-equilibrium free energy minimization of the relatively simple EEI model, based on disordered jamming at ϕ _c, can serve surprisingly well in describing the collective behavior of ionic colloidal emulsions.

This EEI model, in combination with the two universal fit parameters that we have determined, can be used to predict rheological regimes of a wide variety of ionic emulsions. These entropic, electrostatic, and interfacial regimes reflect the dominance of a particular term in the free energy, and we have mapped boundaries of these regimes as a function of droplet radius and volume fraction for different Debye screening lengths. Moreover, we have explicitly shown the relative contributions to the free energy, osmotic pressure, and shear modulus that each of these terms makes. Although this EEI model provides a powerful predictive platform for emulsion rheology, it nevertheless must be used with discretion; as we have shown, introduction of non-amphiphilic salt can alter important parameters, such as the interfacial tension and the surface potential, in addition to the Debye screening length.

In future work, it would be interesting to test the utility of the model’s predictions for monodisperse disordered microscale and nanoscale emulsions that have a wider range of ionic amphiphile and non-amphiphile concentrations. Likewise, it would be interesting to perform multi-scale Brownian or molecular dynamics simulations, which can incorporate complex behavior such as entropy contribution of ions, on dense disordered systems of constant-volume droplets stabilized by ionic surfactants to arrive at predictions for the two universal parameters. A more sophisticated model or simulation could be developed to incorporate the microscopic details of the system, such as the local coordination number and the distribution of the degree of deformation of constituent droplets, into predictions for Π(ϕ) and G′_p(ϕ). The EEI model could further be advanced into the regime of attractive ionic emulsions by incorporating the effects of secondary minima in the interaction potentials between proximate surfaces of neighboring droplets (Bibette et al. 1993; Mason et al. 1996; Datta et al. 2011; Hegelson et al. 2012). Moreover, the EEI model does not explicitly treat polydispersity, which can alter ϕ _c and also change the shape of G′_p(ϕ) and Π(ϕ) of emulsions. While challenging, extending the EEI model and simulations to include polydispersity, such as a peaked monomodal distribution, would also be useful.