1 Introduction

In rheology, viscoelasticity is the property of materials that exhibit both viscous and elastic characteristics when undergoing deformation. Generally, the elastic effect is related to the shear-induced first normal stress difference (N1S), \(N_{1}^{{\text{S}}} = \tau_{11} - \tau_{22}\), wherein \(\tau_{11}\) and \(\tau_{22}\) denote the normal stresses in the principal flow and gradient directions, respectively. For a particular point of interest, extensional viscosity \(\eta_{{\text{E}}}\) is the ratio of “net tensile stress”, \(\sigma_{{\text{E}}} = \tau^{\prime}_{11} - \tau^{\prime}_{22}\), to extension rate \(\dot{\varepsilon }\), namely, \(\eta_{{\text{E}}} = \sigma_{{\text{E}}} /\dot{\varepsilon }\), wherein \(\tau^{\prime}_{11}\) and \(\tau^{\prime}_{22}\) denote the normal stresses in the principal stretch and shrink directions, respectively. Thus, \(\sigma_{{\text{E}}}\) is defined as the extensional-viscosity generating first normal stress difference (N1E), \(N_{1}^{{\text{E}}}\). However, it is not normal to discuss the competitive role of N1S and N1E coexisting in complex flows for viscoelastic fluids of polymer melts.

Early on, Debbaut and Crochet [1] considered the effect of extensional viscosity as a cause of corner vortex in abrupt 4:1 contraction flow simulations. In addition, they concluded the conflicting effects of the extensional viscosity and \(N_{1}^{{\text{S}}}\) on vortex activity. Later, Walters et al. [2] used the Oldroyd B viscoelastic constitutive model to show the potential importance of \(N_{1}^{{\text{S}}}\) in axisymmetric contraction flows for Boger fluids. Specifically, they summarized that high \(\eta_{{\text{E}}}\) can retard the flow, whereas high \(N_{1}^{{\text{S}}}\) can have the opposite effect. James [3] investigated the possible role of shear-generated normal stresses to be extensional in nature. For Boger fluids flowing through arrays of rods, the increased flow resistance is related to the elasticity property \(N_{1}^{{\text{S}}}\), and not to the extensional viscosity stress \(N_{1}^{{\text{E}}}\). Although \(N_{1}^{{\text{S}}}\) is small, it cannot be ignored. However, their numerical results did not evidently demonstrate the opposite effect of \(N_{1}^{{\text{S}}}\) and \(N_{1}^{{\text{E}}}\) in those articles aforementioned.

In the rheology, the Deborah number De and Weissenberg number Wi are key dimensionless number to indicate the viscoelastic character of polymer melts [4]. Experimentally, De is defined as the ratio of the characteristic time of the fluid \(\lambda\) to the characteristic time of the flow \(t_{{\text{f}}}\):

$${\text{De}} = \lambda /t_{{\text{f}}}$$
(1)

Theoretically, Wi is the product of the shear rate \(\dot{\gamma }\) and relaxation time \(\lambda\):

$${\text{Wi}} = \lambda \dot{\gamma }.$$
(2)

At a large Weissenberg number or Deborah number, \({\text{Wi}} > > 1\) or \({\text{De}} > > 1\), the fluid will respond with elastic behavior like that of a solid. For \({\text{Wi}} < < 1\) or \({\text{De}} < < 1\), a liquid-like viscous state is expected, while there is sufficient time to relax during deformation. \({\text{Wi}} \approx 1\) or \({\text{De}} \approx 1\) implies the viscoelastic fluid. Addiontally, Pipkin diagram [5] is the relationship between De and Wi to represent different flow regimes of a material regarding viscometric flows, linear viscoelasticity, and nonlinear viscoelasticity.

Recently, Tseng [6] derived a potential weighted shear/extensional viscosity, called the GNF-X (Generalized Newtonian Fluid eXtended) model. For the 3D (three-dimensional) entry flow simulation of a low-density polyethylene (LDPE) melt, he [6], therefore, demonstrated the vortex formation in terms of the weighted viscosity and extensional flow. The earlier White–Metzner (WM) constitutive equation [7] expresses a relatively simple nonlinear viscoelastic fluid. Based on the GNF-X model, Tseng continued to develop a modification of the WM constitutive equation, called the WMT-X (WM eXtended by Tseng) model [8,9,10]. Such a model can pretty well fit the first normal stress difference for characterizing a fluid’s elasticity, as well as its shear viscosity and extensional viscosity. The predicted vortex sizes are in good agreement with the experimental data. In the WMT-X numerical calculation carried out over a wide range of Deborah numbers, it is stably convergent.

Using the WMT-X viscoelastic fluid model, the primary objective of the present study is, therefore, to demonstrate the competitive role of shear and extension-induced first normal stress differences coexisting in complex flows of polymer melts. Additionally, one can derive \(N_{1}^{{\text{S}}}\) and \(N_{1}^{{\text{E}}}\) related to Weissenberg’s number and Trouton’s ratio. In contraction flow simulations, the numerical predictions of slit-die velocity profile at different viscous and viscoelastic constitutive equations, including GNF, GNF-X, and WMT-X, are compared with related experimental data. The governing equations and constitutive equations of polymer melts are introduced in the next section for completeness.

2 Theoretical background

The actual flow of polymer melts is complicated. In non-Newtonian fluid mechanics, the polymer processing is highly nonlinear, as the material properties are dependent upon flow and temperature conditions. For completeness, the governing equations of fluid dynamics, including those on continuity, motion, and energy, are addressed:

$$\frac{\partial \rho }{{\partial t}} + \nabla \cdot \rho {\mathbf{v}} = 0$$
(3)
$$\frac{\partial }{\partial t}(\rho {\mathbf{v}}) + \nabla \cdot (\rho {\mathbf{vv}}) = - \nabla P + \nabla \cdot {{\varvec{\uptau}}} + \rho {\mathbf{g}}$$
(4)
$$\rho C_{P} \left( {\frac{\partial T}{{\partial t}} + {\mathbf{v}} \cdot \nabla T} \right) = \nabla \cdot (k\nabla T) + {{\varvec{\uptau}}}:{\mathbf{D}},$$
(5)

where \(\rho\) is the density; v is the velocity vector; t is the time; P is the pressure; \({{\varvec{\uptau}}}\) is the extra stress tensor; g is the acceleration vector of gravity; Cp is the specific heat; T is the temperature; k is the thermal conductivity. Note that the velocity gradient tensor \(\nabla\) v, rate-of-deformation tensor D, and vorticity tensor W are kinematic tensors; their relationships are expressed as follows:

$${\mathbf{D}} = \frac{{\nabla {\mathbf{v}} + (\nabla {\mathbf{v}})^{T} }}{2}$$
(6)
$${\mathbf{W}} = \frac{{\nabla {\mathbf{v}} - (\nabla {\mathbf{v}})^{T} }}{2},$$
(7)

where D and W are the symmetric and anti-symmetric parts of \(\nabla\) v, respectively.

For different viscous and viscoelastic fluids, a rheological state expression of the stress tensor \({{\varvec{\uptau}}}\) in terms of various kinematic tensors is called the so-called constitutive equation. The constitutive equations of interest, including the standard GNF (generalized Newtonian fluid) viscous model of shear viscosity, the extended GNF (GNF-X) viscous model of weighted shear/extensional viscosity, and the improved White–Metzner viscoelastic model of WMT-X (White–Metzner eXtended by Tseng), are introduced in the present study.

2.1 GNF shear and extensional viscosity

The famous GNF (generalized Newtonian fluid) shear viscosity model [4, 11,12,13] describes the mathematical relationship between the tensors \({{\varvec{\uptau}}}\) and D in a steady-state, homogenous, and generalized 3D deformation, as follows:

$${{\varvec{\uptau}}} = 2\eta_{{\text{S}}} (\dot{\gamma }){\mathbf{D}},$$
(8)

where shear viscosity \(\eta_{{\text{S}}}\), which is a nonlinear function of strain rate, indicates flow resistance in simple shear; the strain rate \(\dot{\gamma }\) is the magnitude of the rate-of-deformation tensor, namely, D: \(\dot{\gamma } = \sqrt {2{\mathbf{D}}:{\mathbf{D}}}\).

The flow curves of shear viscosity dominate the flow behaviors of a variety of materials. Commonly, the Carreau model [12], a type of the GNF shear viscosity model, is often used to fit experimental viscosity data:

$$\eta_{{\text{S}}} (\dot{\gamma }) = \frac{{\eta_{0} }}{{[1 + (\lambda \dot{\gamma })^{2} ]^{{\tfrac{1 - n}{2}}} }},$$
(9)

where \(\lambda\) is the characteristic time; n is the power index; \(\eta_{0}\) is the Newtonian fluid (NF) constant viscosity or the zero-shear-rate viscosity. When \(\dot{\gamma } = 0\), the GNF viscosity returns to the NF viscosity.

In rheology, the Trouton ratio Tr is the uniaxial extensional viscosity \(\eta_{{{\text{UE}}}}\) over shear viscosity \(\eta_{{\text{S}}}\) [13,14,15]:

$${\text{Tr}} = \frac{{\eta_{{{\text{UE}}}} }}{{\eta_{{\text{S}}} }}.$$
(10)

For the isotropic Newtonian viscosity [14], the Trouton ratio ideally equals 3, namely, Tr = 3. In particular, Tseng [6] proposed the Trouton ratio function for an interrelationship between nonlinear shear viscosity and nonlinear extensional viscosity,

$$\eta_{{{\text{UE}}}} (\dot{\gamma }) = \eta_{{\text{S}}} (\dot{\gamma }){\text{Tr}}(\dot{\gamma })$$
(11)
$${\text{Tr}}(\dot{\gamma }) = 3 + \frac{{{\text{Tr}}_{0} }}{{\left[ {1 + (\lambda_{{\text{T}}} \dot{\gamma })^{ - 2} } \right]^{{n_{{\text{T}}} }} }},$$
(12)

where three parameters:\({\text{Tr}}_{0}\), \(\lambda_{{\text{T}}}\), and \(n_{{\text{T}}}\) are the anisotropic factor, characteristic time, and power index, respectively. Equation (12) is an empirical equation fitted by the experimental extension viscosity data to describe the significant extension thinning and extension thickening characteristics,, refer to the previous work of Sarkar and Gupta [15]. Note the maximum value of \({\text{Tr(}}\dot{\gamma })\) at large \(\dot{\gamma }\), namely, maxTr = 3 + \({\text{Tr}}_{0}\).

2.2 GNF-X weighted shear/extensional viscosity

Recently, Tseng [6] derived the weighted shear/extensional viscosity \(\eta_{{\text{W}}} (\dot{\gamma })\), called the eXtended GNF (GNF-X) model, as expressed below:

$${{\varvec{\uptau}}} = 2\eta_{{\text{W}}} {\mathbf{D}}$$
(13)
$$\eta_{{\text{W}}} = (1 - W)\eta_{{\text{S}}} + W\eta_{{\text{E}}}$$
(14)
$$1 - W = \frac{{\dot{\gamma }_{{\text{S}}}^{2} }}{{\dot{\gamma }^{2} }}$$
(15)
$$W = \frac{{\dot{\gamma }_{{\text{E}}}^{2} }}{{\dot{\gamma }^{2} }}$$
(16)
$$\dot{\gamma }^{2} = \dot{\gamma }_{{\text{S}}}^{2} + \dot{\gamma }_{{\text{E}}}^{2} ,$$
(17)

where W is the weighting function, also known as the extension fraction; \(\eta_{{\text{S}}}\) and \(\eta_{{\text{E}}}\) are the generalized shear and extensional viscosities with respect to strain rates, respectively.

\(\dot{\gamma }_{{\text{S}}}\) and \(\dot{\gamma }_{{\text{E}}}\) are characteristic shear and extensional rates, respectively. Note that the weighted function W represents the percentage of extension rate. When W = 0, the GNF-X weighted viscosity returns to the GNF shear viscosity. For the flow classification, \(W = 0\) and \(W = 1\) indicate viscometric (or shear) and extensional (or shearfree) flows, respectively. Notably, it cannot be used to identify a rigid body rotation. Details of the GNF-X weighted viscosity are available elsewhere [6].

However, Park [16] commented the GNF-X model in which those so-called principal shear and extension rates cannot represent the shear and extension rates correctly. Therefore, Tseng [17] have sufficiently demonstrated that the GNF-X numerical algorithm can decompose exact shear and extension rates validated in the analytical center-gated disk flow. Significantly, Wen et al. [18] performed the non-isothermal GNF-X flow simulations to estimate the extensional viscosity for various polymer melts.

Basically, the GNF-X weighted viscosity is similar to the early Schunk-Scriven experiential model of a linear combination (or arithmetic mean) of the two type-Carreau-type shear and extension viscosities [19]. Differently, the Schunk-Scriven weighting function depends on the Astarita flow-classification parameter [20], which is the related to the trace of the relative vorticity and rate-of-deformation tensors. Another alternative to employ, Scriven and coworkers [21] proposed the weighted geometric-mean viscosity. The concept of the mixed viscosity was previously explored in several articles [22,23,24,25].

Additionally, the uniaxial extensional flow is defined as follows:

$$\eta_{{{\text{UE}}}} = \frac{{\tau_{11} - \tau_{22} }}{{\dot{\varepsilon }}}$$
(18)
$${{\varvec{\uptau}}} = \left[ {\begin{array}{*{20}c} {\tau_{11} } & 0 & 0 \\ 0 & {\tau_{22} } & 0 \\ 0 & 0 & {\tau_{33} } \\ \end{array} } \right]$$
(19)
$${\mathbf{D}} = \dot{\varepsilon }\left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & { - \tfrac{1}{2}} & 0 \\ 0 & 0 & { - \tfrac{1}{2}} \\ \end{array} } \right],$$
(20)

where \(\tau_{11}\), \(\tau_{22}\), and \(\tau_{33}\) are the x-axial, y-axial, and z-axial normal stress tensor components, respectively; \(\dot{\varepsilon }\) is an extension rate. Therefore, the generalized extensional viscosity \(\eta_{{\text{E}}}\) is related to the uniaxial extensional (UE) viscosity \(\eta_{{{\text{UE}}}}\),

$$\eta_{{\text{E}}} = \frac{{\eta_{{{\text{UE}}}} }}{3} = \frac{{\tau_{11} - \tau_{22} }}{{3\dot{\varepsilon }}}.$$
(21)

Such an extensional viscosity \(\eta_{{\text{E}}}\) is also known as the stressing viscosity of Meissner et al. [11, 26]. For planar extension, the stressing viscosity equals

$$\eta_{{\text{E}}} = \frac{{\eta_{{{\text{PE}}}} }}{4}.$$
(22)

In previous article of Tseng [6], the key part of Eq. (21) is not discussed for the GNF-X model in relating \(\eta_{{\text{E}}}\) and \(\eta_{{{\text{UE}}}}\). The two most commonly used techniques for measuring extensional viscosity of polymer melts are the rheometric scientific RME (rheometric melt elongation) rheometer and the Münstedt tensile rheometer [27]. In practice, it is difficult to directly measure the steady extensional viscosity of thermoplastic composite materials at high extension rates. The Cogswell analytic method of extensional viscosity was famously derived in the pressure drop of entrance flow for capillary rheometer [28].

2.3 WMT-X viscoelastic constitutive equation

Based on the GNF-X weighed shear/extension viscosity [6], Tseng [8] improved the classic White–Metzner (WM) viscoelastic constitutive equation, named WMT-X (WM eXtended by Tseng):

figure a

where \(\lambda_{{\text{W}}} (\dot{\gamma })\) is Weissenberg’s relaxation time; is the Gordon–Schowalter time derivative [12]. Its complete form is expanded as follows:

$$\begin{aligned} \lambda_{{\text{W}}} (\dot{\gamma })\frac{{\partial {{\varvec{\uptau}}}}}{\partial t} + W_{i} (\dot{\gamma })\left( {\frac{{\mathbf{v}}}{{\dot{\gamma }}} \cdot \nabla {{\varvec{\uptau}}}} \right) \\ \quad - Wi(\dot{\gamma })[({\mathbf{W}}^{*} \cdot {{\varvec{\uptau}}} + {{\varvec{\uptau}}} \cdot {\mathbf{W}}^{*T} ) + C_{{\text{N}}} (\dot{\gamma })({\mathbf{D}}^{*} \cdot {{\varvec{\uptau}}} + {{\varvec{\uptau}}} \cdot {\mathbf{D}}^{*} )] + {{\varvec{\uptau}}} = 2\eta_{{\text{W}}} (\dot{\gamma }){\mathbf{D}} \\ \end{aligned}$$
(24)
$$C_{{\text{N}}} (\dot{\gamma }) = 1 - \xi (\dot{\gamma })$$
(25)
$${\mathbf{D}}^{*} = {\mathbf{D}}/\dot{\gamma }$$
(26)
$${\mathbf{W}}^{*} = {\mathbf{W}}/\dot{\gamma },$$
(27)

where Wi is Weissenberg’s number; D* and W* are dimensionless tensors of the rate-of-deformation tensor D and the vorticity tensor W, respectively; the variable \(C_{{\text{N}}} (\dot{\gamma })\) is the normal stress parameter limited between 0 and 1; the variable \(\xi (\dot{\gamma })\) is a slip factor. When \(\eta_{{\text{W}}} = \eta_{{\text{S}}}\), the WMT-X model returns to the White–Metzner model. Note that \(\xi\) = 0 and 1 signify the upper-convected and corotational forms, respectively. For a constant viscosity and \(\xi\) = 0, WMT-X is equivalent to UCM (upper convected Maxwell).

Especially for the “steady-state” and “homogenous” flows, the WMT-X stress tensor can be simplified to consist of the viscous and elastic terms:

$${{\varvec{\uptau}}} = \underbrace {{2\eta_{{\text{W}}} {\mathbf{D}}}}_{{{\text{viscous}}}} + \underbrace {{{\text{Wi}}[({{\varvec{\uptau}}} \cdot {\mathbf{W}}^{*} + {\mathbf{W}}^{*T} \cdot {{\varvec{\uptau}}}) + C_{{\text{N}}} ({{\varvec{\uptau}}} \cdot {\mathbf{D}}^{*} + {\mathbf{D}}^{*} \cdot {{\varvec{\uptau}}})]}}_{{{\text{elastic}}}}.$$
(28)

This can be known as the informed viscoelastic (iVE) equation, which incorporating the shear and extension viscous contributions, as well as the elastic effects. When Wi equals zero, the WMT-X viscoelastic model returns to the GNF-X viscous model. According to the steady-state and homogenous stress tensor under simple shear flow, the shear stress \(\tau_{12}\), the first normal stress difference N1 and the second normal stress difference N2 are further found as below:

$$\tau_{12} = \frac{{\eta_{{\text{S}}} \dot{\gamma }}}{{1 + {\text{Wi}}^{2} (1 - C_{{\text{N}}}^{2} )}}$$
(29)
$$N_{1} = \tau_{11} - \tau_{22} = 2{\text{Wi}}\tau_{12}$$
(30)
$$N_{2} = \tau_{22} - \tau_{33} = - (1 - C_{{\text{N}}} ){\text{Wi}}\tau_{12}$$
(31)
$$- \frac{{N_{2} }}{{N_{1} }} = \frac{{(1 - C_{{\text{N}}} )}}{2} = \frac{\xi }{2}$$
(32)
$$C_{{\text{N}}} = 1 - 2\left( { - \frac{{N_{2} }}{{N_{1} }}} \right),$$
(33)

where \(\tau_{11}\), \(\tau_{22}\), and \(\tau_{33}\) are the x-axial, y-axial, and z-axial normal stress tensor components, respectively; \(\tau_{12}\) occurs in the xy plane.

During the shear flow, the Weissenberg number Wi has proven invaluable for rheologists in quantifying the viscoelastic effects in a non-Newtonian fluid, which is the product of the strain rate \(\dot{\gamma }\) and the longest relaxation time \(\lambda_{{\text{W}}}\):

$${\text{Wi}} = \lambda_{{\text{W}}} \dot{\gamma }.$$
(34)

At a large Weissenberg number, \({\text{Wi}} > > 1\), the fluid will respond with elastic behavior like that of a solid. For \({\text{Wi}} < < 1\), a liquid-like viscous state is expected, while there is sufficient time to relax during deformation. One can assume the strain-rate dependence of \({\text{Wi}}(\dot{\gamma })\) and \(\lambda_{{\text{W}}} (\dot{\gamma })\). Thus, the relaxation time \(\lambda_{{\text{W}}} (\dot{\gamma })\) is determined via Eq. (34):

$$\lambda_{{\text{W}}} (\dot{\gamma }) = \frac{{{\text{Wi}}(\dot{\gamma })}}{{\dot{\gamma }}}.$$
(35)

For avoiding the high Weissenberg number problem [8] with unstable numerical calculations, one attempts to improve the unconstrained growth of Weissenberg function with respect to strain rates:

$${\text{Wi}}(\dot{\gamma }) = \frac{{{\text{Wi}}_{0} }}{{\left[ {1 + \left( {\frac{{\dot{\gamma }}}{{\dot{\gamma }_{{{\text{CW}}}} }}} \right)^{ - 2} } \right]^{{n_{{\text{W}}} }} }},$$
(36)

where the parameters Wi0, \(\dot{\gamma }_{{{\text{CW}}}}\), and nW are fit by the experimental data of the first normal stress difference. Thus, the unstable high Wi problem is weakened by such a constrained Weissenberg growth function. Details of the WMT-X model scheme are referred to in the previous work of Tseng [8].

In addition, the elastic variable CN is related to the minus-normal-stress-difference ratio of −N2/N1 [see Eq. (33)]. The (−N2/N1) ratio reasonably exists in a region between 0 and 0.5 for general polymer melts. Thus, the ratio is assumed the independence of temperature, and is modeled as a step function of strain rates:

$$\left( { - \frac{{N_{2} }}{{N_{1} }}} \right) = R_{0} + \frac{{0.5 - R_{0} }}{{\left[ {1 + \left( {\frac{{\dot{\gamma }}}{{\dot{\gamma }_{CR} }}} \right)^{2} } \right]^{{n_{{\text{R}}} }} }},$$
(37)

where the parameters \(R_{0}\), \(\dot{\gamma }_{{{\text{CR}}}}\), and nR are fit by the experimental data. When −N2/N1 = 0 and 0.5, the variable CN equals one and zero, respectively.

From theory to practice, the significant constitutive models, GNF-X and WMT-X, were incorporated into commercial simulation software of plastic injection molding, Moldex3D. The state-of-the-art Moldex3D CFD (computational fluid dynamics) framework is developed by the three-dimensional finite volume method (3D-FVM) [29] to numerically solve the transient, non-isothermal governing equations of flow fields for complicated viscoelastic fluids of polymer melts. In addition, the advantage of 3D-FVM with robustness and efficiency is the ability to realize a nonlinear imbalanced flow phenomenon in complex channel geometries.

2.4 Derivation of normal stress differences in hybrid shear/extensional flow

Consider that a hybrid flow of the velocity gradient tensor \(\nabla {\mathbf{v}}\) consists of simple shear and planar extension:

$$\nabla {\mathbf{v}} = \left[ {\begin{array}{*{20}c} { - \dot{\varepsilon }} & 0 & {\dot{\gamma }_{{\text{S}}} } \\ 0 & {\dot{\varepsilon }} & 0 \\ 0 & 0 & 0 \\ \end{array} } \right],$$
(38)

where the compression and stretch deformations are exerted along the x-axial and y-axial directions for the planar extension flow, respectively; the simple shear flow is given in the xz plane; \(\dot{\varepsilon }\) and \(\dot{\gamma }_{{\text{S}}}\) are the diagonal and off-diagonal components, respectively. Thereby, the rate-of-strain tensor D and total strain rate and the total strain rate \(\dot{\gamma }\) are expressed as:

$${\mathbf{D}} = \left[ {\begin{array}{*{20}c} { - \dot{\varepsilon }} & 0 & {\tfrac{1}{2}\dot{\gamma }_{{\text{S}}} } \\ 0 & {\dot{\varepsilon }} & 0 \\ {\tfrac{1}{2}\dot{\gamma }_{{\text{S}}} } & 0 & 0 \\ \end{array} } \right]$$
(39)
$$\dot{\gamma }^{2} = \sqrt {2{\mathbf{D}}:{\mathbf{D}}} = \dot{\gamma }_{{\text{S}}}^{2} + \dot{\gamma }_{{\text{E}}}^{2}$$
(40)
$$\dot{\gamma }_{{\text{E}}} = 2\dot{\varepsilon },$$
(41)

where \(\dot{\gamma }_{{\text{S}}}\) and \(\dot{\gamma }_{{\text{E}}}\) are the characteristic shear and extensional rates, respectively.

According to the upper convected form of the WM model of Eq. (30), the first normal stress difference \(N_{1}^{{\text{S}}}\) (abbreviation: N1S) for the steady-state and homogenous simple shear flow is shown as:

$$N_{1}^{{\text{S}}} = \tau_{11} - \tau_{33} = 2\eta_{{\text{S}}} \dot{\gamma }_{{\text{S}}} {\text{Wi,}}$$
(42)

where \(\tau_{11}\), \(\tau_{22}\), and \(\tau_{33}\) are the x-axial, y-axial, and z-axial normal stress tensor components, respectively. In addition, the planar extensional viscosity is defined as:

$$\eta_{{{\text{PE}}}} = \frac{{\tau_{22} - \tau_{11} }}{{\dot{\varepsilon }}} = \frac{{N_{1}^{{\text{E}}} }}{{\dot{\varepsilon }}},$$
(43)

where \(N_{1}^{{\text{E}}}\) (abbreviation: N1E) is the first normal stress difference due to the planar extension flow.

This is based on the Trouton ratio of Eq. (10):

$$N_{1}^{{\text{E}}} = {\text{Tr}}\eta_{{\text{S}}} \dot{\varepsilon }.$$
(44)

Therefore, the total first normal stress difference \(N_{1}^{{\text{T}}}\)(abbreviation: N1T) for hybrid shear/extension flow is expressed as:

$$N_{1}^{{\text{T}}} = N_{1}^{{\text{S}}} + N_{1}^{{\text{E}}} = \eta_{{\text{S}}} \dot{\gamma }_{{\text{S}}} \left( {2{\text{Wi}} + \frac{1}{2}{\text{Tr}}\frac{{\dot{\gamma }_{{\text{E}}} }}{{\dot{\gamma }_{{\text{S}}} }}} \right).$$
(45)

In dimensional forms, the stresses are written as follows:

$$\frac{{N_{1}^{{\text{T}}} }}{{\eta_{{\text{S}}} \dot{\gamma }_{{\text{S}}} }} = 2{\text{Wi}} + \frac{1}{2}{\text{Tr}}\frac{{\dot{\gamma }_{{\text{E}}} }}{{\dot{\gamma }_{{\text{S}}} }}$$
(46)
$$\frac{{N_{1}^{{\text{S}}} }}{{\eta_{{\text{S}}} \dot{\gamma }_{{\text{S}}} }} = 2{\text{Wi}}$$
(47)
$$\frac{{N_{1}^{{\text{E}}} }}{{\eta_{{\text{S}}} \dot{\gamma }_{{\text{S}}} }} = \frac{1}{2}{\text{Tr}}\frac{{\dot{\gamma }_{{\text{E}}} }}{{\dot{\gamma }_{{\text{S}}} }}.$$
(48)

For the percentage of \(N_{1}^{{\text{E}}}\) and \(N_{1}^{{\text{S}}}\), one can find:

$$\frac{{N_{1}^{{\text{E}}} }}{{N_{1}^{{\text{T}}} }} = \frac{1}{{1 + 4({\text{Wi}}/{\text{Tr}})(\dot{\gamma }_{{\text{S}}} /\dot{\gamma }_{{\text{E}}} )}}$$
(49)
$$\frac{{N_{1}^{{\text{S}}} }}{{N_{1}^{{\text{T}}} }} = 1 - \frac{{N_{1}^{{\text{E}}} }}{{N_{1}^{{\text{T}}} }}.$$
(50)

Thus, the \(N_{1}^{{\text{S}}} /N_{1}^{{\text{E}}}\) ratio is expressed as:

$$\frac{{N_{1}^{{\text{S}}} }}{{N_{1}^{{\text{E}}} }} = 4\frac{{{\text{Wi}}}}{{{\text{Tr}}}}\frac{{\dot{\gamma }_{{\text{S}}} }}{{\dot{\gamma }_{{\text{E}}} }}.$$
(51)

From the GNF-X model of Eq. (16), the \(\dot{\gamma }_{{\text{S}}} /\dot{\gamma }_{{\text{E}}}\) ratio is related to the weighted function W of extension fraction:

$$\frac{{\dot{\gamma }_{{\text{S}}} }}{{\dot{\gamma }_{{\text{E}}} }} = \sqrt {\frac{1 - W}{W}} .$$
(52)

In the next section, dramatic variations of the stresses, \(N_{1}^{{\text{E}}}\) and \(N_{1}^{{\text{S}}}\), with respect to strain rates are investigated in analytical flows of hybrid simple shear/planar extension.

3 Results and discussion

In the present study, the main objective is to demonstrate the conflicting effects in the shear-induced and extension-induced first normal stress difference, \(N_{1}^{{\text{E}}}\) and \(N_{1}^{{\text{S}}}\), which are related to the Trouton ratio and the Weissenberg number, respectively. For the analytical center-gated disk flow of power-law fluid, the primary necessity is to understand the characteristic shear rate and extension rate profiles, as well as the \(N_{1}^{{\text{E}}}\) and \(N_{1}^{{\text{S}}}\) distributions through the normalized thickness at various Weissenberg’s numbers under the fixed higher Trouton ratio. In addition to identifying the WMT-X parameters of material functions for LDPE melt, dramatic changes in \(N_{1}^{{\text{E}}}\) and \(N_{1}^{{\text{S}}}\) with respect to strain rates are investigated herein. As validation for different constitutive equations, including NF, GNF, GNF-X, and WMT-X, the slit velocity profile in contraction flow simulations are performed to explore if the inelastic extensional-viscosity-generating first normal stress difference \(N_{1}^{{\text{E}}}\) can obviously increase flow resistance, whereas the elastic shear-induced first normal stress difference \(N_{1}^{{\text{S}}}\) can have the opposite effect to facilitate flow momentum.

3.1 Analytical center-gated disk flow of power-law fluid

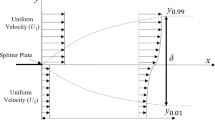
The center-gated disk flow of the velocity gradient tensor is guided by a complex combination flow consisting of the off-diagonal shear component and diagonal extension component, as shown in Fig. 1. For the power-law fluid, the analytical velocity gradient tensor L of the center-gated disk is given to determine the symmetric rate-of-deformation tensor D and the anti-symmetric vorticity tensor W:

$$\eta = \eta_{0} \dot{\gamma }^{n - 1}$$
(53)
$$s = 1/n$$
(54)
$$v_{{\text{r}}} = \frac{Q}{4\pi rb}\left( {\frac{s + 2}{{s + 1}}} \right)\left[ {1 - \left( \frac{z}{b} \right)^{s + 1} } \right],\quad v_{\theta } = 0,\quad v_{z} = 0$$
(55)
$${\mathbf{L}} = \nabla {\mathbf{v}} = \frac{Q}{4\pi rh}\left( {\frac{s + 2}{{s + 1}}} \right)\left[ {\begin{array}{*{20}c} { - \frac{1}{r}\left[ {1 - \left( \frac{z}{h} \right)^{s + 1} } \right]} & 0 & { - \frac{s + 1}{h}\left( \frac{z}{h} \right)^{s} } \\ 0 & {\frac{1}{r}\left[ {1 - \left( \frac{z}{h} \right)^{s + 1} } \right]} & 0 \\ 0 & 0 & 0 \\ \end{array} } \right]$$
(56)
$$= \left[ {\begin{array}{*{20}c} { - L_{{\text{E}}} } & 0 & {L_{{\text{S}}} } \\ 0 & {L_{{\text{E}}} } & 0 \\ 0 & 0 & 0 \\ \end{array} } \right]$$
(57)
$$L_{{\text{S}}} = \frac{Q}{4\pi }\frac{1}{r}\frac{s + 2}{{h^{2} }}\left( \frac{z}{h} \right)^{s}$$
(58)
$$L_{{\text{E}}} = \frac{Q}{4\pi }\frac{1}{{r^{2} }}\frac{1}{h}\left( {\frac{s + 2}{{s + 1}}} \right)\left[ {1 - \left( \frac{z}{h} \right)^{s + 1} } \right],$$
(59)

where Q is the volumetric flow rate; the total gap thickness is 2h; \(v_{i}\) is the velocity component in the \(x_{i}\) direction, with the subscripts \(i,j = r{, }\theta {, }z\) in the cylindrical coordinates; \(0 < r \le R\) is constrained, and R is the disk radius. By using the cylindrical coordinates, the radial distance r describes the flow direction: the azimuth angle \(\theta\) is in the cross-flow direction, and the z axis is in the gradient direction. The velocity gradient tensor component is defined as:\(L_{ij} = \partial v_{i} /\partial x_{j}\). \(L_{{\text{S}}}\) and \(L_{{\text{E}}}\) are the shear and extension components of the velocity gradient tensor, respectively.

Fig. 1
figure 1

Illustration of the center-gated disk flow for the n = 0.5 power-law fluid

Full size image

The rate-of-strain tensor D and total strain rate \(\dot{\gamma }\) depending on \(L_{{\text{S}}}\) and \(L_{{\text{E}}}\) are obtained, as well:

$${\mathbf{D}} = \left[ {\begin{array}{*{20}c} { - L_{{\text{E}}} } & 0 & {\frac{{L_{{\text{S}}} }}{2}} \\ 0 & {L_{{\text{E}}} } & 0 \\ {\frac{{L_{{\text{S}}} }}{2}} & 0 & 0 \\ \end{array} } \right]$$
(60)
$$\dot{\gamma }^{2} = \sqrt {2{\mathbf{D}}:{\mathbf{D}}} = L_{{\text{S}}}^{2} + (2L_{{\text{E}}} )^{2}$$
(61)

The characteristic shear and extension rates, \(\dot{\gamma }_{{\text{S}}}\) and \(\dot{\gamma }_{{\text{E}}}\), can both be discriminated:

$$\dot{\gamma }_{{\text{S}}} = L_{{\text{S}}}$$
(62)
$$\dot{\gamma }_{{\text{E}}} = 2L_{{\text{E}}}$$
(63)
$$\dot{\gamma }^{2} = \dot{\gamma }_{{\text{S}}}^{2} + \dot{\gamma }_{{\text{E}}}^{2} .$$
(64)

In this work, the disk thickness and disk radius are 2h = 0.3 cm and r = 5.0 cm; the flow rate Q = 100 cm3/s is given. For the power-law fluid with the power index n = 0.5, Fig. 2 shows total strain rate, shear rate, and extension rate profiles through the normalized thickness in analytical isothermal center-gated disk flow. Shear rate is the largest proportion of total strain rate. The maximum shear rate \(\dot{\gamma }_{{\text{S}}}^{\max }\) = 212.2 s−1 obviously occurs in the wall boundary (z/h = 1.0), while the zero-shear-rate is found at the flow center (z/h = 0.0). Conversely, the maximum extension rate \(\dot{\gamma }_{{\text{E}}}^{\max }\) = 5.6 s−1 is limited in the center and is close to zero near the wall. In Fig. 3, the extension fraction profile clearly concentrates at the thickness core. As shown in Fig. 4, one can attempt to find the relationship between extension fraction and strain rates. Thereby, the extension fraction or weighted function of the GNF-X model is expressed below:

$$W = \frac{{\dot{\gamma }_{{\text{E}}}^{2} }}{{\dot{\gamma }^{2} }} = \frac{1}{{\left[ {1 + \left( {\tfrac{{\dot{\gamma }}}{{\dot{\gamma }_{{\text{C}}} }}} \right)} \right]^{{N_{{\text{W}}} }} }},$$
(65)

where the critical strain rate is \(\dot{\gamma }_{{\text{C}}} = 10\) s−1; the power index is \(N_{{\text{W}}} = 1.3\).

Fig. 2
figure 2

Total strain rate, shear rate, and extension rate profiles through the normalized thickness for the analytical center-gated disk flow of isothermal power-law fluid (n = 0.5)

Full size image
Fig. 3
figure 3

Extension fraction profiles through the normalized thickness for the analytical center-gated disk flow of isothermal power-law fluid (n = 0.5)

Full size image
Fig. 4
figure 4

Extension fraction against strain rates for the analytical center-gated disk flow of isothermal power-law fluid (n = 0.5)

Full size image

The \(\dot{\gamma }_{{\text{S}}} /\dot{\gamma }_{{\text{E}}}\) ratio is estimated based on Fig. 4 of the extension fraction. In particular, Wi = 0 is given in the preceding Eqs. (49) and (50) so that \(\frac{{N_{1}^{{\text{E}}} }}{{N_{1}^{{\text{T}}} }} = 1\) and \(\frac{{N_{1}^{{\text{S}}} }}{{N_{1}^{{\text{T}}} }} = 0\) are obtained for inelastic power-law fluids with the power index n = 0.5. At various Weissenberg’s numbers (Wi = 0.1, 1.0, and 10) under the fixed higher Trouton ratio of Tr = 30, Fig. 5 shows the percentage of \(N_{1}^{{\text{E}}}\) and \(N_{1}^{{\text{S}}}\) through the normalized thickness from the center core to the wall boundary. Exhibiting the opposite relation between the inelastic extensional-viscosity-generating first normal stress difference \(N_{1}^{{\text{E}}}\) and the elastic shear-induced first normal stress difference \(N_{1}^{{\text{S}}}\) is obvious. In addition, \(N_{1}^{{\text{E}}}\) occurs at the core and \(N_{1}^{{\text{S}}}\) yields near the boundary. For the weak elastic effect with the small Weissenberg number of Wi = 0.1, \(N_{1}^{{\text{E}}}\) almost dominates 90% of whole region, while \(N_{1}^{{\text{S}}}\) occupies about 10%. Increasing the elastic effect at Wi = 1.0, \(N_{1}^{{\text{E}}}\) and \(N_{1}^{{\text{S}}}\) control 40% and 60%, respectively. In particular, due to the strong elastic effect with the extreme value of Wi = 10, it conversely results in 10% of \(N_{1}^{{\text{E}}}\) and 90% of \(N_{1}^{{\text{S}}}\). Therefore, higher \(N_{1}^{{\text{E}}}\) corresponds to lower \(N_{1}^{{\text{S}}}\), and vice versa. When the Weissenberg number of elastic effect is increased, the elastic shear-induced first normal stress difference \(N_{1}^{{\text{S}}}\) becomes stronger, but the inelastic extensional-viscosity-generating first normal stress difference \(N_{1}^{{\text{E}}}\) is weak. Such a result verifies the conflicting role of \(N_{1}^{{\text{E}}}\) and \(N_{1}^{{\text{S}}}\) with respect to Weissenberg numbers in the analytical center-gated disk flow for the non-Newtonian fluid of power-law model.

Fig. 5
figure 5

Percentage of N1S and N1E profiles through the normalized thickness at various Weissenberg’s numbers for the analytical center-gated disk flow of isothermal power-law fluid (n = 0.5)

Full size image

3.2 Variations of N1S and N1E with respect to strain rates

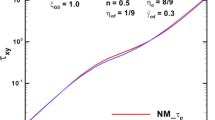
Referring to the previous work of Mitsoulis et al. [30], experimental rheological data on LDPE (low-density polyethylene) melt at the isothermal temperature of 150 °C contain the shear viscosity, the extensional viscosity, and the first normal stress normal difference N1. The WMT-X viscoelastic constitutive Eq. (24) incorporates the Carreau model of shear viscosity of Eq. (9) and the Trouton ratio model of extensional viscosity of Eq. (12), as well as the Weissenberg function of the first normal stress difference of Eq. (36) and the (−N2/N1) ratio of Eq. (37). Figures 6 and 7 show all material functions, including the shear viscosity, the extensional viscosity, and the first normal stress difference, with respect to strain rates. The predictive curves match the related experimental data. Figure 8 presents the Trouton ratio, the Weissenberg function, and the (−N2/N1) ratio. All optimal model parameters are addressed in Table 1. The identified WMT-X parameters are used in the next section for the contraction flow simulations.

Fig. 6
figure 6

Shear viscosity and first normal stress difference against shear rates for molten LDPE at 150 °C; solid symbols and solid lines represent experimental data and fitting curves, respectively

Full size image
Fig. 7
figure 7

Uniaxial extensional viscosity against extension rates for molten LDPE at 150 °C; solid symbols and solid lines represent experimental data and fitting curves, respectively

Full size image
Fig. 8
figure 8

Trouton ratio, Weissenberg number, and −N2/N1 ratio against strain rates for molten LDPE at 150 °C

Full size image
Table 1 Model parameters of material functions for LDPE melt at 150 °C
Full size table

Following the preceding result of the extension fraction with respect to strain rates in Fig. 4 for the hybrid simple shear/planar extension flow, Fig. 9 shows the shear-induced first normal stress difference \(N_{1}^{{\text{S}}}\) and the extensional-viscosity-generating inelastic first normal stress difference \(N_{1}^{{\text{E}}}\) against strain rates \(\dot{\gamma }\) in dimensionless units, as well as the total first normal stress difference \(N_{1}^{{\text{T}}}\). A critical strain rate is found: \(\dot{\gamma }^{\prime}_{{\text{C}}} = 50\) s−1; the critical strain rate is influenced by the Weissenberg number and the Trouton ratio. Obviously, \(N_{1}^{{\text{S}}}\) dominates at high strain rates of \(\dot{\gamma } > \dot{\gamma }_{C}\), whereas \(N_{1}^{{\text{E}}}\) occurs at low strain rates of \(\dot{\gamma } < \dot{\gamma }_{C}\). In addition, \(N_{1}^{{\text{E}}}\) is larger than \(N_{1}^{{\text{S}}}\). Furthermore, Fig. 10 presents the \(N_{{1}}^{{\text{S}}}\)/\(N_{1}^{{\text{E}}}\) ratio to reveal \(N_{1}^{{\text{S}}}\) and \(N_{1}^{{\text{E}}}\) at the high and low strain rates, respectively. The competing roles of \(N_{1}^{{\text{S}}}\) and \(N_{1}^{{\text{E}}}\) percentage distributions with respect to strain rates in Fig. 11 are clearly indicated as well.

Fig. 9
figure 9

Dimensionless N1S, N1E, N1T against strain rates for molten LDPE at 150 °C

Full size image
Fig. 10
figure 10

The ratio of N1S to N1E against strain rates for molten LDPE at 150 °C

Full size image
Fig. 11
figure 11

The percentage of N1S and N1E against strain rates for molten LDPE at 150 °C

Full size image

3.3 Slit velocity profile in contraction flow simulation

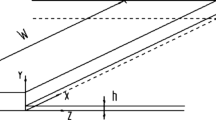
Following the same used material of 150 °C LDPE melt aforementioned, the experimental data of Schmidt et al. [31] regarding the slit velocity profile within a inhomogenous 14:1 planar contraction flow were of interest herein. The primary objective is to demonstrate \(N_{1}^{{\text{S}}}\) facilitating flow and \(N_{1}^{{\text{E}}}\) hindering flow for the velocity profile. Figure 12 illustrates the half symmetric geometry of 14:1 planar contraction flow, which includes two parts: the upstream channel of fluid reservoir and the downstream channel of slit die. The square cross section of the reservoir is 14 × 14 mm2 and its length is 100 mm. The contraction ratio is 14 wherein the height of the reservoir and die is 14 and 1 mm, respectively. The die length is 50 mm. The apparent shear rate of 227 s−1 (or flow rate of about 300 mm3/s) is given for the slit die. Figure 13 shows the trustworthy experimental velocity profile within the slit die measured by Schmidt et al. [31]. They ensured the homogenous temperature distribution in the measurements and avoided some problems of flow instability and wall slip. The velocity profile presents a typical plug-like shape; this result realistically confirms the general understanding of the theoretical analysis in rheology.

Fig. 12
figure 12

The half symmetric geometry of 14:1 planar contraction flow with slit die

Full size image
Fig. 13
figure 13

Velocity profiles within the die slit for the LDPE melt at 150 °C and 227 s−1 for differential viscous and viscoelastic constitutive models

Full size image

Referring to the previous work of Schmidt et al. [31], a research version of the commercial injection molding simulation software, Moldex3D (CoreTech System Co., Taiwan) was adopted to perform the contraction flow simulation in the present work. The number of 3D cells is about 1,000,000 hexagonal elements used in the flow computation for the contraction geometry in Fig. 12. The Cartesian coordinate system was defined in the description and analysis of the velocity fields. The identified viscous and viscoelastic parameters of the NF, GNF, GNF-X, and WMT-X models are addressed in Table 1.

The early studies indicated that the temperature increase leads to opposite variations of the viscosity [32]. For high shear rates, shear heating viscous dissipation will increase substantially the downstream slit-wall temperature in the contraction flow. Typically, note that a pressure drop of 10 MPa will induce a temperature increase of around 2 °C. At a high shear rate of 10,000 s−1 and a high pressure drop of 100 MPa, the mean temperature rise could be as high as 20 °C which will influence the viscosity. In the present study, such a slit-contraction flow simulation was performed by the Moldex3D software kept at the isothermal temperature of T = 150 °C at the lower appear shear rate of 227 s−1. Recently, Wen et al. [18] performed the non-isothermal GNF-X flow simulations to estimate the extensional viscosity for various polymer melts.

As a result, the predictions of velocity profiles for different constitutive models of viscous and viscoelastic fluids are shown in Fig. 13. For the linear NF constant viscosity and the nonlinear GNF shear viscosity, the predicted velocity profile clearly presents the parabolic curve with over-estimation as compared with the experimental date. Basically, the nonlinear GNF shear viscosity increases the flow resistance. In addition, the GNF-X model results in the plug-flow distribution with under-prediction. Obviously, the central velocity slows down due to the resistance contribution of extensional viscosity. It is significant that the predictive curve by the WMT-X viscoelastic model is close to the experimental data of Schmidt et al. [31]. Therefore, one can focus the whole velocity profile especially for GNF-X and WMT-X models, confirming the importance of the elastic effect of the first normal stress difference to accelerate the flowing speed, whereas the GNF-X model with extensional viscosity provides the attaining of a flowing resistance. Previously, the WMT-X viscoelastic model was used to find the vertex growth phenomenon [6, 8], which was slightly affected by the elastic effect of the first normal stress difference. Notably, the inelastic extensional-viscosity-generating first normal stress difference \(N_{1}^{{\text{E}}}\) hinders flow, whereas the elastic shear-induced first normal stress difference \(N_{1}^{{\text{S}}}\) can have the opposite effect in facilitating the flow. Therefore, it evidently demonstrates the opposite effect of the normal stresses \(N_{1}^{{\text{S}}}\) and \(N_{1}^{{\text{E}}}\) for the slit velocity in the contraction flow of LDPE melt.

In particular, a comparison of extensional-thickening and extensional-thinning viscosity curves at low extension rates shown in Fig. 14.The extensional viscosity model parameters of Trouton ratio are addressed in Table 2. Thereby, Fig. 15 presents that the central velocity of the extensional-thinning fluid is faster than that of the extensional-thinning fluid. It is evident to explore the difference between extensional-thinning and extensional-thinning.

Fig. 14
figure 14

Extensional viscosity curves for extensional-thickening and extensional-thinning

Full size image
Table 2 Trouton ratio for extensional-thickening and extensional-thinning
Full size table
Fig. 15
figure 15

Velocity profiles for extensional-thickening and extensional-thinning

Full size image

4 Conclusions

Using the WMT-X viscoelastic model, the ultimate goal was to demonstrate the conflicting roles of the inelastic extensional viscosity-generating first normal stress difference \(N_{1}^{{\text{E}}}\) and the elastic shear-induced first normal stress difference \(N_{1}^{{\text{S}}}\) in hybrid shear/extension flow. As a whole. \(N_{1}^{{\text{E}}}\) is larger than \(N_{1}^{{\text{S}}}\). Although \(N_{1}^{{\text{S}}}\) is somewhat small, it cannot be ignored. In addition, \(N_{1}^{{\text{S}}}\) and \(N_{1}^{{\text{E}}}\) dominate at high and low strain rates, respectively. When the Weissenberg number of elastic effect is increased, \(N_{1}^{{\text{S}}}\) becomes stronger, while \(N_{1}^{{\text{E}}}\) is relatively weak. For predicting the slit velocity profile in contractions flow simulations, it is significant to show \(N_{1}^{{\text{S}}}\) facilitating flow, albeit \(N_{1}^{{\text{E}}}\) has the opposite effect in hampering flow. In particular, it is evident to explore that the central velocity of the extensional-thinning fluid is faster than that of the extensional-thinning fluid.