From substrate disorder to contact angle hysteresis, and back

Abstract

Based on Monte Carlo simulation of the contact line as a long-range elastic model, we develop tools relating substrate traps, trapping time and trapping length. We demonstrate the possibility of retrieving some information on the substrate topography from measurements of contact line motion, near the threshold in forced spreading or near the advancing angle in spontaneous spreading.

Introduction

The dynamics of wetting plays a key role in many practical phenomena where a liquid has to wet a surface, such as in the chemical, automotive or glass industries. Both liquids and solids can vary extensively, as can the spreading processes. The liquid may be, for example, a paint or a lubricant, which has to cover a surface, such as textile, metal, wood or glass. An adhesive, ink or colourant is required to wet and to stick to the corresponding substrate. Another example is the surface treatment, where a substrate is wetted with a coating for a certain application, such as window coating to avoid water and dust deposit. Wetting is also important in agriculture, where pesticides have to spread rapidly on plants to maximise their action. It also plays an important role in life science: the rise of sap in plants, the wetting of the eye cornea, adhesion of parasites on wetted surfaces, insect motion on water, etc.

Each application needs precise understanding of the wetting details, such as the spreading velocity, the wettability properties of the surfaces and the liquid properties, in order to control or modify the liquid/solid pair to obtain the desired wetting behaviour. The driving force for wetting is the out-of-balance surface tension arising from the non-equilibrium shape of the drop on the solid. For a given system under a given set of conditions, the dynamic contact angle $\theta_\textrm{D}$ appears to be a function of the velocity of the moving contact line, $\theta_\textrm{D} = f(v_\textrm{CL})$. In drop spreading, a third parameter, the dynamic base radius R, is sometimes introduced.

In forced spreading (where the contact line is made to move by an external force), for a given configuration and force, a characteristic contact line velocity and a characteristic dynamic contact angle are observed for a given system. Upon varying the conditions, other sets of velocities and angles are observed. It is widely believed that there is a unique relationship between $v_\textrm{CL}$ and $\theta_\textrm{D}$. Experimentally, this relationship is a monotonically increasing function for advancing contact angles and monotonically decreasing for receding angles.

If, on the other hand, we deposit a drop on a solid, which leads to spontaneous spreading, $\theta_\textrm{D}$ will relax from 180° towards its equilibrium value. The contact-line velocity decreases from its initial value to 0 at equilibrium. Here, it is obvious that only one unique velocity can exist for each value of $\theta_\textrm{D}$. Forced spreading and spontaneous spreading are both examples of moving contact lines, and as such, they should be described in some universal way.

This relationship is experimentally shown to be well described by theoretical models considering the energy dissipation occurring via different mechanisms. First, the hydrodynamic model, based on continuum fluid dynamics, considers the dissipation due to flow in the edge of the droplet [1, 2]. Second, the molecular-kinetic theory neglects this mechanism and prefers to consider the friction dissipation between liquid and solid at the contact line, at an atomic level [3, 4]. Current experimental observations seem to give support to both models, depending on the kind of liquid, on the wettability as well as on the timescale of the process.

In practice however, it is almost impossible to deal with perfect solid surfaces. There are always some physical defects (roughness) or chemical heterogeneities either at the microscopic or macroscopic scales. It is now understood that these defects will induce some pinning of the three-phase contact line [5]. Theoretically, only one equilibrium configuration exists. In practice, even small irregularities on the solid, chemical or geometric, induce metastable configurations, having a contact angle that differs from the true equilibrium contact angle. This phenomenon is called contact angle hysteresis, i.e. the value of the static contact angle depends on the history of the system. The angle varies according to whether the liquid tends to advance across or recede from the solid surface. The limiting angles obtained just prior to the movement of the contact line are known as the advancing and receding contact angles. The values for the advancing and receding contact angles tend to be reproducible and are often used to characterise the solid substrate.

The situation is thus as follows. Once we have heterogeneities, we know that there will be some hysteresis. Here, we address the complementary question: Can we infer the type of heterogeneities from the hysteresis measurement?

Using Monte Carlo simulation of the contact line as a long-range elastic model, we exhibit relations between substrate traps, trapping time and trapping length. The Monte Carlo method has the advantage of being sufficiently fast so that the long-range interaction within the line [6, 7] can be taken into account and updated at each time step. Qualitative results and insight into contact angle hysteresis can thus be obtained. Other aspects have been uncovered using hydrodynamics [8], molecular dynamics [9] or a Ginzburg–Landau phase field [10].

The model used in simulations is defined in Section “Forced spreading simulation”. The corresponding contact line velocity and contact line roughness exponent are analysed in Section “Macroscopic observables”. Traps, trapping time and trapping length are analysed in Section “Traps, trapping time and trapping length”. Tools for the inverse problem, inferring the substrate from contact line motion, are developed in Section “Inferring the substrate from contact lines”. The feasibility of using these tools for experimental data is explored in Section “Experiments”. Concluding remarks are given in Section “Conclusion”.

Forced spreading simulation

We start at time t = 0 with a straight line of length N at position 0 in the spreading direction, h(0) = (0,0,...0). At time t = 1,2,..., the line will be described as h( t) = (h ₁(t),h ₂(t),...h _N (t)), with h _i  ∈ ℝ and i ∈ ℤ/Nℤ, corresponding to periodic boundary conditions. The line represents the contact line of a liquid spreading on a disordered substrate, made of delta-function dots of random wettability at integer coordinates (i,k) on top of a uniform substrate of wettability μ. The disorder ξ(i,k) is present only in the half space in front of the initial line, k ∈ ℤ₊. The elastic energy of the contact line is inherited from the liquid surface tension, leading to a long-range interaction [6, 7] between h _i and h _j decreasing as the inverse squared distance |i − j|^− 2 as |i − j|→ ∞. This leads to a Hamiltonian

$$\label{H} H=J\sum\limits_{i,j=1}^N\frac{(h_i-h_j)^2}{1+d(i,j)^2}-\sum\limits_{i=1}^N\mu_i(\xi,h_i) $$

(1)

where $d(i,j)=\min\bigl(|i-j|,N-|i-j|\bigr)$ and

$$\begin{array}{rll} \mu_i(\xi,h_i)&=&\int_0^{h_i}dh_i\left(\mu-\sum\limits_{k\in\mathbb{Z}_+}\delta(h_i-k)\xi(i,k) \right)\nonumber\\ &=&\mu h_i -\sum\limits_{k=1}^{{\rm int}(h_i)}\xi(i,k). \end{array}$$

(2)

The disorder ξ(i,k) is an independent random variable at each site (i,k), with a Gaussian distribution of mean 0 and variance b ². The model has an approximate scale invariance, which allows to fix one parameter: J = 1. The different regimes will be obtained by varying the remaining two parameters μ and b.

We then run a Monte Carlo dynamics obeying detailed balance with respect to the measure $\exp(-H)\prod_{i=1}^Ndh_i$: At each Monte Carlo step, a site i is chosen at random uniformly in {1,...,N}; then, a tentative move δh _i is drawn from a Gaussian distribution of mean 0 and variance 1. This move would lead to a change ΔH of the Hamiltonian. The move is accepted with probability $\min(1,\exp(-\Delta H))$. Then, N such Monte Carlo steps make up a unit of time or Monte Carlo step per site (MCS/S). Figure 1 shows a small sample. Note that there is disorder at every point of integer coordinates (i,k), but only peaks of disorder, obstacles to wetting, are shown.

Fig. 1

Contact line after 10⁴ MCS/S, with N = 100, b = 3.0 and μ = 0.15. Dots indicate points where ξ(i,k) > 1.2 b

Contact angle hysteresis occurs when the spreading velocity vanishes before reaching equilibrium: At some advancing angle larger than the equilibrium angle, there is still a positive drift but peaks of disorder oppose line motion, in such a way that the velocity is effectively 0 for a macroscopic sample. In order to understand this stopping mechanism, we analyse the contact line with a constant drift μ in the limit of a small resulting mean velocity, corresponding to a contact angle slightly larger than the advancing angle. We focus our attention on a strong disorder regime, where the rms deviation of the disorder, b = 3.0, is not small with respect to surface tension, encapsulated in the coupling constant J = 1.0.

Macroscopic observables

Contact line velocity

The following quantities are defined in the limit $N\nearrow\infty$ (first) and $t\nearrow\infty$ (second):

$$ v(b,\mu)\sim(\mu-\mu_\textrm{c}(b))^\beta\quad{\rm as}\quad \mu\searrow\mu_\textrm{c}(b). $$

(3)

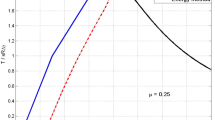
The velocity is obtained from a linear fit of $\bar h(t)={1\over N}\sum_i h_i(t)=a+vt$ for N = 50,000 and t ∈ [10⁵,10⁶] MCS/S, see Fig. 2. Near the threshold, for μ between 0.09 and 0.14, the simulation was run twice with different compilers and random number generators, hence the two markers for each μ in the figure. Beyond μ = 0.2, the velocity is very close to linear in μ along the slope starting on the right part of the plot. Below μ = 0.13, relaxation is very slow and sample dependent. Whenever N < ∞ and μ > 0, the velocity in the limit $t\nearrow\infty$ will be positive but will tend to 0 as $N\nearrow\infty$ for $\mu\le\mu_\textrm{c}$. The results favour β = 1 for the model at hand, with $\mu_\textrm{c}(3)\simeq0.12$.

Fig. 2

Velocity v(b,μ) for b = 3.0 and N = 50,000, in per MCS/S

The threshold in forced spreading allows to compute the advancing angle in spontaneous spreading, in the corresponding model. For the model at hand, spontaneous spreading implies [5] adding a term

$${J\over L}\sum\limits_ih_i^2 $$

(4)

in the Hamiltonian Eq. 1, where L is the length perpendicular to the substrate. The spreading coefficient when the contact line reaches $\bar h$ then becomes

$$ \mu-2J\bar h/L=\mu-2J\cot\theta $$

(5)

with $\cot\theta=\bar h/L$. Spontaneous spreading stops at the advancing angle, where the contact line velocity vanishes, $\mu-2J\cot\theta_\textrm{a}=\mu_\textrm{c}$, instead of the true equilibrium, $\mu-2J\cot\theta_\textrm{eq}=0$. Therefore,

$$ \cot\theta_\textrm{eq}-\cot\theta_\textrm{a}={\mu_\textrm{c}\over2J} $$

(6)

$${\cot\theta_\textrm{a}\over\cot\theta_\textrm{eq}}=1-{\mu_\textrm{c}\over\mu}\simeq0.88 $$

(7)

which is compatible with data from spontaneous spreading simulations [5].

From

$$ v\ \sim\ \mu-2J\bar h/L-\mu_\textrm{c}\ \sim\ \cot\theta_\textrm{a}-\cot\theta $$

(8)

and dθ~vdt, the time to reach the advancing angle is given by a mildly divergent integral:

$$ \int dt\ \sim\ \int{d\theta\over\cot\theta_\textrm{a}-\cot\theta}\ =\ +\infty $$

(9)

Contact line roughness

The contact line roughness exponent ζ is defined by

$$\label{zeta} \lim\limits_{t\nearrow\infty}\lim\limits_{N\nearrow\infty}\langle(h_{i+j}-h_i)^2\rangle \sim j^{2\zeta}\quad{\rm as}\quad j\nearrow\infty. $$

(10)

The initial condition is a straight line. At short times, say until 10³ MCS/S, $\langle(h_{i+j}-h_i)^2\rangle(t)$ thermalises in the same way as in the absence of disorder, leading to $\langle(h_{i+j}-h_i)^2\rangle(t)\sim\log(j)$. Then, at longer times, the correlation becomes $\langle(h_{i+j}-h_i)^2\rangle(t)\sim j^{2\zeta(t)}$, with a dynamical roughness exponent ζ(t) which converges slowly to a stationary value. Figure 3 shows ζ(t) for μ = 0.14, slightly above threshold. The fit yields ζ = ζ( ∞ ) ≃ 0.41. The roughness exponent ζ was computed for a similar model with Langevin dynamics by Rosso and Krauth [11] who found ζ = 0.388±0.002 at the depinning threshold, $\mu=\mu_\textrm{c}$.

Fig. 3

Contact line roughness exponent as a function of time for b = 3, μ = 0.14 and N = 10⁵

More sophisticated models have been considered, see e.g. [12–15], but here we focus our attention on the relation between contact line trapping and substrate topography, see the following sections, for which the linear-elastic long-range model with disorder is already very rich.

Traps, trapping time and trapping length

Trapping analysis from a set of contact lines

A given point of the contact line at time t, say h _i (t), will be considered as “trapped” for a duration τ if for a fixed small ε ≥ 0, we have

$$ V_{i}^{\tau }\left( t\right) =h_{i}^{{}}(t+\tau )-h_{i}^{{}}(t)\leq \varepsilon. \label{eqvcond} $$

(11)

Similarly, a portion of the contact line of length ℓ starting at i will be considered as trapped at time t for a duration τ if

$$ \left\{ \begin{array}{lcc} V_{i-1}^{\tau }\left( t\right) >\varepsilon & & \\ V_{i+j}^{\tau }\left( t\right) \leq \varepsilon & \textrm{for} & 0\leq j<\ell \\ V_{i+\ell }^{\tau }\left( t\right) >\varepsilon. & & \end{array} \right. \label{eqV} $$

(12)

This portion of contact line faces a portion of substrate where the rescaled deviation from average wettability is

$$ -\Delta\xi=-\frac{1}{\sqrt{\ell }}\sum\limits_{j=0}^{\ell -1}\xi \left( i+j,\;\;\left[ h_{i+j}\left( t\right) \right] +1\right) \label{Deltaxi} $$

(13)

where $\left[ \cdot \right]$ denotes the integer part.

Figure 4 is taken from a simulation where 100 contact lines were stored at time intervals of T = 10⁴ MCS/S. The times t and τ in Eqs. 11, 12 and 13 are taken as multiples of T. For each such τ, we collect all events obeying Eq. 12, and the corresponding Eq. 13. The number of events is 3,693.

Fig. 4

Trapping time, length and disorder. N = 20,000, μ = 0.14

It is remarkable that the events collapse on a two-dimensional surface. This implies that fixing one coordinate, the other two are function one of the other, which may provide a clue to the inverse problem.

Trapping analysis from sojourn times

The idea is that the line is blocked at some scale by some kind of large deviation of the noisy substrate. Here, we describe one possibility of analysing this phenomenon.

A grid of squares was used with size one (namely, the same size as the substrate-noise grid). Every 100 MCS/S, the position of the line was registered with respect to the grid. More precisely, each square of the grid has a counter initially set to 0. The counter of a square of the grid is increased by one if at the time of measurement the line passes through this square. One obtains at the end a histogram of the time the line has spent in every square. Given a threshold, one can determine the squares where sojourn time is larger than this threshold. The positions of these squares are then plotted (in red) in Fig. 5 for μ = 0.15 and for μ = 0.19. The grid has a width N = 20,000 and a length corresponding to the distance travelled by the contact line during the run: approximately 250 for μ = 0.15 and approximately 500 for μ = 0.19.

Fig. 5

In black is the substrate filtered above a threshold defined by $\texttt{facsubf}=0.5$ and l = 100. In red is the sojourn time filtered above a threshold defined by $\texttt{facsej}=0.3$ and l = 100. Bottom μ = 0.19, top μ = 0.15

The substrate is filtered horizontally using a Gaussian filter of standard deviation l. Given a threshold, one can determine the squares where the filtered substrate is larger than this threshold. The positions of these squares are then plotted (in black) in Fig. 5.

For convenience, the thresholds are not fixed in absolute value but as fractions of the maximum value, called facsej and facsubf, respectively. Hence, there are three parameters: l, facsej and facsubf.

Contact angle hysteresis can thus be seen as a collective effect of the traps (in black) blocking the contact line (in red where blocked). The analysis requires a non-zero mean velocity, here μ > 0.12 as can be seen in Fig. 2, corresponding to a contact angle slightly larger than the advancing angle. The contact line may be seen as an exploration device, doing a more precise job at smaller velocities (μ = 0.15 compared to μ = 0.19). It does not work at, or very near, the transition $\mu_\textrm{c}\simeq0.12$, where the velocity vanishes and the correlation length is expected to diverge.

Inferring the substrate from contact lines

Let us now consider the problem of estimating the substrate topography to a given scale using the motion of the contact line on it. It is the inverse problem. The reconstruction is done as follows, using data from simulations. We have 100 lines, each made of 20,000 points. At each of the 2.10⁶ x,y points, a velocity $V_{xy}^\tau$ is computed, like in Eq. 11. Then,

$$ \tau_{xy}=\max\{\tau':V_{xy}^{\tau'}<\epsilon\}. $$

(14)

The matrix τ is lacunary: Only 3,693 matrix elements are non-zero, like in Fig. 4. Summing over ℓ and i allows to build an empirical distribution function of a random variable ω distributed like τ. At each (x,y), a consistent random guess for ξ _xy  = Δξ defined by Eq. 13 at x,y is

$$ \widetilde\xi_{xy}=\alpha\log(\beta\omega_{xy}\tau_{xy}) $$

(15)

where α and β are normalising constants and ω _xy is an independent drawing of ω.

Figure 6 shows a region of the true substrate and the same region of the reconstructed substrate. Similarities are easy to localise. In order to compare quantitatively the digital image $\left( \xi _{l,\,k}\right)$ of the substrate used in the Monte Carlo simulations to its inferred image $(\,\widetilde{\xi }_{l,\,k}^{{}}\,)$, we use the digital cross-correlation measure defined as [16]

$$ C_{i,\,j}\left( \xi ,\,\widetilde{\xi }\right) =\frac{1}{NL} \sum\limits_{l=0}^{N-1}\sum\limits_{k=0}^{L-1}\xi _{l,\,k} \widetilde{\xi }_{l+\left|i\right| ,\,k+\left| j\right| }^{{}} $$

(16)

where $\widetilde{\xi }_{x,y}=0$ if x ≥ N or y ≥ L. This is a standard technique to estimate the likeness of two digital images. This measure is able to tack, very well, all changes in an image. It is scale insensitive. Its maximum over i and j achieves maximum similarity of the involved images. When images are almost identical, up to a scale factor, this maximum is achieved for i = j = 0. This is what Fig. 7 exhibits: The maximum is near the origin i = j = 0, and the decrease from the centre is monotonic.

Fig. 6

True substrate ξ _{l, k} (left) and reconstructed $\widetilde\xi _{l,\,k}$ (right)

Fig. 7

Correlation $C_{i,\,j}(\,\xi,\,\widetilde\xi\,)$ between true and reconstructed substrates

Experiments

A glass slide of 2.5 cm width was cleaned with sulfochromic acid. Then, perfluorodecyltrichlorosilane spots were deposited using a plastic Pasteur pipette rinsed with isopropanol. The spot size was about a few millimetre. This glass slide was penetrated and removed at a constant speed of 0.24 mm/s in a glass cell filled with water.

The camera provides 20,000 successive contact lines, each line consisting of approximately 600 points. At each of the 20,000×600 corresponding points with coordinates x,y on the substrate, a velocity $V_{xy}^\tau$ is computed as in Eq. 11. Then, the set of trapped sites is constructed as in Eq. 12. Using the derived empirical distribution, each site is revisited and a most likely random height is generated using Eq. 13. The reconstruction is done in the same way as for data from simulation, Section “Inferring the substrate from contact lines”. The substrate reconstructed in this way from the contact lines is shown in Fig. 8.

Fig. 8

Reconstructed substrate

Conclusion

The three-phase line observed during drop spreading is modelled by a series of partition variables with long-range interactions decreasing as the inverse square distance. The disorder is made of delta-function dots of random wettability given by a Gaussian distribution with mean 0 and variance b ². For a strong disorder, we observe using Monte Carlo simulations that the speed of the three-phase line is proportional to the wettability above a certain threshold. The contact line roughness exponent is shown to be approximately equal to 0.4. It is also possible to compute the trapping time for each portion of the contact line.

From the motion of the contact line, we propose a tool to estimate the substrate topography which is validated by our simulations. We show that this tool can be applied to analyse experimental data.