Single-image super-resolution based on local biquadratic spline with edge constraints and adaptive optimization in transform domain

Abstract

This paper proposes a novel single-image super-resolution method based on local biquadratic spline with edge constraints and adaptive optimization in transform domain. The complex internal structure of the image makes the values of adjacent pixels often differ greatly. Using surface patches to interpolate image blocks can avoid large surface oscillation. Because the quadratic spline has better shape-preserving property, we construct the biquadratic spline surface on each image block to make the interpolation more flexible. The boundary conditions have great influence on the shape of local biquadratic spline surfaces and are the keys to constructing surfaces. Using edge information as a constraint to calculate them can reduce jagged and mosaic effects. To decrease the errors caused by surface fitting, we propose a new adaptive optimization model in transform domain. Compared with the traditional iterative back-projection, this model further improves the magnification accuracy by introducing SVD-based adaptive optimization. In the optimization, we convert similar block matrices to the transform domain by SVD. Then the contraction coefficients are calculated according to the non-local self-similarity, and the singular values are contracted. Experimental comparison with the other state-of-the-art methods shows that the proposed method has better performance in both visual effect and quantitative measurement.

1 Introduction

The purpose of single-image super-resolution (SISR) is to recover high-frequency information from the low-resolution (LR) input images and generate reasonable high-resolution (HR) images that are not conflict with the LR versions. SISR is an important branch of image processing and has applications in many areas, such as medical imaging, security surveillance, satellite imagery, e-commerce and many others. There are two main types of SISR methods: interpolation-based methods and learning-based methods.

Classical polynomial interpolation methods [21,22,23] are extensively used due to their simplicity and speed of computation. However, since these methods use the commonly used polynomial fitting method to construct the interpolation surface of the image, the generated images are often too smooth and appear jagged and ringing effects in texture and edge areas. To solve this problem, some edge-oriented interpolation methods were proposed [5, 20, 29]. The adaptive interpolation method based on covariance was proposed by Li et al. [20]. The method first estimates the local covariance coefficient from the LR image, estimates the HR covariance according to the geometric duality between LR covariance and HR covariance, and then used these covariances to adaptively adjust the interpolation. Chen et al. proposed a fast edge guidance method [5]. Based on the analysis of the local structure of the image, this method divides the image into smooth regions and edge regions, and adopts a specific interpolation method in different regions. The method proposed by Wang et al. [29] realizes the super-resolution reconstruction of a single image through adaptive self-interpolation of gradient amplitude. The basic idea of this method is to first estimate the HR gradient field from the LR image, and then this gradient is used as the gradient constraint in the reconstructed HR image, so that the reconstructed image can retain sharp edges. RFI [35] uses rational fractal interpolation for texture regions and rational interpolation for non-texture regions. These methods use the structural information of images to sharpen the edges, but they are easy to generate noise and distortion in the texture area. Other methods use some constraints to optimize the interpolated HR images. Iterative back projection optimizes the HR image by reducing the error between the down-sampled HR image and the input LR image iteratively, such as IBP [19], BFIBP [7], NLIBP [13], etc. NLFIBP [34] optimizes the interpolation image in combination with the nonlocal mean filter and back projection. The enlarged image has sharp edges, while the accuracy is relatively low. In addition, the nonlocal self-similarity of images is widely used in various image super-resolution methods [18, 25, 37]. BM3D-SR [14] enlarge the image by combining Wiener filtering in transform domain and iterative back projection framework. WSD-SR [6] is improved based on BM3D-SR. The Wiener filter in 3D transform domain is changed into one in 1D similar domain, which not only reduces the computational complexity, but also improves the image quality. LPRGSS [33] uses the self-similarity of images and the sparsity of the global structure as the constraints to optimize the interpolated image, and achieves remarkable results.

The learning-based SISR method learns the mapping from LR to HR images through training sets containing numerous HR and LR image pairs. Learning mapping methods can be divided into two categories: methods that rely on external images as the training data and methods that rely only on input LR images. These methods include sparse dictionary learning [24, 27], manifold learning [4], local linear regression [26] and convolutional neural networks [11]. ANR [27] learns the sparse dictionary on fixed dictionary atoms. SF [30] achieves outstanding performance through clustering and the corresponding learned functions. $A^+$ [28] improves ANR based on the idea of SF, and combines the best characteristics of ANR and SF. The deep learning method SRCNN [10] based on convolutional neural network directly learns the end-to-end mapping between LR and HR images, and achieves remarkable results. FSRCNN [12] raises the speed of enlargement and achieves better image quality by improving the structure of SRCNN. SelfEx [16] is based on image self-similarity. Instead of relying on external data, it learns internal dictionaries from the given image. By expanding the search space of similar blocks, the limitations of internal dictionaries are improved. MMPM [17] proposes mixture prior model to learn image features, and uses the method based on curvature difference to group image blocks. DLD [9] builds a lightweight database and learns adaptive linear regression, which maps LR image blocks directly into HR blocks, and achieves excellent results.

In this paper, we propose a new method based on local biquadratic spline with edge constraints and adaptive optimization in transform domain for SISR. The local biquadratic spline interpolation is divided into four steps. First, we use the image edge information to calculate the boundary conditions. Second, for each $3\times 3$ LR image block, a local biquadratic spline surface is constructed, namely, 9 surface patches. Third, the weighted average of all local biquadratic spline surfaces constitutes the overall bicubic fitting surface. Finally, the sampling density is selected according to the scale factor, and the output HR image is obtained by sampling on the bicubic fitting surface. Subdividing a surface into 9 surface patches gives each surface greater interpolation flexibility. Therefore, the error is smaller in the region where the pixel value varies greatly, which improves the accuracy of the enlarged image. It is inevitable to have approximation error and lose part of high-frequency information when fitting image blocks with surfaces. To overcome these two shortcomings, we use the non-local self-similarity and data fidelity as prior constraints to optimize the image in space and transform domains. For each iteration, the approximation error is reduced in the transform domain by contracting singular values of each similar block matrix. The contraction coefficient is adaptively updated in the iteration. Then in the space domain, the high-frequency information lost in the interpolation is made up by projecting the amplified error image back to the HR image.

The major contributions of our work are summarized as follows:

• 1. We propose a new local biquadratic spline method with edge constraints. Each $3\times 3$ image block is interpolated by nine $C^{1}$ continuous surface patches, which improves the interpolation accuracy and the flexibility of surface to approximate the shape of the image block.

• 2. A new method for calculating the boundary conditions of biquadratic spline surfaces is presented. The edge information is introduced as a constraint to reduce the jagged and mosaic effect of the enlarged image edge. The two-step method improves the image accuracy and reduces the computation.

• 3. We construct a novel adaptive optimization in transform domain. Compared with the traditional iterative back-projection method, the proposed model incorporates the adaptive optimization based on SVD. By using the non-local self-similarity, the interpolation error is reduced, and the quality of the convergent image is improved greatly.

The rest of the paper is arranged as follows. Section 2 describes the problems and introduces the overall process of the proposed method. In Sect. 3, the details of local biquadratic spline with edge constraints are described. Section 4 describes the adaptive optimization in transform domain and analyzes the structure of the optimization model. Section 5 evaluates the performance of the proposed method in terms of visual effect and quantitative measurement. A summary of the paper is given in Sect. 6.

2 Problem description and algorithm framework

The object of SISR is to recover HR image containing high- frequency information from the known degraded LR image. The image degradation process can be expressed as follows:

$$\begin{aligned} Y=(f_g\otimes X)\downarrow ^s \end{aligned}$$

(1)

where X and Y represent HR and LR images, respectively. $f_g$ is fuzzy filtering, and ’$\otimes$’ is the convolution operation. ’$\downarrow ^s$’ represents the down-sampling operation with scale factor s. Ideally, the reconstructed HR image should degrade to produce the same image as the known LR image. However, with only a small amount of LR information, it is difficult to restore an ideal HR image. There will be errors between the LR image generated by the actual generated HR image and the input image. Iterative back-projection is a method to obtain HR image by minimizing reconstruction errors. Specifically, after the initial HR image $X^0$ is obtained by interpolation method, the back-projection operation is performed iteratively. Each iteration is divided into two steps: calculating the error image and projecting the enlarged error image back to HR image. The formula is as follows:

$$\begin{aligned} X^{t+1}=X^t+U((Y-(f_g\otimes X^t)\downarrow ^s),s) \end{aligned}$$

(2)

where $X^t$ represents the HR image obtained after the t-th iteration, and $U(\cdot ,s)$ represents the interpolation for super-resolution, with the scale factor of s. The error image between the degraded image of $X^t$ and the input LR image Y is calculated and enlarged. Then, the reconstructed error image is projected back to $X^t$ to complete a back-projection operation of the error image. As the number of iterations increases, the error between the enlarged image and the input image decreases gradually. When the stop condition is reached, the final HR image is output.

The optimization model of iterative back-projection is based on the objective function of minimizing the error between the iterative convergence result and the input image. But the solution of this objective function is an indeterminate problem. In other words, there may be multiple different solutions that satisfy the optimal solution. Several different HR images may degenerate into the same LR image, and the convergence result may be quite different from the ideal HR image. Therefore, the interpolation function U has an important influence on the accuracy of the output image. Traditional image interpolation algorithms, such as bicubic spline interpolation, construct a whole surface to interpolate the entire image. The disadvantage of the overall construction surface is that much local information in the image is ignored. When the pixel values are greatly different between neighborhoods, the high-frequency components of the image are easily damaged. Thus the details degrade due to the wiggle of the polynomial spline functions. The main reason for this phenomenon is that the same kernel function is used in different regions. The methods lack adaptability and are prone to produce zigzag effect on the edge areas.

In addition, the errors between the HR image and the input image are mainly distributed in the image edges and texture areas. The back-projection operation of the reconstructed error image can make up the missing high-frequency information. However, there are inevitably errors in the way that polynomial interpolation surface is used to fit the original image surface. After the degradation of the HR image, partial errors will not be reflected in the error image. Therefore, this part of errors cannot be reduced by back-projection operation, but accumulate in the iterative process, making the final convergence result far from the ideal image. Therefore, ignoring the interpolation error and directly carrying out the back-projection operation will limit the improvement of the image accuracy, resulting in fuzzy effect.

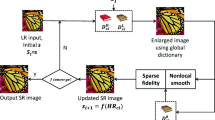
Through the above analysis, we propose a SISR method based on local biquadratic spline with edge constrains and adaptive optimization model in transform domain. The proposed algorithm first obtains the initial HR image by local biquadratic spline with edge constraints (LBSEC), and then iteratively optimalizes it to obtain the final HR image. Figure 1 shows the overall process.

Fig. 1

The flowchart of the proposed algorithm. LBSEC represents the local biquadratic spline with edge constraints. $X^0$ is the initial HR image amplified by LBSEC from the input LR image, and $X^t$ is the optimized HR image obtained in the tth iteration. Mse denotes the mean square error between the degraded HR image and the input LR image, and T is the maximum of iterations

Each iteration is divided into two steps: optimization in transform domain and back-projection of the error image. First, the optimization in the transform domain is carried out. The similar block matrices are obtained by matching blocks. And the singular values of each matrix are contracted adaptively to get the updated image blocks. Then we aggregate the blocks to obtain the optimized HR image. Second, back-projection is accomplished by enlarging the error image with LBSEC and then projecting it to the reconstructed HR image. Continue iterating until the stop condition is reached, and output the final HR image.

3 Local biquadratic spline with edge constraints

The traditional interpolation algorithms use the method of constructing the whole surface, and uses the same kernel function in different areas. In this way, the high-frequency information of the image is easily lost, resulting in smooth and ringing effect. Therefore, we propose a new local biquadratic spline with edge constraints method. We construct a local biquadratic spline surface containing 9 surface patches on each $3\times 3$ grid. Different boundary conditions are adopted in different areas. This way improves the shape preserving ability of the surfaces, and reduces the loss of the high frequency components in the regions with large image gradient. Because the biquadratic spline surface is constructed on a small $3\times 3$ image block containing 9 pixels, the boundary conditions have great influence on the shape of the surface. They are the key to construct an ideal surface. The meaning of the ideal surface here is that the surface not only approximates the image block with high precision, but also has the shape of the image block. Constructing biquadratic spline surface is divided into two steps: calculating the boundary conditions and constructing surface. After constructing all local biquadratic spline surfaces, the integral bicubic fitting surface is formed by surface fusion.

3.1 Calculate the boundary conditions

The boundary conditions to be computed are the first partial derivatives at the pixel points. The interpolation accuracy of biquadratic splines can reach the accuracy of biquadratic polynomials. Therefore, the computational boundary conditions need to have the precision of biquadratic polynomials. When calculating the boundary conditions, we introduce the structure information of the image as a constraint. So the first partial derivative not only has high accuracy, but also keeps the shape of the edge, thus reducing the sawtooth effect of the edge region. Assuming that the pixel values of the input LR image are sampled per unit area on the continuous original surface. The piecewise surface $g_{i,j}$ is used to approximate the original surface. Then, the pixel value can be defined as

$$\begin{aligned} P_{i,j}=\int _{j-0.5}^{j+0.5}\int _{i-0.5}^{i+0.5}g_{i,j}(x,y)dxdy \end{aligned}$$

(3)

To make the boundary conditions have biquadratic polynomial accuracy, we use the biquadratic polynomial to construct $\scriptstyle {g_{i,j}}$ on the $5\times 5$ image block (Fig. 2). That is, in the $\scriptstyle {[i-2.5,i+2.5]\times [j-2.5,j+2.5]}$ region of xy plane. $g_{i,j}(x,y)$ can be written as

$$\begin{aligned} g_{i,j}(x,y)= & {} a_0u^2v^2+a_1u^2v+a_2uv^2+a_3u^2\nonumber \\&+a_4uv+a_5v^2+a_6u+a_7v+a_8 \end{aligned}$$

(4)

where $u=x-i,y=y-j$, $a_0,a_1,\ldots ,a_8$ are the unknown surface coefficients.

The first partial derivatives $a_6,a_7$ in the surface patch $\scriptstyle {g_{i,j}(x,y)}$ are the boundary conditions to be solved. There are 9 unknowns in (4). If they all participate in the calculation of $a_6$ and $a_7$, a large amount of calculation is required. To reduce the calculating amount, we solve $a_6$ and $a_7$ through the first-order difference quotient. There are 25 pixels on the $5\times 5$ image block in Fig. 2. According to (3) and (4), 8 first-order difference quotients including $a_1$, $a_2$, $a_6$ and $a_7$ can be obtained from 8 directions in Fig. 2. And $a_6$ and $a_7$ can be solved by the 8 first-order difference quotients. In order to improve the fitting accuracy, we hope that the pixels on the inner $3\times 3$ image block play a greater role in determining $a_6$ and $a_7$. Therefore, we use the following two-step method to calculate $a_6$ and $a_7$.

Next, we introduce the solution method of $a_6,a_7$. Based on (3) and (4), the following four equations can be obtained from the first-order difference quotient:

$$\begin{aligned} \begin{aligned}&\tfrac{1}{12}a_2+a_6=\frac{P_{i+1,j}-P_{i-1,j}}{2}=c_1,\\&\tfrac{1}{12}a_1+a_7=\frac{P_{i,j+1}-P_{i,j-1}}{2}=c_2,\\&\tfrac{13}{12}a_1+\tfrac{13}{12}a_2+a_6+a_7=\frac{P_{i+1,j+1}-P_{i-1,j-1}}{2}=c_3,\\&\tfrac{13}{12}a_1-\tfrac{13}{12}a_2-a_6+a_7=\frac{P_{i-1,j+1}-P_{i+1,j-1}}{2}=c_4 \end{aligned} \end{aligned}$$

(5)

As shown in Fig. 2, $c_1, c_2, c_3, c_4$ represent the first-order difference quotients in the four directions indicated by the red arrows, respectively.

Fig. 2

First-order difference quotients in eight directions on the $5\times 5$ image block

The expressions of $a_6,a_7$ as linear combinations of $a_1,a_2$ are obtained by using the least square method with constraints. The objective function is defined as

$$\begin{aligned} \begin{aligned} G_1(a_1,a_2,a_6,a_7)=&\; w_1(\tfrac{1}{12}a_2+a_6-c_1)\\&+\,w_2(\tfrac{1}{12}a_1+a_7-c_2)\\&+\,w_3(\tfrac{13}{12}a_1+\tfrac{13}{12}a_2+a_6+a_7-c_3)\\&+\,w_4(\tfrac{13}{12}a_1-\tfrac{13}{12}a_2-a_6+a_7-c_4) \end{aligned} \end{aligned}$$

(6)

where $w_1,w_2,w_3,w_4$ are the weights. By minimizing the objective function $\scriptstyle {G_1(a_1,a_2,a_6,a_7)}$, that is, setting its partial derivatives with respect to $a_6,a_7$ as zero, we can obtain the expression of $a_6,a_7$ as follow:

$$\begin{aligned} \begin{aligned}&a_6=\beta _{11}a_1+\beta _{12}a_2+\beta _{13},\\&a_7=\beta _{21}a_1+\beta _{22}a_2+\beta _{23} \end{aligned} \end{aligned}$$

(7)

The second step is to solve $a_1,a_2$. From (3) and (4), we can get that

$$\begin{aligned} \begin{aligned}&\tfrac{13}{6}a_1+\tfrac{49}{12}a_2+a_6+2a_7=\frac{P_{i+1,j+2}-P_{i-1,j-2}}{2}=c_5,\\&\tfrac{13}{6}a_1-\tfrac{49}{12}a_2-a_6+2a_7=\frac{P_{i-1,j+2}-P_{i+1,j-2}}{2}=c_6,\\&\tfrac{49}{12}a_1+\tfrac{13}{6}a_2+2a_6+a_7=\frac{P_{i+2,j+1}-P_{i-2,j-1}}{2}=c_7,\\&\tfrac{49}{12}a_1-\tfrac{13}{6}a_2-2a_6+a_7=\frac{P_{i-2,j+1}-P_{i+2,j-1}}{2}=c_8 \end{aligned} \end{aligned}$$

(8)

where $c_5, c_6, c_7, c_8$ correspond to the first-order difference quotients in the four directions indicated by the blue arrows in Fig. 3.

Fig. 3

The $3\times 3$ image block is divided into 9 regions, and the adjacent regions are separated by different colors. The red arrows represent the boundary conditions. They are the first partial derivatives of the corresponding pixels. The arrow direction is the partial derivative direction

Substitute (7) into (5) and (8) to get the 8 equations $h_i(a_1,a_2)=c_i,i=1,2,\ldots ,8$ about $a_1,a_2$. And the $a_1,a_2$ are determined by least square method again, namely, by minimizing the following formula:

$$\begin{aligned} G_2(a_1,a_2)=\sum _{i=1}^8w_i(h_i(a_1,a_2)-c_i)^2 \end{aligned}$$

(9)

The weights in (6) and (9) are defined as follows:

$$\begin{aligned} w_i=\frac{1}{1+(\Delta _i/d_i)^2} \end{aligned}$$

(10)

where $\Delta _i$ is the second-order difference quotients in corresponding directions, and $d_i$ is the distance between adjacent pixels. The image edges have a significant impact on the visual effect. To reflect the image edge features better, the approximate surface should be closer to the original one in the edge directions than in other directions. A smaller change of the pixel values means that the direction is more likely to be the direction of the image edge, which should be given a larger weight. Finally, the $a_6,a_7$ are obtained by bringing $a_1,a_2$ into (7).

In the two-step solution, $a_6$ and $a_7$ are expressed as functions of other coefficients $a_1,a_2$. This way makes full use of the structural information of the image, so that the pixels on the inner $3\times 3$ image block play a greater role in determining $a_6$ and $a_7$. Thereby, the calculated boundary conditions are more reasonable. Compared with the overall solution, the two-step one improves the fitting precision. In addition, the overall solution is that 9 unknown coefficients are all involved in the calculation. For each pixel, the unknown coefficients are solved by a nine-element linear equation set. The two-step solution is to obtain $a_6$ and $a_7$ by solving the binary linear equation set twice, which requires less calculation. In order to test the performance, we magnify images by LBSEC based on overall and two-step solutions respectively. As shown in Table 1, the latter can effectively improve the quality of enlarged images while reducing the time cost.

Table 1 PSNR (dB) and running time results of LBSEC based on overall and two-step solutions on Set5, Set14, BSD100 and Urban100 by a factor of 2

3.2 Construct local biquadratic spline surface

For each $3\times 3$ image block, we construct a biquadratic spline surface patch, which consists of 9 subsurface patches. As shown in Fig. 3, the neighborhood $\scriptstyle {[i-1,i+1]\times [j-1,j+1]}$ of pixel point $\scriptstyle {(i,j)}$ is divided into 9 subregions, each containing a pixel point. We construct a biquadratic surface patch on each subregion, denoted by $s_{m,n}$, and the formula is as follows:

$$\begin{aligned} s_{m,n}(x,y)= & {} b_0^{m,n}u^2v^2\!+\!b_1^{m,n}u^2v\!+\!b_2^{m,n}uv^2\!+\!b_3^{m,n}u^2 \nonumber \\&+b_4^{m,n}uv\!+\!b_5^{m,n}v^2\!+\!b_6^{m,n}u\!+\!b_7^{m,n}v\!+\!b_8^{m,n}\nonumber \\ \end{aligned}$$

(11)

where $\scriptstyle {(m,n)}$ is the coordinates of pixel points contained in the subregion, $m=i\pm 1,i,n=j\pm 1,j$. $u=x-m,v=y-n$, and $\scriptstyle {b_0^{m,n},b_1^{m,n},\ldots ,b_8^{m,n}}$ are the unknown surface coefficients.

Because of $\scriptstyle {C^1}$ continuity of biquadratic spline surface, the function value and first partial derivative of subsurface patches are continuous at the junction. For example, at the boundary curves $\scriptstyle {x=i\pm 0.5}$ in the y direction, the function value being continuous is the sufficient condition for $\scriptstyle {\frac{\partial s_{m,n}}{\partial y}}$ being continuous. So here, we only consider the continuity of $\scriptstyle {\frac{\partial s_{m,n}}{\partial x}}$, regardless of $\scriptstyle {\frac{\partial s_{m,n}}{\partial y}}$. Then, the adjacent subsurface patches at the junction of $\scriptstyle {x=i\pm 0.5}$ satisfy the following conditions:

$$\begin{aligned} \begin{aligned}&s_{m,n}(m+0.5,y)=s_{m+1,n}(m+0.5,y),\\&\frac{\partial s_{m,n}}{\partial x}(m+0.5,y)=\frac{\partial s_{m+1,n}}{\partial x}(m+0.5,y) \end{aligned} \end{aligned}$$

(12)

where $m=i-1,i,n=j\pm 1,j$. The same is true for the interface curves in the x direction. In addition, for each pixel value $P_{m,n},m=i\pm 1,i,n=j\pm 1,j$,

$$\begin{aligned} s_{m,n}(m,n)=b_8^{m,n}=P_{m,n} \end{aligned}$$

(13)

We use the known conditions to solve the unknown coefficients by group way. The first group is $\scriptstyle {b_3^{m,n},b_6^{m,n}}$. The first partial derivatives of x and y directions at point $\scriptstyle {(m,n)}$ obtained above are $\scriptstyle {a_6^{m,n},a_7^{m,n}}$ respectively. We assign $\scriptstyle {a_6^{m,n},a_7^{m,n}}$ to $\scriptstyle {b_6^{m,n},b_7^{m,n}}$, which are the first partial derivatives of the subsurface patches $s_{m,n}$ in the corresponding regions. As shown in Fig. 3, the red arrows indicate the first partial derivatives. Different regions adopt different boundary conditions. Then, the boundary conditions can be expressed by the formula as follows:

$$\begin{aligned} \begin{aligned} b_6^{m,n}&=a_6^{m,n},m=i\pm 1,n=j\pm 1,j,\\ b_7^{m,n}&=a_7^{m,n},m=i\pm 1,i,n=j\pm 1 \end{aligned} \end{aligned}$$

(14)

According to (12), the coefficients of same order term on both sides of equal sign are same, we can obtain a set of equations about $\scriptstyle {b_3^{m,n}}$,$\scriptstyle {b_6^{m,n}}$:

$$\begin{aligned} \begin{aligned}&\tfrac{1}{4}b_3^{m,n}\!+\!\tfrac{1}{2}b_6^{m,n}\!+\!b_8^{m,n}\!=\!\tfrac{1}{4}b_3^{m+1,n}\!-\!\tfrac{1}{2}b_6^{m+1,n}\!+\!b_8^{m+1,n}\\&b_3^{m,n}\!+\!b_6^{m,n}\!=\!-b_3^{m+1,n}\!+\!b_6^{m+1,n} \end{aligned} \end{aligned}$$

(15)

where $m=i-1,i$, $n=j\pm 1,j$. Substitute (13) and (14) into (15), and the solutions of the rest $\scriptstyle {b_3^{m,n}}$, $\scriptstyle {b_6^{m,n}}$ can be obtained. Similarly, $\scriptstyle {b_5^{m,n}}$, $\scriptstyle {b_7^{m,n}}$ can be obtained.

Then, we solve for $\scriptstyle {b_0^{m,n}}$, $\scriptstyle {b_1^{m,n}}$, $\scriptstyle {b_2^{m,n}}$, $\scriptstyle {b_4^{m,n}}$. We set the second mixed partial derivatives of the surface at four vertices of the rectangular region as zero, which can be formulated as

$$\begin{aligned} \begin{aligned} \frac{\partial ^2 s_{m,n}}{\partial x\partial y}=b_4^{m,n}=0,m=i\pm 1,n=j\pm 1 \end{aligned} \end{aligned}$$

(16)

A set of equations about $\scriptstyle {b_0^{m,n}}$, $\scriptstyle {b_1^{m,n}}$, $\scriptstyle {b_2^{m,n}}$, $\scriptstyle {b_4^{m,n}}$ can be derived from the continuity constraint at the junction of x and y directions. Substituting the known $\scriptstyle {b_4^{m,n}}$, $\scriptstyle {b_6^{m,n}}$ and $\scriptstyle {b_7^{m,n}}$ into them, the unknown $\scriptstyle {b_0^{m,n}}$, $\scriptstyle {b_1^{m,n}}$, $\scriptstyle {b_2^{m,n}}$, $\scriptstyle {b_4^{m,n}}$ can be solved.

The nine subsurface patches are jointed together to form the fitting surface patch at the center pixel point, denoted as $\scriptstyle {f_{i,j}(x,y)}$.

3.3 Surface fusion

Each biquadratic spline surface patch $\scriptstyle {f_{i,j}(x,y)}$ is divided into nine subsurface patches. In this way, the surface can fit the image block more flexibly and the interpolation precision is higher. All biquadratic spline surfaces are fused into the overall bicubic fitting surface $\scriptstyle {F(x,y)}$ by weighted average. The formula is as follows:

$$\begin{aligned} \begin{aligned} q_{i,j}(x,y)&=(1-u)(1-v)f_{i,j}+u(1-v)f_{i+1,j}\\&\quad \, + (1-u)vf_{i,j+1}+uvf_{i+1,j+1} \end{aligned} \end{aligned}$$

(17)

where $u=x-i$, $v=y-j$, $\scriptstyle {f_{i,j}}$, $\scriptstyle {f_{i+1,j}}$, $\scriptstyle {f_{i,j+1}}$ and $\scriptstyle {f_{i+1,j+1}}$ are the surfaces at four vertices of quadrilateral region. The representation of $\scriptstyle {F(x,y)}$ in this region is $\scriptstyle {q_{i,j}(x,y)}$. All the surface $\scriptstyle {q_{i,j}(x,y)}$ joint together to form the whole fitting surface $\scriptstyle {F(x,y)}$. The HR image is obtained by sampling at the corresponding density on $\scriptstyle {F(x,y)}$.

4 Adaptive optimization model in transform domain

The adaptive optimization model in transform domain is improved on the basis of traditional iterative back-projection framework. Before the operation of back-projection, we optimize the interpolated image by using the non-local self-similarity, which effectively reduces the approximation error of the interpolation surface. Compared with the traditional framework, the proposed model further improves the accuracy of enlarged image and reduces the sawtooth and mosaic effect of image edges.

4.1 Adaptive optimization in transform domain

In the process of biquadratic spline interpolation, the fitting surface inevitably has approximation errors, which make the sampled HR pixel easily distorted. Therefore, we design a new adaptive optimization in transform domain to reduce the error. The interpolation algorithm which uses only local information of the image cannot reconstruct HR images with high quality. So we use the non-local self-similarity to optimize the image. The optimization includes three steps: similar block matching; calculating the contraction coefficient and contracting the singular value; block fusion.

First, similar blocks are searched in a search window centered on the reference block $R_{i},i=1,2,\ldots ,n$. By comparing the distance between $R_i$ and all blocks in the window, we find K blocks which are most similar to the central one and form a similar block matrix $M_{i}$.

Second, due to the similarity between the blocks, the column vectors of the similar block matrix are highly correlated. Thus, the similar block matrix is low-rank. Moreover, the singular value often contains important information of the corresponding matrix, and the importance is positively correlated with the singular value. Thus, the low rank indicates that most energy of the matrix is contained in a few large singular values. However, the fitting error will cause the fluctuation of singular values. This problem leads to small singular values, and increases the rank of similar block matrices. According to this principle, we contract the singular values to ensure the low rank of the matrices and reduce the errors. The formula of SVD for similar block matrices is:

$$\begin{aligned} M_{i}=U_{i}\Sigma _{i}V_{i}, i=1,2,\ldots ,n \end{aligned}$$

(18)

where $M_{i}$ is the similar block matrix of the reference block $R_i$ and $\Sigma _{i}$ is the singular value matrix. The greater the singular value is, the more effective information it contains, which should be dealt with a smaller contraction. So we set the soft threshold as $\scriptstyle {thr_{j}=\zeta /(\sigma _j+\tau )}$. $\sigma _{j}$ is the first j singular value from big to small order. $\tau$ is a small positive number to ensure that the denominator is not zero. $\zeta$ is the contraction factor. The greater $\zeta$ the more information amputated, and the optimized image will be smoother. We design the contraction factor to be adaptively updated, rather than predetermined. The formula is as follows:

$$\begin{aligned} \zeta =\frac{\Big \Vert Y-(f_g\otimes X)\downarrow ^s\Big \Vert _2^2}{2m} \end{aligned}$$

(19)

where Y denotes the input LR image,and X is the HR image to be optimized. $f_g$ represents a fuzzy filter, ”$\scriptstyle {\downarrow ^s}$” is a down-sampling operation with scale factor s, and m is the number of pixels in Y. In the initial iteration, the fitting error of interpolation surface and the error between the degraded HR image and the input LR image are both large, so a larger scaling factor is applied. As the number of iterations increases, the sawtooth of HR images decreases, and fitting errors are gradually eliminated. Then, a smaller contraction factor is applied. So $\zeta$ shrinks gradually in the iterations. The diagonal matrix of contracted singular value is donated as $\hat{\Sigma }_{i}$. And the first j diagonal element of it is as $\scriptstyle {\hat{\sigma }_j=max\{\sigma _j-thr_j,0\}}$. Then, by replacing $\Sigma _{i}$ with $\hat{\Sigma }_{i}$ in (18), the updated similar block matrix is obtained.

Third, for different estimates ${\scriptstyle {p^{k}},k\,=\,1,2,\ldots ,K}$ of the image block p, their weights are set according to the ranks $\scriptstyle {r^k}$ of the matrices where they are located. The low rank matrix contains blocks with high similarity, and the estimated results are more reliable. So we set a larger weight for it. The fused image block $\hat{p}$ is obtained by weighted averaging of multiple estimates as follows:

$$\begin{aligned} \hat{p}=\frac{1}{W}\sum _{k=1}^{K}(1-\frac{r^{k}}{N+1})p^{k} \end{aligned}$$

(20)

where $r\le N$, and the denominator is set as $N+1$ to ensure weights are not zeros. $\scriptstyle {\frac{1}{W}}$ is the normalization factor. After the fusion of different estimated blocks, we fuse the overlapped pixels of image blocks with a simple averaging strategy. Then, the complete reconstructed HR image is obtained.

4.2 Analysis of optimization model structure

In this section, three different optimization model structures are compared. We use ’BP’ to represent the traditional iterative back-projection structure, that is, each iteration contains only the back-projection operation of the reconstructed error image. The optimization model structure in [34] is to first optimize the enlarged error image, and then project it back to the HR image in each iteration. We call this structure ’BP+Opt(e)’. Different from  [34], we carry out the optimization for the intact HR image instead of the error image. We call it ’BP+Opt(h)’. We test the performance of three different structures of optimization model, as show in Fig. 4.

Compared with ’BP’ that only has a back-projection operation, the optimization of HR image can reduce the fitting error and make the image accuracy higher when iterative convergence. It can be seen from the figure that ’BP+Opt(h)’ effectively increases the growth rate of PSNR during iteration and further improves image quality.

Fig. 4

Performance comparison of ‘BP’, ‘BP+Opt(e)’ and ‘BP+Opt(h)’ optimization sructures on woman image with the magnification $\times 2$

In addition, it can be seen from the figure that ‘BP + Opt (h)’ achieves much better amplification effect than ’BP + Opt (e)’. Through adaptive optimization in transform domain, ‘BP+Opt(e)’ structure can use the non-local self-similarity of the image to guide the direction of iterative convergence. It can improve the quality of the final output image. However, because HR images contain more complete structural information, the results of non-local optimization for HR images are more reliable than those for error images. In this way, the error image obtained from the optimized HR image contains more useful information than that from the non-optimized HR image. Thus, the improvement space will be larger when the error image is back projected. In summary, we adopt the ‘BP + Opt (h)’ optimization model structure.

The overall process of the proposed single-image super-resolution algorithm based on local biquadratic spline with edge constraints and adaptive optimization in transform domain (LBSAO) is shown in Algorithm 1.

5 Experiments and analysis

This section verifies the effectiveness of the proposed algorithm. We first test the performance of local biquadratic spline with edge constraints (LBSEC) and adaptive optimization in transform domain (AOTD) respectively. Second, we give the setting of experimental parameters. Finally, the overall effectiveness of the proposed SISR method is verified by comparing it with different state-of-the-art methods in terms of quantitative measurement and visual effect.

5.1 LBSEC and AOTD performance

This section is divided into two parts to evaluate the effectiveness of the proposed LBSEC and AOTD respectively.

Table 2 PSNR (dB) comparison among different SISR interpolation algorithms on Set5 by a factor of 2

Fig. 5

PSNR (dB) comparison among different SISR interpolation algorithms on Set14 by a factor of 2

Fig. 6

Performance of different SISR interpolation algorithms on Baby image ($\times 3$)

In the first part, we compare LBSEC with bicubic, CCEM [3], and EDD [32]. CCEM combines the edge information to construct the cubic fitting surface, which makes the edge of the interpolation image smoother and the visual effect is better. EDD can effectively preserve the edge structure of the image through directional filtering and data fusion based on linear minimum mean square-error estimation (LMMSE) technology. Table 2 shows the PSNR comparison result on Set5. It can be seen that LBSEC achieves the highest magnification accuracy for each image. Also as shown in Fig. 5, in the PSNR comparison results on Set14, our method also surpasses other methods. Figure 6 is a visual comparison of the methods. At the texture of the woolen cap in the image, the results of bicubic and CCEM have different degrees of blurring. In comparison, the texture of LBSEC result is clearer. There are some color blocks in the result of EDD, while the result of LBSEC has more delicate texture and better visual effect. From the above, the proposed LBSEC can reduce the interpolation error effectively and improve the accuracy of the enlarged images.

Then, we compare the AOTD with non-local mean filter (NMF). NMF reconstruct the image by replacing the reference block with weighted average of the similar blocks. Both of NMF and AOTD make use of the self-similarity of the image and operate in blocks. The main difference of them is that the former operates in the spatial domain, while the latter operates in the transform domain. We replace AOTD of the proposed algorithm with NMF and compare it with the original algorithm. The comparison results in Table 3 are about Set5 [2] and Set14 [31] by different scale factors. It shows clearly that the SISR algorithm using AOTD has a improvement of magnification accuracy than the one using NMF, and achieves better performance. As can be seen from the results in Fig. 7, for the letter ”D” in the figure, the edge of NMF result is blurred, and artifacts appear at the connection with the letter ”o”. However, the results of the method in this paper have a sharper and smooth edge, and the letters ”D” and ”o” are clearly separated, which is obviously better than the NMF result. Therefore, the enhancement of similarity in the transform domain can reduce the approximation error of interpolating surface and achieve sharper edges.

Table 3 PSNR (dB) comparison between NMF and AOTD on Set5 and Set14 ($\times 2,\times 3,\times 4$)

Fig. 7

Performance of NMF and AOTD on ppt3 image ($\times 3$)

5.2 Experimental setting

To verify the effectiveness of the proposed algorithm, experiments for three different scale factors (2, 3 and 4) are carried out on the test images. The publicly available image sets Set5 [2], Set14 [31], BSD100 [1]and Urban100 [16] are used as the test benchmarks, which are widely used in performance testing of super- resolution methods. In the experiment, the corresponding LR images are obtained from these HR images by bicubic interpolation.

The proposed method is compared with eight different methods, which include interpolation-based methods and learning-based methods for SISR. Bicubic is a classical interpolation algorithm. And rational fractal interpolation (RFI) [35] is a method combining rational interpolation and fractal interpolation for image super-resolution. NLFIBP [34] is based on non-local feature interpolation and iterative back projection. LPRGSS [33] utilizes low-rank patch regularization and global structure sparsity for image restoration. SelfEx [16], FSRCNN [12], MMPM [17] and DLD [9] are four learning-based methods. Among them, FSRCNN and MMPM train the model by using external training data while SelfEx and DLD depend on internal data.

The parameter setting will affect the performance of the algorithm, and we choose the appropriate parameter values through experiments. With similar block matching, the larger the search window is, the more non-local information of the image will be obtained. However, it is also more likely to find blocks with small distances but different structures. We chose a compromise size $45\times 45$ by experimental comparison. The selection of image block size also has a crucial impact on the performance of the method. Similar blocks matched with larger block size are more reliable, but the cost is that the algorithm will require more computation. According to the data in Table 4, we select the block size $4\times 4$.

Table 4 PSNR (dB) comparison among different image block sizes ($3\times 3 \sim 8\times 8$) on lena image ($\times 2,\times 3,\times 4$)

As for the number of similar blocks, if it is large, the information in the similar block matrix is more sufficient, but some image blocks which are not similar enough may be matched. From the comparison shown in Table 5, we set the number of similar blocks as 30.

Table 5 PSNR (dB) comparison among different number of similar blocks ($25\sim 50$) on lena image ($\times 2,\times 3,\times 4$)

5.3 Overall quantitative comparison

Table 6 PSNR (dB) (the first row) and SSIM (the second row) results of nine SISR methods on Set5, Set14, BSD100 and Urban100 image sets with scale factors 2, 3 and 4. The best results are in red and the secondary is in blue

Fig. 8

PSNR (dB) comparison among nine SISR methods on Urban100 image set ($\times 2$)

For quantitative evaluation, we use PSNR (dB) and SSIM indicators to evaluate quality. Table 6 shows the results of all compared methods on Set5, Set14, BSD100 and Urban100 image sets. The best results are shown in red and the secondary in blue. It can be seen from the table that the PSNR and SSIM of the proposed method are much higher than those of the interpolation-based methods with scale factors of 2, 3, and 4. Among the four learning-based comparison methods, FSRCNN achieves the best results in natural images in Set5 and Set14, while SelfEx has the most advantage in image with high self-similarity in Urban100. Compared with the learning-based SISR methods, the proposed method also achieves the best results on Set5, Set14 and Urban100 image sets with all scale factors. On BSD100 data set, the results of our method are only worse than the best. Figure 8 shows the comparison of PSNR of different methods on Urban100 image set. It can be seen that the proposed method achieves the best results on most images. It is further proved that the proposed method can improve the accuracy and quality of enlarged image.

5.4 Overall visual comparison

Figure 9, 10, 11 and 12 shows the visual effect of test images magnified by eight different SISR methods with scale factors 2, 3 and 4. The corresponding PSNR (dB) and SSIM values are below the pictures. Figure 9 shows the images with a scale factor 2. It can be seen that the edge contour of bicubic result at the butterfly wings is severely blurred, and the edge artifacts of NLFIBP and RFI results are also heavy. The results of the other four comparison methods show that the image edge is improved compared with the previous three methods, but there is also a fuzzy effect, and the proposed method achieves a sharper edge.

Fig. 9

Super-resolution comparison on butterfly image ($\times 2$): a original, b bicubic, c NLFIBP, d RFI, e LPRGSS, f MMPM. g FSRCNN, h DLD, i proposed

Fig. 10

Super-resolution comparison on bird image ($\times 3$): a original, b bicubic, c NLFIBP, d RFI, e LPRGSS, f MMPM, g FSRCNN, h DLD, i proposed

Fig. 11

Super-resolution comparison on lena image ($\times 4$): a original, b bicubic, c NLFIBP, d RFI, e LPRGSS, f MMPM, g FSRCNN, h DLD, i proposed

Figure 10 show the results of different methods using a scale factor 3. The bicubic and NLFIBP results show that the edge of parrot’s beak is not clear and distorted, while the RFI and LPRGSS results show that an edge breaks into two parts that are not connected, both of which produce unnatural edges. The result of MMPM method can see the outline of image edge, but it is not clear enough. The right side of the black edge of the DLD method is fused with the green mouth to produce a transition zone, and the resulting image is too smooth. Compared with MMPM and DLD, the result of FSRCNN has better details, but the edges are also fuzzy, and the results of the proposed method can better retain the edge details.

Fig. 12

Super-resolution comparison on foreman image ($\times 4$): a original, b bicubic, c NLFIBP, d RFI, e LPRGSS, f MMPM, g FSRCNN, h DLD, i proposed

Figures 11 and 12 show the images with a upscaling factor 4. In Fig. 11, both the bicubic and RFI results produce severe jagged edges in the brim, resulting in missing image details. LPRGSS produces artifacts with severely distorted edges. The MMPM result is sharp on the outermost brim edge, but the brim on the upper left edge has a smooth effect, and the image does not contain fine textures. FSRCNN result also has a certain degree of fuzziness. The result of DLD has similar problems, with clear outer edges, but the inner edges are also clearly jagged and some details are distorted. Our method effectively reduces the jagged effect of the enlarged image at the texture and edge, and is closer to the original image.

As shown in Fig. 12, the boundary between collar and background in the bicubic image is not clear and the artifacts are serious. Serious mosaic effect appears in RFI images. LPRGSS results show a fault in the part below the collar edge, resulting in image distortion, while the magnification effect of the other four comparison methods has varying degrees of blurring effect. Compared with other methods, the method in this paper can better retain the edge, as shown in the collar part, and the algorithm can get the sharp edge without jagging.

5.5 Comparison with recent state-of-the-art methods

In this section, we compare the performance of the proposed method with that of recently proposed state-of-the-art denoising methods, including RDN [36], SAN [8], DBPN [15]. As we know, deep-learning-based techniques for SISR have been recently attracting considerable attentions due to its remarkable performance, and there are many successful schemes that have been published recently. For all the competing methods, the source codes are obtained from the original authors.

Table 7 PSNR (dB) result of different SISR methods ($\times 3$)

we compare the accuracy of the enlarged images by our method, RDN, SAN and DBPN in Table 7. The proposed method is lower than the other competing methods. The learning-based approach can achieve excellent results but it also has some problems. First, methods that rely on external training data will be limited in the application of image enlargement according to the type of training images. Second, some methods need a lot of time to train the model, especially the method based on CNN. Third, the learned model can only be used for the magnification of a fixed scale, and the model needs to be retrained for different scales. Our interpolation-based method is not as good as deep learning method in common image accuracy, which is the place we need to learn and improve in the next work.

Table 8 PSNR (dB),SSIM and running time (min) results of different SISR methods on lena image ($\times 3$)

5.6 Running time

LBSEC is mainly divided into three steps. The first step is to calculate the first-order partial derivatives at each pixel of the LR image. The second step is to construct the biquadratic spline surface at each pixel according to the boundary conditions. The last is to calculate the HR image pixels by weighting and averaging the pixels of four overlapping surfaces. Because the complexities of the above three steps are all O(n), the complexity of LBSEC is O(n), which is the same as Bicubic and Ecubic. In addition, AOTD uses the non-local structure information of the image, which can effectively reduce the interpolation error of the HR image. Same as NMF, its complexity is O(n). Although it is time-consuming to find similar blocks, the running time can be reduced by adjusting the step size and reducing the search frequency. In summary, the complexity of the entire algorithm is O(mn), and m is the number of iterations.

As for running time, the maximum of iterations T will control the times of iteratios, thus affecting the running time of the algorithm. In a certain range, if the value of T is larger, the magnified image will have higher accuracy, but the corresponding running time will be longer. So here we choose a compromise value $T=100$. Meanwhile, the threshold of mean square error $\varepsilon$ can also control the number of iterations. Through experiments, we set $\varepsilon =0.25$. We compare the proposed method with different image super-resolution methods. As shown in Table 8, LPRGSS takes much longer time than ours, but the image magnification accuracy is much lower. The block matching and SVD operations of proposed method require a large amount of computation. So ours is slower than RFI, but it has more advantages in enlarged image quality.

6 Conclusions

This paper presents a new method for SISR which is realized by two steps. First, a local biquadratic spline surface based on edge constraints is constructed on each small area of the image. And then, the enlarged image generated by biquadratic spline surface is adaptive optimized in transform domain. Biquadratic spline interpolation computes nine $C^1$ continuous biquadratic surface patches in the $3\times 3$ neighboring region of each pixel, constrained by the edge information. The whole fitting surface is constructed by weighted averaging of the surface patches. The interpolation algorithm improves the accuracy of the enlarged image, and has good shape preserving ability, which reduces the sawtooth shape and mosaic effect of the image. A new adaptive optimization in transform domain is proposed to reduce the unavoidable approximation error of the interpolation surface. The optimization model combines the proposed optimization with the iterative back-projection framework to optimize the enlarged image iteratively. According to the non-local self-similarity, we compute the contraction factor and adaptively contract the singular values of similar block matrices to reduce errors. The global structure can make up for the limitation of biquadratic spline algorithm that constructing HR pixels with only local pixels. Finally, the reconstructed error image is projected back to make up the lost high-frequency information. By introducing the adaptive optimization into the traditional iterative back-projection framework, the quality of output image can be greatly improved. Compared with the state-of-the-art methods, our method achieves better results in terms of visual effects and quantitative indicators. In future work, we will consider adding more constraints to the optimization model to improve the amplification effect.