A Surface Fitting Image Super-Resolution Algorithm Based on Triangle Mesh Partition

Abstract

High-frequency information such as image edges and textures have an important influence on the visual effect of the super-resolution images. Therefore, it is vital to maintain the edge and texture features of the super-resolution image. A surface fitting image super-resolution algorithm based on triangle mesh partitions is proposed in this study. Different from the traditional image interpolation algorithm using quadrilateral mesh, this method reconstructs the fitting surface on the triangle mesh to approximate the original scene surface. LBP algorithm and second-order difference quotient are combined to divide the triangular mesh accurately, and the edge angle is utilized as a constraint to makes the edge of the constructed surface patch more informative. By the area coordinates as weighting coefficients to perform weighted averaging on the surface patches at the vertices of the triangle mesh, the cubic polynomial surface patches are obtained on the triangle mesh. Finally, a global structure sparse regularization strategy is adopted to optimize the initially super-resolution image and further eliminate the artifacts at the image edges and textures. Since the new method proposed in this study utilizes numerous information about local feature (e.g. edges), compared to other state-of-the-art methods, it provides clear edges and textures, and improves the image quality greatly.

1 Introduction

Image super-resolution is a technology about how to get information-rich high-resolution (HR) images from low-resolution (LR) images through magnification and reconstruction, and the purpose is to improving the resolution of the image and restoring the details of the image. Image super-resolution plays an important role in scientific research fields including computer graphics, artificial intelligence, and computer vision. Based on different reconstruction methods, image super-resolution algorithms can be classified into two categories: interpolation-based algorithms and learning-based algorithms. This paper mainly studies the method based on interpolation.

Interpolation-based algorithms [1,2,3,4] are the process of constructing curves or curved surfaces [5,6,7] of LR images in a certain area through a specific function and predicting the HR images. Previous classical algorithms based on interpolation are nearest neighbor algorithm, bilinear interpolation [8, 9], and bicubic interpolation [10,11,12]. Although the interpolation functions used by these three methods are relatively simple, the HR images obtained by interpolation are severely distorted and have obvious aliasing and ringing effects. Zhang et al. proposed an interpolation method for soft decision estimation [13]. Compared to the traditional methods for decision estimation of each pixel, this method estimated missing high-resolution pixels in units of image patches. Besides, the model parameters can be adaptively adjusted according to the pixels of the LR image that is provided as inputs in the interface. Therefore, this method is simple, efficient, and adaptable. Although the method has improved the objective quantification of data, the subjective visual effect has not been significantly improved. The study conducted by Takuro et al. (2017) proposed a single image super-resolution algorithm based on multiple filtering and weighted average [14]. The algorithm utilized local functions to reduce blur and introduced new weight to improve the reliability of local functions. Besides, this method adopted convolution of small filters to replace the calculation of each local function, which can reduce the calculation cost. High-quality, non-aliased, and blur-free output images can be obtained by using this method in a short calculation time. In 2018, Yang et al. proposed a method of fractional gradient interpolation [15]. By selecting an appropriate fractional gradient operator, not only the high-frequency components of the signal are protected, but also the low-frequency components of the signal are retained nonlinearly. The algorithm can effectively process the pixels with similar gray values in the smooth area. The enlarged image effectively preserved the texture details, highlighted the edges, and avoided the ringing and step effects. Liu et al. proposed an image enlargement method based on cubic fitting surfaces with local features as constraint [16]. For the input image and the error image, the quadratic polynomial surface patches are constructed in regions of different sizes, and the enlarged image has a better visual effect. But for complex edge regions, the enlarged image obtained by this method is relatively smooth. Literature [17] enlarged a given LR input image to a HR image while retaining texture and structure information. This algorithm has achieved high numerical accuracy, but there are high-frequency information missing or artifacts at complex edges and texture details. In 2020, Zhang et al. proposed a more advanced image super-resolution method [18]. Creative and innovative results have been achieved on LR images that are down-sampled by interlacing and inter-column, but the magnification effect is poor for other down-sampled LR images.

This paper proposes a surface fitting image super-resolution algorithm based on triangle mesh partition, mainly focuses on the edges of the quadrilateral meshes inclined at 45° and 135°. The innovations are as follows:

• 1. This paper puts forward a strategy for triangle mesh partition that consists of the neighboring pixels. By the combination of LBP algorithm and simple second-order difference quotient, the strong edges and texture details of image are effectively extracted.

• 2. An edge angle is proposed to constraint the process of solving the coefficients of the quadratic polynomial surface.

• 3. The initially reconstructed HR images is optimized by the global structure sparse regularization strategy. The artifacts in edge and texture of the image are eliminated during the iterations, improving the visual effect.

The rest of this paper is as follows. Section 2 is the overall description of the method. Section 3 compares the experimental results of different methods. Section 4 is the summary of the method and the next step of this work.

2 Methodology

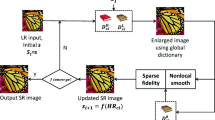
For a low-resolution image, the first step is to detected edge and texture image by using the combination of the LBP algorithm and the second-order difference quotient method (SODQ). The triangle meshes that consists of the neighboring pixels are obtained, taking the edge and texture image as the guide. The algorithm constructs a cubic polynomial triangle surface patch on each triangle mesh, and stitches these surface patches together to approximate the original surface. Then, it resamples on the fitting surface to obtain the preliminary reconstructed HR image Y. Since there are unavoidable errors of the fitting surface, and the edges and textures of HR image Y are unsatisfactory, the next step is to optimize image Y. The image Y is decomposed into a smooth component $f_{1} \otimes Y_{1}$, where $Y_{1}$ is a low-frequency feature map of the image, and a sparse residual $Y_{r}$ representing the global structure of this image. This operation ensures that the smooth component contains low frequencies. The low-frequency feature map $Y_{1}$ are enforced to be smooth (i.e., to have a weak response to an edge-filter) by a gradient operator along horizontal or vertical direction. The polished $Y_{1}$ is superimposed with $Y_{r}$ and then an optimized image is obtained. By repeating this process, the final enlarged image H can be obtained. The flowchart of the proposed method is shown in Fig. 1.

Fig. 1.

Flowchart of the proposed method.

2.1 Divide Triangle Mesh

Since the edge of the image will have a great influence on the visual effects of the enlarged images, dividing the mesh according to the edge situation can depict the edge of the image better when reconstructing the image. Since we only need to consider the edges in the 45° and 135° directions, the paper firstly extracts strong edges according to the LBP algorithm and determines the mesh division scheme according to the element jump rule at the diagonal. The details are as follows:

The binary number is the LBP value of the central pixel, reflecting the information in the neighborhood. The algorithm only processes the uniform patterns among them. Uniform mode refers to the mode in which the repeated binary digits corresponding to LBP can, at most, transform twice between 0 and 1. Therefore, a rule can be obtained, namely when the number of transformations equals 2 and such transformations occur at diagonal positions, the edge inclined at this position equals to 45° or 135°. According to this rule, precise division of strong edge meshes in the directions of 45° and 135° can be obtained. The principle is simple while the edge accuracy is high.

Then, for the remaining undivided area, a rough mesh is divided according to the simple second-order difference in the diagonal direction. According to the nature of the image, the changing rate of the pixel values in the image along the edge is relatively small. Therefore, for the remaining undivided areas (usually texture and flat areas), we can calculate the simple second-order difference quotient of the image in the directions of 45° and 135°, namely the rate of change. According to the rate of change in the two directions, the quadrilateral mesh can be generated by using the adjacency relationship of the pixels, and then a rough triangular mesh division scheme can be obtained.

The rate of change at the point $P_{i,j}$ is shown in Fig. 2. Where the red dotted line indicates the change along the 45° direction, and the blue dotted line indicates the change along the 135° direction. The simple second-order difference quotient in the 45° and 135° directions can be defined as follows:

$$ \begin{gathered} g_{45} \left( {i,j} \right) = P_{i + 1,j + 1} - 2P_{i,j} + P_{i - 1,j - 1} \hfill \\ g_{135} \left( {i,j} \right) = P_{i - 1,j + 1} - 2P_{i,j} + P_{i + 1,j - 1} \hfill \\ \end{gathered} $$

(1)

If $g_{45} < g_{135}$, it means that the rate of change of the image in the 45° direction is small, and then the quadrilateral grid is divided into two triangular meshes along the red dotted line to obtain a 45° division scheme. Otherwise, the division occurs along the blue dotted line to get the 135° division scheme.

The combination of LBP algorithm and second-order difference quotient methods can effectively extract the edge and texture, makes the division of triangle meshes more accurate and efficient.

Fig. 2.

Coarse division.

Fig. 3.

$3 \times 3$ Image patch.

Fig. 4.

Area coordinate weighted average.

2.2 Construct Fitting Surface

This paper firstly constructs a quadratic polynomial surface patch centered on each pixel. Then, the weighted average area coordinate is used to obtain the cubic polynomial surface patch on the triangular mesh, so as to approximate the original surface.

2.2.1 Construct a Quadratic Polynomial Surface Patch at a Pixel

Pixel can be regarded as the discrete data sampled from the surface.

$$ P_{i,j} = \int_{j - 0.5}^{j + 0.5} {\int_{i - 0.5}^{i + 0.5} {g_{i,j} } } (x,y)dxdy $$

(2)

The $3 \times 3$ image patch (shown in Fig. 3) is constructed using a double quadratic polynomial $g_{i,j}$, that is, $g_{i,j}$ defined in the $xy$ area of the plane $[i - 1.5,i + 1.5] \times [j - 1.5,j + 1.5]$. We construct the following quadratic polynomial fitting surface patch centred at pixel $P_{i,j}$.

$$ g_{i,j} (u,v) = a_{1} u^{2} + a_{2} uv + a_{3} v^{2} + a_{4} u + a_{5} v + a_{6} $$

(3)

in which, $u = x - i,v = y - j$, $a_{1} ,a_{2} , \cdot \cdot \cdot ,a_{6}$ are unknown patch coefficients of $g_{i,j}$.

Figure 5(a)–(f) are the interpolated images obtained when only the corresponding coefficients $a_{i} (i = 1,2, \cdot \cdot \cdot ,6)$ are retained and the other coefficients are 0, and (g) is the original image. Cleaned up for presentation purposes, the gray values of Fig. 5(a)–(e) are magnified 5 times. The results in Fig. 5(a)–(e) imply that coefficients a_i(i = 1, 2, …, 5) provide more image details. Image edge information is mainly provided by Fig. 5(d), (e), and (f), while Fig. 5(a), (b), and (c) provide limited information.

Fig. 5.

The result of magnifying the image using only individual coefficients $a_{i} (i = 1,2, \cdot \cdot \cdot ,6)$.

The above-mentioned information shows that different coefficients have different effects on the edges and texture of the image. As $i(i = 1,2, \cdot \cdot \cdot ,6)$ continuously increasing, more low-frequency information and less high-frequency information can be obtained. In the solution process, the low-frequency information of the image needs to be determined first. Therefore, the algorithm firstly considers how to accurately solve the coefficients of the constant term $a_{6}$, and then solve the remaining coefficients. Here, the method proposed by Zhang [24] is used to solve the polynomial coefficients.

From Eqs. (2) and (3), we can get:

$$ P_{i + m,j + n} = a_{1} m^{2} + a_{2} mn + a_{3} n^{2} + a_{4} m + a_{5} n + a_{6} + \frac{{a_{1} + a_{3} }}{12},\quad m,n = - 1,0,1 $$

(4)

Equation (5) can be inferred from Eq. (6):

$$ a_{6} = P_{i,j} - \frac{1}{12}a_{1} - \frac{1}{12}a_{3} $$

(5)

As shown in Fig. 5, the first-order deviations along the four directions at the points are:

$$ \begin{gathered} x:\lambda_{1} = (P_{i + 1,j} - P_{i - 1,j} )/2 \hfill \\ y:\lambda_{2} = (P_{i,j + 1} - P_{i,j - 1} )/2 \hfill \\ x + y:\lambda_{3} = (P_{i + 1,j + 1} - P_{i - 1,j - 1} )/2 \hfill \\ x - y:\lambda_{4} = (P_{i + 1,j - 1} - P_{i - 1,j + 1} )/2 \hfill \\ \end{gathered} $$

(6)

From Eqs. (4) and (6), we can get:

$$ a_{4} = \lambda_{1} ,a_{5} = \lambda_{2} ,a_{4} + a_{5} = \lambda_{3} ,a_{4} - a_{5} = \lambda_{4} $$

The unknown coefficients $a_{4}$ and $a_{5}$ can be obtained by constrained least squares using Eq. (7):

$$ CLS(a_{4} ,a_{5} ) = \omega_{1} (a_{4} - \lambda_{1} )^{2} + \omega_{2} (a_{5} - \lambda_{2} )^{2} + \omega_{3} (a_{4} + a_{5} - \lambda_{3} )^{2} + \omega_{4} (a_{4} - a_{5} - \lambda_{4} )^{2} $$

(7)

Unlike Zhang, the algorithm in this study introduces an edge angle $\theta$ to define the weight function $\omega_{i}$:

$$ \omega_{i} = \frac{1}{{1 + \mu_{i}^{2} \left| {\cos \theta } \right|}} $$

(8)

$\mu_{i}$ in Eq. (9) is the second-order difference quotient of the corresponding equation along the same direction. For example, the definition of $\mu_{i}$ along the $x$ direction is as follows:

$$ x:\mu_{1} = \frac{{P_{i + 1,j} - 2P_{i,j} + P_{i - 1,j} }}{2} $$

(9)

The edge angle $\theta$ is defined as: $\theta = 0^{ \circ }$ in x, y direction, $\theta = 45^{ \circ }$ in $x + y$ direction, $\theta = 135^{ \circ }$ in $x - y$ direction. If there is a linear function $g_{i,j} (x,y)$ along the $45^{^\circ }$ edge direction, the determination of the weight function should make the $\lambda_{3}$ on the $x + y$ direction play a major role on the determination of $a_{4} + a_{5}$ on this direction. That being said, the weighted value $\omega_{3}$ in Eq. (8) should be a larger value. The edge angle makes the weight bigger, and it plays a greater role in determining the direction coefficient, which is consistent with the edge characteristics of the surface and effectively improves the accuracy of the surface.

In order to obtain the remaining unknown coefficients $a_{1}$,$a_{2}$, and $a_{3}$, the corresponding conditions can be obtained by using the 8 pixel points around the point $P_{i,j}$ into Eq. (10).

$$ P_{i + m,j + n} = a_{1} m^{2} + a_{2} mn + a_{3} n^{2} + a_{4} m + a_{5} n + P_{i,j} ,\;\;m,n = - 1,0,1,\;m \ne n = 0 $$

(10)

in which, $m,n = - 1,0,1$ and $m \ne n = 0$.

Similarly, the least-square method with constraints is used to obtain the unknown coefficients $a_{1}$,$a_{2}$, $a_{3}$.The minimum objective function is as follows:

(11)

The weight function $\omega$ is determined in the same direction by using Eq. (8) in the same way.

2.2.2 Constructing Cubic Polynomial Surface Patches on Triangular Mesh

As shown in Fig. 4, $f_{i} (x,y)$, $f_{j} (x,y)$, $f_{k} (x,y)$ are quadratic polynomial surface patches constructed by using three vertices $P_{i}$,$P_{j}$,$P_{k}$ as the centers, respectively. The triangular surface patch $f_{i,j} (x,y)$ is obtained by weighted average of these three surface patches:

$$ f_{i,j} (x,y) = lif_{i} (x,y) + ljf_{j} (x,y) + lkf_{k} (x,y) $$

(12)

To simplify the process of surface construction, the definition of area coordinates is introduced. As shown in Fig. 7, the area coordinates $(li,lj,lk) = (li(x_{i} ,y_{i} ),lj(x_{j} ,y_{j} ),lk(x_{k} ,y_{k} ))$ of triangle M are defined as:

$$ \begin{gathered} li = \frac{1}{2S}[y_{j} x_{k} - y_{k} x_{j} + (x_{j} - x_{k} )y + (y_{k} - y_{j} )x] \hfill \\ lj = \frac{1}{2S}[y_{k} x_{i} - y_{i} x_{k} + (x_{k} - x_{i} )y + (y_{i} - y_{k} )x] \hfill \\ lk = \frac{1}{2S}[y_{i} x_{j} - y_{j} x_{i} + (x_{i} - x_{j} )y + (y_{j} - y_{i} )x] \hfill \\ \end{gathered} $$

(13)

in which S represents the area of the triangle M. According to the nature of the area coordinates, we can get $li + lj + lk = 1$. The obtained triangular surface pieces $f_{i,j} (x,y)$ are spliced together to obtain a continuous and curved surface $f(x,y)$.

2.3 Global Structure Sparse Regularization Optimization

There are inevitable errors in fitting the curved surfaces with surface patches, and it is unrealistic to process the details of some edges and textures. Therefore, to reduce the reconstructed artifacts of the enlarged image, this paper adopts a global structure sparse regularization strategy to optimize the enlarged image.

The key of the strategy is to decompose the smooth component of the image [28]. Y is the enlarged image after the preliminary reconstruction. Y₁ is the low-frequency feature map of the image, and the residual component $Y_{r}$ that mainly containing the high-frequency information of the image (i.e. edge texture and other details). The global structure of the image can be expressed as:

$$ Y = f_{l} \otimes Y_{l} + Y_{r} $$

(14)

in which $f_{l}$ is a 3×3 low-pass filter, $\otimes$ represents the convolution operation.

To construct the regularized function, two prerequisites need to be provided. One is $\left\| {Y_{r} } \right\|_{p}$, indicating the residual component is sparse in $l_{p}$ norm. Given this study considers convexity, the $L_{1}$ norm is used. In addition, the low-frequency feature map Y₁ needs to be enhanced to smooth the image. This process is expressed as $\left\| {g_{d} \otimes Y_{l} } \right\|_{2}^{2}$, in which $g_{d} = [1,2]$ and $d \in \left\{ {1 = level,2 = vertical} \right\}$ indicates the gradient operator in the horizontal or vertical direction. Based on these two prerequisites, we can get a regularized function as follows:

$$ R_{g} = \left\| {Y_{r} } \right\|_{1} + \varphi \sum\limits_{d = 1}^{2} {\left\| {g_{d} \otimes Y_{l} } \right\|_{2}^{2} } $$

(15)

Where $\phi$ controls the smoothness of the low-frequency feature map. The larger the $\phi$ is, the more image information the residual components contain. At the same time, the image is smoother. As regularization enhances sparsity, the gradient of the reconstructed image is reduced, which can effectively reduce artifacts at edges and textures.

At this time, the image reconstruction can be written as:

$$ \arg \;{\text{min}}_{(\lambda ,\xi )} \,\;\left\| {Y{ - }f_{l} \otimes Y_{l} { - }Y_{r} } \right\|_{{2}}^{{2}} + R_{g} $$

(16)

3 Results and Discussion

3.1 Parameter Settings

The downsampled images of all experiments in this paper are obtained by averaged downsampling. The parameters φ in the global structure sparse regularization strategy are set to 1 empirically. The algorithm termination threshold $\xi$ is set as $e^{ - 5}$_.The maximum number of iterations is set to 4 to balance the time complexity and the obtained image quality. Our experiments show that the time increases as the number of iterations increasing. However, the PSNR value of the algorithm does not increase significantly after 4 iterations. The maximum number of iterations is set to 4 to balance the image quality obtained and the time complexity.

3.2 Analysis of Results

The experiment is divided into two parts. The first part is a comparison experiment of 10 representative images listed in Table 1. The second part is to compare the dataset images, the dataset includes Set5, Set14, BSD100 and Urban 100. This paper compares 8 methods: Bicubic [12], LGS [28], FRI [17], Zhang [27], NLFIP [24], NARM [29], SelfEx [25] and ANR [30].

Figures 6 and 7 show the results of nine representative methods of two images. To facilitate observation, the nearest neighbor interpolation method is used to enlarge the red area with a scale factor of 3 or 4.

Edges and textures are important indicators for evaluating high-resolution image quality. Compared to other methods, the method proposed in this paper can keep edges and texture well. Figures 6 and 7 mainly compare the effectiveness of the methods at the edges. In Fig. 6, Bicubic, Zhang, NLFIP, ANR and NARM at the edges are relatively blurry, and there is obvious aliasing at the stripes of LGS, SelfEx and FRI. In Fig. 7, it can be seen that the proposed method can display the sloping edges clearly. On the contrary, LGS, SelfEx and FRI have obvious aliasing, and Bicubic, Zhang, NLFIP, ANR and NARM have obvious fuzziness.

Fig. 6.

(a) NARM. (b) ANR. (c) Bicubic. (d) LGS. (e) Zhang. (f) NLFIP. (g) SelfEx. (h) FRI. (i) Ours. (j) GroundTruth.

Fig. 7.

(a) NARM. (b) ANR. (c) Bicubic. (d) LGS. (e) Zhang. (f) NLFIP. (g) SelfEx. (h) FRI. (i) Ours. (j) GroundTruth.

In this paper, the objective quantitative analysis uses peak signal-to-noise ratio (PSNR) and structural similarity (SSIM) as the indicators to test the image quality. Table 1 lists the PSNR and SSIM values of the images enlarged by 6 methods and the scale factor is 2. The last line shows the average PSNR and SSIM values for each method. The maximum value of the PSNR and SSIM are marked in bold. The higher the PSNR and SSIM values are, the better the image quality is. As shown in Table 1, the PSNR and SSIM values of the method proposed in this paper are the largest except the SSIM value of Baboon. Therefore, compared to the other methods, the method developed in this paper can provide the best image quality.

Table 1. The PSNR and SSIM of six methods

This paper tested the images from several datasets, including Set5, Set14, BSD100, and Urban100, which are all classic datasets commonly used in image super-resolution algorithms. According to the results shown in Table 2, the method proposed in this paper leads to the largest average PSNR and SSIM values, implying the advantage of the method proposed in this paper compared to other previous methods.

Table 2. Results of nine methods on different data sets

4 Conclusions

The paper proposes a surface fitting image super-resolution algorithm based on triangle mesh partition. This method not only effectively improves the quality of the enlarged image edges and textures but also provides a better visual effect. By applying global structure sparse regularization strategy on iterative optimization, the time complexity of the algorithm is increased. Therefore, how to further improve the image quality and effectively shorten the time are the focus of the next step.