An isogeometric analysis-based topology optimization framework for 2D cross-flow heat exchangers with manufacturability constraints

Abstract

Heat exchangers (HXs) have gained increasing attention due to the intensive demand of performance improving and energy saving for various equipment and machines. As a natural application, topology optimization has been involved in the structural design of HXs aiming at improving heat exchange performance (HXP) and meanwhile controlling pressure drop (PD). In this paper, a novel multiphysics-based topology optimization framework is developed to maximize the HXP for 2D cross-flow HXs, and concurrently limit the PD between the fluid inlet and outlet. In particular, an isogeometric analysis solver is developed to solve the coupled steady-state Navier–Stokes and heat convection–diffusion equations. Non-body-fitted control mesh is adopted instead of dynamically remeshing the design domain during the evolution of the boundary interface. The method of moving morphable voids is employed to represent and track boundary interface between the hot and the remaining regions. In addition, various constraints are incorporated to guarantee manufacturability of the optimized structures with respect to practical considerations in additive manufacturing, such as removing sharp corners, controlling channel perimeters, and minimizing overhangs. To implement the iterative optimization process, the method of moving asymptotes is employed. Numerical examples show that the HXP of the optimized structure is greatly improved compared with its corresponding initial design, and the PD between the fluid inlet and outlet is controlled concurrently. Moreover, a smooth boundary interface between the channel and the cold fluid, and improved manufacturability are simultaneously obtained for the optimized structures.

1 Introduction

Topology optimization [1] has been widely applied to many fields for the purpose of improving performance of the structural systems. The optimization objectives include static compliance [2,3,4], structural stress [5], fundamental vibration frequency [6], thermal conduction [7], and thermo-elasticity [8]. In recent years, increasing attention has been paid to topology optimization of multiphysics systems such as vibration-acoustic structures [9, 10] and thermal fluid structures [7, 11,12,13]. The studies in Refs. [14, 15] are particularly relevant, because they address topology optimization of 3D cross-flow HXs with solid fins at high temperature. Other multiphysics topology optimization reports address fluid–structure interaction (FSI) systems [16,17,18] and thermal-electric energy structure [19], which shows a promising trend in the development and application of topology optimization.

Among the multiphysics systems, heat exchangers (HXs) attract strong interest and attention, since they are widely used as an important component in modern industries [7, 20, 21]. However, the structural design of HXs is challenging, because the fluid mechanics and heat transfer phenomena involved in HXs are complicated. Early research focused on either fluid domain optimization based on fluid mechanics [13, 22,23,24], or thermal optimization in terms of thermal conduction and convection condition [25,26,27]. Nonetheless, there are examples of coupled multiphysics investigations for real fluid–fluid and even fluid–solid–fluid HX systems that aim to improve the performance of HXs based on topology optimization [28,29,30].

Common topology optimization methods include homogenization [1, 31], solid isotropic material with penalization (SIMP) [32, 33], level-set method (LSM) [34, 35], and bi-directional evolutionary structure optimization (BESO) [36, 37]. In addition, methods such as moving morphable components (MMCs) [38] and voids (MMVs) [39] have been proposed recently as novel tools for explicit topology optimization. SIMP is simple to implement and straightforwardly shows the material layout in structures. LSM can provide a smooth boundary interface between different material filling states and avoid gray elements with intermediate density in the optimized structures, which, by contrast, is a common drawback of the SIMP method. The MMC/MMV method performs explicit topology optimization by representing the evolving material layouts based on components or voids defined by explicit mathematical equations. This method also has promise for generating smooth boundary interfaces and removing gray elements in the optimized topology.

Regarding topology optimization of HXs, many works employ the density-based approach [29, 30] to find optimal structures. However, it is difficult to guarantee a smooth and explicit boundary interface between different filling states with respect to the fluid–fluid or fluid–solid phase fields owing to gray elements with intermediate densities [15, 40]. Moreover, a material or phase interpolation model is usually needed for the density-based framework to link the topological density with the multiphysics equations. This increases the complexity of the multiphysics topology optimization framework, especially when geometric constraints such as the minimum length/thickness constraint are included. Recently, LSM was successfully applied to topology optimization of both FSI systems [18, 41, 42] and cross-flow HXs [28], where different phases such as solid and fluid are described based on an explicit discretization of the design domain. Specific geometric constraints such as a non-mixing restriction between different fluids and minimum channel thickness can be applied. Given an explicit discretization, fine body-fitted meshes [28, 35, 43] and remeshing for the design domain [28] are required in the iterative optimization process, which results in high computational cost. Moreover, because of the implicit description of boundary interface, it is challenging to derive the sensitivity when a gradient-based optimization method is employed.

Although many have addressed structural design of HXs, there are few that include practical manufacturability of the final numerical design. It is very common to encounter complex internal configurations in the optimized design, including highly curved surfaces and sharp features (see, e.g., [28]). Here, we consider a cross-flow HX with thin-walled channels. With conventional machining and tooling methods, it would be very difficult to manufacture the complex optimized designs. Additive manufacturing, however, provides a fabrication solution with more freedom for complex components. Interested readers are referred to Liu et al. [44] who review the current progress and future trends in topology optimization for additive manufacturing. They discuss optimized designs limited to 2D planar geometries and 3D HX models are constructed based solely on normal extrusion. By contrast, additive manufacturing is suitable for fabricating complex 3D designs in near net-shape fashion with minimal wasted material. Specific technologies such as laser powder bed fusion (LPBF) and directed energy deposition (DED) with wire or powder are generally applicable. For designs that have extrudable profiles, extrusion from solid billets can be employed to print the 3D HXs. Certain manufacturability constraints are typically considered for all three techniques, such as avoiding sharp corners and overhang features in the optimized designs.

In addition, most reports employ conventional finite-element method (FEM) to conduct multiphysics simulation for HXs in the topology optimization framework. As an advanced finite-element tool, isogeometric analysis (IGA) [45, 46] has seen rapid development in both theory and application in different fields. Compared to conventional FEM, IGA enables direct and seamless integration of geometry modeling and analysis, using smooth splines as basis functions to accurately represent complex computer-aided design (CAD) models and formulate numerical solutions. IGA has demonstrated higher computational efficiency with fewer degrees of freedom used for the same problem setting, and better performance in numerical accuracy and stability over conventional FEM. Thanks to these advantages, IGA has been widely applied to shell structure analysis [47,48,49], biomedical field [50,51,52,53,54], and FSI simulation [55,56,57]. IGA has been incorporated into commercial software such as Abaqus [58, 59] and LS-Dyna [60, 61]. Moreover, IGA has been utilized as the solver for heat transfer [62], and has been incorporated in topology optimization of mechanical systems [39, 63, 64].

Here, we develop a novel multiphysics IGA framework for the topology optimization of 2D HXs. New contributions include: (1) Truncated hierarchical B-splines (THB-splines) that describe accurately the design domain and boundary interface curves between different fluid phase fields. An IGA-based solver is developed to solve the governing equations in multiphysics simulation for the HXs; (2) an explicit topology optimization framework is developed based on the MMV method to guarantee a pure “black-and-white” material layout with a smooth boundary interface between different fluid phase fields in the optimized structures for 2D cross-flow HXs; (3) a non-body-fitted control mesh is adopted for the 2D design domain. The computational cost can be substantially reduced, since no dynamic remeshing is needed regardless of the evolving boundary interface between different fluid phase fields in the iterative topology optimization process; and (4) a gradient-based optimization module is established to perform iterative topology optimization. Manufacturability constraints are also considered in topology optimization with respect to the additive manufacturing process, such as removing sharp corners, constraining channel perimeters, and minimizing overhangs for printing the cross-flow HXs.

The body of the paper is organized as follows. The problem description and an overview of the developed framework are given in Sect. 2 in terms of major computational modules, the multiphysics system, and numerical methods. Section 3 introduces the mathematical governing equations and IGA solver for multiphysics simulation in HXs. Section 4 presents the mathematical model of topology optimization for HXP maximization while considering pressure drop (PD) as a specific constraint. In particular, the MMV method is adopted for the topology optimization of the cross-flow HXs. A specific optimization engine based on MMA [65, 66] is also introduced. Section 5 presents numerical examples to demonstrate the effectiveness of the proposed topology optimization framework for cross-flow HX design. A validation study first shows good accuracy from employing a non-body-fitted control mesh and MMV-based description for the 2D domain, followed by an investigation of the influence of different factors on the topology optimization. Section 6 shows how to improve manufacturability in a practical sense. Finally, conclusions and future work are given in Sect. 7.

2 Problem description and framework overview

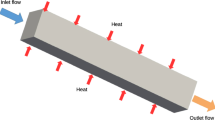
In the HXs, fluids such as air and oil can be characterized by the flow velocity and pressure field. A simplification is applied to the hot fluid channels by assuming zero velocity and constant temperature. In other words, we did not consider fluid flow in the out-of-plane “pipes”; see Fig. 1. The pressure drop in the embedded channels is disregarded. The constant temperature assumption for hot fluid channels is appropriate for solid pin-fins of a heat sink. The detailed inner structure of the cross-flow HX without accessories like front and rear headers is shown in Fig. 1. The 2D design domain can be extruded into a 3D cross-flow HX in practice. When the 3D problem is considered, the out-of-plane flow in the embedded channels should be fully simulated, e.g., [14, 67]. In this paper, the cold fluid is always assumed to enter the domain $\varOmega _{f}$ from the left side as the inlet ($\partial \varOmega _{f\_{\mathrm{in}}}$). The hot fluid is contained in the tubes/channels represented by the voids (see the red circles in Fig. 1). The right side ($\partial \varOmega _{f\_{\mathrm{out}}}$) of the HX domain is assumed to be the outlet. Flow velocity, pressure, and temperature fields in the 2D domain are investigated in this paper.

Fig. 1

2D design domain of a 5-channel cross-flow HX: hot fluid inlet (red circles) is perpendicular to the inlet of cold fluid (blue bold arrows, $\partial \varOmega _{f\_{\mathrm{in}}}$); the cold fluid always flows out from the right end (red bold arrow, $\partial \varOmega _{f\_{\mathrm{out}}}$) after exchanging heat; non-slip boundary condition (BC) is applied to the upper and lower boundary of the domain ($\partial \varOmega _{f\_{\mathrm{wall}}}$) (color figure online)

Fig. 2

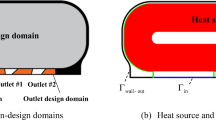
An overview of the developed topology optimization framework for 2D cross-flow HXs. The framework mainly consists of the IGA and optimization modules. Multiphysics simulation is implemented based on the IGA solver to obtain the fluid velocity, pressure, and temperature fields. Then, the HXP and PD are taken as the objective function and constraint for the optimization module, respectively. Through the gradient-based optimization process using MMA, the optimized structure is found to maximize the HXP and control the PD of the design domain

Figure 2 shows an overview of the proposed topology optimization framework for 2D HXs. Two major modules are included in the framework. The IGA module includes an IGA-based solver to perform multiphysics simulation for the HXs. The optimization module involves an MMA-driven topology optimization model to find the optimized structures with the goal of HXP maximization and PD minimization. The problem settings of the involved multiphysics system including the governing equations, major numerical analysis methods, and optimization algorithms are listed as below.

• 1. In the IGA module, multiphysics simulation is performed to obtain the fluid velocity, pressure and temperature fields in the 2D cross-flow HXs. In particular, the fluid velocity and pressure fields are solved first based on the steady-state Navier–Stokes (N–S) equations. Then, the fluid velocity solution is taken as the input to solve the temperature field based on the steady-state heat convection–diffusion (C–D) equation. The MMV method is employed to track the boundary interface between cold and hot fluids in the design domain. By moving the center position and changing the shape and topology of the MMVs, different patterns of the hot fluid regions are generated. IGA is employed to solve the multiphysics governing equations and non-body-fitted control mesh is adopted for the design domain of 2D HXs. After the fluid velocity, pressure, and temperature fields are obtained, HXP and PD between the fluid inlet and outlet are calculated accordingly.

• 2. In the optimization module, the HXP is adopted as the objective function for the topology optimization model, while the PD is treated as a constraint. Sensitivity analysis is performed first to obtain gradient information. The direct finite difference method is employed to solve the derivatives of the objective function and constraint equations with respect to the design variables. MMA iteratively updates the design variables. Three influence factors are studied in detail, such as angular division, initial design, and inlet velocity. Moreover, certain manufacturing-related constraints are incorporated in the optimization module, including design variable filtering, boundary perimeter constraint, and cell-based optimization. Finally, an optimized solution is obtained as the output of the optimization process with simultaneous HXP maximization and PD control.

3 Multiphysics IGA solver for HXs

In this section, a multiphysics IGA solver is developed to model the cross-flow HXs. The fluid velocity ${\varvec{u}}$ and pressure p in the HXs are first obtained by solving the incompressible steady-state N–S equations

$$\begin{aligned} {\left\{ \begin{array}{ll} \nabla \cdot (\rho {\varvec{u}} \otimes {\varvec{u}}) + \nabla p = \nu \varDelta {\varvec{u}} + f &{} \text {in } \varOmega _{f} \text {,}\\ \nabla \cdot {\varvec{u}} = 0 &{} \text {in } \varOmega _{f} \text {,} \\ {\varvec{u}} = {\varvec{u}}_{\mathrm{in}} &{} \text {at the inlet of cold fluid } \partial \varOmega _{f\_{\mathrm{in}}} \text {,} \\ {\varvec{u}} = {\varvec{0}} &{} \text {at the upper and lower wall }\partial \varOmega _{f\_{\mathrm{wall}}} \text {,} \\ {\varvec{u}} = {\varvec{0}} &{} \text {in the regions of hot fluid,} \end{array}\right. } \end{aligned}$$

(1)

where $\varOmega _{f}$ represents the fluid domain in HXs, $\nu$ denotes the dynamic fluid viscosity, $\rho$ denotes the fluid density, and f denotes the body force such as gravity in the fluid system. For simplicity, the body force term is ignored in this paper. The non-slip BC is applied to the upper and lower boundary of the 2D design domain ($\partial \varOmega _{f\_{\mathrm{wall}}}$; see Fig.  1). Since the flow direction of the hot fluid in cross-flow HXs is perpendicular to the 2D design domain in Fig. 1, the fluid velocity at the hot fluid regions is set to zero. Regarding the inlet for cold fluid ($\partial \varOmega _{f\_{\mathrm{in}}}$), we adopt a constant inlet velocity ${\varvec{u}}_{\mathrm{in}}$ in all numerical examples.

Taking the velocity field ${\varvec{u}}$ as input, the fluid temperature field T is then determined by solving the steady-state heat C–D equation

$$\begin{aligned} {\left\{ \begin{array}{ll} -\nabla \cdot (k_f \nabla T) + \rho c_p {\varvec{u}} \cdot \nabla T = 0 &{} \text {in } \varOmega _{f} \text {,}\\ -k_f \dfrac{\partial T}{\partial {\varvec{n}}} = 0 &{} \text {at the upper and lower wall }\partial \varOmega _{f\_{\mathrm{wall}}} \text {,} \\ T = T_{\mathrm{in}} &{} \text {at the inlet of cold fluid } \partial \varOmega _{f\_{\mathrm{in}}} \text {,} \\ T = T_{\mathrm{hot}} &{} \text {in the regions of hot fluid,} \end{array}\right. } \end{aligned}$$

(2)

where $c_p$ denotes the heat capacity coefficient and $k_f$ denotes the thermal conductivity coefficient. ${\varvec{n}}$ is the normal of the boundary. $T_{\mathrm{in}}$ and $T_{\mathrm{hot}}$ denote the temperatures imposed at the cold fluid inlet and the hot fluid regions, respectively. Specifically, a fixed high temperature is enforced on all hot-channel regions of the non-body-fitted mesh representing the design domain.

For the steady-state N–S equations and the heat C–D equation, Reynolds number (Re) and Péclet number (Pe) are defined as

$$\begin{aligned} {\mathrm{Re}} = \dfrac{\rho \Vert {{\varvec{u}}_{\mathrm{in}}}\Vert _{\infty } L}{\nu }, \quad Pe = \dfrac{\rho c_p \Vert {{\varvec{u}}_{\mathrm{in}}}\Vert _{\infty } L}{k_f}, \end{aligned}$$

(3)

where $\Vert {{\varvec{u}}_{\mathrm{in}}}\Vert _{\infty }$ denotes the fluid velocity magnitude infinitely far away from the inlet, and L denotes the characteristic length of the HXs. In this paper, the width/height is selected as the characteristic length. Meanwhile, the fluid density $\rho$ and the heat capacity coefficient $c_p$ take unit value to simplify the computation of Re and Pe. Since the characteristic length L is constant, only the fluid dynamic viscosity $\nu$ and the thermal conductivity coefficient $k_f$ are adjusted to achieve different Re and Pe values.

In this paper, we only consider the incompressible steady-state N–S equations without turbulence. Therefore, the Re value is restricted to the range of [10, 200], and we choose 40 and 160 in our study. The Pe value ranges from 200 to 2000 in all numerical examples. Moreover, we only study the cross-flow HXs with the cold flow and hot channels perpendicular to each other. In practical applications, there are other types of shell-tube HXs where the two fluids flow parallelly or anti-parallelly to each other. In this case, the wall thickness has to be considered for the solid tubes/channels to ensure a non-mixing condition for the two fluids. This issue has been successfully considered in several previous works [28, 30]. In particular, the heat convection on the solid interface would have to be considered and a separate thermal diffusion equation would be necessary to determine the temperature distribution in the solid wall. This would increase the difficulty in obtaining the velocity and temperature solution to the shell-tube HX and is beyond the scope of this paper.

The numerical implementation of our solver is based on IGA. Compared with traditional FEM, IGA directly integrates geometric modeling with numerical simulation using the same smooth spline basis functions. Therefore, the use of IGA ensures an accurate and high continuity representation of the optimized structure during topology optimization, which leads to better accuracy than FEM. Also, the optimized designs represented by spline basis functions can be easily converted to CAD files to meet the requirements of the practical manufacturing. These benefits motivate us to develop the optimization framework based on IGA. Herein, we adopt the cubic THB spline as basis functions [68,69,70] and develop the solver based on the PETSc package [71] for better computational efficiency with parallel computing. To handle the numerical oscillation issue of the solution related to the convection term in the governing equations, we implement the variational multiscale (VMS) method [72, 73] for the N–S solver and the streamline upwind/Petrov–Galerkin (SUPG) method [74, 75] for the C–D solver. The detailed implementation of our IGA solver is available at https://github.com/CMU-CBML/HXTO.

4 MMV-based topology optimization with manufacturing constraints

In this section, the MMV method is first introduced for tracking the boundary interface of hot fluid regions in the design domain. Then, the objective functions and the design variables of the topology optimization framework are demonstrated. Then, the manufacturability constraints for additive manufacturing are presented. Finally, MMA is introduced as the engine to drive the topology optimization process.

4.1 MMV for tracking hot fluid regions

The MMV method is employed to track evolution of the shape of hot fluid regions in the design domain (see voids in Fig. 1). When these regions/voids move and deform, overlapping may occur among different voids. By merging multiple voids into a new one, topology of the design domain is changed accordingly. Closed B-spline curves are adopted to describe the boundary interface of these regions/voids. Assume that $m_{\xi }+1$ real numbers, $\xi _0$, $\xi _1$, ..., $\xi _{m_\xi }$, are arranged in a non-descending group $\Xi = \{ \xi _0, \xi _1, ..., \xi _{m_\xi -1}, \xi _{m_\xi } \}$, satisfying the condition $\xi _i \le \xi _{i+1}$ for $i= 0, 1, ..., m_\xi -1$. The group $\Xi$ is called a knot vector and used to define a series of B-spline basis functions. For a s-degree B-spline, the i^th basis function for $s = 0$ is defined as

$$\begin{aligned} N_{i,0}(\xi ) = {\left\{ \begin{array}{ll} 1, &{} \text {if } \xi _i \le \xi \le \xi _{i+1} , \\ 0, &{} \text {otherwise.} \end{array}\right. } \end{aligned}$$

(4)

Then, the remaining B-spline basis functions for $s = 1, 2, ...$ are constructed recursively according to

$$\begin{aligned} N_{i,s}(\xi ) = \frac{\xi - \xi _i}{\xi _{i+s} - \xi _i} N_{i,s-1}(\xi ) + \frac{\xi _{i+s+1} - \xi }{\xi _{i+s+1} - \xi _{i+1}} N_{i+1,s-1}(\xi ). \end{aligned}$$

(5)

Given $n_{\xi }+1$ control points $\{P_i\}$ = $\{P_0$, $P_1, ..., P_{n_\xi -1}, P_{n_\xi }\}$ corresponding to the constructed s-degree basis functions, a s-degree B-spline curve is formulated as

$$\begin{aligned} C(\xi ) = \sum _{i=0}^{n_{\xi }} N_{i,s}(\xi ) P_i , \end{aligned}$$

(6)

where $n_{\xi }$ and $m_{\xi }$ satisfy

$$\begin{aligned} m_{\xi } = n_{\xi } + s + 1. \end{aligned}$$

(7)

A closed curve can be constructed when the first and last control points are identical. As shown in Fig. 3, we demonstrate how a closed curve like circle can be represented using quadratic ($s=2$) B-spline basis functions and further used in the MMV method. Suppose the circle is equally divided into $N_{\mathrm{div}} = 12$ parts with the division angle $\varphi = 2\pi /N_{\mathrm{div}}$, 14 ($n_\xi + 1$, $n_\xi = 13$) control points ($P_0$, $P_1$, ..., $P_{13}$) are needed to define the circle and the corresponding knot vector is $\Xi = (0,0,0,\frac{1}{N_{\mathrm{div}}}, \frac{1}{N_{\mathrm{div}}}, \ldots , 1, 1, 1)$. Here, $(x_c, y_c)$ is the center point of the enclosed void, ($r_1$, $r_2$, ..., $r_i$, ..., $r_{N_{\mathrm{div}}}$) denote radii of all control points. A similar approach to shape design parameterization was reported in [27] where concurrent shape and topology optimization of steady conjugate heat transfer was addressed. The void in Fig. 3 is morphable by changing the center point location and the radii of control points. Therefore, the center position and radii of all control points are selected as the design variables in MMV-based topology optimization. Assuming $N_v$ voids are employed in the design domain, the design variables involved in the MMV-based topology optimization framework can be written as ${\mathrm{var}} = ({\mathrm{var}}_1, {\mathrm{var}}_2, ..., {\mathrm{var}}_j, ..., {\mathrm{var}}_{N_v})$, where ${\mathrm{var}}_j = (x_{c,j}, y_{c,j}, r_{1,j}, r_{2,j}, ..., r_{i,j}, ..., r_{N_{\mathrm{div}},j})^\text {T}$ are control variables for the jth void, leading to $(N_{\mathrm{div}}+2) \times N_v$ design variables in total.

Fig. 3

A circular void enclosed by a closed curve with $N_{\mathrm{div}}$ angular divisions ($\varphi = \frac{2 \pi }{N_{\mathrm{div}}}, N_{\mathrm{div}} = 12$ for this figure) constructed using B-spline basis functions with 14 control points $P_0, P_1, ..., P_{13}$. By changing the center point ($x_c, y_c$) and radius of each control point ($r_1, r_2, ..., r_i, ...$), the void can be moved and deformed simultaneously

When multiple MMVs move and deform simultaneously during the optimization process, merging may occur between two or more voids. If merging of MMVs is detected, the control points located in the overlapping region are labeled as inactive ones for each individual MMV. Accordingly, derivatives of the radius variables corresponding to the inactive control points are enforced to zero. Moreover, as a specific case, splitting of an individual MMV is allowed for the symmetric topology optimization problem in this paper. The initial, intermediate, and final optimized structures are symmetric as a default setting. The MMVs initialized in the centerline of the design domain may move away from the centerline, resulting in a duplicate MMV in a mirroring manner. The same group of radius variables is assigned to the duplicate MMVs correspondingly. This explains the specific numerical implementation of the MMV splitting in this work. Since the MMVs are accurately described with B-spline basis functions, we always have explicit and smooth boundary curves for the channels in the optimized structure.

4.2 Objective function of topology optimization

Maximizing HXP of the cross-flow HXs is the major objective of our topology optimization framework. The HXP is determined by the heat energy exchanged between the cold and hot fluids based on the following equation:

$$\begin{aligned} \text{ HXP } = \int _{\varOmega _f} \rho c_p {\varvec{u}} \cdot \nabla T \, \text {d} \varOmega , \end{aligned}$$

(8)

where $\varOmega _f$ denotes the entire fluid domain (see Fig. 1). Standard units are adopted according to the International System of Units (SI) for all the involved terms in the equations. We use kg/m³ for $\rho$, J/(m K) for $c_p$, m/s for ${\varvec{u}}$, K for T and meter for dx. Finally, the units of HXP and PD are Watt (W) and Pa, respectively. For Re and Pe in Eq. (3), kg/(m s) is used for $\nu$ and W/(m K) is used for $k_f$.

Meanwhile, the minimization of PD is considered concurrently. The PD between the fluid inlet and outlet of a cross-flow HX is calculated by

$$\begin{aligned} \begin{aligned} g(\varOmega _f) = \frac{\int _{\partial \varOmega _{f{\_{\mathrm{in}}}}} p \, \text {d} S}{\int _{\partial \varOmega _{f{\_{\mathrm{in}}}}} \text {d} S} - \frac{\int _{\partial \varOmega _{f{\_{\mathrm{out}}}}} p \, \text {d} S}{\int _{\partial \varOmega _{f{\_{\mathrm{out}}}}} \text {d} S}, \end{aligned} \end{aligned}$$

(9)

where $\partial \varOmega _{f{\_{\mathrm{in}}}}$ and $\partial \varOmega _{f{\_{\mathrm{out}}}}$ denote the cold fluid inlet and outlet boundary, respectively (see Fig. 1). Equation (9) applies to general scenarios where the fluid inlet and the outlet may have different areas. Note that fluid pressure field is solved in an atmospheric environment.

We consider PD as a constraint on the maximization of HXP. Normally, a minimization form of the objective function is adopted. Since the fluid density $\rho$ and thermal capacity coefficient $c_p$ are assigned unit values, the mathematical model of the topology optimization framework is simplified as

$$\begin{aligned} \begin{aligned} \text{ min }&f(\varOmega _f) = -\text {HXP} = -\int _{\varOmega _f} {\varvec{u}} \cdot \nabla T \, \text {d} \varOmega , \\&\text {s.t.} \quad \text {PD} \le {\overline{PD}} \\&\quad {\mathrm{var}} \subset D ({\mathrm{var}}), \end{aligned} \end{aligned}$$

(10)

where $\varOmega _f$ denotes the entire design domain containing the cold fluid and hot regions represented by the MMVs, and $D({\mathrm{var}})$ is the admissible design space for the design variables. ${\overline{{\mathrm{PD}}}}$ is the upper limit of PD. The value of ${\overline{{\mathrm{PD}}}}$ can be determined empirically according to practical requirement for the cross-flow HXs.

In the optimized designs, complex channel shapes are present. After normal extrusion, the obtained thin-walled tubes or solid fins are difficult to fabricate by conventional machining and tooling methods as mentioned in the introduction. Moreover, material would be wasted in producing the thin walls. Additive manufacturing is able to overcome these difficulties. Given a specific additive manufacturing technique such as LPBF, DED or material extrusion, and assuming a constant wall thickness of the hot fluid channels, the material consumption is mainly determined by the perimeter of the cross sections of thin-walled channels in the cross-flow HXs. Therefore, the boundary perimeter constraint is employed to control the material consumption for the optimized structures in some of our numerical examples. A general form of the boundary perimeter constraint can be written as follows:

$$\begin{aligned} \begin{aligned} L_{\mathrm{hot}} \le L_u, \end{aligned} \end{aligned}$$

(11)

where $L_{\mathrm{hot}}$ is the boundary perimeter of the hot-channel regions enclosed by the MMVs in the design domain, and $L_u$ denotes the upper bound of the boundary perimeter.

4.3 Optimization engine: MMA

MMA [65, 66] is a well-known gradient-based search method with wide applications to nonlinear optimization problems. The fundamental idea of MMA is to use a series of strictly convex sub-problems to approximate the original problem. The “moving asymptotes” are employed to control the generation of these convex sub-problems. The numerical implementation generates and solves the sub-problems iteratively. This iterative process stops when certain stopping criteria such as a small tolerance are satisfied. An optimized solution to the original optimization problem is obtained after stopping.

MMA has several unique advantages. First, the special feature of “moving asymptotes” can improve stability and accelerate the convergence speed of general optimization process. Second, MMA has proved to be effective for highly nonlinear and non-convex optimization problems. Therefore, in addition to general optimization problems, it is also popular in the field of structural and topological optimization. A crucial input to MMA implementation is the system gradient information. Therefore, sensitivity analysis of the objective functions and constraint equations is required with respect to the design variables. Usually, this procedure is very time consuming when a large number of design variables are involved as in the density-based topology optimization methods. In this paper, one major challenge is that the design variables for MMVs are not explicitly incorporated in the objective functions and the multiphysics governing equations; thus, an explicit form for the sensitivity analysis is not available. To resolve this issue, we employ the direct finite difference method to solve for the gradient information, taking into account the small number of design variables using MMVs and the efficient IGA solver. To determine the step size used in the forward difference method, we take the mesh size as reference and test three different values. A proper step size is selected to balance the derivative accuracy and the computational efficiency. The detailed testing examples are given in Sect. 5.2. Nonetheless, as the number of design variables increases, there may come a point at which the direct finite difference method for sensitivity analysis may be too expensive (computationally).

The detailed procedures of our topology optimization framework incorporating IGA as the multiphysics solver, MMVs as the design variables and MMA as the optimization tool, are summarized in Algorithm 1. In this paper, both the maximum iteration number and a small tolerance between two consecutive iterations are adopted as the stopping criteria of optimization. In this way, the computational cost can be effectively controlled within an acceptable range.

Remark

The proposed method is different from the density-based and level-set-based methods for topology optimization. For the density-based topology optimization, it is common to encounter elements with intermediate densities, resulting in blurring of the boundary interface between solid and fluid phases. Moreover, the resulting boundary interface lacks an accurate description which introduces difficulties when converting the optimized design into a CAD file. For the level-set-based topology optimization, since the boundary interface between different material phases is always accurate, the intermediate element issue can be avoided if a boundary conforming scheme is employed such as the body-fitted method. However, the boundary interface is implicitly represented by the level-set function. The proposed method overcomes the above two issues using MMVs to explicitly represent the boundary interface between the cold and hot regions. As a result, it is straightforward to convert the optimized designs into CAD files for practical manufacturing use. Nonetheless, due to using the non-body-fitted mesh, boundary conditions are not applied to the boundary curves accurately, causing a numerical issue similar to the intermediate densities. This comparison highlights the features of the proposed topology optimization framework.

5 Numerical studies of topology optimization

In this section, a validation study on MMV-based representation using non-body-fitted mesh is presented first with a comparison to literature results. Then, the topology optimization results are presented to investigate the influence of angular division, initial design, and inlet velocity. The parameters involved in this section are given in Table 1. Given symmetric design domain, mesh, and velocity and temperature BCs, the topology optimization problem is inherently symmetric in this paper. The optimized structure should be symmetric after the optimization process. However, since the MMA solves the original optimization problem through generating a series of approximate sub-problems, the symmetry of the optimized structure cannot be guaranteed. Therefore, geometrical symmetry is considered as a default setting for the design domain in our optimization process. As a result, the number of design variables in terms of the MMVs is reduced by half. Whereas for the cell-based design in Sect. 6.3, the symmetry constraint is removed and the whole design domain needs to be involved. To maintain consistency, the entire domain is employed throughout the paper.

Table 1 Parameters for solving the fluid velocity, pressure and temperature fields

5.1 Verification study on MMV-based representation using non-body-fitted mesh

In this section, we verify our IGA solver by comparing our results in the non-body-fitted mesh with the FEM results in the body-fitted mesh of the same MMV-represented geometry. We adopt a quadrilateral control mesh to represent the 2D domain for the cross-flow HXs. Since the MMV method can generate highly curved voids containing the hot fluid, it is time-consuming to dynamically remesh the remaining cold fluid domain with a high-quality body-fitted mesh whenever the domain is updated. Therefore, a non-body-fitted control mesh is employed and the entire rectangle design domain is represented by a structured grid. Regarding the control points within the hot fluid regions, zero velocity and the identical high temperature are imposed for solving the N–S equations and heat C–D equation, respectively. One advantage of this approach is that no dynamic remeshing is needed for the design domain. Moreover, the same non-body-fitted control mesh can be used no matter how the fluid–fluid interfaces evolve based on the MMVs during the iterative topology optimization process.

An example from [28] is considered in this verification study. Since the detailed design information was not provided in [28], image analysis is employed to obtain the channel configuration. An in-house Matlab code is used to extract the boundary features of the design image including the curly shape of the optimized channels. Then, the 2D model is reconstructed based on the extracted features. To compare with the result in [28], the same 2D design domain is used with the size of $0.85 \times 1.0$ (length $\times$ width). The initial design containing five circular voids is represented by a uniform control mesh with $210 \times 248$ quad elements. There are $211 \times 249$ control points, resulting in 157,617 and 52,539 degrees of freedom for solving the N–S and C–D equations, respectively. The Re, Pe, fluid inlet velocity, and temperature for the cold fluid inlet and hot fluid region are shown in Table 1. The number of angular divisions for a single MMV is set to 72 to capture the geometrical details like the sharp and curly corners as observed in the literature results. In other words, 72 radius variables and then 2 variables for the central point coordinates are used to describe a single void, resulting in a total of 370 variables for 5 voids. This setup is only used for reconstructing the design in [28]. In the optimization examples later, we adopt fewer angular divisions for each void to improve computational efficiency. By tuning the center positions and radii of the control points, a proper set of variables are determined for the MMVs to reconstruct the hot fluid regions as in the literature.

Figure 4a shows our reconstructed structure based on the MMVs and the non-body-fitted mesh with red and blue colors representing hot regions and cold fluid, respectively. In our implementation, the BCs for fluid velocity and temperature fields are applied on control points. The control points of the design domain are classified into four categories based on their locations: (1) on the fluid inlet; (2) on the non-slip walls; (3) within hot fluid regions; and (4) the remaining ones. In particular, for the third category, the closed curves of hot regions are constructed using B-spline basis functions and refined by knot insertion. As a result, the closed curves are divided into 200 segments and approximated by polygons. Then, the built-in function named “inpolygon” in Matlab is employed to determine whether a control point is contained in the voids or not. For the control points in the first category, the parabolic velocity distribution and a fixed cold fluid temperature are applied as the BCs. For the control points in the second category, zero velocity and no specific temperature setting are applied as the BCs. For the control points in the third category, zero velocity and a fixed high temperature are enforced as their BCs. No BC is enforced for the fourth category. Specifically, for comparison to [28], material properties such as the thermal conductivity coefficient are set to very small values ($1.0 \times 10^{-6}$) to eliminate the contribution from the elements inside the voids.

The fluid velocity and temperature fields are shown in Fig. 4b, c. The computed HXP and PD are 459 and 2785, respectively. In addition, the geometry is further solved by FEM using a body-fitted mesh, as shown in Fig. 4d. There are 5711 triangular elements and 3722 nodes in the body-fitted mesh, and the minimal element size is the same as used in the non-body-fitted mesh. The obtained velocity and temperature profiles are shown in Fig. 4e and f with 467 and 2933 as the HXP and the PD, respectively. To compare results in these two different meshes, the results from the non-body-fitted mesh are mapped to the body-fitted mesh through interpolation. The FEM results are taken as the reference to calculate the differences. The differences are normalized to percentage errors by the range of the results (102 for the velocity and 90 for the temperature). The nodal relative error for the velocity and temperature fields are shown in Fig. 4g and h, respectively. The maximum error is 6.6% and 7.7% for the velocity and temperature fields, respectively. Moreover, the average difference over the entire domain is within 5% for both fields, which is more relevant to the following topology optimization study, because the HXP is computed using area integration based on the velocity and temperature fields. In addition, both the HXP and the PD using the non-body-fitted and body-fitted meshes are close to the results (476 for the HXP and 2847 for the PD) in [28]. Based on our observation, the MMVs are able to generate the structure with similar concavity and protruding corners in the hot fluid channels. These protruding corners make the fluid velocity change drastically, which helps the heat exchange in these local regions.

Fig. 4

a–c The non-body-fitted control mesh and the obtained fluid velocity and temperature fields using our B-spline based IGA and MMVs. Red color in a represents the channels. d–f The body-fitted mesh with the obtained fluid velocity and temperature fields using FEM. g, h The difference profiles for the velocity and temperature fields (color figure online)

Nonetheless, some differences are observed between the velocity and temperature solutions using the non-body-fitted and body-fitted meshes. The velocity and temperature fields obtained using the non-body-fitted mesh do not have the flow separation features at the sharp corners compared to the conformal mesh case, and obvious differences are found in the corresponding locations from the error plots. The major reason for this issue is that the no-flow BCs for the MMV-represented regions are strongly imposed on the non-body-fitted mesh by assigning zero velocity and hot fluid temperature to the control points inside the voids. Compared to the body-fitted mesh used in FEM, the boundary geometry cannot be accurately described and we can only approximately impose the boundary condition. Therefore, layer effects are not accurately captured for the sharp and thin corners, which affects the velocity and temperature fields in these regions. In fact, the non-conforming boundary condition imposition causes the numerical issue similar to the intermediate density elements in the density-based topology optimization. This is a limitation for the current non-body-fitted mesh-based framework. The immersed boundary method is a promising solution to this issue, and it will be incorporated into our framework in the future. When compared to [28], the geometrical differences are observed between the channels of these two structures, resulting in some differences between the velocity and temperature profiles, especially for regions nearby the sharp tips. It is challenging to employ MMVs to obtain exactly the same solution as in [28]. In particular, due to the sequential angular division-based construction format of MMVs, as shown in Fig. 3, it is hard to represent the enclosed voids with complex concave shapes and sharp corners using a small number of divisions. It is also challenging to represent the concave and sharp corners, since the rays connecting control points and the center may intersect with each other. Though this issue can be ameliorated by increasing the number of control points for an MMV, the computational cost will increase significantly due to the increase of design variables. Relaxing coordinates of all control points as design variables could be another promising solution to this issue. Overall, the current framework is limited to design the structure including sharp and thin features due to the use of MMVs and the non-body-fitted mesh. From the view of practical AM process, the sharp and thin corners in the component are usually ignored and removed. Therefore, the proposed framework is capable of supporting the manufacturability-oriented topology optimization in the following sections.

In summary, we have verified the effectiveness of the proposed module employing MMVs, non-body-fitted mesh, and IGA despite the aforementioned limitation. This solution module will be utilized to compute the objective function with constraints as well as their derivatives in the optimization process. In comparison to [28], a unique feature of our topology optimization framework is that the boundary curves are accurately and explicitly represented by B-splines. They can be easily extracted and converted into a 3D cross-flow HX model for practical additive manufacturing. The 3D extruded structures based on the 2D configuration in Fig. 4b are shown in Fig. 5. Both solid fins and thin-walled channels can be formed based on extrusion.

Fig. 5

3D reconstructed models of the cross-flow HX containing a the solid fins and b the thin-walled channels

5.2 Topology optimization results for HXs

In this subsection, several numerical examples are shown to demonstrate the effectiveness of the developed topology optimization framework for cross-flow HXs. We take the same $0.85 \times 1.0$ rectangle as the design domain. The problem settings keep the same to Sect. 5.1 including BCs, Re, and Pe values. Regarding the lower and upper bounds of the design variables, all the radii are limited to [0.03, 0.425]. This lower bound (0.03) is determined according to the geometrical limitation for vertical voids given a specific 3D printer like EOS M290. The center point movement range is limited to $[-0.425, 0.425]$. To determine a reasonable maximum iteration number as one stopping criterion for MMA, a series of numerical experiments are conducted. It is found that the iteration history curve generally becomes stable after at least 40 iterations, and therefore, the maximal iteration number is set to 60 for MMA. Meanwhile, we use another stopping criterion to detect whether the maximum change of the design variables is smaller than a tolerance (e.g., 0.001). These settings are used in the remaining numerical examples. All the examples were run on the Pittsburgh Supercomputing Center (PSC) Bridges-2 system [76] using 128 cores on one computing node.

Angular division Three different angular division numbers (16, 24, and 36) are adopted to study their influence on the topology optimization results. Correspondingly, there are 90, 130, and 190 design variables involved, respectively. An initial design containing 5 distributed circular voids is adopted. The initial radii of all the control points are 0.05. The fluid velocity and temperature fields are listed in the first row of Table 2. The HXP and PD are 210 and 681, respectively. The boundary truncation gap for the MMVs is set to 0.05. A low-pressure drop constraint (2800) is adopted specifically. It takes the PD value of 2847 in [28] as the reference for our first test.

For the MMA-driven topology optimization process, a sensitivity study is needed. Herein, we computed the derivatives of the design variables with the forward difference method and the step size is determined based on the mesh size of 0.004. In particular, we compared the derivative computation of the same design variable with three different step sizes: 0.01, 0.008, and 0.006 (i.e., 2.5, 2.0, and 1.5 times of the mesh size). All these three step sizes yield stable derivatives with small difference (within 5%). Considering computational efficiency with the fewest iterations, we selected 0.01 (2.5 times of the mesh size) as the step size in our study. The computational cost depends on the number of design variables in each numerical example. For instance, for the 5-MMV case using 16 angular divisions, there are 90 design variables involved. The finite difference computation needs to run 90 times in each optimization iteration. Using the IGA solver, each computation takes nearly 1.0 s. In other words, the computational cost of the finite difference computation is nearly 90 s for one optimization iteration in this case.

The corresponding optimized structures, HXP, and PD values are shown in Table 2. Compared with the initial design, the optimized HXP values show large improvement, while the optimized PD values increase. To verify the optimization result, the optimized structure for the 16-division case is further solved by FEM using a body-fitted mesh. The computed HXP and PD values are 632 and 2870, respectively, which are similar to 654 and 2789 in the first column of Table  2. Regarding the optimization process for maximizing the HXP, a general finding is that the PD can be actively controlled to meet the constraint. However, compared with the initial design, the PD value may increase as the trade-off of improving the HXP. This feature was also reported in [28]. Moreover, according to Table 2, the MMVs tend to evolve into larger and curved channels to increase the channel surface area when only a small number of MMVs are employed as shown in this example. The shape of the optimized voids resembles some results in [27] where a similar shape parameterization approach was employed. In addition, when more angular divisions are used, better HXP results can be obtained for some local features like the spike-like protrusions appear in the shape of MMVs to enhance local heat exchange efficiency. As a comparison test, we enforce the same PD value to the initial design and compare the HXP with the optimized structure. In particular, the pressure on the inlet and the outlet are set to 2800 and 0, respectively. In this case, the computed HXP value is 332 which is much smaller compared with the HXP value 692 of the optimized structure. This comparison verifies that structural design optimization can help improve the HXP significantly.

Table 2 Topology optimization results with varying number of angular divisions for single MMV

Figure 6 shows the evolving intermediate configurations of the design domain using 16 angular divisions. In the first several iterations, significant change occurs in the shape of the central void compared to the remaining four voids; see Fig. 6a and b. It indicates that HXP improvement is more sensitive to the shape of central void. In the meantime, relative position of the remaining voids changes obviously, resulting in narrow paths and large fluid velocities in some local regions. With the increase of iterations, all the voids deform significantly and evolve into highly curved channels, providing larger contact area and thus improving local heat exchanging between the cold and hot fluids. Specifically, the central void moves gradually from the center position to the right boundary of the design domain. After nearly 40 iterations, the optimized structure becomes stable with only minor and local adjustments occurring in the MMVs. The corresponding HXP and PD values are also listed in the figure. It is observed that the HXP value increases monotonously, and the PD value is well constrained below the upper limit (2800) with oscillating changes during iterations. This observation can verify that the optimizer works correctly, and the PD constraint is enforced effectively in the iterative optimization process.

Fig. 6

MMV-based intermediate topological designs with the fluid velocity profiles, and corresponding HXP and PD values in the evolution history of the MMA-driven topology optimization for the case using 16 angular divisions. Note that the initial design containing 5 circular voids is considered as iteration 0

The convergence history curves of the HXP and PD values are shown in Fig. 7. As the objective function, the HXP value increases with slight oscillation during the entire iterative topology optimization process. One possible reason is that the complex multiphysics topology optimization problem is non-convex and highly nonlinear in nature. For the gradient-based optimization method, it is likely to encounter some issues in stability and show oscillation in the convergence curves. Approximate gradients from the finite difference method also contribute to the oscillation. Nonetheless, in all three cases, the overall trend of the HXP is increasing and the constraint for PD is well satisfied. In summary, this example indicates that the proposed IGA-MMV-MMA topology optimization framework can effectively handle the simultaneous maximization of HXP and control of PD for 2D cross-flow HXs. Regarding the efficiency, the computational time is nearly 12, 18, and 24 h for the cases using 16, 24, and 36 angular divisions, respectively.

Fig. 7

Convergence history curves of the HXP (solid line) and PD (dash line) values in the gradient-based topology optimization process. Iteration 0 indicates the values corresponding to the initial design. The horizontal dash line denotes the upper limit (2800) for the PD as the constraint

Initial design In addition to the 5-void case, four different initial designs containing various numbers of circular voids are employed. The number of angular divisions is set to 16 to reduce the total number of design variables and computational cost. The PD upper limit for this optimization is 5600, which doubles the upper limit from Table 2. The same constraint is adopted for all four cases. The initial designs and the corresponding optimized structures are shown in Table 3. We observe that the optimized structures are highly dependent on the initial designs. Generally, the MMVs tend to keep separate from each other, while they deform the shape, leading to structural shape optimization. Similar finding is also revealed in [28]. It seems that the scattered channels are more helpful from the point view of maximizing HXP for the cross-flow HXs. The possible reason is that these scattered channels can better heat up the surrounding cold fluid through heat conduction and convection. Meanwhile, the PD can be reduced due to small cross section and smooth shape of the channels.

Table 3 Topology optimization results using different initial designs

Nonetheless, merging of two MMVs is observed in local regions in the 25-void case, as shown in Fig. 8a. It is found that merging two MMVs is helpful in reducing PD, but may decrease the HXP of the design domain. The splitting of an individual MMV is observed in the 12-void case as seen in Fig. 8b, leading to more voids in the optimized structure, and thus, the largest HXP improvement (232%) is observed in this case. When checking the evolution history, we find that the MMV splitting occurs very early (after iteration 5) before significant deformation of the void shape is observed. It suggests that the HXP improvement is more sensitive to the location of the MMVs in the 12-void case. Note splitting can only occur for those MMVs initialized on the centerline. Due to the default symmetric setting, when an individual MMV moves entirely away from the centerline, a complete MMV is generated symmetrically in the opposite half design domain, resulting in the observation of MMV splitting as shown in the 12-void case. In addition, we observe that some MMVs move across the boundary of the design domain, and finally disappear in the 30-void case. This results in only 26 channels remained in the optimized configuration. The reduction in the number of MMVs helps decrease pressure of the design domain, and guarantee the optimized structure to satisfy our PD constraint.

Fig. 8

Observation of the a MMV merging in the 25-void case and b MMV splitting in the 12-void case. The regions filled with black color represent hot channels with fixed high temperature in the cross-flow HX

Inlet velocity We vary the fluid inlet velocity to study its effect on topology optimization results. The variation in the inlet velocity results in variations in the Re and Pe values. For heat transfer problems, the Pe value denotes the ratio between the energy exchanged by heat convection and conduction. The configuration containing 25 circular voids is taken as the initial design. A tight PD constraint is employed and the upper limit for PD is set to $1.25\times \text {PD}_0$ where $\text {PD}_0$ is the initial PD value. This upper limit is chosen as an example to set a tight constraint. Using such a setting helps us observe MMV merging in the optimized structure. The initial design is taken as the reference to calculate $\text {PD}_0$ for each of the four cases.

Table 4 shows the velocity, temperature profiles, and the HXP and PD values for the initial and optimized structures with different inlet velocities. Before discussing the observation, we also perform a cross-check analysis by evaluating the performance of each optimized structure under different inlet velocities. The PD values of the 4 designs are also checked to ensure the constraint is satisfied in each design condition. As shown in Table 5, each optimized design performs the best under its corresponding design condition.

By observing temperature profiles in different initial designs in Table 4, we find that the tail-like field behind each circular channel shows a wider influential area with higher temperature when the fluid inlet velocity is small. The reason is that the Pe value is small and heat conduction dominates the heat exchange process in the slow-moving fluid. In the optimized structures, we observe that most of the MMVs stay separate from each other, as noted in the previous subsection. Meanwhile, some MMVs deform with stronger curvature which increases the hot-channel surface area. In addition, in the first and second cases, we observe the merging of two MMVs in the optimized structure. As a result of the moving, deforming, and merging of these MMVs, the cold fluid domain contains many branching channels between the voids. The complex configuration forms smooth tail-like flow streamlines as observed in the temperature fields. Through tracking evolution of the middle three voids, MMV splitting is observed in the third case of Table 4, leading to an increase of the total number of voids in the final design. More scattered channels (26) are generated in the optimized structure compared with the remaining three cases. As a result, the HXP improvement from the initial design is up to 32%, which is slightly higher than the remaining three cases.

Table 4 Topology optimization results with different fluid inlet velocities

Table 5 Cross-check analysis for HXP of the optimized structures with different fluid inlet velocities

6 Manufacturability improvement

In this section, we take into account the manufacturability of HX and study its influence on the optimized HX design from topology optimization. First, variable filtering is presented to eliminate spike features in the MMV-described channels. Then, boundary perimeter constraint is considered to control the material consumption with respect to a practical additive manufacturing process. Following that, cell-based topology optimization results are presented to consider thin-walled channels as support structures. Some discussions are given in the end.

6.1 Variable filtering

Variable filtering is employed to adjust the boundary curve shape of the MMVs. The reason for using this technique is that some features like thin and sharp spikes are observed in the optimized structures (see Table 2). Given the melting used in LPBF and DED manufacturing, these thin and sharp protrusions may cause large thermal distortion in the bottom-up layer-wise deposition process. Moreover, the distorted build (through local uplift) may collide with the recoater that spreads metal powders back and forth, which may further result in failure of the build. Therefore, the spike-like features should be avoided in the optimized structures. Filtering is a specific technique used to avoid unwanted features in topology optimization. For example, density filtering is widely employed to eliminate the checkerboard problem in the conventional element-based topology optimization as in, e.g., the SIMP method. In this paper, filtering is specifically applied to the radius variables for each individual MMV. Each radius variable is filtered with respect to its neighboring radius variables to eliminate sharp spikes. A general form of variable filtering for the ith MMV control point is shown as follows:

$$\begin{aligned} \begin{aligned} {\hat{r}}_i = \sum _{j=1}^{{\hat{n}}_i} \alpha _j \, r_j, \end{aligned} \end{aligned}$$

(12)

where $i=1,2,...,N_{\mathrm{div}}$, ${\hat{r}}_i$ denotes the radius variable after filtering. $\alpha _j \in [0,1]$ denotes the filtering coefficient and $\sum _{j=1}^{{\hat{n}}_i} \alpha _j = 1$. ${\hat{n}}_i$ is the number of the radius variables located in a specific neighborhood of the ith MMV control point. In this section, a specific filtering manner is adopted and each radius variable $r_i$ is averaged with its adjacent two radius variables. We have

$$\begin{aligned} \begin{aligned} {\hat{r}}_i = \frac{r_{i-1}+4r_i+r_{i+1}}{6}, \end{aligned} \end{aligned}$$

(13)

where $i=1,2,...,N_{\mathrm{div}}$, and $r_{i+1} = r_1$ when $i=N_{\mathrm{div}}$.

Table 6 shows the optimized results using the 5-void configuration as the initial design together with the variable filtering technique. Compared with the optimization results without filtering (see Table 2), the spike-like features are effectively removed, leading to optimized configurations that are more friendly to the additive manufacturing process. However, the optimized HXP values decrease in all these three cases. The decrease in the optimized HXP values is expected, since the spike-like protrusions (see Table 2) effectively enhance local heat exchange, but are flattened by the variable filtering. The final PD values all satisfy the prescribed constraint despite the imposition of variable filtering. In addition, the filtering effect weakens as the number of angular divisions is increased. The sharp spikes may return when the number of divisions increases. Therefore, if more convex shaped channels are preferred for the 36-division case, the variable filtering operation can be extended to a larger neighborhood containing five or more radii of control points. Fortunately, the additional computational time for implementing variable filtering is negligible compared with the filtering-free cases.

Table 6 Topology optimization results using variable filtering for radii of the MMV control points

6.2 Boundary perimeter constraint

This constraint can provide active control of material usage amount if an optimized structure for the cross-flow HX is fabricated into thin-walled channels by additive manufacturing process in practice. Specifically, the perimeter of the MMV-represented regions is constrained below an upper bound which should be determined according to the practical manufacturing requirement. The perimeter of the rectangle design domain (3.70) is considered as a reference value. Two different initial designs containing 5 and 12 voids, respectively, are employed in this example. For the 5-void case, the upper bound of boundary perimeter is set to 3.70. For the 12-void case, the boundary perimeter limit is set to 5.55, which is 1.5 time of the perimeter of the rectangle design domain. The upper bounds of PD for the two cases keep the same as in Sect. 5. Meanwhile, the effect of variable filtering is studied by comparing with the result without variable filtering.

Table 7 shows the optimized structure, maximized HXP, final boundary perimeter, and final PD for each case. We observe that the optimized HXP becomes better when the upper bound of the boundary perimeter increases. This phenomenon is expected, since larger perimeter of the deformed MMVs leads to larger contact area between the cold and hot fluids, which will improve the heat exchange efficiency. With the boundary perimeter constraint enforced, very curly channel shapes are avoided in the optimized structure for the 5-void case compared with Table 2. Moreover, for the 12-void case, though splitting is still observed for some MMVs in the middle region, there are only 11 voids in the optimized structure compared with the result containing 15 voids in Table 3. Some of the MMVs disappear to ensure the optimized structure satisfy the boundary perimeter constraint. Due to variable filtering, boundary curves of the MMVs in the optimized structures become further flattened as mentioned in Sect. 6.1. As a result, there is a slight decrease in the optimized HXP values compared to the results without filtering. In addition, by adjusting the settings such as initial designs, it is likely to find other solutions to the topology optimization problem using the same design domain. Given different solutions, by considering their HXP and material consumption in the additive manufacturing process, it is feasible to select a compromise design for practical applications.

Table 7 Topology optimization results with different boundary perimeter constraints

To show the stability of our IGA–MMV–MMA topology optimization framework considering two constraint functions (PD and boundary perimeter), the convergence history curves are shown in Fig. 9 for the 5-void case with and without variable filtering as the example. We observe some oscillations in the HXP, PD, and boundary perimeter curves. The reason for such oscillation is related to high non-linearity of our multiphysics topology optimization problem. Using the approximate gradients from the forward difference method also contributes to the oscillation. Moreover, the boundary perimeter is satisfied strictly in the optimization process. It is observed that the PD value may slightly violate its upper bound in some iteration steps, indicating that the PD is sensitive to the influence of other constraints like the boundary perimeter constraint. Despite the slight oscillations in the convergence history curves and slight violation for the PD constraint, the proposed topology optimization framework shows good stability in this example.

Fig. 9

Evolution history curves of HXP, PD, and boundary perimeter values for the 5-void case a without and b with variable filtering in the MMA-driven iterative optimization process; the data point at iteration 0 denotes the values corresponding to the initial design

6.3 Cell-based optimization

When the optimized configurations are converted into CAD files for cross-flow HXs, bottom and top caps (headers) are added to encapsulate the thin-walled channels containing hot fluid. In the aforementioned examples, the distance between two channels in the optimized structure can be very large. Consequently, when the HX is printed in an arrangement where the thin-walled channels are vertical, significant overhang features will occur for the plate-like top cap. Therefore, the cross-flow HX cannot be fabricated successfully by a powder-based additive manufacturing process like LPBF and DED. Therefore, we propose to use the cell-based optimization as a promising solution to address this printability problem in this subsection. The basic idea is to divide the entire design domain into cells with the same size, and perform optimization based on the cell domain. The optimized configuration of the cell is distributed over the entire design domain, forming the optimized structure of the cross-flow HX. In this way, the distance between two channels can be controlled in the optimized structure. When fabricated by a powder-based additive manufacturing process, the cell-based channels themselves can be treated as vertical support structures for the top cap. Another benefit is that the number of design variables is reduced, and the computational cost is greatly reduced for the cell-based optimization. As a clarification, it would be possible to optimize each cell independently while restricting the voids to be present in each cell. In that way, the number of design variables would increase and the computational cost would increase dramatically. In this paper, we focus on demonstrating the concept of cell-based design to address potential overhang issues in practical additive manufacturing.

Table 8 Cell-based topology optimization results using different initial designs

Table 8 shows the cell-based optimization results using two different initial topological designs containing 24 and 28 voids, respectively. Either geometrically mirrored or periodic cell distribution is considered for the final optimized structure as a comparison. For the mirrored distribution, with reference to the horizontal center line, the cells in the lower half are mirrored to the upper half domain. For the periodic cell distribution, the same shape is repeated for all the cells in the design domain. This is the difference between these two distribution patterns. The variable filtering technique and boundary perimeter constraint are not involved in this example. It is observed that the cell-based optimization tends to generate the airfoil-like voids. Moreover, the mirrored designs can give better HXP values than the repeated designs, indicating the necessity of taking symmetry as the default setting in the previous examples. In addition, the initial topology of the design domain has a significant influence on the optimization results. According to our observation, it is better to arrange the cells in a staggered manner like the 28-void case, because this arrangement leads to larger HXP values in both the initial and optimized designs than the 24-void case with a uniform distribution. When practical fabrication is considered by additive manufacturing, the voids can be extruded into thin-walled channels and printed layer-by-layer in the vertical direction without difficulty. The vertical channels naturally act as the support structures for printing the top cap of the cross-flow HX. As a benefit, additional support structures are not needed and powder feedstock can be saved. Moreover, it avoids the difficulty in removing additional support structures inserted between channels during postprocessing.

6.4 Discussion

There are many parameters and influential factors in the proposed multiphysics topology optimization framework for cross-flow HXs with respect to the practical additive manufacturing requirement. This discussion is intended to provide some suggestions on how to employ the proposed framework to address the potential industry-related problems. First, using 16 angular divisions is sufficient to give good topology optimization results as demonstrated in this paper. When more angular divisions are employed, further improvement in the final HXP is expected with increasing complexity of the optimized structure. To avoid unwanted features like spike-like protrusions, the variable filtering technique is recommended as a default setting. When choosing initial designs, a staggered arrangement for the initial circular voids is recommended. An initial design containing 10–30 voids is appropriate in relation to the computational cost. For the inlet fluid velocity and upper bound of the PD constraint, their values should be determined according to practical working conditions for the cross-flow HXs. In terms of manufacturability, the boundary perimeter constraint should be applied to minimize feedstock consumption. To determine the boundary perimeter limit, the perimeter of the design domain can be taken as a good reference. In addition, if after an optimized structure is converted into a CAD file for additive manufacturing and an overhang issue is detected for the top cap, we recommend switching to the cell-based optimization mode and using the packed vertical channels as the inherent support structures for successful printing.

7 Conclusions and future work

In this paper, an IGA-based topology optimization framework for the design of 2D cross-flow HXs has been established. The optimization maximizes the HXP while taking into account the PD constraint and some manufacturability issues. The framework is built on an IGA-based multiphysics solver to solve the steady-state incompressible N–S equations and heat C–D equation and obtain the fluid velocity, pressure, and temperature fields in the 2D cross-flow HXs. The MMV method is employed to explicitly describe the shape and topology of the hot fluid regions in the design domain. Each void is enclosed by a closed curve constructed based on B-spline basis functions. Both the center position and shape of the voids can be changed during topology optimization. MMA is selected as the optimization engine in the optimization process. The HXP maximization is considered as the objective function, while the PD control is taken as a constraint. Based on the MMV method, explicit and smooth boundary interfaces of the optimized hot fluid regions are obtained.

Several influential factors of the HX design are studied including angular division, initial design, and fluid inlet velocity. With more angular divisions for an individual MMV, larger HXP values can be obtained, and more local features are obtained such as the curly boundary curves and spike-like protrusions in the optimized structures. We find that the topology optimization results are highly dependent on the initial designs. Both splitting of a single MMV and merging of two MMVs are observed. Moreover, when using the identical 25-void initial design, the optimized structures tend to have larger HXP values with larger fluid inlet velocity. Most of the MMVs are scattered in the design domain, which can enhance both conduction and convection-related heat transfer between the cold and hot fluids. To guarantee good manufacturability of the optimized structures for the additive manufacturing process, both filtering and geometrical constraint have been incorporated in the topology optimization framework. First, variable filtering is employed to eliminate the thin and protruding spikes in the cross section of thin-walled channels. Second, boundary perimeter constraint for hot fluid regions is also considered to control material consumption. We demonstrate that this constraint may help flatten the shape of the deformed MMV, and the optimized HXP value may increase along with the upper bound of the boundary perimeter. It is necessary to find a balance between maximizing the HXP and reducing the practical material usage. Moreover, the cell-based optimization is carried out to provide support structures for top cap with respect to a powder-based additive manufacturing process. We recommend arranging the cells in a staggered layout to generate larger HXP values.

In terms of computational efficiency, most numerical examples take 15–20 h to finish the MMA-driven optimization process within 60 iterations. Nonetheless, there are slight variations in computational time because of varying complexity of the design domain. In addition, when more design variables are involved, the computational cost increases nearly proportionally from using the direct finite difference method. In the future, we plan to extend our framework to the topology optimization of 3D HXs including the cross-flow, parallel-flow, and anti-parallel-flow HXs. An internal flow model will be strictly necessary for the channels in the 3D HXs. Moreover, we will implement the immersed boundary method to improve the computational accuracy and incorporate machine learning method into our framework to enhance the computational efficiency. The source code for our work is available for downloading from https://github.com/CMU-CBML/HXTO. The input files such as the control mesh and BC settings for every numerical example in this paper are also provided in the repository folder.