1 Introduction

With the development of electronic equipment toward the trends of high-degree integration, reduced size, and high performance, the resulting considerable amount of heat flux is greatly increased (Xu 2011; Moore and Shi 2014). However, excessive temperature degrades the performance of electronic devices and even cause failure (Xu 2011). This contradiction has triggered high desires toward research about heat management systems for high heat flux cooling (McGlen et al. 2004; Garimella et al. 2008). As a competitive solution, forced convection cooling systems exhibit high heat dissipation efficiency, low requirement of flow rate, and low noise (Lin et al. 2011; Christen et al. 2017). It has been widely adopted in many industrial fields, such as engines, motors, power plants, and high-performance computers.

Forced convection heat sinks are usually composed of flow channels built from highly conductive materials and moving fluids which transport the heat away from the device (Dilgen et al. 2018). Their heat dissipation performance depends on the amount of conductive material and its distribution, the contact area between the fluid and the channel, the fluid velocity distribution, fluid temperature, and fluid thermal capacity (Dbouk 2017; Dilgen et al. 2018). After basic materials and boundary conditions are determined, the structural topology plays a crucial role in the heat dissipation performance of the designed heat sinks. The main subject of this paper is to optimize the structural topology of forced convection heat sinks for maximizing their heat dissipation performance.

Many efforts have already been investigated by researchers and engineers in designing heat sinks with high cooling efficiency. The classical design approaches are to optimize parameters of channels under predefined layout schemes, including the size optimization and the shape optimization methods (Zhao et al. 2018). Related methods have been well established and widely reported in the literature (Fabbri 2004; Manzan et al. 2008; Ahmed and Ahmed 2015; Tan et al. 2016). Many basic topologies of channels have been studied, such as the fractal tree-like channel nets, parallel channels, and snake-like channels (Wan et al. 2011; Yenigun and Cetkin 2016). The size and shape parameters of these basic topologies are adopted as variables to optimize the heat sink’s performance. Usually considered parameters includes the thickness, width, and length of channels; the distance between channels; and the coordinates of key points in the boundary (Fabbri 2004; Manzan et al. 2008; Jarrett and Kim 2011; Mitropoulou et al. 2013; Ahmed and Ahmed 2015; Tan et al. 2016). However, the initial channel layout setting is crucially important for achieving high-performance devices, and the optimal solution strongly depends on this initial setting (Yaji et al. 2015).

Topology optimization theory is an effective way to overcome the limitations of initial configurations. It is a mathematical theory that optimizes material layout within the design domain under given objectives and constraints (Bendsøe and Sigmund 2003). Due to its high degree of design freedom, it has a large advantage in achieving innovative designs, compared with the size and shape optimization methods (Bendsøe and Sigmund 2003). Since Dede (2009) first introduced this theory into thermal-fluid coupling problems, it has attracted extensive research interest in heat sink design problems. Recently, many novel channels with greatly improved cooling efficiency were designed through topology optimization in various engineering cases including air/water cooled problems (Dede et al. 2015; Qian et al. 2018), natural/forced convection problems (Yoon 2010; Alexandersen et al. 2014), steady/unsteady flow problems (Yaji et al. 2018), and laminar/turbulent flow problems (Yu et al. 2019).

In thermal-fluid coupling problems, three kinds of topology optimization methods were adopted by existing researches: the density method, the level set method, and the moving morphable component (MMC) method. Among these methods, the density method is most widely used because it is easy to be understood and implemented. In density-based related researches, the design variable “porosity” is defined on each element or point in the design domain to represent the material here, which is bounded between 0 and 1. In fluid-solid problems, generally, 1 corresponds to the fluid and 0 corresponds to the solid material. Therefore, the structural topology is characterized by the controlled porosity field. Through the constructed interpolation model between material properties and the porosity value, fluid flow and heat transfer governing equations under specific porosity fields can be solved. And the porosity field is iterated for optimizing the concerned thermal or flow performances.

In the level set method, the level set function is adopted as the design variable. Boundaries of the design are defined by the zero level contours of the level set function and the structure is defined by the domain where the level set function takes positive values (Sigmund and Maute 2013). Compared with the density method, this method obtains structures with a clearer fluid/solid interface and so to avoid grayscales.

The previous two methods describe the structural topology implicitly. In the MMC method, the structural topology is explicitly characterized by predefined MMCs as the primary building blocks. Moving and morphable parameters are adopted as design variables. The advantage of this method is that it obtains proper design freedom with fewer design variables and the feature size can be easily controlled (Guo et al. 2016). Numerical results indicated that different models may lead to different topologies depending upon the type and the number of features (Yu et al. 2019). So, how to design proper components and its quantities based on specific problems needs to be further studied.

In these topology optimization researches, most of them focus on optimizing the topology of the internal flow channel under preset inlet/outlet schemes. Only a few works evaluate the variation of inlet/outlet schemes (Kontoleontos et al. 2013; Marck et al. 2013; Matsumori et al. 2013; Zhao et al. 2018; Scholten 2017). However, as a part of the flow channel, the number, position, and shape of inlets and outlets also have significant effects on the performance of the optimized heat sink. Scholten (2017) evaluated optimized heat sinks under eight combinations of inlet and outlet positions. The maximum difference in the performance of optimized designs reached 38.2%. Similarly, in Zhao’s (2018) work, heat sinks were optimized under two kinds of inlet/outlet position schemes. The maximum difference in the mean temperature (the optimization objective) between the two designs is 377.9%. In Matsumori’s (2013) work, the difference in the design objective between the single outlet scheme and the double outlet scheme is greater than 100%. The basic approach to design inlets and outlets in these researches is to apply optimization algorithms among limited inlet/outlet schemes and select a relative best design scheme among them (Scholten 2017). This exhaustive-based option exhibits extremely expensive computational requirements, and the optimized inlet/outlet scheme is dependent on the selection of initial candidate schemes. Recently, a preliminary related research was presented (Zhao et al. 2019). The topology of straight channel cooling structures was optimized on the structural cross section. In the concerned straight channel, the inlet, outlet, and internal channel share the same topology. Thus, they are optimized in a specific application. And in this work, we intend to solve more general problems.

This paper addresses a concurrent design method of the internal flow channel, inlets, and outlets in design problems of forced convection heat sinks. In this method, the topology of the internal channel and the position/shape parameters of inlets/outlets are defined as design variables. Topologies of the inlet/outlet design domains and the internal design domain are described by MMCs and the porosity field, respectively. Taking design problems of water-cooled heat sinks as examples, a MMC that contains the length, angle, and position variables is constructed to represent inlets and outlets. A corresponding topology description transformation function is constructed to transfer the topology of inlet/outlet design domains into porosity fields for subsequent analysis. Besides, continuous design-dependent governing equations of inlets are established to model design-dependent flow and temperature boundary conditions of inlets. Further, the flow and heat transfer governing equations, materials interpolation model, optimization model, and implementation details are presented. All design variables are concurrently optimized with the sensitivity information. Design problems of minimizing the average temperature of heat sources in water-cooled heat sinks are presented as numerical examples. To validate the applicability of this method, problems with inlet pressure, inlet flow flux, and inlet velocity boundary conditions are considered. Compared with the discrete optimization approach, the concurrent method efficiently achieves competitive solutions.

The reminder of this paper is organized as follows. The problem and proposed method are outlined in Section 2. Section 3 introduces the basic MMC and the corresponding topology description transformation function. Section 4 presents the thermal-fluid governing equations and materials interpolation functions. Optimization problems and implementation details are given in Section 5. Varies numerical examples are presented in Section 6. Finally, discussions and conclusions are given in Section 7 and 8, respectively.

2 Problem setup and method overview

2.1 Problem setup

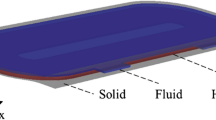
The ketch of the considered heat sink design problem in this work is shown in Fig. 1. This problem comes from the cooling demand of the Lorentz motor in an ultra-precision stage. The whole structure contains four domains: the inlet design domain, the internal channel design domain, the outlet design domain, and the non-design domains (the walls). A coil-like heat source with constant heat flux is defined under the heat sink. Γin indicates the entry boundary of the inlet design domain and is referred to as the extended inlet boundary. Similarly, Γout indicates the exit boundary of the outlet design domain and is referred to as the extended inlet boundary. Γwall − out indicates the extra outer boundary and Γwall − in indicates the internal boundary. The channel’s topology determines the flow field that further influences the effect of convective heat dissipation. So this work intends to optimize the structural topology for better cooling performances.

Fig. 1
figure 1

Schematic figures of the considered heat sink optimization problem

Full size image

In most cases, the topologies of inlets and outlets are often regular shapes (such as cylinders and cubes). Meanwhile, inlets and outlets are defined as components that are relatively narrow along the flow direction. Considering these factors, MMCs are adopted to describe the topology of inlet and outlet design domains. On the other hand, the porosity field is adopted to characterize the topology of the internal channel design domain. So, the design variables of this problem are MMC parameters and the internal porosity field.

2.2 Method overview

Figure 2 illustrates the overview of the proposed concurrent optimization method. Each process and important details are briefly introduced below.

Fig. 2
figure 2

Overview of the proposed concurrent design method

Full size image

2.2.1 Topology description scheme

In the internal design domain, the porosity field γ consists of porosity values γ that are defined on each element (or node). Noted that, γ is a continuous variable defined from 0 (solid) to 1 (fluid). It indicates the volume fraction of fluid. Before solving fluid flow and heat transfer governing equations, the internal porosity field is filtered and projected to avoid numerical instabilities and obtain clear layouts. Noted that, the projected porosity field γp characterizes the internal topology and the original porosity field γ only acts as design variables. The filtering and projections processes are presented in detail in Section 5.

In the inlet and outlet design domains, elements (or nodes) that are inside MMCs are defined as fluids and those that are outside MMCs are defined as solids. MMCs are controlled by their position and shape parameters. And these parameters in the inlet and outlet design domains are indicated by vectors α and β, respectively. Different topologies can be achieved through moving, overlapping, hiding, or even removing of these MMCs. Further, in the thermal-fluid analysis process, MMC-described inlet/outlet domains are transferred to porosity-described domains by the topology description transformation function. Take calculating the inlet porosity field γin as an example, the topology transformation function is shown as follows:

$$ {\gamma}_{in}(x)=\left\{\begin{array}{c}1,\mathrm{if}\ x\in {\mathrm{M}}_{in}\kern2em \\ {}0,\mathrm{if}\ x\in {\Omega}_{in}\backslash {\mathrm{M}}_{in}\end{array}\right. $$
(1)

where x represents the coordinate of elements (or nodes) in the inlet design domain. Μinindicates the domain composed of all inlet MMCs. Ωin indicates the inlet design domain. Similarly, the outlet porosity field γout can also be obtained. The constructed MMC and corresponding issues are presented in detail in Section 3.

2.2.2 Porosity-interpolated thermal-fluid model

To evaluate the concerned performance of the porosity-described heat sink, fluid flow and heat transfer models of this problem are constructed. The material interpolation model is constructed to interpolate the flow and heat transfer properties between fluids and solids with porosity values. With porosity-interpolated properties, the flow and temperature fields can be solved under the current porosity field.

Particularly, inlet flow and temperature boundary conditions should be defined on actual inlet boundaries. While the actual inlet components always change during the optimization process. So, to ensure accurate inlet flow and temperature boundary conditions, design-dependent boundary governing equations are established on the extended inlet boundary Γin.

The constructed model is presented in detail in Section 4.

2.2.3 Optimization issues

A general heat sink’s structure optimization problem is defined as follows:

$$ {\displaystyle \begin{array}{l} find\ \boldsymbol{\upalpha}, \boldsymbol{\beta}, \boldsymbol{\gamma} \\ {}\min\ \mathrm{O}\left(\mathbf{u}\left(\boldsymbol{\upalpha}, \boldsymbol{\beta}, \boldsymbol{\gamma} \right),T\left(\boldsymbol{\upalpha}, \boldsymbol{\beta}, \boldsymbol{\gamma} \right)\right)\\ {}S.t.\kern0.5em {G}_U\left({\boldsymbol{\gamma}}_{in},{\boldsymbol{\gamma}}_{out},\boldsymbol{\gamma}, \mathbf{u}\right)=0\\ {}\kern1.75em {G}_T\left({\boldsymbol{\gamma}}_{in},{\boldsymbol{\gamma}}_{out},\boldsymbol{\gamma}, \mathbf{u},T\right)=0\\ {}\kern1.75em {\mathrm{g}}_i\left(\boldsymbol{\upalpha}, \boldsymbol{\beta}, \boldsymbol{\gamma} \right)\le 0,i=1,\dots, N\end{array}} $$
(2)

where O is the optimization objective; u and T are the solved discrete state variables representing the flow and temperature fields, respectively. GU and GT are governing equations of the flow and heat transfer problems. The set gi represents additional inequality constraints. Commonly used inequality constraints include the flow dissipation constraint, the maximum temperature constraint, the volume fraction constraint, and so on.

To optimize this problem, sensitivity information of the objective and constraint functions to the design variables is computed and applied to iterate all design variables. Noted that, all optimization objectives and constraints should be defined to be continuous and differentiable to all variables. When the convergence criterion is satisfied, the iteration stops and the optimized heat sink is obtained.

Adopting the considered heat sink as an example, Sections 3, 4, and 5 present the proposed method in detail.

3 MMC and topology description transformation function

As is shown in Fig. 3a, a parallelogram MMC is adopted as the primary building block. Each MMC is controlled by three parameters: the position parameter l, the wide parameter w, and the angle parameter θ. The centroid of the MMC is defined as the origin of its local coordinate system. And the angle between the local and global coordinate systems is θ. Different inlet/outlet schemes can be achieved by different parameter combinations of MMCs. Figure 3 b illustrates the movement, deformation, overlap, and hiding of two components.

Fig. 3
figure 3

a The constructed quadrilateral MMC. b Different combinations of two MMCs

Full size image

Topology description function (TDF) is used for describing the geometry of a structural component using explicit parameters (Guo et al. 2014). And the basic rule is to calculate whether the point is inside the concerned MMC or not. To accomplish this, global coordinates of each point are transferred into the local coordinates of the concerned MMC. The transfer process is accomplished by coordinate translation and rotation between global and local Cartesian coordinate systems. It is formulated as follows:

$$ \left\{\begin{array}{c}{x}_j^{\prime}\\ {}{y}_j^{\prime}\end{array}\right\}=\left[\begin{array}{cc}\cos {\theta}_j& \sin {\theta}_j\\ {}-\sin {\theta}_j& \cos {\theta}_j\end{array}\right]\left\{\begin{array}{c}x-{xc}_j\\ {}y-{yc}_j\end{array}\right\} $$
(3)

where \( {\mathbf{x}}_j^{\prime }=\left({x}_j^{\prime },{y}_j^{\prime}\right) \) is the local coordinate of point x = (x, y). (xcj, ycj) is the global coordinate of the centroid of the jth MMC.

Considering that the inlet/outlet domains are parallelogram domains, the local vertical coordinate of the concerned point determines whether this point locates in the MMC or not. For points whose local vertical distance to the centroid of the jth MMC is bigger than w ∗ cos θ/2, this point is outside the concerned MMC. The TDF of the jth MMC is written as follows:

$$ {\chi}_j\left(\mathbf{x}\right)=1-H\left({\left({y}^{\prime }/\left(0.7\ast w\ast \cos \theta \right)\right)}^2\right)=\left\{\begin{array}{c}1,\kern0.5em \mathrm{if}\kern0.5em \mathbf{x}\in {\mathrm{M}}_j\kern0.75em \\ {}0,\kern0.5em \mathrm{if}\kern0.5em \mathbf{x}\in \Omega \backslash {\mathrm{M}}_j\end{array}\right. $$
(4)

where Μj represents the close domain formulated by the jth MMC. H is modified from a smoothed Heaviside function (Wang et al. 2011) to make the TDF continuous and differential. It is formulated as follows:

$$ H(z)=\left\{\begin{array}{c}\frac{\tanh \left({a}_1{b}_1\right)+\tanh \left({a}_1\left(z-{b}_1\right)\right)}{\tanh \left({a}_1{b}_1\right)+\tanh \left({a}_1\left(1-{b}_1\right)\right)}\ 0\le \mathrm{z}\le 1\\ {}\kern3.5em 1\kern5.25em \mathrm{z}>1\end{array}\right. $$
(5)

where a1 is a parameter controlling the projection steepness. b1 is the projection threshold parameter and is set to 25/49 in this work. Then, TDF of each point is used to calculate corresponding porosity values. Ideally, for points whose TDF to at least one MMC is 1, their porosity values equal 1. Taking the inlet porosity field as an example, the topology description transformation function is formulated as follows:

$$ {\boldsymbol{\upgamma}}_{\boldsymbol{in}}\left(\mathbf{x}\right)=1-\prod \limits_j\left(1-{\boldsymbol{\upchi}}_{\boldsymbol{j}}\left(\mathbf{x}\right)\right)=\left\{\begin{array}{l}1,\mathrm{if}\kern0.5em \mathbf{x}\in {\mathrm{M}}_{in}\\ {}0,\mathrm{if}\kern0.5em \mathbf{x}\in {\Omega}_{in}\backslash {\mathrm{M}}_{in}\end{array}\right. $$
(6)

4 Thermal-fluid model

4.1 Fluid flow model

In this paper, a steady-state, incompressible, laminar flow with constant fluid properties is assumed. The continuity equation and Navier-Stokes equation for this problem are given as follows (Dede 2009; Yoon 2010):

$$ {\rho}_f\left(\nabla \cdot \mathbf{u}\right)=0 $$
(7)
$$ \left(\mathbf{u}.\nabla \right)\mathbf{u}=-\frac{1}{\rho_f}\nabla \mathbf{p}+{\nu}_f{\nabla}^2\mathbf{u}-\frac{12{\nu}_f\mathbf{u}}{d^2}+\mathbf{f} $$
(8)

where ρf and νf are the density and viscosity coefficient of the fluid phase, p indicates the pressure field, and \( -\frac{12{\nu}_f\mathbf{u}}{d^2} \) is the shallow channel approximation term. It takes the effect of z-direction boundaries into account by adding a drag term. d represents the thickness of the heat sink. f is the Brinkman friction term. This term is used in flow problems to penalize flow through solid materials within the design domain and corresponds to the force exerted on a fluid flowing through an ideal porous medium (Olesen et al. 2006). It’s defined as:

$$ \mathbf{f}=\hbox{-} {I}_1\left(\gamma \right)\mathbf{u} $$
(9)

where I1(γ) is the inverse permeability term function. Ideally, I1(γ = 1) is set to be an infinitely number to prevent any fluid from flowing across solid areas. By contrast, I1(γ = 0) is set 0 because this term does not exist in the actual fluid flow.

In this paper, three kinds of classical inlet flow boundary conditions are considered. The first one is the inlet pressure boundary condition:

$$ {\mathbf{n}}^T\left(-p\mathbf{I}+{\nu}_f\left(\nabla \mathbf{u}+{\left(\nabla \mathbf{u}\right)}^T\right)\right)\mathbf{n}=-{p}_0\kern1em \mathrm{on}\kern1em {\boldsymbol{\Gamma}}_{\mathrm{in}} $$
(10)

where p0 is the defined inlet pressure. n is the normal vector and I is the identity matrix.

The second boundary condition, the inlet flow flux boundary condition, is defined as:

$$ m=-\int {\rho}_f\left(\mathbf{u}\cdot \mathbf{n}\right)d\mathrm{d}\Gamma \kern1em \mathrm{on}\kern1em {\boldsymbol{\Gamma}}_{\mathrm{in}} $$
(11)

where m is the normal mass flow rate.

The third boundary condition, the inlet velocity condition, is defined as:

$$ {\mathbf{u}}_{in}={\boldsymbol{\upgamma}}_{in}{f}_u\left(\boldsymbol{\upalpha} \right)\kern1em \mathrm{on}\kern1em {\boldsymbol{\Gamma}}_{in} $$
(12)

where fu is the inlet velocity function. It is defined as the function of inlet parameters. γin penalties the velocity of solid boundaries into 0. Thus, the inlet velocity condition is applied on the actual inlet boundary and changes along with corresponding inlet MMCs.

Except the extended inlet and outlet boundaries, other boundaries of the flow field are defined as the non-slip boundary condition:

$$ \mathbf{u}=0\kern1em \mathrm{on}\kern1em {\boldsymbol{\Gamma}}_{\mathrm{wall}\hbox{-} \mathrm{in}} $$
(13)

4.2 Heat transfer model

In the non-design domains composed of solid materials, the 2D thermal diffusion equation is given by (Haertel et al. 2018):

$$ \nabla \cdot \left({k}_s\nabla \mathbf{T}\right)+\frac{\mathbf{Q}}{d}=0 $$
(14)

where ks is the thermal conductivity of the solid phase and Q represents the heat generated by heat sources.

In the design domain where fluids and solids are mixed, the 2D thermal convection-diffusion coupling equation is given by Dede (2009):

$$ {I}_2\left(\gamma \right){\rho}_f{C}_f\mathbf{u}\cdot \nabla \mathbf{T}=\nabla \cdot \left(k\left(\gamma \right)\nabla \mathbf{T}\right)+\frac{\mathbf{Q}}{d} $$
(15)

where I2(γ) is an interpolation function for the convection term. For solid phases, the convection term is punished to be 0 by I2(γ = 0) = 0. And the convection terms of fluid phases are not punished by I2(γ = 1) = 1. k(γ) is the interpolated thermal conductivity between solid and fluid phases. Cf is the heat capacity of the fluid phase.

Typically, a fluid temperature boundary condition is set in the actual inlet boundary. However, positions of actual inlet boundaries are unknown before optimization and are changing during the optimization process. Therefore, a design-dependent governing equation is defined in the extended inlet boundary. It is formulated as follows:

$$ {\boldsymbol{\upgamma}}_{in}{h}^{\ast}\left(\mathbf{T}-{T}_0\right)=\left(1-{\boldsymbol{\upgamma}}_{in}\right)\mathbf{n}\cdot \mathbf{q}\kern1em \mathrm{on}\kern1em {\boldsymbol{\Gamma}}_{\mathrm{in}} $$
(16)

where h∗ is the unit heat transfer coefficient and is set to 1 W/(mK). Equation (16) determines the boundary conditions at each point by the porosity value here. For boundaries belonging to the current actual inlet components, their temperatures are defined to be a constant value T0. And extra boundaries are defined to be thermal insulation.

In this problem, other external boundaries of the heat sink are defined to be thermal insulation:

$$ -\mathbf{n}\cdot \mathbf{q}=0\kern1em \mathrm{on}\kern1em {\boldsymbol{\Gamma}}_{\mathrm{wall}\hbox{-} \mathrm{out}} $$
(17)

4.3 Material interpolation model

In the constructed fluid flow and heat transfer models, three interpolation functions are defined to interpolate corresponding terms in the governing equations between solid and fluid phases. In this problem, interpolation functions of the Brinkman friction term and the heat conduction term adopt the RAMP-style model (Stolpe and Svanberg 2001). The heat convection term adopts the linear model. Corresponding interpolation functions are given as follows:

$$ {I}_1\left(\gamma \right)=\frac{{\mathrm{b}}_{\mathrm{max}}\left(1-\gamma \right)}{1+{c}_1\gamma } $$
(18)
$$ k\left(\gamma \right)=\frac{\gamma \left({k}_f\left(1+{c}_2\right)-{k}_s\right)+{k}_s}{1+{c}_2\gamma } $$
(19)
$$ {I}_2\left(\gamma \right)=\gamma $$
(20)

where bmax is the inverse permeability of solid phases, kf is the thermal conductivity of the fluid phase, and c1 and c2 are interpolation convexity parameters.

5 Optimization setup and implementations

5.1 Optimization problem

In this work, the optimization objective is to minimize the average temperature in the heat source domain. We will respectively formulate three optimization problems under three kinds of inlet boundary conditions.

  1. (I)

    Problem under the inlet pressure boundary condition

In this problem, the concurrent optimization problem is written mathematically as:

$$ {\displaystyle \begin{array}{l} find\kern0.75em \boldsymbol{\upalpha}, \boldsymbol{\upbeta}, \boldsymbol{\upgamma} \\ {}\min {T}_{ave}=\int {Td\varOmega}_H/\int {ld\varOmega}_H-273.15K\\ {}\begin{array}{l}S.t.\kern0.5em f\int {1d\varOmega}_d-\int {\boldsymbol{\upgamma} d\varOmega}_d\ge 0\\ {}\kern2.25em 0\le \boldsymbol{\upgamma} \le 1\\ {}\kern2.25em \begin{array}{l}{\alpha}_i^{low}\le {\alpha}_i\le {\alpha}_i^{up}\\ {}{\beta}_i^{low}\le {\beta}_i\le {\beta}_i^{up}\\ {} Governing\ eqautions\ \left(7,8,10\right),\left(14-17\right)\end{array}\end{array}\end{array}} $$
(21)

where Tave indicates the concerned temperature index in the heat source domain \( {\varOmega}_H \). It is calculated by the fourth-order surface integration in the finite element model. \( \mathtt{f} \) is the preset maximum fluid volume ratio in the internal design domain \( {\varOmega}_{\mathtt{d}} \). The second to the fourth constraints indicates the bounds of the internal porosity field and the MMC parameters. \( {\alpha}_i^{low} \) and \( {\alpha}_i^{up} \) are the lower and upper limits of parameter αi, respectively. Similarly, \( {\beta}_i^{low} \) and \( {\beta}_i^{up} \) are corresponding limits of parameter βi, respectively.

  1. (II)

    Problem under the inlet flow flux boundary condition

To avoid ill-posed optimization problem which would go to tremendously high pressure drops to slightly improve the thermal performance, the pressure drop Δp is also considered the objective. The objective function is defined as the standard weighted sum of the two objectives (average temperature and pressure drop). In subsequent numerical examples, weights of the two objectives are set equal. The objective function is formulated as follows:

$$ \min \kern0.5em {T}_{ave}+\int {\boldsymbol{\upgamma}}_{in}\mathbf{p}d{\Gamma}_{in}/\int {\boldsymbol{\upgamma}}_{in}d{\Gamma}_{in}-\int {\boldsymbol{\upgamma}}_{out}\mathbf{p}d{\Gamma}_{out}/\int {\boldsymbol{\upgamma}}_{out}d{\Gamma}_{out} $$
(22)

where ∫γinpdΓin/ ∫ γindΓin and ∫γoutpdΓout/ ∫ γoutdΓout represent average pressures of the actual inlet boundary and the actual outlet boundary, respectively. The optimization variables and constraints in this problem is the same as those in problem (I), except the governing (10) is replaced by (11).

  1. (III)

    Problem under the inlet velocity boundary condition

This problem has the same variables, objectives and constraints with problem (II), except the governing (11) is replaced by (12).

5.2 Porosity filtering and projection

To avoid ill-posedness numerical problems in the optimization framework, a Helmholtz-type partial differential equation in previous works (Sigmund and Petersson 1998; Lazarov and Sigmund 2011) was adopted to filter the porosity field of the internal design domain. It is formulated as follows:

$$ -{r}^2{\nabla}^2{\boldsymbol{\upgamma}}_f+{\boldsymbol{\upgamma}}_f=\boldsymbol{\upgamma} $$
(23)
$$ -{\mathbf{n}}_{\Gamma_d}\cdot \left(-{r}^2\nabla {\gamma}_f\right)=0 $$
(24)

where γf is the filtered porosity field and r is the filtering radius. Equation (24) represents a zero flux state defined on the boundary of the internal design domain. \( {\mathbf{n}}_{\Gamma_d} \) is the normal vector of the boundary.

To obtain a clear topology layout, a common approach is to project the filtered porosity with a smoothed Heaviside function (Wang et al. 2011):

$$ {\boldsymbol{\upgamma}}_p=\frac{\tanh \left({a}_2{b}_2\right)+\tanh \left({a}_2\left({\boldsymbol{\upgamma}}_f-{b}_2\right)\right)}{\tanh \left({a}_2{b}_2\right)+\tanh \left({a}_2\left(1-{b}_2\right)\right)} $$
(25)

where γp is the projected porosity field. Same as (5), a2 and b2 are the steepness and threshold parameters, respectively. Further, γp is applied in governing equations to solve the flow and temperature fields.

5.3 Sensitivity analysis

In this paper, the gradient information is adopted to iterate design variables. So, sensitivity analysis is essential and meaningful. Taking the objective function as an example, its sensitivity with respect to design variables γ and α can be calculated by chain rules:

$$ \frac{\partial \mathbf{O}}{\partial \boldsymbol{\upgamma}}=\frac{\partial \mathbf{O}}{\partial {\boldsymbol{\upgamma}}_p}\frac{\partial {\boldsymbol{\upgamma}}_p}{\partial {\boldsymbol{\upgamma}}_f}\frac{\partial {\boldsymbol{\upgamma}}_f}{\partial \boldsymbol{\upgamma}} $$
(26)
$$ \frac{\partial \mathbf{O}}{\partial \boldsymbol{\upalpha}}=\frac{\partial \mathbf{O}}{\partial {\boldsymbol{\upgamma}}_{in}}\frac{\partial {\boldsymbol{\upgamma}}_{in}}{\partial \boldsymbol{\upchi}}\frac{\partial \boldsymbol{\upchi}}{\partial \boldsymbol{\upalpha}} $$
(27)

where \( \frac{\partial \mathbf{O}}{\partial {\boldsymbol{\upgamma}}_p} \) and \( \frac{\partial \mathbf{O}}{\partial {\boldsymbol{\upgamma}}_{in}} \) are sensitivities derived from the flow and heat transfer governing equations based on the adjoint approach. Sensitivity analysis of the thermal-fluid problems to the porosity field has been already investigated in previous researches (Koga et al. 2013; Kontoleontos et al. 2013; Alexandersen et al. 2014; Yu et al. 2019; Zhao et al. 2019). Interested readers can refer to the related reference for details. \( \frac{\partial {\boldsymbol{\upgamma}}_p}{\partial {\boldsymbol{\upgamma}}_f} \) and \( \frac{\partial {\boldsymbol{\upgamma}}_f}{\partial \boldsymbol{\upgamma}} \) can be derived from (25) and (23), respectively. \( \frac{\partial {\boldsymbol{\upgamma}}_{in}}{\partial \boldsymbol{\upchi}} \) and \( \frac{\partial \boldsymbol{\upchi}}{\partial \boldsymbol{\upalpha}} \) can be derived from (3)–(6).

5.4 Iteration and convergence

In this work, the Globally Convergent Method of Moving Asymptotes (GCMMA) (Svanberg 1987) was applied as the optimization algorithm for its advantages in strongly nonlinear problems. As the commercial software COMSOL Multiphysics was adopted in many thermal-fluid topology optimization researches (Dede 2009, 2012; Matsumori et al. 2013; Dede et al. 2015; Haertel et al. 2018; Qian et al. 2018; Zeng et al. 2018; Zhao et al. 2018; Yu et al. 2019), it is used to solve the multiphysics problem with the finite element method in this work. The whole optimization process is achieved in MATLAB.

Noted that, like most previous works, the continuous strategy was introduced. It achieves a clear topology layout through several continuous steps. The parameters of interpolation and projection functions are different in each continuous step. The optimized layout of the current step is taken as the initial layout of the next step.

In each continuous step, the convergence criterion is defined as the norm of the residual vector in the KKT (Karush-Kuhn-Tucker) condition not exceeding 0.001 or the optimization loop exceeding 100.

6 Numerical examples

6.1 Parameter setup

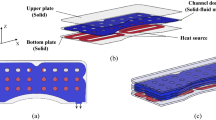
Sizes of the heat sink in x-y direction are shown in Fig. 4b. The height of the heat sink is set to 0.7 mm. Values of the heating power, the inlet temperature, and the pressure of the outlet are set to 100 W, 293.15 K, and 0 Pa, respectively. The maximum volume fraction of the fluid phase in the internal design domain is set to 0.8. Materials of the solid and fluid phases are designated as aluminum alloy and water, respectively. Thermophysical properties of materials are assumed constant. The resulting values are given in Table 1.

Fig. 4
figure 4

a Sizes of the considered heat sink (unit: mm). b The created mesh for topology optimization

Full size image
Table 1 Constant thermophysical properties of materials used in this work
Full size table

Taking the midpoint of the lower boundary of the heat sink as the origin (as shown in Fig. 4a), x-direction bounds of the inlet and outlet design domains are [− 47 mm, − 2 mm] and [2 mm, 47 mm], respectively. The triangular mesh is used to discretize the model. Maximum element sizes of the internal design domain, the inlet/outlet design domains, and the wall domains are set to 0.5 mm, 0.2 mm, and 1.0 mm, respectively. In total, 115,278 elements are created (as shown in Fig. 4b). The filtering radius r and the projection parameters a1 and b2 are set to 1.5 mm, 100, and 0.5, respectively.

Two continuous steps are set. Unless specifically mentioned, in the first step, c1, c2, a2, and bmax are set to 3, 3, 10, and 2 × 106 Pa s/m2, respectively. And they are set to 1, 1, 15, and 10 × 106 Pa s/m2, respectively, in the second step. The constraint factor in the GCMMA algorithm is set to 3000.

6.2 Single inlet/outlet problems

In order to evaluate the quality of the obtained solutions and the efficiency of the proposed concurrent method more conveniently, single inlet/outlet problems that only consider location variables of the inlet/outlet components are first presented. Meanwhile, optimized heat sinks in this section are considered the benchmark in the further section.

To verify the applicability of the proposed method, optimized heat sinks under three typical inlet boundary conditions are shown. In all examples, the width and angle of the inlet/outlet components are set to 10 mm and 0°, respectively. The bounds of the location variables of inlet and outlet components are defined to [− 42 mm, − 7 mm] and [7 mm, 42 mm], respectively. Noted that, in implementation, the normalized location variable \( \overline{\mathrm{l}} \) is applied as design variables. \( \overline{\mathrm{l}}=0 \) and \( \overline{\mathrm{l}}=1 \) correspond to the lower and upper limits of the location variable, respectively. \( \overline{\mathrm{l}} \) of the inlet and outlet components are referred to as \( {\overline{\mathrm{l}}}_{i1} \) and \( {\overline{\mathrm{l}}}_{o1} \), respectively.

6.2.1 Problem (I)

In this problem, the inlet pressure is defined to p0 = 50 Pa. The initial porosity field is set to be uniform with γp = 0.8. Initial values of \( {\overline{\mathrm{l}}}_{i1} \) and \( {\overline{\mathrm{l}}}_{o1} \) are set to 0.4 and 0.6, respectively. Iteration histories of the objective and inlet/outlet parameters in the first continuous step are shown in Fig. 5. The objective is effectively minimized and converges well. In the initial stage of optimization, the inlet/outlet components both converged to the rightmost side of corresponding design domains. Later, the inlet component converges to the left boundary and stabilizes to the end of optimization.

Fig. 5
figure 5

Iteration history of Tave (in a) and lil and lol (in b)

Full size image

The optimized physical porosity field and extracted geometry model are shown in Fig. 6 a and b, respectively. Tave of the optimized heat sink is 89.94 K. The optimized internal solid features exhibit a clear topology and streamlined boundaries. Optimized inlet and outlet components are symmetrical about the origin. The optimized topology enhances the flow resistance of the short-distance flow path and decreases that of the long-distance flow path. So that each part of the coil-like heat source is sufficiently cooled. The temperature field in Fig. 6c is solved by the optimized porosity field and the constructed porosity-interpolated thermal-fluid model. And the temperature field in Fig. 6d is solved by the extracted geometry model and standard fluid-solid thermal-fluid model. It can be observed that two color maps show good consistency. It indicates that the constructed model, especially the established design-dependent inlet governing equations, is very effective in predicting the thermal-fluid performance of the considered heat sink.

Fig. 6
figure 6

Optimized porosity-described structure in (a), extracted geometry model in (b), and corresponding temperature fields in (c) and (d) (unit: K)

Full size image

To validate the quality of the concurrently optimized solution, the considered problem is also solved with a traditional discrete method. In the discrete method, the internal topology is optimized under preset inlet/outlet schemes. Inspired by the concurrently optimized heat sink, inlet and outlet components are defined to be symmetrical about the origin. Meanwhile, the maximum element size of the inlet/outlet design domains are modified to be the same with that of the internal design domain. In all, about 81,000 elements are created during the discrete way. Several discrete optimized heat sinks are presented in Fig. 7. The concurrently optimized solution is also mark by a red circle in Fig. 7. It can be seen that the proposed concurrent optimization method obtains a competitive solution.

Fig. 7
figure 7

Optimized heat sinks of problem (I) under different inlet/outlet schemes and corresponding objective value

Full size image

In this numerical example, all computing works were conducted on the same hardware (Intel(R) Core(TM) i7-7700K CPU, 32.0G RAM). The time consuming of this concurrent case and two discrete cases is summarized in Table 2.

Table 2 Time consuming of the concurrent approach and the discrete approach
Full size table

It can be seen from Table 2 that the average time consuming of each inner iteration of the concurrent approach is about 1.37 times that of the discrete approach under one inlet/outlet scheme. This is mainly caused by the increased number of finite elements in the concurrent case. On the other hand, the whole iteration numbers of the two methods are very close. Considering that a considerable number of inlet/outlet schemes will be evaluated in the discrete method, the proposed concurrent method exhibits a great improvement in efficiency.

6.2.2 Problem (II)

Here, the inlet flow flux is defined to m = 3.5 × 10−4 kg/s (corresponding Reynolds number equal to 500). Initial values of all design variables are set to be the same with the previous problem. To ensure more accurate flow/pressure fields in inlet/outlet design domains, bmax is set to a larger value 10 × 106 Pa s/m2 in the first continuous step.

Figure 8 illustrates the iteration history and the optimized heat sink. Similarly, the inlet and outlet components converge to the leftmost and the rightmost sides of their respective design domains. And the internal solid features show streamlined boundaries. This problem is also solved with the discrete optimization method with different symmetrical inlet/outlet schemes. Obtained topologies and corresponding performance are presented in Fig. 9. It can be observed that the proposed concurrent method achieves a competitive solution in problem (II), compared with the discrete method.

Fig. 8
figure 8

Iteration history of the objective in a, the location variables in b, and the optimized topology in c

Full size image
Fig. 9
figure 9

Optimized heat sinks of problem (II) under different inlet/outlet schemes and corresponding objective value

Full size image

6.2.3 Problem (III)

Here, a parabola inlet velocity profile is defined on the actual inlet boundary. The velocity function is defined as follows:

$$ {f}_{\mathrm{u}}=0.0018\left(x-{l}_{\mathrm{i}1}+5\right)\left(-x+{l}_{\mathrm{i}1}+5\right)\ \left(\mathrm{m}/\mathrm{s}\right) $$
(28)

With the constructed boundary governing (12), this profile is design-dependent with the inlet component. Implementation parameters are set to be the same with those in the previous problem.

The optimization history and the optimized heat sink are illustrated in Fig. 10. The objective converges well and the inlet/outlet components also converge to the two sides. Optimized structures by the discrete method and corresponding performance are shown in Fig. 11. It can be observed that the proposed concurrent method achieves a competitive solution in problem (III), compared with the discrete method.

Fig. 10
figure 10

Iteration history of the objective in a, the location variables in b, and the optimized topology in c

Full size image
Fig. 11
figure 11

Optimized heat sinks of problem (III) under different inlet/outlet schemes and corresponding objective value

Full size image

6.3 Multiple inlet/outlet problems

In this section, a double inlet/outlet problem is first presented. Location variables of inlet and outlet components are limited in [− 42 mm, − 7 mm] and [7 mm, 42 mm], respectively. Width variables of all components are limited in [6 mm, 12 mm]. Angle variables of all components are limited in [−π/4, π/4]. The problem is optimized under an inlet pressure boundary condition with p0 = 50 Pa. Similarly, all inlet/outlet design variables are normalized in implementation. The normalized width and angle variables are indicated by \( \overline{\mathrm{w}} \) and \( \overline{\theta} \).

The initial porosity field is set to be uniform with γp = 0.8. Initial values of all \( \overline{\mathrm{w}} \) and \( \overline{\theta} \) are set to 0.5. To evaluate the influence of initial location variables to the optimization result, four optimized topologies (as shown in Fig. 12) were obtained under four sets of initial values of \( \overline{\mathrm{l}} \) (as listed in Table 3).

Fig. 12
figure 12

Optimized heat sinks under different initial value sets and corresponding Tave

Full size image
Table 3 Four initial value sets of inlet/outlet location variables
Full size table

Several aspects can be observed in Fig. 12. First, benefiting from the increased design space, all optimized double inlet/outlet heat sinks exhibit higher heat dissipation performance than the optimized single inlet/outlet heat sink in Section 6.2.2. Second, optimized heat sinks under initial value set 1 and 4 show similar topologies. The two inlet components combined into one component. Third, optimized heat sinks under initial value set 2 and 3 show similar topologies. There are two main flow channels. The left inlet and the right outlet are connected with a long-distance flow channel. The right inlet and left outlet are connected with a short-distance flow channel. Fourth, to investigate these two kinds of topology, Fig. 13 presents some intermediate steps of optimization processes under initial value set 1 and 3. The difference between the two topologies is mainly due to the initial distance between the two inlet components.

Fig. 13
figure 13

Some intermediate steps of the concurrent optimization. a Initial value set 1. b Initial value set 3

Full size image

Further, a triple inlet/outlet problem under the same boundary condition is presented. Bounds of all inlet/outlet parameters are the same with those in the double inlet/outlet problem. Initial values of three normalized inlet/outlet location variables are set to 0, 0.5, and 1.0, respectively. Initial values of other design variables and implementation parameters are the same with the previous problem.

The optimized structure is shown in Fig. 14. It shows similar topology features with optimized structures in Fig. 12 b and c. The left inlet is a combination of inlet components 1 and 2. And the right outlet is a combination of outlet components 2 and 3. The optimized structure exhibits a little enhancement in the cooling performance (Tave = 76.39 K), compared with those in the previous examples.

Fig. 14
figure 14

The optimized heat sink in the triple inlet/outlet problem

Full size image

7 Discussions

7.1 The influence of angled inlets/outlets

To the best of the authors’ knowledge, in previous similar works based on topology optimization, heat sinks with angled inlets/outlets have not been investigated. In this work, the proposed method enables inlet/outlets to be optimized with greater design freedom. Especially, several optimized heat sinks with angled inlets/outlets are presented in Section 6.3.

In order to evaluate the influence of angled inlets/outlets, the double inlet/outlet problem in Section 6.3 is optimized with fixed-angle inlets/outlets in this section. Angle variables of all inlet/outlet components are set to 0. Settings of other parameters remain the same as those in Section 6.3. This problem is also solved under four sets of initial values (as listed in Table 3). Table 4 presents Tave of optimized heat sinks with fixed-angle inlets/outlets. Additionally, Tave of optimized heat sinks in Section 6.3 is listed as comparisons.

Table 4 Tave of optimized heat sinks with fixed-angle and changeable-angle inlets/outlets under four sets of initial values
Full size table

It can be seen from Table 4 that Tave of optimized heat sinks with fixed-angle inlets/outlets is 1.69 K higher than that of heat sinks with changeable-angle inlets/outlets on average. In numerical, the performance advantage of heat sinks with angled inlets/outlets comes from greater design freedom. As the focus of this work is to present a concurrent optimization approach of inlets/outlets and internal channels, the performance advantage of angled inlet/outlets needs to be further studied in terms of the heat convection mechanism.

7.2 A more general numerical example

In Section 6, the proposed concurrent method is presented with design problems that come from the cooling demand of the Lorentz motor in an ultra-precision stage. To some extent, the design domains of inlets/outlets in these problems are limited. In order to validate the applicability of the proposed method, a more general design case is presented in this section.

Figure 15 a illustrates the schematic figure of the considered heat sink design problem in this section. Almost all external domains of the heat sink are defined as inlet/outlet design domains. As is shown in Fig. 15), a new MMC is adopted as the primary inlet/outlet building block. The position of each MMC is controlled by the rotation variable θ. Heat sources are not uniformly distributed in the design domain (as shown in Fig. 15c).

Fig. 15
figure 15

a An additional heat sink optimization problem. b A new inlet/outlet MMC. c Size and heat sources (areas in red) of the considered heat sink in a (unit: mm). The height is set to 0.7 mm

Full size image

Similarly to (4), the TDF of the jth MMC is written as follows:

$$ {\chi}_j\left(\mathbf{x}\right)=1-H\left({\left(\left(\arctan \left(\frac{y-{yc}_j}{x-{xc}_j}\right)-{\theta}_j\right)/\left(0.7\ast {\theta}_w\right)\right)}^2\right) $$
(29)

where θw is the angle between two straight sides of the MMC. θw is set to π/15 in this section.

The considered problem is a single inlet/outlet problem under the inlet flow flux boundary condition. The inlet flow flux is defined to m = 2.1 × 10−4 kg/s (corresponding Reynolds number equal to 300). The optimization objective is to minimize the sum of the average temperature in blue areas and the average pressure of the inlet. Meanwhile, the maximum volume fraction of the fluid phase is set to 0.5.

In order to avoid the weak flow and convection effects in solid domains of the inlet/outlet design domains, bmax of the inlet/outlet design domains is set as a function of corresponding rotation variables. Taking bmax of the inlet design domain as an example, it is formulated as follows:

$$ {b}_{\mathrm{max}}\left(\mathbf{x}\right)={\left(\left(\arctan \left(\frac{y-{yc}_j}{x-{xc}_j}\right)-{\theta}_j\right)/\left(0.7\ast {\theta}_w\right)\right)}^{4/3}\ast {b}_0 $$
(30)

where b0 = 107 Pa s/m2. This function ensures that bmax is large enough in areas far from the actual inlets/outlets in the inlet/outlet design domains.

Except for the details introduced above, other parameter settings and implementation details of this problem are defined to be the same as those in Section 6.2.2.

Figure 16 presents optimized structures with the concurrent method and the discrete method (under three sets of predefined inlet/outlet). The values of optimized objective functions are listed below each structure. It can be found that positions of the inlet and outlet have a great impact on the objective performance of the obtained structures. In addition, compared with optimized structures in Fig. 16b–d, the obtained structure by the proposed method exhibits better objective performance

Fig. 16
figure 16

Optimized heat sinks with the concurrent method (in a) and the discrete method (in b–d)

Full size image

8 Conclusions

This paper investigates a concurrent optimization design method of the internal flow channel, the inlets, and the outlets in forced convection heat sinks. The porosity field and MMCs are adopted to describe topologies of the internal design domain and the inlet/outlet design domains, respectively. A parallelogram inlet/outlet component with three design variables and its topology description function are constructed. A porosity-interpolated thermal-fluid model is constructed to solve the fluid flow and heat transfer problem. Particularly, design-dependent governing equations of the extended inlet boundary are established under three classical unlet boundary conditions, thus ensuring meaningful inlet flow and temperature conditions.

The proposed concurrent method and implementation issues are detailed presented with several numerical examples. The single inlet/outlet cases demonstrate the applicability of the proposed method and design-dependent thermal-fluid model in three classical inlet boundary conditions. Meanwhile, compared with the discrete method, the proposed concurrent method achieves competitive solutions and is very efficient. Further, the proposed method obtains satisfactory solutions and novel topologies in multiple inlet/outlet problems.

In the discussion section, the performance of heat sinks with angled inlets/outlets is preliminarily investigated. Changeable-angle inlets/outlets allow for greater design freedom and the designed heat sinks exhibit better objective performance. Additionally, the applicability of the proposed method is validated in a more general numerical example that the inlet/outlet is moveable almost throughout the external boundary of the heat sink.