Prediction of axial load capacity of rectangular concrete-filled steel tube columns using machine learning techniques

Abstract

This work aims to develop a novel and practical equation for predicting the axial load of rectangular concrete-filled steel tubular (CFST) columns based on soft computing techniques. More precisely, a dataset containing 880 experimental tests was first collected from the available literature for the development of an artificial neural network (ANN) model. An optimization strategy was conducted to obtain a final set of ANN’s architecture as well as its weight and bias parameters. The performance of the developed ANN was then compared to current codes (AS, EN, AIJ, ACI, AISC, LRFD, and DBJ) and existing empirical equations. The accuracy of the present model was found superior to the results obtained by others when predicting the axial load of rectangular CFST columns. For practical application, an explicit equation and an Excel-based Graphical User Interface were derived based on the ANN model. The graphical user interface is provided freely for all interested users, to support the design, teaching, and interpretation of the axial behavior of CFST columns.

1 Introduction

Concrete filled steel tube (CFST) columns have gained significant popularity in modern construction [1,2,3,4]. They constist of a hollow steel section, either hot rolled or cold-formed or welded, filled with concrete, normally without any other longitudinal reinforcement or stirrups. This combination offers a number of advantages. No formwork for the casting of concrete is needed, since the hollow section serves this purpose, reducing labour costs. Furthermore, the steel tube, offers the required confinement conditions for the concrete, to deliver its compressive capacity and maintain its ductility. On the other hand, the concrete core, blocks the potential for any inward movement of the steel tube, enhancing this way its overall resistance against local buckling. Global buckling is enhanced, as well, due to the combined contribution to the overall stiffness of the steel and concrete parts. More slender steel sections can be used, as a consequence, that would otherwise be susceptible to premature instabilities. As a result, a CFST column, achieves increased stiffness, strength, and ductility, surpassing the respective characteristics of its individual components. Other practical advantages include the increased floor space, a hard to damage the final surface, and improved fire resistance. Compared to a reinforced concrete construction, however, CFST columns require more complicated beam-to-column joints, that must typically be prepared in-shop, as well as anti-corrosion finishing for the exposed steel.

Several cross-sectional shapes for CFSTs are in use nowadays. Circular hollow sections are quite common, due to the excellent confinement conditions they can offer. Square or rectangular hollow sections are also increasingly used, offering easier manufacturing of the beam to column joints, and aesthetics. However, they provide less confinement to the concrete core, compared to the circular tubes. Other shapes, such as octagonal, hexagonal or elliptic are also in use, though less commonly, Steel and composite codes, worldwide facilitate the design of CFSTs, with provisions for their axial and flexural capacity, and stability. Specifically, available codes include EN1994 [5] in Europe, AISC-360 [6] and ACI-318 [7] in North America, AIJ [8] in Japan, DBJ13-51 [9] in China and AS4100 [10] in Australia. Also, an increasing number of analytical models becomes available in the literature for the prediction of CFST behavior. Considering the axial compressive capacity, analytical methodologies are proposed, among others, by Uy [11], Sakino et al. [12], Han et al. [13], Yu et al. [14], Ding et al. [15], Du et al. [16], Wang et al. [17], Chen et al. [18].

In recent years, soft computing techniques have gradually become popular and applied in many different fields [19,20,21,22,23]. Artificial neural network (ANN) method uses existing experimental data to train neural networks to generalize and predict the behavior of the same material under different testing conditions and has become the most commonly used machine learning algorithm [19]. Many studies related to ANN applied to the behavior of steel–concrete pipe columns subjected to different types of loads have been conducted, such as prediction of fire resistance of concrete-filled tubular steel columns [24]; prediction of biaxial bending behavior of steel–concrete composite beam-columns [25]; concrete-filled steel tube ultrasonic [26]. Du et al. [27] utilized ANN to predict the axial bearing capacity of rectangular CFST columns using the parameters such as sectional length and width, thickness, steel, and concrete strength. In such a study, 305 experimental data were collected, in which 275 samples were used to train the ANN model, whereas 30 samples were used for the validation phase. The predicted values are more accurate than standards such as ACI and EC4. In Wei et al. [28], an ANN model was developed to evaluate the seismic properties of high-strength reinforced concrete columns with concrete-filled steel tube core. In addition, by using neural networks and input parameters such as yield limit of steel tube, the compression strength of concrete, diameter, and height of circular concrete-filled steel tube, and wall thickness of steel tube, a network for strength prediction of columns was proposed with high level of accuracy and precision [29]. The results obtained from the literature demonstrate that ANN could predict the behavior of concrete-filled steel tubes with a high degree of accuracy.

2 Research significance

The present paper focuses on the prediction of the ultimate compressive load of rectangular CFSTs, using an artificial neural network approach. Ultimate compressive load represents the main design variable of a CFST column, under axial loading. Numerous literature studies are devoted towards its experimental characterization and several analytical models are proposed either by design codes [5,6,7,8,9,10] or research works, as will be seen later in text. However, in a structural design situation, a column is normally expected to withstand a more complex loading condition, that may include flexural bending, shear and torsion. Nevertheless, even in these cases, the compressive capacity remains a crucial parameter that affects the final capacity under the interaction of loading modes.

While the estimation of the compressive capacity, through closed-formed analytical models, is always a sought-after solution, sometimes it becomes necessary to look for a numerical solution, such as a finite element model. For example, the currently available design codes [5,6,7,8,9,10], place certain limits on their application, regarding the use of high-strength steel and concrete, or the slenderness of the cross-section. However, due to the excellent confinement conditions, a CFST can offer, the opportunity arises in practice, to take advantage of high-strength concrete, in an effective and simple manner. Similarly, the inner restraint offered by the concrete core, to the steel section, enhances its resistance against local buckling, so that the use of high-strength steel and thin-walled sections becomes viable and effective. In such cases, the verification of the CFST compressive capacity can rely on experimental testing or advanced finite element modeling. Both solutions, however, are expensive in time and financial resources, and not scalable to every structure. A neural network model, on the other hand, if trained with a sufficient number of experimental specimens, can offer a reliable estimation, that can cover a broad field of application, in a scalable manner. The final implementation of such a model can be of comparable complexity, with an analytical methodology. The high number of experimental tests, available in the literature nowadays, regarding the compressive response of CFSTs, facilitates the training of a neural network model, in an extended field of application, that includes high-strength materials and thin-walled sections.

3 Literature review on concrete-filled steel tube columns under axial loading

3.1 Experimental works

Extended experimental work has been conducted in the past, helping to establish a solid understanding on the mechanisms that contribute to the ultimate response of CFSTs under axial compression. Several common aspects of their design have been explored in the literature, such as, the shape of the tube, its aspect ratio, the column slenderness, the load eccentricity, the influence of stiffeners as well the use of innovative materials, including high strength steel, high strength concrete, and self-consolidating concrete.

Early experimental studies, by Kloppel and Goder [30], Furlong [31] and by Knowles and Park [32] report tests on circular and square CFSTs. Gardner and Jacobson [33], examined rectangular CFSTs with varying aspect ratios. Tomii et al. [34] reported a large number of tests for circular, square and octagonal shaped CFSTs. More recent tests on square CFSTs include the works by Uy [35], Varma et al. [36], Mursy and Uy [37, 38], Sakino [12], Lam and Willimas [39], Tao et al. [40], Yu et al. [14], Aslani et al. [41], Liew et al. [2], Dundu [42], Khan et al. [43, 44], Xiong et al. [45], Zhu et al. [46], Chen et al. [18].

In the case of a rectangular sections, the aspect ratio, $H/B$, of the two section sides, affects the concrete confinement conditions. This in turn can negatively affect both strength and ductility of the column. Experimental evidence, in this context, is reported by Han [47], who tested sections with $1 \le H/B \le 1.75$, Liu et al. [48] and Liu [49], who tested high strength CFSTs, with $1 \le H/B \le 2$, Du et al. [50] who tested high strength CFSTs, with $1.17 \le H/B \le 1.5$. . On a different approach, Evirgen et al. [51] examined different CFSTs shapes including square, as well as rectangular ones, with $H/B = 1.67$. The latter proved much less effective in enhancing the axial lo, compared to to the square ones. Similarly, Ibanez et al. [52] examined different shapes of high strength CFSTs, including rectangular ones, with $H/B = 1.5$, concluding that the latter offer reduced confinement levels, compared to square and circular sections, with similar section area.

A crucial factor, that determines the behavior of CFSTs, under compressive loading, is the width-to-thickness ratio $B/t$, of the steel tube. Higher values of this ratio, result in local buckling phenomena to the steel section, reducing the overall column capacity. Rectangular or square tubes prove more susceptible to local buckling, compared to circular ones. Uy [53] tested square concrete filled box columns, with $40 \le B/t \le 100$, and proposed slenderness limits for the steel section, before local buckling prevents the column from reaching its yield capacity, accounting also for residual stresses. Sakino et al. [12] tested square CFSTsm with $18.4 \le B/t \le 73.9$, as well as circular ones. For the square tubes, they proposed a strength reduction factor, due to steel tube local buckling. Chitawadagi et al. [54], among other parameters, investigated experimentally the width-to-thickness ratio of cold-formed rectangular CFSTs, taking values between 9.4 and 25. It is found that larger wall thickness leads to increased load carrying capacity, by postponing local buckling. Similar conclusions are drawn by Evirgen et al. [51], who tested circular, hexagonal, square, and rectangular CFSTs, with four $B/t$ ratios, between 18.75 and 100. Chen et al. [18], who tested circular and square CFSTs, with varying $B/t$ ratio, between 13.2 and 48.9, and concrete strength, reported that with higher $B/t$ ratios, local buckling becomes more critical, resulting in a loss of concrete confinement, though this phenomenon is postponed with higher concrete strengths.

An effective measure against local buckling involves the use of longitudinal stiffeners. To this end, the performance of several inner stiffener layouts, for square CFSTs has been investigated by Tao et al. [40, 55] and by Zhu et al. [46], for cold-formed steel tubes. Similar investigation for inner, as well as outer longitudinal stiffeners, for square and rectangular CFSTs has been performed by Tao et al. [56]. Ding et al. [15] evaluated the axial load carrying response of square CFSTs with stiffeners, as well as, three different stirrup configurations. They conclude that inner stiffeners improve mainly the ductility of the column, however, stirrups were able to enhance capacity as well.

More than often, the experimentally tested CFST specimens are short in length, for easier construction and testing. However, the evaluation of the column behavior, under global buckling conditions, requires the testing of long specimens. Han and Yao [57], tested rectangular CFSTs with varying length-to-width ratio, $L/B$, up to 18, under different conditions of concrete compaction. Mursi and Uy [38] examined long, square, high strength CFSTs, with $L/B$ taking values between 11.6 and 27.5. Lue et al. [58] tested rectangular CFSTs with an $L/B$ ratio equal to 18.55, that failed either due to global buckling, local buckling or a combination of the two. Yu et al. [59] examined the performance of circular and square CFSTs, with high-performance concrete, using three different lengths and $L/B$ ratios reaching 30. Dundu [42] examined square CFSTs, using both mild and high strength steel and $L/B$ ratios up to 45. Failure modes included global buckling mostly, as well as local buckling. Also, Khan et al. [43] tested square, high strength CFSTs, with three different lengths and varying slenderness that failed either due to global or local buckling, or a combination of both.

Extensive experimental studies investigate the performance of high-strength CFSTs. The use of high strength concrete (HSC) or ultra-high-strength concrete (UHSC) has been investigated by Lam and Williams [39] and Khan et al. [43, 44], for square CFSTs, by Liu et al. [48], Liu and Gho [60] and Lue et al. [58], for rectangular CFSTs, by Yu et al. [59], Liew et al. [2], Xiong et al. [45] and Chen et al. [18], for square and circular CFSTs, by Ibanez et al. [52] for circular, square and rectangular CFSTs, by Zhu et al. [61] for octagonal, circular and square CFSTs. On the other hand, experimental tests with high strength steel tubes are reported by Liu et al. [48], Sakino et al. [12], Mursi and Uy [38], Liu and Gho [60], Aslani et al. [41], Liew et al. [2], Dundu [42], Du et al. [16], Xiong et al. [45], Khan et al. [43, 44]. Other investigations focus on the use of stainless steel tubes (Young and Ellobody [62], Uy et al. [63]), the use of self-consolidating concrete (Han and Yao [64], Han et al. [13], Yu et al. [49]), the preloading of the steel tube (Han and Yao [65]).

3.2 Available proposals

The design of CFST columns against axial compression is supported by many steel and composite design codes. These include European EN1994 [5], American LRFD [66], AISC 360 [6] and ACI 318 [7], Japanese AIJ [8], Chinese DBJ 13-51-2010 [9], Australian AS5100 [10]. Almost all codes restrict their field of application, limiting the range of acceptable steel material strength $f_{{\text{y}}}$, concrete strength $f_{{\text{c}}}^{'}$, and excluding very slender steel sections. Some codes also limit the steel percentage in the composite section. The limits differ greately between codes, as can be seen in Table 1.

Table 1 Field of application of various code standards for the design of CFST columns

Hereafter, a concise description of each of the aforementioned design codes is made, regarding the estimation of the compressive axial capacity of rectangular CFST columns. Safety factors are omitted from the presentation here, aiming for a more objective comparison between different codes that are undertaken in this work. Also, a number of analytical methodologies, available in the literature, for the estimation of the ultimate axial load of the square of rectangular CFSTs, is described in the remaining of this section.

3.2.1 Eurocode EN1994

According to Eurocode 4 [5], the squash load of a CFST column, under axial compression, is calculated by combining the individual resistances of the steel section and the concrete core:

$$N_{{{\text{pl}}}}^{{}} = f_{{\text{y}}} A_{{\text{s}}} + f_{{\text{c}}}^{'} A_{{\text{c}}} ,$$

(1)

The effect of column slenderness is taken into account through a reduction factor $\chi$, so that the column axial capacity is found as:

$$N_{{}}^{{{\text{EC4}}}} = \chi N_{{{\text{pl}}}}^{{}} ,\quad {\text{with}}\quad \chi \le 1.$$

(2)

Factor $\chi$ is found through buckling curves, provided by EN1993 [67], using an effective slenderness $\bar{\lambda }$ that combines contributions to stiffness from the steel and concrete components. The formulas in this case are:

$$\bar{\lambda } = \sqrt {\frac{{N_{{{\text{pl}}}} }}{{\frac{{\pi ^{2} \left( {{\rm E}{\rm I}} \right)_{{{\text{eff}}}} }}{{L_{{\text{e}}} ^{2} }}}}}$$

$$\left( {{\rm E}{\rm I}} \right)_{{{\text{eff}}}} = E_{{\text{s}}} I_{{\text{s}}} + 0.6E_{{\text{c}}} I_{{\text{c}}}$$

(3)

where, $L_{{\text{e}}}$ is the critical buckling length, $I_{{\text{s}}}$, $I_{{\text{c}}}$ the moments of inertia of the steel section and the concrete core, respectively, $E_{{\text{s}}} ,E_{{\text{c}}}$ the moduli of elasticity for the same components. The later can be calculated using the EN1992 [68] formula: $E_{{\text{c}}} = 22,000\left( {0.1f_{{\text{c}}}^{'} + 0.8} \right)^{{0.3}}$ (in MPa).

3.2.2 AISC 360-16

American standard AISC360-16 [6], takes into account the strength of the steel and concrete parts of CFST columns, as well as the slenderness of the column member, providing the following formula for the calculation of their axial compressive capacity:

$$N_{{}}^{{{\text{AISC360}}}} = \left\{ {\begin{array}{*{20}c} {N_{{{\text{no}}}} \left( {0.658^{{\left( {\frac{{N_{{{\text{no}}}} }}{{N_{{{\text{cr}}}} }}} \right)}} } \right),} & {{\text{if }}\;\frac{{N_{{{\text{no}}}} }}{{N_{{{\text{cr}}}} }} \le 2.25} \\ {0.877N_{{{\text{cr}}}} ,} & {{\text{if}}\;\frac{{N_{{{\text{no}}}} }}{{N_{{{\text{cr}}}} }} > 2.25} \\ \end{array} } \right.,$$

(4)

where $N_{{{\text{no}}}}$ is related to the strength of the total section, depending on its classification against local buckling phenomena, while $N_{{{\text{cr}}}}$ is the elastic critical buckling load of the member. The former, is found with the following expression:

$$N_{{{\text{no}}}} = \left\{ {\begin{array}{*{20}l} {N_{{{\text{pl}}}} ,} \hfill & {{\text{if}}\;\lambda < \lambda _{{\text{p}}} } \hfill \\ {N_{{{\text{pl}}}} - \left( {N_{{{\text{pl}}}} - N_{{\text{y}}} } \right)\frac{{\left( {\lambda - \lambda _{{\text{p}}} } \right)^{2} }}{{\left( {\lambda _{{\text{r}}} - \lambda _{{\text{p}}} } \right)^{2} }},} \hfill & {{\text{if }}\;\lambda _{{\text{p}}} \le \lambda < \lambda _{{\text{r}}} } \hfill \\ {\frac{{9E_{{\text{s}}} A_{{\text{s}}} }}{{\lambda ^{2} }} + 0.7f_{{\text{c}}}^{\prime } A_{{\text{c}}} ,} \hfill & {{\text{if }}\;\lambda \ge \lambda _{{\text{r}}} } \hfill \\ \end{array} } \right..$$

(5)

Loads $N_{{{\text{pl}}}}$ and $N_{{\text{y}}}$ are related to the combined plastic and yield, respectively, strength of the steel and concrete parts of the total section, while $\lambda _{p}$ and $\lambda _{p}$ are classification limits for the width-to-thickness ratio, $\lambda$, of the steel section.

$$\left\{ {\begin{array}{*{20}l} {N_{{{\text{pl}}}} = f_{{\text{y}}} A_{{\text{s}}} + 0.85f_{{\text{c}}}^{\prime } A_{{\text{c}}} } \hfill \\ {N_{{\text{y}}} = f_{{\text{y}}} A_{{\text{s}}} + 0.7f_{{\text{c}}}^{'} A_{{\text{c}}} } \hfill \\ {\lambda = \left( {H - 2t} \right)/t} \hfill \\ {\lambda _{{\text{p}}} = 2.26\sqrt {E_{{\text{s}}} /f_{{\text{y}}} } } \hfill \\ {\lambda _{{\text{r}}} = 3.00\sqrt {E_{{\text{s}}} /f_{{\text{y}}} } } \hfill \\ \end{array} .} \right.$$

(6)

On the other hand, for the calculation of the elastic buckling load $N_{{{\text{cr}}}}$, that is used in Eq. (4), an effective flexural stiffness of the total cross section is employed, equal to:

$$\left( {{\rm E}{\rm I}} \right)_{{{\text{eff}}}} = E_{{\text{s}}} I_{{\text{s}}} + C_{3} E_{{\text{c}}} I_{{\text{c}}} ,$$

$$C_{3} = 0.45 + \frac{{3A_{{\text{c}}} }}{{A_{{{\text{sc}}}} }} \le 0.9.$$

(7)

For the estimation of the modulus of elasticity of concrete $E_{{\text{c}}}$, an empirical expression is provided by AISC360-16 [6] ($E_{{\text{c}}} = 0.043\rho ^{{1.5}} \sqrt {f_{{\text{c}}}^{'} }$, in MPa, where $\rho$ the density of concrete in kg/m³).

3.2.3 LRFD 1999

The older version of American standard LRFD 1999 [66], provides a simpler path for the estimation of the axial capacity of CFST columns, compared to AISC 360 [6]. Along with its newer counterpart, LRFD 1999, takes into consideration the strength of the steel and concrete components, as well as the slenderness of the column member, but without accounting for the classification of the steel section against local buckling. Specifically, the capacity of the CFST column, under axial compression, is given by the following expression:

$$N_{{}}^{{{\text{LRFD}}}} = \left\{ {\begin{array}{*{20}l} {A_{{\text{s}}} f_{{{\text{my}}}} 0.658^{{\left( {\lambda _{{\text{c}}} ^{2} } \right)}} ,} \hfill & {{\text{if}}~~~\lambda _{{\text{c}}} \le 1.5} \hfill \\ {A_{{\text{s}}} f_{{{\text{my}}}} \frac{{0.877}}{{\lambda _{{\text{c}}} ^{2} }},} \hfill & {{\text{if}}~~~\lambda _{{\text{c}}} > 1.5} \hfill \\ \end{array} } \right.,$$

(8)

where $\lambda _{{\text{c}}}$ is the slenderness of the column given by:

$$\lambda _{{\text{c}}} = \left( {\frac{{L_{{\text{e}}} }}{{\pi \sqrt {I_{{\text{s}}} /A_{{\text{s}}} } }}} \right)\sqrt {\frac{{f_{{{\text{my}}}} }}{{E_{{\text{m}}} }}} ,$$

(9)

and $f_{{{\text{my}}}}$, $E_{{\text{m}}}$ are effective yield stress and modulus of elasticity, of the composite section, accounting for contributions from both the steel and concrete parts:

$$\left\{ {\begin{array}{*{20}c} {f_{{{\text{my}}}} = f_{{\text{y}}} + 0.85f_{{\text{c}}}^{'} A_{{\text{c}}} /A_{{\text{s}}} } \\ {E_{{\text{m}}} = E_{{\text{s}}} + 0.4E_{{\text{c}}} A_{{\text{c}}} /A_{{\text{s}}} } \\ \end{array} .} \right.$$

(10)

For the estimation of the modulus of elasticity of concrete $E_{{\text{c}}}$, an empirical expression is provided by LRFD 1999 [66] ($E_{{\text{c}}} = 0.041\rho ^{{1.5}} \sqrt {f_{{\text{c}}}^{'} }$, in MPa, where $\rho$ the density of concrete in kg/m³).

3.2.4 AS 5100

Australian code AS 5100 [10], follows a similar path with EN1994 [5], for the calculation of the capacity of a CFST columns, under axial compression. The squash load of the section is found by combining the individual resistances of the steel section and the concrete core. Ignoring safety factors, this is written as:

$$N_{{{\text{pl}}}}^{{}} = f_{{\text{y}}} A_{{\text{s}}} + f_{{\text{c}}}^{'} A_{{\text{c}}} .$$

(11)

The effect of column slenderness is then taken into account through a reduction factor $a_{c}$, so that the column axial resistance is found as:

$$N_{{}}^{{{\text{AS5100}}}} = a_{{\text{c}}} N_{{{\text{pl}}}}^{{}} ,\quad {\text{with}}\quad a_{{\text{c}}} \le 1.$$

(12)

Factor $a_{{\text{c}}}$ depends on a relative column slenderness, $\lambda _{{\text{r}}} = \sqrt {N_{{{\text{pl}}}}^{{}} /N_{{{\text{cr}}}}^{{}} }$, where $N_{{{\text{cr}}}}^{{}}$ the elastic critical buckling load of the column. The latter is evaluated using an effective flexural stiffness, taking into account both the steel and concrete components:

$$N_{{{\text{cr}}}}^{{}} = \pi ^{2} \frac{{E_{{\text{s}}} I_{{\text{s}}} + E_{{\text{c}}} I_{{\text{c}}} }}{{L_{{\text{e}}} ^{2} }}.$$

(13)

The calculation of factor $a_{{\text{c}}}$ is based on the following formulas:

$$\begin{array}{*{20}l} {a_{{\text{c}}}^{{}} = \xi \left[ {1 - \sqrt {1 - \left( {\frac{{90}}{{\xi \lambda }}} \right)^{2} } } \right]} \hfill \\ {\lambda = 90\lambda _{{\text{r}}} + a_{{\text{a}}} a_{{\text{b}}} } \hfill \\ {\xi = \frac{{\left( {\lambda /90} \right)^{2} + 1 + \eta }}{{2\left( {\lambda /90} \right)^{2} }}} \hfill \\ {a_{{\text{a}}} = \frac{{2100\left( {90\lambda _{{\text{r}}} - 13.5} \right)}}{{8100\lambda _{{\text{r}}} ^{2} - 1377\lambda _{{\text{r}}} + 2050}}} \hfill \\ {\eta = 0.00326\left( {13.5 - \lambda } \right) \ge 0} \hfill \\ \end{array} .$$

(14)

In the above expressions, $\eta$ represents a geometrical imperfection factor, while $a_{{\text{b}}}$ accounts for the impact of residual stresses (for tubular sections, not classified as slender, it is, $a_{{\text{b}}} = - 1$).

3.2.5 AIJ

Japanese code AIJ [8] covers the design of circular and square CFSTs under axial compression. The axial capacity, for a square section, having width $B$, can be calculated through the following three expressions, which take into consideration both the strength of the section and the stability of the member, depending on its slenderness:

$$N_{{}}^{{{\text{AIJ}}}} = \left\{ {\begin{array}{*{20}l} {A_{{\text{s}}} f_{{\text{y}}} + 0.85A_{{\text{c}}} f_{{\text{c}}}^{\prime } ~~~\left( { = N_{{{\text{pl}}}} } \right),} \hfill & {{\text{if: }}L_{{\text{e}}} /B \le 4 } \hfill \\ {N_{{{\text{pl}}}} - 0.125\left( {N_{{{\text{pl}}}} - N_{{\text{b}}} } \right)\left( {\frac{{{\text{ }}L_{{\text{e}}} }}{B} - 4} \right),} \hfill & {{\text{if: 4}} < L_{{\text{e}}} /B \le 12 } \hfill \\ {N_{{\text{b}}}^{{\text{c}}} + N_{{\text{b}}}^{{\text{s}}} ~~\left( { = N_{{\text{b}}} } \right),} \hfill & { {\text{if: }}L_{{\text{e}}} /B > 12} \hfill \\ \end{array} } \right.,$$

(15)

where, $L_{{\text{e}}}$ the effective length of the member and $N_{{\text{b}}}^{{\text{c}}}$, $N_{{\text{b}}}^{{\text{s}}}$, the buckling capacities of the concrete and steel parts of the section, respectively. The first branch in the formula, corresponds to the squash load of the section, while the third one to flexural buckling capacity. In both cases, the contributions of the steel and concrete parts are evaluated separately and then are combined together, in the above formulation. The global buckling capacity of the concrete is evaluated using the following procedure:

$$N_{{\text{b}}}^{{\text{c}}} = \left\{ {\begin{array}{*{20}l} {\frac{2}{{1 + \sqrt {\bar{\lambda }_{{\text{c}}}^{4} + 1} }}0.85A_{{\text{c}}} f_{{\text{c}}}^{\prime } ,} \hfill & {{\text{if: }}\overline{{ \lambda }} _{{\text{c}}} \le 1 } \hfill \\ {0.83e^{{\left[ {C_{{\text{c}}} \left( {1 - \overline{{ \lambda }} _{{\text{c}}} } \right)} \right]}} 0.85A_{{\text{c}}} f_{{\text{c}}}^{\prime } ,} \hfill & {{\text{if: }}\bar{\lambda }_{{\text{c}}} > 1} \hfill \\ \end{array} } \right.,$$

(16)

where:

$$\left\{ {\begin{array}{*{20}l} {\bar{\lambda }_{{\text{c}}} = \lambda _{{\text{c}}} \sqrt {\varepsilon _{{\text{u}}}^{{\text{c}}} } /\pi } \hfill \\ {\varepsilon _{{\text{u}}}^{{\text{c}}} = 0.00093\left( {0.85f_{{\text{c}}}^{'} } \right)^{{0.25}} } \hfill \\ {C_{{\text{c}}} = 0.568 + 0.00612f_{{\text{c}}}^{'} } \hfill \\ \end{array} } \right..$$

(17)

Buckling capacity of the steel tube is evaluated using the following procedure:

$$N_{{\text{b}}}^{{\text{s}}} = \left\{ {\begin{array}{*{20}l} {A_{{\text{s}}} f_{{\text{y}}} ,} \hfill & {{\text{if: }}\overline{{{\text{ }}\lambda }} _{{\text{s}}} < 0.3{\text{ }}} \hfill \\ {\left[ {1 - 0.545\left( {\overline{{{\text{ }}\lambda }} _{{\text{s}}} - 0.3} \right)} \right]{\text{ }}A_{{\text{s}}} f_{{\text{y}}} ,} \hfill & {{\text{if: }}0.3 \le \bar{\lambda }_{{\text{s}}} < 1.3{\text{ }}} \hfill \\ {\frac{1}{{1.3}}\frac{{\pi ^{2} E_{{\text{s}}} I_{{\text{s}}} }}{{L_{{\text{e}}} ^{2} }},} \hfill & {{\text{if: }}\bar{\lambda }_{{\text{s}}} \ge 1.3} \hfill \\ \end{array} } \right.,$$

(18)

where:

$$\bar{\lambda }_{{\text{s}}} = \frac{{\lambda _{{\text{s}}} }}{\pi }\sqrt {\frac{{f_{{\text{y}}} }}{{E_{{\text{s}}} }}} .$$

(19)

In the above expressions, $\lambda _{{\text{c}}}$ and $\lambda _{{\text{c}}}$ are the slenderness ratios of the concrete and steel parts of the column.

3.2.6 DBJ 13-51-2010

Chinese code DBJ 13-10-2010 [9] employs a combined yield stress $f_{{{\text{sc}}}}$, for the calculation of the squash load of the composite CFST section. The following expression is used for rectangular tubes:

$$f_{{{\text{sc}}}} = f_{{\text{c}}}^{'} \left( {1.18 + 0.85\xi } \right),$$

(20)

where, $\xi$ is a confinement factor, expressed through the following:

$$\xi = \frac{{{\rm A}_{{\text{s}}} f_{{\text{y}}} }}{{{\rm A}_{{\text{c}}} f_{{\text{c}}}^{'} }}.$$

(21)

The compressive resistance of the composite section is then found as:

$$N_{{}}^{{{\text{DB}}J13 - 51}} = f_{{{\text{sc}}}} \left( {A_{{\text{s}}} + A_{{\text{c}}} } \right).$$

(22)

3.2.7 ACI 318-14

American standard ACI 318-14 [7] recommends the following relationship for the ultimate capacity of a CFST column (ignoring the accidental eccentricity factor):

$$N_{{}}^{{{\text{ACI318}}}} = A_{{\text{s}}} f_{{\text{y}}} + 0.85A_{{\text{c}}} f_{{\text{c}}}^{'} .$$

(23)

The effect of column slenderness is considered in the standard, but through a magnification factor for the applied moments.

3.2.8 Sakino et al. [12]

Sakino et al. [12] proposed a strength reduction factor, for square-shaped tubes, that accounts local buckling phenomena. The ultimate resistance of square CFSTs is given by:

$$N_{{}}^{{{\text{Sakino 2004}}}} = A_{{\text{s}}} \sigma _{{{\text{scr}}}} + A_{{\text{c}}} \gamma _{{\text{U}}} f_{{\text{c}}}^{\prime } ,$$

(24)

where the influence of steel section slenderness is considered, through a critical stress $\sigma _{{{\text{scr}}}}$:

$$\sigma _{{{\text{scr}}}} = {\text{S}}f_{{\text{y}}} \le f_{{\text{y}}} ,$$

(25)

$$\frac{1}{S} = 0.698 + 0.128\left( {\frac{H}{t}} \right)^{2} \frac{{f_{{\text{y}}} }}{{E_{{\text{s}}} }}\frac{{4.00}}{{6.97}}.$$

(26)

Factor $\gamma _{{\text{U}}}$ accounts for the scale effects of the concrete strength:

$$\gamma _{{\text{U}}} = 1.67D_{{\text{c}}}^{{ - 0.112}} ,$$

(27)

where $D_{{\text{c}}}$ the diameter of an equivalent circle, with same sectional area.

3.2.9 Han et al. [13]

Han et al. [13], proposed a numerical and a simplified analytical model for the prediction of the nonlinear force–deformation curve of circular and square CFST columns, under axial compression. For the latter, the capacity of the composite section is estimated through combined yield stress:

$$N_{{}}^{{{\text{Han}}2005}} = f_{{{\text{scy}}}} \left( {A_{{\text{s}}} + A_{{\text{c}}} } \right),$$

(28)

$$f_{{{\text{scy}}}} = f_{{\text{c}}}^{'} \left( {1.18 + 0.85\xi } \right).$$

(29)

The formula for $f_{{{\text{scy}}}}$, in Eq. (28), is proposed for square sections. The authors introduce $\xi = {\rm A}_{{\text{s}}} f_{{\text{y}}} /{\rm A}_{{\text{c}}} f_{{\text{c}}}^{'}$, as a confinement factor, with a valid range between 0.1 and 5. The expressions proposed by the Chinese code DBJ 13-10-2010 [9], are identical to the ones proposed by Han et al. [13].

3.2.10 Ding et al. [15]

Ding et al. [15] proposed a simplified methodology for the estimation of the compressive capacity of stirrup confined, square, CFST columns. For stub columns, their approach results in the following relationship:

$$N_{{}}^{{{\text{Ding}}2014}} = f_{{\text{c}}}^{'} A_{{\text{c}}} + 1.2f_{{\text{y}}} A_{{\text{s}}} .$$

(30)

3.2.11 Wang et al. [17]

Wang et al. [17] proposed a simplified model for the prediction of compressive stiffness, the strain at ultimate strength and the ultimate axial load of circular and rectangular CFST columns. The latter is given by the following formula:

$$N_{{}}^{{{\text{Wang 2017}}}} = \eta _{\alpha } f_{{\text{y}}} A_{{\text{s}}} + \eta _{{\text{c}}} f_{{\text{c}}}^{\prime } A_{{\text{c}}} ,$$

(31)

where parameter $\eta _{\alpha }$, is a reduction factor accounting for concrete confinement demands to the steel section and potential local buckling, while parameter $\eta _{{\text{c}}}$ is an amplification factor accounting for concrete confinement. For rectangular tubes, these parameters are calibrated to:

$$\left\{ {\begin{array}{*{20}l} {\eta _{\alpha } = 0.91 + \left( {7310f_{{\text{y}}} - \left( {128 + 2.26f_{{\text{y}}} } \right)\left( {\frac{W}{t}} \right)^{2} } \right)10^{{ - 8}} } \hfill \\ {\eta _{c} = 0.98 + 29.5f_{{\text{y}}}^{{ - 0.48}} k_{{\text{s}}}^{{0.2}} \left( {\frac{{tf_{{\text{y}}} }}{{Wf_{{\text{c}}}^{\prime } }}} \right)^{{1.3}} } \hfill \\ \end{array} } \right.,$$

(32)

where $W = \sqrt {H^{2} + B^{2} }$, the diagonal length of the rectangular tube, and $k_{{\text{s}}}$ a confinement coefficient given by:

$$k_{{\text{s}}} = \frac{1}{3}\left( {\frac{{B - 2t}}{{H - 2t}}} \right)^{2} .$$

(33)

3.2.12 Du et al. [16] and Chen et al. [18]

Du et al. [16] proposed a calculation method, which was calibrated with experimental CFSTs, using high-strength steel. The following expression is proposed:

$$N_{{}}^{{{\text{Du 2016}}}} = f_{{\text{y}}} A_{{\text{s}}} + \left( {1 + k} \right)f_{{\text{c}}}^{'} A_{{\text{c}}} ,$$

(34)

where $k$, is an augmentation factor that reflects the enhancement caused by the steel tube to the concrete core, given by:

$$k = 0.5668 - 0.0039\frac{H}{t}\sqrt {\frac{{f_{{\text{y}}} }}{{235}}} .$$

(35)

The same expression was also calibrated by Chen et al. [18] for ultra-high-performance concrete. This time the augmentation factor, is given by the following equation (for square sections):

$$k = 0.3 - 0.004\frac{B}{t}\sqrt {\frac{{f_{{\text{y}}} }}{{235}}} .$$

(36)

3.2.13 Tran et al. [69]

Tran et al. [69] developed a neural network model, for the prediction of the axial compressive capacity of square CFST columns, taking into account the width and thickness of the steel tube, the column length and yield limit of the steel and concrete materials. Based on this model, an empirical expression was also proposed:

$$N_{{}}^{{{\text{Tran 2020}}}} = Q_{{\text{u}}}^{{\text{*}}} C_{{\text{L}}} C_{{\text{t}}} C_{{f_{{\text{y}}} }} C_{{f_{{\text{c}}}^{'} }} ,$$

(37)

where $Q_{{\text{u}}}^{{\text{*}}}$ is a the capacity, as a function of only the steel tube height $H$, which proved the most sensitive input parameter, given by:

$$Q_{{\text{u}}}^{*} = 0.0429H^{2} + 7.7943H + 300.2900,$$

(38)

and $C_{{\text{L}}}$, $C_{{\text{t}}}$, $C_{{f_{{\text{y}}} }}$, $C_{{f_{{\text{c}}}^{{\text{'}}} }}$ correction factors, accounting for the other 4 input parameters, calibrated to the following formulas:

$$\left\{ {\begin{array}{*{20}l} {C_{{\text{L}}} = - 0.0002\left( {\frac{L}{{800}}} \right)^{3} + 0.0011\left( {\frac{L}{{800}}} \right)^{2} - 0.0065\left( {\frac{L}{{800}}} \right) + 1.0055} \hfill \\ {C_{{\text{t}}} = - 0.0256\left( {\frac{t}{5}} \right)^{3} + 0.1297\left( {\frac{t}{5}} \right)^{2} + 0.1332\left( {\frac{t}{5}} \right) + 0.7633} \hfill \\ {C_{{f_{{\text{y}}} }} = - 0.0235\left( {\frac{{f_{{\text{y}}} }}{{500}}} \right)^{3} + 0.1259\left( {\frac{{f_{{\text{y}}} }}{{500}}} \right)^{2} + 0.0683\left( {\frac{{f_{{\text{y}}} }}{{500}}} \right) + 0.8295} \hfill \\ {C_{{f_{{\text{c}}}^{'} }} = - 0.0450\left( {\frac{{f_{{\text{c}}}^{'} }}{{60}}} \right)^{3} + 0.2906\left( {\frac{{f_{{\text{c}}}^{'} }}{{60}}} \right)^{2} + 0.1182\left( {\frac{{f_{{\text{c}}}^{'} }}{{60}}} \right) + 0.6348} \hfill \\ \end{array} } \right..$$

(39)

4 Materials and methods

4.1 Metaheuristic models

In this section, the basic principles and the constitutive rules followed by Artificial Neural Networks (ANNs) will be presented, focusing on the specific ANNs type known as back-propagation neural networks (BPNNs), as well as on other metaheuristic method such as balancing composite motion optimization (BCMO).

4.1.1 Artificial neural network

Artificial neural network (ANN) is a mathematical computational model that was inspired by the biological neural networks in the human brain [70]. By conception, the ANN exhibits the ability to learn from observed data and then make generalizations [22]. It is efficient in both cases of discrete and continuous functions by mapping the relationships between input variables and output response [71]. As proved by many investigations in the literature, the ANN possesses a strong ability to model complex nonlinear problems in civil engineering applications, where conventional techniques fail. For example, Ali et al. [72] for estimating the fire capacity of structural members, Asteris and Mokos [20] for predicting concrete compressive strength, and Hasanzadehshooiili et al. [73] for investigating buckling capacity of steel arch-shells. Therefore, the ANN is the most commonly employed AI-based model in civil engineering applications, thanks to its simplicity [74]. The ANN model consists of three layers of neurons namely input, hidden, and output layers. In such an architecture, each node is linked to all of the nodes in the next layer. However, there is no connection among the nodes on the same layer. The number of nodes in the input layer is the number of input variables, whereas the number of nodes in the output layer depends on the output variables of the considered problem. The information about the relationship between the inputs and output is represented by the weight and bias parameters. These weights and bias are the goal of the optimization problem, in minimizing errors between observed and predicted data [75,76,77].

The structure of an ANN model composes of three layers including input (variables), hidden (functional layer), and output layers (network’s outcomes). These layers are connected by the artificial computational neurons, which compute the weight parameters of the model. For a problem with one output response, the following nonlinear function is generalized by the ANN model [78,79,80]:

$$f:X \in \mathbb{R}^{N} \mapsto Y \in \mathbb{R}^{1} ,$$

(40)

where X is the input vector and Y is the predicted variable. The function f could be fully detailed, as follows [21, 81]:

$$X \mapsto f\left( X \right) = f_{{\text{o}}} \left( {L_{{\text{W}}} \times \left( {f_{{\text{h}}} \left( {b_{{\text{i}}} + I_{{\text{W}}} \times X} \right)} \right) + b_{{\text{o}}} } \right),$$

(41)

where I_W, f_h and b_i are the weight matrix, activation function and bias vector of the hidden layer; whereas L_W, f_o and b_o are the weight matrix, activation function and bias vector of the output layer, respectively.

4.1.2 Other metaheuristic method: balancing composite motion optimization

Balancing composite motion optimization (BCMO) is a novel population-based optimization technique, proposed by Le-Duc et al. [82]. The method is described as simple without following any natural or human behaviors [82]. The main idea of BCMO is that the searching motions of the population are equalized following a composite manner. In other words, a candidate solution can move in both global and local space, which is assumed Cartesian. The movement in the local space allows the candidate to find if there are any better solutions in the local region, whereas the other movement in the global space is useful in exploring sufficiently the search space. In terms of concept, a mathematical, probabilistic model for ensuring the equalization controls these movements. This concept allows obtaining a self-balance of the method during the optimization process, as the motions of a candidate solution are equalized in both exploration and exploitation. The performance of BCMO was checked against various classical benchmark functions such as unimodal, multimodal, as well as noisy quartic [83]. The BCMO method consists of the following main steps:

• Initialization: in this step, the population is initialized in the search space following a uniform distribution. The objective function is then evaluated and sorted for ranking all initial individuals.

• Determination of instant global point: in this step, an instant global point is determined based on both the best individual of the previous iteration and individual trial vector.

• Determination of the best individual: in this step, the best individual is assigned to be the instant global point determined previously.

• Calculation of the global movement in the search space for each individual.

• Calculation of the movement of each individual in the local region.

• Updating of the population: the position of each individual is updated, ready for the next iteration.

• Ranking of all individuals by their objective function values.

• Reaching of stopping condition, post-processing of results: if the maximum iteration is reached, the algorithm is stopped. The final population is stored for post-processing.

As recommended by Le-Duc et al. [82], the BCMO can be applied in various optimization problems because of the following reasons:

• The only parameter of BCMO to be controlled is its population size; therefore, it can be quickly employed for solving various types of optimization problems,

• BCMO is developed based on the mechanism of both mutation and crossover. Therefore, the individuals in the population are implicitly balanced based on the proposed random probabilistic model. Such self-organizing characteristics allow BCMO to be efficient in solving many other optimization problems.

Finally, more details on the BCMO method could be consulted in Le-Duc et al. [82].

4.2 Experimental database

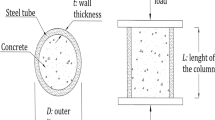
A database of experimental tests, available in the literature, for rectangular or square concrete-filled steel tube columns has been constructed and is presented herein. A number of 65 different literature sources have been collected, amounting to 880 individual experimental specimens, as presented in Table 2. A generalized experimental setup is shown in Fig. 1. The geometric configuration of each specimen depends on 4 parameters:

• the tube section external dimensions, $H$ and $B$ (with $H \ge B$),

• the tube wall thickness, $t$,

• and the column effective length, $L_{{\text{e}}}$.

Table 2 Data from experiments published in literature

Fig. 1

Rectangular concrete-filled steel tube columns under uniaxial compressive loading

Furthermore, three more parameters, relevant to the steel and concrete materials are recorded for each test:

• modulus of elasticity of the steel, $E_{{\text{s}}}$,

• yield limit of the steel $f_{{\text{y}}}$,

• and the cylinder strength of the concrete $f_{{\text{c}}}^{'}$.

Together, these 4 geometric and the 3 material parameters are considered the input variables of each experimental test. The effective length $L_{{\text{e}}}$ coincides with the physical length $L$, for short columns. For long columns, however, its value depends on the end support conditions of the specimen. When both ends are pinned, it is taken $L_{{\text{e}}} = L$. In other cases, different effective lengths are reported in the sources, and these values are assigned to $L_{{\text{e}}}$.

Table 3, presents a statistical analysis on the values these variables take in the database, which includes their minimums and maximums, their mean average and the standard deviation. Considering material properties, it can be seen that a vast range of steel yield limits is covered, which includes mild and high strength steels too (maximum value 835 MPa). Similarly, a very wide range of concrete strengths from 8.51 to 151 MPa is present in the database. Regarding geometry, the database includes both short and slender columns, as well as, compact and thin-walled ones. The output variable from each experimental test, is the ultimate axial compressive force, $N$, that was recording during testing (depicted schematically in Fig. 1). Table 3 presents the range of $N$ throughout the whole database. A quite extended sample of ultimate axial compressive forces is included, ranging from 105 kN up to 7780 kN.

Table 3 The input and output parameters used in the development of BPNNs (all datasets)

Table 4 presents the correlation between all variables, both input and output, in the database. Specifically, the Pearson correlation coefficient $R$, is shown between the values of every pair of variables in the database. Figure 2 displays a graphical representation of the correlation coefficients. Regarding input parameters, a high coefficient is generally unwanted, since it implies a linear relationship between the involved variables, resulting in a reduced generality of the database. Except for the high coefficient, between $B$ and $H$ (which is expected for the rectangular tubes that are practically available), it can be seen, that the correlation coefficient is indeed low for all other pairs of input parameters ($< 0.5$), which means that the input variables are indeed sufficiently scattered. The stronger correlations exist between the steel and concrete strengths, $f_{{\text{y}}}$ and $f_{{\text{c}}}^{'}$, with $R = 0.48$, and between the steel strength $f_{{\text{y}}}$ and the tube thickness $t$, with $R = 0.43$. For the remaining pairs the coefficient is quite lower.

Table 4 Correlation matrix of the variables

Fig. 2

Correlogram of the variables (input and output parameters)

Regarding the correlation between the input parameters and the output, the lower coefficients are found for the column length $L_{{\text{e}}}$, and for the modulus of elasticity of steel, $E_{{\text{s}}}$. These parameters are related with the failure of the column due to flexural buckling and they are considered irrelevant when material strength determines failure. In this context, the low coefficients between the output and the $L_{{\text{e}}}$, $E_{{\text{s}}}$ parameters, indicate that most of the test columns in the database, are not very slender, so that buckling failure would be critical. On the other hand, the stronger correlations between input and output parameters are found for the tube dimensions $B$ and $H$, with coefficients 0.67 and 0.63, respectively.

Figures 3, 4 and 5 demonstrate the scatter of the input and output variables in the database. More specifically, for each variable, a scatter plot is presented, depicting, for all the available tests, the values the variable takes and the respective values of the output (the ultimate axial force N). Also, for each variable, a histogram is shown, that groups the total number of tests, in predetermined sub-ranges. Regarding the steel tube dimensions, $B$ and $H$, it can be seen that most of the specimens involve lower values of sectional width and height, with most dominant, the 100.1–150 mm value range. For higher values, the number of specimens gradually decreases. In particular, a quite low number of available specimens is found for the 250.1–300 mm range, which highlights the need for more experimental testing in this particular area. Similarly, for the tube thickness $t$, most of the specimens involve values at the lower ranges, with more than half in between the 3.01–6.00 mm range. Very few specimens are available for thicknesses greater than 9 mm.

Fig. 3

Histograms of the parameters: length of tubes section (B); height of tubes section (H); thickness of tubes section (t)

Fig. 4

Histograms of the parameters: effective length of steel tube column (L_e); steel yield limit (f_y); steel modulus of elasticity (E_s)

Fig. 5

Histograms of the parameters: concrete compressive strength ($f_{{\text{c}}}^{\prime }$); axial load (N)

Regarding the column effective length $L_{{\text{e}}}$, a strong preference for lengths below 1 m is observed. The distribution of the specimens to larger lengths is almost uniform though, except for the higher range (> 3 m). The preference for smaller lengths downgrades the member stability as a possible failure mode and explains the small correlation between the column length and the output axial load, mentioned earlier. Continuing to steel yield limit $f_{{\text{y}}}$, a rather broad scatter of its value can be seen, throughout the specimens. The majority of the specimens feature $f_{{\text{y}}}$ values between 201 and 400 MPa, which are typical for mild steel grades. However, there is a considerable number of specimens involving high-strength steels, particularly in the ranges over 700 MPa. On the other hand, the steel modulus of elasticity $E_{{\text{s}}}$ demonstrates a predominant presence of specimens in the 191–200 GPa range. Many specimens are stacked in key $E_{{\text{s}}}$ values, indicating a possible reference to nominal material properties, rather than measured ones. Regarding the concrete strength $f_{{\text{c}}}^{'}$, a broad scatter of its value is observed. Most specimens feature concrete strengths in the range 21–40 MPa, followed closely by the 41–60 range. The number of specimens decreases gradually for larger $f_{{\text{c}}}^{'}$ values.

4.3 Sensitivity analysis of the parameters affecting the axial load capacity of CSFT based on the experimental database

In general, sensitivity analysis (SA) of a numerical model is a technique used to determine if the output of the model is affected by changes in the input parameters. This provides feedback as to which input parameters are the most significant, and thus, by removing the insignificant ones, the input space will be reduced, and subsequently the complexity of the model, as well as the time required for its training, will be also reduced. To identify the effects of model inputs on the outputs, the SA can be conducted on the database. Sometimes, the results of SA helps researchers/designers to remove one or more input parameters from the database to obtain better analyses with a higher level of performance prediction. To perform the SA, the cosine amplitude method (CAM), which has been used by many researchers [111,112,113] was selected and implemented. In CAM, data pairs will be used to construct a data array, X, as follows:

$$X = \left\{ {x_{1} ,x_{2} ,x_{3} , \ldots ,x_{i} , \ldots ,x_{n} } \right\}.$$

(42)

Variable $x_{i}$ in array, $X$, is a vector of length m, defined as:

$$x_{i} = \left\{ {x_{{i1}} ,x_{{i2}} ,x_{{i3}} , \ldots ,x_{{im}} } \right\}.$$

(43)

The relationship between $R_{{ij}}$ (strength of the relation) and datasets of $X_{i}$ and $X_{j}$ is presented by the following equation:

$$R_{{ij}} = \frac{{\mathop \sum \nolimits_{{k = 1}}^{m} x_{{ik}} x_{{jk}} }}{{\sqrt {\mathop \sum \nolimits_{{k = 1}}^{m} x_{{ik}}^{2} \mathop \sum \nolimits_{{k = 1}}^{m} x_{{ik}}^{2} } }}.$$

(44)

The relative strength of effect (RSE) values $R_{{ij}}$ between the compressive strength and the input parameters are shown in Fig. 6. This analysis reveals that, the width and the height of the steel tubes cross-section have the greatest influence on axial load capacity values, with strength values of 0.8889 and 0.8754 respectively, followed by steel yield limit, $f_{{\text{y}}}$ (0.8626), thickness of tube walls, $t$ (0.8584), concrete compressive strength,$f_{{\text{c}}}^{\prime }$ (0.8136), steel modulus of elasticity, $E_{{\text{s}}}$ (0.7986) and, the parameter with the lowest influence on axial load capacity seems to be the effective column length, $L_{{\text{e}}}$ (0.5460).

Fig. 6

Sensitivity analysis of axial load capacity of rectangular concrete-filled steel tube columns

4.4 Performance indices

Three different statistical parameters were employed to evaluate the performance of the derived model as well as the available in the literature formulae, including the root mean square error (RMSE), the mean absolute percentage error (MAPE), and the coefficient of determination (R²). Lower RMSE and MAPE values represent more accurate prediction results (a null value indicates a perfect fit), while higher R² values represent a better fit between the analytical and predicted values (a unit value indicates a perfect fit). The aforementioned statistical parameters have been calculated by the following expressions [114]:

$${\text{RMSE}} = \sqrt {\frac{1}{n}\mathop \sum \limits_{{i = 1}}^{n} \left( {x_{i} - y_{i} } \right)^{2} } ,$$

(45)

$${\text{MAPE}} = \frac{1}{n}\mathop \sum \limits_{{i = 1}}^{n} \left| {\frac{{x_{i} - y_{i} }}{{x_{i} }}} \right|,$$

(46)

$$R^{2} = 1 - \left( {\frac{{\mathop \sum \nolimits_{{i = 1}}^{n} \left( {x_{i} - y_{i} } \right)^{2} }}{{\mathop \sum \nolimits_{{i = 1}}^{n} \left( {x_{i} - \bar{x}} \right)^{2} }}} \right),$$

(47)

where, $n$ denotes the total number of datasets, and $x_{i}$ and $y_{i}$ represent the predicted and target values, respectively.

The reliability and accuracy of the developed neural networks were evaluated using R² and RMSE. RMSE presents information on the short term efficiency which is a benchmark of the difference of predicated values in relation to the experimental values. The lower the RMSE, the more accurate the evaluation is. The R² measures the variance that is interpreted by the model, which is the reduction of variance when using the model. R² values ranges from 0 to 1 while the model has healthy predictive ability when it is near 1 and is not currently analyzing, when it is near 0. These performance metrics are a good measure of the overall predictive accuracy.

It should be highlighted that, amongst the statistical indices available, the majority of researchers use the R², in order to evaluate the effectiveness of the developed computation model. The R², is a measure of the linear correlation between two variables X and Y. For forecasting models, such as AI models, X and Y represent the predicted and target values, respectively. According to the Cauchy–Schwarz inequality [115], the coefficient R has a value between + 1 and − 1. The further away R is from zero, the stronger the linear relationship is between the two variables. The sign of R corresponds to the direction of the relationship. If R is positive, then as one variable increases, the other tends to also increase. If R is negative, then as one variable increases, the other tends to decrease. A perfect linear relationship (R = − 1 or R = 1) means that one of the variables can be perfectly explained by a linear function of the other. As aforementioned, the reliability of a model’s forecasting ability increases as the R² value approached + 1. Despite the fact that this index is widely used by the majority of researchers, it is in fact the most unreliable amongst the available statistical indices, an observation which can be illustrated through the following example. Supposed that a model predicts a constant value Χ for all data, in accordance to the following function:

$$X = c,$$

(48)

where, c is a constant. This would result in the model forecasting the constant value c for any target value, as depicted in Fig. 7.

Fig. 7

Correlation coefficient between two variables X and Y

Often, the Pearson correlation coefficient is used to calculate the slope of the linear relationship between two variables, in accordance to the following linear expression:

$$X = aY + c.$$

(49)

When two forecasting models present different R values, as well as different slope values, comparison between the models is impossible. Even more so, when evaluating neural networks developed through different architectures. Therefore, the following new engineering index, the a20-index, has been recently proposed [20, 116,117,118,119,120,121,122,123,124,125] for the reliability assessment of the developed SC techniques:

$${\text{a}}20 - {\text{index}} = \frac{{{\text{m}}20}}{M}$$

(50)

where, M is the number of dataset sample and m20 is the number of samples with a value of (experimental value)/(predicted value) ratio, between 0.80 and 1.20. Note that for a perfect predictive model, the values of a20-index values are expected to be the unit value. The proposed a20-index has the advantage of a physical engineering meaning, as it declares the amount of the samples that satisfy the predicted values with a deviation of ± 20%, compared to experimental values.

5 Methodology

Methodology for predicting axial load of CFST columns can be divided into the following four main steps:

Step 1: Dataset preparation: the data were randomly split into 3 parts: the first 66.70% of data values (587 samples) were used for training the models, while the remaining 16.60 and 16.70% of data (146 and 147 samples, respectively) were taken for validating and testing the models.

Step 2: Building models: parametric studies, including with or without normalization of data, number of neurons in hidden layer, activation functions, with or without Young’s modulus of steel, etc, were conducted for developing the machine learning models.

Step 3: Validating models: the ANN model was validated using the validating dataset, using different performance indices such as a-20 index, RMSE, MAPE, VAF, and R.

Step 4: Comparing models: the performance of the developed model was compared with different standards and existing empirical equations.

Step 5: Proposed explicit equation and Graphical User Interface: an explicit equation for the prediction of axial load of CFST columns was proposed in a matrix form, together with an Excel-based Graphical User Interface (appended to this paper), for a practical application purpose.

6 Results and discussion

6.1 ANN models

6.1.1 Development of ANN models

Based on the above, different architecture ANNs were developed and trained. More specifically, during the development and training of the ANN models the following steps (which are summarized in Table 5) were followed:

• The 880 datasets comprising the database used for the training and development of the ANN models were divided into three separate sets. Specifically, 587 of 880 (66.70%) datasets were designated as Training datasets, 146 (16.60%) as Validation datasets, while 147 (16.70%) datasets were used as Testing datasets.

• During the training phase of the ANNs, the above datasets were used with and without normalization. In the case were normalization of the data was conducted, the minmax normalization technique in the range [0.10, 0.90] was implemented.

• The Levenberg–Marquardt algorithm [126] was used for the training of the ANNs.

• 10 different initial values of weights and biases were applied for each architecture.

• ANNs with only one hidden layer were developed and trained.

• The number of neurons per hidden layer ranged from 1 to 250, by an increment step of 1.

• Two functions, the mean square error (MSE) and sum square error (SSE) functions, were used as cost function, during the training and validation process.

• 10 functions, as presented in Table 5, were used as transfer or activation functions.

Table 5 Training parameters of ANN models

The above steps resulted in the development of 100.000 different ANNs. It is worth noting that only the use of 10 different transfer function results in 100 different ANNs, for each architecture with the same number of neurons, as a result of 100 (= 10²) different dual combinations of the 10 transfer functions investigated.

6.1.2 Optimum parameters for modelling the axial load capacity

Regarding the simulation of the axial load capacity of the rectangular concrete-filled steel tube columns, it is particularly important to select the main parameters which affect its obtained value. In the present section, four different cases are examined (Table 6), regarding the parameters, which will be taken into account as influencing, for the development of axial load capacity.

Table 6 Cases of variables used for the estimation of the axial load capacity of the rectangular concrete-filled steel tube columns

As stated in Table 6, case scenario I is the reference scenario, where the six (6) basic input parameters, influencing axial load capacity, are taken into consideration. Namely, the parameters: the width of tubes section (B), the height of tubes section (H), the thickness of tubes (t), the length of steel tube column (L_e), the steel yield limit (f_y) and the concrete compressive strength ($f_{{\text{c}}}^{\prime }$). In case scenario II, the input parameters are increased to seven (7), to also include the steel modulus of elasticity (E_s).

To evaluate which of the two above cases is the most appropriate for the most accurate prediction of axial load capacity, and taking into account the steps, described in the previous section, 400.000 ANNs were developed, trained and evaluated. The optimum architectures are presented in Table 7.

Table 7 Optimum architectures for the two cases of variables (input parameters) investigated for the estimation of axial load capacity

Results presented in Table 7, highlight no important effect of steel modulus of elasticity (E_s) on the value of axial load capacity of concrete-filled steel tube columns, in accordance with the same finding of sensitivity analysis, which has been presented in the previous section (Fig. 6). At this point, it is worth noting that for both two cases examined, the best results were obtained with normalization of the data, using minmax technique (Table 7).

6.1.3 Optimum ANN models

In this section, the key points process for the development of the optimum ANN model for the prediction of the axial load capacity (N) of concrete-filled steel tube columns are presented in detail. Based on the previous investigation, the best input parameters are those corresponding to Case I. Therefore, using only six input parameters (excluding the steel modulus of elasticity), a plethora of different ANN models have been trained and developed with the following parameters:

• six (6) input parameters, for the modelling of axial load capacity which is the only output parameter,

• use of datasets with and without normalization technique (minmax in the range 0.10–0.90),

• architectures with only one hidden layer,

• neurons per hidden layer from 1 to 50 by step 1,

• use two cost functions. Namely, mean square error (MSE) and sum square error (SSE), and

• use as activation functions in hidden and output layer, 100 different combinations, based on the ten functions presented in Table 5.

The above parameters result in the development of 400.000 different architectures of ANN models. The top 20 architectures, based on the value of RMSE, for Testing Datasets, are presented in Table 8. All the top 20 ANN models have excellent performance, with values of R greater than 0.9930. Among them, the optimum ANN model, based on the value of RMSE of Testing Datasets, is the BPNN 6-27-1 model that corresponds to a NN structure with 27 neurons and the use of minmax normalization technique in the range 0.10–0.90 (Fig. 8). On the other hand, even though the BPNN 6-17-1 model presents slightly lower performance indices, it is superior in terms of simplicity, as the hidden layer contains only 17 neurons, without using any normalization technique, in contrast to the 27 neurons of the (statistically) optimum ANN.

Table 8 Architectures of top ten ANNs based on testing datasets root mean square error (RMSE)

Fig. 8

The architecture of the optimum 6-27-1 ANN

Furthermore, in Table 9 and Fig. 9, a detailed presentation of the performance of the optimum ANN model, including the a20-index, is presented. It is clearly highilited that the developed optimum model, based on all the 5 used performance indices, is a reliable tool for the prediction of the steel tubes axial load capacity. Specifically, the value of a 20-index is equal to 0.8980, for the case of testing datasets. In physical terms, this means that for 89.80% of the samples, the predicted values of the axial load satisfy a deviation of ± 20%, compared to experimental values.

Table 9 Summary of prediction capability of the optimum 6-27-1 BPNN

Fig. 9

Experimental vs predicted axial load for the optimum 6-27-1 BPNN

Based on the results presented in Table 8, the following key findings have been revealed, regarding the transfer functions of the best 20 ANN models:

• The most appropriate transfer functions for the hidden layer, are the log-sigmoid transfer function (LS), the positive linear transfer function (PLi), the normalized radial basis transfer function (NRB) and the hyperbolic tangent sigmoid transfer function (HTS).

• Concerning the output layers, the most appropriate functions seem to be the hyperbolic tangent sigmoid transfer function (HTS), the linear transfer function (Li) and the symmetric saturating linear transfer function (SSL).

6.2 Optimization of BPNN 6-27-1 model by BCMO algorithm

In this section, the BPNN 6-27-1 model, obtained previously, is optimized using the BCMO algorithm. The weights and bias of the BPNN 6-27-1 model were employed directly, as initial values of the optimization problem. It is noted, that there were 217 optimizable parameters of the BPNN 6-27-1 model (6 input variables, 27 neurons in the hidden layer and one output variable). The BCMO algorithm was conducted using a population size of 50, as recommended by Duong et al. [22], for an optimization problem with six design variables. A maximum number of 9 × 10⁵ iterations was employed, as the stopping criterion, during optimization by BCMO. Figure 10 presents the evaluation of performance indices R, RMSE, MAPE, and VAF, during the optimization process. Performance indices for training, validating and testing datasets, as well as, for all datasets, are included. It is seen that the selection of 9 × 10⁵ iterations is significant to obtain optimized results, with respect to all performance criteria.

Fig. 10

Evolution of performance indices over 9 × 10⁵ iterations: a R, b RMSE, c MAPE and d VAF

Weight and bias parameters obtained at the last iteration were extracted for constructing the final prediction model. This model was then used as a numerical prediction function, investigating parametrically the deviation of performance criteria, in function weight parameters. This parametric study could be helpful to verify if the results provided by the BCMO algorithm are unique, i.e. if the BCMO allowed reaching the global optimum of the problem. For illustration purposes, only the four first weight parameters are plotted. Figure 11a presents the evolution of RMSE, while varying weight parameters (N°1 and N°2), from their lowest to highest values. In the same context, Fig. 11b–d present the evolution of RMSE, while varying weight parameters (N°1 and N°3), (N°2 and N°3), and (N°3 and N°4), from their lowest to highest values. It can be seen, that the global optimum points of these RMSE surfaces match the final set provided by the BCMO algorithm. This remark confirms that the BCMO technique succesfully reached the global optimum of the optimization problem, providing this way the final prediction model.

Fig. 11

Verification of global optimum provided by the BCMO. The surfaces of RMSE show unique optimal solution, which minimizes the value of RMSE: a between weight parameters N°1 and N°2, b between weight parameters N°1 and N°3, c between weight parameters N°2 and N°3, d between weight parameters N°3 and N°4. Optimal points obtained by BCMO are marked by black cross

Finally, in Table 10 and Fig. 12, a detailed presentation of the performance of the BPNN 6-27-1-BCMO model, including a comparison with the BPNN 6-27-1 model, is presented. It is clearly highlighted that the BPNN 6-27-1-BCMO model exhibits a better performance than the BPNN 6-27-1 model.

Table 10 Summary of prediction capability of the optimum 6-27-1 BPNN and 6-27-1 BPNN optimized by BCMO

Fig. 12

Experimental vs predicted axial load for the optimum 6-27-1 BPNN and 6-27-1 BPNN-BCMO

6.3 Comparison with code standards

In Table 11 the performance of the optimum BPNN 6-27-1 model and of its optimized BPNN 6-27-1-BCMO version is compared with the available methodologies in design codes [5,6,7,8,9,10], that were described earlier in text. For the calculations, the design formulas are applied without safety factors. Only the specimens in the Testing Dataset are included in the results presented in Table 11. The models are sorted according to their RMSE (mean square) index. A significantly improved performance is observed for the BPNN 6-27-1 model, scoring about 38% smaller RMSE index from the next model, that is the Australian AS5100 [10] one. Also, the performance for the other indices is clearly improved. The performance of the BPNN 6-27-1-BCMO model, however, is even better, in every index, achieving a 12% smaller RMSE, compared to its non-optimized variant (or 46% compared to the most performant code). The a20-index is also significantly improved.

Table 11 Ranking of developed soft computing models BPNN 6-27-1-BCMO and BPNN 6-27-1 against available procedures in design codes, based on RMSE values for the case of testing datasets

Comparing between the codes, it is found that AS5100 [10] manages to offer a better performance overall, closely followed by the Eurocode EN1994 [5]. Japanese AIJ [8] and the American LRFD 1999 [66] are following with approximately 25% higher RMSE index, compared to the Australian code. The newer American AISC360 [6] falls further behind, having 41% higher RMSE index, however, its correlation coefficient R is better. For the Chinese code DBJ13-51-2010 [9], the RMSE index is much worse than the others. This could be attributed to the missing of any calculation for stability phenomena, however, a similar performance cannot be seen for the ACI 318 [7] code, which also misses stability calculations, but manages to achieve comparable to others performance, despite its simplicity.

The performance indices shown in Table 11 involve all the specimens in the Testing Dataset. However, every code places some limits for its field of application. Table 1, earlier in the text, presents these limits for every code. Not all specimens in the Testing Dataset satisfy these limits. It is interesting, to compare the different codes, only for those specimens that meet their respective field of application. Table 12, presents the performance indices, for such a subset in the Testing Dataset (different subset for each code), as well as the number of specimens in the subset. More inclusive proves the American AISC 360 [6] code, which covers, in its field of application 88 out of 147 specimens, more than any other code. On the other hand, it is the code with the worst RMSE, as well as a20-index. Less inclusive is the Australian AS5100 [10] code, with only 26 out of 147, specimens satisfying its requirements. All the codes achieve improved RMSE indices compared to the complete testing dataset, but their remaining indices deteriorate. Despite this improvement, the proposed ANN models, outperform all codes, in every index, while covering the complete Testing Dataset. Between the different codes, EN1994 [5] achieves the best RMSE index, very close to the BPNN 6-27-1 model. Also, its other performance indices are also better. American ACI 318 [7], despite its simplicity, manages to perform better than most other codes, achieving the second better RMSE index.

Table 12 Ranking of developed soft computing models BPNN 6-27-1-BCMO and BPNN 6-27-1 against available procedures in design codes, based on RMSE values for the case of testing datasets, considering application limits

In Fig. 13, the scatter plots for the experimental vs, predicted axial load, for the specimens in the testing dataset, are presented, for the BPNN 6-27-1-BCMO and BPNN 6-27-1 models, as well as, for the models recommended by the available design codes [5,6,7,8,9,10]. For the latter, the points in gray color represent specimens that do not satisfy the respective code field of application. The ANN models appear to converge to the experimental values, much more closely than the design code models, throughout the entire range of axial loads. Commenting on the performance of different codes, it appears that EN1994 [5] and AS5100 [10] produce an almost balanced output, around the experimental mean. A potential for widening their field of application can therefore be seen from these results. On the other hand, AISC 360 [6] as well as, AIJ [8] and LRFD 1999 [66], to a less extent, appear to underestimate the load values, particularly for the lower end of the load range. DBJ13-51-2010 [9], to the contrary, overestimates the load values, throughout the available load range.

Fig. 13

Comparison of developed soft computing models BPNN 6-27-1-BCMO and BPNN 6-27-1 (top row) against available procedures in design codes

6.4 Comparison with other models from the literature

In Table 13, the performance of the BPNN 6-27-1-BCMO and BPNN 6-27-1 models is compared against available methodologies in the literature [12, 13, 15,16,17,18, 69], presented earlier. Only the specimens in the testing dataset are included. The models are sorted accorded to their RMSE (mean square) index. It is observed that the proposed ANN models, outperform all other models, achieving significantly improved performance indices (about 58% smaller RMSE for the BPNN 6-27-1-BCMO, compared to the higher sorted one, from Sakino et al. [12]). The models proposed by Sakino et al. [12] and Wang et al. [17], both of which take into account the section slenderness, appear to perform better that the others, particularly in terms of RMSE. The model of Chen et al. [18], achieves the higher a20-index, among the analytical models, though it is still considerably lower, compared to the ANN models.

Table 13 Ranking of developed soft computing models BPNN 6-27-1-BCMO and BPNN 6-27-1 against available in literature proposals, based on RMSE values for the case of testing datasets

In Fig. 14, the scatter plots for the experimental vs, predicted axial load, for the specimens in the Testing Dataset, are presented, for the BPNN 6-27-1-BCMO and BPNN 6-27-1 models, as well as for the examined literature models. Again, the proposed models seem to converge considerably better to the experimental values. The models by Sakino et al. [12], Wang et al. [17] and Chen et al. [18], appear to produce a rather balanced output, around the experimental mean, compared to the other models. The models by Han et al. [13] (which employs the same formulation with Chinese code DBJ13-51-2010 [9]), by Ding et al. [15] and by Du et al. [16] consistently overestimate the load value. On the other hand, the model by Tran et al. [69], appears to significantly overestimate the axial load for the lower end of the load range, while underestimating it for the upper end.

Fig. 14

Comparison of developed soft computing models BPNN 6-27-1-BCMO and BPNN 6-27-1 (top row) against available proposals in the literature

6.5 Proposed explicit equation and graphical user interface

In this section, we present the close form of the explicit equations for the prediction of axial load of CFST columns, based on the optimal machine learning model, presented previously. It is not convenient for engineers/researchers to use machine learning models in practice, because such a “black-box” model composes of weights and bias, together with activation functions. Thus, explicit equations based on the developed machine learning model should be derived for a direct and efficient application. The proposed mathematic calculation for the prediction of axial load of CFST columns is presented in a matrix form in Eq. (51):

$$N_{{\text{u}}}^{{{\text{predicted}}}} = {\text{tansig}}\left( {\left[ {L_{{\text{W}}} } \right] \times \left[ {{\text{logsig}}\left( {\left[ {I_{{\text{W}}} } \right] \times \left[ {x_{n} } \right] + \left[ {b_{{\text{i}}} } \right]} \right)} \right] + \left[ {b_{{\text{o}}} } \right]} \right),$$

(51)

where $\left[ {x_{n} } \right]$ is a 6 × 1 input vector; $\left[ {I_{{\text{W}}} } \right]$ is a 27 × 6 matrix containing weights of the hidden layer; $\left[ {L_{{\text{W}}} } \right]$ is a 1 × 27 vector containing weights of the output layer; $\left[ {b_{{\text{i}}} } \right]$ is a 27 × 1 vector containing bias of the hidden layer; and $\left[ {b_{{\text{o}}} } \right]$ is a 1 × 1 vector containing bias of the output layer. Vector $\left[ {x_{n} } \right]$ is given by:

$$\left[ {x_{n} } \right] = \frac{5}{2} \times \left( {\left[ \begin{gathered} x_{B} \hfill \\ x_{H} \hfill \\ x_{t} \hfill \\ x_{{L_{{\text{e}}} }} \hfill \\ x_{{f_{{\text{y}}} }} \hfill \\ x_{{f_{{\text{c}}}^{'} }} \hfill \\ \end{gathered} \right] - 0.1} \right) - 1,$$

(52)

where

$$\left\{ \begin{gathered} x_{B} = 0.8\left( {B - B_{{\min }} } \right)/\left( {B_{{\max }} - B_{{\min }} } \right) + 0.1 \hfill \\ x_{H} = 0.8\left( {H - H_{{\min }} } \right)/\left( {H_{{\max }} - H_{{\min }} } \right) + 0.1 \hfill \\ x_{t} = 0.8\left( {t - t_{{\min }} } \right)/\left( {t_{{\max }} - t_{{\min }} } \right) + 0.1 \hfill \\ x_{{L_{{\text{e}}} }} = 0.8\left( {L_{{\text{e}}} - L_{{{\text{e}}\min }} } \right)/\left( {L_{{{\text{e}}\max }} - L_{{{\text{e}}\min }} } \right) + 0.1 \hfill \\ x_{{f_{{\text{y}}} }} = 0.8\left( {f_{y} - f_{{y\min }} } \right)/\left( {f_{{{\text{y}}\max }} - f_{{{\text{y}}\min }} } \right) + 0.1 \hfill \\ x_{{f_{{\text{c}}}^{'} }} = 0.8\left( {f_{{\text{c}}}^{'} - f_{{{\text{c}}\min }}^{'} } \right)/\left( {f_{{{\text{c}}\max }}^{'} - f_{{{\text{c}}\min }}^{'} } \right) + 0.1 \hfill \\ \end{gathered} \right.,$$

(53)

Minimum and maximum values of input variables are given in Table 3. On the other hand, $\left[ {I_{{\text{W}}} } \right]$, $\left[ {L_{{\text{W}}} } \right]$, $\left[ {b_{{\text{i}}} } \right]$ and $\left[ {b_{{\text{o}}} } \right]$ are given by:

$$\left[ {I_{{\text{W}}} } \right] = \left[ {\begin{array}{*{20}c} { - 0.6842} & { - 5.8840} & {6.0732} & { - 0.2371} & {2.3141} & { - 1.1916} \\ {4.4341} & { - 6.9129} & { - 0.2506} & { - 2.7163} & { - 1.9236} & {5.1724} \\ { - 6.1348} & { - 1.4091} & {1.9660} & { - 2.3765} & {0.2505} & {1.0817} \\ { - 1.7979} & { - 2.2308} & { - 0.5994} & {5.8943} & {3.2321} & { - 1.1338} \\ {2.2898} & {2.8668} & { - 1.7847} & { - 0.5836} & {1.2450} & { - 1.8966} \\ { - 2.0614} & {6.1328} & {2.1043} & { - 1.9921} & { - 3.2341} & {3.6724} \\ { - 0.3125} & {1.6238} & {1.8828} & {2.7811} & { - 1.4969} & { - 0.0494} \\ {1.7406} & { - 0.6431} & { - 2.0980} & {1.5658} & { - 0.3078} & { - 3.1920} \\ {5.1810} & { - 0.3230} & {4.6036} & {1.0361} & {4.1943} & {0.9496} \\ {5.7311} & {0.1348} & { - 2.7615} & { - 1.7411} & { - 6.4058} & { - 0.7156} \\ {1.9401} & {0.7519} & { - 6.5444} & { - 7.1657} & {5.8021} & {5.2713} \\ { - 7.1872} & { - 5.0112} & {4.0393} & {4.0989} & { - 0.1379} & {5.9474} \\ {5.0587} & {1.6659} & { - 1.9654} & {3.9619} & { - 2.3001} & { - 7.0451} \\ {4.4040} & {4.4280} & { - 3.1617} & {3.3130} & { - 3.4476} & { - 6.3119} \\ { - 3.1581} & {0.7416} & {1.0388} & {4.4699} & {1.7863} & { - 5.3506} \\ {4.6719} & { - 7.1352} & { - 1.9883} & {0.0733} & { - 2.7178} & { - 1.8665} \\ {0.4226} & {0.3173} & { - 2.8865} & {4.6372} & { - 4.6964} & { - 1.8046} \\ { - 4.4317} & {3.4197} & { - 7.1785} & {5.4733} & { - 1.8705} & {4.7364} \\ { - 1.9748} & { - 0.2925} & {0.7026} & { - 5.8795} & { - 2.9754} & { - 3.4682} \\ {1.4463} & {0.3188} & {2.7898} & { - 1.6934} & {2.8816} & { - 1.8081} \\ { - 0.3032} & {5.8290} & { - 4.9297} & { - 2.3103} & {2.1232} & { - 1.0433} \\ { - 0.9655} & { - 3.3258} & { - 3.6768} & { - 4.5653} & {2.4464} & { - 2.6838} \\ { - 0.0849} & {2.5787} & { - 3.7486} & { - 3.0462} & {2.8743} & {0.5642} \\ {3.6757} & { - 4.3359} & { - 0.6372} & {2.3030} & {3.2193} & {0.9106} \\ { - 2.2291} & { - 2.0756} & { - 3.3454} & { - 3.8062} & {1.1501} & { - 4.1052} \\ {3.7204} & {4.2145} & {1.9023} & { - 0.2873} & { - 1.0326} & { - 2.1055} \\ { - 5.5265} & { - 1.7746} & {6.1162} & {0.6304} & {0.6606} & {1.9640} \\ \end{array} } \right],$$

(54)

$$\left[ {b_{{\text{i}}} } \right] = \left[ {\begin{array}{*{20}c} {6.1185} \\ { - 7.1877} \\ {5.7092} \\ { - 2.7414} \\ { - 7.1877} \\ {3.3939} \\ {2.3079} \\ { - 3.0312} \\ { - 4.4045} \\ {0.5886} \\ {5.7489} \\ {4.4240} \\ {0.2204} \\ {1.0986} \\ {0.1183} \\ {4.0449} \\ {2.6714} \\ {1.6212} \\ { - 2.2771} \\ {1.3121} \\ {4.2471} \\ { - 2.3960} \\ {4.6779} \\ {5.8968} \\ { - 3.8083} \\ {5.9148} \\ { - 3.3276} \\ \end{array} } \right]\quad \left[ {L_{{\text{W}}}^{{}} } \right]^{{\text{T}}} = \left[ {\begin{array}{*{20}c} { - 0.4314} \\ {0.9021} \\ { - 1.0456} \\ { - 0.5849} \\ { - 2.9228} \\ { - 0.4687} \\ {1.0860} \\ { - 1.1392} \\ {1.3276} \\ {0.3430} \\ {0.0962} \\ { - 0.3027} \\ { - 0.6035} \\ {0.5117} \\ { - 0.4309} \\ { - 0.0817} \\ { - 0.7523} \\ {0.3551} \\ { - 0.6640} \\ {0.7115} \\ {1.0261} \\ { - 0.4895} \\ { - 1.1446} \\ {0.7812} \\ {0.6088} \\ {0.7326} \\ {0.1510} \\ \end{array} } \right],$$

(55)

$$\left[ {b_{{\text{o}}} } \right] = \left[ {0.2359} \right].$$

(56)

For practical purposes, an Excel-based Graphical User Interface (GUI) was developed, incorporing the prediction of axial load of CFST columns, using Eq. (51). Figure 15, presents a screenshot of this GUI (also appended to this paper as supplemenraty material). Since it is provided freely, all interested users can download it for practical application. The use of the GUI is straightforward. After selecting the value of input variables (or using the scrollbars), the prediction of axial load will be displayed directly. With a simple matrix form, the proposed model can be used in practice. Moreover, if more experimental data are available in the future, the model can be improved (i.e. for a wider range of data).

Fig. 15

Excel-based Graphical User Interface for prediction of axial load of CFST columns based on the optimal machine learning model

7 Conclusions

The research, presented in this paper, proposes a robust numerical tool, for the estimation of the capacity of rectangular CFST columns, under axial compressive load. The steps for the setup, training, validation, optimization, and testing of the proposed model are presented in detail. The model is evaluated against a wide range of available design codes and methodologies from the literature. The following conclusions summarize the developed methodology and the obtained results presented in the paper:

• An experimental dataset was collected from the available literature, for the development of computational predictive models, including two categories of input variables for each specimen: the geometric dimensions and the mechanical properties of steel and concrete materials. In total, 880 specimens were collected, covering an extended field of the input variables, that include among others, high strength materials, long columns and slender steel tubes;

• An optimization procedure was performed to obtain a final set of ANN model including its architecture, activation function, cost function, weight, and bias parameters;

• The developed ANN model was compared in performance to current codes and standards (AS, EN, AIJ, ACI, AISC, LRFD and DBJ), and existing empirical equations in the literature, using various performance indices such as R, RMSE, MAPE, and VAF. The performance of the proposed ANN model was significantly better in every performance index;

• It is found that the proposed model, produces a quite balanced prediction of the compressive capacity, over the entire field of input variables in the testing dataset that is significantly broader, compared to the application limits of available design codes.

• An Excel-based Graphical User Interface that impements the proposed optimum model was developed and is provided freely for researcher/engineer/interested users.

The results of the present work could simplify the design of CFST columns. The optimum model proposed in this study facilitates the quick and accurate prediction of the axial compressive capacity of rectangular CFST columns, for practical design applications, covering a wide range of the input variables, including high strength steel, high strength concrete, slender sections, and long columns.