1 Introduction

The term convective heat transport is simply recognized as convection used in the phenomenon of heat transportation through the random motion of nanofluids particles. Convection plays an important role in heat transportation in liquids as well as gasses. Convective heat transport is a transfer of heat between stirring liquid and compact surface at dissimilar temperatures. Such transport can be judged by the growing thermal conductivity of the fluid. The researchers investigated the thermal conductivity of regular liquids through the suspension of greater or micro-sized dense particles in the liquid. The theory of heat transference of liquid related dense particles was presented by Maxwell [1] and some recent study based on the convection of heat transport is provided in the references [2, 3].

Mass convection under the influence of chemical reaction–diffusion for the description of cell polarity is described by Latos et al. [4]. The impression of radiative and convective heat transference with convective thermocapillary for a high Prandtl number considered by Yano and Nishino [5]. Steady solutions of compressible fluid with high density, chemical reaction and transport limit of singularly perturbed convection–diffusion are studied by [6, 7]. The leading factor of heat transference on the fluid bridge with a free surface for mixed cases. When the instructions of thermocapillary and vapor flow coincide, the radiative factor can be surpassed even under circumstances via durable gas flow.

The nanofluid is a fluid that contains the smallest structure and size of particles having their nanometer sized. These fluids are organized on the base of the fluid as a suspension. Nanoparticles are usually made of oxides, metals, carbon nanotubes and carbides. The small dust and fog are examples of such flow, which have been extensively utilized in warmth exchangers, solar energy structures, electrical chips, and automobile heaters. In the solar energy structure, nano liquids have massively probable that have been by Wahab et al. [8]. Some real confines and massive tasks of nano liquids were considered by Shah et al. [9]. The results of the thermic recital of the photovoltaic thermal mass utilizing CuO-water along a nano liquid were inspected by Michael et al. [10]. It is perceived that the thermic proficiency grows up to 45.76% of CuO-water nano liquid with 0.05% capacity fraction along with the water at a mass drift rate is 0.01 kg/s. The solar thermic conversion proficiency augmented with intensification in nanoparticle absorption of mixed walled carbon nanotubes was considered by Chen et al. [11]. Yurddas [12] debated mathematically the thermal presentations of nanofluids in the exiled tube solar. Enhancement of the photovoltaic thermal structures was derived by Abbas et al. [10,11,12,13]. It is observed that the volume segment of nanoparticle absorption less than 5% was apposite to evade the clustering procedure of the nanoparticles. A new way to calm absorbed photovoltaic structures by utilizing an extensive microchannel heat sink along nanofluids was provided by Radwan et al. [14]. Mercan and Yurddas [15] debated both mathematically and experimentally the consequences of several factors based on the heat transfer of expatriate tube.

A boundary layer in the fluid flow is referred to a thin layer of a flowing material having its contact with a surface, like the wing of an airplane and the surface inside of a pipe. Such boundary layer flows show the laminar category generally. The boundary layer flow through the deformable sheets is studied by many researchers using several industrial applications, namely, smooth extrusion of flexible sheets, boundary layer with fluid film, reduces progression of the copper plate and polymer trades. Also, such flows have a promising tender in the extrusion of polymer sheets using the portrayal of flexible films. The production of the mentioned sheet and afterward strained to accomplish in the anticipated width. The conventional result for the boundary layer flow of the viscid liquid thru deformable sheet, stirring along velocity fluctuating linearly discussed by Crane [16]. Mukhopadhyay [17] explored properties of MHD slip on boundary layer flow through exponentially extending sheet with puff and thermic radiation. The thermic radiation impacts on micropolar fluid and heat transfer through the permeable deformable sheet were inspected by Bhattacharyya et al. [18]. Results for 2-D laminar electrically conducting flow along continuously extending sheet dormant couplings strain liquid was scrutinized by Turkyilmazoglu [19]. The outcomes of absorption to the stagnation point with the convective condition have been considered by Alsaedi et al. [20].

A cross-fluid lies in that category of generalized Newtonian fluid where variable viscosity is taken at a shear rate. This fluid is based on the classification of the rheology. The existing inquiries depict the structure of non-Newtonian and Newtonian axis symmetric liquid flow. Investigational inquiry of the cross-liquid problem was performed by Escudier et al. [21] via suitable non-Newtonian fluid with the cross-equation, which is presented by fluid-flow and Xanthan gum data. In the power-law structure, we have restricted viscosity on the shear rate turns out to be zero with cross-fluid. The cross-fluid problem is useful in the combination of various polymeric solutions, namely blood and Xanthan gum, which was explored by Barnes et al. [22]. Xie et al. [23] used the WC-MPS technique to scrutinize the flow of free surface non-Newtonian fluids and determined four borders of the cross-fluid problem. The heat transfer of cross-fluid and boundary layer flow was done by Khan et al. [24]. Cross-fluid model contains time continuity, which is utilized in numerous engineering problems provided in references [25,26,27,28].

The basic aim of this study is to investigate the melting heat transport of blood with a cross-fluid model and solution of PDEs by the mentioned model. These PDEs are passed through the mechanism of similarity variable and made the conversion into nonlinear differential equation ODEs. Moreover, the shooting technique rescued and made the system of nonlinear ODEs of the first order. For comparison and numeric solution, bvp4c method built in Matlab program and Keller–Box methodology is adopted.

The rest of the paper sections are provided on the physical model, validity of study, analysis and solver a numeric methodology, Keller–Box technique, discussion of the numerical results and conclusion.

2 Origination of PDEs of cross-fluid model

The vector form of equation of continuity and momentum is given as:

$${\text{div}}V = 0,$$
(1)
$$\rho \frac{{{\text{d}}v}}{{{\text{d}}t}} = {\text{div}}\tau + b,$$
(2)
$$\tau = - pI + \mu A_{1} ,$$
(3)
$$\mu = \mu_{\infty } + \left( {\mu_{0} - \mu_{\infty } } \right)\left[ {\frac{1}{{1 + (\lambda r^{ \cdot } )^{n} }}} \right],$$
(4)
$$\mu = \mu_{0} \left[ {\frac{1}{{1 + (\lambda r^{ \cdot } )^{n} }}} \right],$$
(5)
$$A_{1} = {\text{grad}}V + ({\text{grad}}V)^{{\text{T}}} , \dot{\gamma } = \sqrt {\frac{1}{2}tr(A_{1} )^{2} } ,$$
(6)

Velocity profile

$$V = \left[ {u\left( {x,y} \right),v\left( {x,y} \right),0} \right],$$
(7)
$$\dot{\gamma } = \left[ {4\left( {\frac{\partial u}{{\partial x}}} \right)^{2} + \left( {\frac{\partial u}{{\partial y}} + \frac{\partial v}{{\partial x}}} \right)^{2} } \right]^{1/2} ,$$
(8)

Using the requirements of (1) and (2), we have

$$\frac{\partial u}{{\partial x}} + \frac{\partial v}{{\partial y}} = 0,$$
(9)
$$\begin{gathered} \rho \left( {u\frac{\partial u}{{\partial x}} + v\frac{\partial u}{{\partial y}}} \right) = - \frac{\partial p}{{\partial y}} + \eta_{0} \left( {2\frac{{\partial^{2} v}}{{\partial x^{2} }} + \frac{{\partial^{2} v}}{{\partial y^{2} }} + \frac{{\partial^{2} u}}{\partial x\partial y}} \right)\left[ {1 + \lambda^{n} \left\{ {4\left( {\frac{\partial u}{{\partial x}}} \right)^{2} + \left( {\frac{\partial u}{{\partial y}} + \frac{\partial v}{{\partial x}}} \right)^{2} } \right\}^{n/2} } \right]^{ - n} \hfill \\ + 2\eta_{0} \frac{\partial u}{{\partial y}}\frac{\partial }{\partial y}\left[ {1 + \lambda^{m} \left\{ {4\left( {\frac{\partial u}{{\partial x}}} \right)^{2} + \left( {\frac{\partial u}{{\partial y}} + \frac{\partial v}{{\partial x}}} \right)^{2} } \right\}^{n/2} } \right]^{ - 1} \hfill \\ + \eta_{0} \left( {\frac{\partial u}{{\partial y}} + \frac{\partial v}{{\partial x}}} \right)\frac{\partial }{\partial y}\left[ {1 + \lambda^{m} \left\{ {4\left( {\frac{\partial u}{{\partial x}}} \right)^{2} + \left( {\frac{\partial u}{{\partial y}} + \frac{\partial v}{{\partial x}}} \right)^{2} } \right\}^{n/2} } \right], \hfill \\ \end{gathered}$$
(10)

as \(v = \frac{{\eta_{0} }}{\rho }\) utilizing in 10, we get

$$\begin{gathered} u\frac{\partial u}{{\partial x}} + v\frac{\partial u}{{\partial y}} = - \frac{1}{\rho }\frac{\partial p}{{\partial x}} + \nu \left( {2\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial^{2} u}}{{\partial y^{2} }} + \frac{{\partial^{2} v}}{\partial x\partial y}} \right)\left[ {1 + \lambda^{n} \left\{ {4\left( {\frac{\partial u}{{\partial x}}} \right)^{2} + \left( {\frac{\partial u}{{\partial y}} + \frac{\partial v}{{\partial x}}} \right)^{2} } \right\}^{m/2} } \right]^{ - 1} + 2\nu \frac{\partial u}{{\partial x}}\frac{\partial }{\partial x}\left[ {1 + \lambda^{n} \left\{ {4\left( {\frac{\partial u}{{\partial x}}} \right)^{2} + \left( {\frac{\partial u}{{\partial y}} + \frac{\partial v}{{\partial x}}} \right)^{2} } \right\}^{n/2} } \right]^{ - 1} \hfill \\ + \nu \left( {\frac{\partial u}{{\partial y}} + \frac{\partial v}{{\partial x}}} \right)\frac{\partial }{\partial y}\left[ {1 + \lambda^{n} \left\{ {4\left( {\frac{\partial u}{{\partial x}}} \right)^{2} + \left( {\frac{\partial u}{{\partial y}} + \frac{\partial v}{{\partial x}}} \right)^{2} } \right\}^{\frac{n}{2}} } \right]^{ - 1} . \hfill \\ \end{gathered}$$
(11)
$$\begin{gathered} \left( {u\frac{\partial u}{{\partial x}} + v\frac{\partial u}{{\partial y}}} \right) = - \frac{1}{\rho }\frac{\partial p}{{\partial y}} + \upsilon \left( {2\frac{{\partial^{2} v}}{{\partial x^{2} }} + \frac{{\partial^{2} v}}{{\partial y^{2} }} + \frac{{\partial^{2} u}}{\partial x\partial y}} \right)\left[ {1 + \lambda^{n} \left\{ {4\left( {\frac{\partial u}{{\partial x}}} \right)^{2} + \left( {\frac{\partial u}{{\partial y}} + \frac{\partial v}{{\partial x}}} \right)^{2} } \right\}^{n/2} } \right]^{ - 1} + 2\upsilon \frac{\partial u}{{\partial y}}\frac{\partial }{\partial y}\left[ {1 + \lambda^{n} \left\{ {4\left( {\frac{\partial u}{{\partial x}}} \right)^{2} + \left( {\frac{\partial u}{{\partial y}} + \frac{\partial v}{{\partial x}}} \right)^{2} } \right\}^{n/2} } \right]^{ - 1} \hfill \\ + \upsilon \left( {\frac{\partial u}{{\partial y}} + \frac{\partial v}{{\partial x}}} \right)\frac{\partial }{\partial y}\left[ {1 + \lambda^{n} \left\{ {4\left( {\frac{\partial u}{{\partial x}}} \right)^{2} + \left( {\frac{\partial u}{{\partial y}} + \frac{\partial v}{{\partial x}}} \right)^{2} } \right\}^{\frac{n}{2}} } \right]^{ - 1} . \hfill \\ \end{gathered}$$
(12)

Equations (11) and (12) are further scrutinized with the concepts of boundary layer along with the mass and momentum form is given as:

$$\frac{\partial u}{{\partial x}} + \frac{\partial v}{{\partial y}} = 0,$$
(13)
$$u\frac{\partial u}{{\partial x}} + v\frac{\partial u}{{\partial y}} = - \frac{1}{\rho }\frac{\partial p}{{\partial x}} + \nu \frac{{\partial^{2} u}}{{\partial y^{2} }}\left[ {1 + \lambda^{n} \left( {\frac{\partial u}{{\partial y}}} \right)^{n} } \right]^{ - 1} + \nu \frac{\partial u}{{\partial y}}\frac{\partial }{\partial y}\left[ {1 + \lambda^{n} \left( {\frac{\partial u}{{\partial y}}} \right)^{n} } \right]^{ - 1} ,$$
(14)

Pressure along y-axis has no contribution so Eq. (12) disappears due to zero pressure.

$$\begin{aligned} u\frac{\partial u}{{\partial x}} + v\frac{\partial u}{{\partial y}} + \frac{\partial u}{{\partial t}} &= \nu \left[ {\left( {\left( {\Gamma \frac{\partial u}{{\partial y}}} \right)^{n} + 1} \right)^{ - 1} } \right]\frac{{\partial^{2} u}}{{\partial y^{2} }}, \hfill \\ &\quad - \left( {\frac{\partial u}{{\partial y}}} \right)^{n} \frac{{\partial^{2} u}}{{\partial y^{2} }}\left[ {1 + \left( {\Gamma \frac{\partial u}{{\partial y}}} \right)^{n} } \right]^{ - 2} \nu \Gamma^{n} n + g\beta_{nf} \left( {T_{1} - T_{2} } \right) \hfill \\ \end{aligned}$$
(15)

2.1 Origination of PDEs for energy equation

The vector form of energy equation is given as:

$$\rho c_{{\text{p}}} \frac{{{\text{d}}T}}{{{\text{d}}t}} = \tau \cdot L - {\text{div}}(q),$$
(16)
$$q = \left( { - k\nabla T} \right),L = \nabla V.$$
(17)

3 Geometry related physical model

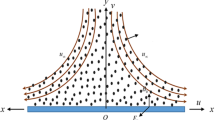
Incompressible and 2-D flow with convection boundary layer conditions of cross-nanofluid (blood), which contains nanoparticles of iron oxides (Fe3O4) is flowing along a vertical surface. Table 1 describes the thermophysical properties, which are related to the nanofluids (blood). The fluid (blood) is flowing along the x‐axis, which is admitted along the vertical surface and the y‐axis is placed orthogonal to the x-axis, which is clear in the figure of geometry 1. The flow is bounded within the regime of upper the y-axis that is in y > 0. Surface temperature is Tm, and T2 (constant temperature) of the ambient medium. It is noted here that Tm is lower than the T2 (Fig. 1).

Table 1 Fluid properties along with its units and blood ratio
Full size table
Fig. 1
figure 1

Geometry of flow

Full size image

Being processing the approximations of boundary layer, the governing community of equations for a cross-nanofluid for 2-D is mentioned below [29]:

$$\frac{\partial \left[ u \right]}{{\partial x}} + \frac{\partial \left[ v \right]}{{\partial y}} = 0,$$
(18)
$$u\frac{\partial u}{{\partial x}} + v\frac{\partial u}{{\partial y}} + \frac{\partial u}{{\partial t}} = \frac{{\mu_{{{\text{nf}}}} }}{{\rho_{{{\text{nf}}}} }}\left[ {\left( {\left( {\Gamma \frac{\partial u}{{\partial y}}} \right)^{n} + 1} \right)^{ - 1} } \right]\frac{{\partial^{2} u}}{{\partial y^{2} }} - \left( {\frac{\partial u}{{\partial y}}} \right)^{n} \frac{{\partial^{2} u}}{{\partial y^{2} }}\left[ {1 + \left( {\Gamma \frac{\partial u}{{\partial y}}} \right)^{n} } \right]^{ - 2} \frac{{\mu_{{{\text{nf}}}} }}{{\rho_{{{\text{nf}}}} }}\Gamma^{n} n + g\beta_{{{\text{nf}}}} \left( {T_{1} - T_{2} } \right),$$
(19)
$$v\frac{{\partial T_{1} }}{\partial y} + u\frac{{\partial T_{1} }}{\partial x} + \frac{{\partial T_{1} }}{\partial t} = \alpha_{{{\text{nf}}}} \frac{{\partial^{2} T_{1} }}{{\partial y^{2} }}.$$
(20)

For above-mentioned mathematical system, BCs are

$$u = u_{{\text{w}}} \left( {x,t} \right)\;{\text{where}}\;u_{{\text{w}}} \left( {x,t} \right) = \frac{ax}{{1 - ct}},\;T_{1} = T_{{\text{m}}} ,\;{\text{at}} y = o,$$
(21)
$${\text{for}} \, y \to \infty ,\left( - \right)\left\{ {K_{{{\text{nf}}}} \frac{{\partial T_{1} }}{\partial y}} \right\}_{y = 0} = \langle \lambda^{*} - \left( {T - T_{{{\text{mo}}}} } \right)c_{{\text{s}}}\rangle v\left( {x,o} \right)\rho_{{\text{f}}} .$$
(22)

The mentioned Eq. (4) is known for melting heat transport. Such transportation imparts that heat of melting surface + Heat required for raising solid temperature T0 to its melting temperature Tm = Heat of melting. Below given transformation satisfies the equation of the continuity, so by this transformation it is confirmed that flow is possible and now using Eqs. (19) and (20), we get

$$\left| {\begin{array}{*{20}l} {\psi = \sqrt {\frac{{\upsilon_{{\text{f}}} c}}{{\left( {1 - \alpha t} \right)}}} xf\left( \eta \right)} \\ {\eta = y\sqrt {\left( {\frac{{\left( {1 - \alpha t} \right)^{ - 1} c}}{{\upsilon_{{\text{f}}} }}} \right)} ,} \\ {u = \frac{\partial \psi }{{\partial y}} = \left( {\frac{{\left( {1 - \alpha t} \right)^{ - 1} c}}{{x^{ - 1} }}} \right)f^{\prime}\left( \eta \right),} \\ {v = - \frac{\partial \psi }{{\partial x}} = yag^{\prime}\left( \eta \right),} \\ {\theta \left( \eta \right) = \left[ {\frac{{T_{1} - T_{2} }}{{T_{2} - T_{{\text{m}}} }}} \right],} \\ \end{array} } \right|,$$
(23)
$$\left| {\begin{array}{*{20}l} {\mu_{{{\text{nf}}}} = \left[ {\frac{1}{{(1 - \phi )^{ - 5/2} }}} \right]\mu_{{\text{f}}} ,} \\ {\alpha_{{{\text{nf}}}} = \frac{{k_{{{\text{nf}}}} }}{{\left( {\rho C_{{\text{p}}} } \right)_{{{\text{nf}}}} }} = \frac{1}{{(1 - \phi )^{ - 1} }}\left( {\rho C_{{\text{p}}} } \right)_{{\text{f}}} + \phi \left( {\rho C_{{\text{p}}} } \right)_{{\text{s}}} } \\ {\rho_{{{\text{nf}}}} = \left( {1 - \phi } \right)\rho_{{\text{f}}} + \phi \left( \rho \right)_{{\text{s}}} .} \\ {\frac{{k_{{{\text{nf}}}} }}{{k_{{\text{f}}} }} = \left[ {\frac{{\left( {2k_{{\text{s}}} + k_{{\text{f}}} } \right) - 2\left( {k_{{\text{f}}} - 2k_{{\text{s}}} } \right)\phi }}{{\left( {2k_{{\text{s}}} + k_{{\text{f}}} } \right) + \left( {k_{{\text{f}}} - 2k_{{\text{s}}} } \right)\phi }}} \right]} \\ {\beta_{{{\text{nf}}}} = \left( {1 - \phi } \right)\beta_{{\text{f}}} + \phi \beta_{{\text{s}}} } \\ \end{array} } \right|.$$
(24)

Fulfilling all requirements for Eqs. (2) and (3), the highly nonlinear differential equations take the form as:

$$A\left[ {f^{\prime} + \frac{\eta }{2}f^{\prime\prime}} \right]\left( {1 + \left( {{\text{we}}f^{\prime\prime}} \right)^{n} } \right)^{2} = \left[ {\left\{ {\left( {1 - \phi } \right) + \phi \frac{{\rho_{{\text{s}}} }}{{\rho_{{\text{f}}} }}} \right\}\left\{ {\left( {1 - \phi } \right)^{2.5} } \right\}} \right]^{ - 1} \left[ {\left( {1 - \left( {n - 1} \right)\left( {{\text{we}}f^{\prime\prime}} \right)^{n} } \right)} \right]f^{\prime\prime\prime} + \left\{ {\left( {1 - \phi } \right) + \phi \frac{{\beta_{{\text{s}}} }}{{\beta_{{\text{f}}} }}} \right\}\lambda \theta - f^{{\prime}2} - ff,^{\prime \prime }$$
(25)
$$\theta ^{\prime\prime} - \Pr \frac{{k_{{\text{f}}} }}{{k_{{{\text{nf}}}} }}\left\{ {\left( {1 - \phi } \right) + \phi \frac{{\left( {\rho C_{{\text{p}}} } \right)_{{\text{s}}} }}{{\left( {\rho C_{{\text{p}}} } \right)_{{\text{f}}} }}} \right\}\left\{ {A\left( {\frac{{\eta \theta^{\prime}}}{2} + 2\theta } \right) - \theta^{\prime}f + 2\theta f^{\prime}} \right\} = 0.$$
(26)
$$\left| {\begin{array}{*{20}l} {f^{\prime} = 1,} \\ {\theta ^{\prime} = 1,\;{\text{at}}\;\eta = 0} \\ {f^{\prime} \to 0,\theta ^{\prime} \to 0,\;{\text{at}}\;\eta = \infty } \\ {M\theta ^{\prime}\left( 0 \right) + \Pr f\left( 0 \right) = 0} \\ \end{array} } \right|.$$
(27)

Important physical quantities are

$$C_{{{\text{fx}}}} = \frac{{2\tau_{{\text{w}}} \mu_{{{\text{nf}}}} }}{{\rho_{{\text{f}}} u_{{\text{w}}}^{2} }}\left( {\frac{\partial u}{{\partial y}}} \right)_{y = 0} ,$$
(28)
$${\text{Nu}}_{x} = \frac{{ - xk_{{{\text{nf}}}} \left( {T_{\infty } - T_{{\text{m}}} } \right)^{ - 1} x}}{{k_{{\text{f}}} }}\left. {\frac{{\partial T_{1} }}{\partial y}} \right|_{y = 0} ,$$
(29)

Similarity variables becomes as:

$$Cf_{x} \left( {{\text{Re}}_{x} } \right)^{1/2} = \frac{1}{{\left( {1 - \phi } \right)^{2.5} }}\frac{2f^{\prime\prime}\left( 0 \right)}{{\left[ {1 + \left( {{\text{We}}_{1} f^{\prime\prime}\left( 0 \right)} \right)^{n} } \right]}},$$
(30)
$${\text{Nu}}_{x} \sqrt {\left( {{\text{Re}}_{x} } \right)^{ - 1} } = \left( {\frac{{k_{{{\text{nf}}}} }}{{k_{{\text{f}}} }}} \right)\left( { - \theta^{\prime}\left( 0 \right)} \right).$$
(31)

3.1 Validness of study

Table 2 encourages to move forward to get advance result and discussion, because this Table 2 approves the current work due to agreement of these value of \(-{\theta }^{^{\prime}}(0)\) with existing literature (Fig. 2).

Table 2 Comparison of the literature work for (− θ′(0)) by fixing A = ϕ = We = λ = 0
Full size table
Fig. 2
figure 2

Graphical validity of the study

Full size image

4 Numerical procedure for the solution and programing methodology

This section provides a brief explanation to solve the ODEs given in (8) and (9) along with the boundary condition. Due to non-availability of the solutions in the literature, the shooting technique is applied that works to convert the BVPs into IVPs along with the Runge–Kutta Fehlberg 45th‐order method. The procedure steps of the shooting methodology [33,34,35,36,37,38,39,40,41,42,43] are given as (Fig. 3):

$$\left| {\begin{array}{*{20}l} {f = E_{1} ,} \\ {f^{\prime} = {\rm E}_{2} ,f^{\prime\prime} = {\rm E}_{3} ,} \\ {f^{\prime\prime\prime} = {\rm E}_{3}^{^{\prime}} ,\theta = {\rm E}_{4} ,\theta ^{\prime} = {\rm E}_{5} ,} \\ {\theta ^{\prime\prime} = {\rm E}_{6} ,} \\ {E_{3} ^{\prime} = \frac{{A\left[ {E_{2} + \frac{\eta }{2}E_{3} } \right]}}{{\Omega_{1} \times \Omega_{2} }} - \left\{ {\left( {1 - \phi } \right) + \phi \frac{{\beta_{{\text{s}}} }}{{\beta_{{\text{f}}} }}} \right\}\lambda E_{4} + E_{2}^{2} + E \times E_{3} } \\ {E_{6} = \frac{{k_{{\text{f}}} }}{{k_{{{\text{nf}}}} }} - \Omega_{3} \left\{ {A\left( {2E_{4} + \frac{{\eta E_{5} }}{2}} \right) + 2E_{4} E_{2} - E_{5} E_{1} } \right\}} \\ {{\text{where}}\, \Omega_{1} = \left[ {\left\{ {\left( {1 - \phi } \right) + \phi \frac{{\rho_{s} }}{{\rho_{{\text{f}}} }}} \right\}\left\{ {\left( {1 - \phi } \right)^{2.5} } \right\}} \right]^{ - 1} } \\ {\Omega_{2} = \left[ {\left( {1 - \left( {n - 1} \right)\left( {{\text{we}}_{1} E_{3} } \right)^{n} } \right)\left( {1 + \left( {{\text{we}}_{1} E_{3} } \right)^{n} } \right)^{ - 2} } \right]} \\ {\Omega_{3} = \left\{ {\left( {1 - \phi } \right) + \phi \frac{{\left( {\rho C_{{\text{p}}} } \right)_{{\text{s}}} }}{{\left( {\rho C_{{\text{p}}} } \right)_{{\text{f}}} }}} \right\}} \\ \end{array} } \right|.$$
(32)
Fig. 3
figure 3

Flowchart of the through programming scheme

Full size image

BCs are

$${\rm E}_{2} = 1,\;{\rm E}_{4} = 1,\;{\text{at}}\;\eta = 0,\;{\rm E}_{2} \to 0,{\rm E}_{5} \to 0,\;{\text{at}}\;\eta = \infty ,\;M\;{\rm E}_{5} \left( 0 \right) + \Pr {\rm E}\left( 0 \right) = 0.$$
(33)

5 Keller–Box method

Fast convergence method-based Keller–Box technique to solve the differential Eqs. (25)–(27). This method is explained in four approaches.

Approach 1 The higher order differential systems (25–26) are needed to process for converting in system of first-order differential equations. To get this purpose, following substitutions are made:

$$f^{\prime} = H,\theta ^{\prime} = L,$$
(34)

Using Eqs. (25–26)

$$A\left[ {H + \frac{\eta }{2}H^{\prime}} \right]\left( {1 + \left( {{\text{we}}H^{\prime}} \right)^{n} } \right)^{2} = \left[ {\left\{ {\left( {1 - \phi } \right) + \phi \frac{{\rho_{{\text{s}}} }}{{\rho_{{\text{f}}} }}} \right\}\left\{ {\left( {1 - \phi } \right)^{2.5} } \right\}} \right]^{ - 1} \left[ {\left( {1 - \left( {n - 1} \right)\left( {{\text{we}}H^{\prime}} \right)^{n} } \right)} \right]H^{\prime\prime} + \left\{ {\left( {1 - \phi } \right) + \phi \frac{{\beta_{{\text{s}}} }}{{\beta_{{\text{f}}} }}} \right\}\lambda L - H^{2} - Hf,$$
(35)
$$L^{\prime} - \Pr \frac{{k_{{\text{f}}} }}{{k_{{{\text{nf}}}} }}\left\{ {\left( {1 - \phi } \right) + \phi \frac{{\left( {\rho C_{{\text{p}}} } \right)_{{\text{s}}} }}{{\left( {\rho C_{{\text{p}}} } \right)_{{\text{f}}} }}} \right\}\left\{ {A\left( {\frac{\eta L}{2} + 2\theta } \right) - Lf + 2\theta H} \right\} = 0.$$
(36)

The BCs take the form as:

$$\left| {\begin{array}{*{20}l} {H = 1,} \\ {L = 1,\;{\text{at}} \eta = 0} \\ {H \to 0,L \to 0,\;{\text{at}} \eta = \infty } \\ {ML\left( 0 \right) + \Pr f\left( 0 \right) = 0} \\ \end{array} } \right|.$$
(37)

Approach 2 Formulation of grid points are needed to be set and described as:

$$\eta_{0} = 0,\eta_{j} = \eta_{j - 1} + h_{j} ,j = 1,2,3, \ldots ,J,\eta_{J} = \eta_{\infty } .$$
(38)

The central difference approximations method is utilized considering arbitrary points.

$$\frac{{f_{j} - f_{j - 1} }}{{h_{j} }} = H_{{j - \frac{1}{2}}} ,\frac{{\theta_{j} - \theta_{j - 1} }}{{h_{j} }} = L_{{j - \frac{1}{2}}} ,\;{\text{and}}\;f_{{j - \frac{1}{2}}} = \frac{{f_{j} + f_{j - 1} }}{2},$$
(39)
$$\begin{gathered} A\left[ {H_{{j - \frac{1}{2}}} + \frac{\eta }{2}\left( {U_{{j - \frac{1}{2}}} } \right)} \right]\left( {1 + \left( {{\text{we}}\left( {H_{{j - \frac{1}{2}}} } \right)} \right)^{n} } \right)^{2} = \left[ {\left\{ {\left( {1 - \phi } \right) + \phi \frac{{\rho_{{\text{s}}} }}{{\rho_{{\text{f}}} }}} \right\}\left\{ {\left( {1 - \phi } \right)^{2.5} } \right\}} \right]^{ - 1} \times \hfill \\ \left[ {\left( {1 - \left( {n - 1} \right)\left( {{\text{we}}\left( {H_{{j - \frac{1}{2}}} } \right)} \right)^{n} } \right)} \right]\left[ {\frac{{H_{j} - H_{j - 1} }}{{h_{j} }}} \right] + \left\{ {\left( {1 - \phi } \right) + \phi \frac{{\beta_{{\text{s}}} }}{{\beta_{{\text{f}}} }}} \right\}\lambda l_{{j - \frac{1}{2}}} - \left( {H_{{j - \frac{1}{2}}} } \right)^{2} - H_{{j - \frac{1}{2}}} f_{{j - \frac{1}{2}}} , \hfill \\ \end{gathered}$$
(40)
$$\left[ {\frac{{L_{j} - L_{j - 1} }}{{h_{j} }}} \right] - \Pr \frac{{k_{{\text{f}}} }}{{k_{{{\text{nf}}}} }}\left\{ {\left( {1 - \phi } \right) + \phi \frac{{\left( {\rho C_{{\text{p}}} } \right)_{{\text{s}}} }}{{\left( {\rho C_{{\text{p}}} } \right)_{{\text{f}}} }}} \right\}\left\{ {A\left( {\frac{{\eta V_{{j - \frac{1}{2}}} }}{2} + 2\theta_{{j - \frac{1}{2}}} } \right) - Lf + 2\theta_{{j - \frac{1}{2}}} H_{{j - \frac{1}{2}}} } \right\} = 0.$$
(41)

Approach 3 The obtained system is nonlinear, so we cannot move further without linearizing the system. Therefore, \(\left( {j + 1} \right)\)th iteration we write this in way of \(f_{j + 1} = f_{j} + \delta f_{j}\) and continuing the process for all involved independent variables. Ignoring the second-order well as higher order terms for \(\delta f_{j}\) and continuing the process, as result tridiagonal system of linear equations goes in matrix form.

$$A\delta = r^{*} .$$
(42)

In which

$$A = \frac{{\partial^{2} }}{{\partial x^{2} }}\left[ {\begin{array}{*{20}c} {\left[ {A_{1} } \right]} & {\left[ {C_{1} } \right]} & - & - & {} & {} \\ {\left[ {B_{2} } \right]} & {\left[ {A_{2} } \right]} & {} & {\left[ {C_{2} } \right]} & {} & {} \\ {\begin{array}{*{20}c} {} \\ {} \\ \end{array} } & {\begin{array}{*{20}c} {} \\ {} \\ \end{array} } & {\begin{array}{*{20}c} {} \\ {} \\ \end{array} } & {\begin{array}{*{20}c} {} \\ \ddots \\ \end{array} } & {\begin{array}{*{20}c} {} \\ \ddots \\ \end{array} } & {\begin{array}{*{20}c} {} \\ {} \\ \end{array} } \\ {\begin{array}{*{20}c} {} \\ {} \\ \end{array} } & {\begin{array}{*{20}c} \ddots \\ {} \\ \end{array} } & {\begin{array}{*{20}c} \ddots \\ \ddots \\ \end{array} } & {\begin{array}{*{20}c} \ddots \\ {} \\ \end{array} } & {\begin{array}{*{20}c} {} \\ {} \\ \end{array} } & {\begin{array}{*{20}c} {} \\ {} \\ \end{array} } \\ {} & {} & {} & {\left[ {B_{j - 1} } \right]} & {\left[ {C_{j - 1} } \right]} & {\left[ {C_{j - 1} } \right]} \\ {} & {} & {} & {} & {\left[ {B_{j} } \right]} & {\left[ {A_{j} } \right]} \\ \end{array} } \right],\;\delta = \left[ {\begin{array}{*{20}c} {\left[ {\delta_{1} } \right]} \\ {\left[ {\delta_{2} } \right]} \\ \ddots \\ \ddots \\ \ddots \\ \ddots \\ {\left[ {\delta_{j - 1} } \right]} \\ {\left[ {\delta_{j} } \right]} \\ \end{array} } \right],r^{*} = \left[ {\begin{array}{*{20}c} {\left[ {r_{1} } \right]} \\ {\left[ {r_{2} } \right]} \\ \ddots \\ \ddots \\ \ddots \\ \ddots \\ {\left[ {r_{j - 1} } \right]} \\ {\left[ {r_{j} } \right]} \\ \end{array} } \right],$$
(43)

Now, we suppose that

$$A = L^{*} U,$$
(44)

where

$$L^{*} = \left[ {\begin{array}{*{20}c} {} & {\left[ {a_{1} } \right]} & {} & {} \\ {\left[ {b_{2} } \right]} & {\left[ {a_{2} } \right]} & {} & {} \\ {\begin{array}{*{20}c} \ddots \\ {} \\ \end{array} } & {\begin{array}{*{20}c} \ddots \\ \ddots \\ \end{array} } & {\begin{array}{*{20}c} {} \\ \ddots \\ \end{array} } & {\begin{array}{*{20}c} {} \\ {} \\ \end{array} } \\ {} & {} & {\left[ {b_{j} } \right]} & {\left[ {a_{j} } \right]} \\ \end{array} } \right],\;U = \left[ {\begin{array}{*{20}c} {\left[ I \right]} & {} & {\left[ {\Gamma_{1} } \right]} & {} & {} \\ {} & {\left[ I \right]} & {} & {\left[ {\Gamma_{1} } \right]} & {} \\ {} & \ddots & {} & \ddots & {} \\ {} & {} & \ddots & {} & \ddots \\ {} & {\begin{array}{*{20}c} {\left[ I \right]} \\ {} \\ \end{array} } & {\begin{array}{*{20}c} {} \\ {} \\ \end{array} } & {\begin{array}{*{20}c} {\left[ {\Gamma_{J - 1} } \right]} \\ {} \\ \end{array} } & {\begin{array}{*{20}c} {} \\ {\left[ I \right]} \\ \end{array} } \\ \end{array} } \right],$$
(45)

Here, unit matrix is [I], the matrices \(\left[ {ai} \right]\) and \(\left[ {\Gamma i} \right]\) have 5 × 5 order and process of calculating its element as

$$\left[ {a_{i} \left] \, = \, \right[A_{i} } \right],$$
(46)
$$\left[ {A_{1} } \right]\left[ {\Gamma_{1} } \right] = \left[ {C_{1} } \right]$$
(47)
$$\left[ {a_{j} } \right] = \left[ {A_{j} } \right] - \left[ {B_{j} } \right]\left[ {\Gamma_{j - 1} } \right],j = 1,2,3, \ldots ,J,$$
(48)
$$\left[ {a_{i} } \right]\left[ {\Gamma_{1} } \right] = \left[ {C_{j} } \right],j = 1,2,3, \ldots ,J$$
(49)
$$L^{*} U\delta = r^{*} .$$
(50)

Assume that,

$$U\delta = P,$$
(51)

and

$$L^{*} P = r^{*} .$$
(52)

Here

$$P = \left[ {\begin{array}{*{20}c} {\left[ {P_{1} } \right]} \\ {\left[ {P_{2} } \right]} \\ {\left[ {P_{3} } \right]} \\ {\begin{array}{*{20}c} {\left[ {P_{4} } \right]} \\ {\left[ {P_{5} } \right]} \\ \end{array} } \\ \end{array} } \right],$$
(53)

where \(\left[ {P_{j} } \right]\) inculpates column matrices having \(5 \times 5\) order, and computation process is given below:

$$\left[ {a_{1} } \right]\left[ {P_{j} } \right] = \left[ {r_{1} } \right],$$
(54)
$$\left[ {a_{j} } \right]\left[ {P_{j} } \right] = \left[ {r_{j} } \right] - \left[ {B_{j} } \right]\left[ {P_{j - 1} } \right].$$
(55)

To get the results of P, \(\delta\) elements are calculated by the below relation as:

$$\left[ {\delta_{j} } \right] = \left[ {Z_{j} } \right],$$
(56)
$$\left[ {\delta_{j} } \right] = \left[ {Z_{j} } \right] - \left[ {\Gamma_{j} } \right]\left[ {\delta_{j + 1} } \right].$$
(57)

Approach 4 After reaching this stage, final form of system of linear equations are passed through block technique. Continuous iterations are going on until achieving the absolute difference which is kept less than \(10^{ - 6}\) in two consecutive iterations.

6 Results

The present section describes the results of the blood flow carrying of nanoparticles of iron oxide. The numerical outcomes are placed in tabular form and sketched through geometrical data. Different parameters and their impact on velocity and temperature of nanofluid (blood) is elaborated through figures and tables. Physical quantities are also there with a reasonable explanation. The impact of different parameters is shown for shear thinning/thickening n = 0.5 and n = 1.5, respectively. Present assumed problem goes into the category of the steady case when we substitute A = 0. The numerical attitude of quantities Skin friction and Nusselt number is explained by Table 4 with variation of parameters \(\phi\), \(\lambda\), \(\beta\) and \(A\). Parameter Pr puts the direct effect of motion and temperature of the fluid, and this fact is shown geometrically through sketching 14 (a, c, d, e) (Fig. 4).

Fig. 4
figure 4

Flowchart of the complexity analysis

Full size image

The influence of the parameters through the geometry of the problem is illustrated in Figs. 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16. The velocity profile is derived for both cases n < 1 keeping fixed that is n = 0.5 (shear thinning) and n > 1 keeping fixed n = 1.5 (thickening case). Highlighting the impact of A on f ′(η) of nanofluid (blood) is plotted in Fig. 5. An increase in A responses decrement in f′(η). As A is time related parameter so the time is consuming due to this boundary layer thickness decreases and as a result velocity downs for both cases (n > 1 ^ n < 1). Figure 6 discusses the effect of λ on f ′(η) and it presents velocity and momentum boundary layer thickness is growing because of step-up in λ in (n > 1 ^ n < 1). Physical point of view, growth in λ leads the enhancement of convection currents. As melting parameter grows as a result velocity gets up for (n > 1 ^ n < 1) due to melting of fluid this fact is seen in Fig. 7. Figure 8 depicts that cross-index responsible for higher velocity. Figure 9 provides that the gradual increment in \(\phi\) and the velocity of the nanofluid (blood) behaves alike, but opposite behavior is found in Fig. 10 for Prandtl number in both cases (n > 1 ^ n < 1). Increment in Prandtl number causes to lose the temperature and motion of nanoparticle that’s why velocity gets down. As we is related with relaxation time due to this increment in it causes to slow velocity this fact is shown in Fig. 8.

Fig. 5
figure 5

\(f\left( \eta \right) \;{\text{for}} \;A\) (n > 1 ^ n < 1)

Full size image
Fig. 6
figure 6

\(f\left( \eta \right) \;{\text{with}}\; \lambda\) (n > 1 ^ n < 1)

Full size image
Fig. 7
figure 7

\(f\left( \eta \right) \;{\text{with}} \; M\) (n > 1 ^ n < 1)

Full size image
Fig. 8
figure 8

\(f\left( \eta \right)\; {\text{with }}\;n\)

Full size image
Fig. 9
figure 9

\(f\left( \eta \right)\; {\text{with}}\; \phi \left( {n > 1^{n} < 1} \right)\)

Full size image
Fig. 10
figure 10

\(f\left( \eta \right)\;{\text{with}}\;\Pr \left( {n > 1^{n} < 1} \right)\)

Full size image
Fig. 11
figure 11

\(f\left( \eta \right)\, {\text{with}}\, {\text{We}}\)

Full size image
Fig. 12
figure 12

\(\theta \left( \eta \right) \,{\text{with}} \; A\)

Full size image
Fig. 13
figure 13

\(\theta \left( \eta \right)\, {\text{with }}\, \lambda\)

Full size image
Fig. 14
figure 14

\(\theta \left( \eta \right)\, {\text{with}}\, M\)

Full size image
Fig. 15
figure 15

\(\theta \left( \eta \right) \;{\text{with}}\, \phi\)

Full size image
Fig. 16
figure 16

\(\theta \left( \eta \right) \,{\text{with}} \,{\text{Pr}}\)

Full size image

The effects of A causes to increase the thermal boundary layer thickness due to this temperature gets high by increasing A that is shown in Fig. 12. Effects of surface convection parameter on temperature of nano-cross-fluid (blood) in the boundary layer region is shown in Fig. 13. Observation is made that temperature (nanofluid blood) decreases on increasing this said parameter, because boundary layer region and is maximum at the surface of the plat thus, the thermal boundary layer thickness decreases with the increase convection parameter. It is found that when M takes it larger value, the temperature of ambient fluid loses, because the motion of the fluid reduces, due to this temperature of nanofluid (blood) loses that is in Fig. 14. Interpretation-related solid volume fraction of nanofluid (blood) parameter ϕ on θ (η) is made through Fig. 15 which illuminates that developing the ϕ temperature downs. Physically, this implies that when solid friction of nanoparticle become high then liquid friction down so, due to less friction in blood temperature loses. Pr has affect which reduces the velocity profile, which implies that when nanofluid velocity becomes lower, so it results the lower diffusion so temperature downs with growing Pr and this fact is shown in Fig. 16. Easiest way to understand of debate on results is elaborated through Table 3.

Table 3 Tabular representation of results and discussion
Full size table

7 Conclusions

The main causes to present this numerical work through the melting phenomenon of heat transport with the boundary layer flow for cross-nanofluid in the influence of the convection way of heat transport. Characteristic of flow and temperature profile of cross-fluid (blood) is presented in detail in tabular as well as geometrical interpretation. Few key findings of the current research study are presented below as (Fig. 17) (Table 4):

  • Velocity magnitude is larger in cross-fluid with gradual increment in n.

  • Variation in the Prandtl number it responses lower the velocity and temperature of the blood.

  • (\({f}^{^{\prime}}(\eta )\)) and (\(\theta (\eta )\)) of nanofluid (blood) decreases by increasing the melting parameter M, because when melting occurs temperature loses.

  • The stickiness of the nanofluid is being enhanced for uplifting the numeral values of \(\phi\)

  • Convection currents enhance for rise in λ and due to this increment in velocity and reverse attitude is found for temperature.

Fig. 17
figure 17

a–d Geometrical behavior of physical quantities

Full size image
Table 4 Interpretation of drag force (\(C_{{\text{x}}} \sqrt {\left( {{\text{Re}}_{x} } \right)}\)) and rate of heat transport (Nusselt number) (\({\text{Nu}}_{{\text{f}}} \sqrt {\left( {{\text{Re}}_{x} } \right)}\)) keeping its viscosity constant for both cases with melting effect (M = 0.5) and without melting effects (M = 0)
Full size table