Biomedical aspects of entropy generation on electromagnetohydrodynamic blood flow of hybrid nanofluid with nonlinear thermal radiation and non-uniform heat source/sink

Abstract

The current article aims to develop a theoretical model for electromagnetohydrodynamic flow over a stagnation point flow of hybrid nanofluid with nonlinear thermal radiation and non-uniform heat source/sink. This mathematical model is implemented to blood-based nanofluids for two different nanoparticles. The linear and nonlinear thermal radiations are chosen to be varying the purpose, to see the temperature modifications in this model. For simplifying the governing flow equations, appropriate conversions are taken into interpretation to switch appropriately the ensuing partial differential equations to ordinary differential equations. The rehabilitated mathematical formulations are solved numerically via an effective procedure based on RK 4th order via a shooting scheme. The consequences of sundry variables are established via pictorial representations. The attained outcomes of this model meticulously match with those existing in the literature for some limiting conditions. The outcomes of this study are of repute in the valuation of the effect of some important design parameters on heat transfer and therefore in the optimization of industrial processes. This theoretical model consists of the EMHD and thermal radiation cases through blood flow and it has a significant attitude on the magnetic delivery in blood, the therapeutic procedure of hyperthermia, magnetic endoscopy, understanding/regulating blood flow, transport of complex bio-waste fluids and heat transfer in capillaries, etc.

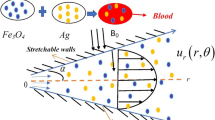
Graphic abstract

Schematic diagram of the physical problem

1 Introduction

Nanofluids are a new category of fluids that are designed by dispersing nanomaterials into base fluids like water, oil, ethylene, and glycol. The concept of nanofluid was first introduced by Choi [1]. Such nanofluids have numerous applications in industries, engineering, biomedical, scientific processes, mechanical, microelectronics, heat exchangers, transportation and drug delivery, etc. [2,3,4,5]. Ghosh and Mukhopadhyay [6] analyzed the nanofluid flow and heat transfer with heat and mass flux over an exponentially shrinking porous surface. However, nanofluids do not have complete high stability and high thermal conductivity in hydrothermal properties. Because of these factors, several researchers have proposed the new nanofluid form, which is a hybrid nanofluid. Here hybrid nanofluid is the mixture of two or more nanoparticles suspended in the base fluid. These hybrid nanofluids have a wide range of applications in medical, acoustics, naval structures, defense, propulsive, cooling and heating in buildings, drug reduction, microscopic, micro-electric cooling of transformer oil, tubular heat exchanger and so on [7,8,9]. Waini et al. [10] studied the effect of transpiration and flow and heat transfer on hybrid nanofluid over a stretching/shrinking surface for uniform shear flow.

The investigation on thermal radiation phenomenon in blood flow and heat transfer has a wide range of applications in biomedical engineering and numerous medical handling methods, predominantly in thermal therapeutic dealings, industrial and space technological products such as furnace design nuclear reactor safety, fire spreads, solar fans, fluidized bed heat reactors, turbid water bodies, photochemical reactors, etc. [11,12,13,14]. Linear thermal radiation is only effective when there is a very low-temperature gradient. However, it is not useful when the temperature gradient changes dramatically. Due to these reasons, we consider the nonlinear thermal radiation. The nonlinear thermal radiation has numerous applications in many engineering and physical procedures such as aircraft, combustion chambers, propulsion devices, chemical processes at high employing temperature, unoriented power innovation, reentry aero-thermodynamics, and furnace operations[15,16,17]. Specifically, the thermal radiation effect considers an invaluable job in dealing the heat transfer process in the polymer processing industry [18]. Reddy et al. [19] investigated the influence of nonlinear thermal radiation on the steady three-dimensional hydromagnetic flow of Eyring–Powell nanofluid over a slendering stretchable sheet. Ghadikolaei et al. [20] analyzed steady 2D mixed convection on MHD flow of Casson nanofluid over a stretching sheet in the occurrence of heat generation and nonlinear thermal radiation.

Many researchers study the impact of magnetic and electric fields endowed with unbelievable uses in engineering, sciences, and medicine such as cooling of nuclear reactors, metal coating, receiving and transmitting antennas, purification of liquid metals, magnetic resonance imaging equipment, magnetohydrodynamic electric power generator, radiofrequency ablation used in cardiology, cure of skin disorders, treatment of malaria infection, etc. [3, 21,22,23,24,25,26,27]. Daniel et al. [28] analyzed unsteady 2D mixed convection flow of electromagnetohydrodynamic (EMHD) conducting nanofluid and heat transfer over a permeable linear stretching sheet. Daniel et al. [29] investigated two-dimensional unsteady free convection flow of electromagnetohydrodynamic (EMHD) conducting nanofluid over a stretching sheet.

Entropy generation is a measure of dissipated useful energy and attention to reduce the efficiency of engineering systems such as dispersion depends on the irreversible conditions in a process; transportation and rate processes. Above survey illustrations, very little research has been done on the entropy generation analysis with an electromagnetic field at stagnation point flow of hybrid nanofluid. Having these realities in this mind, the theoretical study has been performed on the entropy generation minimization on the electromagnetic field at the stagnation point flow of hybrid nanofluid thru non-uniform heat source/sink and nonlinear thermal radiation. Cu and ${\hbox {CoFe}_2\hbox {O}_4}$ nanoingredients with blood as hosts are measured. Consequential nonlinear ODEs are solved numerically. Necessary diagrams and tables are shown to attain valuable conclusions and their limitations. Comparative deliberations nonlinear and linear radiations succor for the engineering requirements. Also, the use of blood instead of other normal liquids would conceivably provide well compatibility. Thus, we trust that the execution of such innovative hybrid colloidal suspension will benefit engineers to project or apply nanoingredients in the most auspicious mode. This theoretical model explained systematically the mathematical analysis, physical quantities of interest, analysis of entropy generation, numerical methodology, justification of results, significant findings, remarkable conclusions.

2 Mathematical construction

We ponder the scenario of steady 2D EMHD stagnation point flow of an incompressible Newtonian fluid flow in the prevalence of hybrid nanofluids $(\hbox {Cu}+\hbox {CoFe}_{\mathrm {2}}\hbox {O}_{\mathrm {4}})$ with blood as a base fluid. The electric and magnetic field inspirations are conforming the Ohm’s law, which are pondered on hybrid nanofluid. Furthermore, the stagnation model is used and the source term of the non-uniform heat source/sink and nonlinear thermal radiation influence has designated for numerous forms of hybrid nanofluids. For abridging more clearly the physical explanation of the current boundary layer flow problem, the geometry of the hybrid nanofluid flow model is demonstrated in Fig. 1 and the equations for mass conservation, momentum and energy equations for hybrid nanofluids are as follows (see Daniel et al. [28], Reddy et al. [19] and Ghadikolaei et al. [20]):

$$\begin{aligned}&\frac{\partial u}{\partial x}+\frac{\partial u}{\partial y}=0, \end{aligned}$$

(1)

$$\begin{aligned}&u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=u_{\infty } \frac{du_{\infty } }{dx}+\upsilon _{hnf} \frac{\partial ^{2}u}{\partial y^{2}}+\frac{\sigma E_{0} B_{0} }{\rho _{hnf} }-\frac{\sigma B_{0} ^{2}}{\rho _{hnf} }\left( {u-u_{\infty } } \right) , \end{aligned}$$

(2)

$$\begin{aligned}&\left( {\rho c_{p} } \right) _{hnf} \left( {u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}} \right) =k_{hnf} \frac{\partial ^{2}T}{\partial y^{2}}+\mu _{hnf} \left( {\frac{\partial u}{\partial y}} \right) ^{2}\nonumber \\&+\,\sigma \left( {E_{0} -B_{0} \left( {u-u_{\infty } } \right) } \right) ^{2}-\frac{\partial q_{r} }{\partial y}+{q}'''. \end{aligned}$$

(3)

In Eq. (3), the term ${q}'''$ is the non-uniform heat source/sink, which is modeled as

$$\begin{aligned} {q}'''=\frac{k_{hnf} u_{w} }{x\upsilon _{hnf} }\left[ {A^{*}(T_{w} -T_{\infty } ){f}'+B^{*}(T-T_{\infty } )} \right] . \end{aligned}$$

(4)

Here, we measured $A^{*}>0,\,B^{*}>0$ and $A^{*}<0,\,B^{*}<0$ as internal heat generation and absorption, respectively.

Fig. 1

Schematic diagram of the physical problem

Thermal radiation is invented with the Rosseland diffusion approximation ,and in accordance with this, the radiative heat flux $q_{r}$ is given by

$$\begin{aligned} q_{r} =-\frac{4\sigma ^{*}}{3k^{*}}\frac{\partial T^{4}}{\partial y}. \end{aligned}$$

(5)

By substituting Eqs. (4) and (5) in Eq. (3), we have:

$$\begin{aligned} \begin{array}{l} \left( {\rho c_{p} } \right) _{hnf} \left( {u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}} \right) =k_{hnf} \frac{\partial ^{2}T}{\partial y^{2}}+\mu _{hnf} \left( {\frac{\partial u}{\partial y}} \right) ^{2}+\sigma \left( {E_{0} -B_{0} \left( {u-u_{\infty } } \right) } \right) ^{2} \\ +\,\frac{16\sigma ^{*}T^{3}}{3k^{*}}\frac{\partial }{\partial y}\left( {T^{3}\frac{\partial T}{\partial y}} \right) +\frac{k_{hnf} u_{w} }{x\upsilon _{hnf} }\left[ {A^{*}(T_{w} -T_{\infty } ){f}'+B^{*}(T-T_{\infty } )} \right] . \\ \end{array} \end{aligned}$$

(6)

The thermophysical properties and its corresponding values of hybrid nanofluid with water as a based fluid are demonstrated in Table 1.

Table 1 Thermophysical properties of base fluids and nanoparticles

The accompanying boundary conditions are:

$$\begin{aligned} u=u_{w} +N\mu _{hnf} \frac{\partial u}{\partial y}, \quad v=V_{w} , \quad T=T_{w} +K\frac{\partial T}{\partial y} \hbox { at } y=0, \nonumber \\ u\rightarrow u_{\infty } , \quad T\rightarrow T_{\infty } \hbox { as } y\rightarrow \infty , (7) \end{aligned}$$

(7)

where $V_{w}$represents the

$$\begin{aligned} V_{w} =\sqrt{\frac{\upsilon _{f} u_{w} }{x}} \quad f(0), \quad y\rightarrow \infty . \end{aligned}$$

(8)

Equation (8) infers that the mass transfer at the surface of the capillary wall take place with a velocity $V_{w}$. Here $V_{w} > 0$ and $V_{w} < 0$ are the cases of injection and suction in equation (7), respectively.

The similarity variables are as:

$$\begin{aligned} \eta =\left( {\frac{u_{w} }{\nu _{f} x}} \right) ^{\frac{1}{2}}y, \varphi =\left( {\nu _{f} xu_{w} } \right) ^{\frac{1}{2}}f\left( \eta \right) , \quad T{=}T_{\infty } \left[ {1{+}\left( {\theta _{w} -1} \right) \theta \left( \eta \right) } \right] ,\,\,\theta {=}\frac{T{-}T_{w} }{T_{w} -T_{\infty } }, \end{aligned}$$

(9)

where $\eta$ and $\varphi$ consider as the similarity variable and stream functions, respectively, and $\theta _{w} =\frac{T_{w} }{T_{\infty } }.$ The velocity components are

$u=\frac{\partial \varphi }{\partial y},v=-\frac{\partial \varphi }{\partial x}\quad ,$ which gratifies Eq. (1).

By consuming similarity variables (9), Eqs. (2) and (6) are altered as:

$$\begin{aligned}&\frac{\mu _{hnf} }{\mu _{f} }{f}'''+\frac{\rho _{hnf} }{\rho _{f} }\left( {-{f}'^{2}+f{f}''+A^{2}} \right) +M\left( {A+E-{f}'} \right) , \end{aligned}$$

(10)

$$\begin{aligned}&\frac{k_{hnf} }{k_{f} }{\theta }''+R\left[ {{\theta }''\left( {1+\left( {\theta _{w} -1} \right) \theta } \right) ^{3}+3\left( {\theta _{w} -1} \right) {\theta }'^{2}\left( {1+\left( {\theta _{w} -1} \right) \theta } \right) ^{2}} \right] \nonumber \\&\frac{\left( {\rho c_{p} } \right) _{hnf} }{\left( {\rho c_{p} } \right) _{f} }Pr(f\theta '-f'\theta )+\Pr \left( \frac{\mu _{f} }{\mu _{f} }\text {Ec}\,\left( {{f}''} \right) ^{2}+M\,\text {Ec}\left( {E-\left( {{f}'-A} \right) } \right) ^{2} \right) \nonumber \\&\quad +A^{*}{f}'+B^{*}\theta , \end{aligned}$$

(11)

Where $A=\frac{a_{0} }{a}$,$M=\frac{\sigma B_{0}^{2}}{\rho _{f} a}$, $E=\frac{E_{0} }{B_{0} ax}$, $u_{\infty } =a_{0} x$, $\Pr =\frac{\left( {\mu c_{p} } \right) _{f} }{k_{f} }$, $u_{w} =ax$, $\text {Ec}=\frac{u_{w}^{2} }{\left( {c_{p} } \right) _{f} \left( {T_{w} -T_{\infty } } \right) },R=\frac{16\sigma ^{*}T_{\infty }^{3}}{3k_{f} k^{*}}$. It is dynamic to mark that for $\theta _{w} =1$ and $\theta _{w} >1$, which converge to simple radiative case and the nonlinear radiative aspects, respectively.

The associated boundary conditions are as follows:

$$\begin{aligned} f=s, {f}'=1+s_{f} \frac{\mu _{hnf} }{\mu _{f} }{f}'', \theta =1+s_{t} {\theta }', {f}'\rightarrow A, \theta \rightarrow 0 \hbox { as } n\rightarrow \infty . \end{aligned}$$

(12)

Here $\theta _{w} =1$ and $\theta _{w} >1$ signify the radiative and nonlinear radiative aspects. Thermophysical attributes of hybrid nanofluid is taken from the reference Ghadikolaei and Gholinia [8].

Physical extents that are remarkable in engineering characteristics to manufacture equipments at non-dimensions are skin friction and Nusselt number, which are outlined mathematically as:

$$\begin{aligned} C_{f} =\frac{2\mu _{hnf} \left( {\frac{\partial u}{\partial y}} \right) _{y=0} }{\rho _{hnf} u_{w}^{2} }, \quad \hbox {Nu}=\frac{h}{k_{f} \left( {T_{w} -T_{\infty } } \right) }\left( {q_{r} -k_{hnf} \frac{\partial T}{\partial y}} \right) _{y=0} . \end{aligned}$$

(13)

Retaining the non-dimensional amendments as in Eq. (9) into Eq. (13), we get the ensuing skin friction coefficient and Nusselt number as:

$$\begin{aligned} \left. {\begin{array}{l} C_{f} \hbox {Re}_{_{x} }^{1/2} /2=\frac{1}{\left( {1-\phi _{1} } \right) ^{2.5}\left( {1-\phi _{2} } \right) ^{2.5}}f''\left( 0 \right) \text{, }\,\, \\ \hbox {Nu}_{x} \hbox {Re}_{_{x} }^{-1/2} =-\frac{k_{hnf} }{k_{f} }\left( {1+R\left( {1+\left( {\theta _{w} -1} \right) \theta \left( 0 \right) } \right) ^{3}} \right) \theta '\text{(0). }\, \\ \end{array}} \right\} \end{aligned}$$

(14)

3 Entropy generation study

The entropy generation rate per unit volume for viscous fluid in the occurrence of an electric and magnetic field is demarcated as (see Kefayati and Tang [26] and Hayat et al. [5])

$$\begin{aligned} S_{G} =\frac{k_{hnf} }{T_{\infty }^{2}}\left( {\frac{\partial T}{\partial y}} \right) ^{2}+\frac{k_{hnf} }{T_{\infty }^{2}}\frac{16\sigma T^{3}}{3k_{f} k^{*}}\left( {\frac{\partial T}{\partial y}} \right) ^{2}+\frac{\mu _{hnf} }{T_{\infty } }\left( {\frac{\partial u}{\partial y}} \right) ^{2}+\frac{\sigma }{T_{\infty } }\left( {B_{0} u-E} \right) ^{2}. \end{aligned}$$

(15)

In Eq. (15), the first term is entropy production due to heat transfer, the second term is entropy production due to fluid friction, and third term is entropy production due to Joule heating.

With the assistance of Eq. (9), Eq. (15) is renewed as follows:

$$\begin{aligned} N_{G}= & {} \frac{k_{hnf} }{k_{f} }\alpha _{1} \left( {1+R\left( {1+\left( {\theta _{w} -1} \right) \theta } \right) ^{3}} \right) {\theta }'^{2}+\frac{\text {Br}}{\left( {1-\phi _{1} } \right) ^{2.5}\left( {1-\phi _{2} } \right) ^{2.5}}{f}''\nonumber \\&+M\text {Br}\left( {{f}'-E} \right) ^{2},\nonumber \\ N_{G}= & {} \frac{S_{G} \nu _{f} T_{\infty } }{k_{f} a\Delta T}, \quad \alpha _{1} =\frac{\Delta T}{T_{\infty } } \hbox { and } \text {Br}=\frac{\mu u_{w} ^{2}}{k\Delta T}. \end{aligned}$$

(16)

The Bejan number is delineated as

$$\begin{aligned} \text {Be}= & {} \frac{\hbox {Entropy generation due to heat}}{\hbox {Total entropy generation}},\nonumber \\ \text {Be}= & {} \frac{\frac{k_{hnf} }{k_{f} }\alpha _{1} \left( {1+R\left( {1+\left( {\theta _{w} -1} \right) \theta } \right) ^{3}} \right) {\theta }'^{2}}{\frac{k_{hnf} }{k_{f} }\alpha _{1} \left( {1+R\left( {1+\left( {\theta _{w} -1} \right) \theta } \right) ^{3}} \right) {\theta }'^{2}+\frac{Br}{\left( {1-\phi _{1} } \right) ^{2.5}\left( {1-\phi _{2} } \right) ^{2.5}}{f}''+MBr\left( {{f}'-E} \right) ^{2}}.\nonumber \\ \end{aligned}$$

(17)

4 Scheme of solution and justification

The nonlinear boundary value Eqs. (10)–(12) and are transformed into a set of order one initial equations by considering new dependent variables. Missed preliminary conditions are attained with the assistance of shooting technique (see Fig. 2). Later, a finite value for $\eta$ at $\infty$ is preferred in such a way that all the far-field boundary conditions are fulfilled asymptotically. Our majority calculations are pondered with the various values at $\eta _{\infty }$ which is necessary to realize the far-field boundary circumstances asymptotically for all values of the parameters are pondered. The value of $\eta _\infty$ depends greatly on the set of the physical parameters. Step size $\nabla _{\eta } =0.01$ and the convergence standards $1\times 10^{-6}$ due to its order sixth truncation error, this applied method has profits over numerous other numerical methods. To check the validity of our present mathematical model, we compared the prior works of Bidin and Nazar [30], El-Aziz [31], Ishak [32], Mukhopadhyay and Reddy [33] for precise values on the heat transfer $-{\theta }'\left( 0 \right)$ with several values of Prandtl numbers when $\phi _{1} =\phi _{2} =M=E=A=R=\text {Ec}=0,A^{*}=0,\,\,B^{*}=0,S_{f} =0,S_{t} =0,$ and it parades well agreement, which parades in Table 2.

Fig. 2

Schematic diagram of shooting scheme

Table 2 Comparison $-\theta '(0)$ for several values of Prandtl number when $\phi _{1} =\phi _{2} =M=E=0,$ $A=R=\text {Ec}=0 \quad A^{*}=0,\,\,B^{*}=0, \quad s_{f} =0,s_{t} =0$

Fig. 3

Influence of M on ${f}'(\eta )$

Fig. 4

Influence of E on ${f}'(\eta )$

Fig. 5

Influence of $S_{f}$ on ${f}'(\eta )$

Fig. 6

Influence of A on ${f}'(\eta )$

Fig. 7

Influence of M on $\theta (\eta )$

Fig. 8

Influence of E on $\theta (\eta )$

Fig. 9

Influence of $A^{*}$ on $\theta (\eta )$

Fig. 10

Influence of $B^{*}$ on $\theta (\eta )$

Fig. 11

Influence of $\Pr$ on $\theta (\eta )$

Fig. 12

Influence of Ec on $\theta (\eta )$

Fig. 13

Influence of $S_{t}$ on $\theta (\eta )$

Fig. 14

Influence of A on $\theta (\eta )$

5 Outcomes and conversation

In this segment, we explore the consequences of involved governing flow parameters on velocity $\left( {{f}'\left( \eta \right) } \right)$ , temperature $\left( {\theta \left( \eta \right) } \right)$ , local entropy generation $\left( {N_{G} } \right)$, Bejan number $\left( {Be} \right) ,$ surface drag force $\left( {C_{f} \hbox {Re}_{_{x} }^{1/2} /2} \right)$ and the rate of heat transfer$\left( {\hbox {Nu}_{x} \hbox {Re}_{_{x} }^{-1/2} } \right)$ of our model. Computer code has been established for these numerical outcomes which are prompted with graphical portrayals and tables.

For this computation, we have established upon the values of pertinent parameters as $M=0.5,\,E=0.01,\,A=0.1,\,S_{f} =0.5,R=1.0,A^{*}=0.1,B^{*}=0.1,S_{t} =0.5,\theta _{w} =1.0,\Pr =21$(human blood [12]), $\text {Ec}=0.01,S=0.2,\alpha _{1} =0.5,Br=1.0,\phi _{1} =0.01$ and $\phi _{2} =0.01$, else otherwise specified.

Consequences of flow parameters discrepancies on velocity profiles

The numerical fallouts of the established numerical results of fluid velocity dispersions on suction and blowing are presented explicitly in Figs. 3, 4, 5 and 6. It might be realized from Fig. 3 that the fluid velocity decreases with the rise in magnetic field for the cases of suction and blowing. This dropdown in velocity silhouettes is owed to rise in the Lorentz force with rise in magnetic field which retards the fluid motion. Figure 4 portrays the inspirations of electric field on the fluid velocity disseminations for the cases of suction and blowing. The outcome of Fig. 4 shows that as electric field rises, the velocity profile and boundary layer of the fluid increase. This scenario in velocity outcomes is due to rise in the Lorentz force with the rise in electric field which roots the resistance to the fluid motion. In Fig. 5, the stimulation of slip velocity on velocity outlines is exemplified. It is sensed that the velocity profile reduces as the slip velocity parameter increases. Figure 6 is pinched to see the belongings of stagnation parameter on fluid velocity outlines. It might be perceived from this figure that the fluid velocity increases with the increase in the stagnation parameter.

Impression of flow parameters discrepancies on temperature sketches

The impression of magnetic field, electric filed, space-dependent heat source/sink, temperature-dependent heat source/sink, Prandtl number, Eckert number, thermal slip and stagnation parameters on the temperature profiles is shown in Figs. 7, 8, 9, 10, 11, 12, 13 and 14 for the cases of linear radiation and nonlinear radiation. The temperature outlines of the fluid become broader with the growing values of magnetic parameter as revealed in Fig. 7. This situation in temperature outcomes is due to the rise in the Lorentz force with the rise in magnetic field which roots the resistance to the temperature of the fluid. Additionally, the nonlinear radiation transmits reasonably enhanced thermal profiles. From Fig. 8, it might be seen that the temperature of the fluid decays with the growing values of electric field. This dropdown in temperature silhouettes is due to the rise in the Lorentz force with the rise in electric field which retards the fluid temperature. Also, it has to be perceived that the temperature profiles of nonlinear radiation are comparably greater equated to linear radiation case. Figures 9 and 10 specify that the temperature is intense by increasing space-dependent heat source/sink and temperature-dependent heat source/sink. The temperature outlines become thinner for the larger values of Prandtl number as revealed in Fig. 11. This dropdown in temperature silhouettes is due to the rise in the Prandtl number, the thermal conductivity of the fluid diminutions and hence temperature decays. The temperature outlines of the fluid become broader with the growing values of Eckert number as revealed in Fig. 12. This circumstances in temperature outcomes is due to rise in Eckert number expands the frictional forces within the fluid which roots the fluid temperature to increase. Moreover, the nonlinear radiation transmits reasonably enhanced thermal profiles. The temperature outline pronounces the same behavior for thermal slip and stagnation parameters in Figs. 13 and 14, respectively.

Influences of flow parameter discrepancies on entropy generation rate

The inspirations of ratio parameter, Brinkman number, nanoparticles volume fractions $\left( {\phi _{1} ,\phi _{2} } \right) ,\,$ magnetic field and electric field on local entropy generation rate is exemplified in Figs. 15, 16, 17, 18, 19 and 20 , respectively. We perceived from Fig. 15 that the local entropy generation rate rises immensely with the values of ratio parameter. This situation in entropy generation rate outcomes is because the rise in ratio parameter boosts the heat transfer rate and friction at the surface, which ultimately results in enrichment of entropy generation. Figure 16 authenticates that for higher values of Brinkman number, the entropy generation rate rises. This situation in entropy generation rate outcomes is because viscous effects have become stronger with the increase in Brinkman number. From Figs. 17 and 18, we see that the rate of entropy generation is increased by enhancing $\phi _{1}$ and $\phi _{2}$. Figure 19 directs the entropy generation intensifications with rising values of magnetic field. Physically, the enhancement of Lorentz force with the intensification in magnetic parameter results in more friction which causes the entropy generation rate to enhancement. From Fig. 20, we observe that the entropy generation rate decreases with intensifying values of electric field.

Fig. 15

Influence of $\alpha _{1}$ on $N_{G}$

Fig. 16

Influence of Br on $N_{G}$

Fig. 17

Influence of $\phi _{1}$ on $N_{G}$

Fig. 18

Influence of $\phi _{2}$ on $N_{G}$

Fig. 19

Influence of M on $N_{G}$

Influences of flow parameter discrepancies on Bejan number

Figures 21, 22, 23, 24, 25 and 26 exhibit the impression of Bejan number for the different values of ratio parameter, Brinkman number, nanoparticles volume fractions $\left( {\phi _{1} ,\phi _{2} } \right) ,\,$ magnetic field and electric field, respectively. It could be seen from Fig. 21 that the Bejan number increases immensely with the values of ratio parameter. Additionally, the nonlinear radiation transmits reasonably enhanced Bejan number profiles. Figure 22 indorses that for higher values of Brinkman number, the Bejan number rises. Also, it has to be perceived that the temperature profiles of nonlinear radiation are comparably greater compared to linear radiation case. From Figs. 23 and 24, we see that the Bejan number is increased by enhancing $\phi _{1}$ and $\phi _{2}$. Figure 25 directs that the Bejan number increases with rising values of magnetic field. From Fig. 26, we observe that the Bejan number reduces with intensifying values of electric field. Moreover, the nonlinear radiation transmits reasonably enhanced thermal profiles.

Fig. 20

Influence of E on $N_{G}$

Fig. 21

Influence of $\alpha _{1}$ on Be

Fig. 22

Influence of Br on Be

Fig. 23

Influence of $\phi _{1}$ on Be

Fig. 24

Influence of $\phi _{2}$ on Be

Fig. 25

Influence of M on Be

Fig. 26

Influence of E on Be

Fig. 27

Influence of $\phi _{1}$ and Mon $\hbox {Re}_{x}^{1/2}C_{f} /2$

Fig. 28

Influence of $\phi _{1}$ and M on $\hbox {Nu}_{x} \hbox {Re}_{x} ^{-1/2}$

Fig. 29

Influence of $\phi _{2}$ and M on $\hbox {Re}_{x}^{1/2}C_{f} /2$

Fig. 30

Influence of $\phi _{2}$ and M on $\hbox {Nu}_{x} \hbox {Re}_{x} ^{-1/2}$

Fig. 31

Influence of $\phi _{1}$ and E on $\hbox {Re}_{x}^{1/2}C_{f} /2$

Fig. 32

Influence of $\phi _{1}$ and E on $\hbox {Nu}_{x} \hbox {Re}_{x} ^{-1/2}$

Fig. 33

Influence of $\phi _{2}$ and E on $\hbox {Re}_{x}^{1/2}C_{f} /2$

Fig. 34

Influence of $\phi _{2}$ and E on $\hbox {Nu}_{x} \hbox {Re}_{x} ^{-1/2}$

Fig. 35

Influence of $\phi _{1}$ and $\alpha _{1}$ on $\hbox {Re}_{x} ^{1/2}C_{f} /2$

Fig. 36

Influence of $\phi _{1}$ and $\alpha _{1}$ on $\hbox {Nu}_{x} \hbox {Re}_{x}^{-1/2}$

Influences of flow parameter discrepancies on skin friction coefficient and Nusselt number

Influence of magnetic field, electric field, nanoparticles volume fractions $\left( {\phi _{1} ,\phi _{2} } \right) ,\,$ ratio parameter and Brinkman number on skin friction coefficient and the Nusselt number is depicted in Figs. 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, and 42. From these sketches, it might be understood that the skin friction coefficient reduces when rising the values of magnetic field, $\phi _{1}$, $\phi _{2} ,$ ratio parameter and Brinkman number; however, the conflicting tendency is noticed in the case of electric field. Moreover, the heat transfer rate increases when increasing the values of $\phi _{1} ,\phi _{2} ,$ electric field, ratio parameter and Brinkman number, whereas the contradictory tendency is perceived in the case of magnetic field.

Fig. 37

Influence of $\phi _{2}$ and $\alpha _{1}$ on $\hbox {Re}_{x} ^{1/2}C_{f} /2$

Fig. 38

Influence of $\phi _{2}$ and $\alpha _{1}$ on $\hbox {Nu}_{x} \hbox {Re}_{x}^{-1/2}$

Fig. 39

Influence of $\phi _{1}$ and Br on $\hbox {Re}_{x}^{1/2}C_{f} /2$

Fig. 40

Influence of $\phi _{1}$ and Br on $\hbox {Nu}_{x} \hbox {Re}_{x}^{-1/2}$

Fig. 41

Influence of $\phi _{2}$ and Br on $\hbox {Re}_{x}^{1/2}C_{f} /2$

Fig. 42

Influence of $\phi _{2}$ and Br on $\hbox {Nu}_{x} \hbox {Re}_{x} ^{-1/2}$

6 Conclusions

In this article, entropy generation on EMHD blood flow of hybrid nanofluid with nonlinear thermal radiation and non-uniform heat source/sink has been explored. The governing equations for the blood flow problem are demonstrated with the assistance of continuity, momentum and energy equations. The ensuing PDE’s are converted into a system of coupled nonlinear ODE’s with the assistance of similarity variables and are solved with the assistance of RK 4th order method with shooting technique. The foremost consequences for the current analysis are:

• 1. Velocity outlines increase with the rise in electric filed, whereas the temperature reduces with electric field.

• 2. The velocity sketches increase with an increase in stagnation parameter, whereas the contradictory tendency is perceived for the temperature case.

• 3. The local entropy generation increases, when increasing the values of the magnetic parameter, ratio parameter, and the Brinkman number, whereas the contradictory tendency is perceived in the case of electric field.

• 4. The skin frication coefficient increases when rising the electric field but decreases when increasing the magnetic field.

• 5. The nonlinear radiation is comparably greater compared to linear radiation for all the situations.

The current hypothetical model will be very interesting to clinicians for their treatment to the patients more accurately in thermal therapeutic procedures (i.e., treatment for relieving pain, muscle spasms, chronic widespread pain, etc.), treatment for tumors, cancers, malaria by using the electromagnetic hyperthermia, heat dose sensitivity tests, arterial diseases, etc. Likewise, the current mathematical model will be beneficial in judging the accurateness of forthcoming studies in this path, considering a better number of physical parameters.