A multi-constraint failure-pursuing sampling method for reliability-based design optimization using adaptive Kriging

Abstract

Using surrogate models to substitute the computationally expensive limit state functions is a promising way to decrease the cost of implementing reliability-based design optimization (RBDO). To train the models efficiently, the active learning strategies have been intensively studied. However, the existing learning strategies either do not individually build the models according to importance measurement or do not completely relate to the reliability analysis results. Consequently, some points that are useless to refine the limit state functions or far away from the RBDO solutions are generated. This paper proposes a multi-constraint failure-pursuing sampling method to maximize the reward of adding new training points. A simultaneous learning strategy is employed to sequentially update the Kriging models with the points selected in the current approximate safe region. Moreover, the sensitive Kriging model as well as the sensitive sample point are identified based on the failure-pursuing scheme. A new point that is highly potential to improve the accuracy of reliability analysis and optimization can then be generated near the sensitive sample point and used to update the sensitive model. Besides, numerical examples and engineering application are used to validate the performance of the proposed method.

1 Introduction

Reliability-based design optimization (RBDO) is an effective tool to consider the various uncertainties in the initial design stage. The optimal solution of RBDO can achieve the balance between the performance and the reliability of a product. The formulation of RBDO is generally defined as [1,2,3,4]

$${\text{Find }}\mu_{X} {\text{Min }}f(\mu_{X} ) {\text{S.t. Prob}}(g_{c} (\mathbf{X}) \le 0) \le P_{f,c}^{t} , \, c = 1,\ldots,N_{c} \, \, \mu_{X}^{L} \le \mu_{X} \le \mu_{X}^{U}$$

(1)

where ${{\mathsf{\mu }}_{\mathbf{X}}}$ are the mean values of random design variables ${\mathbf{X}}$, $\mathcal{\mu }_{{\mathbf{X}}}^{L}$ and $\mathcal{\mu }_{{\mathbf{X}}}^{U}$ are the lower and upper bounds of $\mathcal{\mu }_{{\mathbf{X}}}$ respectively. Due to the uncertainties that exists in ${\mathbf{X}}$, the failure probability is used to measure the reliability of a certain design. In the probabilistic constraint, it is defined that the failure probability calculated by ${\text{Prob(}} \cdot )$ should be smaller than the maximum allowable failure probability $P_{f,c}^{t}$. The failure event occurs when the limit state function (i.e. performance function) ${\text{g}}_{c} ({\mathbf{X}})$ is smaller than or equal to zero. Correspondingly, the failure probability is calculated by [5,6,7]

$$\text{Prob(}{{\text{g}}_{c}}({\mathbf{X}})\le 0) =\int_{{{\varOmega }_{f,c}}}{{{f}_{\mathbf{X}}}(\mathbf{X})}{\rm d}{\mathbf{X} }$$

(2)

where ${{f}_{\boldsymbol{X}}}(\boldsymbol{X})$ is the joint probability density function, and ${{\varOmega }_{f,c}}$ is the failure region of the c-th probabilistic constraint.

In practice, the limit state function ${{\text{g}}_{c}}({\mathbf{X}})$ is usually the time-consuming model, such as the finite element analysis (FEA), computational fluid dynamics (CFD) and true physics model, which means calculating the complex integration in Eq. (2) is computationally prohibitive. Since the estimation of failure probability is an essential part of RBDO (i.e. Eq. (2) is a part of Eq. (1)), the computational cost of RBDO is more expensive. Therefore, both the reliability analysis methods and RBDO methods have been intensively studied. On one hand, many analytical reliability analysis methods [8,9,10,11] and well-known analytical RBDO approaches, roughly classified into double-loop methods [12], decoupled methods [13, 14] and single-loop methods [15, 16], are developed. However, the former performs poorly sometimes when the limit state function is highly nonlinear, while the latter gets stuck in the tradeoff between the accuracy and efficiency. On the other hand, another alternative, i.e. surrogate model, has been used to approximate the implicit limit state function in reliability analysis and RBDO during the last two decades [17]. The surrogate model is trained by a set of sample points, and then it can be combined with the simulation method for analysis and optimization. Because the true function evaluations for training the surrogate model are much smaller than those required by direct simulation method, the computational cost is sharply reduced. The commonly used surrogate models include response surface method (RSM) [18, 19], artificial neural network (ANN) [20], support vector machine (SVM) [21], and Kriging [22,23,24,25,26]. In this paper, the Kriging model that has been widely used in reliability analysis [27,28,29], system reliability analysis [30,31,32] and time-dependent reliability analysis [33,34,35,36] is employed due to its feature in providing the mean prediction and variance.

Kriging-based RBDO methods can be divided into one-shot sampling methods [37] and sequential sampling methods [38]. In one-shot sampling methods, Kriging model is trained with the sample points generated by factorial design [39], central composite design [40] or Latin hypercube designs [41]. The performance of one-shot sampling method relies on the number and location of sample points, which cannot accommodate the unknown outline of complex functions. Different from one-shot sampling methods, the latter adds new points and update Kriging model sequentially. During the refinement of Kriging, the sequential sample points are selected according to some learning strategies. Therefore, the sequential sampling process can be adjusted based on the results of reliability analysis or RBDO, which tends to build a more accurate Kriging model with fewer samples [42].

In sequential sampling methods, the Kriging model can be built by the global modeling strategy in the design domain or the local modeling strategy driven by the iterative optimization. The goal of global modeling strategy is to accurately approximate the whole constraint boundary in the design domain [43, 44]. When the Kriging model reaches the predetermined precision, the RBDO process is conducted to search the optimal solution according to the constructed Kriging model. The local modeling strategy driven by the iterative optimization focuses on the local region where the optimal solution may exist, since the accuracy of the constraint boundary in that local region plays an important role on the accuracy of the optimal solution [45,46,47,48,49]. In the local modeling strategy driven by the iterative optimization, new samples near the current optimization solution of each iteration step are selected to update the Kriging model, and then the next optimization solution is searched according to the updated model. The Kriging modeling and design optimization are conducted sequentially until the optimal solution is found.

Although great progress has been made in Kriging-based RBDO methods, there are still some challenges. For example, some methods treat all the constraints equally and update all the Kriging models with the same training points. However, some sample points may be not the optimal choice of all the constraints, and some points may be wasted for the inactive constraints. Moreover, some learning strategies are not able to make full use of the results of reliability analysis and RBDO, leading to the fact that some sample points make little contribution to the improvement of prediction accuracy. To address these issues, we propose a multi-constraint failure-pursuing sampling (MCFPS) method. For the RBDO problems with multiple probabilistic constraints, MCFPS separately updates the Kriging models with different points by the simultaneous learning strategy. All the candidate points are selected from the safe region determined by the current Kriging models. Furthermore, we propose an error measurement that can calculate the sensitivity of existing sample points to the accuracy of estimated failure probability. According to the error measurement, the sensitive sample point that is the most important to the accuracy improvement of Kriging model can be identified for every constraint. Correspondingly, the sensitive constraint that should be updated can also be identified.

The remainder of this article is organized as follows. Section 2 introduces two typical Kriging-based RBDO methods that are compared with our proposed method. Section 3 provides the details of the proposed method. Section 4 demonstrates the performance of the proposed method through three numerical examples and one engineering application. Section 5 summarizes the contributions.

2 The multi-constraint failure-pursuing sampling method

For the Kriging -based RBDO problems with multiple probabilistic constraints, there are still some challenges: (1) How to update the Kriging models of different probabilistic constraints in an effective sequence; (2) How to identify the active probabilistic constraints important for RBDO and the inactive constraints useless for RBDO; (3) How to generate the new training point for the refinement of the most important Kriging model. To address these important issues, this work proposes a multi-constraint failure-pursuing sampling (MCFPS) method, and the following subsections will introduce how MCFPS answers these questions one by one.

2.1 Simultaneous learning strategy

The basic idea of Kriging -based RBDO is to substitute the time-consuming limit state function with cheap Kriging model. Since each probabilistic constraint contains a limit state function, several Kriging models are required when there are multiple probabilistic constraints. To train the Kriging models, the most popular way is generating the same sample points for all the limit state functions, just like what CBS and LAS have done. However, the design optimization problems in engineering often involve multiple constraints, and each constraint may correspond to different disciplines. This means that for each constraint, the corresponding response value needs to be obtained through separate simulation or experiment. Therefore, generating the same sample points for all the limit state functions may waste the computational resource, as most sample points may be only important for part of constraints rather than all constraints. If we can separately identify the most useful points for every constraint while training the Kriging models, then the wasted points will be reduced as much as possible. Therefore, we employ the simultaneous learning strategy in MCFPS.

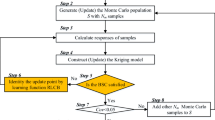
In simultaneous learning strategy, different Kriging models only share the same initial sample point set ($E{{D}_{0}}={{\mathbf{X}}_{initial}},c=1,\cdots ,{{N}_{c}}$), which is uniformly generated in the design space. Following the initialization, only one Kriging model of the constraint will be updated in each iteration of the sequential refinement, and we name the updated constraint as sensitive constraint. Figure 1 illustrates this strategy by three consecutive iterations. In the k-th iteration, the Kriging model (${{\hat{\text{g}}}_{2}}$) of the second constraint is selected to be updated based on some criteria, while the other two constraints are not updated. After that, the sensitive constraint will shift from ${\hat{\text{g}}}_{2}$ to ${\hat{\text{g}}}_{3}$ in the next iteration shown in Fig. 1b. Based on the same criteria, the constraint that is the most important to the RBDO result will be identified and updated one by one. As a result, the sample sets $E{{D}_{c}}(c=1,\cdots ,{{N}_{c}})$ of different constraints vary from each other after the sequential sampling.

Fig. 1

The illustration of simultaneous learning strategy

Moreover, to avoid adding the points that make few contributions in the simultaneous learning process, all the new sample points are only selected in the safe domain that plays a significant role in searching the RBDO solution. The main reason for sampling in the safe area is to improve the sampling efficiency by reducing the sampling region. Moreover, by adding the sequential sample points in the safe area, the fitting accuracy of the constraint boundary is gradually updated and finally meets the accuracy requirements. To avoid the possible influence of sampling in the safe area on the sampling accuracy or efficiency, the introduction of the conservative boundary will be considered in the follow-up study. The existing constraint boundary will be offset to the failure domain by a certain amount, and then the sequential sampling will be carried out in the shifted safe area. The specific offset distance and sampling effect will be the focus of future research.

The safe region is defined by

$${{\varOmega }_{safe}}=\left\{ \mathbf{x}\in {{\mathbf{R}}^{d}}|{{{\hat{g}}}_{c}}(\mathbf{x})\ge 0,\forall c\in [1,{{N}_{c}}] \right\},$$

(3)

where ${{\hat{g}}_{c}}(\mathbf{x})$ is the Kriging model of the c-th limit state function. Since the safe region is determined by the current Kriging models, it can be also observed from Fig. 1 that the size of the safe region is updated with the update of the Kriging models. Obviously, the safe region deeply affects the generation of sample points and the search of RBDO solution. If we update all the Kriging models in each iteration, some constraints will be updated by some useless points that have a higher probability to be located outside the safe region actually. The simultaneous learning strategy can reduce the risks of wasting sample resource. Next, we will discuss how to identify the sensitive constraint and how to add new training point for the constraint.

2.2 Identification of sensitive constraint and sensitive point

Motivated by the failure-pursuing sampling framework proposed by the authors [50], MCFPS identifies the sensitive constraint from all constraints as well as the sensitive point from the existing training point set before adding new sample points. It is worth noting that the failure-pursuing sampling framework is developed for reliability analysis, while MCFPS is proposed for RBDO. Their different aims indicate that their identification strategies vary from each other, let alone the generation of new training points.

In Kriging-based RBDO, it is vital to accurately approximate the constraint boundaries that are potential to be visited by the optimal solution. However, the approximation accuracy of the constraint boundaries around the current design point is not able to be calculated directly. To add more sample points that are highly potential to improve the approximation accuracy, MCFPS validates the approximation accuracy by calculating the estimation accuracy of failure probability at the current design point. Consequently, MCFPS employs an error measurement defined by

$$e_{{{{\hat{p}}}_{f}}}^{c,i}=\left| {{{\hat{p}}}_{f,c}}-\hat{p}_{f,c}^{{{\mathbf{X}}_{c}}/\mathbf{x}_{c}^{i}} \right|,c=1,\ldots ,{{N}_{c}}, \, i=1,\ldots ,N_{sample}^{c},$$

(4)

where ${{\hat{p}}_{f,c}}$ is the failure probability of the c-th constraint predicted by the current Kriging model ${{\hat{g}}_{c}}(\mathbf{x})$, $\hat{p}_{f,c}^{{{\mathbf{X}}_{c}}/\mathbf{x}_{c}^{i}}$ is the predicted failure probability after removing the sample point $\mathbf{x}_{c}^{i}$ from the training set of current Kriging model ${{\hat{g}}_{c}}(\mathbf{x})$, $N_{sample}^{c}$ is the current number of sample points for c-th constraint, and ${{N}_{c}}$ is the total number of probabilistic constraints. It is observed based on Eq. (7) that the larger the error is, the less the accuracy of constraint boundary is.

Additionally, since the computational cost will grow with the increase of number of training points, the efficient importance sampling technique [51] is adopted while calculating the failure probability, and the most probable point is found by the iterative control strategy [15].

In each iteration, the error measurement will be calculated for every constraint and every existing sample point. As a result, the indices of sensitive point and sensitive constraint can be identified by

$$i_{sen}^{c}=\underset{i=1,\cdots,N_{sample}^{c}}{\mathop{\arg \max}}\,e_{{{{\hat{p}}}_{f}}}^{c,i},c=1,\ldots,{{N}_{c}}$$

(5)

and

$${{c}_{sen}}=\underset{c=1,\cdots,{{N}_{c}}}{\mathop{\arg \max}}\,(e_{{{{\hat{p}}}_{f}}}^{c,i_{sen}^{c}}).$$

(6)

The constraint with the maximal error, i.e. sensitive constraint, will be updated to maximize the accuracy improvement of the safe region. Correspondingly, the new added point will be highly related to the corresponding sensitive point ${{\mathbf{x}}_{{{c}_{sen}},{{i}_{sen}}}}$, as the point is the most sensitive to the estimation accuracy of failure probability. Based on this strategy, the active constraints that determine the location of RBDO solution will be identified and updated, while the inactive constraints will remain unchanged. Moreover, it is worth noting that the sample points that are far away from the current design point have less effect on the estimation of failure probability. Therefore, the sensitive point will be often located around the current design point, which means the more computational resource will be focused on the local region visited by RBDO optimizer.

Figure 1 illustrates the identification process of sensitive constraint and sensitive point. In each iteration, the error measurement in Eq. (7) is used to evaluate the sensitiveness of all existing samples (blue “x”). Then the sample with the maximal error is regarded as the sensitive point (blue “x” with a green dotted circle). At the sensitive point, the constraint with the maximum error is regarded as the sensitive constraint. In the k-th iteration, constraint 3 is regarded as the sensitive constraint and new sample (black “*” in Fig. 1b) is added to only update constraint 3. Then in the (k + 1)-th iteration, constraint 1 is regarded as the sensitive constraint and new sample (black “*” in Fig. 1c) is added to only update constraint 1.

2.3 Generation of new training point

In general, the points around the sensitive point ${\mathbf{x}}_{{c_{sen} }}^{{i_{sen}^{c} }}$ of the sensitive constraint have a high probability to improve the accuracy of the corresponding Kriging model. Moreover, the points that are close to the constraint boundary or with large prediction uncertainty should also be selected. Therefore, the learning function (LF) for adding the new training points can be defined as follows

$$\text{LF}(\mathbf{x})=\frac{\left| \hat{g}(\mathbf{x}) \right|}{{{\sigma }_{{\hat{g}}}}(\mathbf{x})\cdot corr(\mathbf{x},\mathbf{x}_{{{c}_{sen}}}^{i_{sen}^{c}})}$$

(7)

where $\hat{g}(\mathbf{x})$ and ${{\sigma }_{{\hat{g}}}}(\mathbf{x})$ are the mean prediction and error prediction of Kriging model respectively. $corr(\mathbf{x},\mathbf{x}_{{{c}_{sen}}}^{i_{sen}^{c}})$ is the correlation between the candidate points and the sensitive point, which is expressed using the minimum distance to the existing samples.

The learning function is derived from the U function [52]. The difference is that the correlation between the candidate points and the sensitive point is considered in the proposed method. To compare the two sequential sampling methods, an example taken from [53] is applied. The function is given as

$$\text{g}({\mathbf{X}})=\frac{({{(1.5+{{X}_{1}})}^{2}}+4)((2.5+{{X}_{2}})-1)}{20}-\sin \frac{5(1.5+{{X}_{1}})}{2}-2$$

(8)

The initial Kriging model is constructed using 6 Latin Hypercube samples. The Kriging model is then updated by U function and proposed learning function when new samples are added. Figure 2 depicts the true function (${{g}_{t}}$, Blue lines), the function from Kriging model (${{g}_{\text{p}}}$, Grey lines), the initial training points (Black circles), and the sequential samples (Blue boxes) of U function and proposed methods. It illustrates that the proposed method effectively reduces the number of training points used in U function. The reason is that some sequential samples in U function are too close to the existing samples. These samples which are less important to the update of the Kriging model are labeled as red “x” in Fig. 2. However, if the correlation between the candidate points and the existing sample points are considered, this situation will be solved.

Fig. 2

The comparison of U function and Proposed Sampling Criterion

Based on Eq. (10), the point that minimizes LF and is located at the safe region ${{\varOmega }_{safe}}$ will be selected to update the Kriging model, and the newly added point is represented by

$$\mathbf{x}_{{{c}_{sen}}}^{new}=\left\{ \mathbf{x}\in {{\varOmega }_{safe}}\left| \hbox{min} \left( LF(\mathbf{x}) \right) \right. \right\}.$$

(9)

Then the sample set of the sensitive constraint is updated as $E{{D}_{{{c}_{sen}}}}=[{{\mathbf{X}}_{{{c}_{sen}}}};\mathbf{x}_{{{c}_{sen}}}^{new}]$.

Additionally, the local refinement of Kriging models around the current design point is stopped when $e_{{{{\hat{p}}}_{f}}}^{{{c}_{sen}},i_{sen}^{c}}\le 0.1$, and a new optimization is performed to search the next design point. The local refinement and optimization are sequentially repeated until the design point satisfies the following stopping condition

$$\left\| \frac{\mathbf{x}_{opt}^{k+1}-\mathbf{x}_{opt}^{k}}{\mathbf{x}_{opt}^{k}} \right\|\le {{\varepsilon }_{opt}},$$

(10)

where $\mathbf{x}_{opt}^{k}$ is the design point in the k-th optimization iteration, ${{\varepsilon }_{opt}}$ is a predefined threshold for the optimization.

2.4 The flowchart of MCFPS method

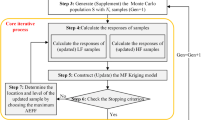
The flowchart of MCFPS method is shown in Fig. 3. For initialization, the initial sample points are uniformly generated in the whole design space, the initial design point and the corresponding candidate point set are also determined. After that, the Kriging models are built and the current safe region is determined. Then the sensitive constraint and sensitive point are identified according to the methods proposed in Sect. 3.2. Meanwhile, the sequential sample is obtained from the current safe region to update the sensitive constraint by LF criterion. To avoid the waste of samples, the simultaneous learning strategy is adopted to only update one Kriging model in each iteration during the refinement. The local refinement of Kriging models around the current design is stopped when the stopping condition shown in Sect. 3.3 is satisfied. After that, reliability analysis and corresponding sensitivity analysis are carried out based on the updated Kriging models, and the design solution get updated until it meets the accuracy requirements. It’s worth noting that, the optimization algorithm used in this paper is sequential quadratic programming, which is a kind of gradient-based optimization algorithm. In addition, other algorithms, including global optimization algorithm, can be used in the proposed method [54].

Fig. 3

The flowchart of MCFPS method

3 Examples

In this section, three classic numerical examples and the EDM process parameter optimization example are used to demonstrate the performance of the proposed method. By comparing with the one-time sampling method (Latin hypercube sampling, LHS), constraint boundary sampling (CBS) and local adaptive sampling (LAS), the performance of the proposed method is validated. The Kriging parameter set for all the four examples is as follows. The initial value $\theta$ is 10 and the lower and upper bounds of $\theta$ is 0.1 and 30. To demonstrate the robustness of each method, all experiments are repeated 10 times, and the average value is taken as the final optimization solution. The errors between the optimization results of each method ($\mu_{\mathbf{X}}^{opt}$) and the reference value ($\mu_{\mathbf{X}}^{ANA}$) are calculated by ${{\varepsilon }_{d}}=(\left| \mu_{\mathbf{X}}^{ANA}-\mu_{\mathbf{X}}^{opt} \right|)/\left| \mu_{\mathbf{X}}^{ANA} \right|$. In addition, the relative error between Kriging failure probability and actual failure probability are calculated by ${{\varepsilon }_{c}}=(\left| P_{f}^{ANA}-P_{f}^{Kriging} \right|)/\left| P_{f}^{ANA}+eps \right|$. $eps$ is used here to avoid the 0 denominator.

The convergence conditions of all methods are given by

$$\left\| \frac{\mu_{\mathbf{X}}^{k+1}-\mu_{\mathbf{X}}^{k}}{\mu_{\mathbf{X}}^{k+1}} \right\|\le {{10}^{-3}},$$

(11)

where $\mu_{\mathbf{X}}^{k}$ is the design point of the k-th iteration. ${{10}^{-3}}$ is a relatively reasonable value obtained by experiments, which can obtain the balance between accuracy and efficiency. ${{10}^{-1}}$ or ${{10}^{-4}}$ can also be used here, but the former may cause inaccurate RBDO solution and the latter may cause inefficient RBDO solution for the examples used in this paper. The influence of design point norm, problem dimensions, nonlinearity to the termination criteria will be the next research content.

3.1 Numerical example 1

This is a two-dimensional problem with three nonlinear probabilistic constraints [4, 14]. The two variables follow the normal distribution ${{X}_{i}} \sim {\ }N(\mu_{{{X}_{i}}}^{{}},{{0.3}^{2}})i=1,2$. The target reliability is set to 3 for all the probabilistic constraints, which means the corresponding failure probability is $P_{f,c}^{t}= 0. 1 3 50 \%$. The initial design point is ${\mu}_{{\mathbf{X}}}^{0} = [5,5]$. The RBDO model is formulated as follows

$$\begin{aligned} & {\text{Find }}\varvec{\mu}_{{\mathbf{X}}}^{{}} = [\mu_{{X_{1} }}^{{}} ,\mu_{{X_{2} }}^{{}} ] \hfill \\ & {\text{Min }}\mu_{{X_{1} }}^{{}} + \mu_{{X_{2} }}^{{}} \hfill \\ & {\text{S}} . {\text{t}} . {\text{ Prob}}(g_{c} ({\mathbf{X}}) \le 0) \le P_{f,c}^{t} \, c = 1,2,3 \hfill \\ & \, 0 \le \mu_{{X_{1} }}^{{}} \le 10, \, 0 \le \mu_{{X_{2} }}^{{}} \le 10, \hfill \\ & {\text{g}}_{1} ({\mathbf{X}}) = 1 - X_{1}^{2} X_{2} /20 \hfill \\ & {\text{g}}_{2} ({\mathbf{X}}) = (X_{1} + X_{2} - 5)^{2} /30 + (X_{1} - X_{2} - 12)^{2} /120 - 1 \hfill \\ & {\text{g}}_{3} ({\mathbf{X}}) = 1 - 80/(X_{1}^{2} + 8X_{2} + 5) \hfill \\ \end{aligned}$$

(12)

The optimization results are shown in Table 1. For sequential sampling methods, 10 same LHS sample points are used to construct the initial Kriging models. “45/45/45″ means the number of sample points needed to construct the Kriging model for each constraint, respectively. The results of ANA are obtained by directly calling the real performance functions. The error results for numerical example 1 is shown in Table 2. As can be seen from Table 2, all the methods show small errors ranging from 0.0827 to 0.2234%. Therefore, all the methods are in good precision. The error of the optimal design point calculated by MCFPS is small, and the failure probability error of each constraint is closer to the result of ANA, which means the proposed method has high accuracy.

Table 1 RBDO results for numerical example 1

Table 2 Error results for numerical example 1

On the other hand, the total numbers of sample points are gradually decreased from LHS to MCFPS. Many samples that are meaningless to the Kriging modeling are selected in LHS, thus it has the lowest efficiency. The sequential samples of CBS are mainly located near the constraint boundaries, but some of them are useless to the solution of RBDO. In LAS, the sequential samples are mainly selected within a small region around the current iteration design point. Therefore, its sampling efficiency is higher than that of LHS and CBS. But in LAS, the same sample points are selected for all the constraints, which wastes the computational resource because most sample points may only be important for part of constraints rather than all constraints. This issue is solved by MCFPS, thus it has the highest efficiency. Seen in Table 1, there is no sequential sample added for the third constraint in MCFPS, the reason is that the third constraint is identified as the inactive constraint in each iteration of the refinement. Moreover, the maximum number of samples for single constraint approximation in MCFPS (21) is less than that of LAS (22), which indicates that the learning function (LF) for adding the new training samples in MCFPS is effective.

Figure 4 shows the positions of samples for each method. The samples of LHS are uniformly distributed in the whole design space, and the samples of CBS, LAS and MCFPS are mainly located near the constraint boundary. Most samples of LAS concentrate on the local region of current iterative design points, so LAS has higher efficiency. Different from other methods which share the same samples for all constraints, MCFPS handles the constraints separately. In Fig. 4d, the blue squares and red squares are the sequential samples of constraint 1 and constraint 2, respectively. The number of samples is different for each constraint in MCFS method, where most samples are identified near the corresponding constraint boundary (Table 2).

Fig. 4

The positions of sample points for numerical example 1

3.2 Numerical example 2

This is a two-dimensional problem with two probabilistic constraints, where the first constraint is strongly nonlinear and the second constraint is linear [43, 45]. The two variables follow the normal distribution ${{X}_{i}}\sim {\ }N(\mu_{{{X}_{i}}}^{{}},0.{ 1^{2}})i=1,2$. The target reliability for both constraints is 2, while the corresponding target failure probability is $P_{f,c}^{t}= 2. 2 7 5 0\%, \, c=1,2$. The initial design point is $\mu_{\mathbf{X}}^{0} = \text{ }\!\![\!\!\text{ 2} . 5 , 2. 5 \text{ }\!\!]\!\! \,$. This problem is formulated as follows

$$\begin{aligned} & {\text{Find}}\quad\varvec{\mu}_{{\mathbf{X}}} = [\mu_{{X_{1} }}^{{}} ,\mu_{{X_{2} }}^{{}} ]^{T} \hfill \\ & {\text{Min}}\quad f(\varvec{\mu}_{{\mathbf{X}}} ) = (\mu_{{X_{1} }}^{{}} - 3.7)^{2} + (\mu_{{X_{2} }}^{{}} - 4)^{2} \hfill \\ & {\text{S}} . {\text{t}} .\quad \;\,{\text{Prob}}(g({\mathbf{X}}) \le 0) \le \varPhi ( - \beta^{t} ) \hfill \\ & g_{1} ({\mathbf{X}}) = - X_{1} \sin (4X_{1} ) - 1.1X_{2} \sin (2X_{2} ) \hfill \\ & g_{2} ({\mathbf{X}}) = X_{1} + X_{2} - 3 \hfill \\ & 0.0 \le \mu_{{X_{1} }}^{{}} \le 3.7,\;\;0.0 \le \mu_{{X_{2} }}^{{}} \le 4.0 \hfill \\ \end{aligned}$$

(13)

The optimization results are shown in Table 3. All the methods show small errors ranging from 0.0149 to 0.0909%. Therefore, all the methods are in good precision. The error of the optimal design point calculated by MCFPS is small, and the failure probability error of each constraint is closer to the result of ANA, which means the proposed method has high accuracy. Compared with other methods, the proposed MCFPS method obtains the optimal solution with the least sample points (38.2 samples). One reason is that the two constraints are considered respectively in the sequential sampling process of MCFPS method. The linear constraint (constraint 2) can be accurately fitted using the initial samples, which will not be updated afterwards. Therefore, sequential sampling is only conducted for the highly nonlinear constraint (constraint 1). Another reason is that the learning function (LF) used for adding the new training samples in MCFPS is efficient. Figure 5 further compares the sample position of each method. For sequential sampling methods, 10 same LHS sample points are used to construct the initial Kriging models. The samples of LHS are uniformly distributed in the whole design space, where many samples are located at the meaningless area (such as the lower-left corner), so the efficiency of LHS is very low. Most samples of CBS are located near the constraint boundary, but there are still some samples at the meaningless constraint boundary, resulting in a waste of computing resources. In LAS and MCFPS, the sequential samples are selected in areas which have the important influence on the solution of RBDO, thus they have higher efficiency. However, the same samples are shared for both constraints in LAS, its sampling efficiency is thus lower than that of MCFPS method.

Table 3 RBDO results for numerical example 2

Fig. 5

The positions of sample points for numerical example 2

3.3 RBDO of the speed reducer

The speed reducer is regularly used to test the performance of RBDO methods [45, 55]. There are 7 independent random variables and 11 probabilistic constraints in this problem. The random design variables are termed as gear width ${{X}_{1}}$, gear module ${{X}_{2}}$, the number of pinion teeth ${{X}_{3}}$, distance between bearings $({{X}_{4}},{{X}_{5}})$ and the shaft diameters $({{X}_{6}},{{X}_{7}})$. The optimization objective is to minimize the weight of the speed reducer. The constraints are related to bending stress, contact stress, longitudinal displacement, stress of the shaft and geometry. The target reliability is set to 3 for all the probabilistic constraints, which means the corresponding failure probability is $P_{f,c}^{t}= 0. 1 3 50\%$. The initial design point is $\left[ 3.20,\;0.75,\;23.00,\;8.00,\;8.00,\;3.60,\;5.00 \right]$. The RBDO model of the speed reducer is formulated as:

$$\begin{array}{ll} {\text{find}}:\quad d = \left[ {d_{1} ,d_{2} ,d_{3} ,d_{4} ,d_{5} ,d_{6} ,d_{7} } \right]^{T} \hfill \\ { \hbox{min} }:\quad f\left( d \right) = 0.7854d_{1} d_{2}^{2} \left( {3.3333d_{3}^{2} + 14.9334d_{3} - 43.0934} \right) \hfill \\ \, - 1.5080d_{1} \left( {d_{6}^{2} + d_{7}^{2} } \right) + 7.4770\left( {d_{6}^{3} + d_{7}^{3} } \right) + 0.7854(d_{4} d_{6}^{2} + d_{5} d_{7}^{2} ) \hfill \\ s.t.:\quad P\left[ {g_{i} \left( X \right) > 0} \right] \le \varPhi \left( { - \beta_{i}^{t} } \right),i = 1, \cdots ,11 \hfill \\ where\;\;g_{1} \left( {\bf X} \right) = \frac{27}{{{\bf X}_{1} X_{2}^{2} X_{3} }} - 1,g_{2} \left( X \right) = \frac{397.5}{{{\bf X}_{1} X_{2}^{2} X_{3}^{2} }} - 1 \hfill \\ g_{3} \left( {\bf X} \right) = \frac{{1.93X_{4}^{3} }}{{{\bf X}_{2} X_{3} X_{6}^{4} }} - 1,g_{4} \left( {\bf X} \right) = \frac{{1.93X_{5}^{3} }}{{{\bf X}_{2} {\bf X}_{3} {\bf X}_{7}^{4} }} - 1 \hfill \\ g_{5} \left( {\bf X} \right) = \frac{{\sqrt {(745 {\bf X}_{4} /({\bf X}_{2} {\bf X}_{3} ))^{2} + 16.9 \times 10^{6} } }}{{0.1 {\bf X}_{6}^{3} }} - 1100 \hfill \\ g_{6} \left( X \right) = \frac{{\sqrt {(745 {\bf X}_{5} /({\bf X}_{2} {\bf X}_{3} ))^{2} + 157.5 \times 10^{6} } }}{{0.1 {\bf X}_{7}^{3} }} - 850 \hfill \\ g_{7} \left( {\bf X} \right) = {\bf X}_{2} {\bf X}_{3} - 40,g_{8} \left( {\bf X} \right) = 5 - \frac{{{\bf X}_{1} }}{{{\bf X}_{2} }} \hfill \\ g_{9} \left( {\bf X} \right) = \frac{{{\bf X}_{1} }}{{{\bf X}_{1} }} - 12,g_{10} \left( {\bf X} \right) = \frac{{1.5 {\bf X}_{6} + 1.9}}{{{\bf X}_{4} }} - 1 \hfill \\ g_{11} \left( {\bf X} \right) = \frac{{1.1X_{7} + 1.9}}{{{\bf X}_{5} }} - 1, {\bf X}_{j} \sim N\left( {d_{j} ,0.005^{2} } \right),j = 1, \cdots ,7. \hfill \\ 2.6 \le d_{1} \le 3.6,0.7 \le d_{2} \le 0.8,17 \le d_{3} \le 28 \hfill \\ 7.3 \le d_{4} \le 8.3,7.3 \le d_{5} \le 8.3,2.9 \le d_{6} \le 3.9 \hfill \\ 5.0 \le d_{7} \le 5.5 \hfill \\ \end{array}$$

(14)

The RBDO results for the speed reducer are shown in Table 4. The MCS results of different methods are shown in Table 5. The Summary of failure probability error results for speed reducer is shown in Table 6. The number of initial samples for sequential sampling methods (CBS, LAS and proposed methods) is 396 (36*11) using LHS.

Table 4 Summary of RBDO results for speed reducer

From Table 4, it can be seen that all the methods show small errors ranging from 0.0115 to 0.0754%. Therefore, all the methods are in good precision. The average sample number of MCFPS is 443.6, which is much less than that of other methods, so it is very efficient. Moreover, the error of the optimal design point calculated by MCFPS is small, and the failure probability error of each constraint is closer to the result of ANA, which means the proposed method has high accuracy.

Table 5 Summary of failure probability results for speed reducer (%)

Table 6 Summary of failure probability error results for speed reducer (%)

3.4 RBDO of EDM process parameters

Electrical discharge machining (EDM) is an effective tool to deal with difficult-to-machining materials (such as super-hard materials) and complicated configurations [56]. In EDM, the instantaneous high temperature produced by pulse discharge between two poles (workpiece and tool) are used to melt and remove the material, so as to process the required shape [57]. After being electrified, the pulse voltage breaks through the insulating medium between the two poles to form a discharge channel, and then forms a plasma composed of charged particles and neutral particles. The charged particles which are moving at high speed collide with the electrode to form an instantaneous high-temperature heat source. Then the workpiece around the discharge point is separated from the local materials due to the influence of high temperature. When the pulse stops, the ion channel is closed, and the heated workpiece is rapidly cooled by the circulating coolant. Then the insulation between the two electrodes is restored until the next cycle. The duration of single spark discharge is very short, thus there are very few materials to be removed. However, EDM can remove a certain amount of metal due to multiple pulse discharge per second. Due to the high temperature in the discharge process and the erosion of workpiece materials, the air particle pollution near the EDM machine tool is formed. In addition, there are surface quality requirements in engineering practice. Therefore, the unit energy consumption (UEC), surface roughness (SR), PM2.5 and PM10 indices in EDM process are considered and analyzed in this paper.

There are many factors that affect the unit energy consumption, surface roughness, PM2.5 and PM10 indices in EDM process, among which peak current (A), cycle rate (s) and efficiency are the most important ones. Therefore, peak current, cycle rate and efficiency are regarded as the design variables in EDM of 304 steel. In EDM processing process, these three parameters have certain uncertainty, thus RBDO is conducted to obtain the optimal unit energy consumption with reliability requirement of the surface roughness (SR), PM2.5 and PM10. The RBDO model of EDM process parameters is formulated as follows

$$\begin{array}{ll} {\text{Find}}\quad \mu_{\mathbf{X}} = [\mu_{{{\mathbf{X}}_{1} }}^{{}} ,\;\mu_{{{\mathbf{X}}_{2} }}^{{}} ,\;\mu_{{{\mathbf{X}}_{3} }}^{{}} ]^{T} \hfill \\ {\text{Min}}\quad f(\mu_{\mathbf{X}} ) = UEC \hfill \\ {\text{S}} . {\text{t}} .\quad \;\,{\text{Prob}}(g({\mathbf{X}}) < 0) \le \varPhi ( - \beta^{t} ) \hfill \\ g_{1} ({\mathbf{X}}) = 6.3 - SR \hfill \\ g_{2} ({\mathbf{X}}) = 100 - PM2.5 \hfill \\ g_{3} ({\mathbf{X}}) = 150 - PM10 \hfill \\ 4{\text{A}} \le \mu_{{{\mathbf{X}}_{1} }}^{{}} \le 10{\text{A}},\;100\;\mu s \le \mu_{{{\mathbf{X}}_{2} }}^{{}} \le 500\;\mu s,\;0.3 \le \mu_{{{\mathbf{X}}_{3} }}^{{}} \le 0.7 \hfill \\ {\mathbf{X}}_{1} \sim N(\mu_{{{\mathbf{X}}_{1} }}^{{}} ,\,0.1^{2} ),\;{\mathbf{X}}_{2} \sim N(\mu_{{{\mathbf{X}}_{2} }}^{{}} ,\,10^{2} ),{\mathbf{X}}_{3} \sim N(\mu_{{{\mathbf{X}}_{3} }}^{{}} ,\,\;0.01^{2} ), \hfill \\ \beta_{i}^{t} = 2.0,\;i = 1,\;2,\;3,\;\mu_{\mathbf{X}}^{0} = [7,300,0.5] \hfill \\ \end{array}$$

(15)

where UEC is the unit energy consumption (Kwh/cm³), which is the power consumption per unit processed volume. The first constraint means that the roughness of the machined surface should be less than the given value to ensure the surface quality of the workpiece. The second and third constraints are the requirements about PM2.5 (${ \, \!\!\mu\!\!\text{ g}}/{{{\text{m}}^ 3}}\;$) and PM10 (${ \, \!\!\mu\!\!\text{ g}}/{{{\text{m}}^ 3}}\;$), which should be less than the given value to ensure the health of operators. The EDM process and the machined workpiece are shown in Fig. 6.

Fig. 6

EDM of 304 steel

The RBDO results of EDM process parameters are shown in Table 7. Except LHS, 10 same initial sample points are used to construct the initial Kriging models. It can be observed that the optimal solutions are obtained by all the methods, where the proposed method is the most efficient one. For the surface roughness constraint, LAS is as efficient as MCFPS, but the fitting efficiency of the other two constraints in the proposed method is much higher than that of LAS. Therefore, using MCFPS to optimize the EDM process parameters, the optimal unit energy consumption can be obtained with reliability requirement of the surface roughness (SR), PM2.5 and PM10.

Table 7 RBDO results for EDM process parameters

4 Conclusions

In this paper, a sampling method, named as MCFPS, is proposed to improve the efficacy of the Kriging-based RBDO. The contribution of this work is as follows

• A simultaneous learning strategy is employed to update the different constraint functions sequentially. Since some unimportant constraint or inactive constraint will be rarely updated, the sample points are saved.

• An error index is proposed to identify the constraint as well as the sample point that are the most sensitive to the accuracy of the failure probability at the current design point. The sensitive constraint will be updated by the new training point identified from the neighborhood of the sensitive sample point.

• A learning function is developed to add the sample point that has the maximum probability to improve the accuracy of Kriging model.

Three numerical examples and RBDO of the EDM process parameters are used to validate the efficacy of MCFPS. The comparison results demonstrate that MCFPS can identify both the important sampling regions and the inactive constraints, then more computational resource is allocated to the important regions. As a result, MCFPS is more efficient than the typical constraint boundary sampling method and local adaptive sampling method. In future work, we will take into account the influence of objective function in the sampling strategies.

Appendix

1.1 Kriging model

Kriging model has been widely used to approximate the implicit performance responses in engineering applications [58]. In Kriging, the predicted response value at a point not only depends on the design parameters but also is affected by the sample distribution [46].

Kriging model is based on the assumption that the response function $\hat{g}(\varvec{x})$ is composed of a regression model $f(\varvec{x})^{T}\varvec{\beta}$ and stochastic process $Z(\varvec{x})$ as follows:

$$\hat{g}(\varvec{x}) = f(\varvec{x})^{T}\varvec{\beta}{ + {\rm Z}(}\varvec{x}\text{)}$$

(16)

where $f(\varvec{x})$ is the prediction trend which is expressed by polynomial function and with the coefficient vector $\varvec{\beta}$;${{\rm Z}}(\varvec{x})$ is a Gaussian process with zero mean and covariance between points $\varvec{x}$ and $\varvec{w}$ as follows:

$$Cov[Z(\varvec{x}),Z(\varvec{w})] =\varvec{\sigma}_{Z}^{2} \varvec{R}(\varvec{\theta}\text{,}\varvec{x}\text{,}\varvec{w})$$

(17)

where $\varvec{\sigma}_{Z}^{2}$ is the process variance and $\varvec{R}(\varvec{\theta}\text{,}\varvec{x}\text{,}\varvec{w})$ is the correlation function defined by parameter $\varvec{\theta}$.

The squared-exponential function (also named anisotropic Gaussian model) is commonly used to define the correlation function [53, 58]:

$$\varvec{R}\text{(}\varvec{\theta},\varvec{x},\varvec{w}) = \prod\nolimits_{1}^{n} {exp[ - \theta_{i} (x_{i} - w_{i} )}^{2} ]$$

(18)

Where $x_{i}$ and $w_{i}$ are the ith coordinates of points $\varvec{x}$ and $\varvec{w}$, n is the dimension of points $\varvec{x}$ and $\varvec{w}$, and θ_i is a scalar which gives the multiplicative inverse of the correlation length in the ith direction [46]. An anisotropic correlation function is preferred here because in reliability analysis and RBDO the random variables are often of different natures [52].