1 Introduction

Tensegrity structures are self-equilibrated spatial assemblages of one-dimensional tension and compression carrying elements, cables and struts. While capable of carrying external loads, in their basic form, force balance at each connection point (node) is satisfied by the introduced prestress. Although the “classical” definition of tensegrity involves struts connected to other struts only via cables, other definitions allow struts connected at nodes for better structural performance [1]. To distinguish between the classical and other kinds of tensegrity structures, a categorization based on the maximum number of struts connected to each other at a node is suggested [2]. Tensegrity structures that have k struts in contact are called Class-k tensegrities, while classical tensegrities having no strut-to-strut connection are called Class-1. The main performance difference between these classes is increased stiffness resulting from strut-to-strut contact—thus, Class-k structures typically yield higher stiffness.

The invention of tensegrity structures dates back to the 1950s, accomplished by Kenneth Snelson (in collaboration with Buckminster Fuller). Over the years, the attention given to tensegrity structures has grown and they have found applications in civil engineering, mechanical engineering, bio-medical engineering, and mathematics. Furthermore, systematic methods have been developed to study the mechanics of tensegrity structures and engineers began to exploit their unique features for lightweight applications [2,3,4,5]. The unique features of tensegrity structures such as light weight, reconfigurability, deployability, and ability to withstand large deformations have the potential to provide novel solutions to many engineering problems. Since tensegrity structures are composed only of axial load-carrying elements, bending loads are (ideally) not experienced by these elements individually and instead structures deform as a whole. Furthermore, their stiffness can be adjusted by varying the prestress levels [6]. Therefore, tensegrity structures have potential to provide solutions for a variety of structural problems.

The design of tensegrity structures not only involves form finding under internal loads, towards which considerable effort has pursued better ways to obtain solutions [7,8,9,10,11], but also requires determination of the response of the structure to external loads. Once the structural configuration is determined by form finding, kinematic and static properties can be investigated to analyze the performance of tensegrity structures.

Design of a real engineering structure can benefit from an optimization step to use materials efficiently and effectively. The most commonly studied optimization problems in the structural engineering field are the minimization of mass under a given set of constraints, which is also known as sizing optimization. However, despite the fact that tensegrity structures have been studied for some time, the majority of the research is devoted to form finding and deployment, and only a few studies have addressed structural design optimization. Furthermore, these optimization studies are mostly related to controllability and deployment. The research on sizing and structural optimization of tensegrity structures for minimum mass with adequate stiffness is quite limited.

Structural optimization of tensegrity structures was first considered by De Jager and Skelton [12]. They investigated the stiffness of tensegrity structures symbolically and conducted optimization studies. Masic and Skelton [13] used a gradient method to select initial prestress levels for LQR performance of tensegrity structures and showed that a linear decrease in the objective function is attainable with proper selection of prestress levels. Masic et al. [14] utilized nonlinear programming to optimize the stiffness-to-mass ratio of tensegrity structures. They concluded that there are three ways to increase the stiffness-to-mass ratio: increasing prestress levels, adding extra elements to lock infinitesimal mechanisms, and changing the topology to a Class-2 tensegrity structure.

Considering the nonlinear behavior of tensegrity structures, which limits the use of classical optimization techniques, and significant improvement in computational capabilities over time, the trend in optimization methods shifted to numerical optimization techniques. Raja and Narayanan [15] employed a genetic algorithm to simultaneously optimize the geometry and the control performance of a two-bay three-strut tensegrity structure. Ali et al. [3] also utilized a genetic algorithm to optimize the design of a tensegrity footbridge for finding a cost-effective design that satisfies a set of given static and dynamic requirements. Lee and Lee [16] also used a genetic algorithm-based optimization technique to maximize the fundamental natural frequencies of different tensegrity configurations appeared in the literature. Their work can be described as a prestress optimization as the member cross sections are pre-defined and the only design variable is the prestress level. Another genetic algorithm-based design was performed by Dalilsafaei et al. [4] to achieve sizing and prestress optimization of tensegrity structures. Class-1 and Class-2 tensegrity structures and a truss structure having the same dimensions were optimized and compared.

Another aspect of optimization for tensegrity structures is topology optimization, which combines sizing optimization with form finding. Kanno [17, 18] used mixed-integer linear programming to investigate Class-1 tensegrity structures to minimize the strain energy at the equilibrium state under self-weight and external loads, respectively, starting with initial tensegrity shapes. Marzari [19] addressed topology optimization of two-dimensional cantilevered tensegrity structures for minimum mass and, in most cases, found that tensegrity structures can yield lighter structures with proper material selection for cables. In another study by Xu et al. [20], topology optimization of tensegrity structures with buckling constraints was considered. Their aim was to minimize the mass of the structure using mixed-integer linear programming. However, some of the design variables were selected from a set of given values or some predetermined values were used rather than searching for the optimum design variables.

Depending on the design requirements, in certain engineering problems, more than one quantity may be the subject of optimization. Such optimization problems are called multi-objective optimization, and from a structural engineering point of view, the objective functions may be related to combinations of mass, stiffness, controllability, etc. Such multi-objective optimization problems may be cast into single-objective form by different approaches. These approaches include conversion of objective functions to constraints until only one objective function remains and combination of objective functions into a single one through prioritization and assignment of weight coefficients.

Zhang and Ohsaki studied a multi-objective optimization problem for a given tensegrity configuration and obtained Pareto-optimal solutions [21]. They attempted to maximize the stiffness of the structure while minimizing the deviation of element forces. However, in their study, no real engineering constraints such as cable yielding or strut buckling were considered. Multi-objective optimization of tensegrity structures was pursued by Ashwear et al. [22] with an aim to design a tensegrity structure with a relatively high fundamental natural frequency, with the others well separated for structural health monitoring purposes. However, the constraints considered in their study included neither cable yielding nor strut buckling. More recently, Xu et al. [23] used mixed integer linear programming formulation to investigate multi-objective topology optimization of tensegrity structures for enhanced controllability.

For practical aerospace engineering applications, it is a challenging and critical task to design structures that comply with the given requirements, while reasonable structural failure modes are taken into account. In this study, sizing and prestress optimization of tensegrity booms with given topologies are studied for space applications, including practical constraints such as cable yielding and strut buckling. Particle swarm optimization (PSO) is used to pursue optimization of tensegrity booms while considering their nonlinear behavior. Two numerical examples are considered, one with a single-objective function and another with multiple objective functions. This paper serves the following purposes: designing a tensegrity structure with a given topology for space boom applications, assessing how the optimized structure compares with more conventional state-of-the-art booms, and evaluating the robustness of PSO in large-scale optimization problems. To achieve these goals, many practical, reasonable, and realistic constraints are taken into account.

The first example attempts to maximize the bending stiffness-to-mass ratio of a tensegrity boom with given global or large-scale dimensions. A representative deployable space boom is selected, and its geometry is used to guide the design and optimization of a tensegrity alternative. The effective bending stiffness of the boom is evaluated by continuum beam modeling. The second example examines another tensegrity structure and considers two objective functions that conflict with each other: minimum mass and minimum lateral tip displacement. The multi-objective optimization yielded Pareto-optimal solutions that can be used to provide insight in the design decision-making process.

This paper is organized as follows: first, analysis methods for tensegrity structures are explained along with the fundamental assumptions. Then, the continuum beam modeling approach is briefly described. The optimization method utilized in this study, particle swarm optimization, is outlined and selection of the parameters is explained. Numerical examples for both the single- and multi-objective function cases are given, and the results are presented and discussed.

2 Analysis of tensegrity structures

Tensegrity structures inherently exhibit geometric nonlinearity and can experience large displacements. The prestress state contributes to the overall stiffness of the structure, which can vary with changes in orientation and geometry [5, 24, 25]. Therefore, nonlinear modeling and analyses considering geometric nonlinearity are required to analyze the behavior and deflection of tensegrity structures under external loads.

The nonlinear structural analysis scheme used employs a modified Newton–Raphson procedure to solve the equilibrium equations incrementally [6]. The fundamental assumptions are listed as follows:

  • Materials exhibit linear elastic behavior.

  • Elements carry solely axial loads.

  • Cables and struts are capable of only carrying tension and compression, respectively (unilateral element behavior).

  • External loads act only at the nodes and the self-weight of the structure is neglected.

The assumptions listed above indicate that tensegrity structures can be modeled in a way similar to truss structures except for the inherent geometric nonlinearity associated with member preloads. This modeling approach has been employed by several researchers and shown to be accurate [6, 24,25,26,27]. The equilibrium equations relating the tangent stiffness matrix and the displacement vector to the external load vector can be represented as follows:

$$\begin{aligned} {K}_{T} \varDelta {U}=P-F, \end{aligned}$$
(1)

where \({K}_T\), U, P, and F denote the tangent stiffness matrix, the displacement vector, the external load vector, and the internal load vector, respectively. Additionally, \(\varDelta \) stands for the iterative changes.

The tangent stiffness matrix consists of linear and geometric stiffness matrices. The linear stiffness matrix is the same stiffness matrix used for linear analyses of truss structures, while the geometric stiffness matrix originates from prestress. Expressions for the stiffness matrices, derivations of which can be found in several studies [6, 24, 26], are given as follows:

$$\begin{aligned}&\begin{array}{lll} {K}_L&{}=&{} \!\dfrac{E_iA_i}{L_i}\begin{bmatrix} {I}_1 &{} -{I}_1 \\ -{I}_1 &{} {I}_1 \\ \end{bmatrix} \end{array}; \qquad \begin{array}{lll} {I}_1&{}=&{} \!\begin{bmatrix} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ \end{bmatrix} \end{array}, \end{aligned}$$
(2)
$$\begin{aligned}&\begin{array}{lll} {K}_\mathrm{{NL}}&{}=&{} \!\dfrac{F_i}{L_i}\begin{bmatrix} {I}_3 &{} -{I}_3 \\ -{I}_3 &{} {I}_3 \\ \end{bmatrix} \end{array}; \qquad \begin{array}{lll} {I}_3&{}=&{} \!\begin{bmatrix} 1 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 \\ \end{bmatrix} \end{array}, \end{aligned}$$
(3)

where \({K}_L\) and \({K}_\mathrm{{NL}}\) are the linear and geometric stiffness matrices, respectively. \(E_i\), \(A_i\), \(L_i\), and \(F_i\) denote the modulus of elasticity, the cross-sectional area, the length of the element, and the prestress force carried by the element, respectively. The tangent stiffness matrix can be obtained as follows where the superscript \((')\) denotes a transformation from local to global coordinates:

$$\begin{aligned} {K}_T={K}_L^{'}+{K}_\mathrm{{NL}}, \end{aligned}$$
(4)

The geometric stiffness matrix is invariant to coordinate transformation and identified as ‘isotropic’, and thus, no transformation is required [26, 28]. The geometric stiffness matrix is linear in the prestress; however, due to large deformations or displacements, it can vary remarkably and results in notable effective changes in stiffness. From the stiffness matrix formulation, its contribution to the tangent stiffness matrix is evident, indicating the important role prestress levels play. The prestress levels can be adjusted to regulate the stiffness levels of tensegrities to some extent [6, 22, 29, 30] and to delay cable slackening as noted by Skelton et al. [31].

Once the tangent stiffness of each element is calculated, the traditional finite-element assembly process can be carried out to obtain the global stiffness matrix. Then, Eq. (1) can be solved iteratively with linear response assumption around the equilibrium state for small external load changes. Since the slope of the linear response is different in each iteration, the collection of these reveals an overall nonlinear response.

For complex structures with a large number of elements that exhibit nonlinear behavior, structural analyses can be tedious to formulate and may take a long time to solve. One approach to alleviating this complexity and computational expense is the use of continuum beam modeling. Such continuum beam modeling works best for long lattice beam-like structures. The goal is to determine a set of effective beam stiffness properties such as axial (EA), bending (EI), and torsional rigidities (GJ). This modeling approach allows relatively rapid evaluation of the stiffness of the long lattice structures and quick comparison of alternative structures.

Tensegrity booms with many repeating bays can thus be modeled as three-dimensional continuum beams and their effective stiffness properties can be obtained. This modeling technique reduces the number of degrees of freedom considerably and the effective stiffness properties can be used to estimate the global behavior rapidly and accurately. One of the methods for continuum beam modeling is called energy equivalency, and it establishes a relation between the actual structure and the continuum beam model, so that they exhibit the same strain energy when deformed the same.

Continuum beam modeling methods have been developed initially by Noor et al. [32] for simple lattice trusses. Then, Dow et al. [33] developed a numerical approach that uses the displacement field developed by Noor and the truss finite-element stiffness matrix. Later, Kebiche et al. [34] adapted Dow’s numerical approach to prestressed structures by including the geometric stiffness. More recent work by Yildiz and Lesieutre [35] modified the approach suggested by Kebiche et al. to make it more straightforward for application to tensegrity structures. In this paper, the method developed by Yildiz and Lesieutre is implemented to evaluate the effective stiffness properties. The method begins with the approximation of the displacement field, and represents the stiffness matrix of the structure in terms of strains and strain derivatives. Depending on the repeating unit of the lattice structure, the strain parameters that are not exhibited by the structure are eliminated, and after a parameter transformation step, the stiffness matrix is reduced to the size of a continuum beam, written in terms of associated strain terms. Then, the diagonal and off-diagonal terms represent the effective stiffness properties and the coupling terms.

3 Particle swarm optimization

Optimization of tensegrity structures can potentially be very complex due to their nonlinear behavior. Static analyses under external loads require numerical solution methods such as nonlinear finite-element analyses with a modified Newton–Raphson algorithm to account for the geometric nonlinearity and the effect of prestress. Therefore, employing the traditional optimization techniques such as gradient methods is excessively expensive in terms of computational effort, and it may even be effectively impossible when considering all design variables and a vast number of constraints simultaneously.

To tackle the optimization of such nonlinear problems, heuristic optimization algorithms are gaining favor. Among a variety of heuristic optimization techniques, in this work, particle swarm optimization is used. PSO is a method developed by Eberhart and Kennedy which is similar to genetic algorithms, as it starts with a population in the search space and seeks an optimum solution [36]. To achieve that, a fitness function (objective function) is iteratively evaluated and potential solutions are updated based on the current best solutions across the population. It does not involve any gradient calculation and has proven to work robustly in many situations [37,38,39,40].

The PSO algorithm randomly generates a population in the search space (design space) in which each individual design is called a particle. Then, each particle is assigned a position and a velocity which are used to determine its iteratively updated position via simple mathematical expressions. The fitness function is evaluated for each particle to determine the best individual and global positions in the swarm. The velocity and position of each particle are then updated using the following expressions:

$$\begin{aligned} v_{i,j}^{k+1}= & {} w \times v_{i,j}^{k}+c_1 \times r_1 \times (p_{i,j}^k-x_{i,j}^k)+c_2 \times r_2 \times (g_{j}^k-x_{i,j}^k), \end{aligned}$$
(5)
$$\begin{aligned} x_{i,j}^{k+1}= & {} x_{i,j}^k+v_{i,j}^{k+1}, \end{aligned}$$
(6)

where \(x_{i,j}^k\) and \(v_{i,j}^k\) are the \(i^\mathrm{{th}}\) particle’s position and velocity components in the \(j^\mathrm{{th}}\) direction, respectively. The superscript k represents the iteration number, while \(r_1\) and \(r_2\) are random numbers between (0, 1). \(p_{i,j}\) is the \(j^\mathrm{{th}}\) component of the best position of the \(i^\mathrm{{th}}\) particle, while \(g_{j}\) is the \(j^\mathrm{{th}}\) component of the best position achieved by the whole swarm up to the \(k^\mathrm{{th}}\) iteration. w is the inertia weight, suggested by Shi and Eberhart [41] which scales the effect of the particle’s velocity from the previous iteration to regulate between local or global minima. In a subsequent study, Eberhart and Shi [42] stated that a using a linearly decreasing inertia weight from 0.9 to 0.4 improves the algorithm performance. Additionally, the parameters \(c_1\) and \(c_2\) were set to 2 initially by Eberhart and Kennedy. Assigning higher values to \(c_1\) or \(c_2\) makes particles tend more towards the best individual position or the best global position, respectively.

For constrained optimization problems, several approaches have been suggested in the literature for heuristic techniques. In this study, the penalty approach is employed, which adds a relatively large number to the fitness function if any of the constraints are violated. By doing so, solutions that violate any constraints would be worse compared to other ones and thus avoided. Additionally, the particles violating the boundary of the design space due to their velocities were relocated at the boundary. The main drawback of the PSO in large-scale and complex problems can be identified as the particles converging to local minima prematurely due to initial random scattering. To avoid such cases, the population size should be selected sufficiently large and the analyses should be repeated at least a few times.

PSO can also be adapted to treat multi-objective optimization problems that have conflicting objective functions. Several variations are suggested by researchers [43,44,45], while two fundamental methods, namely weighted sum and \(\varepsilon \)-constraint, require very minor modifications prior to application of optimization methods. The first one assigns weights (preferably with a sum of 1.0) to the individual objective functions to generate a single-objective function, while the second one converts individual objective functions into constraints until a single-objective function remains. Very recently, a PSO application to tensegrity structures appeared in the literature that determines the optimal feasible prestress modes using weighted sum method [46]. In this study, both the weighted sum and \(\varepsilon \)-constraint methods are utilized to increase confidence in the results.

4 Numerical examples

In this section, sizing and prestress optimization of tensegrity booms is addressed. The main focus is minimizing mass and increasing stiffness by determining the cross-sectional areas and the prestress levels of the elements. A high stiffness-to-mass ratio is of great importance for tensegrity structures used in civil and aerospace applications. The tensegrity structures considered in this work are Class-2 cylindrical tensegrity booms—as they yield greater stiffness-to-mass ratio as compared to Class-1 cylindrical tensegrity booms [1, 3, 5, 47].

Class-2 cylindrical tensegrity booms are built by stacking tensegrity units on top of each other. To generate a self-equilibrated cylindrical tensegrity unit, a twist angle between the top and bottom faces is required, and its direction can be reversed with each subsequent tensegrity unit to reduce twist-extension and bending-twist couplings. The twist angle has a unique value, \(\alpha =(\pi /2)-(\pi /n)\), where n is the number of struts in each bay. However, previous studies showed that addition of extra elements called reinforcing cables can provide design flexibility to the twist angle and define a feasible range such as \(\alpha =(\pi /2-\pi /n,\pi /2)\) rather than a unique value, while increasing stiffness as the infinitesimal mechanisms are locked [48,49,50]. While it is not addressed in detail in this work, stability is an important consideration in the design and analysis of tensegrity structures. Class-2 cylindrical boom configurations considered in this work can be shown to be prestress-stable but not superstable [51].

A close investigation of Class-2 cylindrical tensegrity booms shows that elements within the structures can be classified based on the prestress forces which they carry. The top and bottom cables, vertical cables, saddle cables, optional reinforcing cables, and struts are shown with black, blue, green, orange, and red lines on a two-bay Class-2 cylindrical tensegrity boom in Fig. 1. Figure 2 shows the twist angle using a top view of the boom.

Fig. 1
figure 1

Two-bay tensegrity boom

Full size image
Fig. 2
figure 2

Top view of the boom

Full size image

The first optimization problem is selected as maximization of bending stiffness-to-mass ratio, a single-objective problem. This is somewhat similar to the work by Ashwear et al. [22] in which the first vibration mode of the structure investigated was a bending mode. In such cases, the corresponding natural frequency can be considered an indication of bending stiffness-to-mass ratio. On the other hand, the second is a multi-objective optimization problem that aims to minimize the mass and the tip displacement under loads simultaneously. For both optimization problems, the population size is selected as 200, and three analyses with 100 iterations are performed. The tensegrity booms to be optimized are chosen to consist of three struts per bay, since this configuration exhibits the least number of mechanisms [52]. A representative multi-bay Class-2 tensegrity boom is shown in Fig. 3.

Fig. 3
figure 3

A multi-bay tensegrity boom

Full size image

The optimization problems presented in this study consider the Canister Astromast as a representative deployable space structure and use its global geometry [53]. It is 14 m long with a radius of 0.254 m. As the design loads for the Canister Astromast are not public information and may depend on the mission, the loading scenario in this study is determined based on the following information: Garrett and Pike [54] stated that the loads acting on a spacecraft due to its operating equipment are typically between 0.001 and 10 N. Therefore, to test the limits of Class-2 cylindrical tensegrity booms as deployable space booms, in the first optimization problem, lateral loads of 20 N are applied at the three nodes at the tip of the structure, resulting in 60 N. On the other hand, the second optimization problem addresses a vertical civil engineering structure subjected to 10 N of lateral loads at the tip which may represent mild wind conditions. Furthermore, for both optimization problems, the constraints are defined as: unilateral element behavior and cable slackness (cables carry only tension; struts always carry compression); stress limit for cables; and global (Euler) and local (wall) buckling of struts.

4.1 Class-2 tensegrity boom—single-objective function

In this example, the tensegrity boom is chosen to be a Class-2 tensegrity with reinforcing cables. The objective function is maximization of the bending stiffness-to-mass ratio. The bending stiffness and the other effective stiffness properties of the boom are determined using the modified energy equivalency method [35]. Lateral loads of 20 N in the y direction are applied at the top nodes, while the bottom nodes are fixed. Unless such a realistic loading scenario is applied to the structure, the optimization algorithm converges to a solution with low prestress levels and low cable cross-sectional areas to minimize the mass. This behavior can be explained by the lesser influence of prestress on the stiffness compared to axial stiffness (\(E_iA_i\)) of the elements [28]. However, when a lateral load is applied, the cables can go slack easily. To prevent cable slackness in the results, a realistic loading scenario must be considered, even though it has little direct influence on the determination of effective stiffness properties.

Struts are assumed to be hollow tubes, while the cables have solid cross sections. The design variables are chosen as: radii of four different groups of cables; inner and outer radii of struts; prestress coefficient; twist angle; and the number of bays, resulting in nine total design variables. The cables are assumed to be made of Kevlar 49 resin-impregnated strands, since it provides a great tensile strength of \(\sigma _Y=3600\) MPa. The modulus of elasticity of Kevlar 49 is \(E=124\) GPa, and the density is \(\rho =1440\) kg/m3. For struts, unidirectional Mitsubishi K13C2U UHN/epoxy (60% fiber volume fraction) is chosen due to its low density and high modulus of elasticity [4, 55]. The modulus of elasticity, Poisson’s ratio, and the density are \(E=536\) GPa, \(\nu =0.39\), \(\rho =1840\) kg/m3. These materials might be considered to be representative of an aerospace structure.

The lower and upper bounds of the cable radii, inner and outer strut radii, and the prestress coefficient are selected as 2 and 10 mm, 1 and 30 mm, and, 0.1 and 20 N/mm, respectively. The twist angle bounds are determined to be 62\(^{\circ }\) and 88\(^{\circ }\)  since struts collide at 60\(^{\circ }\) and vertical cables become slack at 90\(^{\circ }\). As the geometry of the structure changes based on the twist angle selection, normalized force-density values carried by each element to satisfy force balance are determined by the force finding method developed by Tran and Lee [56]. These normalized force-density values can be multiplied by the prestress coefficient, which is a scaling factor, and the length of the elements to find the actual prestress forces carried by the elements. The prestress forces in elements can be found as follows:

$$\begin{aligned} {F} = P_s{L}{q}, \end{aligned}$$
(7)

where F is a column vector which stores the prestress force values in each element. \(P_s\) is the prestress coefficient, L is a diagonal matrix of member lengths, and q is the force-density vector.

Based on the preceding information, the optimization problem can be stated as follows:

$$\begin{aligned} \begin{array}{ll} \underset{X}{\text {min}} &{} \quad -\mathrm {EI}(X,{q}(X))/M(X) \\ \text {subject to} &{} \quad -{q}(X)<0, \; \text{ for } \text{ cables } \\ &{} \quad \sigma _{c_i} \le \sigma _Y, \; \text{ for } \text{ cables } \\ &{} \quad {q}(X)<0, \; \text{ for } \text{ struts } \\ &{} \quad T_{\mathrm{{st}}_i} \le P_\mathrm{{eu}}, \; \text{ for } \text{ struts } \\ &{} \quad \sigma _{\mathrm{{st}}_i} \le \sigma _\mathrm{{cr}}, \; \text{ for } \text{ struts }, \\ \end{array} \end{aligned}$$
(8)

where \(\mathrm {EI}\), M, and X, denote the bending rigidity, the mass of the boom, and the configuration, respectively. \(\sigma _{c_i}\), \(T_{\mathrm{st}_i}\), \(P_{\mathrm{eu}}\), \(\sigma _{\mathrm{st}_i}\), and \(\sigma _{\mathrm{cr}}\) are the axial stress in the \(i^{\mathrm{th}}\) cable, the compression force in the \(i^{\mathrm{th}}\) strut, the Euler buckling load, the axial stress in the \(i^{\mathrm{th}}\) strut, and the critical stress for wall buckling, respectively. The Euler buckling load and the critical stress for wall buckling can be expressed as follows [57]:

$$\begin{aligned} P_\mathrm{{eu}}= & {} \frac{\pi ^2\mathrm {EI}}{L^2}, \end{aligned}$$
(9)
$$\begin{aligned} \sigma _\mathrm{{cr}}= & {} \frac{\gamma E}{\sqrt{3(1-\nu ^2)}}\frac{r_o-r_i}{r_o}, \end{aligned}$$
(10)

where \(\gamma \) is a correlation coefficient defined as follows:

$$\begin{aligned} \gamma= & {} 1-0.901(1-e^{-\phi }), \end{aligned}$$
(11)
$$\begin{aligned} \phi= & {} \frac{1}{16}\sqrt{\frac{r_o}{r_o-r_i}}, \end{aligned}$$
(12)

where \(r_i\) and \(r_o\) represent the inner and outer strut radii, respectively.

Initial results revealed that the maximum bending stiffness-to-mass ratio is obtained using only a few bays. However, this requires very long struts which may not be feasible for a space application as it would hinder compact stowing for launch. Considering the limited cargo volume of launch vehicles, an increased number of bays would allow shorter struts. Therefore, to develop better insight and understanding on how the bending stiffness-to-mass ratio is affected by the number of bays, further optimization analyses are conducted for fixed numbers of bays.

The total number of design variables are reduced by one once the number of bays is fixed, and the optimization analyses are conducted with an even number of bays to eliminate any potential couplings, between 2 and 50. Selecting such a wide range for the number of bays and carrying out optimization analyses within could provide better insight in the design of deployable tensegrity structures for space applications in which the length of the struts is very important for stowage for launch. Figures 4, 5, 6, 7, 8, 9 show the bending rigidity, the bending rigidity per unit mass, the torsional rigidity, the torsional rigidity per unit mass, the total mass, and the tip deflection, respectively. The results are also tabulated in Table 1.

Fig. 4
figure 4

Variation of bending rigidity

Full size image
Fig. 5
figure 5

Variation of bending rigidity per unit mass

Full size image
Fig. 6
figure 6

Variation of torsional rigidity

Full size image
Fig. 7
figure 7

Variation of torsional rigidity per unit mass

Full size image
Fig. 8
figure 8

Variation of mass

Full size image
Fig. 9
figure 9

Variation of tip deflection

Full size image

The optimization results show that the maximum bending rigidity per unit mass is achieved when the number of bays equals 8, while the minimum mass occurs with 14 bays. The results also reveal that it is possible to design a competitive tensegrity structure with much greater bending rigidity-to-mass ratio than that of the Canister Astromast, which has a bending rigidity-to-mass ratio of 1.25\(\times \)103 Nm2/kg. Increasing the number of bays for the stowing purposes decreases the bending rigidity and bending rigidity-to-mass ratio which can be attributed to the fact that the struts are less aligned with the long axis of the boom.

Table 1 Bending and torsional stiffnesses of the booms optimized for EI/Mass
Full size table

The design variables for the optimum solutions are given in the Appendix. The design variables reveal that the outer radius of the struts tends to converge to the extreme bound to avoid strut buckling by increasing the moment of inertia and maximizing the Euler buckling load. Additionally, the struts get thinner as the number of bays increases, implying that the struts are the major load-carrying elements of the tensegrity booms with fewer bays. In all cases, the radius of the reinforcing cables is found to be the upper bound, meaning that they are also key in resisting bending loads. In addition, tensegrity booms with a few bays have small cross-sectional top and bottom cables, while the vertical cables have large cross sections. This behavior is reversed when the number of bays increases. Furthermore, the twist angle is close to its lower bound for tensegrity booms with fewer bays, while it approaches the upper bound for increased numbers of bays. The prestress coefficient is found to increase with increasing numbers of bays to keep the axial forces in the (shorter) cables at similar levels to prevent cable slackening and increase overall stiffness.

4.2 Class-2 tensegrity boom—multi-objective function

In this second optimization example, the tensegrity boom considered is selected to be a 20-bay three-strut Class-2 tensegrity boom with no reinforcing cables exhibiting the same global dimensions as in the previous example. Therefore, the twist angle is set to \(\alpha =\pi /6\) to ensure a self-equilibrated geometry. The optimization problem is defined to be multi-objective, aiming to minimize both the mass of the boom and the tip displacement at the same time. These two objective functions conflict with each other, and therefore, there is no single optimum solution. Yet, a set of optimum solutions can be found in such cases. These solutions are called Pareto-optimal solutions and none of the objective functions can be improved without making the others worse. With no further information beyond than the objective function values, a comparison of the Pareto-optimal solutions is ill-defined and they are all considered to be valid.

Since reinforcing cables are not present in this tensegrity boom example and the twist angle has a unique value, the radius of the reinforcing cables and the twist angle are no longer design variables. Therefore, the design variables are: the radii of three different groups of cables; the inner and outer radii of the struts (assuming hollow struts); and the prestress coefficient. The upper and lower bounds of the design variables are the same as in the first example with one exception: the lower bounds of the cable radii are chosen as 1 mm. The same constraint set stated for the first optimization problem is directly applied to this problem.

The cables and struts are assumed to be made of steel and aluminum, respectively. The modulus of elasticity of the cables and struts are \(E=210\) GPa and \(E=70\) GPa, respectively. The density of the cables and struts are \(\rho =7850\) kg/m3 and \(\rho =2700\) kg/m3, respectively. The Poisson’s ratio of the struts are assumed to be \(\nu =0.32\). These materials might be considered to be representative of civil structures. The tensegrity boom is designed to be a vertical tower, fixed at the bottom, and lateral loads of 10 N are applied at the top nodes in the y direction to simulate mild wind conditions. The self-weight of the structure is neglected, since it acts in the orthogonal direction to the applied loads and, therefore, it has a little effect on the tip deflection.

Several methods have been suggested by researchers to address multi-objective optimization problems. These methods can be represented in four different categories which are reviewed extensively by Cui et al. [58]. In this study, two of these methods, namely weighted sum and \(\varepsilon \)-constraint methods, are used and a Pareto-optimal set is obtained.

The weighted sum method assigns positive weights (\(w_i\)) to individual objective functions based on their importance in the optimization, and generates a single-objective function. Then, by varying these weights, optimization analyses can be performed repeatedly to obtain Pareto-optimal solutions. This multi-objective (two-objective) optimization can be formulated as follows:

$$ \begin{gathered} \mathop {\min }\limits_{X} \quad \;\;\,\,\,\,\,w_{1} d\left( {X,q\left( X \right)} \right) + w_{2} M\left( X \right) \hfill \\ {\text{subject}}\;{\text{to}}- q\left( X \right){\text{ < }}0,\;{\text{for}}\;{\text{cables}} \hfill \\ \quad \quad \quad \quad \,\sigma _{{c_{i} }} \le \sigma _{Y} ,\;{\text{for}}\;{\text{cables}} \hfill \\ \quad \quad \quad \quad \,q\left( X \right){\text{ < }}0,\;{\text{for}}\;{\text{struts}} \hfill \\ \quad \quad \quad \quad \,T_{{{\text{st}}_{i} }} \le P_{{{\text{eu}}}} ,\;{\text{for}}\;{\text{struts}} \hfill \\ \quad \quad \quad \quad \,\sigma _{{{\text{st}}_{i} }} \le \sigma _{{{\text{cr}}}} ,\;{\text{for}}\;{\text{struts}} \hfill \\ {\text{where}}\quad \;\;\;w_{1} + w_{2} = 1, \hfill \\ \end{gathered} $$
(13)

where d represents the tip displacement. The assigned weights are then varied between 0 and 1 to obtain Pareto-optimal solutions. The case where \(w_1=1\) and \(w_2=0\) is not considered as it would return the design variables equal to their upper bounds, which is not a practical result.

Alternatively, the \(\varepsilon \)-constraint method suggested by Haimes et al. [59] converts the objective functions into inequality constraints except for one, which is then used as the single-objective function. In this study, the objective function associated with the minimization of mass is converted into a constraint with an upper bound of \(\varepsilon \). Then, the optimization problem is written as follows:

$$\begin{gathered} \mathop {\min }\limits_{X} \quad \;\;\,\,\,\,\,\,d\left( {X,q\left( X \right)} \right) \hfill \\ {\text{subject}}\;{\text{to}}\;\,M\left( X \right) \le \varepsilon \hfill \\ \quad \quad \quad \quad \, - q\left( X \right){\text{ < }}0,\;{\text{for}}\;{\text{cables}} \hfill \\ \quad \quad \quad \quad \,\sigma _{{c_{i} }} \le \sigma _{Y} ,\;{\text{for}}\;{\text{cables}} \hfill \\ \quad \quad \quad \quad \,q\left( X \right){\text{ < }}0,\;{\text{for}}\;{\text{struts}} \hfill \\ \quad \quad \quad \quad \,T_{{{\text{st}}_{i} }} \le P_{{{\text{eu}}}} ,\;{\text{for}}\;{\text{struts}} \hfill \\ \quad \quad \quad \quad \,\sigma _{{{\text{st}}_{i} }} \le \sigma _{{{\text{cr}}}} ,\;{\text{for}}\;{\text{struts,}} \hfill \\ \end{gathered} $$
(14)

Then, the \(\varepsilon \) value is varied between 15 and 150 kg, and the optimization analyses are repeated to obtain Pareto-optimal solutions. Representing these Pareto-optimal solution sets visually show the Pareto frontier which can be used for design decision-making purposes as noted by Zhang and Ohsaki [21].

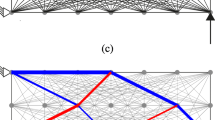
Figure 10 shows the sets of Pareto-optimal solutions along with the Pareto frontier. It also reveals the nonlinear trade-off between the two objective functions: minimum mass and minimum tip displacement. The Pareto frontier shows that the heavier the designed boom, the smaller the tip displacement and vice versa. This plot can be used for decision-making purposes for a given design problem. Treating the multi-objective optimization problem with two different methods and obtaining results that demonstrate similar trends also increases the reliability of the results. The mass and tip displacement values of the optimized booms are shown in Table 2, while the associated design variables can be found in the Appendix.

Fig. 10
figure 10

Pareto-optimal solutions

Full size image
Table 2 Mass and tip displacement values of the optimized booms
Full size table

The design variables reveal that in all cases, the radius of the top and bottom cables takes the lower bound value, indicating that they do not play an important role in resisting the lateral loads. Additionally, the outer radii of the struts are found to converge to the upper bound to maximize the moment of inertia and thus the buckling load. In addition, the radii of the vertical and saddle cables increase with increasing displacement weight, \(w_1\), or increasing \(\varepsilon \) values. For increased mass weight, \(w_2\), or smaller \(\varepsilon \) values, the optimum outer and inner radii of the struts are found to be the same in different cases, which can be interpreted as pursuing the smallest possible cross-sectional area and moment of inertia that will prevent buckling. Furthermore, similar to the first example, the prestress coefficient increases with increased importance of minimum displacement to increase overall stiffness and prevent cable slackening.

5 Conclusions

Tensegrity structures offer the potential for lightweight solutions to a wide range of engineering problems. However, optimization is needed to guide the design of tensegrity structures that are capable of resisting external loads effectively without losing their lightweight feature. To address this need, the optimization of tensegrity structures was investigated using the particle swarm optimization algorithm.

A model of tensegrity structures was described in which individual struts and cables are modeled using one-dimensional two-noded axial load-carrying finite elements. The linear and geometric stiffness matrices, which originate from the axial stiffness and the prestress in the elements, were provided, and the assembly of the global stiffness matrix followed. A computational nonlinear analysis scheme to study the behavior tensegrity structures under external loads was described. Continuum beam modeling was used for rapid estimation and evaluation of the global stiffness properties of prestressed lattice structures.

Since the behavior of tensegrity structures is generally nonlinear in nature, the traditional optimization techniques are very difficult to implement. Therefore, a heuristic optimization technique, the particle swarm optimization algorithm was employed in this research. The PSO algorithm was described, along with variations appropriate for the treatment of multi-objective optimization problems.

Two numerical examples focusing on sizing and prestress optimization of tensegrity structures were presented. The first example investigated the single-objective optimization of three-strut multi-bay tensegrity booms with an aim to maximize the bending stiffness-to-mass ratio. The bending stiffness of the booms was evaluated by the modified energy equivalency method under a set of constraints that include realistic challenges such as cable slackness and yielding, and strut buckling. The second example addressed the multi-objective optimization of tensegrity booms under external lateral loads with conflicting objectives: minimization of mass and minimization of tip displacement. The multi-objective optimization problem was treated by two different methods, namely weighted sum and \(\varepsilon \)-constraint.

The optimization results revealed that it is possible to design tensegrity booms which exhibit greater bending stiffness-to-mass ratio than that of the representative deployable space boom, the Canister Astromast. The multi-objective optimization results showed the robustness of the particle swarm optimization technique: application of the weighted sum and \(\varepsilon \)-constraint approaches both yielded similar results.

The use of PSO in the optimization of nonlinear tensegrity structures showed that a complete design and optimization of a tensegrity boom with a given set of realistic constraints can be achieved. The nature of the optimization problem is non-convex and, thus, global optima cannot be guaranteed. However, repeated analyses with similar results assure that PSO works robustly even for challenging multi-objective design optimization problems. While the problems considered involve Class-2 tensegrity structures, the procedure can be readily adapted to other tensegrity classes and larger multi-objective optimization problems. For example, Pareto frontiers could be represented by multi-dimensional surfaces rather than curves in the case of a multi-objective optimization with three or more objective functions and higher numbers of objective functions could require more complex visualization techniques. Overall, PSO can be a very powerful tool for future optimization problems related to the design of optimum tensegrity structures for aerospace and civil applications.