1 Introduction

Strong earthquakes such as USA Northridge (1994) and Japan Kobe (1995) provoked engineers and researchers to devise a new seismic design procedure for structures that was conventionally strength based. Although the casualties in these events were not significant, the damages incurred by structural components were enormous. This led the engineering community to develop the performance-based seismic design (PBSD) framework in which structures are designed to endure a specific damage level to satisfy the desired performance level of serviceability and strength in the face of future extreme events. The Federal Emergency Management Agency (FEMA) introduced several useful guidelines in PBSD; in this respect, one can refer to (FEMA-273 1997; FEMA-356 2000; FEMA-440 2005). Although these codes were originally meant to be used for evaluation and retrofit purposes, they opened a new horizon for designing of structures based on performance-based design (PBD) philosophy. Later, the ASCE 41–17, which is based on the aforementioned FEMA guidelines, opened a path to design new structures based on PBD concept other than evaluation and retrofit aims.

Many researchers have addressed the challenges of the PBD in recent years such as Saadat et al. 2014; Liu et al. 2013; Mansouri and Maheri 2019; and Khalilian et al. 2021.

According to ASCE 41–17, for the risk category of II, the performance levels for designing new structures based on PBSD framework are as follows:

  • Life safety (LS)

  • Collapse prevention (CP)

At the LS level of performance, the structure is allowed to have damaged components, but it remains safe for occupants to evacuate the building. The CP performance level is defined as the state in which the structure has damaged components and retains no margin against collapse; however, it continues to tolerate gravity loads (ASCE41-17 2017).

In order to construct a cost-efficient structure, different earthquakes with various hazard levels are assumed to occur for a specific structure, and the structure is designed to have a particular performance level under those levels of an earthquake. The structure's performance level depends on the importance of the structure and the stakeholders’ preference. The hazard level associated with the LS and CP performance levels for the new buildings in risk category of II is called BSE-1 N and BSE-2 N in ASCE 41–17, respectively. BSE-2 N denotes the basic safety earthquake-2 assumed as the ground shaking based on the risk-targeted maximum considered earthquake (\({MCE}_{R}\)), and BSE-1 N shows the basic safety earthquake-1 or called the design earthquake (DE) taken as the two-thirds of the BSE-2 N at a site (ASCE7-16 2016).

In order to evaluate the seismic response of the structure, the nonlinear static procedure, also known as pushover analysis (POA), is often an attractive choice due to its simplicity and ability to identify component- and system-level deformation demands with accuracy comparable to dynamic analysis (Shayanfar et al. 2013). Under the FEMA-273, FEMA-356, and ASCE 41–17 approach, in which the acceptance criteria of a given performance level are determined based on component-level responses, the constraints are implemented such that each component’s response is calculated and then compared to the allowable threshold.

The PBSD is a complex problem that entails adjusting many parameters; thus, it is difficult for designers to know whether the current design is the best or still there is a more desirable one. For this purpose, advancements in structural optimization have made it possible to move from traditional trial-and-error procedures toward an automatic approach (Fragiadakis and Lagaros 2011). Metaheuristic algorithms have gained growing popularity recently due to their efficiency in solving engineering problems in suitable time duration and acceptable accuracy for engineering objectives (Kaveh et al. 2018, 2013; Safari et al. 2021; Kaveh and Malakoutirad 2010; Makiabadi and Maheri 2021; Sedlar et al. 2021). Usually, the common characteristic of metaheuristic algorithms is the inspiration from natural or man-made phenomena. The water strider algorithm (WSA) is a new metaheuristic algorithm proposed by Kaveh and Dadras (2020). The viability of the algorithm in optimizing mathematical functions and size optimization of structures has formerly been investigated. Subsequently, Kaveh et al. proposed an improved water strider algorithm (IWSA) which uses opposition-based learning (OBL) and a mutation technique to enhance the standard WSA (Kaveh et al. 2020). The superiority of IWSA over WSA and many classical and well-established modern metaheuristics have already been demonstrated in their article.

The main purpose of structural optimization algorithms is to minimize the constructional cost of structures by building the lightest possible structure while satisfying several design constraints (Kaveh and Ghazaan 2018). In the framework of PBSD, structural optimization via metaheuristic algorithms has received considerable attention in recent years. Kaveh et al. used the ant colony optimization (ACO) algorithm for PBSD of steel moment-resisting frames (MRFs) and showed the superiority of ACO in comparison with the genetic algorithm (GA) for the discussed problems (Kaveh et al. 2010). Kaveh and Nasrollahi employed charged system search (CSS) algorithm for PBSD of steel frames and used POA based on semirigid connections and compared the results with the GA and ACO (Kaveh and Nasrollahi 2014). Gholizadeh used a modified firefly algorithm (MFA) and a new neural network for PBSD of steel structures (Gholizadeh 2015). They also used an improved quantum particle swarm optimization (Gholizadeh and Moghadas 2014) and Newton metaheuristic algorithm in this issue (Gholizadeh et al. 2020). Eftekhar et al. utilized a hybrid metaheuristic in this framework to obtain designs with lighter weights and higher convergence rate than all the existing results in the literature (Eftekhar et al. 2021). Degertekin et al. employed school-based optimization (SBO) for PBSD of steel frames (Degertekin et al. 2020) and compared the results with other metaheuristic algorithms, showing the outperformance of the SBO algorithm to others.

Although WSA and IWSA algorithms have shown promising results in size optimization of space structures such as double-layer barrel vaults (Kaveh and Dadras Eslamlou 2020; Kaveh et al. 2020), the literature review reveals that these algorithms have not been used in PBSD problems or a complex engineering optimization problem so far. Furthermore, by studying the literature carefully, one realizes that the majority of articles have only considered system-level response such as inter-story drift ratio (IDR) for the entire optimization process, neglecting the component-level response; however, neglecting this fact is not allowed in FEMA-273, FEMA-356 or ASCE 41 since the acceptance criteria for the specified performance are measured based on component-level response. Moreover, it has been stated in Table C1-3 of FEMA-356 that the drift criterion is only a qualitative assessment of the performance of the structure. In this regard, there are a few studies in the literature taking into consideration the component-level response. For example, Wang et al. considered the strength and elements rotation ratio in the performance-based seismic design optimization (PBSDO) of two MRFs and conducted nonlinear time history analysis (Wang et al. 2019); nevertheless, they only deemed CP performance level for their optimization process and did not check geometric constraint (constructability) in the optimization. Fathali and Hoseini Vaez performed the optimum performance-based design of eccentrically braced frames (Fathali and Hoseini Vaez 2020), taking component- and system-level constraints into account. Fathizadeh et al. considered soil–structure effects on PBSDO of MRFs using an engineered cluster-based genetic algorithm (Fathizadeh et al. 2021). Hassanzadeh and Gholizadeh performed a collapse-performance-aided design of steel concentrically braced frames (Hassanzadeh and Gholizadeh 2019). Therefore, considering all the essential constraints to simulate a PBSD procedure according to ASCE 41 for MRFs have not been properly addressed in the literature yet. The strong capability of WSA and IWSA in search space exploration and achieving a suitable solution in a reasonable time inspired us to examine their ability on such problems as PBSDO. Thus, this study is herein proposed to investigate the efficiency of WSA and IWSA in solving a challenging and computationally demanding engineering problem, perform a comparative study on PBSDO problems, and extend their application. To the best of the authors’ knowledge, this is the first time that steel MRFs are optimally designed using metaheuristic algorithms considering all of the essential constraints according to the ASCE 41–17 provisions.

To further investigate the competitiveness of the newly developed metaheuristic algorithms, particle swarm optimization (PSO) and enhanced colliding bodies optimization (ECBO) are utilized in this article to perform a comparative study. In fact, it has been demonstrated that PSO is the best performing algorithm in comparison with GA, ACO, and harmony search (HS) algorithms in the framework of PBSD of steel frames (Gholizadeh et al. 2013). Therefore, selecting PSO as the representative of a classical optimization method is justified. Moreover, ECBO has shown to be a robust optimization algorithm in structural optimization problems, including performance-based design optimization (Kaveh and Ilchi Ghazaan 2014; Kaveh and Farhadmanesh 2019; Fathali and Hoseini Vaez 2020). Thus, it is selected for a more comprehensive comparative study.

2 Performance-Based Seismic Design

The performance of structures is determined based on demand and capacity. The demand of the structure is defined given the expected earthquake, which is dependent on the level of the seismic hazard level, implying the rate of occurrence of the event. On the other hand, capacity is expressed by the design parameters of the structure, including the strength of elements, ductility, and proportioning. Thus, given the earthquake hazard level and the structures’ capacity, performance levels are determined (Degertekin et al. 2020). In PBSD, a performance level is chosen for a specific hazard level. Commonly, for new buildings, the hazard level associated with 10 and 2% of probability of exceedance in 50 years has been respectively considered for the performance levels of LS and CP before the introduction of risk-targeted maximum considered earthquake (\({\mathrm{MCE}}_{R}\)) as new seismic design basis in ASCE 7. This earthquake is defined as the 1% probability of collapse of building in 50 years. Accordingly, the hazard level at the design earthquake (\(\mathrm{DE}\)) is a uniform reduction of \({MCE}_{R}\). These earthquakes correspond to the mean return period of 475 (\(\mathrm{DE}\)) and 2475 years (\({\mathrm{MCE}}_{R}\)) (ASCE41-17 2017).

In order to assess the seismic response of the structure, a nonlinear static procedure or POA is adopted in this article. Different methods have been proposed to conduct the POA recently (Shayanfar et al. 2019). Among the various methods, herein, the displacement coefficient method is employed (Hasan et al. 2002). In POA, the structure is subjected to increasing lateral loads until a predefined target displacement is reached. The monitored node for this displacement control analysis is taken as the center of mass for the roof story. The target displacement is calculated as follows according to ASCE41-17 2017:

$$\delta_{t} = C_{0} C_{1} C_{2} S_{a} \frac{{T_{e}^{2} }}{{4\pi^{2} }}g$$
(1)

where \({C}_{0}\), \({C}_{1}\), and \({C}_{2}\) are the coefficients defined thoroughly in ASCE 41–17, \({S}_{a}\) is the spectral response acceleration, \(g\) is the gravity acceleration, and \({T}_{e}\) is the effective fundamental period defined as:

$$T_{e} = T_{i} \sqrt {\frac{{K_{i} }}{{K_{e} }}}$$
(2)

where \({T}_{i}\) is the fundamental elastic period, \({K}_{i}\) is the elastic lateral stiffness, and \({K}_{e}\) is the effective lateral stiffness. Since the determination of the target displacement is dependent on the bilinearization of the pushover curve, an iterative process might be necessary. In POA, the vertical distribution of the seismic forces is considered to be proportional to the shape of the fundamental mode:

$$C_{vx} = \frac{{w_{x} h_{x}^{k} }}{{\mathop \sum \nolimits_{i = 1}^{ns} w_{i} h_{i}^{k} }}$$
(3)

where \({C}_{vx}\) represents the vertical distribution factor at each story level and \({w}_{x}\) and \({w}_{i}\) denote the portion of the total weight of the structure located at floor level \(x\) and \(i\), respectively. \({h}_{x}\) and \({h}_{i}\) are the height from the base to floor level \(x\) and \(i\), respectively. The parameter \(k\) is obtained by the following equation:

$$k = \left\{ {\begin{array}{*{20}c} {1\;T \le 0.5\;{\text{sec}}} \\ {2\;T \ge 2.5\;{\text{sec}}} \\ {0.5\;T + 0.75\;{\text{else}}} \\ \end{array} } \right.$$
(4)

Additionally, spectral acceleration (\({S}_{a}\)) can be calculated for the two performance levels as follows (ASCE41-17 2017):

$$\begin{gathered} S_{a} = S_{{XS}} \left[ {\left( {\frac{5}{{B_{1} }} - 2} \right)\frac{T}{{T_{s} }} + 0.4} \right]\;if\;0 < T < T_{0} \hfill \\ S_{{XS}} /B_{1} \;if\;T_{0} < T < T_{s} \hfill \\ S_{{X1}} /(B_{1} T)\;if\;T_{s} < T < T_{L} \hfill \\ T_{L} S_{{X1}} /(B_{1} T^{2} )\;if\;T > T_{L} \hfill \\ \end{gathered}$$
(5)

where \({S}_{X1}={F}_{v}{S}_{1}\), \({S}_{XS}={F}_{a}{S}_{s}\), \({T}_{s}={S}_{X1}/{S}_{XS}\), \({T}_{0}=0.2{T}_{s}\), \({B}_{1}=4/[5.6-\mathrm{ln}(100\beta )]\).

In the above equations, T is the fundamental period of the structure, \({S}_{XS}\) is the spectral response acceleration parameter at short periods, \({S}_{X1}\) is the spectral response acceleration parameters at a 1-s period, \({F}_{a}\) and \({F}_{v}\) are the site coefficients, and \(\beta\) is the effective viscous damping ratio. A site with highly seismicity in Los Angeles (latitude: 34.05 longitude: − 118.24) is considered in this study. \({S}_{s}\) and \({S}_{1}\) are determined based on the 11.4.2 provision of ASCE 7–16. Also, \({F}_{a}\) and \({F}_{v}\) are obtained from Table 11.4–1 and Table 11.4–2 of ASCE 7–16, respectively. These values are tabulated in Table 1. The damping ratio (\(\beta\)) of the structures is assumed to be \(5\%\).

Table 1 Seismic design parameters of site class D, risk category II, and located in Los Angeles
Full size table

It is worth mentioning that \({S}_{XS}\) and \({S}_{X1}\) are the notation used in the code for the selected seismic hazard, either DE or MCE. The site parameters for the MCE (denoted by \({S}_{MS}\) and \({S}_{M1}\)) are determined first, and the corresponding values for the DE (denoted by \({S}_{DS}\) and \({S}_{D1}\)) are obtained by the following equations (ASCE7-16 2016):

$$\left\{ {\begin{array}{*{20}c} {S_{DS} = \frac{2}{3}S_{MS} } \\ {S_{D1} = \frac{2}{3}S_{M1} } \\ \end{array} } \right.$$
(6)

3 Metaheuristic Algorithms

In this research, four metaheuristics consisting of WSA, IWSA, PSO, and ECBO are employed for the optimization process. In the following subsections, these algorithms are briefly explained.

3.1 Water Strider Algorithm

The water strider algorithm is a novel population-based metaheuristic inspired by the life cycle of water striders that uses swarm intelligence. This algorithm employs territorial behavior, mating style, intelligent ripple communication, feeding mechanism, and succession of water strider insects to establish an efficient optimization algorithm that is competitive to many renowned classical optimization algorithms as well as the modern ones despite using simple mathematical equations. Water striders (WS) establish territories which are often inhabited by two WSs, one female and one male (keystone). Using a ripple communication system, the keystone sends ripples to the female WS to mate. The probability of attraction or repulsion from the female WS is supposed to be \(p=50\%\). The next position of the keystone based on the reaction of the female is obtained as:

$$\left\{ \begin{gathered} {\text{WS}}_{i}^{{t + 1}} = {\text{WS}}_{i}^{t} + {\text{R}}{\text{.rand; if mating happens}}\left( {{\text{with probability of }}p} \right) \hfill \\ {\text{WS}}_{i}^{{t + 1}} = {\text{WS}}_{i}^{t} + R.\left( {1 + {\text{rand}}} \right);\;{\text{otherwise}} \hfill \\ \end{gathered} \right.$$
(7)

The length of \(R\) equals the distance between the male and female WS:

$$R = {\text{WS}}_{F}^{t - 1} - {\text{WS}}_{i}^{t - 1}$$
(8)

where \({\mathrm{WS}}_{i}^{t}\) and \({\mathrm{WS}}_{F}^{t}\) represent the male and female WS positions in the \({\mathrm{t}}^{\mathrm{th}}\) cycle, respectively. If the keystone’s fitness is not improved in the new position, it moves towards the best candidate solution. There, the fitness value of the keystone is evaluated again. In case it decreases, a new WS will be generated to substitute it. These steps are repeated for other keystones as well. When all keystones’ positions are updated, the WSs are assigned to new territories to start another loop. For a more comprehensive study of the steps of the algorithm, the reader can refer to (Kaveh and Dadras Eslamlou 2020).

3.2 Improved Water Strider Algorithm (IWSA)

There are two techniques incorporated in WSA to make it a more suitable global optimization algorithm. The first idea is based on OBL initially proposed by Tizhoosh for machine learning (Tizhoosh 2005), and the second idea is inspired by the mutation operator utilized in the GA.

Generalized space transformation search (GSTS) is utilized as the new formulation for OBL (Zhang and Jin 2020) to be applied to the initial population to provide a more promising search space for IWSA. The initial population plays an important role in the efficiency of the metaheuristic algorithms. In fact, random initialization might increase the probability of searching fruitless regions of search space. Utilizing OBL increases the ability of the optimization algorithms in terms of search space exploration and near-optimum exploitation of the search space. Moreover, in order to enhance the convergence speed, employing random numbers and their opposite is more beneficial than using pure randomness to generate initial estimates in the absence of prior knowledge about the solutions, as this method searches in two directions simultaneously (Rahnamayan et al. 2008).

To strengthen the exploration ability of the standard WSA algorithm, a mutation operator is added to enrich the algorithm to search more promising regions of the search space and assist it in escaping local optimums, which is an important issue in metaheuristics. The mutation technique is applied on the best-so-far solution in each iteration with a probability called \(pro\).

Regarding the computational complexity of the IWSA, let \(C\) be the number of cycles that the algorithm needs to run, \(T\) the number of territories, and \(N\) the population size (number of water striders); then, the computational complexity of the IWSA can be calculated as follows: In the initialization part of the algorithm, the complexity of randomly initiating the population corresponds to \(O(N)\) complexity and evaluating their opposites requires \(O(N)\) complexity as well which leads to \(O(2N)\) complexity for the initialization of IWSA. Then, for the updating part of the algorithm, the complexity is at least \(O(CT)\) and at most \(O(3CT)\) depending on the fitness of the keystone (similar to the standard WSA). Furthermore, after this updating process, the mutation operator is applied which corresponds to \(O(0)\) or \(O(CT)\) computational complexity based on the probability of the mutation. Therefore, the computational complexity of IWSA is between \(O(2N+CT)\) and \(O(2N+4CT)\).

In this study, similar to the source article, the number of WSs and the territories are set as nws = 50 and nt = 25 for both WSA and IWSA algorithms.

3.3 Particle Swarm Optimization (PSO)

Particle swarm optimization (PSO) is one of the most well-known classical metaheuristics introduced by Kennedy and Eberhart. In PSO, the candidate solutions, so-called particles, are randomly initiated in the search space, and their positions are updated regarding the velocity of each particle. It is assumed that particles remember their best experienced position so far (\({\mathrm{xbest}}_{i}\)), and the whole swarm’s best position (\(\mathrm{xgbest}\)) as yet. Each particle’s velocity is updated based on the following equation (Kennedy and Eberhart 1995):

$$v_{i,j}^{k + 1} = wv_{i,j}^{k} + c_{1} r_{1} \left( {{\text{xbest}}_{i,j}^{k} - x_{i,j}^{k} } \right) + c_{2} r_{2} \left( {{\text{xgbest}}_{j}^{k} - x_{i,j}^{k} } \right)$$
(9)

where \({x}_{i,j}^{k}\) and \({v}_{i,j}^{k}\) represent the \({j}^{th}\) component of the position and velocity vector of the \({i}^{th}\) particle in the \({k}^{th}\) iteration, respectively. \({r}_{1}\) and \({r}_{2}\) are two random numbers generated in [0,1]. \({c}_{1}\) and \({c}_{2}\) are constant numbers representing the cognitive and social behavior parameters, respectively. w is the inertia weight which is chosen to decrease linearly from 0.9 to 0.4 during the optimization (Eberhart and Shi 2000). The time step is considered to be unit. Thus, the particles’ positions are updated as:

$$x_{i,j}^{k + 1} = x_{i,j}^{k} + v_{i,j}^{k + 1}$$
(10)

In this study, the internal parameters of PSO are set as: \({c}_{1}={c}_{2}=2\), and the population size is set to 50 as in WSA and IWSA algorithms.

3.4 Enhanced Colliding Bodies Optimization (ECBO)

Colliding bodies optimization (CBO) is a multi-agent algorithm that originated from collision laws in physics. In this algorithm, each candidate solution is called a colliding body (CB). The population is divided into two groups of stationary and moving groups, and the collision occurs between them to obtain a new position for each candidate solution. Enhanced colliding bodies optimization (ECBO) was introduced to improve the performance of CBO in terms of convergence speed and avoiding local optimums. In order to enhance the convergence rate, a memory is used to save some of the historically best solutions by defining a memory called colliding memory (CM). The CBs saved in CM are added to the population in each iteration, and the same number of current worst CBs is deleted. To help the CBO algorithm evade local optimums, a probability like \(pro\) is introduced, and for each CB, with a probability of \(pro\), one of its components is regenerated randomly. Herein, the internal parameters of ECBO are selected as: \(\mathrm{Population size}=50, pro=0.3\). For a more comprehensive explanation of the ECBO algorithm, the reader may refer to Kaveh and Ilchi Ghazaan 2014.

4 Performance-Based Seismic Design Optimization Procedure

In this section, the formulation for PBSDO is presented. The optimization procedure can be mathematically expressed as follows:

Find \(\left\{X\right\}=[{x}_{1},{x}_{2}, \dots ,{x}_{ng}]\)

$${\text{to minimize}} W\left( {\left\{ X \right\}} \right) = \mathop \sum \limits_{i = 1}^{ng} x_{i} \mathop \sum \limits_{j = 1}^{nm\left( i \right)} \rho_{j} L_{j}$$
(11)

subjected to:\(\left\{ \begin{gathered} g_{j} \left( {\left\{ X \right\}} \right) \le 0,j = 1,2, \ldots ,nc \hfill \\ x_{{i\min }} \le x_{i} \le x_{{i\max }} \hfill \\ \end{gathered} \right.\)where \(\left\{X\right\}\) is the design variables vector chosen from the 267 wide flange sections provided in the AISC database. The sections are sorted based on their cross-section areas in the first place and for equal cross-sectional areas, the moment of inertia (\({I}_{x}\)) sorts the list. \(W\left(\left\{X\right\}\right)\) represents the weight of the structure, \(ng\) is the number of design groups, \(nm(i)\) is the number of members associated with the \({i}{th}\) group, and \({\rho }_{j}\) and \({L}_{j}\) indicate the density of the material and the length of the \({j}{th}\) member, respectively. \({g}_{j}\left(\left\{X\right\}\right)\) represents the design constraints of the problem specified by the standard codes, and \(nc\) is the number of constraints. \({x}_{imin}\) and \({x}_{imax}\) are the lower bound and the upper bound of the variable \({x}_{i}\), respectively. For constraints handling, the well-known penalty approach is utilized here. Thus, the objective function is redefined as follows:

$$P\left( {\left\{ X \right\}} \right) = \left( {1 + \alpha G} \right) \times W\left( {\left\{ X \right\}} \right)$$
(12)

where \(P\left(\left\{X\right\}\right)\) is the penalized weight or objective function to be minimized and \(\alpha\) represents the penalty coefficient which is set as a large number (equal to 100 herein as being suitable for the problems). \(G\) denotes the sum of the violations of the design constraints and is calculated as follows:

$$G = \mathop \sum \limits_{i = 1}^{n} \max \left( {g_{i} , 0} \right)$$
(13)

where \({g}_{i}\) is the \({i}{th}\) constraint considered and \(n\) is the number of constraints of the problem.

5 Optimization Constraints

To ensure that the desired design is obtained, five types of constraints consisting of seismic and non-seismic ones are taken into account during the optimization.

5.1 Non-Seismic Constraints

Non-seismic constraints include geometric and strength constraints that are checked here before conducting the POA.

5.1.1 Geometric Constraint

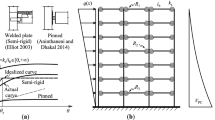
In order to make the structure constructable, certain geometric constraints must be met during the optimization process as seen in Fig. 1. Therefore, Eq. (14) is checked in each node to make sure the beams and columns dimensions are compatible. In the following equations, \({{(b}_{\mathrm{beam}})}_{i}\) and \({{(b}_{\mathrm{column}})}_{i}\) are the flange width of the \({i}^{th}\) beam and column, respectively, and \({n}_{BC}\) is the number of beam-column connections. \({{(d}_{n+1})}_{j}\) and \({{(d}_{n})}_{j}\) are the depth of the \({j}^{th}\) column at the \({(n+1)}^{th}\) and \({n}^{th}\) story. In addition, \({n}_{CC}\) and \({n}_{s}\) show the number of column-column connections and the number of stories in the structure, respectively.

$$g_{1} = \left\{ {\begin{array}{*{20}c} {(b_{{{\text{beam}}}} )_{i} /(b_{{{\text{column}}}} )_{i} - 1 \le 0; i = 1, 2, \ldots , n_{{{\text{BC}}}} } \\ {(d_{n + 1} )_{j} /(d_{n} )_{j} - 1 \le 0; j = 1, 2, \ldots , n_{{{\text{CC}}}} ;s = 1, 2, \ldots , n_{s} - 1} \\ \end{array} } \right.$$
(14)
Fig. 1
figure 1

Geometry of frames’ connections for constructability

Full size image

5.1.2 Strength Constraint

In terms of strength constraint, all of the structural members are assessed whether they sustain the following gravity load combination (ASCE7-16 2016):

$$Q_{G}^{{{\text{type1}}}} = 1.2DL + 1.6LL$$
(15)

where DL and LL denote the dead load and live load, respectively (\(DL=2500kgf/m\),\(LL=1000kgf/m\)). The strength constraint is expressed by flexural moment-axial force interaction relation according to (AISC360-16 2016):

$$g_{2} = \left\{ {\begin{array}{*{20}c} {\frac{{P_{u} }}{{2\varphi_{c} P_{n} }} + \left( {\frac{{M_{ux} }}{{\varphi_{b} M_{nx} }} + \frac{{M_{uy} }}{{\varphi_{b} M_{ny} }}} \right) - 1.0 \le 0.0 if\frac{{P_{u} }}{{\varphi_{c} P_{n} }} < 0.2 } \\ {\frac{{P_{u} }}{{\varphi_{c} P_{n} }} + \frac{8}{9}\left( {\frac{{M_{ux} }}{{\varphi_{b} M_{nx} }} + \frac{{M_{uy} }}{{\varphi_{b} M_{ny} }}} \right) - 1.0 \le 0.0 if\frac{{P_{u} }}{{\varphi_{c} P_{n} }} \ge 0.2} \\ \end{array} } \right.$$
(16)

where \({M}_{ux}\) and \({M}_{uy}\) are the required flexural strength in respect to the strong and weak axes, respectively; \({M}_{nx}\) and \({M}_{ny}\) are the nominal flexural strength in respect to the strong and weak axes, respectively; \({P}_{u}\) and \({P}_{n}\) denote the required and nominal axial strength, respectively, \({\varphi }_{c}\) is the resistance factor (\({\varphi }_{c}\) = 0.9 for tension or compression), and \({\varphi }_{b}\) is the flexural resistance factor equal to 0.9.

5.2 Seismic Constraints

According to ASCE 41–17, the gravity loads assigned to the structure before starting the POA are considered to be:

$$Q_{G}^{{{\text{type2}}}} = DL + LL$$
(17)

where \(DL\) is the dead load and \(LL\) is the effective live load equal to 25% of unreduced design live load.

5.2.1 Inter-Story Drift Ratio Constraint (IDR)

The IDR constraint is calculated for each performance level by the following equation:

$$g_{3} = \frac{{d_{k}^{i} }}{{d_{all}^{i} }} - 1 \le 0.0 i = {\text{LS}},{\text{CP}};\; k = 1, 2, \ldots ,{\text{ns}}$$
(18)

where \(ns\) indicates the number of stories, \({d}_{k}^{i}\) denotes the IDR of the \({k}{th}\) story for performance level of \(i\), and \({d}_{all}^{i}\) is its allowable value. The allowable IDRs are considered to be 2.5% and 5% for the LS and CP performance level, respectively, as recommended by FEMA-365 2000.

5.2.2 Deformation-Controlled Members Constraints

Plastic hinge distribution plays an important role in performance-based design by showing the element-level behavior of structures. In addition, the element-level performance can predict collapse mechanisms and the formation of soft stories during extreme events. Herein, the plastic hinge growth of the frames of this study has been investigated for each defined performance level. The criteria by which the performance levels are determined are in accordance with ASCE 41–17 provisions for structural steel components. According to this standard, members that are able to show inelastic behavior are classified as deformation-controlled and their rotation must satisfy the following relation:

$$g_{4} = \frac{{\theta_{j}^{i} }}{{\theta_{{{\text{AC}}, j}}^{i} }} - 1 \le 0;\; j = 1, 2, \ldots , {\text{ne}} i = {\text{LS, CP}}$$
(19)

In the above equation, \({\theta }_{j}^{i}\) and \({\theta }_{\mathrm{AC}, j}^{i}\) denote the absolute value of the rotation of the \({j}^{th}\) plastic hinge, and its acceptance criterion for the \({i}^{th}\) performance level, respectively. Considering the compactness of the sections used herein, the acceptance criteria for this study are provided in Table 2 where \({P}_{G}\) represents the axial force component of the gravity load obtained by exerting \({Q}_{G}^{\mathrm{type}2}\), and the yield rotation of the members, \({\theta }_{y}\), is calculated by the following formulas (ASCE41-17 2017):

$$\left\{ \begin{gathered} \theta _{y} = \frac{{M_{{pe}} L\left( {1 + \eta } \right)}}{{6EI}}\;{\text{for beams}} \hfill \\ \theta _{y} = \frac{{M_{{pce}} L\left( {1 + \eta } \right)}}{{6\left( {\tau _{b} E} \right)I}}\;{\text{for columns}} \hfill \\ \end{gathered} \right.$$
(20)

where

$$\eta = \frac{12EI}{{L^{2} GA_{s} }}$$
$$\left\{ \begin{gathered} \tau _{b} = 1.0\;for\;\frac{{\left| P \right|}}{{P_{{ye}} }} \le 0.5 \hfill \\ \frac{{4\left| P \right|}}{{P_{{ye}} }}\left( {1 - \frac{{\left| P \right|}}{{P_{{ye}} }}} \right)\;for\;\frac{{\left| P \right|}}{{P_{{ye}} }} > 0.5 \hfill \\ \end{gathered} \right.$$
$$\left\{ {\begin{array}{*{20}c} {M_{{CE}} = M_{{pe}} \;{\text{for beams}}} \\ {M_{{CE}} = M_{{pce}} = \left\{ \begin{gathered} M_{{pe}} \left( {1 - \frac{{\left| P \right|}}{{2P_{{ye}} }}} \right)\;for\;\frac{{\left| P \right|}}{{P_{{ye}} }} < 0.2 \hfill \\ M_{{pe}} \frac{9}{8}\left( {1 - \frac{{\left| P \right|}}{{P_{{ye}} }}} \right)\;for\;\frac{{\left| P \right|}}{{P_{{ye}} }} \ge 0.2\;{\text{for columns}} \hfill \\ \end{gathered} \right.} \\ \end{array} } \right.$$
(21)
Table 2 Acceptance criteria for nonlinear procedures
Full size table

In the above equations, \(E\) is the modulus of elasticity, \(F_{{{\text{ye}}}}\) is the expected yield stress, \(L\) denotes the length of the beam or column members, \(M_{{{\text{CE}}}}\) is the expected flexural strength of the member, \(I\) is the moment of inertia of the beam or column members, \(G\) is the shear modulus, \(A_{s}\) is the effective shear area of the cross section, \(M_{{{\text{pe}}}}\) is the expected plastic moment capacity of the section about the bending axis calculated as \(M_{{{\text{pe}}}} = {\text{ZF}}_{{{\text{ye}}}}\) (\(Z\) denotes the plastic section modulus), \(P\) is the axial force in the member at the target displacement, and \(P_{{{\text{ye}}}}\) shows the expected axial yield force of the member (\(= A_{g} F_{{{\text{ye}}}}\)). Herein, the value of \(\eta\) is set equal to zero as permitted by the code for the sections and mathematical modeling of this study. Moreover, the expected values of the parameters are set equal to their original values.

5.2.3 Force-Controlled Members Constraints

According to ASCE 41–17 and ignoring the lateral-torsional buckling, the columns that their modeling parameter, \(a\), as provided in Table 2, is equal to zero or where \({P}_{G}/{P}_{ye}>0.6\), shall remain elastic for flexure, and are not expected to develop ductile behavior. Hence, they are considered force-controlled in this study. These columns shall also satisfy the following constraint in addition to the criteria of Table 2:

$$g_{5} = \left\{ \begin{gathered} \frac{{\left| P \right|}}{{2P_{{yLB}} }} + \frac{{M_{x} }}{{M_{{pLBx}} }} + \frac{{M_{y} }}{{M_{{pLBy}} }} - 1 \le 0\;for\;\frac{{\left| P \right|}}{{P_{{yLB}} }} > 0.2 \hfill \\ \frac{{\left| P \right|}}{{P_{{yLB}} }} + \frac{8}{9}\left( {\frac{{M_{x} }}{{M_{{pLBx}} }} + \frac{{M_{y} }}{{M_{{pLBy}} }}} \right) - 1 \le 0\;for\;\frac{{\left| P \right|}}{{P_{{yLB}} }} \ge 0.2 \hfill \\ \end{gathered} \right.$$
(22)

where \(P\) denotes the required axial force of the column, \({M}_{x}\) and \({M}_{y}\) are, respectively, the required bending moments about the \(x\)- and \(y\)-axis, and all calculated at the target displacement. \({P}_{yLB}\) represents the lower bound of the axial yield strength of the member (\(={A}_{g}{F}_{yLB}\)), \({M}_{pLBx}\) and \({M}_{pLBy}\) are the lower bound plastic moment capacity of the section about the \(x\)- and \(y\)-axis, respectively. \({M}_{pLBx}\) and \({M}_{pLBy}\) can be obtained using Eq. (21). Also, the lower bound values of the parameters are set to their original values in the article.

To reduce the computational cost due to excessive numbers of pushover analyses, firstly, the non-seismic constraints are checked, and then, in case of zero penalty, the algorithm proceeds to assess the seismic constraints. Also, it is noteworthy to mention that the candidate solutions are rejected if they do not satisfy the non-seismic constraints by applying a large penalty coefficient (\(\alpha ={10}^{9}\)); otherwise, POA is performed to determine the IDR and deformation or force-controlled members' constraints. The proposed method’s flowchart is depicted in Fig. 2.

Fig. 2
figure 2

Flowchart of the proposed method

Full size image

6 Simulation

Two structures consisting of 6- and 12-story MRFs are studied here for PBSDO. Considering the practical aspects of the construction and the symmetry of the structures, the frames are grouped into 9 and 24 design variables, as shown in Fig. 3. Since the objective function evaluation is costly and time-consuming, the MaxNFE of 20,000 is considered the algorithms’ termination criterion for the two frames. In each iteration, a vector of design variables, herein columns and beams’ sections, is returned to OpenSees (Mazzoni et al. 2006) so as to calculate the model response under lateral loadings that are incremented to reach the target displacement. To this end, the distributed plasticity simulation has been adopted, and the fiber model is employed to simulate the nonlinear behavior. The bilinear constitutive model is then used for nonlinear behavior via steel01 uniaxial material with a 3% strain-hardening ratio. The element nonlinearBeamColumn is utilized with the intended w-sections assigned; also, the number of integration points is assumed to be 7 along each element. The connections of all the frames are assumed to be fully restrained, and for the sake of reducing the computation burden, deformation of panel zones and nonlinear behavior of connections have been idealized using equalDof command. In order for diaphragms, herein beams, to simulate rigid behavior, a constraint is employed in the horizontal direction between beams’ nodes so that rigid diaphragm behavior realizes. After computing the eigenvalues of the model and deriving the fundamental period, gravity analysis is done. Afterwards, POA is applied to compute the models’ seismic constraints for a specific target displacement determined according to the intended performance level.

Fig. 3
figure 3

Schematic of the two frames considered for PBSDO; a the 6-story frame b the 12-story frame

Full size image

Mechanical properties of the steel are assumed as shown in Table 3:

Table 3 Mechanical properties of the considered steel
Full size table

The estimated coefficients for the target displacement for each frame are provided in Table 4. It is worth mentioning that \({{\varvec{C}}}_{0}\) was calculated using Table 7–5 of the ASCE 41–17, and the other two coefficients were approximately estimated by a process of trial and error for these structures.

Table 4 Coefficients for calculating the target displacement
Full size table

7 Results and Discussions

In this section, the results of designing the two frames by the algorithms are discussed. The 1st example is run 10 times independently, and 6 independent runs were carried out for the 2nd one to provide reasonable statistical results.

7.1 6-story Frame

The first example is a 3-bay, 6-story frame depicted in Fig. 3a. The design variables include 6 groups for columns and 3 groups for beams as demonstrated in Fig. 3a. The best designs achieved by the algorithms without any constraint violations are shown in Table 5. As can be seen, the best design of IWSA (bolded in the table) is 4.2 and 10% better than its standard version and PSO, respectively. In addition, it is 3.5% lighter than the best result of ECBO. For a better insight into the performance of the three algorithms in the ten runs, the average optimized weight is also provided in Table 5. As shown, the average optimized weight of IWSA is 21171.56 kg which is 6.2% and 9.8% lighter than WSA and PSO, respectively. This shows the superiority of the IWSA over its standard version and PSO in the optimization process. However, the mean result of ECBO is slightly better than IWSA. This number, along with a low value of the standard deviation of ECBO, shows the satisfactory performance of this metaheuristic in the ten independent runs.

Table 5 The best design achieved by the algorithms for the 6-story frame
Full size table

The convergence curves for the best design of the algorithms are shown in Fig. 4. It can be seen that the IWSA has the highest convergence rate in comparison with the other metaheuristics. It is worth mentioning that despite beginning the optimization with a similar initial solution to the WSA, the higher convergence rate of IWSA is evident in later stages of the optimization. This demonstrates that the strategies utilized in IWSA were instrumental in enhancing the convergence speed of the algorithm.

Fig. 4
figure 4

Convergence history for the best design of the 6-story frame

Full size image

The IDR for the best design by IWSA is shown in Fig. 5, which shows that the final design also meets the drift ratio constraints. However, the values for the IDR of the frames are far from their allowable threshold which can be construed that this constraint has not controlled the design.

Fig. 5
figure 5

Inter-story drift ratio for the best design obtained by IWSA algorithm for the 6-story frame

Full size image

Figure 6 shows the rotation of plastic hinges for the best solution obtained for the 6-story frame (the left and the right bar plot belong to the columns and beams, respectively). In this figure, the numbering for columns and beams is started from the first story up to the last one and from left to right. For each column, the numbering begins with the lower plastic hinge and then the upper one, and for each beam, it begins with the left plastic hinge to the right one. For each plastic hinge, the existing value of the rotation is divided by the maximum allowable value of rotation (\(\theta /{\theta }_{A.C}\)) so that the values of the vertical axis are normalized for a better insight. This figure illustrates that the rotation of hinges has not exceeded the allowable values. However, this value for the CP performance level controls the designing process.

Fig. 6
figure 6

Plastic hinges rotation for the best design of the 6-story frame

Full size image

The strong column-weak beam (SCWB) criterion is checked using the following equation according to (AISC341-16 2016):

$$\frac{{\sum M_{pb} }}{{\sum M_{pc} }} \le 1$$
(23)

where \(\sum {M}_{pb}\) denotes the sum of plastic moments in the beams projected at the centerline of the column and \(\sum {M}_{pc}\) is the sum of plastic moments in the column below and above the joint at the intersection of the beam and column centerline. The SCWB graph for the best design is plotted in Fig. 7. In this figure, Nij denotes the \({j}^{th}\) node of the \({i}^{th}\) story, counting from left to right. The values for \(\sum {M}_{pb}/\sum {M}_{pc}\) are directly affected by the design and classification of variables and are determined at the CP performance level. The values denoting the ratio of the leftmost nodes are slightly less than the rightmost ones; this conclusion is drawn based on the higher axial load of the right columns at CP performance level, which increases this ratio. The difference grows more noticeable as the section sizes reduce. It can be seen that in each beam-column intersection, the value of \(\sum {M}_{pb}/\sum {M}_{pc}\) is less than unity, showing that this criterion is met for the best design achieved by IWSA algorithm.

Fig. 7
figure 7

Strong column-weak beam ratio plot for the best design of the 6-story frame

Full size image

7.2 12-story Frame

The second example evaluates a 4-bay, 12-story frame. The schematic of the frame, along with the groupings of columns and beams, is shown in Fig. 3b. This example is a more complex problem than the first one and consists of 24 design variables and numerous seismic constraints which makes it an arduous task for metaheuristics to converge to a feasible solution. For this example, WSA and PSO could not obtain an acceptable result without constraint violation in the six independent runs. Furthermore, since the optimization of this structure entails much more time than the first structure, and considering the outperformance of IWSA and ECBO in the previous problem, the sheer further studies of these two algorithms is justified.

Table 6 shows the best design obtained by IWSA and ECBO and the average value of the optimized weight. As shown, the best design of IWSA weighs 68,663.54 kg (bolded in the table), whereas this value for ECBO equals 77,628.72 kg. In other words, IWSA has outperformed ECBO by 11.6% in the best optimization process. In terms of the average optimized weight, Table 6 shows that IWSA has also performed better than ECBO in the six optimization runs since the mean value of IWSA is 10% less than ECBO.

Table 6 The best design achieved by the algorithms for the 12-story frame
Full size table

The best design convergence curve is depicted in Fig. 8. It is seen that IWSA has a faster convergence rate than ECBO to a large extent. For such a complex problem, a mechanism is required for an optimization algorithm to escape from the local optimum and to navigate it towards the near-optimal solution. This mechanism is designed in IWSA by the mutation of the best-so-far solution which assists it to approach the optimal solution rather than getting trapped in local optimum or searching fruitless areas of the search space.

Fig. 8
figure 8

Convergence history for the best design of the 12-story frame

Full size image

The IDR of the best design of the IWSA algorithm is depicted in Fig. 9, demonstrating that it has satisfied this constraint successfully.

Fig. 9
figure 9

Inter-story drift ratio for the best design obtained by IWSA algorithm for the 12-story frame

Full size image

In Figs. 10 and 11, the plastic hinge rotation of columns and beams is demonstrated. As can be seen, the orange bars (CP performance level) are near their maximum allowable values for both the columns and beams plastic hinges while for the most of the plastic hinges, the LS bars are far from their maximum allowable values. This shows that the plastic hinges rotation for the CP performance level dominates the optimization process.

Fig. 10
figure 10

Plastic hinges rotation of columns for the best design of IWSA for the 12-story frame

Full size image
Fig. 11
figure 11

Plastic hinges rotation of beams for the best design of IWSA for the 12-story frame

Full size image

In Fig. 12, the SCWB criterion is investigated for the best design of IWSA. This figure demonstrates that the SCWB criterion is satisfied for most of the nodes except a few nodes belonging to the 9th and 10th story. Since the strong column-weak beam criterion has not been explicitly taken into account as a design constraint, a few columns exhibit a ratio larger than unity. For the design of special moment frames, this criterion should be assumed as a constraint, and thus after achieving a final design with no violation of constraint, this criterion would also be satisfied.

Fig.12
figure 12

Strong column-weak beam ratio plot for the best design of the 12-story frame

Full size image

7.3 Hinge Formation of the Optimal Designs

Since the CP performance-level acceptance criteria were the predominant constraints in the optimization process for the two frames considered, the distribution of the rotation of elements' endings at CP performance level is of interest to us. Figure 13 illustrates the amount of rotation ratio for each element with respect to its corresponding yield rotation, \({\theta }_{y}\). The red circle in this figure denotes the location in which the maximum rotation ratio has occurred in either the beams or columns. By observing this figure, one can discern the critical elements in the frames which have undergone a large deformation, and the critical elements that can potentially induce soft story mechanism can be identified for prospective rehabilitation purposes.

Fig. 13
figure 13

Elements rotation ratios with respect to yield rotation, \({\theta }_{y}\), for the two optimally designed frames at CP performance level (the active constraint) denoted by the blue circles; a) the 6-story frame b) the 12-story frame. The red circle shows the hinge in which the maximum rotation has occurred

Full size image

8 Conclusion

The recently developed metaheuristic algorithm called IWSA was tested in a complex performance-based design optimization problem with system- and component-level seismic and non-seismic constraints, and the results were compared to its standard version and two other well-established metaheuristic algorithms, namely PSO and ECBO. Two MRFs were studied in this article with 9 and 24 discrete design variables for PBSDO to challenge the four algorithms and illustrate their computational performance. The following conclusions can be drawn based on the results of this paper:

  • For both of the problems, the CP performance level governed the optimization process. This can be construed that while CP tends to occur in the aftermath of stronger earthquakes and less frequently than the LS performance level, the allowable damage level is so strict that its imposed design controls those of the LS performance level.

  • The acceptance criteria for the plastic hinge rotation of the members at the CP performance level were the active constraint.

  • The comparison of the metaheuristics shows that the IWSA algorithm is superior to its standard version and PSO in terms of accuracy of the final result as well as the required number of structural analyses.

  • IWSA is competitive with one of the most successful, state-of-the-art metaheuristic algorithms, ECBO.

  • An acceptable average value and standard deviation for the independent runs for the two examples clearly proved that the algorithm is also robust without sensitivity to the initial random population generated.

  • The mechanisms embedded in IWSA were useful for a successful optimization process. The GSTS as an opposition-based learning method guided the algorithm towards more promising areas of the search space, thereby increasing the convergence speed of the algorithm. The mutation technique utilized in IWSA also did a successful job in assisting IWSA to achieve a near-optimum solution, especially in the second example. Therefore, we can utilize these mechanisms in other metaheuristic algorithms to attempt to enhance their performance.

Furthermore, IWSA can also be applied in a different framework such as reliability-based design optimization (RBDO) problems, especially system reliability problems in which the failure domain involves non-convex functions with various constraints. These topics are of interest for prospective studies in this respect.