1 Introduction

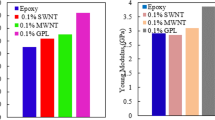
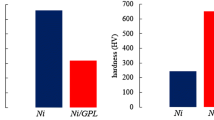
According to the recent advantages in nanoscience and technology (Olia et al. 2019; Hosseini et al. 2018), the GNP reinforcement has attracted considerable attention. Recently, Li et al. (2018) studied the effect of GNP on grain size and hardness of GNP/Ni micro/nano composites. Their result showed that the grains of the GNP/Ni composites are finer than pure Ni and the hardness of this composite is higher than the pure Ni, So that they produced micro gear by using the GNP/Ni composite. Rafiee et al. (2009) compared the mechanical properties of epoxy refined by 1% value fraction of the single walled carbon nanotubes (SWNT), multi walled carbon nanotube (DWNT) and GNP with each other. They reported that \( E \), \( \sigma_{UTS} \) and fracture toughness of the composite reinforced by GNPs is higher than other composites. So, GNP is a good alternative for SWCNTs and MWCNTs in many applications. In the field reinforced structures, some researches showed that Habibi et al. (2016, 2017, 2018a, b), Fazaeli et al. (2016), Hosseini et al. (2018), Ghazanfari et al. (2016) and Torabi and Shafieefar (2015) with the aid of some methods the mechanical properties of macro-structures is improved.

Some researches demonstrated that subjoining a very meager value of graphene into the primary polymer matrix can improve mechanical, thermal and electrical properties of the structure (Ebrahimi et al. 2018; Safarpour et al. 2018a, b; Esmailpoor Hajilak et al. 2019; Pourjabari et al. 2019; Habibi et al. 2019; Zehtabiyan-Rezaie et al. 2019; Makki et al. 2019). It is worth mentioning that the nanostructures reinforced by GNP are more applicable in engineering design, so that focus on the dynamic modeling of the nanostructure reinforced by GNP reinforcement is an important issue. For this reason, the investigation of the mechanical characteristics of the reinforced strictures have a great importance for engineering design and manufacture. Song et al. (2017) demonstrated the post buckling of the FG reinforced GNPs nanobeams. They indicated that the GNPs have substantial reinforcing effect on the buckling and post buckling of the beams. In another paper, Feng et al. (2017) studied the nonlinear bending of the GNPs reinforced beams. They showed that the high value of GNPs and symmetric distribution in such directions are less susceptible to the nonlinear behavior. According to many researcher’s reports, the size effects have a significant role on the mechanical behaviors of the micro/nano structures (Ghadiri et al. 2017; Ghadiri and SafarPour 2017; Mahinzare et al. 2017; Mohammadi et al. 2018). Thus, overlooking these effects may lead to obtain wrong results in designing and manufacturing. It should worth mentioning that classical continuum theory (Shamloofard and Assempour 2019; Shamloofard and Movahhedy 2015) is not validated for modeling any micro/nano structures. Therefore, some methods, such as: molecular dynamic (MD) simulations (Shayan-Amin et al. 2009; Mohammadi et al. 2017, 2018; Tsai and Tu 2010) and non-classical continuum theory are used to study nanostructures. MD simulation includes complicated and time-consuming calculations which are not efficient. In contrast, simple and efficient, higher order continuum mechanic theories, have recently attracted researcher’s attentions. As studying the mechanical behaviors of nanoshells relates to submicron dimensions, they could not be correctly predicted by the classical theory. Thus taking into consideration the size effect, higher order continuum theories are used. As an example for size-dependent theories: Ghayesh et al. (2018) demonstrated nonlinear vibration of a FG microplate based on a modified version of the couple stress theory. In their result showed that FG volume fraction, parameters of length-scale, and external force have special effect on the response of the structure. Vibrational behavior of FGM nanobeam based on nonlocal strain gradient elasticity theory (NSGT) is examined by Hadi et al. (2018). Also, they solved those equations with the aid of GDQM. They concluded that, NSGT is the best theory for their problem. Ghayesh and Farajpour (2018) discussed on the nonlinear forced vibration of the nanoscale tubes using NSGT. They developed the equations of the problem by Hamilton’s principle. As their interesting results, they showed that, external force has important role on the dynamics behavior. Farokhi and Ghayesh (2018) investigated the effects of DC and AC voltages on the static and dynamic instability of microelectromechanical plate. They employed the modified couple stress theory (MCST) for considering the size effect. Ghayesh (2018) presented the force vibration of the FG viscoelastic microbeams using MCST. In their results, effects of the FG volume fraction, amplitude load and viscoelastic parameters on the forced vibration of the structures are investigated. Khaniki (2018) used Eringen’s theory for analyzing of the vibrational behavior of the two-layered nanobeam. The porosity effect on vibrational behavior of the nanotubes based on NSGT is investigated by She et al. (2018). In their work, the effects of temperature variations, porosity and material parameters on the vibrational behavior of the nanotubes are studied. Ke et al. (2012) discussed on the vibration of the FG microbeams with the aid of MCST. In addition, for solving the equations using boundary conditions they used DQM. Shafiei and She (2018) investigated the vibrational characteristics of the FG tubes with the aid of NSGT. They used GDQM for solving the equations. In the results section, they demonstrated the effects of the different boundary condition, material variation, temperature variation, and nonlocal parameter on the vibrational behavior of the structure. Sahmani and Aghdam (2017) studied nonlinear instability of FG-GNPRC nanoshells under hydrostatic pressure using NSGT. Sahmani et al. (2018) investigated the nonlinear vibration of the FG porous GNP micro and nano plates with the aid of NSGT. Barati (2018) studied the forced vibration of the porous plates using NSGT. They showed that, the porosity pattern, nonlocal parameter and the location of the dynamic load have significant effects on the forced vibrational behavior of the nanoplates. Therefore, it is a great significance to study the forced vibration characteristics of a porous GNPRC cylindrical nanoshell using FMCS parameter for the first time.

To the best of our knowledge, no papers have been reported in the literature concerning the forced vibrational behavior of the porous GNPRC nanoshells using FMCS parameter. It is noted that, pervious papers have not considered the effects of porosity, thermal environment, dynamic load, porous GNPRC and size effect on the resonance frequencies and dynamic deflections of the porous GNPRC nanoshell using FMCS parameter and the first order shear deformation (FSDT). The novelty of this paper is considering the porosity, GNPRC, different temperature distributions, size effects and dynamic load implemented on the proposed model based on FSDT. Finally, in the results section show that the GNP distribution patterns, modified couple stress parameter, porosity and thermal environment have important roles on the resonance frequencies, relative frequency changes, and dynamic deflections of the porous GNPRC cylindrical nanoshell in thermal environments.

2 Multilayer polymer porous composites reinforced GNPs formulations

Here, a cylindrical nanoshell under the dynamic load is modeled. R, h and l are middle surface radius, thickness and length of the cylindrical nanoshell, respectively. Applied dynamic load is shown by \( q_{0} \) (Fig. 1).

Fig. 1
figure 1

Geometry of a cylindrical GNPRC nanoshell under dynamic load

Full size image

The cylindrical nanoshell is made of composite material. For better grasp of the importance and applications of the current model, Fig. 2 shows a multi-layer GNP/polymer nanocomposite shell. As Fig. 2 displays GNPs are regularly dispersed in each layer of polymer matrix, but in each layer the weight fraction is different from another. Pattern 1 is an isotropic homogeneous plate that GNPs (wt% of GNPs 1%) are regularly distributed, and pattern 2 shows that GNPs weight fraction (wt%) changes since layer to layer along the thickness. As shown in pattern 3 the weight fraction in midplane is the highest and increases layer to layer towards the top layer. In comparison with pattern 2, pattern 3 shows the maximum weight fraction on both top layers, and it decreases to the lowest amount in the midplane. Pattern 4 is a non-symmetrical pattern in which weight fraction increments linearly from top to inner surface.

Fig. 2
figure 2

Different distributions of GNP in GNPRCs cylindrical nanoshell

Full size image

In addition, three different nonuniform patterns for the porous material are shown in Fig. 3.

Fig. 3
figure 3

Schematic representation of the FG porous cylindrical nanoshell with various porosity dispersion

Full size image

The volume fraction functions of these four patterns have been represented by

$$ {\text{Pattern}}\,1{:}\quad U - GNPRC{:}\,V_{GNP} (k) = V_{GNP}^{*} $$
(1)
$$ {\text{Pattern}}\,2{:}\quad X - GNPRC{:}\,V_{GNP} (k) = 2V_{GNP}^{*} \left| {2k - N_{L} - 1} \right| /N_{L} $$
(2)
$$ {\text{Pattern}}\,3{:}\quad O - GNPRC{:}\,V_{GNP} (k) = 2V_{GNP}^{*} \left[ {1 - \left( {\left| {2k - N_{L} - 1} \right| /N_{L} } \right)} \right] $$
(3)
$$ {\text{Pattern}}\,4{:}\quad A - GNPRC{:}\,V_{GNP} (k) = 2V_{GNP}^{*} (2k - 1) /N_{L} $$
(4)

where k is the number of layers of the nanoshell, \( N_{L} \) and \( V_{{GNP}}^{*} \) are total number of layers and GNPs volume fraction. Relation of \( V_{GNP}^{*} \) and \( g_{GNP} \) can be defined by:

$$ V_{GNP}^{*} = \frac{{g_{GNP} }}{{g_{GNP} + (\rho_{GNP} /\rho_{m} )(1 - g_{GNP} )}} $$
(5)

in which, GNPs mass densities and polymer matrix are \( \rho_{GNP} \) and \( \rho_{m} \). Based on Tsai–Halpin model, the elastic modulus of composites reinforced by GNPs approximated by:

$$ \begin{aligned} E & = \frac{3}{8}E_{L} + \frac{5}{8}E_{T} , \\ E_{L} & = \frac{{1 + \xi_{L} n_{L} V_{GPL} }}{{1 - n_{L} V_{GPL} }}E_{m} ,\quad E_{T} = \frac{{1 + \xi_{T} n_{T} V_{GPL} }}{{1 - n_{T} V_{GPL} }}E_{m} \\ \end{aligned} $$
(6)

where E is the effective modulus of composites reinforced by GNPs. In addition, for unidirectional lamina, EL and ET are longitudinal and transverse moduli. In Eq. (6) the GNP geometry factors (\( \xi_{L} \) and \( \xi_{T} \)) and other parameters are given by:

$$ \begin{aligned} \xi_{L} & = 2({\mathbb{Z}}_{GNP} /h_{GNP} ),\quad \xi_{t} = 2(b_{GNP} /h_{GNP} ), \\ n_{L} & = \frac{{(E_{GNP} /E_{M} ) - 1}}{{(E_{GNP} /E_{M} ) + \xi_{L} }},\quad n_{T} = \frac{{(E_{GNP} /E_{M} ) - 1}}{{(E_{GNP} /E_{M} ) + \xi_{T} }} \\ \end{aligned} $$
(7)

where \( {\mathbb{Z}}_{GNP} \), \( h_{GNP} \), \( R_{GNP} \) are the average length, thickness and radius of the GNPs. By using rule of mixture, young’s module (\( \bar{E} \)), Mass density (\( \bar{\rho } \)), Poisson’s ratio (\( \bar{\nu } \)), and thermal expansion (\( \bar{\alpha } \)) of the GNP/polymer composite are expressed as:

$$ \begin{aligned} \bar{E} & = E_{GNP} V_{GNP} + E_{M} V_{M} , \\ \bar{\rho } & = \rho_{GNP} V_{GNP} + \rho_{M} V_{M} , \\ \bar{\nu } & = \nu_{GNP} V_{GNP} + \nu_{M} V_{M} , \\ \bar{\alpha } & = \alpha_{GNP} V_{GNP} + \alpha_{M} V_{M} . \\ \end{aligned} $$
(8)

The mechanical properties of the porous GNPRC cylindrical shell are presented by (Sahmani et al. 2018):

$$ \begin{aligned} E_{eff} & = \bar{E}\left[ {1 -\Gamma _{P} S(z)} \right], \\ \rho_{eff} & = \bar{\rho }\left[ {1 -\Gamma _{m} S(z)} \right], \\ \alpha_{eff} & = \bar{\alpha }\left[ {1 -\Gamma _{p} S(z)} \right], \\ \nu_{eff} & = 0.221\left( {1 - \frac{{\rho_{eff} }}{{\bar{\rho }}}} \right) + \bar{\nu }\left[ {1 + 0.342\left( {1 - \frac{{\rho_{eff} }}{{\bar{\rho }}}} \right)^{2} - 1.21\left( {1 - \frac{{\rho_{eff} }}{{\bar{\rho }}}} \right)} \right] \\ \end{aligned} $$
(9)

where

$$ \begin{aligned} S(z) & = \left\{ {\begin{array}{*{20}l} {\cos \left( {\frac{\pi z}{2h} + \frac{\pi }{4}} \right)} \hfill & {for\,imperfection\,1} \hfill \\ {\cos \left( {\frac{\pi z}{h}} \right)} \hfill & {for\,imperfection\,2} \hfill \\ {1 - \cos \left( {\frac{\pi z}{h}} \right)} \hfill & {for\,imperfection\,3} \hfill \\ \end{array} } \right. \\\Gamma _{m} & = 1.121\left[ {1 + ( - 1 +\Gamma _{p} S(z))^{1/2.3} } \right] /S(z) \\ \end{aligned} $$
(10)

In Eqs. (9) and (10) \( \Gamma _{p} \) and \( \Gamma _{m} \) are porosity and density coefficients, respectively.

2.1 Mathematical modeling

According to the Taylor’s series expansion, displacement components are as below (Ebrahimi et al. 2019; Safarpour et al. 2019):

$$ \begin{aligned} u(x,\theta ,z,t) & = u_{0} (x,\theta ,t) + zu_{1} (x,\theta ,t) \\ v(x,\theta ,z,t) & = (1 + z /R)v_{0} (x,\theta ,t) + zv_{1} (x,\theta ,t) \\ w(x,\theta ,z,t) & = w_{0} (x,\theta ,t) \\ \end{aligned} $$
(11)

Here, \( u_{0} (x,\theta ,t) \), \( v_{0} (x,\theta ,t) \) and \( w_{0} (x,\theta ,t) \) indicate the displacements of the neutral surface along x, \( {\theta } \) and z directions respectively. Also, \( u_{1} (x,\theta ,t) \) and \( v_{1} (x,\theta ,t) \) represent the rotations of a cross section around \( \uptheta \) and x-directions. In addition, the three-dimensional stress–strain relation can be expressed as follows:

$$ \left[ {\begin{array}{*{20}l} {\sigma_{xx} } \hfill \\ {\sigma_{\theta \theta } } \hfill \\ {\sigma_{zz} } \hfill \\ {\sigma_{x\theta } } \hfill \\ {\sigma_{xz} } \hfill \\ {\sigma_{\theta z} } \hfill \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\bar{Q}_{11} } & {\bar{Q}_{12} } & {\bar{Q}_{13} } & 0 & 0 & 0 \\ {\bar{Q}_{12} } & {\bar{Q}_{22} } & {\bar{Q}_{23} } & 0 & 0 & 0 \\ {\bar{Q}_{13} } & {\bar{Q}_{23} } & {\bar{Q}_{33} } & 0 & 0 & 0 \\ 0 & 0 & 0 & {\bar{Q}_{44} } & 0 & 0 \\ 0 & 0 & 0 & 0 & {\bar{Q}_{55} } & 0 \\ 0 & 0 & 0 & 0 & 0 & {\bar{Q}_{66} } \\ \end{array} } \right] \left[\begin{array}{*{20}l} {\varepsilon_{xx} - \alpha_{1}\Delta T} \hfill \\ {\varepsilon_{\theta \theta } - \alpha_{2}\Delta T} \hfill \\ {\varepsilon_{zz} - \alpha_{3}\Delta T} \hfill \\ {\varepsilon_{x\theta } } \hfill \\ {\varepsilon_{xz} } \hfill \\ {\varepsilon_{\theta z} } \hfill \\ \end{array}\right] $$
(12)

In Eq. (12) thermal expansion and temperature changes are \( \alpha \) and \( \Delta T \), respectively. The minimum potential energy for motion and boundary conditions equations states that:

$$ \int_{{t_{1} }}^{{t_{2} }} {(\delta T - \delta U + \delta W_{1} - \delta W_{2} )dt = 0} $$
(13)

The strain energy (Zahabi et al. 2018) of the nanoshell is:

$$ U = \frac{1}{2}\iiint\limits_{V} {(\sigma_{ij} \varepsilon_{ij} + m_{ij}^{s} \chi_{ij}^{s} )R\,dxd\theta dz} $$
(14)

In Eq. (14), strain and stress components are \( \varepsilon_{ij} \) and \( \sigma_{ij} \), which are presented by Barooti et al. (2017). In addition, \( m_{ij} \) and \( \chi_{ij}^{s} \) are the components of the symmetric rotation and higher order stress tensor, which can be expressed as:

$$ \begin{aligned} \chi_{ij}^{s} & = \frac{1}{2}(\varphi_{i,j} + \varphi_{j,i} ) \\ m_{ij}^{s} & = 2l^{2} \mu \chi_{ij}^{s} \\ \end{aligned} $$
(15)

where \( \emptyset_{\text{i}} \) and \( l \) represent the extremely small rotation vector and FMCS parameter is symmetric rotation, and can be shown as below:

$$ l = l_{GNP} V_{GNP} + l_{M} V_{M} \,\,\, $$
(16)

Moreover, the kinetic energy of the GNPRC cylindrical nanoshell considering FMCS parameter can be obtained as:

$$ T = \frac{1}{2}\int\limits_{Z} {\iint\limits_{A} {\rho \left\{ {\dot{u}^{2} + \dot{v}^{2} + \dot{w}^{2} } \right\}}} R\,dz\,dx\,d\theta $$
(17)

For a typical isotropic cylindrical shell which is in exposure to high temperature environment, it is assumed that the temperature distributed across its thickness. Hence, work done of temperature change can be obtained as:

$$ W_{1} = \frac{1}{2}\iint\limits_{A} {\left[ {N_{1}^{T} \left( {\frac{{\partial w_{0} }}{\partial x}} \right)^{2} + N_{2}^{T} \left( {\frac{{\partial v_{0} }}{\partial x}} \right)^{2} } \right]}R\,dx\,d\theta $$
(18)

where thermal resultants are \( N_{1}^{T} \) and \( N_{2}^{T} \). Both of them can be obtained as:

$$ \begin{aligned} N_{1}^{T} & = \int_{ - h/2}^{h/2} {(\bar{Q}_{11} + \bar{Q}_{12} + \bar{Q}_{13} )\,\alpha (T - T_{0} )dz,} \\ N_{2}^{T} & = \int_{ - h/2}^{h/2} {(\bar{Q}_{21} + \bar{Q}_{22} + \bar{Q}_{23} )\,\alpha (T - T_{0} )dz.} \\ \end{aligned} $$
(19)

Coefficients of thermal expansion are presented as:

$$ \alpha = \left[ {\alpha_{xxe} \,\,\,\alpha_{\theta \theta e} \,\,\,\alpha_{zze} \,\,\,\,0\,\,\,\,0\,\,\,\,0} \right]^{T} $$
(20)

Temperature changes linearly along the thickness from \( T_{m} \) (at the outer surface) to \( T_{c} \) (at the inner surface) is supposed. The work done of applied forces obtained as:

$$ W_{2} = \frac{1}{2}\left\{ {q_{dynamic} w^{2} } \right\}\,R\,dV $$
(21)

In which, qdynamic is applied dynamic load. Substituting Eqs. (14), (17), (18) and (21) into Eq. (13) the motion equations of the porous GNP cylindrical nanoshell in thermal environment can be obtained as follows:

$$ \begin{aligned} & \left[ {\frac{{\partial N_{xx} }}{\partial x} + \frac{1}{R}\frac{{\partial N_{x\theta } }}{\partial \theta } + \frac{1}{{2R^{2} }}\left( - \frac{{\partial Y_{\theta \theta } }}{\partial \theta } + \frac{{\partial Y_{zz} }}{\partial \theta }\right) + \frac{1}{2R}\frac{{\partial^{2} Y_{zx} }}{\partial \theta \,\partial x} + \frac{1}{{2R^{2} }}\frac{{\partial^{2} Y_{\theta z} }}{{\partial \theta^{2} }}} \right]\delta u \\ & \quad + \,\left[ {\frac{{\partial N_{x\theta } }}{\partial x} + \frac{1}{R}\frac{\partial }{\partial \theta }N_{\theta \theta } + \frac{{Q_{z\theta } }}{R} + \frac{1}{2}\left\{ {\frac{1}{R}\frac{\partial }{\partial x}( - Y_{xx} + Y_{\theta \theta } ) - \frac{1}{{R^{2} }}\frac{{\partial Y_{\theta x} }}{\partial \theta } - \frac{{\partial^{2} Y_{xz} }}{{\partial x^{2} }} - \frac{{Y_{xz} }}{{R^{2} }} - \frac{1}{R}\frac{{\partial^{2} Y_{z\theta } }}{\partial \theta \,\partial x}} \right\}} \right]\delta v \\ & \quad - \,N_{2}^{T} \frac{{\partial^{2} v}}{{\partial x^{2} }}\delta v + \left[ {\frac{{\partial Q_{xz} }}{\partial x} + \frac{1}{R}\frac{{\partial Q_{z\theta } }}{\partial \theta } - \frac{{N_{\theta \theta } }}{R} - \frac{1}{{2R^{2} }}\frac{{\partial^{2} Y_{\theta x} }}{{\partial \theta^{2} }} - \frac{1}{{2R^{2} }}\frac{{\partial Y_{zx} }}{\partial \theta } + \frac{1}{2R}\frac{{\partial Y_{\theta z} }}{\partial x} + \frac{{\partial^{2} Y_{x\theta } }}{{2\partial x^{2} }}} \right]\delta w_{0} \\ & \quad + \,\left[ { - \frac{1}{2R}\frac{{\partial^{2} }}{\partial \theta \,\partial x}(Y_{xx} - Y_{\theta \theta } ) - N_{1}^{T} \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right]\delta w \\ & \quad + \,\left[ {\frac{{\partial M_{xx} }}{\partial x} + \frac{1}{R}\frac{{\partial M_{\theta \theta } }}{\partial \theta } - Q_{xz} + \frac{1}{2}\frac{{\partial Y_{\theta x} }}{\partial x} - \frac{1}{2R}\frac{\partial }{\partial \theta \,}(Y_{zz} - Y_{\theta \theta } )} \right]\delta u_{1} \\ & \quad + \,\left[ {\frac{{Y_{zz} }}{R} + \frac{1}{2R}\frac{{\partial^{2} T_{zx} }}{\partial \theta \,\partial x} + \frac{1}{{2R^{2} }}\frac{{\partial^{2} T_{\theta z} }}{{\partial \theta^{2} }}} \right]\delta u_{1} \\ & \quad + \,\left[ {\frac{1}{R}\frac{{\partial M_{\theta \theta } }}{\partial \theta } + \frac{{\partial M_{x\theta } }}{\partial x} - Q_{z\theta } + \frac{1}{2}\frac{\partial }{\partial x}\left( {Y_{zz} - Y_{xx} + \frac{{T_{\theta \theta } }}{R}} \right)} \right]\delta v_{1} \\ & \quad + \,\left[ { - \frac{1}{2}\frac{{\partial Y_{\theta x} }}{\partial \theta } + \frac{{Y_{xz} }}{2R} - \frac{1}{2R}\frac{{\partial^{2} T_{\theta z} }}{\partial \theta \,\partial x} - \frac{1}{2}\frac{{\partial^{2} T_{zx} }}{{\,\partial x^{2} }}} \right]\delta v_{1} \\ & \quad = \,\left\{ {I_{0} \frac{{\partial^{2} u}}{{\partial t^{2} }} + I_{1} \frac{{\partial^{2} \psi_{x} }}{{\partial t^{2} }}} \right\}\delta u + \left\{ {I_{0} \frac{{\partial^{2} v}}{{\partial t^{2} }} + I_{1} \frac{{\partial^{2} \psi_{\theta } }}{{\partial t^{2} }}} \right\}\delta v \\ & \quad + I_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }}\delta w_{0} + \left\{ {I_{1} \frac{{\partial^{2} u}}{{\partial t^{2} }} + I_{2} \frac{{\partial^{2} \psi_{x} }}{{\partial t^{2} }}} \right\}\delta u_{1} \\ & \quad + \left\{ {I_{1} \frac{{\partial^{2} v}}{{\partial t^{2} }} + I_{2} \frac{{\partial^{2} \psi_{\theta } }}{{\partial t^{2} }}\,} \right\}\delta v_{1} + q_{dynamic} \delta w \\ \end{aligned} $$
(22)

where parameters used in Eq. (22) are presented as:

$$ \begin{aligned} & (N_{xx} ,N_{\theta \theta } ,N_{x\theta } ) = \int_{ - h/2}^{h/2} {(\sigma_{xx} ,\sigma_{\theta \theta } ,\sigma_{x\theta } )dz,} \\ & (M_{xx} ,M_{\theta \theta } ,M_{x\theta } ) = \int_{ - h/2}^{h/2} {(\sigma_{xx} ,\sigma_{\theta \theta } ,\sigma_{x\theta } )zdz} , \\ & (Q_{xz} ,Q_{z\theta } ) = \int_{ - h/2}^{h/2} {k_{s} (\sigma_{xz} ,\sigma_{z\theta } )dz} , \\ & (Y_{xx} ,Y_{\theta \theta } ,Y_{zz} ,Y_{x\theta } ,Y_{xz} ,Y_{z\theta } ) = \int_{ - h/2}^{h/2} {(m_{xx} ,m_{\theta \theta } ,m_{zz} ,m_{x\theta } ,m_{xz} ,m_{z\theta } )dz,} \\ & (T_{xx} ,T_{\theta \theta } ,T_{zz} ,T_{x\theta } ,T_{xz} ,T_{z\theta } ) = \int_{ - h/2}^{h/2} {(m_{xx} ,m_{\theta \theta } ,m_{zz} ,m_{x\theta } ,m_{xz} ,m_{z\theta } )zdz} . \\ \end{aligned} $$
(23)

2.2 Solution procedure

In this section, analytical method is implemented to solve the governing equations of MSGT-based on GPLRC nanoshell. In addition, in this research, the proposed model is simply supported in x = 0, L and \( \theta = \pi /2,\,3\pi /2 \). Thus, the displacement fields can be calculated as:

$$ \left\{ \begin{aligned} u_{0} (x,\theta ,t) \hfill \\ v_{0} (x,\theta ,t) \hfill \\ w_{0} (x,\theta ,t) \hfill \\ u_{1} (x,\theta ,t) \hfill \\ v_{1} (x,\theta ,t) \hfill \\ \end{aligned} \right\} = \sum\limits_{m = 1}^{\infty } {\sum\limits_{n = 1}^{\infty } {\left\{ {\begin{array}{*{20}l} {U_{0mn} \,\cos \,\left( {\frac{m\pi }{L}x} \right)\,\cos \,(n\theta )} \hfill \\ {V_{0mn} \,\sin \,\left( {\frac{m\pi }{L}x} \right)\,\sin \,(n\theta )} \hfill \\ {W_{0mn} \sin \,\left( {\frac{m\pi }{L}x} \right)\,\cos \,(n\theta )} \hfill \\ {U_{1mn} \,\cos \,\left( {\frac{m\pi }{L}x} \right)\,\cos \,(n\theta )} \hfill \\ {V_{1mn} \,\sin \left( {\frac{m\pi }{L}x} \right)\,\sin \,(n\theta )} \hfill \\ \end{array} } \right\}} } \sin (\omega t) $$
(24)

where \( \left\{ {U_{0mn} ,V_{0mn} ,W_{0mn} ,\Psi _{xmn} ,\Psi _{\theta mn} } \right\} \) are the unknown Fourier coefficients that need to be determined for each n and m values. Also, n and m are the circumferential and axial wave numbers, respectively. For vibration analysis of the structure, by substituting Eq. (24) into Eq. (22), one obtains:

$$ \begin{aligned} & \left( {\left\{ {\begin{array}{*{20}c} {k_{1,1} } & {k_{1,2} } & {k_{1,3} } & {k_{1,4} } & {k_{1,5} } \\ {k_{2,1} } & {k_{2,2} } & {k_{2,3} } & {k_{2,4} } & {k_{2,5} } \\ {k_{3,1} } & {k_{3,2} } & {k_{3,3} } & {k_{3,4} } & {k_{3,5} } \\ {k_{4,1} } & {k_{4,2} } & {k_{4,3} } & {k_{4,4} } & {k_{4,5} } \\ {k_{5,1} } & {k_{5,2} } & {k_{5,3} } & {k_{5,4} } & {k_{5,5} } \\ \end{array} } \right\} - \omega_{ex}^{2} \left\{ {\begin{array}{*{20}c} {m_{1,1} } & {m_{1,2} } & {m_{1,3} } & {m_{1,4} } & {m_{1,5} } \\ {m_{2,1} } & {m_{2,2} } & {m_{2,3} } & {m_{2,4} } & {m_{2,5} } \\ {m_{3,1} } & {m_{3,2} } & {m_{3,3} } & {m_{3,4} } & {m_{3,5} } \\ {m_{4,1} } & {m_{4,2} } & {m_{4,3} } & {m_{4,4} } & {m_{4,5} } \\ {m_{5,1} } & {m_{5,2} } & {m_{5,3} } & {m_{5,4} } & {m_{5,5} } \\ \end{array} } \right\}} \right)\left( \begin{aligned} U_{0} \hfill \\ V_{0} \hfill \\ W_{0} \hfill \\ \psi_{x} \hfill \\ \psi_{\theta } \hfill \\ \end{aligned} \right) \\ & \quad = \left[ {\begin{array}{*{20}l} 0 \hfill \\ 0 \hfill \\ {q_{dynamic} } \hfill \\ 0 \hfill \\ 0 \hfill \\ \end{array} } \right]\left( \begin{aligned} U_{0} \hfill \\ V_{0} \hfill \\ W_{0} \hfill \\ \psi_{x} \hfill \\ \psi_{\theta } \hfill \\ \end{aligned} \right) \\ \end{aligned} $$
(25)

In which, \( \omega_{ex} \) is the excitation frequency and applied dynamic load (\( q_{dynamic} \)) is defined as:

$$ q_{dynamic} = \sum\limits_{m = 1}^{\infty } {\sum\limits_{n = 1}^{\infty } {q_{0} \sin \,\left( {\frac{m\pi }{L}x} \right)\,\cos \,(n\theta )} } \sin (\omega t), $$
(26)

Solution of Eq. (26) gives the dynamic deflection and excitation frequency of the porous FG-GPLRC cylindrical nanoshell. The dimensionless excitation frequency and forced vibration amplitude are defined as:

$$ \Omega = 10 \times \omega_{ex} L\sqrt {\rho /E} ,\quad \bar{W}_{uniform} = W_{0mn} \frac{{10Eh^{3} }}{{L^{4} q_{0} }}. $$
(27)

3 Results and discussion

In the result section, a porous GNP cylindrical nanoshell in thermal environment is modeled with the simply supported boundary conditions. After modeling the current structure, the effects of the porosity, patterns of GNP distribution, FMCS parameter, radius to length ratio, mode number and thermal environment on resonance frequencies and dynamic deflections are studied in detail. Generally, the first part of our result is validation of the model with the aid of previous papers in literature. In the second part, effects of porosity and some various parameters on resonance frequencies and dynamic deflections of the porous GNP nanoshell in thermal environments are investigated.

3.1 Model validation

According to Fig. 3, in these value of length scale parameter (l = R/3), MCST has a better agreement with the results of MD simulation which is reported by Ansari et al. (2012). So, considering the three value of length scale parameter (l = R/3) is a good suggestion for dynamic analysis of a nanoshell using MCST (Fig. 4).

Fig. 4
figure 4

Comparison of the natural frequency of cylindrical nanoshell with the results obtained by MD simulation (Ansari et al. 2012)

Full size image

Table 1 presents a comparison study between obtained natural frequencies of simply supported nanoshells with considering FMCS parameter from current study and previous papers. High agreement between the dimensionless natural frequency of current study and those of Tadi Beni et al. (2016) is shown.

Table 1 Dimensionless natural frequencies of isotropic homogeneous nanoshells
Full size table

As another verification, Table 2 compares the results for dimensionless natural frequency of the cylindrical shell with different GNP distribution patterns with the reported results with those obtained by Liu et al. (2018).

Table 2 dimensionless natural frequency of GNPRC nanoshells
Full size table

3.2 Parametric results

In this section the analytical results are presented for a simply supported porous GNP cylindrical nanoshell using FMCS parameter in thermal environment. The model is a cylindrical shell with the total thickness of hGNP = 1.5 nm, length of aGNP = 2.5 μm and radius of RGNP = 0.75 μm. Table 3 gives the mechanical properties of GNP. The property parameters of epoxy are assumed to be temperature-dependent. In the following sections the effects of different parameters on the excitation frequency, dimensionless amplitude and relative frequency changes of the structure are investigated.

Table 3 Epoxy and GNP properties (Wu et al. 2017)
Full size table

Temperature dependency of the porous materials are defined as follows:

$$ \alpha_{m} = \frac{{45(0.0005\Delta T + 1)}}{{10^{6} \times K}}\,{\text{and}}\;E = \left( { - 3.52 + 0.0034T} \right)\,{\text{GPa}},\,{\text{in}}\,{\text{which}}\,T =\Delta T + T_{0} . $$

3.3 The effects of different parameter on excitation frequency and dimensionless amplitude

The effect of weight function on dynamic deflection and resonance frequency of the GNPRC cylindrical nanoshell is shown in Fig. 5. In this figures, different values of weight function (gGPL) are examined. It is evident that dynamic deflection of the GNPRC cylindrical nanoshell is affected by the magnitude of excitation frequency of dynamic load. In fact, dynamic deflection increases smoothly with the increase of excitation frequency. At a certain value of excitation frequency, a considerable increase is observed in deflection of GNPRC cylindrical nanoshell. The reason is that the excitation frequency of dynamic load coincides with the natural frequency of the GNPRC cylindrical nanoshell which leads to the resonance phenomena. It is seen that resonance frequency of the GNPRC cylindrical nanoshell decreases by decreasing the weight function. This is because of an increase in the weight function which leads to an increase in the stiffness of structure, and causes resonance frequency and stability to increase.

Fig. 5
figure 5

Resonance frequency and dynamic deflection of the cylindrical nanoshell for different weight fraction (\( \Delta T = 20K \), l = R/3, Pattern 2, L/R = 10, R/h = 10 and n = m = 1)

Full size image

The effects of different GPL distribution patterns on the dynamic deflection and resonance frequency of the GPLRC cylindrical nanoshell is illustrated in Fig. 6. It can be seen that as GPL distribution patterns increases from 1 to 4, the resonance frequency increases, this leads to an increase in the instability of structure. In other words, pattern 4 gives larger resonance frequencies than other patterns. This behavior stems from the mathematical function which was presented in previous section. It is worth mentioning that, the resonance frequency of the structure in patterns 3 and 4 are close to each other.

Fig. 6
figure 6

Resonance frequency and dynamic deflection of the cylindrical nanoshell for different GNP distribution patterns (\( \Delta T = 20K \), l = R/3, L/R = 10, R/h = 10 and n = m = 1)

Full size image

In Fig. 7, the effect of FMCS parameter on the excitation frequency and dynamic deflection of the porous GNP cylindrical nanoshell is studied for X-GNPRC pattern. As an important result, the FMCS parameters have a remarkable effect on the resonance frequencies of the structure. An increase in the FMCS parameters leads to increase the resonance frequency so that this matter can cause an improvement in the stability of the porous GNP cylindrical.

Fig. 7
figure 7

Resonance frequency and dynamic deflection of the cylindrical nanoshell for different modified couple stress parameter (\( \Delta T = 20K \), Pattern 2, L/R = 10, R/h = 10 and n = m = 1)

Full size image

The effects of R/h and temperature changes on resonance frequency of the porous GNP cylindrical nanoshell are presented in Figs. 8 and 9. Based on Fig. 8, by increasing the R/h, the resonance frequency and stability decline. In addition, Fig. 8 indicates that an increase in the temperature changes cause to increase in the resonance frequency, and leads to decline the stability of structure.

Fig. 8
figure 8

Resonance frequency and dynamic deflection of the cylindrical nanoshell for different radius to thickness ratios (\( \Delta T = 0K \), l = R/3, Pattern 4, L/R = 10 and n = m = 1)

Full size image
Fig. 9
figure 9

Resonance frequency and dynamic deflection of the cylindrical nanoshell for different temperature changes (l = R/3, Pattern 4, L/R = 10, R/h = 10 and n = m = 1)

Full size image

3.4 Different parameters effects on relative frequency change

The percentage value in parentheses denotes the relative frequency increase \( (\omega_{C} - \omega_{M} ) \), where \( \omega_{C} \) and \( \omega_{M} \) are natural frequencies with and without GPL, respectively. Figure 10 show the relative frequency changes of the FG-GPLRC cylindrical nanoshell with different total number of layers (NL). As expected, the fundamental frequencies of the structure with GPL distribution pattern 1 are not affected by NL since they are homogeneous. For the cylindrical nanoshells with pattern 2 in which GPLs are non-uniformly dispersed, their fundamental frequencies decrease with increasing the total number of layers to NL = 7, then they remain almost unchanged when NL is further increased. In contrast, this trend is reversed for GPL distribution pattern 3. Among the three non-uniform patterns considered, the fundamental frequency of the structure with GPL pattern 1 is least affected by the change in NL. As a good suggestion, the multilayer shell is modeled in the current study. According to Fig. 10 by increasing the number of layers (1 < NL < 7) the natural frequency and stability of the nanostructure change (for non-uniform GPL distribution patterns 2 and 3). It is observed that, in the non-uniform GPL distribution pattern 3, by increasing of the number of layers, the natural frequency and stability of the nanostructure increase. Also, for the other uniform and non-uniform distribution patterns, number of layers of the GPL is not important. The other amazing result is that, by increasing the number of layers in the non-uniform GPL distribution pattern 2, the natural frequency and stability decrease.

Fig. 10
figure 10

The effect of NL on the relative frequency change for different patterns of GNP/epoxy (\( \Delta T = 10K \), l = R/3, Pattern 2, L/R = 10, R/h = 10 and n = m = 1)

Full size image

Figures 11 and 12 show the effects of FMCS parameters and temperature changes on the relative frequency of the porous GNPRC cylindrical nanoshell, respectively. Based on Fig. 10, an increase in the material length parameter leads to an increase in the natural frequency and a decrease in the stability of the structure. At a certain value of temperature change, a considerable increase is observed in deflection of GNPRC cylindrical nanoshell. The reason of this trend is that the buckling phenomena occurs in this temperature. According to Fig. 12, by increasing the FMCS parameters, an enhancement for relative frequency of the structure is observed. The amazing result is that; mode number has any effect on the relative frequency changes of the porous GNP cylindrical nanoshell. By increasing the weight fraction, the structure becomes softer, so that it is a reason for increasing the relative frequency changes.

Fig. 11
figure 11

The effect of the temperature changes on the relative frequency change for different FMCS parameter (Pattern 2, L/R = 10, R/h = 10 and n = m = 1)

Full size image
Fig. 12
figure 12

The effect of weight fraction on the relative frequency change for different mode numbers (\( \Delta T = 10K \), l = R/3, Pattern 2, L/R = 10, R/h = 10)

Full size image

Figures 13, 14 and 15 illustrate the effect of porosity coefficient, and temperature changes on natural frequency (THz) for different porosity distributions using non-classical continuum theory. According to figures, by decreasing the temperature changes, stability and natural frequency of the nanoshell see a decrease. The figure shows that an increase in porosity coefficient increases the natural frequency and causes an increase in stability of nanostructure. The difference between Figs. 13, 14 and 15 is that, by increasing the porosity coefficient in porosity distribution 1, the natural frequency increases in the form of nonlinear changes. Porosity distribution 2 has similar trend as can be seen in Fig. 14, but by increasing the porosity coefficient in porosity distribution 3, the natural frequency increases in the form of linear changes.

Fig. 13
figure 13

The effects of temperature changes and porosity coefficient on the natural frequency (THz) of the simply supported porous GNPRC nanoshell with considering imperfection 1

Full size image
Fig. 14
figure 14

The effects of temperature changes and porosity coefficient on the natural frequency (THz) of the simply supported porous GNPRC nanoshell with considering imperfection 2

Full size image
Fig. 15
figure 15

The effects of temperature changes and porosity coefficient on the natural frequency (THz) of the simply supported porous GNPRC nanoshell with considering imperfection 3

Full size image

4 Conclusions

In this article, size-dependent thermal buckling, forced and free vibrational characteristics of a porous composite cylindrical nanoshell reinforced by GNPs in thermal environment are presented. The size-dependent porous GNP nanoshell is analyzed using FMCS parameter. At the first time, in this article, FMCS constant which changes along the thickness direction is considered. With the aid of the Hamilton’s principle, the motion equations and non-classic boundary conditions are obtained. Excellent agreements are observed with comparison the results of this research and those of others and MD simulation which confirmed the accuracy and validity of this continuum mechanic model. The influences of some key parameters such as, GNP distribution patterns, FMCS parameter, length to radius ratio, mode number, and thermal environment on the resonance frequencies, relative frequency change and dynamic deflections are studied. The main results of this article are presented as below:

  1. 1.

    It is observed that the resonance frequency increases as the FMSC parameter and weight fraction increase, and it decreases as the temperature difference increases.

  2. 2.

    The results show that A-GNP pattern presents larger resonance frequency than other patterns.

  3. 3.

    An increase in the temperature change causes to increase in the relative frequency which decreases the stability of the structure, however this trend is reversed for weight fraction of GNP.

  4. 4.

    By increasing R/h parameter, the resonance frequency and stability of the porous GNP cylindrical nanoshell tends to increase.

  5. 5.

    By increasing the porosity coefficient in imperfection 1, the natural frequency increases as nonlinear changes and the imperfection 2 has a similar trend with imperfection 1, but effect of porosity coefficient on natural frequency in imperfection 3 is linear.