Buckling and post-buckling behaviors of higher order carbon nanotubes using energy-equivalent model

Abstract

This paper aims to investigate the size scale effect on the buckling and post-buckling of single-walled carbon nanotube (SWCNT) rested on nonlinear elastic foundations using energy-equivalent model (EEM). CNTs are modelled as a beam with higher order shear deformation to consider a shear effect and eliminate the shear correction factor, which appeared in Timoshenko and missed in Euler–Bernoulli beam theories. Energy-equivalent model is proposed to bridge the chemical energy between atoms with mechanical strain energy of beam structure. Therefore, Young’s and shear moduli and Poisson’s ratio for zigzag (n, 0), and armchair (n, n) carbon nanotubes (CNTs) are presented as functions of orientation and force constants. Conservation energy principle is exploited to derive governing equations of motion in terms of primary displacement variable. The differential–integral quadrature method (DIQM) is exploited to discretize the problem in spatial domain and transformed the integro-differential equilibrium equations to algebraic equations. The static problem is solved for critical buckling loads and the post-buckling deformation as a function of applied axial load, CNT length, orientations and elastic foundation parameters. Numerical results show that effects of chirality angle, boundary conditions, tube length and elastic foundation constants on buckling and post-buckling behaviors of armchair and zigzag CNTs are significant. This model is helpful especially in mechanical design of NEMS manufactured from CNTs.

1 Introduction

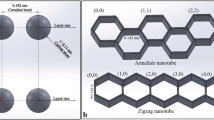
Since 1991, carbon nanotubes (CNTs), discovered by Iijima, have received widespread interest of researchers due to their extraordinary mechanical, thermal, physical and electrical properties. CNTs are considered the strongest and most resilient material known until now, [32]. In general, geometrical and mechanical properties of CNTs are controlled by two parameters [12], which are the orientation of the chiral angle and the carbon diameter. The chiral vector and tube radius ($R$) of CNTs can be portrayed by

$${\overrightarrow{C}}_{h}=n{\overrightarrow{a}}_{1}+ m {\overrightarrow{a}}_{2},$$

(1.a)

$$R={l}_{0}\sqrt{3\left({n}^{2}+{m}^{2}+n\mathrm{*}m\right)}/2\pi .$$

(1.b)

In which the unit vectors are ${\overrightarrow{a}}_{1}$ and ${\overrightarrow{a}}_{2}$, and $\left(n, m\right)$ is integer pair that specifies the structure orientation of CNTs [i.e.: zigzag at $\left(n, 0\right)$, armchair at $\left(n, n\right)$, and chiral orientation at $\left(n, m\right)$ for $m\ne n$ or 0] as presented in Fig. 1. The C–C bond length here is ${l}_{0}=0.142$ $\mathrm{n}\mathrm{m}$. Zigzag and armchair nanotubes radii are calculated by $R=\frac{\sqrt{3}n{l}_{0}}{2\pi }$ and by $R=\frac{3n{l}_{0}}{2\pi }$, respectively.

Fig. 1

Schematic diagram of the chiral vector and the choral angle of CNTs, [42]

Nasdala et al. [34] illustrated that the standard truss and beam elements can be represented atomic interactions accurately. Energy-equivalent model, resulting from the foundation of molecular and continuum mechanics, considers the mechanical properties of CNTs (i.e.; Young’s modulus, shear modulus, and Poisson’s ratio) as a material size dependent by many researchers. Leung et al. [27] proposed a combined model of molecular and continuum mechanics to investigate mechanical properties of zigzag SWCNTs. Wu et al. [42] derived the equivalent Young’s and shear moduli for both armchair and zigzag SWCNTs by combining molecular and continuum mechanics methods. In [30], derived an exact elastica solution for a clamped-simply (C-S) SWCNT by the elliptic integral technique. Aydogdu [1] studied, free vibration of simply supported (S–S) multi-walled carbon nanotubes (MWCNTs) using the higher order shear deformation beam theory (HOSDT). Mayoof and Hawwa [29] investigated nonlinear vibration of CNT with waviness along its axis based on classical continuum theory. Shodja and Delfani [38] and Shokrieh and Rafiee [39] presented analytical formulations to predict the elastic moduli of graphene sheets and CNTs using a linkage between lattice molecular structure and equivalent discrete frame structure. Joshi et al. [23] modeled the elastic behavior of CNT-reinforced composites using the multiscale representative volume element approach. Wang et al. [40, 41] studied the vibrations of S–S double-walled CNTs subjected to a moving harmonic load using nonlocal Euler and Timoshenko beam theories. Mohammadi et al. [33] investigated the static instability of an imperfect nonlocal Eringen nanobeam embedded in elastic foundation. Khater et al. [25] studied buckling behavior of curved nanowires including a surface energy under a thermal load. Ghadyani and Ochsner [19] presented an expression for the stiffness of SWCNTs as function of nanotube thickness. Eltaher and Agwa [9] presented a modified continuum energy-equivalent model to investigate the vibration of a pretension CNTs carrying a concentrated mass as a mass sensor.

Gholami et al. [20] analyzed the nonlinear resonant of imperfect HOSDT functionally graded carbon nanotube-reinforced composite beams subjected to a harmonic transverse load. Kordkheili et al. [26] employed nonlocal continuum theory of Eringen and Von Karman nonlinear strains to study a linear and nonlinear dynamics of SWCNTs conveying fluid with different boundary conditions. Mohamed et al. [31] exploited modified differential–integral quadrature method to analyze nonlinear free and forced vibrations of buckled curved beams resting on nonlinear elastic foundations. Maneshi et al. [28] presented closed-form expression for geometrically nonlinear large deformation of nanobeams subjected to end force. Emam et al. [18] investigated the post-buckling and free vibration response of geometrically imperfect multilayer nanobeams under pre-stress compressive load. Eltaher et al. [12] and Mohamed et al. [32] presented a novel numerical procedure to predict nonlinear buckling and post-buckling stability of imperfect clamped–clamped (C–C) SWCNTs surrounded by nonlinear elastic foundation using energy-equivalent model. Eltaher et al. [13] illustrated the influence of periodic (sine and cosine) and nonperiodic imperfection modes on buckling, post-buckling and dynamics of beam rested on nonlinear elastic foundations. Dehghan et al. [6] investigated the wave propagation of fluid-conveying magneto-electro-elastic nanotube incorporating fluid effect. Eltaher et al. [14] characterized Young’s modulus and evaluated vibration and buckling behaviors of CNTs by equivalent-continuum mechanics approach. Karimiasl et al. [24] studied post-buckling behaviors of multiscale composite sandwich doubly curved piezoelectric shell with a flexible core by employing Homotopy Perturbation Method in hygrothermal environment. Eltaher et al. [15, 16] illustrated the effect of imperfections and vacancies on vibration and modal participation factor of CNTs using energy-equivalent model. Ebrahimi and Hosseini [7] presented the nonlinear vibration behavior and dynamic instability of Euler–Bernoulli nanobeams (EBT) under thermo-magneto-mechanical loads. Ebrahimi et al. [8] evaluated the damping forced harmonic vibration characteristics of magneto-electro-viscoelastic nanobeam embedded in viscoelastic foundation based on nonlocal strain gradient elasticity theory.

Based on both material and size dependency, many researchers studied buckling and vibration behaviors of CNTs. Baghdadi et al. [2] presented thermal effect on vibration of armchair and zigzag SWCNTs using nonlocal parabolic beam theory. Benguediab et al. [4] studied buckling properties of a zigzag double-walled CNT with both chirality and small-scale effects using Timoshenko beam. Semmah et al. (2015) presented the thermal buckling properties of a zigzag SWCNT based on the nonlocal Timoshenko beam and energy-equivalent model. Bedia et al. [3] studied analytically thermal buckling of armchair SWCNT embedded in an elastic medium. On the basis of the continuum mechanics and the single-elastic beam model, Besseghier et al. [5] investigated the nonlinear vibration of zigzag SWCNT embedded in elastic medium. Heshmati et al. [21] studied the vibrational behavior of CNT-reinforced composite beams and presented the effects the interface, waviness, agglomeration, orientation and length on the behavior of CNTs. Eltaher et al. [9] illustrated nonlinear static behavior of size-dependent and material-dependent nonlocal CNTs using nonlocal differential form of Eringen and energy-equivalent method. Eltaher et al. [11] presented a modified continuum model included energy-equivalent model and modified couple stress theory to investigate the vibration behavior of CNTs.

According to the best of the authors' knowledge and literature review, it can be concluded that no researchers have attempted to investigate buckling and post-buckling of higher order shear deformation CNTs by considering material size dependency. The present study intends to fill this gap in the literature by considering the energy-equivalent method along with HOSDT. This paper is organized as follows. Section 2 describes the mathematical formulation of the equivalent energy model for armchair and zigzag SWCNTs continuum. Main formulations and equilibrium governing equations of CNTs modeled by higher order shear deformation theory are presented. In Sect. 3, differential–integral quadrature method is presented and developed to solve equilibrium differential equations of material size-dependent carbon nanotube. Analytical solution and closed form for critical buckling load are presented through Sect. 4. Numerical results are presented and discussed in Sect. 5. Most findings and concluding remarks are summarized in Sect. 6.

2 Mathematical formulation

2.1 Chemical energies vs. mechanical energies

Comparing microscopic chemistry and the macroscopic mechanics energies, covalent bonds between carbon atoms can be represented by forces, which are functions of bond lengths and bond angles. Therefore, the force filed through bonding can be described by potential energies as [35]

$$\mathrm{P}\mathrm{E}={\mathrm{P}\mathrm{E}}_{L}+{\mathrm{P}\mathrm{E}}_{\theta }+{\mathrm{P}\mathrm{E}}_{T}+{\mathrm{P}\mathrm{E}}_{\omega }.$$

(2)

In which ${\mathrm{P}\mathrm{E}}_{L}$, ${\mathrm{P}\mathrm{E}}_{\theta }$, ${\mathrm{P}\mathrm{E}}_{T}$, and ${\mathrm{P}\mathrm{E}}_{\omega }$ are bond stretching, angle variation, torsion and inversion (out of plane) energies. In 2D loading, the most significant energies are bending angle energies and bond stretching and the other energies can be neglected. Therefore, Eq. (2) can be simplified as [14,15,16]

$$\mathrm{P}\mathrm{E}={\mathrm{P}\mathrm{E}}_{L}+{\mathrm{P}\mathrm{E}}_{\theta }=\frac{1}{2}\sum_{i}{K}_{i} {\left(d{R}_{i}\right)}^{2}+\frac{1}{2}\sum_{j}{C}_{j} {\left(d{\theta }_{j}\right)}^{2},$$

(3)

where ${K}_{i}$ is the stretching constant, $d{R}_{i}$ is the elongation of the bond $i$, ${C}_{j}$ is the angle variance constant, $d{\theta }_{j}$ is the variance of bond angle $j$. Young’s modulus and Poisson’s ratio for CNTs, for armchair and zigzag orientations, can be represented by Mohamed et al. [32]

$${E}_{a}=\frac{4\sqrt{3}}{3}\frac{KC}{3 Ct+4 K {l}_{0}^{2} t \left({\lambda }_{a1}^{2}+2 {\lambda }_{a2}^{2}\right)},$$

(4a)

$${\upsilon }_{a}=\frac{{\lambda }_{a1 }{l}_{0}^{2} K-C}{{\lambda }_{a1 }{l}_{0}^{2} K+3 C},$$

(4b)

$${E}_{z}=\frac{4\sqrt{3}KC}{9 C t+4 K {l}_{0}^{2} t \left({\lambda }_{z1}^{2}+2 {\lambda }_{z2}^{2}\right)},$$

(4c)

$${\upsilon }_{z}=\frac{{\lambda }_{z1 }{l}_{0}^{2} K+\sqrt{3}C}{{\lambda }_{z1 }{l}_{0}^{2} K-3\sqrt{3} C},$$

(4d)

where $t$ is the thickness of a nanotube. Subscripts $a$ and $z$ represent armchair and zigzag, respectively. ${\lambda }_{1}$ and ${\lambda }_{2}$ are geometrical-dependent parameters, which can be evaluated by

$${\lambda }_{a1 }\left(n\right)=\frac{4-{\mathrm{c}\mathrm{o}\mathrm{s}}^{2}\left(\pi /2n\right)}{16+2{\mathrm{c}\mathrm{o}\mathrm{s}}^{2}\left(\pi /2n\right)},$$

(5a)

$${\lambda }_{a2 }\left(n\right)=\frac{-\sqrt{12-3 {\mathrm{c}\mathrm{o}\mathrm{s}}^{2}\left(\pi /2n\right)} \mathrm{c}\mathrm{o}\mathrm{s}\left(\pi /2n\right)}{32+4{\mathrm{c}\mathrm{o}\mathrm{s}}^{2}\left(\pi /2n\right)},$$

(5b)

$${\lambda }_{z1 }\left(n\right)=\frac{-3\sqrt{4-3 {\mathrm{c}\mathrm{o}\mathrm{s}}^{2}\left(\pi /2n\right)} \mathrm{c}\mathrm{o}\mathrm{s}\left(\pi /2n\right)}{8\sqrt{3}-2\sqrt{3}{\mathrm{c}\mathrm{o}\mathrm{s}}^{2}\left(\pi /2n\right)},$$

(5c)

$${\lambda }_{z2 }\left(n\right)=\frac{12-9 {\mathrm{c}\mathrm{o}\mathrm{s}}^{2}\left(\pi /2n\right)}{16\sqrt{3}-4{\sqrt{3}\mathrm{c}\mathrm{o}\mathrm{s}}^{2}\left(\pi /2n\right)},$$

(5d)

2.2 Geometrical formulation of CNTs

The displacement fields of the higher order shear deformation CNTs are represented by Aydogdu [1]

$${U}_{0}\left(x,z,t\right)=u\left(x,t\right)-\mathrm{z}\frac{\partial w\left(x,t\right)}{\partial x}+f\left(z\right)\phi \left(x,t\right),$$

(6a)

$${W}_{0}\left(x,z,t\right)=w\left(x,t\right),$$

(6b)

where ${U}_{0}$, and ${W}_{0}$ are denoting the displacement components along the $x$- and $z$-directions, respectively. $u$ and $w$ represent middle surface displacement components along the $x$- and $z$-directions, respectively. $\phi$ is an unknown function that represents the effect of transverse shear strain on the beam middle surface, and $f\left(z\right)$ represents the shape function determining the distribution of the transverse shear strain and stress through the thickness, which can be described by Reddy [36]

$$f\left(z\right)=z\left(1-\frac{4{\mathrm{z}}^{2}}{3{h}^{2}}\right),$$

(7)

The nonzero strains of the CNTs associated with the displacement field given in Eq. (6) can be computed by

$${\upvarepsilon }_{xx}=\frac{\partial {U}_{0}}{\partial x}+\frac{1}{2}{\left(\frac{\partial {W}_{0}}{\partial x}\right)}^{2}={\varepsilon }_{x}^{\left(0\right)}+\mathrm{z}{\varepsilon }_{x}^{\left(1\right)}+f\left(z\right) {\varepsilon }_{x}^{\left(2\right)},$$

(8a)

$${\upgamma }_{xz}=\frac{\partial {U}_{0}}{\partial z}+\frac{\partial {W}_{0}}{\partial x}=\frac{df}{\partial z}{\gamma }_{xz}^{\left(0\right)},$$

(8b)

in which

$${\varepsilon }_{x}^{\left(0\right)}=\frac{\partial \mathrm{u}}{\partial x}+\frac{1}{2}{\left(\frac{\partial w}{\partial x}\right)}^{2}; {\varepsilon }_{x}^{\left(1\right)}=-\frac{{\partial }^{2}\mathrm{w}}{\partial {x}^{2}} ; {\varepsilon }_{x}^{\left(2\right)}=\frac{\partial \phi }{\partial x} ; {\gamma }_{xz}^{\left(0\right)}=\phi .$$

(9)

However, the stress constitutive equations may be written in the form

$${\upsigma }_{xx}=E{\upvarepsilon }_{xx}=E\left[{\varepsilon }_{x}^{\left(0\right)}+\mathrm{z}{\varepsilon }_{x}^{\left(1\right)}+f\left(z\right) {\varepsilon }_{x}^{\left(2\right)}\right],$$

(10a)

$${\uptau }_{xz}=G{\upgamma }_{xz}=\frac{E}{2\left(1+\mu \right)}\frac{\partial f}{\partial z}{\gamma }_{xz}^{\left(0\right)}.$$

(10b)

Hence, force and moment resultants may be written in the form

$$\left\{\begin{array}{c}N\\ M\\ P\end{array}\right\}=\left[\begin{array}{ccc}{A}_{1}& {A}_{2}& {A}_{3}\\ {A}_{2}& {A}_{4}& {A}_{5}\\ {A}_{3}& {A}_{5}& {A}_{6}\end{array}\right]\left\{\begin{array}{c}{\varepsilon }_{x}^{\left(0\right)}\\ {\varepsilon }_{x}^{\left(1\right)}\\ {\varepsilon }_{x}^{\left(2\right)}\end{array}\right\},$$

(11a)

$$Q={A}_{7} {\gamma }_{xz}^{\left(0\right)},$$

(11b)

where ${A}_{j}$ stiffness coefficients can be evaluated by

$$\left({A}_{1},{A}_{2},{A}_{3, } {A}_{4},{A}_{5},{A}_{6},{A}_{7}\right)=\underset{A}{\int }E\left(z\right)\left[1,{z,f,z}^{2},zf,{f}^{2},{\left(\frac{df}{dz}\right)}^{2} \right]dA.$$

(12)

Based on the conservation of energy, which states that variation of energy will be equal to zeros

$$\delta \Pi =\delta U+\delta V=0,$$

(13)

where $\delta U$ is the virtual strain energy, $\delta V$ is the virtual work done by external forces, and

$$ \begin{aligned}\delta U&=\frac{1}{2}\delta \left[{\int }_{\Omega } \left({\upsigma }_{xx}{\upvarepsilon }_{xx}+{\uptau }_{xz}{\upgamma }_{xz}\right) d\Omega \right]+\frac{1}{2}\stackrel{-}{N}\delta {\int }_{0}^{L}{\left(\frac{\partial w}{\partial x}\right)}^{2}dx\\ &=\underset{0}{\overset{L}{\int }}\left[N\delta {\varepsilon }_{x}^{\left(0\right)}+M\delta {\varepsilon }_{x}^{\left(1\right)}+P\delta {\varepsilon }_{x}^{\left(2\right)}+Q\delta {\gamma }_{xz}^{\left(0\right)}\right]dx\\ &\quad+\stackrel{-}{N}{\int }_{0}^{L}\left(\frac{\partial w}{\partial x}\right)\left(\frac{\partial \delta w}{\partial x}\right)dx,\end{aligned} $$

(14a)

$$\delta V=-\delta \left[{\int }_{\Gamma } \left({\upsigma }_{xx}u+{\uptau }_{xz}w\right) d\Gamma \right],$$

(14b)

where $\Omega$ and $\Gamma$ denote domain and boundary of the beams. After performing variation operations, one can obtain

$$\delta u : \frac{\partial N}{\partial x}=0,$$

(15a)

$$\delta w : \frac{{\partial }^{2}\mathrm{M}}{\partial {x}^{2}}+\frac{\partial }{\partial x}\left(N\frac{\partial \mathrm{w}}{\partial x}\right)-\left(\stackrel{-}{N}-{\stackrel{-}{k}}_{s}\right)\frac{{\partial }^{2}\mathrm{w}}{\partial {x}^{2}}-{\stackrel{-}{k}}_{L}w-{\stackrel{-}{k}}_{NL}{w}^{3}=0,$$

(15b)

$$\delta \varphi : \frac{\partial P}{\partial x}-Q=0,$$

(15c)

where the shear layer, linear and nonlinear Winkler stiffness are ${\stackrel{-}{k}}_{s}$,${\stackrel{-}{k}}_{L}$ and ${\stackrel{-}{k}}_{NL}$, respectively. The equilibrium equations can be represented in terms of displacements as

$${A}_{1}\frac{d}{dx}\left[\frac{du}{dx}+\frac{1}{2}{\left(\frac{dw}{dx}\right)}^{2}\right]-{A}_{2}\frac{{d}^{3}w}{d{x}^{3}}+{A}_{3}\left(\frac{{d}^{2}\phi }{d{x}^{2}}\right)=0,$$

(16a)

$$ \begin{aligned}&{A}_{1}\frac{d}{dx}\left\{\left[\frac{du}{dx}+\frac{1}{2}{\left(\frac{dw}{dx}\right)}^{2}\right]\frac{dw}{dx}\right\}+{A}_{3}\frac{d}{dx}\left[\frac{dw}{dx}\frac{d\phi }{dx}\right]\\ &\quad+{A}_{2}\frac{{d}^{3}u}{d{x}^{3}}+{A}_{5}\left(\frac{{d}^{3}\phi }{d{x}^{3}}\right)-{A}_{4}\frac{{d}^{4}w}{d{x}^{4}}-\left(\stackrel{-}{N}-{\stackrel{-}{k}}_{s}\right)\\ &\quad\frac{{\partial }^{2}\mathrm{w}}{\partial {x}^{2}}-{\stackrel{-}{k}}_{L}w-{\stackrel{-}{k}}_{NL}{w}^{3}=0,\end{aligned} $$

(16b)

$${A}_{3}\frac{d}{dx}\left[\frac{du}{dx}+\frac{1}{2}{\left(\frac{dw}{dx}\right)}^{2}\right]-{A}_{5}\frac{{d}^{3}w}{d{x}^{3}}+{A}_{6}\frac{{d}^{2}\phi }{d{x}^{2}}-{A}_{7}\phi =0.$$

(16c)

To eliminate the axial displacement $u$ in governing Eq. (16), Integrating Eq. (16a) with respect to the spatial coordinate $x$ two times yields

$$u=-\frac{1}{2}\underset{0}{\overset{L}{\int }}{\left(\frac{dw}{dx}\right)}^{2}dx+\frac{{A}_{2}}{{A}_{1}}\frac{dw}{dx}-\frac{{A}_{3}}{{A}_{1}}\phi +\frac{{C}_{1}}{{A}_{1}}x+{C}_{2}.$$

(17)

The boundary conditions for CNTs with immovable ends can be expressed as

$$u\left(0\right)=u\left(L\right)=0.$$

(18)

After substituting and some manipulations, the following equations can be deduced:

$$\frac{du}{dx}+\frac{1}{2}{\left(\frac{dw}{dx}\right)}^{2}=\frac{1}{2L}\underset{0}{\overset{L}{\int }}{\left(\frac{dw}{dx}\right)}^{2}dx+\frac{{A}_{2}}{{A}_{1}}\frac{{d}^{2}w}{d{x}^{2}}-\frac{{A}_{3}}{{A}_{1}}\frac{d\phi }{dx},$$

(19a)

$$\frac{d}{dx}\left[\frac{du}{dx}+\frac{1}{2}{\left(\frac{dw}{dx}\right)}^{2}\right]=\frac{{A}_{2}}{{A}_{1}}\frac{{d}^{3}w}{d{x}^{3}}-\frac{{A}_{3}}{{A}_{1}}\frac{{d}^{2}\phi }{d{x}^{2}},$$

(19b)

$$\frac{{d}^{3}u}{d{x}^{3}}=-\frac{d}{dx}\left(\frac{dw}{dx}\frac{{d}^{2}w}{d{x}^{2}}\right) -\frac{{A}_{3}}{{A}_{1}}\frac{{d}^{3}\phi }{d{x}^{3}}+\frac{{A}_{2}}{{A}_{1}}\frac{{d}^{4}w}{d{x}^{4}}.$$

(19c)

Substituting Eq. (19) back into Eq. (16) yields

$$ \begin{aligned}& \left(\frac{{A}_{2}^{2}}{{A}_{1}}-{A}_{4}\right)\frac{{d}^{4}w}{d{x}^{4}}+\left[\frac{{A}_{1}}{2L}\underset{0}{\overset{L}{\int }}{\left(\frac{dw}{dx}\right)}^{2} dx-\stackrel{-}{P}+{\stackrel{-}{k}}_{s}\right]\\&\frac{{d}^{2}w}{d{x}^{2}}-{\stackrel{-}{k}}_{L}w-{\stackrel{-}{k}}_{NL}{w}^{3}+\left({A}_{5}-\frac{{A}_{2}{A}_{3}}{{A}_{1}}\right)\frac{{d}^{3}\phi }{d{x}^{3}}=0,\end{aligned} $$

(20a)

$$\left({A}_{6}-\frac{{A}_{3}^{2}}{{A}_{1}}\right)\frac{{d}^{2}\phi }{d{x}^{2}}+\left(\frac{{A}_{2}{A}_{3}}{{A}_{1}}-{A}_{5}\right)\frac{{d}^{3}w}{d{x}^{3}}-{A}_{7}\phi =0.$$

(20b)

Computing the coefficients ${A}_{j}$ and substituting into Eq. (20).

$$ \begin{aligned}& EI\frac{{d}^{4}w}{d{x}^{4}}+\left[\stackrel{-}{P}-{\stackrel{-}{k}}_{s}-\frac{EA}{2L}\underset{0}{\overset{L}{\int }}{\left(\frac{dw}{dx}\right)}^{2}dx\right]\\&\frac{{d}^{2}w}{d{x}^{2}}{+\stackrel{-}{k}}_{L}w+{\stackrel{-}{k}}_{NL}{w}^{3}-\frac{4}{5}EI\frac{{d}^{3}\phi }{d{x}^{3}}=0,\end{aligned} $$

(21a)

$$\frac{68}{105}EI\frac{{d}^{2}\phi }{d{x}^{2}}-\frac{4}{5}EI\frac{{d}^{3}w}{d{x}^{3}}-\frac{8}{15}EA\phi =0,$$

(21b)

where the mass moment of inertia $I=\frac{\pi }{4}\left({\left(R+t\right)}^{4}-{R}^{4}\right)$ and the cross-sectional area $A=\pi \left({\left(R+t\right)}^{2}-{R}^{2}\right)$. Introducing the following nondimensional parameters

$$W=\frac{w}{L}, X=\frac{x}{L},\Phi =\phi .$$

(22)

Equation (21) can be written in a dimensionless form as

$$ \begin{aligned}& \frac{{d}^{4}W}{d{X}^{4}}+\left[P-{k}_{s}-\frac{1}{2}{\gamma }_{0}\underset{0}{\overset{1}{\int }}{\left(\frac{dW}{dX}\right)}^{2}dx\right]\\&\frac{{d}^{2}W}{d{X}^{2}}{+k}_{L}W+{k}_{NL}{W}^{3}-{\gamma }_{1}\frac{{d}^{3}\Phi }{d{X}^{3}}=0,\end{aligned} $$

(23a)

$${\gamma }_{2}\frac{{d}^{2}\Phi }{d{X}^{2}}-{\gamma }_{1}\frac{{d}^{3}W}{d{X}^{3}}-{\gamma }_{3}\Phi =0.$$

(23b)

The coefficients of Eq. (23) are defined as

$$ \begin{aligned}& P=\frac{\stackrel{-}{P}{L}^{2}}{EI},{k}_{s}=\frac{{\stackrel{-}{k}}_{s}{L}^{2}}{EI}, {k}_{L}=\frac{{\stackrel{-}{k}}_{L}{L}^{4}}{EI},{ k}_{NL}=\frac{{\stackrel{-}{k}}_{NL}{L}^{6}}{EI},{\gamma }_{0}=\frac{{L}^{2}}{{S}_{0}},\\& { \gamma }_{1}=\frac{4}{5},{ \gamma }_{2}=\frac{68}{105},{\gamma }_{3}=\frac{8}{15}\frac{{L}^{2}}{{S}_{0}}\;\mathrm{a}\mathrm{n}\mathrm{d}\; {S}_{0}=\frac{I}{A}=\frac{1}{4}\left({\left(R+t\right)}^{2}+{R}^{2}\right).\end{aligned} $$

(24)

The dimensionless boundary conditions can be written as

$$S-S: W=\frac{{d}^{2}W}{d{X}^{2}}=\frac{d\Phi }{dX}=0 \mathrm{a}\mathrm{t} X=\mathrm{0,1},$$

(25a)

$$C-C: W=\frac{dW}{dX}=\Phi =0 \mathrm{a}\mathrm{t} X=0, 1.$$

(25b)

Since the definite integral in Eq. (23.a) can be treated as a constant term, Eq. (23) can be rewritten as

$$\frac{{d}^{4}W}{d{X}^{4}}+{\Gamma }^{2}\frac{{d}^{2}W}{d{X}^{2}}{+k}_{L}W+{k}_{NL}{W}^{3}-{\gamma }_{1}\frac{{d}^{3}\Phi }{d{X}^{3}}=0,$$

(26a)

$${\gamma }_{2}\frac{{d}^{2}\Phi }{d{X}^{2}}-{\gamma }_{1}\frac{{d}^{3}W}{d{X}^{3}}-{\gamma }_{3}\Phi =0.$$

(26b)

In which

$${\Gamma }^{2}=P-{k}_{s}-\frac{1}{2}{\gamma }_{0}\underset{0}{\overset{1}{\int }}{\left(\frac{dW}{dX}\right)}^{2}dx.$$

(26c)

The present model can be reduced to EBT by neglecting Eq. (26b) and substituting $\Phi =0$ into Eq. (26a).

3 Differential–integral–quadrature method (DIQM)

Owing to the presence of higher order nonlinearities, obtaining an analytical solution for the governing equations is too complicated. Therefore, numerical method is a suitable method to solve the buckling problem, Eq. (26). The DIQM presented in [31] is an efficient method to solve the nonlinear integro-differential equation.

In this method, the domain is discretized using the Chebyshev–Gauss–Lobatto as follows:

$${X}_{i}=\frac{1}{2}\left(1-\mathrm{cos}\left(\frac{\left(i-1\right)\pi }{N-1}\right)\right), i=\mathrm{1,2},\dots N,$$

(27)

where $N$ is the number of the grid points. On the basis of DQM, the ${r}^{th}$-order derivatives of $f\left(X\right)$ can be approximated as

$${\left.\frac{{d}^{r}f\left(X\right)}{d{X}^{r}}\right|}_{X={X}_{i}}=\sum_{j=1}^{N}{\mathcal{M}}_{ij}^{(r)}f\left({X}_{j}\right), i=\mathrm{1,2},\cdots N,$$

(28)

where ${\mathcal{M}}_{ij}^{(n)}$ is weighting coefficients of $r\mathrm{t}\mathrm{h}$-order derivates. Quan and Chang (1989) introduced the weighting coefficients for the first-order derivative as

$${\mathcal{M}}_{ij}^{(1)}=\left\{\begin{array}{c}\frac{{\mathcal{L}}^{\left(1\right)}\left({X}_{i}\right)}{\left({X}_{i}-{X}_{j}\right){\mathcal{L}}^{\left(1\right)}\left({X}_{j}\right)} i\ne j i,j=\mathrm{1,2},\dots N\\ -\sum_{j=1,i\ne j}^{N}{\mathcal{M}}_{ij}^{(1)} i=j, i=\mathrm{1,2},\dots N\end{array},\right.$$

(29)

in which ${\mathcal{L}}^{\left(1\right)}\left(x\right)$ is defined as

$${\mathcal{L}}^{\left(1\right)}\left(x\right)=\prod_{j=1,j\ne i}^{N}({X}_{i}-{X}_{j}),$$

(30)

Introducing a column vector ${\varvec{f}}=\left[f({X}_{i})\right]={\left[{f}_{1}, {f}_{2},\dots {f}_{N}\right]}^{T}$, in which $f({X}_{i})$ denotes the nodal value of $f\left(X\right)$ at $X={X}_{i}$. Also, its first derivative vector will be ${\varvec{F}}={\left[{F}_{1}, {F}_{2},\dots {F}_{N}\right]}^{T}$. A differential matrix of the first-order derivative based on Eq. (28) can be written in the form

$${\varvec{F}}={D}^{(1)} {\varvec{f}}.$$

(31)

Meanwhile, ${D}^{(1)}=\left[{\mathcal{M}}_{ij}^{\left(1\right)}\right], i,j=\mathrm{1,2},\dots N$. The higher order derivative matrices can be obtained as

$${D}^{(r)}={D}^{(1)}{D}^{(r-1)}, r>1,$$

(32)

Thereafter, an accurate row vector integral operator for definite integral is introduced. If we have a continuous function $f\left(x\right)$ in a domain $0\le X\le 1$ and

$$\frac{df}{dX}=F\left(X\right),$$

(33)

then

$$\underset{{X}_{i}}{\overset{{X}_{j}}{\int }}F\left(X\right)dx=f\left({X}_{j}\right)-f\left({X}_{i}\right)\cong \sum_{k=1}^{N}\left({\left[\mathcal{B}\right]}_{jk}-{\left[\mathcal{B}\right]}_{ik}\right){F}_{k},$$

(34)

where $\mathcal{B}$ is the pseudo-inverse of matrix ${D}^{(1)}$. From Eq. (34), one can deduce that

$$\underset{0}{\overset{1}{\int }}F\left(x\right)dx\cong \sum_{k=1}^{N}\left({\left[\mathcal{B}\right]}_{Nk}-{\left[\mathcal{B}\right]}_{1k}\right){F}_{k}=\mathcal{R}{\varvec{F}}.$$

(35)

Introducing a column vector ${\varvec{W}}$ and ${\varvec{\Phi}}$ as

$${\varvec{W}}={\left[{W}_{1}, {W}_{2},\dots {W}_{N}\right]}^{T},{\varvec{\Phi}}={\left[{\Phi }_{1}, {\Phi }_{2},\dots {\Phi }_{N}\right]}^{T},$$

(36)

where ${W}_{i}=W\left({X}_{i}\right)$ and ${\Phi }_{i}=\Phi \left({X}_{i}\right)$. Upon using the DIQM, the nondimensional governing Eq. (26) can be discretized as follows:

$$\left({D}^{(4)}+{\Gamma }^{2}{D}^{\left(2\right)}+{k}_{L}I\right){\varvec{W}}+{k}_{NL}{{\varvec{W}}}^{\circ 3}-{\gamma }_{1}{D}^{\left(3\right)}{\varvec{\Phi}}=0,$$

(37a)

$$\left({\gamma }_{2}{D}^{\left(2\right)}-{\gamma }_{3}I\right){\varvec{\Phi}}-{\gamma }_{1}{D}^{\left(3\right)}{\varvec{W}}=0,$$

(37b)

$${\Gamma }^{2}-P+{k}_{s}+\frac{1}{2}{\gamma }_{0}\mathcal{R}\left[{\left({D}^{\left(1\right)}{\varvec{W}}\right)}^{\circ 2}\right]=0,$$

(37c)

in which $I$ is $N\times N$ identity matrix and $\circ$ denotes the Hadamard matrix product. The discretized form of boundary conditions is

$$ \begin{aligned}{W}_{1}&={W}_{N}=\sum_{j=1}^{N}{\left[{D}^{\left(2\right)}W\right]}_{1j}=\sum_{j=1}^{N}{\left[{D}^{\left(2\right)}W\right]}_{Nj}\\ &=\sum_{j=1}^{N}{\left[{D}^{\left(1\right)}\Phi \right]}_{1j}=\sum_{j=1}^{N}{\left[{D}^{\left(1\right)}\Phi \right]}_{Nj}=0,\end{aligned} $$

(38a)

$${W}_{1}={W}_{N}=\sum_{j=1}^{N}{\left[{D}^{\left(1\right)}W\right]}_{1j}=\sum_{j=1}^{N}{\left[{D}^{\left(1\right)}W\right]}_{Nj}={\Phi }_{1}={\Phi }_{N}=0.$$

(38b)

For S–S and C–C CNTs, respectively. Equation (37) forms a system of nonlinear algebraic equations which can be written in the form

$${\mathbb{T}}\left(\mathcal{X},{\Gamma }^{2}\right)=0,{\mathbb{T}}:{\mathbb{R}}^{2N+1}\to {\mathbb{R}}^{2N+1},\mathcal{X}={\left[{{\varvec{W}}}^{T},{{\varvec{U}}}^{T}\right]}^{T}.$$

(39)

Therefore, Eq. (39) can be solved by Newton’s method. The Jacobian matrix of this system can be written as

$${\mathbb{J}}=\left[\begin{array}{ccc}{D}^{(4)}+{\Gamma }^{2}{D}^{\left(2\right)}+{k}_{L}I+3{k}_{NL}\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left({{\varvec{W}}}^{\circ 2}\right)& {\gamma }_{1}{D}^{\left(3\right)}& {D}^{\left(2\right)}{\varvec{W}}\\ -{\gamma }_{1}{D}^{\left(3\right)}& \left({\gamma }_{2}{D}^{\left(2\right)}-{\gamma }_{3}I\right)& {\varvec{Z}}\\ {\gamma }_{0}\mathcal{R}\left(\left[\left({D}^{\left(1\right)}{\varvec{W}}\right){{\varvec{O}}}^{T}\right]\circ {D}^{\left(1\right)}\right)& {{\varvec{Z}}}^{T}& 1\end{array}\right],$$

(40)

where ${\varvec{Z}}$ is a column vector defined as ${{\varvec{Z}}}^{T}={\left[0, 0, \dots 0\right]}_{N\times 1}$ and ${\varvec{O}}$ is defined as ${{\varvec{O}}}^{T}={\left[\mathrm{1,1},\dots 1\right]}_{N\times 1}$. It is worth mentioning that, in Eqs. (39, 40), rows corresponding to boundaries are replaced by the corresponding boundary condition equations. Here, the solution of the linearized form of Eq. (39) is considered as the initial values to the Newton’s method.

4 Analytical solutions

For the purpose of comparison, analytical solutions for post-buckling configuration and critical buckling load of S–S CNT are derived. The constants of elastic foundations are set to zeros (i.e., ${k}_{L}={k}_{s}={k}_{NL}=0$). As consequence, Eq. (23) are reduced to

$$\frac{{d}^{4}W}{d{X}^{4}}+\left[P-\frac{1}{2}{\gamma }_{0}\underset{0}{\overset{1}{\int }}{\left(\frac{dW}{dX}\right)}^{2}dx\right]\frac{{d}^{2}W}{d{X}^{2}}-{\gamma }_{1}\frac{{d}^{3}\Phi }{d{X}^{3}}=0,$$

(41a)

$${\gamma }_{2}\frac{{d}^{2}\Phi }{d{X}^{2}}-{\gamma }_{1}\frac{{d}^{3}W}{d{X}^{3}}-{\gamma }_{3}\Phi =0.$$

(41b)

According to Emam [17], the displacement field can be assumed as

$$W\left(X\right)=a\; \mathrm{s}\mathrm{i}\mathrm{n}\left(\pi \frac{X}{L}\right),$$

(42a)

$$\Phi \left(X\right)=b\; \mathrm{c}\mathrm{o}\mathrm{s}\left(\pi \frac{X}{L}\right),$$

(42b)

where $a$ and $b$ are unknowns to be determined. Substituting Eqs. (42.a, b) into Eqs. (41.a, b), the nondimensional maximum amplitude of post-buckling response of the first mode can be computed as

$$a=\pm \frac{2}{\pi \sqrt{{\gamma }_{0}}}\sqrt{P-{\pi }^{2}+\frac{{\pi }^{2}{\gamma }_{1}^{2}}{{\gamma }_{3}+{\pi }^{2}{\gamma }_{2}}.}$$

(43)

Also, the nondimensional first critical buckling load can be obtained as

$${{\varvec{P}}}_{{\varvec{c}}}={\pi }^{2}\left(1-\frac{{\pi }^{2}{\gamma }_{1}^{2}}{{\gamma }_{3}+{\pi }^{2}{\gamma }_{2}}\right).$$

(44)

5 Numerical results

In this section, numerical results for the critical buckling load and the static response of zigzag and armchair SWCNTs with S–S and C–C boundary conditions are considered. The parameters used in the analysis for zigzag and armchair orientations of SWCNTs are the effective thickness is $t=0.258 \mathrm{n}\mathrm{m}$, the forces constants $K/2=46900 \mathrm{k}\mathrm{c}\mathrm{a}\mathrm{l}/\mathrm{m}\mathrm{o}\mathrm{l}/\mathrm{n}\mathrm{m}$², and $C/2=63 \mathrm{k}\mathrm{c}\mathrm{a}\mathrm{l}/\mathrm{m}\mathrm{o}\mathrm{l}/\mathrm{r}\mathrm{a}\mathrm{d}$².

5.1 Validation

To assure the accuracy of the present numerical method, the nondimensional critical buckling load and the post-buckling configuration of S–S zigzag and armchair SWCNTs without any elastic foundations are compared with analytical ones presented in Sect. 4. Table 1 compares the critical buckling loads of S–S zigzag and armchair SWCNTs obtained via DIQM with those obtained analytically, Eq. (44). As noticed, the DIQM and analytical results are in excellent agreement.

Table 1 Nondimensional first critical buckling load $\left({P}_{c}=\frac{\stackrel{-}{P}{L}^{2}}{EI}\right)$ of S–S zigzag and armchair CNT, $({k}_{L}={k}_{s}={k}_{NL}=0)$

In Fig. 2, the post-buckling equilibrium paths of S–S zigzag and armchair SWCNTs based on the present method and analytical one, Eq. (43), are compared. Again, an excellent agreement is achieved.

Fig. 2

Comparison of the post-buckling equilibrium paths of S–S zigzag and armchair CNT based on the DIQM and the analytical one, $({k}_{L}={k}_{s}={k}_{NL}=0)$

5.2 Parametric studies

5.2.1 Effect of beam theories

The dimensionless first three buckling load of zigzag and armchair CNTs with various boundary conditions using different beam theories are reported in Tables 2 and 3, respectively. Here, the effect of surrounding medium is ignored. It is observed that, the critical buckling load predicted by HOSDT is smaller than those predicted by EBT. The difference between HOSDT and EBT is more pronounced for higher buckling modes and short CNTs. Increasing the CNT length, the results obtained by HOSDT converges to EBT.

Table 2 Nondimensional first three critical buckling loads $( {P}_{c}=\frac{\stackrel{-}{P}{L}^{2}}{EI})$ of ($14, 0$) zigzag SWCNT ($R=5.4802 \AA$)

Table 3 Nondimensional first three critical buckling loads $\left( {P}_{c}=\frac{\stackrel{-}{P}{L}^{2}}{EI}\right)$ of ($\mathrm{14,14}$) armchair CNT ($R=9.4920 \AA$)

Plotting in Fig. 3 are post-buckling equilibrium paths of $(14, 0)$ zigzag CNT with S–S and C–C boundary conditions based on the HOSDT and EBT. Herein, the nondimensional post-buckling amplitude is defined as $\stackrel{-}{W}=\frac{WL}{\sqrt{{S}_{0}}}$. It noted that the shear deformation has a great influence on the post-buckling response of CNT.

Fig. 3

Post-buckling equilibrium paths of S–S and C–C $(14, 0)$ zigzag CNT obtained by HOSDT and EBT, $({k}_{L}={k}_{s}={k}_{NL}=0)$

As noted from Tables 2, 3 and Fig. 3, the shear deformation effect can be neglected when the aspect ratio ($L/D$) reaches $50$. Furthermore, it is observed that the shear deformation effect for C–C boundary conditions is more than S–S ones.

5.2.2 Effect of aspect ratio ($L/D$)

To study the effect of aspect ratio, the buckling load of zigzag and armchair CNTs with S–S and C–C boundary conditions are reported in Table 4. Herein, the elastic foundation constants are set to zeros. The $(14, 0)$ zigzag and $(8, 8)$ armchair CNTs are considered so that they have approximately the same diameters that makes it possible to investigate the effect of chirality. As seen form Table 4, that armchair CNT relatively have a little higher values of critical buckling load compared to zigzag CNT especially for lower aspect ratios. In addition, one can note that, the buckling load of CNTs decreases rapidly as the aspect ratio increases. This can be interpreted since increasing aspect ratio decreases the CNT rigidity. The same conclusion can be drawn from Fig. 4 which contains plots of the critical buckling load versus aspect ratio of $(8, 8)$ armchair S–S and C–C CNTs without any elastic foundations.

Table 4 First critical buckling load $(nN)$ of S–S and C–C zigzag and armchair CNTs, $({k}_{L}={k}_{s}={k}_{NL}=0)$

Fig. 4

Critical buckling load versus aspect ratio of $(8, 8)$ armchair S–S and C–C CNTs, $({k}_{L}={k}_{s}={k}_{NL}=0)$

Figure 5 depicts the post-buckling equilibrium path of $(8, 8)$ armchair S–S and C–C CNTs with different values of aspect ratio. It can be seen that increasing aspect ratio causes the CNTs to behave softer and consequently the maximum deflection to increase.

Fig. 5

Post-buckling equilibrium paths of S–S and C–C $(8, 8)$ armchair CNTs with different values of aspect ratio, $({k}_{L}={k}_{s}={k}_{NL}=0)$

5.2.3 Effect of elastic foundation constants

In Table 5, the influence of elastic foundation constants on the critical buckling loads of S–S and C–C CNTs with aspect ratio $L/D=10$ are studied. Different types of CNTs are considered. Table 5 reveals that the critical buckling load increases by increasing shear and linear elastic foundation parameters. However, the nonlinear elastic foundation parameter has no effect on the critical buckling load. It can easily be seen from Eq. (37.a) and the Jacobian matrix Eq. (40), that the nonlinear elastic foundation parameter ${k}_{NL}$ is multiplied by the static response ${\varvec{W}}.$ In fact, the static response of CNTs in prebuckling state is zero, as shown in Fig. 3. And hence, the nonlinear elastic foundation parameter has no effect on the buckling load of CNTs. Also, it can be noted that the influence of the shear and linear elastic foundation parameters on critical buckling load become more considerable as the chiral number of CNTs increases. Furthermore, it can be observed that the chiral number has a significant effect on the critical buckling load of CNTs. These observations are valid for both zigzag and armchair CNTs.

Table 5 First critical buckling load (nN) of different types of CNT with S–S and C–C boundary conditions ($L/D=10$)

Figure 6 illustrates post-buckling equilibrium paths of S–S and C–C $(7, 7)$ armchair CNTs with various values of elastic foundation constants and aspect ratio $L/D=10$. It can be easily deduced that the responses have a descending trend with respect to the shear foundation constant. The shear stiffness of elastic foundation is more significant than that of the linear and nonlinear elastic foundation constants.

Fig. 6

Post-buckling equilibrium paths of S–S and C–C $(7, 7)$ armchair CNTs with aspect ratio $L/D=10$

6 Conclusions

In the framework of higher order beam theory, buckling and post-buckling behaviors of zigzag and armchair CNTs resting on nonlinear elastic medium were numerically investigated. S–S and C–C boundary conditions are considered. The nonlinear integro-differential equations were solved by DIQM method in combination with Newton method. Also, they are solved analytically for the case of S–S boundary conditions. Results obtained via DIQM method were compared with those obtained by analytical solutions and an excellent agreement was obtained. The most findings of the current analysis are

• The critical buckling load predicted by HOSDT is smaller than those predicted by EBT.

• The difference between HOSDT and EBT is more pronounced for higher buckling modes and short CNTs.

• The armchair CNT relatively have a little higher values of critical buckling load compared to zigzag CNT especially for lower aspect ratios.

• The buckling load of CNTs decreases rapidly as the aspect ratio increases. This can be interpreted since increasing aspect ratio decreases the CNT rigidity.

• The critical buckling load increases by increasing shear and linear elastic foundation parameters. However, the nonlinear elastic foundation parameter has no effect on the critical buckling load.