1 Introduction

After discovering carbon nanotubes (CNTs) [1], many investigations have concentrated on the proper and accurate analysis of single-walled carbon nanotubes (SWCNTs) and their industrial applications. A considerable amount of research is focused on different engineering properties of SWCNTs, due to their superior thermal and electrical conductivity, and mechanical strength. Based on these remarkable properties, SWCNTs may be used for different applications such as nano-probes, nano-composites, nano-sensors, and nano-vessels for in vitro and in vivo implementations [2].

For nano-scale structures, the lengths are in the order of inter-atomic distances, so the nonlocal and small-length scale effects can be significant. There have been many experimental and theoretical studies of SWCNT based on atomistic and molecular simulations and also classical continuum mechanics. However, laboratory and computer experiments are expensive and time-consuming processes. Additionally, classical continuum theories are found to be inadequate because of their scale-free constitutive equations and also atomistic simulations like molecular dynamics (MD) are limited for very small structures with lower number of atoms. Therefore, length-dependent continuum theories have received more attention in modeling of nano-scale structures and devices. Among these, theory of nonlocal continuum mechanics presented by Eringen [3,4,5,6] and Eringen and Edelen [7] has been widely used in nano-mechanics to account for the small-length scale effects such as the internal length-scale and inter-atomic forces. In fact, nonlocal continuum mechanics has been implemented in different areas such as lattice dispersion of phonon waves, fracture mechanics, dislocation mechanics, and surface tension in fluids [5].

For this end, Peddieson et al. [8] for the first time developed a nonlocal Euler–Bernoulli beam model to study the nonlocal effects on the static behavior of micro- and nano-beams. Then, many researchers investigated small-length scale effects on buckling analysis of nano-beams using nonlocal theory [2, 9,10,11,12,13]. Also, Sudak [14] and Zhang et al. [15] investigated the small-length scale effects on buckling of multi-walled carbon nanotubes (MWCNT). In addition, the modified Euler–Bernoulli beam model, based on nonlocal continuum theory and strain gradient approach, was developed to account for small-length scale effects in buckling analysis of SWCNTs [16]. Moreover, Wang et al. [17] investigated the buckling of Timoshenko gradient elasticity beam model and also Ma et al. [18] presented a microstructure-dependent Timoshenko beam model based on a modified couple stress theory. Recently, some researchers investigated the free vibration and wave propagation of SWCNTs using nonlocal beam theories [19,20,21,22].

In fact, the governing differential equation of nano-beams modeled by nonlocal Timoshenko beam theory is sixth-order and consequently requires six dependent boundary conditions including four classic (local) and two non-classic (nonlocal) boundary conditions. However, the absence of non-classic boundary conditions leads to approximate critical buckling strains. Researchers usually solve this equation without considering nonlocal boundary conditions by neglecting the highest-order term in the differential governing equation, because the nonlocal boundary conditions are not derived from a variationally consistent formulation [12]. The aim of this paper is to introduce a novel and more definitive method to derive nonlocal higher-order boundary conditions based on the nonlocal Timoshenko beam theory, strain gradient elasticity and variational method, simultaneously. In previous studies, the necessity of the variational approach based on the nonlocal theories was emphasized for deriving the boundary conditions by different researchers [8, 23]. However, a combination of these two methods gives only four boundary conditions and is not adequate for nonlocal buckling and vibration analysis of CNTs which require six boundary conditions. In the authors’ opinion, the best way for overcoming this problem is to combine the strain gradient elasticity with nonlocal equations and then using the minimum total potential energy principle and the variational method to extract the higher-order terms.

The remainder of this paper is organized as follows: in Sect. 2, the nonlocal elasticity and its constitutive relations are discussed and then the equations for nonlocal Timoshenko beam theory are derived. In Sect. 3, the governing equations and boundary conditions for buckling of a nonlocal Timoshenko beams are derived using variational method. In Sect. 4, the nonlocal boundary conditions and critical buckling strains are presented for different beam types such as simply supported, clamped, cantilever, and propped cantilever beams. In Sect. 5, the numerical results for the axial buckling of SWCNTs are derived and the proposed beam model based on nonlocal boundary conditions is validated through comparison with results from MD simulations, and consistent value for the Eringen’s nonlocal constant of SWCNTs is calibrated. Finally, in Sect. 6, the conclusions are summarized.

2 Nonlocal elasticity and constitutive relations

According to Eringen [3], for homogeneous and isotropic linearly elastic solids, the linear nonlocal theory is expressed by the following constitutive relations:

$$t_{kl} (x) = \int\limits_{V} {\alpha (\,\left| {x - x^{\prime}} \right|\,,\tau )\,\sigma_{kl} (x^{\prime})} \,{\text{d}}v(x^{\prime})\,,$$
(1)
$$\sigma_{kl} (x^{\prime}) = \lambda e_{rr} (x^{\prime})\delta_{kl} + 2\mu e_{kl} (x^{\prime}),$$
(2)

where \(t_{kl}\) is the nonlocal stress tensor at the field point \(x\) in the body. \(\sigma_{kl} (x^{\prime})\) is the macroscopic (classical) stress tensor at \(x^{\prime}\) which is related to the linear strain tensor \(e_{kl} (x^{\prime})\) in domain V at any point \(x^{\prime}\) with Lamé constants, \(\lambda\) and \(\mu\). In addition, \(\alpha \,(\,\left| {x^{\prime} - x} \right|\,,\tau )\) is defined as a nonlocal kernel, depending on the characteristic length ratio \(\frac{a}{l}\), where \(a\) is an internal characteristic length (e.g., a lattice parameter, granular distance) and \(l\) is an external characteristic length (e.g., a wave length, crack length). Thus, nonlocal parameter is defined as below:

$$\tau = \frac{{e_{0} \,a}}{l},$$
(3)

where the Eringen’s nonlocal constant, \(e_{0}\), is a nondimensional material property determined by experiments. Combining the constitutive Eq. (1) with Hooke’s law, the nonlocal constitutive relation for a Hookean solid is derived, but this integro-partial differential equation is mathematically intractable. Thus, the constitutive equation is converted into a partial differential equation by some simplifications as follows:

$$(\,1 - \tau^{2} l^{2} \nabla^{2} )\,\sigma_{ij} \, = C_{ijkl} \varepsilon_{kl} .$$
(4)

In this paper, we are adopting this notation for engineering customary: \(\sigma_{ij}\) denotes the nonlocal stress tensor field.

2.1 Nonlocal beam theory

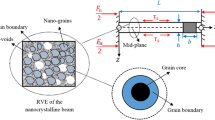
The following coordinate system is set up for establishing boundary value problem of nonlocal Timoshenko beam theory. The x-coordinate is taken along the length of the beam and the z-coordinate along the thickness. We consider instability-induced bending in the xz-plane (See Fig. 1).

Fig. 1
figure 1

Beam configuration and coordinate system

Full size image

According to Timoshenko beam configuration in Fig. 1, the assumed displacement field is

$$u_{1} (x,y,z,t) = u(x,t) + z\phi (x,t)\,,\quad u_{2} (x,y,z,t) = 0\,,\quad u_{3} (x,y,z,t) = w(x,t)\,,$$
(5)

where \(\phi\) denotes the rotation of beam cross section as indicated in Fig. 1. The remaining non-zero axial and transverse shear strains are given by Eqs. (6a), (6b) as follows:

$$\varepsilon_{xx} = \frac{\partial u}{\partial x} + z\frac{\partial \phi }{\partial x},$$
(6a)
$$2\varepsilon_{xz} \equiv \gamma = \phi + \frac{\partial w}{\partial x}\,.$$
(6b)

Using Eq. (4), the non-zero nonlocal stress tensor components of Timoshenko beam theory are assumed as

$$\sigma_{xx} - (e_{0} a)^{2} \frac{{\partial^{2} \sigma_{xx} }}{{\partial x^{2} }} = E\varepsilon_{xx} \,,$$
(7a)
$$\,\sigma_{xz} - (e_{0} a)^{2} \frac{{\partial^{2} \sigma_{xz} }}{{\partial x^{2} }} = 2K_{\text{S}} G\varepsilon_{xz} = K_{\text{S}} G\gamma \,.$$
(7b)

where \(K_{\text{S}}\) is the shear correction factor to account for constant shear strain over the cross section of the beam in Timoshenko beam model. The nonlocal axial and shear force and bending moment are derived from the above equations, respectively, as

$$N_{\text{NL}} - (e_{0} a)^{2} \frac{{\partial^{2} N_{\text{NL}} }}{{\partial x^{2} }} = EA\frac{\partial u}{\partial x}\,,$$
(8)
$$Q_{\text{NL}} - (e_{0} a)^{2} \frac{{\partial^{2} Q_{\text{NL}} }}{{\partial x^{2} }} = K_{\text{S}} GA\gamma \,,$$
(9)
$$M_{\text{NL}} - (e_{0} a)^{2} \frac{{\partial^{2} M_{\text{NL}} }}{{\partial x^{2} }} = EI\frac{\partial \phi }{\partial x}\,,\,\,$$
(10)

where E, G, A, and I are the Young’s modulus, shear modulus, cross-sectional area of beam and area moment of inertia of beam cross section, respectively.

3 Governing equations

The axial and shear stresses in Eqs. (7a), (7b) can be solved to determine nonlocal stress state as a function of strain field. Assuming \((e_{0} a)^{2} < < 1\), and neglecting the higher powers of \((e_{0} a)^{2}\), the solution could be simplified to

$$\sigma (x,z) = E\,\left[ {\varepsilon (x,z) + (e_{0} a)^{2} \frac{{\partial^{2} \varepsilon (x,z)}}{{\partial x^{2} }}} \right]\,,$$
(11)
$$\tau (x) = K_{\text{S}} G\,\left[ {\gamma (x) + (e_{0} a)^{2} \frac{{{\text{d}}^{2} \gamma (x)}}{{{\text{d}}x^{2} }}} \right]\,.$$
(12)

Hence, we obtain the stress resultants from Eqs. (11) and (12) based on the strain gradient theory as follows:

$$N_{\text{NL}}^{\text{SG}} = N_{\text{CL}} + (e_{0} a)^{2} \frac{{\partial^{2} N_{\text{CL}} }}{{\partial x^{2} }}\,,$$
(13)
$$Q_{\text{NL}}^{\text{SG}} = Q_{\text{CL}} + (e_{0} a)^{2} \frac{{\partial^{2} Q_{\text{CL}} }}{{\partial x^{2} }}\,,$$
(14)
$$M_{\text{NL}}^{\text{SG}} = M_{\text{CL}} + (e_{0} a)^{2} \frac{{\partial^{2} M_{\text{CL}} }}{{\partial x^{2} }},$$
(15)

where the classical (local) form of axial force, shear and bending moment acting on the beam cross section are

$$N_{\text{CL}} = EA\frac{\partial u}{\partial x}\,,$$
(16)
$$Q_{\text{CL}} = K_{\text{S}} GA\gamma ,$$
(17)
$$M_{\text{CL}} = EI\frac{\partial \phi }{\partial x}.$$
(18)

Considering  static conditions, for a Timoshenko beam subjected to an external compressive and conservative force field, \(N_{0}\), and laterally distributed load, \(p(x)\), the total potential energy, \(\varPi\), which is given by Kumar et al. [16] is generalized in the presence of shear effect as follows:

$$\begin{aligned} \varPi & = \int\limits_{V} {\left[ {\frac{{E\varepsilon^{2} (x,z)}}{2} - (e_{0} a)^{2} \frac{E}{2}\left( {\frac{\partial \varepsilon (x,z)}{\partial x}} \right)^{2} } \right]} {\text{d}}v + \int\limits_{V} {\left[ {\frac{{K_{\text{S}} G\gamma^{2} (x)}}{2} - (e_{0} a)^{2} \frac{{K_{\text{S}} G}}{2}\left( {\frac{{{\text{d}}\gamma (x)}}{{{\text{d}}x}}} \right)^{2} } \right]{\text{d}}v} \\ & \quad \, + \int\limits_{0}^{L} {\left( {N_{0} \frac{{{\text{d}}u}}{{{\text{d}}x}}} \right)\,{\text{d}}x} - \int\limits_{0}^{L} {p\,w(x)} \,{\text{d}}x - \frac{1}{2}\int\limits_{0}^{L} {N_{0} \left( {\frac{{{\text{d}}w}}{{{\text{d}}x}}} \right)^{2} {\text{d}}x} \,. \\ \end{aligned}$$
(19)

Substituting Eqs. (6a), (6b) into Eq. (19) and integrating over the beam cross-sectional area, the following expression is obtained for \(\varPi\):

$$\begin{aligned} \varPi & = \frac{1}{2}\int\limits_{0}^{L} {\left[ {EA\left( {\frac{{{\text{d}}u}}{{{\text{d}}x}}} \right)^{2} + EI\left( {\frac{{{\text{d}}\phi }}{{{\text{d}}x}}} \right)^{2} + K_{\text{S}} GA\left( {\frac{{{\text{d}}w}}{{{\text{d}}x}} + \phi } \right)^{2} } \right]\,} {\text{d}}x \\ & \quad \, - \frac{1}{2}(e_{0} a)^{2} \int\limits_{0}^{L} {\left[ {EA\left( {\frac{{{\text{d}}^{2} u}}{{{\text{d}}x^{2} }}} \right)^{2} + EI\left( {\frac{{{\text{d}}^{2} \phi }}{{{\text{d}}x^{2} }}} \right)^{2} + K_{\text{S}} GA\left( {\frac{{{\text{d}}^{2} w}}{{{\text{d}}x^{2} }} + \frac{{{\text{d}}\phi }}{{{\text{d}}x}}} \right)^{2} } \right]\,{\text{d}}x} \\ & \quad + \int\limits_{0}^{L} {\left( {N_{0} \frac{{{\text{d}}u}}{{{\text{d}}x}}} \right)\,{\text{d}}x} - \int\limits_{0}^{L} {p\,w(x)} \,{\text{d}}x - \frac{1}{2}\int\limits_{0}^{L} {N_{0} \left( {\frac{{{\text{d}}w}}{{{\text{d}}x}}} \right)^{2} {\text{d}}x} \,. \\ \end{aligned}$$
(20)

Using the definition for \(N_{\text{CL}}\) and ignoring the laterally distributed loads, \(p(x)\), for a buckling analysis, we apply the variational operator, with respect to \(u(x)\), to the functional \(\varPi\). Inserting the equilibrium condition of \(\delta \varPi = 0\) results to

$$\delta_{u} (\varPi ) = \int\limits_{0}^{L} {\left[ {N_{\text{CL}} \left( {\delta \frac{{{\text{d}}u}}{{{\text{d}}x}}} \right) - (e_{0} a)^{2} \frac{{{\text{d}}N_{\text{CL}} }}{{{\text{d}}x}}\left( {\delta \frac{{{\text{d}}^{2} u}}{{{\text{d}}x^{2} }}} \right) + N_{0} \,\left( {\delta \frac{{{\text{d}}u}}{{{\text{d}}x}}} \right)} \right]\,} {\text{d}}x = 0\,.$$
(21)

Integrating by parts and using Eq. (16), we obtain the governing equation and boundary conditions for \(u(x)\) as

$$\frac{\text{d}}{{{\text{d}}x}}(N_{\text{NL}} + N_{0} ) = 0,$$
(22)
$$\left. {(N_{\text{NL}} + N_{0} )\,\delta u} \right|_{x = 0}^{x = L} \, = 0,$$
(23a)
$$- (e_{0} a)^{2} \left. {\left( {\frac{{{\text{d}}N_{\text{CL}} }}{{{\text{d}}x}}} \right)\delta \frac{{{\text{d}}u}}{{{\text{d}}x}}} \right|_{x = 0}^{x = L} = 0.$$
(23b)

Operating the variation with respect to \(w(x)\) on \(\varPi\) in Eq. (20) and equating \(\delta \varPi\) to zero, it gives

$$\begin{aligned} \delta_{w} (\varPi ) & = \int\limits_{0}^{L} {\left[ {K_{\text{S}} GA\left( {\frac{{{\text{d}}w}}{{{\text{d}}x}} + \phi } \right)\delta \frac{{{\text{d}}w}}{{{\text{d}}x}} - (e_{0} a)^{2} K_{\text{S}} GA\left( {\frac{{{\text{d}}^{2} w}}{{{\text{d}}x^{2} }} + \frac{{{\text{d}}\phi }}{{{\text{d}}x}}} \right)\delta \frac{{{\text{d}}^{2} w}}{{{\text{d}}x^{2} }}} \right]\,{\text{d}}x} \\ \, & \quad - \int\limits_{0}^{L} {\left[ {\left( {N_{0} \frac{{{\text{d}}w}}{{{\text{d}}x}}} \right)\delta \frac{{{\text{d}}w}}{{{\text{d}}x}}} \right]\,{\text{d}}x = 0} \,. \\ \end{aligned}$$
(24)

Integrating by parts, we obtain the governing equation for \(w(x)\) as

$$\frac{\text{d}}{{{\text{d}}x}}\left( {Q_{\text{NL}} - N_{0} \frac{{{\text{d}}w}}{{{\text{d}}x}}} \right) = 0,$$
(25)

and the following boundary conditions are derived:

$$\left. {\left( {Q_{\text{NL}} - N_{0} \frac{{{\text{d}}w}}{{{\text{d}}x}}} \right)\delta w} \right|_{x = 0}^{x = L} = 0,$$
(26a)
$$(e_{0} a)^{2} \left. {\left( {\frac{{{\text{d}}Q_{\text{CL}} }}{{{\text{d}}x}}} \right)\delta \frac{{{\text{d}}w}}{{{\text{d}}x}}} \right|_{x = 0}^{x = L} = 0.$$
(26b)

In the same way, applying the variational operator to \(\phi (x)\) for \(\varPi\) in Eq. (20) and equating the result to zero, we obtain

$$\begin{aligned} \delta_{\phi } & = \int\limits_{0}^{L} {\left[ {\left( {EI\frac{{{\text{d}}\phi }}{{{\text{d}}x}}} \right)\delta \frac{{{\text{d}}\phi }}{{{\text{d}}x}} - \left( {(e_{0} a)^{2} EI\frac{{{\text{d}}^{2} \phi }}{{{\text{d}}x^{2} }}} \right)\delta \frac{{{\text{d}}^{2} \phi }}{{{\text{d}}x^{2} }} + K_{\text{S}} GA\left( {\frac{{{\text{d}}w}}{{{\text{d}}x}} + \phi } \right)\delta \phi } \right]\,} {\text{d}}x \\ & \quad \, - \int\limits_{0}^{L} {\left[ {(e_{0} a)^{2} K_{\text{S}} GA\left( {\frac{{{\text{d}}^{2} w}}{{{\text{d}}x^{2} }} + \frac{{{\text{d}}\phi }}{{{\text{d}}x}}} \right)\delta \frac{{{\text{d}}\phi }}{{{\text{d}}x}}} \right]{\text{d}}x = 0} \,. \\ \end{aligned}$$
(27)

Using integration by parts, the governing equation for \(\phi (x)\) is given by

$$\frac{{{\text{d}}M_{\text{NL}} }}{{{\text{d}}x}} = Q_{\text{NL}} ,$$
(28)

and the following boundary conditions are derived

$$\left. {\left[ {M_{\text{NL}} - (e_{0} a)^{2} \frac{{{\text{d}}Q_{\text{CL}} }}{{{\text{d}}x}}} \right]\delta \phi } \right|_{x = 0}^{x = L} = 0,$$
(29a)
$$(e_{0} a)^{2} \left. {\left( {\frac{{{\text{d}}M_{\text{CL}} }}{{{\text{d}}x}}} \right)\delta \frac{{{\text{d}}\phi }}{{{\text{d}}x}}} \right|_{x = 0}^{x = L} = 0.$$
(29b)

Substituting the nonlocal shear force and bending moment defined in Eqs. (9) and (10) into the governing Eqs. (25) and (28) and eliminating \(\phi\) from these two equations, the transverse equilibrium equation in terms of lateral displacement for an axially loaded beam using a nonlocal strain gradient theory is obtained as

$$(e_{0} a)^{2} \left( {\frac{EI\,}{{K_{\text{S}} GA}}} \right)\frac{{{\text{d}}^{6} w}}{{{\text{d}}x^{6} }} + \left[ {\frac{EI}{{N_{0} }} - \frac{EI}{{K_{\text{S}} GA}} - (e_{0} a)^{2} } \right]\frac{{{\text{d}}^{4} w}}{{{\text{d}}x^{4} }} + \frac{{{\text{d}}^{2} w}}{{{\text{d}}x^{2} }} = 0,$$
(30)

where \(N_{0}\) is an external axial compressive load. This equation is similar to that obtained by Reddy and Pang [12] for buckling of the nonlocal Timoshenko beam using the Hamilton’s principle.

In this case, neglecting the nonlocal parameter may result the classic Timoshenko beam model and neglecting the nonlocal parameter and shear deformation gives the buckling equation for Euler–Bernoulli beam model.

In addition, for solving the above equation, six boundary conditions are required (three for each end) but four boundary conditions appear in Eqs. (26a), (26b) and (29a), (29b). It means that there is one additional boundary condition for each end. So, the main objective is to select three independent boundary conditions which can satisfy all boundary conditions for each end. In the next part, the boundary conditions for various beam supports are obtained.

The dimensionless form of Eq. (30) using the length of the beam, \(L\), as a nondimensionalizing parameter can be rewritten as

$$(\,\bar{\mu }\,\bar{\varOmega })\frac{{{\text{d}}^{6} \bar{w}}}{{{\text{d}}\bar{x}^{6} }} + \left( {\frac{1}{{\pi^{2} r}} - \bar{\varOmega } - \bar{\mu }} \right)\frac{{{\text{d}}^{4} \bar{w}}}{{{\text{d}}\bar{x}^{4} }} + \frac{{{\text{d}}^{2} \bar{w}}}{{{\text{d}}\bar{x}^{2} }} = 0,$$
(31)

where \(\bar{w}\), \(\bar{x}\),\(r\), \(\bar{\varOmega }\) and \(\bar{\mu }\) are the nondimensional forms of the deflection, displacement, ratio of the critical buckling loads, shear deformation, and nonlocal parameter, respectively, as follows:

$$\bar{w} = \frac{w}{L},\quad \bar{x} = \frac{x}{L},\quad \,r = \frac{{N_{\text{cr}}^{\text{NL}} }}{{N_{\text{cr}}^{\text{CL}} }}\,,\quad \bar{\varOmega } = \frac{EI}{{K_{\text{S}} GA\,L^{2} }}\,,\quad \bar{\mu } = \tau^{2} = \left( {\frac{{e_{0} a}}{L}} \right)^{2} ,$$
(32)

where \(N_{\text{cr}}^{\text{NL}}\) is obtained by solving Eq. (30) and \(N_{\text{cr}}^{\text{CL}}\) is the buckling load given by classic Euler columns for simply supported end conditions.

We may simply switch to nonlocal Euler–Bernoulli beam model by ignoring the shear deformation terms. Also, the local Timoshenko beam model is obtained by letting the nonlocal parameter to be zero and by setting both the shear deformation and nonlocal parameters to zero, the local Euler–Bernoulli beam model appears.

Also, using the strain gradient form of the nonlocal shear force and bending moment (i.e., the weak form of the nonlocal theory) defined in Eqs. (14) and (15) into the governing Eqs. (25) and (28) and eliminating \(\phi\) from these two equations, the differential equation of buckling in terms of \(w(x)\) for an axially loaded Timoshenko beam is obtained as

$$(e_{0} a)^{2} EI\frac{{{\text{d}}^{6} w}}{{{\text{d}}x^{6} }} + \left( {EI - \frac{EI}{{K_{\text{S}} GA}}N_{0} } \right)\frac{{{\text{d}}^{4} w}}{{{\text{d}}x^{4} }} + N_{0} \frac{{{\text{d}}^{2} w}}{{{\text{d}}x^{2} }} = 0.$$
(33)

The above equation may result the nonlocal Euler–Bernoulli beam model by neglecting the shear deformation term as derived in the literatures [8, 16]. However, using the strain gradient form of the nonlocal shear force and bending moment leads to miss a few terms in Eq. (33) in comparison to its exact form in Eq. (30). It is because of neglecting the higher-order terms of \((e_{0} a)^{2}\) in strain gradient theory and that is why the present study can capture the size effects more exact as compared with other literatures.

4 Nonlocal boundary conditions

We obtain four sets of boundary conditions for each end in Eqs. (26a), (26b) and (29a), (29b). However, one set is redundant for the sixth-order differential equation of buckling in the case of nonlocal Timoshenko beam model. Thus, the main point is to specify six boundary conditions which can satisfy all the boundary conditions in Eqs. (26a), (26b) and (29a), (29b). On the other hand, we have both the essential and natural boundary conditions for each set. Therefore, it is very important to choose essential and natural boundary conditions with respect to the type of the beam supports. In the sequel, we study boundary conditions for various nano-beams with different end conditions by means of the mathematically and variationally consistent formulations.

4.1 Simply supported nano-beams

Considering the classic continuum mechanics for simply supported boundary conditions, the deflection and bending moment are zero at each end (\(x = 0,L\)).

$$w = 0,\quad M_{\text{CL}} = 0\,.$$
(34)

It should be noticed that the essential boundary conditions are the same for the local and nonlocal boundary conditions. However, the natural boundary conditions should be transformed to the nonlocal form, in order to be used in higher-order theories. Hence, the first boundary condition for deflection in Eq. (34), which is an essential boundary condition, is unchanged for this case. By substituting this condition in Eq. (26a), the first set of boundary conditions will be satisfied at each end. Furthermore, for hinged supports, the slope of the beam axis at each end should be non-zero and as we have homogeneous boundary conditions, thus we obtain \(\delta \frac{{{\text{d}}w}}{{{\text{d}}x}} \ne 0\). Therefore, in order to satisfy the second set of boundary conditions in Eq. (26b), we should have

$$(e_{0} a)^{2} \left. {\left( {\frac{{{\text{d}}Q_{\text{CL}} }}{{{\text{d}}x}}} \right)} \right|_{x = 0}^{x = L} = 0.$$
(35)

The above end condition is called a nonlocal boundary condition, because it is length dependent. Inserting this boundary condition in Eq. (29a), and considering that the rotation of transverse normal at two ends should be non-zero for a simply supported beam, (i.e., \(\delta \phi \ne 0\)), so we obtain \(M_{\text{NL}} = 0\) in order to satisfy this boundary condition which was predictable from the previous points about the nonlocal form of the natural boundary conditions like bending moment in Eq. (34).

In order to satisfy the last set of boundary conditions in Eq. (29b), we should set either \(\delta \frac{{{\text{d}}\phi }}{{{\text{d}}x}}\) or \((e_{0} a)^{2} EI\frac{{{\text{d}}^{2} \phi }}{{{\text{d}}x^{2} }}\) to be zero. In this regard, another point is that when the nonlocal bending moment is zero, the classic bending moment should be zero as a special case. In fact, for each value of the nonlocal term, the nonlocal bending moment is zero. Thus, by neglecting the nonlocal term, the nonlocal bending moment for the Timoshenko beam model is transformed to the classic value as follows:

$$M_{\text{CL}} = EI\frac{{{\text{d}}\phi }}{{{\text{d}}x}}.$$
(36)

According to the above equation and in order to have zero bending moment at each end, we obtain \(\frac{{{\text{d}}\phi }}{{{\text{d}}x}} = 0\), which leads to the following equation for the homogeneous boundary conditions:

$$\delta \frac{{{\text{d}}\phi }}{{{\text{d}}x}} = 0.$$
(37)

Substituting the above result in the last set of boundary conditions, Eq. (29b) will be satisfied. We can simplify Eq. (35), using Eq. (37), as follows:

$$\frac{{{\text{d}}^{2} w}}{{{\text{d}}x^{2} }} = 0.$$
(38)

As a result, the generalized boundary conditions for simply supported beams at \(x = 0,L\) are given as

$$w = 0,$$
(39a)
$$\frac{{{\text{d}}^{2} w}}{{{\text{d}}x^{2} }} = 0,$$
(39b)
$$\frac{{{\text{d}}\phi }}{{{\text{d}}x}} = 0.$$
(39c)

However, we should have the boundary conditions in terms of the dependent variable of boundary value problem, i.e., displacement \(w(x)\) in order to solve the buckling differential equation. Using the governing equations, we find

$$\frac{{{\text{d}}\phi }}{{{\text{d}}x}} = \left( {\frac{{N_{0} }}{{K_{\text{S}} GA}} - 1} \right)\frac{{{\text{d}}^{2} w}}{{{\text{d}}x^{2} }} - (e_{0} a)^{2} \left( {\frac{{N_{0} }}{{K_{\text{S}} GA}}} \right)\frac{{{\text{d}}^{4} w}}{{{\text{d}}x^{4} }} = 0.$$
(40)

By substituting Eq. (39b) in the above equation, one obtains

$$\frac{{{\text{d}}\phi }}{{{\text{d}}x}} = - (e_{0} a)^{2} \left( {\frac{{N_{0} }}{{K_{\text{S}} GA}}} \right)\frac{{{\text{d}}^{4} w}}{{{\text{d}}x^{4} }} = 0.$$
(41)

Finally, the generalized boundary conditions in terms of only \(w(x)\) for simply supported beams at \(x = 0,L\) are given by

$$w = 0\,,\quad \frac{{{\text{d}}^{2} w}}{{{\text{d}}x^{2} }} = 0\,,\quad (e_{0} a)^{2} \left( {\frac{{N_{0} }}{{K_{\text{S}} GA}}} \right)\frac{{{\text{d}}^{4} w}}{{{\text{d}}x^{4} }} = 0.$$
(42)

These homogeneous boundary conditions are similar to those obtained in the literature for Euler–Bernoulli beam models using higher-order theories [23]. Based on MNTBT and applying these boundary conditions into Eq. (30), the closed-form critical buckling strains for simply supported nano-beams becomes

$$\varepsilon_{\text{cr}} = \frac{{\pi^{2} I}}{{AL^{2} }}\left[ {\frac{1}{{1 + \pi^{2} (\,\bar{\mu } + \,\bar{\varOmega }\,) + \pi^{4} (\bar{\mu } \times \,\bar{\varOmega }\,)}}} \right]\,.$$
(43)

4.2 Clamped nano-beams

The classic boundary conditions for clamped beams are defined for the deflection and the rotation of transverse normal at the boundaries (\(x = 0,L\)) as follows:

$$w = \phi = 0\,.$$
(44)

The above boundary conditions satisfy two sets of end conditions in Eqs. (26a) and (29a), respectively. In addition, we know that the slope of the beam axis should be zero at the fixed point, (i.e., \(\delta \frac{{{\text{d}}w}}{{{\text{d}}x}} = 0\)), and thus the second set of boundary conditions in Eq. (26b) will be satisfied.

Unlike the simply supported beams, the bending moment should be non-zero at each end. So, the local bending moment in Eq. (36) has to be non-zero. It means that

$$\frac{{{\text{d}}\phi }}{{{\text{d}}x}} \ne 0\,.$$
(45)

Using the above inequality constraint in the last set of boundary conditions in Eq. (29b) and in order to satisfy this homogeneous boundary condition, we have the nonlocal boundary condition as

$$\left. {(e_{0} a)^{2} EI\frac{{{\text{d}}^{2} \phi }}{{{\text{d}}x^{2} }}} \right|_{x = 0}^{x = L} = 0.$$
(46)

Therefore, the general boundary conditions are

$$w = 0\,,$$
(47a)
$$\frac{{{\text{d}}w}}{{{\text{d}}x}} = 0,$$
(47b)
$$(e_{0} a)^{2} EI\frac{{{\text{d}}^{2} \phi }}{{{\text{d}}x^{2} }} = 0.$$
(47c)

Again, in order to have boundary conditions in terms of \(w(x)\), we eliminate \(\phi\) by differentiating Eq. (40) and inserting in Eq. (47c) as follows:

$$\frac{{{\text{d}}^{2} \phi }}{{{\text{d}}x^{2} }} = \left( {\frac{{N_{0} }}{{K_{\text{S}} GA}} - 1} \right)\frac{{{\text{d}}^{3} w}}{{{\text{d}}x^{3} }} - (e_{0} a)^{2} \left( {\frac{{N_{0} }}{{K_{\text{S}} GA}}} \right)\frac{{{\text{d}}^{5} w}}{{{\text{d}}x^{5} }} = 0.$$
(48)

The above equation is called the nonlocal boundary condition because the nonlocal term, \((e_{0} a)^{2}\), appears in it and for clamped beams, the boundary conditions in terms of \(w(x)\) at \(x = 0,L\) are given by

$$w = 0\,,\quad \frac{{{\text{d}}w}}{{{\text{d}}x}} = 0\,,\quad \left( {\frac{{N_{0} }}{{K_{\text{S}} GA}} - 1} \right)\frac{{{\text{d}}^{3} w}}{{{\text{d}}x^{3} }} - (e_{0} a)^{2} \left( {\frac{{N_{0} }}{{K_{\text{S}} GA}}} \right)\frac{{{\text{d}}^{5} w}}{{{\text{d}}x^{5} }} = 0.$$
(49)

It is worth noting that unlike the simply supported boundary conditions, the odd derivatives of \(w(x)\) are appeared in clamped boundary conditions. This result is similar to that obtained by Lim and Wang [23] for Euler–Bernoulli models using higher-order theories.

Solving Eq. (30) using nonlocal boundary conditions derived in Eq. (49), we obtain closed-form critical buckling strains for doubly clamped nano-beams based on MNTBT as follows:

$$\varepsilon_{\text{cr}} = \frac{{4\pi^{2} I}}{{AL^{2} }}\left[ {\frac{1}{{1 + 4\pi^{2} (\,\bar{\mu } + \,\bar{\varOmega }\,) + 16\pi^{4} (\,\bar{\mu } \times \,\bar{\varOmega }\,)}}} \right]\,.$$
(50)

4.3 Cantilever nano-beams

The boundary conditions for the fixed end of a cantilever beams are exactly the same as the clamped boundary conditions derived in Eq. (49). Moreover, we have the classic natural boundary conditions for shear force and bending moment at the free end of a cantilever at \(x = L\) as follows:

$$Q_{\text{CL}} - N_{0} \frac{{{\text{d}}w}}{{{\text{d}}x}} = 0\,,\quad M_{\text{CL}} = 0\,.$$
(51)

As mentioned before, we have to transform these classic natural boundary conditions to nonlocal ones as follows:

$$Q_{\text{NL}} - N_{0} \frac{{{\text{d}}w}}{{{\text{d}}x}} = 0\,,$$
(52a)
$$M_{\text{NL}} = 0\,.$$
(52b)

In the other words, the deflection at the free end should be non-zero, (i.e., \(\delta w \ne 0\)). Thus, we find Eq. (52a) in order to satisfy the first set of boundary conditions in Eq. (26a).

Moreover, we know that the slope of the beam axis at the free end should be non-zero, (i.e., \(\delta \frac{{{\text{d}}w}}{{{\text{d}}x}} \ne 0\)). Therefore, in order to satisfy the second set of boundary conditions in Eq. (26b), we should have

$$(e_{0} a)^{2} \left. {\left( {\frac{{{\text{d}}Q_{\text{CL}} }}{{{\text{d}}x}}} \right)} \right|_{x = 0}^{x = L} = 0.$$
(53)

Applying this boundary condition in Eq. (29a), and considering that the rotation of transverse normal at the free end should be non-zero, (i.e., \(\delta \phi \ne 0\)), we find \(M_{\text{NL}} = 0\) in order to satisfy Eq. (29a), which was obvious from the previous points in Eq. (52b).

In order to satisfy the last set of boundary conditions in Eq. (29b), either the natural boundary condition is zero (i.e., \((e_{0} a)^{2} EI\frac{{{\text{d}}^{2} \phi }}{{{\text{d}}x^{2} }} = 0\)) or the essential boundary condition (i.e., \(\delta \frac{{{\text{d}}\phi }}{{{\text{d}}x}} = 0\)). Considering Eq. (52b) for the special case, when the nonlocal parameter is neglected, and in order to have zero bending moment at the free end, we should have \(\frac{{{\text{d}}\phi }}{{{\text{d}}x}} = 0\), (i.e., \(\delta \frac{{{\text{d}}\phi }}{{{\text{d}}x}} = 0\) for the homogeneous boundary conditions), as a boundary condition for satisfying the last set of boundary conditions. Combining this condition with Eq. (53) results to

$$\frac{{{\text{d}}^{2} w(x = L)}}{{{\text{d}}x^{2} }} = 0\,,$$
(54)

Thus, the general boundary conditions for the free end of a cantilever beam at \(x = L\) are

$$Q_{\text{NL}} - N_{0} \frac{{{\text{d}}w}}{{{\text{d}}x}} = 0\,,$$
(55a)
$$\frac{{{\text{d}}^{2} w}}{{{\text{d}}x^{2} }} = 0\,,$$
(55b)
$$\frac{{{\text{d}}\phi }}{{{\text{d}}x}} = 0.$$
(55c)

Defining the nonlocal shear force \(Q_{\text{NL}}\) in terms of \(w(x)\), using Eqs. (9), (25), and (28), we obtain

$$Q_{\text{NL}} = EI\frac{{{\text{d}}^{2} \phi }}{{{\text{d}}x^{2} }} + (e_{0} a)^{2} N_{0} \frac{{{\text{d}}^{3} w}}{{{\text{d}}x^{3} }}\,.$$
(56)

Eliminating \(\phi\) in the above equation, using the derivative of Eq. (40), we have

$$Q_{\text{NL}} = - (e_{0} a)^{2} \left( {\frac{EI}{{K_{\text{S}} GA}}N_{0} } \right)\frac{{{\text{d}}^{5} w}}{{{\text{d}}x^{5} }} + \left[ {\frac{EI}{{K_{\text{S}} GA}}N_{0} - EI + (e_{0} a)^{2} N_{0} } \right]\frac{{{\text{d}}^{3} w}}{{{\text{d}}x^{3} }}\,.$$
(57)

Using Eqs. (55b) and (40), the boundary condition in Eq. (55c) in terms of \(w(x)\) is derived as

$$\frac{{{\text{d}}^{4} w}}{{{\text{d}}x^{4} }} = 0.$$
(58)

Thus, the general boundary conditions for the free end of a cantilever beam at \(x = L\) in terms of \(w(x)\) are

$$\frac{{{\text{d}}^{2} w}}{{{\text{d}}x^{2} }} = 0\,,\quad \frac{{{\text{d}}^{4} w}}{{{\text{d}}x^{4} }} = 0\,,\quad (e_{0} a)^{2} \left( {\frac{EI\,}{{K_{\text{S}} GA}}} \right)\frac{{{\text{d}}^{5} w}}{{{\text{d}}x^{5} }} + \left[ {\frac{EI}{{N_{0} }} - \frac{EI}{{K_{\text{S}} GA}} - (e_{0} a)^{2} } \right]\frac{{{\text{d}}^{3} w}}{{{\text{d}}x^{3} }} + \frac{{{\text{d}}w}}{{{\text{d}}x}} = 0\,.$$
(59)

According to MNTBT and solving the governing Eq. (30), by means of these boundary conditions, the closed-form of critical buckling strains for cantilever nano-beams becomes

$$\varepsilon_{\text{cr}} = \frac{{\pi^{2} I}}{{4AL^{2} }}\left[ {\frac{1}{{1 + \frac{1}{4}\pi^{2} (\,\bar{\mu } + \,\bar{\varOmega }\,) + \frac{1}{16}\pi^{4} (\,\bar{\mu } \times \,\bar{\varOmega }\,)}}} \right]\,.$$
(60)

4.4 Propped cantilever nano-beams

The boundary conditions for this type are the combination of clamped and simply supported boundary conditions and derived in the previous parts. Assuming the fixed end at \(x = 0\) and hinged end at \(x = L\), we have Eqs. (49) and (42) for the fixed and hinged boundary conditions, respectively. Therefore, the closed-form of critical buckling strain for propped cantilever nano-beams becomes

$$\varepsilon_{\text{cr}} = \frac{{2.0449\,\pi^{2} I}}{{AL^{2} }}\left[ {\frac{1}{{1 + 20.187(\,\bar{\mu } + \,\bar{\varOmega }\,) + 407.515\,(\,\bar{\mu } \times \,\bar{\varOmega }\,)}}} \right]\,.$$
(61)

5 Numerical results and discussion

The critical buckling loads for SWCNTs modeled as nano-beams with different end conditions are investigated with respect to different values of small-scale parameter \((e_{0} a)\) and aspect ratio \((L/d)\). These exact solutions of nonlocal Timoshenko beam model using nonlocal boundary conditions  (MNTBT) are compared with the results of nonlocal Timoshenko beam models (NTBT).

The following effective properties of SWCNTs are used in computing the numerical values [12]:

$$E = 1\,\,({\text{TPa}}),\;G = 420\,\,({\text{GPa}}),\;d = 1\,\,({\text{nm}}),\;K_{\text{S}} = 0.877.$$
(62)

The numerical results for the critical buckling loads of SWCNTs in nano Newton (nN) are presented for the different types of end conditions in Tables 1, 2, 3 and 4 as follows:

Table 1 Comparison of critical buckling loads for simply supported nano-beams
Full size table
Table 2 Comparison of critical buckling loads for clamped nano-beams
Full size table
Table 3 Comparison of critical buckling loads for cantilever nano-beams
Full size table
Table 4 Comparison of critical buckling loads for propped cantilever nano-beams
Full size table

The values of the first row of each table state the classical or local critical buckling loads (i.e., when \(e_{0} a = 0\)). These values are the upper bound of the critical buckling loads and vary monotonically from the classical value to values that are lower.

Clearly, the nonlocal parameter as well as the aspect ratio has the effect of reducing the critical buckling loads. Moreover, the difference between NTBT and MNTBT solutions is the most significant for clamped beams and the least for cantilever beams. This difference decreases by increasing the aspect ratio.

Furthermore, the presented numerical results for critical buckling strains are compared with MD simulations results for validation [11]. We also consider the end conditions with fully clamped boundaries as assumed in Ref. [11]. In addition, CNT (5, 5) is analyzed with a diameter \(d = 0.671\,({\text{nm}})\) and CNT (7, 7) with a diameter \(d = 0.94\,({\text{nm}})\), for different lengths. Both nanotubes are modeled using a wall thickness \(h = 0.066\,({\text{nm}})\), Young’s modulus \(E = 5.5\,\,({\text{TPa}})\), and Poisson’s ratio \(\nu = 0. 1 9\) [24]. The comparison of MD simulations and modified nonlocal Timoshenko beam model are presented for critical buckling strains in Table 5.

Table 5 Comparison of buckling strains for proposed modified nonlocal Timoshenko beam theory and MD simulations [11]
Full size table

Herein, it is illustrated that the critical buckling strains based on nonlocal boundary conditions are in good agreement as compared with MD simulations. In addition, it is shown that presented model can capture correctly the length-dependent buckling strains of SWCNTs, because of using the newly derived boundary conditions. Clearly, the presented beam models in literatures are unable to show the correct and exact trend in critical axial buckling strains of SWCNTs, while the proposed nonlocal beam model shows much better agreement with the molecular dynamics simulation results.

Moreover, based on the MD simulation results, the value of nonlocal constant is calibrated for axial buckling of SWCNTs based on an averaging process. The best match between molecular dynamics simulations and nonlocal formulations is achieved for Eringen’s small length-scale coefficient value of \(e_{0} a = 0.277\,({\text{nm}})\), which is verified by the recent study of Wang et al. for buckling of nonlocal beams with \(e_{0} a = 0.289\,({\text{nm}})\) [13]. In Figs. 2, 3, 4 and 5, the comparison of proposed MNTBT using nonlocal boundary conditions with both nonlocal and classic Timoshenko beam theories are presented for different end conditions.

Fig. 2
figure 2

Comparison of proposed modified nonlocal Timoshenko beam theory (exact) with the other Timoshenko beam theories for simply supported end conditions

Full size image
Fig. 3
figure 3

Comparison of proposed modified nonlocal Timoshenko beam theory (exact) with the other Timoshenko beam theories for clamped end conditions

Full size image
Fig. 4
figure 4

Comparison of proposed modified nonlocal Timoshenko beam theory (exact) with the other Timoshenko beam theories for clamped-free end conditions

Full size image
Fig. 5
figure 5

Comparison of proposed modified nonlocal Timoshenko beam theory (exact) with the other Timoshenko beam theories for propped cantilever end conditions

Full size image

As illustrated in Figs. 2, 3, 4 and 5, classic Timoshenko beam model has the constant upper bound value in each figure because it does not depend on nonlocal parameter. In addition, the proposed modified nonlocal Timoshenko beam theory using nonlocal boundary conditions has the lower values in comparison with the results based on classic boundary conditions for buckling of SWCNTs. It is because of the effect of shear deformation and nonlocal parameters. Moreover, it is clear that both nonlocal Timoshenko beam models have the same value for the classic case (\(\bar{\mu } = 0\)), because the governing equation changed to forth-order in this case (see Eq. 31) and nonlocal boundary conditions are redundant, consequently. However, by increasing the nonlocal parameter, the results of MNTBT model decrease rapidly as compared with NTBT model and it provides a much better fit to MD simulation results for axial buckling of the nano-beams. In addition, it is indicated that nonlocal effect is the most significant for doubly clamped nano-beams and the least significant for cantilever nano-beams.

6 Conclusions

Based on the current study, the governing field equations and nonlocal boundary conditions are derived for nano-beams, using a novel approach based on strain gradient theory and variational methods. The nonlocal Timoshenko beam theory is used here for accounting the nonlocal small-size effects in the normal and transverse shear stress components. In addition, the nonlocal boundary conditions for exact solution of sixth-order governing differential equation are used, and thus the solutions presented herein for axial buckling of SWCNTs are different and more exact as compared with those available in the literatures. Furthermore, some important issues about derivation and specification of the nonlocal boundary conditions are discussed, which could be useful to understand the nature of the higher-order nonlocal boundary conditions.

Finally, numerical results  are compared to the analytical solutions of TBT and NTBT for different end conditions. For each comparison, the modified NTBT based on nonlocal boundary conditions provides a lower bound on the buckling strains of SWCNTs. Moreover, the nonlocal parameter has the effect of reducing the buckling loads. This effect is the most significant for doubly clamped nano-beams and the least significant for cantilever nano-beams. The differences among the results may decrease by increasing the aspect ratio and will be negligible for the aspect ratios more than 20.

In addition, the proposed MNTBT model based on nonlocal boundary conditions is validated through comparison with the results from MD simulations. It is found that the MNTBT model with nonlocal boundary conditions provides a much better fit to MD simulation results as compared with available beam models for axial buckling of SWCNTs. Based on the proposed modified Timoshenko beam model with higher-order nonlocal boundary conditions, we could calibrate the Eringen’s nonlocal coefficient e0 for buckling problems to a constant value (i.e., 0.277 nm) which is in good agreement with the literature [13] using the discrete boundary conditions for the nonlocal beams (i.e., \(e_{0} = 0.289\) nm).