1 Introduction

Presenting superior mechanical and thermal properties, carbonaceous structures are excellent reinforcements for high performance composites materials. Traditional composites with embedded fibers have less strength and stiffness compared to nano-composite materials reinforced by carbonaceous structures such as carbon nanotubes (Thai et al. 2018; Esawi and Farag 2007). This leads to the generation of new composites having different distributions of carbon nanotubes such uniform or functionally graded. In functionally graded nano-composites, carbon nanofillers are non-uniformly dispersed within the matrix phase in order to boost the efficient application of the small percentage of nanofillers in composite materials (Shen 2009). There are also different fabrication techniques for functionally graded nano-composites such as thermal spray, electromechanical deposition and powder metallurgy (Kwon et al. 2011; Bafekrpour et al. 2013). This situation led to attraction of attentions from research and engineering communities for analyzing structural behavior of carbon reinforced nano-composite beams, plates and shells (Mehar et al. 2017; Ansari et al. 2016; Alibeigloo 2014; Ebrahimi and Habibi 2017, 2018; Torabi et al. 2019; Aragh 2017; Rokni et al. 2015).

Moreover, graphene nanoplatelet (GNP) reinforced composites with high strength can prominently decrease weight with a higher efficiency than that of a conventional metal material (Zarasvand and Golestanian 2017). GNP reinforced composite materials with polymer matrix have been broadly utilized in many structural applications, including aerospace and automotive industries in which weight decrement is vital for increased payloads and higher speeds. Graphene sheet can be preferred over conventional carbon nanofillers such as carbon nanotubes because of possessing a higher surface area, tensile strength and thermal/electrical conductivity (Kilic et al. 2018). Structural elements (beams and plates) made of GNP reinforced composites are recently studied in the view point of their static and dynamic behaviors. Analysis of vibration and stability characteristics of GNP reinforced beams having a porous matrix is carried out by Kitipornchai et al. (2016). In another work, Feng et al. (2017) researched free vibrations of a GNP reinforced beam considering geometric nonlinearity. Zhao et al. (2017) researched bending behavior of GNP reinforced plates with trapezoidal shapes. Free vibration characteristics of cylindrical shells made of GNP reinforced composites are studied by Barati and Zenkour (2018). Also, free vibrational behavior of a GNP reinforced plate with different boundary conditions has been investigated by Reddy et al. (2018). Also, geometrically nonlinear vibration of small scale beams made of GNP reinforced composites has been studied by Sahmani and Aghdam (2017) considering strain gradients.

With the prompt expansion of technologies, composite materials with carbon nanofillers have gained a broad attention in micro-mechanics by tailoring their architecture at small scales (Allahkarami and Nikkhah-Bahrami 2018). As stated in Kong et al. (2008), Asghari et al. (2010), Ahouel et al. (2016) and Bessaim et al. (2015), the scale influence becomes very prominent for the mechanical properties of micro-sized structures. Hence, investigation on scale impacts on the mechanical characteristics of a micro-scale beam is of substantial importance. Experiments on micro-sized structures are not easy to execution, therefore it is necessary to employ an easier way which is utilization of non-classical continuum mechanics capturing size effects. For example, it is proved that the essence of size effect at micro scale is related to the micro-rotations of particles inside the material (Toupin 1962). Modified couple stress theory having one scale parameter can capture such size-dependency behaviors (Zeighampour and Beni 2014; Li and Pan 2015; Dai et al. 2015; Hu et al. 2016). The theory is also used to investigate static/dynamic behaviors of micro-sized beams and plates fabricated from carbon nanotube reinforced composites. Analysis of free vibrations and static buckling of a microbeam with embedded carbon nanotubes has been carried out by Shenas et al. (2018). Based on modified couple stress elasticity, Rostami et al. (2018) researched linear forced vibrations of a carbon nanotube reinforced microbeam. Considering viscoelastic effects, Mohammadimehr et al. (2017) re-examined vibration characteristics of a carbon nanotube reinforced microbeam. It can be understand from previous works on nanofiller reinforced microbeams that all of them studied perfect beams only and the influences of geometric imperfection have not been researched. According to real states, structure components may have geometric imperfection that creates within the manufacturing procedure or expand within their operating life (Farokhi et al. 2013; Ghayesh and Farokhi 2017; Farokhi and Ghayesh 2015).

This research deals with nonlinear free/forced vibrational analysis of geometrically imperfect GNP reinforced microscale beams based on modified couple stress elasticity. The imperfect microbeam is rested on a nonlinear hardening elastic medium and a harmonic force is applied to its top surface. Uniform, linear and nonlinear cases of distribution for GNPs have been considered based on Halpin–Tsai micromechanical model. These distributions provide a continual gradation of material property over the thickness. So, the problem of discontinuity stresses at interfaces of a multi-layered GNP reinforced composite has been resolved. Finally, harmonic balance method has been implemented to solve the nonlinear dynamic equation of microbeam having quadratic and cubic nonlinearities. It is shown in this research that GNP weight fraction, GNP distribution, external force and geometric imperfection have great impacts on vibrational behavior of microbeams.

2 Modeling of a GNP-reinforced microbeam

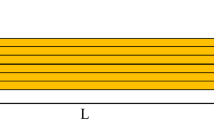
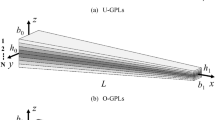
In this research, it is considered that graphene platelets are dispersed uniformly, linearly and nonlinearly thorough the transverse direction, as illustrated in Fig. 1. Also, a GNP-reinforced microbeam lying on elastic foundation has been shown in Fig. 2. Based upon, Halpin–Tsai micromechanical model (Zhao et al. 2017), the GNP volume fraction (VGPL) has the following relation with the weight fraction of GNPs (WGPL) as:

$$V_{GPL} = \frac{{W_{GPL} }}{{W_{GPL} + \frac{{\rho_{GPL} }}{{\rho_{M} }} - \frac{{\rho_{GPL} }}{{\rho_{M} }}W_{GPL} }}$$
(1)

where \(\rho_{GPL}\) and \(\rho_{M}\) denote the mass density of GNPs and polymer matrix, respectively. Then, the elastic moduli of the nanocompoite can be expressed as a function of matrix elastic moduli (EM) as (Zhao et al. 2017):

$$E_{1} = \frac{3}{8}\left( {\frac{{1 + \xi_{L}^{GPL} \eta_{L}^{GPL} V_{GPL} }}{{1 - \eta_{L}^{GPL} V_{GPL} }}} \right)E_{M} + \frac{5}{8}\left( {\frac{{1 + \xi_{W}^{GPL} \eta_{W}^{GPL} V_{GPL} }}{{1 - \eta_{W}^{GPL} V_{GPL} }}} \right)E_{M}$$
(2)

where \(\xi_{L}^{GPL}\) and \(\xi_{W}^{GPL}\) are two geometric parameters showing the influences of GPL shape and size in axial and lateral directions (Zhao et al. 2017):

$$\xi_{L}^{GPL} = \frac{{2l_{GPL} }}{{t_{GPL} }}$$
(3a)
$$\eta_{L}^{GPL} = \frac{{\left( {E_{GPL} /E_{M} } \right) - 1}}{{\left( {E_{GPL} /E_{M} } \right) + \xi_{L}^{GPL} }}$$
(3b)
$$\xi_{W}^{GPL} = \frac{{2w_{GPL} }}{{t_{GPL} }}$$
(3c)
$$\eta_{W}^{GPL} = \frac{{\left( {E_{GPL} /E_{M} } \right) - 1}}{{\left( {E_{GPL} /E_{M} } \right) + \xi_{W}^{GPL} }}$$
(3d)
Fig. 1
figure 1

Three types of GNP distribution over the thickness

Full size image
Fig. 2
figure 2

Functionally graded GPL-reinforced microbeam

Full size image

In above relations, wGPL, lGPL, and tGPL denote GPL average width, length, and thickness, respectively. Also, Poisson’s ratio of nanocomposite material is a function of Poisson’s ratio of GPL and matrix phases as:

$$v_{1} = v_{GPL} V_{GPL} + v_{M} V_{M}$$
(4)

in which \(V_{m}\) represents the volume fraction of matrix phase (\(V_{M} = 1 - V_{GPL}\)).

In this study, GPL dispersion are considered as:

Uniform:

$$W_{GPL} = \lambda_{1} W_{GPL}^{0}$$
(5a)

Linear:

$$W_{GPL} = \lambda_{2} W_{GPL}^{0} \left( {\frac{z}{h} + \frac{1}{2}} \right)$$
(5b)

Nonlinear:

$$W_{GPL} = \frac{{\lambda_{3} W_{GPL}^{0} z^{2} }}{{s^{2} h^{2} (4s^{2} - h^{2} )}}\left[ {4h^{2} z^{2} - h^{4} + \frac{{16s^{2} }}{n}(s^{2} - z^{2} )} \right]$$
(5c)

where \(W_{GPL}^{0}\) is a specific GPL weight fraction which is considered as \(W_{GPL}^{0} = 1\%\); and s = 0.45 h.

This research deals with the analysis of microbeams according to classical beam model having the displacement field as:

$$u_{1} \left( {x,y,z,t} \right) = u\left( {x,y,t} \right) - z\frac{\partial w}{\partial x}$$
(6)
$$u_{3} (x,y,z,t) = w(x,y,t)$$
(7)

in which axial and transverse displacements are respectively denoted by u and w. The strain field containing geometric imperfection and nonlinearity can be introduced as (Farokhi et al. 2013):

$$\varepsilon_{xx} = \frac{{\partial u_{1} }}{\partial x} = \frac{\partial u}{\partial x} - z\frac{{\partial^{2} w}}{{\partial x^{2} }}\, + \frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} + \frac{\partial w}{\partial x}\frac{{\partial w^{*} }}{\partial x}$$
(8)

Modeling of a microbeam according to modified couple stress elasticity needs the components of curvature tensor in the form:

$$\chi_{xy} = - \frac{1}{2}\frac{{\partial^{2} w}}{{\partial x^{2} }},\;\chi_{xx} = \chi_{yy} = \chi_{zz} = \chi_{xz} = \chi_{yz} = 0$$
(9)

Obtained strain and curvature tensors are corresponding to the axial stress and couple stress by the following equations (Dai et al. 2015):

$$\sigma_{xx} = [\lambda_{nc} + 2\mu_{nc} ]\varepsilon_{xx}$$
(10)
$$m_{xy} = 2\mu_{nc} l^{2} \chi_{xy}$$
(11)

in which Láme’s constants may be written as:

$$\lambda_{nc} = \frac{{E_{1} v_{1} }}{{\left[ {1 + v_{1} } \right][1 - 2v_{1} ]}}$$
(12)
$$\mu_{nc} = \frac{{E_{1} }}{{2[1 + v_{1} ]}}$$
(13)

Based on the classical beam model and the procedure explained in Li and Pan ( 2015) and Hu et al. (2016), one can achieve the governing equations by implementing the minimization of the total potential energy:

$$\frac{{\partial N_{x} }}{\partial x} = I_{0} \frac{{\partial^{2} u}}{{\partial t^{2} }} - I_{1} \frac{{\partial^{3} w}}{{\partial x\partial t^{2} }}$$
(14)
$$\begin{aligned} \frac{{\partial^{2} M_{x}^{b} }}{{\partial x^{2} }} + \frac{\partial }{\partial x}\left( {N_{x} \left[ {\frac{\partial w}{\partial x} + \frac{{\partial w^{*} }}{\partial x}} \right]} \right) + \frac{{\partial^{2} Y_{1} }}{{\partial x^{2} }} = q_{ynamic} + I_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }} + I_{1} \left( {\frac{{\partial^{3} u}}{{\partial x\partial t^{2} }}} \right) - I_{2} \nabla^{2} \left( {\frac{{\partial^{2} w}}{{\partial t^{2} }}} \right) \\ & + k_{L} w - k_{P} \nabla^{2} w + k_{NL} w^{3} \\ \end{aligned}$$
(15)

Here, linear, shear and nonlinear elastic substrate parameters are respectively denoted by kL, kp, and kNL and

$$(I_{0} ,I_{1} ,I_{2} ) = \int_{ - h/2}^{h/2} {(1,z_{{}} \,,z_{{}}^{2} )\rho_{1} } dz$$
(16)

Also, the in-plane force (Nx), bending moment (M b x ) and couple stress resultant (Y1) can be expressed by:

$$N_{x} = A_{xx} \left( {\frac{\partial u}{\partial x} + \frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} + \frac{\partial w}{\partial x}\frac{{\partial w^{*} }}{\partial x}} \right) - B_{xx} \frac{{\partial^{2} w}}{{\partial x^{2} }}$$
(17)
$$M_{x}^{b} = B_{xx} \left( {\frac{\partial u}{\partial x} + \frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} + \frac{\partial w}{\partial x}\frac{{\partial w^{*} }}{\partial x}} \right) - D_{xx} \frac{{\partial^{2} w}}{{\partial x^{2} }}$$
(18)
$$Y_{1} = - \tilde{A}\left( {\frac{{\partial^{2} w_{{}} }}{{\partial x^{2} }}} \right)$$
(19)

where

$$\begin{aligned} A_{xx} & = \int_{ - h/2}^{h/2} {\left( {\lambda_{nc} \frac{{1 - v_{1} }}{{v_{1} }}} \right)} dz, \\ B_{xx} & = \int_{ - h/2}^{h/2} {\left( {\lambda_{nc} \frac{{1 - v_{1} }}{{v_{1} }}} \right)z\,} dz, \\ D_{xx} & = \int_{ - h/2}^{h/2} {\left( {\lambda_{nc} \frac{{1 - v_{1} }}{{v_{1} }}} \right)z^{2} \,} dz, \\ \tilde{A} & = \int_{ - h/2}^{h/2} {\mu_{nc} l^{2} } dz, \\ \end{aligned}$$
(20)

Two nonlinear governing equations are obtained for an imperfect microbeam by replacing Eqs. (17)–(19) in Eqs. (14) and (15) as:

$$A_{xx} \left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial w_{{}} }}{\partial x}\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{\partial^{2} w}}{{\partial x^{2} }}\frac{{\partial w^{*} }}{\partial x} + \frac{\partial w}{\partial x}\frac{{\partial^{2} w^{*} }}{{\partial x^{2} }}} \right) - B_{xx} \frac{{\partial^{3} w}}{{\partial x^{3} }} = I_{0} \frac{{\partial^{2} u}}{{\partial t^{2} }} - I_{1} \frac{{\partial^{3} w}}{{\partial x\partial t^{2} }}$$
(21)
$$\begin{aligned} & B_{xx} \frac{\partial }{\partial x}\left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{\partial w}{\partial x}\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{\partial^{2} w}}{{\partial x^{2} }}\frac{{\partial w^{*} }}{\partial x} + \frac{\partial w}{\partial x}\frac{{\partial^{2} w^{*} }}{{\partial x^{2} }}} \right) - (D_{xx} + \tilde{A})\frac{{\partial^{4} w}}{{\partial x^{4} }} \\ &\quad + N_{x} \left( {\left[ {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{\partial^{2} w^{*} }}{{\partial x^{2} }}} \right]} \right) = q_{ynamic} + I_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }} + I_{1} \left( {\frac{{\partial^{3} u}}{{\partial x\partial t^{2} }}} \right) - I_{2} \nabla^{2} \left( {\frac{{\partial^{2} w}}{{\partial t^{2} }}} \right) \\ &\quad + k_{L} w - k_{P} \nabla^{2} w + k_{NL} w^{3} \\ \end{aligned}$$
(22)

By ignoring in-plane inertia \(\left( {I_{0} \frac{{\partial^{2} u}}{{\partial t^{2} }}} \right)\) in Eq. (21) and knowing that the effect of I1 is small, it is possible to express Eq. (21) as:

$$A_{xx} \left( {\frac{\partial u}{\partial x} + \frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} + \frac{\partial w}{\partial x}\frac{{\partial w^{*} }}{\partial x}} \right) - B_{xx} \frac{{\partial^{2} w}}{{\partial x^{2} }} = C_{1}$$
(23)

Simplifiying Eq. (23) yields:

$$\frac{\partial u}{\partial x} = - \frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} - \frac{\partial w}{\partial x}\frac{{\partial w^{*} }}{\partial x} + \frac{{B_{xx} }}{{A_{xx} }}\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{C_{1} }}{{A_{xx} }}$$
(24)

The axial displacement may be obtained by integrating Eq. (24) as:

$$u = - \frac{1}{2}\int_{0}^{x} {\left( {\frac{\partial w}{\partial x}} \right)^{2} } dx - \int_{0}^{x} {\frac{\partial w}{\partial x}\frac{{\partial w^{*} }}{\partial x}} dx + \frac{{B_{xx} }}{{A_{xx} }}\frac{\partial w}{\partial x} + \frac{{C_{1} }}{{A_{11} }}x + C_{2}$$
(25)

Axial displacement are restrained at both ends (u(0) = 0, u(L) = 0) which results in:

$$\begin{aligned} C_{2} & = - \frac{{B_{xx} }}{{A_{xx} }}\frac{\partial w}{\partial x}\left| {_{x = 0} } \right. \\ C_{1} & = \frac{{A_{xx} }}{2L}\int_{0}^{L} {\left( {\frac{\partial w}{\partial x}} \right)^{2} } dx + \frac{{A_{xx} }}{L}\int_{0}^{L} {\frac{\partial w}{\partial x}\frac{{\partial w^{*} }}{\partial x}} dx - \frac{{B_{xx} }}{L}\frac{\partial w}{\partial x}\left| {_{x = L} } \right. + \frac{{B_{xx} }}{L}\frac{\partial w}{\partial x}\left| {_{x = 0} } \right. \\ \end{aligned}$$
(26)

Inserting constant C1 into Eq. (24) gives:

$$\begin{aligned} \frac{\partial u}{\partial x} & = - \frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} - \frac{\partial w}{\partial x}\frac{{\partial w^{*} }}{\partial x} + \frac{{B_{xx} }}{{A_{xx} }}\frac{{\partial^{2} w}}{{\partial x^{2} }} + \\ & + \frac{1}{2L}\int_{0}^{L} {\left( {\frac{\partial w}{\partial x}} \right)^{2} } dx + \frac{1}{L}\int_{0}^{L} {\frac{\partial w}{\partial x}\frac{{\partial w^{*} }}{\partial x}} dx - \frac{{B_{xx} }}{{LA_{xx} }}\frac{\partial w}{\partial x}\left| {_{x = L} } \right. + \frac{{B_{xx} }}{{LA_{xx} }}\frac{\partial w}{\partial x}\left| {_{x = 0} } \right. \\ \end{aligned}$$
(27)

Also, the second derivative of axial displacement can be obtained from Eq. (27) as:

$$\frac{{\partial^{2} u}}{{\partial x^{2} }} = - \frac{\partial w}{\partial x}\frac{{\partial^{2} w}}{{\partial x^{2} }} - \frac{{\partial^{2} w}}{{\partial x^{2} }}\frac{{\partial w^{*} }}{\partial x} - \frac{\partial w}{\partial x}\frac{{\partial^{2} w^{*} }}{{\partial x^{2} }} + \frac{{B_{xx} }}{{A_{xx} }}\frac{{\partial^{3} w}}{{\partial x^{3} }}$$
(28)

Using Eqs. (27) and (28), the nonlinear governing equation of an imperfect microbeam can be simplified as:

$$\begin{aligned} &B_{xx} \frac{\partial }{\partial x}\left( { + \frac{{B_{xx} }}{{A_{xx} }}\frac{{\partial^{3} w}}{{\partial x^{3} }}} \right) - (D_{xx} + \tilde{A})\frac{{\partial^{4} w}}{{\partial x^{4} }} + \left[ {A_{xx} \left( { + \frac{1}{2L}\int_{0}^{L} {\left( {\frac{\partial w}{\partial x}} \right)^{2} } dx + \frac{1}{L}\int_{0}^{L} {\frac{\partial w}{\partial x}\frac{{\partial w^{*} }}{\partial x}} dx - \frac{{B_{xx} }}{{LA_{xx} }}\frac{\partial w}{\partial x}\left| {_{x = L} } \right. + \frac{{B_{xx} }}{{LA_{xx} }}\frac{\partial w}{\partial x}\left| {_{x = 0} } \right.} \right)} \right]\left( {\left[ {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{\partial^{2} w^{*} }}{{\partial x^{2} }}} \right]} \right) \hfill \\&\quad = q_{ynamic} + I_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }} - I_{2} \nabla^{2} \left( {\frac{{\partial^{2} w}}{{\partial t^{2} }}} \right) + k_{L} w - k_{P} \nabla^{2} w + k_{NL} w^{3} \hfill \\ \end{aligned}$$
(29)

3 Solution procedure

Nonlinear vibration problem of geometrically imperfect microbeams is analytically solved in this section. First, the lateral displacement component is considered as (Rostami et al. 2018):

$$w = \sum\limits_{i = 1}^{\infty } {W_{i} \varphi_{i} (x)}$$
(30)

where Wi is the vibration amplitude and \(\varphi_{i} (x) = 0.5\left( {1 - \cos \left( {\frac{2i\pi }{L}x} \right)} \right)\) is trial function to satisfy clamped boundary edges with the following conditions:

$$w\left| {_{x = 0} } \right. = w\left| {_{x = L} } \right. = 0,\frac{{\partial w_{{}} }}{\partial x}\left| {_{x = 0} } \right. = \frac{{\partial w_{{}} }}{\partial x}\left| {_{x = L} } \right. = 0 \,$$
(31)

Also, the geometric imperfection is same as vibration mode (Ghayesh and Farokhi 2017; Farokhi and Ghayesh 2015):

$$w_{{}}^{*} = W_{{}}^{*} \phi_{{}} (x) = 0.5W_{{}}^{*} \left( {1 - \cos \left( {2\pi \frac{x}{L}} \right)} \right)$$
(32)

Inserting Eqs. (30)–(32) into Eq. (29) leads to:

$$K_{{}}^{S} W_{i} + G_{1} W_{i}^{3} + Q_{1} W_{i}^{2} + M\ddot{W}_{i} = F_{1} \cos \left( {\omega t} \right)$$
(33)

in which

$$\begin{aligned} K_{{}}^{S} & = - \left( {D_{xx} + \tilde{A} - \frac{{B_{xx}^{2} }}{{A_{xx} }}} \right)\left( {\varLambda_{40} } \right) - k_{w} \varLambda_{00} + k_{p} \varLambda_{20} + \frac{{A_{xx} }}{L}\varXi_{11} \varGamma_{20} W^{*2} \\ & \quad - \frac{{B_{xx} }}{{LA_{xx} }}\frac{\partial w}{\partial x}\left| {_{x = L} } \right.W^{*} \varGamma_{20} + \frac{{B_{xx} }}{{LA_{xx} }}\frac{\partial w}{\partial x}\left| {_{x = 0} W^{*} \varGamma_{20} } \right. \\ \end{aligned}$$
(34)
$$G_{1} = \frac{{A_{xx} }}{2L}\varLambda_{11} \varLambda_{20} - k_{NL} \tilde{\varLambda }_{00}$$
(35)
$$Q_{1} = \frac{{A_{xx} }}{2L}\varLambda_{11} \varGamma_{20} W^{*} + \frac{{A_{xx} }}{L}\varXi_{11} \varLambda_{20} W^{*} - \frac{{B_{xx} }}{{LA_{xx} }}\frac{\partial w}{\partial x}\left| {_{x = L} } \right.\varLambda_{20} + \frac{{B_{xx} }}{{LA_{xx} }}\frac{\partial w}{\partial x}\left| {_{x = 0} \varLambda_{20} } \right.$$
(36)
$$M = - I_{0} \varLambda_{00} + I_{2} \varLambda_{20}$$
(37)
$$F_{1} = \int_{0}^{L} {f(x,t)} \varphi_{i} dx$$
(38)

where

$$\begin{aligned} \varLambda_{00} = \int_{0}^{L} {\varphi_{i} \varphi_{i} dx} \hfill \\ \varLambda_{20} = \int_{0}^{L} {\varphi_{i}^{''} \varphi_{i} dx} \hfill \\ \varLambda_{40} = \int_{0}^{L} {\varphi_{i}^{''''} \varphi_{i} dx} \hfill \\ \varLambda_{11} = \int_{0}^{L} {\varphi_{i}^{'} \varphi_{i}^{'} dx} \hfill \\ \tilde{\varLambda }_{00} = \int_{0}^{L} {\left( {\varphi_{i} } \right)^{4} dx} \hfill \\ \varXi_{11} = \int_{0}^{L} {\phi_{i}^{'} \varphi_{i}^{'} dx} \hfill \\ \varGamma_{20} = \int_{0}^{L} {\varphi_{i}^{''} \phi_{i} dx} \hfill \\ \varGamma_{40} = \int_{0}^{L} {\phi_{i}^{''''} \phi_{i} dx} \hfill \\ \end{aligned}$$
(39)

Since the vibration of microbeam occurs at both positive and negative transverse directions, Eq. (33) must be re-written as:

$$K_{{}}^{S} W_{i} + G_{1} W_{i}^{3} + Q_{1} W_{i}^{{}} \left| {W_{i} } \right| + M\ddot{W}_{i} = F_{1} \cos \left( {\omega t} \right)$$
(40)

For harmonic oscillation of system, the amplitude of microbeam can be defined as:

$$W_{i} = \tilde{W}\cos \left( {\omega t} \right)$$
(41)

Now, Eq. (41) must be inserted in Eq. (40) to obtain the following equation:

$$\begin{aligned} \frac{{K^{S} }}{M}\tilde{W}\cos (\omega t) + \frac{{G_{1} }}{M}\left( {\tilde{W}\cos (\omega t)} \right)^{3} + \frac{{Q_{1} }}{M}\left( {\tilde{W}\cos (\omega t)} \right)\left| {\tilde{W}\cos (\omega t)} \right| - \tilde{W}\omega^{2} \cos (\omega t) = \frac{{F_{1} }}{M}\cos \left( {\omega t} \right) \hfill \\ \hfill \\ \end{aligned}$$
(42)

Based on the properties of trigonometric functions, Eq. (42) can be simplified as:

$$\begin{aligned} \frac{{K^{*} }}{M}\tilde{W}\cos (\omega t) + \frac{{G_{1} }}{M}\tilde{W}^{3} \left( {\frac{1}{4}\cos (3\omega t) + \frac{3}{4}\cos (\omega t)} \right) \\ & + \frac{{Q_{1} }}{M}\tilde{W}^{2} \cos (\omega t)\left| {\cos (\omega t)} \right| - \tilde{W}\omega^{2} \cos (\omega t) = \frac{{F_{1} }}{M}\cos \left( {\omega t} \right) \\ \end{aligned}$$
(43)

Also, the following relations are needed for further simplifications:

$$\begin{aligned} \left| {\cos (\omega t)} \right| & = \frac{4}{\pi }\left[ {\frac{1}{2} + \frac{1}{3}\cos (2\omega t) - \frac{1}{15}\cos (4\omega t) + \cdots } \right] \\ \cos (\omega t)\left| {\cos (\omega t)} \right| & = \frac{4}{\pi }\left[ {\frac{1}{2}\cos (\omega t) + \frac{1}{3}\cos (2\omega t)\cos (\omega t) - \frac{1}{15}\cos (4\omega t)\cos (\omega t) + \cdots } \right] \\ & = \frac{4}{\pi }\left[ {\frac{1}{2}\cos (\omega t) + \frac{1}{6}(\cos (\omega t) + \cos (3\omega t)) - \frac{1}{15}\cos (4\omega t)\cos (\omega t) + \cdots } \right]= \frac{8}{3\pi }\cos (\omega t) \\ \end{aligned}$$
(44)

Finally, collecting the coefficients of first harmonic gives the governing equation as:

$$\left[ {\frac{{K^{S} }}{M}\tilde{W} + \frac{3}{4}\frac{{G_{1} }}{M}\tilde{W}^{3} + \frac{{8\tilde{W}^{2} }}{3\pi }\frac{{Q_{1} }}{M} - \tilde{W}\omega^{2} - \frac{{F_{1} }}{M}} \right]\cos (\omega t) = 0$$
(45)

Solving the above equation gives the amplitude-frequency curves. To examine free vibrations of the microbeam, it must be considered that F1 = 0. Then, the nonlinear frequency can be found from Eq. (45) as:

$$\omega_{NL} = \sqrt {\frac{{K^{S} }}{M} + \frac{{8\tilde{W}}}{3\pi }\frac{{Q_{1} }}{M} + \frac{3}{4}\frac{{G_{1}^{{}} }}{M}(\tilde{W})^{2} }$$
(46)

In this research, results are presented according to the following non-dimensional quantities:

$$\begin{aligned} K_{L} &= {\text{k}}_{L} \frac{{{\text{L}}^{4} }}{{D_{x} }},K_{p} = {\text{k}}_{p} \frac{{{\text{L}}^{2} }}{{D_{xx} }},K_{NL} = {\text{k}}_{NL} \frac{{{\text{L}}^{4} }}{{A_{xx} }} \hfill \\ \tilde{F}& = f\frac{{L^{2} }}{{A_{xx} h}},\tilde{\omega } = \omega L^{2} \sqrt {\frac{{\rho_{M} A}}{{E_{M} h^{3} }}} \hfill \\ \end{aligned}$$
(47)

4 Results and discussions

Amplitude-frequency curves derived in the previous section are depicted and explained in a number of figures in the present section. Amplitude-frequency curves are illustrated accounting for three cases of GNP distributions which are uniform, linear and non-linear. Last two cases (linear and non-linear) provide a continuous gradation of material property over the thickness, hence, the problem of discontinuity stresses at interfaces of a multi-layered GNP reinforced composite has been resolved.

In Tables 1 and 2, the material characteristics of a GNP reinforced microbeam have been presented. A trigonometric function is introduced to describe the geometric imperfection similar to first mode of vibration. Vibration frequency validation of a perfect GPN reinforced beam has been presented in Fig. 3 with those of Kitipornchai et al. (2016) and an excellent agreement can be seen between two curves. New results obtained in the present research are illustrated in Figs. 4, 5, 6, 7, 8 and 9, and suitable discussions are provided in the following paragraphs.

Table 1 Gradient index effect on total content of GNPs
Full size table
Table 2 Material and geometrical parameters for a GNP-reinforced beam
Full size table
Fig. 3
figure 3

Vibration frequency validation of a GNP reinforced beam (L/h = 20)

Full size image
Fig. 4
figure 4

Vibration frequency versus dimensionless amplitude for different graphene distribution and weight fractions (L/h  = 20, Kw =  0, Kp= 0, W*  = 0.1 h, l/h  = 0.2)

Full size image
Fig. 5
figure 5

Nonlinear vibration frequency versus dimensionless amplitude for different graphene distribution and geometric imperfections (L/h = 20, Kw =  0, Kp =  0, \(\% {\text{W}}_{\text{GPL}}^{*}\) = 1%, l/h  =  0.2)

Full size image
Fig. 6
figure 6

Nonlinear vibration frequency versus dimensionless amplitude for foundation parameters (L/h = 20, l/h  =  0.2, W* = 0.2 h, \(\% {\text{W}}_{\text{GPL}}^{*}\)  = 1%)

Full size image
Fig. 7
figure 7

Dimensionless amplitude frequency curves for various graphene distribution and weight fractions (L/h  = 20, Kw = 0, Kp = 0, W*  = 0.01 h, l/h  = 0.2, \(\tilde{F}\) = 0.01)

Full size image
Fig. 8
figure 8

Dimensionless amplitude frequency curves for different force amplitudes and couple stress parameters (L/h  = 20, W*  = 0.01 h,\(\% {\text{W}}_{\text{GPL}}^{*}\)  = 1%)

Full size image
Fig. 9
figure 9

Dimensionless amplitude frequency curves for different foundation parameters (L/h = 20, l/h  =  0.2, W*  = 0.01 h, \(\% {\text{W}}_{\text{GPL}}^{*}\)  = 1%)

Full size image

Influences of GNP weight fraction and GNP distributions on nonlinear vibrational frequencies of the geometrically perfect/imperfect microbeam are examined in Fig. 4. Based on this figure, the couple stress parameter is set to l/h = 0.2 and imperfection amplitude is W* = 0.1 h. The non-dimensional vibration amplitude changes from − 1 to + 1. Increase of vibration amplitude is corresponding to larger frequencies due to incorporation of nonlinear hardening effects. It is clear that frequency curves for a perfect microbeam are symmetric with respect to the vibration amplitude. It means that the minimum frequency (natural frequency) of perfect microbeams is obtained for \(\tilde{W}\)/h = 0. However, in the case of imperfect microbeams, the frequency curves are un-symmetric with respect to dimensionless amplitude. It means that the nonlinear frequency may decrease with increase of dimensionless amplitude in negative transverse motions.

Another observation from Fig. 4 is that the nonlinear vibration frequency is significantly increased as the value of GNP weight fraction becomes greater. This is due to the reason that GNP nanofillers can elevate the stiffness of microbeam leading to larger frequencies. Also, the magnitude of frequency increment by increasing in GNP weight fraction is dependent on the type of GNP distribution. The highest value of nonlinear vibrational frequency is observed in the case of nonlinear GNP distribution. However, the lowest frequency is observed in the case of linear GNP dispersion in which the GNP weight fraction is zero at lower surface of microbeam.

In Fig. 5, the influence of geometrical imperfection amplitude (W*) on the variation of nonlinear vibration frequencies of the GNP reinforced microbeam versus dimensionless amplitude of motion is studied when l/h = 0.2. Different types of GNP distribution have been considered in this example. One can see that in contrast to the perfect microbeams, the nonlinear frequencies of the counterpart with imperfection reduce by increasing in vibration amplitude \(\tilde{W}\)/h in a given range of vibration amplitude in \(\tilde{W}\)/h < 0. Another conclusion from this figure is that as the magnitude of imperfection amplitude becomes greater, the difference between nonlinear vibration frequencies of perfect and imperfect microscale beams gets larger.

Figure 6 shows the dependency of nonlinear free vibrational behavior of geometrically perfect/imperfect microbeams reinforced by uniform distribution of GNPs on foundation parameters when \(\% {\text{W}}_{\text{GPL}}^{*}\) = 1% and W* = 0.2 h. It is evident from this figure that the influence of nonlinear elastic substrate parameter (KNL) on vibrational frequency is ignorable near the zero vibration amplitude. Thus, its effects becomes more prominent at large negative/positive vibration amplitudes. However, increasing in linear (KL) and shear (KP) foundation parameters only increases the magnitude of nonlinear frequency and their effect is not dependent on the vibration amplitude.

To examine forced vibration behavior of GNP reinforced microbeams, Fig. 7 presents the amplitude-frequency curves for different GNP distributions when the force amplitude is \(\tilde{F} = 0.01\). At first, it should be pointed out that due to the nonlinear hardening effects, the curves are diverted to the right. However, at a specific frequency, the amplitude of vibration becomes very large. This frequency is the resonance frequency of microbeam. This figure shows that by increasing the amount of GNPs, the resonance of microbeam can be postponed. In fact, increasing the magnitude of GNP weight fraction can increase the value of resonance frequency. Also, the highest and lowest resonance frequencies are obtained respectively in the case of nonlinear and linear GNP dispersions.

The effects of couple stress parameter as well as force magnitude on amplitude-frequency curves of a microbeam with uniform GNP reinforcement are presented in Fig. 8. This figure shows that increasing couple stress parameter results in larger resonance frequencies. This is due to stiffness hardening effects provided by particles micro-rotations. Also, one can see that increasing force amplitude only increases the value of maximum deflection (maximum amplitude) while the resonance frequency remains unchanged. This is because the resonance frequency dependent only on linear stiffness and mass density of microbeams. Therefore, by increasing the force magnitude, the amplitude-frequency curves becomes wider.

Forced vibration characteristics of a GNP reinforced microbeam are studied in Fig. 9 for different values of foundation parameters. One can observe that increasing nonlinear elastic foundation parameter leads to the deviation of amplitude-frequency curves to the right due to the enhancement of nonlinear hardening effects. Also, nonlinear foundation parameter cannot change the magnitude of resonance frequency since the resonance frequency is not dependent on nonlinear stiffness. It should be explained that linear and shear foundation parameters do not contribute to the nonlinear stiffness of microbeam. So, increasing their value can only increase the resonance frequency without any change in the deviation of curves.

5 Conclusions

This research dealt with nonlinear free/forced vibrations of a functionally graded graphene nanoplatelet (GNP) reinforced microbeam with geometrical imperfection which is rested on a nonlinear elastic foundation. Graphene Platelets were uniformly and non-uniformly dispersed in the cross section area of the microbeam. Small scale effects were captured by means of modified couple stress theory. Harmonic balance method was implemented to solve the nonlinear governing equation of microbeam having quadratic and cubic nonlinearities. It was observed that the nonlinear vibration frequency increased as the value of GNP weight fraction became greater. Also, the highest and lowest vibration frequencies were obtained respectively in the case of nonlinear and linear GNP dispersions. It the case of forced vibration analysis, it was seen that nonlinear foundation parameter as well force amplitude cannot change the value of resonance frequency. Also, it was reported that the nonlinear frequency of the microbeam with geometric imperfection may reduce by increasing in vibration amplitude within a certain range of vibration amplitude.