Abstract
Given a large enough population of voters whose utility functions satisfy certain statistical regularities, we show that voting rules such as the Borda rule, approval voting, and evaluative voting have a very high probability of selecting the social alternative which maximizes the utilitarian social welfare function. We also characterize the speed with which this probability approaches one as the population grows.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
As a theory of social justice, utilitarianism is quite appealing. But as a practical criterion for collective choice, it has serious shortcomings. To apply the utilitarian criterion, we not only need accurate information about the cardinal utility functions of all individuals in society; we must also know how to make cardinal interpersonal comparisons between these utility functions. Furthermore, an individual might inadvertently misperceive her own utility function, either through lack of self-knowledge, or because she does not fully understand the long-term consequences of the policies under consideration. For these reasons (among others), collective decisions are almost never made by trying to explicitly ascertain the utility functions of the members of society. Instead, collective decisions are usually made by voting.
A scoring rule is a particular kind of voting rule where each voter assigns a “score” to each alternative (with some constraints), and the alternative with the highest aggregate score wins. Well-known scoring rules include the Borda rule, the plurality and anti-plurality rules, evaluative (or “range”) voting, and approval voting. Since they involve maximizing a sum, scoring rules seem like a sort of “ersatz utilitarianism”. We will show that this is more than just a superficial formal resemblance. If the probability distribution of utility functions in a large society satisfies certain conditions, then we will show that a well-chosen scoring rule has a very high probability of selecting the alternative which maximizes the utilitarian social welfare function. For a sufficiently large population, this probability can be made arbitrarily close to certainty. Thus, with the right scoring rule, we can realize the utilitarian ideal, despite the informational problems described above.
The remainder of this paper is organized as follows. Section 2 introduces notation and assumptions which will be maintained throughout the paper. Section 3 considers evaluative voting. Section 4 considers approval voting. Section 5 considers rank scoring rules, such as the Borda rule or the plurality rule. Each of these three sections introduces one or more scenarios (described by hypotheses concerning the probability distribution of utility functions), and then, for each scenario, gives an asymptotic probability result. Appendix A reviews some results from Pivato (2016c) that are used in the other proofs. Appendix B contains the proofs of all the results in the paper.
Related literature The results in this paper are complementary to those in Pivato (2015, (2016a, (2016c). Like the present paper, Pivato (2015) considers conditions under which ordinal voting rules maximize the utilitarian social welfare function (SWF) in a large population. But whereas this paper focuses on scoring rules, Pivato (2015) focuses on Condorcet consistent rules such as the Copeland rule or an agenda of pairwise majority votes. Meanwhile, Pivato (2016c) considers a broader problem: how can we compute (and maximize) the utilitarian SWF when we have only very imprecise information about people’s utility functions and the correct system of interpersonal utility comparisons? Under plausible conditions, Pivato (2016c) shows that, in a large population, we can accurately estimate the utilitarian SWF despite these difficulties. Indeed, Pivato (2016a) shows that this can be done in a strategy-proof way, using a modified version of the Groves–Clarke pivotal mechanism.
We will evaluate ordinal voting rules from a utilitarian perspective. This approach was pioneered by Laplace in 1795,Footnote 1 but then apparently neglected for one hundred seventy years. It was rediscovered by Rae (1969), Taylor (1969) and Weber (1978). Rae and Taylor assumed that all voters had equal preference intensities over a dichotomous choice, given by independent, identically distributed (i.i.d.) random \(\{0,1\}\)-valued utility functions. In this setting, they showed that simple majority vote maximized the expected value of the utilitarian SWF, amongst all anonymous voting rules.Footnote 2 Weber (1978) considered a setting with many alternatives, and variable preference intensities. Assuming that the voters’ utilities for the different alternatives were independent, uniformly distributed (i.u.d.) random variables, he sought the voting rule which maximized the expected value of the utilitarian SWF in a large population. He showed that the Borda rule was the optimal rule in the class of rank scoring rules. The results in Sect. 5 can be seen as a major generalization of this early insight. In the case of exactly three alternatives, Weber (1978) also showed that the approval voting rule slightly outperforms the Borda rule; we will study the utilitarian efficiency of approval voting in Sect. 4.
Shortly after Weber’s foundational work, Bordley (1983, (1985a) and Merrill (1984) used computer simulations to estimate the expected value of the utilitarian SWF for various voting rules. Bordley (1985b, (1986) computed utilitarian-optimal weighted majority voting schemes for dichotomous decisions with correlated voters. But there was no further utilitarian analysis of voting rules for the next 20 years.
Starting in 2005, a literature emerged on the utilitarian analysis of federal representative assemblies. Most of these papers focussed on dichotomous decisions, and assumed that the utility functions of the citizens were i.i.d. random variables. They asked: which voting rule will maximise the expected value of the utilitarian SWF? First, Beisbart et al. (2005) computationally compared the performance of seven benchmark rules, while Barberà and Jackson (2006) gave an exact formula for the utilitarian-optimal weighted majority rule in terms of the distribution of utility functions found within each region. Next, Beisbart and Bovens (2007) and Bovens and Hartmann (2007) investigated the consequences of different population-based weighting formulas with a mixture of theoretical analysis and computational results. Laruelle and Valenciano (2008, Ch.3; 2010, §7) provided a utilitarian rational for the classic Penrose “square root” weighting formula. Macé and Treibich (2012) and Koriyama et al. (2013) derived analytical results in scenarios where voters have non-separable preferences over a series of dichotomies. (This is represented by making the utility of each region a concave function of its frequency of victory in a long series of decisions.) In contrast to all the previously mentioned papers, Fleurbaey (2009) and Beisbart and Hartmann (2010) considered models with correlated voters. In Biesbart and Hartmann’s model, the profile of utility functions is drawn from a multivariate normal distribution, whereas Fleurbaey’s model is extremely general; the correlation structure between voters is completely arbitrary. Finally, Maaser and Napel (2014) used computer simulations to find utilitarian-optimal voting weights in a setting with three or more alternatives arranged on a line (with single-peaked preferences). The overall message of these papers is that, with i.i.d. voters, the expected value of utilitarian social welfare is generally maximized by a “degressive” weighted majority rule, where the weight of each region is a sub-linear function (e.g. square root) of its population. With non-independent and/or non-identical voters, the optimal weights can depend on the correlations and preference intensities.
More recently, a series of papers have considered direct democracies deciding amongst three or more alternatives. Lehtinen (2007, (2008) used computer simulations to show that strategic voting often improves the utilitarian efficiency of the Borda rule and approval voting. Caragiannis and Procaccia (2011) estimated the “distortion” of the plurality, approval, and antiplurality voting rules—that is, the worst-case ratio between the utilitarian social welfare of the optimal alternative, and the utilitarian social welfare of the alternative which actually wins, where the worst case is computed over all possible profiles of “normalized” utility functions. (A utility function is “normalized” if it is positive and the utilities sum to one.) Procaccia and Caragiannis were particularly interested in the asymptotic growth rate of this distortion ratio as the number of voters and/or alternatives becomes large. They showed that, if voters randomly convert their cardinal utility functions into voting behaviours in a plausible way, then the expected distortion ratio grows surprisingly slowly. Their intended application was preference aggregation in a cooperating group of artificially intelligent agents, but their results are also applicable to more traditional social welfare problems. This approach has recently been extended by Boutilier et al. (2012), who study the worst-case and average-case performance of randomized social choice rules.
Given a social welfare function W, and the probability distribution of the voters’ cardinal utility functions, Apesteguia et al. (2011) asked: what ordinal voting rule maximizes the expected value of W? In the case when W is the utilitarian SWF, and the voters’ utilities are i.i.d. random variables, they showed that the W-optimal rule is a rank scoring rule of the kind we consider in Sect. 5. In particular, if the voters’ utilities are i.u.d. random variables, then the W-optimal rule is the Borda rule. The results in Sect. 5 of this paper can be seen as complementary to those of Apesteguia et al. (2011); they showed that a certain scoring rule was better, on average, than any alternative voting rule, whereas we show that, in a large population, it approaches perfect agreement with the utilitarian social choice.
Giles and Postl (2014) conducted a similar investigation for (A, B)-voting rules, a two-parameter family of rules introduced by Myerson (2002), which includes approval vote as well as rank scoring rules. Giles and Postl suppose there are three alternatives, whose utilities for each voter are privately known i.i.d. random variables on the interval [0, 1]. Unlike Apesteguia et al. (2011), they allow strategic voting. Giles and Postl first characterize the symmetric Bayesian Nash equilibrium (BNE) for the N-player strategic voting game for any \(N\ge 2\). Then they numerically compute the expected value of the utilitarian SWF at the three-player BNE for various \((A,B)\in [0,1]^2\) (where the three players’ utilities are i.i.d. random variables drawn from either a uniform distribution or a beta distribution on [0, 1]). The results on approval voting in Sect. 4 of this paper can be seen as complementary to the findings of Giles and Postl (2014), but extended to an arbitrary number of alternatives and a large number of voters.
Kim (2014) pushes this investigation further. In a setting with three or more alternatives, and voters with independent (but not identically distributed) random utilities, he characterizes the rules which are ex ante Pareto efficient in the class of ordinal voting rules: they are “non-anonymous” rank scoring rules (where each voter has perhaps a different score vector). He further shows that, in a “neutral” environment (i.e. all alternatives are ex ante interchangeable), such rules are incentive compatible (i.e. truth-revealing in BNE). Special cases of Kim’s analysis are the rank scoring rules which maximize ex ante utilitarian social welfare over all ordinal rules. In particular, Kim observes that the rank scoring rules of Apesteguia et al. (2011) are incentive-compatible in the i.i.d. environment of their paper.Footnote 3 He then constructs incentive-compatible voting rules which, in terms of the utilitarian SWF, are superior to any ordinal rule (in particular, any scoring rule), but which utilize only a limited amount of cardinal utility information from the voters.
Azrieli and Kim (2014) perform a similar analysis for a dichotomous choice in which voters have independent (but not identically distributed) random utilities. They show that the rule which maximizes ex ante utilitarian social welfare over the class of all incentive compatible rules is a weighted majoritarian rule (where the weight of each voter is determined by the expected value of her utility function). They also obtain a similar characterization of the ex ante and ex interim Pareto-optimal rules in the class of incentive-compatible rules. Meanwhile, Krishna and Morgan (2012) have considered a model where participation itself is a strategic choice. Assuming that voting is costly and participation is voluntary, they showed that simple majority vote will maximize utilitarian social welfare, because voters with weaker preferences will abstain from voting.
The majority of the aforementioned papers deal only with dichotomous decisions, whereas we allow an arbitrary number of alternatives.Footnote 4 Also, except for Fleurbaey (2009), all of the aforementioned papers assumed that cardinal interpersonal utility comparisons are unproblematic. In contrast, we suppose that these interpersonal comparisons themselves are ambiguous in practice (but still meaningful in principle). Finally, except for Weber (1978) and Caragiannis and Procaccia (2011), all of the aforementioned papers deal with “small” populations of voters, whereas we are interested in asymptotic probabilistic results for very large populations.Footnote 5 It is not possible here to adequately summarise the vast and growing literature on the large-population asymptotic probabilistic analysis of voting rules. Instead, we will only briefly touch on two strands of this literature. The first strand is the Condorcet Jury Theorem (CJT) and its many generalizations.Footnote 6 Like the CJT literature, the results of the present paper say that, under certain probabilistic assumptions, a large population using a certain voting rule is likely to arrive at the “correct” decision. But the goal for the CJT literature is to find the correct answer to some objective factual question, whereas the goal in the present paper is to maximize social welfare.
The second strand is the literature on strategic voting and/or strategic candidacy in large populations with some kind of randomness or uncertainty in voters’ preferences. This literature is mainly concerned with characterizing the Nash equilibria of certain large election games. These equilibria occasionally have surprising social welfare properties. For example, Ledyard (1984), Lindbeck and Weibull (1987, (1993), Coughlin (1992; Theorem 3.7 and Corollary 4.4), Banks and Duggan (2004; §4) and McKelvey and Patty (2006) have all shown that, in certain election games, there is a unique Nash equilibrium (sometimes called a “political equilibrium”) where all the candidates select the policy which maximizes a utilitarian SWF. But these utilitarian SWFs are based on somewhat peculiar systems of interpersonal utility comparisons. In these models, voter behaviour is described by a stochastic device: the probability that voter i votes for candidate C (or in some cases, the probability that i votes at all) is a function of the difference between the cardinal utility which i assigns to C and the cardinal utility she assigns to other candidates. Although the different models use different stochastic devices and seek to capture different phenomena (e.g. random private costs for voting, or random private shocks to the utility functions, or random individual errors due to bounded rationality, or other exogenous perturbations), each model assumes that utility functions are translated into voting probabilities in the same way for every voter. In this way, each model smuggles in a system of “implicit” interpersonal utility comparisons via the stochastic device. As observed by Banks and Duggan (2004, p. 29), this means that the normative significance of the “utilitarianism” emerging from these political equilibria is somewhat unclear.
In contrast, this paper assumes that there is a pre-existing, normatively meaningful system of cardinal interpersonal utility comparisions, explicitly described by a set of “calibration constants” which exist independently of the voting rule and any other random factors in the model. The social planner does not know the exact values of these calibration constants, so she regards them as random variables. Our results suggest that it is still possible to closely approximate the utilitarian social choice, even with this kind of uncertainty. However, unlike the political equilibrium literature, we treat the social alternatives as exogenous, rather than endogenizing them as the result of political candidates competing for popularity.
We also differ from the political equilibrium literature in that we do not grapple with strategic voting. However, in a companion paper, Núñez and Pivato (2016) show that all of the voting rules considered in this paper can be “approximately implemented” in large populations. To be precise, given any voting rule F, there is a stochastic voting rule \({\widetilde{F}}\) which has two properties, for any sufficiently large population of voters. First, \({\widetilde{F}}\) selects the same alternative as F, with very high probability. Second, each voter will find it strategically optimal to vote honestly in \({\widetilde{F}}\), with very high probability. This result holds under weak and plausible assumptions about the voters’ beliefs about other voters. Thus, the problem of strategic voting essentially vanishes in a sufficiently large population.
2 Assumptions and notation
We will now fix some notation and assumptions which will be maintained throughout the paper. Let \({\mathbb {R}}\) denote the set of real numbers. For any set \({\mathcal { A}}\) and function \(f:{\mathcal { A}}{{\longrightarrow }}{\mathbb {R}}\), let \({{\mathrm{\mathrm{argmax}}}}_{\mathcal { A}}(f)\) denote the set of elements in \({\mathcal { A}}\) which maximize f. For any random variable X, let \({\mathbb {E}}[X]\) denote its expected value, and let \(\mathrm{var}[X]\) denote its variance.
Let \({\mathcal { A}}\) be a finite set of social alternatives, let \({\mathcal { I}}\) be a set of voters, and let \(I:=|{\mathcal { I}}|\). (We will typically suppose that I is very large; indeed we will be interested in asymptotic phenomena as \(I{\rightarrow }{\infty }\).) For every i in \({\mathcal { I}}\), let \(u_i:{\mathcal { A}}{{\longrightarrow }}{\mathbb {R}}\) be voter i’s cardinal utility function, and let \(c_i>0\) be a “calibration constant”, which we will use to make cardinal interpersonal utility comparisons. We suppose that the functions \(c_i\, u_i\) and \(c_j\, u_j\) are interpersonally comparable for all voters i and j in \({\mathcal { I}}\). In other words, for any alternatives a, b, c, and d in \({\mathcal { A}}\), if \(c_i\,u_i(b)-c_i\,u_i(a)=c_j\,u_j(d)-c_j\,u_j(c)\), then the welfare that voter i gains in moving from alternative a to alternative b is exactly the same as the welfare that voter j gains in moving from c to d. We would therefore like to maximize the utilitarian social welfare function \(U_{\mathcal { I}}:{\mathcal { A}}{{\longrightarrow }}{\mathbb {R}}\) defined by
The models which appear below differ in their assumptions about the functions \(\{u_i\}_{i\in {\mathcal { I}}}\). In Sects. 4 and 5, we will suppose that \(\{u_i\}_{i\in {\mathcal { I}}}\) are unknown to the social planner; from her point of view, they are random functions. However, she knows certain features of their distributions, and can exploit these features in the design of the voting rule. She can then obtain partial and indirect information about \(\{u_i\}_{i\in {\mathcal { I}}}\) from the voters’ responses to this voting rule. In contrast, in Sect. 3 we will suppose that \(\{u_i\}_{i\in {\mathcal { I}}}\) are known functions, ranging over [0, 1]; the only uncertainty lies in the calibration constants \(\{c_i\}_{i\in {\mathcal { I}}}\). Throughout Sects. 3, 4 and 5, we will assume that \(\{c_i\}_{i\in {\mathcal { I}}}\) are unknown to the social planner. We formalize this with the following assumption:
-
(C)
\(\{c_i\}_{i\in {\mathcal { I}}}\) are real-valued random variables, which are independent, but not necessarily identically distributed. There is some constant \(\sigma _c^2\ge 0\) (independent of I) such that \(\mathrm{var}[c_i]\le \sigma _c^2\) and \({\mathbb {E}}[c_i]=1\) for all \(i\in {\mathcal { I}}\).
For some of our results, it will also be convenient to assume the utility profile \(\{u_i\}_{i\in {\mathcal { I}}}\) satisfies the following technical property.
-
\((\Delta )\) There is a constant \(\Delta >0\) (independent of I) such that \(\max _{{\mathcal { A}}} (U_{\mathcal { I}})-U_{\mathcal { I}}(a)>\Delta \) for every \(a\not \in {{\mathrm{\mathrm{argmax}}}}_{{\mathcal { A}}} (U_{\mathcal { I}})\).
Here, \(\Delta \) is the minimum social welfare gap between the optimal policy and the next-best policy. If a voting rule acts as an “estimator” of the utilitarian SWF, then we need the error of this estimate to be smaller than \(\Delta \), in order for the rule to select the optimal policy, and not the next-best policy. (Of course, if \(\Delta \) was very small, then selecting the next-best policy would not be a catastrophe; thus, we will relax condition \((\Delta )\) in Propositions 3.2, 4.3, and 5.3 below.)
It might seem strange that \(U_{\mathcal { I}}\) is defined in formula (1) as the per capita average utility, rather than the total utility. The extra 1 / I factor makes no difference for maximization purposes. So why is it there?
The reason is that we are concerned with assessing how far a particular policy falls short of the theoretical maximum social welfare, and in a large (and growing) population, it makes much more sense to measure such a welfare shortfall in terms of per capita average utility rather than total utility. To see the problem, suppose our voting rule selects some policy P which falls short of the optimal policy Q. If we measure this shortfall as the per capita average utility disparity between P and Q, then our assessment will be independent of the size of the population (ceteris paribus). But if we measured the shortfall as the total utility disparity between P and Q, then an increase in the size of the population would mechanically cause a proportionate increase in our assessment of the “suboptimality” of P, even though nothing else has changed. If we judge the quality of voting rules by the social suboptimality of the policies they produce, then we would spuriously conclude that the larger society had a worse voting rule.
Indeed, policy evaluators usually normalize statistics by population size, precisely to avoid this kind of spurious conclusion. For instance, suppose that a certain traffic law X leads to 100 accidental traffic deaths per year in country A, while an alternative traffic law Y leads to 300 accidental traffic deaths per year in another very similar country B (and otherwise X and Y have identical effects on traffic flow, pollution, etc.). We might naïvely conclude that the traffic law X is safer. But if the population of country B is ten times bigger than country A, then in fact the law Y is safer, in per capita terms.
3 Evaluative voting
The most natural “utilitarian” voting rule simply asks each voter to assign a numerical score to each alternative, presumably reflecting her cardinal utility function. The obvious problem with this approach is that voters could strategically exaggerate these scores. One partial solution is to rescale every voter’s utility function to range over the interval \({\left[ 0,1 \right]}\). The resulting social choice rule has been called evaluative voting (Núñez and Laslier 2014; Baujard et al. 2014), utilitarian voting (Hillinger 2005), or range voting (Smith 2000; Macé 2013).
Formally, in evaluative voting (EV), the vote of each voter i in \({\mathcal { I}}\) takes the form of a function \(v_i:{\mathcal { A}}{{\longrightarrow }}[0,1]\). The EV rule then chooses the alternative(s) in \({\mathcal { A}}\) that maximize the function \(V_{\mathcal { I}}:{\mathcal { A}}{{\longrightarrow }}{\mathbb {R}}\) defined by
Meanwhile, for every voter i in \({\mathcal { I}}\) let \(w_i:{\mathcal { A}}\,{{\longrightarrow }}\,{\mathbb {R}}\) be her “true” utility function. We suppose these utility functions admit one-for-one cardinal interpersonal comparisons. In other words, for any alternatives a, b, c, and d in \({\mathcal { A}}\), if \(w_i(b)-w_i(a)=w_j(d)-w_j(c)\), then the welfare that voter i gains in moving from a to b is exactly the same as the welfare that voter j gains in moving from c to d. We therefore want to maximize the utilitarian SWF \(U_{\mathcal { I}}\) defined by
Let \({\underline{w}}_i:=\min \{w_i(a)\); \(a\in {\mathcal { A}}\}\). By replacing \(w_i\) with the function \({\widetilde{w}}_i:=w_i-{\underline{w}}_i\) if necessary, we can suppose that \(\min \{w_i(a)\); \(a\in {\mathcal { A}}\}=0\), for every voter i in \({\mathcal { I}}\). Clearly this does not affect the maximizer of (3). Now let \(c_i:=\max \{w_i(a)\); \(a\in {\mathcal { A}}\}\), and then define \(u_i(a):= w_i (a)/c_i\), for every voter i in \({\mathcal { I}}\) and every alternative a in \({\mathcal { A}}\). Then formula (3) is clearly equivalent to formula (1). Roughly speaking, \(c_i\) can be seen as a crude measure of the “intensity” of voter i’s preferences regarding the social decision. Of course, the social planner cannot accurately observe these preference intensities. So we will assume that the planner regards \(\{c_i\}_{i\in {\mathcal { I}}}\) is independent random variables, as described by assumption (C) from Sect. 2.
Note that each \(u_i\) ranges over the interval \({\left[ 0,1 \right]}\). If each voter i uses the full range [0, 1] to express her utilities, but is otherwise accurate; then she will set \(v_i=u_i\). (In this case, EV is equivilant to the relative utilitarian social welfare function axiomatized by Dhillon (1998) and Dhillon and Mertens (1999).) However, voter i may misperceive her own utility function. Thus, in general, \(v_i = u_i+\epsilon _i\), where \(\epsilon _i:{\mathcal { A}}\,{{\longrightarrow }}\,{\mathbb {R}}\) is a random “error” function. Suppose \({\underline{a}}_i\) and \({\overline{a}}_i\) are the minimizer and maximizer of \(u_i\) (thus, \(u_i({\underline{a}}_i)=0\) and \(u_i({\overline{a}}_i)=1\)). It is reasonable to suppose that \(v_i({\underline{a}}_i)=0\) and \(v_i({\overline{a}}_i)=1\)—that is, voter i reliably assigns a score of 0 to her worst alternative and a score of 1 to her best alternative. Thus, \(\epsilon _i({\underline{a}}_i)=\epsilon _i({\overline{a}}_i)=0\). However, for the other alternatives in \({\mathcal { A}}\), the errors may be nonzero. We assume they satisfy the following condition:
-
(E)
For each alternative a in \({\mathcal { A}}\), the random errors \(\{\epsilon _i(a)\}_{i\in {\mathcal { I}}}\) are independent, but not necessarily identically distributed. There is some constant \(\sigma _\epsilon ^2>0\) (independent of I) such that \(\mathrm{var}[\epsilon _i(a)]\le \sigma _\epsilon ^2\) and \({\mathbb {E}}[\epsilon _i(a)]=0\) for all \(a\in {\mathcal { A}}\) and \(i\in {\mathcal { I}}\). The random variables \(\{c_i\}_{i\in {\mathcal { I}}}\) are independent of the random functions \(\{\epsilon _i\}_{i\in {\mathcal { I}}}\).
(Note that we do not assume that, for a fixed voter i in \({\mathcal { I}}\), the random errors \(\epsilon _i(a)\) and \(\epsilon _i(b)\) are independent for different alternatives a and b in \({\mathcal { A}}\).) Our first result says that, despite the uncertainties surrounding \(\{c_i\}_{i\in {\mathcal { I}}}\) and \(\{\epsilon _i\}_{i\in {\mathcal { I}}}\), evaluative voting has a very good chance of maximizing the utilitarian social welfare function \(U_{\mathcal { I}}\) in formula (3), when the population is large.
Theorem 3.1
For every voter i in \({\mathcal { I}}\), let \(u_i:{\mathcal { A}}\,{{\longrightarrow }}\, [0,1]\) be a utility function. Suppose that the profile \(\{u_i\}_{i\in {\mathcal { I}}}\) satisfies \((\Delta )\), and suppose \(\{c_i\}_{i\in {\mathcal { I}}}\), \(\{\epsilon _i\}_{i\in {\mathcal { I}}}\) and \(\{v_i\}_{i\in {\mathcal { I}}}\) are randomly variables satisfying (C) and (E). Then
We can refine this result in three ways. First, we can drop condition \((\Delta )\). Second, and relatedly, instead of demanding that the outcome of evaluative voting exactly maximizes \(U_{\mathcal { I}}\), we can allow the possibility that it only almost maximizes \(U_{\mathcal { I}}\)—something which would be almost as good, for practical purposes. Third, we can estimate how large the population needs to be in order to achieve such “almost-maximization” with a certain probability. To achieve these refinements, we need some more notation. For any utility profile \(\{u_i\}_{i\in {\mathcal { I}}}\), if \(U_{\mathcal { I}}\) is as in Eq. (3), then let
This is the theoretical maximum social welfare, which would be obtained from the optimal social alternative. Let \(\delta >0\) represent a “social suboptimality tolerance”, and let \(p>0\) represent the probability that this tolerance will be exceeded (the social planner wants both of these to be small). For any values of \(\delta \) and p, we define
Our next result says that, for any population larger than \({\overline{I}}(\delta ,p)\), any \(V_{\mathcal { I}}\)-maximizing social alternative will produce a utilitarian social welfare within \(\delta \) of the theoretical optimum, with probability at least \(1-p\).
Proposition 3.2
For every voter i in \({\mathcal { I}}\), let \(u_i:{\mathcal { A}}\,{{\longrightarrow }}\, [0,1]\) be a utility function. Suppose \(\{c_i\}_{i\in {\mathcal { I}}}\), \(\{\epsilon _i\}_{i\in {\mathcal { I}}}\) and \(\{v_i\}_{i\in {\mathcal { I}}}\) satisfy (C) and (E). For any \(\delta >0\) and \(p\in (0,1)\), if \(I\ge {\overline{I}}(\delta ,p)\), then \(\mathrm{Prob}\left[ U_{\mathcal { I}}(a)< U^*_{\mathcal { I}}-\delta \right]\ < \ p\), for every a in \({{\mathrm{\mathrm{argmax}}}}_{{\mathcal { A}}} (V_{\mathcal { I}})\).
Remark on strategic voting Theorem 3.1 assumes that everyone tries to vote honestly—i.e. that \(v_i=u_i\) (plus perhaps some error) for all \(i\in {\mathcal { I}}\). But people may vote strategically. Indeed, in a Myerson–Weber model of evaluative voting in a large-population, each voter’s best strategy is to assign a score of either 0 or 1 to each alternative in \({\mathcal { A}}\) (Núñez and Laslier 2014). In this case, evaluative voting would reduces to approval voting. However, Núñez and Pivato (2016, Theorem 4) show that in a sufficiently large population, there is a stochastic voting rule which will produce the same outcome as evaluative voting, with very high probability, and where almost all voters will vote honestly. This result, combined with Theorem 3.1 above, suggests that in a sufficiently large population satisfying hypotheses (C) and (E), this stochastic evaluative voting rule will select the utilitarian-optimum outcome with very high probability, even when voters are strategically sophisticated.
4 Approval voting
Approval voting was originally proposed by Ottewell (1977), Kellett and Mott (1977), and Weber (1978), but the first sustained formal analysis was by Brams and Fishburn (1983), which is now usually regarded as the locus classicus. Laslier and Sanver (2010) provide a recent and comprehensive reference. Informally, the approval voting rule works as follows:
-
1.
Each voter i identifies a subset of alternatives in \({\mathcal { A}}\) which she “approves”.
-
2.
For each social alternative a in \({\mathcal { A}}\), count how many voters approve a.
-
3.
Choose the alternative which is approved by the most voters.
Formally, for every voter i in \({\mathcal { I}}\), let \({\mathcal { G}}_i\subseteq {\mathcal { A}}\) be the set of alternatives which i approves; we refer to \({\mathcal { G}}_i\) as her approval set. Let \({\varvec{{\mathcal { G}}}}:=\{{\mathcal { G}}_i\}_{i\in {\mathcal { I}}}\) be the profile of the voters’ approval sets. For any social alternative a in \({\mathcal { A}}\), we define its approval score by: \(V_{\varvec{{\mathcal { G}}}}(a):=\#\{i\in {\mathcal { I}}\); \(a\in {\mathcal { G}}_i\}\). We then define \(\mathrm{Appr}({\varvec{{\mathcal { G}}}}) := {{\mathrm{\mathrm{argmax}}}}_{\mathcal { A}}(V_{\varvec{{\mathcal { G}}}})\).Footnote 7
Recall that \(u_i:{\mathcal { A}}\,{{\longrightarrow }}\,{\mathbb {R}}\) denotes the cardinal utility function of voter i, and that we wish to maximize the utilitarian social welfare function \(U_{\mathcal { I}}\) defined in Formula (1). If the approval set \({\mathcal { G}}_i\) is a “noisy signal” of \(u_i\) (for every voter i in \({\mathcal { I}}\)), then the aggregate approval score \(V_{\varvec{{\mathcal { G}}}}\) could be seen as a “noisy signal” of the social welfare function \(U_{\mathcal { I}}\). Thus, under the right conditions, approval voting should maximize utilitarian social welfare. Indeed, Weber (1978) showed this was true when there are three alternatives, for which the utilities of the voters are independent random variables uniformly distributed over an interval. The goal of this section is to make this intuition precise in a much more general setting.
Each voter’s true utility function is unknown to the social planner. So is the process by which each voter converts her utility function into an approval set. We capture this lack of knowledge by treating these as random variables, described by some probabalistic model. We will consider two different models: the Threshold Model and the Selection Model. The Threshold Model (Sect. 4.1) first assigns each voter a random utility for each social alternative, and then selects her approval set from these alternatives by means of a randomly determined threshold. The Selection Model (Sect. 4.2) first selects an approval set for each voter (this process may be random or deterministic), and then randomly assigns utilities to each social alternative, according to a probability distribution which depends on whether or not it is in the approval set. Both models yield the same conclusion: in a large population, approval voting maximizes the utilitarian social welfare function, with high probability.
4.1 The threshold model
In this section, we will suppose that each voter i in \({\mathcal { I}}\) identifies an approval threshold \(\theta _i\). She then defines her approval set \({\mathcal { G}}_i\) to be all social alternatives whose utility exceeds \(\theta _i\). That is:
In addition to the assumptions (C) and \((\Delta )\) from Sect. 2, we will now make the following two assumptions:
- \((\Theta 1)\) :
-
The utilities \(\{u_i(a)\); \(a\in {\mathcal { A}}\) and \(i\in {\mathcal { I}}\}\) are i.i.d. random variables with finite variance. The variables \(\{c_i\}_{i\in {\mathcal { I}}}\) and \(\{u_i\}_{i\in {\mathcal { I}}}\) are all jointly independent.
- \((\Theta 2)\) :
-
The thresholds \(\{\theta _i\}_{i\in {\mathcal { I}}}\) are independent random variables (not necessarily identically distributed). For any \(i\in {\mathcal { I}}\), the random threshold \(\theta _i\) may depend on \(\{u_i(a)\}_{a\in {\mathcal { A}}}\). But \(\{\theta _i\}_{i\in {\mathcal { I}}}\) and \(\{c_i\}_{i\in {\mathcal { I}}}\) are independent. Finally, \(0<\mathrm{Prob}[u_i(a)\ge \theta _i]<1\) for all \(a\in {\mathcal { A}}\).
Assumption \((\Theta 1)\) describes the planner’s ignorance about people’s true utility functions, while \((\Theta 2)\) describes her ignorance about how they convert these utility functions into approval sets, except for the fact that they follow rule (6). The condition “\(0<\mathrm{Prob}[u_i(a)\ge \theta _i]<1\)” simply guarantees that the output of rule (6) is almost-surely nondegenerate. The next result says that, if a large population of voters satisfies these hypotheses, then with very high probability, approval voting will maximize the utilitarian social welfare function \(U_{\mathcal { I}}\) in Eq. (1).
Theorem 4.1
Suppose \(\{u_i\}_{i\in {\mathcal { I}}}\), \(\{\theta _i\}_{i\in {\mathcal { I}}}\) and \(\{c_i\}_{i\in {\mathcal { I}}}\) satisfy (C), \((\Delta )\), \((\Theta 1)\), and \((\Theta 2)\), and the approval profile \({\varvec{{\mathcal { G}}}}=\{{\mathcal { G}}_i\}_{i\in {\mathcal { I}}}\) is defined by rule (6). Then
One notable difference between Theorems 3.1 and 4.1 is that the former places essentially no conditions on the utility functions \(\{u_i\}_{i\in {\mathcal { I}}}\), whereas the latter requires these utility functions to be i.i.d. random variables. The reason is that approval voting provides us with less information about individual utility functions than evaluative voting. A voter’s response in evaluative voting tells us her entire utility function, up to a scalar multiple; the only uncertainty is the magnitude of this scalar. But her approval set only tells us whether each she assigns a ‘high’ or ‘low’ utility to each alternative. Thus, without further information about the conditional probability distributions of these ‘high’ and ‘low’ utilities, it is not possible for us to estimate the utilitarian social welfare function.
The total ignorance described by \((\Theta 1)\) implies both a sort of a priori anonymity (i.e. all voters are indistinguishible, a priori) and a priori neutrality (i.e. all social alternatives are indistinguishible, a priori). Thus, it does not allow us to incorporate the knowledge that certain alternatives (e.g. low taxes) tend to be favoured by certain classes of voters (e.g. business owners). Nor does it allow us to incorporate the knowledge that people’s preferences may be correlated (e.g. voters who favour low taxes tend to also favour less regulation, because they are often business owners). Likewise, \((\Theta 2)\) does not allow us to incorporate knowledge that certain types of voters tend to set higher thresholds than others for certain types of policy problems. Thus, when applied to a specific policy problem, these assumptions may be less than optimal; a voting rule more closely optimized to the specific probability distribution of utility functions in a society might yield a higher expected social welfare.Footnote 8 However, in many cases, we might not have such specific information about the distribution of utility functions.
It is important to note that we do not assume that the random threshold \(\theta _i\) is independent of \(u_i\). For example, one very natural threshold for a voter would be the average utility of all alternatives; that is:
Note that a random threshold determined in this way is compatible with hypothesis \((\Theta 2)\).
4.2 The selection model
In our second model, the approval set of each voter is exogenous and arbitrary. Her approval set might be fixed in advance, or it might be generated by some other random process. (If the voters’ approval sets are random variables, then we do not need to assume that they are either independent, or identically distributed.) Each voter assigns random utilities to each alternative, conditional on whether or not it is in her approval set.
Formally, for each i in \({\mathcal { I}}\), let \({\mathcal { G}}_i\) be the (exogenous) approval set of voter i, and let \({\mathcal { B}}_i:={\mathcal { A}}{\setminus }{\mathcal { G}}_i\). Let \(\gamma \) and \(\beta \) be two finite-variance probability measures on \({\mathbb {R}}\), such that the mean value of \(\gamma \) is strictly larger than that of \(\beta \).Footnote 9 In addition to assumptions (C) and \((\Delta )\) from Sect. 2, we now make the following assumption:
- (S) :
-
For all g in \({\mathcal { G}}_i\), \(u_i(g)\) is a \(\gamma \)-random variable. For all b in \({\mathcal { B}}_i\), \(u_i(b)\) is a \(\beta \)-random variable. The random variables \(\{c_i\); \(i\in {\mathcal { I}}\}\) and \(\{u_i(a)\); \(i\in {\mathcal { I}}\) and \(a\in {\mathcal { A}}\}\) are all jointly independent.
The interpretation of (S) is the same as \((\Theta 1)\); it implies both a sort of a priori anonymity and a priori neutrality. The difference is that now we can distinguish between those alternatives which are in a voter’s approval set and those which aren’t, and give them different statistical treatments. Since the approval sets are exogenous, this model is able to cope with situations where a voter’s approval choices are highly correlated, both with other voters and with other known facts about that voter (e.g. the fact that business owners tend to approve of tax reduction and also tend to approve of deregulation). The model in effect makes no assumptions about the statistical distribution of approval sets (it doesn’t even treat them as random). However, the model still does not allow correlations of utility within each voter’s approval set (e.g. a correlation between the utility that a voter assigns to a tax reduction and the utility she assigns to a deregulation policy, given that she has approved of both). Once again, if a large population of voters satisfies these hypotheses, then with very high probability, approval voting will maximize the utilitarian social welfare function \(U_{\mathcal { I}}\) in Eq. (1).
Theorem 4.2
Let \({\varvec{{\mathcal { G}}}}=\{{\mathcal { G}}_i\}_{i\in {\mathcal { I}}}\) be an arbitrary approval profile. If \(\{u_i\}_{i\in {\mathcal { I}}}\) and \(\{c_i\}_{i\in {\mathcal { I}}}\) satisfy hypotheses (C), \((\Delta )\), and (S), then
As in Sect. 3, we would like to refine Theorems 4.1 and 4.2 by dropping condition \((\Delta )\). We would also like to estimate how large the population must be in order for approval voting to “almost-maximize” \(U_{\mathcal { I}}\) with a certain probability, by analogy with Proposition 3.2. For brevity, we will present such a result only for the Selection Model, but a similar result can be proved for the Threshold Model. Let \(U^*_{\mathcal { I}}:=\max \{U_{\mathcal { I}}(a)\); \(a\in {\mathcal { A}}\}\).
Proposition 4.3
Let \({\varvec{{\mathcal { G}}}}=\{{\mathcal { G}}_i\}_{i\in {\mathcal { I}}}\) be an arbitrary approval profile. If \(\{u_i\}_{i\in {\mathcal { I}}}\) and \(\{c_i\}_{i\in {\mathcal { I}}}\) satisfy (C) and (S), then for any \(\delta >0\), we have
Furthermore, if the fourth moments of \(\gamma \) and \(\beta \) are finite,Footnote 10 then there are constants \(C_1,C_2>0\) (determined by \(\gamma \), \(\beta \), and \(\sigma _c^2\)) such that, for any \(p>0\), if \(I\ge C_1/p\) and \(I\ge C_2/p\,\delta ^2\), then \(\mathrm{Prob}\left[ U_{\mathcal { I}}(a)< U^*_{\mathcal { I}}-\delta \right] < p\) for all \(a\in \mathrm{Appr}({\varvec{{\mathcal { G}}}})\).
Remark on strategic voting Theorems 4.1 and 4.2 assumed that each person votes sincerely, meaning that she votes for all and only those alternatives whose utility exceeds some threshold. Such sincerity should not be taken for granted; De Sinopoli et al. (2006) and Núñez (2014) have constructed examples of mixed strategy Nash equilibria and Poisson equilibria with insincere approval voting. However, Núñez and Pivato (2016, Theorem 3) show that in a sufficiently large population, there is a stochastic voting rule which will produce the same outcome as approval voting, with very high probability, and where almost all voters will vote sincerely, using the threshold defined by formula (7). This result, combined with Theorem 4.1, suggests that in a large enough population satisfying hypotheses (C), \((\Delta )\), \((\Theta 1)\), and \((\Theta 2)\), this stochastic approval voting rule will select the utilitarian-optimum outcome with very high probability, even when voters have the option of being insincere.
5 Rank scoring rules
One concern with approval voting is that it gives each voter very little ability to express the intensity of her preference for or against each alternative. For example, if a voter does not include a certain alternative in her approval set, this may be because she actively dislikes this alternative, or it may simply be because she has no strong feelings either way, or perhaps inadequate knowledge of this alternative, and for this reason she “abstains” from endorsing it. Approval voting is unable to distinguish between voting against and abstention. For this reason, Alcantud and Laruelle (2014) propose “dis&approval” voting, which allows a voter three choices for each alternative: approve, disapprove, or abstain. However, “dis&approval” voting still does not distiguish between “strong” (dis)approval and “weak” (dis)approval. For this purpose, we turn to rank scoring rules.
Let \(N:=|{\mathcal { A}}|\). Let \(s_1\le s_2\le \cdots \le s_N\) be real numbers, and define \({\mathbf { s}}:=(s_1,s_2,\ldots ,s_N)\). The \({\mathbf { s}}\) -rank scoring rule on \({\mathcal { A}}\) is defined as follows:
-
1.
For every voter i in \({\mathcal { I}}\), let \(\succ _i\) denote her (strict) ordinal preferences on \({\mathcal { A}}\).
-
2.
For every alternative a in \({\mathcal { A}}\), if a is ranked kth place from the bottom with respect to \(\succ _i\), then voter i gives a the score \(s_k\). (In particular, i gives the score \(s_1\) to her least-prefered alternative, and the score \(s_N\) to her most prefered alternative.)
-
3.
For each alternative in \({\mathcal { A}}\), add up the scores it gets from all voters.
-
4.
The \({\mathbf { s}}\)-rank scoring rule chooses the alternative(s) with the highest total score.
For example, the Borda rule is the rank scoring rule with \({\mathbf { s}}=(1,2,3,\ldots ,N)\). The standard plurality rule is the rank scoring rule with \({\mathbf { s}}=(0,0,\ldots ,0,1)\).
Formally, for every voter i in \({\mathcal { I}}\), if \({\mathcal { A}}=\{a_1,a_2,\ldots ,a_N\}\) and \(a_1\prec _i a_2\prec _i\cdots \prec _i a_N\), then define \(v_i:{\mathcal { A}}{{\longrightarrow }}{\mathbb {R}}\) by setting \(v_i(a_k) := s_k\) for all \(k\in [1\ldots N]\). Let \({\mathcal { P}}_{\mathcal { I}}:=\{\succ _i\}_{i\in {\mathcal { I}}}\) be the profile of ordinal preferences of the voters. For every social alternative a in \({\mathcal { A}}\), define \(V^{\mathbf { s}}_{{\mathcal { P}}_{\mathcal { I}}}(a):=\sum _{i\in {\mathcal { I}}} v_i(a)\). Then define \(\mathrm{Score}_{\mathbf { s}}({\mathcal { P}}_{\mathcal { I}}):={{\mathrm{\mathrm{argmax}}}}_{\mathcal { A}}(V^{\mathbf { s}}_{{\mathcal { P}}_{\mathcal { I}}})\).
Apestequia et al. (2011; Theorem 3.1) have shown that, amongst all voting rules, rank scoring rules are the ones which maximize the expected value of the utilitarian social welfare function (under certain conditions). Furthermore, they characterized the optimal rank scoring rule in terms of the probability distribution of the voters’ utility functions—to be precise, in terms of the expected order statistics of this distribution. Our results in this section are complementary. We work with a much broader class of probability distributions than Apesteguia et al. (2011). We will show that, if the profile \(\{u_i\}_{i\in {\mathcal { I}}}\) arises from this class, then there exists a rank scoring rule which will come arbitrarily close to selecting a utilitarian optimum, with very high probability as \(I{\rightarrow }{\infty }\). Thus, while Apesteguia et al. (2011) show that the optimal rank scoring rule is “better on average” than any other voting rule, we show that it is, in fact “almost perfect”, in the limit of a large population.Footnote 11
As in Sect. 4, we will present two stochastic models of voter preference formation. In the Endogenous Preference model (Sect. 5.1), the voters’ utility functions are i.i.d. random variables, and their ordinal preferences are determined by these utility functions. In the Exogenous preference model (Sect. 5.2), the voter’s ordinal preferences are exogenous and arbitrary, and their utility functions are random variables conditional on these preferences.
5.1 Endogenous preferences
For each voter i in \({\mathcal { I}}\), we will represent her utility function over \({\mathcal { A}}\) as an N-dimensional vector \({\mathbf { u}}^i:=(u^i_a)_{a\in {\mathcal { A}}}\in {\mathbb {R}}^{\mathcal { A}}\) (where \(u^i_a:=u_i(a)\) for all \(a\in {\mathcal { A}}\)). Let \(\mu \) be a probability measure on \({\mathbb {R}}^{\mathcal { A}}\) which has finite variance (i.e. the variance of each one-dimensional marginal of \(\mu \) is finite). We will use \(\mu \) to randomly generate the utility functions of the voters. For any \(a,b\in {\mathcal { A}}\), we assume that \(\mu \{{\mathbf { u}}\in {\mathbb {R}}^{\mathcal { A}}\); \(u_a=u_b\}=0\) (i.e. almost surely, no two alternatives yield the same utility). In addition to hypotheses (C) and \((\Delta )\) from Sect. 2, we will now make the following two assumptions.
- (N1) :
-
The utility functions \(\{{\mathbf { u}}^i\}_{i\in {\mathcal { I}}}\) are independent, \(\mu \)-random vectors. Also, \(\{{\mathbf { u}}^i\}_{i\in {\mathcal { I}}}\) are independent of \(\{c_i\}_{i\in {\mathcal { I}}}\).
- (N2) :
-
\(\mu \) is symmetric under all coordinate permutations.
Note that we do not assume, for any particular voter i, that the utilities she assigns to different alternatives a and b are independent random variables: the probability measure \(\mu \) may allow for arbitrary correlations between \(u^i_a\) and \(u^i_b\). However, assumption (N2) acts as a form of a priori neutrality. It implies that the expected values of the utilities \(u^i_a\) and \(u^i_b\) are the same. Furthermore, the expected value of \(u^i_a\), conditional on some information about the rank of b (say, that b is i’s favourite alternative) is the same as the expected value of \(u^i_b\) conditional on the same information about the rank of a. Hypothesis (N1) is comparable to (S) or \((\Theta 1)\): it is a sort of a priori anonymity, saying that all voters are indistinguishable, a priori. However, (N1) supposes a richer level of knowledge than (S) or \((\Theta 1)\); for example, we might know that, on average, each voter’s second-best and third-best alternatives obtain, respectively 90 and 75 % of the utility of her favourite alternative (assuming her worst alternative has utility 0). We will now see how to incorporate such knowledge into the optimal rank scoring rule.
Let \({\mathbf { u}}\in {\mathbb {R}}^{\mathcal { A}}\) be a \(\mu \)-random vector. Rearrange the coordinates of \({\mathbf { u}}\) in increasing order, to get a vector \({}^{\scriptscriptstyle \uparrow }\!{\mathbf { u}}:=({}^{\scriptscriptstyle \uparrow }\!u_1,\ldots ,{}^{\scriptscriptstyle \uparrow }\!u_N)\), where \({}^{\scriptscriptstyle \uparrow }\!u_1\le {}^{\scriptscriptstyle \uparrow }\!u_2\le \cdots \le {}^{\scriptscriptstyle \uparrow }\!u_N\). For all \(n\in [1\ldots N]\), let \(s_n\) be the expected value of \({}^{\scriptscriptstyle \uparrow }\!u_n\); this yields a vector \({\mathbf { s}}=(s_1,\ldots ,s_N)\). The next result says that, if a large population of voters satisfies our hypotheses, then with very high probability, the \({\mathbf { s}}\)-rank scoring rule will maximize the utilitarian social welfare function \(U_{\mathcal { I}}\) in Eq. (1).
Theorem 5.1
Suppose \(\{{\mathbf { u}}_i\}_{i\in {\mathcal { I}}}\), and \(\{c_i\}_{i\in {\mathcal { I}}}\) satisfy (C), \((\Delta )\), (N1) and (N2), and let \({\mathcal { P}}_{\mathcal { I}}=\) \({\{\succ _i\}_{i\in {\mathcal { I}}}}\) be the ordinal preference profile defined by \(\{u_i\}_{i\in {\mathcal { I}}}\). Then
Impartial culture As we have emphasized, hypothesis (N1) does not require the utilities \(\{u^i_a\}_{a\in {\mathcal { A}}}\) to be i.i.d. random variables, for any particular voter i. However, it is certainly compatible with this additional assumption. This corresponds to the special case of the model where \(\mu \) is a Cartesian product of N copies of some underlying finite-variance, nonatomic probability measure \(\rho \) on \({\mathbb {R}}\). In this case, the utilities \(\{u^i_a\); \(i\in {\mathcal { I}}\) and \(a\in {\mathcal { A}}\}\) are all independent, \(\rho \)-random variables; this is a version of the so-called “Impartial Culture” model. If we make the further assumption that \(\rho \) is absolutely continuous and has compact support, and assume that \(c_i:=1\) for every voter i in \({\mathcal { I}}\), then we obtain the models considered by Weber (1978) and Apesteguia et al. (2011). But the Endogenous Preference model is much more general than the Impartial Culture model. For example, in a large population Impartial Culture model, all elements of \({\mathcal { A}}\) end up with roughly the same average utility (due to the Law of Large Numbers), so that utilitarianism is effectively indifferent between them, and the use of any voting rule is somewhat superfluous. The Endogenous Preference model avoids this unrealistically trivial outcome.
5.2 Exogenous preferences
In our second model, the preference orders of the voters are exogenous and arbitrary. These preference orders may themselves be random variables, or they may be determined in some other way. (If they are random variables, then we do not assume that they are independent or identically distributed, unlike the Impartial Culture model.) The model then assigns each voter a random utility for each alternative, conditional on her preference order.
Formally, let \({}^{^\uparrow }\!{\mathbb {U}}:=\{{}^{\scriptscriptstyle \uparrow }\!{\mathbf { u}}\in {\mathbb {R}}^N\); \({}^{\scriptscriptstyle \uparrow }\!u_1< {}^{\scriptscriptstyle \uparrow }\!u_2< \cdots < {}^{\scriptscriptstyle \uparrow }\!u_N\}\), and let \(\lambda \) be a finite-variance probability measure on \({}^{^\uparrow }\!{\mathbb {U}}\). For every voter i in \({\mathcal { I}}\), let \(\succ _i\) denote i’s (exogenous) preference order over \({\mathcal { A}}\). In addition to assumptions (C) and \((\Delta )\) from Sect. 2, we make the following assumption:
-
(X)
The utility vectors \(\{{\mathbf { u}}^i\}_{i\in {\mathcal { I}}}\) are independent random vectors, generated as follows. For each \(i\in {\mathcal { I}}\), we obtain \({\mathbf { u}}^i\) by taking a \(\lambda \)-random variable \({}^{\scriptscriptstyle \uparrow }\!{\mathbf { u}}^i\) in \({}^{^\uparrow }\!{\mathbb {U}}\), and rearranging the coordinates to agree with the preference order \(\succ _i\). The random variables \(\{{\mathbf { u}}^i\}_{i\in {\mathcal { I}}}\) and \(\{c^i\}_{i\in {\mathcal { I}}}\) are independent.
Once again, we do not assume, for any particular voter i, that the utilities she assigns to different alternatives a and b are independent random variables, even after we condition on \(\succ _i\); the probability measure \(\lambda \) may allow for arbitrary correlations between \(u^i_a\) and \(u^i_b\). However, (X) has a consequence similar to (N2): given two voters i and j, and two alternatives a and b, if a has the same rank with respect to \(\succ _i\) as b does with respect to \(\succ _j\), then the expected value of \(u^i_a\) is the same as that of \(u^j_b\). Hypothesis (X) is also comparable to (N1): it is a sort of a priori anonymity, saying that all voters are indistinguishable, a priori, except for their exogenous ordinal preferences.
For all \(k\in [1\ldots N]\), let \(s_k\) be the expected value of \({}^{\scriptscriptstyle \uparrow }\!u_k\), where \(({}^{\scriptscriptstyle \uparrow }\!u_1,\ldots ,{}^{\scriptscriptstyle \uparrow }\!u_N)\in {}^{^\uparrow }\!{\mathbb {U}}\) is a \(\lambda \)-random variable. Let \({\mathbf { s}}:=(s_1,s_2,\ldots ,s_N)\). The next result says that, if a large population of voters satisfies our hypotheses, then with very high probability, the \({\mathbf { s}}\)-rank scoring rule will maximize the utilitarian social welfare function \(U_{\mathcal { I}}\) in equation (1).
Theorem 5.2
Let \({\mathcal { P}}_{\mathcal { I}}=\{\succ _i\}_{i\in {\mathcal { I}}}\) be an arbitrary ordinal preference profile. Suppose \(\{{\mathbf { u}}_i\}_{i\in {\mathcal { I}}}\), and \(\{c_i\}_{i\in {\mathcal { I}}}\) satisfy (C), \((\Delta )\), and (X). Then the limit (9) holds as \(I{\rightarrow }{\infty }\).
As in Sects. 3 and 4, we would like to refine Theorems 5.1 and 5.2 by dropping condition \((\Delta )\). We would also like to estimate how large the population must be in order for the rank scoring rule to “almost-maximize” \(U_{\mathcal { I}}\) with a certain probability, by analogy with Propositions 3.2 and 4.3. For brevity, we will present such a result only for the Exogenous Preference model, but a similar result can be proved for the Endogenous Preference model. As usual, let \(U^*_{\mathcal { I}}:=\max \{U_{\mathcal { I}}(a)\); \(a\in {\mathcal { A}}\}\).
Proposition 5.3
Let \({\mathcal { P}}_{\mathcal { I}}=\{\succ _i\}_{i\in {\mathcal { I}}}\) be an arbitrary ordinal preference profile. If \(\{u_i\}_{i\in {\mathcal { I}}}\) and \(\{c_i\}_{i\in {\mathcal { I}}}\) satisfy (C) and (X), then for any \(\delta >0\), we have
Furthermore, if the fourth moment of \(\lambda \) is finite,Footnote 12 then there are constants \(C_1,C_2>0\) (determined by \(\lambda \) and \(\sigma _c^2\)) such that, for any \(p>0\), if \(I\ge C_1/p\) and \(I\ge C_2/p\,\delta ^2\), then \(\mathrm{Prob}\left[ U_{\mathcal { I}}(a< U^*_{\mathcal { I}}-\delta \right] < p\), for all \(a\in \mathrm{Score}_{\mathbf { s}}({\mathcal { P}}_{\mathcal { I}})\).
Conditional impartial culture Theorem 5.1 is actually a consequence of Theorem 5.2; in effect, the Exogenous Preference model can be intepreted as the Endogenous Preference model, conditional on a particular realization of the (random) ordinal preference profile \(\{\succ _i\}_{i\in {\mathcal { I}}}\). Theorem 5.2 says that limit (9) holds for any particular realization of \(\{\succ _i\}_{i\in {\mathcal { I}}}\). Theorem 5.1 follows from this fact by integrating over all possible realizations of \(\{\succ _i\}_{i\in {\mathcal { I}}}\). (See Appendix B for details.)
At the end of Sect. 5.1, we explained how the “Impartial Culture” model was a special case of the Endogenous Preferences model. If we condition on a particular realization of \(\{\succ _i\}_{i\in {\mathcal { I}}}\), we obtain the Conditional Impartial Culture model. To be precise, let \(\rho \) be a probability measure on \({\mathbb {R}}\) with finite variance and no atoms. For every voter i in \({\mathcal { I}}\), let \(\succ _i\) be voter i’s (exogenous) ordinal preference relation on \({\mathcal { A}}\). In this case, hypothesis (X) takes the following form:
- (X\('\)):
-
Let \(\{r^i_1,r^i_2,\ldots ,r^i_N\}\) be a sample of N independent, \(\rho \)-random variables. Rearrange this sample in increasing order, to obtain an N-tuple \(({}^{\scriptscriptstyle \uparrow }\!r^i_1,{}^{\scriptscriptstyle \uparrow }\!r^i_2,\ldots ,{}^{\scriptscriptstyle \uparrow }\!r^i_N)\) with \({}^{\scriptscriptstyle \uparrow }\!r^i_{1}< {}^{\scriptscriptstyle \uparrow }\!r^i_{2}< \cdots < {}^{\scriptscriptstyle \uparrow }\!r^i_{N}\).Footnote 13 If \({\mathcal { A}}=\{a_1,a_2,\ldots ,a_N\}\) and \(a_1 \prec _i a_2 \prec _i\cdots \prec _i a_N\), then set \(u_i(a_1):={}^{\scriptscriptstyle \uparrow }\!r^i_{1}\), \(u_i(a_2):={}^{\scriptscriptstyle \uparrow }\!r^i_{2}\), \(\ldots \), and \(u_i(a_N):={}^{\scriptscriptstyle \uparrow }\!r^i_{N}\).
The rank scoring rule described prior to Theorem 5.2 now has the following construction. Take a random sample of N independent random variables drawn from \(\rho \), and compute the order statistics of this sample; this yields N new random variables (which are neither independent, nor identically distributed). Let \(s^{N}_{1}< s^{N}_{2}< \cdots < s^{N}_{N}\) be the expected values of these random variables. Then set \({\mathbf { s}}:=(s^{N}_{1},s^{N}_{2},\ldots ,s^{N}_{N})\).
It is convenient to “renormalize” \(s^{N}_{1},s^{N}_{2},\ldots ,s^{N}_{N}\) to range over the interval \({\left[ -1,1 \right]}\), by defining
This ensures that \({\widetilde{s}}^{N}_{N}=1\) and \({\widetilde{s}}^{N}_{1}=-1\). (For example, if \(N=3\), then we have \({\widetilde{s}}^{3}_{3}=1\) and \({\widetilde{s}}^{3}_{1}=-1\), and only the value of \({\widetilde{s}}^{3}_{2}\) remains to be determined.) If \(\rho \) is a probability distribution symmetrically distributed about some point in the real line, then the values \({\widetilde{s}}^{N}_{1},{\widetilde{s}}^{N}_{2},\ldots ,{\widetilde{s}}^{N}_{N}\) will be symmetrically distributed around zero—that is, \({\widetilde{s}}^{N}_{k} = - {\widetilde{s}}^{N}_{N+1-k}\) for all k in \({\left[ 1\ldots N \right]}\). Thus, if N is odd and \(k=(N+1)/2\), then \({\widetilde{s}}^{N}_{k}=0\). In particular, if \(N=3\), then we must have \({\widetilde{s}}^{3}_{2}=0\), while \({\widetilde{s}}^3_3=1\) and \({\widetilde{s}}^3_1=-1\). Thus, we get the rank scoring rule defined by the scoring vector \((-1,0,1)\), which is just the Borda rule. Thus, Theorem 5.2 implies the next result, which says that the Borda rule is asymptotically utilitarian-optimal for any symmetric measure \(\rho \).
Corollary 5.4
Suppose \(|{\mathcal { A}}|=3\), and let \({\mathcal { P}}_{\mathcal { I}}=\{\succ _i\}_{i\in {\mathcal { I}}}\) be any profile of preference orders on \({\mathcal { A}}\). Let \(\rho \) be any symmetric, finite-variance probability distribution on \({\mathbb {R}}\). If \(\{u_i\}_{i\in {\mathcal { I}}}\), and \(\{c_i\}_{i\in {\mathcal { I}}}\) satisfy (C), \((\Delta )\) and (X\('\)), then
If \(|{\mathcal { A}}|\ge 4\), then the Borda rule is no longer guaranteed to be asymptotically optimal; the optimal rule will depend on the expected values of the order statistics for \(\rho \), which depend on the structure of \(\rho \) itself. For example, suppose \(\rho \) was a standard normal probability distribution and \(|{\mathcal { A}}|=7\). Then we get the following expected order statistics (to 5 significant digits).
By comparision, the Borda rule uses the scoring vector \((-1, -0.6\overline{6}, -0.3\overline{3}, 0, 0.3\overline{3}, 0.6\overline{6}, 1)\).
Unfortunately, the expected values of order statistics are quite hard to compute for many probability distributions. Harter and Balakrishnan (1996) provide tables of these expected values for most of the common probability distributions (e.g. normal, exponential, Weibull, etc.); from this data it is easy to design the appropriate rank scoring rule.
Remark on strategic voting Scoring rules are highly susceptible to strategic voting. Theorems 5.1 and 5.2 do not address this issue. However, given any scoring rule F, Núñez and Pivato (2016, Theorem 1) show that, in a sufficiently large population, there is a stochastic voting rule which will produce the same outcome as F, with very high probability, and where almost all voters will vote honestly. This result, combined with Theorems 5.1 and 5.2, suggests that in a sufficiently large population satisfying hypotheses (C), \((\Delta )\), and either (X) or hypotheses (N1) and (N2), this stochastic scoring rule will select the utilitarian-optimum outcome with very high probability, even when we allow for strategic voting.
6 Conclusion
For a large enough population, our results suggest that simple and popular voting rules such as the Borda rule or approval voting have a very high probability of selecting an alternative which maximizes or almost-maximizes the utilitarian social welfare function. However, our results depend on some substantive assumptions. We will now briefly discuss some of these assumptions.
First, we have often assumed that the random variables associated with different voters are independent. This assumption is shared by virtually all the literature reviewed in Sect. 1.Footnote 14 But it excludes the possibility that voters belonging to a particular community or social group might exhibit correlations in their utility functions, preference intensities, errors, and/or approval thresholds. Empirical data suggests that these independence assumptions are false (Gelman et al. 2004). But they were made for expositional simplicity, rather than technical necessity. The results in this paper are derived using results from Section 2 of Pivato (2016c), which assumes stochastically independent voters. Section 3 of Pivato (2016c) extends these results to correlated voters, assuming the correlation strength is not too strong.Footnote 15 Using this extension, it would be straightforward to extend the results of the present paper to correlated voters.
A major obstacle to any implementation of utilitarian social choice is strategic voting. As we have already noted, Núñez and Pivato (2016) offers a possible solution, which is particularly suitable for the large-population, probabilistic approach taken in this paper. The mechanisms in Núñez and Pivato (2016) make truthful voting an optimal strategy for almost all voters, but at a price: they introduce a tiny probability that the rule will choose a socially suboptimal outcome. (In effect: they induce each voter to reveal her true preferences by offering her a small chance to be a “random dictator”.) This is very similar to the concept of virtual implementation introduced by Matsushima (1988) and Abreu and Sen (1991). Virtual implementation is an extremely powerful and versatile implementation technology; the main idea is that it is sufficient to obtain a very high probability of selecting a socially optimal outcome, rather than certainty. Thus, virtual implementation is also well-suited to the probabilistic approach of the present paper. Another partial solution to strategic voting is suggested by Kim (2014), who shows that, with stochastically independent voters, the rank scoring rules considered in Sect. 5 are truth-revealing in Bayesian Nash equilibrium.
Finally, each of our results depends on specific assumptions about the statistical distribution of utility functions in the population. Thus, to select the best rule, we must know something about this distribution. The statistical distribution of utility functions probably depends on both the society and the particular policy problem. Thus, different voting rules may be optimal in different situations. In some situations, none of the voting rules considered here may be optimal, from a utilitarian perspective. This suggests a two-stage approach. In the first stage, estimate the utility functions of some statistically representative sample of the population (e.g. using a survey). Use this data to estimate the statistical distribution of utilities, and then determine which voting rule (if any) is optimal, given this distribution. If the statistical distribution of utility functions satisfies the hypotheses of one of the results in this paper, then in the second stage, we can use the corresponding voting rule to make the collective decision. Otherwise, we must resort to some other method.
Notes
In fact, Rae and Taylor were interested in maximizing “responsiveness”: the probability that the outcome agrees with the preference of a random individual. But if all voters have equal preference intensities, then maximizing “responsiveness” is equivalent to maximizing the utilitarian SWF. See also Badger (1972), Curtis (1972), Schofield (1972), Straffin (1977), and Dubey and Shapley (1979) for extensions of the Rae–Taylor theorem. Riley (1990) appears to have independently intuited some of the same conclusions. But he did not give any formal proofs. More recently, Fleurbaey (2009) has proved a far-reaching generalization of the Rae–Taylor theorem to a setting where voters may have different preference intensities and arbitrary correlations.
For i.u.d. utilities, this result had been anticipated by Weber (1978, p. 10).
However, approval voting and all rank scoring rules reduce to simple majority vote when there are only two alternatives. Thus, in this setting, our results in Sects. 4 and 5 imply the utilitarian optimality of simple majority voting, and are complementary to the Rae–Taylor theorem and its extensions.
Since they consider a democratic federation of regions, the papers by Barberà and Jackson (2006), Beisbart et al. (2005), Beisbart and Bovens (2007), Beisbart and Hartmann (2010), Laruelle and Valenciano (2008; 2010), etc. presumably posit large populations. However, most of these papers represent each population in reduced form as an averaged utility function, not as a set of individuals, and none of them engage in any sort of asymptotic analysis.
Laslier (2012) discusses several other ways to assign “scores” to alternatives based on the voters’ approval sets, e.g. by computing the stationary probability distribution of an associated Markov process. It might be possible to prove “asymptotic utilitarian” results for these alternative approval scoring systems as well. But for simplicity, we will confine the analysis in this paper to the standard approval scoring system.
Typically, \(\gamma \) and \(\beta \) would have nonoverlapping support; e.g. \(\gamma \) would be a measure on \([0,{\infty })\) while \(\beta \) would be a measure on \((-{\infty },0]\). But we don’t need to assume this. Note that \(\gamma \) and \(\beta \) are not assumed to be Gamma or Beta distributions.
The fourth moment of a probability measure \(\gamma \) is the integral \(\displaystyle \int _{-{\infty }}^{\infty }u^4 \ \mathrm{d}\gamma [u]\). It is finite if d\(\gamma [u]\) decays quickly enough as \(u{\rightarrow }\pm {\infty }\).
The fourth moment of the multivariate probability measure \(\lambda \) is the integral \(\displaystyle \int _{\mathbb {U}}\sum \nolimits _{n=1}^N u_n^4 \ \mathrm{d}\lambda [{\mathbf { u}}]\). It is finite if d\(\lambda [{\mathbf { u}}]\) decays quickly enough as \({\left\| {\mathbf { u}} \right\| _{{}} } {\rightarrow }{\infty }\). For example, the fourth moment of a multivariate normal probability measure is finite.
\(({}^{\scriptscriptstyle \uparrow }\!r^i_1,{}^{\scriptscriptstyle \uparrow }\!r^i_2,\ldots ,{}^{\scriptscriptstyle \uparrow }\!r^i_N)\) are called the order statistics of the sample.
To be more precise, we need an asymptotic condition on the \(L^1\) norm of the covariance matrix of the random variables \(\{c_i\}_{i\in {\mathcal { I}}}\) and \(\{u_i\}_{i\in {\mathcal { I}}}\), as \(I{\rightarrow }{\infty }\).
We do not assume that, for a fixed voter i in \({\mathcal { I}}\), the random errors \(\epsilon _i(a)\) and \(\epsilon _i(b)\) are independent for different alternatives a and b in \({\mathcal { A}}\).
To be precise, we fix an infinite sequence \((\succ _n)_{n=1}^{\infty }\) of ordinal preferences. Then, for any particular value of I, we identify \({\mathcal { I}}\) with \([1\ldots I]\) and let \({\mathcal { P}}_{\mathcal { I}}=\{\succ _n\}_{n=1}^I\). Theorem 5.2 then applies for every possible infinite sequence.
The set of all possible infinite sequences \((\succ _n)_{n=1}^{\infty }\) has a natural sigma-algebra (generated by “cylinder sets”, which are defined by fixing values for any finite number of coordinates). The Endogenous preference model defines a probability measure on this sigma algebra (in fact, it is a Bernoulli stochastic process). In the last step of the proof, we integrate with respect to this probability measure.
References
Abreu D, Sen A (1991) Virtual implementation in Nash equilibrium. Econometrica 59(4):997–1021
Alcantud JCR, Laruelle A (2014) Dis&approval voting: a characterization. Soc Choice Welf 43(1):1–10
Apesteguia J, Ballester MA, Ferrer R (2011) On the justice of decision rules. Rev Econ Stud 78(1):1–16
Azrieli Y, Kim S (2014) Pareto efficiency and weighted majority rules. Int Econ Rev 55(4):1067–1088
Badger WW (1972) Political individualism, positional preferences, and optimal decision-rules. In: Niemi and Weisberg, pp 34–59
Banks J, Duggan J (2004) Probabilistic voting in the spatial model of elections: the theory of office-motivated candidates. In: Austen-Smith D, Duggan J (eds.) Social Choice and Strategic Decisions, Springer, New York, pp 15–56
Barberà S, Jackson MO (2006) On the weights of nations: assigning voting power to heterogeneous voters. J Polit Econ 114(2):317–339
Baujard A, Igersheim H, Lebon I, Gavrel F, Laslier J-F (2014) Who’s favored by evaluative voting? an experiment conducted during the 2012 french presidential election. Elect Stud 34:131–145
Beisbart C, Bovens L (2007) Welfarist evaluations of decision rules for boards of representatives. Soc Choice Welf 29(4):581–608
Beisbart C, Bovens L, Hartmann S (2005) A utilitarian assessment of alternative decision rules in the council of ministers. Eur Union Polit 6(4):395–418
Beisbart C, Hartmann S (2010) Welfarist evaluations of decision rules under interstate utility dependencies. Soc Choice Welf 34(2):315–344
Black DS (1958) Theory of committees and elections. Cambridge University Press, Cambridge
Bordley RF (1983) A pragmatic method for evaluating election schemes through simulation. Am Polit Sci Rev 77:123–141
Bordley RF (1985a) A precise method for evaluating election schemes. Public Choice 46(2):113–123
Bordley RF (1985b) Using factions to estimate preference intensity: improving upon one person/one vote. Public Choice 45(3):257–268
Bordley RF (1986) One person/one vote is not efficient given information on factions. Theory Decis 21(3):231–250
Boutilier C, Caragiannis I, Haber S, Lu T, Procaccia AD, Sheffet O (2012) Optimal social choice functions: a utilitarian view. In: Proceedings of the 13th ACM conference on electronic commerce. EC ’12. ACM, New York, NY, USA, pp 197–214
Bovens L, Hartmann S (2007) Welfare, voting and the constitution of a federal assembly. In: Galavotti MC, Scazzieri R, Suppes P (eds) Reasoning, rationality and probability. CSLI Publications, Stanford
Brams SJ, Fishburn PC (1983) Approval voting. Birkhäuser Boston, Boston
Caragiannis I, Procaccia AD (2011) Voting almost maximizes social welfare despite limited communication. Artif Intell 175(9–10):1655–1671
Coughlin P (1992) Probabilistic voting theory. Cambridge University Press, Cambridge
Curtis RB (1972) Decision-rules and collective values in constitutional choice. In: Niemi and Weisberg, pp 23–33
De Sinopoli F, Dutta B, Laslier J-F (2006) Approval voting: three examples. Int J Game Theory 35(1):27–38
Dhillon A (1998) Extended Pareto rules and relative utilitarianism. Soc Choice Welf 15:521–542
Dhillon A, Mertens J-F (1999) Relative utilitarianism. Econometrica 67:471–498
Dubey P, Shapley LS (1979) Mathematical properties of the Banzhaf power index. Math Oper Res 4(2):99–131
Fleurbaey M (2009) One stake one vote (preprint)
Gelman A, Katz JN, Bafumi J (2004) Standard voting power indexes do not work: an empirical analysis. Br J Polit Sci 34:657–74
Giles A, Postl P (2014) Equilibrium and effectiveness of two-parameter scoring rules. Math Soc Sci 68:31–52
Harter HL, Balakrishnan N (1996) CRC handbook of tables for the use of order statistics in estimation. CRC Press, Boca Raton
Hillinger C (2005) The case for utilitarian voting. Homo Oecon 23:295–321
Kellett J, Mott K, Summer, (1977) Presidential primaries: measuring popular choice. Polity 9(4):528–537
Kim S (2014) Ordinal versus cardinal voting rules: a mechanism design approach (preprint)
Koriyama Y, Laslier J-F, Macé A, Treibich R (2013) Optimal apportionment. J Polit Econ 121(3):584–608
Krishna V, Morgan J (2012) Voluntary voting: costs and benefits. J Econ Theory 147(6):2083–2123
Laruelle A, Valenciano F (2008) Voting and collective decision-making: bargaining and power. Cambridge University Press, Cambridge
Laruelle A, Valenciano F (2010) Egalitarianism and utilitarianism in committees of representatives. Soc Choice Welf 35(2):221–243
Laslier J-F (2012) And the loser is... plurality voting. In: Felsenthal SD, Machover M (eds) Electoral systems: paradoxes, assumptions, and procedures. Studies in choice and welfare. Springer, Berlin, pp 327–351
Laslier J-F, Sanver MR (eds) (2010) Handbook on approval voting. Studies in Choice and Welfare. Springer, Heidelberg
Ledyard JO (1984) The pure theory of large two-candidate elections. Public Choice 44(1):7–41
Lehtinen A (2007) The Borda rule is also intended for dishonest men. Public Choice 133(1–2):73–90
Lehtinen A (2008) The welfare consequences of strategic behaviour under approval and plurality voting. Eur J Polit Econ 24:688–704
Lindbeck A, Weibull JW (1987) Balanced-budget redistribution as the outcome of political competition. Public Choice 52(3):273–297
Lindbeck A, Weibull JW (1993) A model of political equilibrium in a representative democracy. J Public Econ 51(2):195–209
Maaser N, Napel S (2014) The mean voter, the median voter, and welfare-maximizing voting weights. In: Fara R, Leech D, Salles M (eds) Voting power and procedures. Studies in choice and welfare series. Springer, Berlin
Macé A (2013) Voting with evaluations: when should we sum? What should we sum? (preprint)
Macé A, Treibich R (2012) Computing the optimal weights in a utilitarian model of apportionment. Math Soc Sci 63(2):141–51
Matsushima H (1988) A new approach to the implementation problem. J Econ Theory 45(1):128–144
McKelvey RD, Patty JW (2006) A theory of voting in large elections. Games Econ Behav 57(1):155–180
Merrill S (1984) A comparison of efficiency of multicandidate electoral systems. Am J Polit Sci 28:23–48
Myerson RB (2002) Comparison of scoring rules in Poisson voting games. J Econ Theory 103(1):219–251
Niemi RG, Weisberg HF (eds) (1972) Probability models of collective decision making. Charles E Merrill Publishing, Columbus
Nitzan S (2009) Collective preference and choice. Cambridge University Press, Cambridge
Núñez M, Laslier J-F (2014) Preference intensity representation: strategic overstating in large elections. Soc Choice Welf 42(2):313–340
Núñez M, Pivato M (2016) Truth-revealing voting rules for large populations (preprint)
Núñez M (2014) The strategic sincerity of approval voting. Econ Theory 56(1):157–189
Ottewell G (1977) The arithmetic of voting. In: Defense of Variety. http://www.universalworkshop.com/ARVOfull.htm
Pivato M (2013) Voting rules as statistical estimators. Soc Choice Welf 40(2):581–630
Pivato M (2015) Condorcet meets Bentham. J Math Econ 59:58–65
Pivato M (2016a) Dominant strategy utilitarianism in large populations (preprint)
Pivato M (2016b) Epistemic democracy with correlated voters (preprint)
Pivato M (2016c) Statistical utilitarianism. J Theor Polit (to appear)
Rae D (1969) Decision rules and individual values in constitutional choice. Am Polit Sci Rev 63:40–56
Riley J (1990) Utilitarian ethics and democratic government. Ethics 100(2):335–348
Schofield NJ (1972) Is majority rule special? In: Niemi and Weisberg, pp 60–82
Smith WD (2000) Range voting. http://rangevoting.org (unpublished)
Straffin PD Jr (1977) Majority rule and general decision rules. Theory Decis 8(4):351–360
Tangian AS (2000) Unlikelihood of Condorcet’s paradox in a large society. Soc Choice Welf 17(2):337–365
Tanguiane AS (1991) Aggregation and representation of preferences: introduction to mathematical theory of democracy. Springer, Berlin
Taylor M (1969) Proof of a theorem on majority rule. Behav Sci 14:228–231
Weber RJ (1978) Comparison of voting systems. Discussion paper 498, Cowles Foundation for Research in Economics
Acknowledgments
I am grateful to Michel le Breton, Rohan Dutta, Ori Heffetz, Sean Horan, Jérôme Lang, Christophe Muller, Matías Núñez, and Clemens Puppe for helpful comments on earlier versions of this paper. I also thank Gustaf Arrhenius, Miguel Ballester, Marc Fleurbaey, Annick Laruelle, and the other participants of the June 2014 “Workshop on Power” at the Collège d’Études Mondiales in Paris. Finally, I thank two anonymous referees for their careful reading and helpful comments. None of these people are responsible for any errors. Most of this research was done when I was at the Department of Mathematics at Trent Universty, in Canada. This research was supported by NSERC Grant #262620-2008, and by Labex MME-DII (ANR11-LBX-0023-01).
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: Background
The proofs in this paper depend on some results from Pivato (2016c). In this appendix, we briefly review these results.
Pivato (2016c) considers the problem of a utilitarian social planner who can only make noisy observations of the utility functions of the individuals in society and the correct system of interpersonal comparisons. For every i in \({\mathcal { I}}\), let \(u_i:{\mathcal { A}}{{\longrightarrow }}{\mathbb {R}}\) be the true cardinal utility function for voter i, and let \(c_i>0\) be a calibration constant, which we will use to make cardinal interpersonal utility comparisons. We suppose that the social planner wants to maximize the utilitarian social welfare function \(U_{\mathcal { I}}:{\mathcal { A}}{{\longrightarrow }}{\mathbb {R}}\) defined by Formula (1); however, she faces the following informational problems.
- (U1) :
-
\(\{c_i\}_{i\in {\mathcal { I}}}\) are unknown. The planner regards \(\{c_i\}_{i\in {\mathcal { I}}}\) as independent (but not necessarily identically distributed) real-valued random variables. There are constants \({\overline{c}}>0\) and \(\sigma _c^2\ge 0\) (independent of I) such that \({\mathbb {E}}[c_i]={\overline{c}}\) and \(\mathrm{var}[c_i]\le \sigma _c^2\), for all \(i\in {\mathcal { I}}\).
- (U2) :
-
The utility functions \(\{u_i\}_{i\in {\mathcal { I}}}\) are not precisely observable. Instead, for each i in \({\mathcal { I}}\), the planner can only observe a function \(v_i:=u_i+\epsilon _i\), where \(\epsilon _i:{\mathcal { A}}{{\longrightarrow }}{\mathbb {R}}\) is a random “error” term. For each alternative a in \({\mathcal { A}}\), the random errors \(\{\epsilon _i(a)\}_{i\in {\mathcal { I}}}\) are independentFootnote 16 (but not necessarily identically distributed), and they all have an expected value of 0 and a variance less than or equal some constant \(\sigma _\epsilon ^2>0\) (which is independent of I). Finally, the random variables \(\{c_i\}_{i\in {\mathcal { I}}}\) are independent of the random functions \(\{\epsilon _i\}_{i\in {\mathcal { I}}}\).
We assume that the utility profile \(\{u_i\}_{i\in {\mathcal { I}}}\) satisfies one or both of the following conditions.
- (U3) :
-
There is a constant \(\Delta >0\) (independent of I) such that \(\max _{{\mathcal { A}}} (U_{\mathcal { I}})-U_{\mathcal { I}}(a)>\Delta \) for every \(a\not \in {{\mathrm{\mathrm{argmax}}}}_{{\mathcal { A}}} (U_{\mathcal { I}})\).
- (U4) :
-
There is a constant \(M>0\) (independent of I) such that
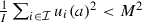 for every a in \({\mathcal { A}}\).
for every a in \({\mathcal { A}}\).
Note that, while we assume that \(\{v_i\}_{i\in {\mathcal { I}}}\) and \(\{c_i\}_{i\in {\mathcal { I}}}\) are random variables, we make no assumptions about the mechanism generating the underlying profile of utility functions \(\{u_i\}_{i\in {\mathcal { I}}}\). These utility functions might be fixed in advance, or they might themselves be generated by some other random process, as long as they satisfy (U4) and (U3). Define the function \(V_{\mathcal { I}}:{\mathcal { A}}{{\longrightarrow }}{\mathbb {R}}\) as in Eq. (2), and define the SWF \(U_{\mathcal { I}}:{\mathcal { A}}\,{{\longrightarrow }}\,{\mathbb {R}}\) as in Eq. (1). Here is Theorem 1 of Pivato (2016c).
Theorem 6.1
For every i in \({\mathcal { I}}\), let \(u_i:{\mathcal { A}}\,{{\longrightarrow }}\, {\mathbb {R}}\) be a utility function. Suppose the profile \(\{u_i\}_{i\in {\mathcal { I}}}\) satisfies (U3) and (U4). If \(\{c_i\}_{i\in {\mathcal { I}}}\), \(\{\epsilon _i\}_{i\in {\mathcal { I}}}\) and \(\{v_i\}_{i\in {\mathcal { I}}}\) are randomly generated according to rules (U1) and (U2), then
For any \(\delta >0\) and \(p\in (0,1)\), we define
Define \(U^*_{\mathcal { I}}:=\max {\left\{ U_{\mathcal { I}}(a) \; ; \; a\in {\mathcal { A}} \right\} }\). Here is Theorem 2 of Pivato (2016c).
Theorem 6.2
Suppose \(\{u_i\}_{i\in {\mathcal { I}}}\), \(\{c_i\}_{i\in {\mathcal { I}}}\), \(\{\epsilon _i\}_{i\in {\mathcal { I}}}\) and \(\{v_i\}_{i\in {\mathcal { I}}}\) satisfy (U1), (U2) and (U4). For any \(\delta >0\) and \(p\in (0,1)\), if \(I\ge {\overline{I}}(\delta ,p)\), then \(\mathrm{Prob}\left[ U_{\mathcal { I}}(a)< U^*_{\mathcal { I}}-\delta \right]\ < \ p\), for all a in \({{\mathrm{\mathrm{argmax}}}}_{{\mathcal { A}}} (V_{\mathcal { I}})\).
Appendix 2: Proofs
Proof of Theorem 3.1
We will derive this from Theorem 6.1. Recall that \(u_i:=w_i/c_i\), so that \(w_i=c_i\,u_i\); with this substitution, formulae (3) and (1) are equivalent. Observe that hypothesis (C) implies (U1) (with \({\overline{c}}:=1\)), hypothesis (E) implies (U2), and hypothesis \((\Delta )\) implies (U3). Meanwhile, hypothesis (U4) is true automatically, with \(M=1\), because the functions \(\{u_i\}_{i\in {\mathcal { I}}}\) range over [0, 1]. The asymptotic probability claim now follows from Theorem 6.1. \(\square \)
Proof of Proposition 3.2
If we set \(M:=1\) in formula (11), we obtain formula (5). The asymptotic probability inequality now follows from Theorem 6.2. \(\square \)
Proof of Theorem 4.1
Let \(g:={\mathbb {E}}[u^i_a\,|\, u^i_a\ge \theta _i]\) and let \(b:={\mathbb {E}}[u^i_a\,|\, u^i_a< \theta _i]\); thus \(g>b\). By \((\Theta 1)\) and \((\Theta 2)\), these values do not depend on i or a. For all \(i\in {\mathcal { I}}\), define \(v_i:{\mathcal { A}}\,{{\longrightarrow }}\,{\mathbb {R}}\) by
[The second equality is by Eq. (6).] Then define \(\epsilon _i(a):=v_i(a)-u_i(a)\) for all \(a\in {\mathcal { A}}\). Thus, \(v_i = u_i+\epsilon _i\). By construction, \({\mathbb {E}}[u_i(a)\,|\,v_i(a)]=v_i(a)\), and thus \({\mathbb {E}}[\epsilon _i(a)]=0\), for all \(i\in {\mathcal { I}}\) and \(a\in {\mathcal { A}}\). Let \({\overline{c}}:=g-b\); then \({\overline{c}}>0\). For all \(i\in {\mathcal { I}}\), let \({\widetilde{u}}_i:=u_i/{\overline{c}}\) and \({\widetilde{c}}_i:={\overline{c}}\cdot c_i\); thus, \(c_i\, u_i = {\widetilde{c}}_i\,{\widetilde{u}}_i\). Thus, \(U_{\mathcal { I}}= \frac{1}{I}\sum _{i\in {\mathcal { I}}} {\widetilde{c}}_i{\widetilde{u}}_i\). For all \(i\in {\mathcal { I}}\), let \({\widetilde{v}}_i:=v_i/{\overline{c}}\) and \({\widetilde{\epsilon }}_i := \epsilon _i/{\overline{c}}\); thus, \({\widetilde{v}}_i = {\widetilde{u}}_i+{\widetilde{\epsilon }}_i\). Let \({\widetilde{V}}_{\mathcal { I}}=\sum _{i\in {\mathcal { I}}} {\widetilde{v}}_i\). Then \({\widetilde{V}}_{\mathcal { I}}=V_{\varvec{{\mathcal { G}}}}+\)(a constant). Thus, \({{\mathrm{\mathrm{argmax}}}}_{\mathcal { A}}({\widetilde{V}}_{\mathcal { I}})={{\mathrm{\mathrm{argmax}}}}_{\mathcal { A}}(V_{\varvec{{\mathcal { G}}}})\). But \({{\mathrm{\mathrm{argmax}}}}_{\mathcal { A}}(V_{\varvec{{\mathcal { G}}}})=\mathrm{Appr}({\varvec{{\mathcal { G}}}})\); thus, it suffices to compute the asymptotic probability that \({{\mathrm{\mathrm{argmax}}}}_{\mathcal { A}}({\widetilde{V}}_{\mathcal { I}})\subseteq {{\mathrm{\mathrm{argmax}}}}_{\mathcal { A}}(U_{\mathcal { I}})\), using Theorem 6.1. To do this, we must verify hypotheses (U1)–(U4). First, let \({\overline{u}}:={\mathbb {E}}[u^i_a]\) and let \(\sigma ^2_u:=\mathrm{var}[u^i_a]\) for any \(i\in {\mathcal { I}}\) and \(a\in {\mathcal { A}}\). By hypothesis \((\Theta 1)\), these values are finite and independent of i and a. Let \(M:={\overline{u}}^2+\sigma _u^2\). \(\square \)
Claim A
\(\displaystyle \lim _{I{\rightarrow }{\infty }} \mathrm{Prob}\quad (M \quad \text {and the profile} \{u_i\}_{i\in {\mathcal { I}}} \ \text {satisfy condition } \; \mathrm{(}U4)) = 1\).
Proof
Fix \(a\in {\mathcal { A}}\). For all \(i\in {\mathcal { I}}\), we have \( {\mathbb {E}}[u_i^2(a)] ={\overline{u}}^2 + \sigma ^2_u = M^2\). Thus, \(\frac{1}{I}\sum _{i\in {\mathcal { I}}} u_i(a)^2\) is an average of I independent random variables (by \((\Theta 1)\)), each with expected value \(M^2\). Thus, the Law of Large Numbers implies that
Thus, since \({\mathcal { A}}\) is finite, the claim follows.\(\diamond \)
Hypotheses \((\Theta 1)\) and \((\Theta 2)\) imply that \(\{{\widetilde{u}}_i\}_{i\in {\mathcal { I}}}\), \(\{{\widetilde{v}}_i\}_{i\in {\mathcal { I}}}\) and \(\{{\widetilde{\epsilon }}_i\}_{i\in {\mathcal { I}}}\) satisfy (U2). Hypothesis (C) implies that \(\{{\widetilde{c}}_i\}_{i\in {\mathcal { I}}}\) satisfies (U1), and hypothesis \((\Delta )\) implies that \(\{{\widetilde{u}}_i\}_{i\in {\mathcal { I}}}\) satisfies (U3) (with \(\widetilde{\Delta }:=\Delta /{\overline{c}}\)). Now apply Claim A and Theorem 6.1 to \(\{{\widetilde{u}}_i\}_{i\in {\mathcal { I}}}\), \(\{{\widetilde{v}}_i\}_{i\in {\mathcal { I}}}\), \(\{{\widetilde{\epsilon }}_i\}_{i\in {\mathcal { I}}}\) and \(\{{\widetilde{c}}_i\}_{i\in {\mathcal { I}}}\) to derive the claimed asymptotic probability. \(\square \)
Proof of Theorem 4.2
The strategy is very similar to the proof of Theorem 4.1. Let g be the mean value of \(\gamma \), and let b be the mean value of \(\beta \); thus \(g>b\). For all \(i\in {\mathcal { I}}\), define \(v_i:{\mathcal { A}}{{\longrightarrow }}{\mathbb {R}}\) by
Then define \(\epsilon _i(a):=v_i(a)-u_i(a)\) for all \(a\in {\mathcal { A}}\). Thus, \(v_i = u_i+\epsilon _i\). By construction, \({\mathbb {E}}[u_i(a)]=v_i(a)\), and thus \({\mathbb {E}}[\epsilon _i(a)]=0\), for all \(i\in {\mathcal { I}}\) and \(a\in {\mathcal { A}}\). Let \({\overline{c}}:=g-b\); then \({\overline{c}}>0\). For all \(i\in {\mathcal { I}}\), let \({\widetilde{u}}_i:=u_i/{\overline{c}}\) and \({\widetilde{c}}_i:={\overline{c}}\cdot c_i\); thus, \(c_i\, u_i = {\widetilde{c}}_i\,{\widetilde{u}}_i\). Thus, \(U_{\mathcal { I}}= \frac{1}{I}\sum _{i\in {\mathcal { I}}} {\widetilde{c}}_i{\widetilde{u}}_i\). For all \(i\in {\mathcal { I}}\), let \({\widetilde{v}}_i:=v_i/{\overline{c}}\) and \({\widetilde{\epsilon }}_i := \epsilon _i/{\overline{c}}\); thus, \({\widetilde{v}}_i = {\widetilde{u}}_i+{\widetilde{\epsilon }}_i\). Let \({\widetilde{V}}_{\mathcal { I}}=\sum _{i\in {\mathcal { I}}} {\widetilde{v}}_i\). Then \({\widetilde{V}}_{\mathcal { I}}=V_{\varvec{{\mathcal { G}}}}+\)(a constant). Thus, \({{\mathrm{\mathrm{argmax}}}}_{\mathcal { A}}({\widetilde{V}}_{\mathcal { I}})={{\mathrm{\mathrm{argmax}}}}_{\mathcal { A}}(V_{\varvec{{\mathcal { G}}}})\). But \({{\mathrm{\mathrm{argmax}}}}_{\mathcal { A}}(V_{\varvec{{\mathcal { G}}}})=\mathrm{Appr}({\varvec{{\mathcal { G}}}})\); thus, it suffices to compute the asymptotic probability that \({{\mathrm{\mathrm{argmax}}}}_{\mathcal { A}}({\widetilde{V}}_{\mathcal { I}})\subseteq {{\mathrm{\mathrm{argmax}}}}_{\mathcal { A}}(U_{\mathcal { I}})\), using Theorem 6.1. \(\square \)
Let \(M_g:=g^2 + \mathrm{var}[\gamma ]\) and \(M_b:=b^2 + \mathrm{var}[\beta ]\). Let \(M:=\sqrt{\max \{M_g,M_b\}}\) and let \({\widetilde{M}}:=M/{\overline{c}}\).
Claim B
\(\displaystyle \lim \limits _{I{\rightarrow }{\infty }} \mathrm{Prob}({\widetilde{M}}\; \text { and the profile } \; \{{\widetilde{u}}_i\}_{i\in {\mathcal { I}}} \; \text { satisfy condition }\; \mathrm{(U4)}) = 1\).
Proof
Fix \(a\in {\mathcal { A}}\). For all \(i\in {\mathcal { I}}\), if \(a\in {\mathcal { G}}_i\), then \({\mathbb {E}}[u_i^2(a)] =M_g\). If \(a\in {\mathcal { B}}_i\), then \({\mathbb {E}}[u_i^2(a)] =M_b\). Either way, \({\mathbb {E}}[u_i^2(a)] \le M^2\). Thus, \(\frac{1}{I}\sum _{i\in {\mathcal { I}}} u_i(a)^2\) is an average of I independent random variables (by (S)), each with expected value \(M^2\). Thus, the Law of Large Numbers implies that
Since \({\widetilde{u}}_i:=u_i/{\overline{c}}\) for all \(i\in {\mathcal { I}}\), it follows that
Thus, since \({\mathcal { A}}\) is finite, the claim follows.\(\diamond \)
Hypothesis (C) implies that \(\{{\widetilde{c}}_i\}_{i\in {\mathcal { I}}}\) satisfies (U1). Define \(\sigma ^2_\epsilon :=\max \{\mathrm{var}(\gamma ),\mathrm{var}(\beta \}/{\overline{c}}^2\). Since \({\widetilde{\epsilon }}_i={\widetilde{u}}_i-{\widetilde{v}}_i\), it follows that \(\mathrm{var}({\widetilde{\epsilon }}_i)\le \sigma ^2_\epsilon \) for all i. Thus, hypothesis (S) implies that \(\{{\widetilde{u}}_i\}_{i\in {\mathcal { I}}}\), \(\{{\widetilde{v}}_i\}_{i\in {\mathcal { I}}}\) and \(\{{\widetilde{\epsilon }}_i\}_{i\in {\mathcal { I}}}\) satisfy (U2). Finally, hypothesis \((\Delta )\) implies that \(\{{\widetilde{u}}_i\}_{i\in {\mathcal { I}}}\) satisfy (U3) (with \(\widetilde{\Delta }:=\Delta /{\overline{c}}\)). Now apply Claim B and Theorem 6.1 to \(\{{\widetilde{u}}_i\}_{i\in {\mathcal { I}}}\), \(\{{\widetilde{v}}_i\}_{i\in {\mathcal { I}}}\), \(\{{\widetilde{\epsilon }}_i\}_{i\in {\mathcal { I}}}\) and \(\{{\widetilde{c}}_i\}_{i\in {\mathcal { I}}}\) to derive the claimed asymptotic probability. \(\square \)
Proof of Proposition 4.3
Define \(\{{\widetilde{u}}_i\}_{i\in {\mathcal { I}}}\), \(\{{\widetilde{v}}_i\}_{i\in {\mathcal { I}}}\), \(\{{\widetilde{\epsilon }}_i\}_{i\in {\mathcal { I}}}\) and \({\widetilde{V}}_{\mathcal { I}}\) as in the proof of Theorem 4.2. From Theorem 6.2, along with Claim B, we immediately obtain the limit Eq. (8). However, to obtain more precise estimates of the convergence speed, we must first estimate the speed of the convergence in Claim B, using the next result. \(\square \)
Claim C
Suppose the fourth moments of \(\gamma \) and \(\beta \) are finite. Then there is some \(C_1>0\) (determined by \(\gamma \) and \(\beta \)) such that, for any \(p\in (0,1)\), if \( I>{C_1}/{p}\), then
The proof is very similar to the proof of Claim E in the proof of Proposition 5.3 (below).
Recall that \(\{{\widetilde{u}}_i\}_{i\in {\mathcal { I}}}\), \(\{{\widetilde{v}}_i\}_{i\in {\mathcal { I}}}\) and \(\{{\widetilde{\epsilon }}_i\}_{i\in {\mathcal { I}}}\) satisfy (U2), with \(\sigma ^2_\epsilon :=\max \{\mathrm{var}(\gamma ),\mathrm{var}(\beta \}/{\overline{c}}^2\). For any \(\delta >0\) and \(p\in (0,1)\), define \({\overline{I}}(\delta ,p)\) as in equation (11). Finally, define \(C_2:=8\,|{\mathcal { A}}|\,({\widetilde{M}}^2\, \sigma _c^2+ \sigma _\epsilon ^2)\). Thus, for any \(p,\delta \in (0,1)\), if \(I>C_2/p\,\delta ^2\), then \(I>{\overline{I}}(\delta ,p/2)\), so that, for any \(a\in \mathrm{Appr}({\varvec{{\mathcal { G}}}})={{\mathrm{\mathrm{argmax}}}}_{\mathcal { A}}({\widetilde{V}}_{\mathcal { I}})\), Theorem 6.2 says
If \(I>C_1/p\) also, then Claim C applies. This, together with inequality (12), implies that \(\mathrm{Prob}\left[ U_{\mathcal { I}}(a)< U^*_{\mathcal { I}}-\delta \right] < \frac{p}{2}+\frac{p}{2} = p\), as desired.
Theorem 5.1 follows from Theorem 5.2, so we will prove that first.
Proof of Theorem 5.2
Since \(\mathrm{Score}_{\mathbf { s}}({\mathcal { P}}_{\mathcal { I}})={{\mathrm{\mathrm{argmax}}}}_{\mathcal { A}}(V^{\mathbf { s}}_{{\mathcal { P}}_{\mathcal { I}}})\), it suffices to compute the asymptotic probability that \({{\mathrm{\mathrm{argmax}}}}_{\mathcal { A}}(V^{\mathbf { s}}_{{\mathcal { P}}_{\mathcal { I}}})\subseteq {{\mathrm{\mathrm{argmax}}}}_{\mathcal { A}}(U_{\mathcal { I}})\), as \(I{\rightarrow }{\infty }\). As usual, we will use Theorem 6.1. Hypothesis (C) implies (U1). For all \(i\in {\mathcal { I}}\) and all \(a\in {\mathcal { A}}\), if we know that i ranks a in kth place (in particular, if we know the preference order \(\succ _i\)), then the expected value of \(u_i(a)\), conditional on this information, is \(s_k\). But, by definition, \(v_i(a)=s_k\). Thus, \({\mathbb {E}}[ u_i(a)|\succ _i]=v_i(a)\). Thus, if we define \(\epsilon _i(a):=u_i(a)-v_i(a)\), then \({\mathbb {E}}[ \epsilon _i(a)|\succ _i]=0\). By hypothesis, the variance of the random variable \(u_i(a)\) is finite; thus, the variance of \(\epsilon _i(a)\) is finite. Finally, by hypothesis (X), the random functions \(\{u_i\}_{i\in {\mathcal { I}}}\) are independent of one another and independent of \(\{c_i\}_{i\in {\mathcal { I}}}\). Thus, the random functions \(\{\epsilon _i\}_{i\in {\mathcal { I}}}\) are independent of one another and independent of \(\{c_i\}_{i\in {\mathcal { I}}}\). This establishes (U2). It remains to verify (U4).
Let \({}^{\scriptscriptstyle \uparrow }\!{\mathbf { u}}=({}^{\scriptscriptstyle \uparrow }\!u_1,\ldots ,{}^{\scriptscriptstyle \uparrow }\!u_N)\in {\mathbb {U}}\) be a \(\lambda \)-random vector. The coordinates \({}^{\scriptscriptstyle \uparrow }\!u_1,\ldots ,{}^{\scriptscriptstyle \uparrow }\!u_N\) are themselves random variables (neither independent, nor identically distributed). Let \(\sigma ^2_1,\ldots ,\sigma ^2_N\) denote their variances. Since \(\lambda \) has finite variance, it is easy to check that \(\sigma ^2_1,\ldots ,\sigma ^2_N\) are all finite. Define \(\sigma ^2_\epsilon :=\max \{\sigma ^2_{1},\sigma ^2_{2},\ldots ,\sigma ^2_{N}\}\). Also, let \(S:=\max \{|s_1|\), \(|s_2|\), \(\ldots ,\) \(|s_N|\}\), and choose any \(M>\sqrt{S^2 + \sigma ^2_\epsilon }\). \(\square \)
Claim D
\(\displaystyle \lim _{I{\rightarrow }{\infty }} \mathrm{Prob}(M \; \text { and the profile }\; \{u_i\}_{i\in {\mathcal { I}}} \; \text { satisfy condition (U4)}) = 1\).
Proof
Fix \(a\in {\mathcal { A}}\). For all \(i\in {\mathcal { I}}\), if a is ranked kth from the bottom by \(\succ _i\), then \(u_i(a)\) is a random variable with mean \(s_k\) and variance \(\sigma ^2_k\). Thus,
Thus, for any \(a\in {\mathcal { A}}\), the sum \(\frac{1}{I}\sum \nolimits _{i\in {\mathcal { I}}} u_i(a)^2\) is an average of I independent random variables, each with expected value smaller than \(M^2\), by inequality (13). Thus, regardless of how the preferences \(\{\succ _i\}_{i\in {\mathcal { I}}}\) are obtained, the Law of Large Numbers implies that
Thus, since \({\mathcal { A}}\) is finite, the claim follows.\(\diamond \)
Finally, hypothesis \((\Delta )\) implies that \(\{u_i\}_{i\in {\mathcal { I}}}\) satisfy (U3). Now apply Claim 1 and Theorem 6.1 to \(\{u_i\}_{i\in {\mathcal { I}}}\), \(\{v_i\}_{i\in {\mathcal { I}}}\), \(\{\epsilon _i\}_{i\in {\mathcal { I}}}\) and \(\{c_i\}_{i\in {\mathcal { I}}}\) to derive the limit (9). \(\square \)
Proof of Theorem 5.1
Define \({\mathbb {U}}\) as in Sect. 5.2, and let \(\lambda \) be the conditionalization of \(\mu \) on \({\mathbb {U}}\). In the Endogenous Preference model of Sect. 5.1, the ordinal preference profile \({\mathcal { P}}_{\mathcal { I}}=\{\succ _i\}_{i\in {\mathcal { I}}}\) is a random variable (determined by the underlying cardinal utility profile \(\{{\mathbf { u}}^i\}_{i\in {\mathcal { I}}}\). (\({\mathcal { P}}_{\mathcal { I}}\) is almost surely a profile of strict preferences, because by hypothesis on \(\mu \), no two alternatives yield the same utility for any voter, almost surely.) However, if we fix a particular realization of \({\mathcal { P}}_{\mathcal { I}}\), then conditional on this realization, the probability distribution of the cardinal profile \(\{{\mathbf { u}}^i\}_{i\in {\mathcal { I}}}\) is described by \(\lambda \) via the Exogenous preference model of Sect. 5.2. Thus, for any particular realization of \({\mathcal { P}}_{\mathcal { I}}\), Theorem 5.2 implies that the limit (9) holds.Footnote 17 Thus, integrating over all possible realizations of \({\mathcal { P}}_{\mathcal { I}}\), and applying Lebesgue’s dominated convergence theorem, we conclude that the limit (9) holds unconditionally.Footnote 18 \(\square \)
Proof of Proposition 5.3
We will apply Theorem 6.2. Define \(\{\epsilon _i\}_{i\in {\mathcal { I}}}\) and M as in the proof of Theorem 5.2. Claim 1 established that \(\lim _{I{\rightarrow }{\infty }} \mathrm{Prob}[M\) and the profile \(\{u_i\}_{i\in {\mathcal { I}}}\) satisfy condition (U4)]\(\,{=}\,\)1. However, to obtain the more precise estimate of convergence speed, we need the next observation.
Claim E
Suppose the fourth moment of \(\lambda \) is finite. Then there is some \(C_1>0\) (determined by \(\lambda \)) such that, for any \(p\in (0,1)\), if \( I>{C_1}/{p}\), then
Proof
If the fourth moment of \(\lambda \) is finite, then there is some \(C'>0\) such that for any \(a\in {\mathcal { A}}\), the fourth moments of each of the random variables \(\{u_i(a)\}_{i\in {\mathcal { I}}}\) is less than \(C'\). In other words, the second moments of each of the random variables \(\{u_i(a)^2\}_{i\in {\mathcal { I}}}\) is less than \(C'\). This implies that there is some \(C''>0\) such that the variance of each of \(\{u_i(a)^2\}_{i\in {\mathcal { I}}}\) is less than \(C''\). Also, these random variables are independent. Thus,
Next, inequality (13) says each of \(\{u_i(a)^2\}_{i\in {\mathcal { I}}}\) has expected value less than \(M^2\). Thus,
Thus, Chebyshev’s inequality and inequalities (14) and (15) imply that there is some \(C_1>0\) (determined by \(C''\)) such that, for any \(p>0\), if \(I>C_1/p\), then
Now, if the profile \(\{u_i\}_{i\in {\mathcal { I}}}\) and M to violate condition (U4), then \(\frac{1}{I}\sum _{i\in {\mathcal { I}}} u_i(a)^2 > M^2\) for some \(a\in {\mathcal { A}}\). Thus, adding together \(|{\mathcal { A}}|\) copies of inequality (16) proves the claim. \(\diamond \)
For any \(\delta >0\) and \(p>0\), let \({\overline{I}}(\delta ,p)\) be as in Eq. (11). Finally, define \(C_2:=8\,|{\mathcal { A}}|\,(M^2\, \sigma _c^2+ \sigma _\epsilon ^2)\). Thus, for any \(p,\delta \in (0,1)\), if \(I>C_2/p\,\delta ^2\), then \(I>{\overline{I}}(\delta ,p/2)\), so that, for all \(a\in {{\mathrm{\mathrm{argmax}}}}_{\mathcal { A}}({\widetilde{V}}_{\mathcal { I}})\), Theorem 6.2 says that
If \(I>C_1/p\) also, then Claim E applies. This, together with inequality (17), implies that \(\mathrm{Prob}\left[ U_{\mathcal { I}}(a)< U^*_{\mathcal { I}}-\delta \right] < \frac{p}{2}+\frac{p}{2} = p\) for any \(a\in {{\mathrm{\mathrm{argmax}}}}_{\mathcal { A}}({\widetilde{V}}_{\mathcal { I}})=\mathrm{Score}_{\mathbf { s}}({\mathcal { P}}_{\mathcal { I}})\), as desired.\(\square \)
Rights and permissions
About this article
Cite this article
Pivato, M. Asymptotic utilitarianism in scoring rules. Soc Choice Welf 47, 431–458 (2016). https://doi.org/10.1007/s00355-016-0971-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00355-016-0971-2




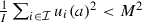 for every a in
for every a in