1 Introduction

High-speed subsonic jets generated by aircraft engines produce intense acoustic waves. Since these acoustic waves cause fatigue damage to a body and also cause environmental noise problems, researches have been conducted for reduction and prediction of acoustic waves from subsonic jets (Jordan and Gervais 2008). These acoustic waves are generated by the convection and fluctuation of eddies in turbulent flow, and their intensity increases in proportion to the eighth power of the jet velocity (Lighthill 1952). Therefore, the behavior of eddies in a jet flow has often been investigated via particle image velocimetry (PIV) (Bridges and Wernet 2011; Rodríguez et al. 2015). PIV is an optical visualization technique for capturing the velocity field and various applications of PIV have been developed such as basic 2D2C-PIV (2 components velocity field in a plane), stereoscopic PIV (2D3C), tomographic PIV (3D3C), Shake-The-Box (3D3C) (Raffel et al. 2018). In the basic 2D2C PIV, a camera and light sheet optics are employed for acquiring paired images of tracer particles in a flow that are taken at a short time interval. The images are divided into small interrogation regions and calculate the cross-correlation between corresponding interrogation regions. The displacements of the particles are determined, and then, the velocity vectors are obtained. One of the challenges of PIV is achieving high spatial resolution with broad field of view (FOV). For example, broad FOV measurement can capture the entire flow, but the resolution of fine local flow fields, such as eddy structures near the shear layer, is reduced. On the other hand, the close-up FOV measurement provides a high-resolution flow field, but it cannot track the fluctuation of the eddies due to the large displacement of the particles on the image.

A lot of efforts have been dedicated to the resolution dilemma in PIV. The first superresolution method in PIV was proposed by Keane et al. (1995) to improve the spatial resolution by combining the advantages of particle-matching velocimetry and particle-tracking velocimetry (PTV). Takehara et al. (2000) proposed a superresolution method based on Kalman filtering and \(\chi ^2\)-testing, and the vector yield is increased by more than five times. These approaches combine correlation analysis with particle tracking, and thus, various superresolution methods have been proposed in PTV community. The time-supersampling of 3D PIV measurements is developed by Schneiders et al. (2014) based on Taylor’s hypothesis of frozen turbulence. The proposed method successfully reconstructed the temporal dynamics because the spatial information can be leveraged to increase the temporal resolution under the assumption. However, the spatial region that can be applied to Taylor’s hypothesis is limited and Taylor’s hypothesis no longer holds true when measuring a entire flow field of a jet with broad FOV. Hypothesis-free superresolution methods that utilize the Navier–Stokes-based data assimilation were also developed in volumetric PTV (Schneiders and Scarano 2016; Gesemann et al. 2016; Mons et al. 2022). Although these methods can spatially and temporally reconstruct both velocity and pressure fields in a single measurement system, they cannot be applied to the basic 2D2C PIV because of the limited measurement quantities. Therefore, superresolution methods for 2D2C PIV requires a specific measurement system and data processing to supplement the missing information.

Spatiotemporal superresolution for 2D2C PIV is often difficult to achieve with a single measurement system. Therefore, it combines point measurement with superior temporal resolution and surface measurement with superior spatial resolution, and achieves a high temporal and spatial resolution that cannot be achieved by each measurement technique alone. The composite measurements dataset is often processed via a data-driven analysis such as the proper orthogonal decomposition (POD) (Berkooz et al. 1993), and the superresolved flow fields are estimated using stochastic estimation as demonstrated in earlier studies (Tinney et al. 2008; Durgesh and Naughton 2010; He and Liu 2017; Zhang et al. 2020). Tu et al. (2013) estimated time-resolved velocity fields using a hot-wire anemometer that measures at a single point with high temporal resolution and a two-dimensional planar PIV that measures the entire flow field with low temporal resolution. They successfully estimated the coherent structures of a wake behind a flat plate in a uniform flow using the linear stochastic estimation combined with POD. Ozawa et al. (2022) constructed a spatiotemporal superresolution method by combining sensors that measure different physical quantities: a microphone and a two-dimensional planar PIV. The spatiotemporal superresolution was also applied to the three-dimensional background-oriented schlieren measurements by Lee et al. (2023).

In recent years, the development of superresolution methods using machine learning has been widely researched as computation performance has improved (Fukami et al. 2023). Some studies developed spatiotemporal superresolution methods using machine learning instead of stochastic estimation and reconstructed the temporal dynamics from sparse sensors (Jin et al. 2020; Manohar et al. 2022; Fukami et al. 2022). The spatial enhancement of PIV is also tried using machine learning. Lee et al. (2017) applied convolutional neural networks to the particle images and extracted the fine-scale structures of the velocity field. A number of studies applied machine learning to PIV and enhanced the spatial resolution of PIV and PTV (Cai et al. 2019; Gao et al. 2021b; Wang et al. 2022a; Tirelli et al. 2023). Fukami et al. (2019) investigated the applicability of machine learning to spatial superresolution by applying convolutional neural network (CNN) and their proposed downsampled skip-connection/multi-scale (DSC/MS) methods. Both CNN and DSC/MS successfully reconstructed low-resolution two-dimensional decaying isotropic turbulence. Also, Gao et al. (2021a) developed physics-informed neural networks (PiNNs) that incorporate the Navier-Stokes equations in the learning process to ensure that the reconstruction results are faithful to the governing equations and not based on the methods developed in the field of image processing. The development of superresolution technology in fluid engineering shows outstanding successes and progress (Lee et al. 2017; Werhahn et al. 2019; Liu et al. 2020; Sun and Wang 2020; Brunton et al. 2020). Although a few studies employ experimental datasets such as PIV and schlieren imaging (Deng et al. 2019; Wang et al. 2022b), most studies adopt artificial low-resolution data generated by pooling or downsampling the reference high-resolution data for training. Training and validation using experimental low and high-resolution datasets are essential for bringing these methods closer to practical use. Also, although PINNs and other methods have made the learning process transparent, it is still difficult to trace the estimation process of high-resolution data using machine learning superresolution.

Therefore, the present study first constructs a database of low and high-resolution paired velocity fields by conducting simultaneous dual PIV measurements on the same plane with different FOV; one is broad FOV and the other is close-up FOV. Then, Bayesian estimation-based superresolution, in which the estimation process is expressed by a mathematical equation, is developed and its applicability is evaluated using the datasets above.

2 Framework of Bayes superresolution

2.1 Overview

The proposed Bayes superresolution framework (hereafter, SR-Bayes) shown in Fig. 1 estimates the probability distribution of latent variables between the low-resolution (LR) and high-resolution (HR) data of the velocity fields by Bayesian estimation. The framework is trained with pair velocity fields of the HR and LR data, and mode coefficients are obtained by modal decomposition of the HR data. It then estimates the latent variable that maximizes the probability distribution under the given LR data and reconstructs it using the estimated latent variable. Bayesian superresolution has been studied in the image processing field after Tipping and Bishop (2002) proposed Bayesian superresolution, such as the development of multi-layer Bayesian superresolution by Kanemura et al. (2009). While other conventional image reconstruction methods, such as bicubic interpolation and machine learning, have been introduced to spatial superresolution, few reports are made on introducing Bayesian superresolution. In the present study, the Bayesian estimation is applied for reconstruction of the LR data based on the HR data.

Fig. 1
figure 1

Overview of the Bayes superresolution (SR-Bayes)

Full size image

2.2 Modal decomposition based on POD

The Bayesian estimation, described in the latter section, requires prior probabilities of latent variables. This method uses mode coefficients of the velocity field of the HR data obtained by POD (Berkooz et al. 1993) as prior probabilities. The velocity fluctuation data of the broad and close-up time-series velocity fields from the PIV measurements are stored in a two-dimensional matrix \({\varvec{X}}\) as described in Eq. (1). \({\varvec{\tilde{u}}}(t)\) and \({\varvec{\tilde{v}}}(t)\) are column vectors storing velocity fluctuation components in the stream-wise direction and the direction perpendicular to the flow at time t, respectively, and N is the number of snapshots.

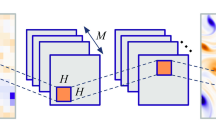
$$\begin{aligned} {\varvec{X}} = \begin{bmatrix} {\varvec{\tilde{u}}}(t=1) &{} {\varvec{\tilde{u}}}(t=2) &{} \cdots &{} {\varvec{\tilde{u}}}(t=N) \\ {\varvec{\tilde{v}}}(t=1) &{} {\varvec{\tilde{v}}}(t=2) &{} \cdots &{} {\varvec{\tilde{v}}}(t=N) \end{bmatrix} \end{aligned}$$
(1)

Singular value decomposition (SVD, Brunton and Kutz (2019)) is applied to the HR data matrix \({\varvec{X}}_{\text {HR}}\) and the POD coefficients are calculated. The data matrix \({\varvec{X}}_{\text {HR}}\) is decomposed into an orthogonal matrix \({\varvec{U}}_{\text {HR}}\) representing the spatial mode, a diagonal matrix \({\varvec{S}}_{\text {HR}}\) with singular values as diagonal components, and an orthogonal matrix \({\varvec{V}}_{\text {HR}}\) representing the temporal mode, as shown in Eq. (2) and Fig. 2.

$$\begin{aligned} {\varvec{X}}_{\text {HR}}={\varvec{U}}_{\text {HR}}{\varvec{S}}_{\text {HR}}{\varvec{V}}^\textsf{T}_{\text {HR}} \end{aligned}$$
(2)

\({\varvec{S}}_{\text {HR}} {\varvec{V}}^\textsf{T}_{\text {HR}}\) are POD coefficients representing the time evolution in the close-up region. The dimension-reduced original data matrix is computed using the upper m modes of the POD modes \((m<N)\), as shown in Eq. (3). Note that the number of POD modes m is a hyperparameter of the proposed framework.

$$\begin{aligned} {\varvec{Z}}_{\text {HR}}={\varvec{S}}^{(m)}_{\text {HR}}{\varvec{V}}^{(m)\textsf{T}}_{\text {HR}} \end{aligned}$$
(3)
Fig. 2
figure 2

Schematic image of POD analysis applied to the velocity data

Full size image

2.3 Bayesian estimation and reconstruction framework

The Bayes theorem expresses that the probability distribution of the latent variable \({\varvec{\theta }}\) under given data \({\varvec{D}}\), \(P({\varvec{\theta }}|{\varvec{D}})\) can be calculated from the prior probability \(P({\varvec{\theta }})\) and the likelihood function \(P({\varvec{D}}|{\varvec{\theta }})\) as follows:

$$\begin{aligned} P({\varvec{\theta }}|{\varvec{D}})=\frac{P({\varvec{D}}|{\varvec{\theta }})P({\varvec{\theta }})}{P({\varvec{D}})}. \end{aligned}$$
(4)

However, since it is difficult to determine the prior probability and likelihood function for complex systems with multiple parameters, the maximum a posteriori (MAP) estimation, and the Bayesian estimation are used as approximate solution estimation methods. In this analysis, the prior probability and likelihood functions are estimated using the Bayesian estimation formulation proposed by Yamada et al. (2021). Yamada et al. defined the noise covariance matrix \({\varvec{R}}\), the expected value \({\varvec{Q}}\) of the square of the latent variable \({\varvec{\theta }}\), and the coefficients \({\varvec{C}}\) of a linear regression of \({\varvec{\theta }}\) and the data \({\varvec{D}}\) as follows:

$$\begin{aligned}{} & {} {\varvec{D}}={\varvec{C}}{\varvec{\theta }}, \end{aligned}$$
(5)
$$\begin{aligned}{} & {} {\varvec{w}}={\varvec{U}}{\varvec{\theta }}-{\varvec{U}}_{\text {est}}{\varvec{\theta }}_{\text {est}}, \end{aligned}$$
(6)
$$\begin{aligned}{} & {} {\varvec{R}} \equiv {E}({\varvec{w}}{\varvec{w}}^\textsf{T}), \end{aligned}$$
(7)
$$\begin{aligned}{} & {} {\varvec{Q}} \equiv {E}({\varvec{\theta }}{\varvec{\theta }}^\textsf{T}). \end{aligned}$$
(8)

Here, the subscript \({_\text {est}}\) indicates the variables estimated by the Bayesian estimation. The prior probability of the POD mode amplitude is obtained as follows:

$$\begin{aligned} P({\varvec{\theta }})\propto {\exp }(-{\varvec{\theta }}^\textsf{T}{\varvec{Q}}^{-1}{\varvec{\theta }}). \end{aligned}$$
(9)

The likelihood function is written as follows:

$$\begin{aligned} P({\varvec{D}}|{\varvec{\theta }})\propto {\exp }(-({\varvec{D}}-{\varvec{C\theta }})^\textsf{T} {\varvec{R}}^{-1}({\varvec{D}}-{\varvec{C\theta }})). \end{aligned}$$
(10)

Then, the posterior probability distribution \(P({\varvec{\theta }}|{\varvec{D}})\) of the latent variable \({\varvec{\theta }}\) becomes as follows:

$$\begin{aligned} \begin{aligned} P({\varvec{\theta }}|{\varvec{D}})&\propto P({\varvec{D}}|{\varvec{\theta }})P({\varvec{\theta }})\\ = {\exp }(-({\varvec{D}}-{\varvec{C\theta }})^\textsf{T} {\varvec{R}}^{-1}({\varvec{D}}-{\varvec{C\theta }}) -{\varvec{\theta }}^\textsf{T}{\varvec{Q}}^{-1}{\varvec{\theta }}). \end{aligned} \end{aligned}$$
(11)

Figure 3 depicts the flowchart of the data processing for the SR-Bayes. The proposed framework assumes that LR data is an observation of HR data degraded by the measurement process or noise. In other words, LR data \({\varvec{X}}_{\text {LR}}\) can be expressed as linear combination of the measurement matrix \({\varvec{C}}\) and POD coefficients of HR data \({\varvec{Z}}_{\text {HR}}\) as follows,

$$\begin{aligned} {\varvec{X}}_{\text {LR}}={\varvec{C}}{\varvec{Z}}_{\text {HR}}. \end{aligned}$$
(12)

This equation means that the HR data is degraded by the measurement matrix C and the LR data is observed. Here, the form of Eq. (12) corresponds to Eq. (5). Thus, the POD coefficients of HR data \({\varvec{Z}}_{\text {HR}}\) is regarded as the latent variable, and the measurement matrix \({\varvec{C}}\) can be obtained as linear regression coefficients by a pseudo-inverse operation: \({\varvec{C}}={\varvec{X}}_{\text {LR}}{\varvec{Z}}_{\text {HR}}^{\dag }\). The noise covariance matrix \({\varvec{R}}\) is the noise contained in the calculated coefficient \({\varvec{C}}\).

$$\begin{aligned} {\varvec{R}}=\frac{1}{N} ({\varvec{X}}_{\text {LR}}-{\varvec{CZ}}_{\text {HR}})({\varvec{X}}_{\text {LR}}-{\varvec{CZ}}_{\text {HR}})^{\textsf{T}} \end{aligned}$$
(13)

The expected value \({\varvec{Q}}\) is assumed as the expected value of POD coefficient \({\varvec{Z}}_{\text {HR}}\), and expressed as follows:

$$\begin{aligned} {\varvec{Q}}\equiv {E}({\varvec{Z}}_{\text {HR}}{\varvec{Z}}^\textsf{T}_{\text {HR}})={\frac{1}{N}}({\varvec{S}}_{\text {HR}}{\varvec{V}}^\textsf{T}_{\text {HR}}{\varvec{V}}_{\text {HR}}{\varvec{S}}_{\text {HR}}) ={\frac{1}{N}}({{\varvec{S}}_{\text {HR}}{\varvec{S}}_{\text {HR}}}). \end{aligned}$$
(14)

Next, the probability distribution of the latent variable \(P({\varvec{Z}}_{\text {HR}})\), and the likelihood function of the LR data, \(P({\varvec{X}}_{\text {LR}}|{\varvec{Z}}_{\text {HR}})\), are calculated using the POD coefficient \({\varvec{Z}}_{\text {HR}}\) as the prior probability by Eqs. (9) and (10). The posterior probability \(P({\varvec{Z}}_{\text {HR}}|{\varvec{X}}_{\text {LR}})\), of the reconstruction velocity field is calculated by Eq. (11) using the obtained probability distribution \(P({\varvec{Z}}_{\text {HR}})\) of the latent variable \({\varvec{Z}}_{\text {HR}}\) and the likelihood function \(P({\varvec{X}}_{\text {LR}}|{\varvec{Z}}_{\text {HR}})\) of the LR data. Then, we will estimate the latent variable \(\hat{{\varvec{Z}}_{\text {HR}}}\) that maximizes the posterior probability \(P({\varvec{Z}}_{\text {HR}}|{\varvec{X}}_{\text {LR}})\).

$$\begin{aligned} \hat{{\varvec{Z}}}_{\text {HR}} = ({\varvec{C}}^\textsf{T}{\varvec{R}}^{-1} {\varvec{C}}+{\varvec{Q}}^{-1})^{-1}{\varvec{C}}^\textsf{T}{\varvec{R}}^{-1} {\varvec{X}}_{\text {LR}} \end{aligned}$$
(15)

The obtained latent variable \(\hat{{\varvec{Z}}}_{\text {HR}}\) is used as the POD coefficient of the reconstructed velocity field \(\hat{{\varvec{X}}}_{\text {HR}}\). The reconstruction is performed using the spatial modes of the HR data.

$$\begin{aligned} \hat{{\varvec{X}}}_{\text {HR}}={\varvec{U}}_{\text {HR}} \hat{{\varvec{Z}}}_{\text {HR}} \end{aligned}$$
(16)

This completes the reconstruction of the velocity field. The performance of the method will be evaluated in Sect. 4.

Fig. 3
figure 3

Flowchart of the data processing for the SR-Bayes

Full size image

3 Experimental apparatus for acquiring HR/LR pair dataset

3.1 Test facility and jet conditions

The present experiment was conducted in an anechoic chamber and a supersonic jet generator at Tohoku University. Refer to Ozawa et al. (2020a, b) for more details of the test facility. A subsonic jet was generated from an axisymmetric convergent nozzle with an exit diameter of \(D=10\) mm. The cross-sectional geometry of the nozzle was based on an article (André et al. 2013). The origin of the coordinate system is at the center of the nozzle exit. The x and r axes are defined as the streamwise and radial directions, respectively. High-pressure air was applied to the stagnation chamber and the pressure ratio between the stagnation chamber and the ambient atmospheric pressure was set to be 1.19 corresponding to the jet Mach number of 0.5. The ambient temperature was 23 degrees centigrade and the temperature ratio between the stagnation chamber and the ambient was 1.0. Reynolds number based on the nozzle diameter was \(1.21\times 10^5\). The estimated maximum velocity at the nozzle exit was \(U_0=165\) m/s under the assumption of isentropic flow.

3.2 Dual PIV measurement system

Figure 4 shows the experimental setup. A dual PIV measurement system was employed for the present experiment, and paired particle images of a broad and close-up view of the jet in the same plane were acquired. One is an LR measurement with broad FOV and the other is an HR measurement with close-up FOV. Each PIV system consists of a double-pulsed laser system and a high-speed camera. Note that each PIV system employs different wavelengths of Nd:YAG (532 nm) and Nd:YLF (527 nm) and optical contamination for each particle image was prevented. Both laser sheets were introduced from the outside of the anechoic chamber through a window. The two high-speed cameras with different optical setups were placed facing each other with respect to the nozzle. Hardware specifications of each PIV system are summarized in Table 1.

Fig. 4
figure 4

Experimental setup of dual PIV measurement system

Full size image

Seeding particles for PIV is generated by Laskin nozzles and a glycerin 50% aqueous solution. The Laskin nozzles are equipped not only in the jet generating system but also in the anechoic room. Therefore, both a subsonic jet and the ambient air were filled with seeding particles. The diameter of the seeding particles is approximately 0.5\(\sim\)2.0 \(\mu\)m (Raffel et al. 2018). The Stokes number derived using the diameter of 1 \(\mu\)m at the maximum velocity of 165 m/s was approximately 0.06. Therefore, the followability of seeding particles is sufficient for the present subsonic jet.

Table 1 Hardware specifications and measurement conditions of dual PIV system
Full size table

The optical magnification of the HR measurements was determined based on the maximum magnification achievable with available optics in the facility. Since the extension tube shortens the shooting distance as well as enlarges the visualized images, the camera optics was selected and the interference between the camera lens and the jet flow was prevented. The details of FOV and measurement conditions are summerized in Table 1. The HR measurement was repeatedly performed with moving FOV as shown in Fig. 5 while the LR measurement always visualizes the entire flow field of the jet. Each area overlaps with \(x/D=0.2\) and the areas 3 to 6 have offset of \(r/D=0.2\) from the areas 1 and 2 to capture the shear layer. The overlap region is arranged because the HR data, which is training data, should be without spatial gaps for the reconstruction of the entire flow field. This overlap region is also used for alignment when synthesizing superresolved data of each area as a single jet. The sampling rate of the paired images was set to 3 kHz, which is the maximum sampling rate at the HR measurement condition.

In this experiment, different time between laser pulses were set for each measurement because the displacement of particles on the image is different between the close-up and broad FOV even in the same flow field as each other. The time between laser pulses for broad FOV was set long (1.06 \(\mu\)s) since the displacement of particles are small. In contrast, the time between laser pulses for close-up FOV was set to be 0.45 \(\mu\)s which is the minimum achievable time for the HR measurement system. The timing chart of the laser and the camera for each measurement system is shown in Fig. 6. The LR and HR measurement systems are synchronized using the function generator as a master trigger. The timing of the first laser pulse was set to be the same for both measurement systems. The timing of the second laser pulse was controlled and the each time between laser pulses was reproduced as described before. Therefore, the measured displacement is not quite at the same time. This effect cannot quantitatively be evaluated and may affect the performance of the superresolution method. Although this effect can be simulated through the synthetic images of PIV using CFD, the detailed evaluation of this effect is out of scope in the present study and left for future work. Since the present study employs the same dataset for all superresolution methods, this does not affect the discussion of the results.

Fig. 5
figure 5

Schematic image of the close-up FOV position in the HR measurement

Full size image
Fig. 6
figure 6

Timing chart of the laser and camera for each measurement system

Full size image

3.3 Details of PIV analysis

Figure 7 shows examples of particle images of LR and HR measurements. The right image is the HR measurement result of the area 3 corresponding to the region of \(4<x/D<6\) and \(-0.4<r/D<1.5\). The left image is a local image corresponding to the area 3 that is cropped out from the broad FOV image of the LR measurement. Both results captured the same structure, implying that the dual PIV measurement system works well.

Fig. 7
figure 7

Particle images of LR and HR measurements. The right image is the HR measurement result of the area 3 corresponding to the region of \(4<x/D<6\) and \(-0.4<r/D<1.5\). The left image is a local image corresponding to the area 3 that is cropped out from the broad FOV image of the LR measurement

Full size image

The details of the particle images and the PIV calculation is summerized in Table 2. The particle images are analyzed by an in-house PIV code written in the MATLAB program that incorporates recursive direct cross-correlation PIV and robust principal component analysis (RPCA) based on gappy POD for denoising. The particle displacement of HR measurement is relatively large due to its magnification and limitation of PIV systems. Therefore, the present study employed direct cross-correlation in which estimation accuracy does not drastically decrease even in the mean displacement becomes large. In addition, direct cross-correlation was recursively applied to the particle images with changing the interrogation window (IW) size and error vectors were suppressed.

Table 2 Parameters for PIV analysis
Full size table

Here, RPCA based on gappy POD was also incorporated into the PIV analysis for the further suppression of error vectors. RPCA is a technique that decomposes a data matrix into a low-rank matrix and a sparse matrix Those matrices represent dominant characteristics and noises of the original data matrix, respectively (Candès et al. 2011; Scherl et al. 2020). Gappy POD is an extension of POD that can restore a gap in an incomplete dataset under the assumption that the gap can be expressed as the superposition of the POD modes. These features are suitable to denoise and restore the outliers in the vector field calculated by direct cross-correlation. Therefore, the group of the present authors extended those techniques to treat the gappy two-component vector data of the velocity field measured by PIV( Abe et al. 2022a, b). This denoising process has a hyperparameter, which is a number of leading POD modes \(\kappa\). This hyperparameter is the number of basis representing the denoised velocity field, and a large number is required for reconstructing the fine-scale structures. The present study determined this hyperparameter based on the energy efficiency of the modal decomposition. Figure 8 shows the partial amount of energy contained in the first \(\kappa\) POD modes of the velocity field in HR measurement. The present study assumed that 80% of energy is sufficient to express the original velocity field, and thus, the number of POD modes was selected as \(\kappa =3000\). Consequently, the calculated velocity field in the present study can be expressed with 3000 modes at the maximum.

Fig. 8
figure 8

Partial amount of energy contained in the first \(\kappa\) POD modes in HR measurement

Full size image

The cutoff wavenumber and the noise level of each PIV system were evaluated based on the article of Foucaut et al. (2004). Figure 9 shows power spectra of displacements along x direction \(E_{11}\) for each PIV system. The power spectra were calculated using a no-flow region of the area 1, which is the outside of the jet and averaged over 7217 snapshots. Equation (17) was fitted to each spectra and the cutoff wavenumber and the noise level were estimated.

$$\begin{aligned} E_{i i}=E_{\text{ noise } }\left( \frac{\sin (k X / 2)}{k X / 2}\right) ^2. \end{aligned}$$
(17)

Here, k, X, and \(E_{\text{ noise } }\) are the wavenumber, the size of IW, and the white noise level obtained by fitting the spectrum with Eq. (17), respectively. The estimated noises were \({E_\text {noise}}=3.4\times 10^{-3}\) and \(1.3\times 10^{-4}\) for LR and HR measurements. The cutoff wavenumber of LR measurement was \(2.8\times 10^{-2}\) rad/pix corresponding to 358 m\(^{-1}\). That of HR measurement was \(1.4\times 10^{-2}\) rad/pix corresponding to 1151 m\(^{-1}\). Therefore, the spatial resolution of the HR measurement was 3.2 times higher than that of the LR measurement.

The spatial resolution is also compared with the actual flow scales. Although there is no reference data on the length scales of the present experimental condition, the turbulence length scales of a high subsonic jet were computationally investigated in a previous study and allows us to evaluate the order of the length scales. Bogey et al. (2003) performed a large eddy simulation of a subsonic jet (\(M=0.9\), \(Re=65000\)) and the longitudinal integral length scale was \(8.9\times 10^{-4}\) m. The corresponding wavenumber is 1124 m\(^{-1}\) which is the same order as the cutoff wavenumber of HR measurement.

Fig. 9
figure 9

Power spectra of displacements along x direction \(E_{11}\) for each PIV system

Full size image

4 Results of the superresolution

4.1 Procedure for performance evaluation

The proposed superresolution method was compared with conventional upscaling methods. The present study employed the conventional bicubic interpolation method by Keys (1981) and the CNN and DSC/MS methods by Fukami et al. (2019) for the comparison. The bicubic interpolation is a cubic convolution interpolation technique that considers 16 pixels in the neighborhood and is simply applied to the present experimental data. The CNN and DSC/MS methods are machine learning-based superresolution methods. The present study determined the settings of the CNN and DSC/MS models based on the article by Fukami et al. (2019). The CNN model is a three-layer model with an example layer. Each layer uses 16 filters with a filter size of \(13\times 13\) pixels and the rectified linear unit (ReLU) was used as the activation function. The DSC/MS model is a hybrid of the CNN model with compression and skipped connections and the multi-scale model by (Du et al. 2018). This improves the performance and robustness of the model. The input data for those machine learning methods were first upscaled by the bicubic interpolation to match the spatial resolution of the HR data. The details of DSC/MS model are referred to the article of Fukami et al. (2019).

The performance of the methods is evaluated by k-fold cross-validation (\(k=5\)), and its error was defined using the Frobenius norm. The k-fold cross-validation is a statistical method for evaluating generalization performance. This validation method first divides the dataset into k segments. Then, one segment is used as test data, and the other \(k-1\) segments are used as training data. This procedure is repeated until all segments have been used as test data once. Here, the reconstruction error of the superresolution methods is defined as follows:

$$\begin{aligned} \text {Error}=\frac{||{\varvec{X}}_{\text {est}}-{\varvec{X}}_{\text {ref}}||_{\text {fro}}}{||{\varvec{X}}_{\text {ref}}||_{\text {fro}}}. \end{aligned}$$
(18)

The subscripts \(_{\text {est}}\) and \(_{\text {ref}}\) indicates the estimated data by the superresolution method and the reference data. The definition of the Frobenius norm is as follows:

$$\begin{aligned} ||{\varvec{X}}||_{\text {fro}} = \sqrt{\sum _{i,j} x_{i,j}^2}. \end{aligned}$$
(19)

4.2 Performance evaluation using artificial LR data

The performance of the superresolution method was first evaluated using an artificial LR data generated by average pooling the experimental HR data. The artificial LR data can eliminate the measurement noise contained in the experimentally measured LR data and evaluate the basic characteristics of the superresolution method. The resolution of the artificial LR data was one-third of that of the HR data and it is matched with the resolution ratio of the experimental HR to LR data. The evaluation was made at the area 4 of \(6<x/D<8\) as a representative.

Figure 10 shows the reconstruction error and the snapshots of the reconstructed velocity field by the superresolution methods using the artificial LR data. The snapshots of velocity field in Fig. 10 are normalized by the nozzle exit velocity \(U_0\). Although the reconstruction error of the SR-Bayes is higher than that of the other conventional methods, the error of the SR-Bayes decreases with the increase in a number of POD modes. This indicates that the high-order modes, which express the small-scale structures, contributes the reconstruction. The reconstructed snapshots of all the superresolution methods were qualitatively agree with the reference HR data. Therefore, the SR-Bayes successfully reconstructed the jet flow. The error deviation of the SR-Bayes at 1500 modes is higher than those of the other cases. In this case, the reconstruction error of the high-order modes was sometimes significantly high. This was not observed when the experimentally measured LR data is used for the SR-Bayes, as described in the latter section. Therefore, this may be due to the averaging pooling of the LR data.

Fig. 10
figure 10

Performance evaluation results using artificial LR data at the area 4 (\(6< x/D < 8\))

Full size image

4.3 Performance evaluation using experimentally measured LR data

This section discusses the reconstruction results using the experimentally measured LR data. This test is more practical and realistic because the LR data contains the measurement noise. Figure 11 shows the reconstruction error and the snapshots of the reconstructed velocity fields for all the superresolution methods. The reconstruction error of all the superresolution methods significantly increases in contrast to that of the artificial LR data. The snapshot of the experimentally measured LR data shown in Fig. 11b is not spatially smooth and a lot of outlier vectors are observed. Moreover, the local maxima and the local minima of the velocity are emphasized in the experimentally measured LR data. These characteristics are not observed in the artificial LR data shown in Fig. 10. This difference indicates that the experimentally measured LR data contains bias errors due to technical issues of the LR measurement. Although Fig. 7 shows that the measured particle images captured the same fluid structures in both FOVs as each other, the particle images of the LR measurement are still not as sharp as the close-up measurement due to the lack of spatial resolution. Also, since the time between laser pulses is very short in the HR measurement, the second laser pulse may be emitted before the first laser pulse has decayed, resulting in an elongated particle image. Such blurring or stretching of the particle image caused a mismatch in the velocity field between FOVs. This causes an increase in the reconstruction error when the experimentally measured LR data is used for the superresolution methods.

The reconstruction error of the SR-Bayes is lower than that of the bicubic interpolation method in all the POD modes, although it is still higher than the other machine learning methods. However, it asymptotic to the reconstruction error of machine learning as the number of POD modes increases. The minimum reconstruction error was approximately 63% when training with the full POD modes of the training data (3000 modes). Meanwhile, the SR-Bayes reconstructed the vortices and shear layers more clearly than the other methods, as shown in the reconstructed velocity fields in Fig. 11. However, the SR-Bayes also reconstructed the outlier vectors and measurement noise in the LR data. This leads the increase in the reconstruction error compared to the CNN and DSC/MS methods. In contrast, the CNN and DSC/MS methods estimated a smoothed velocity field, which filtered out the error vectors and measurement noise, resulting in the suppression of the reconstruction error.

Fig. 11
figure 11

Performance evaluation results using experimentally measured LR data at the area 4 (\(6< x/D < 8\))

Full size image

Figure 12 shows the POD energy distributions of each reconstructed velocity field at the area 4 (\(6<x/D<8\)). The POD energy distribution shows the same trends in all the cases in the low-order modes, while the difference appears in the high-order modes. The input LR data, represented by the black dashed line, overestimated the POD energy of the reference HR data in 40 modes or more. The bicubic interpolation also follows the same trend as the LR data. On the other hand, the SR-Bayes successfully reconstructed the POD energy distribution of the reference HR data up to 200 modes. The CNN and DSC/MS methods underestimate the POD energy of the HR data, and its reconstruction was limited to low-order modes. The CNN and DSC/MS methods are considered to focus on estimating the large-scale structure of the velocity field and did not likely estimate the high-order modes. This is because the high-order modes, which may include the outlier vectors as a fine-scale structure, lead to an increase in the reconstruction error.

Fig. 12
figure 12

POD energy distribution of each reconstructed velocity field at the area 4 (\(6< x/D < 8\))

Full size image

A two-dimensional Fourier transform was applied to the reconstructed velocity fields and the wavenumber-domain analysis of the flow structures are conducted. Figure 13 shows two-dimensional wavenumber spectra at the area 4 of \(6<x/D<8\). The spectra were averaged over the total number of snapshots. The spectrum of the reference HR data showed the wide distribution of wavenumbers from low to high wavenumbers while that of the input LR data do not have the higher wave number components due to its low spatial resolution. The spectrum of the input LR data overestimates the low-wavenumber components and its distribution is blunted compared to that of HR data. The wavenumber spectra of the reconstructed velocity fields are then discussed. The SR-Bayes successfully reconstruct the wavenumber spectrum close to the reference HR data. On the other hand, the reconstruction of the bicubic interpolation is limited to the wavenumber region along the axis and its distribution in the low-wavenumber region is similar to that of the input LR data. Although the wavenumber spectra of the CNN and DSC/MS methods become similar to that of the reference HR data, they still underestimate the high-wavenumber components.

Fig. 13
figure 13

Two-dimensional wavenumber spectrum of the velocity field at the area 4 (\(6< x/D < 8\)). The SR-Bayes result was calcuated using 2000 modes

Full size image

The turbulence statistics of the reconstructed velocity fields are then discussed. The distribution of the Reynolds stress \(\overline{u'v'}\) is shown in Fig. 14a. Reynolds stress profile at the cut line is also shown in Fig. 14b. Reynolds stress of the input LR data slightly underestimates that of the reference HR data. However, the SR-Bayes reconstructed the Reynolds stress of the reference HR data over the entire profile. On the other hand, the bicubic interpolation and the CNN and DSC/MS methods underestimate the Reynolds stress. Although the machine learning-based methods slightly improve its accuracy, the profile of the Reynolds stress is spatially smoothed.

Fig. 14
figure 14

Reynolds stress distribution of the reconstructed velocity field at the area 4 (\(6< x/D < 8\))

Full size image

The turbulent kinetic energy (TKE) at the area 4 of \(6<x/D<8\) is calculated and the statistical characteristics of the reconstructed velocity fields are discussed. Figure 15a shows the TKE of each reconstructed velocity field. Although the LR data overestimated the TKE of the reference HR data over the entire domain, the SR-Bayes recovered the TKE distribution of the HR data. The TKE profile at the cut line indicated in Fig. 15a is also shown in Fig. 15b. The TKE profile of the SR-Bayes agrees very well with the reference HR data. On the other hand, the TKE profile of bicubic interpolation only follows the LR data and does not recover the reference HR data. The CNN and DSC/MS methods fairly underestimate the TKE due to its spatial smoothing of the reconstructed velocity fields.

Fig. 15
figure 15

Turbulent kinetic energy distribution of the reconstructed velocity field at the area 4 (\(6<x/D<8\))

Full size image

The power spectra of the TKE are computed and the enhancement in the spatial resolution was quantitatively evaluated. Figure 16 shows the power spectra of the TKE averaged over the total number of snapshots. The cutoff wavenumbers of the input LR and reference HR data are also plotted as vertical lines in each spectrum. The TKE spectrum of input LR data is higher than that of the reference HR data over the entire wavenumber domain, which is the same trend as indicated in Fig. 15b. Here, the TKE spectrum of the SR-Bayes agrees well with that of the reference HR data while the SR-Bayes slightly underestimates the TKE over \(k\approx 330\). The TKE spectra of the other machine-learning-based methods only agree at the low-wavenumber domain, and they decrease toward the high-wavenumber domain. This is because the CNN and DSC/MS methods spatially average the reconstructed velocity fields and the high-wavenumber components are dumped. The wavenumber where the SR-Bayes slightly deviates from the reference HR data is close to the cutoff wavenumber of the input LR data. However, the estimation accuracy of the SR-Bayes is much better than that of the other methods. Moreover, the difference in the TKE spectra between the SR-Bayes and HR data is still small even above the cutoff wavenumber of the SR-Bayes. Therefore, the SR-Bayes has the potential to estimate turbulence statistics beyond the native spatial resolution.

Fig. 16
figure 16

Power spectra of turbulent kinetic energy at the area 4 of \(6<x/D<8\)

Full size image

4.4 Superresolution of a subsonic jet

This section applies the SR-Bayes to the entire jet and the characteristics of the superresolved velocity fields is discussed. Figure 17 summarizes the superresolved results of the streamwise velocity fields for each area. Note that the SR-Bayes for each area is separately measured and trained, and the snapshots of each area are independent. Although the LR input data is noisy, the velocity fields reconstructed by the SR-Bayes qualitatively agree well with the reference HR data. When the number of POD modes for the SR-Bayes increases, the reconstructed velocity fields exhibit fine-scale structures in a jet.

Figure 18 shows the reconstruction error for each area. The reconstruction error in all the areas decreases as the number of POD modes increases. Moreover, the error decreases in the downstream region where the shear layer thickness is thick. The shear layer thickness at the nozzle exit is supposed to be 0.01D in the present subsonic jet. This corresponds to the wavenumber of 10,000 \(\text {m}^{-1}\). On the other hand, the cutoff wavelength of the HR measurement was 1151 \(\text {m}^{-1}\) as shown in Fig. 9. Therefore, the spatial resolution of the HR measurement is not sufficient for resolving the shear layer near the nozzle exit. Therefore, this insufficient spatial resolution is considered to cause the high reconstruction error in the areas 1 and 2. Morevoer, another reason can be discussed using the POD energy distribution in the LR data shown in the Fig. 19. The POD energy distribution of each area illustrates that the proportion of higher-order mode energies in the total energy increases on the downstream side. In other words, the velocity field at the downstream side has a lot of low-rank components and can be expressed with fewer POD modes. This feature makes the reconstruction easy because the number of variables is small. Therefore, the SR-Bayes can accurately recover the HR data of the velocity field when the LR data can be expressed as low-rank data.

Fig. 17
figure 17

Streamwise velocity fields in each domain for each test datasets. The color contour represents \(u/U_0\)=[0, 1]

Full size image
Fig. 18
figure 18

Reconstruction error in each domain

Full size image
Fig. 19
figure 19

POD energy and its cumulative energy of the LR data in each domain

Full size image

Finally, the superresolution methods were applied to a single snapshot of the entire jet and full reconstruction of a subsonic jet was performed. Figure 20 shows the comparison of the streamwise velocity fields reconstructed by each superresolution methods from the single snapshot of LR data. The area for the superresolution was at the areas 1 to 6 of \(0<x/D<12\) and \(-0.4<r/D<1.4\). Although we do not have HR data of the entire jet to verify the superresolved results, the SR-Bayes successfully reconstructed details of the shear layers and vortices. The SR-Bayes could reconstruct fine-scale structures and suppress error caused by the outlier vectors observed in the LR data. On the other hand, the conventional bicubic interpolation just upscaled the LR input data and its velocity field is not smooth compared with that of the SR-Bayes. Although the machine learning-based methods could suppress the error caused by the outlier vectors observed in the LR data, its reconstructed velocity fields are spatially smoothed and fine-scale structures are lost. Therefore, the SR-Bayes can accurately keep the POD energy, spatial wavenumber distribution, TKE, and Reynolds stress. These are advantages of the SR-Bayes for reconstructing the velocity fields including turbulent structures from PIV.

Fig. 20
figure 20

Reconstructed velocity fields of a subsonic jet from a single snapshot of whole LR PIV data at the area of \(0<x/D<12\) and \(-0.4<r/D<1.4\) The color contour represents \(u/U_0\)=[0, 1]

Full size image

5 Conclusions

The present study proposed the superresolution method based on Bayesian estimation (SR-Bayes) and its applicability was evaluated using the experimental datasets. The SR-Bayes estimates the probability distribution of latent variables, which are POD coefficients, between the LR and HR data of the velocity fields. The experimental datasets consist of two different velocity fields which are simultaneously measured with different magnifications. One is an LR measurement with broad FOV and the other is an HR measurement with close-up FOV. The ratio of the spatial resolution between LR and HR measurements was approximately 1/3.

The performance of the SR-Bayes was compared with conventional upscaling methods: bicubic interpolation method by Keys (1981) and the CNN and DSC/MS methods by Fukami et al. (2019) for the comparison. The present study first evaluates the reconstruction error of the superresolution methods using artificial LR data generated by average pooling of the HR data. This verification test can eliminate the effect of the measurement noise contained in the experimentally measured LR data on the reconstruction error. The SR-Bayes successfully reconstructed the jet flow although the reconstruction error of the SR-Bayes was higher than that of the other conventional methods. The reconstruction error of the SR-Bayes decreases as the number of POD modes increases.

The performance evaluation using experimentally measured LR data was also performed as a practical and realistic test. The minimum reconstruction error of the SR-Bayes was 63 % which is significantly high compared to that of the artificial LR data. This is because the actual particle images of the LR measurement are affected by the blurring or stretching of the particles which leads to a mismatch in the velocity fields of LR and HR measurement. However, wavenumber-domain analysis and turbulence statistics revealed that the SR-Bayes can well reconstruct the turbulence statistics of the velocity fields compared with the other machine learning-based superresolution methods. The enhancement of the spatial resolution was quantitatively evaluated by the TKE spectrum. The TKE spectrum of the SR-Bayes agrees well with that of the reference HR data over a wide range of wavenumbers, although the other superresolution methods can reconstruct only in the low wavenumber components. The SR-Bayes tends to slightly underestimate the TKE spectra over \(k\approx 330\), which is close to the cutoff wavenumber of LR measurement. However, its deviation is still small and the reconstructed spectrum of the SR-Bayes is similar to that of the reference HR data.

The SR-Bayes was finally applied to a single snapshot of the entire jet and a full reconstruction of a subsonic jet was performed. Although the reference HR data of the entire jet is not available, the SR-Bayes successfully reconstructs the fine-scale structures and suppresses the error caused by outlier vectors observed in the LR data. On the other hand, the other machine learning-based methods tend to reconstruct spatially smoothed velocity fields and suppress the error caused by outlier vectors observed in the LR data. This leads to the underestimation of the turbulent statistics in high-wavenumber components. Therefore, the SR-Bayes can reconstruct velocity fields without losing the high-wavenumber components and have the potential to enhance the spatial resolution of various experimental datasets.