Integration of non-time-resolved PIV and time-resolved velocity point sensors for dynamic estimation of velocity fields

Abstract

We demonstrate a three-step method for estimating time-resolved velocity fields using time-resolved point measurements and non-time-resolved particle image velocimetry data. A variant of linear stochastic estimation is used to obtain an initial set of time-resolved estimates of the flow field. These estimates are then used to identify a linear model of the flow dynamics. The model is incorporated into a Kalman smoother, which provides an improved set of estimates. We verify this method with an experimental study of the wake behind an elliptical-leading-edge flat plate at a thickness Reynolds number of 3,600. We find that, for this particular flow, the Kalman smoother estimates are more accurate and more robust to noise than the initial, stochastic estimates. Consequently, dynamic mode decomposition more accurately identifies coherent structures in the flow when applied to the Kalman smoother estimates. Causal implementations of the estimators, which are necessary for flow control, are also investigated. Similar outcomes are observed, with model-based estimation outperforming stochastic estimation, though the advantages are less pronounced.

1 Introduction

Knowledge of the full velocity field can be of great use in identifying and visualizing spatial structures in a flow. For instance, proper orthogonal decomposition (POD) can be used to identify structures with high-energy content (Lumley 1967). However, the data must be time-resolved in order to elucidate the full dynamics of the flow. Certainly, if the data do not resolve the time scales of interest, then the corresponding behaviors will not be captured. If time-resolved velocity fields are available, structures of dynamical importance can be identified using methods such as balanced proper orthogonal decomposition (BPOD) and dynamic mode decomposition (DMD) (Rowley 2005; Rowley et al. 2009; Schmid 2010). Time-resolved, full-field information is also helpful in forming reduced-order models for closed-loop flow control, or for simply visualizing a flow. Unfortunately, time-resolved velocity fields are difficult to obtain.

Particle image velocimetry (PIV) is the standard technique for measuring velocity fields (“snapshots” of a flow), but time-resolved PIV (TRPIV) systems are costly and thus uncommon. In addition, such systems are often restricted to low-speed flows due to the larger time interval needed between snapshots when using a high-speed laser. The required sampling rates can also limit the spatial extent of the data that can be captured (Tinney et al. 2006). As such, typical PIV systems are not time-resolved and as a result are often incapable of resolving the characteristic frequencies of a flow.

On the other hand, many instruments exist for capturing time-resolved “point” measurements, including hot-wire probes and unsteady pressure sensors. Arrays of such instruments can be used to take measurements that span large spatial regions, but these data may not resolve all the spatial scales of interest. The dense arrays necessary to capture small-scale structures are often too intrusive, and any measurement is limited by spatial averaging on the scale of the sensor’s size. Furthermore, point measurements can be sensitive to the placement of the instrument, which is generally predetermined.

In this work, we demonstrate a three-step method that integrates time-resolved point measurements of velocity, non-time-resolved PIV snapshots, and a dynamic model to estimate the time evolution of a velocity field. As we only wish to resolve the dominant coherent structures, we use POD to obtain a low-order description of the flow. First, a variant of linear stochastic estimation (LSE) is used to compute an initial set of time-resolved estimates of the velocity field. We then form a model of the flow physics by combining an analytic characterization of the flow with a stochastic one identified from the initial estimates. The resulting model is used as the basis for a dynamic estimator called a Kalman smoother, with which a second set of estimates is computed.

Whereas the initial LSE estimates are determined by the point measurements alone, the Kalman smoother also incorporates the non-time-resolved PIV snapshots. These two sets of measurements are used to correct an internal, model-based prediction of the estimate. The dynamics of the model prevent the Kalman smoother estimates from evolving on time scales that are fast with respect to the flow physics, filtering out measurement noise. Thus, we can leverage knowledge of the flow physics and a non-time-resolved description of the velocity field to obtain a more accurate and robust set of estimates.

In many ways, this work builds on that of Murray and Ukeiley (2007b), Taylor and Glauser (2004), and Tinney et al. (2008) (among others), who all used LSE-based methods to estimate the time evolution of a flow field. The key difference between our approach and those based solely on LSE is our use of a dynamic model. LSE is a conditional technique for capturing those features of the flow that are correlated with a measurement signal, and does not rely on, nor provide, a model of the flow physics. Our approach also differs from the recent work by Legrand et al. (2011a, b), in which a phase-averaged description of a velocity field is obtained directly from a large ensemble of PIV data. Theirs is a post-processing technique that does not make use of any other measurement signal.

As a proof of concept, we apply this method in a bluff-body wake experiment. A finite-thickness flat plate with an elliptical leading edge and blunt trailing edge is placed in a uniform flow, resulting in oscillatory wake dynamics. We collect TRPIV snapshots, from which we extract the velocity at a single point in the wake, simulating a probe signal. POD modes are computed from the TRPIV data, and a set of basis modes is chosen for approximating the flow field. The TRPIV snapshots are then downsampled (in time), and these non-time-resolved data are fed to the dynamic estimator along with the time-resolved probe signal. This generates an estimated, time-resolved trajectory for each POD mode coefficient.

The estimation error is quantified using the original TRPIV data, with the following analysis applied to both the initial LSE estimates and the Kalman smoother estimates. For each TRPIV snapshot, we compute the difference between the estimated POD representation of the velocity field and its projection onto the POD basis. The kinetic energy contained in this difference is then calculated. We collect the values and find the mean value of the error energy and its distribution. This procedure is then repeated with various levels of artificial noise injected into the probe signal, in order to test each method’s sensitivity to noise. Finally, the estimated flow fields are used to compute DMD modes, testing whether or not the estimates are accurate enough to identify the oscillatory structures in the flow.

This demonstrates the value of our method in post-processing analysis, as DMD would not be possible without time-resolved estimates of the velocity field. Previous work has shown that dynamic estimators and reduced-order models can also be useful in flow control applications. Gerhard et al. (2003) reduced wake oscillations in simulations of the flow over a circular cylinder using a dynamic estimator and a low-dimensional Galerkin model. Li and Aubry (2003) and Protas (2004) achieved similar results using low-order vortex models. Pastoor et al. (2008) used a vortex model to describe the wake behind a D-shaped body (similar to the one analyzed in this work), successfully stabilizing it in experiment using both open- and closed-loop control. In that work, a Kalman filter was applied to dynamically estimate the base pressure fluctuations for vortex shedding synchronization. While the focus of our work is reduced-order estimation and not feedback control, we note that our method can easily be modified for flow control purposes.

The rest of this paper is structured as follows: Sect. 2 provides a brief introduction to the theory of stochastic and dynamic estimation. These estimation techniques are implemented using the numerical methods detailed in Sect. 3 and demonstrated using the experiment described in Sect. 4 The results of this experiment are discussed in Sect. 5, and conclusions drawn therefrom are presented in Sect. 6.

2 Background

2.1 Stochastic estimation

In many instances, we may wish to estimate the value of an event based on the value of another one. Suppose we would like to use the velocity measurement at one point in a flow, ${\underline{u}}(x),$ to estimate the velocity at another point, $\underline{{u}}(x').$ The conditional average

$$ \hat{\underline{{u}}}(x') = \langle\underline{{u}}(x') | \underline{{u}}(x)\rangle$$

(1)

provides the expected value of $\underline{{u}}(x')$ given the measurement $\underline{{u}}(x),$ which is the least-mean-square estimate of $\underline{{u}}(x')$ (Papoulis 1984).

We can estimate the conditional average by measuring $\underline{{u}}(x')$ repeatedly and averaging over those values that occur whenever $\underline{{u}}(x)$ is near a nominal value $\underline{{u}}^*(x)$ (Guezennec 1989). Adrian (1977) introduced stochastic estimation to the turbulence community, approximating the conditional average with the power series

$$ \langle u_i(x') | u_i(x)\rangle \approx A_{ij}(x') u_j(x) + B_{ijk}(x') u_j(x) u_k(x)+\ldots\,, $$

(2)

where summation over repeated indices is implied. In the case of LSE, only the linear coefficients A _ij are retained. These can be computed from the two-point, second-order correlation tensor R _ij (x′) (Adrian 1994).

Similar procedures exist for higher-order estimates, making use of higher-order two-point correlations. While Tung and Adrian (1980) found that higher-order estimation procedures did not provide much additional accuracy, later studies showed that this is not always the case. For instance, quadratic estimation can be more effective when the estimation of a given quantity (e.g., velocity) is based on the measurement of another (e.g., pressure) (Naguib et al. 2001; Murray and Ukeiley 2003).

Other studies achieved improved performance by accounting for time delays between the conditional and unconditional variables (Guezennec 1989). Ewing and Citriniti (1999) developed a multi-time LSE technique in the frequency domain that was a significant improvement over single-time LSE. This multi-time formulation also incorporated global analysis tools, namely POD, that yielded low-dimensional representations of the turbulent jets being studied. The multi-time approach was later translated into the time domain and used to predict future pressure values from past measurements (Ukeiley et al. 2008). Durgesh and Naughton (2010) demonstrated the existence of an optimal range of delays when they estimated the POD mode coefficients of a bluff-body wake in a non-causal, post-processing fashion.

We note that the stochastic estimation of POD coefficients from measurements is typically referred to as modified LSE (mLSE), or more recently, modified linear stochastic measurement. The latter name is used to distinguish this as a measurement estimation as opposed to a plant estimation, which would be typical from a controls perspective (Glauser et al. 2004). In this work, we use the term “LSE” as it is more prevalent in the literature.

It is important to note that stochastic estimation does not involve any modeling of a system’s dynamics. Rather, it simply provides a statistical estimate of a random variable given the knowledge of other random variables (Adrian 1994). We can think of stochastic estimation as a static mapping, computed using a pre-existing dataset, that yields the most statistically likely value of some unknown (conditional) variable, given some other measured (unconditional) data. For a fluid flow, such a method can produce visual representations of the flow field, but cannot suggest, without further analysis, what events should be observed or how they might be related to the underlying flow physics (Cole et al. 1992). Furthermore, in LSE, the estimated values will lie in a subspace whose dimension is limited to the number of conditions. This is especially important when using a small number of measurements to predict a high-dimensional variable, such as a velocity field. Depending on the application, it can be either a limitation or an advantage, unnecessarily restricting the estimates or capturing only the features of interest. The use of a static map can also lead to uniqueness issues, as a particular measurement value will always yield the same estimate. For instance, a pressure sensor may measure the same value at two points in time, leading to identical estimates, even though the corresponding velocity fields are different. Increasing the number of sensors can decrease the likelihood of this happening but is not always feasible.

2.2 Dynamic estimation

Dynamic estimators are a foundational topic in control theory. They estimate a system’s state using a model of its dynamics along with real-time measurement updates. The measurement updates are used to correct the trajectory of the model, which will drift from the true trajectory due to parameter uncertainty, unmodeled dynamics, and external disturbances (process noise). This is in contrast to static estimation techniques, including stochastic estimation, which use a fixed relationship to estimate the system state from a set of measurements. Such an approach does not take advantage of the fact that the equations governing a system’s evolution are often known.

In this work, we focus on the Kalman filter and smoother, both standard subjects in the study of estimation. (For a more in-depth discussion, see any standard text on estimation, for instance the book by Simon 2006.) Suppose we are interested in the evolution of a system described by a linear model

$$ \begin{aligned} \underline{{\xi}}_k &=F \underline{{\xi}}_{k-1} +\underline{{d}}_{k-1} \;\underline{{\xi}} \in{\mathbb{R}}^{N_{\rm s}}\\ \,\, \quad \underline{{\eta}}_k &= H_k\underline{{\xi}}_k + \underline{{n}}_k \quad\underline{{\eta}} \in {\mathbb{R}}^{N_{\rm o}}, \end{aligned} $$

(3)

where $\underline{{\xi}}$ is a vector of N _s state variables, $\underline{{\eta}}$ is a vector of N _o measurements of the state, $\underline{{d}}$ represents process noise, and $\underline{{n}}$ represents sensor noise. At any given iteration k, we assume that we can observe the measurement $\underline{{\eta}}_k.$ From this, we would like to estimate the value of $\underline{{\xi}}_k,$ which is otherwise unknown.

The dimension of $\underline{{\eta}}$ may be smaller than that of $\underline{{\xi}},$ meaning that even without sensor noise, the matrix H relating the two may not be invertible. However, if the system is observable, we can use a knowledge of the system dynamics F and the time history of $\underline{{\eta}}$ to produce an estimate $\hat{\underline{{\xi}}}$ that converges, in the case of no noise, to the true value $\underline{{\xi}}.$ In the presence of noise, the Kalman filter will minimize the expected value of the error

$$ \left(\underline{{\xi}}_k-\hat{\underline{{\xi}}}_k\right)^T \left(\underline{{\xi}}_k-\hat{\underline{{\xi}}}_k\right). $$

The Kalman filter is a causal filter, meaning that only measurements made up to and including iteration k are available in forming the estimate $\hat{\underline{{\xi}}}_k.$ In some situations, we may also have access to measurements occurring after iteration k, for instance in a post-processing application. We can use that information to improve our estimate of $\underline{{\xi}}_k.$ This yields a non-causal filter, generally referred to as a smoother. In this work, we use a variant of the Kalman smoother developed by Rauch, Tung, and Striebel, known as the RTS smoother (cf., Simon 2006). The RTS smoother is a fixed-interval smoother, meaning that all measurements taken over a fixed time interval are used to estimate the state evolution within that interval. Algorithmically, it consists of a forward pass with a Kalman filter followed by a backward, smoothing pass. The specifics of the Kalman filter and RTS smoother algorithms are described in Sect. 3.3

3 Numerical methods

In this section, we detail the various numerical methods used in our estimation procedure. These methods include modal decomposition techniques (used for approximating the flow field and investigating flow physics), stochastic estimation techniques, and dynamic estimation techniques. We also provide a summary of our three-step dynamic estimation procedure, laying out how the numerical methods listed above are used to form a dynamic estimator for experimental applications.

3.1 Modal analysis

3.1.1 Proper orthogonal decomposition (POD)

POD, also known as principal component analysis or Karhunen-Loeve analysis, is a data analysis method that identifies the dominant structures in a dataset (Lumley 1967; Sirovich 1987a; Holmes et al. 1996). More precisely, suppose we wish to project the dataset $\{\underline{{\xi}}_k\}_{k=0}^m$ onto an r-dimensional subspace. Let ${\mathbb{P}_r}$ be the corresponding projection operator. Then the first r POD modes form the orthogonal basis that minimizes the sum-squared error

$$ \sum_{k=0}^m \left\|\underline{{\xi}}_k - {\mathbb{P}}_r \underline{{\xi}}_k\right\|^2. $$

As such, POD modes are naturally ordered, with a smaller mode index indicating a larger contribution to the accuracy of the projection.

When analyzing an incompressible fluid flow, we generally take the data elements to be mean-subtracted velocity fields at given instants in time. That is, we let $\underline{{\xi}}_k = \underline{{u}}_k' = \underline{{u}}'(t_k).$ These elements are commonly referred to as “snapshots.” In this work, the snapshots are collected experimentally using PIV.

POD modes can be computed efficiently using the “method of snapshots” (Sirovich 1987a). Each velocity field is discretized and reshaped into a one-dimensional vector, and then stacked in a data matrix

$$ X =\left[\begin{array}{llll} \vline &\vline & & \vline \\ \underline{{u}}_0'& \underline{{u}}_1' & \cdots & \underline{{u}}_m' \\ \vline & \vline & & \vline\\ \end{array}\right]. $$

(4)

The diagonalization of the correlation matrix X ^T M X is then computed, satisfying

$$ X^T M X = W \Upsigma W^T, $$

(5)

where M is a matrix of inner product weights. (This matrix typically contains grid weights, for instance the scaled identity matrix I dx dy.) The inclusion of M allows us to interpret the vector norm as the integrated kinetic energy:

$$ \left\|\underline{{u}}_k'\right\|^2 = (\underline{{u}}_k')^T M \underline{{u}}_k' = \iint \Big(u'(x, y, t_k)^2 + v'(x, y, t_k)^2\Big) {\hbox {d}}x {\hbox {d}}y. $$

(We note that in this work, we measure only two components of velocity.)

The POD mode $\underline{{\phi}}_j$ is then given by the j + 1th column of the matrix

$$ \Upphi = X W \Upsigma^{-1/2}. $$

(6)

(In this work, we start our indexing from zero, and as such, the “first” mode corresponds to j = 0, the “second” to j = 1, and so on.) The modes form an orthonormal set, satisfying the identity

$$ \underline{{\phi}}_j^T M \underline{{\phi}}_i = \delta_{ij}, $$

(7)

where δ _ij is the Kronecker delta function. As such, the projection of a snapshot $\underline{{u}}_k'$ onto the first r POD modes is given by

$$ {\mathbb{P}}_r \underline{{u}}_k' = \Upphi_r \underline{{a}}_k, $$

(8)

where $\Upphi_r$ contains only the first r columns of $\Upphi,$ and

$$ \underline{{a}}_k = \Upphi_r^T M \underline{{u}}_k'. $$

(9)

We refer to $\underline{{a}}_k$ as the vector of POD coefficients corresponding to the snapshot $\underline{{u}}_k'.$ For a spatially discretized velocity field, the dimension of a POD mode $\underline{{\phi}}_j$ is twice the number of grid points (again assuming we only consider two components of velocity). In contrast, $\underline{{a}}_k$ has only dimension r.

We observe that due to the orthogonality of the POD modes (Eq. 7), the energy in any POD approximation of a velocity field is simply given by

$$ \left\|{\mathbb{P}}_r \underline{{u}}_k'\right\|^2 = \underline{{a}}_k^T \Upphi_r^T M \Upphi_r \underline{{a}}_k = \underline{{a}}_k^T \underline{{a}}_k = \|\underline{{a}}_k\|_2^2. $$

(10)

The kinetic energy captured by the projection itself can be computed as

$$ \sum_{k=0}^m \|{\mathbb{P}}_r \underline{{\xi}}_k\|^2 = \sum_{j=0}^{r-1} \sigma_j, $$

(11)

where the values σ _j are the singular values lying on the diagonal of $\Upsigma.$ If all of the singular values in $\Upsigma$ are included in the right-hand sum, then the above equation yields the maximum possible energy that can be captured by a POD projection.

We emphasize that the first r POD modes form the orthonormal basis that best captures the kinetic energy in a set of velocity fields. For estimation purposes, we would like to approximate the true velocity field as accurately as possible, so POD modes are a natural choice of basis vectors. However, we note that for flow control applications, other bases may be more suitable, as high-energy modes may not always capture the input-output behavior of a system well (Ilak and Rowley 2008). In these cases, control-oriented methods such as balanced POD (Rowley 2005) or the eigensystem realization algorithm (ERA) (Ma et al. 2011) may be advantageous.

3.1.2 Dynamic mode decomposition (DMD)

DMD is a snapshot-based method that identifies oscillatory structures in a flow based on their frequency content (Schmid 2010). This is in contrast to POD, which identifies modes based on their energy content. When a temporal (as opposed to spatial) analysis is performed, these structures can be interpreted in terms of Koopman operator theory (Rowley et al. 2009). For a wake flow that exhibits clear oscillatory behavior, it is natural to apply DMD when trying to identify coherent structures. This is commonly done in numerical studies, but can be difficult in experiments because DMD requires snapshots to be collected at a rate that satisfies the Nyquist sampling criterion. In this work, we use DMD as a benchmark for the accuracy of our method, comparing estimate-based DMD computations with those done using TRPIV data.

To compute the DMD modes from a set of velocity fields $\{\underline{{u}}_k\}_{k=0}^m,$ where again $\underline{{u}}_k = \underline{{u}}(t_k),$ we form the data matrices

$$ K = \left[\begin{array}{lll} \vline & &\vline \\ \underline{{u}}_0 & \cdots & \underline{{u}}_{m-1} \\ \vline & & \vline \end{array}\right], \quad K' = \left[\begin{array}{lll} \vline & & \vline \\ \underline{{u}}_1 & \cdots & \underline{{u}}_m \\ \vline & & \vline \end{array}\right]. $$

(12)

(Note that for DMD, in general the mean is not subtracted from the dataset.)

We then compute the singular value decomposition (SVD) $K = U \Upsigma W^T$ using the method of snapshots, taking advantage of the equivalence of left singular vectors (columns of U) and POD modes:

$$ \begin{aligned} K^T M K &= W \Upsigma^2 W^T \notag \\ U &= K W \Upsigma^{-1}, \end{aligned} $$

(13)

where M is again a matrix of inner product weights (see the discussion of POD above). These matrices are used to solve the eigenvalue problem

$$ (U^T M K' W \Upsigma^{-1}) V = V \Uplambda, $$

(14)

where the columns of V and diagonal elements of $\Uplambda$ are the eigenvectors and eigenvalues, respectively, of $U^T M K' W \Upsigma^{-1}.$

The DMD mode $\underline{{\psi}}_j$ is then given by the j + 1th column of the matrix

$$ \Uppsi = U V, $$

(15)

scaled such that

$$ \sum\limits_{j=0}^{m-1} \underline{{\psi}}_j = \underline{{u}}_0. $$

With this scaling, the DMD modes are related to the original snapshots by the equations

$$ \underline{{u}}_k = \sum_{j=0}^{m-1} \lambda_j^k \underline{{\psi}}_j \quad\quad k=0, \ldots , m-1 \\ $$

(16)

$$ \underline{{u}}_m = \sum_{j=0}^{m-1} \lambda_j^m \underline{{\psi}}_j + \underline{{\epsilon}} \quad\quad \underline{{\epsilon}} \perp \hbox{span}\{\underline{{\psi}}_j\}_{j=0}^{m-1}, $$

(17)

where the values λ _j are the eigenvalues lying on the diagonal of $\Uplambda.$ Each of these eigenvalues is associated with a particular DMD mode $\underline{{\psi}}_j,$ giving each mode an associated growth rate $\|\lambda_j\|$ and oscillation frequency $\hbox{arg}(\lambda_j).$

3.2 Modified stochastic estimation

Stochastic estimation is a means of approximating a conditional average using a knowledge of unconditional statistics. Adrian and Moin (1988) proposed a stochastic estimate of the conditional average by means of a Taylor series expansion

$$ {\hat{a}}_i(t) = \langle a_{i}(t) | p_j(t) \rangle \approx A_{ij} p_j(t) + B_{ijk} p_j(t) p_k(t) + \ldots , $$

(18)

where a _i is the ith POD coefficient, p _j is the jth probe measurement, $\langle\cdot\rangle$ is the expected value, and $\hat{a}_i$ is the estimate of the conditional average. The stochastic estimation coefficients A _ij , B _ijk , and so on are determined by minimizing the mean square error of the estimate

$$ \langle ( \hat{a}_i(t) - a_i(t) )^{2} \rangle, $$

which requires solving a set of linear equations (Guezennec 1989). (We note that in some situations, for instance in the case of periodic flows, additional assumptions may be necessary to uniquely determine the estimation coefficients.)

The particular form of stochastic estimation given in Eq. (18), in which the time-varying POD coefficient is the conditional variable, is referred to as modified stochastic estimation. This approach can be more favorable than estimating a full PIV velocity field, typically consisting of thousands of data points, because the dominant behavior of many flows can be captured by a handful of POD modes. The estimated POD coefficients, paired with the corresponding modes, yield low-dimensional estimates of velocity fields.

Modified stochastic estimation has been applied by Bonnet et al. (1994) and Taylor and Glauser (2004) for linear estimates, Naguib et al. (2001) and Murray and Ukeiley (2007a) for quadratic stochastic estimation, and Durgesh and Naughton (2010) for linear estimates using time delays. In this work, we take the same low-dimensional approach to stochastic estimation, first using it to obtain initial estimates of time-resolved POD coefficients from non-time-resolved PIV measurements and time-resolved point measurements. Based on these initial estimates, it is then used again to estimate model parameters that are later used as part of a dynamic estimator.

3.2.1 Single-time-delay modified linear stochastic estimation

In mLSE, only the linear term in Eq. (18) is retained. Then given the value of the probe measurements, the estimate is

$$ \hat{a}_i(t) = A_{ij} p_j(t - \tau), $$

(19)

where a constant time delay τ is introduced to account for a potential lead or lag between the conditional and unconditional variables. This increases the correlations between $\underline{{a}}(t)$ and $\underline{{p}}(t)$ for some systems (Guezennec 1989; Cole et al. 1992; Schlegel et al. 2012). To calculate the coefficients A _ij , the mean-square error of the estimates must be minimized, which requires solving the equation

$$ A^{T} = \left[PP\right]^{-1} \left[aP\right], $$

(20)

where

$$ \begin{aligned} A^{T} &= \left[\begin{array} {l} A_{1,i} \\ A_{2,i} \\ \vdots \\ A_{N_{\rm p},i}\end{array}\right], \left[ PP \right] = \left[\begin{array}{llll} \overline{p_1 p_1} &\overline{p_1 p_2} & \cdots & \overline{p_1 p_{N_{\rm p}}} \\ \overline{p_2 p_1} & \overline{p_2 p_2} & \cdots & \overline{p_2 p_{N_{\rm p}}} \\ \vdots & \vdots & \ddots & \vdots\\ \overline{p_{N_{\rm p}} p_1} & \overline{p_{N_{\rm p}} p_2} & \cdots &\overline{p_{N_{\rm p}} p_{N_{\rm p}}} \end{array}\right], \hbox{and} \\ \left[aP \right] &= \left[\begin{array}{l} \overline{a_i p_1} \\ \overline{a_i p_2} \\ \vdots \\ \overline{a_i p_{N_{\rm p}}} \end{array}\right]. \end{aligned} $$

(N _p is the number of probe measurements; time dependence in the above equations is neglected for brevity.)

3.2.2 Multi-time-delay modified linear stochastic estimation (MTD-mLSE)

Equation (19) is the “single time” form of mLSE. However, a single delay may increase the correlation between certain pairings of the unconditional and conditional variables but not others. In general, we can account for multiple time delays, summing the correlations over several values of τ (Ukeiley et al. 2008; Durgesh and Naughton 2010):

$$ \hat{a}_i(t) = A_{ijk} p_j (t - \tau_k). $$

(21)

The use of multiple time delays, rather than a single one, is advantageous if the exact time delay is not optimal for all pairings, unknown, or not resolved well enough in time. Multi-time-delay mLSE (MTD-mLSE) has been developed for purely negative time delays, requiring only past data (Ukeiley et al. 2008), as well as for two-sided delays that also use future data (Durgesh and Naughton 2010).

The latter method is applied in this work to estimate the time-dependent POD coefficients $\underline{{a}}(t)$ and is hereafter referred to as MTD-mLSE, unless distinguished as the purely negative delay version. While using both past and future data may strengthen correlations, it comes at the cost of yielding a non-causal process. As such, two-sided MTD-mLSE cannot be used in real-time estimation or flow control applications. For a derivation of the MTD-mLSE algorithm, we refer the reader to Durgesh and Naughton (2010).

We note that Eqs. (19) and (21) provide static maps from the measurement $\underline{{p}}(t)$ to the estimate $\hat{\underline{{a}}}(t).$ When computing the coefficients A _ij and A _ijk , we make sure to average over large datasets, mitigating the effects of sensor noise. However, in using those coefficients to compute an estimate, the static map will respond directly to the probe measurements (without averaging), making the estimates sensitive to noise. The use of a multi-time-delay formulation may increase robustness to sensor noise, but cannot completely overcome this inherent limitation of static estimators.

3.3 Dynamic estimation

3.3.1 Model identification

Our goal is to use a dynamic estimator to estimate the state of a bluff-body wake experiment. We assume that a time-resolved velocity probe signal is available, as well as PIV velocity fields captured at a slower, non-time-resolved sampling frequency. To implement a dynamic estimator, we need a model for the time evolution of the system. A high-fidelity numerical discretization of the Navier-Stokes equation is far too computationally intensive for this purpose, and would in any case be difficult to match to the experiment. As such, we develop an empirically derived, low-order model. We focus on POD-based models, as the first r POD modes optimally capture the kinetic energy contained in a set of snapshots, for any model order r.

From a large, statistically independent ensemble of PIV snapshots, we can compute a single set of well-converged POD modes. For the model identification procedure, we assume only non-time-resolved data are available. (See Sect. 4.3 for a detailed description of the particular dataset used for this computation.) We fix a desired model order r based on the energy content of the modes, which can be determined from the POD eigenvalues. These r modes form a basis for our low-order model.

Due to noise and low spatial resolution, methods such as Galerkin projection can be difficult to apply when using experimentally acquired velocity fields. As such we take a stochastic approach in identifying a dynamic model. First, we collect a set of non-time-resolved PIV snapshots synchronously with a time-resolved probe signal. The PIV data are projected onto the POD basis to get a non-time-resolved set of POD coefficients $\{\underline{{a}}_{N_{\rm ps}k}\},$ where N _ps is the ratio of the probe and PIV sampling rates. (We note that here, the notation $\underline{{a}}_k$ denotes a vector of POD coefficients corresponding to a time t _k , not to be confused with the previous use of a _i to denote the ith element of $\underline{{a}}.$) These coefficients are used along with synchronous probe measurements as “training data” to calculate the linear coefficients for MTD-mLSE, as described above in Sect. 3.2 The MTD-mLSE coefficients are then applied to the full, time-resolved probe signal, providing a set of time-resolved estimates of the POD coefficients, $\{\underline{\hat{a}}_{k}\}.$

We then apply LSE to these vectors, recalling that LSE estimates the expected value of a conditional variable as a linear function of an unconditional variable. If we take $\hat{\underline{{a}}}_k$ to be the conditional variable and $\hat{\underline{{a}}}_{k-1}$ to be the unconditional variable, then we can use LSE to identify a linear, discrete-time dynamical map:

$$ \hat{\underline{{a}}}_{k} \approx \langle \hat{\underline{{a}}}_k | \hat{\underline{{a}}}_{k-1} \rangle \approx F^{\rm LSE} \hat{\underline{{a}}}_{k-1}. $$

(22)

So long as the MTD-mLSE estimates of the POD coefficients are accurate enough, then the resulting model will capture enough of the true dynamics to be used as the basis for a Kalman filter.

Finally, we note that it can be shown that the solution to the above LSE problem is the same as the least-squares, least-norm solution to the problem

$$ {\fancyscript{B}} = F^{\rm LSE} {\fancyscript{A}}, $$

where the columns of $\fancyscript{B}$ are the vectors $\{\hat{\underline{{a}}}_k\}_{k=1}^m$ and the columns of ${\fancyscript{A}}$ are the vectors $\{\hat{\underline{{a}}}_k\}_{k=0}^{m-1},$ collected over all runs. (The proof is simple and omitted here.) As such, F ^LSE can be computed by simply taking the Moore-Penrose pseudoinverse of ${\fancyscript{A}}.$ However, the analogy to LSE provides an additional interpretation to the dynamics it defines, as it provides a linear estimate of the most statistically likely value of $\hat{\underline{{a}}}_k$ given a value of $\hat{\underline{{a}}}_{k-1},$ according to the ensemble defined by ${\fancyscript{A}}$ and $\fancyscript{B}.$ Based on this interpretation, this modeling procedure can naturally be extended using quadratic stochastic estimation (QSE), or even higher-order methods, for which there are no analogs to the pseudoinverse.

The bluff-body wake studied in this work is dominated by a Kármán vortex street. A computational study of a very similar flow shows that this behavior is captured well by the first two POD modes alone, which by virtue of their similarity to the dominant DMD modes, have purely oscillatory dynamics (Tu et al. 2011). To take advantage of this knowledge in developing a model, we decouple the dynamics into two parts: an analytic, oscillatory component describing the Kármán vortex shedding, and a stochastic component describing the dynamics of all the other POD modes. This yields a system with dynamics

$$ \hat{\underline{{a}}}_k = \left[\begin{array}{ll} F^{\rm osc}& 0 \\ 0 & F^{\rm LSE} \end{array}\right] \hat{\underline{{a}}}_{k-1}, $$

(23)

where F ^osc is a 2 × 2 matrix

$$ F^{\rm osc} = \left[\begin{array}{ll} \lambda^{\rm re} &-\lambda^{\rm im}\\ \lambda^{\rm im} & \lambda^{\rm re} \end{array}\right]. $$

(24)

We choose λ = λ ^re + iλ ^im such that arg(λ) is equal to the shedding frequency (identified using an autospectrum of the probe signal), and $\|\lambda\|$ is close to one, indicating nearly perfectly oscillatory dynamics. (In practice we choose $\|\lambda\|=0.999$ to ensure stable dynamics.) The stochastic dynamics F ^LSE are identified using the method discussed above.

We note that in practice, the oscillatory dynamics can be captured directly by the stochastic modeling procedure. This negates the need for an a priori knowledge of the dynamics. For more complex systems, this approach may not suffice, though one could attempt to use more sophisticated system identification tools, for instance the eigensystem realization algorithm (ERA) (Juang and Pappa 1985), the auto-regressive Markov (ARMARKOV) algorithm (Akers and Bernstein 1997; Hyland 1991), or observer Kalman identification (OKID) (Juang et al. 1991; Phan et al. 1993). However, we emphasize that the point of dynamic estimation is to leverage knowledge of a system’s dynamics to estimate its state. As such, the need for a model should not be seen as a hindrance. If a model is not available, this simply indicates that dynamic estimation may not be an appropriate method for the task at hand.

3.3.2 Kalman filter

We use the procedure detailed in the preceding section to model the bluff-body wake as a dynamical system

$$ \begin{aligned} \underline{{a}}_k &= F \underline{{a}}_{k-1} + \underline{{d}}_k\\ \underline{{\eta}}_k &= H_k \underline{{a}}_k + \underline{{n}}_k, \end{aligned} $$

(25)

where $\underline{{a}}$ is a vector of POD coefficients, $\underline{{\eta}}$ is some measured quantity, $\underline{{d}}$ is process noise, and $\underline{{n}}$ is sensor noise. The matrix F is simply the block diagonal matrix given in Eq. (23). The measurement matrix H _k can be varied according to the timestep. At times when a non-time-resolved PIV snapshot is available, we choose H _k  = I, allowing the system access to the POD coefficients of that snapshot. Otherwise, we let H _k be a row vector containing the vertical velocity of each POD mode at the probe location. This makes $\underline{{\eta}}_k$ a POD approximation of the probe signal.

We assume that $\underline{{d}}$ and $\underline{{n}}$ are white, zero-mean, and uncorrelated, with covariances ${\fancyscript{Q}}$ and ${\fancyscript{R}}.$ This yields the equations

$$ \begin{aligned} E[\underline{{d}}_i \underline{{d}}_j^T] &= {\fancyscript{Q}}_i \delta_{ij} \\ E[\underline{{n}}_i \underline{{n}}_j^T] &={\fancyscript{R}}_i \delta_{ij} \\ E[\underline{{d}}_i \underline{{n}}_j^T] &= 0.\\ \end{aligned} $$

${\fancyscript{Q}}$ and ${\fancyscript{R}}$ are user-defined matrices, which we can consider to be design parameters. Their relative magnitudes weigh the relative accuracy of the model versus the sensor and can be used to account for the effects of noise on the system. If we have a very noisy sensor, we want to rely more heavily on the model and make ${\fancyscript{R}}$ large to penalize the sensor noise. On the other hand, if we have an inaccurate model, then we would do better by simply following the sensor, and we increase ${\fancyscript{Q}}$ to penalize process noise. For this particular experiment, we let the covariances ${\fancyscript{Q}}$ and ${\fancyscript{R}}$ vary in time according to which measurement is available. A higher penalty is given to the noisy probe signal, whereas the PIV data (when available) are assumed to be very accurate.

We initialize the Kalman filter with the values

$$ \begin{aligned} \hat{\underline{{a}}}_{f,0}^+ &= E[\underline{{a}}_0] \\ {\fancyscript{P}}_{f,0}^+ &= E[(\underline{{a}}_0-\hat{\underline{{a}}}_0^+) (\underline{{a}}_0-\hat{\underline{{a}}}_0^+)^T], \end{aligned} $$

where ${\fancyscript{P}}$ is the covariance of the estimation error. The filter is then updated using the following equations, for $k=1, 2, \ldots$ (Simon 2006):

$$ {\fancyscript{P}}_{f,k}^-=F{\fancyscript{P}}_{f,k-1}^+F^T+{\fancyscript{Q}}_{k-1 } $$

(26)

$${\fancyscript{K}}_{f,k}=\mathcal{P}_{f,k}^+ H_k^T \mathcal{R}_k^{-1}$$

(27)

$$ \hat{\underline{{a}}}_{f,k}^- = F\hat{\underline{{a}}}_{f,k-1}^+ \\ $$

(28)

$$ \hat{\underline{{a}}}_{f,k}^+ = \hat{\underline{{a}}}_{f,k}^- + {\fancyscript{K}}_{f,k} \left(\underline{{\eta}}_k - H_k \hat{\underline{{a}}}_{f,k}^-\right) $$

(29)

$$ {\fancyscript{P}}_{f,k}^+ = \left(I -{\fancyscript{K}}_{f,k} H_k\right) {\fancyscript{P}}_{f,k}^-. $$

(30)

3.3.3 Kalman smoother

The Kalman filter is a causal estimation technique, using only past and current data in forming a state estimate. In a pure post-processing application, we can make use of data at future timesteps to further improve the estimate. Such non-causal filters are referred to as smoothers. We focus here on fixed-interval smoothing, in which data are available over a fixed interval (here, the duration of the experiment). Specifically, we use a variant of the Kalman smoother called the Rauch–Tung–Striebel (RTS) smoother. RTS smoothing consists of a forward pass over the data using a standard Kalman filter (as described above), followed by a backward pass with the RTS smoother.

We assume that the data are available from timesteps 0 to N _t . After performing a forward pass with a Kalman filter, the smoother is initialized with the values

$$ \begin{aligned} \hat{\underline{{a}}}_{s,N_t} &= \hat{\underline{{a}}}_{f,N_t}^+ \\ {\fancyscript{P}}_{s,N_t} &= {\fancyscript{P}}_{f,N_t}^+. \end{aligned} $$

We then interate over $k=N_t-1, \ldots ,1, 0$ (Simon 2006):

$$ {\fancyscript{I}}_{f,k+1}^- = \left({\fancyscript{P}}_{f,k+1}^-\right)^{-1} $$

(31)

$$ {\fancyscript{K}}_{s,k} ={\fancyscript{P}}_{f,k}^+ F^T {\fancyscript{I}}_{f,k+1}^- $$

(32)

$$ {\fancyscript{P}}_{s,k}= {\fancyscript{P}}_{f,k}^+ - {\fancyscript{K}}_{s,k} \left({\fancyscript{P}}_{f,k+1}^- - {\fancyscript{P}}_{s,k+1}\right){\fancyscript{K}}_{s,k}^T \\ $$

(33)

$$ \hat{\underline{{a}}}_{s,k} = \hat{\underline{{a}}}_{f,k}^+ + {\fancyscript{K}}_{s,k} \left(\hat{\underline{{a}}}_{s,k+1} - \hat{\underline{{a}}}_{f,k+1}^-\right). $$

(34)

3.4 Dynamic estimator implementation

As depicted by the flow chart in Fig. 1, the goal in this work is to leverage the spatial coverage of PIV data with the temporal resolution of point measurements to improve the accuracy of reduced-order flow field estimates. The estimation procedure can be broken into three general tasks:

• 1. Compute an initial set of stochastic estimates.

  • (a) Collect PIV data synchronously with time-resolved probe measurements. The PIV data need not be time-resolved. From the PIV data, compute the dominant POD modes, for instance using Eq. (11) to select modes based on their energy content. This yields a set of r basis vectors $\{\underline{{\phi}}_j\}_{j=0}^{r-1},$ to be used in approximating the flow field.

  • (b) Project the PIV vector fields onto the selected POD modes, yielding a non-time-resolved history of the POD coefficients $\underline{{a}}(t_{N_{\rm ps}k}),$ where N _ps is the ratio of probe and PIV sampling rates. Pair each set of POD coefficients with its corresponding set of probe measurements. Using the POD coefficients as the conditional data and a downsampled subset of the probe measurements as the unconditional data, compute the coefficients in the matrix A for MTD-mLSE.

  • (c) Apply the MTD-mLSE coefficients to the full set of time-resolved probe data. This yields a time-resolved estimate of the time history of the POD coefficients, $\hat{\underline{{a}}}(t_k).$

• 2. Identify a model using the initial estimates.

  Combine physical intuition with the initial, stochastic estimates to form a dynamic model for the evolution of the POD coefficients. For instance, the procedure described in Sect. 3.3 can be used for suitable, well-behaved, oscillatory wakes.

• 3. Compute an improved set of estimates using a model-based dynamic estimator.

  Use the dynamic model constructed above to implement a Kalman smoother. Apply the Kalman smoother, using the time-resolved probe data and non-time-resolved PIV velocity fields (when available) as measurement updates. The time history of the Kalman smoother’s state provides a time-resolved, low-order estimate of the velocity field.

Fig. 1

Flow chart of dynamic estimator implementation

4 Experimental setup

4.1 Facility and instrumentation

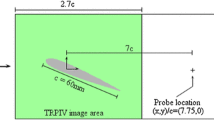
We use TRPIV to measure the velocity in the near wake behind a flat plate model with an elliptical leading edge and blunt trailing edge. The experiments are conducted in an Aerolab wind tunnel at the University of Florida Research and Engineering Education Facility. This open-return, low-speed wind tunnel has a test section that measures 15.3 cm × 15.3 cm × 30.5 cm in height, width, and length, respectively. The test section is preceded by an aluminum honeycomb, an anti-turbulence mesh screen, and a 9:1 area-contraction section. An upstream centrifugal fan, driven by a variable frequency motor, controls the airspeed. The test section velocity is set by referencing the static and stagnation pressures from a Pitot-static tube placed at the inlet of the test section. The pressure differential is read by a Heise ST-2H pressure indicator with a 0–2 in-H₂O differential pressure transducer. For the experimental results that follow, the leading edge of the model is placed a few millimeters downstream of the test section entrance, as seen in Fig. 2.

Fig. 2

Schematic of experimental setup. A laser light sheet for PIV measurements illuminates the region behind the blunt trailing edge of a flat plate model. A probe measurement of v′ is extracted from the TRPIV wake measurements at x/h = 2.24 and y/h = 0.48

The two-dimensional flat plate model has a 4:1 (major axis-to-minor axis) elliptical leading edge, transitioning to a flat portion at the minor axis of the ellipse, and terminating abruptly with a flat trailing edge. Unlike other two-dimensional bluff bodies with similar wake dynamics (e.g., a cylinder), the lack of surface curvature at the trailing edge simplifies the measurement of the near wake region. This geometry allows the PIV laser sheet to illuminate the entire region behind the trailing edge without mirrors or complex laser alignment. The thickness-to-chord ratio is 7.1 %, with a chord of 17.9 cm and a span of 15.2 cm. For this analysis, the freestream velocity $U_{\infty}$ is set to 4.2 m/s, which corresponds to a Reynolds number of 3,600 based on the plate thickness h.

A Lee Laser 800-PIV/40G Nd:YAG system capable of up to 40 W at 10 kHz is paired with appropriate optics to generate a laser sheet for PIV measurements. As shown in Fig. 2, the light sheet enters the test section through a clear floor. The vertically oriented light sheet is aligned with the midspan of the model and angled such that the rays of light run parallel to the trailing edge without grazing the surface. This alignment prevents unwanted, high-intensity surface reflections and is necessary for well-illuminated flow near the trailing edge, where particle densities can be low.

We image the seeded flow with an IDT MotionPro X3 camera and a 60 mm Nikon lens. The camera has a maximum resolution of 1,280 × 1,024 and a sampling rate of 500 Hz for integration of all pixels. A sampling frequency of 800 Hz is achieved by reducing the number of pixels captured for each image, such that the effective image resolution is 600 × 1,024. The laser and cameras are synchronized by a Dantec Dynamics PIV system running Dantec Flow Manager software. The seeding for the freestream flow is produced by an ATI TDA-4B aerosol generator placed upstream of the tunnel inlet. The seed material is olive oil, and the typical particle size is 1 μm.

LaVision DaVis 7.2 software is used to process the PIV data, using the following procedure: first, local minimum-intensity background frames are subtracted from the raw image pairs. This step increases the contrast between the bright particles and the illuminated background by reducing the influence of static background intensities and noise bands. Then, surface regions and areas with poor particle density are masked (ignored) before computing multigrid cross-correlations. The processing consists of three passes with 64 × 64 pixel² interrogation windows and 75 % overlap, followed by two refining passes with 32 × 32 pixel² interrogation windows and 50 % overlap. In between passes, outliers are reduced by applying a recursive spatial outlier detection test (Westerweel 1994). The final vectors are tested for outliers via the universal outlier spatial filter (Westerweel and Scarano 2005) and the multivariate outlier detection test (Griffin et al. 2010), an ensemble-based technique. Holes or gaps left by vector post-processing, which comprise less than 6 % of the total vectors over all ensembles, are filled via gappy POD (Everson and Sirovich 1995; Murray and Ukeiley 2007a). The final spatial resolution of the PIV measurements is approximately 8 % of the trailing edge thickness.

4.2 Data acquisition

We acquire ten records of TRPIV images at a rate of 800 Hz. Each record is comprised of nearly 1,400 sequential image pairs. To obtain a coarsely sampled (in time) set of velocity fields, we simply take a downsampled subset of the original TRPIV data. This is intended to mimic the capture rate of a standard PIV system, which for many flows is not able to resolve all of the characteristic time scales. Typical sampling rates for such commercially available systems are on the order of 15 Hz. For the estimation results that follow, one out of every 25 sequential velocity fields is used for estimation, which corresponds to a sampling rate of 32 Hz. The Nyquist frequency based on this reduced sampling rate is 16 Hz and well below the shedding frequency of about 90 Hz.

We also acquire a time-resolved probe signal by extracting the vertical velocity v from a single point in the TRPIV velocity fields. Because this probe originates from within the velocity field, the probe data are acquired synchronously with the coarsely sampled velocity fields, and span the time intervals between them (Fig. 3). This simulates the type of signal that would be measured by an in-flow sensor like a hot-wire probe. However, in-flow probes are intrusive and may interfere with attempts to take simultaneous PIV measurements, in addition to potentially disturbing the natural flow. Furthermore, such probes are not feasible in real-world applications. To emulate a more realistic flow control setup, other experiments similar to this one have used non-intrusive, surface-mounted pressure sensors to perform stochastic estimation (Durgesh and Naughton 2010; Murray and Ukeiley 2007b), as well as Kalman filter-based dynamic estimation (Pastoor et al. 2006, 2008). Based on their success, the methods developed here can likely be extended to work with surface-mounted sensors as well.

Fig. 3

Cartoon of data acquisition method. Probe data is collected synchronously with TRPIV snapshots. The TRPIV are downsampled to get a non-time-resolved dataset (red). This subset of the TRPIV data is used to develop static and dynamic estimators. Cartoon does not depict actual sampling rates

The dynamic estimators in this work rely, at least partially, on the correlation between point measurements and the time-varying POD coefficients. As such, the time-resolved probe measurements must correlate to structures within the flow field in order for the estimation to work properly. Consequently, the outcome of the estimation can be sensitive to the placement of the sensors (Cole et al. 1992). Motivated by the work of Cohen et al. (2006), we place our sensor at the node of a POD mode (see Fig. 2 for the sensor location). In particular, we choose the point of maximum v-velocity in the third POD mode (Fig. 6d), as a heuristic analysis determined that the dynamics of this mode were the most difficult to estimate.

4.3 Data partitioning

Here, we describe the division of the TRPIV data into two partitions: one for implementation and the other for validation. The first partition consists of five TRPIV records that we use to implement the estimation procedure described in Sect. 3.4 We refer to these records as “training sets.” The remaining five records are reserved for error analysis and validation of the resulting dynamic estimator.

There are only two times when we make use of the full TRPIV records. The first is in the POD computation, where the time-resolved aspect of the records is actually not utilized. The key assumption here is that the POD modes computed from the time-resolved velocity fields are the same as those generated from randomly sampled velocity fields. This is valid in the limit of a large, statistically independent snapshot ensemble. For the remainder of the estimator implementation, we consider only the downsampled subset of the training sets. The second place that we use time-resolved velocity fields is in our error analysis. Here, we make use of the 800 Hz TRPIV data as a basis of comparison for our estimates of the time-resolved velocity field.

5 Results and discussion

The results of the experiment described in Sect. 4 are discussed below. This discussion is broken into two main parts. First, we analyze the dynamics of the wake flow, using POD, DMD, and standard spectral analysis methods. An effort is made to identify key characteristics of the wake, including the dominant frequencies and any coherent structures. In doing so, we allow ourselves access to the TRPIV velocity fields, taken at 800 Hz.

Then the PIV data are downsampled, leaving snapshots taken at only 32 Hz. These velocity fields are combined with time-resolved point measurements of velocity (again at 800 Hz) for use in estimating the time-resolved flow field. We compare the results of MTD-mLSE on the POD coefficients to those of dynamic estimation using a Kalman smoother. As a proof of concept, we also investigate causal implementations of the estimators, which are necessary for flow control applications.

5.1 Wake characteristics

5.1.1 Global/modal analysis

At a thickness Reynolds number of $\text{Re}_h$ = 3,600, the wake behind the flat plate displays a clear Kármán vortex street, as seen in Fig. 4. POD analysis (of the first four training set records, out of five total) shows that 79.6 % of the energy in the flow is captured by the first two modes (Fig. 5). Each subsequent mode contributes only a fraction more energy, with the first seven modes containing 85.0 % in total. As such, for the remainder of this analysis, we take these seven modes as our POD basis. (Though seven modes are required to accurately describe the state, wake stabilization may be possible using fewer (Gerhard et al. 2003; King et al. 2008).)

Fig. 4

Instantaneous spanwise vorticity field computed from PIV data (scaled by the ratio of the freestream velocity $U_\infty$ to the plate thickness h). A clear Kármán vortex street is observed

Fig. 5

Energy content of the first r POD modes (i.e., of a POD basis $\{\underline{{\phi}}_j\}_{j=0}^{r-1}$)

The structure of the dominant modes, illustrated in Fig. 6b, c, demonstrates that they capture the dominant vortex shedding behavior. The lower-energy modes also contain coherent structures, though without further analysis, their physical significance is unclear. All but the third mode (Fig. 6d) resemble modes computed by Tu et al. (2011) for a simulation of a similar flow. However, the modes computed here are not all perfectly symmetric or antisymmetric, as might be expected (Deane et al. 1991; Noack et al. 2003). While it is possible to enforce symmetry by expanding the snapshot ensemble (Sirovich 1987b), we choose not to do so, taking the lack of symmetry in the modes to indicate a possible lack of symmetry in the experiment.

Fig. 6

Spanwise vorticity of POD modes computed from TRPIV fields. The modes are arranged in order of decreasing energy content. Most resemble modes computed by Tu et al. (2011) in a computational study of a similar flow. a Mean flow; b, c dominant shedding modes; d unfamiliar structure, with v-velocity probe location marked by a ; e, g antisymmetric modes; f, h spatial harmonics of dominant shedding modes

DMD analysis of the time-resolved velocity fields (from the first training set record) reveals that the flow is in fact dominated by a single frequency. The spectrum shown in Fig. 7 has a clear peak at a Strouhal number St _h  = 0.27 (based on $U_{\infty}$ and h), with secondary peaks at the near-superharmonic frequencies of 0.52 and 0.79. The dominant frequency is in good agreement with that measured by Durgesh and Naughton (2010). The corresponding DMD modes (Fig. 8) show structures that resemble the POD modes discussed above. Because DMD analysis provides a frequency for every spatial structure, we can clearly identify the harmonic nature of the modes, with the modes in Fig. 8a corresponding to the fundamental frequency, those in Fig. 8b corresponding to its first superharmonic, and those shown in Fig. 8c corresponding to its second superharmonic.

Fig. 7

DMD spectrum. Clear harmonic structure is observed, with a dominant peak at St _h  = 0.27, followed by superharmonic peaks at 0.52 and 0.79

Fig. 8

Spanwise vorticity of DMD modes computed from TRPIV velocity fields. The real and imaginary components are shown in the top and bottom rows, respectively. Note the similarity of these modes to the POD modes depicted in Fig. 6. a Dominant shedding modes; b temporally superharmonic modes, spatially antisymmetric; c further superharmonic modes, spatial harmonics of dominant shedding modes

Furthermore, because DMD identifies structures based on their frequency content, rather than their energy content (as POD does), these modes come in clean pairs. Both DMD and POD identify similar structures for the dominant shedding modes (Figs. 6b, c, 8a), but the superharmonic pairs identified by DMD do not match as well with their closest POD counterparts. For instance, the POD mode shown in Fig. 6e closely resembles the DMD modes shown in Fig. 8b, whereas the mode shown in Fig. 6g does not. Similarly, Fig. 6h depicts a mode resembling those in Fig. 8c, while Fig. 6f does not.

Interestingly, the third POD mode (Fig. 6d) is not observed as a dominant DMD mode. This suggests that the structures it contains are not purely oscillatory, or in other words, that it has mixed frequency content. As such, its dynamics are unknown a priori. This is in contrast to the other modes, whose dynamics should be dominated by oscillations at harmonics of the wake frequency, based on their similarity to the DMD modes. This motivates our placement of a velocity probe at the point of maximum v-velocity in the third POD mode (Cohen et al. 2006), in an effort to better capture its dynamics. This location is shown in Figs. 2 and 6d.

5.1.2 Point measurements

Figure 9 shows a time trace of the probe signal collected in the flat plate wake. We recall that there is no physical velocity probe in the wake. Rather, we simulate a probe of v-velocity by extracting its value from the TRPIV snapshots (see Figs. 2 or 6d for the probe location). Because PIV image correlations are both a spatial average across the cross-correlation windows and a temporal average over the time interval between image laser shots, PIV probe measurements typically do not resolve the fine scale structures of turbulence. To simulate a more realistic probe, Gaussian white noise is artificially injected into this signal, at various levels. We define the noise level γ as the squared ratio of the root-mean-square (RMS) value of the noise to the RMS value of the fluctuating probe signal:

$$ \gamma = \left(\frac{n'_{\rm RMS}}{v'_{\rm RMS}}\right)^2, $$

(35)

where the prime notation indicates a mean-subtracted value. This noise level is the reciprocal of the traditional signal-to-noise ratio. Note that the noise level only reflects the amount of artificially added noise and does not take into account any noise inherent in the velocity probe signal. We consider six noise levels, ranging from 0.01 to 0.36, in addition to the original signal (γ = 0), focusing on the extreme noise levels in the following discussion. Figure 9 shows a comparison of the original signal to artificially noisy signals. We see that though the addition of noise produces random fluctuations, the dominant oscillatory behavior is always preserved.

Fig. 9

Measurement of v′ taken in the wake at x/h = 2.24 and y/h = 0.48, the point of maximum v in the third POD mode (Fig. 6d). The values are extracted from the TRPIV snapshots. Noise is artificially injected to simulate a physical velocity sensor, with the noise level γ defined in Eq. (35). In all cases, clear oscillatory behavior is observed

A spectral analysis of the probe data, seen in Fig. 10, confirms that the shedding frequency is still detected in the presence of the artificially added noise. This is to be expected, as the addition of white noise only adds to the broadband spectrum. The dominant peaks in the autospectra lie at St _h  = 0.27, in agreement with the dominant DMD frequency. This confirms our previous characterization of the dominant DMD (and POD) modes as structures capturing the dominant vortex shedding in the wake.

Fig. 10

Autospectra of probe signals shown in Fig. 9. Clear harmonic structure is observed, with a dominant peak at St _h  = 0.27, which agrees well with the dominant DMD frequency. Superharmonic structure is also seen, again confirming behavior observed using DMD analysis

The autospectra also show clear harmonic structure, again confirming the behavior seen in the DMD spectrum. However, as the broadband noise levels increase, the third and fourth harmonics of the wake frequency become less prominent relative to the noise floor. This loss of harmonic structure carries certain implications for estimation. Most notable is that the fluctuations associated with these higher harmonics do not correlate as strongly with the time-varying POD coefficients. Consequently, the flow field estimates based on the noisy probe signals may not capture the corresponding harmonic structures as well. The inclusion of noise is designed to be a test of estimator robustness. Future work will apply the same general static and dynamic estimators presented here, but with pressure and shear stress sensors, which are inherently noisy (perhaps in a non-Gaussian way).

5.2 Low-dimensional flow-field estimation

5.2.1 Optimal delay interval for MTD-mLSE

We find that with $\tau^{*}$ = 0, MTD-mLSE estimation of the first two POD coefficients is poor, unless multiple probes are used. Here, $\tau^{*}$ is the non-dimensional time delay, defined as

$$ \tau^{*} = \tau U_{\infty}/h. $$

(36)

This follows the results of Durgesh and Naughton (2010), who conducted a very similar bluff-body wake experiment. The cause lies in the fact that there is often a phase difference between the probe signal and the time history of one or more of the POD coefficients, decreasing the magnitude of the LSE cross-correlations.

Durgesh and Naughton (2010) were able to significantly improve their estimates by using MTD-mLSE, which accounts for possible phase mismatches. For that reason, we use the same method in this work. In this variant of MTD-mLSE, to estimate the flow field at a given moment in time, we make use of probe data collected prior to that moment, as well as after. That is, to estimate the flow field at time t, we use probe data collected at times t ± τ _j , for a range of delays τ _j satisfying

$$ \tau_j^{*} \leq \tau_{\rm max} U_{\infty}/h. $$

(37)

Durgesh and Naughton (2010) demonstrated that an optimum bound $\tau^{*}_{\rm max}$ exists for estimating the unknown POD coefficients. In order to determine the optimal value, an estimation error must be computed and evaluated. For the present study, the flow field is approximated using the first seven POD modes. The corresponding vector $\underline{{a}}(t_k)$ of POD coefficients encodes a low-dimensional representation of the velocity field at time t _k , with a corresponding kinetic energy $\|\underline{{a}}(t_k)\|_2^2$ (Eq. 10). We wish to quantify the error between the true coefficients $\underline{{a}}_k$ and the estimated POD coefficients $\hat{\underline{{a}}}(t_k).$ One way to do so is to simply compute the kinetic energy contained in the difference of the two corresponding velocity fields. If we normalize by the mean kinetic energy of the snapshot set, this gives us an error metric

$$ \begin{aligned} e(t_k) &= \frac{\|\hat{\underline{{a}}}(t_k) - \underline{{a}}(t_k)\|_2^2}{\Big<\|\underline{{a}}(t_k)\|_2^2\Big>}\\ &=\frac{\sum_{i=1}^r\Big[\hat{a}_i(t_k) - a_i(t_k)\Big]^2}{\sum_{i=1}^r \Big<a_i(t_k)^2\Big>}. \end{aligned} $$

(38)

This can be interpreted as the fraction of the mean kinetic energy contained in the estimation error.

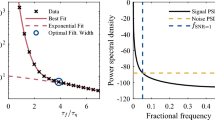
In finding the optimal delay interval for MTD-mLSE, we use only downsampled PIV data (from the first four training set records) to compute the MTD-mLSE coefficients. The estimation error is then evaluated by taking another PIV record (the fifth training set record) and estimating its POD coefficients $\{\hat{\underline{{a}}}_k\}.$ These other PIV velocity fields are also projected onto the POD modes to get their true coefficients $\{\underline{{a}}_k\},$ which we then compare to the estimated coefficients. The mean energy in the error $\overline{e}$ is calculated from these coefficients for values of $\tau^*$ ranging from 0 to 12. The results are plotted in Fig. 11.

Fig. 11

Mean energy in the MTD-mLSE estimation error, for various symmetric time delay intervals. An optimal value of $\tau^*_{\rm max}$ is observed

The minimum value of $\overline{e}$ occurs for a delay interval with $\tau^{*}_{\rm max} = 2.48.$ However, we note that due to the shallow valley around the minimum seen in Fig. 11, similar estimator performance is expected for delays ranging between 1.7 and 3.0 (roughly). Note that the case of $\tau^{*}_{\rm max}$ = 0 empirically demonstrates that mLSE without any time delay yields poor estimates in this experiment (as suggested by theory).

5.2.2 Kalman smoother design

The model for the Kalman smoother is identified using the method described in Sect. 3.3 We recall that this model consists of two decoupled submodels. The first describes the dynamics of the two dominant POD modes, which are assumed to be oscillatory. Figure 10 shows autospectra computed from the time-resolved probe data, which we use to determine the oscillation frequency. The second submodel describes the dynamics of the remaining five modes and is identified using the initial set of MTD-mLSE estimates.

Once the model has been obtained, the Kalman smoother is initialized with the values

$$ \begin{aligned} \hat{\underline{{a}}}_{f,0}^+ &= \underline{{a}}_0 \\ {\fancyscript{P}}_{f,0}^+ &= 5 I, \end{aligned} $$

where I is the identity matrix. We assume that the initial set of POD coefficients $\underline{{a}}_0$ is known, as this is a post-processing application where the PIV data are available at certain (non-time-resolved) instances. The noise covariances are taken to be

$$ {\fancyscript{Q}}_k = \left[\begin{array}{lllllll} 1 & & & & & & 0 \\ & 1 & & & & & \\ & & 0.004 & & & & \\ & & & 0.5 & & & \\ 0 & & & & & \ddots & \end{array}\right] $$

and

$$ {\fancyscript{R}}_k = \left\{\begin{array}{ll} 2 \times 10^4 & \hbox{when only probe data are available} \\ 1 \times 10^{-10} I & \hbox{when PIV data are available.}\end{array}\right.$$

We heavily penalize the time-resolved velocity signal to mitigate the effects of noise (large ${\fancyscript{R}}_k$), while the PIV data are assumed to be very accurate relative to the model (small ${\fancyscript{R}}_k$). In addition, the diagonal matrix ${\fancyscript{Q}}_k$ is designed to account for the observation that the lower-energy POD modes are more sensitive to noise in the probe signal, with the third mode more sensitive than the rest.

5.2.3 Error analysis

We now compare the performance of two estimators: a static MTD-mLSE estimator with an optimal time delay interval and a dynamic Kalman smoother, both described above. We apply each estimator to five PIV records designated for estimator validation. (These records were not used in any way in the development of the estimators.) The estimates of the POD coefficients are evaluated using the error metric e defined in Eq. (18).

The aggregate results are shown in Fig. 12. By definition, e is non-negative, giving it a positively skewed distribution. As such, the spread of these values is not correctly described by a standard deviation, which applies best to symmetric distributions. To account for this, the error bars in Fig. 12 are adjusted for the skewness in the distribution of e (Hubert and Vandervieren 2008). We observe that for all noise levels, the mean error achieved with a Kalman smoother is smaller than that of the MTD-mLSE estimate. Furthermore, the rate of increase in the mean error is slower for the Kalman smoother than for the MTD-mLSE estimate, and the spread is smaller too. As such, we conclude that not only does the Kalman smoother produce more accurate estimates (in the mean), but it is also more robust to noise.

Fig. 12

Mean and distribution of the energy in the estimation error, for various levels of sensor noise (as defined in Eq. (38)). The error energy is normalized with respect to the average energy contained in the (mean-subtracted) velocity field. The Kalman smoother estimates are both more accurate and less sensitive to noise

This robustness comes in two forms. The first is that for a given amount of noise in the signal, the expected value of the estimation error has a wider distribution for MTD-mLSE than for a Kalman smoother. Secondly, as the noise level is increased, the MTD-mLSE estimation error increases more rapidly, indicating a higher sensitivity to the noise level. This is expected, as MTD-mLSE is a static estimation method (as discussed in Sect. 3.2)

The time evolution of the estimates elucidates another advantage of the dynamic estimator. Figure 13a compares the true history of the second POD coefficient to the corresponding MTD-mLSE and Kalman smoother estimates, for the worst-case noise level γ = 0.36. We see that for this particular mode, the Kalman smoother estimates are generally more accurate, deviating less from the true coefficient values. In particular, there is very little error during the instances surrounding a PIV update. This is even more obvious when we consider the evolution of e, which incorporates the errors in all seven mode coefficients (Fig. 13b). Here, we see that for the Kalman smoother alone, local minima in the error line up with the availability of PIV data, indicated by the dashed, vertical lines. (While decreases in the stochastic estimation error sometimes line up with PIV updates, this trend is not observed in general.)

Fig. 13

a Time history of the second POD coefficient (j = 1), along with the corresponding Kalman smoother and MTD-mLSE estimates; b time history of the energy in the estimation error. The vertical, dashed lines mark times when PIV data are available. The square symbols mark the time instance depicted in Figs. 15 and 16. We observe that the Kalman smoother estimates are more accurate overall. Specifically, local minima in the error occur at instances of PIV data assimilation. The MTD-mLSE estimates do not make use of these data, and thus do not show the same general behavior

This is not unexpected, as the stochastic estimates are computed using only the probe signal. In contrast, the Kalman smoother also assimilates PIV velocity fields when they are available, driving the error to nearly zero at each assimilation step. The effects of this improvement are felt for many timesteps following and prior to the PIV update. As such, it is clear that a driving factor in the improved performance of the Kalman smoother is its ability to take advantage of information that MTD-mLSE cannot, in the form of infrequently available PIV velocity fields.

These results are further illustrated by comparing the estimated vorticity fields, for both γ = 0 and γ = 0.36. Figure 14 shows an instantaneous vorticity field and its projection onto the first seven POD modes. (This particular instance in time is denoted by square markers in Fig. 13.) This projection is the optimal representation of the original vorticity field using these POD modes. We observe that the high-energy structures near the trailing edge are captured well, while the far wake structures tend to be more smoothed out. With no noise, the MTD-mLSE estimate of the vorticity field (Fig. 15a) matches the projected snapshot quite well. The spacing and shape of the high-energy convecting structures in the Kármán vortex street are correctly identified. However, when the probe signal is contaminated by noise with γ = 0.36, the estimated vorticity field shown in Fig. 15b bears little resemblance to the projection. In fact, the only structures that match are features of the mean flow (Fig. 6a). Not only are the downstream structures captured poorly, but spurious structures are also introduced. On the other hand, the Kalman smoother estimates match the projected snapshot for both clean and noisy probe data (Fig. 15c, d).

Fig. 14

Comparison of spanwise vorticity fields. a True PIV snapshot; b projection onto a seven-mode POD basis. The first seven POD modes capture the location and general extent of the vortices in the wake, but cannot resolve small-scale features

Fig. 15

Comparison of estimated spanwise vorticity fields. Without noise, both the MTD-mLSE and Kalman smoother estimates match the POD projection shown in Fig. 14b. The addition of noise to the probe signal causes the MTD-mLSE estimate to change dramatically, resulting in a large estimation error. In contrast, the Kalman smoother estimate remains relatively unchanged. a MTD-mLSE with γ = 0; b MTD-mLSE with γ = 0.36; c Kalman smoother with γ = 0; d Kalman smoother with γ = 0.36

5.2.4 Estimation-based global/modal analysis

As a further investigation into the relative merits of MTD-mLSE and Kalman smoother estimation, we use the estimated velocity fields to perform DMD analysis. We recall that DMD analysis requires that the Nyquist sampling criterion is met, for which the sampling rate must be at least double the highest frequency of interest. The DMD modes from the true TRPIV data are shown in Figs. 7 and 8. The key results from the DMD analysis of the estimated flow fields (for both the MTD-mLSE and Kalman smoother estimates) are shown in Fig. 16. Only the minimum and maximum noise levels are considered in this modal analysis.

Fig. 16

Estimation-based DMD modes. Computations of the first and second superharmonic wake modes are shown on the top and bottom rows, respectively. In general, the Kalman smoother results more closely resemble those shown in Fig. 8. For both estimation methods, using a noisier probe signal leads to poorer results. This is especially pronounced for the second superharmonic mode. a MTD-mLSE with γ = 0; b MTD-mLSE with γ = 0.36; c Kalman smoother with γ = 0; d Kalman smoother with γ = 0.36; e MTD-mLSE with γ = 0; f MTD-mLSE with γ = 0.36; g Kalman smoother with γ = 0; h Kalman smoother with γ = 0.36

The fundamental frequency St _h  = 0.27 is captured well by estimation-based DMD for both estimators, for both noise levels. The corresponding modes match as well, and illustrations are therefore neglected. (Refer to Fig. 8a for typical mode structures associated with St _h  = 0.27.) For the superharmonic frequencies, however, the estimation-based DMD modes differ in structure, both among the various estimation cases (across methods, for varying noise levels) and in relation to the DMD modes computed directly from TRPIV data (Fig. 8).

As seen in Fig. 16, both the MTD-mLSE and Kalman smoother estimates capture the first superharmonic (St _h ≈ 0.53) well when no noise is added to the probe signal. However, the Kalman smoother–based mode more accurately captures the expected antisymmetric distribution seen in Fig. 8. When the noise level is increased to 0.36, both of the estimate-based modes deviate from the corresponding TRPIV-based mode, but less so for the Kalman smoother. This is not unexpected, as the Kalman smoother estimates are less sensitive to the addition of noise (Fig. 12).

In contrast, both estimators perform poorly in capturing the DMD mode corresponding to the second superharmonic (St _h ≈ 0.79). Without any artificial noise, the MTD-mLSE and Kalman smoother–based modes are similar to each other and bear some resemblance to the expected mode shape. However, for γ = 0.36, neither displays the correct vorticity distribution nor captures the right frequency. This decreased accuracy for higher harmonics is not unexpected, as the corresponding fluctuations in the probe signals correlate less and less with the POD coefficients as the noise floor increases.

We note that because our estimates are limited to a subspace spanned by only seven POD modes, so are any estimate-based DMD computations. That is, any behavior not captured by the first seven POD modes will not be captured by estimate-based DMD analysis either. Because the dominant POD modes correspond to the highest-energy structures, the estimate-based DMD analysis will also be biased toward high-energy, and typically low-frequency, fluctuations. In this work, we observe that the dominant POD modes are quite similar to the dominant DMD modes. As such, it is no surprise that estimate-based DMD computations are successful in identifying the fundamental shedding mode and its harmonics.

5.3 Causal implementation

The Kalman smoother and MTD-mLSE methods discussed previously are non-causal, requiring future data to estimate the state. This makes them unsuitable for applications that require real-time estimates, such as estimation-based flow control. However, both methods have clear causal counterparts. We recall that the RTS Kalman smoother algorithm consists of a forward, Kalman filter estimation followed by a backward, smoothing correction. By simply not performing the smoothing operation and limiting ourselves to a Kalman filter, we can perform a causal, dynamic estimation that integrates time-resolved point measurements with non-time-resolved PIV snapshots. Similarly, the MTD-mLSE coefficients can easily be computed using one-sided delays only, eliminating the use of future data. We note that in most applications, online processing of PIV velocity fields is currently not feasible, due to computational limitations. However, such systems do exist, though they are generally limited to acquisition rates on the order of 10 Hz (Arik and Carr 1997; Yu et al. 2006). This makes an accurate estimation procedure, which estimates the state of the system between the slow PIV updates, even more critical.

Figure 17 shows that overall, the causal implementations are more error-prone than the non-causal ones (compare to Fig. 12). However, the same trends are observed in comparing the dynamic and stochastic estimates: dynamic estimation yields a lower mean error, a narrower error distribution, and a slower increase in the error with respect to γ. As before, this is not surprising, as the dynamic estimator make uses of not only the point measurements, but also full-field PIV data (when available).

Fig. 17

Mean and distribution of the energy in the estimation error for causal estimation. The same trends are observed as in the non-causal estimation (see Fig. 12), with the Kalman filter estimates more accurate and less sensitive to noise than the MTD-mLSE estimates

When no online PIV system is available, then the best we can do is to estimate the state using the time-resolved point measurements alone. Figure 18 shows that when a Kalman filter is implemented without access to any PIV information, the mean estimation error is nearly the same as that of the MTD-mLSE estimator. For any particular noise level, the distribution is smaller, but only marginally so. The increase in error with respect to noise level is comparable for both methods. As such, we can see that the assimilation of PIV measurements provides a significant benefit, even though it only occurs on relatively slow time scales.

Fig. 18

Mean and distribution of the energy in the estimation error for causal estimation using only point measurements. Without access to any PIV data, the Kalman filter is only marginally more effective than MTD-mLSE. The only benefit is a slight decrease in the sensitivity to noise

6 Conclusions and future work

The three-step estimation procedure presented here proves to be effective in estimating the time-resolved velocity field in a bluff-body wake. Rather than estimate the flow field directly using MTD-mLSE, we use MTD-mLSE to aid in identifying a stochastic model for the lower-energy structures in the flow. This stochastic model is then combined with an analytic model of the dominant vortex shedding in the wake. The result is used to implement a Kalman smoother, whose estimates of the flow field are shown to be more accurate and robust to noise than the stochastic estimates used in the modeling process. A DMD analysis of the Kalman smoother estimates identifies the same coherent structures observed in an analysis of TRPIV data, showing that the estimates correctly capture the oscillatory dynamics of the flow. Similar trends are observed for a Kalman filter implementation, which would be suitable for flow control, whereas the Kalman smoother is limited to post-processing applications.

A natural next step in this work is to apply the same procedure at a higher Reynolds number, where the dynamics are more complex. This will make model identification more difficult and may require approaches different from the one used in this work. If nonlinear models are used, then more advanced filtering techniques (e.g., sigma-point Kalman filters) can be implemented as well. Another direction to pursue is the use of surface sensors, for instance measuring pressure or shear stress, to observe the flow. Because they are (ideally) non-intrusive, they are more practical for use in a flow control experiment than velocity probes placed within the wake.