Homogeneity and isotropy in a laboratory turbulent flow

Abstract

We present a new design for a stirred tank that is forced by two parallel planar arrays of randomly actuated jets. This arrangement creates turbulence at high Reynolds number with low mean flow. Most importantly, it exhibits a region of 3D homogeneous isotropic turbulence that is significantly larger than the integral lengthscale. These features are essential for enabling laboratory measurements of turbulent suspensions. We use quantitative imaging to confirm isotropy at large, small, and intermediate scales by examining one- and two-point statistics at the tank center. We then repeat these same measurements to confirm that the values measured at the tank center are constant over a large homogeneous region. In the direction normal to the symmetry plane, our measurements demonstrate that the homogeneous region extends for at least twice the integral length scale L = 9.5 cm. In the directions parallel to the symmetry plane, the region is at least four times the integral lengthscale, and the extent in this direction is limited only by the size of the tank. Within the homogeneous isotropic region, we measure a turbulent kinetic energy of 6.07 × 10⁻⁴ m² s⁻², a dissipation rate of 4.65 × 10⁻⁵ m² s⁻³, and a Taylor-scale Reynolds number of R _λ  = 334. The tank’s large homogeneous region, combined with its high Reynolds number and its very low mean flow, provides the best approximation of homogeneous isotropic turbulence realized in a laboratory flow to date. These characteristics make the stirred tank an optimal facility for studying the fundamental dynamics of turbulence and turbulent suspensions.

1 Introduction

Homogeneous isotropic turbulence (HIT) is an idealized flow of special interest because it contains all of the basic physical processes of turbulence without the complications commonly found in nature such as mean shear, density stratification, and fluid–solid boundaries (Tsinober 2004). Thus, HIT is an ideal flow with which to understand some of the fundamental mechanisms of turbulence that are at least qualitatively independent of the origin of a specific turbulent flow such as internal intermittency (Douady et al. 1991); the self-amplification mechanisms of velocity derivatives (Galanti and Tsinober 2000); inertial range Eulerian and Lagrangian structure functions (Benzi et al. 2010); and (of particular interest to us) interphase coupling mechanisms in turbulent suspensions (Poelma and Ooms 2006; Lucci et al. 2010; Balachandar and Eaton 2010; Toschi and Bodenschatz 2009).

Despite the simplicity of HIT, it is non-trivial to recreate this condition in a laboratory experiment or in a direct numerical simulation (DNS). In DNS, turbulence either decays with time or must be sustained via an artificial forcing in space or time that introduce biases in the turbulent statistics (Abdelsamie and Lee 2012; Lucci et al. 2010). Turbulent flows in laboratory experiments, on the other hand, are intrinsically inhomogeneous because it is impossible in practice to uniformly distribute turbulent production. At best, laboratory devices can only approximate HIT. In doing so, there has typically been a trade-off between Reynolds number and the size of the HIT region. Herein, we present a new design for a stirred tank that achieves an unprecedented combination of size and Reynolds number, and conduct a thorough characterization.

2 Background

The most common way of generating turbulence for laboratory research is with a steady flow passing through a grid or mesh. These flows exhibit 2D homogeneity and isotropy in planes parallel to the grid (see for example Kurian and Fransson 2009; Krogstad and Davidson 2012, and references therein). Despite the good planar homogeneity, grid-generated turbulence is always anisotropic due to the spatial decay of turbulent kinetic energy (TKE) downstream of the grid. This can make it difficult to compare results between different experimental setups. In fact, the large scatter in decay exponents and empirical coefficients suggests that there may not be a universal state for grid turbulence (George 1992; George and Davidson 2004).

Stationary turbulence with 3D homogeneity and isotropy is produced by a new class of laboratory devices that have flourished in the past decade. These devices stir the flow from multiple locations rather than with a single grid. Stirring is conducted by means of oscillating grids (Srdic et al. 1996; Shy et al. 1997; Villermaux et al. 1995), loudspeaker cones (Hwang and Eaton 2004; Birouk et al. 2003), rotating elements (Liu et al. 1999; Guala et al. 2008; Voth et al. 2002), or synthetic jets (Variano et al. 2004; Krawczynski et al. 2010; Goepfert et al. 2010). An essential feature of these systems is that the stirring elements are arranged symmetrically around some central region. This achieves large-scale isotropy, which in turn fosters small-scale isotropy. Of these symmetric forcing (SF) systems, the most common employ spherically symmetric forcing (SSF). Early implementations of SSF used eight synthetic jets or fans at the corners of a box (see Hwang and Eaton 2004; Birouk et al. 2003, respectively). Extensions of this idea have added more forcing elements and distributed them symmetrically over polygons with more than eight vertices (Chang et al. 2012; Zimmermann et al. 2010).

A drawback of SSF systems is that the flow is optimized only in a limited volume around the point of symmetry. Cylindrical symmetric forcing (CSF) and planar symmetric forcing (PSF) systems allow larger regions of optimal flow conditions because they have a line or plane of symmetry at the tank center. As a result, the optimal region at the tank center has at least one direction in which its homogeneity is limited only by the size of the tank. Because of this, we conclude that PSF systems unite the best aspects of grid turbulence and SF systems. That is, 2D homogeneity and isotropy are present throughout the tank due to the planar forcing, and 3D homogeneity and isotropy are present in a subregion of the tank due to the interaction of two symmetric forcing planes. Herein, we present a PSF system that uses two planar arrays of randomly actuated synthetic jets.

In Table 1, we summarize a subset of the stirred tanks reported in the literature (Srdic et al. 1996; Shy et al. 1997; Villermaux et al. 1995; Hwang and Eaton 2004; Birouk et al. 2003; Liu et al. 1999; Guala et al. 2008; Voth et al. 2002; Goepfert et al. 2010; Zimmermann et al. 2010). Since there are many versions of the SSF cube, we report only a few representative cases; a more thorough comparative summary is given in Chang et al. (2012). We observe in Table 1 a trend in which the flows with large Reynolds number have a small region of HIT, and vice versa. Thus, different stirred tanks will be optimal for different research needs. For our research on particle dynamics, we would like a high Reynolds number (R _λ  >> 100) and a region of homogeneous turbulence that is significantly larger than the integral lengthscale. None of the devices in Table 1 provide both of these traits simultaneously, though those of Zimmermann et al. (2010) and Srdic et al. (1996) are closest. Herein, we present a new device that provides high-Reynolds–number turbulence that is homogeneous and isotropic over a large region.

Table 1 A summary of stirred tank performance focusing on the Reynolds number and size of the homogeneous region

The device we present herein can support a wide variety of investigations into turbulent dynamics. An illustrative example is the measurement of macroscopic particles suspended in turbulent flows. When performing such measurements (Bellani et al. 2012), we require a flow with features that are not found in any other existing device (e.g., Table 1). First, a high Reynolds number is needed to ensure an inertial subrange. Second, the integral lengthscale must be large enough that the inertial subrange will cover the size range of our macroscopic particles (5–30 mm). Having an inertial subrange at such large scales also helps us make unambiguous measurements of small-scale turbulent features (see e.g., Talamelli et al. 2009). The dynamics of particles in suspension demand that we engineer a turbulent flow that is homogeneous and isotropic over as large a region as possible. This is because the equation of motion for suspended drops, bubbles, and particles includes a history term (e.g., Mei 1992). This means that kinematics measured at one location implicitly include the integrated effect of the flow experienced over a particle’s recent trajectory. The flow facility presented here allows us to be more confident that particle kinematics measured at the tank center will represent the effects of only one type of turbulence, because the particles must travel through a large region of homogeneous isotropic turbulence before reaching the tank center. Furthermore, the tank presented herein provides a distinct advantage for studies of buoyant particles: because the tank symmetry is not spherical, the homogeneous isotropic region can be extended indefinitely in the vertical direction, so that the test particles will not rise or fall through the homogeneous region too rapidly.

3 Experimental setup

3.1 Description of the facility

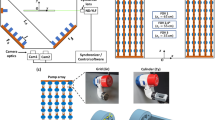
The experimental facility is a tank of dimensions 80 × 80 × 360 cm³. The origin of the coordinate system is at the center of the tank, z is oriented along the axial (longest) dimension of the tank, and y is vertical. The instantaneous velocity vector U(x, y, z, t) = (U, V, W) is defined so that U, V, and W are aligned with the x,  y, and z axes, respectively. The tank is filled with tap water, which is initially filtered to 5 micron and purified by a flow through ultraviolet filter when experiments are not being run.

Stirring is provided by two facing planes of randomly actuated jet arrays, each of them made of 64 individual pumps arranged in an 8 × 8 array as shown in Fig. 1. Each pump is used to create a jet through a cylindrical nozzle with 2.19 cm inner diameter. The nozzle and the pump intake are separated by 7 cm and located in the same volume of fluid; thus, the pump creates a synthetic jet, in the sense that it injects only momentum, and not mass, into the tank. To drive the pumps, we follow the stochastic algorithm developed by Variano and Cowen (2008). The algorithm is a stochastic pattern used to drive the jets in a manner that maximizes the turbulent Reynolds number while also ensuring spatial homogeneity. In this algorithm, an average of eight jets (12.5 % of the total number of jets) are activated on each planar array, with each jet remaining actuated for an average duration, μ _on, of 3 s, followed by an average time turned off, μ _off, of 21 s. The exact duration of a jet’s on/off period is selected from normal probability distributions, where the variance value of each distribution (σ _on; σ _off) is such that σ _on/μ _on = σ _off /μ _off = 1/3. These values were found, experimentally, to maximize Reynolds number by maximizing shear production of turbulence. The stochasticity of the algorithm prevents any tank-scale residual flow from persisting; having negligible mean flow serves experiments in two ways. First, it supports homogeneity and isotropy by reducing advective transport of TKE. Second, it allows the spatial and temporal characteristics of turbulence to be measured independently from a fixed location. Thus, measurements do not need to rely on Taylor’s frozen turbulence hypothesis, allowing a less ambiguous analysis of turbulent structures (Dennis and Nickels 2008; Álamo and Jiménez 2009; Moin 2009).

Fig. 1

Experimental facility. a 4 × 4 array of 4-jet clusters (see closeup), giving an 8 × 8 array of equally spaced jets. Two pumps arrays facing each other (as in sketch b) can produce homogeneous and isotropic turbulence statistics

Turbulence is generated near the jet arrays and decays with distance from them. By combining two arrays in a PSF configuration, it is possible to obtain HIT in a large region in the tank center. The two jet arrays are symmetrically located with respect to the vertical center plane of the tank, at a distance of ±81 cm from the center. This distance is chosen to maximize the isotropy at the tank center by matching the decay curves of the 3 different components of the velocity variance so that they intersect at the tank center.

3.2 Measurement technique

Velocity measurements are performed using particle image velocimetry (PIV) in two different configurations (see Fig. 2). 2D-PIV is used to collect data in the y z plane and stereoscopic PIV (S-PIV) is used to collect data in the x y plane. The imaging setups are shown in Fig. 2. Both PIV configurations use a 1 mm thick laser light sheet (frequency-doubled Nd-YAG), 10 μm tracer particles (silver coated glass spheres), two 12-bit CCD cameras with an 1,600 × 1,200 array of 7.4  μm pixels (Imager PRO-X), image-pair acquisition rate of 0.5 Hz, and either 50 or 105-mm lenses (Nikkor). In the 2-D PIV setup, two cameras (both fitted with a 105-mm Nikkor lens) view two adjacent regions, thus increasing the extent of spatial coverage. These regions are 0.1 cm × 3.5cm × 4.7 volumes centered in the y z plane at y = 0 and y = 10 cm, respectively. In the S-PIV experiments, the two cameras, both fitted with a 105-mm Nikkor lens, view one measurement area from opposite sides of the laser light sheet, each at an angle of 35° relative to the laser’s forward-scatter direction. To avoid image distortion by the air–glass–water interface at the tank walls, two 35° prisms filled with water are attached to the walls. Each camera views the tank through one prism, and images overlap in a 14.7 cm × 8.1   × cm × 0.1cm volume centered in the x y plane at z = 0.

Fig. 2

a Schematic of the imaging setup for 2D-PIV and S-PIV measurements. Pictures of the 2D-PIV and S-PIV setups are shown in b and c, respectively

To compute the velocity fields for both PIV configurations, we use the commercial software Davis 7.2 from LaVision GmbH. The main PIV operating parameters are reported in Table 2. These parameters can greatly effect PIV accuracy in measuring turbulent quantities. The main sources of error in PIV measurements are well understood (Raffel et al. 2001). Particular care is needed near boundaries and in high shear; only the latter is of concern here. For this reason, we use an algorithm with continuous window deformation and reduction that has been shown to perform well in turbulence studies with objective benchmarks (Stanislas et al. 2008). When spatial resolution is coarser than the Kolmogorov microscale, velocity fluctuations and TKE may be underestimated. Of those spatial resolutions reported in Table 2, the coarsest is 2.72 mm. This is about 7 times the size of the Kolmogorov scale, which is fine enough to resolve >95 % of the TKE (Saarenrinne et al. 2001). We explicitly confirm that we have resolved the TKE adequately by comparing the velocity fluctuation magnitudes as measured with two different resolutions (see Fig. 4).

Table 2 Summary of PIV settings

4 Definitions

Turbulent statistics are computed as follows. Expectation values, denoted $\langle \cdot \rangle$, are estimated from appropriate space, time, or ensemble averages.

Coordinate system	$\mathbf{x}=\{x, y, z\}=\{$lateral, vertical, axial}
Velocity field	$\mathbf{U}=\{U, V, W\}$.
Fluctuating field	$\mathbf{u}(\mathbf{x},t)=\mathbf{U}(\mathbf{x}, t)-\langle{\mathbf{U}}(\mathbf{x})\rangle$.
Turbulent kinetic energy (TKE)	$k^2=\frac{1}{2} \langle\mathbf{u}\cdot\mathbf{u}\rangle \approx \frac{1}{2}\langle 2v^2+w^2 \rangle$.
Longitudinal structure function	$S_{\rm L}^{(p)}(\mathbf{r})=\langle\{[\mathbf{u}(\mathbf{x}+\mathbf{r})-\mathbf{u}(\mathbf{x})]\cdot \frac{\mathbf{r}}{|\mathbf{r}|}\}^p\rangle$.
Transverse structure function	$S_{\rm T}^{(p)}(\mathbf{r})=\langle\{[\mathbf{u}(\mathbf{x}+\mathbf{r_T})-\mathbf{u}(\mathbf{x})]\}^p\rangle$, with $\mathbf{r_{\rm T}} \perp \mathbf{u}$.
Longitudinal autocovariance	$C_{\rm L}(\mathbf{r})=\langle\{[\mathbf{u}(\mathbf{x}+\mathbf{r}) \cdot \mathbf{u}(\mathbf{x})]\cdot \frac{\mathbf{r}}{|\mathbf{r}|}\}^p\rangle$.
Transverse autocovariance	$C_{\rm T}(\mathbf{r})=\langle\{[\mathbf{u}(\mathbf{x}+\mathbf{r_T}) \cdot \mathbf{u}(\mathbf{x})]\}^p\rangle$, with $\mathbf{r_{\rm T}} \perp \mathbf{u}$.

5 Results

5.1 Homogeneity and isotropy of single point statistics

At the tank center, statistics of turbulent fluctuations are isotropic, as seen in the velocity pdfs in Fig. 3. The pdfs of the three velocity components (calculated from 1517 S-PIV snapshots) are very similar, and they are very well approximated by a Gaussian distribution.

Fig. 3

a Instantaneous velocity field showing v and w components in the y z plane measured by 2D-PIV. b Probability distribution functions of the three velocity components from S-PIV measurements at the center of the tank (1517 independent snapshots). The dashed line indicates a Gaussian distribution $z=\frac{1}{\sigma\sqrt{2\pi}} e^{-(\frac{x-\mu}{\sigma})^2}$, with σ = v _rms and μ = 0

Fig. 4

a One-point velocity statistics measured with S-PIV on the x y plane and averaged over y. b One-point velocity statistics measured with 2D-PIV on the y z plane and averaged over y. In both plots, $\langle U \rangle\, (\circ), \,\langle V \rangle (\square),\, \langle W \rangle (\triangle)$ and u _rms,  v _rms,   w _rms are the corresponding filled markers. Marker sizes are scaled to show the 95 % CIs. For clarity, only every third sample in space is shown here. Note different spatial scales on the two plots

Figure 4 shows the spatial distribution of mean velocities (with the mean determined over time series at each location). It also shows the magnitude of velocity fluctuations (rms values computed from the temporal variance at each location). Data in Fig. 4a come from S-PIV measurements in the x y plane, while Fig. 4b shows 2D-PIV measurements in the z y plane. This data indicates that, at the center of our tank, the mean flow is negligible compared to the magnitude of velocity fluctuations. A second conclusion from this data is that the mean and rms velocities are homogeneous over the center region of the tank; determining the full extent of the homogeneous region is the topic of Sect. 6.

A summary of the data from Fig. 4b is given in Table 3. This includes a value of rms velocity calculated over both space and time. The spatio-temporal dataset has 7,300 spatial locations (covering the entire 2D PIV image area) and N temporal samples. The N samples can be considered iid (independent and identically distributed) because they are recorded at 0.5 Hz, while the 7,300 spatial locations are spaced too closely to be entirely independent from each other. To evaluate the statistical convergence of the rms velocity value, we consider only the temporal data, because it is iid. At one specific location, we calculate the 95 % CI on rms velocity using the bootstrap. This interval is seen in Table 3, and it appears to be insensitive to increasing N above 400, thus indicating statistical convergence. Having obtained statistical convergence for rms velocity, we evaluate how the rms velocity varies in space. We do so by calculating how rms velocity fluctuations (calculated from N temporal samples) vary across the 7,300 spatial locations. We quantify this spatial variation with a 95 % confidence interval computed with the bootstrap. The resulting intervals (seen in Table 3) overlap the temporal CIs and are similar in size. This indicates that the variation over space is no larger than the uncertainty over time and can be considered a quantitative statement of the spatial homogeneity observed in Fig. 4.

Table 3 Statistical convergence and spatial homogeneity demonstrated using confidence intervals on velocity fluctuation magnitudes calculated over time or space

Figures 3 and 4 and Table 3 allow us to evaluate isotropy at the tank center. In Fig. 3, the pdfs of u and v are nearly identical and the ratio between their standard deviations is u _rms/v _rms ≈ 1. The maximum anisotropy and deviation from a Gaussian behavior is seen in w. This is to be expected because the statistics of  this compnent describe motions that are normal to the symmetry plane. From the data in Table 3 the ratio v _rms/w _rms = 0.95, with a 95 % CI of [0.84 1.09] at any one location, computed via the bootstrap method (Efron and Tibshirani 1994). If we compute the CI of the isotropy ratio using the entire spatial extent of the 2D-PIV measurement at the tank center, it becomes [0.944 0.956]. Thus, the velocity variance at the tank center is either within 10 or 5 % of isotropy, depending on which CI we choose to use. As variance primarily represents the large-scale motions in turbulence, we conclude from these measurements that the flow at the tank center is isotropic at large scales. This large-scale isotropy will promote isotropy at smaller scales, which is investigated below using two-point statistics.

5.2 Two-point statistics and turbulent scales

In HIT, the autocovariances C _L and C _T are isotropic, i.e., independent of the direction of r. Normalizing both by their respective values at r = 0 gives two autocorrelation functions f(r) and g(r). The measurements of these longitudinal and lateral autocorrelation functions f and g are shown in Fig. 5a. Using the continuity equation as a constraint, g can be expressed as a function of f as shown by Eq. 1.

$$g(r)=f(r)+\frac{1}{2}\frac{\partial f(r)}{\partial r}r.$$

(1)

We can test isotropy by comparing the measured g to the prediction obtained from Eq. 1. The g(r) predicted from Eq. (1) is compared to a direct measurement of g(r) in Fig. 5a and the two agree very well to statistical uncertainties. This agreement is a further indication of isotropy between v and w.

Fig. 5

a Longitudinal $({\circ})$ and transverse (square) autocorrelation functions (f(r) and g(r), respectively). The size of the symbols is representative of the 95 % confidence interval (CI). The solid lines show the isotropic prediction of the transverse autocorrelation function g(r) from Eq. 1, with its 95 % CI. The dashed line shows the parabolic fit used to compute the longitudinal Taylor lengthscale from the longitudinal autocorrelation and it 95 % CI. b Compensated second-order structure functions used to determine dissipation rate (dashed line). The error bars represent 95 % CI. The curves are obtained from 1517 independent 2D-PIV measurements

From the autocorrelation curve, it is possible to define the Taylor length scale as $\lambda_f=[-\frac{1}{2}f^{\prime\prime}(0)]^{1/2}$. Equivalently, λ _f is the point at which the parabola p, tangent to f(r) near r = 0, intersects the axis r, so that p(r) = 1 + r ²/λ ² _f . We estimate the coefficients of p by fitting a parabola to the second and third point of f(r). The parabolic fit seen in Fig. 5 gives λ _f  = 15.9 mm, with a 95 % CI of [14.4 16.4] mm. The uncertainty in this value is dominated by the small number of data points used in the fit, which is a consequence of the spatial resolution of our PIV measurements.

We can use λ _f to predict the TKE dissipation rate $\epsilon$, because λ _f is related to fluid velocity gradients as follows (see Pope 2000):

$$\left\langle \left(\frac{\partial u}{\partial x}\right)^{2} \right\rangle =\frac{2u^{'2}}{\lambda_f^{2}}= \frac{4k^{2}}{3\lambda_f^{2}},$$

(2)

where $u' \equiv \sqrt{\frac{2}{3}k^2}$. For flows in which the strain rate tensor is isotropic, Eq. 2 can be combined with the definition of $\epsilon$ to give:

$$\epsilon=15\nu \left\langle \left(\frac{\partial u}{\partial x}\right)^2 \right\rangle=20 \nu \frac{k^2}{\lambda_f^{2}}.$$

(3)

Here, ν is the kinematic viscosity (in our case, for water at 22.8 °C, the value is 0.948 × 10⁻⁶ m² s⁻¹). For λ _f  = 15.9 mm measured from the autocorrelation function and the value of k ² from Table 3, we obtain $\epsilon=4.63 \times 10^{-5} {\rm m}^2{\rm s}^{-3}$, with a 95 % CI of [4.12 5.14].

The dissipation rate can also be computed in a second way, which will allow us to draw further conclusions about isotropy. This calculation uses the following result from Kolmogorov theory (Kolmogorov 1941):

$$S_{\rm L}^{(2)}(r) = C_2 \epsilon^{2/3} r^{2/3},$$

(4)

for r values within the inertial subrange. Although this expression is derived for the case of locally homogeneous and isotropic flows, experimental evidence (Saddoughi and Veeravalli 1994; Sreenivasan 1995) strongly suggests that this holds in heterogeneous flows (e.g., boundary layer) and that C ₂ = 2. In Fig. 5b, we show the compensated structure function S ⁽²⁾_L . The value of the plateau at r > λ _f gives us a dissipation rate of $\epsilon = 4.68\times 10^{-5}\, {\rm m}^2{\rm s}^{-3}$ with a 95 % CI of [4.45 4.78]. This value of $\epsilon$ is in very good agreement with the value obtained above using the Taylor lengthscale. We use this dissipation rate to determine the Kolmogorov lengthscale as $\eta=(\nu^3/\epsilon)^{1/4}=0.37 \hbox{ mm}$, and the Kolmogorov timescale as $\tau_\eta=(\nu/\epsilon)^{1/2}=0.142\,s.$

We use the two-point statistics to evaluate the isotropy across a range of intermediate scales. The distance between the measured and predicted g(r) in Fig. 5a can be seen as a scale-by-scale measure of isotropy. Furthermore, we can compute S ⁽²⁾_L along two orthogonal directions (y and z) shown in Fig. 5b; the distance between these two curves can also be seen as a scale-by-scale measure of isotropy. Both of these measurement methods suggest that the flow is isotropic at all scales. We note that anisotropy at intermediate and large scales, when present, can be a large source of error in estimating the dissipation rate as done above. Thus, the intermediate-scale isotropy seen in Fig. 5 and the large-scale isotropy seen in Fig. 4 support our approaches for estimating the dissipation rate, and the uncertainty in $\epsilon$ is due to statistical fluctuations and not anisotropy.

Integral lengthscales describe the large scales of turbulence, and thus are useful as a scale with which to evaluate the size of the homogeneous region created by our stirred-tank design. This is because the homogeneous region at the tank center will only be ‘truly’ homogeneous if its dimensions are significantly larger than all turbulent scales. We define L as the longitudinal integral length scale, obtained from the integral of the autocorrelation function f(r) from r = 0 to $r=\infty$. Due to practical limitations, it is rare for laboratory measurements to cover a large enough region in space to directly calculate this integral. That is, velocity fields must be measured over a length of 3–5L before f(r) reaches its asymptotic limit at zero. In some flows, this limitation can be overcome by assuming space–time equivalence, such as Taylor’s frozen turbulence hypothesis. However, for the flow considered here, spatial and temporal dynamics cannot be translated in a trivial manner. Thus, to measure L accurately, we combine two strategies. First, we use a pair of simultaneous 2D-PIV measurements to extend the measurement region in space without losing fine-scale resolution. Second, we fit a model function to the curve f(r) (see Fig. 6). This model is valid for the inertial subrange (i.e, where most PIV data are collected) and includes L as one of the two fitting parameters. This method is preferable to the strategy of extrapolating f(r) until it reaches zero, because no universal model exists for f(r > L) (Davidson 2004). Our model of f(r) is obtained from the Kolmogorov hypotheses, specifically by inverse Fourier transform of a power-law model spectrum (see appendix G of Pope 2000). This predicts that the autocorrelation curve within the inertial subrange takes the form:

$$f\bigg(\frac{r}{L}\bigg)=\frac{2}{\Upgamma(q)}\bigg(\frac{r}{2L} \alpha\bigg)^{q} K_q\bigg(\frac{r}{L}\alpha\bigg),$$

(5)

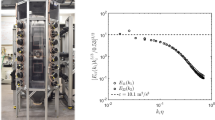
where $\Upgamma$ is the gamma function, K _q is the modified Bessel function of the second kind, and α is determined by the constraint f(0) = 1. Equation 5 has two free parameters: L and q, which are the integral length scale and an algebraic restatement of the velocity power spectrum’s power-law exponent, respectively. Fitting this model to our data at the tank center gives L = 9.50 cm (CI $\in$ [9.45 9.55] cm) and q = 0.353, which corresponds to a spectral power law exponent of 1.70 (CI $\in$ [1.700 1.708]). Although the model is derived to fit data in the inertial subrange, Fig. 6a shows that the fit also provides a good approximation of the autocorrelation curve for large separations (r > L/2). The scaling exponent of the power spectrum can be also obtained directly by computing the power spectrum from the inverse Fourier transform of the measured autocovariance. Figure 6b shows that the spectrum closely matches a κ ^−5/3 slope over about one decade in κ, which indicates the presence of a well-developed inertial range.

Fig. 6

a Longitudinal autocorrelation function extending over a larger region than in Fig. 5a. Symbols indicate the experimental data with 95 % CI, and the solid line shows data interpolation using Bessel function fit performed on the data for λ _f  < r < L/2. b Longitudinal power spectrum E ₂₂ computed from the measured autocovariance. The curves are obtained from 1517 independent 2D-PIV measurements

As a final note on this section, we discuss the relationship between the value of L determined from f(r), and the common approximation $l\equiv \frac{u^{'3}}{\epsilon}$. It is currently an open question whether the ratio $\Upphi \equiv L/l$ is a constant, a function of the Reynolds number, or even a function of the initial and boundary conditions (Batchelor 1953; Sreenivasan 1984; Gamard and George 1999). We are able to add the result of $\Upphi=0.55$ based on the data presented above. This agrees well with the model of Gamard and George (1999), who use scaling arguments to derive weak dependence of $\Upphi$ on the Reynolds number (which they define as Re _G ≡ L/η). They predict $\Upphi=0.64$ at Re _G  = 275, and we measure $\Upphi=0.55$ at Re _G  = 256, with 95 % CI of [0.50 0.60]. Interestingly, this is very close to the one Reynolds number at which the experimental observations by Mydlarski and Warhaft (1996) in grid-generated turbulence disagreed with the theory of Gamard and George. Thus, the support of our measurements is particularly important in evaluating the model.

6 Spatial variation of turbulent quantities

In the previous section, we demonstrated homogeneity and isotropy near the center of our stirred tank. In this section, we investigate turbulent statistics over a larger spatial region. With this, we will assess the full-size of the homogeneous and isotropic region in the tank center. Measurements are done by moving 2D-PIV across four stations in the z-direction, thereby measuring over a distance greater than two integral length scales.

We first analyze one-point statistics, namely TKE and the Reynolds stress tensor. We decompose the Reynolds stress tensor into an isotropic part $\frac{2}{3}k^2\delta_{ij}$, and an anisotropic part $a_{ij}\equiv\langle u_iu_j\rangle-\frac{2}{3}k \delta_{ij}$. The anisotropic part is responsible for the momentum transfer, and it should be zero in a homogeneous flow. Given our 2D data, we can compute three components of the anisotropic stress tensor: a ₂₂,  a ₃₃, and $a_{23}=\langle vw \rangle$. All three components of the anisotropy tensor are seen in Fig. 7, normalized by the local value of TKE. This figure shows that in the region z/L < 1.5, the anisotropic part of the stress tensor remains well below 10 % of the TKE. The distribution of TKE and $\langle vw \rangle$ over y and z are shown in Fig. 8a, b. Both figures indicate that TKE varies by less ≪10% for 0 < z/L < 1 and 0.5 < y/L < 2. Furthermore, we see that $\langle vw \rangle$ is statistically identical to zero, and much smaller than TKE. Together, the one-point statistics shown in Figs. 7 and 8 strongly suggest that the homogeneous isotropic region extends farther than one integral lengthscale from the tank center (eventual conclusions appear in Table 4). Before evaluating this further, we examine the two-point statistics.

Fig. 7

Spatial variation of two diagonal (a ₂₂ and a ₃₃) and one off-diagonal (a ₂₃) components of the anisotropy tensor normalized by the local TKE. The dashed lines show the 10 % variation

Fig. 8

Distribution of TKE $({\circ})$ and Reynolds stress $\langle vw \rangle \,({\diamond})$ in the y z plane. a Data averaged over y. b Data averaged over z. The solid lines indicate mean quantities in the tank center, and percent changes relative to this mean value are shown as dashed (10 % variation) and dashed-dotted (20 % variation) lines. The errorbars represent the 95 % CIs computed by bootstrap method

Values of $\epsilon,\,\lambda_f$, and L are computed at four different locations in z, using the methods described in Sect. 5. The results are shown in Fig. 9 and Table 5. Figure 9a shows that the pattern of the dissipation measurements follows the pattern of the TKE observed in Fig. 8. Figure 9b, c shows that the turbulent lengthscales stay approximately constant over a wider region than any of the other one- and two-point statistics reported here.

Fig. 9

Spatial distribution of turbulent quantities within 0 ≤ z/L ≤ 2.5. The dashed lines show the ±10 % variation with respect to the reference value at the tank center (solid line). The errorbars show the 95 % CI computed via bootstrap method

Given the above results, we conclude that the homogeneous and isotropic region extends at least to z =  −1.0L. A conservative quantitative demarcation of the homogeneous region can be made at z =  −1.0L using the common <10 % variation criterion. If we use instead a < 20 % variation criterion the homogeneous region reaches to z =  −1.5L. At z =  −1.5L, most statistical values are within the 10 % demarcation line, and only the dissipation rate and the TKE are clearly trending away from the reference values in a statistically significant manner.

The size of the homogeneous region in y is larger than that in z; Fig. 8b shows that TKE is constant in y at least to y = 2L. This behavior is expected from the boundary conditions imposed by the tank’s symmetric forcing geometry. That is, we expect the homogeneous region in x and y to be limited only by the size of the tank. Results on shear-free turbulence near an interface (Hunt and Graham 1978; Perot and Moin 1995) suggest that the tank wall at y ≈ 4.3L will begin to influence the flow at y ≈ 2.3L, and strongly influence it for y > 3.3L.

Assuming reflective symmetry about the origin and rotational symmetry between lateral velocity components u and v, we can use the above results to determine the full-size of the homogeneous isotropic region in our stirred tank, which is given in Table 4.

Table 4 Two quantitative demarcations of the size of the region at the tank center that contains homogeneous isotropic turbulence

Table 5 Summary of turbulence quantities

7 Conclusions

Homogeneous isotropic turbulence is of extreme interest for theoretical and engineering problems on turbulent dynamics. However, recreating this idealized situation in a laboratory flow is a formidable challenge due to the local distribution of turbulent production. We have developed a laboratory flow with an unprecedented degree of homogeneity and isotropy, and with negligible mean flow. The flow is obtained by combining the concepts of randomly actuated synthetic jet arrays (Variano and Cowen 2008) and symmetric forcing in a stirred tank.

PIV measurements in this flow show that there is a region at the core of the tank in which the flow is homogeneous over two integral length scales. Several tests of isotropy confirm that the flow in the homogeneous region is isotropic at all scales. The Reynolds number (based on the Taylor microscale) is between 334 < R _λ  < 351 in the homogeneous region. This high-value means that we can expect a large inertial subrange, thereby affording a meaningful approximation to turbulence theory. The mean flow is less than 10% of the turbulent fluctuating velocity magnitude. This low mean flow makes it convenient to investigate the dynamics of turbulence because one can independently measure the Eulerian temporal, Eulerian spatial, and Lagrangian statistics at a single, non-moving, and measurement location.

A conservative demarcation (<10 % variation of turbulent quantities) of the homogeneous isotropic region is 2.3L > x >  −2.3L,  2.3L > y > −2.3L, and 1.0L > z > −1.0L, where L = 9.5 cm. A more liberal quantitative assessment (<20 % variation of turbulent quantities) of the size is 3.3L > x >  −3.3L,  3.3L > y > −3.3L, and 1.5L > z > −1.5L. In either case, this region is much larger than in other laboratory apparatus designed to create homogeneous isotropic turbulence at the same high Reynolds number. The large size of the homogeneous isotropic region is especially important for measuring the dynamics of turbulent particle suspensions. This is because particle motion depends in part on the history of the flow experienced (Mei 1992). Thus, for particle statistics to accurately represent the effects of homogenous isotropic turbulence on particles, they must be measured in a homogeneous region so that they do not include the signature of other regions of the flow. At the center of the stirred tank discussed here, any particle that is measured will have traveled through a large region of homogeneous turbulence, and thus, its motion will be almost entirely due to this flow.

The method of turbulence generation presented here can be extended in a number of possible ways. Tank geometry can be systematically varied to obtain different turbulent parameters at the tank center, covering a range of Reynolds numbers and dissipation rates. The large number of jets offers a significant amount of freedom in driving flow patterns, and thus, different driving algorithms can be used to tune the mean flow and energy-containing scales. If it is important for a study, the fraction of the total tank volume that is occupied by HIT can be directly adjusted by extending the lateral tank boundaries. The method discussed here can also be incorporated in DNS as an alternative forcing mechanism that would likely be better suited for analyzing the effect of turbulence on suspended particles, bubbles, or droplets.