Decomposition of time-resolved tomographic PIV

Abstract

An experimental study has been conducted on a transitional water jet at a Reynolds number of Re = 5,000. Flow fields have been obtained by means of time-resolved tomographic particle image velocimetry capturing all relevant spatial and temporal scales. The measured three-dimensional flow fields have then been postprocessed by the dynamic mode decomposition which identifies coherent structures that contribute significantly to the dynamics of the jet. Both temporal and spatial analyses have been performed. Where the jet exhibits a primary axisymmetric instability followed by a pairing of the vortex rings, dominant dynamic modes have been extracted together with their amplitude distribution. These modes represent a basis for the low-dimensional description of the dominant flow features.

1 Introduction

The description of dominant and coherent flow features and their extraction from experimental data is the goal of many scientific studies of fluid flow. Dominant coherent structures are defined as organized fluid elements that capture the overall dynamics of the flow and are responsible for the bulk of mass, momentum and energy transfer (Hussain 1986). Despite this attempt to describe coherence in fluid flow, no definitive consensus has been reached, and various notions, mostly based on statistical means, are in common use (Antonia 1981). Descriptions by probability density functions (Pope 1994) as well as spatial covariances are among the more popular and successful classifications of fluid elements and the importance of their role in the overall flow dynamics.

As varied as the definition of coherence is the range of numerical algorithms to extract pertinent information from the flow. In experimental settings, conditional averaging (biasing statistics toward specific events in the flow) as well as quadrant analysis (evaluating the occurrence and frequency of specific sign configurations in the velocity fields) was among the early techniques to explore recurring or persistent features of the flow. A less subjective technique is based on the spatial correlation tensor of the flow whose eigenvalues decompose the flow into mutually decorrelated structures. This technique, known as the proper orthogonal decomposition (POD), reorders the flow into a hierarchy of energy-weighted structures that optimally capture the total kinetic energy of the flow when used as a Galerkin basis (Aubry 1991; Berkooz et al. 1993; Lumley 1970; Sirovich 1987). It still enjoys great popularity among experimental and computational fluid dynamicists, which is due to its versatility, its ease of implementation and its convergence properties based on an energy norm.

Computational fluid dynamicists faced the same issues of coherent feature extraction when analyzing the flow fields computed by direct numerical simulations or other techniques. The wealth of data generated by simulations had to be postprocessed to delineate the important dynamic structures from the incoherent, featureless noise. In contrast to experimentalists, however, they could rely on a set of model equations that built the foundation of their simulations, and efficient algorithms could be developed that exploited this fact. Among these algorithms, the Arnoldi method (Greenbaum 1997; Trefethen and Bau 1997) and its variants dominate the quantitative analysis of fluid flow (Edwards et al. 1994). The Arnoldi method, an iterative Krylov subspace technique to compute eigenvalues of large-scale matrices, has rapidly become a standard tool to compute stability information of flows in complex geometries. When coupled with numerical simulations, it produces global stability modes together with their frequency and growth/decay rates. Various modifications have been developed over the years to improve overall performance, to direct convergence toward specific eigenvalues and to add robustness (Lehoucq and Scott1997; Mack and Schmid 2010). Central to the algorithm is the construction of an orthogonal set of vectors (flow fields) onto which the dynamics is projected. This construction depends on the availability of model information, as it requires the evaluation of the underlying equations using a given flow field. While this algorithmic step is easily accomplished by numericists, it constitutes an obstacle for a straightforward application to experimentally generated flow field data. For this very reason, many iterative techniques that are routinely applied within a computational framework are not available to the experimentalists. It is thus fair to say that the range of options for a quantitative analysis of experimental fluid data considerably lags behind the possibilities available to computational fluid dynamicists.

The past years have seen remarkable advances in experimental data acquisition and image analysis, and flow data from experiments rival data from large-scale numerical simulations in spatial and temporal resolution as well as in complexity (Hain et al. 2007; Violato et al. 2009a, b). The analysis of unsteady three-dimensional flow fields is no longer the domain of computational fluid dynamicist owing to the development of time-resolved tomographic PIV techniques (Elsinga et al. 2006). Algorithms for the analysis of these data are now needed to allow the same depth of exploration that is customary in a computational setting. The dynamic mode decomposition (DMD) (Schmid 2009, 2010; Schmid and Sesterhenn 2008) is such a technique as it is solely based on data and does not depend on access to an underlying set of equations. It is related to the Arnoldi method mentioned above but replaces the projection onto an orthogonal basis by a projection onto a snapshot sequence. In this manner, spectral information about the flow can be extracted from the measurements.

DMD represents an approximation of a time-resolved sequence from a nonlinear process by a linear mapping between the samples. Mathematically, it is related to a Koopman analysis of a nonlinear dynamical system (Lasota and Mackey 1994); an application of Koopman analysis to fluid flows has recently been presented and applied to a direct numerical simulation of a jet in cross-flow (Rowley et al. 2009).

After describing the experimental setup and the principles of the dynamic mode decomposition, a set of time-resolved tomographic PIV measurements of a water jet will be processed and analyzed. The obtained results will be presented in form of their spectral characteristics (frequencies, growth/decay rates, wavenumbers and amplitudes) and modal shapes. A discussion of the presented material and an outlook of future applications will conclude this article.

2 Experimental setup and data decomposition

2.1 Experimental setup

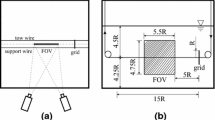
The experiments have been performed in the water jet facility at the Aerodynamic Laboratories of the TU Delft (Violato et al. 2009). The jet exits from a round nozzle of diameter D = 10 mm into an octogonal water tank of 600 mm diameter and 800 mm height whose Plexiglass sides allow full optical access to the illumination and tomographic imaging. For a Reynolds number of Re = 5,000 a jet exit velocity of U = 0.5 m/s has been chosen. Neutrally buoyant polyamide particles (of 56 μm diameter) together with a solid-state Nd/YAG laser provide light-scatter images that are recorded by the tomographic system consisting of four CMOS cameras. Image sequences are acquired by this system at a kilohertz rate over a three-dimensional measurement domain of 50 mm × 50 mm × 32 mm. Three such domains (phase matched across the overlap volumes) cover an extent of 130 mm along the jet axis. Results from the domain closest to the jet nozzle will be reported in this article. The volumetric light intensity is reconstructed using a volume-self-calibration procedure and a MART reconstruction algorithm. Three-dimensional velocity fields are then computed based on a spatial cross-correlation of two subsequent volumes, and data postprocessing using a space-time regression with a 5 pt × 5 pt × 5 pt × 5 pt kernel reduces velocity fluctuations due to measurement or processing noise (Elsinga et al. 2006). A representative snapshot from the experiment is shown in Fig. 3a, visualized by velocity vectors in the axial center-plane.

2.2 Principles of the dynamic mode decomposition

The dynamic mode decomposition (DMD) is a data-based decomposition technique that identifies the dominant coherent motion in a flow field by constructing and subsequently analyzing an approximate linear mapping between time-resolved measurements (Schmid 2009, 2010; Schmid and Sesterhenn 2008). Given a sequence of measured flow fields, denoted by v _j and separated by a constant time-interval $\Updelta t,$ that is,

$$ {\bf V}_1^N = \{ {\bf v}_1, {\bf v}_2, \ldots, {\bf v}_N \} $$

(1)

with N as the total number of flow fields. In what follows we use the short notation V ^N₁ with the subscript ₁ denoting that the first snapshot of the sequence is v ₁ and the superscript ^N denoting that the last snapshot of the sequence is v _N . We assume a linear mapping ${\bf A}_{\Updelta t}$ between each of the snapshots (assumed to be constant over the snapshot sequence); we thus have ${\bf v}_{j+1} = {\bf A}_{\Updelta t} {\bf v}_j.$ Applying the mapping ${\bf A}_{\Updelta t}$ to the entire sequence V ^N₁ results in

$$ {\bf A}_{\Updelta t} {\bf V}_1^N = {\bf V}_2^{N+1}. $$

(2)

For a sufficiently long sequence of snapshots from an experiment, it appears reasonable to assume that the flow fields become linearly dependent. When this limit is reached, it is possible to express any further snapshots by a linear combination of the previous ones; mathematically, this amounts to

$$ {\bf A}_{\Updelta t} {\bf V}_1^N = {\bf V}_2^{N+1} \approx {\bf V}_1^N {\bf S}_{\Updelta t} $$

(3)

where ${\bf S}_{\Updelta t}$ contains the coefficients of the above-mentioned linear combination (Ruhe 1984). In this last equation, the action of ${\bf A}_{\Updelta t}$ on the snapshot sequence V ^N₁ has been approximated by a combination (expressed by ${\bf S}_{\Updelta t}$) of the members of V ^N₁ . Spectral information about the high-dimensional matrix ${\bf A}_{\Updelta t}$ is thus contained in the matrix ${\bf S}_{\Updelta t}$ that can be thought of as a projection of ${\bf A}_{\Updelta t}$ onto the snapshot basis V ^N₁ . This projection is reminiscent of the Arnoldi method where the original large-scale matrix is replaced by a lower-dimensional Hessenberg matrix whose eigenvalues approximate some of the eigenvalues of the original matrix. The orthogonalization step of the Arnoldi method, however, is absent.

The matrix ${\bf S}_{\Updelta t}$ can be computed from the above equation by a least-squares approximation based on the two data sets V ^N₁ and V ^N+1₂ . We obtain

$$ {\bf S}_{\Updelta t} = {\bf R}^{-1} {\bf Q}^H {\bf V}_2^{N+1} $$

(4)

where Q and R stand for the QR-decomposition of the data set V ^N₁ , that is, QR = V ^N₁ . The above procedure holds for a full-rank data matrix V ^N₁ ; for rank-deficiencies or near rank-deficiencies in the data, see Schmid (2010). The eigenvalues of ${\bf S}_{\Updelta t}$ approximate some of the eigenvalues of ${\bf A}_{\Updelta t},$ and the corresponding eigenvectors of ${\bf A}_{\Updelta t}$ are determined by V ^N₁ w where w is an eigenvector of ${\bf S}_{\Updelta t}.$ We will refer to the quantities V ^N₁ w as the dynamic modes of the snapshot series. Due to the nature of the data sequence, the eigenvalues λ of ${\bf S}_{\Updelta t}$ describe the inter-snapshot dynamics. For a sufficiently long data sequence sampled from a nonlinear process (experiment), they approach the unit disk and represent a neutrally stable, oscillatory process (Rowley et al. 2009). We often map the eigenvalues λ of ${\bf S}_{\Updelta t}$ via the transform ${\omega} = \log(\lambda)/\Updelta t;$ unstable eigenvalues ω appear then in the right half-plane.

The reliance on data allows a great deal of flexibility for the dynamic mode decomposition. The inclusion of only parts of the measured flow field in the data sequence V ^N₁ enables the exploration of subdomains where localized instabilities or flow phenomena are expected or observed. In addition, images from high-speed cameras can be as straightforwardly processed as data from time-resolved PIV measurements; the data may even be of a composite nature, combining, for example, PIV velocity measurements with time-synchronous acoustic pressure signals from a microphone array in typical aero-acoustic applications. Even more significantly, the alignment of the snapshots in time represents only one of many options. For example, the data fields v _j could represent measurements at spatial positions x _j separated by $\Updelta x.$ By forming and processing this spatially aligned data sequence, the resulting matrix ${\bf S}_{\Updelta x}$ will contain spectral information about the spatial evolution of the flow. For a more detailed description of DMD, the reader is referred to (Schmid 2010).

The critical parameters of the dynamic mode decomposition are the length N of the snapshot sequence and the (temporal or spatial) separation ${\Updelta t},{\Updelta x}$ between consecutive snapshots. The former parameter can be determined by observing the residual of the least-squares step above. The latter parameter has to be chosen to approximately match the characteristic time/space scale of the fluid flow under investigation, while simultaneously complying with the Nyquist frequency criterion.

3 Results

A sequence of snapshots has been recorded at a sampling frequency of 1 kHz. Each flow field consists of 107 × 62 × 62 three-dimensional velocity vectors. With N + 1 = 201 snapshots in time, the full data array contains more than 82 × 10⁶ entries for each of the three fluid velocity components. In the following temporal and spatial dynamic mode decomposition (DMD) analysis, the full array of data, containing all velocity vectors and all three velocity components, has been used to extract structures of dynamic relevance. The mean flow has not been subtracted from the data.

3.1 Temporal DMD analysis

In a first step, a temporal analysis will be attempted. For this case, the flow fields at each time-step will be reshaped into the columns of a data matrix V ²⁰¹₁ . A mapping between the snapshots (expressed in the snapshot basis) will then be computed following the procedure described above.

A ${\bf S}_{\Updelta t}$-matrix of dimension 200 × 200 results whose eigenvalues λ are shown in Fig. 1a. An eigenvalue near (1,0) signifying the mean flow (i.e. the temporally averaged flow field of the data sequence) has been omitted in the figure. We like to remind the reader, however, that the averaged flow field has not been removed from the processed data. The size and color (from red to blue) of the eigenvalues indicate the amplitude of the respective structure in the data sequence (see below). A magnified view of the relevant section of the unit disk is given in Fig. 1b. We observe stable eigenvalues (inside the unit disk). The clustering of the eigenvalues on the unit disk indicates the convergence toward a linear representation of a saturated nonlinear process. For an even longer data sequence, the eigenvalues are expected to continuously tend toward the unit disk. Due to real input data, the spectra are symmetric with respect to the real axis. A dominant mode (in red) is clearly visible whose Strouhal number, based on the jet diameter and the jet velocity, can be determined as St = 0.325. A second significant eigenvalue corresponds to a Strouhal number of St = 0.646. The amplitude distribution shown in Fig. 2 has been computed by projecting the data sequence onto the identified dynamic modes. The coefficients of this projection indicate the presence of specific dynamic modes in the original data sequence and thus determine their significance; again, the mean flow at ω _r  = 0 has been omitted. A pronounced peak at two frequencies/Strouhal numbers can be observed. Higher-frequency modes contribute less and less to the data sequence, reflected in the decay of their respective amplitudes.

Fig. 1

Decomposition of a three-dimensional low-Mach number jet at Re = 5,000 from time-resolved tomographic PIV measurements: a eigenvalues of the matrix ${\bf S}_{\Updelta t}$ representing the inter-snapshot dynamics; b magnified view of the spectrum near the point (1,0)

Fig. 2

Decomposition of a three-dimensional low-Mach number jet at Re = 5,000 from time-resolved tomographic PIV measurements: amplitude distribution of the dynamic modes versus the Strouhal number St

Figure 3b–d shows the dynamic modes corresponding, respectively, to the mean flow and the two dominant frequencies/Strouhal numbers. All modes are visualized by velocity vectors in the axial center-plane. For the mean flow mode (St = 0), a smooth and homogeneous velocity profile has been detected. The next most dominant dynamic mode is displayed in Fig. 3c. It shows strong vortical structures near the edge of the jet about four diameters downstream from the nozzle, corresponding to vortex rings. The tendency toward an axisymmetric nature of the instability is clearly detectable and confirmed by a radial cut (not shown). The next most dominant dynamic mode is depicted in Fig. 3d. It again features nearly axisymmetric, strong vortex rings, however, concentrated closer to the nozzle, with a reduced axial spacing and correspondingly higher Strouhal number (St = 0.646). A superposition of the three displayed dynamic modes, each weighted by their temporal exponential dynamics $\exp(i\omega t)$ and initialized by a representative flow field, would capture the bulk of the jet dynamics and reproduce the principal features of the original data sequence (see also below). In this sense, the dynamic mode decomposition can be viewed as a model reduction technique, capturing the dynamically most relevant features of the flow.

Fig. 3

Decomposition of a three-dimensional low-Mach number jet at Re = 5,000. a Representative snapshot from the time-resolved tomographic PIV measurements. b–d Three most dominant dynamic modes (DM): mean flow (b) and two dynamic modes with a significant contribution in the original data sequence. a Exp. snapshot, b DM₀  (St = 0), c DM₁  (St = 0.325), d DM₂  (St = 0.646)

Iso-surfaces of the λ₂-criterion, a common technique to identify flow regions of high vorticity (Jeong and Hussain 1995), are displayed in Fig. 4 for the two most dominant dynamic modes, after the mean flow. Nearly axisymmetric vortex rings can be observed that monotonically grow in width and diameter for DM₁, but are concentrated closer to the nozzle exit for DM₂. These features confirm previous observations, but give a more complete picture of the three-dimensional characteristics of the flow and its coherent structures.

Fig. 4

Decomposition of a three-dimensional low-Mach number jet at Re = 5,000. Iso-surfaces of the λ₂-criterion of the two most dominant dynamic modes (besides the mean flow): a DM₁ with St = 0.325, and b DM₂ with St = 0.646. A quarter of the circumferential dependence has been eliminated for an improved visualization

The temporal dynamic mode decomposition has identified two distinct Strouhal numbers in the data sequence; the corresponding structures are characterized by nearly axisymmetric vortical structures superimposed on the cylindrical mean vortex sheet of the jet.

It is apparent that DM₂ describes the primary instability of the jet exiting the nozzle, with a correspondingly high Strouhal number. The first mode (DM₁), on the other hand, captures the vortex pairing of the primary ring vortices. It has a consequently lower Strouhal number and consists of larger vortical structures.

3.2 Temporal POD analysis

Alternative to the dynamic mode decomposition, the proper orthogonal decomposition (POD) can be applied to the data sequence. This approach has been taken in many investigations of fluid flows—ranging from laminar flows that exhibit instabilities to fully developed turbulence—to determine energetic and coherent structures. The technique is based on computing a data correlation matrix that is subsequently diagonalized, thus yielding structures that are physically decorrelated or mathematically orthogonal. POD provides a hierarchical basis that is aligned in the direction of largest data variance and therefore captures a maximal amount of energy in each identified structure while simultaneously maintaining a zero correlation between each structure. This description makes clear that this basis cannot capture the dynamics of the flow, but rather provides a ranking of structures in which the perturbation energy of the flow is captured optimally. To recapture the dynamics of these structures, a projection of a full data sequence onto a finite POD basis, known as a Galerkin projection, is necessary. This step is often taken in investigations that are interested in the low-dimensional description of fluid phenomena; additionally, POD-based reduced models are commonly used in flow control applications.

Applying the proper orthogonal decomposition to our data sequence is equivalent to taking the singular value decomposition (SVD) of the data matrix V ^N₁ according to

$$ {\bf V}_1^N = {\bf U} \Upsigma {\bf V}^H $$

(5)

where the columns of U contain the POD structures, while the entries of the diagonal $\Upsigma$ comprise the energy levels of the various associated structures. The singular values $\sigma = {\hbox{diag}}(\Upsigma)$ are plotted in Fig. 5; for the most dominant singular values, they show a characteristic doubling where two consecutive singular values have nearly the same magnitude. This feature can be attributed to the time-periodic nature of the flow: two mutually orthogonal structure have been identified that carry nearly identical energy levels. In reality, the two associated POD modes correspond to similar but phase-shifted fluid structures. This is depicted in Fig. 6a, b where the first two POD modes (with nearly identical singular values) are shown. The structures of POD₂ appears displaced to the structures of POD₁. Both components are equally important in terms of their contribution to the overall energetic budget. A projection of the data sequence into these two modes reveals two oscillatory signals with a near 90° phase shift. Combined with the respective POD modes, the superposition of these two signal presents a convective and recurring pattern that captures the essence of the observed flow field: vortex rings being convected downstream. Similar conclusions can be drawn for the third and fourth singular values and their associated POD modes (see Fig. 6c, d). Higher singular values do not display any significant doubling, thus suggesting that only two dominant frequencies are present in the flow.

Fig. 5

Singular values of the data matrix V ^N₁ representing the energy content (normalized by the largest singular value) of the associated proper orthogonal (POD) modes

Fig. 6

Decomposition of a three-dimensional low-Mach number jet at Re = 5,000 using a proper orthogonal decomposition. First four POD modes displayed in the axial-radial plane through the centerline of the jet. a POD₁, b POD₂, c POD₃, d POD₄

Comparing the POD spectrum and POD modes with the DMD spectrum and DMD modes, one comes to the same conclusions as to the dynamic features of the processed data sequence. However, this finding is not only an issue of representation, where one decomposition needs two modes to capture the same dynamic that can be represented by one mode of another decomposition. In the proper orthogonal decomposition, the dynamics contained in the data sequence is not captured directly, but has to be recovered by a reprojection of the data onto the extracted basis. In contrast, the dynamic mode decomposition provides both a basis and the temporal dynamics in this basis. Nevertheless, for flow configurations that are dominated by periodic and convective phenomena (which are commonly referred to as oscillator flows), both decompositions yield very similar structures (compare Figs. 4 with 7) and there appears to be a close resemblance of the composite mode POD₁ + iPOD₂ and the mode POD₁; the same can be concluded for POD₃ + iPOD₄ and DMD₂.

Fig. 7

Decomposition of a three-dimensional low-Mach number jet at Re = 5,000 using a proper orthogonal decomposition. Iso-surfaces of the λ₂-criterion of the two most dominant POD modes. A quarter of the circumferential dependence has been eliminated for an improved visualization. a POD₁, b POD₂

For non-periodic or transient flows, this coincidence between POD and DMD no longer holds, and the two decompositions produce different results. In addition, for the spatial analysis, the DMD analysis is the preferred tool (see below).

As mentioned above, POD analysis represents a static (or averaged) decomposition of a temporal process, since the temporal coordinate direction has been used to perform the averages for the spatial correlation matrix. In this way, the time information in the data has been removed from the decomposition. This fact can be made clearer by establishing a mathematical connection between the matrix ${\bf S}_{\Updelta t}$ and the POD decomposition, expressed as a singular value decomposition. A few algebraic steps using Eqs. 3 and 5 yield

$$ {\bf U}^H {\bf A}_{\Updelta t} {\bf U} = \Upsigma {\bf V}^H \, {\bf S}_{\Updelta t} \, {\bf V} \Upsigma^{-1} \sim {\bf S}_{\Updelta t} $$

(6)

where ∼ has been used to indicate equality up to a similarity transformation (in our case, given by $\Upsigma {\bf V}^H$). The above expression establishes a link between the central DMD matrix ${\bf S}_{\Updelta t}$ and the POD modes U: the matrix ${\bf S}_{\Updelta t}$ is given as the correlation matrix between the POD modes U and the POD modes ${\bf A}_{\Updelta t} {\bf U}$ that have been advanced over one time-step by the matrix ${\bf A}_{\Updelta t}.$ It seems possible to recapture the temporal information in the data from this one-step temporal correlation matrix. In numerical simulations, this matrix can be formed by advancing the computed POD modes over one time-step; in physical experiments, this is of course not possible. Nonetheless, the above mathematical expression emphasizes the fact that POD analysis is a statistical technique based on temporal averages, while DMD analysis achieves a decomposition into coherent structures and their temporal dynamics.

3.3 Low-dimensional representation and modeling

Any reduced-order representation of our data sequence can be used to model the flow with a lower number of degrees of freedom. In this section, we will explore and demonstrate the use of DMD to capture the essence of the flow dynamics with a small number of modes.

The procedure follows the standard technique of modal expansions which, in our case, reads

$$ {\bf u}(x,y,z,t) = \sum_{k=1}^N A_k \exp(\omega_k t) \Upphi_k(x,y,z) $$

(7)

where ω _k are related to the eigenvalues λ _k of ${\bf S}_{\Updelta t}$ via $\omega_k = \log(\lambda_k)/\Updelta t,$ and $\Upphi_k$ are given by the eigenvectors w _k of ${\bf S}_{\Updelta t}$ according to $\Upphi_k = {\bf V}_1^N {\bf w}_k.$ The amplitudes A _k are the same as displayed in Fig. 2. The amplitude distribution, with its pronounced peaks at two specific Strouhal numbers, can be taken as a guide for a truncation of the series (7). In this spirit, we only select the two dominant Strouhal numbers and the corresponding spatial structures to give an approximate representation of the principal flow dynamics in the form

$$ {\bf u}(x,y,z,t) \approx A_1 \exp(\omega_1 t) \Upphi_1(x,y,z) + A_2 \exp(\omega_2 t) \Upphi_2(x,y,z) + \hbox{c.c.} $$

(8)

This procedure can be thought of as a filtering approach applied to the data, where the amplitude distribution provides the pass-bands of the filter in the frequency/Strouhal number domain.

The following example shall demonstrate this filtering approach. We extract two signals from the original data sequence at locations in the axisymmetric shear layer of the jet. The locations are indicated in Fig. 8a, superimposed on a snapshot from the data sequence. The first signal (in black) is taken near the nozzle exit where the shear layer shows a primary instability with a well-defined frequency/Strouhal number. The second location is further downstream in the shear layer; at this location, vortex pairing has occurred and a lower Strouhal number prevails, even though the original Strouhal number is still present. The signals from these two locations are plotted (in black and blue) in Fig. 8b, c. After completing the DMD analysis of the entire data set, we compute a superposition of the two dominant DMD modes, properly weighted by their amplitudes. From this superposition, we extract two signals at the same locations as shown in Fig. 8a. The two signals from the low-dimensional DMD representation are shown in red in Fig. 8b, c. We notice that our analysis has produced a filtered representation of the local flow dynamics. For the first signal (closer to the nozzle), only one frequency is detected. This is due to the fact that only the second mode DM₂ with an associated Strouhal number of St = 0.646 has support in this region; the first mode DM₁ has no or negligible support close to the nozzle (see Fig. 4 for a comparison). At the signal location further downstream (blue dot), however, two co-existing frequencies can be observed which yield a modulated signal, with the lower frequency dominating. Again, this can be related to the spatial extent of the associated DMD modes; they are both present in this region, and the mode with the lower Strouhal number, however, has the larger amplitude (see Fig. 2). Incoherent and high-frequency features in the original system have been filtered out, since they do not contribute significantly to the flow dynamics.

Fig. 8

a Two signal have been extracted from the original data sequence: near the nozzle (black dot) and further downstream (blue dot). b Original signal from the upstream (blue) location and equivalent signal (in red) from a two-mode DMD representation of the flow field. c Same for the signal from the downstream (blue) location

The efficient description of dynamic processes by a low-dimensional modal expansion, as shown above, can be used in a variety of ways. Flow control applications often require the application of reduced-order models (ROMs) to compute control and estimation gains. In model-predictive control, low-dimensional models are essential to the design of efficient adaptive control strategies. Moreover, fluid dynamical patterns, for example in dynamic meteorology, are often expressed in low-dimensional form and extended beyond the acquisition horizon to provide approximate forecasts. Even our two-mode representation can be used to extrapolate over a time-interval τ according to

$$ {\bf u}_{\rm pred}(x,y,z,t+\tau) \approx A_1 \exp(\omega_1 (t+\tau)) \Upphi_1(x,y,z) + A_2 \exp(\omega_2 (t+\tau)) \Upphi_2(x,y,z) + \hbox{c.c.} $$

(9)

Since the expansion (7) is continuous in time and only discrete in the number of modes, it also becomes possible to oversample the expression: by evaluating the expansion in time-steps that are shorter than the sampling interval, we can generate flow fields that have an increased resolution in time. Of course, by following this procedure, new information at frequencies beyond the Nyquist cutoff is not contained in the generated flow fields.

In short, any flow field that comprises low-dimensional dynamics or low-frequency patterns can benefit from a truncated modal DMD expansion that can be used to interpolate (oversample) or extrapolate (predict) coherent features extracted from the data sequence.

3.4 Spatial analysis

The previous analysis, detecting a periodic fluid motion with distinct frequencies, suggests to revisit the problem within a spatial framework. As mentioned previously, since the DMD does not depend on a particular model, a simple re-organization of the data array suffices to perform a spatial rather than a temporal analysis. To this end, we align the data fields in our matrix V ^N₁ in the axial direction, that is, each column in V ^N₁ consists of a time record of the three-dimensional flow field in the cross-sectional plane at a given axial location. The number of snapshots is accordingly N + 1 = 107, and the computed matrix ${\bf S}_{\Updelta x}$ is of size 106 × 106 and contains spatial spectral information. The time coordinate becomes an independent variable of the resulting dynamic modes; consequently, the extracted spatial dynamic modes will contain a temporal dependency.

Processing the spatially aligned data matrix with the DMD algorithm results in the spectra displayed in Fig. 9a, b, again in the inter-snapshot format (Fig. 9a) and the more familiar mapped format according to $\alpha = \log(\lambda)/\Updelta x.$ As in the temporal case, we notice a clustering of the eigenvalues near the unit disk and the neutral line, respectively. The “mean flow eigenvalue” has been excluded as before. The spatial DMD detects a marked spatial wavenumber, indicated by the red eigenvalues in either spectrum. The importance and prevalence of this spatial structure is further confirmed in the amplitude distribution (see Fig. 10), which identifies a peak near the spatial wavenumber α _i ≈ 9. On both sides of this peak, the amplitude of other detected wavenumbers decreases notably. The dynamic modes corresponding to the colored peaks in the amplitude distribution depend on the coordinates of the cross-sectional plane and on time (their streamwise dependence is given by $\exp(\alpha x)$ with α as the respective eigenvalue) and are thus difficult to visualize. For this reason, we will first demonstrate the temporal dependence of the two dynamic modes identified in color in the amplitude distribution, evaluated in a one-dimensional cross-sectional cut through the center of the jet. The two modes and their temporal dependence are visualized by contours of one of the cross-sectional velocity component. In addition, the mean flow, visualized by the axial velocity component, is included for completeness (Fig. 11a); it shows a steady velocity component in the center of the interrogation domain. The two displayed dynamic modes exhibit a clear temporal frequency in both velocity components. This should not come as a surprise as the temporal DMD analysis clearly extracted a well-defined Strouhal number from the data.

Fig. 9

Spatial dynamic mode decomposition of a three-dimensional low-Mach number jet at Re = 5,000. a Spatial inter-snapshot spectrum, that is, eigenvalues of ${\bf S}_{\Updelta x}.$ b Spatial DMD spectrum, logarithmically mapped (see text)

Fig. 10

Spatial dynamic mode decomposition of a three-dimensional low-Mach number jet at Re = 5,000. Amplitude distribution of the spatial dynamic modes versus their streamwise wavenumber α _i

Fig. 11

Spatial dynamic mode decomposition of a three-dimensional low-Mach number jet at Re = 5,000. a Spatial dynamic mode associated with the mean flow, visualized by the axial velocity. b and c First spatial dynamic mode, visualized by the velocity components in the cross-sectional plane. d and e Second spatial dynamic mode, visualized by the velocity components in the cross-sectional plane. a Mean flow U, b DM₁ V, c DM₁ W, d DM₂ V, e DM₂ w

In a different visualization (Fig. 12), we display a temporal sequence of velocity vectors for the two dominant DMD modes (after the mean flow mode). In both cases, we observe a circular motion in the cross-sectional plane that reverses direction over the course of the sampling period. This is consistent with the characteristics of the spatial dynamic modes depicted in Fig. 11b–e. The final plot (in blue) represents the flow field associated with the most dominant Fourier mode of the temporal sequence; in this case, the temporal sequence, shown in gray in Fig. 12, has been decomposed into respective frequencies, and the mode corresponding to the peak in the Fourier spectrum has been plotted. For a full appreciation of the three-dimensional dynamics of the dynamic modes, each spatial dynamic mode has to be augmented by an exponential/oscillatory evolution in the streamwise direction according to $\exp(\alpha x).$ Nevertheless, the temporal sequences in Fig. 12 give a first indication of the complexity of the fluid motion captured in the three-dimensional data sequence.

Fig. 12

Decomposition of a three-dimensional low-Mach number jet at Re = 5,000. Temporal sequence (in gray) of the first (left column) and second (right column) spatial dynamic mode, visualized by velocity vectors in the cross-sectional plane; (in blue) most dominant Fourier mode of the temporal sequence

4 Summary, conclusions and outlook

Three-dimensional flow fields of a transitional water jet have been extracted from experiments by means of time-resolved tomographic particle image velocimetry (TR-TOMO-PIV). The flow fields are characterized by a wide range of spatial and temporal scales, but also by the presence of clearly distinguishable frequencies and wavenumbers. A sequence of 201 snapshots in time, each captured with a spatial resolution of 107 × 62 × 62 and three velocity components, has been processed by the dynamic mode decomposition (DMD)—an iterative data-based algorithm for the extraction of dynamically relevant processes from temporally or spatially aligned flow field sequences. In both the temporal and the spatial cases, the DMD method isolated coherent structures and their spectral properties and has proven effective in providing a low-dimensional representation of the coherent dynamics.

As experimental data grow larger in dimensionality and complexity, it becomes more important to develop and apply advanced algorithms that are capable of extracting the essential features and dominant processes from the measurements. In particular, the recent availability of tomographic, three-dimensional and time-resolved data necessitates these types of algorithms to reduce the richness of three-dimensional flows to a few governing mechanisms. By combining TR-TOMO-PIV data with DMD analysis, the current article has attempted to integrate state-of-the-art data acquisition techniques with innovative algorithms for flow pattern extraction.

In a future effort, we will further explore the flow features present in the water jet. This study will include measurements further downstream from the jet nozzle and different nozzle geometries. It is hoped that the synthesis of three-dimensional time-resolved data and efficient, data-based, iterative algorithms (such as DMD) will give new and valuable insight into complex fluid flow, its principal mechanisms and its inherent spatio-temporal scales.