1 Introduction

Over the past two decades, advances in experimental techniques such as time-resolved stereo particle image velocimetry and tomographic particle image velocimetry (Tomo-PIV) (Elsinga et al. 2006) and in direct numerical simulations have enabled the visualization of three-dimensional (3D) velocity fields and vortical structures in various complex flows. Consequently, the datasets collected by high-resolution experimental systems or in high-fidelity simulations have been becoming increasingly difficult to interpret and analyze (Rowley and Dawson 2017; Taira et al. 2017, 2020). The identification of deterministic coherent structures in turbulent flow data thus remains a key challenge in studying various physical processes, such as those of heat and mass transfer and flow noise.

Coherent structures are accompanied by periodicity or energetic dominance, which can be extracted using methods such as classic Fourier decomposition, dynamic mode decomposition (DMD) (Schmid 2010), and proper orthogonal decomposition (POD) (Lumley 1967). In addition, to capture low-energy flow features while determining multiple dominant frequencies, advanced data-driven mode-decomposition algorithms and order-reduction techniques based on POD and DMD have been developed for aerodynamic modeling, e.g., time-domain spectral proper orthogonal decomposition (td-SPOD) (Sieber et al. 2016) and frequency-domain spectral proper orthogonal decomposition (fd-SPOD) (Towne et al. 2018). However, it is non-trivial to determine the most appropriate method for analyzing a particular flow, such as a swirling jet with a low signal-to-noise ratio, and challenging to reconstruct such a flow’s dynamics using modes that contain relevant information (Semeraro et al. 2012). Nevertheless, to solve turbulence problems via data-driven order reduction, it is essential to determine the most appropriate method for analyzing a target flow. It follows that there is a need for a comprehensive understanding of the roles of POD, DMD, td-SPOD, and fd-SPOD in the identification of multi-dominant coherent structures in spatial and spectral domains. Such an understanding would also be useful in engineering applications, because effective mode decomposition can generate ideas for the design or optimization of convoluted industrial flow equipment.

Since the introduction of POD by Lumley (1967) and Sirovich (1987a, b, c), it has been widely applied to acquire coherent structures from flow-field snapshots in fluid dynamic research. Beyond the field of fluid dynamics, POD is also known as principal component analysis (Wall et al. 2003) and Karhunen–Loève decomposition (Berkooz et al. 1993). A POD algorithm constructs a linear superposition using a series of low-order spatially orthogonal bases that best represent the context of the data variance for a given scenario. In the field of fluid dynamics, this data variance represents turbulent kinetic energy: the most energetic coherent structures are represented by POD basis functions and extracted by ranking modes in terms of their energy to create a hierarchy of coherent structures (Holmes et al. 2012). He and Liu (2017) used time-resolved planar laser-induced fluorescence measurements to show that POD convincingly reflected the helical mode and axisymmetric modes buried in jets at various Re. Percin et al. (2017) captured the dominant precessing helical vortex by adopting POD to determine the free annular swirling jet flow in a Tomo-PIV study. POD has also been applied to identify the most energetic structures at a specified azimuthal wavenumber in the large-eddy simulation of a circular jet (He et al. 2018) and in Tomo-PIV measurements (Alekseenko et al. 2018; Markovich et al. 2016). The above studies have demonstrated that the POD algorithm can be used to resolve jets by extracting energetic coherent structures, unless these extracted modes are not ranked correctly in all conditions (Kim et al. 2010).

The temporal periodicity of coherent structures can be extracted by spectral methods such as discrete Fourier transformation (DFT) and DMD (Rowley et al. 2009; Schmid 2010). DMD is a numerical approximation of the use of Koopman modes (Mezić 2005) that involves considering both temporal (spectral) and spatial orthogonality, which enables the extraction of phase/frequency information and the corresponding coherent structures (Zhang et al. 2014). DMD outperforms POD in when applied to a linear dynamic system for mode identification and feature extraction in the case of spatiotemporal coupled modeling. Improved DMD approaches have been introduced to overcome the limitations of DMD for analyzing nonlinear systems (Mezić 2005; Rowley et al. 2009; Williams et al. 2015). Markovich et al. (2014) examined the global inviscid helical instability mode by using DMD to detect conspicuous frequencies of swirl jet flows in stereo-PIV data. Iyer and Mahesh (2016) investigated the shear-layer characteristics of low-speed transverse jets using direct numerical simulation data. Roy et al. (2017) applied DMD to identify and characterize the helical mode and axisymmetric modes of a swirling flow field via stereo PIV. Furthermore, Chen et al. (2012) showed that DMD is formally equivalent to DFT for zero-mean data that are uniformly sampled in time.

The above studies demonstrate that DMD and DFT algorithms’ simple mathematical expression and easy calculation have led to their wide application for the analysis of jet flow phenomena in experiments and numerical simulation. However, although currently available methods involving POD, DMD, or DFT are suitable for the analysis of flows with obvious characteristics, they are often unsuitable for analyzing challenging flows, such as flows with weakly coherent structures (i.e., where the recorded data have low signal-to-noise ratios) and or intermittent dynamics (Sieber et al. 2016). To solve this problem, the current methods have been unified into a more efficient and general approach called time-domain spectral proper orthogonal decomposition (td-SPOD) (Sieber et al. 2016), which could offer possibilities beyond POD and DFT. The key function of the td-SPOD algorithm is to apply a filter operation to the POD correlation matrix and thereby obtain clear temporal dynamics by POD. The td-SPOD algorithm also enables a continuous sweep to be performed from classic POD to DFT by variation of the filter size. Vanierschot et al. (2020) adopted td-SPOD to obtain the temporal flow dynamics of flow structures and to study the shape and dynamics of helical coherent structures found by POD (Percin et al. 2017) of a Tomo-PIV dataset. Sieber et al. (2021a, b) investigated the stochastic dynamics of the global mode in a turbulent swirling jet by reconstruction of the 3D flow field based on planar PIV. In other work, Sieber et al. (2021a, b) examined the interaction between the deterministic contributions representing the global mode and a stochastic contribution representing the intrinsic turbulent forcing. Other recent studies (Lückoff et al. 2018; Sieber et al. 2017; Stöhr et al. 2018) have found that td-SPOD is suitable for feature extraction and the analysis of intermittent dynamics.

Another prominent POD variant is fd-SPOD (Glauser et al. 1987; Taira et al. 2017). Towne et al. (2018) presented a detailed discussion of this approach and currently available methods comprising POD, DMD, and DFT, including an algorithm that considers spectral cross-correlations in actual data using Welch’s method. In the latter approach, a long time series is divided into short segments, each segment is Fourier-transformed in time, and classical POD is applied to the Fourier coefficients at a specific frequency. The strict separation of modes according to frequency means that this approach reveals clear coherent structures in turbulent jets. Schmidt et al. (2018) conducted large-eddy simulations and applied fd-SPOD to explore the deterministic structure of turbulence in jets in subsonic, transonic, and supersonic regimes. Nogueira et al. (2019) evaluated wavenumber spectra and used fd-SPOD to resolve large-scale streaky structures in stereo PIV data of turbulent jets. Nekkanti and Schmidt (2021) used fd-SPOD for low-rank reconstruction, denoising, frequency–time analysis, and prewhitening in large-eddy simulations. fd-SPOD strictly separates energy-dominated modes according to frequency and is thus better suited for capturing deterministic modes than monitoring dynamic processes. Most research based on fd-SPOD has therefore been focused on jet flows at high Mach numbers (Cavalieri et al. 2019; Karami and Soria 2018), and few studies on swirling flows have used fd-SPOD.

The present paper presents a comparative analysis of POD, DFT, td-SPOD, and fd-SPOD strategies for the identification of energetic coherent structures and dominant periodicity buried in 3D swirling jets. The velocity fields of swirling jets at various S are captured and reconstructed by Tomo-PIV, and the flow quality is examined to determine that the data are amenable to mode decomposition. Subsequently, the datasets are directly employed to find differences in the efficacy of POD, td-SPOD, DFT, and fd-SPOD for the identification of multi-dominant coherent structures. Specifically, the mode decomposition, temporal flow dynamics, and low-rank reconstruction of 3D swirling jets by POD, td-SPOD, DFT, and fd-SPOD are compared. The POD, td-SPOD, and DFT data are obtained using the td-SPOD algorithm with various filter sizes to explore the identification of coherent structures in an associated mode pair, and temporal flow dynamics are obtained by determining the time evolution of each mode coefficient. The fd-SPOD data are obtained by dividing a long time series into short segments, Fourier-transforming each segment in time, and applying POD to the Fourier coefficients at each frequency. Analysis of the above data demonstrates that td-SPOD is best for investigating the mode interactions between various wavelengths or the temporal dynamic evolution of modes, whereas fd-SPOD is best for mode extraction, due to its rigorous separation of modes according to frequency.

2 Theoretical background

2.1 POD

Classical POD was proposed by Lumley (1967) and involves the construction of an optimal linear superposition from a series of low-order spatially orthogonal bases that best represent the context of the field description. The resulting Fredholm eigenvalue problem is:

$$\iint {\varvec{C}}\left({\varvec{x}},{{\varvec{x}}}^{\mathrm{^{\prime}}},t,{t}^{\mathrm{^{\prime}}}\right) {{\varvec{\Phi}}}_{i}\left({{\varvec{x}}}^{\mathrm{^{\prime}}},{t}^{\mathrm{^{\prime}}}\right)\mathrm{d}{{\varvec{x}}}^{\mathrm{^{\prime}}}\mathrm{d}{t}^{\mathrm{^{\prime}}}={\lambda }_{i}{{\varvec{\Phi}}}_{i}\left({\varvec{x}},t\right),$$
(2.1.1)

where Φi(x, t) denotes the modes containing the spatiotemporal properties of coherent structures. POD requires the spatiotemporal correlation function C(x, x', t, t') of the dataset. Thus, during measurement, a set of M spatial points over N time steps are collected, where N is usually less than the number of 3D spatial points in a Tomo-PIV measurement. Then, by adopting the snapshot method suggested by Sirovich (1987a, b, c), the correlation function obtained by snapshot POD is expressed as:

$${\varvec{C}}\left( {t,t^{\prime}} \right) = \left\langle {\frac{1}{N}\varvec{u^{\prime}}\left( {{\varvec{x}},t} \right){\varvec{u}}^{{{^{\prime}}*}} \left( {{\varvec{x}},t^{\prime}} \right)} \right\rangle ,$$
(2.1.2)

where the dimensions of the autocorrelation matrix C are N × N and u'(x, t) is the fluctuating part, ⟨⋅⟩ refers to the inner product and the u' ∗ (x, t') indicates the adjoint flow in t' of the stationary flow u'(x, t) in t. Although only the temporal correlation function is considered, spatial and temporal correlations can be exchanged in both discrete and continuous cases (Aubry 1991). The mode coefficient matrix \(\phi_{i} = \left[ {\phi_{i} \left( {t_{1} } \right),\;\phi_{i} \left( {t_{2} } \right), \ldots ,\phi_{i} \left( {t_{N} } \right)} \right]^{T}\) and mode energies λi are obtained using the eigenvectors and eigenvalues of the correlation matrix C,

$${\varvec{C}}\phi_{i} = \lambda_{i} \phi_{i} ,\;\lambda_{1} \ge \lambda_{2} \ge \cdots \ge \lambda_{N} \ge 0,$$
(2.1.3)

where the mode energies λi are sorted in descending order in terms of their content and the eigenvectors are orthogonal to each other. The spatial modes are then calculated as a linear combination of the fluctuation snapshots,

$${{\varvec{\Phi}}}_{i} \left( {\varvec{x}} \right) = \frac{1}{{N\lambda_{i} }}\mathop \sum \limits_{j = 1}^{N} \phi_{i} \left( {t_{j} } \right)\varvec{u^{\prime}}\left( {{\varvec{x}},t_{j} } \right),$$
(2.1.4)

and the flow field is recovered according to

$${\varvec{u}}\left( {{\varvec{x}},t} \right) = \overline{\varvec{u}}\left( {\varvec{x}} \right) + \varvec{u^{\prime}}\left( {{\varvec{x}},t} \right) = \overline{\varvec{u}}\left( {{\varvec{x}},t} \right) + \mathop \sum \limits_{i = 1}^{N} a_{i} \left( t \right){{\varvec{\Phi}}}_{i} \left( {\varvec{x}} \right).$$
(2.1.5)

The mode coefficients ai(t) are obtained from:

$$a_{i} \left( t \right) = \left\langle {\varvec{u^{\prime}}\left( {{\varvec{x}},t} \right),\phi_{i} \left( {\varvec{x}} \right)} \right\rangle .$$
(2.1.6)

2.2 td-SPOD

The td-SPOD algorithm developed by Sieber et al. (2016) estimates the power spectral density (PSD) by the segmentation of time series of limited data and was applied in POD analysis (Taira et al. 2017). Unlike applications that apply a Fourier transform to all segments, td-SPOD multiplies a temporal weighting (window) function with the time series to isolate a segment of the time series. Thus, starting from formulation (2.1.2), the time series is multiplied by a Gaussian function w(τ) = exp (− (τ/T)2) on a short time scale τ:

$$\hat{\varvec{S}}\left( {{\varvec{x}},\varvec{x^{\prime}},\tau ,\tau^{\prime}} \right) = \frac{1}{N}\left\langle {\varvec{u^{\prime}}\left( {{\varvec{x}},t + \tau } \right)w\left( \tau \right){\varvec{u}}\prime^{*} \left( {\varvec{x^{\prime}},t + \tau^{\prime}} \right)w^{*} \left( \tau \right)} \right\rangle ,$$
(2.2.1)

The investigated time-series data of flow should be sufficiently long to allow the flow to pass through every possible state. The POD modes are derived from the integral equation,

$$\iint {\hat{\varvec{S}}\left( {{\varvec{x}},\varvec{x^{\prime}},\tau ,\tau^{\prime}} \right){\hat{\mathbf{\Phi }}}_{i} \left( {\varvec{x^{\prime}},\tau^{\prime}} \right){\text{d}}\varvec{x^{\prime}}{\text{d}}\tau^{\prime} = \hat{\lambda }_{i} {\hat{\mathbf{\Phi }}}_{i} \left( {{\varvec{x}},\tau } \right),}$$
(2.2.2)

and owing to the time window w(τ), the modes \({\hat{\Phi }}_{i}\) retain both their spatial information and temporal evolution. Additionally, it is possible to exchange spatial and temporal correlations in td-SPOD, and the temporal correlation function of td-SPOD is thus written as

$$\hat{\varvec{S}}\left( {t,t^{\prime}} \right) = \frac{1}{N}\left\langle {\varvec{u^{\prime}}\left( {{\varvec{x}},t + \tau } \right)w\left( \tau \right){\varvec{u}}^{{{^{\prime}}*}} \left( {{\varvec{x}},t^{\prime} + \tau } \right)w^{*} \left( \tau \right)} \right\rangle ,$$
(2.2.3)

for data in a discrete time series, with t = kΔt, t' = lΔt, and τ = jΔt. Using a one-dimensional filter gk = ω2(jΔt), the relationship between the temporal correlation matrix of td-SPOD and formulation (2.1.2) is expressed as

$$\hat{\varvec{S}}_{i,j} = \mathop \sum \limits_{{k = - N_{f} }}^{{N_{f} }} g_{k} {\varvec{C}}_{i + k,j + k} .$$
(2.2.4)

This expression was first proposed by Sieber et al. 2016. The size of the filter is 2Nf + 1, where a different value indicates a different window size. The mode coefficient matrix \(\hat{\phi }_{i} = \left[ {\hat{\phi }_{i} \left( {t_{1} } \right),\;\hat{\phi }_{i} \left( {t_{2} } \right), \ldots ,\hat{\phi }_{i} \left( {t_{N} } \right)} \right]^{T}\) and mode energies \(\hat{\lambda }_{i}\) for td-SPOD are obtained from the eigenvectors and eigenvalues of the correlation matrix S,

$$\hat{\varvec{S}}\hat{\phi }_{i} = \hat{\lambda }_{i} \hat{\phi }_{i} ,\hat{\lambda }_{1} \ge \hat{\lambda }_{2} \ge \cdots \ge \hat{\lambda }_{N} \ge 0.$$
(2.2.5)

The mode energies \({\widehat{\lambda }}_{\text{i}}\) are sorted in descending order in terms of their content, and the total energy \(\sum \hat{\lambda }_{i}\) obtained by td-SPOD is equal to the total energy \(\sum \lambda_{i}\) obtained by POD. The spatial modes are then obtained as:

$${\widehat{{\varvec{\Phi}}}}_{i}({\varvec{x}})=\frac{1}{N{\widehat{\lambda }}_{i}}{\sum }_{j=1}^{N}{\widehat{\phi }}_{i}\left({t}_{j}\right){{\varvec{u}}}^{\mathrm{^{\prime}}}\left({\varvec{x}},{t}_{j}\right).$$
(2.2.6)

Subsequently, the flow field obtained by td-SPOD is recovered as:

$${\varvec{u}}\left( {{\varvec{x}},t} \right) = \overline{\varvec{u}}\left( {\varvec{x}} \right) + \mathop \sum \limits_{i = 1}^{N} \hat{a}_{i} \left( t \right){\hat{\mathbf{\Phi }}}_{i} \left( {\varvec{x}} \right).$$
(2.2.7)

The flow field reconstruction is exact if all of the td-SPOD modes are included, and the mode coefficients \(\hat{a}_{i} (t)\) can be obtained as in Eq. (2.1.6).

In one extreme case, the filter size is zero for Nf = 0, which indicates that there is no filtering—and the results of td-SPOD are simply those of POD. In another extreme case, the filter size is extended over the entire time series—which means that Nf is the number of time steps—and the correlation matrix S converges to a symmetric Toeplitz matrix (Gray 2006) that represents the PSD of the entire time series (Wise 1955). By applying periodic conditions at the start and end of this time series and using a box filter having a size equal to the number of snapshots, the symmetric circulant matrix S is obtained, and its eigenvalues and eigenvectors can be calculated by taking the Fourier transform of the first row (Gray 2006). Moreover, td-SPOD in this case is equivalent to DFT. Chen et al. (2012) proved that DMD is formally equivalent to DFT when applied to the analysis of zero-mean data in a periodic time series that are uniformly sampled in time and remains reasonable for the analysis of statistically stationary time series. This equivalency relation has been explained more rigorously by exploring the connection between DMD and Koopman operator theory (Mezić 2005; Rowley et al. 2009) and thus is not discussed in detail here.

According to the description of the td-SPOD framework, the POD, td-SPOD, and DFT methods can be summarized within a framework (coded by Sieber 2015) of td-SPOD with various filter sizes Nf, as expressed by

$${\varvec{S}}_{i,j} = \mathop \sum \limits_{{k = - N_{{\text{f}}} }}^{{N_{{\text{f}}} }} g_{k} {\varvec{C}}_{i + k,j + k} ,\;\left\{ {\begin{array}{*{20}c} {{\text{POD}}} & {N_{{\text{f}}} = 0} \\ {{\text{SPOD}}} & {0 < N_{{\text{f}}} < N} \\ {{\text{DFT}}} & {N_{{\text{f}}} = N} \\ \end{array} } \right..$$
(2.2.8)

2.3 fd-SPOD

fd-SPOD was originally devised as a variation of classical POD. Its development was motivated by the decomposition of the cross-spectral density tensor, where each mode can be extracted at a single frequency (Lumley 1967). The cross-spectral density is usually obtained from time-series data using Welch’s method (Welch 1967). As in the time-domain method, the frequency-domain method requires the segmentation and weighting of a long time series and a Fourier transformation in time τ. For data in a long time series, the correlation function is defined as realizations of the flow in the frequency domain, which are Fourier-transformed in time via

$$\tilde{\varvec{S}}\left( {{\varvec{x}},\varvec{x^{\prime}},f} \right) = \frac{1}{N}\left\langle {\tilde{\varvec{u}}^{^{\prime}} \left( {{\varvec{x}},f} \right)\tilde{\varvec{u}}^{{{^{\prime}}*}} \left( {\varvec{x^{\prime}},f} \right)} \right\rangle .$$
(2.3.1)

here each segment in time τ is Fourier-transformed with a window function w(τ), as follows:

$${\widetilde{{\varvec{u}}}}^{\mathrm{^{\prime}}}\left({\varvec{x}},f\right)=\int {{\varvec{u}}}^{\mathrm{^{\prime}}}\left({\varvec{x}},t+\tau \right)w\left(\tau \right){e}^{-i2\pi f\tau }\mathrm{d}\tau ,$$
(2.3.2)

and the fd-SPOD modes are derived from the integral equation

$$\int \widetilde{{\varvec{S}}}\left({\varvec{x}},{{\varvec{x}}}^{\mathrm{^{\prime}}},f\right){\widetilde{{\varvec{\Phi}}}}_{i}\left({{\varvec{x}}}^{\mathrm{^{\prime}}},f\right)\mathrm{d}{{\varvec{x}}}^{\mathrm{^{\prime}}}={\widetilde{\lambda }}_{i}\left(f\right){\widetilde{{\varvec{\Phi}}}}_{i}\left({\varvec{x}},f\right).$$
(2.3.3)

The relationship between td-SPOD and fd-SPOD was explained rigorously by Sieber (2021). fd-SPOD is identical to the Fourier transformation of td-SPOD modes by formulation (12), that is

$${\widetilde{\Phi }}_{i}\left({{\varvec{x}}}^{\mathrm{^{\prime}}},f\right)=\int {\widehat{\Phi }}_{i}\left({\varvec{x}},\tau \right){e}^{-i2\pi f\tau }\mathrm{d}\tau .$$
(2.3.4)

Similar to the conversion from spatial correlation to temporal correlation in classical POD or td-SPOD, it is possible to exchange spatial and temporal correlations in fd-SPOD, and the snapshot form of fd-SPOD is obtained using the temporal correlation matrix S of fd-SPOD, that is

$$\widetilde{{\varvec{S}}}\left(t,{t}^{\mathrm{^{\prime}}},f\right)=\int \widehat{{\varvec{S}}}\left(t,{t}^{\mathrm{^{\prime}}}\right)w\left(\tau \right){e}^{-i2\pi \tau }\mathrm{d}\tau .$$
(2.3.5)

The mode coefficient matrix \(\tilde{\phi }_{i} = \left[ {\tilde{\phi }_{i} \left( {f_{1} } \right),\;\tilde{\phi }_{i} \left( {f_{2} } \right), \ldots ,\tilde{\phi }_{i} \left( {f_{N} } \right)} \right]^{T}\) and mode energies λi(f) for the snapshot form of fd-SPOD are obtained using the eigenvectors and eigenvalues of the correlation matrix \(\widehat{\text{S}}\), where

$$\tilde{\varvec{S}}\tilde{\phi }_{i} \left( f \right) = \tilde{\lambda }_{i} \left( f \right)\tilde{\phi }_{i} \left( f \right),\tilde{\lambda }_{1} \left( f \right) \ge \tilde{\lambda }_{2} \left( f \right) \ge \cdots \ge \tilde{\lambda }_{N} \left( f \right) \ge 0.$$
(2.3.6)

The mode energies λi(f) are sorted in descending order in terms of their content. The spatial modes at a single frequency are then obtained from

$${\tilde{\mathbf{\Phi }}}_{i} \left( {{\varvec{x}},f} \right) = \frac{1}{{N\overline{\lambda }_{i} \left( f \right)}}\mathop \sum \limits_{i = 1}^{N} \overline{\phi }_{i} \left( f \right)\tilde{\varvec{u}}^{^{\prime}} \left( {{\varvec{x}},f} \right).$$
(2.3.7)

Furthermore, reconstructing the flow field by fd-SPOD requires the following inverse Fourier transformation to be performed:

$$u^\prime (x,f) = \sum\limits_{{i = 1}}^{N} {a_{i} \left( f \right)\Phi _{i} \left( {x,f} \right)} ,$$
(2.3.8)
$${\varvec{u}}\left( {{\varvec{x}},t} \right) = \overline{\varvec{u}}\left( {\varvec{x}} \right) + {\mathcal{F}}^{ - 1} \left( {\tilde{\varvec{u}}^{\prime } \left( {{\varvec{x}},f} \right)} \right),$$
(2.3.9)

where the mode coefficients \(\tilde{a}_{i} (f)\) are obtained as follows:

$$\tilde{a}_{i} \left( f \right) = \left\langle {\tilde{\varvec{u}}^{^{\prime}} \left( {{\varvec{x}},f} \right),\tilde{\phi }_{i} \left( f \right)} \right\rangle .$$
(2.3.10)

However, when applying fd-SPOD as reported by Towne et al. (2018), it is better to segment the flow data into overlapping blocks, each of which containing Nfft snapshots. The data in each block are considered statistically independent and should be sufficiently long to allow the flow to pass through a complete period of the coherent structure. Next, each block is implemented by adopting a weighted temporal discrete Fourier transformation, and the frequency-domain data are subsequently reorganized by frequency. Finally, the data at each frequency are subjected to POD to acquire the modes of fd-SPOD. A more detailed description and a decomposition program have been provided (Schmidt et al. 2018; Towne et al. 2018).

The following two methods can be used for data reconstruction, i.e., the inversion of SPOD (Nekkanti and Schmidt 2021). (1) Frequency-domain reconstruction, which involves computation of the expansion coefficients by considering the inverse of the fd-SPOD problem, and (2) time-domain reconstruction, which involves obliquely projecting the data onto the modal basis. In the current study, fd-SPOD is reconstructed from the frequency domain to compare various methods’ low-rank reconstruction of 3D swirling jets. This approach ensures orthogonality and frequency–mode correspondence.

3 Experimental setup

3.1 Measurement system and data processing

Experiments on swirling jets were conducted in a tall octagonal tank (with sides of 250 mm and a height of 900 mm) filled with tap water (He et al. 2020a, b; 2021; 2022), as shown in Fig. 1a. Owing to this design and its deformable nozzle outlets, the tank could be used to investigate the dynamical behavior of 3D jet flows at various Re and for the visualization 3D jet flows. An overflow chamber controlled the location of the free surface, and a frequency-conversion pump maintained the flow cycle of the jet. A stabilizing chamber at the bottom of the tank, equipped with a cylindrical filter and a honeycomb filter, dampened the large-scale structure and reduced the crosswise velocity upstream of the swirling nozzle (He et al. 2021). Swirling nozzles with a diameter D = 20 mm were installed on top of a pipe using a threaded connection to allow easy exchange, and the pipe extended into the tank for approximately 150 mm to reduce the effect of the wall on the flow field. A fixed Re of 3000 was used, based on the bulk velocity U0 in the nozzle and D. Various swirl strengths were realized by a set of axial swirlers mounted near the exit of the pipe, as shown in Fig. 1b, c. The diameter of the central hub was adjusted to 0.1D to maintain as reasonable a level of axisymmetric according to manufacture capability. Twelve vanes with maximum thickness of 1 mm, an axial length of 0.5D, and a trailing angle β at the half-radius location were uniformly distributed in the azimuthal direction to maintain rigidity, as shown in Fig. 1b. The relationship between β at half radius and vane angle βξ between the leading and trailing edges is expressed semi-empirically (He et al. 2020a, b) as

$$\beta_{\xi } = \beta \sqrt {\frac{2\xi }{D}} ,$$
(3.1)

where ξ is the axial distance to the vane leading edge, as shown in Fig. 1e. β was set to 0°, 30°, or 50° to achieve the desired swirl number S. The intersections of the vanes and cross-sectional planes were set straight by adjusting the vane angles at other radial locations, and possible flow separation from the vane surface was ignored. A mixing section (nozzle mouth) with a length of 0.125D ensured that the wall thickness gradually decreased downstream of the swirler, which attenuated the vane effect by decreasing the non-swirling fluid volume at the start of a slug and the mixing of the flow behind the vanes. In addition, as shown in Fig. 1e, the end surface of the hub was set flush with the vanes on the leeward side and had a streamlined shape on the windward side, which minimized inflow separation (He et al. 2020a, b). All the swirlers were 3D-printed to ensure they had sufficiently smooth surfaces.

Fig. 1
figure 1

a Schematic diagrams of the measurement setup: nozzle exit geometry with b S = 0.0, c S = 0.41, and d S = 0.8; and e the vane parameters

Full size image

S for a specific swirler geometry is defined as the ratio of the axial flux of swirling momentum to that of axial momentum (Candel et al. 2014), as follows:

$$S=1.5\frac{{\int }_{0}^{\infty }{{\varvec{U}}}_{0}{{\varvec{U}}}_{\theta }{r}^{2}\mathrm{d}r}{R{\int }_{0}^{R}{{\varvec{U}}}_{0}^{2}r\mathrm{d}r},$$
(3.2)

where U0 is the axial velocity at the nozzle exit; Uθ is the azimuthal velocity measured by Tomo-PIV at the nozzle exit (Liang and Maxworthy 2005); R is the radius of the swirling nozzle; and r is the radial coordinate defined as \(r = \sqrt {x^{2} + y^{2} }\), with these data interpolated from the Cartesian coordinate system (x, y, z) defined in the reconstructed volume of Fig. 1a to the cylindrical mesh (x, r, θ) with a constant grid step in each direction. The origin is defined as the nozzle center on the swirler exit plane. Infinity is taken as the upper integration range of the swirling momentum term (the numerator) to account for radial diffusion and entrainment. The coefficient of 1.5 is adopted so that formula (3.1) is equivalent to the expression introduced by Liang and Maxworthy (2005). Here, the inflow is realized by solid-body rotation, and

$$S=\frac{\Omega R}{{U}_{0}},$$
(3.3)

where Ω is the rate of the solid-body rotation. A swirl is generated by physically rotating a nozzle, although as this requires solid-body rotation it is difficult to achieve in a complex rig. Thus, axial swirlers that are used in jet engine combustion chambers were employed in this work, as they are easily manufactured and generate satisfactory homogeneity in the azimuthal direction. The S correspond to β and were maintained 0.0, 0.41, and 0.87.

The 3D flow field downstream of the swirling nozzle exit was measured by Tomo-PIV. First, the tank was seeded with 50-μm polyamide tracer particles (Dantech, Denmark) and then volumetrically illuminated with a 25-W continuous-wave laser operating at 532 nm (Millennia EV25S, USA). The volumetric light was expanded and reflected through a flat–concave lens system to ensure that the light shone on the jet longitudinal plane had a thickness of 50 mm. A rectangular tank (with a length of 270 mm, a width of 160 mm, and a height of 115 mm) was placed onto the liquid surface to prevent scattered laser light from directly passing through the free water surface. The particle images were recorded in continuous acquisition mode by two 12-bit complementary metal–oxide-semiconductor cameras (PCO, Germany) with a spatial resolution of 2000 × 2000 pixels, a continuous sampling rate of 1000 image pairs per second, and a time interval between two successive snapshots of 1 ms. The particle size in each image was approximately 3 × 3 pixels, and the particle density was approximately 0.02 particles per pixel. Each camera had two views owing to the use of mirrors, as shown by the green dashed line for the top view of the two cameras and their relative positions in Fig. 1a. This use of an appropriate combination of prismatic and planar mirrors meant that only two cameras were required (Bardet et al. 2010) to obtain four different views with image resolutions of 1000 × 2000 pixels in the radial direction. Further details of the experimental setup can be found in the literature (He et al. 2020a, b; 2021).

Each camera was calibrated using a dotted-array plane with a dot diameter of 1.5 mm and separations of 10 mm, which established volume self-calibration (Wieneke 2008). The 3D volumetric calibration was performed with a 30-mm normal shift of the calibration plate controlled by a traverse mechanism, resulting in calibration error of less than 0.2 pixels. As shown by the reconstructed volume in Fig. 1, a measurement area of 50 mm (2.5D in the x-direction) × 100 mm (5D in the y-direction) × 50 mm (2.5D in the z-direction) was reconstructed with discretization of 11 voxels/mm to obtain the particle field. The velocity vectors were calculated from the raw particle volumes using a graphics processing unit (GPU)-based Tomo-PIV framework developed in-house (Zeng et al. 2022). A GPU-accelerated multiplicative algebraic reconstruction technique was used for image preprocessing to remove noise and improve the volume reconstruction. A concurrent iterative multigrid volumetric cross-correlation approach was applied to recover the displacement field. The interrogation volume was set in turn to 643 and 323 voxels with a 50% overlap, which realized a resolution of 14 vectors per D. Five thousand image sets were recorded and processed using the novel GPU-based Tomo-PIV framework, which gave 2500 frames of 3D flow-field snapshots for each jet.

3.2 Statistical results

Figure 2 presents the 3D mean velocity field and mean fluctuating field for different swirl numbers. The figure also shows the velocity-field slice projection of the Y–Z plane at X = 0 and the mean-fluctuating-field slice projection of the Y–X plane at Z = 0. The time-averaged velocity profiles and the mean fluctuating fields had axisymmetric distributions, and the maximum velocity fluctuation or peak velocity was mainly distributed on the axis around the nozzle. In the case of nonzero S, the axial flow decelerated owing to the swirl-induced pressure gradient and jet expansion (Markovich et al. 2016), but the average mainstream velocity remained positive. Five slices of the velocity field along the axial inflow direction of the jet are also presented in Fig. 2, showing the azimuthal uniformity of the velocity field. In addition, the volumetric measurement was accurate, as confirmed by the uniform azimuthal distribution.

Fig. 2
figure 2

3D mean velocity field and mean fluctuating field: a S = 0.0, b S = 0.41, and c S = 0.87

Full size image

The azimuthal averaged (left half) and fluctuating (right half) streamwise velocity distributions u/U0 at y/D = 0.5, 1.0, 2.0, 3.0, and 4.0 are plotted in Fig. 3a. The normalized axial streamwise velocity distribution and azimuthal averaged velocity for different swirling flows were similar at each position, with a peak near the nozzle edge. The azimuthal averaged velocity distributions Uθ/U0 are shown in the left half of Fig. 3b, where azimuthal velocity profiles close to the central axis resembled those of a solid-body rotation. The time-averaged velocity distribution u/U0 of S = 0.87 shown in the right half of Fig. 3b reveals a central recirculation zone (CRZ) 01, which formed owing to the hub acting as a bluff body against the flow. The central recirculation bubble 02 in the axial downstream was due to vortex breakdown (VB) and its extent depended on the swirl strength (Gan 2010). The detailed reconstruction of the low-swirl nozzle outlet is inadequate because the flow field in this region was the most challenging to measure via Tomo-PIV owing to the high shear strain in the jet shear layer (He et al. 2021; Pawlak et al. 2007). Another reason may be that the particle images had not recorded enough details near the nozzle exit. The cross-section of volumetric light is much larger than the nozzle diameter, with many motionless particles around the nozzle captured on the particle images, which hides the moving particles near and inside the nozzle outlet. Three experimental GIFs under different swirl numbers in supplementary material can better explain the source of this error, showing that the moving particles at the nozzle outlet are blocked. For the non-swirling jet, in the region at y/D ≤ 1.0 near the nozzle, the velocity profiles and velocity fluctuation by Tomo-PIV are quite unreasonable for the continuity of flow, so vectors in this zone were pruned for mode decomposition. The increase of swirl number can improve radial mixing of the jet fluid mass, which causes the movement of motionless particles around the swirling jet nozzle, improving the data quality of the velocity fields at the nozzle exit. Therefore, the displacement field at y/D ≤ 0.5 of swirling jet was considered as inaccurate and removed when comparing different mode decomposition approaches.

Fig. 3
figure 3

a Time-averaged (left half) and fluctuating streamwise velocity distributions u/U0. b (left half) Azimuthal-averaged velocity distributions Uθ/U0 at y/D = 0.5, 1.0, 2.0, 3.0, and 4.0. b (right half) Time-averaged velocity distribution u/U0 of S = 0.87. Only half of the measurement domain is shown, owing to symmetry

Full size image

The uncertainties associated with Tomo-PIV measurements can be affected by main two factors, accuracy of the instantaneous velocity fields and the errors affecting the statistical quantities, respectively. The former aspect contains random and bias error components, caused by experimental instruments, acquisition and processing techniques. Based on the flow continuity in the incompressible flow regime under an ideal condition, the divergence of both the mean U and fluctuating u velocity components should be zero in the absence of measurement error (Atkinson et al. 2011; Scarano et al. 2006). With an assumption of uniform random error distribution in each direction, the random velocity error δ(u) can be obtained as follows (Atkinson et al. 2011). In physical units, when the flow field data is not cut, this returns uncertainty δ(u)/U0 = 3.13%, 4.13%, and 4.70% for S = 0.00, 0.41, 0.87, respectively. The reason for the small random velocity error is that the velocity field has been adjusted by vector validation in Tomo-PIV technology.

In the statistical analysis of flow fields with PIV measurement, the random sampling error is the dominant error, and for the sampling error during the statistical analysis of the flow, uncertainty estimates of the mean flow and the Reynolds stress associated with the sampling of the phenomenon can be expressed as the first-order and second-order moments of the flow, and a detailed error calculation strategy can be found from works by Sciacchitano and Wieneke (2016). The mean relative uncertainty of mean flow is 0.53%, and the statistical uncertainty of origin data is nearly identical to that of data pruning. For Reynolds stress, the mean relative uncertainty is no more than 12% for all swirl number. We must submit that such experimental data are not a perfect measurement due to more noise, while they are a good performance test for mode decomposition methods such as SPOD.

Although these flow data are not perfect, they reveal the basic characteristics of swirling flow, which will be a challenge for the application of different modal extraction methods in those data.

3.3 Spectral analysis

The Tomo-PIV dataset described in Sect. 3.2 was subject to spectral analysis to detect the dominant frequencies of the flow structure. The power spectral densities (PSDs) of the axial y velocity component after azimuthal averaging along the central axis are presented in Fig. 4. The spectra were normalized to the maximum value. Owing to the inaccurate measurement of the outlet velocity of the non-swirl jet (S = 0.0), the PSD results in the zone y/D < 1.0 had no frequency peak. In the zone y/D > 1.0, two obvious peak Strouhal numbers (St = f × D/U0) of St = 0.39 and St = 0.52 were visible (Fig. 4a); these correspond to large-scale vortex ring structures moving in the axial direction that are decomposed and visualized in Sect. 4.1.

Fig. 4
figure 4

Power spectral density [(m/s)2/Hz] of u/U on the central axis of the jet: a S = 0, b S = 0.41, and c S = 0.87. Contours of St-PSD normalized by the maximum value. The contour lines are drawn for values of 0.40, 0.64, 0.88, and 0.96

Full size image

It was difficult to find corresponding flow characteristics for other high frequencies in the data presented in Fig. 4a. In the case of a swirling jet with S = 0.41, the speed information could not be recovered clearly at the nozzle exit and no precession frequency of the CRZ was found. In the region downstream of the VB location (3.5 < y/D < 5.0) with a series of peak St ranging from 0.13 to 0.26, the peaks may represent the precessing frequency of the precessing vortex core (PVC) around the central axis or the dominant frequency of the helical structure. In the case of a swirling jet with S = 0.87, there were two clear St peaks of 0.13 along the central axis, corresponding to a frequency of 1.04 Hz (Fig. 4c). These peaks represent the dominant frequencies of the CRZ near the nozzle exit and the PVC around the central axis. The dominant frequencies of the PVC in this study were less than those obtained by Percin et al. (2017) (St = 0.27 and Jones et al. 2012) (St = 0.35), which was possibly due to the slightly larger S and Re used in these previous studies, and that the nozzle geometry can also affect the Strouhal number of PVC (Syred 2006).

Although the resolution at the exit of the non-swirl and low-swirl jets was poor, Tomo-PIV captured main flow features such as a vortex ring in non-swirling flow and a CRZ in high-swirl flow. To compare direct modal decomposition achieved via various methods in the 3D Tomo-PIV dataset and determine the most appropriate method for analyzing swirl jets having low signal-to-noise ratios, this dataset was further analyzed by POD, DFT, time- and frequency-domain SPOD, as detailed in the following section.

4 Comparative analysis of POD, td-SPOD, DFT, and fd-SPOD

As mentioned in Sect. 2, Sieber et al. (2016) proved that POD, td-SPOD, and DFT methods can be applied within the framework of td-SPOD using various filter sizes Nf (as coded by Sieber 2015). A typical filter size is between one and two periods of the dominant frequency, which can be parsed from the dominant vortex ring in the non-swirl flow jet or the PVC in the swirl jet (Lückoff et al. 2018). The decomposition code of fd-SPOD can be found in the literature (Schmidt et al. 2018; Towne et al. 2018). To enable comparison, the same window size was used in both SPOD methods. The size of the filter in the td-SPOD framework was defined as 2Nf + 1, such that Nf was 256 for a Gaussian window of 513 snapshots. The time series for fd-SPOD was segmented into blocks of 512 snapshots, with a 50% overlap between adjacent blocks. The parameters of the methods are listed in Table 1. All the processed data had a zero mean, i.e., they were data of the fluctuation velocity field.

Table 1 Summary of the various decomposition methods
Full size table

4.1 Modal analysis of a non-swirl jet

Laufer et al. (1974) reported that the basic flow in a turbulent round jet consisted of a street of interacting and coalescing vortex rings. Yule (1978) proved that vortex rings in the round non-swirling jet existed in only a relatively short transitional, Reynolds number dependent, region near the nozzle in the transition region. If the two structures upstream are close enough together, or one of the vortex rings is relatively small, the vortices will merge (Liepmann and Gharib 1992). Then, the amalgamation process continues downstream until the resultant vortex ring is so large that its diameter almost span the radius of the jet, the vortex ring will break down very abruptly into smaller structures (Liepmann and Gharib 1992). After the breakdown, the jet grows linearly with downstream distance. According to the linear stability analysis by Gallaire and Chomaz (2003), modes with m = 0 and ± 1 dominate the non-swirling jets, and m = 0 has the fastest growth for thin shear layers. Further measurements revealed that the heat and mass exchange between the jet and surrounding fluid can be promoted by the large-scale toroidal vortex structures (Demare and Baillot 2001; Kozlov et al. 2011). Alekseenko et al. (2018) applied spatial Fourier transform and POD to evaluate the energies of different azimuthal modes for different cross-sections of the non-swirling jet and to extract coherent structures, manifesting the axisymmetric azimuthal mode has the largest amplitude in the entire measurement domain for both the pressure and velocity fluctuations. The specific structures in the non-swirling jet are suitable for the comparative discussion with different modal decomposition methods.

The results of decomposition of a non-swirl jet at S = 0 using the various methods described above are summarized in Fig. 5. Figure 5a–c compares the normalized eigenvalues obtained by POD, td-SPOD, and DFT against the same background. The percentage energies of the first and second modes obtained by POD were 4.87% and 4.86%, respectively, whereas those of the third and fourth modes were 3.10% and 2.91%, respectively. As the energy ratio decreased more rapidly in the higher-order modes than in the lower-order modes, POD revealed the energy-optimal decomposition modes. The percentage energies of the first four modes obtained by td-SPOD were similar in 2.91%, 2.91%, 2.55%, and 2.55%, respectively. The normalized eigenvalues of DFT declined slowly at higher-order modes because DFT is a frequency-dominated decomposition method. For example, Fig. 5d shows that the normalized eigenvalues of fd-SPOD had a leading mode at each frequency that was substantially more energetic than the suboptimal mode at that frequency (St = 0.39 and St = 0.52, as determined from the PSD in Sect. 3.3). Moreover, the eigenvalues at each frequency were normalized and based on accumulative statistics, which revealed that 50% of the energy was concentrated in the first few modes obtained by fd-SPOD.

Fig. 5
figure 5

Spectra obtained by various methods for a non-swirl jet at S = 0. a, b, c All eigenvalues obtained by POD (Nf = 0), td-SPOD (Nf = 256), and DFT (Nf = 2500). (d) Eigenvalues obtained by fd-SPOD, at St = 0.39 and St = 0.52, normalized by the total energy. e, f, g PSD of the POD/td-SPOD/DFT time coefficients for the first 40 modes. h Percentage of energy obtained by fd-SPOD and accounted for by each mode as a function of frequency. i, j, k Energy contribution of mode pairs to the dynamics of the flow obtained by POD/td-SPOD/DFT, where the diameter and color of the points indicate the harmonic correlation and the mode pairs are numbered according to decreasing harmonic correlation strength. l fd-SPOD eigenvalues as a function of St, normalized by the total flow energy, where shading from red to blue corresponds to the mode ordering \(\left( {\lambda_{1} \, > \,\lambda_{2} \, > \cdots > \,\lambda_{N} } \right)\)

Full size image

The identification of linked modes is important to flow-field analysis and decomposition using POD, td-SPOD, DFT, and fd-SPOD, as linked modes represent dominant coherent structures. The two modes of a mode pair usually have the same spectral content and a fixed phase difference of ± π/2, and the dynamic behavior of a coherent structure in the flow can be expressed by the reconstruction of a mode pair. Sieber et al. (2016) presented an approach for the identification of linked modes that involves checking the harmonic correlation of the eigenvectors of the dynamic mode decomposition of the temporal coefficients, which affords the temporal coefficients of POD, td-SPOD, and DFT within a td-SPOD framework. This unbiased strategy for identifying linked modes provides the harmonic correlation, i.e., a quantitative measure of the dynamic coupling of individual modes through the DMD of the temporal coefficients, as discussed by (Sieber et al. 2016). This powerful approach was used to determine the mode pairs and their associated energy contribution K (defined as \(\left( {\lambda_{i} + \lambda_{j} )/\sum \lambda_{k} } \right)\) obtained by POD, td-SPOD, and DFT, as presented in Fig. 5i, j. The diameter and color of the points indicate the harmonic correlation, and the first four mode pairs are labeled according to weakening harmonic correlation. These four modes of the highest harmonic correlation usually had the highest energy content and hence represented dominant large-scale structures in the flow field. In addition, the DFT results had duplicate harmonic correlations, as indicated by the filled red symbols, and the first four mode pairs were identified by referring to the frequencies detected by td-SPOD at Nf = 256. These results indicate that to obtain meaningful modal pairs, DFT may have to be performed after td-SPOD within the td-SPOD framework.

In fd-SPOD with Fourier transformation, the linked modes comprised real and imaginary parts with a fixed phase difference of ± π/2. Figure 5l shows eigenvalues expressed as a function of St and normalized \(\left( {\lambda_{i} /\sum \lambda_{i} } \right)\) to the total flow energy, where the shading from red to blue corresponds to the mode ordering \(\left( {\lambda_{1} \, > \,\lambda_{2} \, > \, \cdots \, > \,\lambda_{N} } \right)\). There was an energy gap between the leading mode and the following modes at each frequency, which facilitated fd-SPOD-based identification of the energetic mode pair for a low-rank dynamic at a frequency of interest.

Further analysis of temporal flow dynamics could not be performed, owing to the strict separation of the modes according to frequency in fd-SPOD. In contrast, td-SPOD enabled such an analysis, which highlights the key difference between td-SPOD and fd-SPOD. The mode spectra of td-SPOD and fd-SPOD are presented in Fig. 6 to show the differences and similarities of the two techniques. The first eight mode pairs with the highest harmonic correlation in the St range from 0.13 to 1.2 are labeled and plotted together with the fd-SPOD spectrum in Fig. 6b. Interestingly, the scatter plots of the td-SPOD spectrum were similar to the leading mode in line plots of the td-SPOD spectrum at various frequencies, although at a slightly higher energy. This slight energy difference was because the mode obtained by td-SPOD decomposition contained the structures of other frequencies, as later discussed in this section. Additionally, the frequencies of the modal pair obtained by td-SPOD differed slightly from those obtained by fd-SPOD with Fourier transformation, because the former were obtained after DMD of the temporal coefficients and weighting of the relative energy content of a mode pair (Sieber et al. 2016).

Fig. 6
figure 6

SPOD spectra for the time- (a) and frequency-domain (b) decomposition, presented as the percentage of the total turbulent kinetic energy

Full size image

The use of POD, td-SPOD, and DFT within the td-SPOD framework provides a way to examine temporal flow dynamics, and the results for various filter sizes were very different. Figure 5e–g presents the frequency spectra of the temporal coefficients of the first 40 modes, which accounted for approximately 50% of the total energy, and the PSDs of the first four energetic mode pairs extracted by POD, td-SPOD, and DFT are plotted in Fig. 7. The POD results in Fig. 8a show that the phase shift between the two time coefficients was not always π/2, and the Lissajous curves (phase portraits) show that the trajectory of the POD coefficients was not exactly circular (Fig. 8b). These results reveal that a pair of modes extracted by POD had many differences. Modes 1 and 2 obtained by POD shared the same peak St of approximately 0.39, whereas the pair of modes 3 and 4 had a similar distribution and a peak St of 0.26, as seen in Figs. 5e and 7a. The POD results exhibit modes 1 and 2 (hereafter referred to as mode pair (1, 2)) at St = 0.39 and 0.52. Figure 9a visualizes their spatial structure using the Q-criterion (Jeong and Hussain 1995). Figure 9f presents the velocity field reconstructed with only mode pair (1, 2). There was a ring-like vortex (RV) (Alekseenko et al. 2018), the spatial structure of which was easily identified from the instantaneous velocity field and low-order modes. However, the dominant frequency of the RV was not properly resolved by POD. The modes obtained by td-SPOD revealed harmonic correlation, as seen in Figs. 5f and 7b, with a clear peak St of 0.52 for mode pair (1, 2). The first two time coefficients obtained by td-SPOD (Nf = 256) exhibited a phase shift of π/2, as the minima and maxima of one coefficient corresponded to the zeros of the other, and vice versa, as seen in Fig. 8c, d. However, in the case of mode pair (3, 4), coherent structures were not properly resolved as they are in POD, and there were peaks at St = 0.26 and 0.39. Figure 9b shows that the spatial structures obtained by td-SPOD resembled those at St = 0.52 in Fig. 9a, whereas it is difficult to conclude that St = 0.52 represented the dominant frequency of the RV, even though the reconstructed velocity field resembled a fine RV (Fig. 9g). In another decomposition with snapshots, which converged to a DFT, the phase shift between the two time coefficients was a constant π/2 and the Lissajous curve was circular, as seen in Fig. 8e, f. The PSD of temporal coefficients obtained by DFT showed an excellent harmonic correlation and revealed there was a clear dominant frequency for each mode pair, as shown in Figs. 5g and 7c. Peaks of St = 0.52 and 0.26 were found for mode pair (1, 2) and mode pair (3, 4), respectively. The spatial structures obtained by DFT and shown in Fig. 9c resemble the results shown in Fig. 9a, b, but they may have been corrupted by a low-energy structure at the two frequency.

Fig. 7
figure 7

PSD of the first four mode pairs obtained by a POD (Nf = 0), b td-SPOD (Nf = 256), and c DFT (Nf = 2500)

Full size image
Fig. 8
figure 8

Evolution of the temporal coefficients and phase portraits of temporal coefficients of mode pair (1, 2) obtained by (a, b) POD (Nf = 0), (c, d) td-SPOD (Nf = 256), and (e, f) DFT (Nf = 2500)

Full size image
Fig. 9
figure 9

Spatial characteristics and reconstructed velocity field of mode pair (1, 2) for a non-swirl jet at S = 0.0. Iso-contours of Q = 10 U02/D2, where the blue color is the first mode of mode pairs and the red color is the second mode of mode pairs; and m = 0 for axisymmetric mode pairs. a, e POD, b, f td-SPOD, c, g DFT, and d, h fd-SPOD. The light-green color indicates the iso-values of Q = 0.04 U02/D2

Full size image

In summary, the above discussion reveals that the td-SPOD framework with different filter sizes allowed a continuous sweep from classic POD to spectral DFT. Figure 8 presents the temporal coefficients scaled with single-mode energy and reveals how to improve the identification of linked modes by analyzing temporal flow dynamics within the td-SPOD framework. The use of td-SPOD (Nf = 256) effectively improved the extraction of conjugate mode pairs by increasing the diagonal similarity of the correlation matrix C. Most of the detail in the time coefficients was preserved, and the magnitude fluctuation reveals that the VR was not always present in the flow or that its layout varied with time, which could not be revealed by fd-SPOD. The advantage of fd-SPOD is its strict separation of modes according to frequency, and the 3D spatial structures at St = 0.39 and 0.52 obtained by fd-SPOD are shown in Fig. 9d, e. The velocity fields reconstructed by the first two energetic modes at St = 0.39 and 0.52 described the diversity of the RV at respective frequencies, and they had a similar appearance. To confirm the existence of the RV structure at these two frequencies, the instantaneous spatial structures of the RV at two moments were drawn with Q = 0.5 U02/D2, as shown in Fig. 10. Even though the spatial resolution of the Tomo-PIV dataset was poor, some single RVs were observed (Fig. 10a), which corresponds to the vortex rings existed in the transition region near the nozzle (Yule 1978). And the downmost vortex ring was relatively small from Fig. 10, therefore the vortices merge in the downstream in Fig. 10b (Liepmann and Gharib 1992). Then, the amalgamation process continues downstream until the resultant vortex ring was so large that its diameter almost spanned the radius of the jet, the vortex ring break down very abruptly into smaller structures (Liepmann and Gharib 1992). There was an obvious vortex ring break down near the exit of the reconstructed volume as shown in Fig. 10a, b. The reconstructed flow fields suggest that the vortex ring break down corresponded to St = 0.39 due to the RV merging, although the generation frequency of the RV corresponded to St = 0.52. These large-scale ring-like vortex and evolution structures with different frequencies appeared in the instantaneous field, which confirms the effectiveness of fd-SPOD.

Fig. 10
figure 10

Instantaneous spatial structures of a RV and VB at time t1 and b RV merging at time t2. The iso-contours of Q = 0.5 U02/D2 are colored according to the local axial velocity

Full size image

The spatial characteristics of mode pair (3, 4) are presented in Fig. 11. The modal results of POD in Fig. 11a and td-SPOD in Fig. 11b were impure, and thus, valuable modes could not be obtained. The spatial structures of mode pair (3, 4) might have been a single-helix structure (Alekseenko et al. 2018). The 3D spatial mode obtained by fd-SPOD and the Fourier transform in the time domain agree at St = 0.52, as seen in Fig. 9c, e, and at St = 0.26, as seen in Fig. 11c, e, because both methods involve the Fourier transformation of the time-series data. There are differences between Figs. 9c, e and 11c, e, which might have been due to the short time-segment analysis of fd-SPOD and the destruction of features by low-energy structures in DFT.

Fig. 11
figure 11

Spatial characteristics of mode pair (3, 4) for a non-swirl jet at S = 0. The iso-contours of Q = 10 U02/D2 are colored blue (the first mode of mode pairs) and red (the second mode of mode pairs). a POD, b td-SPOD, c DFT, and d fd-SPOD of mode pair (1, 2); and e fd-SPOD mode pair (3, 4). The light-green color indicates the iso-values of Q = 0.04 U02/D2

Full size image

In the decomposition of data of a non-swirl jet flow, neither POD nor DFT provided a sufficiently clear structure, whereas fd-SPOD separated the most energetic structures at each frequency and extracted clear deterministic modes. td-SPOD acquired spatial features and revealed temporal flow dynamics that could be used to monitor the flow process.

4.2 Discussion on the temporal flow dynamics of a low-swirl jet

It is more meaningful to use decomposition methods to extract structures from data of swirling jet flows, including large-scale coherent structures such as VBs and PVCs. The imposition of a swirl on a jet promotes helical instability modes (Gallaire and Chomaz 2003), and as S increases the swirl vortex core becomes destabilized and ultimately breaks down (Billant et al. 1998; Sarpkaya 1979). Under a low swirl number, the spiral-type vortex breakdown occurs during widening of the rotating flow and deceleration of velocity along the vortex core, the flow loses its axial symmetry, and the vortex core takes the shape of a spiral (Alekseenko et al. 2018). Lambourne and Bryer (1961) first reported the two most common breakdown events: bubble breakdown and spiral breakdown. Further increase in the swirl number causes a permanent central reverse flow in the shape of a bubble or cone, corresponding to the bubble-type or cone-type vortex breakdown, respectively (Billant et al. 1998; Sarpkaya 1979; Spall 1996). An axisymmetric recirculation region appears near the central axis of rotation in bubble breakdown, whereas helical structures arise and precess around the central axis in spiral breakdown. After the central recirculation zone appears and it triggers helical instability of the swirling jet's core downstream subsequently (Ruith et al. 2003). In the central reverse flow zone, it will generate a coherent structure consisting of large-scale helical vortices, corresponding to a global self-oscillating mode (Liang and Maxworthy 2005; Oberleithner et al. 2012). 3D helical coherent structures in swirling flows are usually extracted via POD after Fourier transformation over the azimuthal angle (Alekseenko et al. 2018; Markovich et al. 2016). The coherent structures in swirl jets can be extracted directly with the aid of the conditional averaging technique (Sirovich 1987a, b, c), POD (Percin et al. 2017), DMD (Ianiro et al. 2018) and td-SPOD (Vanierschot et al. 2020). In this study, S was fixed at 0.41 or 0.87, and the effectiveness of various methods of decomposition for the extraction of valuable coherent structures were compared.

The snapshots had been decomposed into azimuthal Fourier modes because the swirl jets were periodic along the azimuthal coordinate, and St = 0.13 and 0.26 for the single-helix mode (m = 1) and double-helical mode (m = 2), respectively. This gave the dominant frequencies that were used for finding the two patterns in all the direct vector field decomposition results of a low-swirl jet at S = 0.41 via various methods, as seen in Fig. 12. The energy sequential modes obtained by POD are shown in Fig. 12a. Although the first and second modes had the highest percentage energies (5.27% and 2.37%, respectively), they had a weak harmonic correlation. According to the mode pair labeled as 1 in Fig. 12i and the PSD results in Fig. 13a, mode (3, 4) with St = 0.13 had the highest harmonic correlation, whereas it was difficult to locate the mode pair with St = 0.26 corresponding to the discussion in Sect. 3.3 in Fig. 12e, i. Figure 13a shows a very close mode pair (11, 12), labeled as 3 in Fig. 12i. The PSD of the time coefficients of this mode pair was not completely consistent, indicating that POD cannot distinguish this mode pair from other dynamic structures and noise in the data. Therefore, only mode pair (3, 4) was visualized using the Q-criterion, as shown in Fig. 15a. Each mode comprised a helical structure whose winding opposed the jet swirl direction, and the phase angle between the two modes was π/2, which was also observed at S = 0.36 by Vanierschot et al. (2020). td-SPOD outperformed POD, enabling the collection of mode pairs at St = 0.13 and 0.26, as shown in Fig. 13b. To locate mode pair (6, 7) at St = 0.13 and mode pair (9, 10) at St = 0.26 required the PSD in Fig. 12f, due to no markers associated with frequencies in Fig. 12j. Figure 15b, e presents the 3D modes at St = 0.13 and 0.26, respectively. Figure 15b shows that the spatial structures obtained by td-SPOD resembled those in Fig. 15a, with each mode having a spiral structure. Although this set of mode results appeared incomplete, there might have been a single-helix mode linked to the VB motion in the outer vortex structures near the nozzle rim (Markovich et al. 2016). Similar to the mode pair at St = 0.13, the spatial structures of mode pair (9, 10) were observed as a double-helical shape for each mode, as shown in Fig. 15e.

Fig. 12
figure 12

Spectral results from the various methods for a low-swirl jet at S = 0.41. a, b, c All of the eigenvalues obtained by POD (Nf = 0), td-SPOD (Nf = 256), and DFT (Nf = 2500). d Eigenvalues obtained by fd-SPOD, at St = 0.13 and 0.26, normalized to the total energy. e, f, g PSD of the POD/td-SPOD/DFT time coefficients for the first 40 modes. h Percentage of energy accounted for by each mode as a function of frequency obtained by fd-SPOD. i, j, k Energy contribution of mode pairs to the dynamics of the flow obtained by POD/td-SPOD/DFT, where the diameter and color of the points indicate the harmonic correlation and the mode pairs are numbered according to decreasing harmonic correlation strength. l fd-SPOD eigenvalues as a function of St, normalized to the total flow energy, where shading from dark red to dark blue corresponds to the mode ordering \(\left( {\lambda_{1} \, > \,\lambda_{2} \, > \cdots > \,\lambda_{N} } \right)\)

Full size image
Fig. 13
figure 13

PSD of the first two mode pairs obtained by a POD (Nf = 0), b td-SPOD (Nf = 256), and c DFT (Nf = 2500)

Full size image

Although the frequency of mode pair (9, 10) was twice the frequency of mode pair (6, 7) within PSD numerical accuracy, mode pair (9, 10) was not a higher harmonic of mode pair (6, 7) (Vanierschot et al. 2020). This was shown by the temporal flow dynamics of mode pair (6, 7) and mode pair (9, 10) in Fig. 14. A comparison of the two pairs of time coefficients reveals that the two structures were not always present in the flow; they coexisted in some time intervals, whereas only one existed in other time intervals (Vanierschot et al. 2020). Owing to the higher frequency, increases and decreases in the amplitude of mode pair (9, 10) were more dynamic than those in the amplitude of mode pair (6, 7). The Lissajous curves, which are depicted in Fig. 14e, should have exhibited a figure-of-eight shape if the mode pair (9, 10) was a higher harmonic of the mode pair (6, 7). In addition, under harmonic correlation, the phase angle computed as \(\phi_{{(6, 7)}} = {\text{ arctan}}\left( {a_{{6}} /a_{{7}} } \right)\) or \(\phi_{{(9, 10)}} = {\text{ arctan}}\left( {a_{{9}} /a_{{{1}0}} } \right)\) should have been distributed along the three major diagonals and the histogram of the phase difference of \(2\phi_{(6, 7)} - \phi_{(9, 10)}\) should have exhibited one clear peak. However, the distribution was irregular (Fig. 14f) and the histogram of the phase difference showed no statistical correlation (Fig. 14g), revealing that the double-helix mode was not a higher harmonic of the single-helix mode pair (6, 7).

Fig. 14
figure 14

Evolution and phase portraits of the temporal coefficients for a, b mode pair (7, 8) and c, d mode pair (9, 10). e First temporal coefficient of mode 7 versus mode 9. f Phase angle of mode pair (7, 8) versus mode pair (9, 10). g Histogram of the phase difference between mode pair (7, 8) and mode pair (9, 10)

Full size image

In DFT, two pairs of modes are selected according to the td-SPOD results for the same St, and thus, the spatial structures in Fig. 14c obtained by DFT resembled those in Fig. 14a, b. However, such spatial structures may be destroyed by noise if they do not have a clear or integral helical shape. POD, td-SPOD, and DFT within the td-SPOD framework revealed the spectral characteristics of the dominant frequency for low-swirl flow. These dominant frequencies were clearly obtained from the PSD of the time coefficient (Fig. 13), and yet the spatial modes were quite different, as seen in Fig. 15. As shown in Sect. 4.1, fd-SPOD performed best in mode extraction, and therefore, the swirl data were also resolved by fd-SPOD to verify whether fd-SPOD was effective for swirl jets. Figure 12d, h, l gives the spectral results of fd-SPOD, which revealed that there was an energy gap between the leading mode and following modes at St = 0.13 and 0.26. Figure 12h shows that 50% of the energy was concentrated in the first three modes in fd-SPOD. Figure 12l shows that the first two most energetic modes had St of 0.13 and 0.26, respectively. Figure 15 depicts the 3D spatial modes. Figure 14d shows a more detailed complete helical structure, demonstrating clearly that it wound in the opposite direction to the jet swirl direction. The spatial structure of the mode pair in Fig. 15g suggests that had a double-helical shape, which resulted from the superposition of axial and azimuthal velocities. Both structures represent a counter-winding mode that has been obtained in previous studies using one-dimensional laser Doppler velocimetry (Cala et al. 2006) and two-dimensional particle image velocimetry (Oberleithner et al. 2011).

Fig. 15
figure 15

Spatial characteristics of a non-swirl jet at S = 0.41. Iso-contours of Q = 10 U02/D2, where the blue color indicates the first mode of mode pairs and the red color indicates the second mode of mode pairs, and m = 1 for single-helix mode pairs and m = 2 for double-helical mode pairs. a POD (Nf = 0), b, e td-SPOD (Nf = 256), c, f DFT (Nf = 2500), d, g fd-SPOD

Full size image

As shown in Fig. 15, the results of DFT and fd-SPOD were similar overall but contained some differences. Despite DFT having the same structures as fd-SPOD at the identified frequencies, DFD yielded no information about the frequencies of interest as these structures were usually destroyed by noise at the same frequency (Sieber et al. 2016). The relationship between td-SPOD and fd-SPOD is presented in Fig. 16. The eight pairs of modes in different frequencies with the highest harmonic correlation intensity obtained by td-SPOD agree with the most energetic first-order mode at each frequency obtained by fd-SPOD.

Fig. 16
figure 16

Spectra of the time- a and frequency-domain b SPOD presented as percentages of the total turbulent kinetic energy

Full size image

Overall, the investigation of swirl flow with S = 0.41 shows that the frequency-domain approach is best for mode decomposition in the frequency domain, whereas the time-domain method is best for the investigation of interactions between various structures or the temporal evolution of coherent structures.

4.3 Discussion on the relationship between various SPODs of a high-swirl jet

Formulation (2.3.4) shows that fd-SPOD was identical to the Fourier transform of td-SPOD, and Sects. 4.1 and 4.2 reveal the strong similarity of the results of fd-SPOD and DFT. Therefore, the swirl jet data at S = 0.87 were used to compare the results of the fd-SPOD and td-SPOD for the same segmentation to verify whether there was a conversion relationship between fd-SPOD and td-SPOD, as was proven theoretically by Sieber (2021). Additionally, Sieber (2021) claimed that this relationship was valid, provided that investigation data are statistically stationary. Further investigation showed that this relationship held for the dominant coherent structure in experimental data for a turbulent jet. Thus, it was of interest to determine whether this relationship also held for a high-swirl jet with multi-dominant coherent structures. fd-SPOD was implemented with a time series segmented into blocks with a 50% overlap, with each block comprising 256 snapshots in one period of the periodic structure of the flow field. td-SPOD was analogously computed with the same segmentation from the snapshot correlation. The filtered matrix \(\hat{S}\) obtained by td-SPOD had a 99% segment overlap, according to formulation (2.2.4).

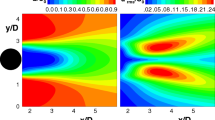
The results of decomposition of a high-swirl jet with S = 0.87 with various methods are summarized in Fig. 17. POD and DFT could not resolve clear coherent structures in the high-swirl jet and thus are not discussed further. The normalized eigenvalues obtained by td-SPOD decreased slowly in Fig. 17f, which might have been because the first several modes had the same energy and had the same frequency as the dominant frequency. This corresponds to the two peaks at St = 0.13 in the PSD results of Fig. 4f. The unbiased strategy of extracting linked modes by DMD of the temporal coefficients appeared to fail in this case, and mode pairs at the PSD dominant frequency could not be found among several linked modes related to the highest harmonic correlation. It was thus necessary to use the PSD results of time coefficients in Fig. 17f to obtain energetic modes at the frequency of interest. fd-SPOD has unique advantages in this field of modal extraction. There was an obvious peak St of 0.13 in Fig. 17l, and the leading mode was substantially more energetic than the suboptimal mode at this frequency. Figure 18 shows that the eight pairs of modes in different frequencies with the highest harmonic correlation intensity obtained by td-SPOD agree with the most energetic first-order mode at each frequency obtained by fd-SPOD, whereas there was no structure of the eight pairs of modes that closely matched a structure at the frequency of interest.

Fig. 17
figure 17

Spectra obtained using various methods for a non-swirl jet at S = 0.87. a, b, c All of the eigenvalues obtained by POD (Nf = 0), td-SPOD (Nf = 256), and DFT (Nf = 2500). d Eigenvalues obtained by fd-SPOD, at St = 0.13, normalized to the total energy. e, f, g Power spectral density of the POD/td-SPOD/DFT time coefficients for the first 40 modes. h Percentage of energy accounted for by each mode as a function of frequency obtained by fd-SPOD. i, j, k Energy contribution of mode pairs to the dynamics of the flow obtained by POD, td-SPOD, and DFT, where the diameter and color of the points indicate the harmonic correlation and the mode pairs are numbered according to decreasing harmonic correlation strength. l fd-SPOD eigenvalues as a function of St, normalized to the total flow energy, where shading from red to blue corresponds to the mode ordering \(\left( {\lambda_{1} \, > \,\lambda_{2} \, > \cdots > \,\lambda_{N} } \right)\)

Full size image
Fig. 18
figure 18

Spectra of time- a and frequency-domain b SPOD presented as the percentage of the total turbulent kinetic energy

Full size image

Figure 19 presents the td-SPOD modes and their Fourier transform, and the fd-SPOD modes. Both td-SPOD and fd-SPOD distinguished various types of structure with large energy differences at the same frequency. td-SPOD then resolved two pairs of different modes, whereas fd-SPOD resolved modes with different energies at the same frequency. fd-SPOD and Fourier transform of td-SPOD modes afforded the same dominant structure, whereas there were differences between the two ways, despite the fact that theory predicts they should be identical. This was probably because of the limited time series, which due to experimental limitations did not cover all observable time scales.

Fig. 19
figure 19

Spatial mode shapes for td-SPOD and fd-SPOD at St = 0.13. a Mode pair (2, 3) and d mode pair (7, 8) obtained by td-SPOD. b, e Fourier decomposition of a, d, and c, f the first two modes obtained by fd-SPOD. The iso-contours of Q = 10 U02/D2, where the blue color is the first mode of mode pairs and the red color is the second mode of mode pairs

Full size image

The swirl jet data for S = 0.87 show that the fd-SPOD and td-SPOD result were directly related through a Fourier transform. These two methods were able to distinguish different types of structures with large energy differences at the same frequency.

4.4 Reconstruction of the 3D flow field

3D instantaneous flow structures with 50% turbulent kinetic energy were reconstructed to further compare the extraction of flow field features by various methods and obtain a clearer coherent structure with a low level of flow noise (Fig. 20). The good-quality data obtained for a non-swirl jet with S = 0 meant that various methods could be used to reconstruct the VC structure in the flow field, thereby retaining many of the flow field details. It was surprising that POD performed better than other methods in flow field reconstruction to reveal flow features. Some flow field details were resolved into higher-order low-energy modes by td-SPOD or DFT, and maintaining 50% energy in td-SPOD or DFT required more high-energy lower-order modes, which resulted in slight differences in the structure of the jet outlet compared with that obtained by POD. The reconstruction by fd-SPOD was based on the frequency domain, which meant that a certain number of modes were retained at each frequency. The process is referred to as nmodes × nfreq mode reconstruction (Nekkanti and Schmidt 2021), where nmodes is the number of modes retained at each frequency in Figs. 5, 12, or 17 and nfreq is given by nfft/2 + 1. Figure 20e shows that fd-SPOD restored more details of the flow field than other methods and revealed a more high-frequency structure. The dominant coherent structures of swirl jets at S = 0.41 and 0.87 were hidden within much high-frequency low-energy noise and they could be extracted in low-order energetic modes.

Fig. 20
figure 20

Reconstructed 3D flow structures with 50% turbulent kinetic energy. a Original, b POD, c td-SPOD, d DFT, and e fd-SPOD. The iso-values of Q = 0.5 U02/D2 are colored according to the local axial velocity

Full size image

As shown in Fig. 20, the central PVC and outer VB in the two swirl flows were clearly visible in the 3D flow fields reconstructed by any of the methods. A complete RV remained near the nozzle exit for swirl jets with S = 0.41, whereas it broke down downstream of the flow because an axial vorticity component was produced that formed a spiral structure that wound in the opposite direction to the jet swirl direction. The isosurface representing Q = 0.5 U02/D2 and colored in terms of its local axial velocity shows that the axial velocity component decreased from approximately 1.1U0 to 0.3U0 along the PVC. Compared to other methods, POD restored more details from the reconstructed 3D flow field of the PVC and peripheral vortex structure in the swirl jets at S = 0.87. In contrast, no complete RV was observed (Fig. 20b), and the outer vortex had the shape of deformed rings, comprising segments with opposite helicity. As the axial vorticity component was generated by the deformation of the vortex rings, these rings broke up downstream into longitudinal vortex filaments with opposite helicity. Therefore, although POD could not effectively distinguish structures at different frequencies, its good performance in principal component extraction suggests that it may be more suitable than other methods for data preprocessing and denoising.

Figure 20b shows that when the axial velocity reached approximately half the velocity at the nozzle exit, the top of the PVC had a defined spiral shape, which was evidence of the spiral-type VB. Four phases of the vortex precession period obtained by POD in the central plane of the jet are shown in Fig. 21. This helical structure wrapped around recirculation zone 2 in a direction opposite to the swirl direction. The helical structure then detached from the PVC and disappeared downstream, as has been reported previously (Alekseenko et al. 2018; Percin et al. 2017).

Fig. 21
figure 21

Instantaneous velocity field at four phases of the vortex precession period in the central plane of the jet, reconstructed by fd-SPOD and colored according to Q = 0.5 U02/D2. The contour lines are local values of the axial velocity

Full size image

5 Conclusion

A comparative analysis of POD, DFT, time-domain SPOD, and frequency-domain SPOD strategies was carried out on Tomo-PIV measurement datasets of swirling jets. The 3D velocity fields of swirling jets at various swirl numbers were reconstructed within the GPU-accelerated Tomo-PIV framework, and the main features of the swirl jet were discussed. Spectral analysis revealed periodic features generated by common structures of the jet, such as an RV, a PVC, and a VB. The jet data were further resolved by POD, DFT, td-SPOD, and fd-SPOD. POD, td-SPOD, and DFT were implemented using the td-SPOD algorithm with various filter sizes. fd-SPOD was implemented by approximating the spectral cross-correlation tensor from experimental data using Welch’s method. The performance of POD, DFT, td-SPOD, and fd-SPOD was compared in terms of their mode decomposition, frequency–time analysis of temporal flow dynamics, and low-rank reconstruction of 3D swirling jets.

The modal analysis of the non-swirl jet reveals that POD and DFT did not provide sufficiently clear structures. POD exhibited non-negligible contamination by other structures at different frequencies because the energetic low-order modes obtained by POD usually merged across several spatial wavelengths and could not be properly separated. Spatial structures at identified frequencies were recognized by DFT, but they were often corrupted with noise or other low-energy structures at the same frequency. fd-SPOD performed best in the identification of coherent structures, as it enabled strict separation of the energy-dominated modes according to frequency. td-SPOD faced problems similar to those faced by POD, with contamination by other structures at different frequencies, but it afforded better correlations of the modal time coefficient of linked modes and revealed temporal flow dynamics that could be used to monitor the flow process. This was most advantageous for the investigation of interactions between different structures of the swirl jet at S = 0.41.

The interactions between the double-helix structure at St = 0.26 and the single-helix structure at St = 0.13 could be analyzed from the time evolution provided by td-SPOD, and the intermittent behaviors of swirl flows were revealed by analyzed by the temporal flow dynamics. It was difficult to examine these dynamic processes by fd-SPOD. The fd-SPOD and td-SPOD results for the swirl jet at S = 0.87 were directly related through a Fourier transformation, and the first several modal pairs with the highest harmonic correlation intensity obtained by td-SPOD agree with the most energetic first-order mode at each frequency obtained by fd-SPOD. The reconstruction of the 3D flow field through mode truncation using the low-order modes shows that POD was suitable for denoising of the flow field.

The comparative analysis of POD, td-SPOD, DFT, and fd-SPOD strategies reveals that fd-SPOD with a strict separation of energy-dominated modes according to frequency was suitable for modal separation and recognition at each frequency, thereby enabling determination of the deterministic mode for flows with convective instabilities. Moreover, the results showed that td-SPOD with a harmonic-related temporal coefficient was suitable for the investigation of mode interactions between different wavelengths and the time dynamic evolution of modes.