1 Introduction

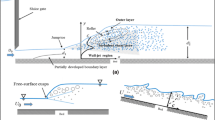
The hydraulic jump is the rapid transition from a supercritical to a subcritical open channel flow. It is characterised by the interaction of a strong turbulence with a free surface leading to air entrainment with macro-scale vortices and kinetic energy dissipation (Fig. 1). A hydraulic jump is defined by its inflow Froude number \( Fr_{1} = V_{1} /{\sqrt {gd_{1} } } \) where V 1 is the inflow velocity, d 1 is the inflow depth and g is the gravity acceleration. Fr 1 is always greater than unity. Air bubble entrainment in a hydraulic jump starts for Fr 1 > 1–1.3 (Chanson 1997; Murzyn et al. 2007). The air entrainment is caused by the strong interaction between turbulence and free surface, which generates disturbances of the air–water interface and vortex formation leading to some air entrapment. Void fraction measurements in hydraulic jumps were first conducted by Rajaratnam (1962). Resch and Leutheusser (1972) performed hot-film probe measurements in the bubbly flow region and showed some effects of the upstream flow conditions. Recent developments included Chanson (1995), Mossa and Tolve (1998), Chanson and Brattberg (2000), Murzyn et al. (2005) and Chanson (2007a).

Fig. 1
figure 1

Air entrainment in a hydraulic jump with partially developed inflow

Full size image

In this study, detailed air–water flow measurements were performed in hydraulic jump flows for two inflow Froude numbers (Fr 1 = 5, 8.5, Re = 38,000, 62,000). The results were compared with an earlier study (Chanson 2006) performed with identical inflow Froude numbers but different geometric scales. The comparative analysis provides an assessment of scale effects affecting void fraction and bubble count rate distributions in hydraulic jumps with partially developed inflow conditions.

1.1 Dimensional analysis and similitude

Theoretical and numerical studies of air bubble entrainment in hydraulic jumps are difficult because of the large number of relevant equations (Chanson 1997; Chanson and Gualtieri 2008). Experimental investigations are performed with geometrically similar models based upon a dimensional analysis and dynamic similitude. In the study of the hydraulic jump, the Froude similitude is commonly used because of theoretical considerations (Bélanger 1828; Henderson 1966). But the turbulent processes in the shear region are dominated by viscous forces (Wood 1991; Chanson 1997).

For a hydraulic jump in smooth, horizontal, rectangular channels, a simplified dimensional analysis showed that the parameters affecting the air–water flow properties at a position (x, y, z) include: (a) the fluid properties including the air and water densities ρair and ρ, the air and water dynamic viscosities μair and μ, the surface tension σ, and the gravity acceleration g, (b) the channel properties including the width W, and, (c) the inflow properties such as the inflow depth d 1, the inflow velocity V 1, a characteristic turbulent velocity u′1, and the boundary layer thickness δ (Chanson 2006, 2007b). In addition, biochemical properties of the water solution must be considered and may have some significant effect. If the local void fraction C is known, the density and viscosity of the air–water mixture may be expressed in terms of the water properties and void fraction only; hence the parameters ρair and μair may be ignored. The result may be expressed in dimensionless terms:

$$ C,\frac{{Fd_{1} }} {{V_{1} }},\frac{V} {{{\sqrt {gd_{1} } }}},\frac{{u'}} {{V_{1} }},\frac{{d_{{{\text{ab}}}} }} {{d_{1} }} \cdots = F_{1} {\left( {\frac{x} {{d_{1} }},\frac{y} {{d_{1} }}\frac{z} {{d_{1} }},Fr_{1} ,\frac{{u^{\prime}_{1} }} {{V_{1} }},Re,Mo,\frac{{x_{1} }} {{d_{1} }},\frac{\delta } {{d_{1} }},\frac{W} {{d_{1} }}, \ldots } \right)} $$
(1)

where F is the bubble count rate, V is the velocity, u′ is a characteristic turbulent velocity, d ab is a bubble size, x is the coordinate in the flow direction measured from the upstream gate, y is the vertical coordinate, z is the transverse coordinate measured from the channel centreline, and x 1 is the distance from the upstream gate (Fig. 1).

In Eq. (1), the dimensionless air–water flow properties at a dimensionless position (x/d 1, y/d 1, z/d 1) within the jump are expressed as functions of the dimensionless inflow properties and channel geometry. In the right hand side of Eq. (1), the fourth, sixth and seventh terms are the inflow Froude number Fr 1, Reynolds number Re = ρV 1 d 1/μ and Morton number Mo = gμ4/ρσ3, respectively. Note that the Weber We was replaced by the Morton number since Mo = We 3/(Fr 2 Re 4). The Morton number is a function only of fluid properties and gravity constant, and it becomes an invariant if the same fluids (air and water) are used in both model and prototype, as in the present study.

The first systematic study of dynamic similarity and scale effects affecting the two-phase flow properties in hydraulic jumps was the work of Chanson (2006, 2007b). For two inflow Froude numbers (Fr 1 = 5.1, 8.5), the experiments tested the validity of the Froude similitude and the effects of the inflow Reynolds number, with all other relevant parameters being constant:

$$ C,\frac{{Fd_{1} }} {{V_{1} }},\frac{V} {{{\sqrt {gd_{1} } }}},\frac{{u'}} {{V_{1} }},\frac{{d_{{{\text{ab}}}} }} {{d_{1} }} \cdots = F_{2} (\text{Re} ) $$
(2)

where the Froude number Fr 1 and the relative channel width W/d 1 were constant: i.e. Fr 1 = 5.1, 8.5, W/d 1 = 20 (Table 1). The results of the Froude-similar experiments showed some scale effect in the smaller hydraulic jumps. In the same study, Chanson (2006) tested the effect of the relative width W/d 1, with all other relevant parameters being constant. That is:

$$ C,\frac{{Fd_{1} }} {{V_{1} }},\frac{V} {{{\sqrt {gd_{1} } }}},\frac{{u'}} {{V_{1} }},\frac{{d_{{{\text{ab}}}} }} {{d_{1} }} \cdots = F_{3} {\left( {\frac{W} {{d_{1} }}} \right)} $$
(3)

where the inflow Froude and Reynolds numbers were constant: Fr 1 = 5, 8.5, Re = 75,000, 95,000 (Table 1). The results showed that the relative channel width had no effect on the air–water flow properties for:

$$ \frac{W} {{d_{1} }} \ge 10\quad {\text{no}}\,{\text{effect}}\,{\text{of}}\,{\text{channel}}\,{\text{width}} $$
(4)
Table 1 Summary of experimental flow conditions for detailed two-phase flow measurements in hydraulic jumps
Full size table

In the present study, two experiments were conducted with the same inflow Froude numbers as the study of Chanson (2006) (Table 1). The instrumentation was similar for the present and earlier investigations, including identical sampling rate (20 kHz) and duration (45 s). A systematic comparison between the present and earlier data provides new information on the validity of the Froude similarity to study the two-phase flow properties in hydraulic jumps, particularly with reference to viscous scale effects. Note that the present study was conducted with a relative channel width W/d 1 = 28 which satisfied Eq. (4).

2 Experimental apparatus and procedures

New experiments were performed in a horizontal rectangular flume at the Gordon McKay Hydraulics Laboratory of University of Queensland (Fig. 2). The channel width was 0.50 m. The sidewall height and flume length were respectively 0.45 and 3.2 m. The sidewalls were made of glass and the channel bed was PVC. This channel was previously used by Chanson (2006, 2007a).

Fig. 2
figure 2

Bubble entrainment in hydraulic jumps. a Fr 1 = 5, Re = 38,000, x 1 = 0.75 m, d 1 = 0.018 m, shutter speed: 1/40 s, flow from right to left. b Fr 1 = 8.3, Re = 62,000, x 1 = 0.75 m, d 1 = 0.018 m, shutter speed: 1/80 s, flow from right to left. The phase-detection probe is visible above the recirculation region

Full size image

The water discharge was measured with a Venturi meter located in the supply line and which was calibrated on-site with a large V-notch weir. The discharge measurement was accurate within ±2%. The clear-water flow depths were measured using rail mounted point gages with a 0.2 mm accuracy. The inflow conditions were controlled by a vertical gate with a semi-circular rounded shape (∅ = 0.3 m) (Fig. 1). The upstream gate aperture was fixed during all experiments (d 1 = 0.018 m).

The air–water flow properties were measured with a double-tip conductivity probe (Fig. 2). The probe was equipped with two identical sensors with an inner diameter of 0.25 mm. The probe was manufactured at the University of Queensland and was previously used in several studies, including Chanson and Carosi (2007a). The conductivity probe is a phase-detection intrusive probe designed to pierce the bubbles. Its principle is based on the difference in electrical resistance between air and water (Crowe at al. 1998; Chanson 2002). The dual-tip probe was excited by an electronic system (Ref. UQ82.518) designed with a response time of less than 10 μs. During the experiments, each probe sensor was sampled at 20 kHz for 45 s. The sampling rate and duration were selected based upon the outcomes of sensitivity analysis performed with phase-detection conductivity probes (Chanson 2006, 2007b). Depending upon the Froude number, three to four vertical profiles were recorded at different cross-sections downstream of the jump toe. Each vertical profile contained at least 30 points. The displacement and the position of the probe in the vertical direction were controlled by a fine adjustment system connected to a Mitutoyo™ digimatic scale unit with a vertical accuracy Δy of less than 0.1 mm.

The analysis of the probe voltage output was based upon a single threshold technique, with a threshold set between 45 and 55% of the air–water voltage range. Below this threshold, the probe was in air whereas it was in water for larger voltage output voltages. The single-threshold technique is a robust method that is well suited to free-surface flows (Toombes 2002; Chanson and Carosi 2007b). The error on the void fraction was expected to be 1% using this technique.

For each experiment, the foot of the jump, or jump toe, was fixed at x 1 = 0.75 m and the upstream flow depth was d 1 = 0.018 m. Based on previous experiments made with the same experimental facility, the inflow was characterised by a partially-developed boundary layer. Further details on the experimental setup and results were reported in Murzyn and Chanson (2007).

3 Experimental results

The hydraulic jump flow was a sudden transition from rapid to fluvial flow motion characterised by the development of large-scale turbulence, surface waves and air entrainment. Air bubbles were entrained at the jump toe into a free shear layer characterised by intensive turbulence production (Figs. 1, 2). The entrained air packets were broken up in very small air bubbles as they were advected in the developing shear region. Once the bubbles were convected into regions of lesser shear, bubble collisions and coalescence led to larger air entities (bubbles, pockets) that were driven by buoyancy upwards to the free surface. In the recirculation region above the mixing layer, strong unsteady flow reversals occurred.

Vertical profiles of void fraction C and bubble count rate F were measured at different longitudinal positions 4.1 < (x–x 1)/d 1 < 34. Figures 3 and 4 present some typical results, where the present data are compared with the earlier data of Chanson (2006). In the developing shear layer, the data compared favourably with an analytical solution of the advective diffusion equation for air bubbles (Chanson 1997):

$$ C = C_{{\max }} \exp {\left( { - \frac{{{\left( {{\left( {y - y_{{C_{{\max }} }} } \right)}/d_{1} } \right)}^{2} }} {{4D^{*} {\left( {x - x_{1} } \right)}/d_{1} }}} \right)} $$
(5)

where C max is the maximum void fraction in the shear layer, \( Y_{{C_{{\max }} }} \) is the vertical elevation of the maximum void fraction C max, D′ is a dimensionless turbulent diffusivity: D′ = D t/(V 1 d 1), D t is the air bubble turbulent diffusivity. Equation (5) is compared with some data in Figs. 3a, 4a and c. The peak of void fraction C max was clearly marked for most investigated conditions (Table 1), but at the lowest Reynolds numbers for Fr 1 = 5.1.

Fig. 3
figure 3

Dimensionless distributions of void fraction and bubble count rate in the hydraulic jump for Fr 1 = 5.1, x 1/d 1 = 42, W/d 1 ≥ 20 and (x–x 1)/d 1 = 8, Re = 25,000, 38,000 and 68,000—data: Chanson (2006) and present study (Re = 38,000). a Void fraction data—comparison with Eq. (5) (solid line). b Dimensionless bubble count rate data F d 1/V 1

Full size image
Fig. 4
figure 4

Dimensionless distributions of void fraction and bubble count rate in the hydraulic jump for Fr 1 = 8.5, x 1/d 1 = 42, W/d 1 ≥ 20 and Re = 38,000, 62,000 and 98,000—data: Chanson (2006) and present study (Re = 62,000). a (x–x 1)/d 1 = 12, void fraction data—comparison with Eq. (5) (solid line). b (x–x 1)/d 1 = 12, bubble count rate data F d 1/V 1. c (x–x 1)/d 1 = 17, void fraction data—comparison with Eq. (5) (solid line). d (x–x 1)/d 1 = 17, bubble count rate data F d 1/V 1

Full size image

Figures 3b, 4b and d present some typical vertical distributions of dimensionless bubble count rate F d 1/V 1. The bubble count rate F is defined the number of air bubbles detected by the probe-leading sensor per unit time and it is proportional to the specific air–water interface area. All the data exhibited a major peak of bubble count rate F max in the developing shear region. It is suggested that this peak was linked with high levels of turbulent shear stresses that break up the entrained air bubbles into finer air entities. Figure 4 shows further some results at two dimensionless longitudinal positions. A comparison between Fig. 4a and c, and between Fig. 4b and d, illustrates the de-aeration of the flow with increasing distance from the jump toe.

Figure 5 shows some dimensionless bubble chord time probability distribution functions in the developing shear layer. The data were recorded at the location where the bubble count rate was maximum (F = F max). For each figure, the caption provides the location ((x–x 1)/d 1, y/d 1), local air–water flow properties (C, F), and number of recorded bubbles N ab. The bubble chord time was proportional to the bubble chord length and inversely proportional to the velocity. Small bubble chord times corresponded to small bubbles passing rapidly in front the probe sensor, while large chord times implied large air packet flowing slowly past the probe sensor. For intermediate chord times, there were a wide range of possibilities in terms of bubble sizes depending upon the bubble velocity. The present results showed a number of typical trends: (a) a broad spectrum of bubble chord time at each location, (b) a preponderance of small bubble chord times relative to the mean with a shape that followed in average a log—normal distribution, and (c) a similar shape at most vertical elevation y/d 1 in both shear and recirculation regions.

Fig. 5
figure 5

Dimensionless probability distribution functions of bubble chord time \( t_{{{\text{ch}}}} {\sqrt {g/d_{1} } } \) in the developing shear layer of hydraulic jumps at F = F max for x 1/d 1 = 42, W/d 1 ≥ 20 and Re = 38,000, 62,000, 98,000—data: Chanson (2006) and present study (Re = 62,000)

Full size image

4 Dynamic similarity in air–water flow properties

The present experiments were compared with the earlier data sets of Chanson (2006). The three data sets were designed to be geometrically similar based upon a Froude similitude with undistorted scale (Table 1). The geometric scaling ratio was L scale = 2.0 between the largest and smallest series of experiments (d 1 = 0.024 and 0.012 m, respectively), where L scale is the geometric scaling ratio defined as the ratio of prototype to model dimensions, and L scale = 1.33 between the largest series of experiments and the present data set (d 1 = 0.024 and 0.018 m, respectively). Similar experiments were conducted for two inflow Froude numbers Fr 1 = 5 and 8.5 with identical upstream distance x 1/d 1 between gate and jump toe, and with Reynolds numbers ranging from 25,000 to 98,000. For a given Froude number, the two-phase flow measurements were performed in the developing air–water flow region at identical cross-sections (x–x 1)/d 1 ≤ 34.

Typical comparative results are presented in Figs. 3, 4 and 5. The data showed drastic scale effects in the smaller hydraulic jumps in terms of void fraction and bubble count rate distributions. The results highlighted consistently a more rapid de-aeration of the jump roller with decreasing Reynolds number for a given inflow Froude number, an absence of self-similarity of the void fraction profiles in the developing shear layer for Re < 40,000 and Fr 1 = 5 (Fig. 3a), and an increasing dimensionless bubble count rate with increasing Reynolds number for a given inflow Froude number (Figs. 3b, 4b). In Fig. 3a, the distributions of void fraction in the shear layer followed Eq. (5) for Re = 68,000 but were basically flat for Re = 25,000 and 38,000. The bubble chord time distributions were not scaled according to a Froude similitude. Comparatively larger bubble chord times were observed at low Reynolds numbers (Fig. 5a, b).

The effects of the Reynolds number on the two-phase flow properties were particularly marked in the developed shear layer. This is illustrated in Fig. 6 showing the maximum void fraction C max and maximum dimensionless bubble count rate F max d 1/V 1 in the shear layer as functions of the inflow Reynolds number Re. Figure 6a presents the relationship between C max and Re, and Fig. 6b shows the variation of F max d 1/V 1 with Re. The results highlighted some monotonic increase in maximum void fraction and maximum dimensionless bubble count rate in the mixing layer with increasing Reynolds number. The rate of increase was about the same for both inflow Froude numbers Fr = 5 and 8.5. Further no asymptotic limit was observed within the range of the experiments (Table 1). The relationships in maximum void fraction and bubble count, and Reynolds number were correlated by:

$$ C_{{\max }} = \frac{{0.745Re}} {{Re + 1.20 \times 10^{5} }}\quad 2 \times 10^{4} < Re < 10^{5} $$
(6)
$$ \frac{{F_{{\max }} d_{1} }} {{V_{1} }} = 0.73 \times Ln(Re) - 7.38\quad 2 \times 10^{4} < Re < 10^{5} $$
(7)

with a normalised coefficient of correlation of 0.978 and 0.984, respectively.

Fig. 6
figure 6

Effects of the inflow Reynolds number on the maximum void fraction C max and maximum dimensionless bubble count rate F max d 1/V 1 in the developing shear layer—data: Chanson (2006) and present study. a Maximum void fraction C max—comparison with Eq. (6). b Maximum bubble count rate F max d 1/V 1—comparison with Eq. (7)

Full size image

The comparative analysis highlighted that (1) the experimental data obtained with Re = 25,000 could not be scaled up to Re = 98,000, and that (2) the data sets with Reynolds numbers up to 98,000 could not be extrapolated to large-size prototype structures without significant scale effects in terms of void fraction and bubble count rate distributions. This result has important implications in terms of civil, environmental and sanitary engineering design. In hydraulic structures, storm water systems and water treatment facilities, hydraulics jumps operate typically with inflow Reynolds numbers ranging from 106 to over 108.

5 Conclusion

Detailed air–water flow measurements were conducted in hydraulic jumps with partially developed inflow conditions. The void fraction distributions showed the presence of an advective shear layer in which the air concentration distributions followed an analytical solution of the diffusion equation, while the bubble count rate distributions exhibited a marked maximum in the mixing layer. Similar experiments were conducted with identical inflow Froude numbers (Fr 1 = 5 and 8.5) and Reynolds numbers between 24,000 and 98,000 (Table 1). The results of Froude-similar experiments showed some drastic scale effects in the smaller hydraulic jumps in terms of void fraction, bubble count rate and bubble chord time distributions. Void fraction distributions implied comparatively greater detrainment at low Reynolds numbers yielding to lesser overall aeration of the jump roller, while an absence of self-similarity was observed for Fr 1 = 5 and Re < 40,000. The dimensionless bubble count rates were significantly lower at low Reynolds numbers, especially in the mixing layer. The bubble chord times were comparatively larger at low Reynolds numbers.

In a physical model, the flow conditions are said to be similar to those in the prototype if the model displays similarity of form, similarity of motion and similarity of forces. Equation (1) highlighted that the study of air bubble entrainment in hydraulic jumps required a large number of relevant parameters. The present comparative analysis demonstrated quantitatively that dynamic similarity of two-phase flows in hydraulic jumps cannot be achieved with a Froude similitude unless working at full-scale (1:1). In experimental facilities with Reynolds numbers up to 105, some viscous scale effects were observed in terms of the rate of entrained air, air–water interfacial area and bubble size populations.