Introduction

Nanomaterials have emerged as a potential element in numerous researches of modern science and technology. Nanomaterials [1] can be distinguished from their bulk counterparts by their exceptional properties such as high strength and stiffness, high thermal conductivity, etc. Because of these properties, nanomaterials become a very attractive component in the application of nano-scale electromechanical systems. During this application, nanomaterials are subjected to various forces such as compression, tension, and vibration. To overcome the adverse effects of these forces, effective modeling is very essential. The classical linear theory of elasticity is not sufficient for the analysis of nanomaterials, because this theory cannot incorporate the small-scale effect [2]. Therefore, researchers extensively used two different types of gradient elasticity theories [3,4,5,6,7,8] such as strain gradient theory and stress gradient theory. In strain gradient theory, the material response at a point depends not only on the classical strain but also on the strain gradients of differential orders. On the other hand, in stress gradient theory, the material response depends on the stress as well as on the stress gradients up to some orders. Nonlocal elasticity theory is one of the forms of stress gradient theory. Generally, the nonlocal elasticity theory is an integro-differential equation whose solution is difficult. Eringen [9] proposed equivalent differential nonlocal elasticity which has been widely accepted to analyze the nanomaterials.

In this paper, an axially graded [10,11,12,13] beam is considered as a kind of nonhomogeneous beam where the material properties are varying along the x-axis exponentially. The axially graded beam [14,15,16] is a type of composite where the material properties are varying smoothly from one end to another end for eliminate the stress concentration at any specific cross-section. The demand for new advanced materials is increasing day by day. The axially functionally graded material is one of the exceptional innovations of recent science and technology that satisfy the growing demand for advanced materials having essential properties for high-quality design. In addition, these materials are a special type of composite that can mitigate the disadvantage of conventional composites.

In most cases, the thermal effect [17,18,19] is ignored in the research. A small change in temperature can change the dynamic behavior of the beam which may cause the failure of the beam. When heat is applied to a body, it stores energy in its atom as kinetic energy that increases the vibration of the atom against the intermolecular forces. Due to this vibration, atoms move away from each other which increases the material size. Due to the rise in temperature, expansion occurs. On the other hand, contraction occurs because of loss of temperature. This expansion or contraction is proportional to the change in temperature. This proportionality can be expressed as linear thermal expansion of the material. According to the assumption of thermo-elasticity, thermal strain can be added with mechanical strain linearly. That is why, the equation of equilibrium is compatible with the thermal load.

A crack is a newly created surface that partially separates the body. Crack is not only a common defect but also very difficult to control [20]. Multiple cracks also can occur in nanomaterials. Formulation of multiple cracks problem is difficult and analysis is time-consuming. Cracks can decrease stiffness and reduce the natural frequency [21,22,23,24,25,26]. Therefore, cracks affect the dynamic behaviors of structures significantly. Cracks can be detected by modal parameters, such as natural frequencies, mode shapes, and damping factors [27]. The mode shape of the vibration of nanomaterials is significantly changed by the presence of cracks. Mode shape is one of the popular techniques to detect a crack [28, 29]. The mode shape diagram is very sensitive to cracks. The lower mode shape is less sensitive than the higher mode shape. Mode shape also explains the effects of crack severity very effectively.

The vibration of nanobeam has been analyzed using several techniques. Roostai and Haghpanahi [30] studied the vibration of nanobeam with multiple cracks. They applied a modified exact solution technique to analyze the multi-cracked nanobeam. Similarly, Loghmani and Yazdi [31] examined the vibration of multi-cracked and stepped nanobeams. They employed the wave approach to analyze their model. Aria et al. [32] investigated the thermal vibration of cracked nanobeams on an elastic matrix. They described the effectiveness of the finite-element method to analyze the model. Esen et al. [33] represented free vibration of cracked FG microbeam embedded in elastic matrix with magnetic and thermal effect. They scrutinized this problem using the analytical method. Their results showed that the magnetic field could be used to eliminate the negative effects of the temperature. Basically, the exact solution technique, perturbation method [34, 35], differential quadrature method [36, 37], and differential transform method [38-40] are very popular among researchers to investigate the dynamic behavior of beams. Similarly, the power series solution technique [41] has been used by a limited number of researchers for analyzing the dynamic problem of structures. However, this technique is rare to study the multi-cracked nanobeam.

In this paper, the power series solution technique is applied to investigate the effects of crack severity, crack location, nonhomogeneity, thermal effect, nonlocal parameter, and different boundary conditions on the vibration of axially graded multi-cracked nanobeams. The governing equation is derived by applying the Euler–Bernoulli beam theory and the theory of nonlocal elasticity. The beam is considered axially graded from one end to another end. Thermal load is also applied axially. Multiple stable and open cracks are considered on the beam where each crack is replaced by a rotational spring for modeling. Mode shape diagrams are also analyzed to describe the effect of nonhomogeneity and thermal load on the vibration of cracked nanobeams. In this paper, the effects of single and multiple cracks, location of cracks, nonhomogeneity, temperature, and nonlocal parameter on the vibration of nanobeams are studied. The outcomes of this analysis are examined with the outcomes of other researchers in the existing literature.

Mathematical Model

Description of the Problem

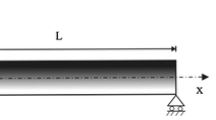
The geometry of an axially graded multi-cracked nanobeam is illustrated in Fig. 1. The left endpoint of the beam is located at the origin of the coordinate system. The neutral axis of the beam overlaps with the x-axis and the height of the beam is placed along the z-axis. L, b, and h describe the length, width, and height of the beam, respectively. Multiple open cracks are considered at the distance of \(a_i\) to \(a_n\) from the left endpoint. The material of the beam is axially graded along the x-axis. E and \(\rho\) are the elasticity and density varying exponentially from one end to another end. The objective of this analysis is to examine the natural vibration of axially graded multi-cracked nanobeams.

Fig. 1
figure 1

An axially graded multi-cracked nanobeam

Full size image

Beam Theory with Nonlocal Elasticity

Euler–Bernoulli beam theory is extensively acceptable to the researcher to analyze the structural elements. This theory is based on some assumptions [42,43,44] such as cross-sections of the beam are plane and perpendicular to the neutral axis during bending, transverse deformation is considered very small and shear deformation is neglected, and the beam is linearly elastic based on Hooke’s law. According to the Euler–Bernoulli theory, the displacement fields [45] can be expressed as

$$\begin{aligned} V_1(x,z,t)=V(x,t)-z \frac{\partial W(x,t)}{\partial x} \end{aligned}$$
(1)
$$\begin{aligned} V_2(x,z,t)=0 \end{aligned}$$
(2)
$$\begin{aligned} V_3(x,z,t)=W(x,t), \end{aligned}$$
(3)

where \(V_1\), \(V_2\), and \(V_3\) express the deflection in x, y, and z axis, respectively, and W(x, t) and V(x, t) define the transverse and axial deflection, respectively. One can write the axial strain as

$$\begin{aligned} \varepsilon _{xx}=\frac{\partial V}{\partial x}-z \frac{\partial ^2 W}{\partial x^2}. \end{aligned}$$
(4)

Considering axial load N and moment M, the Euler–Bernoulli equation for vibration can be presented as

$$\begin{aligned} \frac{\partial ^2 M}{\partial x^2}+ \frac{\partial }{\partial x} \left(N \frac{\partial W}{\partial x}\right) -m_0 \frac{\partial ^2 W}{\partial t^2} =0, \end{aligned}$$
(5)

where \(m_0=\rho A\) is the mass per unit length. However, this theory directly is not applicable to nanomaterials. The physical properties of nano-scale materials are different from macro-materials. To incorporate this scale effect, Eringen proposed the nonlocal theory of elasticity. According to his theory, the stress–strain relationship [46, 47] for a three-dimensional isotropic elastic solid can be expressed as

$$\begin{aligned} \sigma _{ij}(x)=\int _{V} \alpha (\mid x-x^\prime \mid ,\tau ) t_{ij}(x^\prime ) dV(x^\prime ), \end{aligned}$$
(6)

where

$$\begin{aligned} t_{ij}(x^\prime )=\psi \varepsilon _{rr} (x^\prime ) \delta _{ij}+2\phi \varepsilon _{ij}(x^\prime ), \end{aligned}$$
(7)

where \(\psi\) and \(\phi\) represent Lame’s constants. \(t_{ij}(x^\prime )\) and \(\varepsilon _{ij}(x^\prime )\) are the classical stress tensor and linear strain tensor at any point \(x^\prime\) in the body, respectively. \(\alpha (\mid x-x^\prime \mid , \tau )\) represents the nonlocal modulus to indicate the nonlocal effects into the constitutive equation for the reference point x and source point \(x^\prime\), respectively. In Eq. (6), \(\mid x^\prime -x \mid\) represents the Euclidean distance and \(\tau\) can be presented as

$$\begin{aligned} \tau = \frac{e_0 a}{l}; \end{aligned}$$
(8)

\(\tau\) is a constant that indicates the ratio of internal and external characteristic length of the nanomaterial, where \(e_0\) is the material constant. According to the theory of nonlocal elasticity, the integral constitutive relations can be transformed into the equivalent differential equation by substituting the kernel \(\alpha (\mid x^\prime -x \mid ,\tau )\) as below

$$\begin{aligned} (1-(e_0a)^2 \Delta ^2) \sigma _{kl} = t_{kl}, \end{aligned}$$
(9)

where \(\Delta ^2\) indicates the Laplacian operator. Nonlocal theory depends on internal characteristic length a. When a becomes zero, the nonlocal constitutive relations transform to the classical theory of elasticity. In the one-dimensional case, the nonlocal stress–strain relationship can be presented as

$$\begin{aligned} \sigma (x)-(e_0a)^2 \frac{\partial ^2 \sigma (x)}{\partial x^2} =E \varepsilon (x), \end{aligned}$$
(10)

where \(\sigma (x)\) and \(\varepsilon (x)\) represent the stress and strain along the x-axis. Therefore, the nonlocal elasticity theory can be presented in terms of bending moment M, as follows:

$$\begin{aligned} M - (e_0a)^2 \frac{\partial ^2 M}{\partial x^2} = EI \left(-\frac{\partial ^2 W}{\partial x^2}\right). \end{aligned}$$
(11)

Combining the nonlocal theory (11) and Euler–Bernoulli theory (5) can be presented as

$$\begin{aligned} \begin{aligned} \frac{\partial ^2}{\partial x^2} \left(EI \frac{\partial ^2 W}{\partial x^2}\right) - (e_0a)^2 \frac{\partial ^2}{\partial x^2} \left[\rho A \frac{\partial ^2 W}{\partial t^2}- \frac{\partial }{\partial x} \left(N \frac{\partial W}{\partial x}\right)\right] \\ -\frac{\partial }{\partial x} \left(N \frac{\partial W}{\partial x}\right) + \rho A \frac{\partial ^2 W}{\partial t^2} =0. \end{aligned} \end{aligned}$$
(12)

Axially Graded Beam

An axially graded beam is a type of composite element that can avoid the point of stress concentration. It distributes stress gradually from one end to another end. Over the cross-section, the material properties are constant. Modulus of elasticity E and density \(\rho\) are varying along the length exponentially [48, 49]. These can be expressed as

$$\begin{aligned} E=E_0 e^{\lambda \frac{x}{L}}, \rho =\rho _0 e^{\lambda \frac{x}{L}}, \end{aligned}$$
(13)

where \(E_0\) and \(\rho _0\) are the modulus of elasticity and density at the point \(x=0\), and \(\lambda\) is the coefficient of nonhomogeneity.

Thermal Load

Thermal load is created by the contraction and expansion of the material due to the temperature change. This load act as an axial load on the beam element. Thermal load [50] can be expressed as

$$\begin{aligned} N=-EA\alpha _t \theta . \end{aligned}$$
(14)

Considering the varying modulus of elasticity, the thermal load can be presented as

$$\begin{aligned} N=-E_0 e^{\lambda \frac{x}{L}} A \alpha _t \theta , \end{aligned}$$
(15)

where \(\alpha _t\) is the coefficient of thermal expansion. According to the theory of Zarzycki 1982 and Kittel 1983 [51], the coefficient of thermal expansion can be presented as

$$\begin{aligned} \alpha _t=\frac{\gamma _G \rho c_V}{3E}, \end{aligned}$$
(16)

where \(\gamma _G\) is the Grüneisen constant. Here, \(\alpha _t\) depends on density and modulus of elasticity. Both of these parameters are varying equally along the x-axis. Therefore, \(\alpha _t\) is constant over the length.

Modeling of Cracks

The mechanical properties of multiple open and stable cracks can be analyzed using the classical local stiffness model. According to this model, the beam is separated into two sub-beams for each crack at the crack position. Every crack in the beam is replaced by a mass-less rotational spring that connects the two neighboring segments together. In this model, the crack creates a discontinuity in the rotational angle at the location of the crack. Due to the presence of a crack, the beam achieves additional strain energy to the rotational spring. Strain energy is the result of bending moment and axial stress. The change of strain energy [32] can be presented as

$$\begin{aligned} \Delta s_c = \frac{1}{2} M \Delta \theta + \frac{1}{2} N \Delta u, \end{aligned}$$
(17)

where M and N represent the bending moment and axial load respectively. \(\Delta \theta\) indicates the rotational angle because of the spring and \(\Delta u\) represents the axial displacement at the location of the crack. Therefore, these can be expressed as

$$\begin{aligned}&\Delta \theta = K_{MM} \frac{\partial ^2 W}{\partial x^2}+K_{MN} \frac{\partial U}{\partial x} \end{aligned}$$
(18)
$$\begin{aligned}&\quad \Delta u = K_{NN} \frac{\partial U}{\partial x} + K_{NM} \frac{\partial ^2 W}{\partial x^2}, \end{aligned}$$
(19)

where \(K_{MM}\), \(K_{MN}\), \(K_{NN}\), and \(K_{NM}\) are the flexibility constants. When the beam is subjected to transverse vibration, longitudinal displacement \(\Delta u\) and the flexibility constants \(K_{MN}\), \(K_{NN}\), and \(K_{NM}\) are very small which can be neglected. Therefore, the discontinuity at the location of the crack can be expressed as

$$\begin{aligned} \Delta \theta = \frac{K_{MM}}{L} \frac{\partial ^2 W(x)}{\partial x^2} \mid _{x=a}, \end{aligned}$$
(20)

where \(\frac{K_{MM}}{L}\) can be replaced by K as

$$\begin{aligned} \Delta \theta = K \frac{\partial ^2 W(x)}{\partial x^2} \mid _{x=a}; \end{aligned}$$
(21)

here, K is the crack severity. The crack severity depends on the crack depth and rotational spring stiffness. It can be expressed as follows [52]:

$$\begin{aligned} K= \frac{EI}{L} \frac{1}{\kappa _s}, \end{aligned}$$
(22)

where \(\kappa _s\) is the spring stiffness. It can be written as

$$\begin{aligned} \kappa _s = \frac{EI}{h} \frac{1}{C(\gamma )}; \end{aligned}$$
(23)

here, \(\gamma =\frac{d_{cr}}{h}\) is the crack depth and beam height ratio. \(C(\gamma )\) is the local compliance that can be computed from the strain energy density function as follows:

$$\begin{aligned} \begin{aligned} C(\gamma )&=5.346 ( 1.86\gamma ^2-3.95\gamma ^3+16.375\gamma ^4-37.226\gamma ^5 \\&\quad + 76.81\gamma ^6 \\&\quad -126.9\gamma ^7+172\gamma ^8-143.97\gamma ^9+66.56\gamma ^{10}). \end{aligned} \end{aligned}$$
(24)

Crack severity can be written from Eqs. (22) and (23) as

$$\begin{aligned} K=\frac{h}{L} C(\gamma ). \end{aligned}$$
(25)

Crack severity does not depend on the modulus of elasticity and density of the beam. Therefore, crack severity (K) is constant over the length of the axially graded beam.

Derivation of Governing Equation

In this paper, the beam is axially graded and also subjected to thermal load. Therefore, the material properties such as elasticity and density are varying along the x-axis. Similarly, the thermal load is also varying as an axial load. Considering these variations, Eq. (12) can be expressed as

$$\begin{aligned} \begin{aligned}&\frac{\partial ^2}{\partial x^2} \left(E(x)I\frac{\partial ^2W}{\partial x^2}\right) - (e_0a)^2 \frac{\partial ^2}{\partial x^2} \\&\quad \left[\rho (x)A \frac{\partial ^2W}{\partial t^2} - \frac{\partial }{\partial x} \left(N(x)\frac{\partial W}{\partial x}\right)\right] \\&\quad -\frac{\partial }{\partial x} \left(N(x)\frac{\partial W}{\partial x}\right)+\rho (x)A \frac{\partial ^2 W}{\partial t^2}=0. \end{aligned} \end{aligned}$$
(26)

Applying the variable separation technique, deflection can be presented as

$$\begin{aligned} W(x,t)=\bar{W} (x) e^{i\omega _ct}. \end{aligned}$$
(27)

Using the above function (27), the partial differential form (26) can be converted into the ordinary differential equation as

$$\begin{aligned} \begin{aligned}&\frac{d^2}{dx^2}(E(x)I \frac{d^2 \bar{W}}{dx^2})+(e_0a)^2 \frac{d^2}{dx^2}(\rho (x)A{\omega _c}^2\bar{W})\\&\quad +(e_0a)^2 \frac{d^3}{dx^3} \left(N(x)\frac{d\bar{W}}{dx}\right) \\&\quad -\frac{d}{dx} \left(N(x)\frac{d\bar{W}}{dx}\right)-\rho (x)A{\omega _c}^2\bar{W}=0. \end{aligned} \end{aligned}$$
(28)

Applying the conditions of nonhomogeneity and thermal effect from (13), (15), then Eq. (28) can be written as

$$\begin{aligned} \begin{aligned}&E_0I \frac{d^2}{dx^2} \left(e^{\lambda \frac{x}{L}}\frac{d^2\bar{W}}{dx^2}\right)+(e_0a)^2\\&\quad \rho A {\omega _c}^2 \frac{d^2}{dx^2}(e^{\lambda \frac{x}{L}}\bar{W}) \\&\quad -(e_0a)^2 E_0A\alpha _t\theta \frac{d^3}{dx^3} \left(e^{\lambda \frac{x}{L}}\frac{d\bar{W}}{dx}\right) \\&\quad +E_0A\alpha _t\theta \frac{d}{dx} \left(e^{\lambda \frac{x}{L}}\frac{d\bar{W}}{dx}\right) \\&\quad -\rho _0 e^{\lambda \frac{x}{L}}A{\omega _c}^2\bar{W}=0. \end{aligned} \end{aligned}$$
(29)

After differentiating (29), it can be written as

$$\begin{aligned} \begin{aligned}&E_0I \left(\frac{\lambda ^2}{L^2}\frac{d^2 \bar{W}}{dx^2}+2 \frac{\lambda }{L} \frac{d^3 \bar{W}}{dx^3}+\frac{d^4 \bar{W}}{dx^4}\right)\\&\quad +(e_0a)^2\rho _0A{\omega _c}^2 \left(\frac{\lambda ^2}{L^2}\bar{W}+2\frac{\lambda }{L} \frac{d\bar{W}}{dx^2}\right) \\&\quad - (e_0a)^2 E_0A\alpha _t\theta (\frac{\lambda ^3}{L^3}\frac{d\bar{W}}{dx}\\&\quad +3\frac{\lambda ^2}{L^2}\frac{d^2\bar{W}}{dx^2}+3\frac{\lambda }{L}\frac{d^3\bar{W}}{dx^3}+\frac{d^4\bar{W}}{dx^4}) \\&\quad +E_0A\alpha _t\theta \left(\frac{\lambda }{L}\frac{d\bar{W}}{dx}+\frac{d^2 \bar{W}}{dx^2}\right)-\rho _0A{\omega _c}^2\bar{W}=0 \end{aligned} \end{aligned}$$
(30)

The nondimensional parameters can be introduced as follows:

$$\begin{aligned}&\xi =\frac{x}{L}, w=\frac{\bar{W}}{L}, \mu =\frac{e_0a}{L}, n=\frac{E_0A\alpha _t\theta L^2}{E_0I},\\&\quad \omega ^2=(\bar{\omega })^4={\omega _c}^2 L^4 \frac{\rho _0 A}{E_0I}. \end{aligned}$$

Using the nondimensional parameters, Eq. (30) can be transformed as

$$\begin{aligned} \begin{aligned}& \left(\lambda ^2 \frac{d^2w}{d \xi ^2}+2 \lambda \frac{d^3w}{d \xi ^3}+\frac{d^4w}{d \xi ^4}\right)\\&\quad +\mu ^2 \omega ^2 \left(\lambda ^2 w+2 \lambda \frac{d w}{d \xi }+ \frac{d^2 w}{d \xi ^2}\right) \\&\quad -\mu ^2 n (\lambda ^3 \frac{d w}{d \xi }+3 \lambda ^2 \frac{d^2 w}{d \xi ^2}\\&\quad +3 \lambda \frac{d^3 w}{d \xi ^3}+ \frac{d^4 w}{d \xi ^4})+n \left(\frac{dw}{d\xi }+\frac{d^2 w}{d \xi ^2}\right)-\omega ^2 w=0 \end{aligned} \end{aligned}$$
(31)

Therefore, Eq. (31) can be presented in a simplified form as

$$\begin{aligned} \frac{d^4w}{d\xi ^4}+\beta _1 \frac{d^3w}{d\xi ^3}+\beta _2 \frac{d^2w}{d\xi ^2}+\beta _3 \frac{dw}{d\xi}+\beta _4 w=0, \end{aligned}$$
(32)

where

$$\begin{aligned} \begin{aligned} \beta _1=\frac{2\lambda -2\lambda \mu ^2n}{1-\mu ^2n}, \beta _2=\frac{\lambda ^2+\mu ^2\omega ^2-3\mu ^2n\lambda ^2+n}{1-\mu ^2n}, \\ \beta _3=\frac{2\mu ^2\omega ^2\lambda -\mu ^2n\lambda ^3+n}{1-\mu ^2n}, \beta _4=\frac{\mu ^2\omega ^2\lambda ^2-\omega ^2}{1-\mu ^2n}. \end{aligned} \end{aligned}$$

In this nanobeam, multiple cracks are considered where n number of cracks separates the beam into \(n+1\) segments. Finally, the governing equations for \(n+1\) number of segments can be expressed as

$$\begin{aligned} \frac{d^4 w_i}{d \xi ^4}+\beta _1 \frac{d^3 w_i}{d \xi ^3}+\beta _2 \frac{d^2 w_i}{d \xi ^2}+\beta _3 \frac{d w_i}{d \xi }+\beta _4 w_i=0, \end{aligned}$$
(33)

where \(i=1, 2, 3, ..., n+1\). Equation (33) represents the set of governing equations considering the \(n+1\) segments that are separated at the location of cracks \(a_j\). Where \(j=1, 2, ..., n\). Boundary conditions for the beam can be presented as follows:

For the simply supported beam:

$$\begin{aligned} w_1(0)=0, \frac{d^2 w_1(0)}{d\xi ^2}=0, w_{n+1}(1)=0,\frac{d^2 w_{n+1}(1)}{d\xi ^2}=0. \end{aligned}$$

For the fully clamped beam:

$$\begin{aligned} w_1(0)=0, \frac{d w_1(0)}{d\xi }=0, w_{n+1}(1)=0,\frac{d w_{n+1}(1)}{d\xi }=0. \end{aligned}$$

For the clamped simply beam:

$$\begin{aligned} w_1(0)=0, \frac{d w_1(0)}{d\xi }=0, w_{n+1}(1)=0,\frac{d^2 w_{n+1}(1)}{d\xi ^2}=0. \end{aligned}$$

For the clamped free beam:

$$\begin{aligned} w_1(0)=0, \frac{d w_1(0)}{d\xi }=0, \frac{d^2 w_{n+1}(1)}{d^2\xi } =0,\frac{d^3 w_{n+1}(1)}{d\xi ^3}=0. \end{aligned}$$

In-between conditions at the location of cracks are as follows:

$$\begin{aligned}&w_i(a_i)-w_{i+1}(a_i)=0 \\&\quad \frac{d w_i(a_i)}{d\xi }+K\frac{d^2 w_i(a_i)}{d\xi ^2}-\frac{d w_{i+1}(a_i)}{d\xi }=0 \\&\quad \frac{d^2 w_i(a_i)}{d\xi ^2}-\frac{d^2 w_{i+1}(a_i)}{d\xi ^2}=0 \\&\frac{d^3 w_i(a_i)}{d\xi ^3}+\mu ^2\omega ^2\frac{d w_{i}(a_i)}{d\xi }-\frac{d^3 w_{i+1}(a_i)}{d\xi ^3}\\&\quad -\mu ^2\omega ^2\frac{d w_{i+1}(a_i)}{d\xi } =0. \end{aligned}$$

One can solve these equations (33) by applying in-between conditions at the crack locations and any one set of end conditions for the boundary supports.

Power Series Solution

The power series solution [41] is a semi-analytical technique. In this technique, a power series is considered as a solution of the function. Therefore, the differential equation transforms into a set of algebraic equations. Linear, and nonlinear differential equations can be solved using the power series solution technique. Let us consider a series for the deflection of the beam as

$$\begin{aligned} w=\sum _{k=0}^{\infty } A_k \xi ^k. \end{aligned}$$
(34)

Similarly, derivatives of deflection can be written as

$$\begin{aligned} \frac{dw}{d\xi }= & {} \sum _{k=1}^{\infty }k A_k \xi ^{k-1} \end{aligned}$$
(35)
$$\begin{aligned} \frac{d^2w}{d\xi ^2}= & {} \sum _{k=2}^{\infty }k(k-1) A_k \xi ^{k-2} \end{aligned}$$
(36)
$$\begin{aligned} \frac{d^3w}{d\xi ^3}= & {} \sum _{k=3}^{\infty }k(k-1)(k-2) A_k \xi ^{k-3} \end{aligned}$$
(37)
$$\begin{aligned} \frac{d^4w}{d\xi ^4}= & {} \sum _{k=4}^{\infty }k(k-1)(k-2)(k-3) A_k \xi ^{k-4}. \end{aligned}$$
(38)

Substituting above derivatives into Eq. (33) as follows:

$$\begin{aligned} \begin{aligned}&\sum _{k=4}^{\infty } k(k-1)(k-2)(k-3) A_k \xi ^{k-4}\\&\quad +\beta _1 \sum _{k=3}^{\infty } k(k-1)(k-2) A_k \xi ^{k-3} \\&\quad +\beta _2 \sum _{k=2}^{\infty }k(k-1)A_k\xi ^{k-2}\\&\quad +\beta _3 \sum _{k=1}^{\infty } k A_k \xi ^{k-1} +\beta _4 \sum _{k=0}^{\infty } A_k \xi ^k =0. \end{aligned} \end{aligned}$$
(39)

Shifting the power of \(\xi\), Eq. (39) can be written as

$$\begin{aligned} \begin{aligned}&\sum _{k=0}^{\infty } (k+4)(k+3)(k+2)(k+1) A_{k+4} \xi ^{k} \\&\quad +\beta _1 \sum _{k=0}^{\infty } (k+3)(k+2)(k+1) A_{k+3} \xi ^{k}\\&\quad +\beta _2 \sum _{k=0}^{\infty }(k+2)(k+1)A_{k+2}\xi ^{k} \\&\quad +\beta _3 \sum _{k=0}^{\infty } (k+1) A_{k+1} \xi ^{k}\\&\quad +\beta _4 \sum _{k=0}^{\infty } A_k \xi ^k =0. \end{aligned} \end{aligned}$$
(40)

Equating the coefficients of \(\xi ^k\) can be expressed as

$$\begin{aligned} \begin{aligned}&(k+4)(k+3)(k+2)(k+1) A_{k+4}\\&\quad +\beta _1 (k+3)(k+2)(k+1) A_{k+3} \\&\quad +\beta _2 (k+2)(k+1)A_{k+2} +\beta _3 (k+1) A_{k+1}\\&\quad +\beta _4 A_k =0. \end{aligned} \end{aligned}$$
(41)

Simplifying Eq. (41) can be written as

$$\begin{aligned} \begin{aligned}&A_{k+4}= - \frac{\beta _1}{(k+4)} A_{k+3}\\&\quad - \frac{\beta _2}{(k+4)(k+3)} A_{k+2} \\&\quad - \frac{\beta _3}{(k+4)(k+3)(k+2)} A_{k+1}\\&\quad - \frac{\beta _4}{(k+4)(k+3)(k+2)(k+1)} A_k. \end{aligned} \end{aligned}$$
(42)

Using the above relation (42), one can calculate the series coefficients as follows:

$$\begin{aligned}&A_4=-\frac{1}{4} \beta _1 A_3 - \frac{1}{12} \beta _2 A_2 -\frac{1}{24} \beta _3 A_1 -\frac{1}{24} \beta _4 A_0 \end{aligned}$$
(43)
$$\begin{aligned}&\quad A_5=\frac{1}{20} (\beta _1^2-\beta _2)A_3 + \frac{1}{60} (\beta _1\beta _2-\beta _3) A_2 \nonumber \\&\quad +\frac{1}{120} (\beta _1 \beta _3-\beta _4) A_1 +\frac{1}{120} \beta _1 \beta _4 A_0 \end{aligned}$$
(44)
$$\begin{aligned}&\quad A_6=-\frac{1}{120} (\beta _1^3-2\beta _1 \beta _2+\beta _3)A_3 \nonumber \\&\quad - \frac{1}{360} (\beta _1^2\beta _2-\beta _1\beta _3-\beta _2^2+\beta _4) A_2 \nonumber \\&\quad -\frac{1}{720} (\beta _1^2\beta _3- \beta _1\beta _4-\beta _2\beta _3) A_1 -\frac{1}{720} (\beta _1^2\beta _4-\beta _2 \beta _4) A_0. \end{aligned}$$
(45)

Applying the series coefficients, the solution for the each segment of the beam can be written as

$$\begin{aligned} w_i=A_{i,0}+A_{i,1}\xi +A_{i,2}\xi ^2+A_{i,3}\xi ^3+\sum _{k=4}^{\infty }A_{i,k}\xi ^k, \end{aligned}$$
(46)

where \(i=1, ..., n+1\). Using the simply supported boundary conditions and intermediate conditions for cracks, one can eliminate constant coefficients (\(A_{i,k}\) ) and solve these equations to form matrix as follows:

$$\begin{aligned} \begin{bmatrix} m_{1,1} &{} ... &{} ... &{} m_{1,4(n+1)} \\ ... &{} ... &{} ... &{} ... \\ ... &{} ... &{} ... &{} ... \\ m_{4(n+1),1} &{} ... &{} ... &{} m_{4(n+1),4(n+1)} \end{bmatrix} \begin{bmatrix} A_{1,0} \\ ... \\ ... \\ A_{(n+1),3} \end{bmatrix}. \end{aligned}$$
(47)

The value of natural frequency for multi-cracked nanobeams can be determined by solving the above matrix. In this paper, single, double, and triple cracked nanobeams are analyzed.

Numerical Results and Discussion

In this section, parametric analysis is performed to scrutinize their impacts on the natural frequency of axially graded multi-cracked nanobeams in a thermal environment. First of all, the efficiency of the solution technique is measured by comparing the obtained results with the results of relevant papers in the existing literature. In addition, the influences of crack position on the various modes of natural frequency for several values of the gradient parameter are studied and presented graphically. Moreover, the effects of temperature and nonhomogeneity on the frequency ratio of intact and cracked nanobeams are illustrated. Furthermore, the effects of temperature, nonhomogeneity, and nonlocal parameter on the natural frequency are presented in tabular forms. Finally, the mode shapes are depicted to investigate the axially graded multi-cracked nanobeam with different support conditions, and to study the effects of nonhomogeneity, temperature, and a number of cracks on the transverse deflection.

Comparison of Results

In this section, the outcomes of the study are compared with the outcomes of some benchmark studies in the existing literature. This comparison is performed by investigating the effects of nonlocal parameter \((\mu )\), thermal load (n), and crack severity on different modes of natural frequency. In Table 1, the first mode of natural frequency (square root) for simply supported and fully clamped nanobeam is presented. The effect of crack is not considered as well as the beam is considered uniform and homogeneous in this section of calculation. Different values of nonlocal parameter \((\mu )\) and thermal load (n) are considered. It is understandable from these tabular data that natural frequency decreases for the increase of the nonlocal parameter. Therefore, the natural frequency increases for the decrease of temperature. Outcomes are verified with the results of Esen et al. [33] and Aria et al. [32] where they analyzed the cracked nanobeam on elastic matrix with temperature. During this comparison, specific results are selected from their paper where those data ignore the effects of crack and elastic matrix. Similarly, in Table 2, different modes of natural frequency (square root) for simply supported single cracked nanobeam are demonstrated. Nonhomogeneity of nanobeam is ignored in this section of calculation. Different values of crack positions (a), crack severity (K), and nonlocal parameter \((\mu )\) are also considered. It is comprehensible from these tabular data that the natural frequency decreases for the increase of crack severity. Frequency shows the lower value at the crack position of \(a=0.5\) than \(a=0.25\) . This table data also matched with the results of Esen et al. [33] and Aria et al. [32]. However, specific tabular data are selected from their paper where these data ignore the effect of elastic matrix and temperature. These evaluations show a good understanding of these outcomes. In Table 3, different modes of natural frequency for a double-cracked beam with different values of the nonlocal parameter and crack severity are studied. Two cracks in the beam are located at \(a_1=0.3\) and \(a_2=0.7\), respectively. It is obvious from these tabular data that frequency decreases with the increases of the nonlocal parameter. The crack severity and boundary supports also influence the values of frequency. These table data also compare with the results of Roostai and Haghpanahi [30]. This comparison shows a close match among these results.

Fig. 2
figure 2

Frequency ratio versus crack position (SS, 1st Mode)

Full size image
Fig. 3
figure 3

Frequency ratio versus crack position (SS, 2nd Mode)

Full size image
Fig. 4
figure 4

Frequency ratio versus crack position (CC, 1st Mode)

Full size image
Fig. 5
figure 5

Frequency ratio versus crack position (CC, 2nd Mode)

Full size image

Effect of Crack Locations

The crack location is also crucial like crack severity for analyzing the cracked beam. In Figs. (2, 3, 4 and 5), different modes of frequency and two different support systems such as simply supported and fully clamped nanobeam are demonstrated. Thermal load is ignored in this section of the calculation. The frequency ratio is calculated by the frequency at any point with nonhomogeneity and the frequency at the initial point without considering nonhomogeneity. In this section, nonlocal parameter \(\mu =0.1\) and crack severity \(K=0.35\) are applied. It is evident from these figures that in the case of simply supported and the first mode of frequency, the frequency ratio slightly decreases for the presence of nonhomogeneity. However, in other cases, frequency increases with the presence of nonhomogeneity. It is very important in these curves that the frequency ratio is not affected by the positive or negative sign of nonhomogeneity. The effect of crack location is also influenced by the end support systems.

Table 1 Natural frequency (square root) for varying nonlocal parameter, thermal load, and different end supports
Full size table
Table 2 Natural frequency (square root) for simply supported cracked nanobeams in different modes with varying nonlocal parameter
Full size table
Table 3 Natural frequency for double-cracked beams with different values of nonlocal parameter and crack severity
Full size table
Fig. 6
figure 6

Mode shape for different values of gradient parameter (1st mode, SS)

Full size image
Fig. 7
figure 7

Mode shape for different values of gradient parameter (1st mode, CC)

Full size image
Fig. 8
figure 8

Mode shape for different values of gradient parameter (2nd mode, SS)

Full size image
Fig. 9
figure 9

Mode shape for different values of gradient parameter (2nd mode, CC)

Full size image
Fig. 10
figure 10

Mode shape for different values of thermal load (1st mode, SS)

Full size image
Fig. 11
figure 11

Mode shape for different values of thermal load (1st mode, CC)

Full size image
Fig. 12
figure 12

Mode shape for different values of thermal load (2nd mode, SS)

Full size image
Fig. 13
figure 13

Mode shape for different values of thermal load (2nd mode, CC)

Full size image
Fig. 14
figure 14

Mode shape for double cracks and different values of crack severity (1st mode, SS)

Full size image
Fig. 15
figure 15

Mode shape for double cracks and different values of crack severity (1st mode, CC)

Full size image
Fig. 16
figure 16

Mode shape for double cracks and different values of crack severity (2nd mode, SS)

Full size image
Fig. 17
figure 17

Mode shape for double cracks and different values of crack severity (2nd mode, CC)

Full size image
Fig. 18
figure 18

Mode shape for triple cracks and different values of crack severity (1st mode, SS)

Full size image
Fig. 19
figure 19

Mode shape for triple cracks and different values of crack severity (1st mode, CC)

Full size image
Fig. 20
figure 20

Mode shape for triple cracks and different values of crack severity (2nd mode, SS)

Full size image
Fig. 21
figure 21

Mode shape for triple cracks and different values of crack severity (2nd mode, CC)

Full size image
Fig. 22
figure 22

Mode shape for double cracks and different values of nonhomogeneity (1st mode, SS)

Full size image
Fig. 23
figure 23

Mode shape for double cracks and different values of nonhomogeneity (1st mode, CC)

Full size image
Fig. 24
figure 24

Mode shape for double cracks and different values of nonhomogeneity (2nd mode, SS)

Full size image
Fig. 25
figure 25

Mode shape for double cracks and different values of nonhomogeneity (2nd mode, CC)

Full size image
Table 4 Natural frequency for triple cracked nanobeams with several values of nonlocal parameter and crack severity
Full size table
Table 5 Frequency for several values of nonlocal parameter, thermal load, and nonhomogeneity without crack
Full size table
Table 6 Frequency for several values of nonlocal parameter, thermal load, and nonhomogeneity with crack
Full size table

Frequency for Axially Graded Intact and Cracked Nanobeams Under Thermal Load

In Table 4, the natural frequency for a triple cracked beam with several values of the nonlocal parameter and crack severity is demonstrated. Three specific cracks are considered at the position of \(a_1=0.3\), \(a_2=0.5\), and \(a_3=0.7\), respectively. The effects of nonhomogeneity and temperature are not considered. It is understandable in these tabular data that the frequency decreases for the increase of the value of the nonlocal parameter and crack severity. In this section, Table 5 and Table 6 represent the effect of temperature on natural frequency for axially graded intact or cracked nanobeam, respectively. The interactions between temperature, nonhomogeneity, nonlocal parameter, end supports, and different modes of frequency of intact and cracked nanobeam are very diverse. Table 5 represents the relationship between the nonlocal parameter, thermal load, and nonhomogeneity in absence of crack. In this section, three different values of the nonlocal parameter, thermal load from − 2 to 2, and nonhomogeneity − 2 to 2 are considered. The effect of crack is ignored in this part of the calculation. It is very clear that the frequency decreases for the increase of the nonlocal parameter. On the other hand, frequency increases for the decrease of temperature. The relationship between thermal load, nonhomogeneity, and natural frequency is very fluctuating for the mode of frequency and end supports. Table 6 represents the relationship between the nonlocal parameter, thermal load, and nonhomogeneity in the presence of a crack. In this section, different values of the nonlocal parameter, thermal load, and nonhomogeneity are considered as like in Table 4. In addition, a crack is considered at crack location \(a=0.25\) with the crack severity \(K=0.35\). The relationship between thermal load, nonhomogeneity, and natural frequency becomes more changeable in the presence of crack for various modes of frequency and various support systems.

Mode Shape Illustration

Mode shape is one of the very important characteristics that explain the vibration of structural components. It describes the transverse displacement from the beam axis during vibration. It is a very significant measure that exhibits the pattern of vibration. In this section, the effects of nonhomogeneity, thermal load, and the number of cracks on the mode shape of cracked nanobeam are illustrated for different support systems. To understand the dynamic behavior of cracked nanobeam, mode shape analysis is necessary. In this section, three different sets of mode shape diagrams are presented for different values of nonhomogeneity and thermal load. In Figs. (6, 7, 8, 9, 10, 11, 12 and 13), different support conditions of the nanobeam are demonstrated where the location of crack \(a=0.25L\), value of the nonlocal parameter \(\mu =0.1\), and crack severity \(K=0.35\) are considered. Figures (6, 7, 8 and 9) represent mode shapes of axially graded cracked nanobeam for different values of nonhomogeneity. In this section of calculation, thermal load \(n=1\) is considered. Different values of nonhomogeneity \(\lambda =2\), \(\lambda =0\), and \(\lambda =-2\) are applied. It is comprehensible from these figures that mode shapes of cracked nanobeam are considerably changed by the nonhomogeneity. Variation changes with the change of the value of nonhomogeneity. This variation also increases in the higher mode of frequency. Figures (9, 10, 11, 12 and 13) represent mode shapes of axially graded cracked nanobeam for various values of thermal load. In this section of calculation, nonhomogeneity \(\lambda =1\) is considered. Three different values of thermal load \(n=2\), \(n=0\), and \(n=-2\) are applied. It is very clear from these figures that mode shapes are slightly influenced by the thermal load. It can be concluded that the nonhomogeneity is more effective on mode shape than the thermal load. Figures (14, 15, 16, 17, 18, 19, 20 and 21) represent the mode shapes of double and triple cracked nanobeam with fully clamped and simply supported boundary conditions. The nonhomogeneity and thermal effect are not considered. Three specific values of crack severity \(K=0\) , \(K=0.3\) , \(K=0.7\) are used. Figures (14, 15, 16 and 17) describe the mode shape for double-cracked nanobeam. Two similar cracks at \(a=0.3\) and \(a=0.7\) are considered. Similarly, Figs. (18, 19, 20 and 21) reveal the mode shape for triple cracked nanobeam. Three similar cracks at \(a=0.2\), \(a=0.4\), and \(a=0.7\) are considered, respectively. From these figures, it is seen that the number of cracks significantly changes the mode shape diagram. Figures (22, 23, 24 and 25) reveal the mode shapes of double-cracked nanobeam with various nonhomogeneity. In these figures, crack severity \(K=0.35\), crack locations \(a=0.3, b=0.7\), nonlocal parameter \(\mu =0.1\), and thermal load \(n=0\) are considered. Three different values of nonhomogeneity are used in this analysis. It is evident that the mode shape is significantly affected by the nonhomogeneity of the beam.

Conclusion

In this study, the dynamic behavior of axially graded cracked nanobeams with thermal load is analyzed using the power series solution technique. Mode shapes have been illustrated to analyze the effects of nonhomogeneity and thermal load on the vibration of cracked nanobeams. The power series solution technique is employed to study the problem and to illustrate the mode shapes that analyze the natural vibration of multi-cracked nanobeams. Frequency is affected by the crack position as well as the nonhomogeneity. It is shown that the effects of nonhomogeneity and thermal load together on intact and cracked nanobeams are very diverse in different modes of frequency and different end supports. It is evident from these mode shape studies that mode shapes of the single- and multi-cracked nanobeams are very fluctuating for the nonhomogeneity of the material. The thermal load is less effective on the mode shape of cracked nanobeams than the nonhomogeneity. This analysis can be used to design nano-scale electromechanical systems.