Coexistence, Extinction, and Optimal Harvesting in Discrete-Time Stochastic Population Models

Abstract

We analyze the long-term behavior of interacting populations which can be controlled through harvesting. The dynamics is assumed to be discrete in time and stochastic due to the effect of environmental fluctuations. We present powerful extinction and coexistence criteria when there are one or two interacting species. We then use these tools in order to see when harvesting leads to extinction or persistence of species, as well as what the optimal harvesting strategies, which maximize the expected long-term yield, look like. For single species systems, we show under certain conditions that the optimal harvesting strategy is of bang-bang type: there is a threshold under which there is no harvesting, while everything above this threshold gets harvested. We are also able to show that stochastic environmental fluctuations will, in most cases, force the expected harvesting yield to be lower than the deterministic maximal sustainable yield. The second part of the paper is concerned with the analysis of ecosystems that have two interacting species which can be harvested. In particular, we carefully study predator–prey and competitive Ricker models. We are able to analytically identify the regions in parameter space where the species coexist, one species persists and the other one goes extinct, as well as when there is bistability. We look at how one can find the optimal proportional harvesting strategy. If the system is of predator–prey type, the optimal proportional harvesting strategy is, depending on the interaction parameters and the price of predators relative to prey, either to harvest the predator to extinction and maximize the asymptotic yield of the prey or to not harvest the prey and to maximize the asymptotic harvesting yield of the predators. If the system is competitive, in certain instances it is optimal to drive one species extinct and to harvest the other one. In other cases, it is best to let the two species coexist and harvest both species while maintaining coexistence. In the setting of the competitive Ricker model, we show that if one competitor is dominant and pushes the other species to extinction, the harvesting of the dominant species can lead to coexistence.

1 Introduction

A fundamental problem in population biology has been to find conditions for when interacting species coexist or go extinct. Since the dynamics of interacting populations is invariably influenced by the random fluctuations of the environment, realistic mathematical models need to take into account the joint effects of biotic interactions and environmental stochasticity. A successful way of analyzing the persistence and extinction of interacting species has been to look at Markov processes, in either discrete or continuous time, and describe their asymptotic properties. There has been a recent resurgence in stochastic population dynamics, and significant progress has been made for stochastic differential equations (Schreiber et al. 2011; Hening and Nguyen 2018), piecewise deterministic Markov processes (Hening and Strickler 2019; Hening and Nguyen 2020), and stochastic difference equations (Benaïm and Schreiber 2019). The first focus of this paper is to present new results for persistence and extinction in the setting of stochastic difference equations when there are one or two interacting species. These results significantly generalize the work by Chesson and Ellner (1989), Ellner (1989) which only treated competition models and had no extinction results, as well as the more recent work by Benaïm and Schreiber (2019) which only looks at compact state spaces. We are able to give explicit conditions for extinction and persistence in the setting of competitive or predator–prey Ricker equations with random coefficients, adding to the previously known results by Ellner (1989), Vellekoop and Högnäs (1997), Fagerholm and Högnäs (2002), Schreiber et al. (2011). Our results involve computing the invasion rates (Turelli 1978; Chesson 1982; Ellner 1984; Chesson and Ellner 1989) of each species into the random equilibrium of the other species. We show that if both invasion rates are strictly positive, there is coexistence. If, instead, one invasion rate is positive and one is negative, the species with the positive invasion rate persists, while the one with the negative invasion rate goes extinct. If there is coexistence, we prove that under natural conditions, the populations converge to a unique invariant probability measure. If there is extinction, we show that, with probability one, one or both species go extinct exponentially fast. The general theory for the setting with $n>2$ interacting species will appear in future work by the author and his collaborators (Hening et al. 2020).

Once criteria for persistence and extinction are established; our focus shifts towards a key problem from conservation ecology: what is the optimal strategy for harvesting species? This is a delicate issue as overharvesting can sometimes lead to extinction while underharvesting can mean the loss of precious economic resources. In continuous time models, recent studies have been able to find the optimal harvesting strategy, which maximizes either the discounted total yield or the asymptotic yield under very general assumptions if the ecosystem has only one species (Alvarez and Shepp 1998; Hening et al. 2019; Alvarez and Hening 2019). For multiple species, the theory is less developed. Nevertheless, partial results exist (Lungu and Øksendal 1997; Alvarez et al. 2016; Tran and Yin 2015, 2016; Hening et al. 2019; Hening and Tran 2020).

Quite often harvesting models are intrinsically discrete in time. For example, if one looks at the management of fisheries, most models (Getz and Haight 1989; Hilborn and Walters 1992; Clark 2010; Hilker and Liz 2019) assume that the population in a given year can be described by a single continuous variable, and that without harvesting the population levels in successive years are related by

$$\begin{aligned} x_{n+1}=F(x_n) \end{aligned}$$

where F is the so-called recruitment function or the reproduction function. Most discrete time harvesting results ignore random environmental fluctuations and their effects on the availability of food, competition rates, growth and death rates, strength of predation and other key factors. Ignoring environmental stochasticity can create significant problems, in some cases making the models unrealistic (May et al. 1978) and hard to fit to data (Larkin 1973). A series of key studies where environmental fluctuations are included was done by Reed (1978, 1979). Reed looked at the setting where there is one species whose dynamics in the absence of harvesting is given by

$$\begin{aligned} X_{n+1}=Z_n F(X_n) \end{aligned}$$

where $(Z_n)_{n\in {\mathbb {Z}}_+}$ is a sequence of i.i.d. random variables. We extend Reed’s analysis in two ways. First, we study the more general stochastic difference equation

$$\begin{aligned} X_{n+1}=F(X_n, \xi _{n+1}) \end{aligned}$$

where $(\xi _n)_{n\in {\mathbb {Z}}_+}$ is an i.i.d. sequence. Second, we are able to analyze systems of two interacting species. To our knowledge, these are the first results in discrete time that study the harvesting of multiple species.

1.1 Single Species Ecosystem

We are able to give exact conditions under which harvesting leads to persistence or to extinction. In particular, we show that if there is only one species present, then the criteria for persistence only involve the harvesting rate of the population at 0. We are able to find the maximal harvesting rate which does not lead to extinction. If the species $Y_t$ undergoing harvesting persists, we prove it converges in law to a random variable $Y_\infty$ and, if the fraction of the population that gets harvested is given by the strategy h(y), we show that the long run average and the expected long-term harvest both converge to ${\mathbb {E}}h(Y_\infty )$. In many applications, one is interested in seeing how the environmental fluctuations change the long-term yield. We show that in most settings the environmental fluctuations are detrimental and lower the harvesting yield. Only in special cases can we have that the maximum deterministic sustainable yield is equal to the steady-state harvest yield of the stochastic system.

An interesting corollary of our results is that threshold harvesting strategies (also called constant-escapement strategies), where one does not harvest anything below a threshold and harvests everything above that threshold, do not influence the persistence of species as long as the threshold at which one starts harvesting is strictly positive. We showcase two examples where environmental fluctuations are not detrimental for threshold harvesting: (1) The threshold w at which we harvest is self-sustaining, i.e., if at the start of the year we are at level w, the fluctuations of the environment cannot push the population’s size under w. In this setting, the expected value of the long-term yield in the stochastic model equals the yield from the equivalent deterministic model. The downside is that the variance of the yield is higher due to the environmental fluctuations. 2) The threshold w is not self-sustaining, and the maximum yield of the dynamics happens at a self-sustaining threshold ${{\overline{x}}}<w$. In this case, the expected yield of the constant escapement strategy is strictly greater than the yield of the same strategy in the deterministic system.

When looking at constant effort harvesting strategies, where a constant proportion of the return is captured every year, we show that even though the deterministic model might say that we harvest at a sustainable rate, the environmental fluctuations might lead to extinction.

We are able to say more in the setting of the Ricker model. We give conditions under which we can get the same maximal yield in the deterministic and stochastic settings. This includes giving information about the threshold for which the yield is maximized. We also find the optimal harvesting strategy if we restrict ourselves to proportional harvest strategies.

1.2 Two Interacting Species

We analyze a system of two interacting species that can be exploited through harvesting. We show that threshold harvesting strategies do influence the persistence criteria, unlike in the single species setting. In order to be able to compute things explicitly, we focus on Ricker models, also called discrete time Lotka–Volterra models, and assume that the harvesting strategy is of proportional type, where we harvest a fraction $q\in [0,1]$ of the first species and a fraction $r\in [0,1]$ of the second species.

The first studied model is a predator–prey system where species 1 is the prey and species 2 the predator. We give analytical expressions for when one has the persistence of both species, the persistence of the prey and the extinction of the predator as well as the extinction of both species. These expressions tell us exactly for which rates q, r we get one of the three scenarios above. Which strategy, among all proportional harvesting strategies, maximizes the expected long-term harvesting yield? We find by using both analytical results and numerical simulations that it is never optimal to harvest both the predator and the prey. Either we drive the predator extinct and we harvest the prey or we do not harvest the prey at all and we harvest the predator.

The second model we look at consists of an ecosystem where the two species compete with each other for resources. We show that depending on the inter- and intracompetition coefficients of the system, one can have two different regimes each having three regions which depend on the harvesting rates q, r:

• (a) (I) Persistence of species 1 and extinction of species 2; (II) Extinction of species 1 and persistence of species 2; (III) Coexistence

• (b) (I) Persistence of species 1 and extinction of species 2; (II) Extinction of species 1 and persistence of species 2; (III) Bistability, i.e., with probability $p_{x,y}>0$, which depends on the initial abundances (x, y) of the two species, that species 1 persists and species 2 goes extinct, and with probability $1-p_{x,y}>0$ the opposite happens.

We show that harvesting can facilitate coexistence in certain cases. When species 1 is dominant and drives species 2 extinct in the absence of harvesting, it is possible to harvest species 1 and ensure the persistence of both species.

Finally, we look at the optimal harvesting strategies for the competitive system. Combining analytical proofs and numerical simulations, we see that in contrast to the predator–prey setting, it can be optimal, depending on the inter and intra competition rates, to harvest one or both of the species.

2 Stochastic Population Dynamics

We start by describing the stochastic population models we will be working with. To include the effects of random environmental fluctuations, ecologists and mathematicians often use stochastic difference equations of the form:

$$\begin{aligned} X^i_{t+1} = X_t^i f_i({\mathbf {X}}_t, \xi _{t+1}). \end{aligned}$$

(2.1)

here the vector ${\mathbf {X}}_t:=(X_t^1,\ldots ,X_t^n)\in {\mathcal {S}}\subset {\mathbb {R}}_+^n$ records the abundances of the n populations at time $t\in {\mathbb {Z}}_+$ and $\xi _{t+1}$ is a random variable that describes the environmental conditions between time t and $t+1$. The subset ${\mathcal {S}}$ will denote the state space of the dynamics. It will either be a compact subset of ${\mathbb {R}}_+^n$ or all of ${\mathbb {R}}_+^n$. The coexistence set is the subset ${\mathcal {S}}_+=\{{\mathbf {x}}\in {\mathcal {S}}~|~x_i>0, i=1,\ldots n\}$ of the state space where no species is extinct. The real function $f_i({\mathbf {X}}_t,\xi _{t+1})$ captures the fitness of the i-th population at time t and depends both on the population sizes and the environmental state. Models of this type can capture complex short-term life histories and include predation, cannibalism, competition, and seasonal variations.

We have to differentiate between the setting where the dynamics is bounded, and the process enters and remains in a compact set, and the case when the dynamics is unbounded. We will make the following assumptions throughout the paper:

(A1):

$\xi _1,\ldots ,\xi _n,\ldots$ is a sequence of i.i.d. random variables taking values in a Polish space E.

(A2):

For each i the fitness function $f_i({\mathbf {x}},\xi )$ is continuous in ${\mathbf {x}}$ on ${\mathcal {S}}$, measurable in $({\mathbf {x}},\xi )$ and strictly positive.

Assumptions (A1) and (A2) ensure that the process ${\mathbf {X}}_t$ is a Feller process that lives on ${\mathcal {S}}_+$, i.e., ${\mathbf {X}}_t\in {\mathcal {S}}_+, t\in {\mathbb {Z}}_+$ whenever ${\mathbf {X}}_0\in {\mathcal {S}}_+$. One has to make extra assumptions (see (A3) or (A4) in “Appendix A”) in order to ensure the process does not blow up or fluctuate too abruptly between 0 and $\infty$. We note that most ecological models will satisfy these assumptions. For more details see the work by Benaïm and Schreiber (2019), Hening et al. (2020).

Remark 2.1

Suppose the dynamics is given by the more general model of the type

$$\begin{aligned} X^i_{t+1} = F_i({\mathbf {X}}_t, \xi _{t+1}). \end{aligned}$$

(2.2)

Note that (2.2) reduces to (2.1) if $F_i$ is $C^1$ and $F_i({\mathbf {x}})=0$ whenever $x_i=0$. This means that $F_i$ is a nice, sufficiently smooth, vector field which takes the value 0 if species i is extinct—this is a natural assumption as there is no reason the population should be able to come back from extinction. Under these assumptions, we can see that (2.1) is satisfied by setting

$$\begin{aligned} f_i({\mathbf {x}},\xi ) = {\left\{ \begin{array}{ll} \frac{F_i({\mathbf {x}},\xi )}{x_i} &{}\quad \text {if } x_i>0,\\ \frac{\partial F_i({\mathbf {x}},\xi )}{\partial x_i} &{}\quad \text {if } x_i = 0. \end{array}\right. } \end{aligned}$$

We will sometimes compare the stochastic model (2.1) with its averaged deterministic counterpart

$$\begin{aligned} {\mathbf {x}}_{t+1}^i=x_t^i {{\overline{f}}}_i({\mathbf {x}}_t) \end{aligned}$$

(2.3)

where ${{\overline{f}}}_i({\mathbf {x}}) := {\mathbb {E}}f_i({\mathbf {x}},\xi _1)$. Note that

$$\begin{aligned} {\mathbb {E}}[X^i_{t+1}~|~{\mathbf {X}}_t={\mathbf {x}}] = x^i{\mathbb {E}}f_i({\mathbf {x}},\xi _1) = x^i {{\overline{f}}}_i({\mathbf {x}}), \end{aligned}$$

so that (2.3) is the average of (2.1) in this sense.

For example, if $f(x,\xi )=\xi u(x)$ and $\xi _1$ is a random variable with expectation ${\mathbb {E}}\xi _1=1$, then

$$\begin{aligned} {\mathbb {E}}[X^i_{t+1}~|~{\mathbf {X}}_t={\mathbf {x}}] = x^i u({\mathbf {x}}). \end{aligned}$$

This is the setting used by Reed (1978).

2.1 Stochastic Persistence

We define the extinction set, where at least one species is extinct, by

$$\begin{aligned} {\mathcal {S}}_0:={\mathcal {S}}\setminus {\mathcal {S}}_+=\{{\mathbf {x}}\in {\mathcal {S}}~:~\min _i x_i=0\}. \end{aligned}$$

The transition operator $P: {\mathcal {B}}\rightarrow {\mathcal {B}}$ of the process ${\mathbf {X}}$ is an operator which acts on Borel functions ${\mathcal {B}}:=\{h:{\mathcal {S}}\rightarrow {\mathbb {R}}~|~h~\text {Borel}\}$ as

$$\begin{aligned} Ph({\mathbf {x}})={\mathbb {E}}_{\mathbf {x}}[h({\mathbf {X}}(1))]:={\mathbb {E}}[h({\mathbf {X}}(1))~|~{\mathbf {X}}(0)={\mathbf {x}}], ~{\mathbf {x}}\in {\mathcal {S}}. \end{aligned}$$

The operator P acts by duality on Borel probability measures $\mu$ by $\mu \rightarrow \mu P$ where $\mu P$ is the probability measure given by

$$\begin{aligned} \int _{{\mathcal {S}}}h({\mathbf {x}}) (\mu P)(\mathrm{d}{\mathbf {x}}):=\int _{{\mathcal {S}}}P h({\mathbf {x}}) \mu (\mathrm{d}{\mathbf {x}}) \end{aligned}$$

for all $h\in C({\mathcal {S}})$. A Borel probability measure $\mu$ on ${\mathcal {S}}$ is called an invariant probability measure if

$$\begin{aligned} \mu P = \mu \end{aligned}$$

where P is the transition operator of the Markov process ${\mathbf {X}}_t$. An invariant probability measure or stationary distribution is a way of describing a ‘random equilibrium’. If the process starts with ${\mathbf {X}}_0$ having an initial distribution given by the invariant probability measure $\mu$, then the distribution of ${\mathbf {X}}_t$ is $\mu$ for all $t\in {\mathbb {Z}}_+$. In a sense this is the random analogue of a fixed point of a deterministic dynamical system. It turns out that a key concept is the realized per-capita growth rate (Schreiber et al. 2011) of species i when introduced in the community described by an invariant probability measure $\mu$

$$\begin{aligned} r_i(\mu ) =\int _{{\mathbb {R}}_+^n}{\mathbb {E}}[\ln f_i({\mathbf {x}},\xi _1)]\,\mu (\mathrm{d}{\mathbf {x}}) = \int r_i({\mathbf {x}})\mu (\mathrm{d}{\mathbf {x}}) \end{aligned}$$

(2.4)

where

$$\begin{aligned} r_i({\mathbf {x}}) = {\mathbb {E}}[\ln f_i({\mathbf {x}},\xi _1)] \end{aligned}$$

is the mean per-capita growth rate of species i at population state ${\mathbf {x}}$. This quantity tells us whether species i tends to increase or decrease when introduced at an infinitesimally small density into the subcommunity described by $\mu$. If the ith species is among the ones supported by the subcommunity given by $\mu$, i.e., i lies in the support of $\mu$, then this species is in a sense ‘at equilibrium’ and one can prove that

$$\begin{aligned} r_i(\mu )=0. \end{aligned}$$

(2.5)

The only directions i in which $r_i(\mu )$ can be nonzero are those which are not supported by $\mu$.

One can show that the invariant probability measures living on the extinction set ${\mathcal {S}}_0$, together with some tightness assumptions, fully describe the long-term behavior of the system. In a sense, if any such invariant probability measure is a repeller which pushes the process away from the boundary in at least one direction, then the system persists. Let ${{\,\mathrm{Conv}\,}}({\mathcal {M}})$ denote the set of all invariant probability measures supported on ${\mathcal {S}}_0$. In order to have the convergence of the process to a unique stationary distribution, one needs some irreducibility conditions which keep the process from being too degenerate (Hening et al. 2020; Meyn and Tweedie 1992). The following theorem characterizes the coexistence of the ecosystem.

Theorem 2.1

Suppose that for all $\mu \in {{\,\mathrm{Conv}\,}}({\mathcal {M}})$ we have

$$\begin{aligned} \max _{i} r_i(\mu )>0. \end{aligned}$$

(2.6)

Then, the system is almost surely stochastically persistent and stochastically persistent in probability. Under additional irreducibility conditions, there exists a unique invariant probability measure $\pi$ on ${\mathcal {S}}_+$ and as $t\rightarrow \infty$ the distribution of ${\mathbf {X}}_t$ converges in total variation to $\pi$ whenever ${\mathbf {X}}(0)={\mathbf {x}}\in {\mathcal {S}}_+$. Furthermore, if $w:{\mathcal {S}}_+\rightarrow {\mathbb {R}}$ is bounded, then

$$\begin{aligned} \lim _{t\rightarrow \infty }{\mathbb {E}}w({\mathbf {X}}_t) = \int _{{\mathcal {S}}_+} w({\mathbf {x}})\,\pi (\mathrm{d}{\mathbf {x}}). \end{aligned}$$

A sketch of the proof of this result appears in “Appendix A”.

2.2 Classification of Two Species Dynamics

Sometimes one is not only interested in persistence and coexistence, but also in conditions which lead to extinction. Extinction results are more delicate and require a technical analysis. Some extinction results appeared in work by Hening and Nguyen (2018), Benaïm and Schreiber (2019). We restrict our discussion to a system with two species. In this setting, (2.1) becomes

$$\begin{aligned} \begin{aligned} X^1_{t+1}&=X^1_t f_1(X^1_t, X^2_t,\xi _{t+1}),\\ X^2_{t+1}&=X^2_t f_2(X^1_t, X^2_t,\xi _{t+1}). \end{aligned} \end{aligned}$$

(2.7)

The exact assumptions and technical results are found in “Appendix B”. We can classify the dynamics as follows. We first look at the Dirac delta measure $\delta _0$ at the origin (0, 0)

$$\begin{aligned} r_i(\delta _0) = {\mathbb {E}}[\ln f_i(0,\xi _1)], i=1,2. \end{aligned}$$

If $r_i(\delta _0)>0$, then species i survives on its own and converges to a unique invariant probability measure $\mu _i$ supported on ${\mathcal {S}}_+^i := \{{\mathbf {x}}\in {\mathcal {S}}~|~x_i\ne 0, x_j=0, i\ne j\}$. The realized per-capita growth rates can be computed as

$$\begin{aligned} r_i(\mu _j)=\int _{(0,\infty )}{\mathbb {E}}[\ln f_i(x,\xi _1)]\mu _j(\mathrm{d}x). \end{aligned}$$

• (i) Suppose $r_1(\delta _0)>0, r_2(\delta _0)>0$.

  • If $r_1(\mu _2)>0$ and $r_2(\mu _1)>0$, we have coexistence and convergence of the distribution of ${\mathbf {X}}_t$ to the unique invariant probability measure $\pi$ on ${\mathcal {S}}_+$.

  • If $r_1(\mu _2)>0$ and $r_2(\mu _1)<0$, we have the persistence of $X^1$ and extinction of $X^2$.

  • If $r_1(\mu _2)<0$ and $r_2(\mu _1)>0$, we have the persistence of $X^2$ and extinction of $X^1$.

  • If $r_1(\mu _2)<0$ and $r_2(\mu _1)<0$, we have that for any ${\mathbf {X}}_0={\mathbf {x}}\in {\mathcal {S}}_+$

    $$\begin{aligned} p_{{\mathbf {x}},1}+ p_{{\mathbf {x}},2}=1, \end{aligned}$$

    where $p_{{\mathbf {x}},j}>0$ is the probability that species j persists and species $i\ne j$ goes extinct.

• (ii) Suppose $r_1(\delta _0)>0, r_2(\delta _0)<0$. Then, species 1 survives on its own and converges to its unique invariant probability measure $\mu _1$ on ${\mathcal {S}}^1_+$.

  • If $r_2(\mu _1)>0$, we have the persistence of both species and convergence of the distribution of ${\mathbf {X}}_t$ to the unique invariant probability measure $\pi$ on ${\mathcal {S}}_+$.

  • If $r_2(\mu _1)<0$, we have the persistence of $X^1$ and the extinction of $X^2$.

• (iii) Suppose $r_1(\delta _0)<0, r_2(\delta _0)<0$. Then, both species go extinct with probability one.

We note that our results are significantly more general than those from Ellner (1989). In Ellner (1989), the author only gives conditions for coexistence and does not treat the possibility of the extinction of one or both species.

Example 2.1

The simplest case is when the noise is multiplicative, that is

$$\begin{aligned} \begin{aligned} X^1_{t+1}&=X^1_t Z_{t+1}^1f_1(X^1_t, X^2_t)\\ X^2_{t+1}&=X^2_t Z_{t+1}^2 f_2(X^1_t, X^2_t), \end{aligned} \end{aligned}$$

(2.8)

where $Z^1_{1}, Z^1_{2},\ldots$ is an i.i.d. sequence of random variables and $Z^2_{1}, Z^2_{2}, \ldots$ is an independent sequence of i.i.d. random variables. In this case for $i=1,2$ we have

$$\begin{aligned} \begin{aligned} r_i(\delta _0)&= {\mathbb {E}}[\ln (Z_{t+1}^i f_i(0))]\\&= {\mathbb {E}}\ln Z_1 + \ln f_i(0). \end{aligned} \end{aligned}$$

(2.9)

The growth rates at 0 in the stochastic model differ from the growth rates at 0 of the deterministic model only by the term ${\mathbb {E}}\ln Z_1$.

2.3 Harvesting

We next describe how the harvesting effects are taken into account. We assume that the harvesting takes place during a short harvest season. The size of the population at the beginning of the harvest season in year t will be denoted by ${\mathbf {Y}}_t$ and will be called return in year t. If we assume the harvest season is short so that growth and natural mortality can be neglected during the harvesting and that the harvesting strategy is stationary, i.e., the size of the harvest in any year depends only on the size of the population return ${\mathbf {Y}}$ in that year, we can write

$$\begin{aligned} X^i_t = Y_t^i - h_i({\mathbf {Y}}_t) = u_i({\mathbf {Y}}_t) \end{aligned}$$

(2.10)

where $X^i_t$ is the escapement of the ith population from the harvest and $h_i({\mathbf {Y}}_t)$ is the amount of species i that is harvested at time t. The function $u_i$ is called the escapement function and measures how much is left after harvesting. Note that since we cannot harvest a negative amount or more than the total population size, we will always have

$$\begin{aligned} 0\le h_i({\mathbf {y}})\le y_i. \end{aligned}$$

Set ${\mathbf {u}}({\mathbf {y}}):=(u_1({\mathbf {y}}),\ldots ,u_n({\mathbf {y}}))$. Once the harvesting is done, the population evolves according to (2.1) so that the size of the return in year $t+1$ is related to the escapement in year t via

$$\begin{aligned} Y^i_{t+1} = X_t^i f_i({\mathbf {X}}_t, \xi _{t+1}). \end{aligned}$$

(2.11)

Combining (2.10) and (2.11), we get

$$\begin{aligned} Y^i_{t+1} = u_i({\mathbf {Y}}_t) f_i({\mathbf {u}}({\mathbf {Y}}_t), \xi _{t+1}). \end{aligned}$$

(2.12)

In order to be able to analyze the process ${\mathbf {Y}}_t$, we have to make sure that it can be written in the Kolmogorov form (2.1). In order to get this, we assume that

Assumption 2.1

For all $i=1,\ldots ,n$ the following properties hold

• (a) The function $u_i$ is strictly positive on ${\mathcal {S}}_+$, with

  $$\begin{aligned} u_i({\mathbf {y}}) \le y_i. \end{aligned}$$

• (b) The function $u_i$ is continuous on ${\mathcal {S}}$ and continuously differentiable at $y_i=0$.

Remark 1

Note that Assumption 2.1 implies that $u_i({\mathbf {y}})=0$ if $y_i=0$ and

$$\begin{aligned} \frac{\partial u_i}{\partial y_i}({\mathbf {y}})=\lim _{y_i\rightarrow 0} \frac{u_i({\mathbf {y}})}{y_i}\le 1 \end{aligned}$$

if ${\mathbf {y}}\in {\mathcal {S}}$ with $y_i=0$.

2.4 Persistence with Harvesting

Since overharvesting can lead to extinction, we want to find sufficient conditions which ensure the process ${\mathbf {Y}}_t$ converges to a unique invariant probability measure on ${\mathcal {S}}$. Note that we need to put (2.12) into the form (2.1). For this, using Remark 2.1, let

$$\begin{aligned} g_i({\mathbf {x}},\xi ) := {\left\{ \begin{array}{ll} \frac{u_i({\mathbf {x}})}{x_i} f_i({\mathbf {u}}({\mathbf {x}}), \xi )&{}\quad \text {if } x_i>0,\\ \left( \frac{\partial u_i}{\partial x_i}({\mathbf {x}})\right) f_i({\mathbf {u}}({\mathbf {x}}), \xi ) &{}\quad \text {if } x_i = 0. \end{array}\right. } \end{aligned}$$

(2.13)

We can write (2.12) as

$$\begin{aligned} Y^i_{t+1} = Y^i_t g_i({\mathbf {Y}}_t, \xi _{t+1}). \end{aligned}$$

(2.14)

In order to use Theorem 2.1, we have to make sure that conditions (A1)–(A4) are satisfied that the process ${\mathbf {Y}}_t$ is $\phi$-irreducible and that (2.6) holds. If $\mu$ is an invariant probability measure of ${\mathbf {Y}}_t$ living on the extinction set ${\mathcal {S}}_+$, the realized per capita growth rates will be given by

$$\begin{aligned} r_i(\mu ) =\int _{ {\mathcal {S}}}{\mathbb {E}}[\ln g_i({\mathbf {x}},\xi _1)]\,\mu (\mathrm{d}{\mathbf {x}}). \end{aligned}$$

(2.15)

Specifically, if we look at the Dirac mass at 0, we get

$$\begin{aligned} \begin{aligned} r_i(\delta _0)&=\int _{{\mathcal {S}}_0}{\mathbb {E}}[\ln g_i({\mathbf {x}},\xi _1)]\,\delta _0(\mathrm{d}{\mathbf {x}})\\&= {\mathbb {E}}[\ln g_i(0,\xi _1)] \\&= {\mathbb {E}}\left[ \ln \left( \frac{\partial u_i}{\partial x_i}(0)f_i(0, \xi )\right) \right] . \end{aligned} \end{aligned}$$

(2.16)

Example 2.2

If the noise is multiplicative and we are in the setting of Example 2.1, i.e.,

$$\begin{aligned} \begin{aligned} Y^i_{t+1}&=Y^i_t Z_{t+1}^ig_i({\mathbf {Y}}_t), \end{aligned} \end{aligned}$$

(2.17)

then

$$\begin{aligned} \begin{aligned} r_i(\delta _0)&= {\mathbb {E}}[\ln (Z_{t+1}^i g_i(0))]\\&= {\mathbb {E}}\ln Z_1 +\ln \left( \frac{\partial u_i}{\partial x_i}(0)f_i(0)\right) \\&= {\mathbb {E}}\ln Z_1 +\ln \left( \frac{\partial u_i}{\partial x_i}(0)\right) + \ln f_i(0). \end{aligned} \end{aligned}$$

(2.18)

Biological interpretation The above equation showcases the additive contributions of the random environmental fluctuations, the intrinsic growth rate at 0 of the population and harvesting to the persistence of the population. Suppose first there is no harvesting. Suppose for simplicity that ${\mathbb {E}}Z_1=1$. Then, the population persists if

$$\begin{aligned} {\mathbb {E}}\ln Z_1 + \ln f_i(0) >0, \end{aligned}$$

that is when

$$\begin{aligned} f_i(0)-1> e^{-{\mathbb {E}}\ln Z_1}-1=:A. \end{aligned}$$

Note that $f_i(0)-1$ represents the limiting expected annual growth rate at the zero population level, also called the average intrinsic annual growth rate. The above tells us that there is a threshold A above which the average annual growth rate has to be so that the population persists. The quantity A measures the dispersion or spread of the distribution of the environmental fluctuations around their mean value. In other words, A is a measure of the degree of environmentally induced fluctuations. For example, if $Z_1$ has a log-normal distribution with mean one and variance $\sigma ^2$, one can show that

$$\begin{aligned} A=\sqrt{1+\sigma ^2}-1. \end{aligned}$$

This shows that the critical value of the average intrinsic annual growth rate necessary for survival has to be higher in an environment with a high degree of fluctuation that in an environment with a low degree of fluctuation. Next, let us assume there is harvesting. Since $\frac{\partial u_i}{\partial x_i}(0)\le 1$, we always have $\ln (\frac{\partial u_i}{\partial x_i}(0))\le 0$ so that, as expected, harvesting is always detrimental to the survival of each individual species. Arguing as above, we get that for persistence, the minimal escapement rate is such that

$$\begin{aligned} \frac{\partial u^{\mathrm{min}}_i}{\partial x_i}(0) > e^{- ({\mathbb {E}}\ln Z_1 + \ln f_i(0))} = \frac{ e^{- {\mathbb {E}}\ln Z_1}}{ f_i(0)}. \end{aligned}$$

Since $h_i({\mathbf {y}})=1-u_i({\mathbf {y}})$, this implies that the maximal harvesting rate satisfies

$$\begin{aligned} \frac{\partial h^{\mathrm{max}}_i}{\partial x_i}(0) < 1- e^{- ({\mathbb {E}}\ln Z_1 + \ln f_i(0))}=1- \frac{ e^{- {\mathbb {E}}\ln Z_1}}{ f_i(0)}. \end{aligned}$$

If $Z_1$ has a log-normal distribution with mean one and variance $\sigma ^2$, we get that the maximal harvesting rate is

$$\begin{aligned} 1- \frac{\sqrt{1+\sigma ^2}}{ f_i(0)}. \end{aligned}$$

This shows that high environmental fluctuations are detrimental to harvesting and cannot be neglected. The effects of environmental variability have been seen especially in fishing. In four case studies from marine fisheries, including northern cod, haddock, oysters and krill Hofmann and Powell (1998) argue that exploited fisheries must include the effects of environmental fluctuations.

3 Single Species Harvesting

This section explores the setting when there is only one species in the ecosystem. The results can be seen as an extension of the results from Reed (1978). Our results show that environmental fluctuations are usually detrimental to the optimal harvesting yield. Actually, only under very special conditions, it is possible for the stochastic dynamics to have the same maximal expected long-term yield as the related deterministic dynamics. Even in that case, the nonzero variance of the stochastic long-term yield makes it more risky than its deterministic analogue.

We can show that in some special cases of constant-escapement strategies, it is possible for the stochastic expected long-term yield to be higher than the deterministic yield.

One can see from (2.14) that the dynamics of the return will be given by

$$\begin{aligned} Y_{t+1} = Y_t g(Y_t, \xi _{t+1}) \end{aligned}$$

(3.1)

for

$$\begin{aligned} g(x) := {\left\{ \begin{array}{ll} \frac{u(x)}{x} f(u(x), \xi )&{}\quad \text {if } x>0,\\ \left( \frac{\partial u}{\partial x}(0)\right) f(u(0), \xi ) &{}\quad \text {if } x = 0. \end{array}\right. } \end{aligned}$$

We will work under the assumption that without harvesting we have

$$\begin{aligned} {\mathbb {E}}\left[ \ln \left( f(0, \xi _1)\right) \right] >0 \end{aligned}$$

(3.2)

so that the species persists. Suppose the assumptions of one of the Theorems A.1, A.2, A.3 or 2.1 hold. Then, in order to have persistence we need

$$\begin{aligned} r_1(\delta _0) =\int _{\partial {\mathbb {R}}_+}{\mathbb {E}}[\ln g(x,\xi _1)]\,\delta _0(\mathrm{d}x) = {\mathbb {E}}\left[ \ln \left( \left( \frac{\partial u}{\partial x}(0)\right) f(0, \xi _1)\right) \right] >0 \end{aligned}$$

(3.3)

where $\delta _0$ is the point mass at 0 and we made use of (2.15) and Assumption 2.1. We can express this result as

$$\begin{aligned} \frac{\partial u}{\partial x}(0)> e^{- {\mathbb {E}}\ln f(0, \xi _1)}. \end{aligned}$$

(3.4)

Let us next compute the expected long-term harvest yield. If the assumptions of Theorem 2.1 are satisfied we will have

$$\begin{aligned} Y_{t}\rightarrow Y_\infty \end{aligned}$$

in distribution as $t\rightarrow \infty$. Here $Y_\infty$ is a random variable whose distribution equal to the invariant probability measure $\pi _u$. In many models, and for well-behaved functions h one can show by Theorem 2.1 that ${\mathbb {E}}h(Y_\infty )$ exists and is finite. As a result, we have that with probability one

$$\begin{aligned} \lim _{T\rightarrow \infty } \frac{\sum _{t=0}^Th(Y_t)}{T} = {\mathbb {E}}h(Y_\infty ). \end{aligned}$$

This tells us that the long-run average harvest yield converges to a steady yield ${\mathbb {E}}h(Y_\infty )$. Furthermore, we can also see that expected yield also converges to the same quantity

$$\begin{aligned} \lim _{T\rightarrow \infty } {\mathbb {E}}h(Y_T) = {\mathbb {E}}h(Y_\infty ) = \int _{(0,\infty )}h(x)\,\pi _u(\mathrm{d}x). \end{aligned}$$

From now on we will call ${\mathbb {E}}h(Y_\infty )$ the expected steady-state yield. In general, it is not possible to find ${\mathbb {E}}h(Y_\infty )$. However, in certain instances we can exploit the fact that, at stationarity, the realized per-capita growth rates in the directions supported by the measure $\pi _u$ are all zero (Hening et al. 2020). In other words,

$$\begin{aligned} 0=r_1(\pi ) = \int _{(0,\infty )}{\mathbb {E}}\left[ \ln \left( \frac{u(x)}{x} f(u(x), \xi _1)\right) \right] \,\pi _u(\mathrm{d}x). \end{aligned}$$

(3.5)

3.1 Stochastic Versus Deterministic Harvesting

Let us compare the stochastic dynamics (3.1) with its deterministic average

$$\begin{aligned} x_{t+1}=x_t {{\overline{f}}}(x_t) \end{aligned}$$

(3.6)

where ${{\overline{f}}}(x) := {\mathbb {E}}f(x,\xi _1)$ and ${{\overline{F}}}(x) := x {{\overline{f}}}(x)$. If h is any stationary harvesting strategy, the deterministic equilibrium return y satisfies

$$\begin{aligned} y={{\overline{F}}}(u(y)) \end{aligned}$$

and the equilibrium yield is

$$\begin{aligned} h(y)=y-u(y) = {{\overline{F}}}(u(y))-u(y)={{\overline{G}}} (u(y)) \end{aligned}$$

where ${{\overline{G}}}(x):={{\overline{F}}}(x)-x$. The deterministic maximum sustainable yield (DMSY) is obtained by keeping the escapement u(y) at the level $x_1$ at which ${{\overline{G}}}$ attains its maximum, i.e., at the point $x_1$ where

$$\begin{aligned} 0={{\overline{G}}}'(x_1)={{\overline{F}}}'(x_1)-1={{\overline{f}}}(x_1) + x_1 {{\overline{f}}}'(x_1)-1. \end{aligned}$$

The DMSY $M_{\det }$ will be

$$\begin{aligned} M_{\det } = {{\overline{G}}}(x_1)=x_1{{\overline{f}}}(x_1)-x_1. \end{aligned}$$

Theorem 3.1

The expected value of the steady state harvest yield ${\mathbb {E}}h(Y_\infty )$ of any stationary harvesting policy h of the model (3.1) is always dominated by the maximum deterministic sustainable yield of the equivalent deterministic model (3.6),

$$\begin{aligned} {\mathbb {E}}h(Y_\infty ) \le M_{\det }. \end{aligned}$$

The only way to achieve an equality in the above is when the following conditions are satisfied:

• (1) The unharvested dynamics $X_{t+1}=X_tf(X_t,\xi _{t+1})$ is able to go to a level greater or equal to $x_1$.

• (2) The harvesting policy is bang-bang with threshold $x_1$, that is

  $$\begin{aligned} h^*(y) := {\left\{ \begin{array}{ll} y-x_1 &{}\quad \text {if } y>x_1,\\ 0 &{}\quad \text {if } y\le x_1. \end{array}\right. } \end{aligned}$$

• (3) The level $x_1$ is self-sustaining, i.e., the stochastic effects do not make the population ever go below $x_1$ once it reaches this level.

Proof

Let $G(x,\xi ):= x f(x,\xi )-x$ and note that ${\mathbb {E}}G(x,\xi _1)= {{\overline{G}}}(x)$. For the stochastic model, if we use the harvesting policy h, the long-run average yield is

$$\begin{aligned} \begin{aligned} {\mathbb {E}}h(Y_\infty )&= {\mathbb {E}}Y_\infty - {\mathbb {E}}[u(Y_\infty )] \\&= {\mathbb {E}}u(Y_\infty ) f(u(Y_\infty ),\xi _1) - {\mathbb {E}}[u(Y_\infty )] \\&= {\mathbb {E}}G(u(Y_\infty )),\xi _1)\\&= \int \int G(u(y), \xi ) {\mathbb {P}}(Y_\infty \in \mathrm{d}y, \xi _1\in \mathrm{d}\xi )\\&= \int \int G(u(y), \xi ) {\mathbb {P}}(Y_\infty \in \mathrm{d}y){\mathbb {P}}(\xi _1\in \mathrm{d}\xi )\\&= \int \left( \int G(u(y), \xi ){\mathbb {P}}(\xi _1\in \mathrm{d}\xi )\right) {\mathbb {P}}(Y_\infty \in \mathrm{d}y)\\&= {\mathbb {E}}{{\overline{G}}} (u(Y_\infty )) \end{aligned} \end{aligned}$$

(3.7)

where we used the fact that $Y_\infty$ and $u(Y_\infty ) f(u(Y_\infty ),\xi _1)$ have the same distribution and $Y_\infty$ is independent of $\xi _1$. Since ${{\overline{G}}}$ attains its maximum at $x_1$, we have

$$\begin{aligned} {\mathbb {E}}h(Y_\infty ) = {\mathbb {E}}{{\overline{G}}} (u(Y_\infty ))\le {{\overline{G}}}(x_1)= M_{\det }. \end{aligned}$$

(3.8)

In order to have equality in (3.8), we need the law of $u(Y_\infty )$ to be the point mass $\delta _{x_1}$ at $x_1$. This means that with probability 1

$$\begin{aligned} Y_\infty - h(Y_\infty ) = x_1. \end{aligned}$$

One can achieve this if:

• (1) the population can get to a level that is equal or greater to $x_1$,

• (2) one uses the bang-bang, also called constant escapement or threshold, harvest policy at the level $x_1$

  $$\begin{aligned} h^*(y) := {\left\{ \begin{array}{ll} y-x_1 &{}\quad \text {if } y>x_1,\\ 0 &{}\quad \text {if } y\le x_1, \end{array}\right. } \end{aligned}$$

  and

• (3) once the population reaches the level $x_1$, it never decreases to a lower level, that is, if $X_t=x_1$, then

  $$\begin{aligned} Y_{t+1} = X_1f(X_1,\xi _1)=x_1f(x_1,\xi _1) \ge x_1 \end{aligned}$$

  with probability 1.

The last property is equivalent to having ${\mathbb {P}}(f(x_1,\xi _1)\ge 1)=1$—if this is true, we say that the level $x_1$ is self-sustaining. $\square$

Biological Interpretation In general, it is not possible to have the same maximal yield in the stochastic setting as in the deterministic setting. Due to environmental fluctuations the expected long-term yield of any harvesting strategy h will be dominated by the deterministic maximum sustainable yield. The only case when the maximal yields in the stochastic and deterministic setting are equal, is when one uses a constant escapement strategy with threshold $x_1$ (which maximizes the deterministic MSY), the stochastic dynamics can reach levels greater or equal to $x_1$ and $x_1$ and then never goes below $x_1$ due to environmental fluctuations. These very specific conditions will not usually hold. As such, for most situations we cannot expect to get the same optimal harvesting yields in the deterministic and stochastic settings. This is the case for natural populations. In Bayliss (1989), the author shows that the effects of variable rainfall decrease the maximum harvest rate and the maximum harvest yield for magpie geese by $25\%$. Since the magpie goose is one of the most important game species in Australia, it is key to take into account environmental fluctuations. In general, sustainable harvesting strategies will be overestimated if one ignores environmental fluctuations. As a result, one needs to adjust harvesting strategies in order to adapt to increasing environmental variability (Hulme 2005). The greater the environmental variation, the greater the proportion of time a population is likely to spend below its carrying capacity, making the population more prone to extinction.

We note that threshold (or bang-bang) harvesting strategies do not influence the persistence criterion in the one-dimensional case. The unharvested system

$$\begin{aligned} X_{t+1} = X_t f(X_t, \xi _{t+1}) \end{aligned}$$

(3.9)

has

$$\begin{aligned} r^X_1(\delta _0) = {\mathbb {E}}\ln f(0,\xi _1) >0. \end{aligned}$$

If one adds harvesting, then

$$\begin{aligned} Y_{t+1} = Y_t g(Y_t, \xi _{t+1}) \end{aligned}$$

where

$$\begin{aligned} g(x) := {\left\{ \begin{array}{ll} \frac{u_w(x)}{x} f(u_w(x), \xi )&{}\quad \text {if } x>0,\\ \left( \frac{\partial u_w}{\partial x}(0)\right) f(u_w(0), \xi ) &{}\quad \text {if } x = 0. \end{array}\right. } \end{aligned}$$

The bang-bang strategy

$$\begin{aligned} h_w(y) := {\left\{ \begin{array}{ll} y-w &{}\quad \text {if } y>w,\\ 0 &{}\quad \text {if } y\le w, \end{array}\right. } \end{aligned}$$

with $w>0$ also has

$$\begin{aligned} r^Y_1(\delta _0) = {\mathbb {E}}\ln g(0,\xi _1)= {\mathbb {E}}\ln \left( \frac{\partial u_w}{\partial x}(0)\right) f(u(0), \xi ) = {\mathbb {E}}\ln f(0,\xi _1)=r^X_1(\delta _0). \end{aligned}$$

This implies that a constant escapement strategy with a threshold $w>0$ does not change the per-capita growth rate and thus does not interfere with persistence. This is one reason why bang-bang harvesting strategies are robust and make sense when there is only one species present. This is not the case anymore when there are multiple species present.

Biological Interpretation At any sustainable harvesting level, the a threshold harvesting strategy produces a lower risk of depletion or extinction than any other strategy. This is because threshold harvesting keeps the population at relatively high levels by allowing it to recover at the natural rate, without harvesting, when its population is below the threshold. Furthermore, at any level of risk of depletion or extinction, the optimal threshold strategy produces a higher mean annual yield than any other strategy.

3.2 Constant Effort Harvesting

Quite often in fisheries a constant effort harvesting method is used. These strategies are such that the same fixed proportion of the return is captured every year. In other words, for some fixed $\theta \in (0,1)$ we have

$$\begin{aligned} h_\theta (x)= \theta x \end{aligned}$$

and

$$\begin{aligned} u_\theta (x)=(1-\theta )x. \end{aligned}$$

The persistence criteria (3.4) become

$$\begin{aligned} \theta < \theta _{\max } := 1 - e^{-{\mathbb {E}}\ln f(0,\xi _1)} \end{aligned}$$

where $\theta _{\max }$ is the maximum sustainable rate of exploitation. Let us compare this with the deterministic system

$$\begin{aligned} x_{t+1}=x_t {{\overline{f}}}(x_t) ={{\overline{F}}}(x_t) \end{aligned}$$

where ${{\overline{f}}}(x) = {\mathbb {E}}f(x,\xi _1)$. In this setting, the maximum sustainable rate of exploitation $\theta _{\det }$ is given by

$$\begin{aligned} \theta _{\det } = 1 - \frac{1}{{{\overline{f}}}(0)}=1- e^{-\ln {\mathbb {E}}f(0,\xi _1) }. \end{aligned}$$

Since the logarithm is a concave function, Jensen’s inequality implies that

$$\begin{aligned} {\mathbb {E}}\ln f(0,\xi _1) \le \ln {\mathbb {E}}f(0,\xi _1), \end{aligned}$$

with equality if and only if $f(0,\xi _1)$ is constant with probability one. As a result,

$$\begin{aligned} \theta _{\max }<\theta _{\det }, \end{aligned}$$

which was shown by Reed (1978) in a simpler model.

Biological Interpretation If one neglects environmental fluctuations, one might use a rate of exploitation that seems sustainable $\theta <\theta _ {\det }$. However, if one has $\theta \in (\theta _{\max }, \theta _{\det })$, this constant effort harvesting with rate of exploitation $\theta$ will lead to extinction. This inequality is important because it shows that one is in danger of driving species extinct if environmental stochasticity is neglected. This analysis provides theoretical evidence for the ‘harvest-interaction hypothesis’ (Shelton and Mangel 2011; Rouyer et al. 2012; Cameron et al. 2016; Gamelon et al. 2019) from conservation ecology which says that certain harvesting strategies might increase the risk of extinction.

It is well known that in the setting of (3.6) the deterministic maximum sustainable yield (DMSY) is achieved when the rate of exploitation is

$$\begin{aligned} \theta _{\mathrm{DMSY}} = 1 - \frac{1}{{{\overline{f}}}(x_1)} \end{aligned}$$

for $x_1$ satisfying

$$\begin{aligned} {{\overline{f}}}'(x_1)=1. \end{aligned}$$

Under environmental conditions which are large enough, we can have

$$\begin{aligned} e^{-\ln {\mathbb {E}}f(0,\xi _1) } > \frac{1}{{{\overline{f}}}(x_1)} \end{aligned}$$

which implies

$$\begin{aligned} \theta _{\mathrm{DMSY}} = 1 - \frac{1}{{{\overline{f}}}(x_1)} > \theta _{\max } = 1 - e^{-{\mathbb {E}}\ln f(0,\xi _1)} \end{aligned}$$

Biological Interpretation If the environmental fluctuations are significant, one has $\theta _{\mathrm{DMSY}}>\theta _{\max }$. This shows that if large environmental fluctuations are possible and we harvest the population according to the deterministic MSY rate of exploitation, we will drive it to extinction. This provides more evidence that environmental fluctuations are of fundamental importance when considering harvesting strategies. This result is important for resource management as a theoretical example of how harvesting can alter the dynamics of the exploited species and lead to extinction. It supports the conclusion of the empirical study Anderson et al. (2008) which shows that fishing can increase the fluctuations in fish abundance by increasing the dynamic instability of populations.

Theorem 3.2

If the deterministic averaged system (3.6) has a strictly concave ${{\overline{F}}}$, and the dynamics (3.9) is not purely deterministic, then the asymptotic expected yield of any constant effort harvest strategy is strictly lower than the deterministic yield of that harvesting policy.

Proof

For a constant-effort policy $h_\theta (y)=\theta y$, the asymptotic expected yield is given by

$$\begin{aligned} {\mathbb {E}}h_\theta (Y_\infty )=\theta {\mathbb {E}}Y_\infty . \end{aligned}$$

Set $u_\theta (y)=(1-\theta )y$. Using that $u_\theta (Y_\infty ) f(u_\theta (Y_\infty ),\xi _1)$ and $Y_\infty$ have the same distribution, an argument similar to the one from (3.7) shows that

$$\begin{aligned} {\mathbb {E}}Y_\infty = {\mathbb {E}}Y_\infty f(u_\theta (Y_\infty ),\xi _1) = \frac{1}{1-\theta }{\mathbb {E}}{{\overline{F}}}(u_\theta (Y_\infty )). \end{aligned}$$

If the function

$$\begin{aligned} {{\overline{F}}} (y) = y {\mathbb {E}}f(y,\xi _1) \end{aligned}$$

is strictly concave, then by Jensen’s inequality

$$\begin{aligned} \frac{1}{1-\theta }{\mathbb {E}}{{\overline{F}}}(u_\theta (Y_\infty )) \le \frac{1}{1-\theta } {{\overline{F}}}({\mathbb {E}}u_\theta (Y_\infty )). \end{aligned}$$

(3.10)

One can have equality in (3.10) only if $Y_\infty$ is with probability one a constant random variable. This implies that

$$\begin{aligned} {\mathbb {E}}Y_\infty \le {{\overline{F}}} ((1-\theta ) {\mathbb {E}}Y_\infty ). \end{aligned}$$

As we know, in the deterministic model, using the same policy with harvest rate $\theta$, the equilibrium return ${{\widehat{y}}}_\theta$ satisfies

$$\begin{aligned} {{\widehat{y}}}_\theta = {{\overline{F}}}((1-\theta ){{\widehat{y}}}_\theta ). \end{aligned}$$

This together with the strict concavity of ${{\overline{F}}}$ implies that

$$\begin{aligned} {\mathbb {E}}Y_\infty \le {{\widehat{y}}}_\theta . \end{aligned}$$

Equality can only hold if $Y_\infty$ is with probability one a constant, which means the dynamics is deterministic. $\square$

3.3 Bang-Bang Threshold Harvesting

Bang-bang or constant-escapement harvesting strategies are important and are used in many theoretical models as well as in actual harvesting situations, like fisheries. These policies have been shown to be optimal in many instances both for the continuous (Lungu and Øksendal 1997; Alvarez and Shepp 1998; Hening et al. 2019; Alvarez and Hening 2019) and discrete time (Reed 1978, 1979) settings. Constant escapement strategies turned out to be optimal for maximizing discounted yield, asymptotic yield, as well as discounted economic revenue under many different conditions. In discrete time, the work by Reed (1979) implies that a bang-bang policy maximizes the expected discounted net revenue in a discrete time stochastic model. It has not been shown in discrete time, to our knowledge, that the expected steady-state yield is always maximized under a bang-bang strategy. However, both heuristic arguments and analytical results in specific cases hint that these strategies are probably the ones that will in general be optimal. In addition, these are the strategies that are most widely used in fisheries, where the escapement is controlled. We will explore how well these bang-bang strategies do in the stochastic harvesting setting (3.1) in comparison with the deterministic setting (3.6).

Suppose we harvest according to the bang-bang strategy

$$\begin{aligned} h_w(y) := {\left\{ \begin{array}{ll} y-w &{}\quad \text {if } y>w,\\ 0 &{}\quad \text {if } y\le w, \end{array}\right. } \end{aligned}$$

(3.11)

with $w>0$. Let $r_s$ be the maximum self-sustaining level

$$\begin{aligned} r_s = \max \{x~|~{\mathbb {P}}(f(x,\xi _1)\ge 1)=1\}. \end{aligned}$$

We have to differentiate between two cases:

• (1) The level w is self-sustaining, i.e.,

  $$\begin{aligned} {\mathbb {P}}(f(w,\xi _1)\ge 1)=1. \end{aligned}$$

• (2) The level w is not self-sustaining.

Proposition 3.1

If the threshold level w is self-sustaining, then the expected value of the long-term yield ${\mathbb {E}}h_w(Y_\infty )$ is equal to the deterministic yield of the same strategy ${{\overline{G}}} (w)$. The variance of the yield $h_w(Y_\infty )$ is given by

$$\begin{aligned} \sigma ^2(h_w(Y_\infty )):=w^2 {\mathbb {E}}[f^2(w,\xi _1)- {{\overline{f}}}(w)^2]. \end{aligned}$$

Proof

Suppose w is self-sustaining. Then,

$$\begin{aligned} {\mathbb {E}}h_w(Y_\infty )={\mathbb {E}}(Y_\infty -w) = {\mathbb {E}}w f(w,\xi _1)-w={{\overline{F}}}(w)-w={{\overline{G}}}(w). \end{aligned}$$

For the variance of the yield, we get

$$\begin{aligned} \begin{aligned} \sigma ^2(h_w(Y_\infty ))&= {\mathbb {E}}[h_w(Y_\infty )^2] - ({\mathbb {E}}h(Y_\infty ))^2\\&= {\mathbb {E}}[(wf(w,\xi _1)-w)^2] - ({{\overline{F}}}(w)-w)^2\\&={\mathbb {E}}w^2 f^2(w,\xi _1) -2 w^2 {\mathbb {E}}f(w,\xi _1) + w^2 -{{\overline{F}}}^2(w) + 2{{\overline{F}}}(w) w - w^2\\&=w^2 {\mathbb {E}}[f^2(w,\xi _1)-({\mathbb {E}}f(w,\xi _1))^2]. \end{aligned} \end{aligned}$$

This completes the proof. $\square$

Biological Interpretation A self-sustaining threshold w is one where, once the population size goes above w, the environmental fluctuations can never push the population’s size under this threshold. Only in this very special case, it is possible to have the same yield in the stochastic and deterministic settings. Nevertheless, the environmental fluctuations make the variance of the yield increase, which is bad since it can lead to economic losses.

Proposition 3.2

Suppose the following properties hold:

• w is not self-sustaining

• All the levels $x\in [0,r_s]$ are self-sustaining

• ${{\overline{G}}}(x)=x{{\overline{F}}}(x) - x$ is unimodal with its maximum at ${{\overline{x}}}$

• ${{\overline{x}}}$ is self-sustaining.

The expected steady-state yield of the harvesting strategy $h_w$ is strictly greater than the deterministic nominal yield of the same strategy

$$\begin{aligned} {\mathbb {E}}h_w(Y_\infty )>{{\overline{G}}}(w). \end{aligned}$$

Proof

If $h_w$ is given by (3.11) for some $w>0$, then

$$\begin{aligned} u_w(y) := {\left\{ \begin{array}{ll} w &{}\quad \text {if } y>w,\\ y &{}\quad \text {if } y\le w. \end{array}\right. } \end{aligned}$$

(3.12)

Note that $Y_\infty$ will be supported by a subset of $[r_s,\infty )$. By assumption $w>r_s>{{\overline{x}}}$, so that

$$\begin{aligned} {{\overline{G}}}(y) > {{\overline{G}}}(w), y\in [r_s,w]. \end{aligned}$$

This implies that with probability one

$$\begin{aligned} {{\overline{G}}}(Y_\infty ) {\mathbf {1}}\{Y_\infty \in [r_s,w]\}>{{\overline{G}}}(w){\mathbf {1}}\{Y_\infty \in [r_s,w]\}. \end{aligned}$$

Using that the function ${{\overline{G}}}$ is nonincreasing on $[r_s,w]$ together with (3.12) and the last inequality, we see that

$$\begin{aligned} \begin{aligned} {\mathbb {E}}h_w(Y_\infty )&= {\mathbb {E}}{{\overline{G}}}(u_w(Y_\infty ))\\&={\mathbb {E}}[{{\overline{G}}}(Y_\infty ) {\mathbf {1}}\{Y_\infty \in [r_s,w]\} ] + {\mathbb {E}}[{{\overline{G}}}(w) {\mathbf {1}}\{Y_\infty> w\}]\\&> {\mathbb {E}}[{{\overline{G}}}(w) {\mathbf {1}}\{Y_\infty \in [r_s,w]\} ] + {\mathbb {E}}[{{\overline{G}}}(w) {\mathbf {1}}\{Y_\infty > w\}]\\&= {{\overline{G}}}(w). \end{aligned} \end{aligned}$$

with $w>0$. $\square$

Biological Interpretation Suppose one picks a harvesting threshold w which is not self-sustaining, while the maximum yield of the deterministic dynamics happens at a threshold ${{\overline{x}}}<w$ which is self-sustaining. Then, the expected yield of the constant escapement strategy with threshold w for the stochastic dynamics is strictly greater than the expected yield of the same strategy in the deterministic system. The environmental fluctuations will push the population size into the region $({{\overline{x}}}, w)$ and in this region, the function ${{\overline{G}}}$, which measures the size of the deterministic harvest, is strictly decreasing. This makes it more favorable to go below w, something which is not possible in the deterministic dynamics.

4 The Ricker Model: Single Species

In this section, we will provide an in-depth analysis of the Ricker model. Its dynamics is given by the functional response:

$$\begin{aligned} f(x,\xi ) = e^{\rho -\alpha x}. \end{aligned}$$

Here, the randomness comes from $\xi :=(\rho ,\alpha )$. The quantity $\rho _t$ is the fluctuating growth rate and $\alpha _t$ is the competition rate. We assume that $\rho _1, \rho _2,\ldots$ are i.i.d. random variables on ${\mathbb {R}}$, and $\alpha _1,\ldots$ are independent i.i.d. random variables supported on ${\mathbb {R}}$. In this setting, one can see that without harvesting

$$\begin{aligned} r^X(\delta _0) = {\mathbb {E}}\rho _1 \end{aligned}$$

while with harvesting strategy h(y) (or escapement strategy u(y))

$$\begin{aligned} r^Y(\delta _0)= \ln \left( \frac{\partial u}{\partial x}(0) \right) + {\mathbb {E}}\rho _1. \end{aligned}$$

The maximal harvesting rate at 0 which does not lead to extinction is

$$\begin{aligned} \frac{\partial h}{\partial x}(0)<1- e^{- {\mathbb {E}}\rho _1}. \end{aligned}$$

4.1 Maximum Sustainable Yield

We want to see when we can apply the results of Theorem 3.1. Suppose that $\rho _1$ is such that ${\mathbb {E}}e^{\rho _1} = K_1>0$ and assume for simplicity that $\alpha _1>0$ is a constant. Then,

$$\begin{aligned} {{\overline{f}}} (x) = {\mathbb {E}}e^{\rho _1-\alpha _1 x} = K_1 e^{-\alpha _1 x}, \end{aligned}$$

${{\overline{F}}}(x) = x {{\overline{f}}} (x)= xK_1 e^{-\alpha _1 x}$ and ${{\overline{G}}}(x) = x K_1 e^{-\alpha _1 x} - x$. By the analysis from Section 3.1, the deterministic maximum yield is achieved at the point $x_1$ where

$$\begin{aligned} {{\overline{G}}}'(x_1)={{\overline{f}}}(x_1) +x_1 {{\overline{f}}}'(x_1) -1 = K_1e^{-\alpha _1 x_1}-\alpha _1 x_1 K_1e^{-\alpha _1 x_1} - 1=0. \end{aligned}$$

Define the function

$$\begin{aligned} q(x) = K_1 e^{-\alpha _1 x} - \alpha _1 K_1x e^{-\alpha _1 x} - 1, x\in {\mathbb {R}}_+. \end{aligned}$$

Lemma 4.1

If $q(0)<0$, then the equation $q(x)=0$ has no solutions on $(0,\infty )$. If instead $q(0)>0$, then the equation $q(x)=0$ has exactly one solution $x_1>0$.

Proof

Note that

$$\begin{aligned} q'(x)= \alpha _1K_1 e^{-\alpha _1 x}(-2+\alpha _1x) \end{aligned}$$

and

$$\begin{aligned} q''(x)=-\alpha _1^2 K_1 e^{-\alpha _1 x} (-2+\alpha _1 x) + \alpha _1^2 K_1 e^{-\alpha _1 x}. \end{aligned}$$

This shows that starting from $x=0$, the function q decreases to its minimum at $x=\frac{2}{\alpha _1}$ and then increases from there on forever. However, once q goes below zero, it will never go above zero again. This happens because of the above properties and the fact that

$$\begin{aligned} \lim _{x\rightarrow \infty } q(x) =\lim _{x\rightarrow \infty } (K_1 e^{-\alpha _1 x} - \alpha _1 K_1x e^{-\alpha _1 x} - 1)=-1. \end{aligned}$$

This implies that if $q(0)<0$, there are no solutions to $q(x)=0$. If we assume $q(0)>0$, we get in combination with $\lim _{x\rightarrow \infty }<0$ by the intermediate value theorem that there exists a solution to $q(x)=0$. It is also clear by the properties of q(x) that there exists exactly one solution to $q(x)=0$ and the solution has to lie in the interval $(0, \frac{2}{\alpha _1})$. $\square$

In order to be able to achieve this yield in the stochastic setting, according to Theorem 3.1, we need to ensure that $x_1$ is self-sustainable. This boils down to

$$\begin{aligned} {\mathbb {P}}\left( f(x_1,\xi )\ge 1\right) ={\mathbb {P}}\left( e^{\rho _1-\alpha _1 x_1}\ge 1\right) =1, \end{aligned}$$

or

$$\begin{aligned} {\mathbb {P}}\left( \rho _1\ge \alpha _1 x_1 \right) =1. \end{aligned}$$

Since $x_1\in (0, \frac{2}{\alpha _1})$, we see that if $\rho _1\ge 2$ with probability one, then the self-sustaining harvesting policy given by

$$\begin{aligned} h^*(y) := {\left\{ \begin{array}{ll} y-x_1 &{}\quad \text {if } y>x_1,\\ 0 &{}\quad \text {if } y\le x_1, \end{array}\right. } \end{aligned}$$

where $x_1$ is the unique solution to $q(x)=0$, maximizes the expected long-term yield and makes it equal to the deterministic maximal sustainable yield. The value of the optimal expected long-term yield will be

$$\begin{aligned} {\mathbb {E}}h^*(Y_\infty ) = {{\overline{G}}}(x_1) = x_1(K_1 e^{-\alpha _1 x_1}-1). \end{aligned}$$

4.2 Maximal Constant Effort Policy

Suppose we use a constant effort policy $h(x)=\theta x$ for some $\theta \in (0,1)$ and that both $\rho _1$ and $\alpha _1$ are random. The condition for persistence (see Theorems 2.1 and A.3) is given by

$$\begin{aligned} {\mathbb {E}}\rho _1 + \ln (1-\theta )> 0. \end{aligned}$$

This forces that $\theta \in \left( 0,1-e^{-{\mathbb {E}}\rho _1}\right)$. Assume this condition holds so that $Y_t$ converges to a stationary distribution $\pi _\theta$. Then, (3.5) becomes

$$\begin{aligned} 0 = \ln (1-\theta ) +{\mathbb {E}}\rho _1 - (1-\theta ) {\mathbb {E}}\alpha _1 \int _{(0,\infty )}x\,\pi _\theta (\mathrm{d}x). \end{aligned}$$

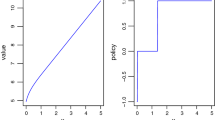
We can use this to show that the long run expected yield is given by (Fig. 1)

$$\begin{aligned} H(\theta ):={\mathbb {E}}h(Y_\infty ) = \int _{(0,\infty )}h(x)\,\pi _\theta (\mathrm{d}x) = \frac{\theta ({\mathbb {E}}\rho _1 +\ln (1-\theta ))}{(1-\theta ) {\mathbb {E}}\alpha _1}. \end{aligned}$$

Fig. 1

Graph of the long-run average yield $H(\cdot )$ as a function of the harvesting rate $\theta$ when ${\mathbb {E}}\rho _1=1$ and ${\mathbb {E}}\alpha _1=1, 2, 3, 4$

The intermediate value theorem shows there is a solution $\theta ^*\in \left( 0,1-e^{-{\mathbb {E}}\rho _1}\right)$ to

$$\begin{aligned} 0=H'(\theta ^*)=\frac{{\mathbb {E}}\rho _1-\theta ^* + \ln (1-\theta ^*)}{ {\mathbb {E}}\alpha _1(1-\theta ^*)^2}. \end{aligned}$$

(4.1)

Since the function $p(x)=\ln (1-x)-x$ is strictly decreasing on (0, 1), we also get that the solution $x^*$ is unique. Taking another derivative, evaluating at $x^*$ and using (4.1) we get

$$\begin{aligned} H''(\theta ^*)= \frac{2{\mathbb {E}}\rho _1-\theta ^*+ 2\ln (1-\theta ^*)-2}{{\mathbb {E}}\alpha _1(1-\theta ^*)^3} = \frac{\theta ^*-2}{{\mathbb {E}}\alpha _1(1-\theta ^*)^3}<0. \end{aligned}$$

This implies that $\theta ^*$ is a global maximum of $H(\theta )$ on $\left[ 0,1-e^{-{\mathbb {E}}\rho _1}\right]$. The maximal expected constant effort harvesting yield will be

$$\begin{aligned} H(\theta ^*) = \frac{(\theta ^*)^2}{(1-\theta ^*) {\mathbb {E}}\alpha _1}. \end{aligned}$$

5 Harvesting of two Interacting Species

In this section, we analyze the situation when there are two interacting species that can be harvested. The system is modeled in the absence of harvesting by

$$\begin{aligned} \begin{aligned} X^1_{t+1}&=X^1_{t} f_1(X^1_t, X^2_t,\xi _{t+1}),\\ X^2_{t+1}&=X^1_{t} f_2(X^1_t, X^2_t,\xi _{t+1}). \end{aligned} \end{aligned}$$

As the theory from “Appendix B” shows, one needs to first look at the quantities

$$\begin{aligned} r_i(\delta _0) = {\mathbb {E}}[\ln f_i(0,\xi _1)], i=1,2. \end{aligned}$$

If $r_i(\delta _0)>0$, then species i survives on its own and converges to a unique invariant probability measure $\mu _i$ supported on $(0,\infty )$. Suppose $r_1(\delta _0)>0, r_2(\delta _0)>0$. The realized per-capita growth rates can be computed via

$$\begin{aligned} r_i(\mu _j)=\int _{(0,\infty )}{\mathbb {E}}[\ln f_i(x,\xi _1)]\mu _j(\mathrm{d}x). \end{aligned}$$

If $r_1(\mu _2)>0$ and $r_2(\mu _1)>0$ by Theorem 2.1, we have the convergence to a unique stationary distribution $\pi$ supported on ${\mathcal {S}}_+$.

5.1 Two Species with Harvesting

Assume next that we harvest according to the strategies $h_1(x_1,x_2)$ and $h_2(x_1, x_2)$. Using (2.13) and (2.14) the dynamics becomes

$$\begin{aligned} Y^i_{t+1} = Y^i_t g_i({\mathbf {Y}}_t, \xi _{t+1}). \end{aligned}$$

(5.1)

where for $i=1,2$

$$\begin{aligned} g_i(y_1,y_2,\xi ) := {\left\{ \begin{array}{ll} \frac{u_i(y_1,y_2)}{y_i} f_i(u_1(y_1,y_2), u_2(y_1,y_2), \xi )&{}\quad \text {if } y_i>0,\\ \left( \frac{\partial u_i}{\partial x_i}(y_1,y_2)\right) f_i(u_1(y_1,y_2), u_2(y_1,y_2), \xi ) &{}\quad \text {if } y_i = 0. \end{array}\right. } \end{aligned}$$

(5.2)

Species $Y^i$ persists on its own with harvesting if

$$\begin{aligned} \begin{aligned} r^Y_i(\delta _0)&= {\mathbb {E}}[\ln g_i(0,0,\xi _1)]\\&= {\mathbb {E}}\ln \left[ \left( \frac{\partial u_i}{\partial x_i}(0,0)\right) f_i(u_1(0,0), u_2(0,0), \xi _1)\right] \\&= \ln \left( \frac{\partial u_i}{\partial x_i}(0,0)\right) + {\mathbb {E}}\ln f_i(0,0, \xi _1)\\&>0. \end{aligned} \end{aligned}$$

(5.3)

or equivalently

$$\begin{aligned} \frac{\partial u_i}{\partial x_i}(0,0)> e^{- {\mathbb {E}}\ln f_i(0,0, \xi _1)}. \end{aligned}$$

(5.4)

At this point, there are three possibilities one may want to look at:

• (1) ${\mathbb {E}}\ln f_i(0,0, \xi _1)>0, i=1,2$ and $\frac{\partial u_i}{\partial x_i}(0,0)> e^{- {\mathbb {E}}\ln f_i(0,0, \xi _1)}, i=1,2$ so that both harvested species persist on their own and have unique invariant probability measures $\mu _1$ and $\mu _2$ on the two positive axes. This describes the harvesting of a competitive system.

• (2) ${\mathbb {E}}\ln f_i(0,0, \xi _1)>0, i=1,2$, $\frac{\partial u_1}{\partial x_1}(0,0)> e^{- {\mathbb {E}}\ln f_1(0,0, \xi _1)}$ and $\frac{\partial u_2}{\partial x_2}(0,0)< e^{- {\mathbb {E}}\ln f_2(0,0,\xi _1)}$. In this case, there are two species which compete with each other, both species persist on their own when there is no harvesting, and species 1 persists with harvesting on its own, while species 2 goes extinct if it is on its own and gets harvested.

• (3) ${\mathbb {E}}\ln f_1(0,0, \xi _1)>0$, ${\mathbb {E}}\ln f_2(0,0, \xi _1)<0$, and $\frac{\partial u_1}{\partial x_1}(0,0)> e^{- {\mathbb {E}}\ln f_1(0,0, \xi _1)}$. In this setting, species 1 is a prey that persists on its own both with harvesting and without harvesting while species 2 is a predator that cannot persist on its own.

Example 5.1

Assume we work with constant threshold harvesting strategies, so that we harvest species 1 according to

$$\begin{aligned} h(y_1,y_2) := {\left\{ \begin{array}{ll} y_1-w &{}\quad \text {if } y_1>w,\\ 0 &{}\quad \text {if } y_1\le w \end{array}\right. } \end{aligned}$$

where $w>0$. We will suppose species 2 does not get harvested. As we have seen in Sect. 3.1, constant escapement harvesting strategies do not influence the persistence of a single species (as long as the threshold is strictly positive). However, we can show that they do change the persistence criteria if there are two interacting species.

Suppose species 1 persists one its own: ${\mathbb {E}}\ln f_1(0,0, \xi _1)>0$. Without harvesting it converges to a stationary distribution ${{\tilde{\mu }}}_1$, while with harvesting it converges to a different stationary distribution $\mu ^{h}_1$. Without harvesting we have

$$\begin{aligned} r_2(\mu _1) = \int _{(0,\infty )}{\mathbb {E}}[\ln f_2(x,0,\xi _1)]{{\tilde{\mu }}}_1(\mathrm{d}x) \end{aligned}$$

while with harvesting

$$\begin{aligned} \begin{aligned} r_2(\mu _1^{h})&= \int _{(0,\infty )}{\mathbb {E}}[\ln g_2(x,0,\xi _1)]\mu _1^{h}(\mathrm{d}x) \\&= \int _{(0,\infty )}{\mathbb {E}}[\ln f_2(u_1(x_1,0),0,\xi _1)]\mu _1^{h}(\mathrm{d}x_1)\\&=\int _{(0,w)}{\mathbb {E}}[\ln f_2(x_1,0,\xi _1)]\mu _1^{h}(\mathrm{d}x_1) + \int _{(w,\infty )}{\mathbb {E}}[\ln f_2(w,0,\xi _1)]\mu _1^{h}(\mathrm{d}x_1). \end{aligned} \end{aligned}$$

(5.5)

We see that in general, since $\mu _1^{h}\ne {{\tilde{\mu }}}_1$, we will have $r_2(\mu _1)\ne r_2(\mu _1^{h})$. Therefore, the persistence criteria are influenced by the threshold policies.

5.2 Two-Dimensional Lotka–Volterra Predator–Prey Model

Suppose that we have model with a predator and a prey, that get harvested proportionally at rates $q,r\in (0,1)$. This means that $u_1(y_1,y_2)=(1-q)y_1$ and $u_2(y_1,y_2)=(1-r)y_2$. Using this in (5.1), we get

$$\begin{aligned} Y^1_{t+1}= & {} Y^1_t \exp \left( \rho _{t+1}+\ln (1-q)-\alpha _{t+1}(1-q)Y^1_t-a_{t+1}(1-r)Y^2_t\right) \\ Y^2_{t+1}= & {} Y^2_t \exp \left( -d_{t+1}+\ln (1-r)-c_{t+1}(1-r)Y^2_t+b_{t+1}(1-q)Y^1_t\right) \end{aligned}$$

where the random coefficients have the following interpretations: $d_{t+1}>0$ is the predator’s death rate, $a_{t+1}>0$ is the predator’s attack rate on the prey, $b_{t+1}>0$ is the predator’s conversion rate of prey, $c_{t+1}>0$ is the predator’s intraspecific competition rate. Let $d_r:={\mathbb {E}}[d_1]-\ln (1-r)>0, \rho _q:={\mathbb {E}}[\rho _1]+\ln (1-q)$ and assume $(\rho _t)_{t\in {\mathbb {Z}}_+}, (\alpha _t)_{t\in {\mathbb {Z}}_+}, (a_t)_{t\in {\mathbb {Z}}_+}, (d_t)_{t\in {\mathbb {Z}}_+}, (c_t)_{t\in {\mathbb {Z}}_+}$ and $(b_t)_{t\in {\mathbb {Z}}_+}$ form independent sequences of i.i.d. random variables. We assume for simplicity that the different random variables have compact support and are absolutely continuous with respect to Lebesgue measure. Then, one can show by Hofbauer et al. (1987), Benaïm and Schreiber (2019) that there is $K>0$ such that the process ${\mathbf {Y}}_t$ eventually enters and then stays forever in the compact set ${\mathcal {K}}=[0,K]^2$. We assume that the boundaries $\{0\}\times (0,K)$ and $(0,K)\times \{0\}$ are accessible for all $q,r\in (0,1)$. This can be easily checked, for example, if $\rho _1$ has (0, L) for some $L>0$ in its support.

As long as $\rho _q>0$, by our previous results, there exists a unique stationary distribution $\mu ^q_1$ on $(0,\infty )\times \{0\}$ and

$$\begin{aligned} \int x_1\,\mu ^q_1(\mathrm{d}x_1) =\frac{\rho _q}{(1-q){\mathbb {E}}\alpha _1} = \frac{{\mathbb {E}}[\rho _1]+\ln (1-q)}{(1-q){\mathbb {E}}\alpha _1}. \end{aligned}$$

This can be used to get

$$\begin{aligned} r_2(\mu ^q_1) = -d_r +{\mathbb {E}}[b_1] \frac{\rho _q}{{\mathbb {E}}\alpha _1}= -({\mathbb {E}}[d_1]-\ln (1-r)) +{\mathbb {E}}[b_1] \frac{{\mathbb {E}}\rho _1 + \ln (1-q)}{{\mathbb {E}}\alpha _1}. \end{aligned}$$

If $r_2(\mu _1^q)<0$, the predator $Y^2$ will go extinct with probability one. This means that, for a given harvesting rate $q\in \left( 0, 1 - e^{-{\mathbb {E}}\rho _1}\right)$ of the prey, the maximal harvesting rate of the predator that does not lead to its extinction is

$$\begin{aligned} r_{\max } = 1- \exp \left( {\mathbb {E}}d_1 - {\mathbb {E}}[b_1] \frac{{\mathbb {E}}\rho _1 + \ln (1-q)}{{\mathbb {E}}\alpha _1} \right) . \end{aligned}$$

As long as $r_2(\mu _1^q)>0$, or equivalently

$$\begin{aligned} \frac{d_r}{\rho _q}< \frac{{\mathbb {E}}b_1}{{\mathbb {E}}\alpha _1}, \end{aligned}$$

we get the existence of a unique invariant probability measure $\mu ^{q,r}_{12}$ supported on a subset of $(0,\infty )^2$. Putting all the conditions together, we get the following classification of the harvested dynamics:

• If

  $$\begin{aligned} \begin{aligned} 0&<q< 1 - e^{-{\mathbb {E}}\rho _1}\\ 0&<r<r_{\max }=1- \exp \left( {\mathbb {E}}d_1 - {\mathbb {E}}[b_1] \frac{{\mathbb {E}}\rho _1 + \ln (1-q)}{{\mathbb {E}}\alpha _1} \right) , \end{aligned} \end{aligned}$$

  then the two species coexist and there is a unique invariant probability measure when

• If

  $$\begin{aligned} \begin{aligned} 0&<q< 1 - e^{-{\mathbb {E}}\rho _1}\\ 1&>r\ge r_{\max }=1- \exp \left( {\mathbb {E}}d_1 - {\mathbb {E}}[b_1] \frac{{\mathbb {E}}\rho _1 + \ln (1-q)}{{\mathbb {E}}\alpha _1} \right) , \end{aligned} \end{aligned}$$

  then the prey persists and the predator goes extinct with probability 1.

• If

  $$\begin{aligned} 1>q\ge 1 - e^{-{\mathbb {E}}\rho _1}, \end{aligned}$$

  then both the prey and the predator go extinct with probability 1.

We depict one example of the three possible regions in Fig. 2. Suppose next that the two species persist. If we set ${{\overline{Y}}}^1 := \int _{(0,\infty )^2} x_1\mu ^{q,r}_{12}(\mathrm{d}u), {{\overline{Y}}}^2 := \int _{(0,\infty )^2} x_2\mu ^{q,r}_{12}(\mathrm{d}u)$, since by (2.5) the per-capita growth rates at stationarity are zero, we get

$$\begin{aligned} r_1(\mu ^{q,r}_{12})= & {} 0 = \rho _q-{\mathbb {E}}[\alpha _{1}](1-q){{\overline{Y}}}^1-{\mathbb {E}}[a_{1}](1-r){{\overline{Y}}}^2\\ r_2(\mu ^{q,r}_{12})= & {} 0=-d_r-{\mathbb {E}}[c_{1}](1-r){{\overline{Y}}}^2+(1-q){\mathbb {E}}[b_{1}]{{\overline{Y}}}^1. \end{aligned}$$

Solving this linear system, we get the unique solution

$$\begin{aligned} \begin{aligned} {{\overline{Y}}}^1&= \frac{{\mathbb {E}}[c_1]\rho _q+{\mathbb {E}}[a_1]d_r}{1-q}\frac{1}{{\mathbb {E}}[\alpha _1]{\mathbb {E}}[c_1]+{\mathbb {E}}[a_1]{\mathbb {E}}[b_1]}\\ {{\overline{Y}}}^2&=\frac{{\mathbb {E}}[b_1]\rho _q-{\mathbb {E}}[\alpha _1]d_r}{1-r}\frac{1}{{\mathbb {E}}[\alpha _1]{\mathbb {E}}[c_1]+{\mathbb {E}}[a_1]{\mathbb {E}}[b_1]} \end{aligned} \end{aligned}$$

(5.6)

Fig. 2

The regions of the harvesting rates q, r for which both species persist, for which just the prey persists and for which both species go extinct. The parameters are ${\mathbb {E}}a_1={\mathbb {E}}d_1= {\mathbb {E}}\alpha _1 = {\mathbb {E}}\rho _1 =1, {\mathbb {E}}b_1=2, {\mathbb {E}}c_1=1.5$

On the other hand, if $r_2(\mu _1^q)<0$, we get by the results from “Appendix B” that $\lim _{t\rightarrow \infty }\frac{\ln Y_t^2}{t}=r_2(\mu _1^q)<0$ so that the predator goes extinct exponentially fast.

Proposition 5.1

If $r_2(\mu _1^q)<0$ and $r_1(\delta _0)=\rho _q>0$, the prey will persist and ${\mathbb {E}}Y_t^1\rightarrow \frac{\rho _q}{(1-q){\mathbb {E}}[\alpha _1]}$ as $t\rightarrow \infty$.

Proof

Pick $\varepsilon , \delta >0$ small. We know that $r_2(\mu _1^q)<0$ implies that $Y^2_t\rightarrow 0$ almost surely as $t\rightarrow \infty$. Because of this, we can find $T>0$ and $\Omega _\delta \subset \Omega$ such that on $\Omega _\delta$ one has $Y^2_t<\varepsilon$ for $t>T$ and ${\mathbb {P}}(\Omega _\delta )\ge 1-\delta$. In other words with probability at least $1-\delta$ one has $Y^2_t<\varepsilon$ for $t>T$. As a result for $t>T$, it is true that

$$\begin{aligned} \begin{aligned} Y^1_t e^{ \rho _{t+1}+\ln (1-q)-\alpha _{t+1}(1-q)Y^1_t-a_{t+1}(1-r)\varepsilon }&<Y^1_{t+1} \\&= Y^1_t e^{ \rho _{t+1}+\ln (1-q)-\alpha _{t+1}(1-q)Y^1_t-a_{t+1}(1-r)Y^2_t} \\&<Y^1_t e^{\rho _{t+1}+\ln (1-q)-\alpha _{t+1}(1-q)Y^1_t} \end{aligned}\nonumber \\ \end{aligned}$$

(5.7)

on $\Omega _\delta$. Let $\mathbb {1}_U$ be the indicator function of the set $U\subset \Omega$. This means that if $\omega \in U$, then $\mathbb {1}_U(\omega )=1$ and if $\omega \notin U$, then $\mathbb {1}_U(\omega )=0$. Define the processes $(Y_t^\varepsilon )_{t\in {\mathbb {Z}}_+}$ and $({{\tilde{Y}}}_t)_{t\in {\mathbb {Z}}_+}$ via

$$\begin{aligned} \begin{aligned} Y_{t+1}^\varepsilon&= Y^\varepsilon _t e^{ \rho _{t+1}+\ln (1-q)-\alpha _{t+1}(1-q)Y^\varepsilon _t-a_{t+1}(1-r)\varepsilon }\\ {{\tilde{Y}}}^1_{t+1}&={{\tilde{Y}}}^1_t e^{\rho _{t+1}+\ln (1-q)-\alpha _{t+1}(1-q){{\tilde{Y}}}^1_t} \end{aligned} \end{aligned}$$

and assume that $Y^\varepsilon _0= {{\tilde{Y}}}^1_0=Y^1_0$. By the results from “Appendix A”, it is easy to see that

$$\begin{aligned} \lim _{t\rightarrow \infty } {\mathbb {E}}{{\tilde{Y}}}^1_{t+1}= \frac{{\mathbb {E}}\rho _1 + \ln (1-q)}{(1-q){\mathbb {E}}\alpha _1} \end{aligned}$$

and

$$\begin{aligned} \lim _{t\rightarrow \infty } {\mathbb {E}}Y^\varepsilon _{t+1}= \frac{{\mathbb {E}}\rho _1 + \ln (1-q)-\varepsilon }{(1-q){\mathbb {E}}\alpha _1}. \end{aligned}$$

By (5.7), we get

$$\begin{aligned} \limsup _{t\rightarrow \infty } {\mathbb {E}}\left[ Y_t^1\right] \le \lim _{t\rightarrow \infty } {\mathbb {E}}{{\tilde{Y}}}^1_{t+1}= \frac{{\mathbb {E}}\rho _1 + \ln (1-q)}{(1-q){\mathbb {E}}\alpha _1} \end{aligned}$$

(5.8)

We let $\Omega _\delta ^C=\Omega \setminus \Omega _\delta$ and note that ${\mathbb {P}}(\Omega ^C_\delta )\le \delta$. Using (5.7) again

$$\begin{aligned} \begin{aligned} \lim _{t\rightarrow \infty } {\mathbb {E}}{{\tilde{Y}}}^\varepsilon _{t+1}-\lim _{t\rightarrow \infty } {\mathbb {E}}\left[ \mathbb {1}_{\Omega ^C_\delta }{{\tilde{Y}}}^\varepsilon _{t+1}\right]&= \lim _{t\rightarrow \infty } {\mathbb {E}}\left[ \mathbb {1}_{\Omega _\delta }{{\tilde{Y}}}^\varepsilon _{t+1}\right] \\&\le \liminf _{t\rightarrow \infty } {\mathbb {E}}\left[ (1-\mathbb {1}_{\Omega ^C_\delta })Y_t^1\right] \\&\le \liminf _{t\rightarrow \infty } {\mathbb {E}}Y_t^1 + \limsup _{t\rightarrow \infty }\left( -{\mathbb {E}}\left[ \mathbb {1}_{\Omega ^C_\delta }Y_t^1\right] \right) \\&\le \liminf _{t\rightarrow \infty } {\mathbb {E}}Y_t^1 - \liminf _{t\rightarrow \infty } {\mathbb {E}}\left[ \mathbb {1}_{\Omega ^C_\delta }Y_t^1\right] . \end{aligned} \end{aligned}$$

The last sequence of inequalities yields

$$\begin{aligned} \lim _{t\rightarrow \infty } {\mathbb {E}}{{\tilde{Y}}}^\varepsilon _{t+1}-\lim _{t\rightarrow \infty }{\mathbb {E}}\left[ \mathbb {1}_{\Omega ^C_\delta }{{\tilde{Y}}}^\varepsilon _{t+1}\right] + \liminf _{t\rightarrow \infty } {\mathbb {E}}\left[ \mathbb {1}_{\Omega ^C_\delta }Y_t^1\right] \le \liminf _{t\rightarrow \infty } {\mathbb {E}}Y_t^1. \end{aligned}$$

Since ${\mathbb {P}}(\Omega ^C_\delta )\le \delta$, we can let $\delta \downarrow 0$ to get

$$\begin{aligned} \frac{{\mathbb {E}}\rho _1 + \ln (1-q)-\varepsilon }{(1-q){\mathbb {E}}\alpha _1}=\lim _{t\rightarrow \infty } {\mathbb {E}}{{\tilde{Y}}}^\varepsilon _{t+1}\le \liminf _{t\rightarrow \infty } {\mathbb {E}}Y_t^1. \end{aligned}$$

(5.9)

Combining (5.8) and (5.9) forces

$$\begin{aligned} \frac{{\mathbb {E}}\rho _1 + \ln (1-q)-\varepsilon }{(1-q){\mathbb {E}}\alpha _1}= & {} \lim _{t\rightarrow \infty } {\mathbb {E}}{{\tilde{Y}}}^\varepsilon _{t+1}\le \liminf _{t\rightarrow \infty } {\mathbb {E}}Y_t^1\le \limsup _{t\rightarrow \infty } {\mathbb {E}}Y_t^1 \le \lim _{t\rightarrow \infty } {\mathbb {E}}{{\tilde{Y}}}^1_{t+1}\\= & {} \frac{{\mathbb {E}}\rho _1 + \ln (1-q)}{(1-q){\mathbb {E}}\alpha _1} \end{aligned}$$

Letting $\varepsilon \downarrow 0$ in the above gives us

$$\begin{aligned} \lim _{t\rightarrow \infty }{\mathbb {E}}Y_t^1= \frac{\rho _q}{(1-q){\mathbb {E}}[\alpha _1]} \end{aligned}$$

which finishes the proof. $\square$

Suppose we want to find the optimal harvesting strategy. Since the profit from harvesting prey or predators might be different, we let $\beta > 0$ represent the relative value of the predator compared to the prey. The problem then becomes maximizing the function

$$\begin{aligned} H(q,r)&:=\lim _{T\rightarrow \infty } {\mathbb {E}}[h_1( Y^1_T)+\beta h_2(Y^2_T)] = \lim _{T\rightarrow \infty } {\mathbb {E}}[q Y^1_T+\beta r Y^2_T]\\&=\lim _{T\rightarrow \infty } \frac{\sum _{n=1}^T q Y^1_n+r\beta Y^2_n}{T} = q {{\overline{Y}}}^1 + r\beta {{\overline{Y}}}^2, \end{aligned}$$

for $q,r\in [0,1]^2$. Using the expressions for ${{\overline{Y}}}^1$, ${{\overline{Y}}}^2$ from (5.6) together with Proposition 5.1, with the understanding that we set ${{\overline{Y}}}^1=\frac{\rho _q}{(1-q){\mathbb {E}}[\alpha _1]}, {{\overline{Y}}}^2=0$ if the prey persists and the predator goes extinct, and the domain regions identified above we get

$$\begin{aligned} H(q,r) = \left\{ \begin{array}{ll} \left( \frac{{\mathbb {E}}[c_1]q\rho _q+{\mathbb {E}}[a_1]qd_r}{1-q} + \frac{\beta {\mathbb {E}}[b_1]r\rho _q-\beta {\mathbb {E}}[\alpha _1]rd_r}{1-r}\right) \frac{1}{{\mathbb {E}}[\alpha _1]{\mathbb {E}}[c_1]+{\mathbb {E}}[a_1]{\mathbb {E}}[b_1]} &{} \quad r<r_{\max }, 0<q< 1 - e^{-{\mathbb {E}}\rho _1} \\ \frac{q\rho _q}{(1-q){\mathbb {E}}[\alpha _1]} &{} \quad r\ge r_{\max }, 0<q< 1 - e^{-{\mathbb {E}}\rho _1}\\ 0&{}\quad q\ge 1 - e^{-{\mathbb {E}}\rho _1}. \end{array} \right. \end{aligned}$$

Fig. 3

The graph of H(q, r). The parameters are $\beta = {\mathbb {E}}a_1={\mathbb {E}}d_1= {\mathbb {E}}\alpha _1 = {\mathbb {E}}\rho _1 =1, {\mathbb {E}}b_1=2, {\mathbb {E}}c_1=1.5$

Fig. 4

The graph of H(q, r). The parameters are $\beta = 5, {\mathbb {E}}a_1={\mathbb {E}}d_1= {\mathbb {E}}\alpha _1 = {\mathbb {E}}\rho _1 =1, {\mathbb {E}}b_1=2, {\mathbb {E}}c_1=1.5$

Economic Interpretation We present the first rigorous results regarding the harvesting of both species from a predator–prey system. First of all, we are able to describe the results of harvesting by splitting the $q-r$ plane, where q and r represent the prey and predator proportional harvest rates, into a region where both species go extinct, a region where the species coexist, and a region where only the prey persists—see Fig. 2. It is never optimal to harvest both the predator and the prey. If the relative price $\beta$ of the predator compared to the prey is low, it is always optimal to harvest the predator to extinction (see Fig. 3). This then lets the prey population increase, and one gains by harvesting the prey. If instead the relative price $\beta$ is high, it is optimal to never harvest the prey (see Fig. 4). This leads to an increase in the predator population, which then increases the harvesting yield of the predators. This result is the first of its kind for stochastic harvesting—it complements the deterministic results of Myerscough et al. (1992), Dai and Tang (1998), Martin and Ruan (2001), Xia et al. (2009).

5.3 Two-Dimensional Lotka–Volterra Competition Mode

We look at a two-species discrete Lotka–Volterra competition model when the two species get harvested proportionally at rates $q,r\in (0,1)$. The harvested dynamics is given by

$$\begin{aligned} Y^1_{t+1}= & {} Y^1_t \exp \left( \rho ^1_{t+1}+\ln (1-q)-\alpha _{t+1}(1-q)Y^1_t-a_{t+1}(1-r)Y^2_t\right) \\ Y^2_{t+1}= & {} Y^2_t \exp \left( \rho ^2_{t+1}+\ln (1-r)-c_{t+1}(1-r)Y^2_t-b_{t+1}(1-q)Y^1_t\right) \end{aligned}$$

We set ${\overline{\rho }}^1_q:={\mathbb {E}}[\rho ^1_1]+\ln (1-q)$ and ${\overline{\rho }}^2_q:={\mathbb {E}}[\rho ^2_1]+\ln (1-r)>0$. We assume the different random coefficients are independent and form sequences of i.i.d. random variables. Furthermore, we make the same assumptions that were made in the predator–prey system. These ensure that the state space is compact and that the boundaries are accessible.

As long as ${\overline{\rho }}^1_q, {\overline{\rho }}^2_r>0$, by our previous results, there exists a unique stationary distribution $\mu ^q_1$ (respectively $\mu ^r_2$) on $(0,\infty )\times \{0\}$ (respectively, $\{0\}\times (0,\infty )$) and

$$\begin{aligned} \int x_1\,\mu ^q_1(\mathrm{d}x_1) =\frac{{\overline{\rho }}^1_q}{(1-q){\mathbb {E}}\alpha _1}= & {} \frac{{\mathbb {E}}[\rho ^1_1]+\ln (1-q)}{(1-q){\mathbb {E}}\alpha _1},\\ \int x_2\,\mu ^r_2(\mathrm{d}x_2) =\frac{{\overline{\rho }}^2_r}{(1-r){\mathbb {E}}c_1}= & {} \frac{{\mathbb {E}}[\rho ^2_1]+\ln (1-r)}{(1-r){\mathbb {E}}c_1}. \end{aligned}$$

One can then compute the per-capita growth rates

$$\begin{aligned} r_1(\mu ^r_2)= & {} {\overline{\rho }}_q^1 - {\mathbb {E}}a_1 (1-r) \int x_2\,\mu ^r_2(\mathrm{d}x_2) \\= & {} ({\mathbb {E}}[\rho ^1_1]+\ln (1-q)) -{\mathbb {E}}a_1 \frac{{\mathbb {E}}\rho ^2_1 + \ln (1-r)}{{\mathbb {E}}c_1}, \end{aligned}$$

and

$$\begin{aligned} r_2(\mu ^q_1)= & {} {\overline{\rho }}_r^2 - {\mathbb {E}}b_1 (1-q) \int x_1\,\mu ^q_1(\mathrm{d}x_1) \\= & {} ({\mathbb {E}}[\rho ^2_1]+\ln (1-r)) -{\mathbb {E}}b_1 \frac{{\mathbb {E}}\rho ^1_1 + \ln (1-q)}{{\mathbb {E}}\alpha _1}. \end{aligned}$$

We get the following classification of the dynamics:

• If

  $$\begin{aligned} \begin{aligned} 0&<q< 1 - e^{-{\mathbb {E}}\rho ^1_1}\\ 0&<r< 1 - e^{-{\mathbb {E}}\rho ^2_1}\\ \frac{{\mathbb {E}}a_1}{{\mathbb {E}}c_1}&< \frac{{\mathbb {E}}\rho ^1_1 +\ln (1-q)}{{\mathbb {E}}\rho ^2_1 + \ln (1-r)} < \frac{{\mathbb {E}}\alpha _1}{{\mathbb {E}}b_1}, \end{aligned} \end{aligned}$$

  then the two species coexist and the process converges to its unique invariant probability measure.

• If

  $$\begin{aligned} \begin{aligned} 0&<q< 1 - e^{-{\mathbb {E}}\rho ^1_1}\\ 0&<r< 1 - e^{-{\mathbb {E}}\rho ^2_1}\\ \frac{{\mathbb {E}}a_1}{{\mathbb {E}}c_1}&< \frac{{\mathbb {E}}\rho ^1_1 +\ln (1-q)}{{\mathbb {E}}\rho ^2_1 + \ln (1-r)}\\ \frac{{\mathbb {E}}b_1}{{\mathbb {E}}\alpha _1}&> \frac{{\mathbb {E}}\rho ^2_1 +\ln (1-r)}{{\mathbb {E}}\rho ^1_1 + \ln (1-q)}, \end{aligned} \end{aligned}$$

  then species 1 persists and species 2 goes extinct with probability 1.

• If

  $$\begin{aligned} \begin{aligned} 0&<q< 1 - e^{-{\mathbb {E}}\rho ^1_1}\\ 0&<r< 1 - e^{-{\mathbb {E}}\rho ^2_1}\\ \frac{{\mathbb {E}}a_1}{{\mathbb {E}}c_1}&> \frac{{\mathbb {E}}\rho ^1_1 +\ln (1-q)}{{\mathbb {E}}\rho ^2_1 + \ln (1-r)}\\ \frac{{\mathbb {E}}b_1}{{\mathbb {E}}\alpha _1}&< \frac{{\mathbb {E}}\rho ^2_1 +\ln (1-r)}{{\mathbb {E}}\rho ^1_1 + \ln (1-q)}, \end{aligned} \end{aligned}$$

  then species 2 persists and species 1 goes extinct with probability 1.

• If $(Y_0^1, Y_0^2)=(x,y)\in (0,\infty )^2$, then let $p_{x,y} = {\mathbb {P}}(Y_t^1\rightarrow \mu _1^q, Y_t^2\rightarrow 0~|~(Y_0^1, Y_0^2)=(x,y))$. If

  $$\begin{aligned} \begin{aligned} 0&<q< 1 - e^{-{\mathbb {E}}\rho ^1_1}\\ 0&<r< 1 - e^{-{\mathbb {E}}\rho ^2_1}\\ \frac{{\mathbb {E}}a_1}{{\mathbb {E}}c_1}&> \frac{{\mathbb {E}}\rho ^1_1 +\ln (1-q)}{{\mathbb {E}}\rho ^2_1 + \ln (1-r)}\\ \frac{{\mathbb {E}}b_1}{{\mathbb {E}}\alpha _1}&> \frac{{\mathbb {E}}\rho ^2_1 +\ln (1-r)}{{\mathbb {E}}\rho ^1_1 + \ln (1-q)} \end{aligned} \end{aligned}$$

  then we have bistability, that is, $p_{x,y}\in (0,1)$ and $1-p_{x,y}= {\mathbb {P}}(Y_t^2\rightarrow \mu _2^r, Y_t^1\rightarrow 0~|~(Y_0^1, Y_0^2)=(x,y))$.

Note that for a given set of coefficients one cannot have all the 4 regions if we vary q and r. There are two possibilities, each having three regions. One is to have coexistence, the persistence of species 1 and extinction of species 2, or the extinction of species 1 and the persistence of species 2 (see Fig. 5). The other possibility is to have bistability, the persistence of species 1 and extinction of species 2, or the extinction of species 1 and the persistence of species 2 (see Fig. 6).

Biological Interpretation An important controversy in ecology addressed the relative importance of competition and predation in determining the structure of food chains—ultimately it was shown that predation can be just as important as competition (Sih et al. 1985). There is strong evidence from multiple ecological systems, that predation is capable of forcing coexistence among competing species, some of which would go extinct in the absence of predation (Caswell 1978; Crowley 1979; Hsu 1981). Our results show that harvesting can have similar effects to a predator which can lead two competitors to coexist due to predator-mediated coexistence. This leads to the concept of harvesting-mediated coexistence. For example, suppose that

$$\begin{aligned} \frac{{\mathbb {E}}a_1}{{\mathbb {E}}c_1}< \frac{{\mathbb {E}}\alpha _1}{{\mathbb {E}}b_1}< \frac{{\mathbb {E}}\rho ^1_1 }{{\mathbb {E}}\rho ^2_1 }. \end{aligned}$$

This implies that if there is no harvesting species 1 persists and species 2 goes extinct. It is clear that there exists $q\in (0,1)$ such that

$$\begin{aligned} \frac{{\mathbb {E}}a_1}{{\mathbb {E}}c_1}< \frac{{\mathbb {E}}\rho ^1_1 +\ln (1-q)}{{\mathbb {E}}\rho ^2_1 } < \frac{{\mathbb {E}}\alpha _1}{{\mathbb {E}}b_1} \end{aligned}$$

which leads to coexistence. This shows that if one species has a competitive advantage so that without harvesting it drives the other competitor extinct, one can harvest this dominant species and get coexistence. This result is similar to the setting studied by Slobodkin (1961) who showed that by removing a constant fraction of the prey population continuously one could reverse the outcome of competition if the losing competitor has a higher growth rate at low densities. In the harvesting setting, similar results have been shown by Yodzis (1976) where the author studied constant-catch harvesting, i.e., one harvests the same amount every year. Yodzis showed that such harvesting can possibly eliminate competitive dominance and result in stable coexistence. However, if there are environmental fluctuations, the harvesting can increase (Yodzis 1977) the niche separation for stable coexistence which can lead to extinctions.

Fig. 5

Figure showing the regions of the harvesting rates q, r for which both species persist, for which just the species 1 persists, and the region for which just species 2 persists. The parameters are ${\mathbb {E}}a_1={\mathbb {E}}b_1=1, {\mathbb {E}}c_1={\mathbb {E}}\alpha _1=1.5, {\mathbb {E}}\rho ^1_1 =1, {\mathbb {E}}\rho ^2_1 =1.5$

Fig. 6

Figure showing the regions of the harvesting rates q, r for which there is bistability, for which just the species 1 persists, and the region for which just species 2 persists. The parameters are ${\mathbb {E}}a_1=1.5, {\mathbb {E}}b_1=2, {\mathbb {E}}c_1=1, {\mathbb {E}}\alpha _1=1, {\mathbb {E}}\rho ^1_1 =1, {\mathbb {E}}\rho ^2_1 =1.5$

Fig. 7

The graph of H(q, r). The parameters are $\beta =1, {\mathbb {E}}a_1={\mathbb {E}}b_1=1, {\mathbb {E}}c_1={\mathbb {E}}\alpha _1=1.5, {\mathbb {E}}\rho ^1_1 =1, {\mathbb {E}}\rho ^2_1 =1.5$

Fig. 8

The graph of H(q, r). The parameters are $\beta =1, {\mathbb {E}}a_1={\mathbb {E}}b_1=1, {\mathbb {E}}c_1={\mathbb {E}}\alpha _1=1.5, {\mathbb {E}}\rho ^1_1 =1.4, {\mathbb {E}}\rho ^2_1 =1.5$

Fig. 9

The graph of H(q, r). The parameters are $\beta =1, {\mathbb {E}}a_1={\mathbb {E}}b_1=1.4, {\mathbb {E}}c_1={\mathbb {E}}\alpha _1=1.5, {\mathbb {E}}\rho ^1_1 =1.4, {\mathbb {E}}\rho ^2_1 =1.5$

If there is coexistence and the system converges to an invariant probability measure $\mu _{12}^{q, r}$ on $(0,\infty )^2$, we see by (2.5) that the per-capita growth rates at stationarity are zero. This shows that

$$\begin{aligned} r_1(\mu _{12})=0= & {} {\overline{\rho }}_q^1-{\mathbb {E}}[\alpha _{1}](1-q){{\overline{Y}}}^1-{\mathbb {E}}[a_{1}](1-r){{\overline{Y}}}^2\\ r_2(\mu _{12})=0= & {} {\overline{\rho }}_r^2-{\mathbb {E}}[c_{1}](1-r){{\overline{Y}}}^2-(1-q){\mathbb {E}}[b_{1}]{{\overline{Y}}}^1, \end{aligned}$$

whereas before ${{\overline{Y}}}^1 = \int _{(0,\infty )^2} x_1\mu ^{q,r}_{12}(du), {{\overline{Y}}}^2= \int _{(0,\infty )^2} x_2\mu ^{q,r}_{12}(du)$ are the expected values of the two species at stationarity. Solving this linear system yields the unique solution

$$\begin{aligned} {{\overline{Y}}}^1= & {} \frac{{\mathbb {E}}[c_1]{\overline{\rho }}^1_q-{\mathbb {E}}[a_1]{\overline{\rho }}^2_r}{1-q} \frac{1}{{\mathbb {E}}[\alpha _1]{\mathbb {E}}[c_1]-{\mathbb {E}}[a_1]{\mathbb {E}}[b_1]}\\ {{\overline{Y}}}^2= & {} \frac{{\mathbb {E}}[\alpha _1]{\overline{\rho }}^2_r-{\mathbb {E}}[b_1] {\overline{\rho }}^1_q}{1-r}\frac{1}{{\mathbb {E}}[\alpha _1]{\mathbb {E}}[c_1]-{\mathbb {E}}[a_1]{\mathbb {E}}[b_1]}. \end{aligned}$$

One can prove the following analogue of Proposition 5.1.

Proposition 5.2

If $r_2(\mu ^q_1)<0$ and $r_1(\mu ^r_2)>0$, then species 1 will persist and ${\mathbb {E}}Y_t^1\rightarrow \frac{{\overline{\rho }}^1_q}{(1-q){\mathbb {E}}[\alpha _1]}$ as $t\rightarrow \infty$. If $r_1(\mu ^r_2) <0$ and $r_2(\mu ^q_1)>0$, then species 2 will persist and ${\mathbb {E}}Y_t^2\rightarrow \frac{{\overline{\rho }}^2_r}{(1-r){\mathbb {E}}[c_1]}$ as $t\rightarrow \infty$.

Suppose the coefficients are such that the coexistence of the two species is possible. We are interested in maximizing the function

$$\begin{aligned} H(q,r)=\lim _{T\rightarrow \infty } {\mathbb {E}}[q Y^1_T+\beta rY^2_T] =\lim _{T\rightarrow \infty } \frac{\sum _{n=1}^T q Y^1_n+r\beta Y^2_n}{T} = q {{\overline{Y}}}^1 + r\beta {{\overline{Y}}}^2, \end{aligned}$$

where $\beta > 0$ represents the relative value of species 2 compared to species 1. Using the expressions for ${{\overline{Y}}}^1$, ${{\overline{Y}}}^2$, together with Proposition 5.2 and the domain regions identified above we get

$$\begin{aligned} H(q,r) = \left\{ \begin{array}{ll} \left( q\frac{{\mathbb {E}}[c_1]{\overline{\rho }}^1_q-{\mathbb {E}}[a_1]{\overline{\rho }}^2_r}{1-q} + \beta r\frac{{\mathbb {E}}[\alpha _1]{\overline{\rho }}^2_r-{\mathbb {E}}[b_1]{\overline{\rho }}^1_q}{1-r}\right) \frac{1}{{\mathbb {E}}[\alpha _1]{\mathbb {E}}[c_1]-{\mathbb {E}}[a_1]{\mathbb {E}}[b_1]} &{} \quad r_2(\mu ^q_1)>0, r_1(\mu ^r_2)>0 \\ q \frac{{\overline{\rho }}^1_q}{(1-q){\mathbb {E}}[\alpha _1]} &{} \quad r_2(\mu ^q_1)<0, r_1(\mu ^r_2)>0\\ \beta r\frac{{\overline{\rho }}^2_r}{(1-r){\mathbb {E}}[c_1]} &{} \quad r_2(\mu ^q_1)>0, r_1(\mu ^r_2)<0\\ 0&{}\quad q\ge 1 - e^{-{\mathbb {E}}\rho ^1_1}, r\ge 1 - e^{-{\mathbb {E}}\rho ^2_1}. \end{array} \right. \end{aligned}$$

Economic Interpretation Depending on the interaction coefficients, growth rates, and the relative value of the species there are three possible scenarios for the optimal harvesting strategy. In one case, we harvest species 1 to extinction and maximize the yield from harvesting species 2. In other instances, it is best to harvest species 2 to extinction and maximize the harvest from species 1. The third instance is the one of coexistence: the optimal harvesting strategy is to keep both species alive. In Fig. 7, we can see that since the growth rate of species 2 is greater than that of species 1, while the other coefficients are identical, it is optimal to harvest species 1 to extinction and to get a higher harvesting yield from species 2. In the example from Fig. 8, when the species are similar to each other, it is optimal to keep both species alive. However, once we increase the competition, it becomes optimal to drive one species extinct through harvesting (see Fig. 9). These examples show that there is a delicate balance one has to take into account when looking for the optimal harvesting strategies. The intra- and interspecific competition rates, growth rates, and the prices of the species turn out to play key roles. These results show that trying to maximize economic gain in a multispecies competitive ecosystem can lead to the extinction of the species which are not as valuable economically. If one wants to conserve species, this has to be factored in and a more complex harvesting model has to be considered.

Appendices

Appendix A. Criteria for Persistence and Extinction

1.1 Single Species System

Suppose we have one species whose dynamics is given by

$$\begin{aligned} X_{t+1} = X_t f(X_t, \xi _{t+1}) \end{aligned}$$

(A.1)

We present a few known results which give the existence of a unique invariant probability measure. These results appear in work by Ellner (1984, 1989), Vellekoop and Högnäs (1997), Fagerholm and Högnäs (2002), Schreiber (2012).

Theorem A.1

Assume that $F(x,\xi )=xf(x,\xi )$ is continuously differentiable and strictly increasing in x, and $f(x,\xi )$ is strictly decreasing in x. If ${\mathbb {E}}[\ln f(0,\xi _1)]>0$ and $\lim _{x\rightarrow \infty } {\mathbb {E}}[\ln f(x,\xi _1)]<0$, then there exists a positive invariant probability measure $\mu$ and the distribution of $X_t$ converges weakly to $\mu$ whenever $X_0=x>0$.

Sometimes, if monotonicity fails, one can make use of the following result (Vellekoop and Högnäs 1997).

Theorem A.2

Assume that

$$\begin{aligned} f(x,\xi )=\lambda h(x)^{-\xi } \end{aligned}$$

where g is a positive differentiable function such that $x\mapsto xh'(x)/h(x)$ is strictly increasing on $[0,\infty )$. Assume ${\mathbb {E}}\xi _1, {\mathbb {E}}\xi _1^2 <\infty$ and $\xi _1$ has a positive density on (0, L) for some $0<L<\infty$. Then, there is a positive invariant probability measure $\mu$ and the distribution of $X_t$ converges to $\mu$ whenever $X_0=x>0$.

We note that the above theorem provides a classification of the stochastic Ricker model if the random variable $\xi _1$ has a density and is supported on (0, L) for some $L>0$. One can also fully classify (Fagerholm and Högnäs 2002) the stochastic Ricker model if the random coefficients do not have compact support.

Theorem A.3

Consider the stochastic Ricker model $X_{t+1} = X_t \exp (r_{t+1}-a_{t+1}X_t)$ where

• $r_1,\ldots$ is a sequence of i.i.d. random variables such that ${\mathbb {E}}[r_1]<\infty$ and $r_1$ has positive density on $(-\infty ,+\infty )$,

• $a_1,\ldots$ is a sequence of positive i.i.d. random variables independent of $r_t$ such that ${\mathbb {E}}[a_1]<\infty$ and

• there exists $x_c$ such that ${\mathbb {E}}[\exp (r_1x)]<\infty$ for all $x\in [0, x_c]$.

Then, if ${\mathbb {E}}[r_1]<0$, $X_t\rightarrow 0$ with probability 1, while if ${\mathbb {E}}[r_1]>0$, there is a positive invariant measure $\mu$ such that $X_t$ converges weakly to $\mu$.

1.2 Two Species Systems

Suppose we have a two species system. The following result appeared in work by Ellner (1989).

Theorem A.4

Assume the following assumptions are satisfied

• For each $i=1,2$, there exists a positive invariant measure $\mu _i$ such that the distribution $\mu _i$ such that the distribution of $X_t^i$ converges to $\mu _i$ weakly whenever $X_0^i>0$ and $X_0^j=0$.

• The mean per capita growth rates $r_i({\mathbf {x}})$ are continuous functions.

• The process ${\mathbf {X}}$ is irreducible on $(0,\infty )\times (0,\infty )$,

• For any Borel measurable $A\subset {\mathbb {R}}_+^2$ we have ${\mathbb {P}}({\mathbf {X}}_1\in A|{\mathbf {X}}_0={\mathbf {x}}_n) \rightarrow {\mathbb {P}}({\mathbf {X}}_1\in A|{\mathbf {X}}_0={\mathbf {x}})$ whenever ${\mathbf {x}}_n\rightarrow {\mathbf {x}}$.

• For any ${\mathbf {x}}\in {\mathbb {R}}_+^2$, $\sup _{t>0}{\mathbb {E}}[\ln ^+ X_t^i~|~{\mathbf {X}}_0={\mathbf {x}}]<\infty$ for $i=1,2$.

If $r_1(\mu _2)>0$ and $r_2(\mu _1)>0$, then there exists a unique positive invariant measure $\mu$ and the distribution of ${\mathbf {X}}_t$ converges to $\mu$ weakly whenever $X_0^1, X_0^2>0$.

1.3 General Criteria for Coexistence

Assume we have a general n species system modeled by

$$\begin{aligned} X^i_{t+1} = X_t^i f_i({\mathbf {X}}_t, \xi _{t+1}), i=1,\ldots ,n. \end{aligned}$$

(A.2)

The subset ${\mathcal {S}}\subset {\mathbb {R}}_+^n$ will denote the state space of the dynamics. It will either be a compact subset of ${\mathbb {R}}_+^n$ or all of ${\mathbb {R}}_+^n$. The coexistence set is the subset ${\mathcal {S}}_+=\{{\mathbf {x}}\in {\mathcal {S}}~|~x_i>0, i=1,\ldots n\}$ of the state space where no species is extinct. We will make the following assumptions:

(A1):

$\xi _1,\ldots ,\xi _n,\ldots$ is a sequence of i.i.d. random variables taking values in a Polish space E.

(A2):

For each i the fitness function $f_i({\mathbf {x}},\xi )$ is continuous in ${\mathbf {x}}$, measurable in $({\mathbf {x}},\xi )$ and strictly positive.

(A3):

If the dynamics is unbounded: There exists a function $V:{\mathcal {S}}_+\rightarrow {\mathbb {R}}_+$ and constants $\gamma _1,\gamma _3, C>0$ and $\rho \in (0,1)$ such that for all ${\mathbf {x}}\in {\mathcal {S}}_+$ we have

(i):

$V({\mathbf {x}})\ge |{\mathbf {x}}|^{\gamma _1}+1$,

(ii):

${\mathbb {E}}\left[ V({\mathbf {x}}^\top f({\mathbf {x}},\xi _1))\ell ({\mathbf {x}},\xi _1)\right] \le \rho V({\mathbf {x}})+C$, where

$$\begin{aligned} \ell ({\mathbf {x}},\xi ):=\left( \max _{i=1}^n \left\{ \max \left\{ f_i({\mathbf {x}},\xi ), \frac{1}{f_i({\mathbf {x}},\xi )}\right\} \right\} \right) ^{\gamma _3}. \end{aligned}$$

(A4):

If the dynamics is bounded: There exists a constant $\gamma _3>0$ such that for all ${\mathbf {x}}\in {\mathcal {S}}_+$ we have

$$\begin{aligned} {\mathbb {E}}\left[ \ell ({\mathbf {x}},\xi _1)\right] <\infty . \end{aligned}$$

Remark A.1

In particular, if one supposes the conditions

• 1) There is a compact subset $K\subset {\mathbb {R}}_+^n\times {\mathbb {R}}^{\kappa _0}$ such that all solutions ${\mathbf {X}}_t$ satisfy ${\mathbf {X}}_t\in K$ for $t\in {\mathbb {Z}}_+$ sufficiently large;

• 2) For all $i=1,2,\ldots ,n$,

  $$\begin{aligned} \sup _{{\mathbf {x}},\xi }|\ln f_i({\mathbf {x}},\xi )|<\infty ; \end{aligned}$$

then assumption (A4) is satisfied.

Assumptions (A1) and (A2) ensure that ${\mathbf {X}}_t$ is a Feller process that lives on ${\mathcal {S}}_{+}$, i.e., ${\mathbf {X}}_t\in {\mathcal {S}}_+, t\in {\mathbb {Z}}_+$ whenever ${\mathbf {X}}_0\in {\mathcal {S}}_{+}$. One has to make the extra assumptions (A3) or (A4) in order to ensure the process does not blow up or fluctuate too abruptly between 0 and $\infty$. We note that most ecological models will satisfy these assumptions. For more details see the work by Benaïm and Schreiber (2019), Hening et al. (2020).

We will follow the notation, methods and results developed by Meyn and Tweedie (1992). A point ${\mathbf {y}}\in {\mathbb {R}}_+^n$ is said to be accessible from ${\mathbf {x}}\in {\mathcal {S}}_+$ if for every neighborhood U of y, there exists $t\ge 0$ such that $P_t({\mathbf {x}},U)>0$. Define

$$\begin{aligned} \Gamma _{\mathbf {x}}:=\{{\mathbf {y}}\in {\mathcal {S}}_+ ~|~{\mathbf {y}}~\text {is accessible from}~{\mathbf {x}}\} \end{aligned}$$

and for $A\subset {\mathbb {R}}_+^n$

$$\begin{aligned} \Gamma _A=\bigcap _{{\mathbf {x}}\in A}\Gamma _{\mathbf {x}}. \end{aligned}$$

Note that $\Gamma _A$ is the set of points which are accessible from every point of A. We say a set A is accessible if for all ${\mathbf {x}}\in {\mathbb {R}}_+^{n,\circ }$

$$\begin{aligned} \Gamma _{{\mathbf {x}}}\cap A\ne \emptyset . \end{aligned}$$

Suppose there exist ${\mathbf {x}}^*\in \Gamma _{{\mathcal {S}}_+}$, a neighborhood U of ${\mathbf {x}}^*$, and a nonzero measure $\phi$ on ${\mathcal {S}}_+$, such that for any ${\mathbf {x}}\in U$ there is $m^*\in {\mathbb {Z}}_+$ such that

$$\begin{aligned} {\mathbb {P}}_ {\mathbf {x}}({\mathbf {X}}_{m^*}\in \cdot )\ge \phi (\cdot ). \end{aligned}$$

We will assume that such conditions are satisfied in our models. In many cases, it is not hard to check that these conditions hold—see Ellner (1989), Hening et al. (2020). Suppose the dynamics happens in either a compact subset of ${\mathbb {R}}_+^n$ or in ${\mathbb {R}}_+^n$. We denote the state space of the dynamics by ${\mathcal {S}}$. We define the extinction set, where at least one species is extinct, by

$$\begin{aligned} {\mathcal {S}}_0:=\{{\mathbf {x}}\in {\mathcal {S}}~:~\min _i x_i=0\}. \end{aligned}$$

For any $\eta >0$ let

$$\begin{aligned} {\mathcal {S}}_\eta :=\{{\mathbf {x}}\in {\mathcal {S}}~:~\min _i x_i\le \eta \} \end{aligned}$$

be the subset of ${\mathcal {S}}$ where at least one species is within $\eta$ of extinction. Denote by ${\mathcal {M}}$ the set of all ergodic invariant probability measures supported on ${\mathcal {S}}_0$ and by ${{\,\mathrm{Conv}\,}}({\mathcal {M}})$ the set of all invariant probability measures supported on ${\mathcal {S}}_0$. We say (A.2) is stochastically persistent in probability (Chesson 1982) if for all $\varepsilon >0$ there exists $\eta (\varepsilon )=\eta >0$ such that for all ${\mathbf {x}}\in {\mathcal {S}}_+$

$$\begin{aligned} \liminf _{t\rightarrow \infty } {\mathbb {P}}_{{\mathbf {x}}}\{{\mathbf {X}}_t\notin S_\eta \}>1-\varepsilon . \end{aligned}$$

For any $t\in {\mathbb {N}}$ define the normalized occupation measure

$$\begin{aligned} \Pi _t(B):=\frac{1}{t}\sum _{s=1}^t\delta _{{\mathbf {X}}(s)}(B) \end{aligned}$$

where $\delta _{{\mathbf {X}}(s)}$ is the Dirac measure at ${\mathbf {X}}(s)$ and B is any Borel subset of ${\mathcal {S}}$. Note that $\Pi _t$ is a random probability measure and $\Pi _t(B)$ tells us the proportion of time the system spends in B up to time t. Denote the (random) set of $\hbox {weak}^*$-limit points of $(\Pi _t)_{t\in {\mathbb {N}}}$ by ${\mathcal {U}}={\mathcal {U}}(\omega )$. We say (A.2) is almost surely stochastically persistent (Schreiber 2012; Benaïm and Schreiber 2019) if for all $\varepsilon >0$ there exists $\eta (\varepsilon )=\eta >0$ such that for all ${\mathbf {x}}\in {\mathcal {S}}_+$

$$\begin{aligned} \liminf _{t\rightarrow \infty } \Pi _t({\mathcal {S}}\setminus {\mathcal {S}}_\eta )>1-\varepsilon , ~{\mathbf {X}}(0)={\mathbf {x}}. \end{aligned}$$

The following general theorem gives us persistence for a general n species system.

Theorem A.5

Suppose that for all $\mu \in {{\,\mathrm{Conv}\,}}({\mathcal {M}})$ we have

$$\begin{aligned} \max _{i} r_i(\mu )>0. \end{aligned}$$

(A.3)

Then, the system is almost surely stochastically persistent and stochastically persistent in probability. Under additional irreducibility conditions, there exists a unique invariant probability measure $\pi$ on ${\mathcal {S}}_+$ and as $t\rightarrow \infty$ the distribution of ${\mathbf {X}}_t$ converges in total variation to $\pi$ whenever ${\mathbf {X}}(0)={\mathbf {x}}\in {\mathcal {S}}_+$. Furthermore, if $w:{\mathcal {S}}_+\rightarrow {\mathbb {R}}$ is continuous and either bounded or satisfies

$$\begin{aligned} w({\mathbf {x}})\le {\mathbb {E}}\left[ V({\mathbf {x}}^\top f({\mathbf {x}},\xi _1))\ell ({\mathbf {x}},\xi _1)\right] , {\mathbf {x}}\in {\mathcal {S}}_+ \end{aligned}$$

then

$$\begin{aligned} {\mathbb {E}}w({\mathbf {X}}_t) \rightarrow \int _{{\mathcal {S}}_+} w({\mathbf {x}})\,\pi (\mathrm{d}{\mathbf {x}}). \end{aligned}$$

Sketch of proof

First, using the Markov property and Assumption A3) one can show that for all $t\in {\mathbb {Z}}_+$ and ${\mathbf {x}}\in {\mathcal {S}}$

$$\begin{aligned} {\mathbb {E}}_{\mathbf {x}}(V({\mathbf {X}}_t)\le \rho ^t V({\mathbf {x}})+\dfrac{C}{1-\rho }, \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} {\mathbb {E}}_{\mathbf {x}}\ell ({\mathbf {X}}_t, \xi _{t+1})&\le \rho ^{t+1} V({\mathbf {x}})+\dfrac{C}{1-\rho }. \end{aligned} \end{aligned}$$

As a next step, one can show that if a continuous function w satisfies $\lim _{{\mathbf {x}}\rightarrow \infty } \frac{w({\mathbf {x}})}{{\mathbb {E}}[V({\mathbf {x}}^T {\mathbf {f}}({\mathbf {x}},\xi _t))\ell ({\mathbf {x}},\xi _t)]}=0$, then w is $\mu$-integrable for any invariant probability measure $\mu$ of ${\mathbf {X}}$. Moreover, the strong law of large numbers for martingales will show that

$$\begin{aligned} \lim _{T\rightarrow \infty } \frac{1}{T} \sum _0^T\left( \log f_i({\mathbf {X}}_{t+1})-P \log f_i({\mathbf {X}}_t)\right) =0, \,\text {when}~ {\mathbf {X}}(0)={\mathbf {x}}\end{aligned}$$

(A.4)

where P is the transition operator of ${\mathbf {X}}_t$. This combined with arguments by Benaïm and Schreiber (2019) implies that if $\mu ({\mathcal {S}}_+)=1$ then $r_i(\mu )=0$ for any $i\in I$.

The next step is to show that there exist $M, C_2, \gamma _4>0,\rho _2\in (0,1)$ such that

$$\begin{aligned} {\mathbb {E}}_{\mathbf {x}}\left[ V({\mathbf {X}}_1)\prod _{i=1}^n X_i^{p_i}(1)\right] \le \left( {\varvec{1}}_{\{|{\mathbf {x}}|<M\}}(C_2-\rho _2)+\rho _2\right) V({\mathbf {x}})\prod _{i=1}^nx_i^{p_i}, ~{\mathbf {x}}\in {\mathcal {S}}\end{aligned}$$

for any ${\mathbf {p}}=(p_1,\ldots ,p_n)\in {\mathbb {R}}^n$ satisfying

$$\begin{aligned} |{\mathbf {p}}|_1:=\sum |p_i|\le \gamma _4. \end{aligned}$$

(A.5)

It is shown in Schreiber et al. (2011) by the min-max principle that Assumption (A.3) is equivalent to the existence of ${\mathbf {p}}>0$ such that

$$\begin{aligned} \min \limits _{\mu \in {\mathcal {M}}}\left\{ \sum _{i}p_i r_i(\mu )\right\} :=2r^*>0. \end{aligned}$$

(A.6)

One can then prove, using arguments by Hening and Nguyen (2018), that there exists an integer $T^*>0$ such that, for any $T>T^*$, ${\mathbf {x}}\in {\mathcal {S}}_0, |{\mathbf {x}}|<M$ one has

$$\begin{aligned} \sum _{t=0}^T{\mathbb {E}}_{\mathbf {x}}\left( \ln V({\mathbf {X}}_{t+1})-\ln V({\mathbf {X}}_t)-\sum p_i\ln f_i({\mathbf {X}}_t, \xi _{t+1})\right) \le -r^*(T+1). \end{aligned}$$

(A.7)

Define $U:{\mathcal {S}}_+\rightarrow {\mathbb {R}}_+$ by

$$\begin{aligned} U({\mathbf {x}})=V({\mathbf {x}})\prod _{i=1}^nx_{i}^{-p_i} \end{aligned}$$

with ${\mathbf {p}}$ and $r^*$ satisfying (A.6). Let $n^*\in {\mathbb {N}}$ be such that

$$\begin{aligned} \rho _2^{1-n^*}>C_2. \end{aligned}$$

(A.8)

Using the previous results, as well as the analysis developed by Hening and Nguyen (2018) one can prove the following: There exist numbers $\theta \in \left( 0,\frac{\gamma _4}{2}\right)$, $K_\theta >0$, such that for any $T\in [T^*,n^*T^*]\cap {\mathbb {Z}}$ and ${\mathbf {x}}\in {\mathcal {S}}_+, \Vert {\mathbf {x}}\Vert \le M$,

$$\begin{aligned} {\mathbb {E}}_{\mathbf {x}}U^\theta ({\mathbf {X}}_T)\le U^\theta ({\mathbf {x}})\exp \left( -\frac{1}{2}\theta r^*T\right) +K_\theta . \end{aligned}$$

One can show that the process $(\rho ^{-t}_2 U({\mathbf {X}}(t)))_{t\ge 0}$ is a supermartingale and use this in conjunction with the Markov property to show that there exist numbers $\kappa =\kappa (\theta ,T^*)\in (0,1)$ and ${{\tilde{K}}}={{\tilde{K}}}(\theta ,T^*)>0$ such that

$$\begin{aligned} {\mathbb {E}}_{\mathbf {x}}U^\theta ({\mathbf {X}}_{n^*T^*})\le \kappa U^\theta ({\mathbf {x}})+{{\tilde{K}}}\,\text { for all }\, {\mathbf {x}}\in {\mathcal {S}}_+. \end{aligned}$$

(A.9)

If the Markov chain ${\mathbf {X}}_t$ is irreducible and aperiodic on ${\mathcal {S}}_+$, and a compact set is petite, then one can use the well-known results by Meyn and Tweedie (1992) in conjunction with the Lyapunov condition (A.9) to conclude that there is $c_4>1$ such that for all ${\mathbf {x}}\in {\mathcal {S}}_+$

$$\begin{aligned} c_4^t\Vert P_t({\mathbf {x}},\cdot )-\pi (\cdot )\Vert _{TV}\rightarrow 0\text { as } t\rightarrow \infty , \end{aligned}$$

where $\Vert \cdot \Vert _{TV}$ is the total variation distance. In particular, this implies that the distribution of ${\mathbf {X}}_t$ converges weakly to $\pi$ as $t\rightarrow \infty$. $\square$

Appendix B. Two Species Systems

In general, one needs stronger assumptions for extinction. We will assume for simplicity $n\le 2$, so that we have one or two species. We need one more condition for extinction. This condition makes sure that the martingale part of ${\mathbf {X}}_t$ is bounded and that the family of occupation measures $(\Pi _t)_{t\in {\mathbb {Z}}_+}$ is tight.

A5) There exists a function $\phi :{\mathcal {S}}\rightarrow (0,\infty )$ and constants $C, \delta _\phi >0$ such that for all ${\mathbf {x}}\in {\mathcal {S}}$

$$\begin{aligned} {\mathbb {E}}_{\mathbf {x}}V({\mathbf {X}}_1)\le V({\mathbf {x}})-\phi ({\mathbf {x}})+C \end{aligned}$$

and

$$\begin{aligned} {\mathbb {E}}_{{\mathbf {x}}}\left( V({\mathbf {X}}_1)-{\mathbb {E}}_{\mathbf {x}}V({\mathbf {X}}_1)\right) ^2+{\mathbb {E}}\left| \log f({\mathbf {x}},\xi _1)-{\mathbb {E}}\log f({\mathbf {x}},\xi _1)\right| ^2\le \delta _\phi \phi ({\mathbf {x}}). \end{aligned}$$

Define ${\mathcal {S}}^j:=\{{\mathbf {x}}\in {\mathcal {S}}~|~x_i=0, i\ne j\}$ to be the subspace supported by the species j. If we restrict the process to ${\mathcal {S}}^j$, then the extinction set is given by ${\mathcal {S}}_0:=\{0\}$ and the persistence set by ${\mathcal {S}}_+^j:={\mathcal {S}}^j\setminus \{0\}$. Let ${\mathcal {M}}^j:=\{\mu \in {\mathcal {M}}~|~\mu ({\mathcal {S}}^j)=1\}, {\mathcal {M}}^{j,+}:=\{\mu \in {\mathcal {M}}~|~\mu ({\mathcal {S}}_+^j)=1\}$ be the sets of ergodic probability measures on ${\mathcal {S}}^j$ and ${\mathcal {S}}^{j}_+$. We also assume that the subspaces ${\mathcal {S}}_0^1, {\mathcal {S}}_0^2, {\mathcal {S}}_+$ are accessible, i.e., we can get close to them from any starting point ${\mathbf {x}}\in {\mathcal {S}}_+$ with positive probability, and each subspace supports at most one ergodic probability measure. Consider two species interacting via the general system

$$\begin{aligned} \begin{aligned} X^1_{t+1}&=X^1_t f_1(X^1_t, X^2_t,\xi _{t+1}),\\ X^2_{t+1}&=X^2_t f_2(X^1_t, X^2_t,\xi _{t+1}), \end{aligned} \end{aligned}$$

(B.1)

The results by Chesson and Ellner (1989), Ellner (1989) assumed some type of monotonicity and only looked at competitive behavior. They can be generalized as follows (see Hening et al. 2020 for proofs). We first look at the Dirac delta measure $\delta _0$ at the origin (0, 0)

$$\begin{aligned} r_i(\delta _0) = {\mathbb {E}}[\ln f_i(0,\xi _1)], i=1,2. \end{aligned}$$

If $r_i(\delta _0)>0$, then species i survives on its own and converges to a unique invariant probability measure $\mu _i$ supported on ${\mathcal {S}}_+^i := \{{\mathbf {x}}\in {\mathcal {S}}~|~x_i\ne 0, x_j=0, i\ne j\}$. Remember that the (random) set of $\hbox {weak}^*$-limit points of the family of occupation measures $(\Pi _t)_{t\in {\mathbb {N}}}$ is denoted by ${\mathcal {U}}={\mathcal {U}}(\omega )$. Thus, if we say that ${\mathcal {U}}(\omega )=\{\mu _1\}$, this means that for the realization $\omega$ we have $\Pi _t \rightarrow \mu _1$ weakly.

• (i) Suppose $r_1(\delta _0)>0, r_2(\delta _0)>0$. The realized per-capita growth rates can be computed via

  $$\begin{aligned} r_i(\mu _j)=\int _{(0,\infty )}{\mathbb {E}}[\ln f_i(x,\xi _1)]\mu _j(\mathrm{d}x). \end{aligned}$$

  • If $r_1(\mu _2)>0$ and $r_2(\mu _1)>0$, we have coexistence and convergence of the distribution of ${\mathbf {X}}_t$ to the unique invariant probability measure $\pi$ on ${\mathcal {S}}_+$.

  • If $r_1(\mu _2)>0$ and $r_2(\mu _1)<0$, we have the persistence of $X^1$ and extinction of $X^2$. In other words, for any ${\mathbf {x}}\in {\mathcal {S}}_+$

    $$\begin{aligned} {\mathbb {P}}_{\mathbf {x}}\left\{ {\mathcal {U}}(\omega )=\{\mu _1\} ~\text {and}~\lim _{t\rightarrow \infty }\frac{\ln X^2_t}{t}=r_2(\mu _1)<0, \right\} =1. \end{aligned}$$

  • If $r_1(\mu _2)<0$ and $r_2(\mu _1)>0$, we have the persistence of $X^2$ and extinction of $X^1$. In other words, for any ${\mathbf {x}}\in {\mathcal {S}}_+$

    $$\begin{aligned} {\mathbb {P}}_{\mathbf {x}}\left\{ {\mathcal {U}}(\omega )=\{\mu _2\} ~\text {and}~\lim _{t\rightarrow \infty }\frac{\ln X^1_t}{t}=r_1(\mu _2)<0, \right\} =1. \end{aligned}$$

  • If $r_1(\mu _2)<0$ and $r_2(\mu _1)<0$, we have that for any ${\mathbf {x}}\in {\mathcal {S}}_+$

    $$\begin{aligned} p_{{\mathbf {x}},j}:={\mathbb {P}}_{\mathbf {x}}\left\{ {\mathcal {U}}(\omega )=\{\mu _j\} ~\text {and}~\lim _{t\rightarrow \infty }\frac{\ln X^i_t}{t}=r_i(\mu _j)<0, i\ne j \right\} \end{aligned}$$

    and

    $$\begin{aligned} p_{{\mathbf {x}},1}+ p_{{\mathbf {x}},2}=1. \end{aligned}$$

• (ii) Suppose $r_1(\delta _0)>0, r_2(\delta _0)<0$. Then, species 1 survives on its own and converges to its unique invariant probability measure $\mu _1$ on ${\mathcal {S}}^1_+$.

  • If $r_2(\mu _1)>0$, we have the persistence of both species and convergence of the distribution of ${\mathbf {X}}_t$ to the unique invariant probability measure $\pi$ on ${\mathcal {S}}_+$.

  • If $r_2(\mu _1)<0$, we have the persistence of $X^1$ and the extinction of $X^2$. In other words, for any ${\mathbf {x}}\in {\mathcal {S}}_+$

    $$\begin{aligned} {\mathbb {P}}_{\mathbf {x}}\left\{ {\mathcal {U}}(\omega )=\{\mu _1\} ~\text {and}~\lim _{t\rightarrow \infty }\frac{\ln X^2_t}{t}=r_2(\mu _1)<0, \right\} =1. \end{aligned}$$

• (iii) Suppose $r_1(\delta _0)<0, r_2(\delta _0)<0$. Then, both species go extinct with probability one. In other words, for any ${\mathbf {x}}\in {\mathcal {S}}_+$

  $$\begin{aligned} {\mathbb {P}}_{\mathbf {x}}\left\{ \lim _{t\rightarrow \infty }\frac{\ln X^i_t}{t}=r_i(\delta _0)<0 \right\} , i=1,2. \end{aligned}$$

We note that our results are significantly more general than those from Ellner (1989). In Ellner (1989), the author only gives conditions for coexistence and does not treat the possibility of the extinction of one or both species.