Complex Dynamics in a Unified SIR and HIV Disease Model: A Bifurcation Theory Approach

Abstract

This paper is concerned with complex dynamical behaviors of a simple unified SIR and HIV disease model with a convex incidence and four real parameters. Due to the complex nature of the disease dynamics, our goal is to explore bifurcations including multistable states, limit cycles, and homoclinic loops in the whole parameter space. The first contribution is the proof of the existence of multiple limit cycles giving rise from Hopf bifurcation, which further induces bistable or tristable states because of the coexistence of stable equilibria and periodic motion. Next, we propose that the existence of Bogdanov–Takens (BT) bifurcation yields the bifurcation of homoclinic loops, which provides a new mechanism for generating disease recurrence, for example, the relapse–remission, viral blip cycles in HIV infection. Last, we present a novel method for the derivation of the normal forms of codimension two and three BT bifurcations. The method is based on the simplest normal form theory from Yu’s previous works.

1 Introduction

Susceptible-infected-recovered epidemiological models are well-known to predict possible disease outbreaks and design disease controls. But the complex disease dynamics are rarely explored in whole parameter space analytically due to the complexity of the model (including the model dimension and the number of parameters), model reduction techniques, and the computation capacity. Therefore, before carrying out the rigorous mathematical analysis, we first introduce the derivation of the simplest two-dimensional models. The basic SIR compartment frame is described as follows (Liu et al. 1986):

$$\begin{aligned} \displaystyle \frac{\mathrm{d}S}{\mathrm{d}t}= & {} \lambda - G(I,\,S) - d\,S + \gamma \, R, \nonumber \\ \displaystyle \frac{\mathrm{d}I}{\mathrm{d}t}= & {} G(I,\,S) - (d+v)\,I, \nonumber \\ \displaystyle \frac{\mathrm{d}R}{\mathrm{d}t}= & {} v\,I - (d+\gamma )\,R. \end{aligned}$$

(1)

We assume the per capita death rate is d for three population compartments, see Earn et al. (2000). The newborns are all susceptibles and contribute to the susceptible population at the rate of $\lambda$. The infection duration is $v^{-1}$. The infection rate, $G(I,\,S)$, is a function in terms of both susceptible and infected populations. It follows from Griffin (1995) that the recovered population gets lifelong immunity (so that $\gamma =0$), model (1) is reduced to a two-dimensional model, given by

$$\begin{aligned} \displaystyle \frac{\mathrm{d}S}{\mathrm{d}t}= & {} \lambda - G(I,\,S) - d\,S , \nonumber \\ \displaystyle \frac{\mathrm{d}I}{\mathrm{d}t}= & {} G(I,\,S) - (d+v)\,I. \end{aligned}$$

(2)

Considering the global incidence rate function in further studies, for example, see Korobeinikov and Maini (2005), Wang et al. (2010), Hethcote and van den Driessche (1991), Liu et al. (1986), the infection rate takes a special case:

$$\begin{aligned} G(I,\,S)\,=\, h(I)\,I\, S = \big (\beta _0 + \textstyle \frac{k \, I}{1+m\,I} \big )\, I\,S, \end{aligned}$$

(3)

where $\beta _0$, k and m are positive constants, and thus the model (2) is rewritten as

$$\begin{aligned} \displaystyle \frac{\mathrm{d}S}{\mathrm{d}t}= & {} \lambda -\big (\beta _0 + \textstyle \frac{k \, I}{1+m\,I} \big )\, I\,S- d\,S , \nonumber \\ \displaystyle \frac{\mathrm{d}I}{\mathrm{d}t}= & {} \big (\beta _0 + \textstyle \frac{k \, I}{1+m\,I} \big )\, I \,S- (d+v)\,I. \end{aligned}$$

(4)

To simplify the analysis, we introduce the change of state variables, $S\,=\,\frac{\lambda }{d+v}\,X$, $I\,=\,\frac{\lambda }{d+v}\,Y$, and the time rescaling, $t\,=\,\frac{1}{d+v}\,\tau$, into (4) to obtain the following dimensionless model,

$$\begin{aligned}&\displaystyle \frac{\mathrm {d}X}{\mathrm {d}\tau }= 1 - D\,X - \big (B+ \textstyle \frac{A\,Y}{Y+C} \big )\,X\,Y ,\nonumber \\&\displaystyle \frac{\mathrm {d}Y}{\mathrm {d}\tau }= \big (B+ \textstyle \frac{A\,Y}{Y+C} \big )\,X\,Y -Y, \end{aligned}$$

(5)

where the new parameters are defined as

$$\begin{aligned} A=\displaystyle \frac{k\,\lambda }{m\,(d+v)^2}, \quad B=\displaystyle \frac{\lambda \beta _0}{(d+v)^2}, \quad C=\displaystyle \frac{d+v}{m\,\lambda }, \quad D=\frac{d}{d+v}. \end{aligned}$$

(6)

All these parameters take positive real values.

Next, we consider a four-dimensional in-host HIV model which was developed by van Gaalen and Wahl (2009) and used to study the viral blips phenomenon in Zhang et al. (2013, 2014a, b). The model is described by the following ordinary differential equations:

$$\begin{aligned} \displaystyle \frac{\mathrm{d}x}{\mathrm{d}t}= & {} \lambda _x - d_x x - (1-\epsilon ) \beta (r)xy,\nonumber \\ \displaystyle \frac{\mathrm{d}y}{\mathrm{d}t}= & {} (1-\epsilon )\beta (r)xy - d_yy, \nonumber \\ \displaystyle \frac{\mathrm{d}r}{\mathrm{d}t}= & {} \lambda _r + ky - mar - d_r r, \nonumber \\ \displaystyle \frac{\mathrm{d}a}{\mathrm{d}t}= & {} \lambda _a + \alpha - par - d_a a, \end{aligned}$$

(7)

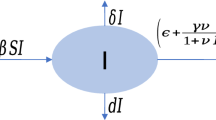
where $x, \, y, \, r, \,$ and $\, a\,$ represent the population densities of the uninfected $\mathrm{CD4}^+$ T cells, infected $\mathrm{CD4}^+$ T cells, reactive oxygen species (ROS), and antioxidants, respectively. The constant $\lambda _x$ is the production rate of $\mathrm{CD4}^+$ T cells, and $d_x x$ denotes the death rate. The infectivity $\beta (r)$ which plays an important role in the infection process is modeled as a positive, increasing, and saturating function with respect to the concentration of ROS, r,

$$\begin{aligned} \beta (r) = b_0 + \frac{r (b_{\mathrm{m}}-b_0)}{r+r_{ 1 / 2}}, \end{aligned}$$

(8)

where $b_0$ represents the infection rate in the ROS-absent case, while $b_{\mathrm{m}}$ denotes the maximum infection rate, and $r_{ 1 / 2}$ is the ROS concentration at half maximum. Then, $(1-\epsilon )\beta (r)xy$ represents the rate at which uninfected cells become infected, where $\epsilon \in (0,1)$ is the effectiveness of drug therapy, and $d_y$ is the per capita death rate of infected $\mathrm{CD4}^+$ T cells. The ROS are produced naturally at rate $\lambda _r$, and by the infected cells at rate $k\,y$; but decay at rate $d_r\,r$ and are eliminated by interaction with antioxidants at rate mar. Antioxidants are introduced into the model via natural dietary intake at a constant rate $\lambda _a$ and through antioxidant supplementation at rate $\alpha$, and are eliminated from the system by natural decay at rate $d_a a$ and by reacting with the ROS at rate par, where p is much smaller than m. All the parameters in (7) and (8) are positive, and their typical values have been chosen with careful reference to clinical studies, as given in van Gaalen and Wahl (2009), Zhang et al. (2014a, b).

We apply the quasi-steady state assumption (Flach and Schnell 2006; Korobeinikov et al. 2005; Boie et al. 2016) to reduce the four-dimensional system (7) to a two-dimensional system. To achieve this, we note from Zhang et al. (2013, 2014a, b) that parameters $\lambda _a$, $\alpha$, $\lambda _r$ and k typically have much bigger values than other parameters in the corresponding equations. Thus, a is obtained by solving the equation $\frac{da}{dt} = 0$ as

$$\begin{aligned} a = \frac{\lambda _a + \alpha }{d_a + p\, r} > 0, \quad (r \ge 0); \end{aligned}$$

and analogously r from the equation $\frac{\mathrm{d}r}{\mathrm{d}t} = 0$ as

$$\begin{aligned} r= & {} \textstyle \frac{-\big [ d_a d_r +m (\alpha +\lambda _a) - p(\lambda _r + ky) \big ] + \sqrt{[ d_a d_r +m (\alpha +\lambda _a) - p(\lambda _r + ky) ]^2 + 4 p d_a d_r (\lambda _r + k y ) }}{2\,p\, d_r } \nonumber \\= & {} \textstyle \frac{ 2 d_a \, (\lambda _r + ky)}{ d_a d_r +m (\alpha +\lambda _a) - p(\lambda _r + ky) + \sqrt{[ d_a d_r +m (\alpha +\lambda _a) - p(\lambda _r + ky) ]^2 + 4 p d_a d_r (\lambda _r + k y ) }} > 0, \,\, (y \ge 0).\nonumber \\ \end{aligned}$$

(9)

Then, the above solutions a and r are substituted into the first two equations in system (7) to obtain

$$\begin{aligned} \frac{\mathrm{d}x}{\mathrm{d}t} = \lambda _x -d_x x - \beta (y) xy, \qquad \frac{\mathrm{d}y}{\mathrm{d}t} = \beta (y) xy - d_y y, \end{aligned}$$

(10)

where $\beta (y)$ is derived from $(1- \varepsilon ) \beta (r)$ with the use of (8) and (9), given by

$$\begin{aligned} \beta (y) = (1 - \varepsilon ) \Big [ b_0 + \frac{ 2 d_a (b_\mathrm{m}-b_0) (\lambda _r + k y)}{ 2 d_a (\lambda _r + k y) + \widetilde{r}_{ 1 / 2}(y) } \Big ], \end{aligned}$$

(11)

in which $\widetilde{r}_{ 1 / 2}(y)$ is defined as

$$\begin{aligned} \widetilde{r}_{ 1 / 2}(y)= & {} r_{ 1 / 2} \big \{ d_a d_r +m (\alpha +\lambda _a) - p(\lambda _r + ky) \\&+\, \sqrt{[ d_a d_r +m (\alpha +\lambda _a) - p(\lambda _r + ky) ]^2 + 4 p d_a d_r (\lambda _r + k y ) } \big \} > 0, \quad (y \ge 0). \end{aligned}$$

To reveal the complex disease dynamics, we focus on bifurcation analysis (i.e., on the asymptotic behavior of the system when the system reaches its steady state). Noting that the value of y is much smaller than that of x, see Zhang et al. (2013, 2014a, b), we may further simplify the two-dimensional system (10) by taking the average value of $\widetilde{r}_{ 1 / 2}(y)$, given by

$$\begin{aligned} \bar{r}_{ 1 / 2}= & {} \displaystyle \lim _{h \rightarrow \infty } \textstyle \frac{1}{h} \int _0^h \widetilde{r}_{ 1 / 2}(y) \, dy = r_{ 1 / 2} \displaystyle \lim _{h \rightarrow \infty } \textstyle \frac{1}{h} \big \{ \big [ d_a d_r - p \lambda _r + m (\alpha +\lambda _a) \big ] h - \textstyle \frac{1}{2}\, p k h^2 \\&+\, \frac{1}{2} p k \big [ \big ( h + \frac{ d_a d_r + p \lambda _r - m (\alpha +\lambda _a)}{pk} \big )^2\\&+ \frac{4 d_a d_r m (\alpha + \lambda _a)}{p^2 k^2} \ln \big ( 2 \big ( h + \frac{ d_a d_r + p \lambda _r - m (\alpha +\lambda _a) }{pk} \big ) \big ) \big ] \big \} \\= & {} 2 d_a d_r r_{ 1 / 2}, \end{aligned}$$

and obtain the new infectivity function,

$$\begin{aligned} \beta (y) = b + \frac{ay}{y+c}, \end{aligned}$$

(12)

where

$$\begin{aligned} a = \displaystyle \frac{(1 - \epsilon ) d_r r_{ 1 / 2} (b_{\mathrm{m}}-b_0)}{\lambda _r + d_r r_{ 1 / 2}}, \quad b = \displaystyle \frac{ (1 - \epsilon ) ( \lambda _r b_{\mathrm{m}} + d_r r_{ 1 / 2} b_0 )}{ \lambda _r + d_r r_{ 1 / 2}} , \quad c = \displaystyle \frac{ \lambda _r + d_r r_{ 1 / 2} }{ k},\nonumber \\ \end{aligned}$$

(13)

all of them are positive since $\epsilon \in (0,1)$ and $b_{\mathrm{m}} > b_0$.

The verification of the averaging step is demonstrated by using the original function $\widetilde{r}_{ 1 / 2}(y)$ and the averaged function $\bar{r}_{ 1 / 2}$ to simulate system (10) with typical values in Zhang et al. (2013, 2014a, b), Yu et al. (2016). The simulation comparison in Fig. 1a, b indeed shows a very good agreement, which implies that the average is reliable and yields very good approximation to the original system.

Fig. 1

Simulation of system (10) showing the comparison on y using the original $\widetilde{r}_{ 1 / 2}(y)$ (red color curve) and $\bar{r}_{ 1 / 2}$ (blue color curve), with the parameter values used in Zhang et al. (2013, 2014a, b), Yu et al. (2016) (Color figure online)

Finally, we introduce the scaling: $x = \textstyle \frac{\lambda _x}{d_y} \, X$, $y = \frac{\lambda _x}{d_y}\, Y$, $t = \frac{1}{d_y}\, \tau$, and the new defined parameters:

$$\begin{aligned} A = \displaystyle \frac{a \lambda _x}{d_y^2}, \quad B = \frac{\lambda _x b}{d_y^2}, \quad C = \frac{c d_y}{\lambda _x}, \quad D = \frac{d_x}{d_y}, \end{aligned}$$

(14)

to transform the model (10) into the dimensionless system (5). Thus, with appropriate parameter values, the unified model (5) represents either an SIR epidemiological model (susceptible and infected individuals) with parameters given in (6) or an in-host infection (susceptible and infected cells) model with parameters given in (14). It is noted that the key difference between system (5) and the class of models studied in Korobeinikov et al. (2005) is that the incidence function in system (5), $(\frac{B + AY}{Y+C})XY$, is convex, while that considered in Korobeinikov et al. (2005) is concave.

Recently, the model (5) was considered by Yu et al. (2016) to demonstrate various dynamics. However, a large part of the analysis, in particular on Hopf bifurcation and Bogdanov–Takens bifurcation is restricted to a two-dimensional parameter space with parameters B and D fixed. Moreover, some part of previous work in (Yu et al. 2016) are heavily dependent upon simulations. Therefore, in this contribution, we shall explore dynamical behaviors of the model (5) in the full four-dimensional parameter space, particularly for the analysis on Hopf and generalized Hopf bifurcations, and BT bifurcation. In this paper, we will first give an analysis on dynamics and bifurcation of system (5), which is different from that given in (Yu et al. 2016), and we then particularly focus on more generic dynamical study of the system in the four-dimensional (A, B, C, D) parameter space. We will focus on the properties of multistable states, limit cycles and homoclinic loops, showing complex behaviors in diseases. In particular, we use theory of Hopf and generalized Hopf bifurcations to prove the existence of multiple limit cycles, giving rise to a different type of bistable or tristable states, with coexistence of stable equilibria and periodic motion. Further, we will carry out the analysis on the BT bifurcation to show homoclinic loop bifurcation, which leads to a new mechanism of generating disease recurrence, that is, cycles of remission and relapse such as the viral blips observed in HIV infection.

The rest of the paper is organized as follows. In the next section, we consider basic solution properties of system (5), and study stability of and bifurcations from the equilibrium solutions of this system. Hopf and generalized Hopf bifurcations will be studied in detail in Sect. 3. In Sect. 4, BT bifurcation and homoclinic bifurcation are investigated, giving rise to a new scenario/mechanism for generating recurrence. Simulations are given in Sects. 3 and 4 for various cases to confirm analytical predictions. Finally, conclusions are drawn in Sect. 5.

2 Dynamics and Bifurcation of System (5)

In this section, we consider general solution properties of system (5), and study stability and bifurcations of its equilibrium solutions. For convenience, define the parameter space as

$$\begin{aligned} {{\gamma }} = (A,B,C,D) \in R_+^4, \end{aligned}$$

(15)

where $R_+^4$ means that all the four parameters take positive real values. Further, define the trapping region,

$$\begin{aligned} \Omega = \big \{ (X,Y)| X\ge 0, \ Y \ge 0, \ X+Y \le \max \big \{1, \textstyle \frac{1}{D} \big \} + \varepsilon \big \}, \end{aligned}$$

(16)

where $0 < \varepsilon \ll 1$. Then it can be shown (Yu et al. 2016) that for any set of parameter values belonging to $\gamma$, all solutions of system (5) are nonnegative provided initial conditions are taken nonnegative. Moreover, all solutions are attracted into $\Omega$ and so bounded.

System (5) has two equilibrium solutions:

$$\begin{aligned} \begin{array}{ll} \mathrm{disease\text {-}free \ equilibrium:} &{} \mathrm{E_0} = \big ( \frac{1}{D}, \, 0 \big ),\\ \mathrm{endemic \ equilibrium:} &{} \mathrm{E_1} = \big (X_1,Y_1 \big ) = \big ( X_1, \, 1 - D X_1 \big ), \end{array} \end{aligned}$$

(17)

where $X_1$ is determined from the equation,

$$\begin{aligned} F_1(X) = D(A+B) X^2 - (A+B+D+BC) X + C+1 = 0. \end{aligned}$$

(18)

The solutions of $F_1(X)=0$ can be written as

$$\begin{aligned} X_{\pm } = \textstyle \frac{ (A+B+D+BC) \pm \,\sqrt{ \Delta }}{2 D (A+B)}, \end{aligned}$$

(19)

in which

$$\begin{aligned} \Delta= & {} (A+B+D+BC)^2- 4 D (1+C)(A+B) \nonumber \\= & {} (A+B-D-BC)^2- 4 C(A+B)(D-B). \end{aligned}$$

(20)

Further, define the reproduction number as

$$\begin{aligned} R_0 = \frac{B}{D}. \end{aligned}$$

(21)

Then the dynamical behavior of system (5) can be conveniently analyzed according to $R_0 < 1$, $R_0 > 1$ and $R_0 = 1$. Note that $\mathrm {E}_0$ is a boundary equilibrium (on the X-axis), while $\mathrm {E}_1$ is a positive (an interior) equilibrium.

We choose D as the bifurcation parameter (which is fixed in the study Yu et al. (2016)) and treat other parameters $A,\,B$ and C as control parameters, then consider the solution X(D) determined by the graph $F_1(X) = 0$, as shown in the D-X plane (see Fig. 2). It will be seen later that the relation between the control parameters also plays an important role on bifurcation property and dynamical behavior of the system. We define the saddle-node bifurcation point and transcritical bifurcation point, respectively, as

$$\begin{aligned}&(D_s,X_s)= (D_-,\, X_{s-}) \quad \mathrm{and} \quad (D_t,X_t)= \big (B, \textstyle \frac{1}{B}\big ), \nonumber \\&\quad \mathrm{where} \quad X_{s\pm } = \textstyle \frac{A+B+BC+D_\pm }{2(A+B)D_\pm }, \quad D_\pm = A + B + BC + 2AC \nonumber \\&\qquad \pm \,2\sqrt{AC(1 + C)(A + B)}. \end{aligned}$$

(22)

Note that $\Delta = 0$ at $(D_{\pm },X_{s\pm })$.

An elementary proof based on the function $F_1$ leads to the following result for the property of the solution $X_1$.

Lemma 2.1

In the D-X plane, the function X(D) has two horizontal asymptotes: $X = 0$ and $X = \frac{1}{A+B}$; and two vertices at $D = D_\pm$. The property of the function X(D) is given in the following table.

X	D	X(D) monotonically
$\in (-\infty ,0)$	$\in (-\infty ,0)$	$\searrow$
$\in (0, X_{s+})$	$\in (D_{+},+\infty )$	$\searrow$
$\in (X_{s+},\frac{1}{A+B})$	$\in (D_{+},+\infty )$	$\nearrow$
$\in (\frac{1}{A+B},X_s)$	$\in (-\infty , D_s)$	$\nearrow$
$\in (X_s, +\infty )$	$\in (0,D_s)$	$\searrow$

Fig. 2

Bifurcation diagrams for system (5): a in the whole D-X plane; b in the biologically meaningful part with $A < BC$; c in the biologically meaningful part with $A = BC$; and d in the biologically meaningful part with $A > BC$, with $\mathrm{E_0}$ in red and $\mathrm{E_1}$ in blue, and stable in solid and unstable in dotted curves, respectively. The green line in a, and black dotted lines in b–d denote the same asymptote $X=\frac{1}{A+B}$ to the biologically meaningful solution $X_\pm$, which satisfies $X_\pm \le X_0$ (Color figure online)

Therefore, the biologically meaningful equilibria (nonnegative solutions) are defined as

$$\begin{aligned} \begin{array}{lll} \mathrm{E_0} : &{} (X_0,Y_0)=\big (\textstyle \frac{1}{D},0), &{} \mathrm{for} \ \ D > 0, \\ \mathrm{E_{1 \pm }} : &{} (X_1,Y_1) = \big ( X_\pm , \, Y_\pm \big ) = \big ( X_\pm , \, 1 - D X_\pm \big ), &{} \mathrm{for} \ \ 0 \le X_\pm \le \textstyle \frac{1}{D}, \end{array} \end{aligned}$$

(23)

where the condition $0 \le X_\pm \le \textstyle \frac{1}{D}$ comes from $Y_1 = 1 - DX_1 \ge 0$. This means that the biological reasonable equilibrium solutions in Fig. 2a–d can only locate in the first quadrant.

We have the following lemma.

Lemma 2.2

The disease-free equilibrium solution $X_0 = \frac{1}{D}$ is a monotonic function of D. The solution curves $X_0$ and $X_1$ have a unique intersection point at $(D,X) = (D_t,X_t) = (B,\frac{1}{B})$. The biologically meaningful endemic equilibrium solution $X_1$ only exists for $\frac{1}{A+B}< X < \frac{1}{B}$ and below the curve $X = \frac{1}{D}$. Moreover, the equilibrium solution $X_1$ has a turning point at $(D,X) = (D_s,X_s)$, which is above the curve $X = \frac{1}{D}$ if $A < BC$, below the curve if $A > BC$, and on the curve if $A = BC$.

Proof

It is obvious that the function $X = \frac{1}{D}$ is monotonic with respect to D. It is easy to show that the two curves $X = \frac{1}{D}$ and $F_1 = 0$ have a unique intersection point by solving $F_1(\frac{1}{D}) = 0$, yielding $D = B$ and thus $X = \frac{1}{B}$, which results in a critical point at $(D,X) = (D_t,X_t) = (B,\frac{1}{B})$. The biologically meaningful solution curve $X_1$ must be below the curve $X = \frac{1}{D}$ since it requires $D X_\pm < 1$, i.e., $X_\pm < X_0$. It is easy to see from Fig. 2 that $X_1 > \frac{1}{A+B}$ for $D < D_s$. More precisely, a direct computation shows that

$$\begin{aligned} D < D_s \ \Longleftrightarrow \ A+B+BC-D> 2 \sqrt{4 D (1+C)(A+B)} - 2AC > 0 , \end{aligned}$$

and then

$$\begin{aligned}&X_-> \tfrac{1}{A+B} \ \Longleftrightarrow \ A+B+D+BC - \sqrt{\Delta }> 2D \\&\quad \Longleftrightarrow \ A+B+BC -D> \sqrt{\Delta } \ \Longleftrightarrow \ AC > 0. \end{aligned}$$

Now, we show that the part of solution $X_1$ for $D \ge D_+$ is above the curve $X = \frac{1}{D}$, see Fig. 2a. To achieve this, we only need to prove that $X_- > \frac{1}{D}$ for $0< X < \frac{1}{A+B}$ and $D > D_+$, which is equivalent to

$$\begin{aligned} \begin{array}{ll} X_-> \frac{1}{D} &{} \Longleftrightarrow \ BC + D - A - B> \sqrt{(A + B + BC + D)^2 - 4D(1 + C)(A + B)} \\ &{} \Longleftrightarrow \ (D-B)C >0, \end{array} \end{aligned}$$

which is true since $D> D_+ > A + B$.

For the last conclusion in this lemma, since the two curves $X_0 = \frac{1}{D}$ and $X_1 = X(D)$ have a unique intersection point at $(D,X) = (D_t,X_t) = (B,\frac{1}{B})$, it suffices to show that $X_s > X_t$ (or $X_s < X_t$) if and only if $A < BC$ (or $A > BC$). A direct calculation yields that

$$\begin{aligned} \begin{array}{rl} X_s - X_t = \frac{A+B+BC+D_s}{2(A+B)D_s} - \frac{1}{B} = \frac{ -\,(A-BC)\, A \,(A+B+B C)}{B D_s \big [ A (1+2 C) (A+B) +(2 A+B) \sqrt{A C (1+C) (A+B)} \big ] }, \end{array} \end{aligned}$$

which clearly shows that the conclusion holds, and the proof is complete. $\square$

The three different cases for $A < BC$, $A = BC$ and $A > BC$ are depicted in Fig. 2b–d, respectively. These figures are actually bifurcation diagrams for system (5), but only the red curve and the part of the blue curve below the red cure are biologically meaningful. The $D_s$, $D_t$ and $D_h$ denote the saddle node, transcritical and Hopf bifurcations, respectively, and $D_t = B$, implying that at the transcritical point $R_0 = 1$. The difference on the conditions of $A < BC$ and $A > BC$ causes a fundamental effect on the dynamics and stability of system (5). In particular, when $A > BC$, the system exhibits bistable phenomena if $R_0 < 1$ (i.e., $D > B$), which may involve two stable equilibrium solutions $\mathrm{E_0}$ and $\mathrm{E_{1-}}$, or stable equilibrium $\mathrm{E_0}$ and stable limit cycles. This can not happen if $A \le BC$. The condition $A = BC$ distinguishes the system into two fundamental different types of bifurcations: forward bifurcation when $A \le BC$, and the other backward bifurcation when $A > BC$. Backward bifurcation usually exhibits more complex dynamical behaviors such as bistable phenomena (Zhang et al. 2016). Biologically, the threshold value of the contact rate at $A=BC$ means that the interaction between X and Y produces sufficient infection such that Y persists even there exists stable disease-free equilibrium $\mathrm{E_0}$.

Stability analysis on the equilibria of a two-dimensional dynamical system is usually not difficulty. However, if the system contains multiple parameters, then it is not easy to find the explicit stability conditions expressed in terms of the system coefficients. For our purpose of studying stability and bifurcation of the equilibrium $\mathrm{E_1}$, define

$$\begin{aligned} \begin{array}{rl} I_B &{} = \big (0, \textstyle \frac{1}{4} \big ), \quad \ A_l = \frac{4 B^2}{1- 4B}, \quad \ A_u = \left\{ \begin{array}{ll} \frac{B\,(2B +\sqrt{B})}{1-4B}, &{} \mathrm{if} \ \ A \le BC , \\ + \infty , &{} \mathrm{if} \ \ A > BC, \end{array} \right. \\ C_{l_2} &{} = \textstyle \frac{A - \sqrt{A^2(1-4B)-4AB^2}}{2B}, \quad C_{u_1} = \textstyle \frac{C_{l_2}}{B} - \big (\frac{A}{B} + 1 \big ), \quad \ C_{u_2} = \min \big \{ \frac{A}{B}, C_{u_1} \big \},\\ C_{l_1} &{} = \textstyle \frac{2 B (A+B) C_{u_1}}{ 2B(1+A+B)+A - \sqrt{A^2(1-4B)-4AB^2} }, \\ D_h &{} = \textstyle \frac{B \big [ 2(A+B)(A+B+BC) -C \big ( A+ \sqrt{A^2(1-4B)-4 A B^2} \big ) \big ] }{(A+B) \big [ A+2 B- \sqrt{ A^2 (1-4B)-4 A B^2 } \big ] },\\ v_0 &{} = - \frac{1}{4 (A+B) D^2/(\sqrt{\Delta }} \big \{ (A+B) \big [ (A+B) (B C-D^2)+2 B C^2 (B-D)-B C D\\ &{} \ \ \ +\, D^2 (D - B C - 2 A C) \big ] + B^2 C^2 (D + B C)\\ &{}\ \ \ - \big [ B C (A + B + B C) + (A + B) D^2 \big ] \sqrt{\Delta } \big \}\\ \mathrm{H_1} &{} = \big \{ B \in I_B, \ A \in (A_l, A_u), \ C \in (C_{l_1}, C_{u_1}) \big \} ,\\ \mathrm{H_2} &{} = \big \{ B \in I_B, \ A \in (A_l, + \infty ), \ C \in (C_{l_1}, C_{u_2}) \big \} ,\\ \mathrm{H_3} &{} = \big \{ B \in I_B, \ A \in (A_l, + \infty ), \ C \in (C_{l_1}, C_{l_2}) \big \} , \end{array} \end{aligned}$$

(24)

where $D_h$ defines a Hopf critical point when D is treated as a bifurcation parameter, and $v_0$ (which is borrowed from the notation used in normal forms) denotes its transversality condition with respect to D.

Then, we have the following result.

Theorem 2.3

For system (5), the stability of equilibrium solutions and bifurcation properties are given in the following table.

Equilibrium		$A \le BC$	$A > BC$
$\mathrm{E_0} \$		GAS for $D \ge D_t$	GAS for $D \ge D_s$, LAS for $D_t<D< D_s$
$\, \mathrm{E_{1+}}$		Saddle	Saddle
	Hopf at $D = D_h$	$\mathrm{H_1} \bigcup D \in (D_h, D_t)$	$\mathrm{H_2} \bigcup D \in (D_h, D_s)$
$\begin{array}{c} \mathrm{E_{1-}} \\ \mathrm{LAS} \end{array}$	$\begin{array}{c} \mathrm{Otherwise,} \\ \mathrm{No \ Hopf} \end{array}$	$D \in (0, D_t)$	$D \in (0, D_s)$
$\begin{array}{c} \mathrm{Bistable^*} \\ \mathrm{States} \end{array}$		No	$\begin{array}{ll} \mathrm{H_3 \bigcup D_h \in (D_t, D_s) }\\ (\mathrm{E_0}, \mathrm{E_1})\ \mathrm{for} \ \, D\in (D_h,D_s) \\ (\mathrm{E_0}, \mathrm{LC}) \ \ \mathrm{for} \ \, D\in (D_t,D_h) \end{array}$

1. where GAS, LAS and LC denote the Globally asymptotically stable, Locally asymptotically stable and Limit cycle, respectively. Moreover, no limit cycles can bifurcate from homoclinic orbits if $A \le BC$

Note in Theorem 2.3 that for the bistable states involving limit cycles, the results on the stability of limit cycles will be given in next section (see Theorems 3.2, 3.3, 3.4 and 3.5).

Proof

The disease-free equilibrium, $\mathrm {E}_0 = (\frac{1}{D},0)$, is a boundary equilibrium, located on the X-axis. Evaluating the Jacobian matrix of system (5) at the $\mathrm{E_0}$ yields two eigenvalues, $\xi _1 = -D$ and $\xi _2 = R_0-1$, showing that $\mathrm{E_0}$ is asymptotically stable (a stable node) if $R_0 < 1$ (i.e., $D > D_t$) and unstable (a saddle) if $R_0 > 1$ (i.e., $D< D_t$). To prove the global stability, first note that all trajectories are attracted into the trapping region $\Omega$. Secondly, if $A \le BC$, then when $D \ge B$ (i.e., $R_0 \le 1$), there exists only one stable equilibrium $\mathrm{E_0}$ on the boundary of $\Omega$, thus all trajectories converge to the stable equilibrium $\mathrm{E_0}$. If $A > BC$, then when $D > D_s$ (i.e., $R_0 < \frac{B}{D_s}$), there again exists only one stable equilibrium $\mathrm{E_0}$ on the boundary of $\Omega$, thus all trajectories converge to the stable equilibrium $\mathrm{E_0}$.

Next, for stability of the $\mathrm{E_1}$, we evaluate the Jacobian matrix of system (5) at the endemic equilibrium $\mathrm{E_1}$ to obtain

$$\begin{aligned} \begin{array}{rl} J_1 = J(\mathrm {E}_1) = \left[ \begin{array}{cc} -\, \frac{1}{X_1} &{}\quad -\, 1 - \frac{AC X_1 Y_1}{(Y_1+C)^2} \\ \frac{1}{X_1}-D &{}\quad \frac{AC X_1 Y_1}{(Y_1+C)^2} \end{array} \right] , \end{array} \end{aligned}$$

(25)

which, together with (19) and (20), in turn results in

$$\begin{aligned} \begin{array}{rl} \det (J_1) =&\frac{-\,(1-DX_1)}{2 D (A+B)(1-D X_1 +C) X_1} \, \sqrt{\Delta } \big [ \sqrt{\Delta } \pm (A+B+D+BC \big ) \big ]. \end{array} \end{aligned}$$

(26)

If we first solve C from the equation $F_1 = 0$ and then obtain the trace of $J_1$ as

$$\begin{aligned} \begin{array}{rl} C \ \ = &{} \frac{1-D X_1}{1-B X_1} \, \big [ (A+B) X_1-1 \big ], \\ \mathrm{Tr}(J_1) = &{} -\, \frac{1}{A X_1} \big \{ \big [ (A+B) X_1-1 \big ] (B X_1-1)+A \big \}. \end{array} \end{aligned}$$

(27)

Note that at the critical point $R_0 = 1$ (i.e., $D = B$), $X_1 = X_0 = \frac{1}{B}$.

We first consider the equilibrium $\mathrm{E_{1+}} : (X_{+},Y_{+})$. Since the term in the square bracket of $\det (J_1)$ (taking the positive sign) is positive, and the biologically meaningful solution requires $0< D X_{+} < 1$, it is obvious that $\det (J_1) < 0$, implying that $\mathrm{E_{1+}}$ is a saddle.

Now, for the equilibrium $\mathrm{E_{1-}}$, we only need to consider the biologically meaningful solution $\mathrm{E_{1-}} : (X_-,Y_-)$ in the first quadrant with $\frac{1}{A+B}< X_{-} < \frac{1}{D}$ (see Fig. 2b–d). At the critical point $D = D_t = B$, $X_{-} = X_0 = \frac{1}{B}$, with a zero eigenvalue at this point, indicating that $R_0 = 1$ is a transcritical bifurcation point, though $\mathrm{E_{1-}}$ does not biologically exist for $R_0 < 1$. For stability of the $\mathrm{E_{1-}}$, first it is seen from (26) that $\det (J_1) > 0$ since $D X_- < 1$ and the term in the square bracket in (26) with the negative sign is negative, and thus the stability is determined by the sign of $\mathrm{Tr}(J_1)$. Since $X_{-} > \frac{1}{A+B}$, $D X_{-} < 1$, and $X_{-} < X_t = \frac{1}{B}$, yielding $B X_{-} < 1$, $C>0$ is guaranteed. However, the term in the bracket of the trace $\mathrm{Tr}(J_1)$ given in (27) can be positive or negative for $D \in (0,D_t)$ if $A \le BC$ (see Fig. 2b, c) or for $D \in (0,D_s)$ if $A > BC$ (see Fig. 2d and note that when $A > BC$, $\mathrm{E_{1+}}$ is a saddle for $D \in (D_t,D_s)$). This indicates that the only possible bifurcation from the $\mathrm{E_{1-}}$ is Hopf bifurcation, arising from a critical point at which $\mathrm{Tr}(J_1) = 0$. In order to determine the Hopf critical point, we solve the two equations in (27) for D and $X_-$ to obtain

$$\begin{aligned} D_h = \textstyle \frac{(A+B+BC) X_- - (1+C)}{X_{-} [(A+B) X_- -1]}, \end{aligned}$$

(28)

where $X_{-}$ is given by

$$\begin{aligned} X_{-} = \textstyle \frac{ A+2B - \sqrt{ A^2(1-4B)-4 AB^2}}{2(A+B)B}, \end{aligned}$$

(29)

which is positive when $B \in I_B = (0,\frac{1}{4})$ and $A > A_l = \frac{4B^2}{1-4B}$. Substituting (29) into (28) results in the expression of $D_h$ given in (24). To find the transversality condition $v_0$, we solve $F_1 = 0$ for $X_1$, which is substituted into $\mathrm{Tr}(J_1)$, and then take the derivative of the resulting trace to obtain

$$\begin{aligned} \left. \textstyle \frac{1}{2} \textstyle \frac{\partial \, \mathrm{Tr}(J_1)}{\partial D} \right| _{\mathrm{E}_{1-}} = \textstyle \frac{1}{2} \, \textstyle \frac{\partial \ }{\partial D} \left[ - \frac{1}{X_1} + \frac{AC X_1 (1-D X_1)}{ (1+C - D X_1)^2} \right] = v_0, \end{aligned}$$

where $v_0$ is given in (24). In general, $v_0 \ne 0$, implying that Hopf bifurcation occurs at the critical point $D=D_h$.

It is clear that no Hopf bifurcation occurs for $D_h \le 0$. To have $D_h > 0$, one more condition is required from $X_{-} > \frac{1+C}{A+B+BC}$, which in turn yields $0< C < C_{u_1}$. So when the above conditions are satisfied, we have $D_h > 0$. However, note that only if $D_h < D_t$ (i.e., $X_{-} < X_t$) when $A \le BC$, or $D_h < D_s$ (i.e., $X_{-} < X_s$) when $A > BC$, then $D_h > 0$ defines a true Hopf critical point. Hence, we need to consider two cases: $A \le BC$ and $A > BC$.

• (a) $A \le BC$. For this case, the disease-free equilibrium $\mathrm{E_0}$ is globally asymptotically stable if $R_0 \le 1$ (for which $\mathrm{E_{1-}}$ does not biologically exist), and unstable if $R_0 > 1$ (i.e., $D < D_t$) for which $\mathrm{E_{1-}}$ emerges to exist. To have a Hopf bifurcation from $\mathrm{E_{1-}}$, it needs $X_{-} < X_t = \frac{1}{B}$, which is easy to be proved by using (27) to obtain $BX_{-} - 1 < 0$ because of $C>0$. On the other hand, the condition $A \le BC$, or $C \ge \frac{A}{B}$, together with $C< C_{u_1}$ yields $C \in [ \frac{A}{B}, C_{u_1})$. Further, it requires that $C_{u_1} > \frac{A}{B}$, yielding $A < A_u = \frac{ B \, \left( 2B + \sqrt{B} \right) }{1 - 4B}$ (for $B \in I_B$). Hence, for this case, Hopf bifurcation appears from the equilibrium $\mathrm{E_{1-}}$ at the critical point $D = D_h$ if the parameters satisfy $B \in I_B$, $A \in (A_l,A_u)$, $C \in (0, C_{u_1})$ and $D_h \in (0, D_t)$.

• (b) $A > BC$. For this case, the turning point $(D,X) = (D_s,X_s)$ is below the curve $X = \frac{1}{D}$ and so $X_{-}$ must be below the curve $X = \frac{1}{D}$ as well. To have a Hopf bifurcation, the condition, $\frac{1+C}{A+B+BC}< X_{-} < X_s$, needs to be satisfied for $D_h>0$. The condition for $\frac{1+C}{A+B+BC} < X_{-}$ is obtained in part (a) as $C < C_{u_1}$, while the condition for $X_{-} < X_s$ yields $C > C_{l_1}$. In addition, to determine if Hopf bifurcation can occur for $D_h \in (D_t, D_s)$, which may lead to bistable phenomenon involving the stable equilibrium $\mathrm{E}_0$ and a stable limit cycle, we find another critical point at the second intersection point of $X_{-}$ with the vertical line $D = D_t$, where $X_{-} = \frac{1+C}{A+B}$. Then, $\frac{1+C}{A+B} < X_s$ yields the critical point $C_{l_2}$. Finally, we need to ensure that $A > BC$ for this case, which is guaranteed by simply defining $C_{u_2} = \min \big \{\textstyle \frac{A}{B}, \, C_{u_1} \big \}$. It is easy to show that $C_{l_2} < \frac{A}{B}$ and $C_{l_2} < C_{u_1}$, implying that $C_{l_2} < C_{u_2}$. Moreover, it can be shown that $C_{l_1} < C_{l_2}$, and thus we have $C_{l_1}< C_{l_2} < C_{u_2}$. Therefore, for this case, Hopf bifurcation occurs from $\mathrm{E_{1-}}$ at the critical point $D = D_h$ for the parameters satisfying $B \in I_B$, $A > A_l$ and $C \in (C_{l_1}, C_{u_2})$; and $\mathrm{E_{1-}}$ is asymptotically stable for $D \in (D_h,D_s)$. In particular, when $C \in (C_{l_1}, C_{l_2})$ and $D_h \in (D_t,D_s)$, bistable phenomena happen, with the coexistence of stable equilibria $\mathrm{E_0}$ and $\mathrm{E_{1-}}$ for $D \in (D_h,D_s)$, and the coexistence of stable equilibrium $\mathrm{E_0}$ and stable limit cycles for $D \in (D_t,D_h)$. While when $C \in (C_{l_2}, C_u)$ and $D_h \in (0,D_t)$, only stable equilibria $\mathrm{E_0}$ and $\mathrm{E_{1-}}$ coexist for $D \in (D_t,D_s)$.

Finally, to prove that no limit cycles can bifurcate from homoclinic orbits if $A \le BC$, note that $\mathrm{E_0}$ becomes a saddle when $A \le BC$. If a limit cycle bifurcates from a homoclinic orbit, there must exist a homoclinic loop which connects $\mathrm{E_0}$, i.e., leaving the $\mathrm{E_0}$ along the unstable manifold and return to it along the stable manifold. But we know that stable manifold of the $\mathrm{E_0}$ is the X-axis which is an invariant manifold of the system. Thus, connecting the unstable manifold to the stable manifold must violate the uniqueness of the solutions of the system, and so it is not possible to have limit cycles bifurcating from homoclinic orbits when $A \le BC$.

The proof for Theorem 2.3 is complete. $\square$

3 Hopf and Generalized Hopf Bifurcations

In this section, we consider bifurcation of limit cycles due to Hopf and generalized Hopf bifurcations. In particular, we shall consider the existence of multiple limit cycles due to generalized Hopf bifurcation and prove that the maximal number of limit cycles is two for the whole four-dimensional $\gamma$ parameter space. All Hopf bifurcations occur from the equilibrium $\mathrm{E_{1-}}$, which can be classified into three categories according to $R_0 = 1$, $R_0 < 1$ and $R_0 > 1$, namely $D = B$, $D > B$ and $D < B$, respectively. Since the treatment for the cases $R_0 < 1$ and $R_0 > 1$ are similar, we will combine the latter two cases as one: $R_0 \ne 1$. Also, the treatment is same for $A \le BC$ and $A > BC$, we will not distinguish the two cases.

3.1 Case $R_0 = 1$ ($D = B$)

When $R_0 = 1$ (or $D = B)$, system (5) is in a critical situation, i.e., the two equilibria $\mathrm{E_0}$ and $\mathrm{E_1}$ exchange their stability at the critical point and complex dynamics of the system happens on the center manifold which is characterized by a single zero eigenvalue (the other eigenvalue is $-B$).

Since in general we treat D as a bifurcation parameter and define $D_t = B$, to avoid confusing in this subsection we let $D=B$ and choose B as a bifurcation parameter. Then, when $D=B$ (i.e., at $R_0 = 1$), the equilibrium solutions become

$$\begin{aligned} \mathrm{E}_{1+} = \mathrm{E}_0 = \big ( \textstyle \frac{1}{B},\, 0 \big ) \quad \mathrm{and} \quad \mathrm{E}_{1-} = \big (\frac{1+C}{A+B},\, \frac{A-BC}{A+B}\big ), \ \ \big (B \le \frac{A}{C} \, \big ), \end{aligned}$$

(30)

where the existence condition $A \ge BC$ also guarantees $Y_{1-} \ge 0$ and $X_{1-} \le \frac{1}{B}$. Note that when $A=BC$, the equilibrium $\mathrm{E_{1-}} \equiv \mathrm{E_1}$ also coincides with $\mathrm {E}_0$, at which a bifurcation occurs. For this case, we define a new reproduction number as

$$\begin{aligned} B_t = \frac{A}{C}. \end{aligned}$$

(31)

Then, $\mathrm{E_1}$ emerges to exist for $B < B_t$, which requires $A> BC$. In order to study the stability of $\mathrm{E_0}$, we need to find the center manifold at the critical point.

3.1.1 Center Manifold Reduction and Stability Analysis

We first use the center manifold theory to find the differential equation describing dynamics on the center manifold, and then discuss the stability of $\mathrm{E_0}$. To achieve this, we first introduce an affine transformation, given by

$$\begin{aligned} \left( \begin{array}{c} X \\ Y \end{array} \right) = \left( \begin{array}{c} \frac{1}{B} \\ 0 \end{array} \right) + \left[ \begin{array}{cc} 1 &{} 1 \\ -B &{} 0 \end{array} \right] \left( \begin{array}{c} u_1 \\ u_2 \end{array} \right) , \end{aligned}$$

(32)

into (5) with $D=B$ to obtain a system,

$$\begin{aligned}&\frac{\mathrm{d} u_1}{\mathrm{d} \tau } = B u_1 u_2 - \frac{1}{C}(A-BC)\, u_1^2 - \frac{AB}{C} \, u_1^2 u_2 + \cdots , \nonumber \\&\frac{\mathrm{d} u_2}{\mathrm{d} \tau } = -B u_2 + B(B-1) u_1 u_2 + \frac{1}{C} (A-BC)(1-B) u_1^2 + \frac{AB}{C}(1-B) u_1^2 u_2 + \cdots ,\nonumber \\ \end{aligned}$$

(33)

whose linear part is in Jordan canonical form with eigenvalues 0 and $-B$. To find the center manifold, let $u_2 = h(u_1) = \eta u_1^2 + O(u_1^3)$ and then use (33) to find $\eta = \frac{(1-B)(A-BC)}{BC}$. Therefore, the center manifold up to second order is given by

$$\begin{aligned} W^C = \big \{\big (u_1,u_2 \big ) \, \big | \, u_2 = \textstyle \frac{(1-B)(A-BC)}{BC}\, u_1^2 + O(u_1^3) \big \}, \end{aligned}$$

and the differential equation describing the dynamics on the center manifold is given by

$$\begin{aligned} \frac{\mathrm{d} u_1}{\mathrm{d} \tau } = \textstyle \frac{1}{C}(A-BC)\, \big [ -u_1^2 + (1-B)\, u_1^3 + O(u_1^4) \big ]. \end{aligned}$$

(34)

Since when $D = B$, the system still has three free parameters A, B and C, we will give a brief analysis on the dynamics and bifurcation of the system when $R_0 = 1$. Now system has only two equilibria $\mathrm{E_0}$ and $\mathrm{E_1 }$, given in (30). Note that for this critical case, $Y = 1- BX$ still holds and the equilibrium solution $X_1$ for $\mathrm{E_1}$, given by $X_1 = \frac{1 +C}{A+B}$, is monotonically decreasing as B increases, indicating that no backward bifurcation can occur, and so bistable equilibria are not possible. Define

$$\begin{aligned} B_h = \textstyle \frac{A(C-A)}{A+C^2}. \end{aligned}$$

(35)

Then, we have the following theorem for this critical case.

Theorem 3.1

For system (5), when $R_0 = 1$ (i.e., $D = B$), the disease-free equilibrium $\mathrm{E_0}$ is globally asymptotically stable for $B > B_t$ and unstable for $B < B_t$ for which $\mathrm{E_1}$ emerges to exist. $\mathrm{E_1}$ is asymptotically stable for $B < B_t$ if $A \ge C$; and Hopf bifurcation occurs from $\mathrm{E_1}$ at $B = B_h$ if $A < C$ for which $\mathrm{E_1}$ is asymptotically stable for $B_h< B < B_t$ and unstable for $B < B_h$.

Proof

For the stability of the equilibrium $\mathrm{E_0}$, linearization does not work since one eigenvalue is zero. However, we can apply Eq. (34) to study its stability because $(u_1,u_2)$ represents small perturbation from this equilibrium. Since $Y = -B u_1$, Y decreases from a positive initial point if $u_1$ is increasing, implying that Y is stable and converges to zero. It follows from (34) that $u_1$ is increasing if $A < BC$, or $B > B_t$. Recall that the X-axis is invariant and this trajectory converges to $\mathrm{E_0}$ along the X-axis. Therefore, $\mathrm{E_0}$ is a degenerate stable node when $B > B_t$, and a degenerate saddle when $B < B_t$. Note that $\mathrm{E_1}$ does not exist for $B > B_t$, and there exists only one stable equilibrium $\mathrm{E_0}$ on the boundary of the trapping region $\Omega$, and thus all trajectories converge to $\mathrm{E_0}$, implying that $\mathrm{E_0}$ is globally asymptotically stable for $B > B_t$.

To find the stability of the $\mathrm{E_1}$, evaluating the Jacobian of (5) when $D=B$ at $\mathrm{E_1}$ yields the trace and determinant as

$$\begin{aligned} \mathrm{Tr}(J_1) = \textstyle \frac{(C^2+A)(B_h-B)}{A (1+C)} \quad \mathrm{and} \quad \det (J_1) = \textstyle \frac{C^2(B-B_h)^2}{ A(1+C)}>0. \end{aligned}$$

Hence, the equilibrium $\mathrm{E_1}$ is asymptotically stable if $\max \{0,B_h \}< B < B_t$. Hopf bifurcation occurs from $\mathrm{E_1}$ at $B = B_h$, if $B_h > 0$, and $\mathrm{E_1}$ is unstable for $B \in (0, B_h)$.

$\square$

Further, transforming (33) with (34) back to the original coordinates (X, Y), we obtain the equations describing the dynamics on the center manifold, given by

$$\begin{aligned} \begin{array}{ll} \displaystyle \frac{\mathrm{d}X}{\mathrm{d}\tau } =&{} 1 - B X - \textstyle \frac{1}{B}\, Y + (1-B)\, XY - \frac{A-BC}{CB^2}\, Y^2 + \cdots , \\ \displaystyle \frac{\mathrm{d}Y}{\mathrm{d}\tau } =&{} \textstyle \frac{A-BC}{C B^2} \big [ B + (1-B) Y \big ]\, Y^2 + \cdots , \end{array} \end{aligned}$$

(36)

which clearly indicates that for small positive initial conditions, Y converges to zero if $A < BC$, i.e., $B > B_t$. Moreover, the non-trivial equilibrium solution of (36), given by $(X,Y) = \big (1 - \frac{A}{C(B-1)^2}, \frac{B}{B-1} \big )$, shows that the graph $(1 - X) (B - 1)^2 = \frac{A}{C}$ in the B-X plane does not have a turning point, again indicating that no backward bifurcation can occur. The bifurcation diagram for this special case is shown in Fig. 3.

Fig. 3

Bifurcation diagram for system (5) when $R_0 = 1$ ($D = B$)

3.1.2 Hopf Bifurcation

For convenience, define a subset in the $\gamma$-parameter space,

$$\begin{aligned} \gamma _1 = \big \{ \gamma \,|\, C=(\rho +1) A,\ 0<B< \textstyle \frac{1}{\rho +1}, \ \rho >0 \big \}, \end{aligned}$$

(37)

and let

$$\begin{aligned} \bar{A}= & {} \textstyle \frac{ \sqrt{\rho ^4 + 4 \rho ^2 (\rho +1)^2 + 4 (\rho +1)} \,-\, \rho ^2 }{ 2 (\rho +1) \left[ \, \rho ^2 (\rho +1)+1 \right] }\nonumber \\= & {} \frac{2}{ \sqrt{\rho ^4 + 4 \rho ^2 (\rho +1)^2 + 4 (\rho +1)} \,+\, \rho ^2 } \in (0,1), \ \ (\rho > 0). \end{aligned}$$

(38)

Then, we have the following result.

Theorem 3.2

For system (5), when $R_0 = 1$, Hopf bifurcation occurs from the equilibrium $\mathrm{E_1}$ at the critical point $B = B_h$, if the parameter values are taken from the set $\gamma _1$. The bifurcation is supercritical (or subcritical) if $A > \bar{A}$ (or $A < \bar{A}$), and a family of bifurcating limit cycles is stable (unstable), enclosing an unstable (a stable) focus at $\mathrm{E_1}$.

Proof

First, the necessary conditions for having a Hopf bifurcation from $\mathrm{E_1}$ are obtained from the Hopf critical condition $B_h > 0$ and $B < B_t$ as $C> A > BC$, yielding $0< B < 1$. Further, let $C = (\rho + 1) A \ (\rho > 0)$, under which the above two conditions become $0< B < \frac{1}{\rho +1}$. In order to apply normal form theory to calculate the first-order focus value (or the first Lyapunov constant), we first multiply the equations in (5) by $Y + C>0$ and then introduce the affine transformation, given by

$$\begin{aligned} \left( \begin{array}{c} X \\ Y \end{array} \right) = \left( \begin{array}{c} \frac{1+C}{A + B} \\ \frac{A - B C}{A + B} \end{array} \right) + \left[ \begin{array}{cc} 1 &{} 0 \\ \frac{-CA}{C^2 + (1+C)A} &{} \frac{-C \omega _c }{C^2 + (1+C)A} \end{array} \right] \left( \begin{array}{c} u_1 \\ u_2 \end{array} \right) , \end{aligned}$$

(39)

where $\omega _c = \frac{A}{C} \sqrt{(1+C)A}$, into the resulting equations to yield a system to be expanded around $(u_1,u_2)=(0,0)$ up to third-order terms. Next, we apply the Maple program for computing the normal forms associated with Hopf and generalized Hopf bifurcations (Yu 1998) to the new system to obtain the normal form in polar coordinates up to third-order terms as follows:

$$\begin{aligned} \displaystyle \frac{\mathrm{d}r}{\mathrm{d}\tau } = r \,\big [ v_0\, \mu + v_1 \, r^2 + O(r^4) \big ], \quad \displaystyle \frac{\mathrm{d} \theta }{\mathrm{d}\tau } = \omega _c + t_0\, \mu + t_1 \, r^2 + O(r^4) , \end{aligned}$$

(40)

where $\mu = B_h - B$, is a perturbation parameter, and $v_0$ and $v_1$ are the zero-order and the first-order focus values. The first equation of (40) can be used to perform bifurcation analysis and the sign of $v_1$ determines whether the Hopf bifurcation is supercritical or subcritical. The values $v_0$ and $t_0$ can be found from a linear analysis, while $v_1$ and $t_1$ are obtained by applying the Maple program. The calculation shows that

$$\begin{aligned} v_0 = -\,\textstyle \frac{(A+C^2)^2}{2 A C(1+C)}, \qquad t_0 = -\, \textstyle \frac{(A+C^2)^2}{C^2 \sqrt{(1+C)A}}, \end{aligned}$$

(41)

and the output from the Maple program gives $v_1$ and $t_1$ as

$$\begin{aligned} v_1 = \textstyle \frac{-A^3 C^2}{8 (A + AC + C^2 ) (C^2+A)^2} \, \big [ (\rho +1)(\rho ^3+\rho ^2+1) A^2 + \rho ^2 A -1 \big ] \end{aligned}$$

(42)

and

$$\begin{aligned} \begin{array}{ll} t_1 = &{} \frac{-\,A^3 C \sqrt{(1+C) A}}{24 (1+C) (A+ A C+C^2) (C^2+A)^2} \big [ (\rho +1)^2 (\rho ^4+12 \rho ^3+20 \rho ^2+13 \rho +5) A^3 \\ &{} +\, (\rho + 1) (10 \rho ^3 + 44 \rho ^2 + 45 \rho +13) A^2 + (25 \rho ^2 + 45 \rho + 21) A + 13 \big ]. \end{array} \end{aligned}$$

It is easy to verify that when $A > \bar{A}$ (or $A < \bar{A}$), $v_1 < 0$ (or $v_1 > 0$), yielding a supercritical (subcritical) Hopf bifurcation and so the bifurcating limit cycles are stable (unstable). $\square$

To illustrate the theoretical result, we present a simulation using the following parameter values:

$$\begin{aligned} A = \textstyle \frac{6937}{65600}, \quad C = \frac{96}{205}, \quad D=B = \frac{73}{625} = 0.1168, \end{aligned}$$

(43)

yielding $B_h \approx 0.117947$ at which $\mathrm{Tr(J_1)} = 0$ (or $v_0\, \mu = 0$), as well as $v_0 \approx -\,0.726539$ and $v_1 \approx -0.002351$, indicating that the Hopf bifurcation is supercritical and the bifurcating limit cycle is stable. To estimate the amplitude of the limit cycle, we note that $\mu = B_h - B = 0.001147$, which implies that B is decreasing to pass the Hopf critical point $B_h$ as $v_0 < 0$ indicates. Thus, it is easy to use the truncated normal form $\, v_0 \mu + v_1 r^2$ to obtain the estimate of the amplitude of the bifurcating limit cycle as $r \approx 0.5954$. The simulation of this stable limit cycle is shown in Fig. 4a as the red curve, and the green curve in the same figure denotes the first-order approximation of the analytical prediction, which is obtained by using the transformation (39), the normal form (40) together with (41) as well as the following additional transformation,

$$\begin{aligned} u_1 = r \cos (\omega _c t), \quad u_2 = - r \sin (\omega _c t). \end{aligned}$$

The simulation shows an excellent agreement with the analytical prediction.

Fig. 4

A stable limit cycle of system (5) when $R_0 = 1$ for $A = \frac{6937}{65600}$, $C = \frac{96}{205}$, $B = D = \frac{73}{625}$: a phase portrait with the red and green color curves denoting the simulation and the estimation from normal form (with amplitude $r \approx 0.5954$), respectively; and b the time history of the stable limit cycle (Color figure online)

3.1.3 Multiple Limit Cycles Bifurcation

In the previous subsection, we have shown that system (5) always exhibits limit cycles due to Hopf bifurcation. But it is limited to a single limit cycle for a given set of parameter values. Now, we want to ask: for what feasible parameter values in the $\gamma _1$ set, we can obtain maximal number of limit cycles bifurcating from the Hopf critical point near the equilibrium $\mathrm{E_1}$? Here, “feasible” means that the values of the chosen parameters must be positive and the equilibrium solution for the chosen parameter values must be also positive. Bifurcation of multiple limit cycles here is related to the so-called generalized Hopf bifurcation. The condition for a generalized Hopf bifurcation is that at least the first-order focus value vanishes, i.e., $v_1 = 0$. When more focus values vanish, the generalized Hopf bifurcation is more degenerate and more limit cycles can bifurcate from the critical point. More precisely, we rewrite the first equation of (40) as

$$\begin{aligned} \displaystyle \frac{\mathrm{d}r}{\mathrm{d} \tau } = r \,\big [ v_0\, \mu + v_1 \, r^2 + \cdots + v_{k-1}\, r^{2k-2} + v_k \, r^{2k} + O(r^{2k+2}) \big ], \end{aligned}$$

where all the focus values $v_i$’s are expressed in terms of the system parameters. If we can find the conditions on k parameters, say, $\mu = (\mu _1,\, \mu _2, \, \dots ,\, \mu _k)$, such that $v_0=v_1 = \cdots = v_{k-1} = 0$, but $v_k \ne 0$, at the critical point defined by $\mu _c = (\mu _{1c},\, \mu _{2c}, \, \dots , \, \mu _{kc})$ and

$$\begin{aligned} \mathrm{rank} \left[ \frac{ \partial (v_0,\, v_1, \, \dots , \, v_{k-1})}{ \partial (\mu _1,\, \mu _2,\, \dots ,\, \mu _k) } \right] _{\mu = \mu _c} = k, \end{aligned}$$

then k limit cycles can bifurcate from the critical point near the equilibrium by using appropriate perturbations on $\mu$. More details on the topic of bifurcation of limit cycles can be found, for example, in the book Han and Yu (2012).

For multiple limit cycles bifurcation when $R_0 = 1$, we have the following theorem.

Theorem 3.3

For system (5), when $R_0 = 1$, there exist feasible parameter values in the set $\gamma _1$ such that maximal two small-amplitude limit cycles can bifurcate from the endemic equilibrium $\mathrm{E_1}$ due to generalized Hopf bifurcation. The outer limit cycle is stable while the inner one is unstable, and both of them enclose the stable equilibrium $\mathrm{E_1}$.

Proof

To prove this theorem, we need to compute the focus values up to $v_3$ since there are two free parameters A and C. However, we will show that $v_3$ is not needed since no feasible parameter values can be chosen such that $v_2 = 0$. Actually, taking $A = \bar{A}$ we have $v_1=0$, and then $v_2$ is obtained from the Maple program (Yu 1998) as

$$\begin{aligned} v_2= & {} -\,\textstyle \frac{4 \rho ^2 (\rho +1)^2 C^4 \bar{A}^7}{192 (1+C)(C^2+ \bar{A})^4 (C^2+ \bar{A} + \bar{A}C)^4 (\rho ^3 + \rho ^2 +1)^6 } \big [ 7 \rho ^{14} + 54 \rho ^{13}\\&\quad +\, \textstyle 182 \rho ^{12} + 384 \rho ^{11} + 656 \rho ^{10} + 998 \rho ^9\\&\quad +\, \textstyle 1269 \rho ^8 + 1344 \rho ^7 + 1303 \rho ^6+1110 \rho ^5 +791 \rho ^4\\&\quad +\,\textstyle 527 \rho ^3+276 \rho ^2+117 \rho +54 \quad \\&\quad +\,\textstyle \bar{A} \, (\rho +1)( 4 \rho ^{15}+33 \rho ^{14}+127 \rho ^{13} +315 \rho ^{12}\\&\quad +\,\textstyle 565 \rho ^{11}+821 \rho ^{10} +1071 \rho ^9+1272 \rho ^8\\&\quad +\,\textstyle 1262 \rho ^7+1153 \rho ^6+966 \rho ^5 +656 \rho ^4 + 449 \rho ^3\\&\quad +\,\textstyle 234 \rho ^2+90 \rho +54) \big ] < 0, \quad \mathrm{for} \ \ \rho >0. \end{aligned}$$

This clearly shows that there are no feasible parameter values that can yield three limit cycles. There exist infinitely many solutions for the existence of two limit cycles since there are two free parameters, as long as the conditions satisfy $v_1 =0$ with $v_2 < 0$. $\square$

Fig. 5

Two limit cycles of system (5) when $R_0 = 1$ with $A = 0.2095365226$, $C = 0.5$ and $B = D = 0.1324446775$: a the phase portrait with the simulations in red and blue colors and the normal form predictions in green color (with amplitudes $r_1 \approx 0.1839$ and $r_2 \approx 0.3067$); and b the time history of the stable (outer) limit cycle (Color figure online)

To give an example to demonstrate the bifurcation of two limit cycles, we take $\rho = 1.397661 \cdots$, which gives $A = \bar{A} = 0.208536 \cdots$, $C = 0.5$, and $B = B_h = 0.132553 \cdots$, resulting in $v_0 = v_1 = 0$ and $v_2 = -\,0.000222 \cdots < 0$, as expected. Then, we perturb the parameters A and B such that $v_1 > 0$, $v_0 < 0$ and $|v_0| \ll v_1 \ll |v_2|$, and so two limit cycles can be obtained. More precisely, let $A = 0.208536 + \varepsilon _1$ and $B = B_h + \varepsilon _2$, where $\varepsilon _1 = 10^{-3}$ and $\varepsilon _2 = - 7 \times 10^{-6}$, which yield $A = 0.209536, \ B = 0.132444$ and

$$\begin{aligned} v_0 \mu = -\,0.731036 \times 10^{-6} , \ \ v_1 = 0.293971 \times 10^{-4} , \ \ v_2 = -\,0.229863 \times 10^{-3} .\nonumber \\ \end{aligned}$$

(44)

Note that $\varepsilon _2 < 0$ again implies that B is decreasing to pass the Hopf critical point $B_h$ since $v_0 \approx -\,0.672163 < 0$. Thus, the truncated normal form equation $v_0 \mu + v_1 \, r^2 + v_2 \, r^4 = 0$ has two real roots: $r_1 \approx 0.1839$ and $r_2 \approx 0.3067$, which approximate the amplitudes of the two limit cycles. Since $v_2 < 0$, the outer limit cycle is stable while the inner one is unstable, and the equilibrium solution at this critical point is a stable focus.

The simulation, shown in Fig. 5, takes the exact parameter values:

$$\begin{aligned} A = 0.2095365226, \quad C = 0.5, \quad D=B = 0.1324446775. \end{aligned}$$

The simulated phase portrait is shown in Fig. 5a where the stable (the larger one) and unstable (the smaller one) limit cycles are denoted by the red and blue curves, respectively. Analytic predictions based on the normal form are also shown in Fig. 5a as the green curves. It indeed indicates a good agreement between the simulations and the analytic predictions. Figure 5b depicts the time history of the stable (outer) limit cycle. Note that the simulation for the unstable limit cycle (or the unstable periodic motion) is obtained by using a negative time step in a fourth-order Runge–Kutta integration scheme.

3.2 Case $R_0 \ne 1$

When $R_0 \ne 1$ (i.e., $D \ne D_t = B$), the Hopf bifurcation conditions are given in Theorem 2.3, and the critical point is defined in (24) as $D_h$. However, unlike the case $R_0 = 1$ considered in the previous subsection, using the explicit solution of $X_{-}$ will cause difficulty in computing the focus values (or the normal form), in particular for higher-order focus values. Thus, instead of using the explicit expression $X_{-}$, we use the parameter A to solve the equation $F_1 = 0$ and then use the parameter D to solve the trace of the Jacobian of the system to obtain

$$\begin{aligned} A = \textstyle \frac{(1- B X_{-})(1+C-D X_-)}{X_- (1- D X_{-})} \quad \mathrm{and} \quad D = D_h = \frac{1 + C (1 - X_- + B X_-^2)}{X_-} , \end{aligned}$$

(45)

where $D = D_h$ denotes a Hopf critical point. Note that solving $X_{-}$ from (45) yields the solution $X_-$ given in (29). It follows from $A > 0$ that $1 - X_{-} + B X_{-}^2 < 0$.

3.2.1 Hopf Bifurcation

To study Hopf bifurcation which arises from the equilibrium $\mathrm{E_{1-}}$, we use the Hopf bifurcation conditions given in Theorem 2.3 to define a subset $\gamma _2$ in the $\gamma$-parameter space as

$$\begin{aligned} \gamma _2 = \big \{ \gamma \, \big |\, B \in I_B,\ A \in (A_l,A_u), \ C \in (C_l,C_u), \ D \in \big (0, \textstyle \frac{1}{2} \big ) \big \}, \end{aligned}$$

(46)

where

$$\begin{aligned} I_B = \big (0,\textstyle \frac{1}{4}\big ), \quad C_l = C_{l_1}, \quad C_u = \left\{ \begin{array}{ll} C_{u_1}, &{}\quad \mathrm{if} \ \ A \le BC, \\ C_{u_1}, &{}\quad \mathrm{if} \ \ A > BC, \end{array} \right. \end{aligned}$$

and $A_l$, $A_u$, $C_{l_1}$, $C_{u_1}$ and $C_{u_2}$ are defined in (24). Then for the parameter values taken from $\gamma _2$, Hopf bifurcation occurs at the critical point $D=D_h$.

We have the following theorem for Hopf bifurcation when $R_0 \ne 1$.

Theorem 3.4

For system (5), when $R_0 \ne 1$ and the parameter values are taken from the $\gamma _2$ set, Hopf bifurcation occurs from the equilibrium $\mathrm{E_{1-}}$ at the critical point $D_h$. The bifurcation is supercritical (subcritical) if the first-order focus value $v_1$ is negative (positive), and a family of bifurcating limit cycles is stable (unstable), enclosing the unstable (stable) focus $\mathrm{E_{1-}}$.

Proof

First, note that the equilibrium solution satisfies $Y_{-} = 1 - D X_{-} > 0$ (i.e., $0< X_{-} < \frac{1}{D}$), and $1 - X_{-} + B X_{-}^2 < 0$ yields

$$\begin{aligned} \textstyle \frac{1 - \sqrt{1-4B}}{2 B}< X_{-}< \frac{1 + \sqrt{1-4B}}{2B}, \quad 0<B< \frac{1}{4}. \end{aligned}$$

Under these conditions, the frequency at the Hopf bifurcation point can be obtained as

$$\begin{aligned} \omega _c = \textstyle \frac{(1 - D X_{-})(1 - B X_{-})}{-1 + X_{-} - B X_{-}^2} \sqrt{ X_{-} ( 1- D - D X_{-})}. \end{aligned}$$

(47)

The condition $\omega _c > 0$ yields $0< X_{-}< \textstyle \frac{1}{D} - 1 \ (0< D < 1)$, and so we have

$$\begin{aligned} \textstyle \frac{1 - \sqrt{1 - 4B}}{2 B}< X_{-}< \min \big ( \frac{1 + \sqrt{1 - 4B}}{2B},\, \frac{1}{D} - 1 \big ), \quad 0< B < \frac{1}{4}. \end{aligned}$$

(48)

Further, note that

$$\begin{aligned} \begin{array}{ll} &{} 1 - B X_{-}> 1 - \textstyle \frac{1+ \sqrt{1-4B}}{2} = \frac{1- \sqrt{1-4B}}{2} = \frac{2B}{1 + \sqrt{1-4B}}> B, \\ &{}\mathrm{and} \ \ X_{-}> \frac{1 -\sqrt{1-4B}}{2B} = \frac{2}{1 + \sqrt{1-4B}} \in (1,2) \ \Longrightarrow \ \frac{1}{D}-1>1 \ \Longrightarrow \ D < \frac{1}{2}. \end{array} \end{aligned}$$

So the condition (48) becomes

$$\begin{aligned} \textstyle \frac{1 - \sqrt{1 - 4B}}{2 B}< X_{-}< \min \big ( \frac{1 + \sqrt{1 - 4B}}{2B},\, \frac{1}{D} - 1 \big ), \quad 0< B< \frac{1}{4}, \ \ 0< D < \frac{1}{2}. \end{aligned}$$

(49)

Summarizing the above conditions defines the subset $\gamma _2$. Note that if the equilibrium solution $X_- > \frac{1}{D} - 1$, then it follows from (47) that the $\mathrm{E_{1-}}$ is a saddle point, rather than an elementary center.

Now, multiplying $Y+C$ to system (5) and applying the transformation,

$$\begin{aligned} \left( \begin{array}{c} X \\ Y \end{array} \right) = \left( \begin{array}{c} X_{-} \\ 1 - D X_{-} \end{array} \right) + \left[ \begin{array}{cc} 1 &{} 0 \\ \frac{-1}{1 + X_{-} } &{} -\, \frac{\omega _c}{C(1 + X_-)(1- B X_- )} \end{array} \right] \left( \begin{array}{c} u_1 \\ u_2 \end{array} \right) , \end{aligned}$$

to the resulting system yields a system with its linear part in Jordan canonical form, and then using the Maple program (Yu 1998), we obtain the first focus value, given by

$$\begin{aligned} v_1= & {} \frac{-1}{8 X (1+X ) (1-B X) (1-D-D X) (-1+X -B X^2)}\nonumber \\&\big \{ (1 + X)^2 (1 - B X )^2 (1 - X + B X^2 ) C^2\nonumber \\&+\, \big [ (X + 3) (1 - X + B X^2)^2 +(3B X+2 X+B-4) (1-X+B X^2)\nonumber \\&+\,3-B-4 B X \big ] C + 1 \big \}, \end{aligned}$$

(50)

where $X = X_-$. Note that $v_1$ can be positive or negative for taking suitable parameter values, and its sign determines the stability of bifurcating limit cycles. In order to determine the critical condition such that $v_1 =0$. We substitute $X_{-}$ given in (29) into (50) to obtain an equation which is equivalent to $v_1 =0$:

$$\begin{aligned} F_{v_1}= & {} A^2 B^2 \big [(1+ B)^2 + (B + 2) A \big ]^2 C^4 + A \big [ 2 (B-1) (B^2+10 B-2) A^4 \nonumber \\&+\,2 (B-1) (3 B^3+29 B^2+3 B-2) A^3\nonumber \\&+\,(6 B^5+48 B^4-42 B^3 -36 B^2 + 5 B + 1) A^2\nonumber \\&+\,2 B (B^5 + 6 B^4 - 12 B^3 - 18 B^2 - 2 B + 1) A -2 B^3 (B+3) (B+1)^2 \big ] C^3\nonumber \\&+\,\big [ (B^2 + 14 B - 3) A^6 + 2 (26 B^2 + 2 B^3 +\, 4 B - 3) A^5\nonumber \\&+\, (6 B^4 + 68 B^3 + 19 B^2 + 14 B - 6) A^4 \nonumber \\&+\,(4 B^5 + 32 B^4 - 20 B^3 + 54 B^2 + B - 2) A^3 \nonumber \\&+\,B (B^5-2 B^4 -49 B^3+48 B^2+20 B-3) A^2 \nonumber \\&-\,2 B^2 (2 B^4+10 B^3-10 B^2 -11 B+1) A +B^4 (B+3)^2 \big ] C^2\nonumber \\&-\,(A+B) \big [ 2 (B-1) A^5 \nonumber \\&+\,2 (B + 1) (4 B - 1) A^4 +2 (6 B^3 + 14 B^2 + 4 B - 1) A^3 \nonumber \\&+\,(8 B^4 + 28 B^3 + 16 B^2 + 4 B - 1) A^2\nonumber \\&+\, 2 B^2 (B^3 + 3 B^2 + 3) A -2 B^4 (B+3) \big ] C +(A+B)^6 \nonumber \\= & {} 0. \end{aligned}$$

(51)

Therefore, for any values given in $B \in I_B$ and $A \in (A_l,A_u)$, we can use (51) to solve for C and then use (24) to get $D_h$. Further, we again use (24) to verify if these obtained parameter values satisfy $C \in (C_l,C_u)$; and if $D_h \in (0,D_t)$ when $A \le BC$, or $D_h \in (0,D_s)$ when $A > BC$. If all the conditions are satisfied, we have identified the critical point such that $v_1 = 0$. In next subsection, we will present a different method to investigate multiple limit cycles bifurcation. $\square$

To this end, before considering multiple limit cycle bifurcation, we present several numerical examples to show supercritical and subcritical Hopf bifurcations, arising from the equilibrium $\mathrm{E_{1-}}$.

• (1) Taking $D = D_h = \frac{1}{10}$ and $B = \frac{7}{64}$ gives $R_0 >1$ (i.e., $D < B$). Using (48) we obtain $\frac{8}{7}< X_- < 8$, and choose, for instance, $X_- = 7$, and use (45) to obtain $C = \frac{96}{205}$ and then $A = \frac{225}{2624}$. For these parameter values, we have $v_1 = -\, \frac{23}{17220}$ which indicates that the Hopf bifurcation is supercritical and the bifurcating limit cycle is stable. More precisely, it can be shown by using (45) and (50) that for $D = \frac{1}{10}$ and $B = \frac{7}{64}$, we have $v_1 < 0$ if $X_- \in (\frac{8}{7}, 2.419645) \cup (6.017355, 8)$; and $v_1 > 0$ if $X_- \in (2.419645, 6.017355)$.

• (2) Choosing $D = D_h = \frac{1}{10}$ and $B = \frac{9}{100}$ yields $R_0 < 1$ (i.e., $D > B$), and $\frac{10}{9}< X_- < 9$. We take $X_- = 4$, and similarly use (45) and (50) to find $C = \frac{5}{13}$, $A = \frac{256}{975}$, and $v_1 = \frac{431}{133120}$. Thus, the Hopf bifurcation is subcritical and the bifurcating limit cycle is unstable. As a matter of fact, we can also use (45) and (50) to show that for $D = \frac{1}{10}$ and $B = \frac{9}{100}$, $v_1 < 0$ if $X_- \in (\frac{10}{9}, 2.116127)$; and $v_1 > 0$ if $X_- \in (2.116127, 9)$.

However, it is noted that all the parameter values of A, B and C in the above examples belong to the category $A > BC$. This suggests that it is pretty easy to find Hopf bifurcation when $A > BC$. Now we want to find Hopf bifurcation when $A \le BC$. We use the conditions on B and A defined in $\gamma _2$ and then apply (51) to determine the value of parameter C. We will give a couple of examples to show that for the case $A < BC$, $v_1$ can also be positive or negative. Let $B = 0.05 \in (0,0.25)$. We take $A = 0.0156 \in (A_l,A_u) = (0.0125,0.020225)$. Then we solve (51) for C to obtain two positive solutions: $C = 0.097104 \cdots$ and $C = 0.461628 \cdots$, both of them are located in the interval $(C_l,C_u) = (C_{l_1},C_{u_1}) = (0.031912,0.564006)$. However, only the second solution satisfies $v_1 = 0$. Thus, we choose two values for C: $C = 0.458 < 0.461628 \cdots$ and $C = 0.476 > 0.461628 \cdots$, both of them yield $A < BC$. For the former, the Hopf critical point is given by $D_h = 0.011272 < 0.05 = D_t$, and we obtain $v_1 = 0.381609 \times 10^{-6} > 0$, showing a subcrtical Hopf bifurcation; while for the latter, the Hopf critical point is $D_h = 0.009358 < 0.05 = D_t$, and the first-order focus value becomes $v_1 = -0.149416 \times 10^{-5} < 0$, indicating a supercritical Hopf bifurcation.

The above examples indicate that Hopf bifurcations can be either supercritical or subcritical for both cases $A \le BC$ and $A > BC$, implying that two limit cycles are possible to occur from the equilibrium $\mathrm{E_{1-}}$, which will be considered in the next subsection by using a different method.

For simulation, we give two examples, one for $R_0 > 1$ and one for $R_0 < 1$.

(i) For $R_0 > 1$, we choose $A=\frac{225}{2624},\, B = \frac{7}{64}$ and $C=\frac{96}{205}$. Then, $D_h = \frac{1}{10}$ under which $\mathrm{Tr(J)} = 2 v_0\, \mu = 0$ (due to $\mu = 0$), where $v_0 = 0.058427>0$. As shown in above, $v_1 = - \frac{23}{17220}$, indicating that the Hopf bifurcation is supercritical and the bifurcating limit cycle is stable. To achieve a stable limit cycle, we need to perturb some parameter such that $\mu > 0$, yielding $\, v_0 \mu > 0$. We add the perturbation $\mu = \frac{1}{500}$ to D so that $D = \frac{1}{10} + \mu = \frac{51}{500}$, for which $v_1$ is unchanged, and obtain $v_0 \mu \approx 0.000116854$. Then the truncated normal form equation, $v_0 \mu + v_1 r^2 = 0$ gives an estimation for the amplitude of the stable limit cycle as $r \approx 0.2958$. The comparison between the analytical prediction (the green curve) and the simulation (the red curve) is depicted in Fig. 6a, which again shows an excellent agreement and the time history of the stable limit cycle is given in Fig. 6b.

Fig. 6

A stable limit cycle of system (5) for $R_0 > 1$ ($A > BC$) with $A = \frac{225}{2624}$, $C = \frac{96}{205}$, $B = \frac{7}{64}$ and $D = \frac{51}{500}$: a phase portrait with the red and green curves denoting the simulation and the estimation from normal form (with amplitude $r \approx 0.2958$), respectively; and b the time history of the stable limit cycle (Color figure online)

Fig. 7

An unstable limit cycle of system (5) for $R_0 < 1$ ($A > BC$) with $A = \frac{121}{1440}$, $C = \frac{16}{75}$, $B = \frac{3}{32}$ and $D = \frac{199}{2000}$: a phase portrait with the red and green curves denoting the simulation and the estimation from normal form (with amplitude $r \approx 0.6111$), respectively; and b the time history of the unstable limit cycle (Color figure online)

(ii) For $R_0 < 1$, we again choose $D_h = \frac{1}{10}$, but $B = \frac{3}{32} < D_h$. If we choose $A = \frac{121}{1440}$ and $C = \frac{16}{75}$, and get $v_1 = \frac{3}{3850} > 0$, indicating that this case is a subcritical Hopf bifurcation and the bifurcating limit cycle is unstable. Since $v_0 = 0.581928 > 0$, in order to obtain this unstable limit cycle, we take $\mu = - \frac{1}{2000}$ and let $D = \frac{1}{10} + \mu = \frac{199}{2000}$, yielding $v_0 \mu \approx -\,0.0002910$, showing that the equilibrium $\mathrm{E_1}$ is a stable focus and the limit cycle is unstable. The estimation of the amplitude of the unstable limit cycle can be found from the normal form as $r \approx 0.6111$. The simulation is shown in Fig. 7a, where the unstable limit cycle (in red color) is obtained by using a negative time step in the numerical integration scheme. The green curve again denotes the normal form prediction, showing a good prediction even for a pretty large unstable limit cycle. Figure 7b shows the time history of the unstable limit cycle.

3.2.2 Multiple Limit Cycles Bifurcation

Since it has been shown in previous subsection that $v_1$ can be positive or negative by taking appropriate parameter values, it implies that $v_1$ can be zero and more limit cycles may bifurcate from the Hopf critical point. This is a more challenging task since the system contains four free parameters and in general it may exhibit at most four limit cycles. However, we will show that four and three limit cycles are not possible due to the physical restriction on the parameters, and there can still exist maximal two limit cycles even now it allows $B \ne D$. For this case, we obtain the focus values $v_2, \, v_3$ and $v_4$ in terms of the parameters $B,\,D$ and $X_{-}$. We omit the lengthy expressions of these focus values for brevity. We have the following theorem for this case.

Theorem 3.5

For system (5), when $R_0 \ne 1$, there exist feasible parameter values in the $\gamma _2$ set such that maximal two small-amplitude limit cycles can bifurcate from the endemic equilibrium $\mathrm{E_{1-}}$ due to generalized Hopf bifurcation. The outer limit cycle is stable while the inner one is unstable, and both of them enclose the stable equilibrium $\mathrm{E_{1-}}$.

Proof

Here, we use the parameters A and C to solve the equation $F_1 = 0$ and the trace of the Jacobian of the system to get

$$\begin{aligned} A = \textstyle \frac{(1- B X_-)^2}{ -1+ X_- - B X_-^2} \quad \mathrm{and} \quad C = \textstyle \frac{1-D X_-}{ -1+ X_- - B X_-^2}, \end{aligned}$$

(52)

Note that $-1+ X_- - B X_-^2 >0$ under the condition (49).

Since now there are three free variables B, D and $X_-$ in the expressions of the focus values $v_i$ ($i \ge 1$), the best expected result is to find the conditions such that $v_1 = v_2 = v_3 = 0$, but $v_4 \ne 0$, which implies possible existence of four limit cycles. We first consider whether there exist three limit cycles, i.e., to find the solutions such that $v_1 = v_2 = 0$, but $v_3 \ne 0$. $v_1$ is given in (50). Eliminating B from the two equations $v_1 = 0$ and $v_2 = 0$ we obtain $B = \frac{B_N}{B_D}$, where

$$\begin{aligned} B_N= & {} 4 D^3 (4 D^2-9 D+3) X^7 +12 D^2 (2 D^3-6 D^2+9 D-3) X^6 \nonumber \\&-\, D (17 D^4-51 D^3-34 D^2\nonumber \\&+\,102 D-36) X^5 - 2 (20 D^5-84 D^4 +145 D^3 -59 D^2 \nonumber \\&-\,12 D +\,6) X^4 - (13 D^5 - 75 D^4\nonumber \\&+\,240 D^3 - 316 D^2 + 132 D - 6) X^3 \nonumber \\&+\,2 (D^5-7 D^4+15D^3+\,28 D^2-54 D+18) X^2\nonumber \\&-\, (D-1) (8 D^3-43 D^2+48 D+6) X -6 (2-D) (1-D)^2,\nonumber \\ B_D= & {} 4 D^3 (4 D^2-9 D+3) X^8 + 6 D^2 (5 D^3-17 D^2+20 D-6) X^7\nonumber \\&-\,2 D (5 D^4-6 D^3-62 D^2\nonumber \\&+\,69 D-18) X^6 -(45 D^5-224 D^4 +289 D^3 -34 D^2\nonumber \\&-\, 60 D+12) X^5 -(20 D^5 - 162 D^4\nonumber \\&+\,472 D^3 - 441 D^2 + 114 D + 6) X^4 \nonumber \\&+\,(D^5+2 D^4-\,101D^3+308 D^2 -237 D+42) X^3\nonumber \\&-\,(14 D^4-88 D^3 +79 D^2+48 D-42) X^2 - (1-D) (25 D^2\nonumber \\&-\,69 D+6) X -12 (1-D)^2, \end{aligned}$$

(53)

and a resultant:

$$\begin{aligned} R_{12} = D X (1+X) (1-D X) (1-D-D X)\, R_{12a} R_{12b}, \end{aligned}$$

where

$$\begin{aligned} R_{12a}= & {} D (1-X)^2-X +2 , \nonumber \\ R_{12b}= & {} 12 D^2 (3 D - 1) X^4 + 24 D (2 D^2 - 4 D + 1) X^3 \nonumber \\&+ (13 D^3 - 55 D^2 + 84 D - 12) X^2\nonumber \\&-(1-D) (D^2+30 D+24) X + 15 (1-D)^2. \end{aligned}$$

(54)

Note in the above expressions that $X = X_{-}$. It is seen from (49) that $1< \frac{1-\sqrt{1-4B}}{2 B}< X_- < \frac{1}{D}-1$ for which the $\mathrm{E_{1-}}$ is an elementary center; and the $\mathrm{E_{1-}}$ is a saddle if $X_- > \frac{1}{D}-1$.

To find the roots of $R_{12}$, first letting $R_{12a} = 0$ gives two real solutions:

$$\begin{aligned} X_-^{\pm } = \textstyle \frac{1}{2D}\big ( 1 + 2D \pm \sqrt{ 1- 4D} \big ), \quad \mathrm{for} \ \ 0 < D \le \textstyle \frac{1}{4}. \end{aligned}$$

(55)

It is easy to show that $X_-^+ > \frac{1}{D} -1$ for $0< D < \frac{1}{4}$, and at $D = \frac{1}{4}$, $X_-^+ = X_-^- = 3$, leading to BT bifurcation. Thus, $X_-^+$ is not a feasible solution for bifurcation of multiple limit cycles from a Hopf critical point. Moreover, it can be verified that the solution $X_-^-$ together with the solution $B = \frac{B_N}{B_D}$ results in $v_1 = v_2 = v_3 = v_4 = \cdots = 0$, implying that this is a center condition. As a matter of fact, the above solution $X_-^-$ yields

$$\begin{aligned} A = \textstyle \frac{1}{1+D}, \quad B = \frac{D}{1+D}, \quad C = 1+D, \quad D \in \big (0,\textstyle \frac{1}{4}\big ], \end{aligned}$$

(56)

under which (5) is an integrable system having the first integral,

$$\begin{aligned} F(X,Y) = X+Y + \ln \left( \textstyle \frac{ Y^{1+D}}{|1-D X-X Y|} \right) . \end{aligned}$$

(57)

Note that this integral system belongs to the case $A > BC$. We will not discuss this integral system further in this study.

Next, we consider the factor $R_{12b}$ and will show that $R_{12b} = 0$ does not have feasible solutions to yield three limit cycles. First, for the solution $B = \frac{B_N}{B_D}$ and the equation $R_{12b} = 0$, a more precise upper bound for D can be obtained by considering the restriction $B \in (0, \frac{1}{4})$ on the solution $B = \frac{B_N}{B_D}$. To achieve this, we may use the two equations $R_{12b} = 0$ and $B = \frac{B_N}{B_D} = \frac{1}{4}$ to solve X and D, yielding the maximal value $D_{\max } = 0.252605 \cdots$. Thus, we only need to consider the values of D in the interval $D \in (0, D_{\max })$ for the case of three limit cycles. Further, we want to prove that $R_{12b}=0$ does not have real solutions for $X \in (1, \frac{1}{D}-1)$. It is easy to verify that for $D \in (0,D_{\max })$,

$$\begin{aligned} \begin{array}{ll} \left. R_{12b} \right| _{X \rightarrow - \infty } = -\infty , \\ \left. R_{12b} \right| _{X=0} = 15 (1-D)^2 > 0, \\ \left. R_{12b} \right| _{X=1} = -21 + 72 D - 119 D^2 + 98 D^3< 0, \\ \left. R_{12b} \right| _{X= \frac{1}{D}-1} = -10 (1-D)^2 < 0, \\ \left. R_{12b} \right| _{X \rightarrow \infty } = -\infty , \end{array} \end{aligned}$$

which shows that the polynomial $R_{12b}$ has at least one real root for $X<0$ and at least one real root for $0<X<1$. Then, if the $R_{12b}$ has four real roots, then at most two real roots for $X> 1$. In fact, by using Sturm’s theorem, we can show that the polynomial $R_{12b}$ always has four real solutions for $X \in (-\infty ,\infty )$ with $D \in (0,D_{\max })$. An example is shown in Fig. 8. However, since $R_{12b} < 0$ at $X=1$, $X=\frac{1}{D} - 1$ and $X = +\infty$, the number of the roots of $R_{12b}$ which can occur for $X>1$ must be even, i.e., either two or zero, one is not possible.

Fig. 8

Graph $R_{12b}(X)$ for $D = 0.2$ with two vertical lines (in green color) at $X = 1$ and $X = \frac{1}{D} - 1$, respectively (Color figure online)

More precisely, we can show that exactly one real root of $R_{12b}$ is in the interval $X \in (-\infty ,0)$ and one real root in the interval $X \in (0,1)$. Thus, two real roots must appear in the interval $X \in (1, \infty )$, and they must both appear either in the interval $X \in (1, \frac{1}{D} - 1)$ or in the interval $X \in (\frac{1}{D} - 1, \infty )$ due to $R_{12b} < 0$ at $X=1$, $X=\frac{1}{D} - 1$ and $X = \infty$. In the following, we will show that the two real roots must locate in the interval $X \in (\frac{1}{D} - 1, \infty )$. To achieve this, consider the derivative,

$$\begin{aligned} \begin{array}{rl} \frac{\mathrm{d} R_{12b}}{\mathrm{d} X} = &{} -\,48 D^2 (1-3 D ) X^3 + 72 D (1 - 4 D + 2 D^2 ) X^2 \\ &{} +\, 2 (13 D^3 - 55 D^2 + 84 D - 12) X -(1-D) (24 + 30 D + D^2), \end{array} \end{aligned}$$

whose discriminant is

$$\begin{aligned} \begin{array}{rl} \mathrm{Disc} = &{} -\, \textstyle \frac{1}{746496 D^6(1-3D)^4} \, \big (432-2592 D+12744 D^2-43200 D^3+56979 D^4 \\ &{} +\, 80784 D^5 - 421418 D^6 + 397326 D^7 + 5556 D^8 - 171736 D^9 + 1425 D^{10} \big ). \end{array} \end{aligned}$$

It can be shown that $\mathrm{Disc} < 0$ for $D \in (0,0.34)$, and thus $\frac{\mathrm{d} R_{12b}}{\mathrm{d} X}$ has (maximal) three distinct real solutions in $X \in (-\infty , \infty )$ for any value of $D \in (0, D_{\max })$. Further, for $D \in (0, D_{\max })$ we have

$$\begin{aligned} \begin{array}{ll} \left. \frac{\mathrm{d} R_{12b}}{\mathrm{d} X} \right| _{X \rightarrow - \infty } = + \infty ,\\ \left. \frac{\mathrm{d} R_{12b}}{\mathrm{d} X} \right| _{X=0} = -\,(1-D)(24+30D+D^2)< 0, \\ \left. \frac{\mathrm{d} R_{12b}}{\mathrm{d} X} \right| _{X=1} = -\,48 + 234 D - 417 D^2 + 315 D^3 < 0, \\ \left. \frac{\mathrm{d} R_{12b}}{\mathrm{d} X} \right| _{X=\frac{1}{D}-1} = (1-D) ( 24 - 44 D + 25 D^2) >0, \\ \left. \frac{\mathrm{d} R_{12b}}{\mathrm{d} X} \right| _{X \rightarrow \infty } = - \infty , \end{array} \end{aligned}$$

where $\left. \frac{\mathrm{d} R_{12b}}{\mathrm{d} X} \right| _{X=1} < 0$ is due to $\left. \frac{\mathrm{d} R_{12b}}{\mathrm{d} X} \right| _{X=1,D=0} = -48 < 0$, $\left. \frac{\mathrm{d} R_{12b}}{\mathrm{d} X} \right| _{X=1,D=D_{\max }} = -10.421481 \cdots < 0$, and $\frac{\mathrm{d} }{\mathrm{d} D}\big ( \left. \frac{\mathrm{d} R_{12b}}{\mathrm{d} X} \right| _{X=1}) = 234 - 834 D + 945 D^2 > 0$ for $D \in (0, D_{\max })$. Therefore, the three real critical roots, $X_{ic}$, of $\frac{\mathrm{d} R_{12b}}{dX}$ are located in the intervals, $X_{1c} \in (-\infty ,0)$, $X_{2c} \in (1, \frac{1}{D} - 1)$ and $X_{3c} \in (\frac{1}{D} - 1, \infty )$, respectively, yielding local maximum of $R_{12b}$ at $X = X_{ic}, \, i=1,3$, and local minimum at $X = X_{2c}$ (see black circles in Fig. 8). Moreover, by noticing

$$\begin{aligned} \left. R_{12b} \right| _{X=1}< 0, \quad \left. R_{12b} \right| _{X=\frac{1}{D}-1}< 0, \quad \left. \textstyle \frac{\mathrm{d} R_{12b}}{\mathrm{d} X} \right| _{X=1} < 0, \quad \left. \textstyle \frac{\mathrm{d} R_{12b}}{\mathrm{d} X} \right| _{X=\frac{1}{D}-1} > 0, \end{aligned}$$

we know that $R_{12b} < 0$ for $X \in (1,\frac{1}{D}-1)$. Now, it is easy to see the distribution of the four real roots of $R_{12b}$: one in the interval $X \in (-\infty ,0)$, one in the interval $X \in (0,1)$, and two in the interval $X \in (1, \infty )$, see the circles in Fig. 8.

Summarizing the above results indicates that there are no feasible parameter values in the $\gamma _2$ set, which can yield three limit cycles. Hence, the best result is two limit cycles. The existence of two limit cycles for $R_0 \ne 1$ is obvious since we have already shown that there are two limit cycles for the case $R_0 = 1$ which has restriction $D = B$.

The remaining question is about the sign of $v_2$. Because we have shown that the maximal number of limit cycles is two for feasible parameter values, $v_2$ must keep the sign unchanged for feasible parameter values; otherwise, we have found solutions such that $v_2=0$. To determine the sign of $v_2$, we only need to use a special solution under which $v_1 = 0$ and then find the sign of $v_2$. We take $B = \frac{1}{8}$ which yields $A_l = \frac{1}{8}$, and then choose $A = \frac{1}{4} > A_l$ and use (29) to obtain $X_{-} = 4$. Next, using (51) to solve C we obtain $C = \frac{9 +\sqrt{481}}{50}$, which satisfies $A > BC$. Further, we use (24) or (28) to get $D_h = \frac{41-\sqrt{481}}{200}$, and finally substitute these parameter values into $v_2$ and $\omega _c$ to obtain $v_2 = \frac{\sqrt{481}-191}{1228800} < 0$ and $\omega _c^2 = \frac{253+17 \sqrt{481}}{3125} > 0$. This indicates that $v_2$ is always negative for feasible parameter values when $v_1 = 0$. Therefore, like the case $R_0 = 1$, if there exist two limit cycles bifurcating from a Hopf critical point for the case $R_0 \ne 1$, the outer one must be stable. $\square$

Now, we present several simulations of multiple limit cycles bifurcation from a Hopf critical point, for $R_0 > 1$ and $R_0 < 1$ with either $A > BC$ or $A < BC$.

• (1) First, consider $R_0 > 1$ with $A > BC$. We choose $D = \frac{1}{10}, \, B = \frac{7}{64}$ and then use (45) and (50) to obtain $X_- = 6.017354 \cdots$. Further, it follows from (52) that $A = 0.110556 \cdots$ and $C = 0.376772 \cdots$ for which $\, v_0 \mu = v_1 = 0$ and $v_2 = -\,0.000100 \cdots < 0$, indicating that the larger one of the two limit cycles is stable, as expected. In order to have an unstable smaller limit cycles and stable equilibrium $\mathrm{E_1}$, we need perturbations such that $v_1 > 0$ and $v_0 \mu < 0$ satisfying $-v_0 \mu \ll v_1 \ll -v_2$. To achieve this, we choose perturbations such that $A = 0.110934$ and $C = 0.376594$, which results in $v_0 \mu = -0.889 \times 10^{-7}$, $v_1 \approx 0.0000101$, and $v_2 \approx -\,0.000103$, yielding the approximate amplitudes of the two limit cycles: $r_1 \approx 0.098849$ and $r_2 \approx 0.297144$. As depicted in Fig. 9a, the simulations given in red color (for the stable limit cycle) and blue color (for the unstable limit cycle) agree very well with the analytic predictions in green color. The time history of the stable (outer) limit cycle is shown in Fig. 9b. This example clearly indicates a bistable phenomenon involving a stable equilibrium and a stable (outer) limit cycle with an unstable (inner) limit cycle as their separatory.

• (2) Next, consider $R_0 < 1$ with $A > BC$. Similarly we choose $B = \frac{3}{32} < D = \frac{1}{10}$ and then get $X_- = 8.129787 \cdots$, yielding $A = 0.060591 \cdots$ and $C = 0.200338 \cdots$ for which $\, v_0 \mu = v_1 = 0$ and $v_2 = -0.000182 \cdots < 0$, implying that the larger one of the two limit cycles is stable. Then, we add perturbations to the parameters A and C to obtain $A = 0.06085981$ and $C = 0.20023941$, which yields $v_0 \mu = -0.17779 \times 10^{-6}$, $v_1 \approx 0.0000196$, and $v_2 \approx -0.0001863$, from which we obtain the amplitudes of the two limit cycles as $r_1 \approx 0.1003$ and $r_2 \approx 0.3081$. These two limit cycles (see Fig. 10a) are similar to those shown in Fig. 9a for $R_0 > 1$, but for this case $R_0 < 1$, the phase portrait is different since the system in addition has a stable node at $\mathrm{E}_0$ besides a saddle point at $\mathrm{E}_1^+$ and a stable focus at $\mathrm{E}_1^-$. Thus, this example indeed shows a tristable phenomenon with two stable equilibria (one node and one focus) and one stable limit cycle (another limit cycle is unstable, as a separatory between the stable focus and the stable limit cycle). The simulations (in red/blue color) and analytical predictions (in green color) are shown in Fig. 10a, again indicating a good agreement. The time history of the stable (outer) limit cycle is depicted in Fig. 9b.

• (3) Note that the above two examples belong to the category $A > BC$. The easiness of finding feasible parameter values for two limit cycles when $A > BC$ indeed shows that the system is more likely to exhibit bistable or even tristable complex dynamics. For an illustration, we give an example to satisfy $A < BC$, yielding bistable phenomenon. As discussed above, we may take $B = 0.05$ and $A = 0.0156$, and then use (51) to find $C = 0.461627 \cdots$ and (24) to obtain $D = D_h = 0.010886 \cdots$ such that $v_0 = v_1 = 0$ and $v_2 = -0.771730 \cdots \times 10^{-5} < 0$, as expected. Further, taking perturbations on C and D as $C = 0.4616276809 - 0.005 = 0.4566276809$ and $D = 0.011418264 + 0.00000005 = 0.011418314$, for which we have $v_0 \mu = -\,0.513018 \times 10^{-7}$, $v_1 \approx 0.190025 \times 10^{-5}$ and $v_2 \approx -\,0.797500 \times 10^{-5}$. Thus the truncated normal form equation yields the approximations for the amplitudes of the two limit cycles: $r_1 \approx 0.1065$ and $r_2 \approx 0.4764$. The simulations and analytic predictions as depicted in Fig. 11 show a good agreement. For this case, bistable phenomenon appears to involve a stable equilibrium and a stable periodic motion.

Fig. 9

Two limit cycles of system (5) for $R_0 > 1$ ($A > BC$) with $A = 0.110934$, $B = 0.109375$, $C = 0.376594$ and $D = 0.1$, showing a bistable phenomenon: a phase portrait with the red/blue and green color curves denoting the simulations and the estimations from normal form (with amplitudes $r_1 \approx 0.0989$ and $r_2 \approx 0.2971$), respectively; and b the time history of the stable (outer) limit cycle (Color figure online)

Fig. 10

Two limit cycles of system (5) for $R_0 < 1$ ($A > BC$) with $A = 0.06085981$, $B = 0.09375$, $C = 0.20023941$ and $D = 0.1$, showing a tristable phenomenon: a phase portrait with the red/blue and green color curves denoting the simulations and estimates from the normal form (with amplitude $r_1 \approx 0.1003$ and $r_2 \approx 0.3081$), respectively; and b time history of the stable (outer) limit cycle (Color figure online)

The results obtained in this section, in particular for Theorems 3.3 and 3.5, indicate that regardless whether $R_0 = 1$ or $R_0 \ne 1$, system (5) can always exhibit complex dynamics including different types of bistability or even tristablity, due to multiple limit cycles arising from Hopf bifurcation. This suggests that the real situation could be very complex, showing the coexistence of a stable disease-free equilibrium, stable endemic equilibria, and even stable oscillating motion, all of which are possible depending upon the initial conditions.

Fig. 11

Two limit cycles of system (5) for $R_0 > 1$ ($A < BC$) with $A = 0.0156$, $B = 0.05$, $C = 0.4566276809$ and $D = 0.011418214$: a phase portrait with the red/blue and green color curves denoting the simulations and estimates from normal form (with amplitude $r_1 \approx 0.1065$ and $r_2 \approx 0.4764$), respectively; and b time history of the stable (outer) limit cycle (Color figure online)

3.3 Recurrence Phenomenon (Viral Blips)

It has been shown in Zhang et al. (2013, 2014a, b),Yu et al. (2016) that the recurrence phenomenon can often appear in many disease models. It is characterized by short episodes of high viral reproduction, separated by long periods of relative quiescence. This recurrent pattern is observed in many persistent infections, including the “viral blips” observed during chronic infection with the human immunodeficiency virus (HIV). In fact, the model (5) considered in this paper indeed shows recurrence behavior for a very large parameter region, see Zhang et al. (2013, 2014a, b) in which how this phenomenon occurs is discussed using dynamical system theory. Mathematically speaking, such “slow-fast” motion is a special type of limit cycles. However, it has been shown that such “slow-fast” motion cannot be analyzed by the well-known geometric singular perturbation theory (GSPT). It has been proposed that if the following conditions hold:

$\mathrm{P}_1$::

there exists at least one equilibrium solution;

$\mathrm{P}_2$::

there exists a saddle-node or transcritical bifurcation;

$\mathrm{P}_3$::

there is a Hopf bifurcation; and

$\mathrm{P}_4$::

there is a “window” between the Hopf bifurcation point and the saddle-node/transcritical bifurcation point in which oscillation continuously exists,

then the system exhibits relaxtion-type slow-fast motions. Note that Hopf bifurcation is necessary since it is the source of oscillations. To verify these conditions for higher-dimensional dynamical systems, identifying Hopf bifurcation (condition $\mathrm{P}_3$) becomes crucial.

However, although such slow-fast oscillations are closely related to Hopf bifurcation, Hopf bifurcation cannot be used to predict or estimate such motions because normal form theory is no longer applicable for such a large perturbation, that is, such special bifurcating limit cycles are far away from the equilibrium. To illustrate this fact, we give simulations for three different cases: $R_0=1$, $R_0>1$ and $R_0<1$.

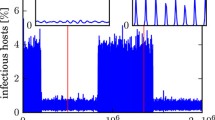
First we consider $R_0=1$. For this case, we use the same values of A and C given in (43), yielding the same $B_h$, $v_0$ and $v_1$ as that example shown in Fig. 4, but change B and D to $D=B = \frac{1}{10}$. For a comparison, we still use the normal form to estimate the amplitude of the oscillation. Here, $\mu = B_h - B = 0.017947$, and so the truncated normal form gives the approximation of the amplitude as $r \approx 2.3551$, which is very large, implying that the Hopf bifurcation theory and associated normal form are no longer applicable. The simulation is depicted in Fig. 12a as the red curve, where the green curve again denotes the normal form estimate, which indeed shows a very large deviation from the simulation, even with a negative part, implying that normal form theory is no longer applicable. The simulated time history given in Fig. 12b clearly shows the recurrence infection (viral blips) phenomenon, and this recurrence for the case $R_0=1$ was not considered in Zhang et al. (2013, 2014a, b), Yu et al. (2016).

For the case $R_0>1$, we take the perturbation on A as $\mu = \frac{1}{50}$ so that $A = \frac{225}{2624} + \mu = \frac{6937}{65600}$, and again take $C = \frac{96}{205}$ and $D = \frac{1}{10}$. Note that this set of parameter values (except B) is exactly the same as that for the case $R_0=1$, see Fig. 12. Now we apply the truncated normal form to obtain $r \approx 2.4778$, which is again very large and normal form theory is not applicable. The simulated phase portrait is given in Fig. 13a (see the red colored curve) and the green curve in this figure shows the normal form prediction, indicating a large discrepancy. The simulated time history given in Fig. 13b again shows the recurrence infection.

Fig. 12

Simulated recurrence oscillation of system (5) for $R_0 = 1$ with $A = \frac{6937}{65600}$, $C = \frac{96}{205}$, $B = D = \frac{1}{10}$: a phase portrait with the red and green color curves denoting the simulation and the estimation from normal form (with amplitude $r \approx 2.3551$), respectively; and b the time history of the stable oscillation (Color figure online)

Fig. 13

Simulated recurrence oscillation of system (5) for $R_0 > 1$ ($A > BC$) with $A = \frac{6937}{65600}$, $C = \frac{96}{205}$, $B = \frac{7}{64}$ and $D = \frac{1}{10}$: a phase portrait with the red and green color curves denoting the simulation and the estimation from normal form (with amplitude $r \approx 2.4778$), respectively; and b the time history of the stable oscillation (Color figure online)

Fig. 14

Simulated recurrence oscillation of system (5) for $R_0 < 1$ ($A > BC$) with $A = \frac{749}{7200}$, $C = \frac{16}{75}$, $B = \frac{3}{32}$ and $D = \frac{1}{10}$: a phase portrait with the red and green color curves denoting the simulation and the estimation from normal form (with amplitude $r \approx 1.9346$), respectively; and b the time history of the unstable oscillation (Color figure online)

Finally for the case $R_0<1$, we again choose $D = \frac{1}{10}$, but $B = \frac{3}{32} < D$. If we choose $A = \frac{121}{1440}$ and $C = \frac{16}{75}$, then we have $v_1 = \frac{3}{3850} > 0$. To estimate the amplitude of this unstable limit cycle, we take $\mu = \frac{1}{50}$ and let $A = \frac{121}{1440} + \mu = \frac{749}{7200}$, yielding $r \approx 1.9346$. The simulation is shown in Fig. 14, where the unstable limit cycle is obtained by using a negative time step in a numerical integration scheme. Again, the green curve denotes the normal form prediction, showing a large difference from simulation. This recurrence for $R_0 < 1$ was also not studied in Zhang et al. (2013, 2014a, b), Yu et al. (2016).

The above three examples for the three different cases: $R_0>0, R_0=0$ and $R_0<0$ exhibit the recurrence phenomenon, which cannot be predicted by normal form theory or analyzed by using geometric singular perturbation theory. However, we have shown that the slow-fast motions can be induced from Hopf bifurcation if the four conditions $\mathrm{P_1}$–$\mathrm{P_4}$ are satisfied. This provides a mechanism to generate the recurrence behavior in disease models and has been discussed in Zhang et al. (2013, 2014a, b). In next section, we will provide another new mechanism of generating recurrence from homoclinic loops arising from BT bifurcation.

4 Bogdanov–Takens (BT) Bifurcations

In this section, we study Bogdanov–Takens (BT) bifurcation in system (5), which is characterized by a critical point associated with double-zero eigenvalues. First, BT bifurcation cannot occur (1) at the equilibrium $\mathrm{E_0}=(\frac{1}{D},0)$ with eigenvalues $-D$ and $R_0-1$, because only one eigenvalue can be zero when $R_0=1$; (2) at $\mathrm{E_{1+}}$ because it is a saddle for all parameter values according to the result from Theorem 2.3; and (3) at $\mathrm{E_{1-}}$ when $R_0 \ge 1$, since the determinant of its Jacobian is positive if the trace equals zero. Therefore, BT bifurcation can only occur at $\mathrm{E_{1-}}$ when $R_0<1$, at which the Hopf critical point coincides with the saddle-node point, i.e., $D_h = D_s$. For example, in Fig. 2d, $D_h$ approaches and collides with $D_s$.

First, we derive the parameter conditions for the occurrence of double-zero eigenvalues, that is, $\mathrm{Tr}(J_1) = \mathrm{det}(J_1) = 0$; or the collision of the Hopf and saddle-node bifurcations, namely $(D_h,X_h) = (D_s,X_s)$. Noting from (26) that $\mathrm{Tr}(J_1) = 0$ yields $\Delta = 0$, we solve $\Delta =0$ and $\left. \mathrm{Tr}(J_1) \right| _{\mathrm{E_{1-}}} = 0$ for A and B to obtain

$$\begin{aligned} A = A_0 \equiv \textstyle \frac{ D (C+D)^2}{ C ( 1-D)^2}, \quad B = B_0 \equiv \frac{ D [ C ( 1-2D)-D^2 ] }{ C ( 1-D)^2}. \end{aligned}$$

(58)

The positiveness of $B_0$ requires

$$\begin{aligned} C > \textstyle \frac{D^2}{1 - 2D} \quad \mathrm{and} \quad 0< D < \frac{1}{2}. \end{aligned}$$

(59)

We then define a two-dimensional parameter hypersurface,

$$\begin{aligned} \mathcal {S} : \big \{ \gamma \,|\, A = A_0, \ B = B_0, \ C > \textstyle \frac{D^2}{1 - 2D}, \ 0< D < \frac{1}{2} \big \}. \end{aligned}$$

(60)

System (5) undergoes a BT bifurcation if its paramerers $(A,B,C,D)\in \mathcal {S}$. The projections of $\mathcal {S}$ into the A–B–C space and A–B–D space are shown in Fig. 15a, b, respectively.

Fig. 15

Projection of the hypersurface $\mathcal {S}$ into a the A–B–C space; and b the A–B–D space (Color figure online)

To analyze the BT bifurcation, the first step is usually to find the normal form of the dynamical system and then use the normal form to determine the codimension and unfolding of the BT bifurcation. The general idea of the derivation of normal forms is introducing nonlinear transforms on state variables together with necessary time rescaling. The derivation is standard for codimension-2 BT bifurcation at the BT bifurcation point without unfolding/bifurcation parameter. However, even for codimension-2 BT bifurcation, the normal form computation becomes much more complicated when bifurcation parameters are involved. For codimension-3 BT bifurcation, the computation burden is even heavier. The 6-step transformations approach developed by Dumortier et al. (1987) becomes a standard method and applied by researchers to find the parametric normal form for codimension-3 BT bifurcation. Some cases of codimension-4 BT bifurcation have been discussed in the literature (e.g., see Li and Rousseau 1989) by using a similar multiple-step transformation method to find the normal form. Multiple-step transformation method is tedious and yet hard to verify. Besides, the transformation between the original variables and the new variables in the last step of transformations is difficult to achieve. We are not aware of any work on developing one-step transformation and obtain explicit expressions for the transformation between the original variables and new variables. We have used the simplest normal theory (e.g., see Yu (1999); Yu and Leung (2003); Gazor and Yu (2010, 2012); Gazor and Moazeni (2015)) to develop a one-step transformation approach to find the parametric simplest normal form and associated transformations. Our new method not only gives the direct relation between original variables (including both state and parameter variables) but also yields results which can be easily verified. Programs based on a computer algebra system, Maple, and the new method and algorithm will be available in one of our forthcoming papers.

In order to determine the codimension of the BT bifurcation, we first find the equilibrium $\mathrm{E_{1-}}$, under the conditions given in (58), as

$$\begin{aligned} \mathrm{E_{1-}} = \big ( \textstyle \frac{1}{D}-1, \, D \big ), \quad \mathrm{for} \ \ D \in \big (0, \frac{1}{2} \big ). \end{aligned}$$

and then introducing the following change of state variables,

$$\begin{aligned} \left( \begin{array}{c} X \\ Y \end{array} \right) = \left( \begin{array}{c} \frac{1}{D}-1 \\ D \end{array} \right) + \left[ \begin{array}{rc} \textstyle \frac{1}{D-1} &{} 0\\ \textstyle \frac{D}{1-D} &{} 1 \end{array} \right] \left( \begin{array}{c} u_1 \\ u_2 \end{array} \right) , \end{aligned}$$

(61)

into (5) we obtain

$$\begin{aligned} \displaystyle \frac{d u_1}{d \tau } = u_2 + f(u_1,u_2) , \qquad \displaystyle \frac{d u_2}{d \tau } = f(u_1,u_2), \end{aligned}$$

(62)

where

$$\begin{aligned}&f(u_1,u_2)\nonumber \\&\quad = \frac{-[Du_1+(1-D)u_2]\{D(1+C)[D(1-D)u_1+Du_{1}^{2}+(1-D)u_1 u_2]-C(1-D)^3u_2\}}{(1-D)^3 [ (1-D) (C+D)+D u_1+(1-D) u_2]}\nonumber \\ \end{aligned}$$

(63)

Now, expanding $f(u_1,u_2)$ in Taylor series around $(u_1,u_2)=(0,0)$ and applying the simplest normal form theory, we introduce the following seventh-order near-identity nonlinear transformation,

$$\begin{aligned} u_1 = x_1 + \displaystyle \sum _{i+j=2}^7 a_{ij} x_1^i x_2^j, \qquad u_2 = x_2 + \displaystyle \sum _{i+j=2}^7 b_{ij} x_1^i x_2^j, \end{aligned}$$

(64)

where $a_{ij}$ and $b_{ij}$ are constant coefficients, expressed in terms of C and D, and the time rescaling

$$\begin{aligned} \tau = \big [ 1 + \textstyle \frac{C}{2 (1-D)(C+D)} \,x_1 + x_1^3 \big ]\, \tau _1, \end{aligned}$$

(65)

into (62) to obtain the following simplest normal form up to seventh-order terms:

$$\begin{aligned} \begin{array}{rl} \displaystyle \frac{\mathrm{d} x_1}{\mathrm{d} \tau _1} = &{} x_2 + \mathcal {O}(| (x_1,x_2) |^8), \\ \displaystyle \frac{\mathrm{d} x_2}{\mathrm{d} \tau _1} = &{} a_1 \, x_1^2 + a_2 \, x_1 x_2 + a_3 \, x_1^3 x_2 + a_4 \, x_1^4 x_2 + a_5 \, x_1^6 x_2 + \mathcal {O}(|(x_1,x_2)|^8). \end{array} \end{aligned}$$

(66)

Comparing the above simplest normal form with the conventional normal form (e.g., see Guckenheimer and Holmes (1993),

$$\begin{aligned} \begin{array}{rl} \displaystyle \frac{\mathrm{d} x_1}{\mathrm{d} \tau _1} = &{} x_2 + \mathcal {O}(| (x_1,x_2) |^{n+1}), \\ \displaystyle \frac{\mathrm{d} x_2}{\mathrm{d} \tau _1} = &{} \displaystyle \sum _{k=2}^n a_k \, x_1^k + b_k \, x_1^{k-1} x_2 + \mathcal {O}(| (x_1,x_2) |^{n+1}), \end{array} \end{aligned}$$

(67)

it is seen that the simplest normal form (66) has less half of the terms in the conventional normal form (67).

Further, introducing the transformation,

$$\begin{aligned} x_1 \rightarrow x_1, \quad x_2 + \mathcal {O}(|(x_1,x_2)|^8) \rightarrow x_2, \end{aligned}$$

into (66), we obtain

$$\begin{aligned} \begin{array}{rl} \displaystyle \frac{\mathrm{d} x_1}{\mathrm{d} \tau _1} = &{} x_2, \\ \displaystyle \frac{\mathrm{d} x_2}{\mathrm{d} \tau _1} = &{} a_1 \, x_1^2 + a_2 \, x_1 x_2 + a_3 \, x_1^3 x_2 + a_4 \, x_1^4 x_2 + a_5 \, x_1^6 x_2 + \mathcal {O}(|(x_1,x_2)|^8), \end{array} \end{aligned}$$

(68)

where the coefficients $a_i$’s are given in terms of C and D. In particular,

$$\begin{aligned} \begin{array}{rl} a_1 =&-\, \textstyle \frac{(1+C) D^3}{(C+D)(1-D)^3 } \quad \mathrm{and} \quad a_2 = \textstyle \frac{D [C(1-3 D)-D(1+D)]}{(C+D) (1-D)^3}. \end{array} \end{aligned}$$

(69)

It is obvious that $a_1 < 0$ due to $0< D < \frac{1}{2}$, and it is easy to show that

$$\begin{aligned} \begin{array}{ll} a_2 < 0 &{}\quad \mathrm{for} \ D \in \big [ \textstyle \frac{1}{3}, \textstyle \frac{1}{2} \big ), \ \mathrm{or} \ \mathrm{if} \ C \in \big ( \textstyle \frac{D^2}{1-2D}, \textstyle \frac{D(1+D)}{1-3D} \big ) \ \mathrm{for} \ D \in \big (0,\textstyle \frac{1}{3} \big ), \\ a_2> 0 &{}\quad \mathrm{if} \ C > \textstyle \frac{D(1+D)}{1-3D} \ \mathrm{for} \ D \in \big (0,\,\textstyle \frac{1}{3} \big ), \\ a_2 = 0 &{}\quad \mathrm{if} \ C = \textstyle \frac{D(1+D)}{1-3D} \ \mathrm{for} \ D \in \big (0,\,\textstyle \frac{1}{3} \big ). \end{array} \end{aligned}$$

(70)

Therefore, if $a_2 \ne 0$, i.e., when $\frac{1}{3} \le D < \frac{1}{2}$ or $0< D < \frac{1}{3}$ with $C \ne \frac{D(1+D)}{1 - 3D}$, the BT bifurcation is codimension 2.

When $C = C_0 = \frac{D(1+D)}{1 - 3D}, \ (0< D < \frac{1}{3})$, $a_2 = 0$, and $a_1$, $a_3$, $a_4$ and $a_5$ become

$$\begin{aligned} \begin{array}{rl} a_1 = &{} -\, \textstyle \frac{D^2}{2(1-D)^2} , \quad a_3 = \textstyle \frac{(1-4D) D(1+D)}{8(1-D)^5}, \quad a_4 = -\, \textstyle \frac{(1-4D)D(1+D)(1-11D)}{64 (1-D)^7}, \\ a_5 = &{} \textstyle \frac{(1-4D) D (68480D^5+3206517D^4+2472332D^3 -837530D^2-107396D+60077)}{7741440 (1-D)^{11}}. \end{array} \end{aligned}$$

(71)

It can be seen that $a_1 < 0$, and $a_3 \ne 0$ for $D \ne \frac{1}{4}$. More precisely, we have

$$\begin{aligned} a_3 = \textstyle \frac{(1-4D)D(1+D)}{8(1-D)^5} \left\{ \begin{array}{ll} >0 &{}\quad \mathrm{if} \ \ 0< D< \frac{1}{4}, \\ =0 &{}\quad \mathrm{if} \ \ D = \textstyle \frac{1}{4}, \\<0 &{}\quad \mathrm{if} \ \ \textstyle \frac{1}{4}< D < \frac{1}{3}. \end{array} \right. \end{aligned}$$

(72)

Thus, when $D \in (0,\frac{1}{4})\bigcup (\frac{1}{4},\frac{1}{3})$, the BT bifurcation is codimension 3.

When $D = \frac{1}{4}$, $a_3 = a_4 = a_5 = 0$. In fact, at this critical value, we obtain $C_0 = \frac{5}{4}$, yielding $A_0 = \frac{4}{5}$ and $B_0 = \frac{5}{4}$, which satisfy the center condition (56). That is, under these parameter values, system (5) is an integral system with the first integral (57), having a nilpotent point at $(X,Y) = (3,\frac{1}{4})$. We shall not discuss this special case in this paper. Finally, note that a necessary condition for the existence of the equilibrium $\mathrm{E_{1-}}$ is $\Delta >0$, which is equivalent to

$$\begin{aligned} \Delta _1 = A+B-D-BC - 2\sqrt{C(A+B)(D-B)} >0. \end{aligned}$$

(73)

Summarizing the above results we have the following theorem.

Theorem 4.1

For system (5), when $R_0 < 1$ (i.e., $D > B$) and $\Delta _1> 0 \ (\text {so} \ A > BC)$, BT bifurcation occurs from the endemic equilibrium $\mathrm{E_{1-}} : (\frac{1}{D} - 1, D)$ at the critical point $(A,B) = (A_0,B_0) = \big (\frac{D(C+D)^2}{C(1-D)^2}, \frac{D[C(1-2D)-D^2]}{C(1-D)^2} \big )$, with $C > \frac{D^2}{1-2D}$, $D \in (0,\frac{1}{2})$. Moreover, the BT bifurcation is

• (i) codimension 2 if $D \in [\frac{1}{3}, \frac{1}{2})$ or $\, D \in (0,\frac{1}{3})$ with $C \ne \frac{D(1+D)}{1-3D}$; and

• (ii) codimension 3 if $C = \frac{D(1+D)}{1-3D}$ with $D \in (0,\frac{1}{4}) \bigcup (\frac{1}{4},\frac{1}{3})$.

In the following two subsections, we will consider the two BT bifurcations with condimensions 2 and 3, respectively.

4.1 Codimension-2 BT Bifurcation

Suppose the condition (i) in Theorem 4.1 holds, under which $a_2 \ne 0$. To obtain the normal form with unfolding, we introduce the parameter transformation,

$$\begin{aligned} A = A_0 + \mu _1, \qquad B = B_0 + \mu _2, \end{aligned}$$

(74)

together with the change of state variables (61), into (5) and expanding the resulting system around the critical point $(u_1, u_2, \mu _1, \mu _2 ) = (0,0,0,0)$ yields

$$\begin{aligned} \begin{array}{rrl} &{} \displaystyle \frac{\mathrm{d} u_1}{\mathrm{d} \tau } = &{} u_2 + f_2(u_1,u_2,\mu ) + \mathcal {O}(|(u_1,u_2,\mu )|^3) , \\ &{} \displaystyle \frac{\mathrm{d} u_2}{\mathrm{d} \tau } = &{} f_2 (u_1,u_2,\mu ) + \mathcal {O}(|(u_1,u_2,\mu )|^3), \end{array} \end{aligned}$$

(75)

where $\mu =(\mu _1,\mu _2)$ and $f_2$ as follows:

$$\begin{aligned} f_2= & {} \textstyle (1-D)^2 \left[ \frac{D}{C+D }\, \mu _1 + \mu _2 \right] \\&+ \textstyle \left[ \frac{ D \left[ CD + (2 C + D)(1- 2D) \right] }{ (C+D)^2 } \, \mu _1 + (1- 2 D)\, \mu _2 \right] u_1\\&+ \, \textstyle (1-D)^2 \left[ \frac{2 C+D}{ (C+D)^2 }\, \mu _1 +\frac{1}{D}\, \mu _2 \right] u_2 - \frac{(1+C)\, D^3}{(C+D) (1-D)^3 }\, u_1^2\\&+ \textstyle \frac{D \left[ C(1 -2D)- D \right] }{ (1-D)^2 (C+D) }\, u_1 u_2 +\frac{C}{C+D}\, u_2^2. \end{aligned}$$

It should be pointed out that even the recurrence infection (viral blips) phenomenon has been studied in Zhang et al. (2013, 2014a, b), no detailed dynamical analysis is given for the two-dimensional model (5). In our later work (Yu et al. 2016), BT bifurcation is discussed with two pairs of parameter values on B and D, that is, $(B,D)=(\frac{27}{500}, \frac{57}{1000})$ and $(\frac{27}{500},\frac{87}{1000})$. Therefore, the BT critical point is completely determined by the parameters $A=A(B,D)$ and $C=C(B,D)$. In fact, only two BT critical points on $\mathcal {S}$ are considered in (Yu et al. 2016):

$$\begin{aligned} (A,B,C,D)= \big (\textstyle \frac{3078507}{206879500}, \frac{27}{500}, \frac{61731}{827518}, \frac{57}{1000} \big ), \ \big (\frac{118428267}{2237439500}, \frac{27}{500}, \frac{219501}{8949758}, \frac{57}{1000} \big ). \end{aligned}$$

The dynamical behaviors from Yu et al. (2016) is limited. To get a global dynamical behavior in the whole parameter space, this paper studies the whole feasible parameter region near $\mathcal {S}$. Instead of fixing $A,\,C$ and D in Zhang et al. (2013, 2014a, b) or B and D in Yu et al. (2016), this paper studies all parameter set $(A,B,C,D) \in \mathcal {S}$ in (60). In addition, bifurcation diagrams are given in terms of parameters $A = A_0(C,D)$ and $B=B_0(C,D)$ to show the global influence of control parameters C and D on the system’s dynamical behavior.

Next, we apply the parametric simplest normal form theory (Yu and Leung 2003; Gazor and Yu 2010, 2012; Gazor and Moazeni 2015) to get the parametric normal form (up to second order) via the transformations of state variables and parameters. Note that unlike the series of transformations applied in many articles in the literature, here we only need to use one transformation to obtain the normal form. In general, the transformation is not unique, but in order to obtain the simplest parameterization, we use the following change of state variables,

$$\begin{aligned} \begin{array}{rl} u_1 = &{} \frac{1}{a_1} \left[ - y_1 - \frac{(1-D)^2 [D+C(1-D)]}{2 (1+C) D^3} \, \xi _1 + \frac{D^2 (1+C)}{(1-D) (C+D)}\, \xi _2 - \frac{C(2 -3 D) +D(1-2 D) }{D (C+D)}\, \xi _2 y_1 \right. \\ &{} \quad \ - \frac{(1-D) [D(C+D)-C(1-D^2)]}{2 D^3 (1+C)}\, y_1^2 + \frac{(1-D)^3 [ C^2(4 D^2 + D+1)+ CD(3 D+4) +D^2 ]}{6 D^5 (1+C)^2} \, y_1 y_2 \\ &{} \left. \quad \ -\frac{(1-D)^3 [ C^2 ( 3 D^3-3 D^2 + 7 D-3) + 2 C D ( D^2+4 D-2) + D^2 ( 3 D-1) ]}{8 D^6 (1+C)^2} \, y_2^2 \right] ,\\ u_2 = &{} \frac{1}{a_1} \left[ - y_2 + \xi _1 - \frac{(1-D)^3 [ C^2( D^3+D^2-9 D+3) + 4 C D(D^2-4 D+1 ) +D^2(1-5 D)]}{4 D^6 (1+C)^2}\, \xi _1 (\xi _1 - y_2 ) \right. \\ &{} \quad \ + \frac{ D (1-3 D)+2 C(1- 2D)}{D (C+D)}\, \xi _2 (\xi _1 - y_2) + y_1^2 + \frac{(1-D)^3 C}{ D^3 (1+C)} \, y_1 y_2\\ &{} \quad \ \left. - \frac{(1-D)^3 [C^2 (2 D^2 -D-1) + CD (3 D-4)-D^2]}{6 D^5 (1+C)^2} \, ( \xi y_1 + y_2^2) \right] , \end{array} \end{aligned}$$

(76)

and then obtain the following simplest parameterization,

$$\begin{aligned} \begin{array}{rl} \mu _1 = &{} -\,\frac{(1-D)(C+D)^2}{D^4 (1+C)}\, \xi _1 + \frac{2 D (1+C) (C+D)}{C (1-D)^2}\, \xi _2 , \\ \mu _2 = &{} -\,\frac{2 (1+C) D^2}{C (1-D)^2}\, \xi _2 - \frac{D (1+C)}{(1-D)(C+D)}\, \xi _2^2. \end{array} \end{aligned}$$

(77)

Implicit function theorem implies that local perturbations on $\xi _1$ and $\xi _2$ near the critical poin $(\xi _1,\xi _2)=(0,0)$ is topologically equivalent to local perturbations on $\mu _1$ and $\mu _2$ near $(\mu _1,\mu _2)=(0,0)$ since

$$\begin{aligned} \det \left[ \tfrac{ \partial (\mu _1, \mu _2)}{ \partial (\xi _1, \xi _2)} \right] = \tfrac{ 2(C+D)^2}{C D^2(1-D)} + \mathcal {O}(\xi ) \ne 0 \ \ \text {for small} \ \ \xi =(\xi _1,\xi _2). \end{aligned}$$

Under the above transformations (76) and (77), (75) becomes

$$\begin{aligned} \begin{array}{rl} \displaystyle \frac{\mathrm{d} y_1}{\mathrm{d} \tau } = &{} y_2 + \mathcal {O}(|(y_1,y_2,\xi )|^3), \\ \displaystyle \frac{\mathrm{d} y_2}{\mathrm{d} \tau } = &{} \xi _1 + \xi _2 \, y_2 + y_1^2 - \frac{a_2}{a_1} \, y_1 y_2 + \mathcal {O}(|(y_1,y_2,\xi )|^3), \end{array} \end{aligned}$$

where $a_1$ and $a_2$ are given in (69). To remove the higher-order terms $O(|(y_1,y_2,\xi )|^3)$ in the first equation of the above equations, we introduce an additional transformation:

$$\begin{aligned} y_1 = x_1, \quad y_2 + \mathcal {O}(|(y_1,y_2,\xi )|^3) = x_2, \end{aligned}$$

into the above equations to obtain the normal form with unfolding up to second-order terms:

$$\begin{aligned} \begin{array}{rl} \displaystyle \frac{\mathrm{d} x_1}{\mathrm{d} \tau } = &{} x_2 , \\ \displaystyle \frac{\mathrm{d} x_2}{\mathrm{d} \tau } = &{} \xi _1 + \xi _2 \, x_2 + x_1^2 - \frac{a_2}{a_1} \, x_1 x_2 + \mathcal {O}(|(x_1,x_2,\xi )|^3), \end{array} \end{aligned}$$

(78)

where the coefficient $-\frac{a_2}{a_1}$ not being normalized to $\pm 1$ is for us to easily see the effect of the original parameters C and D. Note that $-\frac{a_2}{a_1}$ has the same sign of $a_2$ due to $a_1 < 0$.

Now, we use the normal form (78) to analyze the codimension-2 BT bifurcation. Note that the normal form (78) is in the standard form given in Guckenheimer and Holmes (1993). Thus, we follow the approach described in Guckenheimer and Holmes (1993) to obtain the following theorem.

Theorem 4.2

For system (5), with the conditions given in Theorem 4.1, codimension-2 BT bifurcation occurs for $D \in [\frac{1}{3},\frac{1}{2})$, or for $D \in (0,\frac{1}{3})$ with $C \ne \frac{D(1+D)}{1-3D}$. Moreover, three local bifurcations, with the representations of the bifurcation curves, are given below.

• (1) Saddle-node bifurcation occurs from the bifurcation curve:

  $$\begin{aligned} \mathrm{SN} = \big \{ (\xi _1,\xi _2) \mid \xi _1 = 0 \big \}. \end{aligned}$$

• (2) Hopf bifurcation occurs from the bifurcation curve:

  $$\begin{aligned} \mathrm{H} = \left\{ (\xi _1,\xi _2) \mid \xi _1 = -\, \big (\textstyle \frac{a_1}{a_2} \big )^2 \xi _2^2 \right\} \left\{ \begin{array}{ll} \xi _2>0 \ (a_2< 0), &{} \mathrm{subcritical}, \\ \xi _2<0 \ (a_2 > 0), &{} \mathrm{supercritical}. \end{array} \right. \end{aligned}$$

• (3) Homoclinic orbit occurs from the bifurcation curve:

  $$\begin{aligned} \mathrm{HL} = \left\{ (\xi _1,\xi _2) \mid \xi _1 = -\,\textstyle \frac{49}{25} \big ( \textstyle \frac{a_1}{a_2} \big )^2 \xi _2^2 \right\} \left\{ \begin{array}{ll} \xi _2>0 \ (a_2< 0), &{} \mathrm{unstable}, \\ \xi _2<0 \ (a_2 > 0), &{} \mathrm{stable}. \end{array} \right. \end{aligned}$$

Fig. 16

Bifurcation diagrams for the codimension-2 BT bifurcation based on the normal form (78): a$a_2<0$; and b$a_2>0$

The bifurcation diagrams for the codimsion-2 BT bifurcation are shown in Fig. 16. Note that the above formulas for bifurcation curves given in terms of $(\xi _1,\xi _2)$ can be expressed in terms of $\mu _1$ and $\mu _2$ for the original system (5) by using (77).

The homoclinic loop in the BT bifurcation studied above implies a new mechanism to generate the recurrence phenomenon, which is completely different from what discussed in the previous section, based on the four conditions $\mathrm{P_1}$–$\mathrm{P_4}$ in Sect. 3.3. Here, it is noted that the trajectory starting from a point on the homoclinic loop will approach the saddle point either as $\tau \rightarrow + \infty$ or $\tau \rightarrow - \infty$. Consider the case that a limit cycle near the homoclinic bifurcation curve is stable (see Fig. 16b), we can see that the limit cycle moves extremely slowly near the saddle point but moves fast when it is away. This yields a slow-fast motion which generates recurrence behavior. The first three conditions for this mechanism are same as $\mathrm{P_1}$-$\mathrm{P_3}$, but the last condition should be modified as

$\mathrm{P}_4^*$::

there exists Bogdanov–Takens bifurcation, leading to homoclinic loops near a Hopf bifurcation.

We notice that the new recurrence-generating mechanism offers a small amplitude of oscillation, or extremely slow convergence to the disease-free equilibrium. The big difference between the mechanism discussed in the previous section and the new mechanism is that the former yields very large oscillations in both amplitude and frequency, while the latter only has significant change in frequency, but very little variation in the amplitude. Patients with chronic infections may undergo a short-period of worse symptom.

Fig. 17

Codimension-2 BT bifurcation diagram around the critical point $(A,B,C,D)=(\frac{1}{18},\frac{2}{27},\frac{1}{20},\frac{1}{10})$

To end this subsection, we present simulations for the codimension-2 BT bifurcation. It has been shown that the BT bifurcation can occur only for $R_0 < 1$ (i.e., for $D < B$). It should be also noted that in the neighborhood of the codimension-2 BT critical point, there exists only one limit cycle from the Hopf bifurcation. To give a more direct impression, here we shall use the original equation (5), rather than the normal form (78), to perform the simulation. Since the perturbation parameters A and B are given in terms of C and D, we choose $(C,D) = (\frac{1}{20}, \frac{1}{10})$, then obtain the BT critical point as $(A,B) = (\frac{1}{18}, \frac{2}{27})$, then further have $a_1 = -\frac{7}{729}$ and $a_2 = -\frac{50}{729}$, and $\frac{a_2}{a_1} = \frac{50}{7}$. The bifurcation diagram near the above critical point is shown in Fig. 17.

We can take perturbations on A and B such that $A,\,B$ pass through the blue curve from above, see Fig. 17. To investigate the effect of B on the BT bifurcation, we let $A = \frac{1}{18} + \mu _1$, $B = \frac{2}{27} + \mu _2$, and fix $\mu _1 = \frac{1}{20}$.

Fig. 18

Simulations of system (5) when $A = \frac{19}{180}$, $C = \frac{2}{27}$ and $D = \frac{1}{10}$ for a$B = 0.0460740741$, showing convergence of the half-unstable manifold of the saddle point $\mathrm{E_{1+}}$ to the stable focus $\mathrm{E_{1-}}$; b$B = 0.0457725781$, showing an unstable homoclinic loop enclosing a stable focus; c$B = 0.0440740741$, showing stable focus $\mathrm{E_{1-}}$ enclosed by an unstable limit cycle; and d$B = 0.0400740741$, showing an unstable focus $\mathrm{E_{1-}}$ with a trajectory connecting to half-stable manifold of the saddle point $\mathrm{E_{1+}}$

Taking

$$\begin{aligned} \mu _2 = -0.028, \quad -0.028301496, \quad -0.03, \quad -0.034, \end{aligned}$$

(79)

the four corresponding points $(A,B,C,D) \in \mathcal {S}$ locate from top to the bottom on the blue vertical line segment in Fig. 17. Four corresponding simulations are shown in Fig. 18a–d, respectively. We can use (77) to obtain $\xi _1$ and $\xi _2$ expressed in terms of $\mu _2$ as follows:

$$\begin{aligned} \xi _1 = -\textstyle \frac{7}{27000} + \frac{7}{1500}\, \mu _2 - \frac{98}{675}\, \mu _2^2, \quad \xi _2 = - \frac{9}{7}\, \mu _2- 40\, \mu _2^2 . \end{aligned}$$

The simulations given in Fig. 17a–d correspond to the four phase portraits shown in Fig. 18a. However, note that stability is reversed since the transformation given in (61) yields

$$\begin{aligned} \det \left[ \begin{array}{rc} \textstyle \frac{1}{D-1} &{} 0 \\ \textstyle \frac{D}{1-D} &{} 1 \end{array} \right] = \frac{1}{D-1} < 0, \quad \mathrm{for} \ \ D \in \big (0, \textstyle \frac{1}{2} \big ), \end{aligned}$$

and thus the Hopf and homoclinic bifurcations exchange their positions. Moreover, for the parameter values $(A,B,C,D)=(\frac{1}{18},\frac{2}{27}, \frac{1}{20},\frac{1}{10})$, we can use (61), (76) and (77) to find the coordinates of the focus $\mathrm{E_{1-}}$ and the saddle $\mathrm{E_{1+}}$ in the original system (5), corresponding to the focus $(x_1,x_2)=(-\sqrt{-\xi _1},0)$ and the saddle $(x_1,x_2)=(\sqrt{-\xi _1},0)$, respectively, as

$$\begin{aligned} \big (X_-,Y_- \big )\approx & {} \left( \textstyle \frac{963}{140}-\frac{9\sqrt{210}}{70} +\big ( \frac{324}{7}-\frac{783\sqrt{210}}{980} \big ) \mu _2 , \ \frac{8011729}{28000000} \right. \\&\left. + \textstyle \frac{14193 \sqrt{210}}{612500} -\big ( \frac{717741}{200000} + \frac{94149 \sqrt{210}}{245000} \big ) \mu _2 \right) , \\ \big (X_+,Y_+ \big )\approx & {} \left( \textstyle \frac{963}{140}+\frac{9\sqrt{210}}{70} +\big ( \frac{324}{7}-\frac{783\sqrt{210}}{980} \big ) \mu _2 , \ \frac{8011729}{28000000}\right. \\&\left. +\textstyle \frac{14193 \sqrt{210}}{612500} -\big ( \frac{717741}{200000} - \frac{94149 \sqrt{210}}{245000} \big ) \mu _2 \right) , \end{aligned}$$

which shows that

$$\begin{aligned} X_+ - X_- = \textstyle \frac{9 \sqrt{210}}{490} \big ( 14 + 87 \mu _2)>0, \quad Y_- - Y_+ = \frac{9 \sqrt{210}}{612500} \big ( 3154 - 52305 \mu _2)>0, \quad \end{aligned}$$

for the values of $\mu _2$ given in (79), as expected.

4.2 Codimension-3 BT Bifurcation

In this section, we consider the codimension-3 BT bifurcation under condition (ii) in Theorem 4.1. To find the parametric normal form of BT bifurcation, a widely used method was developed by Dumortier et al. (1987) which involves transformation with six steps. In this paper, we present a one-step transformation method to reach the parametric normal form. This novel method involves transformations on state variables and parameters, as well as a time rescaling. To achieve this, let

$$\begin{aligned} A = \textstyle \frac{4 D^2}{(1+D)(1-3D)} + \mu _1, \quad B = \frac{D}{1+D} + \mu _2, \quad C = \frac{D(1+D)}{1-3D} + \mu _3, \end{aligned}$$

(80)

where $D \in (0,\frac{1}{4}) \bigcup (\frac{1}{4},\frac{1}{3})$. We denote $\mu =(\mu _1,\mu _2,\mu _3)$ and then apply (80) together with (61) into (5) and expand the resulting system around the point $(u_1,u_2,\mu ) = (0,0,0)$ to obtain the following system:

$$\begin{aligned} \begin{array}{rrl} &{} \displaystyle \frac{\mathrm{d} u_1}{\mathrm{d} \tau } = &{} u_2 + f_4(u_1,u_2,\mu ) + \mathcal {O}(|(u_1,u_2,\mu )|^5) , \\ &{} \displaystyle \frac{\mathrm{d} u_2}{\mathrm{d} \tau } = &{} f_4 (u_1,u_2,\mu ) + \mathcal {O}(|(u_1,u_2,\mu )|^5), \end{array} \end{aligned}$$

(81)

where

$$\begin{aligned} f_4= & {} \mathcal {F}_{400}(\mu ) + \mathcal {F}_{310}(\mu ) \, u_1 + \mathcal {F}_{301}(\mu ) \, u_2 + \mathcal {F}_{220}(\mu ) \, u_1^2 + \mathcal {F}_{311}(\mu ) \, u_1 u_2 \\&+ \, \mathcal {F}_{302}(\mu ) \, u_2^2 + \mathcal {F}_{130}(\mu ) \, u_1^3 + \mathcal {F}_{121}(\mu ) \, u_1^2 u_2 + \mathcal {F}_{112}(\mu ) \, u_1 u_2^2 + \mathcal {F}_{103}(\mu ) \, u_2^3 \\&+ \, \textstyle \frac{(1-3 D)(1+D)}{8 (1-D)^3} \, \left[ \frac{D^2}{(1-D)^3} \, u_1^4 + \frac{2 (2-3 D) }{(1-D)^3}\, u_1^3 u_2 + \frac{6(1-2D)}{(1-D)^2}\, u_1^2 u_2^2\right. \\&\left. \textstyle + \frac{2 (2-5D)}{ D (1-D)} \, u_1 u_2^3 + \frac{(1-3D)}{D^2 } \, u_2^4 \right] , \end{aligned}$$

in which $\mathcal {F}_{kij}$ are kth-degree polynomials in $\mu$. Then, we employ the parametric simplest normal form theory (Yu and Leung 2003; Gazor and Yu 2010, 2012; Gazor and Moazeni 2015) to obtain the parametric normal form. More precisely, we apply the following state variables transformation:

$$\begin{aligned} u_1= & {} -\textstyle \frac{2(1-D)^2}{D^2}\, y_1 + \frac{(1-D)^2 (2 D^2 + 3D-3)}{2 D^4}\, \xi _1 + \frac{(1-D)^2}{D}\, \xi _2\nonumber \\&+ \displaystyle \sum _{i+j+k+l+m=2,3,4} \mathcal {U}_{1ijklm} y_1^i y_2^j \xi _1^k \xi _2^l \xi _3^m,\nonumber \\ u_2= & {} -\textstyle \frac{2(1-D)^2}{D^2}\, y_2 + \textstyle \frac{2(1-D)^2}{D^2} \, \xi _1 + \displaystyle \sum _{i+j+k+l+m=2,3,4} \mathcal {U}_{2ijklm} y_1^i y_2^j \xi _1^k \xi _2^l \xi _3^m, \end{aligned}$$

(82)

and a time rescaling:

$$\begin{aligned} \tau \ \rightarrow \ \big [ 1 - \textstyle \frac{1+D}{2 D^2}\, y_1 + \frac{1}{6 D}\, \xi _2 + \frac{D}{3(1+D)}\, \xi _3 \big ] \tau , \end{aligned}$$

(83)

then obtain the parametric normal form,

$$\begin{aligned} \displaystyle \frac{\mathrm{d} y_1}{\mathrm{d} \tau }= & {} y_2 + \mathcal {O}(|y_1,y_2,\xi |^5), \nonumber \\ \displaystyle \frac{\mathrm{d} y_2}{\mathrm{d} \tau }= & {} \xi _1 + \xi _2 \, y_2 + \xi _3 \, y_1 y_2 + y_1^2 - b_1\, y_1^3 y_2 + \mathcal {O}(|(y_1,y_2,\xi )|^5), \end{aligned}$$

(84)

where $b_1 = \frac{(1-4D)(1-D^2)}{D^5}$ for $D \in (0,\frac{1}{4}) \bigcup (\frac{1}{4},\frac{1}{3})$, and the parametrization is given by

$$\begin{aligned} \mu _1= & {} \textstyle \frac{4 (1-D)^2 (8 D^2-3 D-1)}{D^2 (1+D) (1-3 D)^2}\, \xi _1 + \frac{4 D (1-D)}{(1+D)(1-3 D)^2}\, \xi _2 - \frac{8 D^4 (1-D)}{(1+D)^2 (1-3D)^2}\, \xi _3,\nonumber \\&+ \sum \limits _{i+j+k=2,\,3} \textstyle \mathcal {M}_{1ijk} \xi _1^i \xi _2^j \xi _3^k,\nonumber \\ \mu _2= & {} \textstyle - \frac{(1-D)(1-4D)}{D^2 (1+D)}\, \xi _1 - \frac{D}{2(1+D)}\, \xi _2 - \frac{D^3}{(1+D)^2}\, \xi _3 + \displaystyle \sum _{i+j+k=2,3} \mathcal {M}_{2ijk} \xi _1^i \xi _2^j \xi _3^k,\nonumber \\ \mu _3= & {} - \textstyle \frac{(1+D)(1-D)^2 (1-D +4D^2)}{D^3 (1-3 D)^2}\, \xi _1 + \frac{3(1+D) (1-D)^2}{2 (1-3D)^2}\, \xi _2 - \frac{D^2 (1-D)^2}{(1-3D)^2}\, \xi _3\nonumber \\&+ \sum \limits _{i+j+k=2,3} \textstyle \mathcal {M}_{3ijk} \xi _1^i \xi _2^j \xi _3^k - \textstyle \frac{2 D^5 (72 D^5-36 D^4+33 D^3-3 D^2+15 D-1) (1-D)^2}{9 (1+D)^3/(1-3D)^4}\, \xi _3^4.\qquad \end{aligned}$$

(85)

Finally, introducing the transformation:

$$\begin{aligned} y_1 = x_1, \quad y_2 + \mathcal {O}(|(y_1,y_2,\xi )|^5) = x_2, \end{aligned}$$

into (84) yields the normal form with the unfolding up to fourth-order terms:

$$\begin{aligned} \displaystyle \frac{\mathrm{d} x_1}{\mathrm{d} \tau }= & {} x_2, \nonumber \\ \displaystyle \frac{\mathrm{d} x_2}{\mathrm{d} \tau }= & {} \xi _1 + \xi _2 \, x_2 + \xi _3 \, x_1 x_2 + x_1^2 - b_1\, x_1^3 x_2 + \mathcal {O}(|(x_1,x_2,\xi )|^5). \end{aligned}$$

(86)

Note that the coefficient of $y_1$ in the time rescaling (83), $-\,\frac{1+D}{2D^2}$, is actually equivalent to the coefficient of $x_1$ in the time rescaling (65), $\frac{C}{2(1-D)(C+D)} = \frac{1+D}{4 (1-D)^2}$, because there is a scaling $-\frac{2(1-D)^2}{D^2}$ for $u_1$ and $u_2$ in (82). In fact, $\frac{1+D}{4 (1-D)^2} \times \big ( -\frac{2(1-D)^2}{D^2} \big ) = -\frac{1+D}{2D^2}$. For the same reason, we see that $b_1 = \frac{(1-4D)(1-D)^2}{D^5} = -\, \frac{a_3}{a_1} \times \big ( -\frac{2(1-D)^2}{D^2} \big )^2$, where $a_1$ and $a_3$ are given in (71). Thus, due to $a_1 < 0$, $b_1$ has the same sign of $a_3$, which is positive for $D \in (0,\frac{1}{4})$ and negative for $D \in (\frac{1}{4},\frac{1}{3})$. To examine the influence of D on the system’s dynamics, we use $b_1 = \frac{(1-4D)(1-D)^2}{D^5}$ without normalization.

Further, it is easy to use (85) to verify that

$$\begin{aligned} \det \left[ \textstyle \frac{\partial (\mu _1, \mu _2, \mu _3)}{\partial (\xi _1, \xi _2, \xi _3)} \right] = -\, \textstyle \frac{8 D (1-D)^3}{(1+D)(1-3D)^3} + \mathcal {O}(\xi ) \ne 0 \ \ \mathrm{in} \ D \in (0,\textstyle \frac{1}{3}) \ \ \mathrm{for \ small} \ \xi , \end{aligned}$$

which shows that near the critical point $(A,B,C) = (A_0,B_0,C_0)$, system (5) has the same bifurcation set with respect to $\mu$ as system (86) has with respect to $\xi$, up to a homeomorphism in the parameter space.

Now, based on the normal form (86), we can follow a similar procedure used for analyzing the codimension-2 BT bifurcation to obtain the Hopf bifurcation surface and homoclinic bifurcation surface in the $\xi _1$–$\xi _2$–$\xi _3$ parameter space. To achieve this, we first find the two equilibrium solutions $\mathrm{E_\pm }$ as

$$\begin{aligned} \mathrm{E_\pm }= (x_{1 \pm },0), \quad \mathrm{where} \quad x_{1 \pm } = \pm \sqrt{-\xi _1} \quad \mathrm{for} \quad \xi _1 < 0. \end{aligned}$$

(87)

The Jacobian of (86) evaluated at $\mathrm{E_\pm }$ is given by

$$\begin{aligned} J_\pm = \left[ \begin{array}{ll} 0 &{}\quad 1 \\ 2 x_{1 \pm } &{}\quad \xi _2 + \xi _3 x_{1 \pm } - b_1 x_{1 \pm }^3 \end{array} \right] , \end{aligned}$$

(88)

which indicates $\mathrm{E_{1 +}}$ is a saddle, and $\mathrm{E_{1 -}}$ is focus or node. It is easy to see that the plane

$$\begin{aligned} \mathrm{SN} = \big \{ (\xi _1, \xi _2, \xi _3) \mid \xi _1 = 0 \big \}, \end{aligned}$$

(89)

excluding the origin in the parameter space is the saddle-node bifurcation surface.

Next, we consider Hopf bifurcation and generalized Hopf bifurcation from which multiple limit cycles can occur. We have the following result.

Theorem 4.3

For system (86), Hopf bifurcation occurs from the equilibrium solution $\mathrm{E_{-}}$ at any point on the critical surface, defined by

$$\begin{aligned} \mathrm{H} = \left. \Big \{ (\xi _1, \xi _2, \xi _3) \right| \xi _2 - ( \xi _3 + b_1 \xi _1 ) \sqrt{-\xi _1}=0 \, \Big \}. \end{aligned}$$

(90)

The generalized Hopf bifurcation occurs from the equilibrium solution $\mathrm{E_{-}}$ at any point on the critical line which is the intersection of the critical surface $\mathrm{H}$ and the generalized critical surface $\mathrm{GH}$, defined by

$$\begin{aligned} \mathrm{GH} = \left. \Big \{ (\xi _1, \xi _2, \xi _3) \right| \xi _3 + 3 b_1\, \xi _1 =0 \Big \}, \end{aligned}$$

(91)

yielding maximal two small-amplitude limit cycles, and outer one is stable (unstable) if $b_1 > 0$ ($b_1 < 0$).

Proof

It is easy to see from the Jacobian $J_-$ given in (88) that Hopf bifurcation can occur from the equilibrium $\mathrm{E_{1 -}}$ at any point on the critical surface, defined by $\xi _2 + \xi _3 x_{1 -} - b_1 x_{1 -}^3 =0$, which can be written in the form of (90). Note that ignoring the term $b_1 \xi _1$ and letting $\xi _3 = -\frac{a_2}{a_1}$ in (90) yields the Hopf bifurcation curve, $\xi _1 = - (\frac{a_1}{a_2})^2 \xi _2^2$, given in Theorem 4.2, as expected.

To consider the generalized Hopf bifurcation and possible multiple limit cycles bifurcating from the Hopf critical surface (90), we need to find the focus values. Introducing the transformation,

$$\begin{aligned} x_1 = -\sqrt{- \xi _1} + w_1, \quad x_2 = \omega _c \, w_2, \quad \mathrm{where} \quad \omega _c = \sqrt{2 \sqrt{- \xi _1}}, \quad (\xi _1 < 0), \end{aligned}$$

into (86) yields the following system:

$$\begin{aligned} \begin{array}{ll} \displaystyle \frac{\mathrm{d}w_1}{\mathrm{d} \tau } = \omega _c \, w_2, \\ \displaystyle \frac{\mathrm{d} w_2}{\mathrm{d}\tau } = - \omega _c \, w_1 + \textstyle \frac{1}{\omega _c}\, w_1^2 + \big ( \xi _3 - \frac{3 b_1}{4}\, \omega _c^4 \big ) \, w_1 w_2 + \frac{3 b_1}{2} \omega _c^2 w_1^2 w_2 - b_1\, w^3 w_2. \end{array} \end{aligned}$$

(92)

Then applying the Maple program (Yu 1998) we obtain the focus values:

$$\begin{aligned} v_1 = \textstyle \frac{1}{ 32 \omega _c^2} (4 \xi _3+3 b_1 \omega _c^4) = \textstyle \frac{1}{8 \omega _c^2} (\xi _3-3 b_1 \xi _1), \quad \left. v_2 \right| _{v_1 = 0} = -\,\frac{5 b_1}{48 \omega _c^2} \ne 0. \end{aligned}$$

It is easy to find that $v_1 = 0$ leads to

$$\begin{aligned} \xi _3 = -\, 3 b_1\, \xi _1, \quad (\xi _1 < 0), \end{aligned}$$

which defines the generalized Hopf critical surface (91). Since when $v_1=0$, $v_2 \ne 0$, at most two limit cycles can bifurcate from the $\mathrm{E_{-1}}$. Moreover, simple perturbations on $\xi _3$ for $v_1$ and $\xi _2$ for $v_0$ yield $|v_0| \ll |v_1| \ll |v_2|$, implying that two limit cycles do occur, with the outer one stable (unstable) if $b_1>0$ ($b_1<0$). $\square$

It should be noted that the above result on the number of small-amplitude limit cycles bifurcating from the Hopf critical surface (90), near the codimension-3 BT bifurcation point, agrees with that for the general original system (5), given in Theorems 3.3 (for $R_0=1$) and 3.5 (for $R_0 \ne 1$), but the proof here is much simpler.

Now, we turn to consider the homoclinic bifurcation surface as well as the degenerate homoclinic bifurcation points on the surface by following the method described in Han and Yu (2012). For this part, we have the following theorem.

Theorem 4.4

For system (86), homoclinic bifurcation can occur from the critical surface, defined by

$$\begin{aligned} \mathrm{HL} = \left. \Big \{ (\xi _1,\xi _2,\xi _3) \right| \xi _2 - \textstyle \frac{5}{7} \, \big ( \xi _3 + \frac{103 }{55}\,b_1\, \xi _1 \big ) \sqrt{- \xi _1} =0 \Big \}, \end{aligned}$$

(93)

and the degenerate homoclinic bifurcation occurs from any point on the critical line which is the intersection of the critical surface $\mathrm{HL}$ and the degenerate critical surface $\mathrm{DHL}$, defined by

$$\begin{aligned} \mathrm{DHL} = \left. \Big \{ (\xi _1,\xi _2,\xi _3) \right| \xi _2 + \big ( \xi _3 + b_1\, \xi _1 \big ) \sqrt{- \xi _1} = 0 \Big \}, \end{aligned}$$

(94)

leading to bifurcation of two limit cycles.

Proof

We use the method given in Han and Yu (2012) to prove the theorem. We first introduce the following scaling:

$$\begin{aligned}&x_1 = \varepsilon ^{\frac{2}{5}} w_1, \ \ x_2 = \varepsilon ^{\frac{3}{5}} w_2, \ \ \xi _1 = \varepsilon ^{\frac{4}{5}} \nu _1, \ \ \xi _2 = \varepsilon ^{\frac{6}{5}} \nu _2, \nonumber \\&\quad \xi _1 = \varepsilon ^{\frac{4}{5}} \nu _3, \ \ \tau _1 = \varepsilon ^{\frac{1}{5}} \tau , \ \ (0< \varepsilon \ll 1), \end{aligned}$$

(95)

into (86) we obtain

$$\begin{aligned} \displaystyle \frac{\mathrm{d} w_1}{\mathrm{d} \tau _1}= & {} w_2 , \nonumber \\ \displaystyle \frac{\mathrm{d} w_2}{\mathrm{d} \tau _1}= & {} \nu _1 + w_1^2 + \varepsilon \, ( \nu _2 w_2 + \nu _3 w_1 w_2 - b_1 w_1^3 w_2) \equiv \nu _1 + w_1^2 + \varepsilon \, q(w_1,w_2,\nu ),\nonumber \\ \end{aligned}$$

(96)

where $\nu =(\nu _1,\nu _2,\nu _3)$. The system (96)$\big |_{\varepsilon =0}$ is a Hamiltonian system. In order to have the Hamiltonian function given in the form of that in (Han and Yu 2012), we introduce a further transformation,

$$\begin{aligned} w_1 = \bar{\nu }_1 + z_1, \quad w_2 = \sqrt{2 \bar{\nu }_1} \, z_2, \quad \tau _2 = \sqrt{2 \bar{\nu }_1} \, \tau _1, \quad \nu _1 = - \bar{\nu }_1^2 \ \ (\bar{\nu }_1>0), \end{aligned}$$

(97)

into (96) to yield

$$\begin{aligned} \displaystyle \frac{\mathrm{d} z_1}{\mathrm{d} \tau _2}= & {} z_2 , \nonumber \\ \displaystyle \frac{\mathrm{d} z_2}{\mathrm{d} \tau _2}= & {} z_1 + \textstyle \frac{1}{2 \bar{\nu }_1}\, z_1^2 + \textstyle \frac{\varepsilon }{\sqrt{2 \bar{\nu }_1}} \, \big [ ( \nu _2 + \bar{\nu }_1 \, \nu _3 - b_1 \bar{\nu }_1^3 ) z_2 + ( \nu _3 - 3 b_1 \bar{\nu }_1^2 ) z_1 z_2\nonumber \\&-\,3 b_1 \bar{\nu }_1 z_1^2 z_2 - b_1 z_1^3 z_2) \big ] \nonumber \\\equiv & {} z_1 + \textstyle \frac{1}{2 \bar{\nu }_1}\, z_1^2 + \varepsilon \, q(z_1,z_2, \bar{\nu }), \end{aligned}$$

(98)

where $\bar{\nu }=(\bar{\nu }_1,\nu _2,\nu _3)$.

System (98)$\big |_{\varepsilon =0}$ is a Hamiltonian system with two equilibrium solutions:

$$\begin{aligned} \mathrm{\widetilde{E}_-} = ( -2 \bar{\nu }_1,0) \quad \mathrm{and} \quad \mathrm{\widetilde{E}_0} = (0, 0), \end{aligned}$$

(99)

with $\mathrm{\widetilde{E}_- }$ and $\mathrm{\widetilde{E}_0}$ being center and saddle, respectively. These two equilibria correspond to the $\mathrm{E_\pm }$ defined in (87). The Hamiltonian function is

$$\begin{aligned} H(z_1,z_2) = \textstyle \frac{1}{2}\, (z_2^2 - z_1^2) - \frac{1}{6 \bar{\nu }_1} \, z_1^3, \end{aligned}$$

(100)

and the homoclinic orbit connecting $\mathrm{E_0}$ is given by

$$\begin{aligned} \Gamma _0: \quad H (z_1,z_2) = \textstyle \frac{1}{2}\, (z_2^2 - z_1^2) - \frac{1}{6 \bar{\nu }_1} \, z_1^3 = H(0,0) = 0, \end{aligned}$$

(101)

and $H(-2 \bar{\nu }_1,0) = - \frac{2}{3} \, \bar{\nu }_1^2$. Thus, any closed orbit of the Hamiltonian system (98)$\big |_{\varepsilon =0}$ inside $\Gamma _0$ can be described by

$$\begin{aligned} \Gamma _{\mathrm{h}}: \quad H(z_1,z_2,h) = \textstyle \frac{1}{2}\, (z_2^2 - z_1^2) - \frac{1}{6 \bar{\nu }_1} \, z_1^3 - h = 0, \quad h \in \left( - \frac{2}{3} \, \bar{\nu }_1^2, 0\right) . \end{aligned}$$

(102)

Now the Abelian integral or the (first-order) Melnikov function for the perturbed system (98) can be written as

$$\begin{aligned} \begin{array}{rl} M(h,\nu ) &{} = \displaystyle \oint _{\Gamma _{\mathrm{h}}} q (z_1,z_2,\nu ) \, d z_1 - p(z_1,z_2,\nu ) \, d z_2 \mid _{\varepsilon =0} \qquad (p=0) \\ &{} = \displaystyle \oint _{\Gamma _{\mathrm{h}}} q (z_1,z_2,\nu ) \mid _{\varepsilon =0} \, d z_1 = \displaystyle \oint _{\Gamma _{\mathrm{h}}} H_{z_2} q (z_1,z_2,\nu ) \mid _{\varepsilon =0} \, dt \\ &{} = \displaystyle \frac{1}{\sqrt{2 \bar{\nu }_1}} \displaystyle \oint _{\Gamma _{\mathrm{h}}} z_2^2\, \big [ \nu _2 + \bar{\nu }_1 \, \nu _3 - b_1 \bar{\nu }_1^3 + ( \nu _3 - 3 b_1 \bar{\nu }_1^2 ) z_1 - 3 b_1 \bar{\nu }_1 z_1^2 - b_1 z_1^3 \big ] \, d t. \end{array} \end{aligned}$$

(103)

If we consider bifurcation of limit cycles around the center $\mathrm{E_-}$, we may expand the M(h, v) in h for $-\frac{2}{3}\, \bar{\nu }_1^2 < h \ll 1$, which is equivalent to using the method of focus values or normal forms (Tian and Yu 2018), and the same result as that given in Theorem 4.3 will be obtained.

In the following, we consider the limit cycles bifurcating from the homoclinic orbit $\Gamma _0$. We use the method and formulas given in Han and Yu (2012) to expand the Melnikov function $M(h,\nu )$ for $0< -h \ll 1$ to obtain

$$\begin{aligned} M(h,\nu )= & {} C_0(\nu ) + C_1(\nu )\, h \ln |h| + C_2(\nu ) \, h\nonumber \\&+ C_3(h) \, h^2 \ln |h| + \cdots , \quad (0< -h \ll 1), \end{aligned}$$

(104)

where

$$\begin{aligned} C_0(\nu )= & {} \displaystyle \frac{1}{\sqrt{2 \bar{\nu }_1}} \displaystyle \oint _{\Gamma _0} z_2^2 \big [ \nu _2 + \bar{\nu }_1 \, \nu _3 - b_1 \bar{\nu }_1^3 + ( \nu _3 - 3 b_1 \bar{\nu }_1^2 ) z_1 - 3 b_1 \bar{\nu }_1 z_1^2 - b_1 z_1^3 \big ] \, d t, \nonumber \\ C_1(\nu )= & {} a_{10} + b_{01}, \end{aligned}$$

(105)

in which $a_{10}$ and $b_{01}$ are the coefficients in the functions $p(z_1,z_2,\nu )$ and $q(z_1,z_2,\nu )$, given by

$$\begin{aligned} a_{10} =0, \qquad b_{01} = \displaystyle \frac{1}{\sqrt{2 \bar{\nu }_1}} (\nu _2 + \bar{\nu }_1 \, \nu _3 - b_1 \bar{\nu }_1^3 ). \end{aligned}$$

(106)

To compute $C_0(\nu )$, introducing the parametric transformation:

$$\begin{aligned} z_1(t) = - 3 \, \mathrm{sech}^2(t), \quad z_2(t) = 3 \, \bar{\nu }_1^2 \mathrm{sech}^2(t) \, \mathrm{tanh} (t), \end{aligned}$$

(107)

into $C_0(\nu )$ we obtain

$$\begin{aligned} C_0(\nu )&= \displaystyle \frac{1}{\sqrt{2 \bar{\nu }_1}} \displaystyle \int _{-\infty }^\infty \big [ \nu _2 + \bar{\nu }_1 \, \nu _3 - b_1 \bar{\nu }_1^3 + ( \nu _3 - 3 b_1 \bar{\nu }_1^2 ) z_1 - 3 b_1 \bar{\nu }_1 z_1^2 - b_1 z_1^3 \big ] z_2^2 \, d t, \nonumber \\&= \displaystyle \frac{1}{\sqrt{2 \bar{\nu }_1}} \displaystyle \int _{-\infty }^\infty \big [ \nu _2 + \bar{\nu }_1 \, \nu _3 - b_1 \bar{\nu }_1^3 + ( \nu _3 - 3 b_1 \bar{\nu }_1^2 ) z_1 - b_1 z_1^3 \big ] z_2^2 \, d t, \nonumber \\&= \displaystyle \frac{1}{\sqrt{2 \bar{\nu }_1}} \displaystyle \int _{-\infty }^\infty \big [ \nu _2 + \bar{\nu }_1 \, \nu _3 - b_1 \bar{\nu }_1^3 - 3\, ( \nu _3 - 3 b_1 \bar{\nu }_1^2 ) \, \mathrm{sech}^2(t) + 27 \, b_1 \, \mathrm{sech}^6(t) \big ]\nonumber \\&\qquad \qquad \qquad \times \, 9 \, \bar{\nu }_1^4 \mathrm{sech}^4(t) \, \mathrm{tanh}^2 (t) \, d t \nonumber \\&= \textstyle \frac{1}{\sqrt{2 \bar{\nu }_1}} \times \frac{12}{5} \bar{\nu }_1^2 \left[ \nu _2 - \frac{5}{7} \bar{\nu }_1 \, \nu _3 - \frac{103}{77} \, b_1 \bar{\nu }_1^3 \right] = \frac{6 \bar{\nu }_1 \sqrt{2 \bar{\nu }_1}}{5} \left[ \nu _2 - \frac{5}{7} \bar{\nu }_1 \, \nu _3 - \frac{103}{77} \, b_1 \bar{\nu }_1^3 \right] .\nonumber \\ \end{aligned}$$

(108)

Finally, we express $C_0(\nu )$ and $C_1(\nu )$ in terms of the original perturbation parameters $\xi _j$ by using

$$\begin{aligned} \bar{\nu }_1 = \sqrt{-\nu _1} = \sqrt{- \varepsilon ^{-4/5} \, \xi _1} = \varepsilon ^{-2/5} \sqrt{-\xi _1}, \quad \nu _2 = \varepsilon ^{-6/5} \xi _2, \quad \nu _3 = \varepsilon ^{-4/5} \xi _3, \end{aligned}$$

as

$$\begin{aligned} \begin{array}{ll} C_0(\xi ) = \frac{6 \bar{\nu }_1 \sqrt{2 \bar{\nu }_1}}{5} \varepsilon ^{-6/5} \left[ \xi _2 - \frac{5}{7} ( \xi _3 + \frac{103}{55} \, b_1 \xi _1 ) \sqrt{- \xi _1} \right] , \\ C_1(\xi ) = \frac{1}{ \sqrt{2 \bar{\nu }_1}} \left[ \xi _2 + ( \xi _3 + b_1 \xi _1 ) \sqrt{- \xi _1} \right] . \end{array} \end{aligned}$$

(109)

Hence, the homoclinic bifurcation surface is defined by $C_0(\xi ) = 0$, leading to the equation HL given in (93). Again note that ignoring the term $b_1 \xi _1$ and letting $\xi _3 = -\frac{a_2}{a_1}$ in $C_0(\xi ) = 0$ yields the homoclinic curve, $\xi _1 = - \frac{49}{25}\big (\frac{a_1}{a_2}\big )^2 \xi _2^2$, which is exactly the same as that given in Theorem 4.2 for the codimension-2 BT bifurcation, as expected. Further, degenerate homoclinic bifurcation happens at $C_1(\xi ) = 0$, which defines another critical surface DHL given in (94). $\square$

It is obvious that system (86) has no equilibria for $\xi _1 > 0$. So the bifurcation surfaces are in the half space $\xi _1 \le 0$, implying that the bifurcation diagram of system (86) is a cone, which can be represented by its intersection with the 2-sphere,

$$\begin{aligned} S_\sigma = \big \{ (\xi _1,\xi _2,\xi _3) \mid \xi _1^2 + \xi _2^2 + \xi _3^2 = \sigma ^2, \, 0 < \sigma \ll 1 \big \}. \end{aligned}$$

(110)

The intersection curve of the Hopf bifurcation surface (90) and the 2-sphere (110) can be described as

$$\begin{aligned}&\mathrm{H_{curve}}\nonumber \\&\quad = \left. \Big \{ (\xi _2, \xi _3) \, \right| \xi _2 = \Big [ \xi _3 - b_1 \big (\sigma ^2-\xi _2^2-\xi _3^2 \big )^{\frac{1}{2}} \Big ] \big (\sigma ^2 - \xi _2^2 - \xi _3^2 \big )^{\frac{1}{4}}, \ \ \xi _2^2 + \xi _3^2 \le \sigma ^2 \Big \},\nonumber \\ \end{aligned}$$

(111)

which is shown in Fig. 19 as the blue curve. Similarly, we can find the intersection curve of the homoclinic bifurcation surface (93) and the 2-sphere (110) as

$$\begin{aligned}&\mathrm{HL_{curve}} \nonumber \\&\quad = \left. \Big \{ (\xi _2, \xi _3) \, \right| \xi _2 = \textstyle \frac{5}{7} \Big [ \xi _3 - \frac{103}{55} b_1 \big (\sigma ^2-\xi _2^2-\xi _3^2 \big )^{\frac{1}{2}} \Big ] \big (\sigma ^2 - \xi _2^2 - \xi _3^2 \big )^{\frac{1}{4}}, \ \ \xi _2^2 + \xi _3^2 \le \sigma ^2 \Big \},\nonumber \\ \end{aligned}$$

(112)

which is also shown in Fig. 19 as the green curve.

The intersection point of the Hopf and homoclinic bifurcation curves, denoted by C (see Fig. 19), can be obtained from the following equations:

$$\begin{aligned} \mathrm{C}: \,\, \xi _2 = \textstyle \frac{24}{11} \, b_1 \xi _1 \sqrt{-\xi _1}, \,\, \xi _3 = \textstyle \frac{13}{11} \, b_1 \xi _1, \,\, f(\xi _1) = \xi _1 + \sqrt{\sigma ^2 - \xi _2^2 - \xi _3^2 } = 0 \Longrightarrow \xi _1.\nonumber \\ \end{aligned}$$

(113)

Similarly, the GH denotes the intersection point of the Hopf bifurcation (in blue) and the generalized Hopf bifurcation (in pink) curves, and DHL denotes the intersection point of the homoclinic bifurcation (in green) and the degenerate homoclinic bifurcation (in brown) curves. These two points are shown in Fig. 19, determined from the following equations:

$$\begin{aligned} \mathrm{GH}: \quad \left\{ \begin{array}{ll} \xi _2 = -\,2 b_1\, \xi _1 \sqrt{-\xi _1}, \quad \xi _3 = -\,3 \, b_1 \xi _1 , \\ f(\xi _1) = \xi _1 + \sqrt{\sigma ^2 - \xi _2^2 - \xi _3^2 } = 0 \ \Longrightarrow \ \xi _1, \end{array} \right. \end{aligned}$$

(114)

and

$$\begin{aligned} \mathrm{DHL}: \quad \xi _2= & {} \textstyle \frac{4}{11} \, b_1 \xi _1 \sqrt{-\xi _1}, \quad \xi _3 = -\,\textstyle \frac{15}{11} \, b_1 \xi _1,\nonumber \\&f(\xi _1) = \xi _1 + \sqrt{\sigma ^2 - \xi _2^2 - \xi _3^2 } = 0 \ \Longrightarrow \ \xi _1. \end{aligned}$$

(115)

As an example, taking $D = 0.2499$, which yields $b_1 = 0.230923$, and $\sigma = 0.1$, we obtain

$$\begin{aligned} \begin{array}{rlll} \mathrm{C} &{} = \ (\xi _2,\xi _3)_{\mathrm{C}} &{}= (-\,0.014847,-\,0.026036), &{} \ \ \mathrm{for} \ \ \xi _1 = -\,0.095403, \\ \mathrm{GH} &{} = \, (\xi _2,\xi _3)_{\mathrm{GH}} &{} = (0.010790,0.056614), &{} \ \ \mathrm{for} \ \ \xi _1 = -\,0.081721, \\ \mathrm{DHL} &{} = (\xi _2,\xi _3)_{\mathrm{DHL}} &{} = (-\,0.002473,-\,0.030026), &{} \ \ \mathrm{for} \ \ \xi _1 = -\,0.095354, \end{array} \end{aligned}$$

as shown in Fig. 19a.

Fig. 19

Bifurcation curves for the codimension-3 BT bifurcation based on the normal form (86), displayed in the intersection of the cone and the 2-sphere $\xi _1^2 + \xi _2^2 + \xi _3^2 = \sigma ^2$, with red color for saddle-node, blue for Hopf and green for homoclinic, respectively: a with $D = 0.2499$ and $\sigma = 0.1$, where the intersection point of the pink and blue curves is the degenerate Hopf bifurcation, and the intersection point of the brown and green curves denotes the degenerate homoclinic loop bifurcation; and b a schematic bifurcation diagram for $b_1>0$ (i.e., $a_3>0$) (Color figure online)

The two points GH and DHL correspond to the Melnikov function $M(h,\nu )$ given in (103) satisfying $M(h,\nu ) = M_h(h,\nu ) = 0$ at $h= -\frac{2}{3}\,\bar{\nu }_1^2$ and $h=0$, respectively. In fact, for each value of $h \in (-\frac{2}{3}\,\bar{\nu }_1^2, 0)$, one can find a point corresponding to $M(h,\nu ) = M_h(h,\nu ) = 0$. These points form a curve connecting the two points GH and DHL and tangent to the Hopf bifurcation curve at the point GH and to the homoclinic bifurcation curve at the point DHL. This curve is usually called double limit cycle bifurcation curve, denoted as DLC. The existence of this curve is proved by Dumortier et al. (1987), but no explicit formula or computational method given to determine the curve. Figure 19a is an exact bifurcation diagram for $D=0.2499$ and $\sigma =0.1$, where the double limit cycle bifurcation curve DLC is not shown since it is too close to the Hopf and homoclinic bifurcation curves. In order to clearly see the bifurcations we show a schematic general bifurcation diagram in Fig. 19b with associated phase portraits for $b_1>0$ and $0< \sigma \ll 1$. The case $b_1<0$ can be easily obtained from Fig. 19b as a reflection of this figure with stability changed.

We summarize the results for the codimension-3 BT bifurcation as follows (see Fig. 19b).

• (a) Saddle-node bifurcation occurs along the circle, $\xi _2^2 + \xi _3^2 = \sigma ^2$, excluding the two points $S_1$ and $S_2$, while the two points $S_1$ and $S_2$ correspond to the BT bifurcation of condimension two.

• (b) Hopf bifurcation appears along the $\mathrm{H}$ curve excepting the point GH, while the point GH represent the generalized Hopf bifurcation.

• (c) Homoclinic bifurcation happens along the HL curve excluding the point DHL, while the DHL point denotes the degenerate homoclinic bifurcation.

• (d) Double limit cycle bifurcation occurs along the curve DLC, which connects the two points GH and DHL and is tangent to the curves H and HL at these two points, respectively.

5 Conclusions

In this contribution, we have provided a fairly complete dynamical analysis on a two-dimensional disease model, which can be used for either in-host disease modeling or epidemiologic modeling. In particular, we explored the dynamical behaviors of the system in a full four-dimensional parameter space. In particular, we have shown that when the reproduction number $R_0$ is varied near $\mathrm{R_0} = 1$, the system exhibits rich dynamical behaviors, including equilibrium solutions which exchange their stability at the transcritical point $R_0 = 1$. Both Hopf and generalized Hopf bifurcations can occur regardless of whether $R_0<1$ or $R_0 \ge 1$, and yield bistability or even tristability, showing that a simple model can still catch certain types of complexity in a disease model. This new type of bistability or tristability reveals a more complex but more realistic situation: The predicted state may not necessarily be an equilibrium (either the disease-free equilibrium or the endemic equilibrium), but may also involve disease periodic oscillation. This implies that the infective individuals and removed individuals are not necessarily fixed, but in a more realistically, mutually stable periodic motion.

Our study in this paper has also indicated that when $\mathrm{R_0<1}$, the system can have BT bifurcation leading to more complex dynamical behavior such as homoclinic orbit bifurcation. The analysis is based on the parametric normal form for BT bifurcation. We developed a novel computational method to derive the normal form for BT bifurcation of codimension two and three via one-step general nonlinear transformation. The homoclinic loop bifurcation, arising from BT bifurcation provides a new scenario/mechanism for generating recurrence, which is characterized by a special type of oscillation with slow and fast motions on the trajectories. This new mechanism is different with the one proposed in Zhang et al. (2013, 2014a, b).