1 Introduction

Human immunodeficiency virus (HIV), which mainly infects CD4 T cells and other target cells, threatens global human health and society development seriously (Perelson and Nelson 1999; Wodarz and Lloyd 1999). HIV, the cause of acquired immunodeficiency syndrome (AIDS), develops rapidly during the course of infection and the virus can evolve toward faster replication rates during late stages (Perelson and Nelson 1999; Regoes et al. 1998). There are approximately 6000 mm\(^-3\) white blood cells in a healthy body. It is estimated that between 1 and 6% of these are macrophages and approximately \(10\%\) are CD4 T cells Kirschner (1999). Clinical studies show that most viruses come from the infected macrophages during the late stages of the disease. Macrophages play an important role as a viral source and are considered as the second target cell of HIV (Perelson and Essunger 1997; Kirschner 1999). Moreover, macrophages are also the crucial immune responses and can clear certain HIV virus (Adams and Banks 2005; Kirschner 1999).

Mathematical models have made great contributions to getting insights into HIV infection dynamics in vivo. Great efforts were made to describe the interaction between HIV and CD4 T cells (Leenheer and Smith 2003; Hossein et al. 2014; Wang and Wang 2012; Hu and Liu 2010). Some other HIV models consider the interaction process of HIV not only with CD4 T cells but also with macrophages (Elaiw 2010; Adams and Banks 2005; Wodarz and Lloyd 1999; Shu et al. 2013). Generally speaking, the models with two target cells are more suitable than the models with only CD4 T cells (Elaiw 2010; Perelson and Nelson 1999; Kirschner 1999). Particularly, Elaiw proposed one model with two target cells and obtained the global asymptotical stabilities of the equilibria of the model by means of Lyapunov functions in Elaiw (2010). However, we should consider some other features including the proliferation of CD4 T cells stimulated by HIV virus and the loss term of the virus killed by macrophages (Ouattara 2005; Xia 2007). Based on above works, we introduce a four-dimensional model which is formulated by the following system of non-linear differential equations:

$$\begin{aligned} \frac{\mathrm{d}T}{\mathrm{d}t}= & {} \lambda _1-\delta _1 T-\beta _1 Tv+\beta _{12} Tv, \end{aligned}$$
(1)
$$\begin{aligned} \frac{\mathrm{d}T_m}{\mathrm{d}t}= & {} \lambda _2-\delta _2 T_m-\beta _2 T_mv+\beta _{22} T_mv, \end{aligned}$$
(2)
$$\begin{aligned} \frac{\mathrm{d}T^{*}}{\mathrm{d}t}= & {} \beta _1 Tv+\beta _2 T_mv -aT^{*}, \end{aligned}$$
(3)
$$\begin{aligned} \frac{\mathrm{d}v}{\mathrm{d}t}= & {} bT^{*}-cv-\beta _3T_m v. \end{aligned}$$
(4)

We briefly summarize the interpretation of different parameters in the model. \(T, T_m , T^{*},\) and v represent the uninfected CD4 T cells population, the uninfected macrophages population, the infected cells population, and the virus particles population in the blood, respectively. The terms \(\lambda _1\) and \(\lambda _2\) are the constant sources of new CD4 T cells and macrophages, respectively. \(\delta _1, \delta _2, a,\) and c denote the death rates of uninfected CD4 T cells, macrophages, infected cells, and virus particles, respectively. \(\beta _1 Tv\) represents the infection rate of uninfected CD4 T cells by virus. Because the number of CD4 T cells is large, it is reasonable to use the bilinear incidence rate (Elaiw 2010; Wang et al. 2014). \(\beta _{12} Tv\) is a proliferation term due to CD4 T cells immune response. \(\beta _2 T_mv\) and \(\beta _{22} T_mv\) could be explained in the same manner. \(bT^*\) is the source of HIV virus population and the constant b is the production rate of HIV virus by the infected CD4 T cells and infected macrophages. \(\beta _3T_m v\) is the loss term of HIV virus since macrophages can kill virus particles. c is the loss rate of HIV virus because of nature death or other immune response. Suppose all the parameters are nonnegative. Simultaneously, we give some brief definitions and reference values of the model parameters in Table 1. Denote \(\beta '_1=\beta _1-\beta _{12}>0\) and \(\beta '_2=\beta _2-\beta _{22}>0\). System (1–4) becomes the following system:

$$\begin{aligned} \frac{\mathrm{d}T}{\mathrm{d}t}= & {} \lambda _1-\delta _1 T-\beta '_1 Tv, \end{aligned}$$
(5)
$$\begin{aligned} \frac{\mathrm{d}T_m}{\mathrm{d}t}= & {} \lambda _2-\delta _2 T_m-\beta '_2T_mv, \end{aligned}$$
(6)
$$\begin{aligned} \frac{\mathrm{d}T^{*}}{\mathrm{d}t}= & {} \beta _1 Tv+\beta _2 T_mv -aT^{*}, \end{aligned}$$
(7)
$$\begin{aligned} \frac{\mathrm{d}v}{\mathrm{d}t}= & {} bT^{*}-cv-\beta _3T_m v. \end{aligned}$$
(8)
Table 1 Variables and parameters for the model
Full size table

In this paper, we first discuss the positively invariant set, the equilibria and the backward bifurcation. By analyzing the characteristic equations, the local asymptotic stability of an endemic equilibrium of the model is established. Letting \(\beta _3\) be the bifurcation parameter, we show that system (5–8) can undergo Hopf bifurcation, that is, a family of periodic solutions bifurcates from the infected equilibrium when \(\beta _3\) passes through a critical value. To prove the global asymptotical stabilities of the equilibria, we construct Lyapunov functions, which are similar to those in Korobeinikov (2004), Elaiw (2010), Li et al. (2011), Tsuyoshi et al. (2015), Hossein et al. (2014), Roy and Roy (2016).

The intracellular delays, from entry into CD4 T cells or macrophages to the production of new viruses, have been incorporated into biological models in many papers (Wang et al. 2014; Regoes et al. 1998; Culshaw and Ruan 2000; Wang and Zhou 2009; Yuan et al. 2012). In this paper, we establish a delayed model based on system (5–8) to study the influence of the intracellular delays on the infection transmission. We construct Lyapunov functions to prove the global asymptotical stabilities for the delayed model (McCluskey 2010; Huang et al. 2010). It is theoretically shown that time delay has no effect on the asymptotic stability of the equilibria under some conditions.

The paper is ordered as follows: Equilibria and backward bifurcation are studied in Sect. 2. Hopf bifurcation of the model is discussed in Sect. 3. The global asymptotic stabilities of the two equilibria are considered in Sect. 4. Section 5 deals with the extended model with the intracellular delays. Finally, Sect. 6 presents the conclusions of the work.

2 Equilibria and backward bifurcation

In the absence of virus, it is easy to show that the number of CD4 T cells approaches \(T_0=\frac{\lambda _1}{\delta _1}\) and the number of macrophages approaches \(T_{m0}=\frac{\lambda _2}{\delta _2}\). It is straightforward to prove the positive invariance of the nonnegative orthant \(R_{+}^4\) because of biological sense by system (5–8). Furthermore, from (5) and (6), we obtain:

$$\begin{aligned} \frac{\mathrm{d}T}{\mathrm{d}t}\le \lambda _1-\delta _1 T, \quad \frac{\mathrm{d}T_m}{\mathrm{d}t}\le \lambda _2-\delta _2 T_m. \end{aligned}$$

Therefore, we apply comparison lemma in Sharomi and Podder (2007) and obtain:

$$\begin{aligned} 0\le T\le \frac{\lambda _1}{\delta _1}+\left( T(0)-\frac{\lambda _1}{\delta _1}\right) e^{-\delta _1 t}, \quad 0\le T_m\le \frac{\lambda _2}{\delta _2}+\left( T_m(0)-\frac{\lambda _2}{\delta _2}\right) e^{-\delta _2t}, \end{aligned}$$

where \(T(0), T_m(0)\) are the initial conditions. It can be seen that the uninfected CD4 T cells and macrophages are always bounded. For simplicity, we may take

$$\begin{aligned} x=\frac{\beta _1}{\beta '_1}T+\frac{\beta _2}{\beta '_2}T_m +T^*,~ \delta =\min \left\{ \frac{\beta _1\delta _1}{\beta '_1},\frac{\beta _2\delta _2}{\beta '_2},a\right\} , ~\text {and} ~ \varpi =\frac{\beta _1\beta '_2\lambda _1+\beta '_1\beta _2\lambda _2}{\beta '_1\beta '_2}. \end{aligned}$$

From system (5-8), we have,

$$\begin{aligned} \frac{\mathrm{d}x}{\mathrm{d}t}\le \varpi -\delta x. \end{aligned}$$

Therefore, \(T^*\) is bounded. From (8), we know that v is upper bounded too, say by \(M= \frac{b\varpi }{c\delta }.\) Define the region,

$$\begin{aligned} P=\{(T, T_m,T^*,v)\in R_{+}^{4}: 0\le T\le T_0, 0\le T_m\le T_{m0}, x\le \frac{\varpi }{\delta }, v\le M \}. \end{aligned}$$

Then P is positively invariant with respect to system (5–8). Any solution of system (5–8) with initial point in P will stay in P. Furthermore, if \(T> T_0\) and \( T_m> T_{m0}\), either the solution of system (5-8) enters P in finite time, or T approaches \(T_0\) and \(T_m\) approaches \(T_{m0}\) asymptotically. Thus, P attracts all solutions in nonnegative orthant \(R_{+}^{4}\). This leads to the following result:

Proposition 1

The region P is positively invariant and attracting in nonnegative orthant \(R_{+}^{4}\) for system (5–8).

Next, we focus the dynamics behavior of system (5–8) in P. There always exists a disease-free equilibrium \(E_0(T_0, T_{m0},0,0)\), which represents the state with the absence of virus. The Jacobian matrix of system (5–8) at \(E_0\) is given as

$$\begin{aligned} J(E_0) =\left( \begin{array}{cccccclll} -\delta _1 &{} 0 &{} 0&{}-\beta '_1 \frac{\lambda _1}{\delta _1}\\ 0 &{} -\delta _2 &{}0 &{}-\beta '_2 \frac{\lambda _2}{\delta _2}\\ 0&{} 0&{}-a &{} \beta _1\frac{\lambda _1}{\delta _1}+\beta _2\frac{\lambda _2}{\delta _2} \\ 0&{}0&{}b&{}-c-\beta _3\frac{\lambda _2}{\delta _2} \end{array} \right) \end{aligned}$$

with the characteristic equation

$$\begin{aligned}&(\lambda +\delta _1)(\lambda +\delta _2)\left[ \lambda ^2+\left( a+c+\beta _3\frac{\lambda _2}{\delta _2}\right) \lambda \right. \\&\quad \left. +\frac{ac\delta _1\delta _2+\lambda _2\delta _1a \beta _3}{\delta _1\delta _2}\left( 1-\frac{\lambda _1 b\beta _1\delta _2+\lambda _2\delta _1 b\beta _2}{ac\delta _1\delta _2+\lambda _2\delta _1a \beta _3}\right) \right] =0. \end{aligned}$$

According to the fact \(| J(E_0)|=0\), it follows that \(\lambda _1 b\beta _1\delta _2+\lambda _2\delta _1 b\beta _2=ac\delta _1\delta _2+\lambda _2\delta _1a \beta _3\). So, we define the basic reproduction number as

$$\begin{aligned} R_0=\frac{\lambda _1 b\beta _1\delta _2+\lambda _2\delta _1 b\beta _2}{ac\delta _1\delta _2+\lambda _2\delta _1a \beta _3}, \end{aligned}$$

which represents the average number of secondary cases that one infected case can generate. It can be easily verified that, \(E_0\) is locally asymptotically stable when \(R_0<1\) and is unstable when \(R_0>1\) from the characteristic equation.

When \(a\beta _3=b\beta _2\), system (5–8) has no endemic equilibrium if \(R_0\le 1\) and has only one endemic equilibrium \(\bar{E}_1(\bar{T}_1, \bar{T}_{m1},\bar{T^*}_1, \bar{v}_1)\) if \(R_0>1\), where

$$\begin{aligned} \bar{T}_1=\frac{ac}{b\beta _1}, \quad \bar{T}_{m1}=\frac{\lambda _2}{\delta _2+\beta '_2\bar{v}_1}, \quad \bar{T^*}_1=\frac{ac\bar{v}_1}{b}+\beta _3 \bar{T}_{m1}\bar{v}_1, \quad \text {and} ~~\bar{v}_1=\frac{\lambda _1b\beta _1-ac\delta _1}{\beta '_1ac}. \end{aligned}$$

When \(a\beta _3\ne b\beta _2\), it can be computed that \(v\ne 0\) satisfies

$$\begin{aligned} \frac{b\beta _1\lambda _1}{\delta _1+\beta '_1v}+\frac{\lambda _2(b\beta _2-a\beta _3)}{\delta _2+\beta '_2v}=ac, \end{aligned}$$

which is equivalent to the quadratic equation

$$\begin{aligned} pv^2+qv+r =0, \end{aligned}$$
(9)

where

$$\begin{aligned} p= & {} ac\beta '_1\beta '_2, ~q=(ac\delta _1\beta '_2+ac\delta _2\beta '_1+\lambda _2a\beta '_1\beta _3-\lambda _2b\beta '_1\beta _2-\lambda _1b \beta _1 \beta '_2), \\ r= & {} (ac\delta _1\delta _2+\lambda _2\delta _1a \beta _3)(1-R_0). \end{aligned}$$

Therefore, we obtain the following result:

Proposition 2

When \(a\beta _3\ne b\beta _2\), system (5–8) has:

  1. (1)

    a unique endemic equilibrium if \(R_0>1\);

  2. (2)

    a unique endemic equilibrium if \(q<0\), and \(R_0=1\) or \(q^2-4pr=0\);

  3. (3)

    two endemic equilibria if \(R_0<1, q<0\) and \(q^2-4pr>0\);

  4. (4)

    no endemic equilibrium otherwise.

Item (3) in Proposition 2 indicates the possibility of backward bifurcation when \(R_0<1\) (Sharomi and Podder 2007; Zhang and Liu 2008; Feng and Castillo-Chavez 2000). To verify the existence of backward bifurcation, we let the discriminant \(q^2-4pr\) be 0 and solve the equation in term of \(R_0\). We obtain

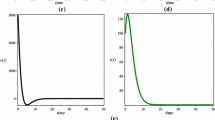
$$\begin{aligned} R^c_0=1-\frac{q^2}{4ac\beta '_1\beta '_2(ac\delta _1\delta _2+\lambda _2\delta _1a \beta _3)}. \end{aligned}$$

It can be shown that backward bifurcation occurs for the values of \(R_0\) if \(R^c_0<R_0<1\). We explore this phenomenon via numerical simulations and use the following parameter values: \(\lambda _1=8; \lambda _2=3; \delta _1=0.008; \delta _2=0.002; \beta '_1=0.000012; \beta '_2=0.0000211; \beta _1=0.0002; \beta _2=0.00025; a=0.48; b=50; c=4.3; \beta _3=0.05\) (Kirschner 1999; Lu and Huang 2014; Xia 2007). Then, we obtain \(R^c_0=0.2321\), \(R_0=0.7553\) and \(R^c_0<R_0<1\). It is clear that system (5–8) has a disease-free equilibrium \(E_0(1000, 1500, 0, 0)\) and two endemic equilibria, \(\hat{E}_1(278.5310,78.0510, 283.2904, 1.7268\times 10^{3})\) and \( \check{E}_1( 801.4765, 547.0186, 104.5313, 165.1315).\) The simulations depicted in Fig. 1 show that \(E_0\) and \(\hat{E}_1\) are locally asymptotically stable and \(\check{E}_1\) is unstable. As a result, a stable endemic equilibrium co-exists with a stable disease-free equilibrium for system (5–8) if \(R_0<1\). A bifurcation diagram is shown in Fig. 2. The above discussion is summarized below.

Theorem 1

System (5–8) exhibits backward bifurcation when \(q<0\), \(q^2-4pr>0\), and \(R^c_0<R_0<1\).

It should be noted that the term \(\beta _3T_mv\) plays an important role on the backward bifurcation. The phenomenon of backward bifurcation has been established in many papers (Sharomi and Podder 2007; Qesmi and Wu 2010; Feng and Castillo-Chavez 2000). It is worth stating that bilinear incidence in our model also can exhibit backward bifurcation (Hadeler and Driessche 1997; Wang and Wang 2012). This phenomenon has an important influence to control the disease. The existence of multiple endemic equilibria indicates that the asymptotical behavior of system (5–8) should depend on initial conditions. It is not enough for the eradication of the disease if \(R_0<1\). Therefore, it is equally important to identify possible backward bifurcation.

Fig. 1
figure 1

Simulations of system (5–8). We choose several different initial conditions

Full size image
Fig. 2
figure 2

Backward bifurcation of the endemic equilibria. The solid line and dashed line stand for stable equilibrium and unstable equilibrium, respectively

Full size image

3 Existence of Hopf bifurcation at the endemic equilibrium

When \(R_0>1\) and \(a\beta _3\ne b\beta _2\), it is easy to derive that system (5–8) has a unique endemic equilibrium \(\tilde{E}_1(\tilde{T}_1, \tilde{T}_{m1},\tilde{T_1^*}, \tilde{v}_1)\), where

$$\begin{aligned} \tilde{T}_1=\frac{\lambda _1}{\delta _1+\beta '_1\tilde{v}_1}, \tilde{T}_{m1}=\frac{\lambda _2}{\delta _2+\beta '_2\tilde{v}_1}, \tilde{T_1^*}=\frac{\beta _1\tilde{T}_1\tilde{v}_1 +\beta _2\tilde{T}_{m1}\tilde{v}_1}{a}, \tilde{v}_1=\frac{-q+\sqrt{q^2-4pr}}{2p}. \end{aligned}$$

Therefore when \(R_0>1\), we always have one endemic equilibrium \(E_1(T_1, T_{m1},{T_1^*}, {v}_1)\), where \(E_1=\bar{E}_1\) if the condition \(a\beta _3= b\beta _2\) is satisfied and \(E_1=\tilde{E}_1\) if the condition \(a\beta _3\ne b\beta _2\) is satisfied. The characteristic equation corresponding to \(E_1\) is given by

$$\begin{aligned} \lambda ^4+a_1\lambda ^3+a_2\lambda ^2+a_3\lambda +a_4=0, \end{aligned}$$
(10)

where

$$\begin{aligned} a_1=a_1(\beta _3)= & {} \delta _1+\beta '_1v_1+\delta _2+\beta '_2v_1+a+c+\beta _3T_{m1}, \\ a_2=a_2(\beta _3)= & {} (\delta _1+\beta '_1v_1)(\delta _2+\beta '_2v_1)+(\delta _1+\beta '_1v_1\\&+\,\delta _2+\beta '_2v_1)(a+c+\beta _3T_{m1})-\beta '_2\beta _3T_{m1}v_1,\\ a_3=a_3(\beta _3)= & {} (\delta _1+\beta '_1v_1)(\delta _2+\beta '_2v_1)(a+c+\beta _3T_{m1})+b\beta '_2\beta _2T_{m1}v_1+b\beta '_1T_1\beta _1v_1 \\&-\,\beta '_2\beta _3T_{m1}v_1(a+\delta _1+\beta '_1v_1),\\ a_4=a_4(\beta _3)= & {} b\beta '_2\beta _2T_{m1}v_1(\delta _1+\beta '_1v_1)+b\beta '_1\beta _1T_1v_1(\delta _2+\beta '_2v_1)\\&-\,\beta '_2\beta _3T_{m1}v_1a(\delta _1+\beta '_1v_1). \end{aligned}$$

By the Routh–Hurwitz criterion, it follows that all eigenvalues of Eq. (10) have negative real parts if and only if

$$\begin{aligned} a_1>0, ~a_4>0,~ a_1a_2>a_3, ~\text {and} ~~ a_3(a_1a_2-a_3)>a^2_1a_4. \end{aligned}$$

By simply calculating, we derive that \(a_1>0, a_2>0, \) and \(a_1a_2>a_3\). Moreover, when \(a\beta _3= b\beta _2\), we can obtain \(a_4>0. \) So we derive the following proposition:

Proposition 3

When \(R_0>1\), the infected equilibrium \(E_1\) of system (5–8) is locally asymptotically stable if

$$\begin{aligned} a_4>0, ~~a_3(a_1a_2-a_3)>a^2_1a_4. \end{aligned}$$
(11)

In the following, we discuss the conditions for which \(E_1\) enters into Hopf bifurcation.

Theorem 2

Suppose \(a_3>0, a_4>0\) and \(R_0>1\). If there exists a critical value \(\beta _{30}>0\) such that \(\phi (\beta _{30})=0\) and \(\phi '(\beta _{30})\ne 0\), Hopf bifurcation occurs at \(E_1\) of system (5–8) when \(\beta _{3}\) passes through \(\beta _{30}\). That is, periodic solutions bifurcate from \(E_1\).

Proof

Suppose \(a_3>0\) and \(a_4>0\). Define the continuously differentiable function of \(\beta _3\):

$$\begin{aligned} \phi (\beta _3)=a_3(\beta _3)(a_1(\beta _3)a_2(\beta _3)-a_3(\beta _3))-a^2_1(\beta _3)a_4(\beta _3). \end{aligned}$$

If there exists \(\phi (\beta _{30})=0\), Eq. (10) becomes

$$\begin{aligned} (\lambda ^2+\frac{a_3(\beta _{30})}{a_1(\beta _{30})})(\lambda ^2+a_1(\beta _{30})\lambda +\frac{a_1(\beta _{30})a_4(\beta _{30})}{a_3(\beta _{30})})=0. \end{aligned}$$
(12)

It is easy to show that (12) has a pair of purely imaginary roots and either another pair of complex roots with negative real parts or two negative real roots. Since \(\phi (\beta _3)\) is one continuous function of all its roots in \(\beta _3\), we can derive that Eq. (10) has a pair of complex conjugate roots in a neighborhood of \(\beta _{30}\), denoted by \(\lambda _1\) and \(\lambda _2\). They are conjugated purely imaginary roots at \(\beta _3=\beta _{30} \). The transversality condition (Roy et al. 2017; Greenhalgh 1997; Liu 1994)

$$\begin{aligned} \frac{\mathrm{d}(Re\lambda _1(\beta _3))}{\mathrm{d}\beta _3}|_{\beta _{30}}\ne 0\end{aligned}$$

is equivalent to

$$\begin{aligned} \phi '(\beta _{30})=\frac{\mathrm{d}(\phi (\beta _3))}{\mathrm{d}\beta _3}|_{\beta _{30}}\ne 0. \end{aligned}$$

This completes the proof.

We present some numerical results of system (5–8) for different values of \(\beta _3\) and use the parameter values as the same as in Sect. 2 except for \(\delta _2=0.008\) and \(\beta _3\). Let initial values be (500, 200, 300, 100). We obtain \(\beta _{30}\approx 0.057\) from \(\phi (\beta _3)=0\). Numerical simulations show that \(E_1\) is locally asymptotically stable if \(\beta _3=0.05< \beta _{30}\) (see Fig. 3). When \(\beta _3=\beta _{30}\), \(E_1\) loses its stability and Hopf bifurcation occurs. When \(\beta _3=0.058>\beta _{30}\), \(E_1\) becomes unstable and there are periodic solutions surrounding \(E_1\) (see Fig. 4).

Fig. 3
figure 3

Simulations of system (5–8). We choose \(\beta _3=0.05<\beta _{30}\). \( E_1 \) is locally asymptotically stable

Full size image
Fig. 4
figure 4

Simulations of system (5–8). We choose \(\beta _3=0.058>\beta _{30}\). The bifurcating periodic solutions from \(E_1\) occur

Full size image

4 Global stability of two equilibria

Theorem 3

If \(R_0\le 1\) and \(b\beta _2\ge a\beta _3\), the disease-free equilibrium \(E_0\) of system (5–8) is globally asymptotically stable in P.

Proof

Define a Lyapunov function

$$\begin{aligned} L_1=\frac{\beta _1}{\beta '_1} \left( T-T_0-T_0\ln \frac{T}{T_0}\right) + \frac{b\beta _2-a\beta _3}{b\beta '_2} \left( T_m-T_{m0}-T_{m0}\ln \frac{T_m}{T_{m0}}\right) +T^*+\frac{a}{b}v. \end{aligned}$$

Calculating the time derivative of \(L_1\) along the solution of system (5–8), we obtain

$$\begin{aligned} \frac{\mathrm{d}L_1}{\mathrm{d}t}= & {} \frac{\beta _1}{\beta '_1}\left( \lambda _1-\delta _1 T-\beta '_1 Tv\right) \left( 1-\frac{T_0}{T}\right) \nonumber \\&+ \frac{b\beta _2-a\beta _3}{b\beta '_2}\left( \lambda _2-\delta _2 T_m-\beta '_2T_mv\right) \left( 1-\frac{T_{m0}}{T_m}\right) \nonumber \\&+\,\beta _1 Tv+\beta _2 T_mv -aT^{*}+aT^{*}-\frac{ac}{b}v-\frac{a\beta _3}{b}T_mv. \end{aligned}$$
(13)

Note that \(\lambda _1=\delta _1 T_0\) and \(\lambda _2=\delta _2 T_{m0} \). It follows from (13) that

$$\begin{aligned} \frac{\mathrm{d}L_1}{\mathrm{d}t}= & {} \frac{\beta _1\lambda _1}{\beta '_1}\left( 2-\frac{T}{T_0}-\frac{T_0}{T}\right) \\&+ \frac{b\beta _2-a\beta _3}{b\beta '_2}\lambda _2\left( 2-\frac{T_m}{T_{m0}}-\frac{T_{m0}}{T_m}\right) +\frac{R_0-1}{\delta _1\delta _2b(ac\delta _1\delta _2+\lambda _2\delta _1a \beta _3)}v. \end{aligned}$$

Apparently, we can obtain \(2-\frac{T}{T_0}-\frac{T_0}{T}\le 0\) and \(2-\frac{T_m}{T_{m0}}-\frac{T_{m0}}{T_m}\le 0\). So we obtain \(\frac{\mathrm{d}L_1}{\mathrm{d}t}\le 0\) if \(R_0\le 1\). The largest compact invariant set in \(\{(T, T_m,T^*,v)\in P: \frac{\mathrm{d}L_1}{\mathrm{d}t}= 0 \}\) is the singleton \(\{E_0\}\). Using the Lasalle invariant principle, we derive that all solutions with initial conditions in P converge to \(E_0\). We complete the proof.

From Theorem 3, we obtain that the virus can be cleared under some conditions. In addition, we easily derive that system (5–8) does not exhibit backward bifurcation if \(b\beta _2\ge a\beta _3\).

Theorem 4

If \(R_0> 1\), \(b\beta _2> a\beta _3\) and \(b\lambda _1\beta _1\beta '_2\beta _3\le \beta '_1(b\beta _2- a\beta _3)(c\delta _2-\lambda _2\beta _3)\), the endemic equilibrium \(E_1\) of system (5–8) is globally asymptotically stable in P.

Proof

We consider a Lyapunov function

$$\begin{aligned} L_2= & {} \frac{\beta _1}{\beta '_1} \left( T-T_1-T_1\ln \frac{T}{T_1}\right) + \frac{b\beta _2-a\beta _3}{b\beta '_2} \left( T_m-T_{m1}-T_{m1} \ln \frac{T_m}{T_{m1}}\right) \\&+\left( T^*-T^*_1-T^*_1\ln \frac{T^*}{T^*_1}\right) +\frac{a}{b}\left( v-v_1-v_1\ln \frac{v}{v_1}\right) . \end{aligned}$$

Calculating the time derivative of \(L_1\) along the solution of system (5–8), we obtain

$$\begin{aligned} \frac{\mathrm{d}L_2}{\mathrm{d}t}= & {} \frac{\beta _1}{\beta '_1}\left( \lambda _1-\delta _1 T-\beta '_1 Tv\right) \left( 1-\frac{T_1}{T}\right) +\frac{b\beta _2-a\beta _3}{b\beta '_2}\left( \lambda _2-\delta _2 T_m-\beta '_2T_mv\right) \left( 1-\frac{T_{m1}}{T_m}\right) \\&+\left( \beta _1 Tv+\beta _2 T_mv -aT^{*}\right) \left( 1-\frac{T^*_1}{T^*}\right) +\frac{a}{b}\left( bT^{*}-cv-\beta _3T_mv\right) \left( 1-\frac{v_{1}}{v}\right) . \end{aligned}$$

From system (5–8), we obtain that

$$\begin{aligned}&\lambda _1=\delta _1 T_1+\beta '_1 T_1v_1, \lambda _2=\delta _2 T_{m1}+\beta '_2T_{m1}v_1, \\&aT^{*}_1=\beta _1T_1v_1+\beta _2 T_{m1}v_1, b(\beta _1T_1+\beta _2T_{m1})=ac+a\beta _3T_{m1}. \end{aligned}$$

Then we get

$$\begin{aligned} \frac{\mathrm{d}L_2}{\mathrm{d}t}= & {} \frac{\beta _1\delta _1T_1}{\beta '_1}\left( 2-\frac{T}{T_1}-\frac{T_1}{T}\right) +\left( \frac{\left( {b\beta _2-a\beta _3}\right) \delta _2T_{m1}}{b\beta '_2}-\frac{a\beta _3T_{m1}v_1}{b}\right) \left( 2-\frac{T_m}{T_{m1}}-\frac{T_{m1}}{T_m}\right) \\&+\,\beta _1T_1v_1\left( 3-\frac{T_1}{T}-\frac{T^*_1Tv}{T^*T_1v_1}-\frac{T^*v_1}{T^*_1v}\right) +\beta _2T_{m1}v_1\left( 3-\frac{T_{m1}}{T}-\frac{T^*_1Tv}{T^*T_{m1}v_1}-\frac{T^*v_1}{T^*_1v}\right) . \end{aligned}$$

If \(b\beta _2> a\beta _3\) and \(b\lambda _1\beta _1\beta '_2\beta _3\le \beta '_1(b\beta _2- a\beta _3)(c\delta _2-\lambda _2\beta _3)\), we can obtain

$$\begin{aligned} v_1<\frac{b\lambda _1\beta _1\beta '_2+\lambda _2\beta '_1\left( b\beta _2- a\beta _3\right) }{ac\beta '_1\beta '_2}<\frac{\left( {b\beta _2-a\beta _3}\right) \delta _2}{a\beta _3\beta '_2}. \end{aligned}$$

Then, we have:

$$\begin{aligned} \frac{\left( {b\beta _2-a\beta _3}\right) \delta _2}{b\beta '_2}-\frac{a\beta _3v_1}{b}>0. \end{aligned}$$

Therefore, the endemic equilibrium \(E_1\) is globally asymptotically stable by the similar analysis in Theorem 3. Especially, we know \(E_1\) is globally asymptotically stable when \(\beta _3=0\). The proof is completed.

5 Analysis of the delayed model

In this section, we consider one differential equation model with a time delay, which denotes the time for the viruses from entry into CD4 T cells or macrophages to the production of new viruses. The model is given as follows:

$$\begin{aligned} \frac{\mathrm{d}T}{\mathrm{d}t}= & {} \lambda _1-\delta _1 T-\beta '_1 Tv, \end{aligned}$$
(14)
$$\begin{aligned} \frac{\mathrm{d}T_m}{\mathrm{d}t}= & {} \lambda _2-\delta _2 T_m-\beta '_2T_mv, \end{aligned}$$
(15)
$$\begin{aligned} \frac{\mathrm{d}T^{*}}{\mathrm{d}t}= & {} \beta _1 T(t-\tau )v(t-\tau )+\beta _2 T_m(t-\tau )v(t-\tau ) -aT^{*}, \end{aligned}$$
(16)
$$\begin{aligned} \frac{\mathrm{d}v}{\mathrm{d}t}= & {} bT^{*}-cv-\beta _3T_mv . \end{aligned}$$
(17)

The positive constant \(\tau \) represents the length of the delay. All the other parameters are the same as in system (5–8). The initial conditions are:

$$\begin{aligned} T(t)=\psi _1(t)\ge 0, T_m(t)=\psi _2(t)\ge 0 , T^*(0)= \psi _3\ge 0, v(t)=\psi _4(t)\ge 0, t\in [-\tau ,0], \end{aligned}$$

where \(\psi _3\) is a given constant, and \(\psi _1,\psi _2, \psi _4 \in C([-\tau , 0],R_{+})\) with \(R_{+}=[0, \infty )\).

Being similar to the analysis of system (5–8), we find system (14–17) always has one disease-free equilibrium \(E_0(T_0, T_{m0},0,0)\) and a unique positive equilibrium \(E_1(T_1, T_{m1}, T^*_1, v_1)\) if \(R_0>1\), where \( T_0, T_{m0}, T_1, T_{m1},T^*_1,\) and \(v_1\) are the same as in Sect. 2.

Let \(\bar{E}(\bar{T},\bar{T_m},\bar{T^*},\bar{v})\) be any equilibrium of system (14–17). Denote \( X =( T,T_m,T^*,v)^T. \) The linearized system in vector form is given as:

$$\begin{aligned} \frac{\mathrm{d}X}{\mathrm{d}t}=A_1X+A_2X(t-\tau ), \end{aligned}$$

where \(A_1\) and \(A_2\) are \(4 \times 4\) matrices given by:

$$\begin{aligned} A_1 =\left( \begin{array}{cccccclll} -\delta _1- \beta '_1\bar{v}&{} 0 &{} 0&{}-\beta '_1 \bar{T}\\ 0 &{} -\delta _2-\beta '_2\bar{v} &{}0 &{}-\beta '_2 \bar{T_m}\\ 0&{} 0&{}-a &{} 0 \\ 0&{}-\beta _3\bar{v}&{}b&{}-c-\beta _3\bar{T}_{m} \end{array} \right) \end{aligned}$$

and

$$\begin{aligned} A_2 =\left( \begin{array}{cccccclll} 0&{} 0 &{} 0&{}0\\ 0 &{} 0 &{}0 &{}0\\ \beta _1\bar{v}&{} \beta _2\bar{v}&{}0 &{} \beta _1\bar{T}+\beta _2\bar{T_m} \\ 0&{}0&{}0&{}0 \end{array} \right) . \end{aligned}$$

The characteristic equation for system (14–17) is given by:

$$\begin{aligned} \det (\lambda I-A_1-A_2e^{-\lambda \tau })=0. \end{aligned}$$

Theorem 5

The disease-free equilibrium \(E_0\) of system (14–17) is locally asymptotically stable for all \(\tau \ge 0\) when \(R_0<1\), and is unstable when \(R_0>1\).

Proof

For the disease-free equilibrium \(E_0\), the characteristic equation reduces to,

$$\begin{aligned}&\left( \lambda +\delta _1\right) \left( \lambda +\delta _2\right) \left( \lambda ^2+\left( a+c+\beta _3\frac{\lambda _2}{\delta _2}\right) \lambda \right. \nonumber \\&\quad \left. +\frac{ac\delta _1\delta _2+\lambda _2\delta _1a \beta _3}{\delta _1\delta _2}\left( 1-R_0 e^{-\lambda \tau }\right) \right) =0. \end{aligned}$$
(18)

When \(\tau =0\), we know that \(E_0\) is locally asymptotically stable if \(R_0<1\) and is unstable if \(R_0>1\) from former analysis. In the following, we discuss the case of \(\tau \ne 0\). Equation (18) has two negative solutions \(\lambda _1=-\delta _1\) and \(\lambda _2=-\delta _2\). The other eigenvalues of Eq. (18) satisfy the following transcendental equation:

$$\begin{aligned} \lambda ^2+\left( a+c+\beta _3\frac{\lambda _2}{\delta _2}\right) \lambda +\frac{ac\delta _1\delta _2+\lambda _2\delta _1a \beta _3}{\delta _1\delta _2}\left( 1-R_0 e^{-\lambda \tau }\right) =0. \end{aligned}$$
(19)

Denote,

$$\begin{aligned} F(\lambda )=\lambda ^2+\left( a+c+\beta _3\frac{\lambda _2}{\delta _2}\right) \lambda +\frac{ac\delta _1\delta _2+\lambda _2\delta _1a \beta _3}{\delta _1\delta _2}\left( 1-R_0 e^{-\lambda \tau }\right) . \end{aligned}$$

For the case of \(R_0>1\), we obtain \(F(0)<0\) and \(F(\lambda )\rightarrow +\infty \) (\(\lambda \rightarrow +\infty \)). Thus, Eq. (19) has at least one positive real root. So \(E_0\) is unstable. For the case of \(R_0<1\), we assume that \(\lambda =i\omega , ~~\omega >0.\) Substituting \(\lambda =i\omega \) into (19), we have:

$$\begin{aligned}&-\,\omega ^2+\left( a+c+\beta _3\frac{\lambda _2}{\delta _2}\right) i\omega +\frac{ac\delta _1\delta _2+\lambda _2\delta _1a \beta _3}{\delta _1\delta _2}-\frac{\lambda _1 b\beta _1\delta _2+\lambda _2\delta _1 b\beta _2}{\delta _1\delta _2}cos(\omega \tau )\\&\quad +\,i\frac{\lambda _1 b\beta _1\delta _2+\lambda _2\delta _1 b\beta _2}{\delta _1\delta _2}sin(\omega \tau )=0. \end{aligned}$$

We separate the real and imaginary parts and obtain,

$$\begin{aligned}&-\omega ^2+\frac{ac\delta _1\delta _2+\lambda _2\delta _1a \beta _3}{\delta _1\delta _2}=\frac{\lambda _1 b\beta _1\delta _2+\lambda _2\delta _1 b\beta _2}{\delta _1\delta _2}cos(\omega \tau ), \end{aligned}$$
(20)
$$\begin{aligned}&\left( a+c+\beta _3\frac{\lambda _2}{\delta _2}\right) \omega =-\frac{\lambda _1 b\beta _1\delta _2+\lambda _2\delta _1 b\beta _2}{\delta _1\delta _2}sin(\omega \tau ) . \end{aligned}$$
(21)

Adding the squared Eqs. (20) and (21), it follows that,

$$\begin{aligned} \omega ^4{+}\left( a^2{+}\left( c{+}\beta _3\frac{\lambda _2}{\delta _2}\right) ^2\right) \omega ^2+\left( \frac{ac\delta _1\delta _2+\lambda _2\delta _1a \beta _3}{\delta _1\delta _2}\right) ^2-\left( \frac{\lambda _1 b\beta _1\delta _2+\lambda _2\delta _1 b\beta _2}{\delta _1\delta _2}\right) ^2=0.\nonumber \\ \end{aligned}$$
(22)

If \(R_0<1\), Eq. (22) has no positive real roots and there is no \(i\omega (\omega \ne 0)\) satisfying Eq. (18). Equation (18) has roots with positive real parts if and only if it has purely imaginary roots by Rouch\(\acute{e}\)’s theorem (Culshaw and Ruan 2000). For all values of the delay \(\tau \ge 0\), all eigenvalues of Eq. (18) have negative real parts. This completes the proof.

Theorem 6

If \(R_0\le 1\) and \(b\beta _2\ge a\beta _3\), the disease-free equilibrium \(E_0\) of system (14–17) is globally asymptotically stable for any time delay \(\tau \ge 0\).

Proof

Define a Lyapunov function \(L_3\) as follows:

$$\begin{aligned} L_3= & {} \frac{\beta _1}{\beta '_1} \left( T-T_0-T_0\ln \frac{T}{T_0}\right) + \frac{b\beta _2-a\beta _3}{b\beta '_2} \left( T_m-T_{m0}-T_{m0}\ln \frac{T_m}{T_{m0}}\right) \\&+\,T^*+\frac{a}{b}v+U_1(t), \end{aligned}$$

where

$$\begin{aligned} U_1(t)=\int ^{t}_{t-\tau }\left[ \beta _1 T(s)v(s)+\beta _2 T_m(s)v(s)\right] \mathrm{d}s. \end{aligned}$$

We calculate the time derivative of \( U_1(t)\),

$$\begin{aligned} \frac{\mathrm{d}U_1(t)}{\mathrm{d}t}=\beta _1 T(t)v(t)+\beta _2 T_m(t)v(t)-\left[ \beta _1 T(t-\tau )v(t-\tau )+\beta _2 T_m(t-\tau )v(t-\tau )\right] . \end{aligned}$$

Calculating the time derivative of \(L_1\) along the solution of system (14-17), we obtain

$$\begin{aligned} \frac{\mathrm{d}L_3}{\mathrm{d}t}= & {} \frac{\beta _1}{\beta '_1}\left( \lambda _1-\delta _1 T-\beta '_1 Tv\right) \left( 1-\frac{T_0}{T}\right) {+}\frac{b\beta _2-a\beta _3}{b\beta '_2}\left( \lambda _2-\delta _2 T_m-\beta '_2T_mv\right) \left( 1-\frac{T_{m0}}{T_m}\right) \\&+\,\beta _1 T(t-\tau )v(t-\tau )+\beta _2 T_m(t-\tau )v(t-\tau )-aT^{*}+aT^{*}-\frac{ac}{b}v-\frac{a\beta _3}{b}T_mv \\&+\,\beta _1 T(t)v(t)+\beta _2 T_m(t)v(t)-\left[ \beta _1 T(t-\tau )v(t-\tau )+\beta _2 T_m(t-\tau )v(t-\tau )\right] . \end{aligned}$$

Note that \(\lambda _1=\delta _1 T_0\) and \(\lambda _2=\delta _2 T_{m0} \). Thus, we obtain

$$\begin{aligned} \frac{\mathrm{d}L_3}{\mathrm{d}t}= & {} \frac{\beta _1\lambda _1}{\beta '_1}\left( 2-\frac{T}{T_0}-\frac{T_0}{T}\right) \\&+ \frac{b\beta _2-a\beta _3}{b\beta '_2}\lambda _2\left( 2-\frac{T_m}{T_{m0}}-\frac{T_{m0}}{T_m}\right) +\frac{R_0-1}{\delta _1\delta _2b\left( ac\delta _1\delta _2+\lambda _2\delta _1a \beta _3\right) }v. \end{aligned}$$

So, it follows that \(\frac{\mathrm{d}L_3}{\mathrm{d}t} \le 0\) if \(R_0\le 1\) and \(b\beta _2\ge a\beta _3\). It is clear that \(E_{0}\) is stable. Furthermore, the largest compact invariant set is the singleton \(\{E_0\}\). Accordingly, it follows from LaSalle invariance principle that \(E_{0}\) is globally asymptotically stable. We complete the proof.

The characteristic equation for the linearized system around the infected equilibrium \(E_1\) is given by

$$\begin{aligned} \lambda ^4+m_1\lambda ^3+m_2\lambda ^2+m_3\lambda +m_4+(m_5\lambda ^2+m_6\lambda +m_7)e^{-\lambda \tau }=0, \end{aligned}$$
(23)

where

$$\begin{aligned} m_1= & {} \delta _1+\beta '_1v_1+\delta _2+\beta '_2v_1+a+c+\beta _3T_{m1},\nonumber \\ m_2= & {} \left( \delta _1+\beta '_1v_1\right) \left( \delta _2+\beta '_2v_1\right) +\left( \delta _1+\beta '_1v_1+\delta _2+\beta '_2v_1\right) \left( a+c+\beta _3T_{m1}\right) \\&+\,a\left( c+\beta _3T_{m1}\right) -\beta '_2\beta _3T_{m1}v_1,\\ m_3= & {} \left( \delta _1+\beta '_1v_1\right) \left( \delta _2+\beta '_2v_1\right) \left( a+c+\beta _3T_{m1}\right) +\left( \delta _1+\beta '_1v_1+\delta _2+\beta '_2v_1\right) a\left( c+\beta _3T_{m1}\right) \\&-\,\beta '_2\beta _3T_{m1}v_1\left( a+\delta _1+\beta '_1v_1\right) ,\\ m_4= & {} \left( \delta _1+\beta '_1v_1\right) \left( \delta _2+\beta '_2v_1\right) a\left( c+\beta _3T_{m1}\right) - \beta '_2\beta _3T_{m1}v_1 a\left( \delta _1+\beta '_1v_1\right) ,\\ m_5= & {} \,-b\left( \beta _1T_1+\beta _2T_{m1}\right) =-a\left( c+\beta _3T_{m1}\right) ,\\ m_6= & {} b\beta '_2T_{m1}\beta _2v_1+b\beta '_1T_1\beta _1v_1-a\left( c+\beta _3T_{m1}\right) \left( \delta _1+\beta '_1v_1+\delta _2+\beta '_2v_1\right) ,\\ m_7= & {} b\beta '_2T_{m1}\beta _2v_1\left( \delta _1+\beta '_1v_1\right) +b\beta '_1\beta _1T_1v_1\left( \delta _2+\beta '_2v_1\right) \\&\,-a\left( c+\beta _3T_{m1}\right) \left( \delta _1+\beta '_1v_1\right) \left( \delta _2+\beta '_2v_1\right) . \end{aligned}$$

Substituting \(\lambda =i\omega \) with \(\omega >0\) into (23) and separating the real and imaginary parts, we yield

$$\begin{aligned}&\omega ^4-m_2\omega ^2+m_4= (m_5\omega ^2-m_7){\text {cos}}\omega \tau -m_6\omega {\text {sin}}\omega \tau , \\&-m_1\omega ^3+m_3\omega = (m_7-m_5\omega ^2){\text {sin}}\omega \tau -m_6\omega {\text {cos}}\omega \tau . \end{aligned}$$

Adding up the squares of above both equations, we obtain

$$\begin{aligned} \omega ^8+p_1\omega ^6+p_2\omega ^4+p_3\omega ^2+p_4=0, \end{aligned}$$
(24)

where

$$\begin{aligned} p_1= & {} m^2_1-2m_2, ~p_2=m^2_2+2m_4-2m_1m_3-m^2_5,\\ p_3= & {} m^2_3+2m_5m_7-2m_2m_4-m^2_6, p_4=m^2_4-m^2_7. \end{aligned}$$

We put \(\omega ^2=\upsilon \) into Eq. (24) and obtain a fourth degree polynomial

$$\begin{aligned} \upsilon ^4+p_1\upsilon ^3+p_2\upsilon ^2+p_3\upsilon +p_4=0. \end{aligned}$$
(25)

By directly calculating, it is easy to show that \(p_1>0\) and \( p_4=(m_4-m_7)(m_4+m_7)>0\) if \(a_4>0\). Furthermore, we also obtain

$$\begin{aligned} p_2> & {} \left( \delta _1+\beta '_1v_1\right) ^2\left( \delta _2+\beta '_2v_1\right) ^2+a^2\left( \left( \delta _1+\beta '_1v_1\right) ^2+\left( \delta _2+\beta '_2v_1\right) ^2\right) >0, \\ p_3= & {} \left( \delta _1+\beta '_1v_1\right) ^2\left[ \beta '_2\beta _3T_{m1}v_1-\left( \delta _2+\beta '_2v_1\right) \left( c+\beta _3T_{m1}\right) \right] ^2+a^2\left( \beta '_2\beta _3T_{m1}v_1\right) ^2 \\&\,+2 a^2\beta '_2\beta _3T_{m1}v_1 \left( \delta _1+\beta '_1v_1\right) ^2 +a^2\left( \delta _1+\beta '_1v_1\right) ^2\left( \delta _2+\beta '_2v_1\right) ^2 \\&+\,2a\left( c+\beta _3T_{m1}\right) \left( b\beta _2T_{m1}\beta '_2v_1\left( \delta _2+\beta '_2v_1\right) +b\beta _1T_{1}\beta '_1v_1\left( \delta _1+\beta '_1v_1\right) \right) \\&-\,2a^2\left( \beta '_2\beta _3T_{m1}v_1\right) \left( \delta _2+\beta '_2v_1\right) \left( c+\beta _3T_{m1}\right) -\left( b\beta _2T_{m1}\beta '_2v_1+b\beta _1T_{1}\beta '_1v_1\right) ^2. \end{aligned}$$

If \( p_3\ge 0\), we know that Eq. (25) has no positive root. The real parts of all eigenvalues of Eq. (23) remain negative for all values of the delay \(\tau >0.\) Considering the special case of \(\beta _3=0\), we can obtain

$$\begin{aligned} p_3\ge (\delta _1+\beta '_1v_1)^2(\delta _2+\beta '_2v_1)^2(a^2+c^2)+(b\beta '_2T_{m1}\beta _2v_1-b\beta '_1T_2\beta _1v_1)^2>0. \end{aligned}$$

Summarizing the above analysis, we have the following theorem.

Theorem 7

Suppose that the conditions in (11), \(R_0>1\) and \(p_3\ge 0\) hold, the infected equilibrium \(E_1\) of system (14–17) is locally asymptotically stable for all \(\tau \ge 0\).

Although we introduce the delay, \(E_1\) is also locally asymptotically stable under some conditions. Under the circumstances, system (14–17) does not undergo Hopf bifurcations.

Theorem 8

If \(R_0> 1\), \(b\beta _2> a\beta _3\) and \(b\lambda _1\beta _1\beta '_2\beta _3\le \beta '_1(b\beta _2- a\beta _3)(c\delta _2-\lambda _2\beta _3)\), the endemic equilibrium \(E_1\) of system (14–17) is globally asymptotically stable for all \(\tau \ge 0\).

Proof

We consider a Lyapunov function

$$\begin{aligned} L_4= & {} \frac{\beta _1}{\beta '_1} \left( T-T_1-T_1\ln \frac{T}{T_1}\right) + \frac{b\beta _2-a\beta _3}{b\beta '_2} \left( T_m-T_{m1}-T_{m1} \ln \frac{T_m}{T_{m1}}\right) \\&+\left( T^*-T^*_1-T^*_1\ln \frac{T^*}{T^*_1}\right) \\&+\frac{a}{b}\left( v-v_1-v_1\ln \frac{v}{v_1}\right) +\beta _1 T_1v_1U_2+\beta _2 T_{m1}v_1U_3, \end{aligned}$$

where

$$\begin{aligned} U_2= & {} \int ^{t}_{t-\tau }\left[ \frac{T(s)v(s)}{ T_1v_1}-1-\ln \frac{ T(s)v(s)}{ T_1v_1}\right] \mathrm{d}s, \\ U_3= & {} \int ^{t}_{t-\tau }\left[ \frac{T_m(s)v(s)}{ T_{m1}v_1}-1-\ln \frac{T_m(s)v(s)}{ T_{m1}v_1}\right] \mathrm{d}s. \end{aligned}$$

Calculating the time derivative of \(L_4\) along the solution of system (14–17), we obtain

$$\begin{aligned} \frac{\mathrm{d}L_4}{\mathrm{d}t}= & {} \frac{\beta _1}{\beta '_1}\left( \lambda _1-\delta _1 T{-}\beta '_1 Tv\right) \left( 1-\frac{T_1}{T}\right) {+}\frac{b\beta _2-a\beta _3}{b\beta '_2}\left( \lambda _2-\delta _2 T_m-\beta '_2T_mv\right) \left( 1{-}\frac{T_{m1}}{T_m}\right) \\&+\left( \beta _1 T\left( t-\tau \right) v\left( t-\tau \right) +\beta _2 T_m\left( t-\tau \right) v\left( t-\tau \right) -aT^{*}\right) \left( 1-\frac{T^*_1}{T^*}\right) \\&+\frac{a}{b}\left( bT^{*}-cv-\beta _3T_mv\right) \left( 1-\frac{v_{1}}{v}\right) +\beta _1 T_1v_1\frac{\mathrm{d}U_2\left( t\right) }{\mathrm{d}t}+\beta _2 T_{m1}v_1\frac{\mathrm{d}U_3\left( t\right) }{\mathrm{d}t}. \end{aligned}$$

We calculate the time derivative of \(U_2(t)\) and \( U_3(t)\),

$$\begin{aligned} \frac{\mathrm{d}U_2(t)}{\mathrm{d}t}= & {} \frac{T(t)v(t)}{T_1v_1}-\frac{T(t-\tau )v(t-\tau )}{T_1v_1}+\ln \frac{T(t-\tau )v(t-\tau )}{T(t)v(t)},\\ \frac{\mathrm{d}U_3(t)}{\mathrm{d}t}= & {} \frac{T_{m}(t)v(t)}{T_{m}v_1}-\frac{T_{m}(t-\tau )v(t-\tau )}{T_{m1}v_1}+\ln \frac{T_{m1}(t-\tau )v(t-\tau )}{T_{m1}(t)v(t)}. \end{aligned}$$

From system (14–17), we obtain that

$$\begin{aligned} \lambda _1= & {} \delta _1 T_1+\beta '_1 T_1v_1, \lambda _2=\delta _2 T_{m1}+\beta '_2T_{m1}v_1,\nonumber \\ aT^{*}_1= & {} \beta _1T_1v_1+\beta _2 T_{m1}v_1, b(\beta _1T_1+\beta _2T_{m1})=ac+a\beta _3T_{m1}. \end{aligned}$$

Note that

$$\begin{aligned}&\ln \frac{T(t-\tau )v(t-\tau )}{T(t)v(t)}={\ln }\frac{T_1}{T(t)}+{\ln }\frac{T^*_1T(t-\tau )v(t-\tau )}{T^*(t)T_1v_1}+{\ln }\frac{T^*(t)v_1}{T^*_1v(t)}, \\&\ln \frac{T_{m}(t-\tau )v(t-\tau )}{T_{m}(t)v(t)}={\ln }\frac{T_{m1}}{T_{m}(t)}+{\ln }\frac{T^*_1T_{m}(t-\tau )v(t-\tau )}{T^*(t)T_{m1}v_1}+{\ln }\frac{T^*(t)v_1}{T^*_1v(t)}. \end{aligned}$$

Then we yield

$$\begin{aligned} \frac{\mathrm{d}L_4}{\mathrm{d}t}= & {} \frac{\beta _1\delta _1T_1}{\beta '_1}\left( 2-\frac{T}{T_1}-\frac{T_1}{T}\right) \\&+\left( \frac{\left( {b\beta _2-a\beta _3}\right) \delta _2T_{m1}}{b\beta '_2}-\frac{a\beta _3T_{m1}v_1}{b}\right) \left( 2-\frac{T_m}{T_{m1}}-\frac{T_{m1}}{T_m}\right) \\&+\,\beta _1T_1v_1\left( 1-\frac{T_1}{T}+\ln \frac{T_1}{T}\right) +\beta _1T_1v_1\left( 1-\frac{T^*_1T\left( t-\tau \right) v\left( t-\tau \right) }{T^*\left( t\right) T_1v_1}\right. \\&\left. +\,\ln \frac{T^*_1T\left( t-\tau \right) v\left( t-\tau \right) }{T^*\left( t\right) T_1v_1}\right) \\&+\,\beta _1T_1v_1\left( 1-\frac{T^*\left( t\right) v_1}{T^*_1v\left( t\right) }+\ln \frac{T^*\left( t\right) v_1}{T^*_1v\left( t\right) }\right) +\beta _2T_{m1}v_1\left( 1-\frac{T_{m1}}{T_{m}\left( t\right) }+\ln \frac{T_{m1}}{T_{m}\left( t\right) }\right) \\&+\,\beta _2T_{m1}v_1\left( 1-\frac{T^*_1T_m\left( t-\tau \right) v\left( t-\tau \right) }{T^*\left( t\right) T_{m1}v_1}+\ln \frac{T^*_1T_m\left( t-\tau \right) v\left( t-\tau \right) }{T^*\left( t\right) T_{m1}v_1}\right) \\&+\,\beta _2T_{m1}v_1\left( 1-\frac{T^*\left( t\right) v_1}{T^*_1v\left( t\right) }+\ln \frac{T^*\left( t\right) v_1}{T^*_1v\left( t\right) }\right) . \end{aligned}$$

It is known that the function \(f(x)=1-x+{\ln }x\) is always non-positive for \(x>0, \) and \(f(x)=0\) if and only if \(x=1\). Therefore, \(E_1\) is globally asymptotically stable by similar analysis as in Theorem 3. Especially, we know \(E_1\) is global asymptotically stable when \(\beta _3=0\). The proof is completed.

We use the parameter values in Sect. 2 except for \(\beta _3=0.01\). The condition (11), \( p_2>0\), and \( p_3>0\) are all satisfied. We also get \(R_0=3.1034>1\). It is shown that \(E_1 (164.3169, 40.7940, 319.2487, 1.3586\times 10^{3})\) is locally asymptotically stable for \(\tau =1 \) and \( \tau =10\) via simulating results (see Fig. 5). Time delay \(\tau \) does not change the stabilities of the equilibrium \(E_1\).

Fig. 5
figure 5

Simulation of system (14–17). We choose the initial condition (200, 100, 100, 500), \(\tau =1 \) and \(\tau =10\). \(E_1\) is locally asymptotically stable

Full size image

6 Discussions and conclusions

In the present paper, we propose a mathematical model, which describe the interactions of HIV virus and two target cells. The model can undergo the phenomenon of backward bifurcation if \(R_0<1\). Meanwhile, we find that Hopf bifurcation occurs under some conditions. By using Lyapunov functions, we obtain sufficient conditions for the global asymptotical stabilities of the equilibria. Especially, the two equilibria are globally asymptotically stable in case of \(\beta _3=0\). We cannot ignore the fact that macrophages really influence dynamics behavior of HIV virus from our analysis. What is more, we establish an extended model, and derive that the local asymptotical stabilities of the uninfected and infected equilibria are independent of the size of the delay if \(\beta _3=0\) by analyzing the transcendental characteristic equations. We also derive that the two equilibria are globally asymptotically stable for the delayed model under some conditions.

Finally, some interesting questions deserve further investigation about our model. One may consider the non-bilinear incidence rate for system (5–8). Moreover, we can study the influence of distributed delays not just discrete delays on system (14–17).