Dynamics of a Stochastic Predator–Prey Model with Stage Structure for Predator and Holling Type II Functional Response

Abstract

In this paper, we develop and study a stochastic predator–prey model with stage structure for predator and Holling type II functional response. First of all, by constructing a suitable stochastic Lyapunov function, we establish sufficient conditions for the existence and uniqueness of an ergodic stationary distribution of the positive solutions to the model. Then, we obtain sufficient conditions for extinction of the predator populations in two cases, that is, the first case is that the prey population survival and the predator populations extinction; the second case is that all the prey and predator populations extinction. The existence of a stationary distribution implies stochastic weak stability. Numerical simulations are carried out to demonstrate the analytical results.

1 Introduction

Classical predator–prey models typically assume that individual predators have the same capability to hunt prey. However, natural populations are more complex; while the mature individuals can hunt for food by themselves, the immature individuals are raised by their mature parents, and the rate at which they attack prey can be ignored. Particularly, we have in mind mammalian populations and some amphibious animals, which exhibit these two stages. Recently, predator–prey models with stage structure for the predator have received much attention and many authors have studied the dynamical behaviour of these models (Freeman and Wu 1991; Wang and Chen 1997; Wang 1997; Wang et al. 2001; Xiao and Chen 2004; Deng et al. 2014; Al-Omari 2015; Xu and Ma 2008; Georgescu et al. 2010). These models typically provide a richer dynamics, leading to better understanding of the interactions within the biological system while they also incorporate important physiological parameters, such as different death rates for immature and mature predators.

Moreover, all predator–prey models use some interaction functions especially Holling interaction functions between predators and preys based on reasonable biological assumptions because these functions do not allow the predators to grow arbitrarily fast, if prey is abundant (Sahoo and Poria 2014). Holling type II functional response captures density-dependent growth rate that is a concave function, leading to a saturation of prey consumption, and it measures the average feeding rate of a predator when it spends some time finding and processing the prey (Skalski and Gilliam 2001). The functional form $f(x)=\frac{bx}{1+mx}$ denotes the Holling type II functional response, b being the search rate and m being the search rate multiplied by the handling time. This type of functional response has been extensively used in biological systems, such as chemostat model (Monod 1950; Novick and Szilard 1950) and epidemic model (Zhang and Teng 2008; Xiang et al. 2009).

A predator–prey model with stage structure for predator and Holling type II functional response was developed by Wang and Chen (1997) and takes the form

$$\begin{aligned} \left\{ \begin{array}{l} x'=x(r-ax)-\displaystyle \frac{bx}{1+mx}z,\\ y'=\displaystyle \frac{kbx}{1+mx}z-(D+d_{1})y,\\ z'=Dy-d_{2}z, \end{array} \right. \end{aligned}$$

(1.1)

where $x=x(t)$ denotes the density of prey at time t and $y=y(t)$ and $z=z(t)$ denote the densities of immature and mature predators at time t, respectively. The parameters r, a, b, m, k, D, $d_{1}$ and $d_{2}$ are positive constants: r represents the intrinsic growth rate of the prey, a denotes the intraspecific competition rate of the prey, k $(k\le 1$ due to its biological significance) is the coefficient in converting prey into a new immature predator, $d_{1}$ and $d_{2}$ represent the death rates of immature and mature predators, respectively, and D denotes the rate at which immature predators become mature predators. By defining the basic reproduction number of the predator

$$\begin{aligned} R_{0}=\frac{kbDr}{d_{2}(a+mr)(D+d_{1})} \end{aligned}$$

as being the average number of offsprings produced by a mature predator in its lifetime when introduced in a prey-only environment with prey at carrying capacity, they have shown that if $R_{0}\le 1$, then the prey-only equilibrium $\left( \frac{r}{a},0,0\right)$ is globally asymptotically stable on $(0,\infty )^{3}$, while if $R_{0}>1$, then the prey-only equilibrium $\left( \frac{r}{a},0,0\right)$ is unstable; there is a unique positive equilibrium. These results can be found in the works (Georgescu and Hsieh 2006; Georgescu and Moroşanu 2006).

However, as a matter of fact, parameters involved in the system are not absolute constants, and they always fluctuate around some average values due to fluctuations in the environment (see e.g. Gard 1984, 1986), such as earthquakes, epidemics, tsunami, malaria and dengue fever. These events are so severe and strong that they can change the population size greatly in a short time. So these sudden events can be described as noise. Introducing environmental noise into the underlying population systems may be a good approach to describe these phenomena. May (2001) has revealed the fact that due to environmental fluctuations, the birth rates, death rates, carrying capacities, competition coefficients and other parameters involved in the system exhibit random fluctuations to a greater or lesser extent, and as a result, the equilibrium population distribution cannot attain a steady value, but fluctuates randomly around some average value (Ji and Jiang 2011). Hence, in order to fit to the reality better, many authors have introduced stochastic perturbations into deterministic models to reveal the effect of environmental variability on the population dynamics in mathematical biology (Zhang et al. 2014; Zhang and Jiang 2015; Liu and Wang 2011). By considering the effect of randomly fluctuating environment, Zhang et al. (2014) considered a predator–prey model with disease in the prey and discussed the asymptotic behaviour of the solution. Moreover, they investigated whether there exists a stationary distribution for the model and if it has the ergodic property. In Zhang and Jiang (2015), Zhang and Jiang discussed a stochastic Lotka–Volterra model with two predators competing for one prey. They obtained sufficient conditions guaranteeing the principle of coexistence for this perturbed model via Markov semigroup theory. Furthermore, they proved that the densities of the distributions of the solutions can converge in $L^{1}$ to an invariant density or can converge weakly to a singular measure under appropriate conditions. Liu and Wang (2011) investigated a stochastic stage-structured predator–prey model with Beddington–DeAngelis functional response. They gave sufficient conditions for global asymptotic stability of the system. For this reason, we study the dynamics of a stochastic predator–prey model with stage structure for predator and Holling type II functional response.

Since the intrinsic growth rate r and death rates $d_{i}$ $(i=1,2)$ are most influential in determining the fate of predators and preys, the literature has mainly focused on studying the effect of random perturbations on these parameters (Beddington and May 1977; Pang et al. 2008; Braumann 2008; Li and Mao 2009; Liu et al. 2011). Consequently, we follow the approach proposed by Liu et al. (2016) and perturb the parameters r, $-d_{1}$ and $-d_{2}$ by

$$\begin{aligned} r\rightarrow r+\sigma _{1}\dot{B}_{1}(t),~-d_{1}\rightarrow -d_{1}+\sigma _{2}\dot{B}_{2}(t),~-d_{2}\rightarrow -d_{2}+\sigma _{3}\dot{B}_{3}(t). \end{aligned}$$

So

$$\begin{aligned}&r\mathrm{d}t\rightarrow r\mathrm{d}t+\sigma _{1}\mathrm{d}B_{1}(t),~-d_{1}\mathrm{d}t\rightarrow -\,d_{1}\mathrm{d}t+\sigma _{2}\mathrm{d}B_{2}(t),~\\&\quad -\,d_{3}\mathrm{d}t\rightarrow -\,d_{3}\mathrm{d}t+\sigma _{3}\mathrm{d}B_{3}(t), \end{aligned}$$

where $B_{1}(t)$ $B_{2}(t)$, $B_{3}(t)$ are mutually independent standard Brownian motions with $B_{1}(0)=B_{2}(0)=B_{3}(0)=0$, $\sigma _{1}^{2}$, $\sigma _{2}^{2}$, $\sigma _{3}^{2}$ are the intensities of the environmental white noise. Then, system (1.1) becomes

$$\begin{aligned} \left\{ \begin{array}{l} \mathrm{d}x=\bigg [x(r-ax)-\displaystyle \frac{bx}{1+mx}z\bigg ]\mathrm{d}t+\sigma _{1}x\mathrm{d}B_{1}(t),\\ \mathrm{d}y=\bigg [\displaystyle \frac{kbx}{1+mx}z-(D+d_{1})y\bigg ]\mathrm{d}t+\sigma _{2}y\mathrm{d}B_{2}(t),\\ \mathrm{d}z=[Dy-d_{2}z]\mathrm{d}t+\sigma _{3}z\mathrm{d}B_{3}(t). \end{array} \right. \end{aligned}$$

(1.2)

Our paper is organized as follows: In Sect. 2, we give some known results, definitions and lemmas which will be used in the following analysis. In Sect. 3, we prove the existence and uniqueness of the global positive solution of system (1.2). In Sect. 4, we establish sufficient conditions for the existence and uniqueness of an ergodic stationary distribution of the solutions to system (1.2). In Sect. 5, we obtain sufficient conditions for extinction of the predator populations in two cases, that is, the first case is that the prey population survival and the predator populations extinction; the second case is that all the prey and predator populations extinction. In Sect. 6, numerical simulations are introduced to illustrate the theoretical results. Finally, some concluding remarks and future directions are presented to end this paper. In order to make our proofs easier to follow, we present some auxiliary results in Appendixes A, B and C.

Throughout this paper, unless otherwise specified, let $(\Omega ,\mathcal {F},\{\mathcal {F}_{t}\}_{t\ge 0},\mathbb {P})$ be a complete probability space with a filtration $\{\mathcal {F}_{t}\}_{t\ge 0}$ satisfying the usual conditions (i.e. it is increasing and right continuous, while $\mathcal {F}_{0}$ contains all $\mathbb {P}$-null sets) and we also let $B_{i}(t)$ be mutually independent standard Brownian motions defined on the complete probability space, $i=1,2,3$. Define

$$\begin{aligned} \mathbb {R}_{+}^{d}= & {} \{x=(x_{1},\ldots ,x_{d})\in \mathbb {R}^{d}:x_{i}>0,1\le i\le d\}~\text {and}~\overline{\mathbb {R}}_{+}^{d}\\= & {} \{x=(x_{1},\ldots ,x_{d})\in \mathbb {R}^{d}:x_{i}\ge 0,1\le i\le d\}. \end{aligned}$$

2 Preliminaries

In this section, we shall present some known results, definitions and lemmas which will be used later. Firstly, we give some basic theory of stochastic differential equations (see Mao 1997 for a detailed introduction).

Consider the d-dimensional Markov process described by the stochastic differential equation

$$\begin{aligned} d(X(t))=f(X(t))\mathrm{d}t+g(X(t))\text {d}B(t)~\text {for}~t\ge t_{0}, \end{aligned}$$

(2.1)

with the initial value $X(0)=X_{0}\in \mathbb {R}^{d}$, where B(t) denotes a d-dimensional standard Brownian motion defined on the complete probability space $(\Omega ,\mathcal {F},\{\mathcal {F}_{t}\}_{t\ge 0},\mathbb {P})$. Denote by $C^{2}(\mathbb {R}^{d};\overline{\mathbb {R}}_{+})$ the family of all nonnegative functions V(X) defined on $\mathbb {R}^{d}$ such that they are continuously twice differentiable in X. The differential operator L of Eq. (2.1) is defined by (Mao 1997)

$$\begin{aligned} L=\sum _{i=1}^{d}f_{i}(X,t)\frac{\partial }{\partial X_{i}}+\frac{1}{2}\sum _{i,j=1}^{d}\left[ g^\mathrm{T}(X,t)g(X,t)\right] _{ij}\frac{\partial ^{2}}{\partial X_{i}\partial X_{j}}. \end{aligned}$$

If L acts on a function $V\in C^{2}(\mathbb {R}^{d};\overline{\mathbb {R}}_{+})$, then

$$\begin{aligned} L(V(X))=V_{X}(X)f(X)+\frac{1}{2}\text {trace}\left[ g^\mathrm{T}(X)V_{XX}(X)g(X)\right] , \end{aligned}$$

where $V_{X}=\left( \frac{\partial V}{\partial X_{1}},\ldots ,\frac{\partial V}{\partial X_{d}}\right)$, $V_{XX}=\left( \frac{\partial ^{2}V}{\partial X_{i}\partial X_{j}}\right) _{d\times d}$. According to Itô’s formula (Mao 1997), if $X(t)\in \mathbb {R}^{d}$, then

$$\begin{aligned} d(V(X(t)))=L(V(X(t)))\mathrm{d}t+V_{X}(X(t))g(X(t))\mathrm{d}B(t). \end{aligned}$$

Definition 2.1

(Has’minskii 1980) The transition probability function P(s, x, t, A) is said to be time homogeneous (and the corresponding Markov process is called time homogeneous) if the function $P(s,x,t+s,A)$ is independent of s, where $0\le s\le t$, $x\in \mathbb {R}^{d}$ and $A\in \mathcal {B}$ and $\mathcal {B}$ denotes the $\sigma$-algebra of Borel sets in $\mathbb {R}^{d}$.

Let X(t) be a regular time-homogeneous Markov process in $\mathbb {R}^{d}$ described by the stochastic differential equation

$$\begin{aligned} d(X(t))=f(X(t))\mathrm{d}t+g(X(t))\mathrm{d}B(t). \end{aligned}$$

The diffusion matrix of the process X(t) is defined as follows

$$\begin{aligned} A(x)=(a_{ij}(x)),~a_{ij}(x)=g^{i}(x)g^{j}(x). \end{aligned}$$

Lemma 2.1

(Has’minskii 1980) The Markov process X(t) has a unique ergodic stationary distribution $\mu (\cdot )$ if there exists a bounded open domain $U\subset \mathbb {R}^{d}$ with regular boundary $\Gamma$, having the following properties:

$A_{1}$ The diffusion matrix A(x) is strictly positive definite for all $x\in U$.

$A_{2}$ There exists a nonnegative $C^{2}$-function V such that L(V) is negative on $\mathbb {R}^{d}\setminus U$.

3 Existence and Uniqueness of the Global Positive Solution

Since x, y, z in system (1.2) denote population densities, they should be nonnegative. So for further study, we should first give some condition under which system (1.2) has a unique global positive solution. To this end, we establish the following theorem.

Theorem 3.1

For any initial value $(x(0),y(0),z(0))\in \mathbb {R}_{+}^{3}$, there exists a unique solution (x(t), y(t), z(t)) of system (1.2) on $t\ge 0$ and the solution will remain in $\mathbb {R}_{+}^{3}$ with probability one, namely $(x(t),y(t),z(t))\in \mathbb {R}_{+}^{3}$ for all $t\ge 0$ almost surely (a.s.).

Proof

Since the coefficients of system (1.2) satisfy the local Lipschitz condition, then for any initial value $(x(0),y(0),z(0))\in \mathbb {R}_{+}^{3}$, there exists a unique local solution $(x(t),y(t),z(t))\in \mathbb {R}_{+}^{3}$ on $t\in [0,\tau _{e})$ a.s., where $\tau _{e}$ denotes the explosion time (Mao 1997). Now we shall prove that this solution is global, i.e. to prove that $\tau _{e}=\infty$ a.s. To this end, let $n_{0}\ge 1$ be sufficiently large such that x(0), y(0) and z(0) all lie within the interval $\left[ \frac{1}{n_{0}},n_{0}\right]$. For each integer $n\ge n_{0}$, define the stopping time as (Mao 1997) $\square$

$$\begin{aligned} \tau _{n}=\inf \bigg \{t\in [0,\tau _{e}):\min \{x(t),y(t),z(t)\}\le \frac{1}{n}~\text {or}~\max \{x(t),y(t),z(t)\}\ge n\bigg \}, \end{aligned}$$

where throughout this paper, we set $\inf \emptyset =\infty$ (as usual $\emptyset$ denotes the empty set). Clearly, $\tau _{n}$ is increasing as $n\rightarrow \infty$. Set $\tau _{\infty }=\lim _{n\rightarrow \infty }\tau _{n}$, whence $\tau _{\infty }\le \tau _{e}$ a.s. If we can verify that $\tau _{\infty }=\infty$ a.s., then $\tau _{e}=\infty$ and $(x(t),y(t),z(t))\in \mathbb {R}_{+}^{3}$ a.s. for all $t\ge 0$. That is to say, to complete the proof all we need to prove is that $\tau _{\infty }=\infty$ a.s. If this assertion is not true, then there exists a pair of constants $T>0$ and $\epsilon \in (0,1)$ such that

$$\begin{aligned} \mathbb {P}\{\tau _{\infty }\le T\}>\epsilon . \end{aligned}$$

Hence, there exists an integer $n_{1}\ge n_{0}$ such that

$$\begin{aligned} \mathbb {P}\{\tau _{n}\le T\}\ge \epsilon ,~\forall n\ge n_{1}. \end{aligned}$$

(3.1)

Define a $C^{2}$-function $V:\mathbb {R}_{+}^{3}\rightarrow \mathbb {R}_{+}$ by

$$\begin{aligned} V(x,y,z)=\bigg (x-c-c\ln \frac{x}{c}\bigg )+\frac{1}{k}(y-1-\ln y)+(z-1-\ln z), \end{aligned}$$

where c is a positive constant to be determined later. The nonnegativity of this function can be seen from

$$\begin{aligned} u-1-\ln u\ge 0,~\forall u>0. \end{aligned}$$

Applying Itô’s formula to V, we have

$$\begin{aligned} \begin{array}{l} d(V)=L(V)\mathrm{d}t+\sigma _{1}(x-c)\mathrm{d}B_{1}(t)+\displaystyle \frac{\sigma _{2}}{k}(y-1)\mathrm{d}B_{2}(t)+\sigma _{3}(z-1)\mathrm{d}B_{3}(t), \end{array} \end{aligned}$$

where, according to the definition of the operator L,

$$\begin{aligned} L(V)= & {} (x-c)\bigg [r-ax-\displaystyle \frac{bz}{1+mx}\bigg ]+\frac{c\sigma _{1}^{2}}{2}+\frac{1}{k}\bigg (1-\frac{1}{y}\bigg )\bigg [\frac{kbxz}{1+mx}-(D+d_{1})y\bigg ]\\&+\,\frac{\sigma _{2}^{2}}{2k } + \bigg (1-\frac{1}{z}\bigg )[Dy-d_{2}z]+\frac{\sigma _{3}^{2}}{2}\\= & {} -\,ax^{2}+(ac+r)x-\displaystyle \frac{bxz}{y(1+mx)}-\frac{Dy}{z}\\&+\,Dy-\frac{D+d_{1}}{k}y+\frac{cbz}{1+mx}-d_{2}z-cr+\frac{c\sigma _{1}^{2}}{2}+\frac{1}{k}\bigg (D+d_{1}+\frac{\sigma _{2}^{2}}{2}\bigg )\\&+\,d_{2}+\displaystyle \frac{\sigma _{3}^{2}}{2}\\\le & {} (-ax^{2}+(ac+r)x)+\displaystyle \frac{(k-1)D}{k}y-\frac{d_{1}}{k}y\\&+\,cbz-d_{2}z+\frac{c\sigma _{1}^{2}}{2}+\frac{1}{k}\bigg (D+d_{1}+\frac{\sigma _{2}^{2}}{2}\bigg ) +d_{2}+\displaystyle \frac{\sigma _{3}^{2}}{2}\\\le & {} (-ax^{2}+(ac+r)x)+\displaystyle \frac{(k-1)D}{k}y+cbz-d_{2}z+\frac{c\sigma _{1}^{2}}{2}\\&+\,\frac{1}{k}\bigg (D+d_{1}+\frac{\sigma _{2}^{2}}{2}\bigg ) +d_{2}+\displaystyle \frac{\sigma _{3}^{2}}{2}\\\le & {} \displaystyle \frac{(ac+r)^{2}}{4a}+(cb-d_{2})z+\frac{c\sigma _{1}^{2}}{2}+\frac{1}{k}\bigg (D+d_{1}+\frac{\sigma _{2}^{2}}{2}\bigg )+d_{2}+\frac{\sigma _{3}^{2}}{2}, \end{aligned}$$

where in the third inequality, we have used the fact that $0<k\le 1$. Choose $c=\frac{d_{2}}{b}$ such that $cb-d_{2}=0$, then we have

$$\begin{aligned} L(V)\le \frac{(ac+r)^{2}}{4a}+\frac{c\sigma _{1}^{2}}{2}+\frac{1}{k}\bigg (D+d_{1}+\frac{\sigma _{2}^{2}}{2}\bigg )+d_{2}+\frac{\sigma _{3}^{2}}{2}\le K, \end{aligned}$$

where K is a positive constant. Hence, one can obtain that

$$\begin{aligned} d(V(x,y,z))\le K\mathrm{d}t+\sigma _{1}(x-c)\mathrm{d}B_{1}(t)+\displaystyle \frac{\sigma _{2}}{k}(y-1)\mathrm{d}B_{2}(t)+\sigma _{3}(z-1)\mathrm{d}B_{3}(t). \end{aligned}$$

(3.2)

Integrating both sides of (3.2) from 0 to $\tau _{n}\wedge T=\min \{\tau _{n},T\}$ yields

$$\begin{aligned}&V(x(\tau _{n}\wedge T),y(\tau _{n}\wedge T),z(\tau _{n}\wedge T))\nonumber \\&\quad \le V(x(0),y(0),z(0))\nonumber \\&+\,K(\tau _{n}\wedge T)+\sigma _{1}\displaystyle \int _{0}^{\tau _{n}\wedge T}x(s)\mathrm{d}B_{1}(s)+\frac{\sigma _{2}}{k}\int _{0}^{\tau _{n}\wedge T}y(s)\mathrm{d}B_{2}(s)\nonumber \\&+\,\sigma _{3}\int _{0}^{\tau _{n}\wedge T}z(s)\mathrm{d}B_{3}(s)\nonumber \\&-\,\sigma _{1}cB_{1}(\tau _{n}\wedge T)-\displaystyle \frac{\sigma _{2}}{k}B_{2}(\tau _{n}\wedge T)-\sigma _{3}B_{3}(\tau _{n}\wedge T)\nonumber \\&{:}{=}\,V(x(0),y(0),z(0))+K(\tau _{n}\wedge T)+M_{1}(\tau _{n}\wedge T)+M_{2}(\tau _{n}\wedge T)+M_{3}(\tau _{n}\wedge T)\nonumber \\&-\,\sigma _{1}cB_{1}(\tau _{n}\wedge T)-\displaystyle \frac{\sigma _{2}}{k}B_{2}(\tau _{n}\wedge T)-\sigma _{3}B_{3}(\tau _{n}\wedge T), \end{aligned}$$

(3.3)

where

$$\begin{aligned}&M_{1}(\tau _{n}\wedge T)\\&\quad {:}{=}\,\sigma _{1}\int _{0}^{\tau _{n}\wedge T}x(s)\mathrm{d}B_{1}(s),~M_{2}(\tau _{n}\wedge T)\\&\quad {:}{=}\,\frac{\sigma _{2}}{k}\int _{0}^{\tau _{n}\wedge T}y(s)\mathrm{d}B_{2}(s),~M_{3}(\tau _{n}\wedge T)\\&\quad {:}{=}\,\sigma _{3}\int _{0}^{\tau _{n}\wedge T}z(s)\mathrm{d}B_{3}(s) \end{aligned}$$

are three local martingales.

Since the solution (x(t), y(t), z(t)) of system (1.2) is $\mathcal {F}_{t}$-adapted, taking the expectation on both sides of (3.3), we have

$$\begin{aligned} \mathbb {E}V(x(\tau _{n}\wedge T),y(\tau _{n}\wedge T),z(\tau _{n}\wedge T))\le V(x(0),y(0),z(0))+K\mathbb {E}(\tau _{n}\wedge T). \end{aligned}$$

Therefore,

$$\begin{aligned} \mathbb {E}V(x(\tau _{n}\wedge T),y(\tau _{n}\wedge T),z(\tau _{n}\wedge T))\le V(x(0),y(0),z(0))+KT. \end{aligned}$$

(3.4)

Let $\Omega _{n}=\{\omega \in \Omega :\tau _{n}=\tau _{n}(\omega )\le T\}$ for $n\ge n_{1}$ and by (3.1), we have $\mathbb {P}(\Omega _{n})\ge \epsilon$. Note that for every $\omega \in \Omega _{n}$, there is $x(\tau _{n},\omega )$ or $y(\tau _{n},\omega )$ or $z(\tau _{n},\omega )$ equals either n or $\frac{1}{n}$. Hence, $V(x(\tau _{n},\omega ),y(\tau _{n},\omega ),z(\tau _{n},\omega ))$ is no less than either

$$\begin{aligned}&\bigg (n-c-c\ln \frac{n}{c}\bigg )\wedge \bigg (n-1-\ln n\bigg )~\text {or}~\bigg (\frac{1}{n}-c-c\ln \frac{1}{nc}=\frac{1}{n}-c+c\ln (nc)\bigg )\\&\quad \,\wedge \bigg (\frac{1}{n}-1-\ln \frac{1}{n}=\frac{1}{n}-1+\ln n\bigg ). \end{aligned}$$

Consequently, one can get that

$$\begin{aligned}&V(x(\tau _{n},\omega ),y(\tau _{n},\omega ),z(\tau _{n},\omega ))\ge \bigg (n-c-c\ln \frac{n}{c}\bigg )\wedge \bigg (n-1-\ln n\bigg )\\&\quad \wedge \,\bigg (\frac{1}{n}-c+c\ln (nc)\bigg )\wedge \bigg (\frac{1}{n}-1+\ln n\bigg ). \end{aligned}$$

It follows from (3.4) that

$$\begin{aligned}&V(x(0),y(0),z(0))+KT\ge \mathbb {E}[I_{\Omega _{n}(\omega )}V(x(\tau _{n},\omega ),y(\tau _{n},\omega ),z(\tau _{n},\omega ))]\\ \\&\quad \ge \epsilon \bigg (n-c-\displaystyle c\ln \frac{n}{c}\bigg )\wedge \bigg (n-1-\ln n\bigg )\wedge \bigg (\frac{1}{n}-c+c\ln (nc)\bigg )\wedge \bigg (\frac{1}{n}-1+\ln n\bigg ), \end{aligned}$$

where $I_{\Omega _{n}}$ denotes the indicator function of $\Omega _{n}$. Letting $n\rightarrow \infty$, then one can see that

$$\begin{aligned} \infty >V(x(0),y(0),z(0))+KT=\infty , \end{aligned}$$

which leads to the contradiction and so we must have $\tau _{\infty }=\infty$ a.s. This completes the proof.

4 Existence of Ergodic Stationary Distribution

In this section, we shall establish sufficient conditions for the existence of a unique ergodic stationary distribution. We first give two lemmas which will be used later.

Lemma 4.1

If $l_{1},l_{2},l_{3}>0$, then

$$\begin{aligned} \displaystyle \frac{l_{1}+l_{2}+l_{3}}{3}\ge \root 3 \of {l_{1}l_{2}l_{3}}, \end{aligned}$$

(4.1)

and the equality holds if and only if $l_{1}=l_{2}=l_{3}$.

Proof

Obviously, (4.1) is equivalent to the following inequality $\square$

$$\begin{aligned} l_{1}^{3}+l_{2}^{3}+l_{3}^{3}\ge 3l_{1}l_{2}l_{3}. \end{aligned}$$

Since

$$\begin{aligned}&l_{1}^{3}+l_{2}^{3}+l_{3}^{3}-3l_{1}l_{2}l_{3}\\&\quad =(l_{1}+l_{2})^{3}-3(l_{1}^{2}l_{2}+l_{1}l_{2}^{2})+l_{3}^{3}-3l_{1}l_{2}l_{3}\\&\quad =(l_{1}+l_{2})^{3}+l_{3}^{3}-3(l_{1}^{2}l_{2}+l_{1}l_{2}^{2})-3l_{1}l_{2}l_{3}\\&\quad =(l_{1}+l_{2}+l_{3})\left[ (l_{1}+l_{2})^{2}-(l_{1}+l_{2})l_{3}+l_{3}^{2}\right] -3l_{1}l_{2}(l_{1}+l_{2}+l_{3})\\&\quad =(l_{1}+l_{2}+l_{3})(l_{1}^{2}+l_{2}^{2}+l_{3}^{2}-l_{2}l_{3}-l_{1}l_{3}-l_{1}l_{2})\\&\quad =\displaystyle \frac{1}{2}(l_{1}+l_{2}+l_{3})\left[ (l_{2}-l_{3})^{2}+(l_{3}-l_{1})^{2}+(l_{1}-l_{2})^{2}\right] \ge 0, \end{aligned}$$

then the assertion in Lemma 4.1 is true. This completes the proof.

Lemma 4.2

For any $\xi >0$, the following inequality holds

$$\begin{aligned} \xi +\frac{2}{3}\xi (1-\xi )\le \xi ^{\frac{1}{3}}. \end{aligned}$$

Proof

Since $\square$

$$\begin{aligned}&\xi +\displaystyle \frac{2}{3}\xi (1-\xi )-\xi ^{\frac{1}{3}}\\&\quad =\xi ^{\frac{1}{3}}\bigg [\xi ^{\frac{2}{3}}-1+\displaystyle \frac{2}{3}\xi ^{\frac{2}{3}}(1-\xi )\bigg ]\\&\quad =\xi ^{\frac{1}{3}}\left( \xi ^{\frac{1}{3}}-1\right) \bigg [\xi ^{\frac{1}{3}}+1-\displaystyle \frac{2}{3}\xi ^{\frac{2}{3}}\left( \xi ^{\frac{1}{3}}+\xi ^{\frac{2}{3}}+1\right) \bigg ]\\&\quad =\xi ^{\frac{1}{3}}\left( \xi ^{\frac{1}{3}}-1\right) \bigg [\xi ^{\frac{1}{3}}+1-\displaystyle \frac{2}{3}\xi -\frac{2}{3}\xi ^{\frac{4}{3}}-\frac{2}{3}\xi ^{\frac{2}{3}}\bigg ]\\&\quad =\displaystyle \frac{1}{3}\xi ^{\frac{1}{3}}\left( \xi ^{\frac{1}{3}}-1\right) \left( -2\xi ^{\frac{4}{3}}-2\xi -2\xi ^{\frac{2}{3}}+3\xi ^{\frac{1}{3}}+3\right) \\&\quad =\displaystyle \frac{1}{3}\xi ^{\frac{1}{3}}\left( \xi ^{\frac{1}{3}}-1\right) \bigg [-2(\xi -1)-2\xi ^{\frac{1}{3}}(\xi -1)-2\xi ^{\frac{2}{3}}+\xi ^{\frac{1}{3}}+1\bigg ]\\&\quad =-\displaystyle \frac{2}{3}\xi ^{\frac{1}{3}}\left( \xi ^{\frac{1}{3}}-1\right) \left( 1+\xi ^{\frac{1}{3}}\right) (\xi -1)-\frac{1}{3}\xi ^{\frac{1}{3}}\left( \xi ^{\frac{1}{3}}-1\right) ^{2}\left( 2\xi ^{\frac{1}{3}}+1\right) \\&\le 0, \end{aligned}$$

then the assertion in Lemma 4.2 is true. This completes the proof.

Theorem 4.1

Assume that $r>\frac{\sigma _{1}^{2}}{2}$ and $R_{0}^{S}=\frac{kbDr}{(a+mr)\left( D+d_{1}+\frac{\sigma _{2}^{2}}{2}\right) \left( d_{2}+\frac{\sigma _{3}^{2}}{2}\right) }\left( 1-\frac{\sigma _{1}^{2}}{2r}\right) ^{3}>1$, then for any initial value $(x(0),y(0),z(0))\in \mathbb {R} _{+}^{3}$, system (1.2) has a unique ergodic stationary distribution $\mu (\cdot )$.

Proof

In order to prove Theorem 4.1, it suffices to validate conditions $A_{1}$ and $A_{2}$ in Lemma 2.1. Now we prove the condition $A_{1}$. The diffusion matrix of system (1.2) is given by $\square$

$$\begin{aligned} A=\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} \sigma _{1}^{2}x^{2}&{}0&{}0\\ 0&{}\sigma _{2}^{2}y^{2}&{}0\\ 0&{}0&{}\sigma _{3}^{2}z^{2} \end{array}\right) . \end{aligned}$$

Obviously, the matrix A is positive definite for any compact subset of $\mathbb {R}_{+}^{3}$; then, the condition $A_{1}$ in Lemma 2.1 is satisfied.

Now we verify Assumption $A_{2}$ by constructing a $C^{2}$-function V(x, y, z) and an open bounded set U such that $L(V)\le -1$ on $\mathbb {R}_{+}^{3}\setminus U$. Define

$$\begin{aligned} V_{1}(x,y,z)= & {} -\ln y+c_{1}x-c_{2}\ln z, \\ V_{2}(x)= & {} \displaystyle \frac{2a}{3r}\frac{x}{r}-\frac{\ln x}{r}, \\ V_{3}(x,y,z)= & {} V_{1}(x,y,z)+\displaystyle 3\root 3 \of {\frac{c_{1}c_{2}kbDr^{2}}{ma}}V_{2}(x), \\ V_{4}(x,y,z)= & {} V_{3}(x,y,z)+\displaystyle \frac{3b}{d_{2}r}\root 3 \of {\frac{c_{1}c_{2}kbDr^{2}}{ma}}z+\frac{3bD}{d_{2}r(D+d_{1})}\root 3 \of {\frac{c_{1}c_{2}kbDr^{2}}{ma}}y, \\ V_{5}(x,y,z)= & {} \displaystyle \frac{1}{\theta +1}\bigg (x+\frac{y}{k}+\frac{D+d_{1}}{2Dk}z\bigg )^{\theta +1}, \end{aligned}$$

where $c_{1}$ and $c_{2}$ are positive constants to be determined later and $\theta >0$ is a sufficiently small constant satisfying $3^{\theta }\theta <\min \left\{ \frac{d_{1}}{4\sigma _{\max }},\frac{d_{2}}{2\sigma _{\max }}\right\}$ and $\sigma _{\max }:=\sigma _{1}^{2}\vee \sigma _{2}^{2}\vee \sigma _{3}^{2}=\max \left\{ \sigma _{1}^{2},\sigma _{2}^{2},\sigma _{3}^{2}\right\}$. Moreover, let

$$\begin{aligned} \tilde{V}(x,y,z)=MV_{4}(x,y,z)+V_{5}(x,y,z)-\ln y, \end{aligned}$$

where M is a positive constant satisfying the following condition

$$\begin{aligned} -M\lambda +B+D+d_{1}+\displaystyle \frac{\sigma _{2}^{2}}{2}=-2 \end{aligned}$$

(4.2)

and

$$\begin{aligned} \lambda :=\bigg (D+d_{1}+\displaystyle \frac{\sigma _{2}^{2}}{2}\bigg )\left( R_{0}^{S}-1\right) >0. \end{aligned}$$

Note that $\tilde{V}(x,y,z)$ is not only continuous, but also tends to $+\infty$ as (x, y, z) approaches the boundary of $\mathbb {R}_{+}^{3}$ and as $\Vert (x,y,z)\Vert \rightarrow \infty$, where $\Vert \cdot \Vert$ denotes the Euclidean norm of a point in $\mathbb {R}_{+}^{3}$. Therefore, it must be lower bounded and achieve this lower bound at a point $(x_{0},y_{0},z_{0})$ in the interior of $\mathbb {R}_{+}^{3}$. Then, we define a nonnegative $C^{2}$-function $V:\mathbb {R}_{+}^{3}\rightarrow \mathbb {R}_{+}\cup \{0\}$ as

$$\begin{aligned} V(x,y,z)= & {} \tilde{V}(x,y,z)-\tilde{V}(x_{0},y_{0},z_{0})=MV_{4}(x,y,z)\\&+\,V_{5}(x,y,z)-\ln y-\tilde{V}(x_{0},y_{0},z_{0}). \end{aligned}$$

It is shown in Appendix B that

$$\begin{aligned} L(V(x,y,z))\le -1,~\forall (x,y,z)\in \mathbb {R}_{+}^{3}\setminus U, \end{aligned}$$

where U is the bounded open set defined as

$$\begin{aligned} U=\bigg \{(x,y,z)\in \mathbb {R}_{+}^{3}:\epsilon<x<\frac{1}{\epsilon },\epsilon ^{3}<y<\frac{1}{\epsilon ^{3}},\epsilon<z<\frac{1}{\epsilon }\bigg \}, \end{aligned}$$

and $0<\epsilon <1$ is a sufficiently small number. Consequently, condition $A_{2}$ in Lemma 2.1 is satisfied and system (1.2) has a unique ergodic stationary distribution $\mu (\cdot )$. This completes the proof.

5 Extinction of the Predator Populations

In this section, we shall establish sufficient conditions for extinction of the predator populations in two cases, that is, the first case is that the prey population survival and the predator populations extinction; the second case is that all the prey and predator populations extinction. We establish the following two theorems.

Theorem 5.1

Let (x(t), y(t), z(t)) be the solution of system (1.2) with any initial value $(x(0),y(0),z(0))\in \mathbb {R}_{+}^{3}$. If $r>\frac{\sigma _{1}^{2}}{2}$, then for almost $\omega \in \Omega$, we have

$$\begin{aligned} \limsup _{t\rightarrow \infty }\frac{1}{t}\ln \bigg (\frac{D}{d_{2}(D+d_{1})}y(t)+\frac{\sqrt{R_{0}}}{d_{2}}z(t)\bigg )\le \upsilon ~\text {a.s.}, \end{aligned}$$

where $\upsilon =\min \{D+d_{1},d_{2}\}(\sqrt{R_{0}}-1)I_{\{\sqrt{R_{0}}\le 1\}}+\max \{D+d_{1},d_{2}\}(\sqrt{R_{0}}-1)I_{\{\sqrt{R_{0}}>1\}}+\frac{kbD\sigma _{1}}{(a+mr)(D+d_{1})}\left( \frac{r}{2R_ {0}}\right) ^{\frac{1}{2}}-\left( 2\left( \sigma _{2}^{-2}+\sigma _{3}^{-2}\right) \right) ^{-1}$ and $R_{0}=\frac{kbDr}{d_{2}(a+mr)(D+d_{1})}$. Particularly, if $\upsilon <0$, then the predator populations y and z die out exponentially with probability one, i.e.

$$\begin{aligned} \lim _{t\rightarrow \infty }y(t)=0,~\lim _{t\rightarrow \infty }z(t)=0~a.s. \end{aligned}$$

Furthermore, the distribution of x(t) converges weakly a.s. to the measure which has the density

$$\begin{aligned} \pi (x)=Q\sigma _{1}^{-2}x^{-2+\frac{2r}{\sigma _{1}^{2}}}\mathrm{e}^{-\frac{2a}{\sigma _{1}^{2}}x},~x\in (0,\infty ), \end{aligned}$$

where $Q=\bigg [\sigma _{1}^{-2}\left( \frac{\sigma _{1}^{2}}{2a}\right) ^{\frac{2r}{\sigma _{1}^{2}}-1}\Gamma \left( \frac{2r}{\sigma _{1}^{2}}-1\right) \bigg ]^{-1}$ is a constant satisfying $\int _{0}^{\infty }\pi (x)\mathrm{d}x=1$. This statement means that if $\mu _{t}(x)$ denotes the probability density of the prey population at time t, then for any (sufficiently smooth) function f(x),

$$\begin{aligned} \displaystyle \lim _{t\rightarrow \infty }\int _{\mathbb {R}_{+}}f(x)\mu _{t}(x)\mathrm{d}x=\int _{\mathbb {R}_{+}}f(x)\pi (x)\mathrm{d}x. \end{aligned}$$

(5.1)

Proof

Since for any initial value $(x(0),y(0),z(0))\in \mathbb {R}_{+}^{3}$, the solution of system (1.2) is positive, and we obtain $\square$

$$\begin{aligned} d(x)\le x(r-ax)\mathrm{d}t+\sigma _{1}x\mathrm{d}B_{1}(t). \end{aligned}$$

Consider the following auxiliary 1-dimensional stochastic differential equation

$$\begin{aligned} d(X)=X(r-aX)\mathrm{d}t+\sigma _{1}X\mathrm{d}B_{1}(t), \end{aligned}$$

(5.2)

with the initial value $X(0)=x(0)>0$.

Setting

$$\begin{aligned} g(x)=x(r-ax),~\sigma (x)=\sigma _{1}x,~x\in (0,\infty ), \end{aligned}$$

we compute that

$$\begin{aligned} \int \frac{g(u)}{\sigma ^{2}(u)}\mathrm{d}u=\frac{1}{\sigma _{1}^{2}}\int \bigg (\frac{r}{u}-a\bigg )\mathrm{d}u=\frac{1}{\sigma _{1}^{2}}(r\ln x-ax)+Q. \end{aligned}$$

Hence,

$$\begin{aligned} \mathrm{e}^{\int \frac{g(u)}{\sigma ^{2}(u)}\mathrm{d}u}=\mathrm{e}^{Q}x^{\frac{r}{\sigma _{1}^{2}}}\mathrm{e}^{-\frac{a}{\sigma _{1}^{2}}x}. \end{aligned}$$

Obviously, we obtain

$$\begin{aligned} \displaystyle \int _{0}^{\infty }\frac{1}{\sigma ^{2}(x)}\mathrm{e}^{\int _{1}^{x}\frac{2g(u)}{\sigma ^{2}(u)}\mathrm{d}u}\mathrm{d}x=\frac{\mathrm{e}^{\frac{2a}{\sigma _{1}^{2}}}}{\sigma _{1}^{2}}\int _{0}^{\infty }x^{-2}x^{\frac{2r}{\sigma _{1}^{2}}}\mathrm{e}^{-\frac{2a}{\sigma _{1}^{2}}x}\mathrm{d}x<\infty . \end{aligned}$$

(5.3)

Therefore, the condition of Theorem 1.16 in Kutoyants (2003) follows clearly from (5.3). So system (5.2) has the ergodic property, and the invariant density is given by

$$\begin{aligned} \pi (x)=Q\sigma _{1}^{-2}x^{-2+\frac{2r}{\sigma _{1}^{2}}}\mathrm{e}^{-\frac{2a}{\sigma _{1}^{2}}x},~x\in (0,\infty ), \end{aligned}$$

where $Q=\bigg [\sigma _{1}^{-2}\left( \frac{\sigma _{1}^{2}}{2a}\right) ^{\frac{2r}{\sigma _{1}^{2}}-1}\Gamma \left( \frac{2r}{\sigma _{1}^{2}}-1\right) \bigg ]^{-1}$ is a constant satisfying $\int _{0}^{\infty }\pi (x)\mathrm{d}x=1$.

Next, we will prove statement (5.1). In order to prove statement (5.1), we only need to validate conditions $A_{1}$ and $A_{2}$ in Lemma 2.1. We first prove the condition $A_{1}$. The diffusion matrix A of system (5.2) is positive definite for any compact subset of $\mathbb {R}_{+}$, so the condition $A_{1}$ in Lemma 2.1 holds.

Now we prove the condition $A_{2}$. To this end, let us define a $C^{2}$-function $\bar{V}:\mathbb {R}_{+}\rightarrow \mathbb {R}$ as

$$\begin{aligned} \bar{V}(X)=\tilde{M}(-\ln X+X)+X, \end{aligned}$$

where $\tilde{M}$ is a positive constant satisfying the following condition

$$\begin{aligned} \tilde{M}=\displaystyle \frac{2}{r-\frac{\sigma _{1}^{2}}{2}}. \end{aligned}$$

(5.4)

Note that $\bar{V}(X)$ is not only continuous, but also tends to $+\infty$ as X approaches the boundary of $\mathbb {R}_{+}$ and as $|X|\rightarrow \infty$, where $|\cdot |$ denotes the modulus of a point in $\mathbb {R}_{+}$. Thus, it must be lower bounded and achieve this lower bound at a point $X_{0}$ in the interior of $\mathbb {R}_{+}$. Then, we can define a nonnegative $C^{2}$-function $V:\mathbb {R}_{+}\rightarrow \mathbb {R}_{+}\cup \{0\}$ as

$$\begin{aligned} V(X)=\bar{V}(X)-\bar{V}(X_{0})=\tilde{M}(-\ln X+X)+X-\bar{V}(X_{0}). \end{aligned}$$

(5.5)

Applying Itô’s formula to (5.5) leads to

$$\begin{aligned} L(V)=-\tilde{M}\bigg (r-\displaystyle \frac{\sigma _{1}^{2}}{2}\bigg )+\tilde{M}aX+rX-aX^{2}. \end{aligned}$$

Define a bounded open set $U_{\epsilon }$ as

$$\begin{aligned} U_{\epsilon }=\bigg \{X\in \mathbb {R}_{+}:\epsilon<X<\frac{1}{\epsilon }\bigg \}, \end{aligned}$$

where $0<\epsilon <1$ is a sufficiently small number. In the set $\mathbb {R}_{+}\setminus U_{\epsilon }$, we can choose $\epsilon$ sufficiently small such that the following conditions hold

$$\begin{aligned} 0<\epsilon \le \displaystyle \frac{1}{\tilde{M}a+r}, \end{aligned}$$

(5.6)

$$\begin{aligned} -\displaystyle \frac{a}{2\epsilon ^{2}}+\sup _{X\in \mathbb {R}_{+}}\bigg \{-\frac{a}{2}X^{2}+\tilde{M}aX+rX\bigg \}\le -1. \end{aligned}$$

(5.7)

For convenience, we can divide $U_{\epsilon }^{c}=\mathbb {R}_{+}\setminus U_{\epsilon }$ into two domains,

$$\begin{aligned} U_{\epsilon }^{1}=\{X\in \mathbb {R}_{+}:0<X\le \epsilon \},~U_{\epsilon }^{2}=\bigg \{X\in \mathbb {R}_{+}:X\ge \frac{1}{\epsilon }\bigg \}. \end{aligned}$$

Obviously, $U_{\epsilon }^{c}=U_{\epsilon }^{1}\cup U_{\epsilon }^{2}$. Next, we prove that $L(V(X))\le -1$ for any $X\in U_{\epsilon }^{c}$, which is equivalent to proving it on the above two domains, respectively.

Case 1 For any $X\in U_{\epsilon }^{1}$, we have

$$\begin{aligned} L(V)\le -\tilde{M}\bigg (r-\displaystyle \frac{\sigma _{1}^{2}}{2}\bigg )+\tilde{M}aX+rX\le -\tilde{M}\bigg (r-\displaystyle \frac{\sigma _{1}^{2}}{2}\bigg )+(\tilde{M}a+r)\epsilon \le -2+1=-1, \end{aligned}$$

(5.8)

which follows from (5.4) and (5.6). Therefore,

$$\begin{aligned} L(V)\le -1~\text {for~any}~X\in U_{\epsilon }^{1}. \end{aligned}$$

Case 2 For any $X\in U_{\epsilon }^{1}$, we obtain

$$\begin{aligned} L(V)\le & {} -aX^{2}+\tilde{M}aX+rX\nonumber \\= & {} -\displaystyle \frac{a}{2}X^{2}-\frac{a}{2}X^{2}+\tilde{M}aX+rX\nonumber \\\le & {} -\,\displaystyle \frac{a}{2}X^{2}+\sup _{X\in \mathbb {R}_{+}}\bigg \{-\frac{a}{2}X^{2}+\tilde{M}aX+rX\bigg \}\nonumber \\&\quad \le -\displaystyle \frac{a}{2\epsilon ^{2}}+\sup _{X\in \mathbb {R}_{+}}\bigg \{-\frac{a}{2}X^{2}+\tilde{M}aX+rX\bigg \}\nonumber \\&\quad \le -1, \end{aligned}$$

(5.9)

which follows from (5.7). Hence,

$$\begin{aligned} L(V)\le -1~\text {for~any}~X\in U_{\epsilon }^{2}. \end{aligned}$$

Clearly, from (5.8) and (5.9), we get that for a sufficiently small $\epsilon$,

$$\begin{aligned} L(V(X))\le -1,~\forall X\in \mathbb {R}_{+}\setminus U_{\epsilon }. \end{aligned}$$

Consequently, the condition $A_{2}$ in Lemma 2.1 holds and system (5.2) has a unique ergodic stationary distribution $\mu _{t}(x)$. In view of Theorem 4.3 of Khasminskii (2012), p.117, we can immediately obtain statement (5.1).

Let X(t) be the solution of Eq. (5.2) with the initial value $X(0)=x(0)>0$; then by the comparison theorem of 1-dimensional stochastic differential equation (Peng and Zhu 2006), we have $x(t)\le X(t)$ for any $t\ge 0$ a.s.

Moreover, let

$$\begin{aligned} \sqrt{R_{0}}(\omega _{1},\omega _{2})=(\omega _{1},\omega _{2})M_{0}, \end{aligned}$$

where $(\omega _{1},\omega _{2})=\left( \frac{D}{d_{2}},\sqrt{R_{0}}\right)$ and $M_{0}=\left( \begin{array}{ccccc} 0&{}\displaystyle \frac{kbr}{(a+mr)(D+d_{1})}\\ \displaystyle \frac{D}{d_{2}}&{}0 \end{array}\right)$.

Define a $C^{2}$-function $V:\mathbb {R}_{+}^{2}\rightarrow \mathbb {R}_{+}$ as

$$\begin{aligned} V(y,z)=\alpha _{1}y+\alpha _{2}z, \end{aligned}$$

where $\alpha _{1}=\frac{\omega _{1}}{D+d_{1}}$, $\alpha _{2}=\frac{\omega _{2}}{d_{2}}$. Making use of Itô’s formula to differentiate $\ln V$ leads to

$$\begin{aligned} d(\ln V)=L(\ln V)\mathrm{d}t+\displaystyle \frac{1}{V}(\alpha _{1}\sigma _{2}y\mathrm{d}B_{2}(t)+\alpha _{2}\sigma _{3}z\mathrm{d}B_{3}(t)), \end{aligned}$$

(5.10)

where

$$\begin{aligned} L(\ln V)=\frac{\alpha _{1}}{V}\bigg [\frac{kbxz}{1+mx}-(D+d_{1})y\bigg ]+\frac{\alpha _{2}}{V}[Dy-d_{2}z]-\frac{\alpha _{1}^{2}\sigma _{2}^{2}y^{2}}{2V^{2}}-\frac{\alpha _{2}^{2}\sigma _{3}^{2}z^{2 }}{2V^{2}}. \end{aligned}$$

In addition, one can get that

$$\begin{aligned} V^{2}=\bigg (\alpha _{1}\sigma _{2}y\displaystyle \frac{1}{\sigma _{2}}+\alpha _{2}\sigma _{3}z\frac{1}{\sigma _{3}}\bigg )^{2}\le \bigg (\alpha _{1}^{2}\sigma _{2}^{2}y^{2}+\alpha _{2}^{2}\sigma _ {3}^{2}z^{2}\bigg )\bigg (\frac{1}{\sigma _{2}^{2}}+\frac{1}{\sigma _{3}^{2}}\bigg ) \end{aligned}$$

(5.11)

and

$$\begin{aligned}&\displaystyle \frac{1}{V}\bigg \{\alpha _{1}\bigg [\frac{kbxz}{1+mx}-(D+d_{1})y\bigg ]+\alpha _{2}[Dy-d_{2}z]\bigg \}\nonumber \\&=\displaystyle \frac{\alpha _{1}z}{V}\bigg (\frac{kbx}{1+mx}-\frac{kb\frac{r}{a}}{1+m\frac{r}{a}}\bigg )\nonumber \\&\quad +\,\frac{1}{V}\bigg \{\alpha _{1}\bigg [\frac{kbr}{a+mr}z-(D+d_{1})y\bigg ] \quad +\alpha _{2}[Dy-d_{2}z]\bigg \}\nonumber \\&=\displaystyle \frac{\alpha _{1}kbz}{V}\frac{x-\frac{r}{a}}{(1+mx)(1+m\frac{r}{a})}\nonumber \\&\quad +\,\frac{1}{V}\bigg \{\frac{\omega _{1}}{D+d_{1}}\bigg [\frac{kbr}{a+mr}z-(D+d_{1})y\bigg ]+ \frac{\omega _{2}}{d_{2}}[Dy-d_{2}z]\bigg \}\nonumber \\&\le \displaystyle \frac{\alpha _{1}kbz}{V}\frac{X-\frac{r}{a}}{1+m\frac{r}{a}}+\frac{1}{V}\bigg \{\frac{\omega _{1}}{D+d_{1}}\bigg [\frac{kbr}{a+mr}z-(D+d_{1})y\bigg ]+\frac{ \omega _{2}}{d_{2}}[Dy-d_{2}z]\bigg \}\nonumber \\&\displaystyle \le \frac{\alpha _{1}}{\alpha _{2}}\cdot \frac{kab}{a+mr}\bigg |X-\frac{r}{a}\bigg |+\frac{1}{V}(\omega _{1},\omega _{2})(M_{0}(y,z)^{T}-(y,z)^{T})\nonumber \\&=\displaystyle \frac{\alpha _{1}}{\alpha _{2}}\cdot \frac{kab}{a+mr}\bigg |X-\frac{r}{a}\bigg |+\frac{1}{V}(\sqrt{R_{0}}-1)(\omega _{1}y+\omega _{2}z)\nonumber \\&=\displaystyle \frac{\alpha _{1}}{\alpha _{2}}\cdot \frac{kab}{a+mr}\bigg |X-\frac{r}{a}\bigg |+\frac{1}{V}(\sqrt{R_{0}}-1)[(D+d_{1})\alpha _{1}y+d_{2}\alpha _{2}z]\nonumber \\&\le \min \{D+d_{1},d_{2}\}(\sqrt{R_{0}}-1)I_{\{\sqrt{R_{0}}\le 1\}}+\max \{D+d_{1},d_{2}\}(\sqrt{R_{0}}-1)I_{\{\sqrt{R_{0}}>1\}}\nonumber \\&\quad +\,\displaystyle \frac{\alpha _{1}}{\alpha _{2}}\cdot \frac{k ab}{a+mr}\bigg |X-\frac{r}{a}\bigg |. \end{aligned}$$

(5.12)

In view of (5.11) and (5.12), we have

$$\begin{aligned}&L(\ln V)\le \min \{D+d_{1},d_{2}\}(\sqrt{R_{0}}-1)I_{\{\sqrt{R_{0}}\le 1\}}\\&\quad +\,\max \{D+d_{1},d_{2}\}(\sqrt{R_{0}}-1)I_{\{\sqrt{R_{0}}>1\}}+\displaystyle \frac{\alpha _{1}}{\alpha _{2}}\cdot \frac{kab}{a+mr}\bigg |X-\frac{r}{a}\bigg |\\&\quad -\left( 2\left( \sigma _{2}^{-2}+\sigma _{3}^{-2}\right) \right) ^{-1}. \end{aligned}$$

It follows from (5.10) that

$$\begin{aligned}&d(\ln V)\le \bigg [\min \{D+d_{1},d_{2}\}(\sqrt{R_{0}}-1)I_{\{\sqrt{R_{0}}\le 1\}}\nonumber \\&\quad +\,\max \{D+d_{1},d_{2}\}(\sqrt{R_{0}}-1)I_{\{\sqrt{R_{0}}>1\}}+\displaystyle \frac{\alpha _{1}}{\alpha _{2}}\cdot \frac{kab}{a+mr}\bigg |X-\frac{r}{a}\bigg |\nonumber \\&\quad -\left( 2\left( \sigma _{2}^{-2}+\sigma _{3}^{-2}\right) \right) ^{-1}\bigg ]\mathrm{d}t\nonumber \\&\quad +\,\displaystyle \frac{\alpha _{1}\sigma _{2}y}{V}\mathrm{d}B_{2}(t)+\frac{\alpha _{2}\sigma _{3}z}{V}\mathrm{d}B_{3}(t). \end{aligned}$$

(5.13)

Integrating (5.13) from 0 to t and then dividing by t on both sides, one obtains

$$\begin{aligned} \displaystyle \frac{\ln V(t)}{t}\le & {} \frac{\ln V(0)}{t}+\,\min \{D+d_{1},d_{2}\}(\sqrt{R_{0}}-1)I_{\{\sqrt{R_{0}}\le 1\}}\nonumber \\&\quad +\max \{D+d_{1},d_{2}\}(\sqrt{R_{0}}-1)I_{\{\sqrt{R_{0}}>1\}}\nonumber \\&\quad +\,\displaystyle \frac{\alpha _{1}kab}{\alpha _{2}(a+mr)t}\int _{0}^{t}\bigg |X(s)-\frac{r}{a}\bigg |\mathrm{d}s-\left( 2\left( \sigma _{2}^{-2}+\sigma _{3}^{-2}\right) \right) ^{-1}\nonumber \\&\quad +\,\frac{1}{t}\int _{0}^{t}\frac{\alpha _{1}\sigma _{2}y(s)}{V(s)}\mathrm{d}B_{2}(s)+\frac{1}{t}\int _{0}^{t}\frac{\alpha _{2}\sigma _{3}z(s)}{V(s)}\mathrm{d}B_{3}(s)\nonumber \\= & {} \displaystyle \frac{\ln V(0)}{t}\nonumber \\&+\min \{D+d_{1},d_{2}\}(\sqrt{R_{0}}-1)I_{\{\sqrt{R_{0}}\le 1\}}\nonumber \\&\quad +\max \{D+d_{1},d_{2}\}(\sqrt{R_{0}}-1)I_{\{\sqrt{R_{0}}>1\}}\nonumber \\&\quad +\,\displaystyle \frac{\alpha _{1}kab}{\alpha _{2}(a+mr)t}\int _{0}^{t}\bigg |X(s)-\frac{r}{a}\bigg |\mathrm{d}s-\left( 2\left( \sigma _{2}^{-2}+\sigma _{3}^{-2}\right) \right) ^{-1}\nonumber \\&\quad +\,\frac{M_{1}(t)}{t}+\frac{M_{2}(t)}{t}, \end{aligned}$$

(5.14)

where $M_{1}(t):=\int _{0}^{t}\frac{\alpha _{1}\sigma _{2}y(s)}{V(s)}\mathrm{d}B_{2}(s)$, $M_{2}(t):=\int _{0}^{t}\frac{\alpha _{2}\sigma _{3}z(s)}{V(s)}\mathrm{d}B_{3}(s)$ are local martingales whose quadratic variations are $\langle M_{1},M_{1}\rangle _{t}=\sigma _{2}^{2}\int _{0}^{t}\left( \frac{\alpha _{1}y(s)}{V(s)}\right) ^{2}\mathrm{d}s\le \sigma _{2}^{2}t$ and $\langle M_{2},M_{2}\rangle _{t}=\sigma _{3}^{2}\int _{0}^{t}\left( \frac{\alpha _{2}z(s)}{V(s)}\right) ^{2}\mathrm{d}s\le \sigma _{3}^{2}t$. Using the strong law of large numbers for local martingales (Mao 1997) yields

$$\begin{aligned} \displaystyle \lim _{t\rightarrow \infty }\frac{M_{i}(t)}{t}=0~\text {a.s.},~i=1,2. \end{aligned}$$

(5.15)

Since X(t) is ergodic and $\int _{0}^{\infty }x\pi (x)\mathrm{d}x<\infty$, we have

$$\begin{aligned}&\displaystyle \lim _{t\rightarrow \infty }\frac{1}{t}\int _{0}^{t}\bigg |X(s)-\frac{r}{a}\bigg |\mathrm{d}s\nonumber \\&\quad =\int _{0}^{\infty }\bigg |x-\frac{r}{a}\bigg |\pi (x)\mathrm{d}x\le \bigg [\int _{0}^{\infty }\bigg (x-\frac{r}{a}\bigg )^{2}\pi (x)\mathrm{d}x\bigg ]^{\frac{1}{2}}\nonumber \\&\quad =\bigg (\frac{r\sigma _{1}^{2}}{2a^{2}}\bigg )^{\frac{1}{2}}, \end{aligned}$$

(5.16)

where a detailed calculation of the last integral can be found in Appendix C.

Taking the superior limit on both sides of (5.14) and combining with (5.15) and (5.16) lead to

$$\begin{aligned} \limsup _{t\rightarrow \infty }\displaystyle \frac{\ln V(t)}{t}\le & {} \min \{D+d_{1},d_{2}\}(\sqrt{R_{0}}-1)I_{\{\sqrt{R_{0}}\le 1\}}\\&\quad +\,\max \{D+d_{1},d_{2}\}(\sqrt{R_{0}}-1)I_{\{\sqrt{R_{0}}>1\}}\\&\quad +\,\displaystyle \frac{\alpha _{1}kab}{\alpha _{2}(a+mr)}\bigg (\frac{r\sigma _{1}^{2}}{2a^{2}}\bigg )^{\frac{1}{2}}-\left( 2\left( \sigma _{2}^{-2}+\sigma _{3}^{-2}\right) \right) ^{-1}\\= & {} \min \{D+d_{1},d_{2}\}(\sqrt{R_{0}}-1)I_{\{\sqrt{R_{0}}\le 1\}}\nonumber \\&\quad +\max \{D+d_{1},d_{2}\}(\sqrt{R_{0}}-1)I_{\{\sqrt{R_{0}}>1\}}\\&\quad +\,\displaystyle \frac{kbD\sigma _{1}}{(a+mr)(D+d_{1})}\bigg (\frac{r}{2R_{0}}\bigg )^{\frac{1}{2}}-\left( 2\left( \sigma _{2}^{-2}+\sigma _{3}^{-2}\right) \right) ^{-1}\\&{:}{=}&\upsilon ~\text {a.s.}, \end{aligned}$$

which is the desired assertion. Furthermore, if $\upsilon <0$, we can easily conclude that

$$\begin{aligned} \limsup _{t\rightarrow \infty }\frac{\ln y(t)}{t}<0,~\limsup _{t\rightarrow \infty }\frac{\ln z(t)}{t}<0~\text {a.s.}, \end{aligned}$$

which implies that $\lim _{t\rightarrow \infty }y(t)=0$ and $\lim _{t\rightarrow \infty }z(t)=0$ a.s. In other words, the predator populations y and z tend to zero exponentially with probability one. This completes the proof.

Theorem 5.2

Let (x(t), y(t), z(t)) be the solution of system (1.2) with any initial value $(x(0),y(0),z(0))\in \mathbb {R}_{+}^{3}$. If $r<\frac{\sigma _{1}^{2}}{2}$, then the prey population x and the predator populations y and z die out exponentially with probability one, i.e.

$$\begin{aligned} \lim _{t\rightarrow \infty }x(t)=0,~\lim _{t\rightarrow \infty }y(t)=0,~\lim _{t\rightarrow \infty }z(t)=0~a.s. \end{aligned}$$

Proof

Applying Itô’s formula to the first equation of system (1.2), we get $\square$

$$\begin{aligned} d(\ln x(t))=\bigg (r-ax-\displaystyle \frac{bz}{1+mx}-\frac{\sigma _{1}^{2}}{2}\bigg )\mathrm{d}t+\sigma _{1}\mathrm{d}B_{1}(t). \end{aligned}$$

(5.17)

Integrating from 0 to t on both sides of (5.17), we obtain

$$\begin{aligned} \ln x(t)-\ln x(0)= & {} \bigg (r-\displaystyle \frac{\sigma _{1}^{2}}{2}\bigg )t-a\int _{0}^{t}x(s)\mathrm{d}s-b\int _{0}^{t}\frac{z(s)}{1+mx(s)}\mathrm{d}s+\sigma _{1}B_{1}(t)\nonumber \\\le & {} \bigg (r-\displaystyle \frac{\sigma _{1}^{2}}{2}\bigg )t+\sigma _{1}B_{1}(t). \end{aligned}$$

(5.18)

Dividing by t on both sides of (5.18) leads to

$$\begin{aligned} \displaystyle \frac{\ln x(t)-\ln x(0)}{t}\le r-\frac{\sigma _{1}^{2}}{2}+\frac{\sigma _{1}B_{1}(t)}{t}. \end{aligned}$$

(5.19)

Taking the superior limit on both sides of (5.19) and noting that $\lim _{t\rightarrow \infty }\frac{B_{1}(t)}{t}=0$ a.s., we obtain

$$\begin{aligned} \limsup _{t\rightarrow \infty }\frac{\ln x(t)}{t}\le r-\frac{\sigma _{1}^{2}}{2}<0~\text {a.s.}, \end{aligned}$$

which implies that

$$\begin{aligned} \lim _{t\rightarrow \infty }x(t)=0~\text {a.s.} \end{aligned}$$

Hence, $x(t)\rightarrow 0$ exponentially a.s. as claimed. In particular, there exists $t_{0}$ and a set $\Omega _{\epsilon }\subset \Omega$ such that $\mathbb {P}(\Omega _{\epsilon })>1-\epsilon$ and $\frac{kbx}{1+mx}\le kbx\le kb\epsilon$ a.s. for $t\ge t_{0}$ and $\omega \in \Omega _{\epsilon }$. To prove that y and z also tend to zero, let $P(t)=y(t)+z(t)$. Applying Itô’s formula to $\ln P(t)$ yields

$$\begin{aligned} d(\ln P(t))= & {} \bigg \{\displaystyle \frac{\frac{kbxz}{1+mx}-d_{1}y-d_{2}z}{y+z}-\frac{\sigma _{2}^{2}y^{2}+\sigma _{3}^{2}z^{2}}{2(y+z)^{2}}\bigg \}\mathrm{d}t+\frac{\sigma _{2}y}{y+z}\mathrm{d}B_{2}(t)\nonumber \\&+\frac{\sigma _{3}z}{y+z}\mathrm{d}B_{3}(t)\nonumber \\\le & {} kbx\mathrm{d}t-\min \{d_{1},d_{2}\}\mathrm{d}t+\displaystyle \frac{\sigma _{2}y}{y+z}\mathrm{d}B_{2}(t)+\frac{\sigma _{3}z}{y+z}\mathrm{d}B_{3}(t)\nonumber \\\le & {} kb\epsilon \mathrm{d}t-\min \{d_{1},d_{2}\}\mathrm{d}t+\displaystyle \frac{\sigma _{2}y}{y+z}\mathrm{d}B_{2}(t)\nonumber \\&+\frac{\sigma _{3}z}{y+z}\mathrm{d}B_{3}(t)~\text {with probability}~1-\epsilon ~\text {when}~t\ge t_{0}. \end{aligned}$$

(5.20)

Integrating (5.20) from 0 to $t\ge t_{0}$ and then dividing by t on both sides, we get

$$\begin{aligned} \displaystyle \frac{\ln P(t)}{t}-\frac{\ln P(0)}{t}\le & {} kb\epsilon -\min \{d_{1},d_{2}\}\nonumber \\&+\frac{1}{t}\int _{0}^{t}\frac{\sigma _{2}y(s)}{y(s)+z(s)}\mathrm{d}B_{2}(s)+\frac{1}{t}\int _{0}^{t}\frac{\sigma _{3}z(s)}{y(s)+z(s)}\mathrm{d}B_{3}(s)\nonumber \\= & {} kb\epsilon -\min \{d_{1},d_{2}\}+\displaystyle \frac{M_{3}(t)}{t}\nonumber \\&+\frac{M_{4}(t)}{t}~\text {with probability}~1-\epsilon , \end{aligned}$$

(5.21)

where $M_{3}(t):=\int _{0}^{t}\frac{\sigma _{2}y(s)}{y(s)+z(s)}\mathrm{d}B_{2}(s)$, $M_{4}(t):=\int _{0}^{t}\frac{\sigma _{3}z(s)}{y(s)+z(s)}\mathrm{d}B_{3}(s)$ are local martingales whose quadratic variations are $\langle M_{3},M_{3}\rangle _{t}=\sigma _{2}^{2}\int _{0}^{t}\left( \frac{y(s)}{y(s)+z(s)}\right) ^{2}\mathrm{d}s\le \sigma _{2}^{2}t$ and $\langle M_{4},M_{4}\rangle _{t}=\sigma _{3}^{2}\int _{0}^{t}\left( \frac{z(s)}{y(s)+z(s)}\right) ^{2}\mathrm{d}s\le \sigma _{3}^{2}t$. Applying the strong law of large numbers for local martingales (Mao 1997) leads to

$$\begin{aligned} \lim _{t\rightarrow \infty }\displaystyle \frac{M_{i}(t)}{t}=0~\text {a.s.},~i=3,4. \end{aligned}$$

(5.22)

Taking the limit supremum of (5.21) as $t\rightarrow \infty$ and combining with (5.22), one obtains

$$\begin{aligned} \limsup _{t\rightarrow \infty }\frac{\ln P(t)}{t}\le -\min \{d_{1},d_{2}\}<0~\text {with probability}~1-\epsilon . \end{aligned}$$

Letting $\epsilon \rightarrow 0$, we have

$$\begin{aligned} \limsup _{t\rightarrow \infty }\frac{\ln P(t)}{t}<0~\text {a.s.}, \end{aligned}$$

which implies that

$$\begin{aligned} \lim _{t\rightarrow \infty }y(t)=0,~\lim _{t\rightarrow \infty }z(t)=0~\text {a.s.} \end{aligned}$$

That is to say, the predator populations y and z die out exponentially with probability one. This completes the proof.

6 Numerical Simulations

In this section, we illustrate our theoretical results using numerical simulations of system (1.2). The initial state of the system is taken fixed at (1.0, 1.0, 1.2). For the numerical simulations, we use Milstein’s higher-order method mentioned in Higham (2001) to obtain the following discretization transformation of system (1.2)

$$\begin{aligned} \left\{ \begin{array}{lll} x^{j+1}=x^{j}+\bigg [x^{j}(r-ax^{j})-\displaystyle \frac{bx^{j}z^{j}}{1+mx^{j}}\bigg ]\Delta t+\sigma _{1}x^{j}\sqrt{\Delta t}\varepsilon _{1,j}+\frac{\sigma _{1}^{2}}{2}x^{j}\left( \varepsilon _{1,j}^{2}-1\right) \Delta t,\\ y^{j+1}=y^{j}+\bigg [\displaystyle \frac{kbx^{j}z^{j}}{1+mx^{j}}-(D+d_{1})y^{j}\bigg ]\Delta t+\sigma _{2}y^{j}\sqrt{\Delta t}\varepsilon _{2,j}+\displaystyle \frac{\sigma _{2}^{2}}{2}y^{j}\left( \varepsilon _{2,j}^{2}-1\right) \Delta t,\\ z^{j+1}=z^{j}+\left[ Dy^{j}-d_{2}z^{j}\right] \Delta t+\sigma _{3}z^{j}\sqrt{\Delta t}\varepsilon _{3,j}+\displaystyle \frac{\sigma _{3}^{2}}{2}z^{j}\left( \varepsilon _{3,j}^{2}-1\right) \Delta t, \end{array}\right. \qquad \end{aligned}$$

(6.1)

where the time increment $\Delta t$ is positive and $\varepsilon _{i,j}$ are the Gaussian random variables which follow the distribution N(0, 1), $i=1,2,3$.

Fig. 1

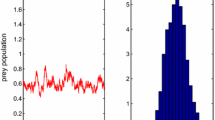
The solution of the stochastic system (1.2) and its histogram. The blue lines represent the solution of system (1.2), and the red lines represent the solution of the corresponding undisturbed system (1.1). The pictures on the right are the histogram of the probability density function for x, y and z populations at $t=300$ for the stochastic system (1.2) with $\sigma _{1}^{2}=0.02$, $\sigma _{2}^{2}=0.1$, $\sigma _{3}^{2}=0.08$. Other parameters are taken in Table 1 (Color figure online)

Table 1 List of parameters

Example 6.1

In order to check the existence of an ergodic stationary distribution, in Fig. 1, we choose the values of the system parameters as follows: $\sigma _{1}^{2}=0.02$, $\sigma _{2}^{2}=0.1$, $\sigma _{3}^{2}=0.08$. Other values of the system parameters, see Table 1. Direct calculation leads to $r=0.6>0.01=\frac{\sigma _{1}^{2}}{2}$ and $R_{0}^{S}=7.3024>1$, where $R_{0}^{S}$ is defined in Theorem 4.1. In other words, the conditions of Theorem 4.1 hold. In view of Theorem 4.1, there is an ergodic stationary distribution $\mu (\cdot )$ of system (1.2). Figure 1 illustrates this. The dynamics of system (1.2) can be visible on a log-linear plot. See Fig. 2.

Example 6.2

In order to illustrate the conclusions of Theorem 5.1, in Fig. 3, we choose the values of the system parameters as follows: $\sigma _{1}^{2}=0.01$, $\sigma _{2}^{2}=2$, $\sigma _{3}^{2}=2$. Other values of the system parameters see Table 1. Direct calculation shows that $\frac{\sigma _{1}^{2}}{2}=0.005<0.6=r$ and $\upsilon =1.2675-2=-0.7325<0$, where $\upsilon$ is defined in Theorem 5.1. Thus, the conditions of Theorem 5.1 hold. According to Theorem 5.1, the distribution of x(t) converges weakly a.s. to the stationary measure and the predator populations y and z tend to zero exponentially. See Fig. 3. The dynamics of system (1.2) can be visible on a log-linear plot. See Fig. 4.

Example 6.3

In order to obtain the extinction of the predator populations, in Fig. 5, we choose the values of the system parameters as follows: $\sigma _{1}^{2}=1.8$, $\sigma _{2}^{2}=1.8$, $\sigma _{3}^{2}=2$. Other values of the system parameters see Table 1. By a simple computation, we obtain $r=0.6<0.9=\frac{\sigma _{1}^{2}}{2}$. That is to say, the condition of Theorem 5.2 is satisfied. By Theorem 5.2, both the prey and predator populations die out exponentially. Figure 5 shows this. The dynamics of system (1.2) can be visible on a log-linear plot. See Fig. 6. From Figs. 3 and 5, we can observe that the larger white noise can lead to the extinction of predator populations.

Fig. 2

Simulation of paths of $\ln x(t)$, $\ln y(t)$, $\ln z(t)$ of model (1.2) with the initial value $(x(0),y(0),z(0))=(1.0,1.0,1.2)$ under the parameter values $r=0.6$, $a=0.1$, $b=0.8$, $m=0.5$, $k=0.8$, $D=0.4$, $d_{1}=0.05$, $d_{2}=0.06$, $\sigma _{1}^{2}=0.02$, $\sigma _{2}^{2}=0.1$, $\sigma _{3}^{2}=0.08$

Fig. 3

The left column shows the paths of x(t), y(t), z(t) of model (1.2) with the initial value $(x(0),y(0),z(0))=(1.0,1.0,1.2)$ under the parameter values $r=0.6$, $a=0.1$, $b=0.8$, $m=0.5$, $k=0.8$, $D=0.4$, $d_{1}=0.05$, $d_{2}=0.06$, $\sigma _{1}^{2}=0.01$, $\sigma _{2}^{2}=2$, $\sigma _{3}^{2}=2$. The blue lines represent the solution of system (1.2), and the red lines represent the solution of the corresponding undisturbed system (1.1). The right column displays the histogram of x(t) with values of $\sigma _{1}^{2}=0.01$, $\sigma _{2}^{2}=2$, $\sigma _{3}^{2}=2$ (Color figure online)

Fig. 4

Simulation of paths of $\ln x(t)$, $\ln y(t)$, $\ln z(t)$ of model (1.2) with the initial value $(x(0),y(0),z(0))=(1.0,1.0,1.2)$ under the parameter values $r=0.6$, $a=0.1$, $b=0.8$, $m=0.5$, $k=0.8$, $D=0.4$, $d_{1}=0.05$, $d_{2}=0.06$, $\sigma _{1}^{2}=0.01$, $\sigma _{2}^{2}=2$, $\sigma _{3}^{2}=2$

Fig. 5

Simulation of paths of x(t), y(t), z(t) of model (1.2) with the initial value $(x(0),y(0),z(0))=(1.0,1.0,1.2)$ under the parameter values $r=0.6$, $a=0.1$, $b=0.8$, $m=0.5$, $k=0.8$, $D=0.4$, $d_{1}=0.05$, $d_{2}=0.06$, $\sigma _{1}^{2}=1.8$, $\sigma _{2}^{2}=1.8$, $\sigma _{3}^{2}=2$. The blue lines represent the solution of system (1.2), and the red lines represent the solution of the corresponding undisturbed system (1.1) (Color figure online)

Fig. 6

Simulation of paths of $\ln x(t)$, $\ln y(t)$, $\ln z(t)$ of model (1.2) with the initial value $(x(0),y(0),z(0))=(1.0,1.0,1.2)$ under the parameter values $r=0.6$, $a=0.1$, $b=0.8$, $m=0.5$, $k=0.8$, $D=0.4$, $d_{1}=0.05$, $d_{2}=0.06$, $\sigma _{1}^{2}=1.8$, $\sigma _{2}^{2}=1.8$, $\sigma _{3}^{2}=2$

7 Concluding Remarks and Future Directions

This paper studied a stochastic predator–prey model with stage structure for predator and Holling type II functional response. Firstly, by constructing a suitable stochastic Lyapunov function, we obtained sufficient conditions for the existence of a unique ergodic stationary distribution of the positive solutions to system (1.2). Then, we established sufficient conditions for extinction of the predator populations in two cases, that is, the first case is that the prey population survival and the predator populations extinction; the second case is that all the prey and predator populations extinction. The existence of a stationary distribution implies stochastic weak stability. More precisely, we have obtained the following results:

$\bullet$ If $r>\frac{\sigma _{1}^{2}}{2}$ and $R_{0}^{S}=\frac{kbDr}{(a+mr)\left( D+d_{1}+\frac{\sigma _{2}^{2}}{2}\right) \left( d_{2}+\frac{\sigma _{3}^{2}}{2}\right) }\left( 1-\frac{\sigma _{1}^{2}}{2r}\right) ^{3}>1$, then for any initial value $(x(0),y(0),z(0))\in \mathbb {R} _{+}^{3}$, system (1.2) has a unique ergodic stationary distribution $\mu (\cdot )$.

$\bullet$ If $r>\frac{\sigma _{1}^{2}}{2}$, then for any initial value $(x(0),y(0),z(0))\in \mathbb {R} _{+}^{3}$, the solution (x(t), y(t), z(t)) of system (1.2) has the following property

$$\begin{aligned} \limsup _{t\rightarrow \infty }\frac{1}{t}\ln \bigg (\frac{D}{d_{2}(D+d_{1})}y(t)+\frac{\sqrt{R_{0}}}{d_{2}}z(t)\bigg )\le \upsilon ~\text {a.s.}, \end{aligned}$$

where $\upsilon =\min \{D+d_{1},d_{2}\}(\sqrt{R_{0}}-1)I_{\{\sqrt{R_{0}}\le 1\}}+\max \{D+d_{1},d_{2}\}(\sqrt{R_{0}}-1)I_{\{\sqrt{R_{0}}>1\}}+\frac{kbD\sigma _{1}}{(a+mr)(D+d_{1})}\left( \frac{r}{2 R_{0}}\right) ^{\frac{1}{2}}-\left( 2\left( \sigma _{2}^{-2}+\sigma _{3}^{-2}\right) \right) ^{-1}$ and $R_{0}=\frac{kbDr}{d_{2}(a+mr)(D+d_{1})}$. Especially, if $\upsilon <0$, then the predator populations y and z die out exponentially with probability one. Moreover, the distribution of x(t) converges weakly a.s. to the measure which has the density

$$\begin{aligned} \pi (x)=Q\sigma _{1}^{-2}x^{-2+\frac{2r}{\sigma _{1}^{2}}}\mathrm{e}^{-\frac{2a}{\sigma _{1}^{2}}x},~x\in (0,\infty ), \end{aligned}$$

where $Q=\bigg [\sigma _{1}^{-2}\left( \frac{\sigma _{1}^{2}}{2a}\right) ^{\frac{2r}{\sigma _{1}^{2}}-1}\Gamma \left( \frac{2r}{\sigma _{1}^{2}}-1\right) \bigg ]^{-1}$ is a constant satisfying $\int _{0}^{\infty }\pi (x)\mathrm{d}x=1$. That is to say, if we use $\mu _{t}(x)$ to denote the probability density of the prey population at time t, then for any (sufficiently smooth) function f(x),

$$\begin{aligned} \displaystyle \lim _{t\rightarrow \infty }\int _{\mathbb {R}_{+}}f(x)\mu _{t}(x)\mathrm{d}x=\int _{\mathbb {R}_{+}}f(x)\pi (x)\mathrm{d}x. \end{aligned}$$

$\bullet$ If $r<\frac{\sigma _{1}^{2}}{2}$, then the prey population x and the predator populations y and z die out exponentially with probability one.

Some interesting problems deserve further consideration. On the one hand, one can propose some more realistic but complex models, such as considering the effects of impulsive perturbations on system (1.2). The motivation for studying this is that ecological systems are often deeply perturbed by natural and human factors, such as planting, drought and flooding. To better describe these phenomena mathematically, impulsive effects should be taken into account (Bainov and Simeonov 1993; Lakshmikantham et al. 1989). On the other hand, while our model is autonomous, it is of interest to investigate the nonautonomous case and study other important dynamical properties, such as the existence of positive periodic solutions, the motivation is that due to the seasonal variation, individual life cycle, food supplies, mating habits, hunting, harvesting and so on, the birth rate, the death rate of the population and other parameters will not remain constant, but exhibit a more or less periodicity. It is also interesting to introduce the coloured noise, such as continuous-time Markov chain, into model (1.2). The motivation is that the dynamics of population may suffer sudden environmental changes, e.g. temperature, humidity, harvesting. Frequently, the switching among different environments is memoryless and the waiting time for the next switch is exponentially distributed; then, the sudden environmental changes can be modelled by a continuous-time Markov chain (see e.g. Luo and Mao 2007; Zhu and Yin 2007). Moreover, for more complex predator–prey systems, the Lyapunov function used in this paper is no longer applicable, and we need to construct new different Lyapunov functions to study the existence and uniqueness of ergodic stationary distributions. These problems will be the subject of future work.

Appendices

Appendix A: Calculation of the Derivation of the Bound

Making use of Itô’s formula leads to

$$\begin{aligned} L(V_{5})= & {} \bigg (x+\displaystyle \frac{y}{k}+\frac{D+d_{1}}{2Dk}z\bigg )^{\theta }\bigg [x(r-ax)\\&-\,\frac{D+d_{1}}{2k}y-\frac{d_{2}(D+d_{1})}{2Dk}z\bigg ]+\frac{\theta }{2} \bigg (x+\displaystyle \frac{y}{k}+\frac{D+d_{1}}{2Dk}z\bigg )^{\theta -1}\\&\times \,\bigg (\sigma _{1}^{2}x^{2}+\displaystyle \frac{\sigma _{2}^{2}}{k^{2}}y^{2}+\frac{(D+d_{1})^{2}}{4D^{2}k^{2}}\sigma _{3}^{2}z^{2}\bigg )\\\le & {} \bigg (x+\displaystyle \frac{y}{k}+\frac{D+d_{1}}{2Dk}z\bigg )^{\theta }\bigg [x(r-ax)-\frac{D+d_{1}}{2k}y-\frac{d_{2}(D+d_{1})}{2Dk}z\bigg ]\\&+\,\frac{\theta }{2}\bigg (x+ \displaystyle \frac{y}{k}+\frac{D+d_{1}}{2Dk}z\bigg )^{\theta +1}(\sigma _{1}^{2}\vee \sigma _{2}^{2}\vee \sigma _{3}^{2})\\\le & {} rx\bigg (x+\displaystyle \frac{y}{k}+\frac{D+d_{1}}{2Dk}z\bigg )^{\theta }-ax^{\theta +2}-\frac{d_{1}}{2k^{\theta +1}}y^{\theta +1}-\frac{d_{2}(D+d_{1})^{\theta +1}}{(2Dk)^{\theta +1}}z^{\theta +1}\\&+\,\frac{\theta }{2}\bigg (x+\displaystyle \frac{y}{k}+\frac{D+d_{1}}{2Dk}z\bigg )^{\theta +1}\times (\sigma _{1}^{2}\vee \sigma _{2}^{2}\vee \sigma _{3}^{2})\\= & {} -\displaystyle \frac{a}{2}x^{\theta +2}-\frac{d_{1}}{4k^{\theta +1}}y^{\theta +1}-\frac{d_{2}(D+d_{1})^{\theta +1}}{2^{\theta +2}(Dk)^{\theta +1}}z^{\theta +1}\\&-\,\frac{a}{2}x^{\theta +2}-\frac{d_{1}}{4k^{\theta +1}}y^{\theta +1}-\frac{d_{2}(D+d_{1})^{\theta +1}}{2^{\theta +2}(Dk)^{\theta +1}}z^{\theta +1}\\&+\,rx\bigg (x+\displaystyle \frac{y}{k}+\frac{D+d_{1}}{2Dk}z\bigg )^{\theta }+\frac{\theta }{2}\bigg (x+\displaystyle \frac{y}{k}+\frac{D+d_{1}}{2Dk}z\bigg )^{\theta +1}(\sigma _{1}^{2}\vee \sigma _{2}^{2}\vee \sigma _{3}^{2})\\\le & {} -\displaystyle \frac{a}{2}x^{\theta +2}-\frac{d_{1}}{4k^{\theta +1}}y^{\theta +1}-\frac{d_{2}(D+d_{1})^{\theta +1}}{2^{\theta +2}(Dk)^{\theta +1}}z^{\theta +1}\\&-\,\frac{a}{2}x^{\theta +2} -\frac{d_{1}}{4k^{\theta +1}}y^{\theta +1}-\frac{d_{2}(D+d_{1})^{\theta +1}}{2^{\theta +2}(Dk)^{\theta +1}}z^{\theta +1}\\&+\,rx\bigg (x+\displaystyle \frac{y}{k}+\frac{D+d_{1}}{2Dk}z\bigg )^{\theta }\\&+\,\frac{3^{\theta }\theta }{2}\bigg (x^{\theta +1}+\bigg (\displaystyle \frac{y}{k}\bigg )^{\theta +1}+\bigg (\frac{D +d_{1}}{2Dk}\bigg )^{\theta +1}z^{\theta +1}\bigg )(\sigma _{1}^{2}\vee \sigma _{2}^{2}\vee \sigma _{3}^{2})\nonumber \\ \end{aligned}$$

$$\begin{aligned}= & {} -\displaystyle \frac{a}{2}x^{\theta +2}-\frac{d_{1}}{4k^{\theta +1}}y^{\theta +1}-\frac{d_{2}(D+d_{1})^{\theta +1}}{2^{\theta +2}(Dk)^{\theta +1}}z^{\theta +1}\\&-\,\frac{a}{2}x^{\theta +2}+\frac{3^{\theta }\theta }{2}(\sigma _{1}^{2}\vee \sigma _{2}^{2}\vee \sigma _{3}^{2})x^{\theta +1}+rx\bigg (x+\displaystyle \frac{y}{k}+\frac{D+d_{1}}{2Dk}z\bigg )^{\theta }\\&-\,\displaystyle \frac{d_{1}}{8k^{\theta +1}}y^{\theta +1}-\frac{d_{2}(D+d_{1})^{\theta +1}}{2^{\theta +3}(Dk)^{\theta +1}}z^{\theta +1}-\bigg (\frac{d_{1}}{8k^{\theta +1}}-\frac{3^{\theta } \theta }{2k^{\theta +1}}(\sigma _{1}^{2}\vee \sigma _{2}^{2}\vee \sigma _{3}^{2})\bigg )y^{\theta +1}\\&-\,\bigg (\displaystyle \frac{d_{2}(D+d_{1})^{\theta +1}}{2^{\theta +3}(Dk)^{\theta +1}}-\frac{3^{\theta }\theta (D+d_{1})^{\theta +1}}{2^{\theta +2}(Dk)^{\theta +1}}(\sigma _{1}^{2}\vee \sigma _{2}^{2}\vee \sigma _{3}^{2})\bigg )z^{\theta +1}\\\le & {} -\displaystyle \frac{a}{2}x^{\theta +2}-\frac{d_{1}}{4k^{\theta +1}}y^{\theta +1}-\frac{d_{2}(D+d_{1})^{\theta +1}}{2^{\theta +2}(Dk)^{\theta +1}}z^{\theta +1}\\&-\,\frac{a}{2}x^{\theta +2}+ \frac{3^{\theta }\theta }{2}(\sigma _{1}^{2}\vee \sigma _{2}^{2}\vee \sigma _{3}^{2})x^{\theta +1}+rx\bigg (x+\displaystyle \frac{y}{k}+\frac{D+d_{1}}{2Dk}z\bigg )^{\theta }\\&-\,\displaystyle \frac{d_{1}}{8k^{\theta +1}}y^{\theta +1}-\frac{d_{2}(D+d_{1})^{\theta +1}}{2^{\theta +3}(Dk)^{\theta +1}}z^{\theta +1}\\= & {} -\displaystyle \frac{a}{2}x^{\theta +2}-\frac{d_{1}}{4k^{\theta +1}}y^{\theta +1}-\frac{d_{2}(D+d_{1})^{\theta +1}}{2^{\theta +2}(Dk)^{\theta +1}}z^{\theta +1}\\&-\,\frac{a}{2}x^{\theta +2}+ \frac{3^{\theta }\theta }{2}\sigma _{\max }x^{\theta +1}+rx\bigg (x+\displaystyle \frac{y}{k}+\frac{D+d_{1}}{2Dk}z\bigg )^{\theta }\\&-\,\displaystyle \frac{d_{1}}{8k^{\theta +1}}y^{\theta +1}-\frac{d_{2}(D+d_{1})^{\theta +1}}{2^{\theta +3}(Dk)^{\theta +1}}z^{\theta +1}\\\le & {} -\displaystyle \frac{a}{2}x^{\theta +2}-\frac{d_{1}}{4k^{\theta +1}}y^{\theta +1}-\frac{d_{2}(D+d_{1})^{\theta +1}}{2^{\theta +2}(Dk)^{\theta +1}}z^{\theta +1}+B, \end{aligned}$$

where

$$\begin{aligned}&\sigma _{\max }{:}{=}\,\sigma _{1}^{2}\vee \sigma _{2}^{2}\vee \sigma _{3}^{2}=\max \{\sigma _{1}^{2},\sigma _{2}^{2},\sigma _{3}^{2}\},\\&\quad B=\sup _{(x,y,z)\in \mathbb {R}_{+}^{3}}\bigg \{-\displaystyle \frac{a}{2}x^{\theta +2}-\frac{d_{1}}{8k^{\theta +1}}y^{\theta +1}-\frac{d_{2}(D+d_{1})^{\theta +1}}{2^{\theta +3}(Dk)^{\theta +1}} z^{\theta +1}\\&+\,\frac{3^{\theta }\theta }{2}\sigma _{\max }x^{\theta +1}+rx\bigg (x+\frac{y}{k}+\frac{D+d_{1}}{2Dk}z\bigg )^{\theta }\bigg \} \end{aligned}$$

and in the third inequality we have used the fact that $|\sum _{i=1}^{k}v_{i}|^{p}\le k^{p-1}\sum _{i=1}^{k}|v_{i}|^{p}$ for $\forall p\ge 1$.

Appendix B: Verification of the Condition $A_{2}$ in Lemma 2.1

By system (1.2), we have

$$\begin{aligned} L(x)=x(r-ax)-\displaystyle \frac{bxz}{1+mx}\le x(r-ax)\le -\frac{r}{m}(1+mx)+\frac{r(a+mr)}{am},\qquad \end{aligned}$$

(B.1)

where the second inequality holds due to the fact that $a(x-\frac{r}{a})^{2}\ge 0$. Moreover, we obtain

$$\begin{aligned} L(-\ln y)=-\displaystyle \frac{kbxz}{(1+mx)y}+D+d_{1}+\frac{\sigma _{2}^{2}}{2} \end{aligned}$$

(B.2)

and

$$\begin{aligned} L(-\ln z)=-\displaystyle \frac{Dy}{z}+d_{2}+\frac{\sigma _{3}^{2}}{2}. \end{aligned}$$

(B.3)

It follows from (B.1), (B.2) and (B.3) that

$$\begin{aligned} L(V_{1})\le & {} -\frac{kbxz}{(1+mx)y}-\frac{c_{1}r}{m}(1+mx)-\frac{c_{2}Dy}{z}+\bigg (D+d_{1}+\frac{\sigma _{2}^{2}}{2}\bigg )\nonumber \\&+\,\frac{c_{1}r(a+mr)}{am}+c_{2}\bigg (d_{2}+\frac{\sigma _{3}^{2}}{2}\bigg )\nonumber \\ {}\le & {} -3\root 3 \of {\displaystyle \frac{c_{1}c_{2}kbDr}{m}}\root 3 \of {x}+\bigg (D+d_{1}+\displaystyle \frac{\sigma _{2}^{2}}{2}\bigg )+\frac{c_{1}r(a+mr)}{am} \nonumber \\&+\,c_{2}\bigg (d_{2}+\frac{\sigma _{3}^{2}}{2}\bigg ), \end{aligned}$$

(B.4)

where in the second inequality we have used Lemma 4.1. Moreover, we get

$$\begin{aligned} L\bigg (\frac{x}{r}\bigg )=x\bigg (1-\frac{ax}{r}\bigg )-\frac{bxz}{r(1+mx)}\le x\bigg (1-\frac{ax}{r}\bigg ) \end{aligned}$$

and

$$\begin{aligned} L\bigg (-\frac{\ln x}{r}\bigg )=-\bigg (1-\frac{ax}{r}\bigg )+\frac{bz}{r(1+mx)}+\frac{\sigma _{1}^{2}}{2r}\le \frac{ax}{r}-1+\frac{b}{r}z+\frac{\sigma _{1}^{2}}{2r}. \end{aligned}$$

In view of Lemma 4.2, we have

$$\begin{aligned} L(V_{2})\le \bigg [\displaystyle \frac{2}{3}\frac{ax}{r}\bigg (1-\frac{ax}{r}\bigg )+\frac{ax}{r}\bigg ]-1+\frac{b}{r}z+\frac{\sigma _{1}^{2}}{2r}\le \root 3 \of {\frac{a}{r}}\root 3 \of {x}-1+ \frac{b}{r}z+\frac{\sigma _{1}^{2}}{2r}.\nonumber \\ \end{aligned}$$

(B.5)

Therefore, by (B.4) and (B.5), one can see that

$$\begin{aligned} L(V_{3})\le & {} -3\root 3 \of {\frac{c_{1}c_{2}kbDr}{m}}\root 3 \of {x}+\bigg (D+d_{1}+\displaystyle \frac{\sigma _{2}^{2}}{2}\bigg )\nonumber \\&+\,\frac{c_{1}r(a+mr)}{am}+c_{2}\bigg (d_{2}+\frac{ \sigma _{3}^{2}}{2}\bigg )+3\root 3 \of {\frac{c_{1}c_{2}kbDr}{m}}\root 3 \of {x}\nonumber \\&-\,3\root 3 \of {\frac{c_{1}c_{2}kbDr^{2}}{ma}}\bigg (1-\frac{\sigma _{1}^{2}}{2r}\bigg )+\frac{3b}{r}\root 3 \of {\frac{c_{1}c_{2}kbDr^{2}}{ma}}z\nonumber \\= & {} \bigg (D+d_{1}+\displaystyle \frac{\sigma _{2}^{2}}{2}\bigg )+\frac{c_{1}r(a+mr)}{am}+c_{2}\bigg (d_{2}+\frac{\sigma _{3}^{2}}{2}\bigg )\nonumber \\&-\,3\root 3 \of {\frac{c_{1}c_{2}kbDr^{2}}{ma}}\bigg (1-\frac{\sigma _{1}^{2}}{2r}\bigg ) +\frac{3b}{r}\root 3 \of {\frac{c_{1}c_{2}kbDr^{2}}{ma}}z. \end{aligned}$$

(B.6)

Taking $c_{1}=\frac{kbDam\left( 1-\frac{\sigma _{1}^{2}}{2r}\right) ^{3}}{(a+mr)^{2}\left( d_{2}+\frac{\sigma _{3}^{2}}{2}\right) }$, $c_{2}=\frac{kbDr\left( 1-\frac{\sigma _{1}^{2}}{2r}\right) ^{3}}{(a+mr)\left( d_{2}+\frac{\sigma _{3}^{2}}{2}\right) ^{2}}$, according to (B.6), we obtain

$$\begin{aligned} L(V_{3})\le & {} \bigg (D+d_{1}+\frac{\sigma _{2}^{2}}{2}\bigg )+\frac{2kbDr}{(a+mr)\left( d_{2}+\frac{\sigma _{3}^{2}}{2}\right) }\bigg (1-\frac{\sigma _{1}^{2}}{2r}\bigg )^{3}\nonumber \\&-\,\frac{3kbDr}{(a+mr)\left( d_{2}+\frac{\sigma _{3}^{2}}{2}\right) }\bigg (1-\frac{\sigma _{1}^{2}}{2r}\bigg )^{3}+\frac{3b}{r}\root 3 \of {\frac{c_{1}c_{2}kbDr^{2}}{ma}}z\nonumber \\= & {} -\bigg (D+d_{1}+\frac{\sigma _{2}^{2}}{2}\bigg )\left( R_{0}^{S}-1\right) +\frac{3b}{r}\root 3 \of {\frac{c_{1}c_{2}kbDr^{2}}{ma}}z, \end{aligned}$$

(B.7)

where

$$\begin{aligned} R_{0}^{S}=\frac{kbDr}{(a+mr)\left( D+d_{1}+\frac{\sigma _{2}^{2}}{2}\right) \left( d_{2}+\frac{\sigma _{3}^{2}}{2}\right) }\bigg (1-\frac{\sigma _{1}^{2}}{2r}\bigg )^{3}. \end{aligned}$$

Noting that

$$\begin{aligned}&L\bigg (\frac{3b}{d_{2}r}\root 3 \of {\frac{c_{1}c_{2}kbDr^{2}}{ma}}z+\frac{3bD}{d_{2}r(D+d_{1})}\root 3 \of {\frac{c_{1}c_{2}kbDr^{2}}{ma}}y\bigg )\nonumber \\&=\frac{3k^{2}b ^{3}D^{2}\left( 1-\frac{\sigma _{1}^{2}}{2r}\right) ^{2}}{d_{2}(D+d_{1})(a+mr)\left( d_{2}+\frac{\sigma _{3}^{2}}{2}\right) }\frac{xz}{1+mx}\nonumber \\&\quad +\,\frac{3bD}{d_{2}r}\root 3 \of {\frac{c_{1}c_{2}kbDr^{2}}{ma}}y-\frac{3bD}{ d_{2}r}\root 3 \of {\frac{c_{1}c_{2}kbDr^{2}}{ma}}y-\frac{3b}{r}\root 3 \of {\frac{c_{1}c_{2}kbDr^{2}}{ma}}z\nonumber \\&=\frac{3k^{2}b^{3}D^{2}\left( 1-\frac{\sigma _{1}^{2}}{2r}\right) ^{2}}{d_{2}(D+d_{1 })(a+mr)\left( d_{2}+\frac{\sigma _{3}^{2}}{2}\right) }\frac{xz}{1+mx}-\frac{3b}{r}\root 3 \of {\frac{c_{1}c_{2}kbDr^{2}}{ma}}z, \end{aligned}$$

(B.8)

then by (B.7) and (B.8), we obtain

$$\begin{aligned} L(V_{4})\le & {} -\bigg (D+d_{1}+\frac{\sigma _{2}^{2}}{2}\bigg )\left( R_{0}^{S}-1\right) +\frac{3k^{2}b^{3}D^{2}\left( 1-\frac{\sigma _{1}^{2}}{2r}\right) ^{2}}{d_{2}(D+d_{1})(a+mr)\left( d_{2}+\frac{\sigma _{3}^{2}}{2}\right) }\frac{xz}{1+mx}\nonumber \\ {}= & {} -\lambda +\frac{3k^{2}b^{3}D^{2}\left( 1-\frac{\sigma _{1}^{2}}{2r}\right) ^{2}}{d_{2}(D+d_{1})(a+mr)\left( d_{2}+\frac{\sigma _{3}^{2}}{2}\right) }\frac{xz}{1+mx}, \end{aligned}$$

(B.9)

where

$$\begin{aligned} \lambda :=\bigg (D+d_{1}+\displaystyle \frac{\sigma _{2}^{2}}{2}\bigg )\left( R_{0}^{S}-1\right) >0. \end{aligned}$$

Furthermore, we have (see Appendix A for a detailed derivation)

$$\begin{aligned} L(V_{5})\le -\displaystyle \frac{a}{2}x^{\theta +2}-\frac{d_{1}}{4k^{\theta +1}}y^{\theta +1}-\frac{d_{2}(D+d_{1})^{\theta +1}}{2^{\theta +2}(Dk)^{\theta +1}}z^{\theta +1}+B, \end{aligned}$$

(B.10)

where B is a positive constant, depending only on the system parameters, whose precise definition can be found in Appendix A.

It follows from (B.2), (B.9) and (B.10) that

$$\begin{aligned} L(V)\le & {} -M\lambda +\displaystyle \frac{3Mk^{2}b^{3}D^{2}\left( 1-\frac{\sigma _{1}^{2}}{2r}\right) ^{2}}{d_{2}(D+d_{1})(a+mr)\left( d_{2}+\frac{\sigma _{3}^{2}}{2}\right) }\frac{xz}{1+mx}-\frac{kbxz}{y(1+mx)} \\&-\,\frac{a}{2}x^{\theta +2}-\frac{d_{1}}{4k^{\theta +1}}y^{\theta +1}-\frac{d_{2}(D+d_{1})^{\theta +1}}{2^{\theta +2}(Dk)^{\theta +1}}z^{\theta +1}\\&+\,B+D+d_{1}+\displaystyle \frac{\sigma _{2}^{2}}{2}\\= & {} -M\lambda +\displaystyle \frac{3Mk^{2}b^{3}D^{2}\left( 1-\frac{\sigma _{1}^{2}}{2r}\right) ^{2}}{d_{2}(D+d_{1})(a+mr)\left( d_{2}+\frac{\sigma _{3}^{2}}{2}\right) }\frac{xz}{1+mx}\\&-\,\frac{kbxz}{y(1+mx)}-\frac{a}{4}x^{\theta +2}-\frac{d_{1}}{4k^{\theta +1}}y^{\theta +1}-\frac{d_{2}(D+d_{1})^{\theta +1}}{2^{\theta +3}(Dk)^{\theta +1}}z^{\theta +1}\\&-\,\displaystyle \frac{a}{4}x^{\theta +2}-\frac{d_{2}(D+d_{1})^{\theta +1}}{2^{\theta +3}(Dk)^{\theta +1}}z^{\theta +1}+B+D+d_{1}+\displaystyle \frac{\sigma _{2}^{2}}{2}. \end{aligned}$$

In order to validate the condition $A_{2}$ in Lemma 2.1 holds, we only need to construct a bounded open set U. Define a bounded open set U as

$$\begin{aligned} U=\bigg \{(x,y,z)\in \mathbb {R}_{+}^{3}:\epsilon<x<\frac{1}{\epsilon },\epsilon ^{3}<y<\frac{1}{\epsilon ^{3}},\epsilon<z<\frac{1}{\epsilon }\bigg \}, \end{aligned}$$

where $0<\epsilon <1$ is a sufficiently small number. In the set $\mathbb {R}_{+}^{3}\setminus U$, we can choose $\epsilon$ sufficiently small such that the following conditions hold

$$\begin{aligned}&\frac{3Mk^{2}b^{3}D^{2}\left( 1-\frac{\sigma _{1}^{2}}{2r}\right) ^{2}\theta \epsilon }{d_{2}(D+d_{1})(a+mr)\left( d_{2}+\frac{\sigma _{3}^{2}}{2}\right) (\theta +1)(1+m\epsilon )}\le 1, \end{aligned}$$

(B.11)

$$\begin{aligned}&\frac{3Mk^{2}b^{3}D^{2}\left( 1-\frac{\sigma _{1}^{2}}{2r}\right) ^{2}\epsilon }{d_{2}(D+d_{1})(a+mr)\left( d_{2}+\frac{\sigma _{3}^{2}}{2}\right) (\theta +1)(1+m\epsilon )}\le \frac{d_{2}(D+d_{1})^{\theta +1}}{2^{\theta +3}(Dk)^{\theta +1}},\qquad \quad \end{aligned}$$

(B.12)

$$\begin{aligned}&0<\epsilon \le \displaystyle \frac{d_{2}(D+d_{1})(a+mr)\left( d_{2}+\frac{\sigma _{3}^{2}}{2}\right) (\theta +2)}{3Mk^{2}b^{3}D^{2}\left( 1-\frac{\sigma _{1}^{2}}{2r}\right) ^{2}(\theta +1)}, \end{aligned}$$

(B.13)

$$\begin{aligned}&0<\epsilon \le \displaystyle \frac{ad_{2}(D+d_{1})(a+mr)\left( d_{2}+\frac{\sigma _{3}^{2}}{2}\right) (\theta +2)}{12Mk^{2}b^{3}D^{2}\left( 1-\frac{\sigma _{1}^{2}}{2r}\right) ^{2}}, \end{aligned}$$

(B.14)

$$\begin{aligned}&-\displaystyle \frac{kb}{\epsilon (1+m\epsilon )}+C\le -1, \end{aligned}$$

(B.15)

$$\begin{aligned}&-\displaystyle \frac{a}{4\epsilon ^{\theta +2}}+C\le -1, \end{aligned}$$

(B.16)

$$\begin{aligned}&-\displaystyle \frac{d_{2}(D+d_{1})^{\theta +1}}{2^{\theta +3}(Dk\epsilon )^{\theta +1}}+C\le -1, \end{aligned}$$

(B.17)

$$\begin{aligned}&-\displaystyle \frac{d_{1}}{4(k\epsilon ^{3})^{\theta +1}}+C\le -1, \end{aligned}$$

(B.18)

where C is a positive constant which will be given explicitly in expression (B.22). For convenience, we can divide $U^{c}=\mathbb {R}_{+}^{3}\setminus U$ into six domains,

$$\begin{aligned} U_{1}= & {} \{(x,y,z)\in \mathbb {R}_{+}^{3}:0<x\le \epsilon \},~U_{2}=\{(x,y,z)\in \mathbb {R}_{+}^{3}:0<z\le \epsilon \},\\ U_{3}= & {} \{(x,y,z)\in \mathbb {R}_{+}^{3}:0<y\le \epsilon ^{3},x>\epsilon , z>\epsilon \},~U_{4}=\bigg \{(x,y,z)\in \mathbb {R}_{+}^{3}:x\ge \frac{1}{\epsilon }\bigg \},\\ U_{5}= & {} \bigg \{(x,y,z)\in \mathbb {R}_{+}^{3}:z\ge \frac{1}{\epsilon }\bigg \},~U_{6}=\bigg \{(x,y,z)\in \mathbb {R}_{+}^{3}:y\ge \frac{1}{\epsilon ^{3}}\bigg \}. \end{aligned}$$

Clearly, $U^{c}=U_{1}\cup U_{2}\cup U_{3}\cup U_{4}\cup U_{5}\cup U_{6}$. Next, we prove that $L(V(x,y,z))\le -1$ for any $(x,y,z)\in U^{c}$, which is equivalent to proving it on the above six domains, respectively.

Case 1 For any $(x,y,z)\in U_{1}$, since $\frac{xz}{1+mx}\le \frac{\epsilon }{1+m\epsilon }z\le \frac{\epsilon }{1+m\epsilon }\frac{\theta +z^{\theta +1}}{\theta +1}=\frac{\theta \epsilon }{(\theta +1)(1+m\epsilon )}+\frac{\epsilon }{( \theta +1)(1+m\epsilon )}z^{\theta +1}$, we have

$$\begin{aligned} L(V)\le & {} -M\lambda +\displaystyle \frac{3Mk^{2}b^{3}D^{2}\left( 1-\frac{\sigma _{1}^{2}}{2r}\right) ^{2}\theta \epsilon }{d_{2}(D+d_{1})(a+mr)\left( d_{2}+\frac{\sigma _{3}^{2}}{2}\right) (\theta +1) (1+m\epsilon )}\nonumber \\&+\,\bigg (\frac{3Mk^{2}b^{3}D^{2}\left( 1-\frac{\sigma _{1}^{2}}{2r}\right) ^{2}\epsilon }{d_{2}(D+d_{1})(a+mr)\left( d_{2}+\frac{\sigma _{3}^{2}}{2}\right) (\theta +1)(1+m\epsilon )}\nonumber \\&-\,\frac{d_{2}(D+d_{1})^{\theta +1}}{2^{\theta +3}(Dk)^{\theta +1}}\bigg )z^{\theta +1}+B+D+d_{1}\nonumber \\&+\,\displaystyle \frac{\sigma _{2}^{2}}{2} \le -2+1+0=-1, \end{aligned}$$

(B.19)

which follows from (4.2), (B.11) and (B.12). Thus

$$\begin{aligned} L(V)\le -1~\text {on}~U_{1}. \end{aligned}$$

Case 2 For any $(x,y,z)\in U_{2}$, since $\frac{xz}{1+mx}\le xz\le \epsilon x\le \epsilon \frac{\theta +1+x^{\theta +2}}{\theta +2}=\frac{(\theta +1)\epsilon }{\theta +2}+\frac{\epsilon }{\theta +2}x^{\theta +2}$, we obtain

$$\begin{aligned} L(V)\le & {} -M\lambda +\displaystyle \frac{3Mk^{2}b^{3}D^{2}\left( 1-\frac{\sigma _{1}^{2}}{2r}\right) ^{2}(\theta +1)\epsilon }{d_{2}(D+d_{1})(a+mr)\left( d_{2}+\frac{\sigma _{3}^{2}}{2}\right) (\theta +2)}\nonumber \\&+\,\bigg (\frac{3Mk^{2}b^{3}D^{2}\left( 1-\frac{\sigma _{1}^{2}}{2r}\right) ^{2}\epsilon }{d_{2}(D+d_{1})(a+mr)\left( d_{2}+\frac{\sigma _{3}^{2}}{2}\right) (\theta +2)}-\frac{a}{4}\bigg )x^{\theta +1}\nonumber \\&+B+D+d_{1}+\displaystyle \frac{\sigma _{2}^{2}}{2}\nonumber \\\le & {} -2+1+0=-1, \end{aligned}$$

(B.20)

which follows from (4.2), (B.13) and (B.14). Hence,

$$\begin{aligned} L(V)\le -1,~\forall (x,y,z)\in U_{2}. \end{aligned}$$

Case 3 For any $(x,y,z)\in U_{3}$, one can get that

$$\begin{aligned} L(V)\le & {} -\displaystyle \frac{kbxz}{y(1+mx)}-\frac{a}{4}x^{\theta +2}-\frac{d_{1}}{4k^{\theta +1}}y^{\theta +1}\nonumber \\&-\frac{d_{2}(D+d_{1})^{\theta +1}}{2^{\theta +3}(Dk)^{\theta + 1}}z^{\theta +1}-\frac{a}{4}x^{\theta +2}-\frac{d_{2}(D+d_{1})^{\theta +1}}{2^{\theta +3}(Dk)^{\theta +1}}z^{\theta +1}\nonumber \\&+\frac{3Mk^{2}b^{3}D^{2}\left( 1-\frac{\sigma _{1}^{2}}{2r}\right) ^{2} }{d_{2}(D+d_{1})(a+mr)\left( d_{2}+\frac{\sigma _{3}^{2}}{2}\right) }\frac{xz}{1+mx}+B+D+d_{1}+\frac{\sigma _{2}^{2}}{2}\nonumber \\ {}\le & {} -\frac{kbxz}{y(1+mx)}-\frac{a}{4}x^{\theta +2}-\frac{d_{1}}{4k ^{\theta +1}}y^{\theta +1}-\frac{d_{2}(D+d_{1})^{\theta +1}}{2^{\theta +3}(Dk)^{\theta +1}}z^{\theta +1}+C\nonumber \\ {}\le & {} -\frac{kbxz}{y(1+mx)}+C\nonumber \\ {}< & {} -\frac{kb\epsilon ^{2}}{\epsilon ^{3}(1+m\epsilon )}+C\nonumber \\ {}= & {} -\frac{kb}{\epsilon (1+m\epsilon )}+C\nonumber \\\le & {} -1, \end{aligned}$$

(B.21)

which follows from (B.15) and

$$\begin{aligned} C= & {} \sup _{(x,y,z)\in \mathbb {R}_{+}^{3}}\bigg \{-\displaystyle \frac{a}{4}x^{\theta +2}-\frac{d_{2}(D+d_{1})^{\theta +1}}{2^{\theta +3}(Dk)^{\theta +1}}z^{\theta +1}\nonumber \\&+\frac{3Mk^{2}b^{3}D^{2}\left( 1 -\frac{\sigma _{1}^{2}}{2r}\right) ^{2}}{d_{2}(D+d_{1})(a+mr)\left( d_{2}+\frac{\sigma _{3}^{2}}{2}\right) }\frac{xz}{1+mx}+B+D+d_{1}+\displaystyle \frac{\sigma _{2}^{2}}{2}\bigg \}.\nonumber \\ \end{aligned}$$

(B.22)

Therefore,

$$\begin{aligned} L(V)\le -1~\text {on}~U_{3}. \end{aligned}$$

Case 4 For any $(x,y,z)\in U_{4}$, one can see that

$$\begin{aligned} L(V)\le & {} -\displaystyle \frac{kbxz}{y(1+mx)}-\frac{a}{4}x^{\theta +2}-\frac{d_{1}}{4k^{\theta +1}}y^{\theta +1}-\frac{d_{2}(D+d_{1})^{\theta +1}}{2^{\theta +3}(Dk)^{\theta + 1}}z^{\theta +1}\nonumber \\&-\,\frac{a}{4}x^{\theta +2}-\frac{d_{2}(D+d_{1})^{\theta +1}}{2^{\theta +3}(Dk)^{\theta +1}}z^{\theta +1}\nonumber \\&+\,\frac{3Mk^{2}b^{3}D^{2}\left( 1-\frac{\sigma _{1}^{2}}{2r}\right) ^{2} }{d_{2}(D+d_{1})(a+mr)\left( d_{2}+\frac{\sigma _{3}^{2}}{2}\right) }\frac{xz}{1+mx}+B+D+d_{1}+\frac{\sigma _{2}^{2}}{2}\nonumber \\\le & {} -\frac{kbxz}{y(1+mx)}-\frac{a}{4}x^{\theta +2}-\frac{d_{1}}{4k ^{\theta +1}}y^{\theta +1}-\frac{d_{2}(D+d_{1})^{\theta +1}}{2^{\theta +3}(Dk)^{\theta +1}}z^{\theta +1}+C\nonumber \\ {}\le & {} -\frac{a}{4}x^{\theta +2}+C\nonumber \\< & {} -\frac{a}{4\epsilon ^{\theta +2}}+C\nonumber \\\le & {} -1, \end{aligned}$$

(B.23)

which follows from (B.16). So

$$\begin{aligned} L(V)\le -1,~\forall (x,y,z)\in U_{4}. \end{aligned}$$

Case 5 When $(x,y,z)\in U_{5}$, one can obtain that

$$\begin{aligned} L(V)\le & {} -\,\displaystyle \frac{kbxz}{y(1+mx)}-\frac{a}{4}x^{\theta +2}-\frac{d_{1}}{4k^{\theta +1}}y^{\theta +1}\nonumber \\&-\,\frac{d_{2}(D+d_{1})^{\theta +1}}{2^{\theta +3}(Dk)^{\theta + 1}}z^{\theta +1}-\frac{a}{4}x^{\theta +2}-\frac{d_{2}(D+d_{1})^{\theta +1}}{2^{\theta +3}(Dk)^{\theta +1}}z^{\theta +1}\nonumber \\&+\frac{3Mk^{2}b^{3}D^{2}\left( 1-\frac{\sigma _{1}^{2}}{2r}\right) ^{2} }{d_{2}(D+d_{1})(a+mr)\left( d_{2}+\frac{\sigma _{3}^{2}}{2}\right) }\frac{xz}{1+mx}+B+D+d_{1}+\frac{\sigma _{2}^{2}}{2}\nonumber \\ {}\le & {} -\frac{kbxz}{y(1+mx)}-\frac{a}{4}x^{\theta +2}-\frac{d_{1}}{4k ^{\theta +1}}y^{\theta +1}-\frac{d_{2}(D+d_{1})^{\theta +1}}{2^{\theta +3}(Dk)^{\theta +1}}z^{\theta +1}+C\nonumber \\\le & {} -\frac{d_{2}(D+d_{1})^{\theta +1}}{2^{\theta +3}(Dk)^{\theta +1}}z^{ \theta +1}+C\nonumber \\< & {} -\,\frac{d_{2}(D+d_{1})^{\theta +1}}{2^{\theta +3}(Dk\epsilon )^{\theta +1}}+C\le -1, \end{aligned}$$

(B.24)

which follows from (B.17). Consequently

$$\begin{aligned} L(V)\le -1~\text {on}~U_{5}. \end{aligned}$$

Case 6 If $(x,y,z)\in U_{6}$, one can see that

$$\begin{aligned} L(V)\le & {} -\,\displaystyle \frac{kbxz}{y(1+mx)}-\frac{a}{4}x^{\theta +2}-\frac{d_{1}}{4k^{\theta +1}}y^{\theta +1}\nonumber \\&-\,\frac{d_{2}(D+d_{1})^{\theta +1}}{2^{\theta +3}(Dk)^{\theta + 1}}z^{\theta +1}-\frac{a}{4}x^{\theta +2}-\frac{d_{2}(D+d_{1})^{\theta +1}}{2^{\theta +3}(Dk)^{\theta +1}}z^{\theta +1}\nonumber \\&+\frac{3Mk^{2}b^{3}D^{2}\left( 1-\frac{\sigma _{1}^{2}}{2r}\right) ^{2} }{d_{2}(D+d_{1})(a+mr)\left( d_{2}+\frac{\sigma _{3}^{2}}{2}\right) }\frac{xz}{1+mx}+B+D+d_{1}+\frac{\sigma _{2}^{2}}{2}\nonumber \\ {}\le & {} -\frac{kbxz}{y(1+mx)}-\frac{a}{4}x^{\theta +2}-\frac{d_{1}}{4k ^{\theta +1}}y^{\theta +1}-\frac{d_{2}(D+d_{1})^{\theta +1}}{2^{\theta +3}(Dk)^{\theta +1}}z^{\theta +1}+C\nonumber \\ {}\le & {} -\frac{d_{1}}{4k^{\theta +1}}y^{\theta +1}+C\nonumber \\ {}< & {} -\frac{d_{ 1}}{4(k\epsilon ^{3})^{\theta +1}}+C\nonumber \\\le & {} -1, \end{aligned}$$

(B.25)

which follows from (B.18). As a result

$$\begin{aligned} L(V)\le -1,~\forall (x,y,z)\in U_{6}. \end{aligned}$$

Obviously, from (B.19), (B.20), (B.21), (B.23), (B.24) and (B.25), we obtain that for a sufficiently small $\epsilon$,

$$\begin{aligned} L(V(x,y,z))\le -1,~\forall (x,y,z)\in \mathbb {R}_{+}^{3}\setminus U. \end{aligned}$$

Hence, the condition $A_{2}$ in Lemma 2.1 holds.

Appendix C: Detailed Calculation of the Last Integral of (5.16)

$$\begin{aligned}&J_{1}{:}{=}\displaystyle \int _{0}^{\infty }x\pi (x)\mathrm{d}x=Q\sigma _{1}^{-2}\int _{0}^{\infty }x^{\frac{2r}{\sigma _{1}^{2}}-1}\mathrm{e}^{-\frac{2a}{\sigma _{1}^{2}}x}\mathrm{d}x\\&\quad =Q\sigma _{1}^{-2}\int _{0}^{\infty }\bigg (\frac{\sigma _{1}^{2}}{2a}\bigg )^{\frac{2r}{\sigma _{1}^{2}}-1}t^{\frac{2r}{\sigma _{1}^{2}}-1}\mathrm{e}^{-t}\frac{\sigma _{1}^{2}}{2a}\mathrm{d}t=Q\sigma _{1}^{-2}\bigg (\frac{\sigma _{1}^{2}}{2a}\bigg )^{ \frac{2r}{\sigma _{1}^{2}}}\Gamma \bigg (\frac{2r}{\sigma _{1}^{2}}\bigg )\\&\quad =\displaystyle \frac{\sigma _{1}^{2}}{2a}\frac{\Gamma \left( \frac{2r}{\sigma _{1}^{2}}\right) }{\Gamma \left( \frac{2r}{\sigma _{1}^{2}}-1\right) }=\frac{\sigma _{1}^{2}}{2a}\bigg (\frac{2r}{\sigma _{1}^{2}}-1\bigg )= \frac{r-\frac{\sigma _{1}^{2}}{2}}{a} \end{aligned}$$

and

$$\begin{aligned}&J_{2}\,{:}{=}\displaystyle \int _{0}^{\infty }x^{2}\pi (x)\mathrm{d}x=Q\sigma _{1}^{-2}\int _{0}^{\infty }x^{\frac{2r}{\sigma _{1}^{2}}}\mathrm{e}^{-\frac{2a}{\sigma _{1}^{2}}x}\mathrm{d}x\\&\quad =Q\sigma _{1}^{-2}\int _{0}^{\infty } \bigg (\frac{\sigma _{1}^{2}}{2a}\bigg )^{\frac{2r}{\sigma _{1}^{2}}}t^{\frac{2r}{\sigma _{1}^{2}}}\mathrm{e}^{-t}\frac{\sigma _{1}^{2}}{2a}\mathrm{d}t=Q\sigma _{1}^{-2}\bigg (\frac{\sigma _{1}^{2}}{2a}\bigg )^{\frac{2r}{\sigma _{1}^{2}}+1}\Gamma \bigg (\frac{2r}{\sigma _{1}^{2}}+1\bigg )\\&\quad =\bigg (\displaystyle \frac{\sigma _{1}^{2}}{2a}\bigg )^{2}\frac{\Gamma \left( \frac{2r}{\sigma _{1}^{2}}+1\right) }{\Gamma \left( \frac{2r}{\sigma _{1}^{2}}-1\right) }\\&\quad =\bigg (\frac{\sigma _{1}^{2}}{2a}\bigg )^{2}\frac{2r}{\sigma _{1}^{2}}\bigg (\frac{2r}{\sigma _{1}^{2}}-1\bigg )=\frac{r\left( r-\frac{\sigma _{1}^{2}}{2}\right) }{a^{2}}. \end{aligned}$$

Hence, we have

$$\begin{aligned} \displaystyle \int _{0}^{\infty }\bigg (x-\frac{r}{a}\bigg )^{2}\pi (x)\mathrm{d}x= & {} \int _{0}^{\infty }\bigg (x^{2}-\frac{2r}{a}x+\frac{r^{2}}{a^{2}}\bigg )\pi (x)\mathrm{d}x=J_{2}-\frac{2r}{a}J_{1}+\frac{r^{2}}{a^{2}}\\= & {} \frac{r\left( r-\frac{\sigma _{1}^{2}}{2}\right) }{a^{2}}-\frac{2r}{a}\cdot \frac{r-\frac{\sigma _{1}^{2}}{2}}{a}+\frac{r^{2}}{a^{2}}=\frac{r\sigma _{1}^{2}}{2a^{2}}. \end{aligned}$$